Как объяснить ребенку умножение и деление?
Развитие ребенка
Как объяснить ребенку умножение и деление?
30 октября 2019 35 036 просмотров
Екатерина Ушахина
Можно заставить ребенка просто решать скучные примеры (и ему будет совсем неинтересно), а можно предложить ему решить забавные текстовые задачки в тетради Kumon или сразиться в межпланетном рыцарском турнире на звание лучшего знатока дробей. Второй подход определенно занимательнее: ребенку гораздо больше понравится учить математику в игре.
Ребятам постарше также по душе будут игровые моменты в обучении. Ведь гораздо веселее изучать математику через яркое домино, чем читать длинные главы в учебнике.
Подготовили для вас несколько советов и подборку книг, которые помогут разложить умножение и деление по полочкам.
Умножаем
Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой.
На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.
Приемы умножения. Некоторые числа легко умножать, зная особые приемы. В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Делим
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Как выполняется деление? Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
Как деление связано с умножением? Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.
Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного делимого (10).
Другой подход к делению. Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное. Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10.
В этом примере 30 футбольных мячей делятся на группы по 3 мяча.
Книги и тетради, которые помогут закрепить навыки
Арифметикум
Домино, с которым ребенок научится хорошо складывать, вычитать, умножать и делить числа до 100. Игрок должен разместить карточку так, чтобы на оказавшихся рядом клеточках был написан пример и правильный ответ или два примера, в результате решения которых получится одно число.
Вокруг любой клеточки можно расположить сразу несколько карточек: по одной у каждой свободной стороны. Проверить вычисления игроки могут по цветным узорам: если узоры совпадают, ход сделан правильно.
Умножариум
Веселая игра поможет освоить математику
Это домино создано специально для легкого и увлекательного изучения таблицы умножения детьми: вместо традиционных точек на каждой карточке нанесены математические примеры и цифры. Совмещая клетку с примером (например, 5×8) и результат умножения (40), ребенок сразу видит, правильно ли он посчитал пример, благодаря цветовому паттерну, который должен совпасть на двух клетках.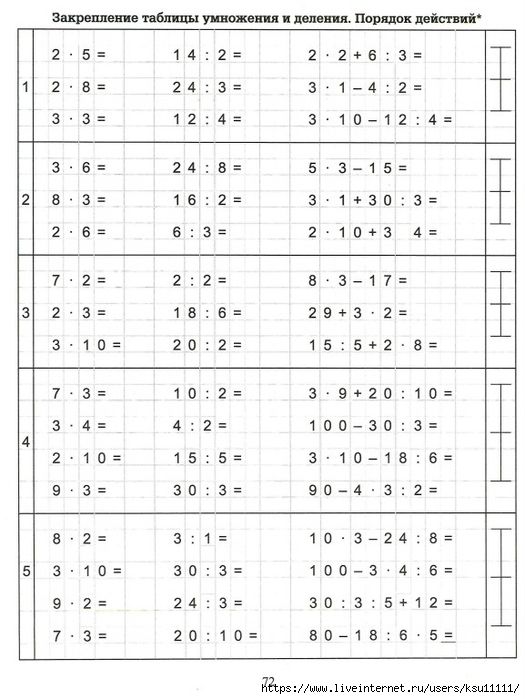
Kumon спешит на помощь
У нас есть множество тетрадей разных уровней сложности, которые помогут выучить таблицу умножения на зубок.
KUMON. Математика. Умножение. Уровень 4
Эта яркая тетрадка научит ребенка умножать многозначные числа в столбик. Шаг за шагом он будет осваивать этот навык, его ждут примеры, которые будут постепенно усложняться, полезные подсказки и, конечно, ключи с ответами в конце тетради для самоконтроля.
Простые задачки научат умножать. Пример из тетради
Kumon. Математика. Деление. Уровень 4
Выполняя задания в этой тетради, ваш ребёнок научится делить многозначные числа в столбик с остатком и без него. Продвигаясь вперёд небольшими последовательными шажками, он обретёт не только математические знания, но и уверенность в своих силах.
Межпланетный рыцарский турнир
Решая примеры из этой книги, ребенок примет участие в настоящем межпланетном состязании! Каждый правильный ответ — ты успешно атаковал противника, каждая ошибка — противник успешно атаковал тебя.
Для убедительности в книге есть изображения персонажей, за которых нужно сыграть юному математику, и их соперников, а также фантастические истории про инопланетян. Всех героев можно раскрасить!
Успешных занятий!
ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 34. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник — страница 34Готовое домашнее задание
Номер 129.
Найди ошибки в вычислениях и реши правильно.
Ответ:
В первом решении ошибка была в том, что второе неполное делимое 45 не смогли разделить, так как оно меньше и сазу снесли следующую цифру, не записав 0 в частном.
Во втором решении ошибка была в том, что третье неполное делимое 600 не разделили, приняв его за остаток.
Номер 130.
Выполни деление с остатком и проверь решение.
Ответ:
Номер 131.
В ящике помещается 20 кг моркови. Сколько потребуется таких ящиков, чтобы отправить в магазин 675 кг моркови? Сколько килограммов моркови будет в последнем ящике?
Ответ:
1 ящ. – 20 кг ? ящ. – 675 кг 675 : 20 = 33 (ост. 15) 33 целых ящика и 1 ящик, в котором будет только 15 кг.
Ответ: 34 ящика потребуется, но в последнем будет 15 кг.
Номер 132.
В каждом ряду кинозала 30 мест. На сеанс продано 942 билета. Сколько полных рядов в этом зале могут занять зрители с билетами?
Ответ:
1 ряд – 30 мест
? рядов – 942 б.
942 : 30 = 31 (ост.
12)
Ответ: 31 ряд могут занять.
Номер 133.
Два лыжника вышли из посёлка одновременно в противоположных направлениях. Один из них шёл со скоростью 12 км/ч, а другой – 10 км/ч. Через сколько часов расстояние между ними будет 44 км? Какое расстояние пройдёт за это время каждый лыжник?
Ответ:
1) 12 + 10 = 22 (км/ч) – скорость удаления лыж. 2) 44 : 22 = 2 (ч) – будут в пути лыж. 3) 12 ∙ 2 = 24 (км) – прошёл 1-ый лыжник. 4) 10 ∙ 2 = 20 (км) – прошёл 2-ой лыжник. Ответ: через 2 часа; 1-ый л. – 24 км.; 2-ой л. – 20 км.
Номер 134.
Из двух посёлков выехали одновременно навстречу друг другу два всадника. Первый ехал со скоростью 200 м/мин, а второй проезжал в минуту на 20 м меньше. Всадники встретились через 50 мин. Найди расстояние между посёлками.
Ответ:
1) 200 − 20 = 180 (м/мин) – скорость второго всадника.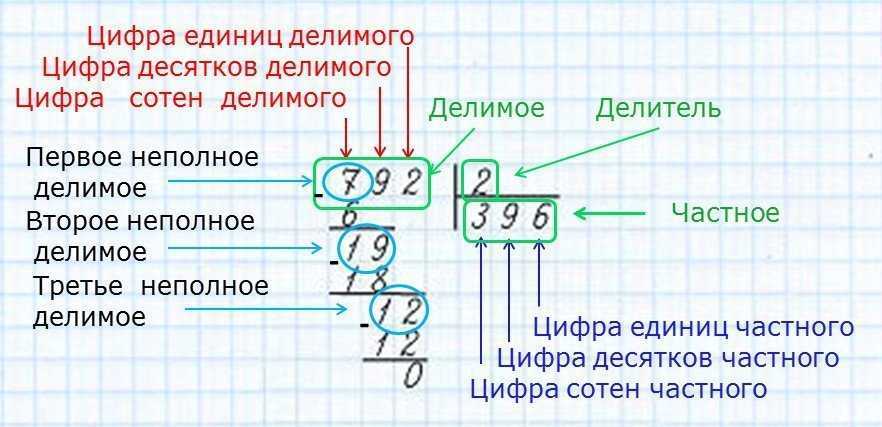
Номер 135.
Найди значение выражения 120 : 4 + 2 ∙ 3. Измени порядок действий в этом выражении с помощью скобок так, чтобы его значение стало равно 60; 96; 12.
Ответ:
120 : 4 + 2 ∙ 3 = 36 120 : (4 + 2) ∙ 3 = 60 (120 : 4 + 2) ∙ 3 = 96 120 : (4 + 2 ∙ 3) = 12
Номер 136.
Выполни деление и проверь умножением.
Ответ:
Номер 137.
Ответ:
Номер 138.
Ответ:
1 ч − 15 мин = 60 мин − 15 мин = 45 мин
1 сут. − 15 ч = 24 ч − 15 ч = 9 ч
1 т − 8 ц = 10 ц − 8 ц = 2 ц
1 ц − 8 кг = 100 кг − 8 кг = 92 кг
Задание на полях страницы
Магический квадрат.
Ответ:
Задание внизу страницы
Проверочные работы с.66 Проверочные работы с.67
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Ваше сообщение отправлено!
+
Wolfram|Alpha Pro: пошаговое обучение арифметике для всех классов — блог Wolfram
В начальной школе арифметические вычисления считаются одним из основных математических навыков.
В последние несколько десятилетий в Соединенных Штатах длинная арифметика традиционно вводилась между первым и пятым классом и остается крайне важной для учащихся всех возрастов.
Стандарты Common Core State по математике указывают, что первоклассники должны научиться складывать «двузначное число и однозначное число». Ко второму классу учащиеся «складывают и вычитают в пределах 1000» и, в частности, «связывают стратегию с письменным методом». В третьем классе вводится умножение на степень 10, а к четвертому классу учащимся ставится задача «использовать понимание разрядного значения и свойства операций для выполнения многозначной арифметики», включая умножение и деление. Ожидается, что пятиклассник будет не только «свободно умножать многозначные целые числа с использованием стандартного алгоритма», но также «складывать, вычитать, умножать и делить десятичные дроби».
Теперь Wolfram|Alpha Pro возвращает пошаговые решения для длинных задач на сложение, вычитание, умножение и деление, в том числе с десятичными или отрицательными числами.
Мы также разработали подробные пошаговые решения для деления целых чисел и отрицательных чисел, а также — для старшеклассников — умножения и деления многочленов.
Длинная арифметика в Wolfram|Alpha
Длинная арифметика используется для решения письменных задач на сложение, вычитание, умножение и деление, часто путем организации чисел друг над другом, с выравниванием цифр в столбцах.
Алгоритмы длинных арифметических операций основаны на концепции разрядности. В нашей системе счисления с основанием 10 каждая цифра представляет собой счет определенного значения, связанного с ее местом в числе. Например, трехзначное число без десятичной точки использует три разряда: сотни, десятки и единицы. Выравнивание чисел на основе их цифр сводится к выравниванию цифр с одинаковыми разрядными значениями. В то время как длинные арифметические алгоритмы могут выполняться без полного продумывания рассуждений о разрядности каждый раз, учащимся может быть концептуально полезно понять процесс, например, умножения единиц, умножения десятков и умножения сотен, а затем объединения эти результаты, чтобы получить окончательный результат.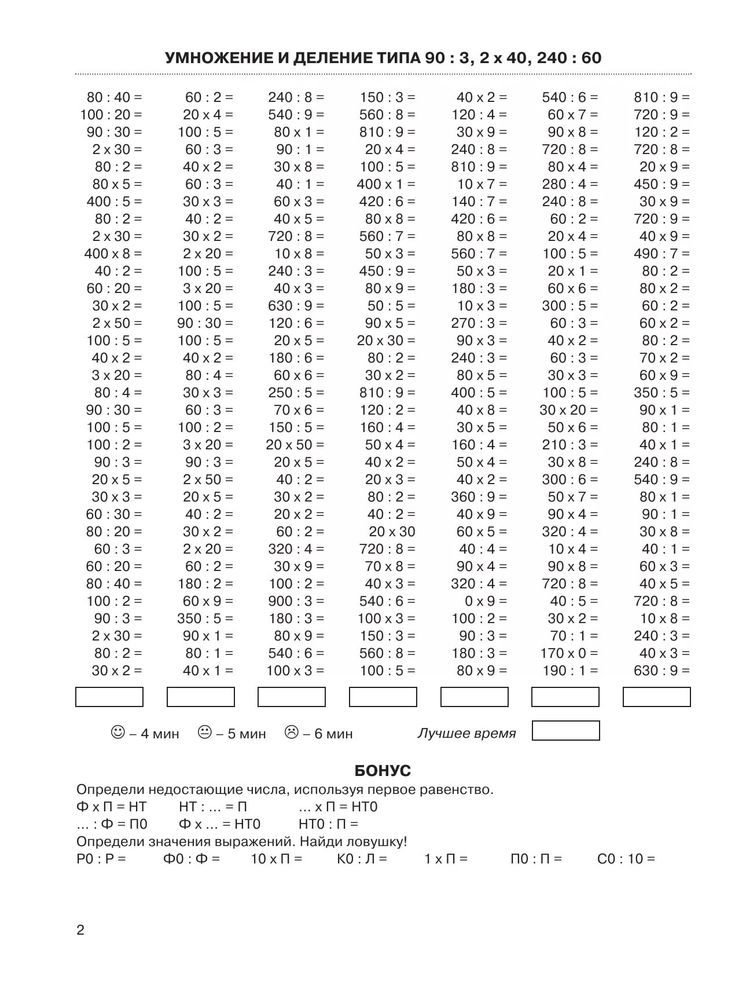
Длинная арифметика может быть сложной для учащихся, впервые сталкивающихся с ней. Более того, поскольку существует множество длинных арифметических методов, родителям может быть сложно помочь своим ученикам. Если вам кажется, что каждое поколение усваивает новый метод длинной арифметики, возможно, это не ваша память! На самом деле, существует множество вариантов длинного арифметического алгоритма, и тот, который вы изучаете в школе, может зависеть от множества факторов, от географического региона до предпочтений учителя и обновлений учебной программы.
Пошаговое решение проблем
Длинное сложение
✕ |
Если вы попросите Wolfram|Alpha сложить несколько чисел, вы сможете просмотреть пошаговое решение, выполняющее вычисления с использованием длинного сложения. Сначала мы распределяем числа по столбцам в зависимости от разрядности, используя десятичную точку в качестве ориентира:
. ✕ |
Wolfram|Alpha затем проведет вас через каждый шаг алгоритма длинного сложения. Как правило, это включает в себя добавление цифр в каждом столбце справа налево. Если сумма цифр в столбце равна 10 или более, мы переносим первую цифру в столбец слева.
Более концептуально, добавление цифр в столбец означает подсчет количества единиц в определенном разряде. На следующем шаге, например, суммирование 6 + 9 + 4 в столбце сотых дает в сумме 19 единиц в столбце сотых. Девятнадцать сотых равны 1 десятой и 9.сотые, и так записываем 9 сотых в столбец сотых и переносим 1 десятый на его собратья десятых в столбце десятых:
✕ |
Пошаговое решение проведет вас через добавление цифр в каждом столбце, после чего вы сможете прочитать окончательный ответ в нижней части сетки:
✕ |
Длинное вычитание
✕ |
Wolfram|Alpha также возвращает пошаговые решения для длительного вычитания меньшего числа из большего.
Постановку задачи начинаем с расстановки цифр на странице:
✕ |
Алгоритм длинного вычитания заключается в вычитании нижней цифры из старшей цифры в каждом столбце. В случае, когда нижняя цифра больше, чем верхняя цифра, мы должны заимствовать из столбцов слева. Мы показываем это на длинной сетке вычитания, заменяя 3 в столбце сотен на 2 и перемещая заимствованную 1 в столбец десятков, чтобы получить 14 десятков:
✕ |
Долгую процедуру вычитания-заимствования можно объяснить с точки зрения разрядных значений. На предыдущем этапе необходимость заимствования возникает в столбце десятков, потому что 4 десятка меньше, чем 9 десятков. Поэтому мы смотрим дальше столбца десятков на столбец сотен, что позволяет нам вместо этого рассмотреть вычитание 9 десятков из 1 сотни и 4 десятков.
Концептуально это меняет соответствующую задачу на вычитание для этого шага с 40 на 9.от 0 до 140 – 90. В длинной сетке вычитания это отображается только как 14 – 9 = 5; разрядные значения цифр закодированы в их позициях в числах в длинной сетке вычитания:
✕ |
Каждый шаг заимствования и вычитания пронумерован в пошаговом решении. Когда в нижнем числе больше нет цифр, мы можем снести все оставшиеся цифры из верхнего числа и прочитать окончательный ответ из нижней части длинной арифметической сетки:
✕ |
Длинное умножение
Для пошагового длинного умножения мы недавно добавили возможность умножать десятичные и отрицательные числа. Выполнение длинного алгоритма умножения с десятичными или отрицательными числами просто включает в себя повторение алгоритма, как для целых чисел, а затем размещение десятичного или отрицательного числа на дополнительном шаге, прежде чем сообщать окончательный ответ.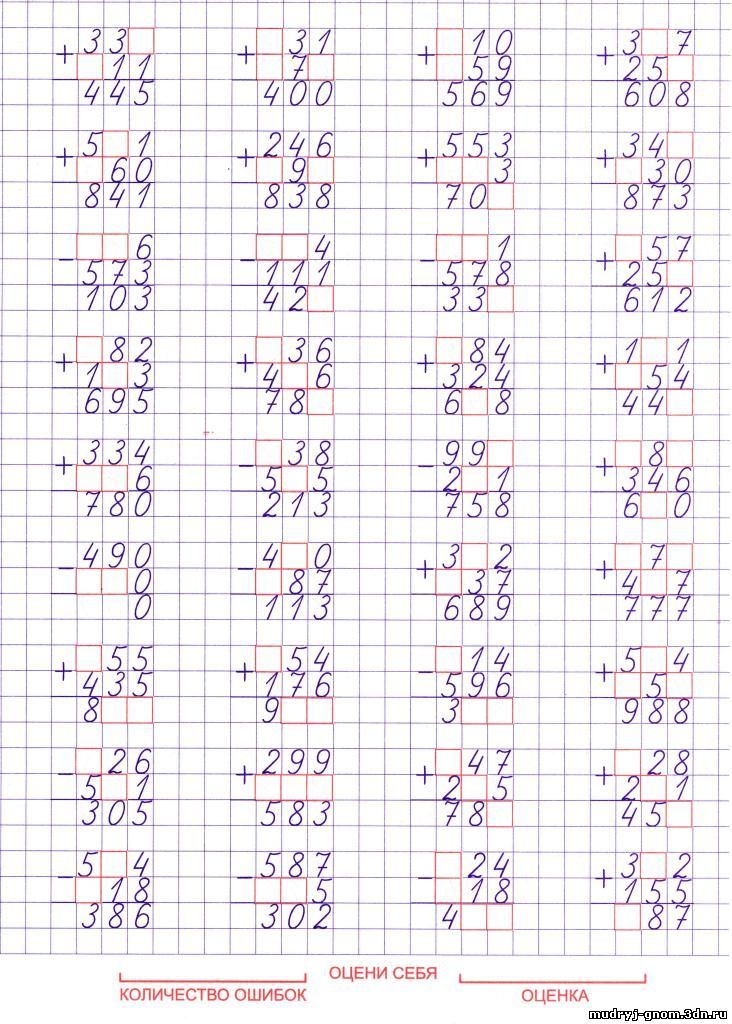
По словам великого Хайме Эскаланте в 1988 фильм Встань и доставь , «Отрицательное, умноженное на отрицательное, становится положительным!» Пошаговое решение для умножения двух отрицательных чисел объясняет, что вы можете эффективно игнорировать отрицательные знаки, прежде чем продолжить алгоритм длинного умножения:
✕ |
Один шаг алгоритма длинного умножения включает умножение цифры второго числа на каждую цифру первого, перенося при необходимости цифру десятков каждого произведения. Каждый шаг суммирован в пошаговом решении:
✕ |
Наконец, если мы умножаем десятичные числа, мы пишем десятичную дробь в окончательном ответе с учетом разрядного значения, что равносильно подсчету количества цифр после десятичной дроби в исходных числах:
✕ |
Длинное деление
Конечный результат длинного деления не всегда дается одним числом.
Когда одно число не делится на другое без остатка, длинное деление показывает и частное, и остаток:
✕ |
✕ |
Еще один способ сообщить о результате задачи деления на длинное — смешанное число, иногда называемое смешанной дробью:
✕ |
Независимо от того, как вы представляете окончательный ответ, шаги для выполнения длинного арифметического алгоритма одинаковы. Начнем с того, что расположим числа немного в другом порядке, используя скобку деления вместо того, чтобы располагать числа вертикально, как в предыдущих алгоритмах. Число слева от скобки — делитель, а число внутри скобки — делимое:
✕ |
Каждый шаг алгоритма длинного деления требует нескольких подшагов.
Во-первых, если у делителя две цифры, как в нашем примере, нужно определить, сколько раз делитель входит в первые две цифры делимого. Запишите это число в верхней части скобки деления, умножьте делитель на это число, вычтите это произведение из делителя и запишите следующую цифру:
✕ |
Фу! Нужны дополнительные разъяснения по этому поводу? Если да, то вы не одиноки. Длинное деление — общеизвестно сложный метод длинной арифметики для обучения или обучения. Таким образом, за кнопкой Несколько промежуточных шагов вы можете увидеть умножение и вычитание, разработанные отдельно, с объяснением каждого добавления в скобку по одному:
✕ |
После выполнения описанных шагов алгоритма деления в длину до тех пор, пока не останется больше цифр делимого, последний шаг проведет вас через процесс нахождения частного и остатка и, при желании, выражения результата в виде смешанного числа:
✕ |
В настоящее время Wolfram|Alpha возвращает только пошаговые решения деления в длину для целых чисел, но не для десятичных чисел.
Мы надеемся, что в ближайшем будущем мы расширим нашу пошаговую поддержку деления на длинные, чтобы включить десятичные дроби.
Полиномиальная арифметика
В старших классах учащиеся расширяют длинную арифметику с помощью чисел, чтобы применить их к математическим выражениям, называемым полиномами. Многочлены представляют собой суммы членов, которые включают переменные и показатели степени, например 3 x 2 + 4 x – 5. Многочлены можно складывать, вычитать, умножать и делить с помощью методов, аналогичных числовой арифметике. В частности, полиномиальное умножение и деление являются важными навыками для занятий по математике в старших классах средней школы и колледжа. Недавно мы расширили пошаговые решения задач полиномиального умножения и деления.
Есть сходство между длинной арифметикой для чисел и многочленов. В то время как цифры в числах могут быть сгруппированы на основе их разрядных значений, члены многочлена могут быть сгруппированы на основе показателей степени переменной.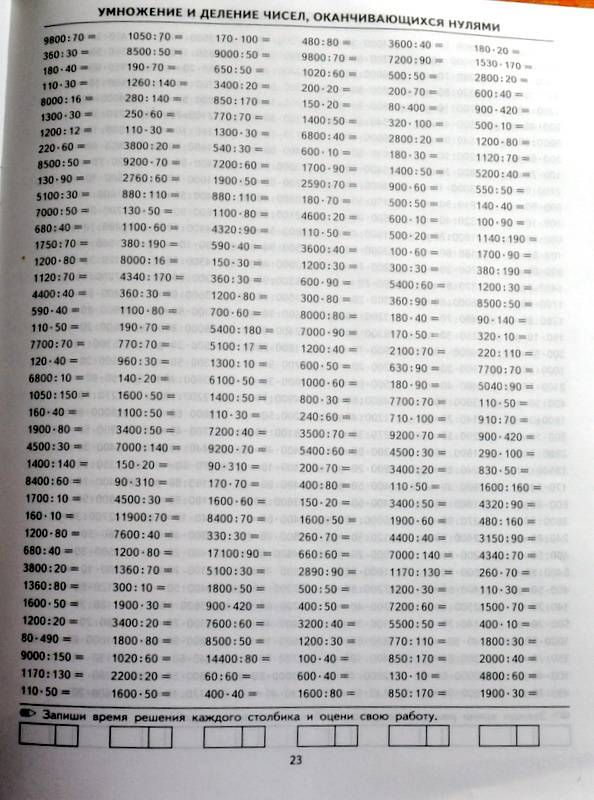
В старших классах учащиеся учатся «складывать, вычитать и умножать многочлены» и, как указано отдельно в другом Общем базовом стандарте, делить многочлены, «используя проверку, длинное деление или, для более сложных примеров, компьютер. система алгебры». Wolfram|Alpha — идеальный инструмент для работы с такими сложными примерами, особенно потому, что мы также показываем, как прийти к решению с помощью пошагового полиномиального деления в длину.
«Метод ящиков» Умножение полиномов
Один из распространенных методов умножения многочленов, часто называемый «методом ящиков», заключается в организации членов многочленов вне сетки. Пошаговое решение объясняет, как определить размер сетки:
✕ |
Затем мы заполняем каждую ячейку в сетке, умножая члены в каждой паре строк-столбцов. Каждый из этих шагов описан в пошаговом решении, а промежуточные шаги содержат подробные сведения о том, как умножать каждую пару полиномиальных членов:
✕ |
Наконец, мы получаем результат задачи полиномиального умножения, суммируя члены во всех полях:
✕ |
Метод ящиков особенно полезен для визуализации попарного умножения членов каждого многочлена.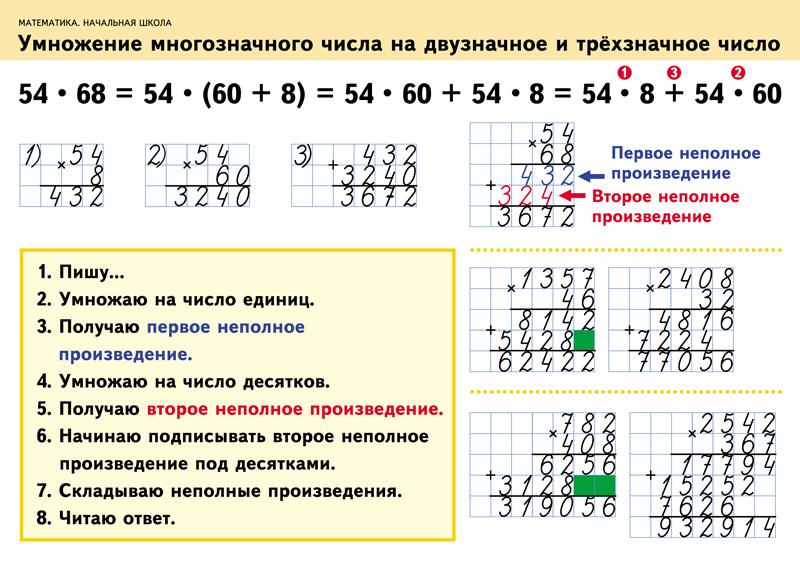
Мы также работаем над разработкой дополнительных методов полиномиального умножения, включая длинное полиномиальное умножение (формат которого аналогичен числовому умножению) и методы «стрелка» и «фольга», которые обычно преподаются в средних школах США.
Полиномиальное длинное деление
И последнее, но не менее важное: мы также улучшили пошаговую поддержку задач полиномиального длинного деления. Полиномиальное длинное деление следует алгоритму, аналогичному целочисленному длинному делению, но с дополнительными требованиями для отслеживания переменных и показателей. Чтобы разделить один многочлен на другой, мы устанавливаем длинную скобку деления с делимым (или числителем) внутри и делителем (или знаменателем) снаружи:
✕ |
✕ |
Структура «умножить, затем вычесть» алгоритма целочисленного деления в длину такая же, как и для полиномиального деления в длину.
Вопрос «Сколько раз делитель входит в первый член (члены) делимого?» можно примерно перевести как что-то вроде «Насколько меньше высших степеней x делитель, чем первый член делимого?» С математической точки зрения мы называем «главным членом» член дивиденда с наивысшей степенью числа 9.0135 x и определите, на что нужно умножить делитель, чтобы он соответствовал старшему члену делимого. Множитель записывается в верхней части скобки, а результат умножения записывается и вычитается в нижней части сетки. Поскольку учащиеся, выполняющие полиномиальное деление в длину, уже знакомы с целочисленным делением в длину, весь этот шаг суммируется в строке:
| . ✕ |
После того, как мы завершили окончательное вычитание, частное и остаток появляются в тех же местах сетки деления, что и при целочисленном делении. Окончательный результат может быть представлен либо в виде дроби, либо в виде умножения частного на делитель, в том, что мы называем «формой частного и остатка»:
✕ |
Будущая работа
Математическая группа Wolfram|Alpha надеется и дальше расширять свое пошаговое покрытие для длинной арифметики.
Мы продолжаем работать над добавлением дополнительных методов для длинной арифметики, включая альтернативные представления одних и тех же алгоритмов. Хотя основные концептуальные арифметические алгоритмы не различаются среди учителей или регионов, существуют некоторые различия в процедурах и методах представления длинных арифметических задач. У разных учителей разные предпочтения в отношении методов передачи содержания своим ученикам, а расположение столбцов и процедуры визуализации арифметики различаются в зависимости от региона.
Мы также работаем над добавлением дополнительных методов помимо традиционных длинных арифметических алгоритмов, таких как визуальные методы, которые подчеркивают различные математические концепции, лежащие в основе арифметики. Мы надеемся предоставить полезные инструменты для учащихся, родителей и учителей, выполняющих длинную арифметику, и приветствуем отзывы или запросы, если есть определенные сложения (или вычитания, умножения и деления), которые вы найдете полезными.
| Зарегистрируйтесь в Wolfram|Alpha Pro, чтобы получить доступ к настраиваемым настройкам, пошаговым решениям, увеличению времени вычислений и многому другому. |
6 простых шагов по обучению умножению в игровой форме для учащихся
Переход от обучения вычитанию и сложению к обучению умножению является одной из самых сложных задач, с которыми учащиеся сталкиваются в школе.
Проблемы с предметом возникают не только у студентов.
При обучении умножению преподаватели часто начинают с неправильных понятий или слишком быстро проводят уроки. Это может обескуражить и запугать учащихся, что в конечном итоге нанесет ущерб результатам обучения.
К счастью, существуют известные стратегии обхода этих препятствий.
Используйте приведенное ниже руководство, чтобы увидеть, как можно упростить преподавание и изучение умножения за шесть простых шагов, которые будут интересны и найдут отклик у учащихся.
Не начинайте с запоминания. Студенты обычно с трудом запоминают факты умножения с первой попытки, и это может привести к страху перед таблицей умножения.
Самый простой способ начать обучение умножению — это закрепить понятие с точки зрения его связи со сложением — операция, с которой ваши ученики уже должны быть знакомы.
Прежде чем двигаться дальше, убедитесь, что ваши ученики усвоили первый столп умножения: это просто повторяющееся сложение.
Используйте соответствующие примеры , подобные приведенному выше, чтобы контекстуализировать этот факт.
Это поможет записать примеры, чтобы учащиеся могли визуализировать идею:
2 x 2 то же самое, что 2 + 2
или
3 x 4 такая же, как 4 4 + 4
2.
СТАРЬ С МЛЯЗАМИ ИСЕЛА И ОДИН. Умножение на ноль: свойство нуля , любые 9Число 0136, умноженное на ноль, также равно нулю:n x 0 = 0
Предложите учащимся найти примеры нулевого свойства в комнате. Например, если в классе 25 стульев, на каждом из которых не сидит ни одной обезьяны, это означает, что в классе нет обезьян.
При желании один забавный пример забавного математического задания для развлечения ваших учеников включает в себя размышление о забавных примерах этого свойства, например 0 x один миллион = 0 … или … 0 x бутерброд с ветчиной = 0.
Источник изображения: Step Into 2nd Class
Умножение на единицу: свойство тождества само: n x 1 = n.Как и в случае с нулевым свойством, подчеркните в своем классе, что умножение числа на единицу дает одно и то же значение.
Чтобы обосновать свойство в контексте реальной жизни, предложите вашему классу подумать о экземплярах свойства идентичности в классе.
Например,
- Одна группа из восьми парт — это восемь парт
- Одна строка календаря, показывающая, что семь дней — это семь дней
Источник изображения: The Classy Teacher
3. Закройте таблицу умножения, начиная с «простыми» числамиДля повторения ваши ученики должны понять, что умножение можно рассматривать как повторяющееся сложение.
Они также должны были потратить время на умножение чисел на ноль и единицу. Хотя им не нужно знать технические термины, понять, как работают нулевое свойство и свойство идентичности.
Теперь пришло время сделать один из самых больших скачков: пройти таблицу умножения.
Один из эффективных подходов работает следующим образом:
- Отобразите диаграмму или слайд таблицы умножения 12 x 12. Если хотите, дополните это студенческими копиями таблицы умножения. Если таблица 12 х 12 кажется слишком сложной, проделайте тот же процесс с таблицей умножения 10 х 10.
- Научите учащихся пользоваться диаграммой и находить продукты, следуя и сопоставляя положение чисел по вертикальной и горизонтальной осям.
- Теперь поговорим о некоторых паттернах, которые вы можете найти на графике. Предложите учащимся подсказки или подсказки. Например, обратите внимание, что каждое число, кратное десяти, заканчивается нулем, а каждое число, кратное пяти, заканчивается нулем или пятью.
- Спросите учащихся, какие факты даются легче всего. Например, единицы и десятки легко. Теперь, когда вы обсудили «простые» факты умножения и то, что делает их легкими, удалите их из таблицы.
Студенты обычно соглашаются, что двойки, пятерки и одиннадцать тоже даются легко. Продолжайте вычеркивать «простые» числа, пока не дойдете до этапа, который выглядит примерно так:
- Посмотрите на оставшиеся числа вместе с классом. Используйте возможность вести динамичную дискуссию и перейти к следующему шагу.
Покажите, как свойство коммутативности упрощает задачу Как и сложение, умножение коммутативно, означает, что порядок множителей не меняет произведение (ответ).
Другими словами, два числа можно умножать в любом порядке, и произведение будет одинаковым. Например, умножение 8 x 2 даст вам тот же ответ, что и умножение 2 x 8.
Когда вы будете эффективно доносить это, это поощрит ваших учеников.
Покажите своим ученикам, что каждый ответ повторяется, поэтому им нужно выучить только половину оставшихся таблиц. Например, объясните, что обучение 3 x 6 — это то же самое, что и обучение 6 x 3!
Если учащиеся уже усвоили факт семейства от 0 до 3, то они также знают четыре числа от 4 до 10.
Чтобы еще больше усилить свойство коммутативности, вы также можете использовать визуальную модель, подобную приведенной выше, и указать, как расположены желтые блоки.
Спросите своих учеников: «Разве эти две аранжировки не одинаковы, а просто разные версии друг друга? Если мы посчитаем общее количество единиц, они одинаковы?»
Помощь учащимся в понимании этого свойства является ключевой частью обучения умножению. Чтобы учащиеся сделали это сами и научились на собственном опыте, попросите класс создать модели, иллюстрирующие эту идею, и доказать, что a x x приводит к тому же результату, что и b x a .
5. Разбейте заучивание на простые шагиТеперь ваши ученики готовы начать заучивание таблицы умножения . Вполне вероятно, что они уже начали это делать.
Имейте в виду, что учащимся не всегда очевидно, зачем им нужно заучивать факты умножения наизусть. Сообщите о важности понимания значения фактов умножения и о том, как их можно использовать в повседневных ситуациях.
Хотя существует множество подходов к запоминанию таблицы умножения, вспомните приведенные выше примеры — «простые» числа — в качестве хорошей отправной точки.
Продолжая урок, соблюдайте следующие правила:
- Поощряйте учащихся и выделяйте время для устной или письменной практики.
- Вводите новые факты умножения один за другим , постепенно и поэтапно открывая концепцию для более сложных шагов умножения на 2, 3, 4 и так далее.
- Дайте учащимся время попрактиковаться в фактах умножения. Найдите ритм, который хорошо работает в вашем классе. Если хотите, воспользуйтесь возможностью взаимного обучения для учащихся, испытывающих затруднения.
- Запомните факты в стратегическом порядке . Как только ваши ученики освоят 0-3 , перейдите к 4-7 , а затем к 8-10 . В зависимости от ваших предпочтений, вы также можете охватить 11 и 12. Добавление более сложных задач в качестве бонуса поможет вам оценить успевающих учеников. Некоторые учителя будут включать несколько более сложных задач в качестве бонуса или для выявления отличников.
Чтобы облегчить запоминание, держите под рукой наглядные материалы в классе. Независимо от того, сколько раз вы повторяете умножение, всегда полезно иметь физическую копию таблицы в вашем классе.
Если у вас его нет, вы можете заказать его онлайн менее чем за 10 долларов. Быстрый поиск на Amazon показывает множество вариантов.
Если у вас уже есть плакат, рассмотрите возможность получения других материалов, которые помогут вам наглядно объяснить функцию умножения.
Например, этот документ является отличным вариантом для дисплеев: он содержит набор из 20 страниц ответов (как тот, что показан ниже) на каждую из таблиц умножения от 1 до 10, закодированных цветом в соответствии с конкретной таблицей, которую они представляют.
6. Познакомить с ассоциативными и дистрибутивными свойствами Хотя эти понятия более сложные, важно, чтобы ваши учащиеся усвоили их. Вы обнаружите, что они могут творить чудеса, улучшая умственные способности ваших учеников.
Примечание: При вводе свойств, указанных ниже, действуйте по своему усмотрению. Они могут быть неприменимы к учащимся любого года младше 4-го класса.
Ассоциативное свойствоПравило 9Ассоциативное свойство 0233
утверждает, что независимо от того, как вы группируете факторы, продукт всегда будет одним и тем же.Например,
( A x B ) x C = A x ( B x C )
6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6)6 ( B x C ). 3 = 1 x (2 x 3)Ваши учащиеся могут понять эту концепцию, связав ее со сложением столбцов, посредством чего они группируют слагаемые, чтобы найти сумму.
Студенты также могут научиться группировать факторы любым удобным для них способом при поиске ответа.
Вы можете объяснить это правило как расширение коммутативного свойства выше.
Свойство распределения обозначается как a(b + c) = (ab) + (ac) 6 90 они уже используют это свойство сами по себе как математический трюк в уме для решения более сложных фактов умножения. Проще говоря, свойство распространяется — или, как следует из его названия, распределяет — значение a поровну на b и c. Например, для 6 x 8 они могут использовать распределительное свойство, чтобы думать: (6 x 5) + (6 x 3) или 30 +18 Чтобы объяснить это свойство визуальным или тактильных учащихся, позвольте детям исследовать распределительное свойство с помощью таких материалов, как чашки и бобы или сетчатая бумага. Математические игры в классе помогут избавиться от страха перед умножением. Константы калькулятора Если калькуляторы в вашем классе имеют функцию констант, предложите учащимся использовать их для определения кратности любого числа, чтобы найти связь между умножением и сложением. Как это работает: Разговор о таблице умножения Это забавное математическое задание, которое мотивирует ваших учеников и закрепляет их знания о таблице умножения. Шаг а) Выберите конкретную таблицу умножения для использования в задании (например, число, кратное пяти) Шаг б) Попросите учащихся встать и расположить их в определенном порядке, чтобы каждый учащийся знал когда подошла их очередь Шаг в) Выберите одного ученика, чтобы считать «один». Таким образом, последовательность будет следующей: раз, два, три, четыре, « жужжание !», шесть, семь… Шаг d) Если учащийся забывает сказать «жужжание» или произносит его в неподходящее время они выходят и садятся. Последовательность подсчета будет продолжаться до тех пор, пока учащиеся не наберут десять раз по пять (или по усмотрению учителя), а затем начнется снова. Окончательными победителями становятся трое последних выживших детей. Рассмотрите возможность награждения победителей как часть вашей стратегии управления классом. Чтобы получить больше вдохновения, просмотрите наш полный список из 20 увлекательных математических игр для развития навыков. Для активного подхода к обучению математике ознакомьтесь с нашими 20 веселыми и творческими математическими заданиями — подходами и упражнениями с компьютерами и без них, которые заставят учащихся с нетерпением ждать ваших уроков математики. В нашем обзоре учебников по математике для учащихся мы нашли список исключительных ресурсов для учителей. Просмотрите номера три, пять и шесть, чтобы найти примеры публикаций, в которых используется умножение и которые помогают поддерживать хорошо структурированную учебную программу по математике. Интернет является домом для огромного количества мощных и полезных образовательных математических веб-сайтов для учителей и учащихся. См. наш список полезных математических веб-сайтов для учителей, пятью из которых вы можете поделиться со студентами. Одним из ресурсов является Prodigy Math Game, математическая игра, ориентированная на учебную программу, которую используют более 800 000 учителей и 30 миллионов учащихся по всему миру. Prodigy предлагает контент по всем основным темам математики, включая умножение, и предназначен для учащихся с 1-го по 8-й класс.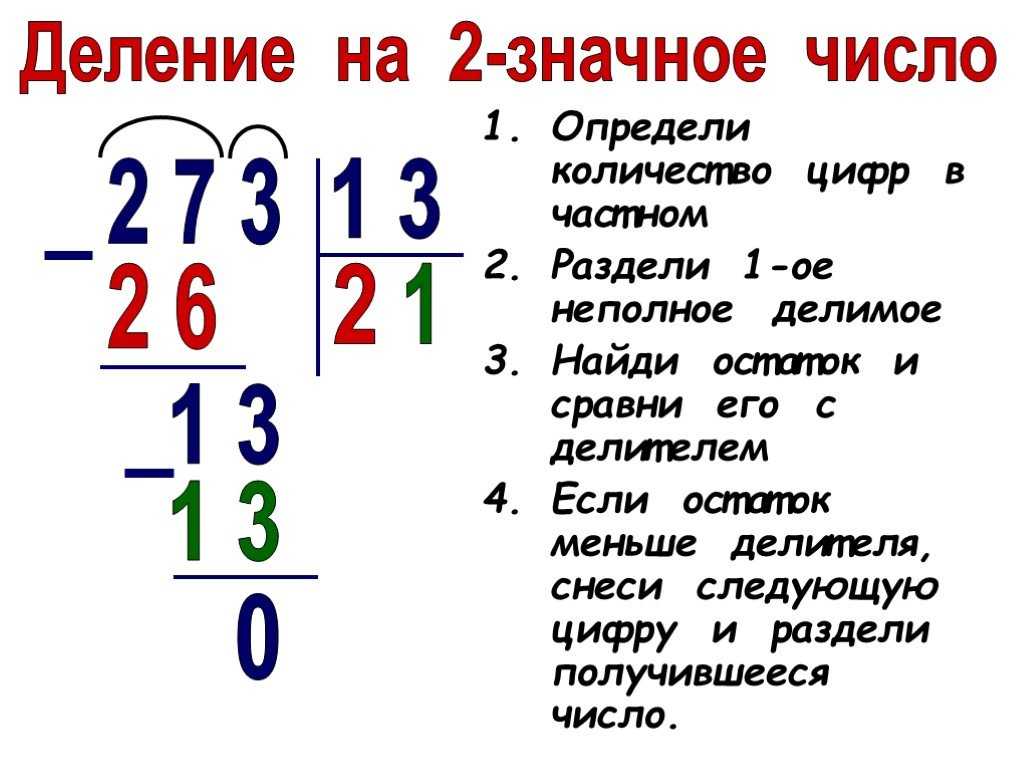
Рассмотрим эти два примера, посвященные умножению:
Затем ребенок слева от него считает «два». Следующий ребенок считает «три» и так далее. Когда последовательность достигает числа, кратного пяти, учащийся выкрикивает «жужжание!»
