Сложение и вычитание столбиком – примеры

4.3

Средняя оценка: 4.3

Всего получено оценок: 280.

4.3

Средняя оценка: 4.3

Всего получено оценок: 280.

Простейшие операции, вроде сложения и вычитания все привыкли выполнять в уме – достаточно немного практики и, кажется, любое выражение такого толка без проблем поддастся решению. Вот только, что делать, если вам попадется сложение или вычитание огромных чисел: пятизначных и больше? Такие числа посчитать в уме не каждому по силам, поэтому придется использовать метод сложения и вычитания в столбик, о котором и пойдет речь сегодня

Сложение

Сложение – это процесс переноса числа по числовой прямой вправо. Если говорить точнее, то перенос по направлению движения числовой прямой.

Направление движения числовой прямой это направление, в котором происходит увеличение, отмечены на прямой чисел. Теоретически, направление может быть любое, но на практике принято считать, что числа увеличиваются при переносе вправо и уменьшаются при переносе влево.

Складывать можно любые рациональные и комплексные числа. При этом, чтобы складывать иррациональные числа, то есть числа под знаком корня, придется использовать какие-либо хитрости или просто вычислить приближенное значение корня и использовать уже его.

Вычитание

Вычитание больше страшит учеников. Проблема в том, что при вычитании ученик в первый раз знакомится с понятием отрицательных чисел, которые в начальных классах все бояться. Тем не менее, принципиально вычитание ничем от сложения не отличается.

В высшей математике, к слову, нет понятия вычитания. Есть «математическая сумма», которая включает в себя и вычитание, как сложение с отрицательным числом.

Сложение и вычитание в столбик

Сложение и вычитание в столбик во многом похожи. Первым делом нужно правильно записать числа. Для этого одно число записывается под другим так, что под единицами записываются единицы, под десятками десятки и так далее. Под числом разряда первого числа всегда записывается число такого же разряда второго числа.

После этого выполняются действия с разрядами. К единицам прибавляются единицы, к десяткам десятки и так далее. В результате правильный ответ как бы формируется сам собой, собираясь из множества простых операций.

Переход через десяток

Отдельно стоит сказать о проходе через десяток. Это явление встречается как в сложении, так и в вычитании. Рассмотрим отдельно переход через десяток в каждой из операций.

В сложении это выглядит следующим образом: вы складываете числа разряда, например, единиц. Но в результате сложения получается число больше 9, что выходит за пределы разряда. Что делать? Нужно просто записать единицы из получившегося числа, а к десяткам прибавить 1 при сложении. Рассмотрим на примере.

1567+154 – распишем по действиям сложение каждого разряда.

4+7=13 – в результат пойдет только число 3, а к сложению десятков нужно прибавить единицу.

6+5+1=12 – по той же схеме, в десятках останется только число 2, а 1 нужно прибавить в следующем действии при сложении уже сотен.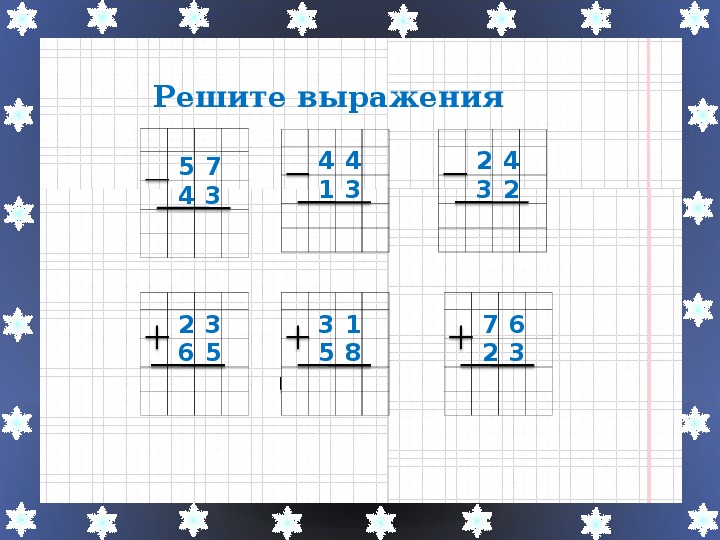

5+1+1=7

Оставшаяся единица в разряде тысяч не имеет пары во втором слагаемом, поэтому просто перепишем ее в результат. Ответом примера будет число: 1723

С вычитанием ситуация похожая, только здесь число в разряде может быть слишком маленьким. Для того, чтобы выполнить вычитание мы занимаем единицу у следующего разряда, которая в настоящем разряде превращается в 10.

Рассмотрим на небольшом примере:

35-16

5-6 – вычитание произвести не получится, но мы можем занять единицу у разряда десятков. Чтобы не забыть о «займе» над разрядом, из которого берут 1 ставят точку.

15-6=9

2-1=1

Результат: 19

Что мы узнали?

Мы узнали, что такое сложение и вычитание. Поговорили о каждой из операций в отдельности, привели примеры сложения и вычитания в столбик.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Елисей Замотаев

  7/10

• Матвей Гавриленко

  8/10

• Даня Акименко

  6/10

• Анна Ножеева

  9/10

• Evgeniy Morozov

  10/10

• Лира Нургалиева

  10/10

• Светлана Быкова

  8/10

• Стас Богданов

  9/10

• Вероника Калачёва

  10/10

• Артём Мещеряков

  6/10

Оценка статьи

4.

3

Средняя оценка: 4.3

Всего получено оценок: 280.

---

А какая ваша оценка?

Сложение и вычитание двузначных чисел в столбик. 2-й класс

Этапы работы	Содержание этапа
1. Организационный момент Цель, которая должна быть достигнута учащимися: подготовиться к продуктивной работе на уроке. Цель, которую учитель хочет достичь на данном этапе: Способствовать подготовке учащихся к продуктивной работе. Задача:  создать положительный эмоциональный настрой; Методы: словесные.	Слайд №1 (Солнышко с лучами) — Добрый день. Я рада снова видеть вас и надеюсь на взаимность. — В жизни человека большую роль играет настроение. С радостным настроением легко получаются любые дела. И наоборот, когда плохое настроение, все “валится из рук”. Давайте пожелаем друг другу хорошего настроения.
2. Изучение учебного материала А) Актуализация опорных знаний. Цель, которая должна быть достигнута учащимися: повторить сложение и вычитание с переходом через разряд, Цель, которую хочет достичь учитель: организовать работу по повторению сложения и вычитания с переходом через разряд, создание ситуации для подведения к теме урока. Методы: побуждающий от проблемной ситуации диалог.	Слайд №2  Как хорошо уметь считать . Прочитайте, что написала второклассница Наташа из города Сызрани. Умеете вы считать? Что значит хорошо считать? Чтобы ответить на этот вопрос, давайте перенесёмся в школу позапрошлого века. Слайд №3 школа Рачинского На уроке в народной школе. Один ученик из этих учеников, когда вырос рассказал о своей любимой школе , о своём любимом уроке этой картиной. Имя художника Богданов – Бельский. Чем она отличается от нашей? Как называется этот урок? Какое задание выполняют ученики? Умеете ли вы считать устно? Вывод: Уметь считать устно – это уметь думать, рассуждать, объяснять. Как получить ответ. 1.Устный счет. ( на доске) 7+7=…-9=…+7=…-8=…+9=…+7=…+10=… (7+7=14-9=5+7=12-8=4+9=13+7=20+10=30) — Что можно сказать о получившемся числе? (двузначное, круглое, четное число
Б) Постановка учебной задачи Цель: обсудить затруднение и сформулировать цель урока.	1. Внимательно посмотрите на числа. — Что между ними общего? Какое число лишнее? (Эти числа двузначные, за исключением числа 8, оно однозначное) 5, 50, 45, 40, 35; 28, 23, 18, 13, 8; 36, 32, 28, 24, 20; 82, 77, 72, 67, 2. — В чём сходство между рядами? (Во всех рядах числа уменьшаются на одно и то же число) — Какой из рядов “лишний”? (В третьем ряду числа уменьшаются на 4, в остальных – на 5; во втором ряду есть однозначное число, а в остальных — нет; в четвёртом ряду есть число, записанное одинаковыми числами, а в остальных — нет). — Назовите в четвёртом ряду самое большое и самое маленькое число (82, 62) — На сколько 82 больше 62? (на 20) — На сколько меньше? (тоже на 20) — Расскажите, что вы знаете о числе 82? (это двузначное число, оно состоит из 8 десятков и двух единиц) — Что получится, если 62 увеличить на 4? (66) — Сложите 62 и 30 (92) (здесь сделать рисунок прибавления чисел) — Cегодня 3 декабря начало зимы, но у нас ещё осень — На ум приходят строчки А.С. Пушкина Унылая пора! Очей очарованье! Приятна мне твоя прекрасная пора Люблю я пышное природы увяданье, В багрец и золото одетые леса. — Какой в этом году была осень для вас? — Чем она вас радовала?
В) Открытие новых знаний Цель: обсудить проект решения учебной задачи и составить алгоритм записи в столбик Методы: учебный диалог, моделирование	Слайд №4 2. Картинка с изображение осени, нарисованная с помощью геометрических фигур. — Посмотрите на картинку. Что можете о ней сказать? — Какие мысли приходят на ум? — Сколько и каких геометрических фигур вы насчитали? (треугольников -.., ломанных -.., ромбов -.., прямоугольников -.., прямых -..) — Осень вам прислала последний подарок. (музыка) и за одно зарядка По классу разбросаны листья, пройдитесь и поднимите тот листик, который соответствует вашему настроению.
3. Закрепление учебного материала Цель: учиться выполнять действия в столбик. Цель, которую ставит перед собой учитель: создать условия для формирования умения записи в столбик. Задачи: — развитие умения выполнять действия в столбик; — развивать умение работать в группе и самостоятельно; — развивать способность сверять свою работу с образцом и самостоятельно и объективно её оценивать. Методы: репродуктивные	— Ребята, а у кого листочек оказался с сюрпризом? Давайте повесим эти листочки на доску. На доске: 62. 36. 53. 76. 23. 56. 98. — Какое задание вы можете предложить? (расположить в порядке возрастания, убывания; представить в виде суммы разрядных слагаемых, сумма цифр) — Выберите то задание, которое вам понравилось. Взаимопроверка тетрадей. — А я хочу вам предложить найти значение суммы 2 самых маленьких чисел. (один ученик у доски решает выражение с пошаговым объяснением) 23+36=(20+3)+(30+6)=(20+30)+(3+6)=50+9=59 — Найдем разность 98 и 45 (второй ученик у доски решает выражение с пошаговым объяснением) 98-45=(90+8)-(40+5)=(90-40)+(8-5)=50+3=53 Учебник стр. 72 № 152 Катя и Женя как решили? Перепиши в тетрадь и ответь на вопросы.
4. Рефлексия Цель: осознание учащимися своей УД, самооценка результатов деятельности своей и класса	Вопросы по слайду. — С какой проблемой сталкиваемся при решении выражений? (длинная запись) — Итак, что нам нужно научиться делать? (учиться делать короткую запись) — Я хочу показать вам короткую запись на доске. Слайд№6 + 23 36 ____ 59 — Сравните новую запись в столбик с записью в строчку? Какая из записей вам нравиться больше? — А кто догадался, почему мы так долго выполняли действия по цепочке?
5. Домашнее задание Цель: закрепить умение выполнять действия в столбик.	Составляли алгоритм записи в столбик Под руководством учителя формулируется алгоритм письменных приёмов сложения и вычитания двузначных чисел: Записать одно число под другим так, чтобы единицы были под единицами, десятки под десятками. Поставить знак действия слева между числами. Подчеркнуть. Сложить единицы, сложить десятки. Прочитать полученный результат. Слайд №7 пишу: единицы под единицами, десятки под десятками; складываю (вычитаю) единицы: …. складываю (вычитаю) десятки: …. ответ: … — Мы решили учебную задачу? Составили алгоритм записи в столбик. — Давайте наше открытие проверим в действии. Откройте учебник с. 72 №152 (3) или на доске решают 46+31 76-13 54+32 63-24 Вычислить выражения в столбик (действия выполняются у доски с комментированием) — Как расположены числа в выражениях? — Где стоят знаки действий? — Чем заменен знак равно? Физминутка для глаз. Слайд на доске “Снежинки” — Ребята, один ум хорошо, а вместе работать лучше и веселей. Работа в группах. Дети берут с подноса по одному жетону (круг, ромб, треугольник, квадрат) и рассаживаются по группам. Каждой группе предстоит измерить длину ломанной. (Вспомнить правила работы в группе, каждая группа называет по одному правилу) Слайд№ 8 — Выберите одну ломанную, длину которой будете измерять. — Почему ломанные разные, а результаты одни? Математика-наука точная, действия выполняются по алгоритму. Давайте вернемся к теме урока, когда учились складывать в столбик. Слайд №9 — Посмотрите на запись. — Что вы видите? — Со всем ли вы согласитесь? — Какую задачу ставили? — Удалось ли решить поставленную задачу? — Кто хочет узнать, почему нельзя записывать “как хочется”? — На следующем уроке мы с вами и разберемся, почему так нельзя записывать. Что нового узнали на этом уроке? Какой этап урока был для тебя самым интересным? Какой этап урока оказался для вас трудным? Как оцениваете свою работу? А работу класса в целом? (для комиссии сделать оценку работы) Слайд №10 Д/з. № 167 стр. 78 Слайд № 11 Спасибо! Молодцы!

Иллюстративная математика

Иллюстративная математика

класс 2

2 класс

2.ОА. 2 класс — Операции и алгебраическое мышление

2.ОА.А. Представлять и решать задачи на сложение и вычитание.

2.ОА.А.1. Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, взятия, сложения, разъединения и сравнения с неизвестными во всех позициях, например, с помощью рисунков и уравнений с символом для неизвестного числа, представляющего проблему. См. Глоссарий, Таблица 1.

• Карандаш и наклейка
• Экономия денег 2

2.ОА.Б. Сложите и вычтите в пределах 20.

2.ОА.Б.2. Свободно складывать и вычитать в пределах 20, используя умственные стратегии. Список умственных стратегий см.

в стандарте 1.OA.6. К концу 2 класса знать наизусть все суммы двух однозначных чисел.
• Стремление к беглости
• Удар по целевому номеру

2.ОА.С. Работайте с равными группами объектов, чтобы получить основу для умножения.

• Запоздалое признание

2.ОА.С.3. Определите, имеет ли группа объектов (до 20) нечетное или четное количество членов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.

• Кнопки нечетные и четные
• Красные и синие плитки

2.ОА.С.4. Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.

• Подсчет точек в массивах
• Разбиение прямоугольника на единичные квадраты

2.

НБТ. 2 класс — Числа и операции с основанием десять

2.НБТ.А. Поймите значение места.

2.НБТ.А.1. Поймите, что три цифры трехзначного числа представляют количество сотен, десятков и единиц; например, 706 равно 7 сотням, 0 десяткам и 6 единицам. Под особыми случаями следует понимать следующее:

• Коробки и коробки карандашей
• Объединение и разделение
• Подсчет марок
• Игра с наибольшим числом
• Глядя на числа в любом направлении
• Изготовление 124
• Один, десять и сто больше и меньше
• Перегруппировка
• Десять 10 долларов составляют 100 долларов.
• Три задачи на композицию/декомпозицию

2.НБТ.А.1.б. Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 относятся к одной, двум, трем, четырем, пяти, шести, семи, восьми или девяти сотням (и 0 десяткам и 0 единицам).

• Пока нет задач, иллюстрирующих этот стандарт.

2.НБТ.А.2. Считать в пределах 1000; пропуск счета на 5, 10 и 100 секунд.

• Экономия денег 2

2.НБТ.А.3. Читать и записывать числа до 1000, используя десятичные числа, имена чисел и расширенную форму.

• Глядя на числа в любом направлении

2.НБТ.А.4. Сравните два трехзначных числа на основе значений цифр сотен, десятков и единиц, используя символы $>$, = и $

<$ для записи результатов сравнения.
• Сравнения 1
• Сравнения 2
• Цифры 2-5-7
• Сравнение числовых строк
• Заказ 3-значных номеров
• Использование изображений для объяснения сравнения чисел

2.НБТ.Б. Используйте понимание значения разряда и свойства операций сложения и вычитания.

2.НБТ.Б.5. Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на разрядности, свойствах операций и/или связи между сложением и вычитанием.


• Форд и Логан Добавляют 45+36
• Банка пенни Джамира
• Экономия денег 1
• Экономия денег 2

2.НБТ.Б.6. Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядности и свойствах операций.

• Головоломка с платным мостом

2.НБТ.Б.7. Складывать и вычитать в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.

• Сколько дней до летних каникул?
• Много способов сделать дополнение 2
• Пейтон и Пресли обсуждают дополнение

2.НБТ.Б.8. Мысленно прибавьте 10 или 100 к заданному числу 100–900 и мысленно вычтите 10 или 100 из заданного числа 100–900.


• Хоровой счет

2.НБТ.Б.9. Объясните, почему стратегии сложения и вычитания работают, используя позиционное значение и свойства операций. Объяснения могут быть подкреплены рисунками или предметами.

• Пейтон и Пресли обсуждают дополнение

2.МД. 2 класс — Измерения и данные

2.МД.А. Измерьте и оцените длину в стандартных единицах.

• Насколько велик фут?

2.МД.А.1. Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, линейки, измерительные рейки и измерительные ленты.

• Определение длины

2.МД.А.2. Дважды измерьте длину объекта, используя для двух измерений единицы длины разной длины; опишите, как два измерения соотносятся с размером выбранной единицы измерения.

• Пока нет задач, иллюстрирующих этот стандарт.

2.

МД.А.3. Оцените длину, используя единицы измерения: дюймы, футы, сантиметры и метры.
• Определение длины

2.МД.А.4. Измерьте, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине с точки зрения стандартной единицы длины.

• Определение длины

2.МД.Б. Свяжите сложение и вычитание с длиной.

2.МД.Б.5. Используйте сложение и вычитание в пределах 100 для решения текстовых задач с длинами, заданными в одних и тех же единицах, например, с помощью рисунков (например, рисунков линеек) и уравнений с символом неизвестного числа для представления задачи.

• Соревнования по прыжкам в высоту

2.МД.Б.6. Представляйте целые числа как длины от 0 на диаграмме числовых линий с точками, расположенными на равном расстоянии друг от друга, соответствующими числам 0, 1, 2, …, и представляйте суммы и разности целых чисел в пределах 100 на диаграмме числовых линий.


• Лягушка и жаба на числовой прямой

2.MD.C. Работа со временем и деньгами.

• Запоздалое признание

2.MD.C.7. Говорите и записывайте время по аналоговым и цифровым часам с точностью до ближайших пяти минут, используя время до и после полудня.

• Время заказа

2.MD.C.8. Решайте словесные задачи с участием долларовых банкнот, четвертаков, десятицентовиков, пятицентовых монет и пенни, используя соответствующие символы \$ и $¢$. Пример: Если у вас есть 2 цента и 3 пенни, сколько у вас центов?

• Александр, который был богат в прошлое воскресенье
• Выбор, выбор, выбор
• Банка пенни Джамира
• Зоомагазин
• Экономия денег 1
• Выбор Сьюзен
• Посещение Аркады

2.МД.Д. Представлять и интерпретировать данные.

2.МД.Д.9. Генерируйте данные измерений, измеряя длину нескольких объектов с точностью до целой единицы или выполняя повторные измерения одного и того же объекта.

Покажите измерения, построив линейный график, где горизонтальная шкала отмечена в целых числах.
• Выращивание бобовых растений
• Измерения размаха рук
• Самая длинная прогулка

2.МД.Д.10. Нарисуйте графическое изображение и столбчатую диаграмму (с единичной шкалой), чтобы представить набор данных с четырьмя категориями. Решайте простые задачи на сборку, разборку и сравнение См. Глоссарий, Таблицу 1, используя информацию, представленную в виде гистограммы.

• Любимый вкус мороженого

2.Г. 2 класс — Геометрия

2.Г.А. Рассуждайте о формах и их атрибутах.

2.Г.А.1. Распознавать и рисовать фигуры с заданными атрибутами, такими как заданное количество углов или заданное количество равных граней. Размеры сравниваются непосредственно или визуально, а не путем измерения. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.


• Полигоны

2.Г.А.2. Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.

• Разбиение прямоугольника на единичные квадраты

2.Г.А.3. Разделите круги и прямоугольники на две, три или четыре равные доли, опишите доли, используя слова

половин , третей , половину , треть и т. д., и опишите целое как две половины, три трети, четыре четверти. Признайте, что равные части одинаковых целых не обязательно должны иметь одинаковую форму.
• Представление половины прямоугольника
• Какие картинки представляют одну половину?
Модель микросхемы

для сложения и вычитания – Другая математика

Около 32 лет назад я только что закончил бакалавриат. по математике и был немедленно нанят преподавать математику в средней школе Рузвельта в Окленде, Калифорния. Я думал, что знаю все, что нужно знать о математических концепциях K-12. Конечно, сложение и вычитание целых чисел!

Однако я почти сразу же был унижен невинным вопросом ученика в классе новичков, который я преподавал. Это был класс, состоящий из студентов, которые были новичками в Соединенных Штатах, и, следовательно, типичный студент в этом классе не имел или не имел никакого предыдущего образовательного опыта в стране, из которой он приехал.

«Почему ты должен вычеркнуть это верхнее число и поставить там маленькую единицу?», — сказала она, указывая на задачу на вычитание, которую я только что искусно решил на доске.

Я дал какой-то неубедительный ответ о том, что у верхнего номера не хватает, поэтому он идет к соседу, чтобы одолжить один … бла … бла … бла. Именно в тот момент я понял, что недостаточно знать алгоритмы, я знал, ПОЧЕМУ они работают, и как объяснить их студентам.

Я полюбил МОДЕЛЬ ЧИПА за визуальное представление четырех операций с целыми числами, потому что это имеет смысл и прямо соответствует стандартному алгоритму.

 

номера моделей

Прежде чем моделировать операции, давайте начнем с использования модели чипа для визуального представления чисел.

268

326

Фишки являются визуальным представлением разрядной системы оценки в математике.

 

Обменный курс

Поскольку мы используем систему с основанием десять, мы можем обменять 10 точек в одном столбце на 1 точку в столбце слева. Если это кажется запутанным, давайте воспользуемся блоками с основанием 10, чтобы взглянуть на ту же идею «обмена».

Десять единичных кубов можно выстроить в ряд, чтобы получить один десятистержень.

Аналогично, 10 десятигранников можно расположить так, чтобы они равнялись одной сотке.

Эти два обмена можно обобщить в одно обобщенное утверждение: десять «маленьких» равны одному «большому»

Использование блоков с основанием десять используется для введения этого обменного курса, потому что относительные размеры блоков пропорциональны друг другу. Стаднеты могут буквально сосчитать, что десять единичных кубов равны 1 десятке, а 10 десяток равны по размеру одной сотке.

Нет необходимости переходить к модели с чипами, пока учащиеся полностью не поймут концепцию обменного курса.

 

Курс обмена с чипами

Обменный курс становится актуальным, когда мы хотим выразить число в его простейшей форме.

Сколько стоят 3 сотни, 2 десятка и 14 единиц?

После моделирования значений мы видим, что есть одна возможность сделать обмен в своей колонке. Поскольку единиц 14, мы можем обменять десять из них на одну точку в столбце десятков.

Вот еще пример, на этот раз потребовалось два обмена.

Сколько стоят 3 сотни, 16 десятков и 13 единиц?

Дополнение с моделью чипа

Предположим, мы хотим сложить 268 и 147, используя модель чипа.

Сначала мы определяем сложение как объединение вещей . Добавление 268 и 147 означает, что мы будем комбинировать точки, представляющие 268, с точками, представляющими 147.

Начните с моделирования обоих чисел на одной и той же диаграмме разрядности. На данный момент мы видим, что неупрощенная сумма равна . 3 сотни и 10 десятков и 15 единиц
Теперь ищем возможности сделать обменный курс 10 маленьких равняется 1 большому . Мы видим, что есть две возможности сделать это, потому что в колонке десятков 10 точек, а в колонке единиц 15 точек. Неважно, какой обмен мы делаем первым, поэтому мы начнем с обмена 10 единиц на 1 десяток.
Теперь мы можем обменять оставшиеся 10 десятков на 1 сотню.
Дополнительных обменов сделать нельзя, поэтому считаем оставшиеся точки в каждом столбце. 4 сотни и 1 десяток и 5 единиц Сумма 415.

Обратите внимание, что вся работа, которую будут выполнять учащиеся, связана с точками. На самом деле мы не записали ни один из шагов стандартного алгоритма. Это по дизайну! Нам нужно дать учащимся большой опыт работы с визуальной моделью, чтобы понять математическую концепцию, прежде чем переходить к более абстрактному алгоритму.

В конце концов, учащиеся покажут модель микросхемы и алгоритм рядом друг с другом, используя модель микросхемы слева и записывая каждый шаг с цифрами справа.

Вкратце, есть только два компонента сложения, которые нам нужно, чтобы учащиеся поняли:

1. Сложение означает объединение вещей
2. Обменный курс: 10 маленьких равны 1 большому

Теперь нам просто нужно предоставить нашим студентам многочисленные возможности для практики. Во время своей практики студенты, естественно, будут искать стратегии, чтобы стать более эффективными.

 

Вычитание с моделью микросхемы

Как упоминалось ранее, мы хотим объяснить вычитание с перегруппировкой математически обоснованным способом, а не прибегать к мнемонике и метафорам. Мы можем достичь этого, используя наше понимание сложения, чтобы понять смысл вычитания.

Два компонента сложения приводят нас к двум компонентам вычитания:

1. Вычесть означает убрать вещи
2. Обменный курс: 1 большой равен 10 маленьким

Выражение 357 – 125 означает, что мы отнимаем 1 сотню и 2 десятка и 5 единиц от точек, которые представляют 357. 

Начните с моделирования числа 357 на диаграмме разряда. Нам не нужно моделировать 125, потому что 125 представляет собой количество, которое нам нужно, чтобы удалить из таблицы стоимостных разрядов.
Смоделируйте вычитание, вычеркнув из точек 1 сотню, 2 десятка и 5 единиц.
Остальные точки обозначают разницу. 2 сотни и 3 десятка и 2 единицы …или проще… 232

 

Предыдущий пример не требовал перегруппировки, поэтому вот пример, в котором она требуется.

326 – 159

Начните с моделирования 326 на диаграмме стоимостей. Технически мы можем вычитать слева направо или справа налево, но для наших целей мы будем двигаться справа налево, чтобы смоделировать стандартный алгоритм в Соединенных Штатах.
Нам нужно удалить 9 единиц, но в нашей модели показано только 6 единиц, поэтому мы используем обменный курс 1 большой равен 10 маленьким , который теперь дает нам 16 единиц.
Теперь мы можем вычеркнуть 9 единиц. Мы используем ✔, чтобы указать, что мы вычеркнули 9 единиц и готовы перейти к колонке десятков.
Теперь нам нужно вычеркнуть 5 десятков, но на данный момент у нас есть только 1 десяток, поэтому мы используем обменный курс 1 большой равен 10 маленьким что теперь дает нам 11 десятков.
Теперь мы можем вычеркнуть 5 десятков. Мы используем ✔, чтобы указать, что мы вычеркнули 5 десятков и готовы перейти к столбцу сотен.
Наш последний шаг — вычеркнуть 1 сотню, что мы можем сделать, потому что у нас осталось 2 сотни в столбце сотен. A ✔ в столбце сотен означает, что мы закончили удаление 1 сотни, 5 десятков и 9те.
Остальные точки обозначают разницу. 1 сотня 6 десятков и 7 единиц …или проще… 167