Задачи на разностное сравнение | План-конспект урока по математике (1 класс) на тему:
Опубликовано 02.11.2017 — 21:35 — Е.B.Корнилова
В материале даны 3 последовательных урока по обучению задачам на разностное сравнение
Скачать:
Предварительный просмотр:
Автор: Корнилова Елена Викторовна, учитель начальных классов МБОУ Устьинская СОШ
Математика – 1 класс
Раздел: Числа от 1 до 10. Число 0.
Сложение и вычитание.
Тема: Задачи на разностное сравнение.
Название номинации: «Реализация системно-деятельностного подхода средствами различных педагогических технологий»
Авторы учебников и печатных тетрадей: В.Г.ДорофеевТ.Н.МираковаТ.Б.Бука Москва «Просвещение» 2012
Формируемые УУД:
Личностные: Формировать положительное отношение к учёбе, воспитывать интерес к урокам математики, осознавать его значение; бережно относиться к учебнику и рабочей тетради; развивать навыки сотрудничества: освоения положительного и позитивного стиля общения со сверстниками и взрослыми в школе и дома; развивать элементарные навыки самооценки результатов своей учебной деятельности.
Регулятивные: Понимать поставленную задачу, соответствующую этапу обучения, понимать выделенные учителем ориентиры действия в учебном материале; адекватно воспринимать предложения учителя; проговаривать вслух последовательность производимых действий; оценивать совместно с учителем результат своих действий, вносить соответствующие коррективы под руководством учителя; составлять план действий для решения несложных учебных задач; выполнять под руководством учителя учебные действия в практической и мыслительной форме; осознавать результат учебных действий, используя математическую терминологию.
Познавательные: Ориентироваться в информационном материале учебника; совместно с учителем или самостоятельно осуществлять поиск необходимой информации, понимать простейшие модели; ориентироваться на разнообразие способов решения задач; учиться строить простые рассуждения.
Коммуникативные: Принимать участие в работе парами и группами; воспринимать различные точки зрения; использовать простые речевые средства; Контролировать свои действия в классе; включаться в диалог со сверстниками и учителем; интегрироваться в группу сверстников, проявлять стремление ладить с собеседниками; совместно со сверстниками определять задачу групповой работы; признавать свои ошибки, озвучивать их, соглашаться , если на ошибки указывают другие.
Задачи на разностное сравнение
Урок 1
Тема урока: Задачи на разностное сравнение
Цель: Формирование умения решать простые задачи на разностное сравнение.
Тип урока: открытие новых знаний
Задачи урока:
Учить решать задачи на разностное сравнение.
Развивать умение работать в группе, оценивать свои результаты.
Учить использовать полученные знания в повседневной жизни.
Воспитывать познавательный интерес, создавать положительную мотивацию учения.
Методы обучения: объяснительно-иллюстративный, словесный, частично-поисковый, практический, проблемный
Формы организации познавательной деятельности: фронтальная, коллективная, индивидуальная, парная
Оборудование урока:алгоритм решения задачи на разностное сравнение чисел, учебник «Математика. 1 класс. Часть 2. Печатная тетрадь 2 часть, веер цифр, сигнальные карточки.
Ход урока
- Организационный момент.
Проверь, дружок,
Готов ли ты начать урок?
Всё ль в порядке
Книжка, ручка и тетрадка?
Проверили? Садитесь!
С усердием трудитесь!
- Актуализация знаний:
Устный счёт.
1) — Счёт до 20 вперёд и обратно.
— Счёт от 9 до 16; от 10 до 3.
– Покажите число, следующее за числом 12 (13).
– Покажите число предыдущее числу 18 (19).
-Какое число стоит слева от 13 на 2 единицы? (11)
— Какое число стоит справа от 9 на 3 единицы? (12)
— Какое число стоит между 3 и 5, 18 и 20? (4, 19)
— Назовите соседей числа 15 (14, 16)
2) — Послушайте внимательно мою задачу. Что в ней неправильно?
«С утра на парковке стояло 8 машин. В полдень несколько машин уехало. Сколько машин осталось стоять на парковке?» (Не хватает данных)
— Исправьте условие и решите задачу.
«С утра на парковке стояло 8 машин. В полдень 5 машин уехало. Сколько машин осталось стоять на парковке?»
3) Задание № 5 на стр. 12
Физкультминутка
Вот мы руки развели,
Словно удивились.
И друг другу до земли
В пояс поклонились!
Наклонились, выпрямились,
Наклонились, выпрямились.
Ниже, ниже, не ленись,
Поклонись и улыбнусь
3. Самоопределение деятельности
Самоопределение деятельности
Практическая работа:
— Положите на парту 5 кружков, а под ними 4 квадрата.
— Как узнать, чего больше? Чего меньше? На сколько?
— Что надо сделать, чтобы узнать, на сколько кружков больше, чем квадратов? (Надо убрать столько кружков, сколько квадратов ).
— Каким действием будем решать эту задачу?
4. Постановка учебной задачи.
— Два разных ученика решили эту задачу по-разному.
Один решил так: 5 – 4
Другой решил так: 4 – 5
— Объясните, кто прав?
Чем будем заниматься на уроке? (Решать задачи на сравнение, то есть определять, на сколько одно число больше или меньше другого)
5. Построение проекта выхода из затруднения.
Вывод: чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.
Выстраивается алгоритм действия.
— Прочитайте правило по учебнику на стр. 11
6. Первичное закрепление.
Выполнение задания 1 на стр.11
VI7. Самостоятельная работа с самопроверкой по эталону.
Самостоятельная работа с самопроверкой по эталону.
№ 2,3 с. 24 в тетради на печатной основе
Физпауза
Вновь у нас физкультминутка,
Наклоняйтесь, ну-ка, ну-ка!
Распремляясь, потянулись,
А теперь назад прогнулись,
Разминаем руки, плечи,
Чтоб сидеть нам было легче.
Голова устала тоже?
Так давайте ей поможем.
Вправо-влево, раз и два –
Думай, думай голова.
Хоть зарядка коротка,
Отдохнули все слегка.
8. Вторичное закрепление
а) Работа в группах. №2 -1группа , №3 -2 группа с иллюстрированием задач с помощью наборного материала (квадратов, кружков, треугольников и д.р.)
б) Выполнение задания №4 с включением выражений «на сколько больше, на сколько меньше» в активную речь учащихся.
в) № 4 с. 25 тетрадь на печатной основе
№ 4, с.112 учебника
9. Рефлексия.
-Было интересно…
-Было трудно…
-Я понял, что…
— Теперь я могу…
— Я научился…
— Мне захотелось…
— На какой ступеньке лесенки вы хотели бы сейчас стоять?
- Ничего не понял на уроке
- Всё понятно
- Хочу знать больше
Предварительный просмотр:
Задачи на разностное сравнение
Урок 2
Цель: Формирование умения решать простые задачи на разностное сравнение.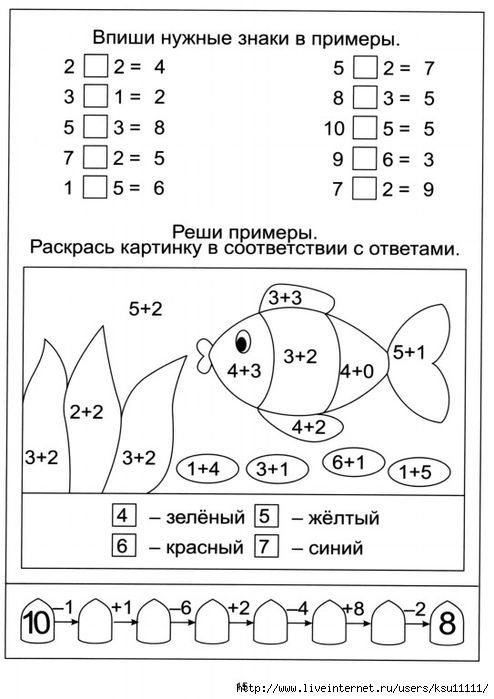
Задачи:
Закрепить правило разностного сравнения чисел.
Учить решать задачи на разностное сравнение.
Закреплять навык счёта в пределах 10
Развивать мыслительные операции, речь, творческие способности учащихся.
Методы обучения: объяснительно-иллюстративный, словесный, частично-поисковый, практический, проблемный
Формы организации познавательной деятельности: фронтальная, коллективная, индивидуальная, парная
Оборудование:алгоритм решения задачи на разностное сравнение чисел, учебник «Математика. 1 класс. Часть 2. Печатная тетрадь 2 часть, веер цифр, сигнальные карточки.
Ход урока
1. Организационный момент.
Доброе утро, друзья! Нашей встрече рада я. А вы?
2. Устный счёт
1)Работа с веером цифр. Покажите ответ.
-Уменьшите 7 на 6 .
— Сложите числа 1 и 5.
— 6 минус 4.
— Найдите сумму чисел 3 и 6.
— Увеличьте 3 на 3 .
— Первое слагаемое 2 второе 7. Найдите сумму.
— Уменьшаемое 8, вычитаемое 2. Вычислите разность.
Вычислите разность.
— На сколько 1 меньше 8?
2) Задания 7, 8 стр.14
2. Сообщение темы урока
— Сегодня нас будут интересовать задачи на нахождение разницы.
— Мы потренировали наш ум, потренируем мышцы.
Физкультминутка:
Шли по крыше 3 кота, 3 кота Василия,
Поднимали 3 хвоста прямо в небо синее.
Сели киски на карниз, посмотрели вверх и вниз.
И сказали 3 кота: «Красота! Красота!»
3. Актуализация знаний
— Кто помнит, с каким правилом мы познакомились на прошлом уроке?
(Чтобы узнать, на сколько одно число больше или меньше другого надо из большего числа вычесть меньшее.)
— Продолжите моё предложение: «Чтобы сравнить два числа, надо из …(большего числа вычесть меньшее)
4. Закрепление правила.Работа в парах
-Составьте в парах задачу на разностное сравнение и предложите способ её решения. Один из пары рассказывает условие задачи, другой – её решение. Остальные ребята проверяют правильность решения сигнальными карточками.
5. Работа над новым материалом.
— Обратимся к № 1 на странице 13. Прочитайте вопросы. Рассмотрим верхний рисунок и верхнюю схему:
— Что обозначает 5 на схеме? (целое — мячики)
— Что обозначает 4? (часть – кубики)
— Что неизвестно? (часть – разница)
— Как найти часть? (из целого вычесть известную часть, из 5-4=1)
— Каким действием можно узнать, на сколько одно число меньше другого?
— Разберём нижний рисунок и нижнюю схему:
Аналогичный разбор.
6. Первичное закрепление.
Попробуем решить задачу №2 на стр. 13 под цифрой 1).
— Прочитайте задачу хором.
— Сколько вопросов в задаче? (два)
— Что надо узнать в задаче? (разность)
-Попробуем на доске изобразить задачу схематически.(Учитель совместно с учениками изображает задачу схематически.)
— Какое правило нам потребуется?
— Запишите самостоятельно решение и ответ. (5-3=2 (р.))
— Проверьте с доски. Ответили ли мы на вопросы задачи?
— Обратите внимание перед нами стояло 2 вопроса, а решение мы записали одно.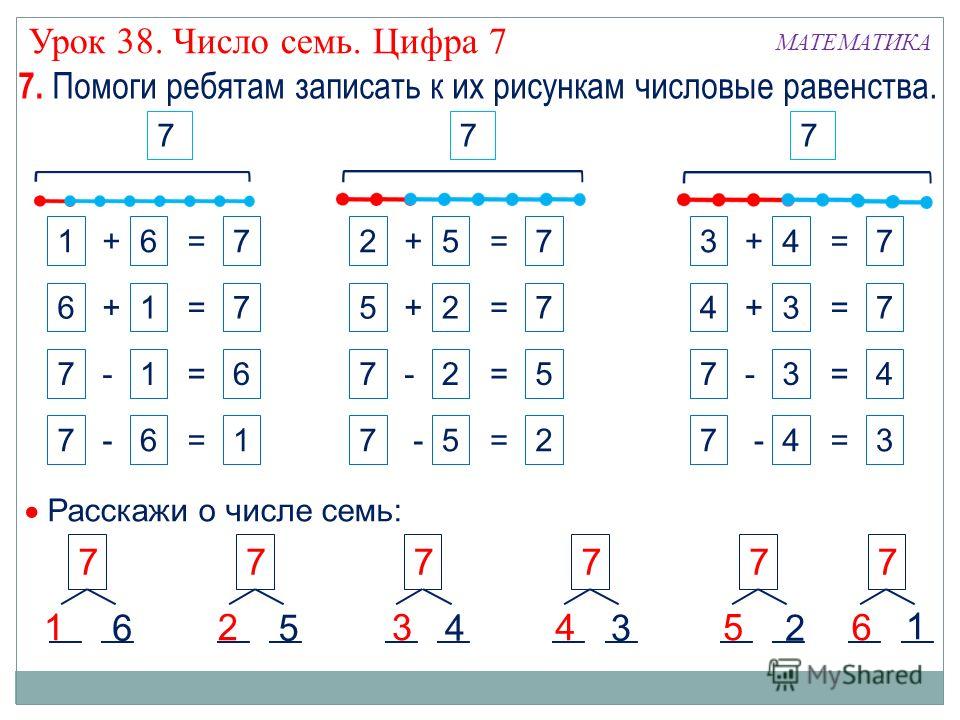 Почему? (решение подходит для ответа на 2 вопроса, так как, чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее)
Почему? (решение подходит для ответа на 2 вопроса, так как, чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее)
Подобный разбор задач под цифрами 2) и 3)
7 Выполнение заданий в тетради на печатной основе
№4 и №5 на стр. 26 решить самостоятельно по вариантам
Физкультминутка.
Стали мы учениками, соблюдаем режим сами:
Утром мы, когда проснулись, улыбнулись, потянулись.
Для здоровья, настроенья делаем мы упражненья:
Руки вверх, руки вниз, на носочки поднялись.
То присели, то нагнулись и, конечно, улыбнулись.
А потом мы умывались, аккуратно одевались.
Завтракали не торопясь, в школу к знаниям стремясь.
7. Повторение ранее изученного материала.
Выполнение заданий № 4 стр. 14 устно, №,5.стр.14 письменно из учебника
№3 стр.26 и №6 стр.27 в печатной тетради.
Итог урока.
— Над какой темой мы сегодня работали?
— Где нам пригодятся полученные знания?
Предварительный просмотр:
Задачи на разностное сравнение
Урок 3
Цель урока: Закрепление умение решать простые задачи на разностное сравнение.
Задачи:
Продолжать учить решать задачи на сравнение
Закреплять навыки счёта в пределах 10.
Развивать навыки контроля и взаимоконтроля.
Учить оценивать результаты своей работы.
Методы обучения: объяснительно-иллюстративный, словесный, частично-поисковый, практический, проблемный.
Формы организации познавательной деятельности: фронтальная, групповная.
Оборудование: Полоски бумаги для составления схем, карточки с задачами, схемы решения задач.
Ход урока
1.Организационный момент.
2. Устный счёт.
Задачи в стихах
1) На подстилке 2 птенца,
Два пушистых близнеца.
И ещё готовы 5 из скорлупок вылезать.
Сколько станет птиц в гнезде, помогите мне. 2+5=7
2) 5 мышат в траве шуршат,
3 забрались под ушат.
2 мышонка спят под ёлкой.
Сосчитать мышей недолго. 5+3+2=10
3)На берёзе 3 синички
Продавали рукавички.
Прилетело ещё 5,
Сколько будут продавать? 3+5=8
4)5 малышек-медвежат
Мама уложила спать.
Одному никак не спится,
А скольким сон хороший снится? 5-1=4
5)Цапля по воде шагала,
Лягушат себе искала.
Двое спрятались в траве,
6 – под кочкой.
Сколько лягушат спаслось?
Только точно! 2+6=8
Игра «Найди закономерность»
1,3.5,7…
10, 9,7,6,4…
Установите закономерность и продолжите числовые ряды.
3. Физкультминутка
«ПРЫГ-СКОК»
Прыг-скок, прыг-скок,
Прыгай веселей, дружок.
Ножки вместе,
Ножки врозь.
Упражненье удалось!
(В конце хлопаем в ладоши)
4.Самоопределение к деятельности
-Решите задачу:
В кружок бальных танцев ходили 8 девочек и 6 мальчиков. На сколько девочек больше, чем мальчиков?
— Как ответить на вопрос задачи? Какое действие надо выполнить?
— Какие задачи мы сегодня будем решать?
5. Работа по теме урока. Работа в группах.
Обучающиеся делятся на несколько групп.
а) Упражнение « Живая природа».
Каждая группа получает комплект карточек «Живая природа» с задачами на разностное сравнение.
— Впишите вместо пропусков подходящие слова: «больше», «меньше», «выше», «ниже», «медленнее», «быстрее», «тяжелее», «легче», «короче», «длиннее», «ниже», «выше».
— Решите задачи, последовательно отвечая на каждый вопрос.
После выполнения заданий результаты обсуждаются и рассуждаются.
Составление схемы решения задач на разностное сравнение.
— Давайте составим карточку – помогайку для решения данного вида задач.
Детям раздаются полоски бумаги для составления схемы. Ученики под руководством учителя составляют схемы.
Упражнение в парах «Сортировка»
Каждая пара получает комплект карточек «Больше – меньше», состоящий из трёх блоков задач с общим сюжетом, и по три схемы: на разностное сравнение, на увеличение и на уменьшение на несколько единиц.
— Определите, какую схему надо использовать к при решении каждой из задач, и поместить карточку под соответствующей схемой.
После выполнения упражнения необходимо проверить, как «рассортированы» задачи, и отметить пары, выполнивших задание правильно.
Физкультминутка.
«Это тоже я могу».
Кто, скажите, сможет, дети,
Повторить движенья эти?
Руки вверх я подниму.
Это тоже я могу.
Вправо-влево разведу
Это тоже я могу.
И, как птица полечу.
Это тоже я могу.
Головою поверчу.
Это тоже я могу.
А потом присяду, встану.
Это тоже я могу.
И нисколько не устану.
Это тоже я могу.
Я попрыгаю немного.
Это тоже я могу.
И пешком пойду в дорогу.
Это тоже я могу.
Если надо, побегу.
Это тоже я могу.
Все на свете я смогу!
Задание «Восстанови задачу»
Учитель вывешивает на доску плакат, на котором дано описание сюжета к задаче и приведены две схемы.
— Глядя на схемы, составьте условия двух задач.
Обсуждаются варианты составленных задач.
Рефлексия.
Поведение итогов работы в группах. Выделение самой активной группы.
— Какие задачи решали на уроке?
— Как найти разницу?
— Оцените свою работу на уроке.
— Кого из одноклассников вы хотели бы поблагодарить за активную работу на уроке?
По теме: методические разработки, презентации и конспекты
задачи на разностное сравнение
представлена презентация для урока математики в 1 классе по теме Задачи на разностное сравнение….
Сравнение чисел. Задачи на разностное сравнение
Урок в 1 классе по учебнику Л.Г. Петерсон…
Разработка к уроку математика. 1 класс. Решение задач. Задачи на разностное сравнение.
Данная работа содержит конспект урока математики в 1 классе и презентацию к нему на тему «Решение задач. Задачи на разностное сравнение. «…
Презентация к уроку математики. Решение задач.Задачи на разностное сравнение. 1класс
Эта презентация разработана учителем начальных классов Ольшанской Екатериной Сергеевной. Презентация к уроку математики на тему «Решение задач.Задачи на разностное сравнение. 1класс» по программе Школ…
3 класс. Карточки. Задачи на разностное сравнение и кратное сравнение.

индивидуальные задания…
Задачи, раскрывающие смысл отношений больше на и меньше на (задачи на разностное сравнение) 1-2 кл
задачи…
Решение задач. Задачи на разностное сравнение.
Предметные:- правильно выполнять сложение и вычитание с использованием таблицы в пределах 10;-наблюдать и объяснять, как связаны между собой две простые задачи;- решать математические выражения.- срав…
Поделиться:
Конспект урока математики в 1 классе «Задачи на сравнение чисел» | План-конспект урока по математике (1 класс):
Тема: Задачи на сравнение чисел
Цели:
— Закрепить правило разностного сравнения чисел, учить решать задачи на разностное сравнение.
— Закреплять навык счёта в пределах 9.
— Развивать мыслительные операции, речь, творческие способности учащихся.
Оборудование: учебники Петерсон Л.Г. «Математика. 1 класс. Часть 2.
Ход урока:
Этапы урока: | Деятельность учащихся | ||||||
1. | |||||||
2. Актуализация знаний 1) минутка чистописания Откройте учебник на с. 61, внизу на этой странице выполните минутку чистописания, проследив закономерность в числах. Что вы заметили? Меняется цифра по середине. Она становится больше на 1. Какое число должно быть следующим? (547,557) 2)Устный счёт. — Счёт до 20 вперёд и обратно. — Счёт от 9 до 16; от 10 до 3. — Назовите последующее число 12 (13). На сколько последующее число больше предыдущего? (на 1) — Назовите предыдущее число 18 (19). На сколько предыдущее число меньше последующего? (на 1) — Какое число следует за числом 6? (б+1) — Какое число предшествует числу 6? (б-1) — Назовите соседей числа 15 (14, 16) | Отвечают на вопросы прописывают Отвечают на вопросы | ||||||
3. ФОРМУЛИРОВАНИЕ ТЕМЫ УРОКА.
— К какому математическому понятию относятся все эти слова? -Значит, какая тема урока? (Решение задач) — Сегодня нас будут интересовать задачи на нахождение разницы. — Мы потренировали наш ум. | Отвечают на вопросы | ||||||
4. Введение в тему урока. — Кто помнит, с каким правилом мы познакомились на прошлых уроках? (Чтобы узнать, на сколько одно число больше или меньше другого надо из большего числа вычесть меньшее.) — Продолжите моё предложение: «Чтобы сравнить два числа, надо из … (большего числа вычесть меньшее) — Закрепим данное правило, поработав на доске: — На сколько 9 больше 6? (на 3) Что вы для этого сделали? (9-6=3) — На сколько 3 меньше 8? (8-3=5) — Что больше 7 или 4 и на сколько? (7-4=3) | Отвечают на вопросы Запись решения и ответов | ||||||
5. — Обратимся к № 3 на странице 60. Прочитайте задачу под буквой а. — О ком задача? (о девочках и мальчиках) -Что мы про них знаем? Девочек -6, а мальчиков не известно сколько? Но что сказано про мальчиков? Что их на 2 меньше. Каков вопрос задачи? (Сколько мальчиков?) Рассмотрим схему и дополним её. Работа со схемой. Девочек больше, значит над большей линией пишем 6. И возле этого отрезка поставим букву «Д». Мальчиков мы не знаем сколько, поэтому над меньшей линией ставим знак ?. И букву «М». Если мальчиков на 2 меньше, значит девочек……) (на 2 больше) Под разницей в отрезках записываем 2. — Каким действием можно узнать сколько мальчиков? 6-2 Запишем это действие в пустой прямоугольник. Можем решить задачу? Запишем решение. 6-2= 4 (м) Как будет звучать ответ? (6 мальчиков) — Переходим к задаче под буквой б): Прочитайте задачу. — О ком эта задача? (Про Таню и Сашу) — Что нам известно? (у Тани 6 марок) -Что значит «их на 2 больше, чем у Саши?» (Значит у Саши на 2 меньше). -Это новый вид задач на сравнение, в которых в косвенной форме подаются для нас данные. И только верно проанализировав данные можно решить их правильно. — Каков вопрос? (Сколько марок у Саши?) -Рассмотрим схему и дополним её. -Больший отрезок -это Таня. Ставим букву «Т». И цифру 6 над отрезком. — Меньший отрезок – это Саша. Ставим букву «С». -Где поставим цифру 2? -Над разницей двух отрезков. Каким действием найдем, сколько марок у Саши? (6-2) Запишите действие. Запишите решение. 6-2=4 (м) Ответ: 4 марки. | Читают задачу, отвечают на вопросы Рассматривают схему, дополняют схему, записывают решение Рассматривают схему, дополняют схему, записывают решение | ||||||
Физкультминутка: Вы, наверное, устали? Ну, тогда все дружно встали. Ножками потопали. Ручками похлопали. Покрутились, повертелись И за парты все уселись. Глазки крепко закрываем, Дружно до пяти считаем. Открываем, поморгаем И работать продолжаем. | Выполнение движений | ||||||
6. Повторение ранее изученного материала. Закрепление навыка счёта в пределах 9. — Мы неплохо разобрали новые задачи. Сейчас стоит повторить решение примеров в пределах 9. Выполним № 4 на стр. 61. Нам нужно дополнить примеры недостающими компонентами так, чтобы результаты были равны. Рассмотрим 1 пример (4+…..). Каков должен быть конечный результат? (Красная точка на 5, значит сумма равна 5.) Сколько нужно добавить к 4, чтобы в сумме получилось 5? (1) Дописываем второе слагаемое, записываем получившийся пример в пустую карточку ниже. Сколько нужно отнять от 9, чтоб в результате получилось 5? (4) Дописываем в пример вычитаемое (9-4), заполняем 2 пустую карточку. Делаем вывод 4+1 = 9-4 (Аналогично 2 рисунок) Сейчас выполним задание №6 на стр. -сколько кругов изображено в 1 рамке? (5) — что нужно с ними сделать? (добавить 2) Значит сколько надо нарисовать синих кругов в следующей рамке?(7) Обратите внимание следующая стрелка направлена в обратную сторону. Что это значит? (Что к какому-то числу прибавили 4 и получили 7) Как узнать это число? (7-4= 3) Сколько кругов нарисуем в последней рамке? Аналогично с красными треугольниками работайте самостоятельно. Проверка. | Самостоятельное решение примеров | ||||||
7. Итог урока. — Над какой темой мы сегодня работали? — Что понравилось больше всего? -Что вызывало затруднения? | Ответы на вопросы |
Сравнение и упорядочивание чисел — значение, шаги, символы, примеры
Давайте сначала вспомним значение сравнения, прежде чем изучать сравнение чисел. Сравнение — это процесс, в ходе которого мы наблюдаем сходные свойства разных предметов или вещей. Сравнение и упорядочивание являются неотъемлемой частью нашей повседневной жизни. Сравнение и упорядочивание чисел — это понятие в математике, при котором мы сравниваем числа в соответствии с их значениями, идентифицируем меньшие и большие числа, а затем упорядочиваем их в порядке возрастания или убывания. Мы сравниваем числа в нашей повседневной жизни, например, сравнивая количество рабочих часов каждый день, мы узнаем, когда мы работали больше. Мы можем сравнивать и упорядочивать числа в порядке возрастания или убывания.
Сравнение и упорядочивание являются неотъемлемой частью нашей повседневной жизни. Сравнение и упорядочивание чисел — это понятие в математике, при котором мы сравниваем числа в соответствии с их значениями, идентифицируем меньшие и большие числа, а затем упорядочиваем их в порядке возрастания или убывания. Мы сравниваем числа в нашей повседневной жизни, например, сравнивая количество рабочих часов каждый день, мы узнаем, когда мы работали больше. Мы можем сравнивать и упорядочивать числа в порядке возрастания или убывания.
В этой статье мы рассмотрим концепцию сравнения и упорядочивания чисел, знаки, используемые для их сравнения, и узнаем о сравнении рациональных и целых чисел. Мы также научимся сравнивать и упорядочивать числа в порядке возрастания и убывания с помощью решенных примеров для лучшего понимания концепции.
| 1. | Что такое сравнение чисел? |
2.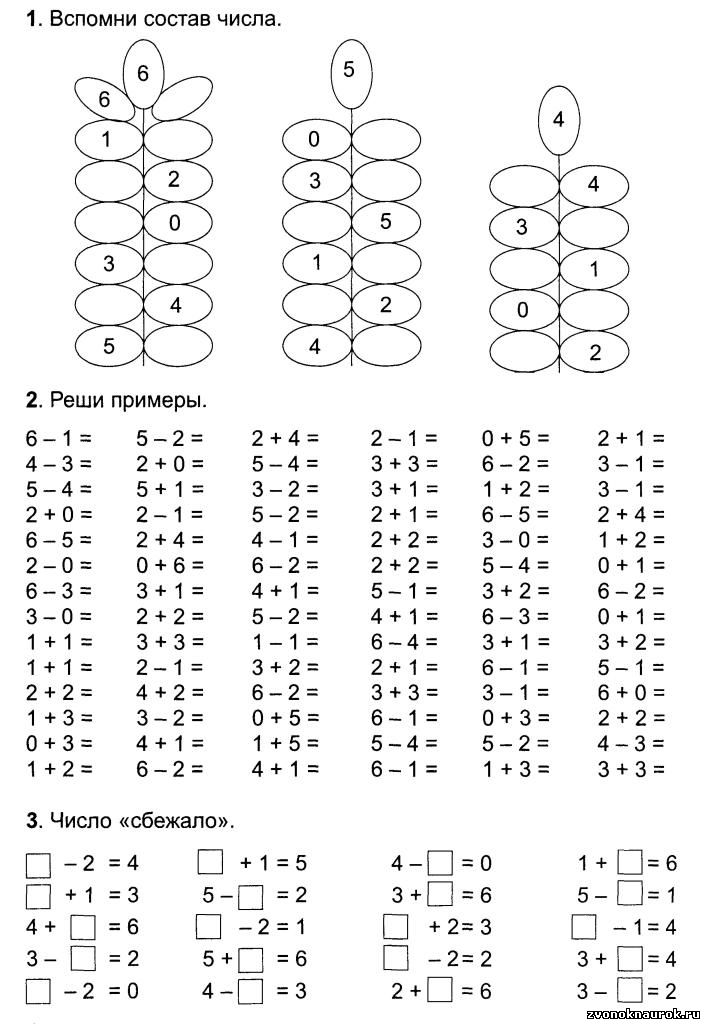 | Сравнение чисел Значение |
| 3. | Что такое номера для заказа? |
| 4. | шагов для сравнения чисел |
| 5. | Символы для сравнения чисел |
| 6. | Сравнение и заказ номеров |
| 7. | Сравнение рациональных чисел |
| 8. | Часто задаваемые вопросы о сравнении чисел |
Что такое сравнение чисел?
Сравнение чисел — это метод сравнения двух или более чисел и определения, является ли одно число равным, меньшим или большим, чем другие числа. Мы используем разные символы для записи сравнения между числами. Мы сравниваем числа в нашей повседневной жизни, например, сравнивая дневную температуру, цены на предметы повседневного обихода, рост, вес и т. д. При сравнении натуральных чисел число с большим количеством цифр больше, чем число с меньшим количеством цифр.
Сравнение значений чисел
Сравнение чисел означает определение числа, которое меньше или больше остальных. Мы можем сравнивать числа, используя различные методы, например, на числовой прямой, путем подсчета или путем подсчета количества цифр, используя разрядные значения чисел и т. д. В нашей повседневной жизни сравнение чисел является обычной практикой, поскольку мы сравниваем числа с аналогичные свойства для определения того, что одно число равно, меньше или больше других чисел.
Мы можем сравнивать числа, используя различные методы, например, на числовой прямой, путем подсчета или путем подсчета количества цифр, используя разрядные значения чисел и т. д. В нашей повседневной жизни сравнение чисел является обычной практикой, поскольку мы сравниваем числа с аналогичные свойства для определения того, что одно число равно, меньше или больше других чисел.
Что такое номера для заказа?
Упорядочивание номеров — это метод их упорядочения — либо от меньшего к большему, либо от большего к меньшему. Когда мы упорядочиваем числа в порядке возрастания, мы упорядочиваем их от меньшего к большему, а когда мы упорядочиваем числа от большего к меньшему, это называется убывающим порядком.
Шаги для сравнения чисел
Чтобы научиться сравнивать числа, давайте пройдем следующие шаги:
- Шаг 1: Сравните количество цифр. Большее количество цифр означает большее число.
- Шаг 2: Если количество цифр одинаковое, сравните старшие разрядные значения.

- Шаг 3: Если цифры совпадают в самом высоком разрядном значении, сравните цифры в следующем разрядном значении справа.
- Шаг 4. Продолжайте сравнивать цифры с одинаковым разрядом до тех пор, пока не найдете цифры, которые отличаются. Тот, у кого выше номинальная стоимость, является большим номером.
Символы для сравнения чисел
Для сравнения чисел мы используем специальные символы для определения большего, меньшего или равного числа. Таких символов три. В приведенной ниже таблице показано значение каждого символа, используемого для сравнения чисел.
| Символ | Значение | Пример |
|---|---|---|
| > | Больше | 5 > 3 |
| < | Менее | 2 < 9 |
| = | равно | 4 = 4 |
Символы меньше и больше выглядят как буква «V», расположенная горизонтально. Простой способ запомнить символы: открытая сторона символа всегда обращена к большему числу, а заостренный конец указывает на меньшее число. Таким образом, если первым идет большее число, то это «больше, чем символ >
Простой способ запомнить символы: открытая сторона символа всегда обращена к большему числу, а заостренный конец указывает на меньшее число. Таким образом, если первым идет большее число, то это «больше, чем символ >
Сравнение и заказ номеров
Теперь, когда мы научились сравнивать числа, мы теперь обсудим, как упорядочивать числа после сравнения. Мы можем расположить числа после их сравнения в порядке возрастания или убывания. Давайте поймем значение двух методов упорядочения:
- Восходящий порядок: расположение данных от наименьшего к наибольшему значению называется возрастающим порядком. Например, 1 < 2 < 3 < 4 < 5,
- Порядок по убыванию: расположение данных от наибольшего к наименьшему значению называется возрастающим порядком. Например, 5 > 4 > 3 > 2 > 1.
Сравнение рациональных чисел
При сравнении рациональных чисел мы берем НОК знаменателей сравниваемых рациональных чисел.
- Все отрицательные рациональные числа меньше 0.
- Все положительные рациональные числа больше 0.
- Все положительные рациональные числа больше всех отрицательных рациональных чисел.
Давайте теперь сравним два рациональных числа, чтобы понять процесс. Сравните 2/3 и 6/7. Во-первых, мы находим НОК знаменателей двух заданных рациональных чисел. НОК(3, 7) = 21. Теперь преобразуйте рациональные числа в подобные рациональные числа.
2/3 = (2 × 7) / (3 × 7) = 14/21
6/7 = (6 × 3) / (7 × 3) = 18/21
Теперь сравним рациональные числа путем сравнения числителей двух одинаковых дробей. Поскольку 18 > 14, значит, 18/21 > 14/21. Следовательно, имеем 6/7 > 2/3.
Важные примечания по сравнению и упорядочению чисел
- Сравнение чисел — это метод сравнения двух или более чисел и определения, является ли одно число равным, меньшим или большим, чем другие числа.

- Мы можем расположить числа в порядке возрастания или убывания.
- Для сравнения чисел используются следующие символы: <, > и =.
☛ Статьи по теме:
- Сравнение десятичных дробей
- Сравнение соотношений
- Сопоставление и сортировка
Часто задаваемые вопросы о сравнении и заказе номеров
Что такое сравнение чисел в математике?
Сравнение чисел — это метод сравнения двух или более чисел и определения, является ли одно число равным, меньшим или большим, чем другие числа.
Каково правило сравнения чисел?
При сравнении натуральных чисел число с большим количеством цифр всегда больше остальных, а число с меньшим количеством цифр всегда наименьшее.
Почему сравнение чисел важно в реальной жизни?
Мы сравниваем числа в повседневной жизни, например, сравнивая дневную температуру, цены на предметы повседневного обихода, рост, вес и т. д. Поэтому важно научиться сравнивать числа.
д. Поэтому важно научиться сравнивать числа.
Что такое сравнение и упорядочивание номеров?
Сравнение и упорядочивание чисел представляет собой концепцию сравнения чисел, а затем их упорядочения в порядке возрастания или убывания.
Как сравнивать целые числа?
Мы можем сравнивать целые числа, используя числовую прямую.
В чем разница между сравнением и заказом номеров?
Сравнение чисел — это просто процесс определения больших и меньших чисел. Упорядочивание номеров включает их сравнение и расположение в порядке возрастания или убывания.
Как сравнивать числа?
Мы можем сравнивать числа, используя различные методы, например, на числовой прямой, путем подсчета или подсчета количества цифр, используя разрядность чисел и т. д.
Сравнение чисел с десятью — 1-й класс сравнив
два числа, мы решаем, является ли число больше , меньше или равно другому числу.
Например:
2 больше 1
3 больше 2
4 больше 3
Также:
1 меньше 2
2 меньше 3
3 меньше 4
и:
5 равно 5
6 равно 6
7 равно 7
Давайте воспользуемся некоторыми объектами для представления чисел, чтобы их было легко сравнивать.
Положим на один рожок 3 шарика мороженого, а на другой рожок 2 шарика мороженого.
Теперь мы можем видеть, что 3 на больше , чем 2 и 2 на меньше , чем 3 !
Проведем еще несколько сравнений.
Положим 1 шарика мороженого на один рожок и 4 шарика мороженого на другой рожок.
Теперь мы можем определенно видеть, что 4 на больше , чем 1 и 1 на меньше , чем 4 !
Мы также можем сравнивать числа, глядя на них на числовой прямой:
Найдите число 8 в числовой строке. Затем найдите число 4 .
Затем найдите число 4 .
Число 8 находится СПРАВА от 4 на числовой прямой.
Это означает, что 8 БОЛЬШЕ, ЧЕМ 4 .
Число 4 находится СЛЕВА от 8 на числовой прямой.
Это означает, что 4 МЕНЬШЕ, ЧЕМ 8 .
Давайте посмотрим на математические символы, которые мы используем для сравнения чисел.
Это:
Если мы хотим сравнить 4 и 3 , это будет выглядеть так:
4 > 3
или
3 Если мы сравниваем два < 4
5
чисел, это будет выглядеть так:4 = 4
Иногда трудно вспомнить, какой символ использовать,
, поэтому представьте символы БОЛЬШЕ и МЕНЬШЕ в виде крокодилов:
Теперь все, что вам нужно запомнить, это то, что крокодил всегда хочет съесть БОЛЬШОЕ число!
Взгляните на эти сравнения. Вы видите, как крокодил жует большее число?
Вы видите, как крокодил жует большее число?
Приготовьтесь к некоторым практическим вопросам по сравнению чисел 1 с 10 !
Практический вопрос 1
Сравним числа 2 и 5 .
2 меньше 5
Верно или неверно?
См. связанные листы:
1 класс
Picture Perfect Puzzle with Penguins
Рабочие листы
Эта головоломка идеально подходит для пингвинов ИЛИ детей! Дети вставят четыре пропущенных числа, связанных с одним числом, а…
1-й класс
Пингвины против волка против медведя
Рабочие листы
Пришло время для небольшого здорового межвидового соревнования! Если число справа самое большое, то пингвин…
1-й класс
Меньше может быть больше
Рабочие листы
У животных в зоопарке чуть менее чем здоровая конкуренция. Пингвины заявили номера…
1-й класс
Величайший перекус Smackdown всех времен
Рабочие листы
Время перекусить в зоопарке! Бегемот, слон и пингвины соревнуются, чтобы заработать дополнительные закуски.
 Организационный момент.
Организационный момент.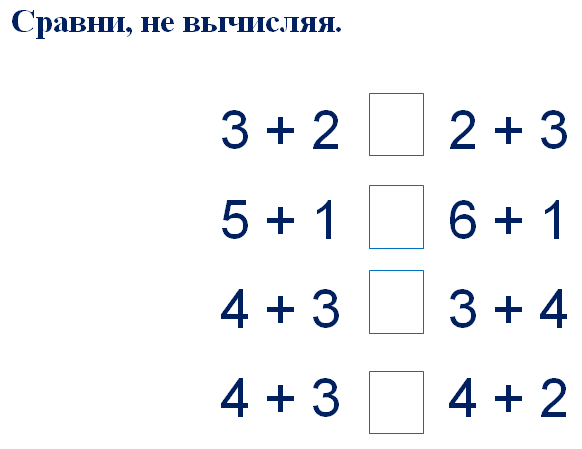
 Работа над новым материалом.
Работа над новым материалом.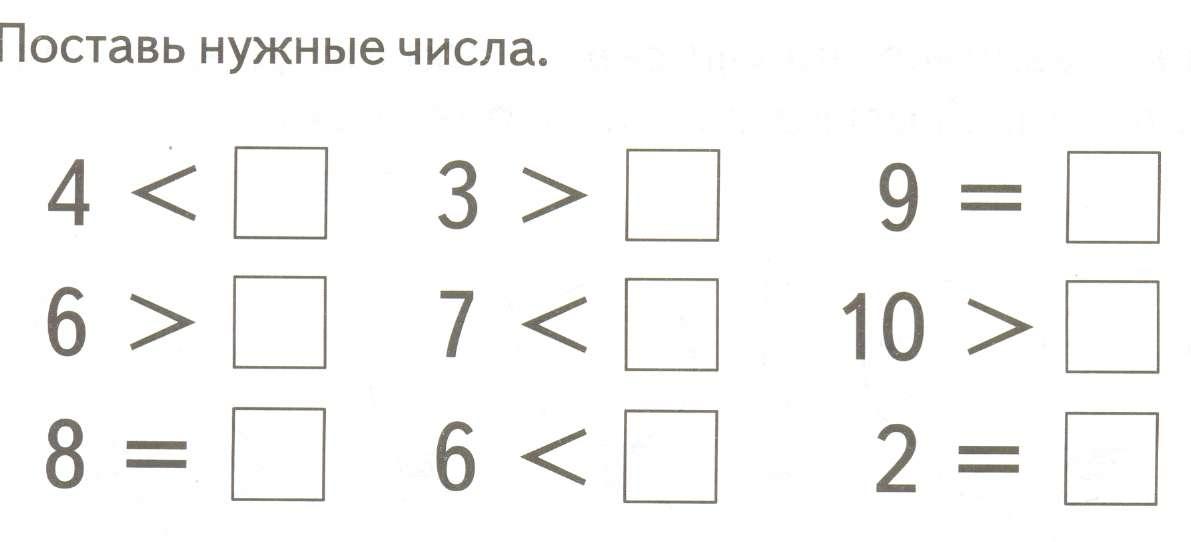
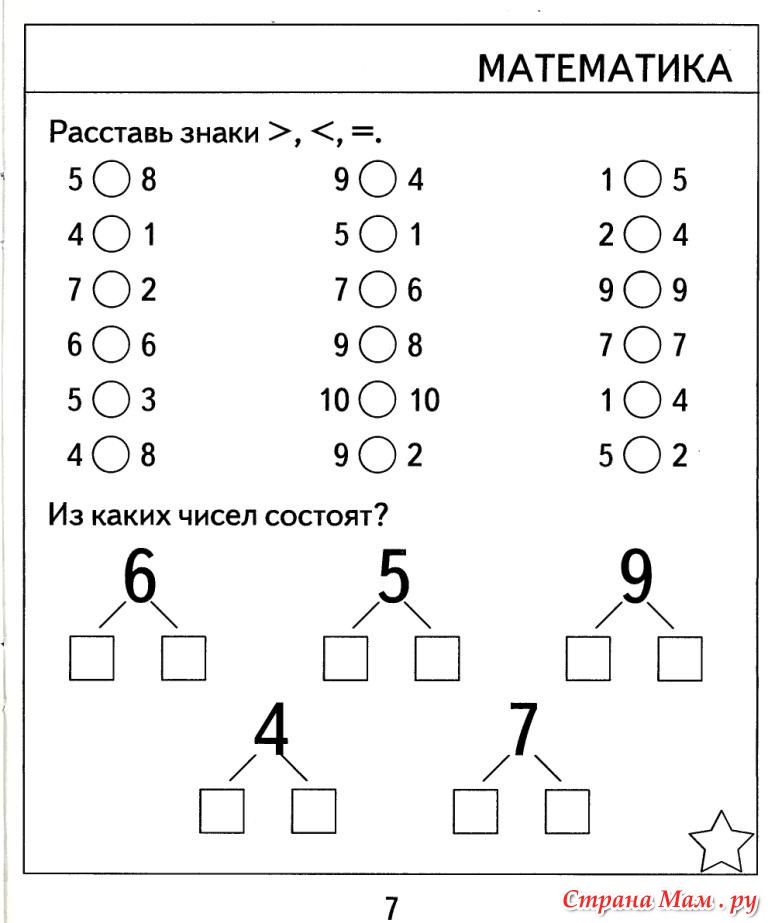
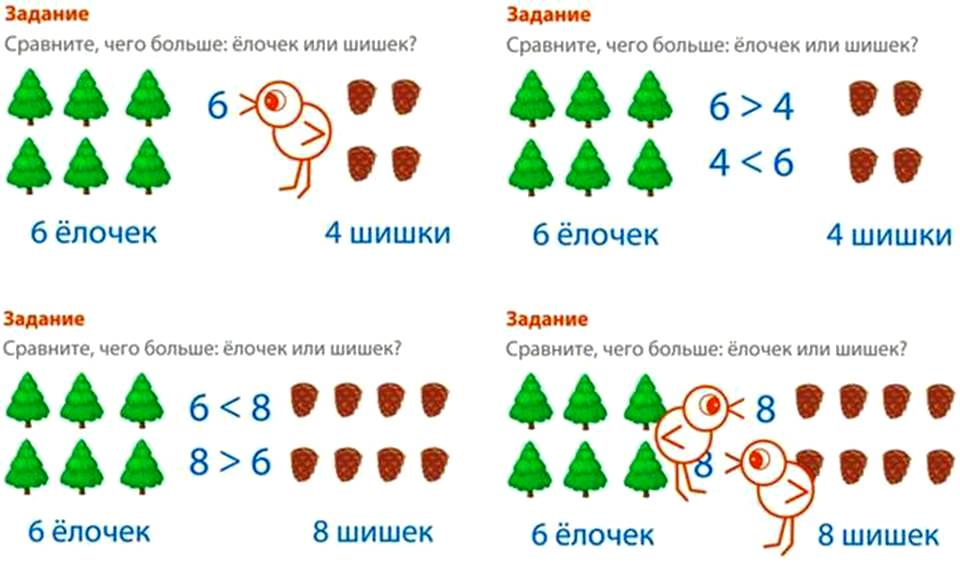 61
61