Числа от 1 до 10. Закрепление. Нумерация чисел от 1 до 10. Сложение и вычитание
Просмотр содержимого документа
«Числа от 1 до 10. Закрепление. Нумерация чисел от 1 до 10. Сложение и вычитание»
Технологическая карта урока
по математике
«Числа от 1 до 10. Закрепление. Нумерация чисел от 1 до 10. Сложение и вычитание»
1 класс
УМК «Школа России»
учитель начальных классов
Зиннурова В.М.
2020-2021 учебный год
Технологическая карта урока
Ф.И.О педагога | Зиннурова Венера Миргалимовна |
Предмет | Математика |
Класс | 1 |
Тема урока | Числа от 1 до 10. |
Тип занятия | Урок закрепления |
Цель занятия | Создать условия для обобщения знаний о числах 1–10. |
Задачи урока | 1.Закрепить знания по нумерации. 2.Развивать вычислительные навыки. 3.Воспитывать интерес к урокам математики. |
Формы организации образовательного пространства на занятии | Индивидуальная, фронтальная |
Средства обучения | Тетрадь, раздаточный материал. |
Этапы урока | Деятельность учителя | Деятельность детей | УУД(универсальные учебные действия) |
I Орг. | Громко прозвенел звонок Начинается урок. К нам сегодня на урок пришли гости. У всех хорошее настроение, все готовы работать! Давайте, вспомним наш девиз: Мы пришли сюда учиться Не лениться, а трудиться Работаем старательно Слушаем внимательно | Самоорганизация. Ученики проверяют свою готовность к уроку. | К(коммуникативные).: -вступать в диалог; -деятельность по решению учебной задачи во внешней речи. Р(регулятивные).: -принимать и сохранять учебную задачу; |
II Сообщение темы урока | Сегодня я приглашаю вас в увлекательное путешествие по стране Математике. Путешествуя по этой стране, мы повторим всё, что уже знаем. На чём же будем путешествовать, мы узнаем отгадав загадку: Железные избушки Прицеплены друг дружке Одна из них с трубой Ведет всех за собой | поезд | К. |
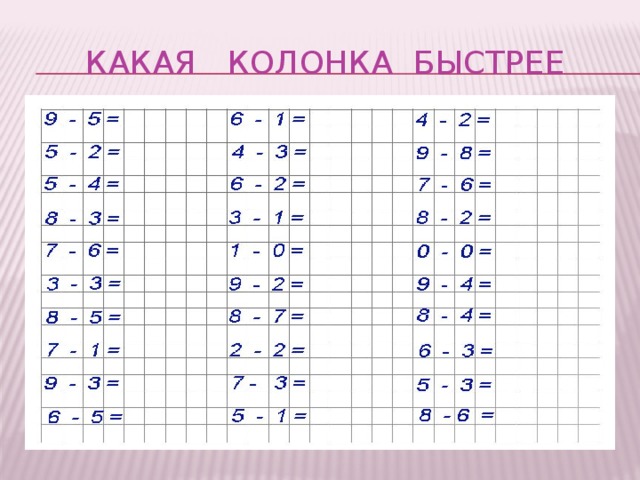
III Устный счёт | А чтобы наш поезд тронулся, мы должны прицепить вагончики, но что бы сделать все правильно нам необходимо повторить счёт. Счёт прямой и обратный 1 ряд — сосчитать от 3 до 8 и обратно. 2 ряд — сосчитать от 5 до 1 и обратно. 3 ряд — сосчитать от 9 до 4 и обратно. — Все вместе считаем от 1 до 10 и обратно. Работа с цифрами. -Какое число предшествует числу 2, 5, 8? -Покажите «соседей» числа 4, 7, 9. Молодцы! Ну, а теперь нам будет просто найти номера вагончиков, решим примеры 2+1 6-5 9-7 А кто из вас расположит их по порядку? А сейчас можно занимать свои места в вагончиках и отправляться в путешествие. | Считают в пределах 10. Ответы детей Решение примеров. Ответы детей. | П(познавательные).: — выполнять классификацию; К.: -слушать и понимать речь других: К.: слушать и понимать речь других; умение с достаточно полнотой и точностью выражать свои мысли. П.: умение ориентироваться в своей системе знаний; овладевать умением поиска и выделения необходимой информации. |
IV Работа над темой урока | На каждой станции нас будет ждать конверт, но взять его мы сможем, если правильно выполним задание. Ну, а открывать конверты будем в конце путешествия, когда все задания будут выполнены. И вот он первый таинственный конверт. Поехали! а).Повторение состава чисел 6 и 7. -А сейчас послушайте загадку: Он мягок, как перина И легок, словно пух Летит, как балерина И все бело вокруг Вот и наша первая станция так и называется «Снегопадная». И снежинки приготовили нам задание на состав чисел 6 и 7: 1 5; 1 6 2 4 ;2 5 3 3 ;3 4 4 2; 4 3 5 1 ;5 2 6 1 Молодцы! Хорошо справились с первым заданием и можем взять конверт. | Зима. Снег Ответы детей Ребята берут конверт М | |
IV Работа над темой урока V Физминутка | б).Решение задач Снежинки покружились, попрощались с нами и улетели, а нам оставили задачи. У маленькой Светы Четыре конфеты. Ещё три дала Алла. Сколько всего стало? Три ромашки — желтоглазки, Два весёлых василька Подарили маме дети. Сколько же цветов в букете? На кустике перед забором Шесть ярко — красных помидоров. Потом четыре оторвалось, А сколько на кусте осталось? — Все задачи решили правильно и можно взять конверт. в).Сравнение чисел. А дальше наша дорога идёт в лес. Прочитайте, как называется наша лесная станция «Угадайкино». Давайте отгадаем загадки о лесных жителях. В птичник повадится — жди беды. Рыжим хвостом заметает следы. Не барашек и не кот, Носит шубу круглый год. Шуба серая — для лета. Для зимы — другого цвета». На овчарку он похож. Что ни зуб — то острый нож! Он бежит, оскалив пасть, На овцу готов напасть. Кто по ёлкам ловко скачет И взлетает на дубы? Кто в дупле орехи прячет, Сушит на зиму грибы? Как можно отгадки назвать одним словом? В какую группу можно объединить этих животных? Отгадали все загадки, получите конверт Ребята, зверята приготовили нам задание. Давайте посмотрим, что же это за задания? •лиса (6*7) •волк (9-1*8) •заяц (10*9) •белка (7+1*7) А кто из вас помнит как называются выражения со знаками » больше» или » меньше»? со знаком » равно»? И с этим заданием справились, возьмём конверт. Ветер дует нам в лицо, Закачалось деревцо. Ветер тише, тише, тише. Деревцо всё выше, выше. е) Повторение геометрического материала. — Все звери разбежались, но оставили на земле свои следы. — Поэтому наша станция и называется — А вот и конверт. ж) Работа в тетради. — Прочитайте название станции: «Тетрадкино». — Вспомним, как правильно пишем цифру 9. Напишите до конца строки по образцу. 5-4 9-3 8+1 3+5 4+4 3-1 10 -2 6+2 — Со всеми заданиями справились, и нас ждёт конверт. Следующая станция Задачкино. Что такое задача? Какие части задачи вы знаете? Слушаем внимательно задачу. Митя поймал 5 рыбок, а Дима- на 3 меньше. Сколько рыб поймал Дима? Сколько всего поймали рыб мальчики? Назовите условие задачи. Что нам известно? Назовите вопрос задачи. Что же нужно найти? Как решим? Справились с заданием, и нас ждет конверт | 7 конфет 5 цветов 2 помидора берут конверт О Ответы детей Лиса Волк Заяц Белка Берут конверт Л Животные Дикие животные \6 9-1=8 109 7+17 неравенство равенство Берут конверт Л Самоорганизация Квадрат, четырех угольник, треугольник,круг. Круг.Нет углов Работа в тетради. Пишут цифру 9. Двое работают у доски, остальные в тетради. Рассказ Условие, вопрос, решение, ответ 5-3=2-Дима 5+2=7-мальчики Схематично нарисовать в тетрадях | К.: вступать в диалог планировать свою деятельность по решению учебной задачи во внешней речи. П.: уметь сравнивать, объясняя выбор для сравнения. К.: слушать и понимать речь других; умение с достаточной полнотой и точностью выражать свои мысли. К.: слушать и понимать речь других уметь с достаточной точностью выражать свои мысли. П.: выполнять классификацию; уметь сравнивать, объясняя выбор критерия для сравнения. выполнять анализ П.: осуществлять анализ учебного материала. К.: устанавливать и соблюдать очередность действий. |
VII Итог урока Рефлексия | А теперь хотите узнать, что находится в конвертах? В каждом конверте лежат буквы. — Давайте прочитаем, что получилось. (МОЛОДЦЫ!) — А теперь сравните себя со смайликами и поднимите руку те, кто считает, что он похож сейчас на улыбающийся красный смайлик, на жёлтый, синий… Со всеми заданиями справились потому, что были внимательны и дружные. | Да Счет от 1 до10. | П.: рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности. Л(личностные).: самооценка на основе критерия успешности; адекватное понимание причин успеха/неуспеха в учебной деятельности. |
Как научить ребенка считать — примеры 1 класс
Счёт – одно из базовых умений, которым должен обладать дошкольник. Научить ребёнка считать несложно, нужно только знать, как правильно организовать учебный процесс. У малышей развивается сначала наглядно-действенное, а затем наглядно-образное мышление, поэтому любые математические операции нужно демонстрировать на практических примерах. Давайте разберёмся, как легко научить ребёнка считать.
Давайте разберёмся, как легко научить ребёнка считать.
Когда начинать учить счёту?
Оптимальный возраст, когда малыша можно начинать обучать счету – это период от 3 до 5 лет. В три годика мышление крохи уже достаточно развито, чтобы освоить этот навык. Некоторых малышей родители учат считать в ещё более раннем возрасте.
Детки, которые ходят в садик, изучают цифры и основы счета именно там. Но если ваш малыш не посещает детский сад, вы можете сами заняться его обучением. Счёт – это один из базовых навыков, которым желательно овладеть до того, как ребёнок пойдёт в школу. Конечно, от первоклассника никто не будет требовать решения сложных математических задач. Но умение складывать и вычитать существенно облегчит школьнику учебный процесс.
Первый шаг, с которого начинается обучение счёту – это знакомство с цифрами. Уже в 1,5–2 годика можно показать крохе цифры и рассказать, как они называются. В этом возрасте малыш еще неспособен сосчитать предметы, даже зная цифры, но он уже понимает разницу между «один» и «много». Для решения это задачи у КУВЫРКОМ есть отличный набор магнитных цифр и знаков.
Для решения это задачи у КУВЫРКОМ есть отличный набор магнитных цифр и знаков.
Начиная с трёх лет кроха может освоить счёт от 1 до 10, используя для этого конкретные осязаемые предметы – конфеты, яблоки, окна в доме или ступеньки лестницы. С 4–5 лет малыш уже способен использовать для счета не предметы, а цифры и считать до 20. А к шести годам он без труда может освоить счёт до 100 (и это не предел), а также обучиться сложению и вычитанию.
Не забывайте, что здесь все индивидуально. Одни детки осваивают устный счёт чуть ли не с пелёнок, а другие до самой школы не могут толком сложить 2 + 2. И, если у вашего малыша пока не получается считать, не расстраивайтесь. Возможно, он ещё маленький и нужно просто немного подождать.
Методы обучения счёту
Способов, как правильно научить ребёнка считать, довольно много. Рассмотрим самые распространённые.
- Счёт на пальцах. Это самый простой и доступный метод, для которого не нужны никакие пособия. Пальцы всегда находятся с малышом, поэтому заниматься можно в любое время и в любом месте, например, во время поездки или стоя в очереди, чтобы скоротать время.
 На пальцах можно научиться считать до десяти. Но крохе сложно запомнить сразу десять цифр, поэтому начинайте с одной руки. Как научите ребёнка считать до 5, можете подключать вторую руку.
На пальцах можно научиться считать до десяти. Но крохе сложно запомнить сразу десять цифр, поэтому начинайте с одной руки. Как научите ребёнка считать до 5, можете подключать вторую руку. - Счётные палочки. Это популярный учебный инструмент, который используют в детском саду, школе, на подготовительных курсах для дошкольников. Такие палочки обычно продаются в канцелярских магазинах и магазинах товаров для школы. Если у вас нет палочек, можно заменить их спичками или зубочистками.
- Счётные карточки. Карточки – это аналог палочек. Вы можете купить набор карточек или изготовить их самостоятельно из картона.
- Методика Монтессори. Научить ребёнка считать методикой Монтессори очень просто. Она похожа на игру в магазин. Вам понадобятся монеты разного достоинства и различные предметы, которые ребёнок будет «покупать».
- Методика Домана. Представляет собой набор карточек с красными точками. На каждой карточке нарисовано определённое количество точек – одна, две, три и т.
 д.
д. - Методика Зайцева. Главная особенность метода в том, чтобы сразу показать крохе числа от 0 до 100. Это нужно для того, чтобы он понял, сколько десятков и единиц входит в каждое число. Для обучения этой методике используется набор специальных карточек с числами.
- Методика Полякова. Этот способ научить ребёнка считать предполагает использование кубиков, специальной коробочки с ячейками для кубиков и набор карточек с цифрами.
Вы можете выбрать любую понравившуюся методику или перепробовать все и остановиться на той, которая больше подойдёт вашему сыну или дочери. Если не хотите покупать учебные пособия и осваивать тонкости разных методик, можно научить считать ребёнка 4–5 лет на пальцах и подручных предметах. А ещё удобно учиться считать через игру. В этом вам могут помочь настолки от КУВЫРКОМ.
Как научить ребёнка считать до 10
Самый простой способ научиться считать до 10 – использовать пальцы. Считать на пальцах можно, даже не зная, как пишутся цифры. Главное, запомнить их название и порядок. Как правило, с эти проблем у малышей не возникает, и они довольно быстро обучаются счету на пальцах. Затем вы можете научить считать ребёнка от 10 до 1 (обратный счёт).
Главное, запомнить их название и порядок. Как правило, с эти проблем у малышей не возникает, и они довольно быстро обучаются счету на пальцах. Затем вы можете научить считать ребёнка от 10 до 1 (обратный счёт).
Чтобы кроха быстрее и легче обучался, делайте следующее:
- Как можно чаще акцентируйте внимание на цифрах. Говорите малышу: «Сейчас тебе три годика, а в следующем году будет четыре», «Я купила пять яблок и три апельсина», «Пора ложиться спать, уже девять часов», «Через два дня к нам в гости придёт бабушка». Ребёнок усвоит, что цифры и числа повсюду присутствуют в повседневной жизни.
- Показывайте картинки, на которых изображены предметы, люди, животные в пределах десяти.
- Постоянно тренируетесь. Предлагайте малышу считать все, что угодно – машины, деревья, игрушки, людей. Заниматься этом можно по дороге в садик, на прогуле, дома.
Купите кубики с цифрами или набор магнитных цифр. Малыш будет с удовольствием играть с ними, параллельно запоминая, как визуально выглядит каждая цифра. Когда он научится уверенно считать до десяти, переходите ко второму десятку.
Когда он научится уверенно считать до десяти, переходите ко второму десятку.
Как научить ребёнка считать до 20
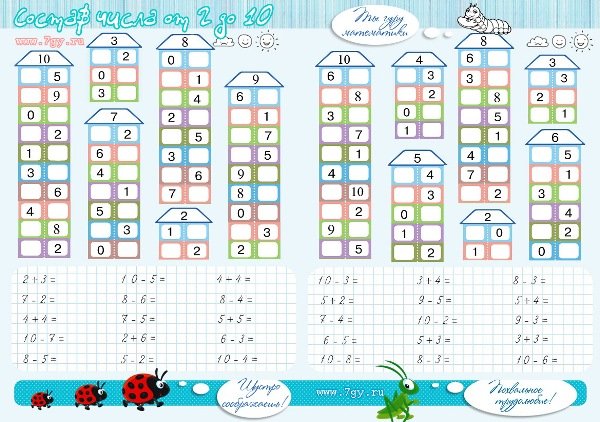
Чтобы научить сына или дочь считать до двадцати, можно задействовать две пары рук – ребёнка и ваши. Для этой цели также подойдут палочки, карточки и любые другие счётные инструменты. Объясните крохе понятие «состав числа». Покажите, как образуются двузначные числа путём добавления одного однозначного числа к другому.
Возьмите 10 счётных палочек или любых других предметов, положите их в ряд. Затем добавьте палочку другого цвета – получится число 11. Таким же образом продемонстрируйте, как получаются числа 12, 13 и т. д. до 20.
Объясните, что слово «дцать» – это устаревшее слово, которое означает «десять». «Один на дцать» – получается 11, «два на дцать» – 12 и т. д. То есть, добавляя число к десятку, получаем новое число и так до того момента, пока не получим «два дцать» – два десятка.
Возьмите двадцать палочек или других предметом для счёта и потренируйтесь на них. Когда малыш научится хорошо считать до 20, можно переходить ко счёту до 30, 40 и т. д. Если он понял, как образуются двузначные числа, трудностей с дальнейшим обучением не возникнет.
Когда малыш научится хорошо считать до 20, можно переходить ко счёту до 30, 40 и т. д. Если он понял, как образуются двузначные числа, трудностей с дальнейшим обучением не возникнет.
Как можно научить ребёнка считать до 100
Если малыш уже умеет уверенно считать до двадцати, можно переходить к счёту до ста. Сначала потренируйтесь в запоминании правильной последовательности десятков чисел: 10, 20, 30, 40 … Когда сын или дочь запомнит последовательность десятков, переходите к добавлению единиц, как описано в примере со счётом до 20.
Не старайтесь выучить сразу все десятки чисел, чтобы не перегружать малыша. Учите по одному десятку в день. Перед тем как взяться за следующий десяток, обязательно повторите предыдущий. Не торопитесь. Переходите к каждому новому десятку чисел только тогда, когда ребёнок твёрдо запомнит предыдущий. В противном случае он запутается и потеряет интерес к обучению. Последовательность и терпение – главные правила обучения.
А ещё у КУВЫРКОМ есть наборы для обучения чтению
Обучение сложению и вычитанию
Во время подготовки к школе полезно не только научить ребёнка быстро считать, но и решать элементарные примеры на сложение и вычитание. Проще всего начать знакомство с базовыми арифметическими действиями с помощью палочек, кубиков или других счётных предметов. Подойдут и пальцы.
Проще всего начать знакомство с базовыми арифметическими действиями с помощью палочек, кубиков или других счётных предметов. Подойдут и пальцы.
Начните учить сына или дочь сложению с самого простого примера: 1+1=2. Возьмите один предмет и добавьте к нему второй. Покажите результат. Теперь прибавьте к первому предмету два, затем три. Пусть кроха сам потренируется, складывая разные числа.
Обязательно расскажите ему о том, что от перемены мест слагаемых сумма не меняется. Пусть он убедится в этом, складывая 3+5 и 5+3, 2+4 и 4+2. После того, как малыш успешно освоит сложение, переходите к вычитанию.
А в этой статье вы можете прочитать про обучение умножению.
Объясните ему, что сложение и вычитание – это взаимосвязанные действия. Покажите эту взаимосвязь на наглядном примере. Возьмите три палочки, добавьте к ней одну – получится четыре. Теперь уберите одну палочку и покажите, что осталось три, как и было вначале. Когда малыш усвоит этот принцип, он легко сможет решать примеры на вычитание.
Чтобы правила лучше запоминались, переводите их в простые, понятные крохе примеры. Например: «У тебя есть три конфеты. Одной ты поделишься с мамой. Сколько у тебя останется?» или «Мама дала тебе два яблока, а папа добавил ещё три. Сколько яблок у тебя стало?». Для большей наглядности можно взять эти конфеты, яблоки, пригласить папу и воспроизвести условия задачи в реальности. Такие занятия вызовут у крохи куда больший интерес, чем скучное заучивание абстрактных чисел.
Игры и весёлые способы, помогающие научить маленького ребёнка считать
Легче всего научить ребёнка считать в игровой форме. В этом вам помогут следующие вспомогательные методы.
Песенки-считалочки
Дети прекрасно воспринимают информацию на слух и легко запоминают песенки и стишки. На Ютубе есть масса весёлых считалочек, помогающих просто научить ребёнка считать. Вы можете включать их крохе, запоминать вместе с ним, а затем напевать в течение дня. С помощью этих забавных песенок можно выучить не только цифры, но и элементарные правила сложения и вычитания.
Сортировка предметов
Купите сыну или дочери сортер – коробочку с прорезями в виде фигур разной формы и набор соответствующих фигурок-вкладышей. Задача малыша – подобрать к каждому отверстию свою фигурку и вставить её туда. Эта развивающая игрушка очень полезна для детей 2–4 лет. С её помощью они учатся различать фигуры по форме и цвету. Процесс сортировки развивает логику и учит основам геометрии. Подойдёт и ещё одна популярная игра — доски Сегена.
Вы можете использовать для этой цели не только сортер, но и подручные предметы. Предложите крохе рассортировать пуговицы по цвету или размеру, ложки и вилки и т. д.
Конструктор Лего
Игры с конструктором превосходно тренируют ум и логическое мышление. Поскольку детали конструктора имеют разную длину и форму, при их сборке малышу приходится размышлять, что к чему присоединить. Пока ребёнок маленький, купите ему универсальный конструктор, состоящий из простых прямоугольных и квадратных блоков. По мере взросления можно покупать тематические наборы, в которых нужно собирать определённую фигуру (машину, корабль, трактор или робота).
Мнемонические карточки
Это вспомогательное пособие помогает научить ребёнка считать быстро и правильно. Купите набор мнемонических карточек, на которых изображены цифры, а рядом – определённые предметы в соответствующем количестве. Например, 1 – одна груша, 2 – два апельсина. Такие карточки создают в детском мозге устойчивую связь между изображением цифры и её фактическим значением.
Хорошо, если карточки будут попадаться на глаза крохе как можно чаще. Есть магнитные модели, которые можно повесить на специальную доску или холодильник. Есть также карточки, оформленные в виде большого плаката, который вешается на стену.
Как понять, что малыш научился хорошо считать?
Математические знания дошкольника можно назвать твёрдыми, если он:
- без запинки перечисляет числа от 1 до 10 (20) и в обратном порядке;
- понимает «соседей» заданного числа: какое из них больше, а какое меньше;
- может сосчитать количество предметов в пределах пяти, лишь мельком взглянув на них;
- умеет считать не только на пальцах и предметах, но и в уме.

Умение считать, как и любой другой навык, совершенствуется путём многочисленных тренировок. Недостаточно просто научить ребёнка считать числа, нужно применять полученные знания на практике. Приучайте малыша считать как можно чаще, чтобы отточить навык до автоматизма.
Здесь вы найдете материалы о том, как научить делению и мотивировать ребёнка к обучению.
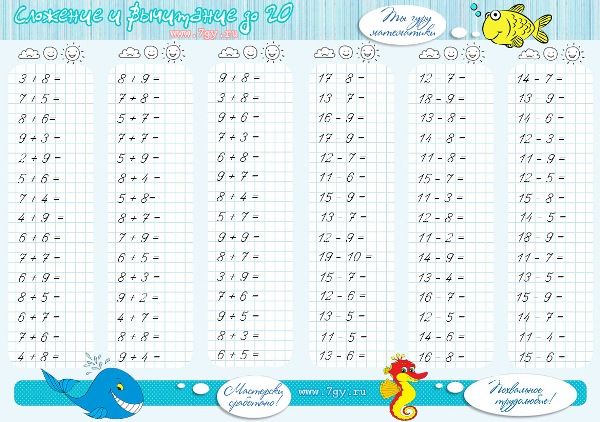
Вычитание от 1 до 200
Главная / Генератор примеров по математике.
Распечатать. Печатается 2 листа. Первый — задания, Второй — задания с ответами.
После решения обязательно проведите проверку !
Задания каждый раз выдаются разные.
Result must be positive numbers.
Задание
Вычитание от 1 до 20015 - 7 = ___
87 - 55 = ___
152 - 130 = ___
193 - 176 = ___
188 - 13 = ___
78 - 41 = ___
41 - 14 = ___
125 - 15 = ___
21 - 19 = ___
181 - 141 = ___
167 - 129 = ___
184 - 62 = ___
184 - 76 = ___
129 - 97 = ___
164 - 28 = ___
42 - 24 = ___
126 - 45 = ___
192 - 78 = ___
200 - 199 = ___
100 - 12 = ___
196 - 2 = ___
96 - 95 = ___
168 - 23 = ___
194 - 70 = ___
193 - 36 = ___
159 - 5 = ___
165 - 65 = ___
150 - 23 = ___
200 - 15 = ___
183 - 104 = ___
56 - 22 = ___
86 - 17 = ___
114 - 110 = ___
134 - 15 = ___
188 - 82 = ___
135 - 121 = ___
200 - 82 = ___
111 - 53 = ___
174 - 49 = ___
177 - 26 = ___
200 - 2 = ___
105 - 75 = ___
106 - 63 = ___
192 - 34 = ___
143 - 46 = ___
123 - 61 = ___
126 - 1 = ___
186 - 179 = ___
152 - 123 = ___
91 - 48 = ___
119 - 5 = ___
168 - 156 = ___
200 - 3 = ___
33 - 20 = ___
188 - 6 = ___
194 - 8 = ___
186 - 1 = ___
127 - 59 = ___
200 - 11 = ___
155 - 26 = ___
171 - 101 = ___
177 - 13 = ___
147 - 81 = ___
156 - 78 = ___
135 - 60 = ___
58 - 25 = ___
168 - 15 = ___
156 - 61 = ___
62 - 50 = ___
184 - 18 = ___
100 - 24 = ___
156 - 39 = ___
155 - 152 = ___
187 - 149 = ___
142 - 85 = ___
119 - 118 = ___
175 - 8 = ___
191 - 1 = ___
133 - 44 = ___
172 - 151 = ___
178 - 65 = ___
195 - 7 = ___
188 - 45 = ___
168 - 8 = ___
196 - 44 = ___
159 - 124 = ___
177 - 8 = ___
180 - 178 = ___
181 - 54 = ___
167 - 115 = ___
32 - 7 = ___
172 - 35 = ___
160 - 127 = ___
89 - 34 = ___
196 - 19 = ___
190 - 103 = ___
143 - 64 = ___
180 - 45 = ___
189 - 138 = ___
144 - 52 = ___
199 - 9 = ___
165 - 118 = ___
139 - 75 = ___
190 - 9 = ___
103 - 20 = ___
131 - 19 = ___
194 - 1 = ___
180 - 65 = ___
191 - 62 = ___
160 - 10 = ___
189 - 41 = ___
63 - 21 = ___
95 - 43 = ___
95 - 3 = ___
178 - 90 = ___
149 - 5 = ___
165 - 12 = ___
167 - 32 = ___
95 - 9 = ___
193 - 48 = ___
Ответы
Вычитание от 1 до 20015 - 7 = 8
87 - 55 = 32
152 - 130 = 22
193 - 176 = 17
188 - 13 = 175
78 - 41 = 37
41 - 14 = 27
125 - 15 = 110
21 - 19 = 2
181 - 141 = 40
167 - 129 = 38
184 - 62 = 122
184 - 76 = 108
129 - 97 = 32
164 - 28 = 136
42 - 24 = 18
126 - 45 = 81
192 - 78 = 114
200 - 199 = 1
100 - 12 = 88
196 - 2 = 194
96 - 95 = 1
168 - 23 = 145
194 - 70 = 124
193 - 36 = 157
159 - 5 = 154
165 - 65 = 100
150 - 23 = 127
200 - 15 = 185
183 - 104 = 79
56 - 22 = 34
86 - 17 = 69
114 - 110 = 4
134 - 15 = 119
188 - 82 = 106
135 - 121 = 14
200 - 82 = 118
111 - 53 = 58
174 - 49 = 125
177 - 26 = 151
200 - 2 = 198
105 - 75 = 30
106 - 63 = 43
192 - 34 = 158
143 - 46 = 97
123 - 61 = 62
126 - 1 = 125
186 - 179 = 7
152 - 123 = 29
91 - 48 = 43
119 - 5 = 114
168 - 156 = 12
200 - 3 = 197
33 - 20 = 13
188 - 6 = 182
194 - 8 = 186
186 - 1 = 185
127 - 59 = 68
200 - 11 = 189
155 - 26 = 129
171 - 101 = 70
177 - 13 = 164
147 - 81 = 66
156 - 78 = 78
135 - 60 = 75
58 - 25 = 33
168 - 15 = 153
156 - 61 = 95
62 - 50 = 12
184 - 18 = 166
100 - 24 = 76
156 - 39 = 117
155 - 152 = 3
187 - 149 = 38
142 - 85 = 57
119 - 118 = 1
175 - 8 = 167
191 - 1 = 190
133 - 44 = 89
172 - 151 = 21
178 - 65 = 113
195 - 7 = 188
188 - 45 = 143
168 - 8 = 160
196 - 44 = 152
159 - 124 = 35
177 - 8 = 169
180 - 178 = 2
181 - 54 = 127
167 - 115 = 52
32 - 7 = 25
172 - 35 = 137
160 - 127 = 33
89 - 34 = 55
196 - 19 = 177
190 - 103 = 87
143 - 64 = 79
180 - 45 = 135
189 - 138 = 51
144 - 52 = 92
199 - 9 = 190
165 - 118 = 47
139 - 75 = 64
190 - 9 = 181
103 - 20 = 83
131 - 19 = 112
194 - 1 = 193
180 - 65 = 115
191 - 62 = 129
160 - 10 = 150
189 - 41 = 148
63 - 21 = 42
95 - 43 = 52
95 - 3 = 92
178 - 90 = 88
149 - 5 = 144
165 - 12 = 153
167 - 32 = 135
95 - 9 = 86
193 - 48 = 145
Перейти, разделить или сделать к следующим 10: стратегии преподавания математики изменились с тех пор, как родители учились в школе
Исследования показывают, что родители оказывают значительное влияние на обучение своих детей, но некоторым не хватает уверенности, чтобы оказывать поддержку дома. Чтобы помочь родителям вовлечь своих детей в изучение математики, программа The Conversation попросила старшего научного сотрудника ACER Кэт Пирн объяснить три стратегии сложения и вычитания, которым теперь обучают в начальной школе.
Чтобы помочь родителям вовлечь своих детей в изучение математики, программа The Conversation попросила старшего научного сотрудника ACER Кэт Пирн объяснить три стратегии сложения и вычитания, которым теперь обучают в начальной школе.
Я уверен, что большинство людей помнят попытки освоить определенное математическое правило или процедуру в начальной или средней школе.
У моей пожилой матери есть история о том, как ее отец помогал ей с домашним заданием по арифметике. Она помнит, как расстроилась из-за того, что ее отец поступил не так, как в школе. Я подозреваю, что ее отец был в состоянии произвести вычисления в уме, а не школьным способом, который заключался в использовании вертикального алгоритма.
CC BY-NDОжидается, что учащиеся сначала будут складывать числа в колонке единиц (справа), а затем в колонке десятков (слева). Задача усложняется, когда сумма столбца единиц превышает 10 — тогда вам нужно «обменять» десять единиц на одну десятку.
Учащиеся, которые дают ответ как 713, а не правильный ответ как 83, возможно, начали сначала со столбца десятков. Или они могли написать 13 в колонке единиц вместо того, чтобы обменивать десять единиц на одну десятку.
Или они могли написать 13 в колонке единиц вместо того, чтобы обменивать десять единиц на одну десятку.
Формальные школьные алгоритмы по-прежнему используются для больших чисел и десятичных знаков, но мы рекомендуем учащимся использовать любую стратегию, которую они предпочитают для сложения двузначных чисел.
Проблема с преподаванием правил заключается в том, что многие ученики с трудом запоминают, когда применять правило, потому что они не понимают, как и почему оно работает.
В австралийской учебной программе: математика говорится, что к концу 2-го года учащиеся будут «выполнять простые вычисления на сложение и вычитание, используя ряд стратегий». К концу 4 года они будут «определять и объяснять стратегии нахождения неизвестных величин в числовых предложениях».
Мы хотим, чтобы дети помнили, как решать эти уравнения в уме, а не полагались на запись процесса. Вот три стратегии, которые школы используют, чтобы научить детей складывать и вычитать двузначные числа.
1. Стратегия разделения
Эту стратегию иногда называют стратегией разложения, разделения или частичной суммы.
Вы можете прибавлять или вычитать десятки отдельно от единиц (или единиц). Например, используя стратегию разделения, чтобы добавить 46 + 23, вы должны:
разделить каждое число (разложить) на десятки и единицы: 46 + 23 = 40 + 6 + 20 + 3
переставить десятки и единицы: 40 + 20 + 6 + 3
добавить десятки, а затем единицы 60 + 9= 69
Использование стратегии разделения для сложения, например 37 + 65, будет аналогичным, но будет дополнительный шаг:
разделить или разложить числа на десятки и единицы: 30 + 7 + 60 + 5
переставить десятки и единицы: 30 + 60 + 7 + 5
добавить десятки, а затем единицы: 90 + 12
разделить 12 (10 + 2), чтобы получить: 90 + 10 + 2 = 100 + 2 = 102
Многие учащиеся считают стратегию разделения более сложной для вычитания, чем для сложения. Это потому, что есть больше шагов, если выполнять эту стратегию в уме.
Это потому, что есть больше шагов, если выполнять эту стратегию в уме.
Для вычитания, например 69-46, вы должны:
разделить или разложить каждое число на десятки и единицы: 60 + 9 – (40 + 6)
снять скобу: 60 + 9 – 40 – 6
переставить десятки и единицы: (60 – 40) + (9 – 6)
вычесть десятки, затем единицы: 20 + 3 = 23
Студенты часто делают ошибки на третьем шаге. Успешные студенты могут сказать: «Я беру 40 из 60, затем 6 из 9». Неуспевающие студенты скажут: «Я отнимаю 40 от 60, затем добавляю 6 и 9».
Учащиеся, успешно использующие эту стратегию, показывают, что они понимают значение разряда (значение каждой цифры в числе) и знают математические правила, необходимые для алгебры.
2. Стратегия перехода
Эту стратегию иногда называют последовательностью или накопительной стратегией суммирования. Реальные предпринятые шаги зависят от уверенности и способностей учащихся.
Некоторые учащиеся добавляют десятки или единицы, в то время как другие добавляют или вычитают десятки, а затем единицы.
Например, сложение 46 + 23 с использованием стратегии прыжка может выглядеть так:
или
Две версии этой стратегии могут быть показаны с помощью пустой числовой строки. Использование пустой или пустой числовой строки позволяет учащимся записывать свои мысли, а учителям анализировать свои мысли и определять стратегию, которую они пытались использовать.
CC BY-NDВычитание 69–46 со стратегией прыжка может быть выполнено с помощью:
или
CC BY-ND3. Стратегия «Дойти до следующих десяти»
Эту стратегию иногда называют компенсационной или сокращенной стратегией. Он включает в себя корректировку одного числа, чтобы упростить решение задачи.
Стратегия «Попасть в следующую десятку» основана на стратегии «Друзья десяти».
Многие учащиеся первых классов начальной школы составляют все комбинации из двух однозначных чисел, которые в сумме дают десять.
9 + 1, 8 + 2, 7 + 3, 6 + 4, 5 + 5 …
Их иногда называют радужными фактами, поскольку дети создают радугу, соединяя два числа вместе. Например, 9 может быть на одном конце цвета радуги, а 1 — на другом.
Объединяя числа таким образом, учителя надеются, что учащиеся поймут, что ответ для 9 + 1 такой же, как 1 + 9.
заданное число (например, следующее кратное десяти), а затем скорректировать число, вычитая то, что было добавлено, или добавляя то, что было вычтено.
На диаграммах отношения обозначены стрелками.
CC BY-NDТаким образом, чтобы добавить 37 + 65, вы должны
прибавьте 3 к 37, чтобы получить 40.
вычесть 3 из 65, чтобы получить 62
получается: 40 + 62 = 102.
Если вычесть 102 – 65, получится:
вычесть 2 из 102, чтобы получить 100
вычесть 2 из 65, чтобы сохранить баланс
это становится 100 — 63 = 37.

Многие учащиеся, использующие эту стратегию, неправильно прибавляют 2 к 65 вместо вычитания 2.
Почему эти стратегии?
Студенты использовали все эти стратегии или некоторые их формы в своей голове на протяжении поколений. Но в течение многих лет ожидалось, что учащиеся будут использовать формальный письменный алгоритм, а не свои собственные мыслительные стратегии.
Введение пустой или пустой числовой строки позволило учащимся записывать свои мыслительные стратегии, что позволяло учителям и родителям их видеть. Именование этих стратегий позволило учителям и учащимся обсудить возможные стратегии, используя общий словарь.
Вместо того, чтобы учить правилам и процедурам, теперь нам нужно поощрять учащихся объяснять свои стратегии, используя как конкретные материалы, так и диаграммы, чтобы продемонстрировать свои знания о сложении и вычитании. ■
Дополнительная информация:
Эта статья Кэт Пирн, старшего научного сотрудника, Австралийского совета по исследованиям в области образования, , переиздана из The Conversation под лицензией Creative Commons. Прочитайте оригинальную статью.
Прочитайте оригинальную статью.
Сложение и вычитание двоичных чисел
Подготовьте ответы на приведенные ниже вопросы и заполните клеточки. Нажми на кнопку, чтобы узнать, правильно ли вы ответили. Если ты прав то появится, и вы должны перейти к следующему вопросу. Если появляется, то ваш ответ неверен. Нажмите на чтобы очистить свой первоначальный ответ и попробовать еще раз. Если вы не можете найти правильный ответ, нажмите на чтобы увидеть ответ.
Вопрос 1Вычислить двоичные числа:
| (a) | 11 + 1 | |
| (b) | 11 + 11 | |
| (c) | 111 + 11 | |
| (d) | 111 + 10 | |
| (e) | 1110 + 111 | |
| (f) | 1100 + 110 | |
| (g) | 1111 + 10101 | |
| (h) | 1100 + 11001 | |
| (i) | 1011 + 1101 | |
| (j) | 1110 + 10111 | |
| (k) | 1110 + 1111 | |
| (l) | 11111 + 11101 |
Вычислить двоичные числа:
| (a) | 11 – 10 | |
| (b) | 110 – 10 | |
| (c) | 1111 – 110 | |
| (d) | 100 – 10 | |
| (e) | 100 – 11 | |
| (f) | 1000 – 11 | |
| (g) | 1101 – 110 | |
| (h) | 11011 – 110 | |
| (i) | 1111 – 111 | |
| (j) | 110101 – 1010 | |
| (k) | 11011 – 111 | |
| (л) | 11110 – 111 |
Вычислить двоичные числа:
| (a) | 11 + 11 | |
| (b) | 111 + 111 | |
| (c) | 1111 + 1111 | |
| (d) | 11111 + 11111 |
| Каким будет следующее число, которое будет соответствовать этому шаблону? |
Вычислить двоичные числа:
| (a) | 10 + 10 | |
| (b) | 100 + 100 | |
| (c) | 1000 + 1000 | |
| (d) | 10000 + 10000 |
| Какое следующее число продолжит ваш двоичный код? |
Решите следующие уравнения, где все числа, включая x , являются двоичными:
| (a) | x + 11 = 1101 | x = | |
| (b) | x – 10 = 101 | x = | |
| (c) | x – 1101 = 11011 | x = | |
| (d) | x + 1110 = 10001 | x = | |
| (e) | x + 111 = 11110 | x = | |
| (f) | x – 1001 = 11101 | х = |
Вычислить двоичные числа:
| (а) | 10 – 1 | |
| (б) | 100 – 1 | |
| (c) | 1000 – 1 | |
| (d) | 10000 – 1 |
| Каким будет следующее число, которое будет соответствовать этому шаблону? |
Четырехзначное двоичное число имеет 2 нуля и 2 единицы.
| (a) Преобразуйте двоичные числа 11101 и 1110 в основание 10. |
| и |
| (b) Сложите два числа с основанием 10. |
| (c) Сложите два двоичных числа. |
| (d) Преобразуйте свой ответ в основание 10 и сравните с вашим ответом на (b). |
Двоичное число состоит из 8 цифр и должно быть преобразовано в основание 10.
| (a) Преобразуйте двоичные числа 11101 и 10111 в систему с основанием 10. |
| и |
| (b) Вычислите разницу между двумя числами с основанием 10. |
| (c) Преобразуйте свой ответ на (b) в двоичное число. |
| (d) Вычислите разницу между двумя двоичными числами и сравните ее со своим ответом на вопрос (c). |
Вот 3 двоичных числа:
| 1110101 | 1011110 | 1010011 |
| Работа в двоичном формате, | |
| (а) сложите вместе два меньших числа, | |
| (b) сложите два больших числа, | |
| (c) отнять наименьшее число от наибольшего, | |
(d) сложите все три числа. |
Вычислить двоичные числа:
| (а) 111+101+100 | |
| (б) 11101+10011+110111 |
Просмотреть дополнение в 10 образовательных ресурсах
Вся библиотекаРабочие листы для печатиИгрыУроки с гидомПланы уроковПрактические занятияИнтерактивные историиОнлайн-упражненияРабочие тетради для печатиНаучные проектыВидео с песнями
497 filtered results
497 filtered results
Addition Within 10
Sort byPopularityMost RecentTitleRelevance
-
Filter Results
- clear all filters
By Grade
- Preschool
- Детский сад
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7th grade
- 8th grade
By Subject
- Coding
- Fine arts
- Foreign language
Math
- Number Sense
Дополнение
- Стратегии добавления
Факты с добавлением
- Дополнение в пределах 5
- .
 0487 Addition Within 10
0487 Addition Within 10- .
- Addition Within 20
- Addition Within 100
- Multi-Digit Addition
- Addition and Missing Addends
- Subtraction
- Multiplication
- Деление
- Смешанные операции
- Дроби
- Десятичные дроби
- 8 процентов, 904 проценты0032
- Algebra
- Geometry
- Measurement
- Time
- Money Math
- Data and Graphing
- Math Word Problems
- Math Головоломки
- Чтение и письмо
- Наука
- Социально-эмоциональное
- 7 20 90 90 90 8 Typing
By Topic
- Arts & crafts
- Coloring
- Holidays
- Offline games
- Pop Culture & Events
- Сезонные
по стандарту
- Common Core
Дополнение 1
7. 0005
0005
Дополнение 1
Умение складывать однозначные числа является основным элементом школьной программы по математике. Вы можете повысить беглость сложения с помощью этого урока с пошаговым руководством, который поможет детсадовцам понять ценности. Дети узнают с целенаправленной инструкцией и попрактикуются в том, что, складывая числа, они получают новое число. По окончании урока дети могут продолжить практиковать сложение с помощью прилагаемых рабочих листов.
Детский сад
Математика
Урок с гидом
Дополнение 2
Урок Урок
Дополнение 2
Гибкость и плавность с добавлением является важной часть получить уверенность с этим навыком. Этот урок, кроме того, предлагает управляемую практику, направленную на улучшение умственной математики и беглости с помощью сложения. Когда ваш ребенок закончит этот урок, вы сможете продолжить сложение, загрузив и распечатав прилагаемые листы сложения.
1 -й класс
MATH
Урок с гидом
Номера зданий
Уровень. мокрый от подсчета и чисел. Эти управляемые упражнения могут дать детям более глубокое понимание смысла чисел, числового порядка и значений. Дошкольники начнут связывать значения с числами и понимать понятия больше и меньше, опираясь на навыки, которые им понадобятся в более поздних классах.
Детский сад
Математика
Урок с подсказкой
Дополнение к 10 образовательным ресурсам Эти рабочие листы и задания на сложение однозначных чисел учат ваших учеников стратегиям сложения чисел до 10 и дают много практики сложения в пределах 10. Есть даже песни и рассказы, которые помогут научить сложению однозначных чисел. Продолжайте бросать вызов своему вундеркинду с нашим дополнением в пределах 20 ресурсов.
Как только ваш ученик поймет, как считать до десяти и что числа представляют количество, пора познакомить его с понятиями сложения. В самом простом случае сложение состоит в том, чтобы взять два отдельных количества и сложить их вместе, создав новое, большее количество.
В самом простом случае сложение состоит в том, чтобы взять два отдельных количества и сложить их вместе, создав новое, большее количество.
Когда ваш ученик впервые знакомится со сложением в пределах 10, важно закрепить понятие количества. Чем больше способов они узнают об этом, тем лучше они поймут, что числа и арифметические операции представляют количества вещей и то, как эти количества изменяются.
- Представление количества в различных формах. Это могут быть пальцы, предметы, звуки вроде хлопков или щелчков или нарисованные изображения.
- Возьмите десять предметов и разделите их на две группы. Например, разделите десять блоков на одну группу из шести блоков и одну группу из четырех блоков.
- Для каждого числа от 1 до 10 определите, какое число нужно прибавить к нему, чтобы получить 10. Понимание этого поможет учащимся быстро решать задачи на сложение двух и трех цифр в будущем. Например, 1+ 9= 10.
Это также когда вы познакомите своего ученика с основными математическими символами, такими как сложение или знак плюс (+) и знак равенства (=), а также с двумя различными формами, которые может принимать уравнение:
1 + 1 = 2
или
1
+1
2
Как и в случае любого математического навыка, повторение является ключом к запоминанию информации.
 Закрепление изученного материала
Закрепление изученного материала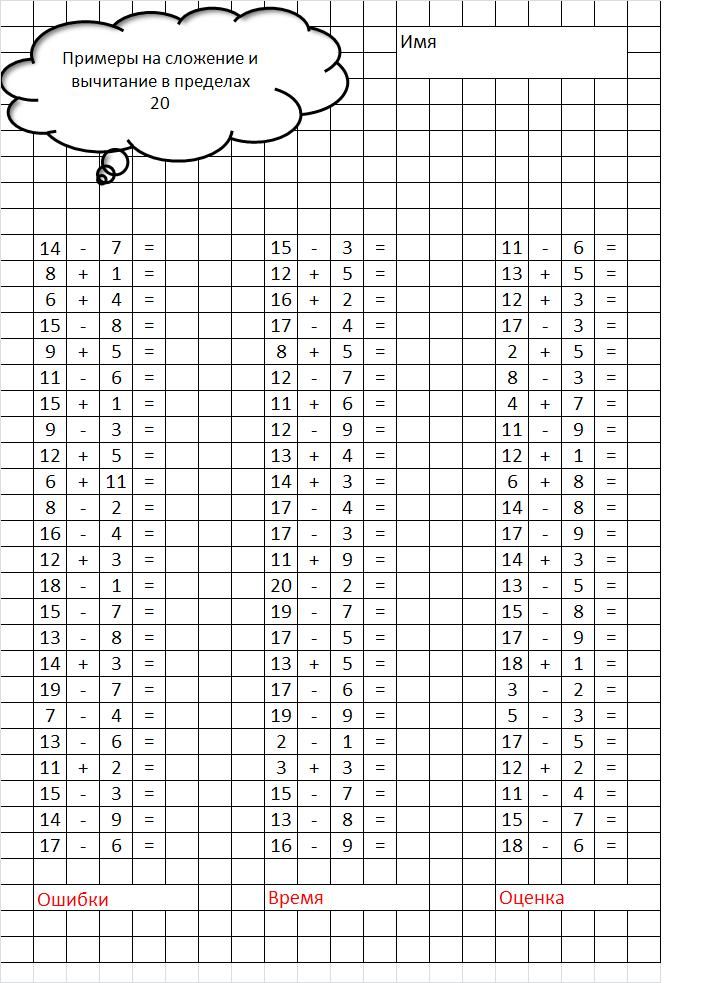 момент
момент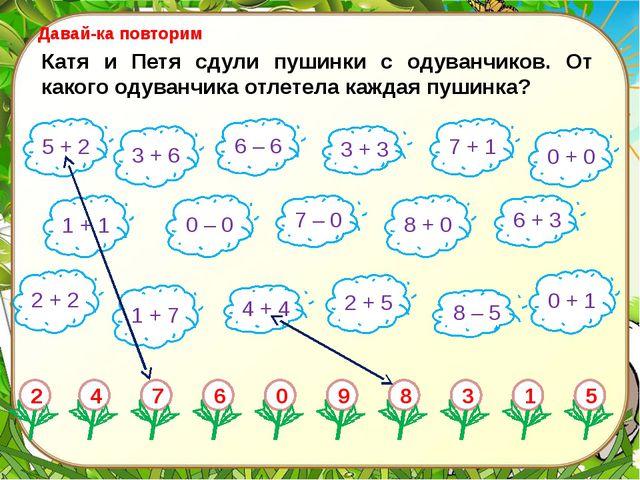 : слушать и понимать речь других
: слушать и понимать речь других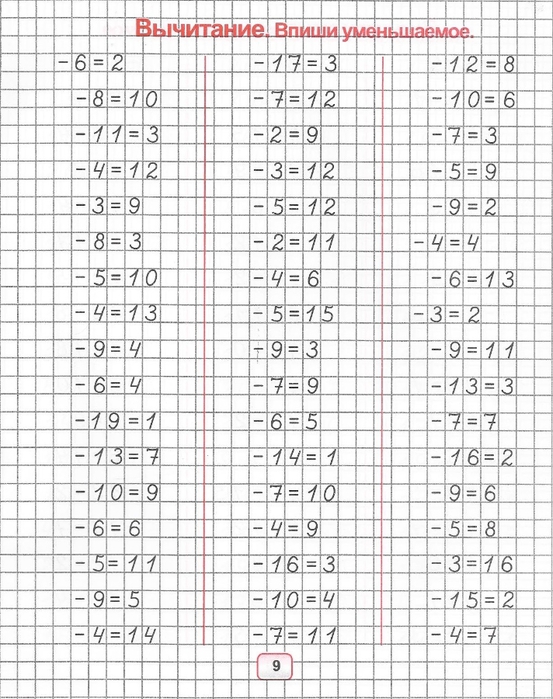



 Один из ребят собирает слово.
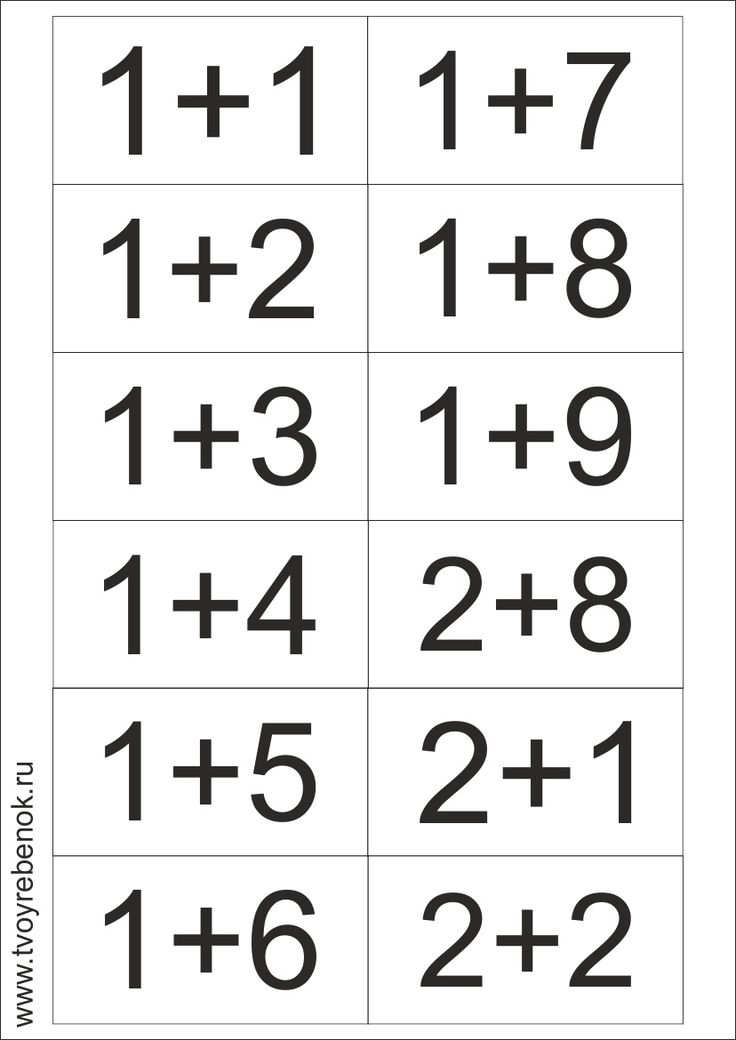
Один из ребят собирает слово. На пальцах можно научиться считать до десяти. Но крохе сложно запомнить сразу десять цифр, поэтому начинайте с одной руки. Как научите ребёнка считать до 5, можете подключать вторую руку.
На пальцах можно научиться считать до десяти. Но крохе сложно запомнить сразу десять цифр, поэтому начинайте с одной руки. Как научите ребёнка считать до 5, можете подключать вторую руку.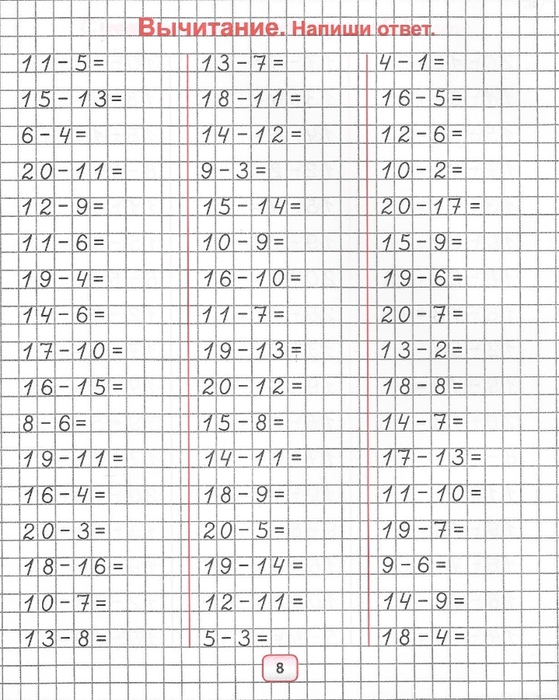 д.
д.

 0487 Addition Within 10
0487 Addition Within 10