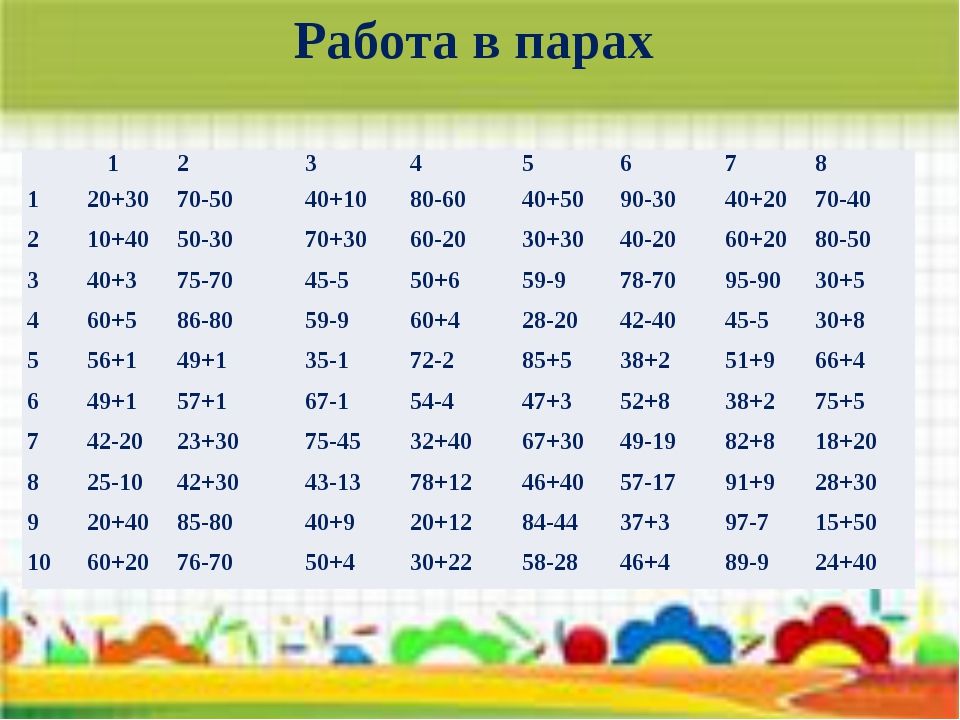
Примеры онлайн на сложение и вычитание двузначных и однозначных чисел
Примеры онлайн на сложение и вычитание двузначных и однозначных чиселПримерОнлайн.ru
Генератор примеров по математике 1-3 класс
Онлайн примеры на сложение однозначных и двузначных чисел позволяют выбрать положение двузначных и однозначных чисел – для тренировки перехода через десяток в разных десятках, или сложение любых двузначных чисел. Пока результат всех примеров не будет превышать 100.
Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.
| Настройка генератора примеров |
|---|
|
|
|
Образец примеров
66 — 39
31 + 29
9 — 7
63 — 14
47 — 32
8 + 17
90 — 67
29 + 23
73 — 54
53 — 28
98 — 71
50 + 31
6 + 65
33 + 33
80 + 18
74 — 49
82 — 61
9 + 66
55 + 32
80 — 20
39 — 3
11 + 23
9 + 29
59 — 15
87 + 6
12 + 79
76 — 29
37 — 5
50 — 2
65 — 6
25 + 11
40 + 1
69 — 17
19 + 54
19 + 15
68 — 20
96 — 41
39 + 46
46 + 4
60 — 52
4 + 87
42 — 18
11 + 31
87 — 69
49 + 33
46 + 14
83 — 28
39 — 25
5 + 86
27 — 12
90 — 36
85 — 38
62 — 49
93 — 40
36 + 40
9 — 4
66 + 1
22 + 20
80 — 34
13 + 20
31 + 12
8 + 25
87 — 44
37 + 9
47 + 43
37 + 40
28 + 36
94 — 23
86 — 78
7 + 20
25 + 68
48 + 22
19 — 4
72 — 54
22 + 2
32 — 6
56 + 29
65 — 38
39 + 7
34 — 5
11 + 82
27 + 26
37 — 22
69 — 29
8 + 77
73 — 37
39 + 21
78 — 57
21 + 30
83 — 63
28 + 48
19 — 15
2 + 22
64 — 33
97 — 73
12 + 17
75 — 67
28 — 10
71 — 61
16 — 6
69 — 65
22 — 17
95 — 5
48 + 38
51 — 19
66 — 29
75 — 62
13 + 57
98 — 68
27 + 30
29 + 70
19 + 36
7 + 4
77 — 62
66 — 28
89 — 54
81 — 24
58 — 50
19 + 71
90 — 40
96 — 3
45 — 5
35 + 59
64 + 11
24 + 26
49 — 49
73 — 30
58 — 41
49 — 1
35 + 57
35 — 22
9 + 64
85 — 41
98 — 29
49 + 25
99 — 89
89 — 72
8 + 74
71 — 9
55 — 24
51 + 43
33 + 26
28 + 52
9 + 8
29 + 18
7 + 58
86 — 46
23 + 2
51 — 16
89 — 80
60 — 27
8 — 1
28 + 64
10 + 26
2 + 34
29 + 53
36 + 50
20 + 15
40 — 26
58 + 13
11 + 2
6 + 85
80 — 58
98 — 38
38 + 34
57 + 29
7 + 10
86 — 69
3 + 70
81 — 16
84 — 11
46 + 17
93 — 36
57 — 41
78 — 43
11 — 2
86 + 8
15 + 7
38 + 28
95 — 42
53 — 39
72 — 65
40 + 43
95 — 65
81 — 46
85 — 50
20 + 38
30 + 7
16 + 64
59 — 48
35 + 52
15 + 22
27 — 24
93 — 29
79 — 10
10 — 8
20 + 2
56 + 3
56 — 6
98 — 17
22 + 55
80 — 75
78 + 12
34 + 4
34 + 21
11 — 11
49 — 10
83 — 79
55 + 43
49 — 36
90 — 48
42 + 20
50 — 36
42 + 41
5 + 9
78 — 61
92 — 15
62 — 35
46 — 11
31 + 6
39 — 18
76 — 64
10 + 44
93 + 3
2 + 45
70 + 19
63 — 54
73 — 66
33 + 10
27 + 64
94 — 53
46 — 29
71 + 28
89 — 30
92 — 63
16 — 8
28 + 40
61 — 40
78 — 46
35 + 6
57 + 15
75 — 21
76 — 69
51 + 31
81 — 63
64 — 61
1 + 39
94 — 11
43 + 25
7 + 29
66 — 48
84 — 32
81 — 51
98 — 76
1 + 90
6 + 82
52 — 32
53 + 46
4 + 70
22 + 28
85 — 55
44 + 55
23 — 1
59 — 57
24 + 46
64 — 61
4 + 75
24 + 24
28 + 22
22 + 3
7 — 5
55 — 34
98 — 82
97 — 13
53 + 41
52 — 43
29 + 35
99 — 3
71 — 35
92 — 71
2 + 86
10 + 63
37 + 58
1 + 17
39 — 11
43 + 436 — 6
89 — 25
38 — 6
10 + 59
61 — 36
71 + 5
31 + 21
65 — 24
16 + 65
71 — 25
45 — 1
16 + 78
57 — 15
82 — 17
39 + 39
9 + 78
22 + 59
64 + 7
51 + 19
19 + 47
30 — 14
7 + 66
89 — 9
45 + 33
81 — 50
73 — 16
57 + 25
34 + 16
72 — 31
98 — 86
48 — 19
29 — 18
64 — 12
76 — 47
78 — 74
6 + 27
49 — 5
81 — 34
96 — 4
86 — 14
42 — 27
57 + 5
64 — 7
22 + 61
24 + 47
92 — 41
66 — 44
58 — 12
81 — 15
10 + 79
96 — 37
19 + 69
76 + 21
10 + 34
26 — 25
68 — 3
99 — 64
88 — 79
77 — 29
74 — 51
64 — 12
94 — 68
18 + 33
88 — 83
3 + 95
76 — 13
90 — 25
91 — 71
11 + 72
49 + 47
29 + 2
96 — 36
62 + 1
7 + 84
81 — 73
71 — 30
85 + 2
18 + 39
32 + 37
83 — 21
46 + 41
34 + 41
30 + 64
79 — 60
40 — 3
71 — 56
17 + 30
30 + 41
3 + 33
94 + 2
14 + 4
84 — 37
59 — 58
37 — 18
12 — 9
17 — 17
72 + 4
53 — 45
12 + 12
72 + 27
73 — 63
94 — 15
95 — 23
27 — 20
54 — 46
83 — 26
95 — 78
56 + 32
24 + 10
37 — 31
58 + 26
17 + 43
10 + 52
62 — 62
57 — 51
32 + 67
42 + 57
65 — 1
96 — 93
64 + 34
13 + 59
52 — 3
76 + 20
61 — 59
73 + 22
67 + 32
97 — 43
21 + 55
41 — 40
5 + 24
69 — 59
26 — 12
31 + 7
95 + 1
16 — 16
88 — 42
20 + 58
67 — 59
71 — 62
27 — 20
94 — 2
46 — 4
95 — 95
68 + 27
41 + 23
1 + 73
38 + 32
16 + 61
51 — 30
1 + 68
35 — 26
63 — 42
63 + 30
42 + 34
10 + 59
35 — 10
58 + 10
69 — 8
86 — 38
1 + 60
49 + 19
79 + 8
45 + 25
56 — 55
24 + 39
29 + 18
85 — 79
48 + 33
99 — 14
65 — 25
79 — 35
62 — 9
3 + 16
88 — 21
96 — 56
52 — 33
30 + 47
51 + 9
57 + 16
23 + 7
39 + 36
17 + 40
39 — 4
90 — 39
66 — 53
3 — 1
26 — 18
45 — 44
35 + 63
25 + 61
92 — 1
58 — 20
21 + 77
6 + 56
46 + 1
75 — 61
90 — 23
89 — 43
34 — 28
58 + 41
78 — 41
68 — 23
84 — 24
38 — 33
95 — 10
10 — 4
74 — 70
31 + 19
74 — 42
64 — 1
38 — 12
Легко и просто учим первоклашку складывать и вычитать двузначные числа
Я уже столько гневных слов написала про учебник Петерсон по математике для 1 класса.
И продолжу утверждать, что он – зло во плоти, уродующее мозги малышей.
Но, справедливости ради, должна рассказать вам про одну вещь, которая подаётся в этом учебнике малышам очень классно: сложение двузначных чисел друг с другом.
Точнее – идея классная, а подачу нужно корректировать. Сейчас расскажу, как – и если ваш малыш уже умеет складывать и вычитать в пределах 10, он будет так же легко и просто складывать в пределах сотни (и метод обучения можно точно так же экстраполировать до тыщи – в конце статьи научу как).
Итак, учиться складывать двузначные числа будем в три этапа.
И еще раз подчеркну: этот метод – для тех детишек, которые уже знают, что такое сложение и вычитание, и умеют складывать и вычитать в пределах десятки.
Этап 1. Коробки и штучкиВозьмите лист, на котором нарисовано много конфет, печенек – чего там ваш малыш любит. Можете сами нарисовать условные изображения. Количество должно быть не кратно 10.
Как-то примерно так:
Коричневые овальчики – это такое печенье )))Попросите малыша «упаковать» печеньки в коробки по 10 штук (обвести в кружочки каждые 10 печенек): «Смотри, на этом листе у нас много печенья.
Давай упакуем их в коробки по 10 штук в каждой».
Когда упаковка завершена, покажите малышу: “У нас получилось столько-то коробок, да еще столько-то печенек остались неупакованными. Почему несколько печенек осталось без упаковки?” – “Правильно, потому что их меньше 10”.
“Давай нарисуем теперь коробки с печеньем, которые у нас получились. И пририсуем к ним рядом неупакованные печеньки”:
Зеленые – это коробки с печеньем, коричневые – отдельные печеньки, которые остались не упакованными
Зеленые упаковки с печеньем и оставшиеся неупакованными 5 печенюшекНа самом деле, у нас получилась условная запись десятков и единиц.
Этап 2. Складываем и вычитаем коробкиРасскажите малышу, что коробки с печеньем и отдельные печенюшки можно складывать и вычитать.
“Давай, как будто у нас на одной полке 2 коробки с печеньем и отдельные 3 печеньки, а на другой полке 1 целая коробка и 4 отдельные печеньки.
Давай посчитаем, сколько всего у нас целых коробок и отдельных печенек.”
Нарисуем условные схемы таким же способом, как мы это делали на предыдущем шаге.
2 коробки и 3 печеньки ПЛЮС 1 коробка и 4 печенькиА теперь отдельно сложим целые коробки, а отдельно – отдельные печенюшки.
Складываем отдельно коробки и отдельно штучкиСкладывайте, начиная с отдельных печенюшек (и оставьте место впереди для “коробок”.
Если малышу будет сложновато складывать по памяти, можно вообще пальцем пересчитывать квадратики (целых коробок) и точечки (отдельных печенек).
Потренируйтесь хорошенько, складывая коробки и штучки. Имеет смысл заменять печеньки на конфеты, яйца, зефир, мыльные пузыри, модели машинок – да что угодно, что малышу нравится. Только обязательно напоминайте ему, что в коробке всегда лежит Десять Штук.
Потом переходите к вычитанию коробками и штучками, придумав простую жизненную ситуацию вроде: “Было 4 коробки и 3 штучки печенья, 2 коробки и одну штучку съели.
Сколько осталось?”
Если у малыша не будет получаться с картинками, можно вообще купить несколько пачек печенья (я покупала “Юбилейное” – в маленьких пачках как раз 10 штучек 🙂 ) и попробовать посчитать прямо на настоящих печеньках.
Этап 3. Наконец-то числаИтак, мы научились мастерски складывать и вычитать коробки и штучки. Теперь нарисуйте схему какого-нибудь “печенькового” примера – пусть малыш ее посчитает – и предложите:
“Давай теперь количество коробок, которое складываем, запишем числом – вот, прямо здесь, под коробками. И запишем количество отдельных штучек, прямо под точечками”:
Подписываем настоящие числа к “коробкам” и “штучкам”“Посмотри, что получилось – 2 и 3. Какое это число?” (Если малыш сразу не может сообразить – можно записать эти числа поближе друг к другу)
Проделайте так с каждым компонентом печенькового примера.
Теперь объясните: “На самом деле так мы можем складывать и вычитать любые двузначные числа. Представь себе, что первая цифра – это количество коробок, а вторая – количество штучек.
И складывай или вычитай точно так же, как делал это со схемами.”
Для удобства – и чтобы не запутаться – можно предложить малышу ставить точечки под цифрами, которые обозначают коробки (или – наоборот – штучки). В моем примере – это красные точечки под десятками – коробками.
И не забывайте, что начинать складывать или вычитать нужно Обязательно со “штучек”, оставляя место под количество “коробок”.
Пока малыш не освоится хорошо с таким счетом, следите внимательно, чтобы сложение / вычитание и десятков, и единиц было всегда в пределах 9 – чтобы не пришлось увеличивать или уменьшать десяток до тех пор, пока малыш не разберется с основами счета.
Когда научится хорошо – можно будет вводить счет с увеличением или уменьшением десятка. Это будет очень просто. Позже я расскажу, как.
А теперь, обещанное выше
А до тыщи слабо?
Если ваш малыш умеет считать (в смысле, просто считать, т.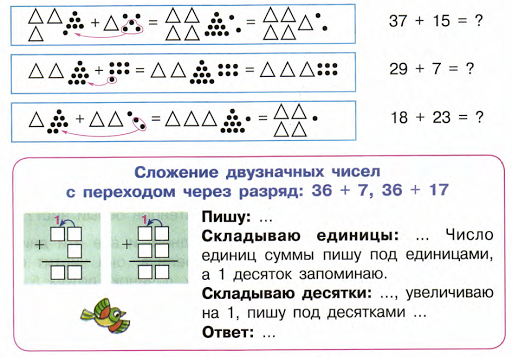
е. знает числа) в пределах тысячи, вы можете так же легко научить его складывать и вычитать трехзначные числа.
Просто добавьте еще одну фигурку – скажем, большоооой прямоугольник, и скажите ему, что “Давай теперь наши коробки с печеньем погрузим в большой ящик по 100 штук в каждом. Это – 10 коробочек по 10 штучек (предложите малышу пересчитать и убедиться, что это – реально 10 по 10). Тогда у нас будут большущие ящики по 100, отдельные коробочки, если количество печенек в них меньше 100, и отдельные штучки, если количество в них меньше 10”
И всё, дальше делаем то же самое, что делали выше. Всё получается так же легко, просто и органично.
_____________________________
А на сегодня у меня всё. Попробуйте этот способ с малышом – уверена, он хорошо и легко сработает.
Успешной учебы вашим детишкам!
Как научить сложным стратегиям вычитания двухзначных чисел
В рамках общего ядра мы даем учащимся множество стратегий, которые помогут им найти ответ на задачи на вычитание двухзначных чисел.
Мне нравится, как эти стратегии вычитания из двух цифр дают учащимся выбор того, как они могут решить проблему. Они помогают создать значение и чувство числа в рамках операции.
Но вот в чем дело… Их может быть много! Иногда наша учебная программа проходит слишком быстро для студентов, и они не совсем усваивают ее и в конечном итоге путаются. Вот почему я делюсь тем, как я преподаю эти стратегии, и упражнениями, которые я даю своим ученикам, чтобы помочь им получить необходимую им практику.
Прежде чем мы начнем, для того, чтобы учащиеся действительно преуспели в этих стратегиях, им нужна прочная основа с математическими фактами. Если учащимся нужно время, чтобы вспомнить или выяснить математический факт, это может запутать их в том, что они делают со стратегией вычитания 2 цифр.
Так что не беспокойтесь, у меня есть для вас кое-что особенное. Я делюсь своими 7 шагами к беглости математических фактов в бесплатной рабочей тетради для учителей 1-го и 2-го классов.
Загрузите бесплатную копию здесь.
Хорошо, давайте начнем со стратегий вычитания двухзначных чисел, которые я преподаю в своем классе.
Стратегии вычитания двухзначных чисел могут быть сложными для учащихся, но есть небольшие хитрости, которые помогут учащимся развить чувство числа и понимание этих стратегий вычитания двухзначных чисел.
Таблица сотен
Во-первых, у нас есть студенты, работающие с таблицей сотен, чтобы решить задачи на вычитание двузначных чисел. Для этой стратегии мне действительно нужно убедиться, что студенты понимают паттерны с диаграммой сотен.
Я хочу, чтобы мои ученики знали, что если они поднимаются вверх по таблице сотен, они вычитают их на десятки. Им нужно знать, если они идут влево на диаграмме сотен, они вычитают на единицы.
Эта стратегия вычитания двух цифр помогает учащимся использовать шаблоны для решения математических задач.
Когда я предлагаю своим ученикам рассмотреть задачу на вычитание двузначных чисел, например 72-35, я сначала спрашиваю, с какого числа мы начинаем в таблице сотен.
Им нужно знать с вычитанием, мы должны начать с большего числа.
Тогда я спрашиваю, сколько десятков в числе 35. Три десятка. Итак, мы поднимаемся на три строки вверх по сотенной диаграмме. Нам все еще нужно убрать единицы из числа 35. Сколько единиц из числа 35? Есть 5 таких. Итак, мы идем налево 5 единиц. Мы приземляемся на 37, так что это наш ответ.
Мои ученики много тренируются с этим. Важно, чтобы им хватило места на чистых сотнях, чтобы не запутаться. Так что я заставляю их работать над сотнями рабочих листов с диаграммами и веселыми занятиями. Их можно использовать как центры или целые групповые занятия. Найдите эти упражнения с диаграммой вычитания сотен здесь.
Открыть числовую строку
С помощью этой стратегии вычитания из двух цифр учащиеся совершают переходы назад по числовой строке. Они также могут рассчитывать на вычитание на числовой прямой. Поначалу это может сбить учащихся с толку, но если они хорошо знакомы с семействами фактов, имеет смысл использовать сложение для вычитания.
Чтобы узнать больше о семействах фактов, прочитайте эту запись в блоге: 3 причины, по которым вам нужно обучать семействам фактов
Стратегия вычитания двухзначного числа из открытой числовой строки может быть очень сложной для учащихся. Вот почему я даю своим ученикам много практики с этой стратегией вычитания двух цифр.
Для обучения этой стратегии я рисую на доске числовую линию и записываю уравнение. Возьмем пример 63-24. Я показываю своим ученикам, что если мы будем вести обратный отсчет по числовой прямой, я начну с того, что поставлю 63 справа.
Затем я спрашиваю, сколько десятков в числе 24. Там 2 десятка, поэтому я сделаю два прыжка назад и назову их.
Затем я спрашиваю, сколько единиц в числе 24. Их 4, поэтому я сделаю 4 прыжка назад и назову их. Я приземлился на 39, так что это ответ.
Учащимся действительно нужно много практиковаться с этой стратегией. Я нахожу полезным, когда даю им достаточно места в числовой строке и напоминаю им оставлять пробелы между своими числами, чтобы они могли действительно прочитать написанное.
Мои ученики практикуются с рабочими листами и беглыми упражнениями. Найдите здесь ресурс «Действия в строке числа с вычитанием двух цифр», который я использую.
Разбить на части
Эта стратегия вычитания 2-значного числа часто нравится моим ученикам. В этой стратегии учащиеся разбивают вычитаемое число на десятки и единицы. Затем разбейте их еще раз, если нужно, чтобы перейти к следующим десяткам, чтобы упростить задачу.
Стратегия разделения на части — любимая учащимися в моем классе!
Это требует некоторой практики. Я просто начинаю с того, что мои ученики тренируются разбивать единицы, чтобы они могли добраться до следующих десятков. Например, я могу показать их, если у нас 45-9., я собираюсь разбить 9 на 4 и 5. Тогда я могу думать об этом как 45-5=40 и 40-4=36.
Потом добавлю к нему десятки, например 45-19. Сначала они просто уберут десятку, чтобы получилось 45-10=35. 35-5=30. 30-4=26.
Мне нравится давать своим ученикам рабочие листы с ячейками, которые помогают им думать о разбиении числа на части.
Здесь вы найдете рабочие листы и другие задания, которые я даю своим ученикам.
Таблица десятков и единиц
Эта стратегия представляет собой обычный алгоритм вычитания двух цифр. Чтобы учащиеся по-настоящему поняли смысл шагов, мы используем модели, рисуем картинки, а затем просто используем числа.
Когда дело доходит до вычитания двузначных чисел с перегруппировкой, учащимся требуется много практики с моделями, картинками и использованием таблиц десятков и единиц.
Мне нравится показывать своим ученикам, когда нам нужно перегруппироваться. Я часто говорю что-то вроде: «Если у меня есть 5 штук, могу ли я убрать 8? Нет, мне нужно перегруппироваться.
Здесь вы найдете рабочие листы и упражнения, которые я использую, чтобы помочь учащимся ответить на вычитание двух цифр с перегруппировкой.
Я надеюсь, что вы нашли много советов, которые помогут учащимся освоить эти стратегии вычитания двухзначных чисел. Это приходит, когда мы учим развивать чувство числа и даем ученикам много практики.
Здесь вы найдете все мои стратегии сложения и вычитания двухзначных чисел в одном наборе.
Для получения дополнительной информации о том, как обучать стратегиям сложения двухзначных чисел, прочитайте эту запись в блоге: Стратегии сложения двухзначных чисел, которые работают
Для получения дополнительной помощи, позволяющей учащимся свободно складывать и вычитать двузначные числа, они должны свободно владеть математическими фактами 1 -20. Загрузите мою бесплатную рабочую книгу, чтобы получить помощь: 7 шагов к беглости математических фактов.
Загрузите его здесь.
Вычитание 2-х цифр — с перегруппировкой
LearnPracticeDownload
Вычитание 2-х цифр
| 1. | Что такое двузначное вычитание? |
| 2. | Вычитание двух цифр без перегруппировки |
| 3. | Вычитание двух цифр с перегруппировкой |
| 4. | Часто задаваемые вопросы о двухзначном вычитании |
Что такое двузначное вычитание?
Вычитание 2-значного числа выполняется путем помещения заданных чисел в столбцы с использованием их соответствующих разрядов, единиц и десятков. При вычитании число, из которого вычитается другое число, называется 9.0095 уменьшаемое
, число, которое нужно вычесть из уменьшаемого, называется вычитаемым . Окончательный результат после вычитания вычитаемого из уменьшаемого называется разностью.Формула вычитания записывается так:
Уменьшаемое — Вычитаемое = Разность .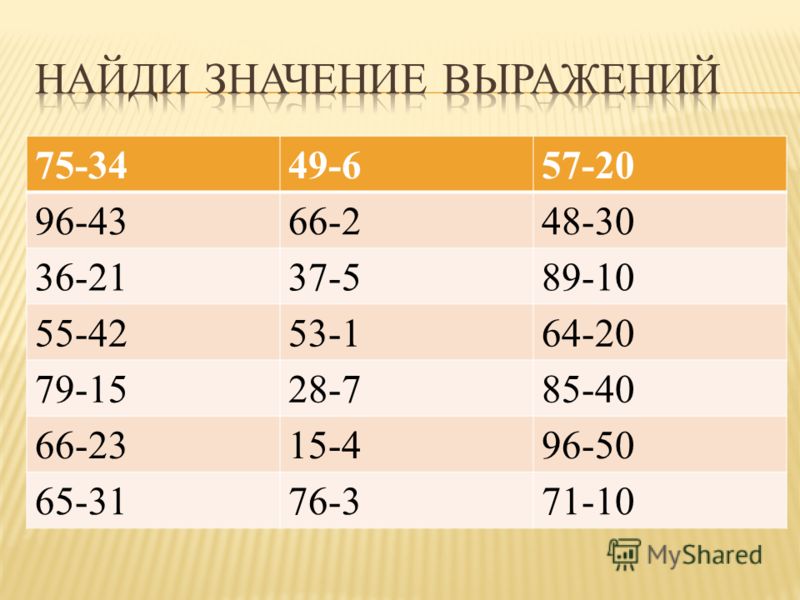
При вычитании двузначных чисел мы в основном используем метод столбца. Следующие шаги объясняют метод вычитания 2-значного числа.
- Шаг 1: Поместите числа друг под другом так, чтобы большее число было наверху, а меньшее — под ним. Мы знаем, что число, стоящее вверху, называется уменьшаемым, а число, расположенное ниже, — вычитаемым.
- Шаг 2: Числа должны быть размещены в соответствии с их разрядностью так, чтобы цифры единиц были выровнены вместе по вертикали, а цифры десятков были выровнены вместе.
- Шаг 3: Начните вычитать цифры из столбца единиц, а затем перейдите к столбцу десятков.
- Шаг 4: После получения разницы соответствующий ответ записывается внизу.
Вычитание двух цифр без перегруппировки
Вычитание двух цифр без перегруппировки означает, что вычитание производится без заимствования. Это относится к случаям, когда каждая цифра уменьшаемого больше соответствующей цифры вычитаемого.
Давайте возьмем пример, чтобы понять это лучше.
Пример: Вычтите 27 из 39.
Решение: Давайте решим это, используя следующие шаги.
- Шаг 1: Расположите числа в соответствии с их разрядностью, как показано ниже.
- Шаг 2: Начните вычитание цифр с единицы. Поскольку число сверху больше, чем число внизу, здесь не требуется перегруппировка/заимствование. После вычитания чисел в столбце с единицами мы получаем 9 — 7 = 2.
- Шаг 3: Теперь вычтите цифры из столбца десятков, и мы получим разницу как 3 — 2 = 1.
Следовательно, после вычитания 27 из 39 получим 12.
Вычитание двух цифр с перегруппировкой
Вычитание 2-значного числа с перегруппировкой также известно как вычитание с заимствованием. Эта перегруппировка требуется, когда любая цифра в уменьшаемом меньше, чем вычитаемое. При перегруппировке мы заимствуем 1 число из предыдущего столбца, чтобы сделать эту меньшую цифру достаточно большой из соответствующего вычитаемого.
Давайте разберемся в этом с помощью примера.
Пример: Вычесть 18 из 55.
Решение: Следующие шаги показывают процедуру вычитания 18 из 55.
- поместите значения, как показано выше.
- Шаг 2: Начните вычитать цифры с разряда единиц. Проверить, больше ли какая-либо цифра в вычитаемом, чем соответствующая цифра в уменьшаемом. В таком случае заимствуйте 1 из столбца десятков и объедините его с меньшим числом, чтобы оно стало больше. Здесь 5 и 8 находятся в столбце единиц, а поскольку 5 меньше 8, мы заимствуем 1 из столбца десятков, и это 5 становится 15. Итак, 15 — 8 = 7. Запишите 7 в столбце единиц.
- Шаг 3: Теперь вычтите числа из столбца десятков. Следует отметить, что после присвоения 1 столбцу единиц число в столбце десятков уменьшится на одно число. Таким образом, 5 в столбце десятков становится 4, потому что это дало 1 столбцу единиц. Теперь 4 — 1 = 3.
- Шаг 4: Затем объедините числа и запишите разницу. Следовательно, разница между 55 и 18 равна 37.
☛ Похожие темы
- Двузначное дополнение
- 2-значное умножение
- 3-значное дополнение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Сложение и вычитание десятичных дробей
- Сложение и вычитание целых чисел
- Вычитание с перегруппировкой
- Вычитание из числовой строки
Примеры двухзначного вычитания
Пример 1: Вычислите разницу между 34 и 9.
Решение: Данное двузначное вычитание можно выполнить следующим образом.
Следовательно, разница между 34 и 9 равна 25.
Пример 2: Вычесть 74 из 89.
Решение: Выполним это вычитание двузначного числа следующим образом.
Таким образом, разница между 89 и 74 составляет 15.
Пример 3: Укажите истинное или ложное значение при вычитании 2-значного числа.
а.) 55 — 11 = 44
б.) 30 — 10 = 10
Решение:
а.) Верно, 55 — 11 = 44
б.) Неверно1, 0 -2002
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по вычитанию двузначных чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о двузначном вычитании
Что такое двузначное вычитание в математике?
Вычитание двух цифр относится к вычитанию чисел, в которых уменьшаемое состоит из двух цифр, а вычитаемое может состоять из одной или двух цифр.
Уменьшаемое — это число, из которого вычитается другое число, а вычитаемое — это число, которое нужно вычесть из уменьшаемого.
Как выполнить вычитание двузначных чисел с перегруппировкой?
Вычитание 2-значного числа с перегруппировкой выполняется, когда любая цифра уменьшаемого меньше соответствующей цифры вычитаемого. Давайте вычтем 17 из 36.
- Шаг 1: Поместите числа одно под другим, выровняв их в соответствии с их разрядами. Здесь 36 будут размещены вверху, потому что они больше, а 17 будут размещены внизу, потому что они меньше.
- Шаг 2: Начните вычитать цифры с разряда единиц. Нам нужно проверить, меньше ли какая-либо цифра в уменьшаемом, чем соответствующая цифра в вычитаемом. В таком случае заимствуйте 1 из столбца десятков и объедините его с меньшим числом. Здесь 6 и 7 находятся в столбце единиц, и поскольку 6 меньше 7, мы заимствуем 1 из столбца десятков, и это 6 становится 16. Итак, 16 — 7 = 9.. Напишите 9 под колонкой единиц.
- Шаг 3: Теперь вычтите числа из столбца десятков. Следует отметить, что после присвоения 1 столбцу единиц число в разряде десятков уменьшится на единицу. Таким образом, 3 в столбце десятков становится 2, потому что это дало 1 столбцу единиц. Теперь 2 — 1 = 1.
- Шаг 4: Наконец, объедините числа и запишите разницу. Следовательно, 36 — 17 = 19 90 150.
Как выполнить вычитание двузначных чисел без перегруппировки?
Вычитание 2-значного числа без перегруппировки — это простое вычитание, при котором нет заимствования, поскольку все цифры уменьшаемого числа больше, чем цифры вычитаемого. Например, давайте вычтем 47 — 32, используя следующие шаги.
- Шаг 1: Расположите числа одно под другим в соответствии с их разрядностью.
- Шаг 2: Вычтите цифры из столбца единиц и запишите разницу. В этом случае 7 — 2 = 5. Поскольку уменьшаемое больше вычитаемого, здесь не требуется перегруппировка/заимствование.
