Урок «Умножение и деление с числами 1, 0. Деление нуля на число. Закрепление изученного»

Тема: «Умножение и деление с числами 1, 0. Деление нуля на число. Закрепление изученного».

Цели: Закреплять правила умножения и деления с числами 1 и 0, знание таблицы умножения и деления, умение решать задачи, изученных видов; учить рассуждать и делать выводы.

Задачи:- Вспомнить правило написания цифры 7;

-научатся решать логические задачи с недостатком и избытком числовых данных и на сообразительность.

-научатся пользоваться таблицей умножения и деления;

— записывать краткое условие задачи в таблицу и составлять план решения задачи;

— изменять вопрос задачи, подходящий к условию и решать задачи изученных видов.

 

ОРГАНИЗАЦИОННЫЙ МОМЕНТ

МИНУТКА ЧИСТОПИСАНИЯ

Ученики вспоминают правила написания цифры 7 по

образцу. (образец в презентации)(слайд1)

ВВОДНАЯ БЕСЕДА

— Вы знаете, что число 7 не простое, а сказочное? Вспомните, в каких сказках оно упоминается? («Волк и семеро козлят», «Сказка о мертвой царевне и семи богатырях», «Белоснежка и семь гномов». )

— Сегодня волшебное число 7 поможет нам побывать в математической сказке. Послушайте ее начало.

Жила-была третьеклассница Соня. Не любила она математику, а задачи даже знать не хотела. Однажды, на уроке математики, когда все решали задачу, девочка заснула.(слайд2) Вдруг оказалась в волшебном лесу и слышит таинственный голос:

— Если ты, Соня, не решишь задачу до конца урока, то навсегда останешься в этом лесу.

Заплакала Соня: не знает, что же ей делать, куда идти, у кого помощи просить?

МАТЕМАТИЧЕСКАЯ РАЗМИНКА

1). Логическая задача с недостатком числовых данных

Тут выскочил зайчик:

— Здравствуй, Соня! Реши мою задачку – помогу тебе.

Делать нечего – согласилась девочка.

Задача зайчика: Из корзины торчат 6 заячьих ушек. Сколько там спряталось зайцев?

— Думала-думала Соня – не может решить задачу. Кто сумеет, ребята, объяснить, в чем трудность этой задачи? (слайд 3)

(В этой задаче только одно числовое данное.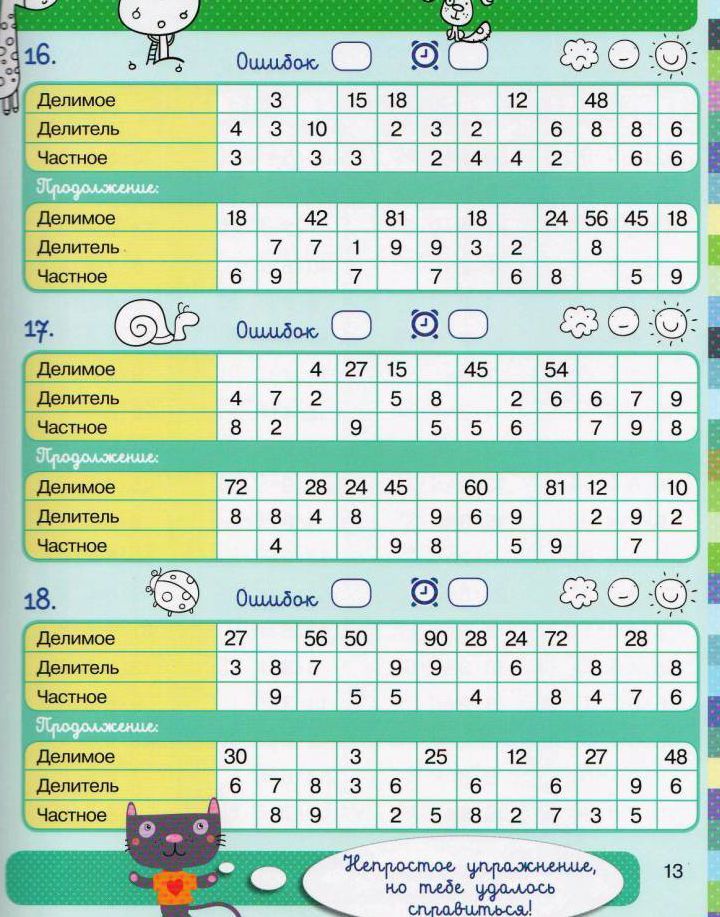 Необходимо добавить второе: у каждого зайчика по два уха, тогда задача будет решена так: 8:2=4(з)).

-Обрадовалась Соня объяснению, сказала ответ зайчику, а он помог девочке пройти к реке, за которой живет фея-Задача. Она-то и научит Соню решать задачи.

2).Логическая задача с избытком данных.

Дошла девочка до реки, а как перебраться — не знает: ни моста, ни лодки. Откуда ни возьмись — лягушка:

— Здравствуй, Соня! Я тебе помогу, если решишь мою задачу.

Согласилась девочка.

Задача лягушки: У животного 2 правые ноги, 2 левые, 2спереди, 2сзади. Сколько ног у этого животного?

— Соня посчитала и сказала ответ, да он оказался неправильным. Давайте ей поможем! Как нужно рассуждать?

(«2 спереди» и «2сзади» — лишние. Это повтор.).

Решение: 2+2=4(н) или 2х2=4(н)

Лягушка за правильный ответ рассказала, что нужно посчитать круговые примеры на рыбках в реке. Рыбки возьмутся за хвосты и образуют мост, по которому можно перейти на другую сторону.

3).Примеры на умножение и деление на рыбках.

3х6 18:2 9х4

36:6 24:8 6:3

2х10 20:5 4х6

Соня плохо знает таблицу. Придется нам ее опять выручать!

(дети решают примеры, читая по-разному)

— Молодцы! Помогли Соне. Переправилась она на другой берег. А дальше куда? Видит Соня – Печка стоит:

— Здравствуйте, Печка! Не подскажете, как фею-Задачу найти?

— Реши мою задачу, подскажу, — говорит печка.

4). Логическая задача на сообразительность

Задача печки.

1 крендель в печи выпекается 10 минут. Сколько минут будут выпекаться 6 кренделей на одном противне?

(10минут, потому,что их ставят впечь одновременно.)

— Молодцы, ребята! Без вашей помощи девочка никогда бы не решила эту задачу. Теперь она знает дорогу к дому феи–Задачи. Надо торопиться! Давайте поможем Соне быстрее дойти.

VФИЗКУЛЬТМИНУТКА

 

Конь меня в дорогу ждет,

Бьет копытом у ворот,

На ветру играет гривой,

Пышной, сказочно красивой.

Быстро я в седло вскочу,

Не поеду – полечу!

Там за дальнею рекой

Помашу тебе рукой!

VIРАБОТА С ЗАДАЧАМИ

— С нашей помощью быстро добралась девочка до нужного места. А там ее уже поджидает фея-Задача. Сама она необычная, и дом у нее непростой. Давайте прочитаем, что написано на этажах. (условие, вопрос, решение, ответ). Это составные задачи.

Отправилась Соня знакомиться с хозяйством феи-Задачи. И мы давайте познакомимся с задачей №2 на с. 76.

Читают и составляют схематический чертеж.

К. П.

 

-Во сколько действий задача? (3)Почему?

-Как узнать общий вес?

— Запишем данные задачи в таблицу.

— О чем идет речь? (конфеты, печенье)

— Что примем за единицу? (массу 1 коробки) (слайд 4)

— Какая будет вторая графа? (количество таких коробок) (слайд 5)

— Третья? (общий вес) (слайд 6)

Заполним таблицу.

— Прочитайте, что сказано о конфетах?

-Куда запишем данные? (слайд7)

-Что сказано о печенье? Прочитайте. Куда запишем данные? (слайд 8)

Прочитайте вопрос задачи. Как показать? (слайд 9)

Посмотрите внимательно на краткую запись: Что можете сказать? (Задача в три действия) Почему?

— Значит, сразу ответить на вопрос задачи мы не можем.

-Чтобы ответить на вопрос задачи, что мы должны знать?

(общий вес конфет и общий вес печенья) (слайд 10))

— Каким действием найдем вес конфет? (умножением)

— А как определить массу печенья? (умножением)

— Как будем находить общее количество печенья?

( сложением)

(Самостоятельно решение задачи выражением. Проверка)Карточки-схемы -тем, кто затрудняется в решении задач.

— Мы справились с решением задачи, а фея-Задача тоже помогла Соне понять и решить задачу.

Тут девочка и проснулась. Вспомнила, что с ней случилось, записала решение задачи в тетрадь и задумалась: « А можно ли решить эту задачу, если изменить вопрос?»

— Давайте и мы подумаем: можно ли поставить к условию задачи другой вопрос? (можно)

— Какой вопрос вы можете задать?( На сколько кг конфет больше , чем печенья? или На сколько кг печенья

меньше, чем конфет?) (слайд11)

Вспомните, к какому типу задач относятся задачи с такими вопросами? (Это задачи на сравнение)

— Кто помнит правило, по которому мы можем правильно решить новую задачу? Как изменится наша схема? ( заменим знак « +» на «-»)

(Самостоятельное решение выражением по вариантам: Iв – на сколько больше привезли конфет, чем печенья?

IIв – на сколько меньше привезли печенья, чем конфет? (первые решивший задачу записывает на доске решение. Проверка)

— Как правильно записать ответ? (На 12 кг больше печенья, чем конфет.

VI I РЕФЛЕКСИЯ

Самостоятельное решение примеров.

7х1 0:4 9х(34-33)

1х8 0х6 0х(43-6)

9х0 0:25 100х0

— Оцените свою работу на уроке.

VIII ИТОГ УРОКА:

— Сколько заданий мы разобрали сегодня на уроке? (7)

— Значит, семерка нам помогла преодолеть все трудности. Поднимите руки, кому понравился сегодняшний урок? Какие задачи вам больше всего запомнились? Подумайте, как вы сами работали сегодня на этом уроке? Поставьте себе карандашом оценку в тетради на полях.

— Хотите ли вы еще встретиться на уроке с Соней?

VIII ДОМАШНЕЕ ЗАДАНИЕ

-Соня передала вам схему задачи, по которой вы составите свою задачу и решите ее разными способами. Что вам напоминает эта схема? На какую схему она похожа? В чем различие?

— Вспомнить пословицы, где упоминается « волшебное» число?

 

 

7

Урок математики в 4 классе.

Тема: «Умножение и деление на 5»

Урок математики в 4 классе

Тема:

«Умножение и деление на 5»

Цели урока:

1.Закрепить знания таблицы умножения и деления на 5; формировать вычислительные навыки, умение решать примеры и задачи в 2 действия.

2. Развивать познавательные процессы, умение сравнивать, доказывать и делать выводы.

3. Воспитывать усидчивость, самостоятельность, аккуратность, работоспособность.

Словарь: умножение, деление, лыжник.

Оборудование: тетради, презентация, счетный материал.

Ход урока

1.Оргмомент.

На уроке математики
Будем очень мы внимательны!
Что учили — повторим,
Все, что знаем — обобщим.
Будем с вами мы считать и решать!

Эмоциональный настрой на урок:

Сегодня на урок к нам пришли гости. Давайте их поприветствуем

— Я желаю вам уверенности в себе, пусть этот урок принесет вам новые знания и умения, а также удачу сегодня и в дальнейшей работе.

2. Задание на внимание.

— Посмотрите на экран. Найдите лишнюю картинку.

(картинки о зиме, 1 с другим временем года).

— Какая картинка лишняя? (осень).

— Почему?

— К какому времени года относятся остальные картинки? (к зиме).

-Что происходит с природой зимой? (она засыпает)

— Да, наступила волшебница- зима. Она прилетела к нам на урок и принесла интересные задания, которые мы постараемся выполнить.

3.Устный счёт.

1) Сколько в классе человек?

2) Прямой и обратный счет по 5 до 50-ти.

5,10,15, 20, 25, 30, 35, 40, 45, 50.

50, 45, 40, 35, 30, 25, 20, 15, 10, 5.

2) Вставь пропущенные числа.

а) 1, …, …, 4, …, …, 7, …, …, 10.

10, 9, 8, …, …, …, 4, 3, …, 1.

б)41, …, …, …, 45, …, …, …, 49,50.

41, 42, 43, 44, 45, 46, 47, 48, 49, 50.

3) Повторить таблицу умножения и деления. (слайд)

4) Решение задач.

Три бельчонка маму-белку
Ждали около дупла
Им на завтрак мама-белка
Девять шишек принесла, 
Разделила на троих.
Сколько каждому из них? (9 : 3 = 3 ш.).

Подарил утятам ежик

Восемь кожаных сапожек.

Кто ответит из ребят,

Сколько было всех утят?

В поле бабочки летали
Лепестки цветов считали
На одном цветке их пять.
Сможете вы сосчитать?
Сколько будет лепестков?
Если шесть всего цветков. (5 х 6 = 30 л.).

Мышка зёрна собирала,
По два зёрнышка таскала.
Принесла девятый раз.

Каков у мышки стал запас? (2 х 9 = 18 з.).

Папа-заяц в сад зашел,

20 спелых груш нашел.

Разделил он их по 5,

Сколько деток — то, зайчат? (20 : 5 = 4 з.)

5. Работа по теме урока.

-Какие действия мы с вами выполняли? (умножение и деление).

— Как вы думаете, какова будет тема нашего урока?

Тема урока «Умножение и деление на 5».

-Мы закрепим знания т/у и т/д на 5, решим задачку, будем стараться доказывать, делать выводы, учиться сравнивать, аккуратно писать.

-Давайте вспомним, как называются числа при умножении?

— Как называются числа при умножении?

Гимнастика для глаз.

Раз- рука, два- рука.

Лепим мы снеговика.

Три-четыре, три-четыре,

Нарисуем рот пошире,

Пять- найдем морковь для носа.

Угольки найдем для глаз.

Шесть – наденем шляпу косо,

Пусть смеется он у нас.

Семь-восемь, семь-восемь,

Танцевать его попросим.

1)Запись числа, классной работы.

2) Решить примеры (работа у доски).

5 х 3 = 45 : 5 =

30 : 5= 5 х 4 =

2) Вставь пропущенные числа ( самостоятельно).

5 х … = 25 … : 5 = 8

…: 5 = 10 5 х … =35

3)Решение задачи. Работа по учебнику у доски.

Откройте учебники на стр. 89 №17.

— Прочитайте задачу внимательно про себя?

В лыжной секции занимается 5 девочек, а мальчиков в 3 раза больше. Сколько детей занимается в лыжной секции?

Чтение задачи учителем.

Кто из вас знает, кто такой лыжник?

— Лыжник – спортсмен, занимающийся лыжным спортом или просто человек, который ходит на лыжах.

— О чем говорится в задаче?(о девочках и мальчиках, которые занимаются в секции).

— Что сказано о девочках?

— Что сказано о мальчиках?

— Какой вопрос задачи?

Давайте вспомним этапы решения задачи.

-Составим краткую запись задачи.

-Какие слова возьмем для краткой записи задачи?

Запись краткой записи у доски.

Девочек — 5 д.

Мальчиков — ? — в 3 раза больше, чем

-Сможем ли мы сразу ответить на вопрос задачи?

-Почему?(мы не знаем сколько мальчиков)

-Что мы найдем в первом действии? (сколько мальчиков)

— Сможем ли мы теперь ответить на вопрос задачи?

-Запишем решение у доски.

1) Сколько мальчиков занимается в секции?

5 × 3 =15(д.)

2) Сколько детей занимается всего?

5 +15= 20(д.)

Ответ: 20 дет

Слабые учащиеся: проверить задания работа по учебнику стр….

4) Физкультминутка.

Раз — подняться, потянуться,

Два — нагнуться, разогнуться,

Три — в ладоши три хлопка,

Головою три кивка.

На четыре — руки шире,

Пять — руками помахать,

Шесть — на место тихо сесть.

Сейчас усложним задание.

5) Решить примеры в два действия. (у доски )

32 : 8 ×2 = 8 40 : 8 × 3 =15

8 : 2× 3 = 12 8 × 4 — 12 = 20

48 : 8 ×2 = 12 8 × 2 + 24 = 40

Слабые учащиеся: решение примеров на карточках

1+3 2 +3

4 +2 4 — 3

5 + 2 6 — 3

6) Геометрический материал.

Посмотрите на экран внимательно. Какие вы видите линии? Назовите их правильно. Посоветуйте зайчику, по какой дороге он быстрее доберется до Новогоднего подарка. Давайте начертим прямую линию.

6.Домашнее задание: повторить т/у и т/д.

7.Итог урока. Оценки.

8. Рефлексия со снежинками.

Чему мы научились сегодня на уроке? (умножать и делить числа).

Что мы для этого делали? (считали устно, решали примеры и задачу).

Молодцы, ребята! Откройте конверты , достаньте снежинки. У вас белая и голубая снежинки. Если у вас хорошее настроение- покажите белую снежинку, кто остался недоволен собой и уроком, то голубую.

Уравнения и неравенства Умножение и деление

Пример задачи

Решите уравнение = 24.

Мы еще не говорили о том, что делать с такого рода уравнением, но вы можете понять это, подумав о весах. Если три копии х весят в сумме 24, то каждая х должна весить треть от 24. То есть x = 24 ÷ 3 = 8. Надеюсь, мы все еще не говорим о мешках, потому что наши лодыжки, вероятно, не могут выдержать такой большой вес.

Другими словами, мы делим обе части 3 x = 24 на 3, чтобы получить само по себе x .

3 x = 24
3 x ÷ 3 = 24 ÷ 3
x = 8

Вот еще один способ подумать об этом: чтобы получить x , умноженное только на обе части уравнения, мы . Не случайно это мультипликативное число, обратное 3. У вас было «ага!» момент? Потому что мы сделали.

В общем, всякий раз, когда мы сталкиваемся с уравнением вида ( коэффициент ) x = ( некоторое значение ), мы умножаем обе части уравнения на обратную величину коэффициента. Поскольку любое число, умноженное на его обратное, равно 1 (просто попробуйте найти число, для которого это не работает — мы смеем вас обмануть), у нас остается уравнение, в котором x  само по себе с одной стороны, и решение к уравнению с другой стороны.

Как и в случае сложения и вычитания, умножение или деление обеих частей уравнения на одну и ту же величину допустимо, если мы не делим на ноль. Помните: все дело в том, чтобы делать с одной стороной то, что вы делаете с другой. Если вы угостите левую сторону, значит, вы принесли достаточно, чтобы поделиться со всем классом.

Будьте осторожны:  При решении уравнения любую операцию, которую вы выполняете с одной стороны, вы также должны выполнять с другой стороны. Мы знаем, что уже говорили это, но мы надеемся, что 47-й раз будет очаровательным. Если вы добавляете 5 к левой части уравнения, вы должны добавить 5 к правой части уравнения. Если вы разделите правую часть уравнения на 3, вам также необходимо разделить левую часть уравнения на 3.

Пример задачи

Как решить задачу 5 х – 10 = 3 х + 8?

Сначала получите все x с одной стороны уравнения, вычитая по 3 x с каждой стороны:

2 x – 10 = 8

Затем добавьте 10 к обеим сторонам:

9 9

x = 18

Наконец, разделите каждую часть уравнения на 2:

x = 9

Вспомните, что деление на 2 равносильно умножению на половину. Если вы хотите увидеть, как кто-то бросит на вас рыбий глаз, попробуйте заказать в Subway фут длиной, а затем спросить, могут ли они умножить ее наполовину.

Мы можем подумать о делении обеих частей уравнения на 2 или умножить обе части уравнения на . Пока мы делаем арифметику правильно, в любом случае мы найдем один и тот же ответ в конце. Однако, когда речь идет о дробях, обычно лучше думать об умножении на обратный мультипликатив, чем о делении на дробь.

Пример задачи

Решите уравнение 

Нам нужно y само по себе, поэтому умножьте обе части уравнения на мультипликативную обратную величину , которая равна . Это сократит дробь в левой части уравнения:

y = 10

Если вы предпочитаете делить обе части уравнения на , обязательно сделайте это. Остерегайтесь любых змей деления, которые могут попытаться укусить вас за лодыжки. Предупреждение: эти змеи могут замаскироваться под цифры.

Одна вещь, которая может сбить нас с толку, если мы не будем осторожны, — это обозначения с отрицательными знаками. Когда в уравнении появляется — x , x умножается на -1. Если вам будет полезно переписать — x как (-1) х , сделайте это. Если кто-то посмеется над вами за это, назовите нам его имя, и о ситуации позаботятся. Мы не говорим, что сделаем  что-нибудь с ними, мы просто говорим. .. позаботимся о .

Умножение и деление чисел — переплетение нитей математики между домом и школой…

Умножение и деление чисел

NZC УРОВЕНЬ 2 Стратегии номеров NAS2-1  Используйте простые аддитивные стратегии с целыми числами и дробями. Знание чисел NAK2-1  Знать последовательности прямого и обратного счета с целыми числами не менее 1000. NAK2-2  Знать основные факты сложения и вычитания. NAK2-3  Знать, сколько единиц, десятков и сотен в целых числах не меньше 1000. NAK2-4  Знать простые дроби в повседневном использовании.

NZC LEVEL 3 Стратегии чисел NAS3-1  Используйте ряд аддитивных и простых мультипликативных стратегий с целыми числами, дробями, десятичными знаками и процентами. Знание чисел NAK3-1  Знать основные факты умножения и деления NAK3-2  Знать последовательности счета для целых чисел. НАК3-3  Знать, сколько десятых, десятков, сотен и тысяч в целых числах. NAK3-4 Знать дроби и проценты в повседневном использовании.

NZC LEVEL 4 Числовые стратегии и знания NA4-1  Используйте ряд мультипликативных стратегий при работе с целыми числами. NA4-2  Понимание сложения и вычитания дробей, десятичных и целых чисел. NA4-3  Найти дроби, десятичные дроби и проценты от сумм, выраженных целыми числами, простыми дробями и десятичными дробями. NA4-4  Применять простые линейные пропорции, включая упорядочение дробей. NA4-5 Знать эквивалентные десятичные и процентные формы для повседневных дробей. NA4-6  Теперь относительный размер и позиционная структура положительных и отрицательных целых чисел и десятичных знаков с точностью до трех знаков после запятой.

NZC LEVEL 5 Число Стратегии и знания NA5-1  Разум с линейными пропорциями.  Используйте простые числа, общие делители, кратные и степени (включая квадратные корни). NA5-3  Понимание операций с дробями, десятичными числами, процентами и целыми числами. NA5-4  Используйте нормы и соотношения. NA5-5 Знайте часто используемые преобразования дробей, десятичных чисел и процентов. NA5-6  Знать и применять стандартную форму, значащие цифры, округление и десятичный разряд.

В этом разделе вы узнаете:
1) Умножение на десятки, сотни и тысячи
​2) Умножение и деление с использованием пропорционального преобразования Квадраты
​5) Использование алгоритмов умножения
​6) Степени
​7) Умножение и деление целых чисел
8) Порядок действий

Понимание умножения и деления

Нажмите на это изображение, чтобы перейти к некоторым удивительным играм на умножение. Ага!

• X, умножить, умножить, произведение и много всего среднего умножения.
• Порядок умножения не имеет значения, т.е. 2 x 3 = 3 x 2.
• Базовый факт можно записать как минимум четырьмя различными способами.
• Два числа, которые умножаются вместе, чтобы получить число, называются его факторами, например. 2 x 3 = 6, поэтому 2 и 3 являются делителями 6.
• Деление противоположно умножению.

---

1) Умножение и деление на десятки, сотни и тысячи

• Использование кратных десятков может упростить некоторые задачи на умножение и деление.

2) Умножение и деление с использованием пропорциональной корректировки

• При умножении удвоение числа и деление пополам другого дает тот же результат.
• Удвоение и деление пополам — это стратегия умножения, которая рекомбинирует множители чисел.
• Треть означает деление числа на 3.
• Утроение означает умножение числа на 3.
• Пропорциональная корректировка — это название, данное этим стратегиям.
• Уменьшение числа пополам и деление пополам равносильно делению на 4.

3) Разбиение на части с использованием разрядного значения

• Числа можно разделить (или разделить) в соответствии с их разрядностью, чтобы упростить умножение и деление. Например, 213 можно записать как 200 + 10 + 3.   213 x 6 = то же самое, что 200 x 6 + 10 x 6 = 3 x 6,9.0279
• Таблицу умножения или (массив) можно использовать для решения задачи на умножение.

4) Кратные, простые числа и квадраты

• Если число имеет только два множителя, оно называется ПРАЙМ .
• Число, умноженное само на себя, является квадратным числом. например 9 это 3 х 3 или 3 в квадрате.
• Подсчет с пропуском дает кратность целого числа. Число, кратное 2, равно 2, 4, 6, 7, 8, 10, 12, 14, 16,…

Посетите эти замечательные веб-сайты, посвященные факторам, кратным и простым числам. Веселиться!


http://www.romsey.hants.sch.uk/maths/number_c.html

http://nrich.maths.org/8705

http://nrich.maths.org/5448/ решение

---

5) Использование алгоритмов умножения

• Мы можем умножать большие числа, используя сетку или стандартный алгоритм.
• Стандартный алгоритм называется длинным умножением, потому что вычисления изложены вдоль страницы.
• Понимание разрядности важно для длинного умножения.
• Важно оценить ответ перед его обработкой, чтобы убедиться, что ваш ответ разумен.

Посмотрите видеоклип, в котором рассказывается об этапах, или зайдите на эти сайты и попробуйте! http://www. homeschoolmath.net/teaching/md/multiplication_algorithm.php https://www.khanacademy.org/math/arithmetic/multiplication-division/multi_digit_multiplication/v/multiplication-6-multiple- цифры-числа http://faculty.atu.edu/mfinan/2033/section13.pdf

6) Степени

• Степень также называют показателем степени или индексом. Если мы говорим о более чем одной степени, мы говорим о степенях, показателях степени или индексах,
• Числа в индексной форме имеют основание и индекс.
• Возведение в квадрат означает степень 2.  4 в квадрате равно 4 x 4.
• Возведение в квадрат — это извлечение квадратного корня.
• Есть и другие полномочия, напр. кубический и кубический корень.

Зайдите на этот сайт, чтобы попробовать EXPONENTS.

Посетите этот сайт. Это приведет вас ко ВСЕМ!

Отличная игра с использованием ПОКАЗАТЕЛЕЙ. Наслаждаться!

Надеюсь, вам понравится эта игра Exponents. Удачи!

7) Умножение и деление целых чисел

• Когда два положительных числа умножаются или делятся, ответ положительный.
• При перемножении положительного и отрицательного числа получается отрицательный результат.
• При делении одного числа на другое, если одно из чисел отрицательное, ответ отрицательный.

• Академия Хана — отличный сайт для посещения, где вы сможете научиться складывать и вычислять целые числа.
  

https://www.khanacademy.org/math/arithmetic/absolute-value/mult_div_negatives/v/multiplying-and-dividing-negative-numbers

• Вот еще один замечательный сайт…
  

http://www.