Примеры на умножение и деление на 4 и 5: Умножение и деление числа на 5, таблица умножения и деления на 5, карточки, задачи и примеры с ответами, скачать

Содержание

Умножение на 4 | Таблица умножения

На этой странице представлены примеры, описывающие умножение на 4 и умножение числа 4, деление, некоторые способы произношения и записи, таблица умножения на 4 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы. Умножение на 4:
1 x 4 = 4
2 x 4 = 8
3 x 4 = 12
4 x 4 = 16
5 x 4 = 20
6 x 4 = 24
7 x 4 = 28
8 x 4 = 32
9 x 4 = 36
10 x 4 = 40

Первый вариант произношения:
1 x 4 = 4 (1 умножить на 4, равно 4)
2 x 4 = 8 (2 умножить на 4, равно 8)
3 x 4 = 12 (3 умножить на 4, равно 12)
4 x 4 = 16 (4 умножить на 4, равно 16)
5 x 4 = 20 (5 умножить на 4, равно 20)
6 x 4 = 24 (6 умножить на 4, равно 24)
7 x 4 = 28 (7 умножить на 4, равно 28)
8 x 4 = 32 (8 умножить на 4, равно 32)
9 x 4 = 36 (9 умножить на 4, равно 36)
10 x 4 = 40 (10 умножить на 4, равно 40)

Второй вариант произношения:
1 x 4 = 4 ( по 1 взять 4 раза, получится 4)

2 x 4 = 8 ( по 2 взять 4 раза, получится 8)
3 x 4 = 12 ( по 3 взять 4 раза, получится 12)
4 x 4 = 16 ( по 4 взять 4 раза, получится 16)
5 x 4 = 20 ( по 5 взять 4 раза, получится 20)
6 x 4 = 24 ( по 6 взять 4 раза, получится 24)
7 x 4 = 28 ( по 7 взять 4 раза, получится 28)
8 x 4 = 32 ( по 8 взять 4 раза, получится 32)
9 x 4 = 36 ( по 9 взять 4 раза, получится 36)
10 x 4 = 40 ( по 10 взять 4 раза, получится 40)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 4, можно легко найти результаты умножения числа 4. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )

Умножение числа 4:

4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24
4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
4 ∙ 10 = 40

Варианты произношения:
4 ∙ 1 = 4 (по 4 взять 1 раз, получится 4)
4 ∙ 2 = 8 (по 4 взять 2 раза, получится 8)
4 ∙ 3 = 12 (по 4 взять 3 раза, получится 12)
4 ∙ 4 = 16 (по 4 взять 4 раза, получится 16)
4 ∙ 5 = 20 (по 4 взять 5 раз, получится 20)
4 ∙ 6 = 24 (по 4 взять 6 раз, получится 24)
4 ∙ 7 = 28 (по 4 взять 7 раз, получится 28)
4 ∙ 8 = 32 (по 4 взять 8 раз, получится 32)
4 ∙ 9 = 36 (по 4 взять 9 раз, получится 36)
4 ∙ 10 = 40 (по 4 взять 10 раз, получится 40)

4 ∙ 1 = 4 (4 умножить на 1, равно 4)
4 ∙ 2 = 8 (4 умножить на 2, равно 8)
4 ∙ 3 = 12 (4 умножить на 3, равно 12)
4 ∙ 4 = 16 (4 умножить на 4, равно 16)
4 ∙ 5 = 20 (4 умножить на 5, равно 20)
4 ∙ 6 = 24 (4 умножить на 6, равно 24)
4 ∙ 7 = 28 (4 умножить на 7, равно 28)
4 ∙ 8 = 32 (4 умножить на 8, равно 32)
4 ∙ 9 = 36 (4 умножить на 9, равно 36)
4 ∙ 10 = 40 (4 умножить на 10, равно 40)

Деление на 4:

4 ÷ 4 = 1
8 ÷ 4 = 2

12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10

4 ÷ 4 = 1 (4 разделить на 4, равно 1)
8 ÷ 4 = 2 (8 разделить на 4, равно 2)
12 ÷ 4 = 3 (12 разделить на 4, равно 3)
16 ÷ 4 = 4 (16 разделить на 4, равно 4)
20 ÷ 4 = 5 (20 разделить на 4, равно 5)
24 ÷ 4 = 6 (24 разделить на 4, равно 6)
28 ÷ 4 = 7 (28 разделить на 4, равно 7)
32 ÷ 4 = 8 (32 разделить на 4, равно 8)
36 ÷ 4 = 9 (36 разделить на 4, равно 9)
40 ÷ 4 = 10 (40 разделить на 4, равно 10)

Картинка:

Деление. Картинка:

Таблица умножения и деления на 4 без ответов (по порядку и вразброс):

1 ∙ 4 =	3 ∙ 4 =	4 ÷ 4 =	36 ÷ 4 =
2 ∙ 4 =	6 ∙ 4 =	8 ÷ 4 =	32 ÷ 4 =
3 ∙ 4 =	1 ∙ 4 =	12 ÷ 4 =	28 ÷ 4 =
4 ∙ 4 =	4 ∙ 4 =	16 ÷ 4 =	24 ÷ 4 =
5 ∙ 4 =	2 ∙ 4 =	20 ÷ 4 =	16 ÷ 4 =
6 ∙ 4 =	7 ∙ 4 =	24 ÷ 4 =	20 ÷ 4 =
7 ∙ 4 =	10 ∙ 4 =	28 ÷ 4 =	12 ÷ 4 =
8 ∙ 4 =	5 ∙ 4 =	32 ÷ 4 =	8 ÷ 4 =
9 ∙ 4 =	9 ∙ 4 =	36 ÷ 4 =	4 ÷ 4 =
10 ∙ 4 =	8 ∙ 4 =	40 ÷ 4 =	40 ÷ 4 =

Способы записи таблицы умножения на 4:

x	Приподнятая точка	*	Знак не указан
1 x 4 = 4	1 ∙ 4 = 4	1 * 4 = 4	1 __ 4 = 4
2 x 4 = 8	2 ∙ 4 = 8	2 * 4 = 8	2 __ 4 = 8
3 x 4 = 12	3 ∙ 4 = 12	3 * 4 = 12	3 __ 4 = 12
4 x 4 = 16	4 ∙ 4 = 16	4 * 4 = 16	4 __ 4 = 16
5 x 4 = 20	5 ∙ 4 = 20	5 * 4 = 20	5 __ 4 = 20
6 x 4 = 24	6 ∙ 4 = 24	6 * 4 = 24	6 __ 4 = 24
7 x 4 = 28	7 ∙ 4 = 28	7 * 4 = 28	7 __ 4 = 28
8 x 4 = 32	8 ∙ 4 = 32	8 * 4 = 32	8 __ 4 = 32
9 x 4 = 36	9 ∙ 4 = 36	9 * 4 = 36	9 __ 4 = 36
10 x 4 = 40	10 ∙ 4 = 40	10 * 4 = 40	10 __ 4 = 40

Способы записи таблицы деления на 4:

/	:	÷	Знак не указан
4 / 4 = 1	4 : 4 = 1	4 ÷ 4 = 1	4 __ 4 = 1
8 / 4 = 2	8 : 4 = 2	8 ÷ 4 = 2	8 __ 4 = 2
12 / 4 = 3	12 : 4 = 3	12 ÷ 4 = 3	12 __ 4 = 3
16 / 4 = 4	16 : 4 = 4	16 ÷ 4 = 4	16 __ 4 = 4
20 / 4 = 5	20 : 4 = 5	20 ÷ 4 = 5	20 __ 4 = 5
24 / 4 = 6	24 : 4 = 6	24 ÷ 4 = 6	24 __ 4 = 6
28 / 4 = 7	28 : 4 = 7	28 ÷ 4 = 7	28 __ 4 = 7
32 / 4 = 8	32 : 4 = 8	32 ÷ 4 = 8	32 __ 4 = 8
36 / 4 = 9	36 : 4 = 9	36 ÷ 4 = 9	36 __ 4 = 9
40 / 4 = 10	40 : 4 = 10	40 ÷ 4 = 10	40 __ 4 = 10

Умножение на:

‹ Умножение на 3 Вверх Умножение на 5 ›

Тренировочные примеры по математике Табличное умножение и деление 2-3 кл Уч пос Кузнецова МИ

Система скидок при заказе с сайта
Сумма заказа	Скидка	Цена товара
до 5000 р.	10%	80
от 5000 р.	15%	76
от 10000 р.	20%	71
от 15000 р.	25%	67

Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения) для начальной школы.
В книге представлен материал, который позволит, с одной стороны, за короткое время выучить таблицу умножения, с другой — эффективно тренировать устойчивость внимания, оперативную память детей, умение сосредоточиться.
Дети, работая с пособием, научатся быстро и правильно умножать и делить числа, выполнять обратные математические операции с натуральными числами.
Для учителя данный материал является хорошим инструментом диагностики причин затруднений каждого ученика.
Пособие является необходимым дополнением к учебникам по математике, рекомендованным Министерством образования и науки Российской Федерации и включённым в Федеральный перечень учебников.
Приказом № 699 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных учреждениях.

Название магазина и адрес		Время работы магазинов		Остаток
Учебно-методический центр «Эдвис» г. Уфа, ул.50 лет СССР, 12 8 (347) 282-52-01		Пн-Сб: 09:00-20:00 Вс: 09:00-19:00		Мало

Название магазина и адрес		Время работы магазинов		Остаток
Учебно-методический центр «Эдвис» г. Уфа, ул.50 лет СССР, 12 8 (347) 282-52-01		Пн-Сб: 09:00-20:00 Вс: 09:00-19:00		Мало

Умножение и деление целых чисел Умножение и деление целых чисел
УМНОЖЕНИЕ
ПРАВИЛО 1: Произведение положительного целого числа на отрицательное число отрицательно.
ПРАВИЛО 2: Произведение двух положительных целых чисел положительно.
ПРАВИЛО 3: Произведение двух отрицательных целых чисел положительно.
Примеров:
Правило 1: 1. (+4) x (-2) = -8 2. (-2) x (+5) = -10
Правило 2: 1. (+6) x (+8) = +48 2. (+6) x (+2) = +12
Правило 3: 1. (-6) x (-8) = +48 2. (-2) x (-4) = +8
ОТДЕЛ
ПРАВИЛО 1: Частное положительного целого числа и отрицательного целого числа отрицательно.
ПРАВИЛО 2: Частное двух положительных целых чисел положительно.
ПРАВИЛО 3: Частное двух отрицательных целых чисел положительно.
Примеры:
Правило 1: 1. (-8) / (+4) = -2 2. (-12) / (+6) = -2
Правило 2: 1. (+6) / (-3) = -2 2. (+24) / (-6) = -4
Правило 3. 1. (+9) / (+3) = +3 2. (+16) / (+4) = +4
Правило 4: 1. (-6) / (-2) = +3 2. (-42) / (-7) = +6
ОБЗОР ПРАВИЛ УМНОЖЕНИЯ И ДЕЛЕНИЯ
Если знаки разные, то ответ отрицательный.
Если знаки одинаковые, ответ положительный
.
Проблемы:
(+3) х (-1) = __________
(+7) х (+6) = __________
(-5) х (-5) = ___________
(-8) х (-6) = ___________
(-12) х (+5) = _________
(+16) х (0) = __________
(-30) х (-3) = __________
(-18) х (+23) = ________
(-40) х (-4) = __________
(-11) х (+4) = _________
(+3) х (-8) = __________
(+15) х (0) = __________
(-7) х (-4) = ___________
(+9) х (+8) = __________
(+9) / (+3) = __________
(+10) /(-5) = __________
(-12) / (-3) = __________
(-25) / (+5) = __________
(-45) / (+15) = _________
(-18) / (-6) = __________
(+52) / (13) = __________
(-30) / (+10) = _________
(+14) / (-2) = __________
(+16) / (-4) = __________
(-42) / (+7) = __________
(4) / (2) = _____________
0 / (-7) = ______________
0 / (6) = ______________

Ключ ответа Умножение и деление целых чисел

42
25
48
60
0
90
414
160
44
24
0
28
72
3
2
4
5
3
3
4
3
7
4
6
2
0
0
Что такое делитель? — Определение, факты и примеры
Что такое делитель?
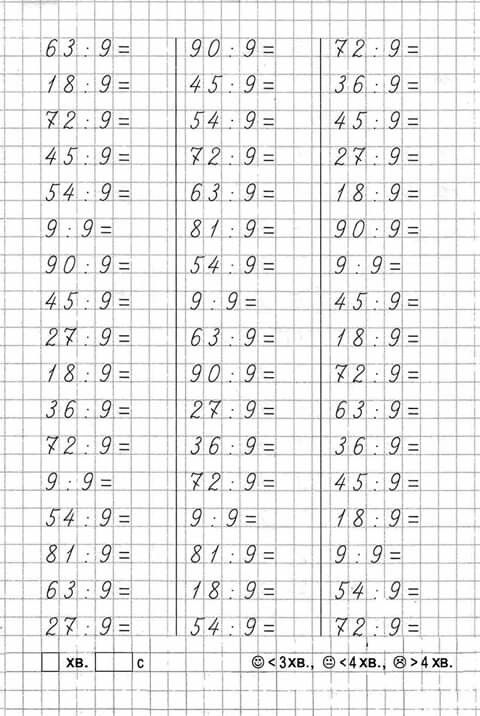
Делитель — это число, которое делит другое число полностью или с остатком.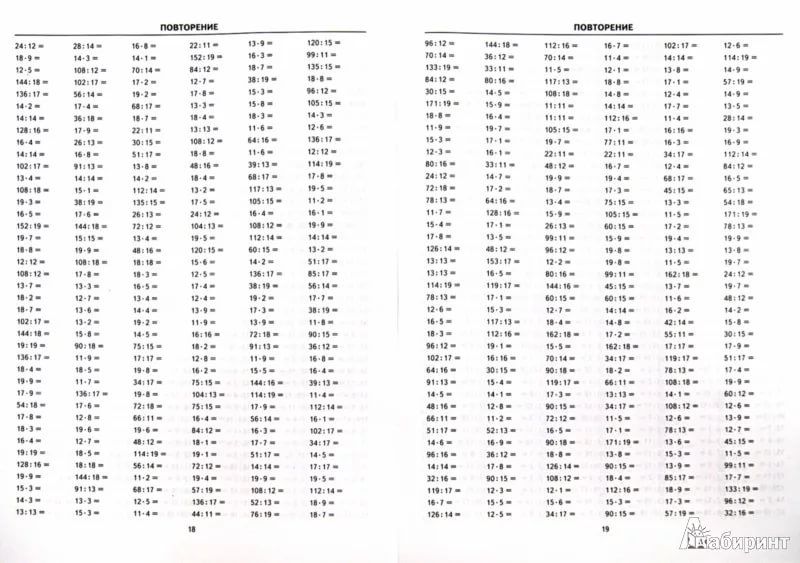
Делитель представлен в уравнении деления как:
Дивиденд ÷ Делитель = Частное.
Разделив 20 на 4, мы получим 5. Здесь 4 — это число, которое полностью делит 20 на 5 частей и называется делителем. Его уравнение деления
Точно так же, если мы разделим 20 на 5, мы получим 4. Таким образом, и 4, и 5 являются делителями 20.
Родственные игры
Делитель и множители
Делитель — это любое число, которое делится на другое число. Однако множитель — это делитель, который полностью делит число и не оставляет остатка. Итак, все делители числа являются его делителями. Но не все делители будут множителями.
В приведенном выше примере 4 и 5 — это множители 20. Если мы разделим 20 на 3, то 20 не будет полностью делиться. Таким образом, 3 не является множителем 20.
Давайте рассмотрим другой пример: 15 разделить на 5 дает 3. Здесь 5 — делитель. Кроме того, при делении 15 на 3 получается 5.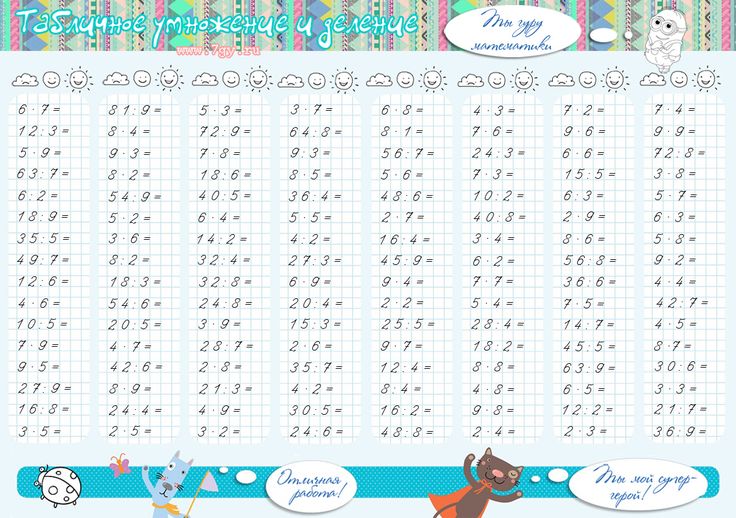 Здесь 3 — делитель.
Делители и делители числа 15: 1, 3, 5, 15
Связанные рабочие листы
Нахождение делителей числа
Чтобы найти делители числа, скажем, 12, выполните указанные шаги:
1 . Начните с 1 и запишите факты умножения так, чтобы произведение было 12, например 1 × 12.
2. Продолжайте таким же образом находить другие факты умножения, пока не найдем пару ближайших множителей или делителей, как указано:
1 × 12 , 2 × 6, 3 × 4
3. Запишите все числа в факте умножения, так как они являются делителями числа 12.
4. Итак, делители или множители числа 12 равны 1 ,2,3,4,6 и 12.
Различные способы представления делителя
Существуют разные стили выражения уравнения деления. На изображениях ниже показаны различные способы записи делителя:
Особые случаи
1. Число 1 является делителем всех чисел.
Причина : Если делитель равен 1, то частное равно делимому.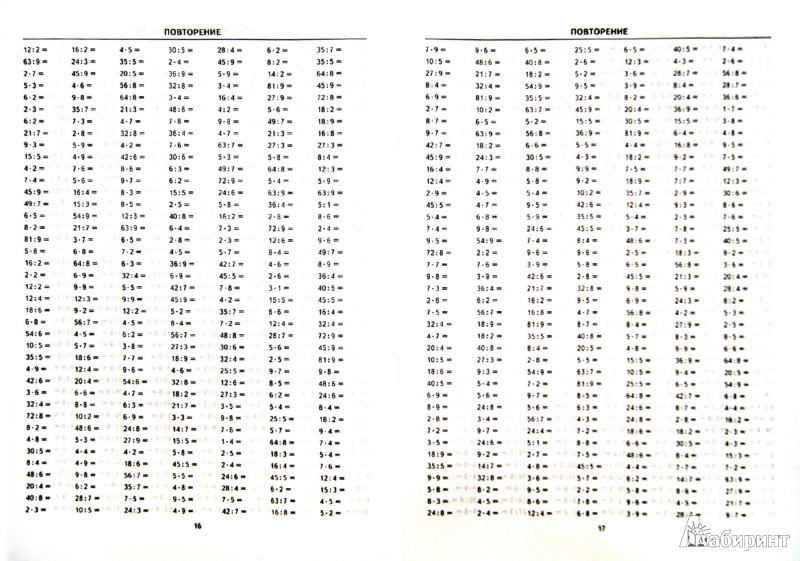
Посмотрите на приведенные примеры,
34 1 = 34
15 1 = 15
2. Само число всегда является одним из делителей числа.
Причина : Когда делитель совпадает с делимым, то ответ на такое деление всегда 1.
Посмотрите на приведенные примеры,
34 34 = 1
15 15 = 1
3. Если делитель меньше числа, чем делимое, то ответом является не целое число, а десятичное число.
Например, 510 = 0,5
Интересные факты
. Если удвоить делитель, частное будет вдвое меньше.
Практические задачи
1
Если 3 является делителем, какой из них даст остаток как 2?
37
47
57
67
Правильный ответ: 47
47 является правильным ответом, так как дает остаток 2 при делении на 3. Какое из следующих чисел имеет наибольшее количество делителей?
44
36
29
47
Правильный ответ: 36
36 имеет наибольшее количество делителей.
Делители 44: 1, 2, 4, 11, 22, 44.
Делители 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Делители 29: 1 и 29
Делители числа 47: 1 и 47
3
Какой наибольший общий делитель чисел 13 и 30?
3
2
1
13
Правильный ответ: 1
Делители 13: 1 и 13 :
1 Наибольший общий делитель чисел 13 и 30: 1
4
Какое из следующих чисел НЕ является делителем 14?
1
2
4
7
Правильный ответ: 4
Делители 14: 1, 2, 7, 14.
Часто задаваемые вопросы
В чем разница между делителем и делимым?
Когда мы делим два числа, то делимое число является делимым, а число, на которое мы делим, является делителем. Например, 12 конфет нужно разделить между 3 детьми. Итак, у нас есть 12 ÷ 3. Здесь 12 — делимое, а 3 — делитель.
Чем делитель отличается от множителя?
Делитель — это любое число, на которое делится другое число.