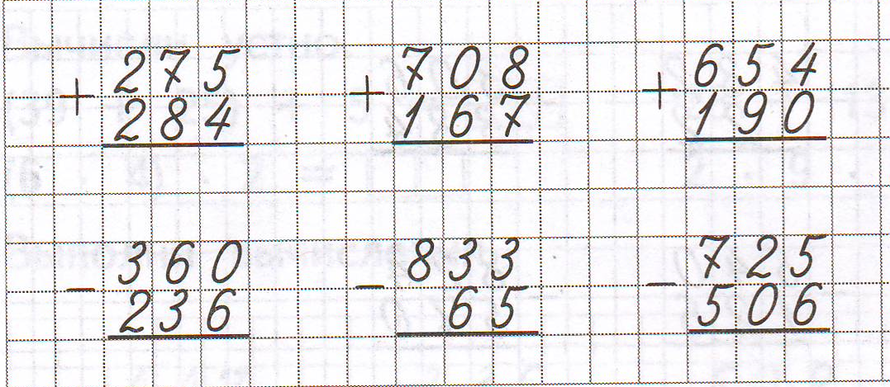Сложение чисел столбиком. Онлайн калькулятор
- Сложение однозначных чисел
- Сложение многозначных чисел
- Сложение столбиком
- Калькулятор сложения столбиком
Сложение однозначных чисел
Однозначные числа складывают, используя таблицу сложения. Таблицу сложения, а точнее результаты сложения однозначных чисел, нужно помнить наизусть.
Пример. Сложим однозначные числа 4 и 9:
4 + 9 = 13.
Сложение многозначных чисел
Многозначные числа складывают по разрядам, используя переместительный и сочетательный законы сложения.
Пример. Сложим двузначные числа 26 и 48:
26 + 48 = (20 + 6) + (40 + 8) = 20 + 6 + 40 + 8 = (20 + 40) + (6 + 8) = 60 + 14 = 60 + (10 + 4) = 60 + 10 + 4 = (60 + 10) + 4 = 70 + 4 = 74.
Сначала мы разложили слагаемые на разряды, затем сгруппировали в одну группу десятки, в другую — единицы и выполнили сложение по разрядам, т. е. сложили десятки с десятками и единицы с единицами, затем один десяток, получившийся от сложения единиц, прибавили к десяткам, которых у нас было 6 от сложения десятков, и в конце сложили десятки с единицами.
е. сложили десятки с десятками и единицы с единицами, затем один десяток, получившийся от сложения единиц, прибавили к десяткам, которых у нас было 6 от сложения десятков, и в конце сложили десятки с единицами.
Форма записи сложения, которую мы использовали, слишком длинная и потому неудобная, поэтому при сложении многозначных чисел обычно используется другая, более удобная форма записи, которая называется сложением столбиком.
Сложение столбиком
Сложение многозначных натуральных чисел удобней выполнять в столбик.
Сложение столбиком — это форма записи и способ сложения, используемый при сложении многозначных чисел. Сложение столбиком иначе ещё называют сложением в столбик.
Рассмотрим сложение столбиком на примере сложения чисел 7056 и 483.
Сложение в столбик записывается так: одно слагаемое записывается под другим так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т.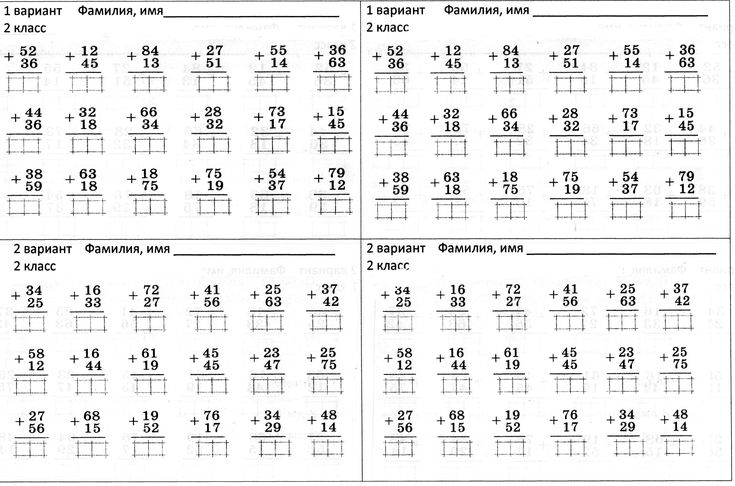 д.). Для удобства обычно меньшее число записывают под большим. Слева между слагаемыми ставится знак плюс, а под нижним слагаемым проводится горизонтальная черта:
д.). Для удобства обычно меньшее число записывают под большим. Слева между слагаемыми ставится знак плюс, а под нижним слагаемым проводится горизонтальная черта:
Полученную запись можно мысленно разбить на столбики так, как это показано на рисунке:
Все дальнейшие действия сводятся к сложению однозначных чисел, которые находятся в одном столбике. Вычисление выполняется поразрядно справа налево, начиная с разряда единиц.
Если в результате сложения получается число меньшее 10, то оно записывается под чертой в этом же разряде.
Начинаем вычисление с разряда единиц: складываем числа 6 и 3. В результате имеем число 9. Так как 9 < 10, то записываем это число под чертой, в том же разряде:
Если в результате сложения получается число, равное 10 или большее 10, то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа запоминается (оно используется на следующем шаге).
Переходим к сложению чисел в следующем разряде, то есть к сложению значений разряда десятков. Складываем числа 5 и 8, получаем число 13. Так как 13 > 10, то под чертой, в том же разряде, записываем число 3 (это значение разряда единиц числа 13), а число 1 запоминаем (это значение разряда десятков числа 13), при этом говорят три пишем, а один в уме
. Чтобы не забыть о запомненном числе, его обычно записывают сверху над следующим (слева) разрядом:
Запомненное число прибавляется к сумме чисел следующего разряда.
Переходим к следующему разряду и складываем числа 0 и 4. В результате имеем 4. К полученному числу прибавляем запомненное число 1, получаем 5. Так как 5 < 10, то под чертой, в том же разряде, записываем число 5:
После этого происходит переход на один разряд влево и действия повторяются. Данный процесс продолжается до тех пор, пока числа не закончатся.
Если в столбике содержится только одно число, и у нас нет запомненного числа (от предыдущего сложения), в этом случае мы просто записываем это число под чертой, в том же разряде.
Так как в следующем столбике находится лишь одно число — 7, и в памяти у нас нет запомненного числа, то мы просто записываем 7 под чертой, в том же разряде:
Дальше никаких чисел нет и в памяти тоже чисел нет. На этом процесс сложения можно считать завершённым. Натуральное число, получившееся под чертой, является результатом сложения данных чисел. Теперь можно записать сумму данных чисел в обычном виде:
7056 + 483 = 7539.
Рассмотрим ещё пару примеров сложения столбиком, чтобы разобраться с оставшимися нюансами.
Пример 1. Сложим числа 29 и 6 столбиком.
Складываем 9 и 6, в результате получаем число 15. Так как 15 > 10, то число 5 записываем, а число 1 запоминаем:
Если в столбике содержится только одно число, и у нас имеется запомненное число (от предыдущего сложения), то запомненное число просто прибавляется к этому одному числу.
В следующем столбике находится лишь одно число — 2. Так как у нас в памяти имеется число 1, то его нужно прибавить к 2. В результате получаем число 3:
В результате получаем число 3:
Дальше никаких чисел нет и запомненного числа тоже нет, следовательно, сложение столбиком завершено.
Пример 2. Сложим столбиком числа 43 и 94.
Складываем 3 и 4. В результате имеем число 7. Так как 7 < 10, то записываем это число под чертой, в том же разряде:
Если в последнем разряде в результате сложения получается число, равное 10 или большее 10, то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа записывается под чертой в следующий разряд.
В следующем разряде складываем числа 4 и 9, получаем число 13. Так как 13 > 10, то под чертой, в том же разряде, записываем число 3, а число 1 записываем под чертой в следующий разряд:
Дальше никаких чисел нет и в памяти числа тоже нет, следовательно, сложение в столбик завершено.
Удобство сложения в столбик заключается в том, что сложение многозначных натуральных чисел фактически сводится к сложению однозначных чисел и запись процесса сложения занимает меньше места.
Калькулятор сложения столбиком
Данный калькулятор поможет вам выполнить сложение столбиком. Просто введите слагаемые и нажмите кнопку Вычислить
.
Комплект карточек (10) «Обучающий калейдоскоп. Сложение и вычитание в столбик»
Навигация:Главная›Для школ›Учебно-наглядные пособия и оборудование›Начальная школа›Математика›Раздаточные пособия›Комплект карточек (10) «Обучающий калейдоскоп. Сложение и вычитание в столбик»
В избранномВ избранное Артикул: 10697 Цена: предоставляется по запросу Задать вопрос по оборудованию | ||||||||||
Назначение Используется вместе с наглядно-дидактическим пособием «Обучающий калейдоскоп» Технические характеристики и комплектность
Пособие состоит из 10 полноцветных, напечатанных на картоне и ламинированных пленкой карточек. Карточки снабжены маркировкой, где буква обозначает предмет, первая цифра – код темы, вторая цифра – порядковый номер (тему) карточки в серии, последняя цифра – вариант (I или II). М18.1.I, М18.1.II. Нахождение числа, записанного словами. Повторение и закрепление знания разрядов многозначных чисел.Рекомендуется использовать во 2, 3 и 4 классах как задания для устного счета. М18.2.I, М18.2.II. Для учащихся 3 и 4 классов. М18.3.I. Для учащихся 3 и 4 классов. Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд. В четырех заданиях из десяти требуется отыскать число, обозначающее пропущенный разряд вычитаемого или одного из слагаемых. М18.3.II. Для учащихся 3 и 4 классов. Действия с многозначными числами, оформленные в таблицу, в которой необходимо правильно выбрать действие сложения или вычитания, опираясь на название компонента действия (уменьшаемое, вычитаемое, разность, слагаемое, сумма), и произвести вычисления, используя данные таблицы.Рекомендуется записывать решения в тетрадь. М18.4.I. Для учащихся 3 и 4 классов. Действия с многозначными числами, оформленные в таблицу, в которой необходимо правильно выбрать действие сложения или вычитания, опираясь на название компонента действия (уменьшаемое, вычитаемое, разность, слагаемое, сумма), и произвести вычисления, используя данные таблицы. М18.4.II. Для учащихся 3 и 4 классов. Действия с трехзначными числами, оформленные в таблицу. Необходимо правильно выбрать действие сложения или вычитания и произвести вычисления, опираясь на данные таблицы, в которой указаны длины сторон треугольника и периметр. Рекомендуется записывать условия и решение в тетрадь. М18.5.I. Для учащихся 3 и 4 классов. Сложные примеры на все действия с определением порядка действий и последовательных вычислений, для которых потребуется вычислять в столбик. Задания оформлены в схемы. Не рекомендуется предлагать учащимся выполнение всех десяти заданий сразу. Рекомендуется использовать в качестве дополнительных упражнений по одному–два задания на уроке.Выполнение заданий развивает логику и требует высокой концентрации внимания. М18.5.II. Текстовые задачи в несколько действий на сложение и вычитание многозначных чисел. ← Назад |
Инженерные классы
Образовательные робототехнические модули
WS Junior — Мехатроника Festo
Учебно-наглядные пособия и оборудование
- Анатомия
- Биология
- География
- ИЗО, МХК
- Иностранный язык
- История
- Литература
- Математика
- Начальная школа
- НВП
- ОБЖ
- Русский язык
- Труд
- Физика
- Химия
- Музыка
- Черчение
- Астрономия
- Информатика
- Физическая культура
Точки роста
Мультимедийное оборудование
3D Принтеры
Учебное оборудование Phywe.
Учебные лаборатории ФГОС.
Инновационное оборудование. Переносные лаборатории
Инновационное оборудование. Цифровые учебные лаборатории
Национальный проект «Образование»
Урок математики в 4 классе
1
#4 класс #Математика #ФГОС #Методические разработки #Урок #Учитель начальных классов #Школьное образование #УМК «Школа России»
Нажмите, чтобы скачать публикацию
в формате MS WORD (*. DOC)
DOC)
Размер файла: 318.16 Кбайт
Скачать
презентацию
Просмотреть
презентацию
Конкурсная работа Всероссийский дистанционный конкурс для учителей начальных классов «Конспект урока с мультимедийным сопровождением» |
План-конспект урока по математике в 4 классе.
Раздел: Числа, которые больше 1000. Сложение и вычитание (1урок)
Тип урока: урок открытия нового знания и комплексного применения знаний.
Цели: Формирование умения письменно и устно складывать многозначные числа.
— Способствовать развитию умений применять переместительное и сочетательное свойства сложения;
— выбирать удобный способ для устных и письменных вычислений;
— решать и составлять текстовые задачи.
Планируемые образовательные результаты:
Предметные: научатся применять переместительное и сочетательное свойства сложения, выбирать удобный способ для устных и письменных вычислений, решать текстовые задачи.
Метапредметные: создать условия для обучающихся: понимать учебную задачу, отвечать на вопросы, обобщать собственные представления; слушать собеседника и вести диалог, оценивать свои достижения на уроке; извлекать информацию из разных источников.
Регулятивные УУД
принимать и сохранять учебную задачу; в сотрудничестве с учителем ставить учебные задачи;
планировать свои действия в соответствии с поставленной задачей;
адекватно воспринимать оценку своей работы учителем и уч-ся;
учиться строить высказывания, определять цели конкретного задания, проверять и оценивать результаты работы.
Познавательные УУД
поиск и выделение необходимой информации
структурирование знаний
постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении примеров
выбор наиболее эффективных способов решения
Коммуникативные УУД
умение с достаточной полнотой и точностью излагать свои мысли
участвовать в коллективном обсуждении проблемы
приходить к общему решению
Личностные: проявляют интерес, переходящий в потребность к расширению знаний, к применению поисковых и творческих подходов к выполнению заданий, использовать в общении правила вежливости.
Технологии: деятельностного и проблемного обучения.
Методы: репродуктивный, частично – поисковый, критического мышления, метод контроля.
Формы: фронтальная, индивидуальная, групповая, парная
Оборудование: мультимедийный проектор, компьютер, презентация,
учебник «Математика» М.И.Моро, 4 класс, 2018г., индивидуальные доски, буклеты «Муйский район», листы самооценки.
Этапы урока:
Мотивация к учебной деятельности (1 мин).
Актуализация знаний и фиксация затруднений в пробном действии (6 мин).
Выявление места и причины затруднения (1 мин).
IV. Построение проекта выхода из затруднения (2 мин).
V. Реализация построенного проекта (10 мин).
VI. Первичное закрепление во внешней речи (5 мин).
Физкультминутка (2 мин).
VII. Самостоятельная работа с самопроверкой по эталону (5 мин).
VIII. Включение в систему знаний и повторения (5 мин).
IX. Рефлексия учебной деятельности (2 мин).
X. Домашнее задание (1мин).
Ход урока:
I.Орг. момент. Мотивация к учебной деятельности.
— Добрый день, друзья! В уголке «Хогвартса» опять письмо! Прочитаем?
Здравствуйте, дорогие ребята 4Б класса!
Мы рады проинформировать вас о том, что для успешного зачисления в Школу чародейства и волшебства «Хогвартс», вам предлагается составить математические задачи для наших учеников. Пожалуйста, отразите в текстах задач сведения про школу, посёлок или район. С нетерпением ждём вашу сову не позднее 1 декабря 2019г. Желаем удачи!
Искренне ваша, заместитель директора Минерва МакГонагалл.
Выполним просьбу? Я предлагаю оставить это задание на математический десерт, т. к. сначала надо изучить тему урока. Хорошее настроение у всех? Пусть для нас всех на уроке сопутствует успех!
к. сначала надо изучить тему урока. Хорошее настроение у всех? Пусть для нас всех на уроке сопутствует успех!
— Запишите в тетрадь — число и классная работа.
II. Актуализация знаний: 1. Мин-ка чистописания: Какое многозначное число можно составить, используя эту информацию? Допишем год. Отделим классы.
— Какое число получилось? (27 11 19)
-Что мы можем сказать о данном числе? — Какие классы присутствуют?
-Назовите единицы каждого разряда в каждом классе. Какой наивысший?
-Запишите соседей числа (271 118, 271 120)
На сколько последующее больше предыдущего? Как узнали?
Мы это всё знаем? Зачем повторяем? (Пригодятся для усвоения новых знаний).
III. Самоопределение к деятельности. 1. Устный счет:
Посмотрите на доску: 164 + 45 + 36 + 355 — Если уметь применять свойства сложения, то значение выражения можно вычислить устно (см. уч-к с.104) — Озвучьте эти св-ва:
уч-к с.104) — Озвучьте эти св-ва:
1)От перестановки слагаемых сумма не изменяется (переместительный) 2)Два соседних слагаемых можно заменить их суммой (сочетательный)
-Какое свойство применим? Вычислите. (164 + 36) + (355 + 45) = 200 + 400 = 600
— Примените правила сложения, выполнив задание на с.60 №260
Работа в парах (В парах по 1 примеру каждому ряду, 1-й все) 2 й– 1 ряд 3 й– 2 ряд 4й –3 ряд ( +, — в листе самооценки).
2. Фиксация затруднений в пробном действии. Выявление места и причины затруднения.
345+345 (690)
3456+3456 (6 912)
34 567 + 34 567 (69 134)
— Выберете себе пример по силам и решите.
Желающие выйдите к доске. Проверьте и поставьте +, — в листе самооценки.
— Чем отличаются примеры? (количеством цифр в числах)
— Объясните решение первого примера, выполнив запись столбиком (в тетради)
— Складывали ли мы четырехзначные числа столбиком? (нет)
— Кто сможет объяснить, как решить второй пример? (Желающий ученик решает пример на доске с объяснением)
— Кто сможет сложить пятизначные числа столбиком? (Желающий ученик решает пример на доске с объяснением)
— А теперь проверьте решение последнего примера вычитанием.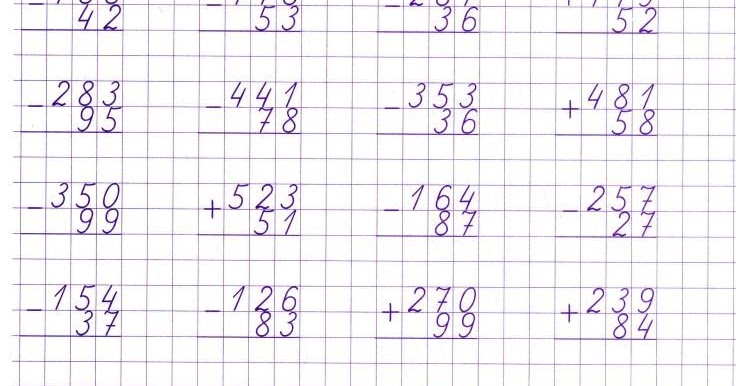 Кто сможет это сделать? (Желающий ученик решает пример на доске с объяснением)
Кто сможет это сделать? (Желающий ученик решает пример на доске с объяснением)
— Какой вывод можно сделать? (многозначные числа складывают и вычитают столбиком так же, как трехзначные).
IV. Сообщение темы, цели урока.
— Какова будет тема урока? (Сложение и вычитание многозначных чисел столбиком).
Что нам нужно вспомнить для данной темы?
(алгоритм сложения и вычитания в столбик, разряды и классы).
— Сформулируйте цели урока.
1. Научимся выполнять сложение и вычитание многозначных чисел столбиком.
2. Повторим алгоритм письменного сложения и вычитания многозначных чисел.
3. Включим новые знания в решение задач и уравнений.
— Начнём выполнять задачи?! Но сначала отдохнём.
Физминутка: «До чего дошёл прогресс» (движения под музыку)Приключения Электроника. mp3
mp3
— Надо ли нам уметь складывать и вычитать многозначные числа, если прогресс довёл человечество до роботов, вычислительной техники?
V. Изучение нового материала. 1.Работа по учебнику.
— Сравним наш вывод с выводом в учебнике. — Прочитайте текст рядом с красной чертой на с.60 — Применяя этот вывод, проверьте решение примеров на слайде №2. Кто прав: Маша или Миша? — Что необходимо знать и уметь, чтобы успешно выполнять +,- многозн.ч.?
— Но для этого составим алгоритм сложения и вычитания многозначных чисел. 2. Работа в парах: Составление алгоритма сложения и вычитания многозначных чисел. Алгоритм:
Работа в парах: Составление алгоритма сложения и вычитания многозначных чисел. Алгоритм:
1. Пишу сотни тысяч под сотнями тысяч, десятки тысяч под десятками тысяч, единицы
под единицами и т.д
2. Складываю единицы
3. Складываю десятки
4. Складываю сотни
Итог: (по слайду №3)
………………………
5. Читаю ответ
(аналогично с вычитанием)
3. Самостоятельная работа. Решите 2 примера самостоятельно с самопроверкой (по слайду №4,5)
385 746 + 23 352 = 409098
409 098 – 385 746 = 23 352
Самооценка в листах.
VI. Первичное закрепление. Разноуровневая самостоятельная работа. (Примеры на слайде №6)
Разноуровневая самостоятельная работа. (Примеры на слайде №6)
– Теперь каждый из вас может попробовать свои силы, выбрав задание. Прочитайте задания на слайде и выберите то, с которым вы справитесь.
Уровень 1.
Выполни вычисления.
+4235 _36798
1943 19467
Уровень 2.
Вычисли, записывая решение столбиком.
18506 + 32993
14238 – 2387
Уровень 3.
Вычисли, записывая решение столбиком, и проверь сложение вычитанием, а вычитание сложением.
13534 + 32994 126547 – 79652
Самопроверка по слайду. Вывод:1.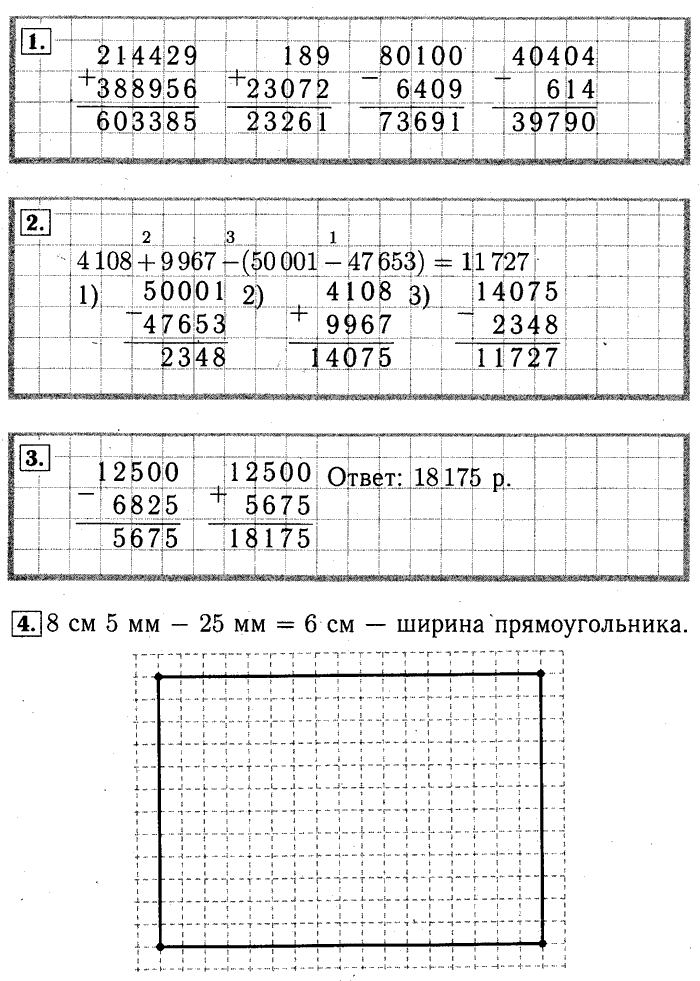 Если надо что-нибудь посчитать устно, то иногда это можно сделать быстрее и легче, пользуясь переместительным и сочетательным свойствами сложения. 2.При сложении и вычитании многозначных чисел числа записывают одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда. 3.Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел. 4.Проверяем сложение вычитанием, а вычитание сложением.
Если надо что-нибудь посчитать устно, то иногда это можно сделать быстрее и легче, пользуясь переместительным и сочетательным свойствами сложения. 2.При сложении и вычитании многозначных чисел числа записывают одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда. 3.Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел. 4.Проверяем сложение вычитанием, а вычитание сложением.
VII. Включение в систему знаний и повторения. Решение задач.
1.Коллективная работа: С. 60 №264— чтение, разбор, решение дифференцированно: сам-но, на индив. досках 2 уч-ся, схемы-опоры для нуждающихся.
60 №264— чтение, разбор, решение дифференцированно: сам-но, на индив. досках 2 уч-ся, схемы-опоры для нуждающихся.
2.Работа в группах. (Письмо с заданием из Хогвартса).
— Давайте выполним просьбу учеников из Хогвартса.
-Наша цель — составить задачи про Муйский район, п.Таксимо. Т.к. тема: сложение вычитание многозначных чисел, то и задачи составим с многозначными ч. Помогут вам буклеты и рекомендации. (Раздаю конверты с материалами).
VIII. Рефлексия:
— Какая цель была поставлена на уроке? — Удалось выполнить?
IX. Итог: Самооценка (лист): —Посчитайте баллы и поставьте себе отметку. Кто желает озвучить свою отметку, пожалуйста!
X. Домашнее задание: (Слайд №7) Стр. 60 № 263, №265, №266 (по выбору 2 номера).
Дополнительно: Посмотрите на №261. Прочитайте (объясни, что обозначают в рамках на полях записи)
(1)Если к числу прибавить 0, то получится тоже самое число;
2)если к 0 прибавить число, то получится тоже самое число;
3)если из числа вычесть 0 – то получится такое же число;
4)если от числа вычесть такое же число, то получится 0)
Эти свойства нам тоже пригодятся при решении примеров.
Приложение 1. Письмо в уголке «Хогвартс»
Приложение 2. Письмо из «Хогвартса».
ШКОЛА ЧАРОДЕЙСТВА И ВОЛШЕБСТВА «ХОГВАРТС»
Здравствуйте, дорогие ребята 4Б класса!
Мы рады проинформировать вас о том, что для успешного зачисления в Школу чародейства и волшебства «Хогвартс», вам предлагается составить математические задачи для наших учеников. Пожалуйста, отразите в текстах задач сведения про школу, посёлок или район. С нетерпением ждём вашу сову не позднее 1 декабря 2019г. Желаем удачи!
Искренне ваша, заместитель директора Минерва МакГонагалл.
Приложение 3. Лист самооценки.
№1 | №2 | №3 | №4 | Итого |
2б –правильно, 1б–частично, 0б — неверно 7-8б – «5», 5-6 б – «4», 3-4б – «3» Твоя оценка: __ Оценка учителя: __ | ||||
Приложение 4. Буклеты «Муйский район»
Буклеты «Муйский район»
Приложение 5. Рекомендации для групп:
№1. Составить текст задачи на +, — многозначных чисел. Например, о горе Таксима.
№2. Составить текст задачи на +, — многозначных чисел. Например, о горе Муйский Гигант.
№3. Составить текст задачи на +, — многозначных чисел. Например, о численности населении Муйского района.
№4.Составить текст задачи на +, — многозначных чисел. Например, о том, сколько лет исполнилось Муйскому району.
№5.Составить текст задачи на +, — многозначных чисел. Например, о том, сколько лет исполнилось п.Таксимо.
Приложение 5. Составленные задачи в группах.
1. Городское население Муйского района составляет 8 431чел, сельское – 1 212 ч. Какова общая численность населения? (9 643)
Какова общая численность населения? (9 643)
2. Посёлок Таксимо официально был основан в 1964 году. Сколько лет нашему посёлку? (55)
3. Образован Муйский район в 1989 г. Сколько лет Муйскому району? (30)
4. Высота г. Таксима 1497м. В первый день туристы забрались на высоту 1050м. На сколько км им осталось подняться?
5. Высота Муйского гиганта 3067 м, Северо-Муйского хребта 2537м. На сколько метров Муйский гигант выше Северо-Муйского хребта?
Приложение 6. Самоанализ урока.
Цель урока включала в себя три аспекта, реализация которых на уроке позволила создать условия для эффективного обучения, развития и воспитания учащихся.
Задачи сформулированы в совместной деятельности с учетом субъективного опыта учащихся. Отражают формирование УУД.
Содержание урока соответствует целям, задачам и дидактическим принципам УМК.
Этапы четкие, логичные, завершенные. Переход к новым этапам осуществляется с помощью проблемных связок. Организация учебной деятельности оптимальная.
Формы адекватны целям и задачам. Организуется включение учащихся в следующие формы УД: индивидуальную, парную, групповую, самостоятельную.
На уроке созданы условия для формирования универсальных учебных действий учащихся.
Познавательные УУД формируются через совместную с учителем работу по извлечению информации из учебника, памяток, буклетов, что позволяет реализовать задачи НРК.
Регулятивные УУД формируются через умение формулировать тему, цели урока, составление алгоритма, контролировать и оценивать свою деятельность с учётом рекомендаций учителя.
Коммуникативные УУД формируются через сотрудничество с учителем и одноклассниками, коллективное обсуждение учебной задачи, работу в паре, участие в групповой работе по созданию текстов задач, слушание выступлений товарищей, дополнение и оценку их ответов.
Личностные УУД формируются через применение субъектного опыта учащихся, проявление интереса, переходящего в потребность к расширению знаний и применению поисковых и творческих подходов в выполнении задания — составление задач о малой родине, соблюдение в работе правил этики.
Задача этапа мотивации направлена на создание положительного эмоционального настроя и предвосхищение интересного окончания урока.
На этапе актуализации знаний и фиксации затруднений в пробном действии создана ситуация успеха через воспроизведение обучающимися знаний, необходимых и достаточных для открытия нового способа.
На этапе выявления причины затруднения и построения проекта выхода из затруднения сформулирована цель урока.
На этапе открытия новых знаний учащиеся построили шаги, которые необходимо сделать для реализации поставленной цели – алгоритм письменного сложения и вычитания многозначных чисел.
В ходе проведения самостоятельной работы учащиеся выполняют задания нового типа, осуществляют самопроверку по образцу, действуя согласно алгоритму, выявляют и корректируют ошибки, определяют способы действий.
На этапе первичного закрепления предложены разноуровневые задания, что создаёт ситуацию успеха для каждого обучающегося.
На этапе включения нового знания в систему знаний и повторения ученикам предложено творческое задание — составление задач, связанных с НРК.
На этапе рефлексии организован анализ учебной деятельности и оценивание учащимися собственных достижений. Учащиеся определили уровень усвоения материала, определили значимость данного урока.
В домашнем задании имело место право выбора. С помощью учителя были определены перспективы дальнейшего обучения по данной теме.
Урок проведён в соответствии с требованиями технологии системно- деятельностного подхода. С целью избегания переутомления использовалась физкультминутка.
На всех этапах урока прослеживалась положительная мотивация к учебной деятельности, создавались ситуации успеха.
Организация контроля рациональна, обеспечивала обратную связь. Оценивание осуществлялось на критериальной основе с помощью оценочных листов, не только по конечному результату, но и в процессе всего урока.
Оценивание осуществлялось на критериальной основе с помощью оценочных листов, не только по конечному результату, но и в процессе всего урока.
Соблюдены принципы построения урока: системно-деятельностный подход, уровневая дифференциация, критериальное оценивание. Таким образом, цели и задачи урока реализованы. Урок соответствует требованиям ФГОС.
Сравнивая желаемый результат с реальным, делаю вывод о том, что поставленные цели, отбор содержания, выбор форм, методов, приемов и средств обучения работали на результат, который показал, что все аспекты цели реализованы с небольшими ошибками.
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
Чтобы написать комментарий необходимо авторизоваться.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Прыгай, разделяй или добирайся до следующих 10: стратегии обучения математике изменились с тех пор, как родители учились в школе
Исследования показывают, что родители оказывают значительное влияние на обучение своих детей, но некоторым из них не хватает уверенности в себе, чтобы оказывать поддержку дома. Чтобы помочь родителям вовлечь своих детей в изучение математики, Беседа попросила старшего научного сотрудника ACER Кэт Пирн объяснить три стратегии сложения и вычитания, которые теперь преподаются в начальной школе.
Я уверен, что большинство людей помнят попытки освоить определенное математическое правило или процедуру в начальной или средней школе.
У моей пожилой матери есть история о том, как ее отец помогал ей с домашним заданием по арифметике. Она помнит, как расстроилась из-за того, что ее отец поступил не так, как в школе. Я подозреваю, что ее отец был в состоянии произвести вычисления в уме, а не школьным способом, который заключался в использовании вертикального алгоритма.
Ожидается, что учащиеся сначала будут складывать числа в столбце единиц (справа), а затем — в столбце десятков (слева). Задача усложняется, когда сумма столбца единиц превышает 10 — тогда вам нужно «обменять» десять единиц на одну десятку.
Учащиеся, ответившие как 713, а не как правильный ответ 83, возможно, начали сначала со столбца десятков. Или они могли написать 13 в колонке единиц вместо того, чтобы обменивать десять единиц на одну десятку.
Формальные школьные алгоритмы по-прежнему используются для больших чисел и десятичных знаков, но мы рекомендуем учащимся использовать любую стратегию, которую они предпочитают для сложения двузначных чисел.
Проблема с преподаванием правил заключается в том, что многие ученики с трудом запоминают, когда применять правило, потому что они не понимают, как и почему оно работает.
В австралийской учебной программе: математика говорится, что к концу 2-го года учащиеся будут «выполнять простые вычисления на сложение и вычитание, используя ряд стратегий». К концу 4 года они будут «определять и объяснять стратегии нахождения неизвестных величин в числовых предложениях».
К концу 4 года они будут «определять и объяснять стратегии нахождения неизвестных величин в числовых предложениях».
Мы хотим, чтобы дети помнили, как решать эти уравнения в уме, а не полагались на запись процесса. Вот три стратегии, которые школы используют, чтобы научить детей складывать и вычитать двузначные числа.
1. Стратегия разделения
Эту стратегию иногда называют стратегией разложения, разделения или частичной суммы.
Вы можете прибавлять или вычитать десятки отдельно от единиц (или единиц). Например, используя стратегию разделения, чтобы добавить 46 + 23, вы должны:
разделить каждое число (разложить) на десятки и единицы: 46 + 23 = 40 + 6 + 20 + 3
переставить десятки и единицы: 40 + 20 + 6 + 3
добавить десятки, а затем единицы 60 + 9= 69
Использование стратегии разделения для сложения, например 37 + 65, будет аналогичным, но будет дополнительный шаг:
разделить или разложить числа на десятки и единицы: 30 + 7 + 60 + 5
переставить десятки и единицы: 30 + 60 + 7 + 5
добавить десятки, а затем единицы: 90 + 12
разделить 12 (10 + 2), чтобы получить: 90 + 10 + 2 = 100 + 2 = 102
Многие учащиеся считают стратегию разделения более сложной для вычитания, чем для сложения. Это потому, что есть больше шагов, если выполнять эту стратегию в уме.
Это потому, что есть больше шагов, если выполнять эту стратегию в уме.
Для вычитания, например 69-46, вы должны:
разделить или разложить каждое число на десятки и единицы: 60 + 9 – (40 + 6)
снять скобу: 60 + 9 – 40 – 6
переставить десятки и единицы: (60 – 40) + (9 – 6)
вычесть десятки, затем единицы: 20 + 3 = 23
Студенты часто делают ошибки на третьем шаге. Успешные студенты могут сказать: «Я беру 40 из 60, затем 6 из 9». Неуспевающие студенты скажут: «Я отнимаю 40 от 60, затем добавляю 6 и 9».
Учащиеся, успешно использующие эту стратегию, показывают, что они понимают значение разряда (значение каждой цифры в числе) и знают математические правила, необходимые для алгебры.
2. Стратегия перехода
Эту стратегию иногда называют последовательностью или накопительной стратегией суммирования. Реальные предпринятые шаги зависят от уверенности и способностей учащихся.
Некоторые учащиеся добавляют десятки или единицы, в то время как другие добавляют или вычитают десятки, а затем единицы.
Например, сложение 46 + 23 с использованием стратегии прыжка может выглядеть так:
или
Две версии этой стратегии могут быть показаны с использованием пустой числовой строки. Использование пустой или пустой числовой строки позволяет учащимся записывать свои мысли, а учителям анализировать свои мысли и определять стратегию, которую они пытались использовать.
CC BY-NDВычитание 69–46 со стратегией перехода может быть выполнено с помощью:
или
CC BY-ND3. Стратегия «Дойти до следующих десяти»
Иногда ее называют компенсационной или сокращенной стратегией. Он включает в себя корректировку одного числа, чтобы упростить решение задачи.
Стратегия «Попасть в следующую десятку» основана на стратегии «Друзья десяти».
Многие учащиеся первых классов начальной школы составляют все комбинации из двух однозначных чисел, которые в сумме дают десять.
9 + 1, 8 + 2, 7 + 3, 6 + 4, 5 + 5 …
Их иногда называют радужными фактами, поскольку дети создают радугу, соединяя два числа вместе. Например, 9 может быть на одном конце цвета радуги, а 1 — на другом.
Объединяя числа таким образом, учителя надеются, что учащиеся поймут, что ответ для 9 + 1 такой же, как 1 + 9.
заданное число (например, следующее кратное десяти), а затем скорректировать число, вычитая то, что было добавлено, или добавляя то, что было вычтено.
На диаграммах отношения обозначены стрелками.
CC BY-NDТаким образом, чтобы добавить 37 + 65, вы должны
прибавьте 3 к 37, чтобы получить 40.
вычесть 3 из 65, чтобы получить 62
получается: 40 + 62 = 102.
Если вычесть 102 – 65, получится:
вычесть 2 из 102, чтобы получить 100
вычесть 2 из 65, чтобы сохранить баланс
это становится 100 — 63 = 37.

Многие учащиеся, использующие эту стратегию, неправильно прибавляют 2 к 65 вместо вычитания 2.
Почему эти стратегии?
Студенты использовали все эти стратегии или некоторые их формы в своей голове на протяжении поколений. Но в течение многих лет ожидалось, что учащиеся будут использовать формальный письменный алгоритм, а не свои собственные мыслительные стратегии.
Введение пустой или пустой числовой строки позволило учащимся записывать свои мыслительные стратегии, что позволяло учителям и родителям их видеть. Именование этих стратегий позволило учителям и учащимся обсудить возможные стратегии, используя общий словарь.
Вместо того, чтобы учить правилам и процедурам, теперь нам нужно поощрять учащихся объяснять свои стратегии, используя как конкретные материалы, так и диаграммы, чтобы продемонстрировать свои знания о сложении и вычитании. ■
Дополнительная информация:
Эта статья Кэт Пирн, старшего научного сотрудника, Австралийского совета по исследованиям в области образования, , переиздана из The Conversation под лицензией Creative Commons.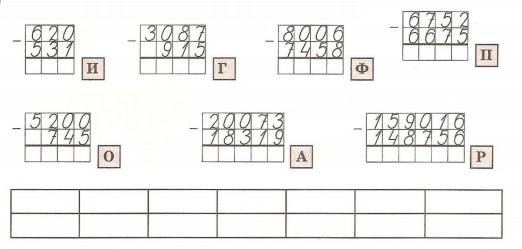 Прочитайте оригинальную статью.
Прочитайте оригинальную статью.
Сложение и вычитание денег | 3 класс
Использование денег — важный жизненный навык.
В этом уроке мы узнаем, как из прибавить и из вычесть деньги .
Добавление денег
Предположим, вы покупаете какие-то товары в супермаркете.
Чтобы узнать общую стоимость товаров, которые вы покупаете, вам нужно добавить денег .
Предположим, вы хотите купить эти два предмета.
Сколько вы должны заплатить за них? 🤔
👉 Сначала напишите суммы в столбце , форме или по вертикали .
Совет: Вам нужно написать только знак доллара с первой цифрой.
Когда вы пишете числа, следите за тем, чтобы десятичные точки были выровнены вверх по правильно.
A десятичное число точка — это точка , которая отделяет доллара на его слева и цента на его справа .
Начнем с добавления крайних правых цифр, затем идем налево.
Не забывайте , чтобы уменьшить десятичную точку и знак доллара , когда будете писать свой ответ.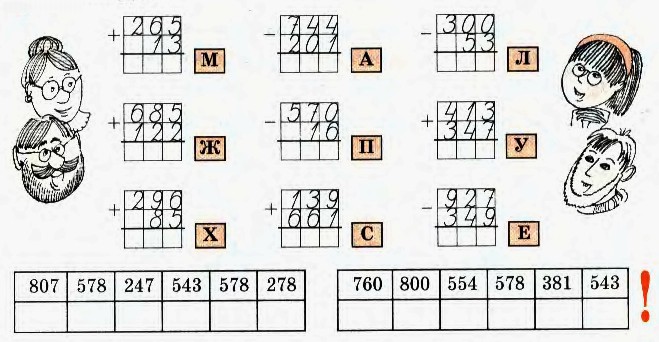
Мы видим, что в сумме получается $2,95 ! ✅
Это 2 доллара и 95 центов. 😃
Другой пример
Вы покупаете два пазла. Каждая головоломка стоит 91 263 $ 2,85 91 264 .
Сколько вы должны заплатить за это? 🤔
Вам просто нужно удвоить сумму . Double означает к добавить сумму к самому .
👉 Теперь мы расставляем числа в столбце из сначала.
Обязательно строка до десятичная точки.
👉 Затем мы добавляем к цифры .
Складываем цифры в столбце Сотые первый .
Совет: Столбец Hundred ths отличается от столбца Hundreds (нет — ths )!
Видим, что нам нужно 9с 1263 по перегруппировать .
Помещаем 0 в разряд сотых и переносим 1 в столбец десятых.
Затем мы добавляем цифры в десятых столбце .
8 + 8 + 1 = 17
Remember to add the 1 that we carried over .
=Мы пишем 7 на десятом месте и переносим 1 в колонку долларов.
Наконец, мы добавляем цифры из столбца долларов .
2 + 2 + 1 = 5
В столбце «Доллар» запишем 5.
😃 Не забудьте написать десятичное число точка между 5 и 7.
✅ Общая сумма, которую вам нужно заплатить, составляет $ 5 . 70 !
Вычитание денег
Еще один навык, который вам необходимо освоить, это вычитание денег .
Представьте, что вы в магазине игрушек.
Вы видите игрушку с надписью «$ 2 . 50 Скидка» .
Скидка означает, что определенная сумма вычитается из первоначальной цены.
Если первоначальная цена составляет 6,50 долларов, как узнать окончательную цену? 🤔
Вычитаешь!
Подсказка: Вычитание денег равно просто как вычитание 3 — цифра цифры .
👉 Сначала запишите числа в столбец форма .
Напишите большее число вверху, а меньшее число внизу. 😃
Убедитесь, что строка до десятичная балла.
👉 Затем из вычесть из чисел, начиная с сотых (крайнее правое место)
Новая цена игрушки $ 4 4 . 00 ! ✅
Вычитание и внесение сдачи
Вы также вычитаете деньги, когда производите сдачу .
Допустим, вы покупаете подарок для своего друга.
Стоит $ 3 . 35 . Вы даете лавочнику 9 долларов1263 5 счет.
35 . Вы даете лавочнику 9 долларов1263 5 счет.
Сколько сдачи вы должны получить? 🤔
Чтобы узнать ответ, нужно из 5 долларов вычесть 3,35 доллара.
Во-первых, запишите числа в столбец форма .
Подсказка: Когда сумма денег не есть десятичная точка, вы всегда можете добавить десятичную дробь и 2 нуля после нее.
Это потому, что 5 долларов равно 5 долларам.
Подсказка: убедитесь, что десятичные точки равны , выровненные вверх по .
 *шир.*выс.), см
*шир.*выс.), см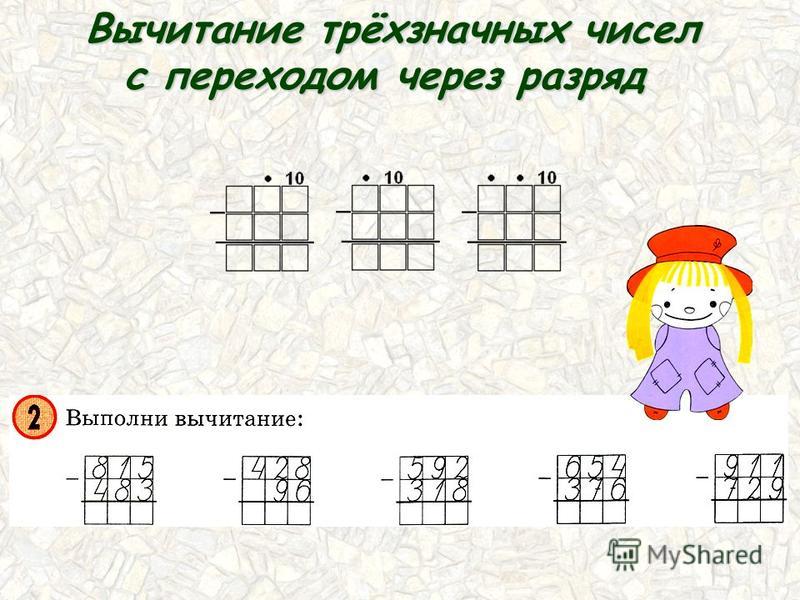 Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд.Рекомендуется записывать решения в тетрадь.
Вычисления в столбик. Сложение и вычитание трех и четырехзначных чисел с переходом через разряд.Рекомендуется записывать решения в тетрадь. 
 В формулировке текста задания используются математические выражения типа «из суммы двух чисел вычти их разность». Рекомендуется использовать в 3 и 4 классах, записывая условия и решение в тетрадь.
В формулировке текста задания используются математические выражения типа «из суммы двух чисел вычти их разность». Рекомендуется использовать в 3 и 4 классах, записывая условия и решение в тетрадь.