Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
- Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
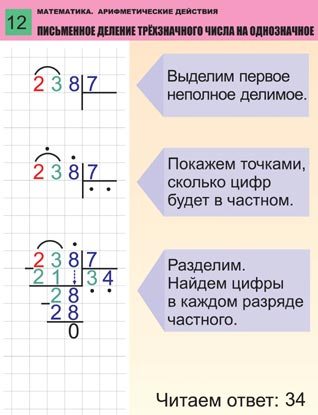
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.
Ответ: 378 : 21 = 18.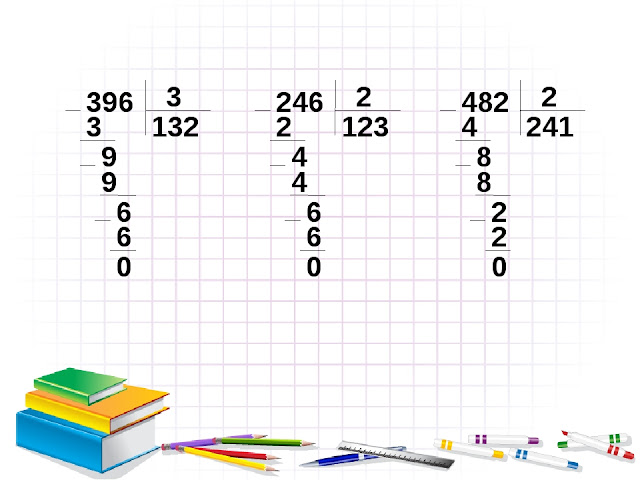
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Деление в столбик — объяснение и примеры…
Привет, мой друг, тебе интересно узнать все про деление в столбик — объяснение , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое деление в столбик — объяснение , настоятельно рекомендую прочитать все из категории Арифметика.
Деление — Арифметическое действие, по к-оторому узнается, сколько раз одно число содержится в другом.
Если вы родитель , то объясните ребенку, что, в математике, действие, противоположное умножению, называется «деление».
Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 3х4=12. результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
В нашем пример разделите получившееся произведение «12» – на любой из множителей – «3» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель, то есть «4» или «3».
Также нужно знать термины, используемые в операции деления – «делимое», «делитель» и «частное».
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.
Посмотрим на примере как делить столбиком.
Вычислить:
Для начала запишем делимое и делитель в столбик . Об этом говорит сайт https://intellect.icu . Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
Начинаем делить 512 на 8 следующим образом:
- Определяем неполное частное. Для этого слева направосравниваем цифры делимого и делитель.

Берем 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого.
- 51 больше 8. Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку.
- Приступаем к делению. Вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение.
6 x 8 = 48
Записываем цифру 6 в частное.Записываем 48 под 51.
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
- В остатке получилось 3. Сравним остаток с делителем.
 3 меньше 8.
3 меньше 8.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого 512 цифру 2 к 3.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение.
8 x 4 = 32В остатке получился ноль. Значит числа разделились нацело (без остатка).
Как ты считаеешь, будет ли теория про деление в столбик — объяснение улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое деление в столбик — объяснение и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но емко про деление в столбик — объяснение
длинная дивизия
длинная дивизияПоказать рекламу
Скрыть рекламу
О рекламе
Ниже
Процесс выписан полностью.
Вы часто будете видеть другие версии, которые, как правило, являются просто укороченной версией процесса ниже .
Вы также можете увидеть это в Long Division Animation.
Посмотрим как это делается с помощью:
- число, на которое нужно разделить, называется делимое
- Число, на которое делится другое число, называется делителем
И вот:
| 4 ÷ 25 = 0 остаток 4 | Первая цифра делимого (4) делится на делитель. | |
| Целое число помещается вверху. Любые остатки в этот момент игнорируются. | ||
| 25 × 0 = 0 | Ответ из первой операции: умножить на делитель. Результат помещается под числом, разделенным на. | |
| 4 − 0 = 4 | Теперь мы вычитаем нижнее число из верхнего числа. | |
| Сократите следующую цифру делимого. | ||
| 42 ÷ 25 = 1 остаток 17 | Разделите это число на делитель. | |
| Целое число помещается вверху. Любые остатки в этот момент игнорируются. | ||
| 25 × 1 = 25 | Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под последним числом, на которое делится. | |
| 42 − 25 = 17 | Теперь мы вычитаем нижнее число из верхнего числа. | |
| Сократите следующую цифру делимого. | ||
| 175 ÷ 25 = остаток 7 0 | Разделите это число на делитель. | |
Целое число помещается вверху. Любые остатки
в этот момент игнорируются. Любые остатки
в этот момент игнорируются. | ||
| 25 × 7 = 175 | Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под числом, разделенным на. | |
| 175 — 175 = 0 | Теперь мы вычитаем нижнее число из верхнего числа. | |
| Больше нет цифр для записи. Ответ должен быть 17 |
Рабочие листы длинного деления
Copyright © 2017 MathsIsFun.com
Многочлен длинного деления | Колледж Алгебра
Результаты обучения
- Используйте длинное деление для деления многочленов.
В следующих двух разделах мы изучим два способа деления многочленов. Эти методы могут помочь вам найти нули многочлена, который нельзя разложить на множители целых чисел.
Мы знакомы с алгоритмом длинного деления для обычной арифметики. Начнем с деления на цифры делимого, имеющие наибольшую разрядную стоимость. Мы делим, умножаем, вычитаем, включаем цифру в следующую разрядную позицию и повторяем. Например, давайте разделим 178 на 3 в длинное деление.
Другой способ взглянуть на решение как на сумму частей. Это должно выглядеть знакомо, так как это тот же метод, который используется для проверки деления в элементарной арифметике.
[латекс]\begin{массив}{l}\left(\text{делитель}\cdot \text{частное}\right)\text{ + остаток}\text{ = делимое}\hfill \\ \left( 3\cdot 59\right)+1 = 177+1 = 178\hfill \end{array}[/latex]
Мы называем это алгоритмом деления и обсудим его более формально после рассмотрения примера.
Деление многочленов, содержащих более одного члена, похоже на деление целых чисел в длинное. Мы можем записать полиномиальное делимое как произведение делителя и частного, прибавленного к остатку.
Мы можем идентифицировать делимое , делитель , частное и остаток .
Запись результата таким образом иллюстрирует алгоритм деления.
Общее примечание: Алгоритм деления
Алгоритм деления утверждает, что при заданном полиномиальном делимом [латекс]f\left(x\right)[/latex] и ненулевом полиномиальном делителе [латекс]d\left (x\right)[/latex], где степень [латекса]d\left(x\right)[/latex] меньше или равна степени [латекса]f\left(x\right)[/ латекс], существуют уникальные многочлены [латекс]q\left(x\right)[/latex] и [latex]r\left(x\right)[/latex] такие, что
[латекс]f\влево(х\вправо)=d\влево(х\вправо)q\влево(х\вправо)+r\влево(х\вправо)[/латекс]
[латекс]q\ left(x\right)[/latex] – частное, а [latex]r\left(x\right)[/latex] – остаток.
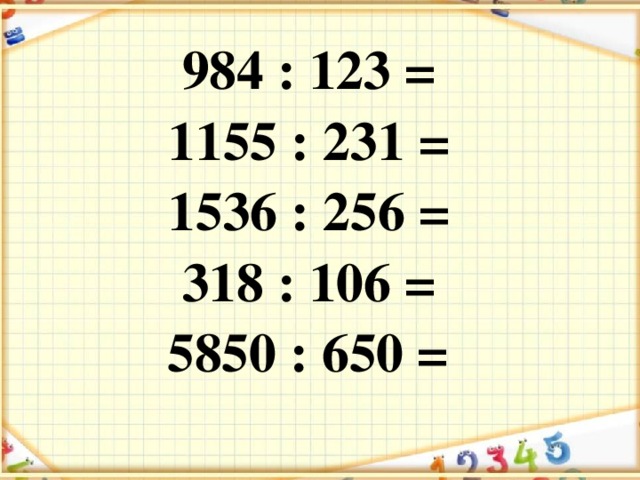 3 меньше 8.
3 меньше 8.