Деление трёхзначного числа на однозначное | Методическая разработка по математике (3 класс) по теме:
Опубликовано 18.03.2012 — 16:48 — Сикорская Валентина Аристафовна
Дидактический раздаточный материал для самостоятельной работы по математике
Скачать:
Предварительный просмотр:
486 : 2
642 :2
693 : 3
848 : 4
936 : 3
264 : 2
996 : 3
555 : 5
966 : 3
484 : 4
488 : 2
963 : 3
448 : 4
639 : 3
684 : 2
777 : 7
674 : 2
896 : 2
678 : 3
892 : 4
676 : 2
954 : 3
490 : 2
860 : 4
580 : 5
678 : 6
896 : 8
798 : 7
476 : 4
687 : 3
585 : 5
654 : 2
876 : 4
298 : 2
675 : 3
468 : 4
595 : 5
684 : 6
872 : 4
146 : 2
219 : 3
196 : 2
332 : 4
335 : 5
288 : 4
370 : 5
291 : 3
408 : 8
426 : 6
330 : 6
455 : 7
567 : 7
549 : 9
684 : 9
504 : 8
486 : 6
728 : 8
595 : 7
531 : 9
168 : 4
189 : 3
405 : 5
260 : 4
232 : 4
504 : 6
592 : 8
252 : 3
432 : 9
539 : 7
516 : 6
376 : 8
570 : 2
672 : 4
792 : 3
828 : 6
840 : 5
936 : 6
920 : 8
912 : 4
882 : 7
965 : 5
738 : 6
801 : 3
708 : 4
903 : 7
822 : 6
895 : 5
984 : 8
852 : 6
973 : 7
936 : 4
875 : 5
572 : 4
855 : 3
976 : 2
918 : 6
966 : 7
992 : 8
792 : 3
996 : 4
894 : 6
889 : 7
952 : 8
612 : 2
927 : 3
540 : 5
828 : 4
648 : 6
921 : 3
742 : 7
963 : 9
864 : 8
745 : 5
872 : 8
954 : 9
536 : 8
861 : 7
576 : 6
436 : 4
530 : 5
856 : 8
648 : 6
836 : 4
972 : 9
675 : 5
954 : 6
896 : 7
Предварительный просмотр:
592 : 8
252 : 3
432 : 9
539 : 7
516 : 6
376: 8
672 : 4
828 : 6
840 : 5
912 : 4
882 :7
570 : 2
936 : 6
920 : 8
828 : 6
840 : 5
936 : 6
920 : 8
278 х 3
157 х 6
186 х5
124 х 8
128 х 7
182 х 4
293 х 3
171 х5
238 х 4
147 х 7
136 х 6
374 х 2
204 х 3
103 х 8
107 х 6
269 х 3
253 х 3
151 х 5
204 х 3
103 х 8
107 х 6
269 х 3
374 х 2
128 х 7
По теме: методические разработки, презентации и конспекты
Математика.
Деление трёхзначного числа на двузначноеДорогие ребята! В этой презентации вашему вниманию представлены тренировочные примеры на деление трёхзначных чисел на двузначные. Удачи! Для скачивания нажмите «скачать»!…
3-4 класс, Интерактивная игра-тренажёр «Африка» (деление трёхзначного числа на однозначное)
Цель: отработка умения делить трёхзначное число на однозначное число.[[{«type»:»media»,»view_mode»:»media_large»,»fid»:»3188798″,»attributes»:{«alt»:»»,»class»:»media-image»,»height»:»351″,»width»:»46…
Карточка «Деление трёхзначного числа на однозначное»
Письменные приёмы деления…
Интерактивная игра «Деление трёхзначного числа на однозначное»
Интерактивная игра «Деление трёхзначного числа на однозначное» по математике создана для учащихся 3-4 класса, УМК любой. Игру можно использовать на этапе изучения или повторения в ходе …
Технологическая карта урока математики » Деление трёхзначного числа на однозначное » 3 класс
Технологическая карта разработана для урока математики по теме «Деление трёхзначного числа на однозначное » в 3 классе УМК «Школа 2100».
…
Интерактивная игра — Деление трёхзначного числа на однозначное
Интерактивная игра — Деление трёхзначного числа на однозначное…
Алгоритм письменного деления трёхзначного числа на однозначное.
Алгоритм письменного деления трёхзначного числа на однозначное. Математика 3 класс….
Поделиться:
Правила делимости на 2, 3, 4, 5, 6, 9 и 10
Число a делится на число b, если a \div b имеет остаток от нуля (0). Например, 15 разделить на 3 равно 5, а это означает, что его остаток равен нулю. Затем мы говорим, что 15 делится на 3.
В другом нашем уроке мы обсуждали правила делимости для 7, 11 и 12. На этот раз мы рассмотрим правила или тесты делимости для 2 , 3 , 4 , 5 , 6 , 9 и 10 . Поверьте мне, вы сможете выучить их очень быстро, потому что вы можете не знать, что у вас уже есть базовое и интуитивное понимание этого.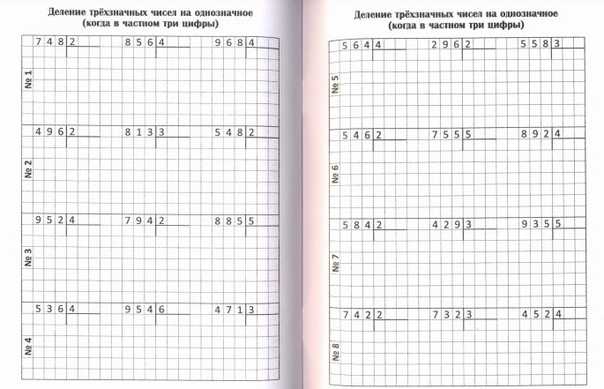
Например, очевидно, что все четные числа делятся на 2. Это в значительной степени правило делимости для 2 . Цель этого урока правил делимости — формализовать то, что вы уже знаете.
Правила делимости помогают нам определить, делится ли одно число на другое, не прибегая к фактическому процессу деления, такому как метод деления в длинное число. Если рассматриваемые числа численно достаточно малы, нам может не понадобиться использовать правила для проверки делимости. Однако для чисел, значения которых достаточно велики, мы хотим иметь некоторые правила, которые служили бы «ярлыками», чтобы помочь нам выяснить, действительно ли они делятся друг на друга.
Число делится на 2, если его последняя цифра 0, 2, 4, 6 или 8.
Пример 1. Делится ли число 246 на 2?
Решение: Поскольку последняя цифра числа 246 оканчивается на 6, это означает, что оно делится на 2.
Пример 2. Какие из чисел 100, 514, 309 и 768 делятся на 2?
Решение: Если мы рассмотрим все четыре числа, то только число 309 не оканчивается на 0, 2, 4, 6 или 8.
Мы можем сделать вывод, что все числа выше, кроме 309делятся на 2.
Число делится на 3, если сумма цифр этого числа делится на 3.
Пример 1. Делится ли число 111 на 3?
Решение: Сложим цифры числа 111. Получим 1 + 1 + 1 = 3. Так как сумма цифр делится на 3, значит, число 111 также делится на 3.
Пример 2: Какое из двух чисел 522 и 713 делится на 3?
Решение: сумма цифр числа 522 (5+2+2=9) равно 9, которое делится на 3. Это делает 522 делящимся на 3. Однако число 713 имеет 11 в виде суммы его цифр, что явно не делится на 3, поэтому 713 не делится на 3. Следовательно, только 522 делится на 3.
Число делится на 4, если две последние цифры числа делятся на 4.
Пример 1. Какое единственное число в приведенном ниже наборе делится на 4?
{945, 736, 118, 429}
Решение: Обратите внимание на две последние цифры четырех чисел в наборе.
Обратите внимание, что 736 — единственное число, в котором две последние цифры (36) делятся на 4. Мы можем заключить, что 736 — единственное число в наборе, которое делится на 4.
Пример 2: верно или неверно. Число 5 554 делится на 4.
Решение: Последние две цифры числа 5 554 равны 54, что не делится на 4. Это означает, что данное число НЕ делится на 4, поэтому ответ ложно .
Число делится на 5, если последняя цифра числа 0 или 5.
Пример 1. Множественный выбор. Какое число делится на 5?
А) 68
B) 71
C) 20
D) 44
Решение. Чтобы число делилось на 5, его последняя цифра должна быть либо 0, либо 5. вариантов, только число 20 делится на 5, поэтому ответом является выбор C .
Пример 2. Выберите все числа, которые делятся на 5.0085 343
E) 600
Решение. И 105, и 600 делятся на 5, потому что они оканчиваются либо на 0, либо на 5.
Таким образом, варианты B и E являются правильными ответами.
Число делится на 6, если оно делится и на 2, и на 3.
Пример 1. Делится ли число 255 на 6?
Решение. Чтобы число 255 делилось на 6, оно должно делиться на 2 и 3. Давайте сначала проверим, делится ли оно на 2. Обратите внимание, что 255 не является четным числом (любое число, оканчивающееся на 0, 2, 4). , 6 или 8), что делает его неделимым 2. Дальше проверять не нужно. Теперь мы можем сделать вывод, что это число не делится на 6. Ответ: 9.0005 НЕТ .
Пример 2. Делится ли число 4608 на 6?
Решение. Число является четным, поэтому оно делится на 2. Теперь проверьте, делится ли оно на 3. Сделаем это, сложив все цифры числа 4 608, что равно 4 + 6+ 0 + 8 = 18. Очевидно, сумма цифр делится на 3, потому что 18 ÷ 3 = 6. Поскольку число 4608 делится и на 2, и на 3, то оно также должно делиться на 6. Ответ: ДА .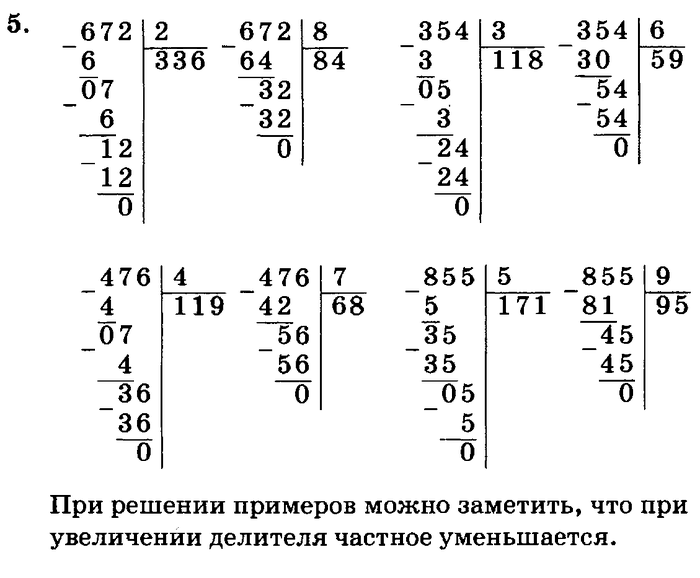
Число делится на 9если сумма цифр делится на 9.
Пример 1. Делится ли число 1764 на 9?
Решение: Чтобы число делилось на 9, сумма его цифр также должна делиться на 9. Для числа 1764 мы получаем 1 + 7 + 6 + 4 = 18. Поскольку сумма цифр равна 18 и делится на 9, поэтому 1764 должно делиться на 9.
Пример 2. Выберите все числа, которые делятся на 9.0085 3 512
C) 8 874
D) 22 778
E) 48,069
Решение: . 7,065, 7 + 0 + 6 + 5 = 18, которое делится на 9.
Число делится на 10, если его последняя цифра равна 0.
Числа 20, 40, 50, 170 и 990 делятся на 10, потому что их последняя цифра равна нулю, 0 С другой стороны, 21, 34, 127 и 468 не делятся на 10, так как они не оканчиваются нулем.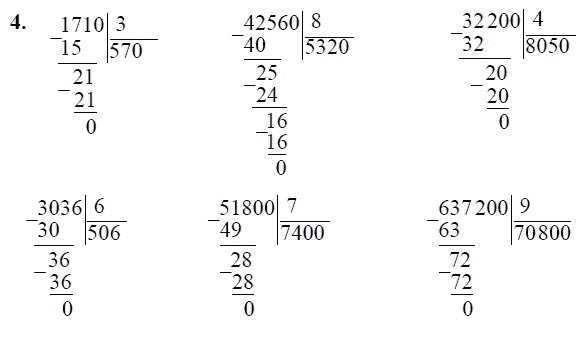
Вас также может заинтересовать:
Правила делимости на 7, 11 и 12
Что такое остаток в математике?
Написано
Malcolm McKinsey
Проверясь по фактам
Пол Маццола
Определение оставшегося
Остальное-это Порция, которая не может быть честным. После деления целых чисел, чтобы найти частное, вы можете получить часть остатка дивиденда; это остаток. Он представляет собой долю дивиденда и может быть записан в виде десятичной или дробной части.
Деление с остатком
Решением или ответом на задачу деления является частное, которое может включать остаток.
Что такое остаток в математике? При делении мы делим отдельные предметы, например торт, и наборы предметов, например кексы, между группами, надеясь, что каждый получит справедливую долю. Любая сумма дивиденда, которая не делится на делитель, является остатком.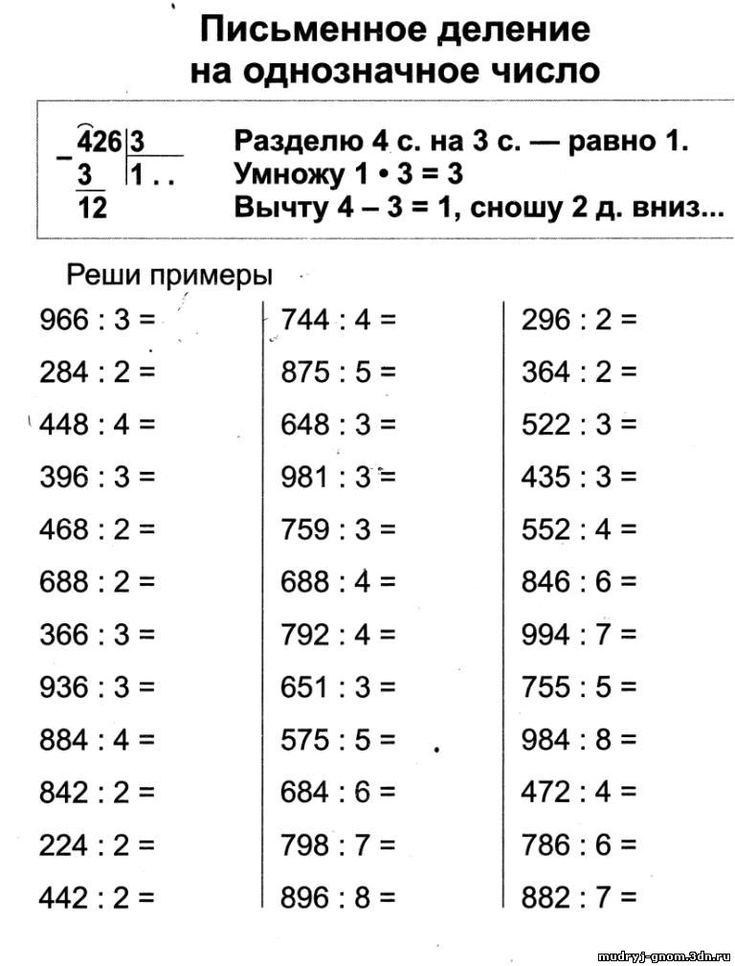
Предположим, мы отмечаем 19-летие школьного математического клуба. У нас есть большой, вкусный листовой пирог, чтобы поделиться со всеми 43 членов. Как мы будем резать торт, чтобы поровну поровну досталось всем?
Мы могли бы разрезать торт по-разному, составляя равные части, но нет способа отрезать ровно 43 частей от прямоугольника. Как бы мы ни разрезали торт, чтобы дать каждому по кусочку, что-то останется. Остаток будет и останется .
Если мы разрежем торт на 5 рядов и 9 столбцов, у нас будет 45 ломтиков, которые можно разделить между 43 человек; каждый получает 1 фрагментов, и у нас остается 2 фрагментов.
Первое число 1 — это частное. 2 это остаток, объедки, часть торта, которую нельзя разумно разделить между всеми 45 членами Математического клуба.
Деление с остатком примерКак найти остаток в делении
Шаги к делению в длинное с остатком легко запомнить с помощью мнемоники (трюка с памятью): D oes M cDonald’s S ell C heese B urgers D aily? :
D OES = D IVIDE (Разделите дивиденд от Divisor)
M Time Partient) Divient The Divient the Divient the Divient the Divient the Divient the Divient the Divient the Divient the Divient the Divient the Divient).
0003S ell = S вычесть (вычесть произведение из первых цифр делимого)
C heese = C разность сравнить с делителем; меньше)
Б ургерс Д айлы = Б кольцо Д собственный (сбей следующую цифру своего дивиденда и начни заново)
0003Если останется разница после выполнения всех шагов все цифры делимого, эта разница равна остаток .
Символ остатка
Чтобы обозначить, что в вашем ответе есть остаток, вы пишете заглавную букву R после частного, за которой следует число, обозначающее остаток. Ответ, или частное, представляет собой целое число, а остаток обозначается буквой R .
Символ остатка Чтобы интерпретировать остаток, вы должны посмотреть на единицы делимого, делителя и частного. Если дивидендом являются кексы, а делитель представляет членов Математического клуба. Затем частное — это кексы на участника, а остаток — это кексы, которые нельзя было справедливо разделить между участниками.
Вот как это выглядит в словесной задаче:
48 кексы можно справедливо разделить между 7 членами Математического клуба. Сколько получит каждый участник и сколько останется?
В виде уравнения это выглядит так:
48 кексов, разделенных между 7 участниками, равно 6 кексов на участника, при этом остается 6 кексов.
Как написать остаток
Существуют разные способы записи остатка в задаче на деление. Остаток может быть целым числом или дробью. Вы всегда пишете остаток после заглавной буквы R, чтобы показать, что это остаток.
Если вы хотите выразить остаток как нечто иное, чем целое число, вы можете превратить его в часть делимого.
Научиться записывать остаток в виде дроби очень просто. Остаток становится числителем, а делитель — знаменателем. Единица для частного и остатка называется делимым и делителем (дивиденд на делитель). Упростите дробь, если это возможно.
Как написать остатокОстаток примеры задач
Вот пример листа пирожных, нарезанных на 44 отдельные пирожные.