ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 35. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник — страница 35Готовое домашнее задание

Номер 1.

Ответ:

84 ∙ 10 − 40 = 840 − 40 = 800 78 ∙ 10 − 700 = 780 − 700 = 80
10 ∙ (920 − 20) = 10 ∙ 900 = 9000 8 ∙ (720 − 700) = 8 ∙ 20 = 160
184 ∙ 100 − 300 = 18400 − 300 = 18100 100 ∙ 391 − 3000 = 39100 − 3000 = 36100

Номер 2.

Ответ:

Номер 3.

Ответ:

Номер 4.

Выполни деление с остатком.

Ответ:

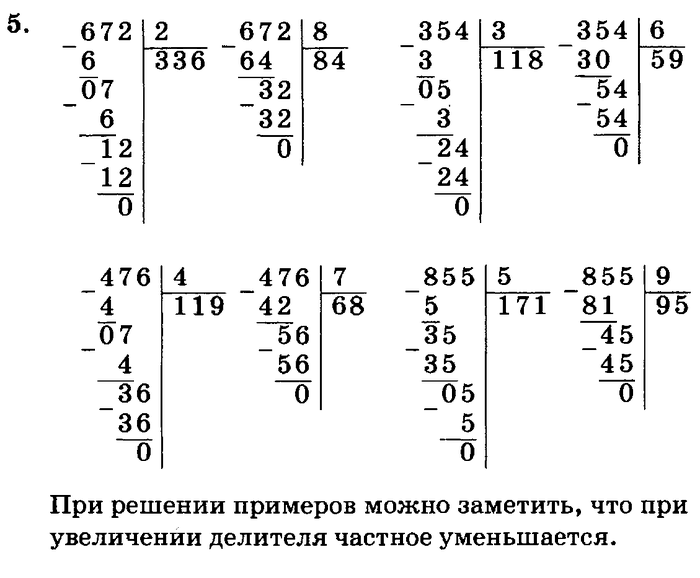
Номер 5.

Вычисли удобным способом.

Ответ:

45 ∙ (2 ∙ 7) = (45 ∙ 2) ∙ 7 = 90 ∙ 7 = 630 720 : (9 ∙ 2) = (720 : 9) : 2 = 80 : 2 = 40 67 ∙ (4 ∙ 25) = 67 ∙ 100 = 6700 17 ∙ 2 ∙ 8 ∙ 125 = 34 ∙ 1000 = 34000

Номер 6.

Ответ:

Номер 7.

Ответ:

Номер 8.

Ответ:

Номер 9.

Ответ:

Номер 10.

Ответ:

Номер 11.

Какими могут быть длины сторон прямоугольника, периметр которого равен 26 см, а площадь – 40 см²?

Ответ:

5 см и 8 см.

Номер 12.

Вычислительная машинка работает так:

Какой ответ будет получаться на выходе из машины, если на входе будет число 47; 53; 28; 94?

Ответ:

47 − 2; 53 − 2; 28 − 1; 94 − 1.

Задание на полях страницы

Сравни площади фигур.

Ответ:

Площади фигур равны.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Деление на 1000 — Математика с мамой

Опубликовано Математика с мамой

Деление на 1000

• Чтобы разделить число на 1000, переместите все его цифры на три разряда вправо.
• Цифра «9» переместится из столбца тысяч в столбец единиц.
• Цифра «0» переместится из столбца сотен в столбец десятых сразу после запятой.
• Цифра «0» в столбце десятков переместится в столбец сотых.
• Цифра «0» в столбце единиц переместится в столбец тысячных
• 9000 ÷ 1000 = 9.000
• Поскольку цифры после запятой все нули, мы их не пишем.
• 9000 ÷ 1000 = 9.
• Поскольку 9000 — это целое число, оканчивающееся тремя цифрами «0», деление его на 1000 дает тот же эффект, что и удаление этих трех нулей.

Чтобы разделить на 1000, переместите все цифры в 3-х разрядном столбце числа вправо.

• Чтобы разделить число на 1000, переместите все его цифры на 3 разряда вправо.
• В этом примере у нас есть 604 ÷ 1000.
• «6» в столбце сотен перемещается в столбец десятых сразу после десятичной точки.
• «0» в столбце десятков перемещается в столбец сотых.
• Цифра «4» в столбце единиц перемещается в столбец тысячных.
• 604 ÷ 1000 = 0,604

Чтобы разделить число на 1000, мы передвигаем

каждая цифра в этом числе три столбца разряда справа .

Деление целого числа , оканчивающегося тремя нулями , на 1000 дает тот же эффект, что и удаление трех нулей.

Этот трюк работает только для целых чисел, оканчивающихся тремя нулями (или чисел, кратных 1000). Вот пример деления такого числа на 1000.

В приведенном выше примере каждая цифра числа 9000 была перемещена на три позиции вправо.

Цифра «9» в столбце тысяч перемещается в столбец единиц.

При делении на одну тысячу любая цифра в столбце тысяч всегда будет перемещаться в столбец единиц слева от десятичной точки.

«0» в столбце сотен перемещается на три позиции в столбец десятых сразу после запятой.

«0» в столбце десятков перемещается на три позиции в столбец сотых.

Наконец, «0» в столбце единиц перемещается в столбец тысячных.

Таким образом, 9000 становится 9000, что равно 9.

Если число имеет только цифру «0» после запятой, то это целое число, и мы не пишем нули или десятичную точку.

Легче написать 9, чем 9.000.

Вы также можете знать, что когда мы делим целое число, оканчивающееся тремя нулями, на 1000, мы можем просто «убрать нули» с конца этого числа.

Этот трюк не сработает, если у нас есть десятичное число.

Важно понимать, как работает деление на 1000, потому что не все числа, которые мы делим на 1000, оканчиваются на три нуля.

Например:

Чтобы разделить 604 на 1000, мы переместим каждой цифры в 604 на три позиции вправо .

Начнем с перемещения «6» из столбца сотен на три позиции вправо в столбец десятых .

Затем «0» и «4» будут следовать за 6 в том же порядке. «0» перемещается из столбец десятков в столбец сотых , а «4» перемещается из столбца единиц в столбец тысячных .

Поскольку в столбце единиц больше нет цифр, мы пишем ноль.

Итак, 604 ÷ 1000 = 0,604.

Мы всегда пишем одну цифру «0» в столбце единиц измерения перед запятой, если там не осталось другой цифры для записи. Неправильно начинать число с десятичной точки, поэтому мы пишем «0,604», а не «0,604». Это позволяет избежать путаницы в письменном тексте с использованием чисел. Это позволяет избежать путаницы между запятыми, точками и десятичными точками.

Десятичная точка маленькая и иногда не замечается. Включение нуля перед десятичной запятой помогает читателю понять, что после нуля, вероятно, будет десятичная точка. Это связано с тем, что целые числа не начинаются с нуля, и единственный способ, которым ноль может быть первой цифрой в числе, — это десятичное число.

В следующем примере мы делим десятичное число на 1000.

Начнем с перемещения цифры «1» три знака вправо . Он перемещается из столбца десятков в столбец сотых . Затем следуют 2 и 8. Мы перемещаем 2 из столбца единиц в столбец тысячных и мы перемещаем 8 из столбца десятых в столбец десятитысячных.

Поскольку ни в столбце единиц, ни в столбце десятых больше нет цифр, мы пишем ноль в каждом из этих пробелов.

Следовательно, 12,8 ÷ 1000 = 0,0128

В следующем примере мы делим десятичное число меньше 1 на 1000.

Для этого переместим цифру ‘5’ на три позиции вправо , из десятого столбца в десятитысячного столбца .

Поскольку ни в столбце десятых, ни в столбце сотых, ни в столбце тысячных нет цифр, мы пишем ноль в каждом из этих столбцов, чтобы показать, что их значения равны нулю.

Следовательно, 0,5 ÷ 1000 = 0,0005.

Теперь попробуйте наш урок на Десятых и сотых , где мы узнаем больше о столбцах десятичных разрядов десятых и сотых.

Вычислить среднее значение группы чисел

Excel

Формулы и функции

Формулы

Формулы

Вычислить среднее значение группы чисел

Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно.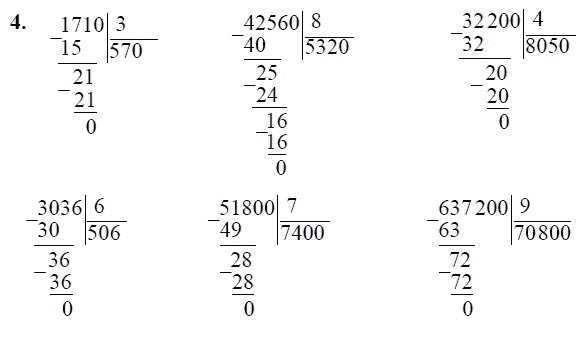 ..Меньше

Предположим, вы хотите найти среднее количество дней, затрачиваемое на выполнение задачи разными сотрудниками. Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.

Функция СРЗНАЧ измеряет центральную тенденцию, то есть положение центра группы чисел в статистическом распределении. Тремя наиболее распространенными показателями центральной тенденции являются:

• Среднее     Это среднее арифметическое, которое рассчитывается путем сложения группы чисел и последующего деления на количество этих чисел. Например, среднее значение 2, 3, 3, 5, 7 и 10 равно 30, разделенному на 6, что равно 5.

• Медиана      Среднее число группы чисел. Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4,9.0005

• Режим     Самое часто встречающееся число в группе чисел. Например, режим 2, 3, 3, 5, 7 и 10 равен 3.

Для симметричного распределения группы чисел все эти три меры центральной тенденции одинаковы. При асимметричном распределении группы чисел они могут быть разными.

Сделайте следующее:

1. Щелкните ячейку ниже или справа от чисел, для которых вы хотите найти среднее значение.

2. org/ListItem»>

   На вкладке Главная в группе Редактирование щелкните стрелку рядом с Автосумма , выберите Среднее и нажмите клавишу ВВОД.

Для выполнения этой задачи используйте функцию СРЕДНЕЕ . Скопируйте приведенную ниже таблицу на пустой рабочий лист.

Формула	Описание (Результат)
=СРЕДНЕЕ(A2:A7)	Усредняет все числа в списке выше (9.5)
=СРЕДНЕЕ(A2:A4,A7)	Усредняет первые три и последний номер в списке (7. 5)
=СРЗНАЧЕСЛИ(A2:A7, «<>0″)	Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11.4)

Для выполнения этой задачи используйте функции СУММПРОИЗВ и СУММ . vВ этом примере вычисляется средняя цена, уплаченная за единицу по трем покупкам, где каждая покупка предназначена для разного количества единиц по разной цене за единицу.

Скопируйте приведенную ниже таблицу на пустой рабочий лист.

1 2 3 4

А Б Цена за единицу Количество единиц 20 500 25 750 35 200 Формула Описание (Результат) =СУММПРОИЗВ(A2:A4;B2:B4)/СУММ(B2:B4) Делит общую стоимость всех трех заказов на общее количество заказанных единиц (24,66)

Для выполнения этой задачи используйте СРЗНАЧ и ЕСЛИ работают.