Математика 4 класс «Деление многозначных чисел на однозначные» (28 слайдов)

Слайд 1

1
Математика 4 класс

Слайд 2

2
Посетите наш зоопарк

Слайд 3

3
Московский зоопарк

Слайд 4

ВЕТЕРИНАРИЯ (от лат. veterinarius) — ухаживающий за скотом, лечащий скот.
Ветеринар
наука
профессия
4

Слайд 5

5
Ветеринар

Слайд 6

6
Ветеринар
медицина биология география химия физика

Слайд 7

7
Тема урока: Деление многозначных чисел на однозначные.
Математика 4 класс

Слайд 8

8
Найди значение частного 4862 : 2
84 : 4 = (80 + 4) : 4 = 21 963 : 3 = (900 + 60 + 3) : 3 = 321 4862 : 2 = (4000 + 800 + 60 + 2) : 2 =

Слайд 9

9
Работай по плану: а) выбираю первое неполное делимое; б) намечаю количество цифр в частном; в) делю первое неполное делимое, подбирая частное; г) делаю проверку: - умножаю частное на делитель, - из делимого вычитаю полученное число, - сравниваю остаток с делителем; д) называю второе неполное делимое. ..

Слайд 10

10
Работай по плану: а) выбираю первое неполное делимое; б) намечаю количество цифр в частном; в) делю первое неполное делимое, подбирая частное; г) делаю проверку: - умножаю частное на делитель, - из делимого вычитаю полученное число, - сравниваю остаток с делителем; д) называю второе неполное делимое…

Слайд 11

Слайд 12

12
Как выполнить деление в столбик любых многозначных чисел на однозначное число?
Вывод: Любые многозначные числа делят на однозначное число так же, как и двузначные и трёхзначные числа: по разрядам, начиная со старшего разряда. При этом сначала выбирают первое неполное делимое и намечают количество цифр в частном.

Слайд 13

13
Проверь себя: 6 : 4 = 1 (ост. 2) 12 : 9 = 1 (ост. 1) 4 : 3 = 1 (ост. 1) 52 : 7 = 7 (ост. 3) 8 : 5 = 1 (ост. 3)
Какие остатки могут получиться при делении чисел на 2? на 3? на 4? на 5? на 6? на 7? на 8? на 9?
Выполни деление с остатком: 6 : 4 4 : 3 8 : 5 12 : 9 52 : 7

Слайд 14

14
1 вариант: 7832 : 2 9852 : 3
2 вариант: 9464 : 4 6765 : 5

Слайд 15

15
1 вариант

Слайд 16

16
2 вариант

Слайд 17

17
Реши уравнения:
(х — 3983) + 7 267 = 12000
х + (3983 + 7267) = 12000
х — 3983 = 12000 + 7267

Слайд 18

18
Реши уравнения:
(х — 3983) + 7 267 = 12000 х – 3983 = 12000-7267 х – 3983 = 4733 х = 4733 + 3983 х = 8716
х + (3983 + 7267) = 12000 х + 11250 = 12000 х = 12000 – 11250 х = 750
х — 3983 = 12000+ 7267 х – 3983 = 19267 х = 19267 + 3983 х = 23250

Слайд 19

В зоопарке есть индийский слон по кличке Раджа, африканская слониха, которую зовут Буба, и жираф по кличке Петька. Масса Раджи равна 3 т 983 кг, масса Бубы — 7 т 267 кг, а масса Раджи, Бубы и Петьки вместе — 12 т. Чему равна масса жирафа Петьки?
19
Реши задачу:
Раджа
Буба
Петя

Слайд 20

В зоопарке есть индийский слон по кличке Раджа, африканская слониха, которую зовут Буба, и жираф по кличке Петька. Масса Раджи равна 3 т 983 кг, масса Бубы — 7 т 267 кг, а масса Раджи, Бубы и Петьки вместе — 12 т. Чему равна масса жирафа Петьки?
1) 3 т 983 кг = 3983 кг 7 т 267 кг = 7267 кг 3983 + 7267 = 11250 (кг)- масса Раджи и Бубы. 2) 12 т = 12000 кг 12000 – 11250 = 750 ( кг) – масса Петьки. Ответ: 750 кг.
20

Слайд 21

В энциклопедии сказано, что масса бурого медведя равна приблизительно 750 кг. Это в 10 раз меньше, чем приблизительная масса африканского слона, и на 480 кг больше, чем масса тигра. Чему приблизительно равна масса африканского слона и чему равна масса тигра?
21
Реши задачу:

Слайд 22

В энциклопедии сказано, что масса бурого медведя равна приблизительно 750 кг. Это в 10 раз меньше, чем приблизительная масса африканского слона, и на 480 кг больше, чем масса тигра. Чему приблизительно равна масса африканского слона и чему равна масса тигра?
Решение: 1) 750 · 10 = 7500 (кг) – масса слона 2) 750 — 480 = 270 (кг) – масса тигра Ответ: 7500 кг, 270 кг.
22

Слайд 23

23
750 кг
7500 кг
270 кг

Слайд 24

24
Масса бурого медведя составляет 3/4 массы белого медведя, а масса белого медведя в 4 раза меньше массы бегемота. Чему равна масса бегемота?

Слайд 25

25
Масса бурого медведя составляет 3/4 массы белого медведя, а масса белого медведя в 4 раза меньше массы бегемота. Чему равна масса бегемота?
750 : 3 · 4 = 1000 (кг) масса белого медведя 2) 1000 · 4 = 4000 (кг) масса бегемота Ответ: 4000 кг

Слайд 26

26
4000 кг
750 кг
1000 кг

Слайд 27

27
Домашнее задание с.71 № 7

Слайд 28

28
Спасибо за работу!

Урок для 4 класса по теме: «Закрепление изученного материала «Деление многозначных чисел на двузначное»»

Открытый урок

по математике в 4 классе

(Закрепление изученного материала

«Деление многозначных чисел на двузначное»)

Составила: Коробейникова Наталья Александровна,

учитель начальных классов

Адрес школы:МБОУ «Солоновская средняя

общеобразовательная школа»

Солоновка

2011 год

Тема урока: Закрепление изученного материала

«Деление многозначных чисел на двузначное»

Цели урока: 1.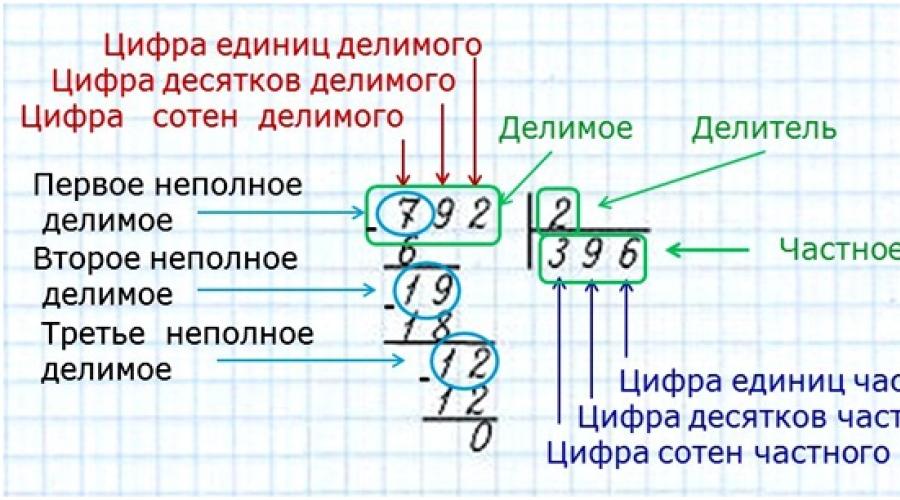 Отработка устных и письменных вычислительных навыков при делении многозначных чисел на однозначное

.

2. Повторение решения уравнений.

3. Совершенствование умения решать текстовые и геометрические задачи.

4. Развивать логическое мышление.

5. Развитие внимания, умения самостоятельно работать.

6. Воспитание уважения и любви к природе.

1. Организационный момент.

Математику, друзья,

Не любить никак нельзя.

Очень точная наука,

Очень строгая наука,

Интересная наука —

Это математика!

Предлагаю вам сегодня отправиться в путешествие на кораблике по морю страны математики. (Слайд №2)

Итак, отправляемся. (песенка бременских музыкантов)

Кораблик быстроходный , потому что за 45 минут мы должны остановиться на 4 островках и выйти на 1 полуострове. (Слайд №3)

Цель урока: А цель нашего путешествия, закрепить знания деления многозначного числа на двузначное. (Слайд №4)

(на магнитной доске висит карта маршрута)

2. Внимание! Кораблик прибыл на остров « Смекалкин». (слайд №5)

— Ребята, нам нужно помочь Колобку добраться до дома, чтобы его не съела лиса.

А еще нам нужно решить примеры. (слайд №6)

2. Отправляемся дальше.

Подплываем к острову «Считалкин». (слайд №7)

• Стр.56 №10

• 1 вариант 2 вариант

• 1,2 ,3 пример 4,5,6 пример

Проверим(слайд №8)

3912:12=326 11206:13=862

6748:14=482 14562:18=809

10635:15=709 15640:17=920

А сейчас я предлагаю немного отдохнуть

Ф и з к у л т м и н у т к а

Повторим таблицу умножения, если я называю пример и правильный ответ, вы хлопаете в ладоши. Если ответ неверный, вы подпрыгиваете и называете верный ответ.

4. Впереди остров« Задачкин». (слайд №9,10,11)

5. Внимание! Приближаемся к полуострову Вычисляйкин» (слайд №12)

Мы на полуострове. Можно выйти прогуляться, но на берегу

случилась экологическая беда.

— Посмотрите, какие поступки людей стали бедой этого берега?

— Что надо сделать ?

— Давайте приведем его в порядок. А для этого решим уравнения. (слайд №14) и проверим друг у друга.

Х*15=640+1235 х+72=3655:17

Х*15=1875 х+72=215

Х=1875:15 х=215-72

Х=125 х=143

125*15=640+1235 143+72=3655:17

1875=1875 215=215

6.Мы подплываем к последнему острову «Занималкину»

1)найти ошибку(слайд №15)

2)помоги мамантенку

3)тест

6. Итог урока. – Как называется море, по которому мы плыли?

— Какие задания выполняли?

7.Домашнее задание.

( отметить работу учеников на уроке)

8. Рефлексия.Колобок сейчас будет прыгать по ступенькам, а вы поставьте номер той ступеньки, которая соответствует вашему настроению.

Стратегии разделения для 4 и 5 классов

Прослушать эту статью

Оценить эту публикацию

---

В этой статье обсуждаются три стратегии разделения. Кроме того, вы найдете решенные примеры с пояснениями и ссылками на рабочие листы для дополнительной практики или оценки.

Что такое подразделение?

Одной из четырех основных математических операций, наряду со сложением, вычитанием и умножением, является деление.

Деление — это процесс разделения большей группы на более мелкие таким образом, чтобы каждая группа содержала равное количество элементов.

Математики используют эту операцию для группировки и равномерного распределения ресурсов.

Деление обратное умножению. При делении чисел мы разбиваем большее число на меньшее так, чтобы произведение меньшего числа было равно большему числу.

Например, 10 ÷ 2 = 5. Мы можем выразить это как факт умножения 2 x 5 = 10,

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Символы деления

Мы можем представить деление двух чисел одним из двух основных символов деления ( ÷ и /).

Например, 10 ÷ 2 = 5, а 10/2 = 5.

Математический символ, который выглядит как небольшая горизонтальная линия с точками над и под ней, чаще всего используется для обозначения деления.

Части деления

Задача на деление состоит из следующих четырех компонентов: делимое, делитель, частное и остаток. В уравнении деления

458 ÷ 3 = 152 R2 ;

• делимое (458) число, которое нужно разделить (первое число слева)
• делитель (3) это число, на которое делим делимое (второе число после знака деления)
• частное (152) — ответ, полученный после выполнения деления (число справа после знака равенства)
• остаток (2) это оставшееся значение, которое меньше делителя (числа, присоединенного к частному)

Стратегии деления

Мы можем использовать таблицу умножения для деления небольших чисел.

Например, чтобы решить 10 ÷ 2, нам нужно только определить, что мы должны умножить на 2, чтобы получить 10 в качестве ответа.

Ясно, что 2 × 5 = 10, поэтому 10 ÷ 2 = 5.

Однако при делении больших чисел практически невозможно использовать этот подход.

Поэтому мы должны придумать альтернативные стратегии для использования при делении больших чисел.

Некоторые из таких стратегий разделения включают;

1. Длинная часть
2. Разделение на частное
3. Зона модельного подразделения

Использование длинного деления в качестве стратегии деления.

Длинное деление — это метод деления больших чисел, который разбивает задачу на несколько шагов, выполняемых в определенном порядке.

Мы сможем делить числа любой длины, как только освоим этапы деления в длинное число.

Как разделить, используя метод деления в длину?

Следуя описанным здесь шагам, вы можете легко разделить, используя деление в большую сторону.

1. Разделить
2. Умножить
3. Вычесть
4. Сбить
5. Повторить процесс

Чтобы лучше понять длинное деление, давайте попробуем это на примере 458 ÷ 3 .

Шаг 1 – Разделить

Составьте уравнение.  

• Нарисуйте символ длинного деления ⟌
• Напишите делитель (3) слева вне символа, а делимое (458) справа под символом деления.

Разделите первую цифру.  

• Работая слева направо, определите, сколько раз делитель может входить в первую цифру делимого, не превышая ее.
• В нашем примере вам нужно знать, сколько раз 3 входит в 4, что равно 1.
• Если делитель больше первой цифры ( 138 ÷ 3) , определите, сколько раз делитель входит в первые две цифры делимого, не превышая его.
• В этом случае вам нужно знать, сколько раз 3 входит в число 13, то есть 4.

Введите первую цифру частного.  

• Поместите количество раз, когда делитель входит в первую цифру (или первые две цифры) делимого сверху символа деления над соответствующей цифрой.
• Длинное деление требует, чтобы числовые столбцы оставались правильно выровненными.
• В 458 ÷ 3 вы должны поставить 1 над 4, так как мы смотрим, сколько раз 3 входит в 4.
• В 138÷3 вы должны поставить 4 над 3, так как мы смотрим, сколько раз 3 входит в 13.

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Шаг 2 – Умножение

Умножение и запись произведения.  

• Умножьте делитель на цифру частного, которую вы только что написали над делимым. (3 х 1 = 3 и 3 х 4 = 12).
• Запишите результат умножения под делимым.
• В первом примере напишите 3 под 4 и 12 под 13 во втором примере, следя за тем, чтобы числа были выровнены.

Шаг 3 – Вычесть

Вычесть произведение.  

• Нарисуйте линию под результатом умножения.
• Вычтите число (произведение умножения) из цифр делимого непосредственно над ним.
• Запишите результат под только что проведенной линией.
• В примерах вычтите 3 из 4, чтобы получить 1, и 12 из 13, чтобы получить 1.

Шаг 4 – Уменьшение

Уменьшение следующей цифры.  

• Поскольку делитель не может входить в результат операции вычитания, необходимо опустить следующую цифру делимого (если она есть).
• В первом примере, поскольку 3 не может войти в 1, не превысив его, вам нужно убрать 5 из 458 и поместить его после 1, получив 15, в которое может войти 3.

Шаг 5. Повторите процесс

Повторите весь процесс.  

• Разделите новое число на делитель и запишите результат над делимым как следующую цифру частного.
• В этом примере определите, сколько раз 3 может составить 15. Запишите это число (5) как следующую цифру частного перед делимым.
• Затем умножьте 3 на 5 и вычтите результат (15) из 15.
• Если в делимом больше цифр, повторяйте этот процесс до тех пор, пока не проработаете их все (пока не получите ноль или число меньше делителя).

Запишите остаток.  

• Запишите, есть ли остаток, т. е. указание того, сколько осталось после того, как вы завершили свое деление.
• В этом примере остаток будет равен 2, потому что 3 не может перейти в 2, и больше нет цифр, которые нужно записывать.
• Поместите остаток после частного с буквой «R» перед ним. В примере ответ будет выражен как «152 R2».

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• Продажа Товар в продаже

  11,25 $ 9 $. 00

  В корзину

  Добавить в список желаний

Те же шаги можно выполнить для деления на двузначные делители.

Здесь вы узнаете, сколько раз двузначный делитель входит в первые две или три цифры делимого.

Это точно так же, как найти, сколько раз однозначный делитель входит в первые одну или две цифры делимого, как обсуждалось в предыдущих шагах.

Использование неполных частных в качестве стратегии разделения.

Деление с частичными частными отличается от стандартного метода.

Метод неполных частных побуждает учащихся разбивать вопросы на деление на «более понятные» части.

Для решения простых задач на деление в подходе с частичными частными используется повторное вычитание.

Как разделить с помощью метода неполных частных?

Выполняя шаги, описанные здесь, вы можете легко делить, используя метод частичных частных.

1. Найти и вычесть простое кратное
2. Повторите процесс
3. Сложить неполные частные

Чтобы лучше понять деление частичных частных, давайте попробуем это на примере 458 ÷ 3 .

Шаг 1. Найдите и вычтите простое кратное.

Нарисуйте вертикальную линию справа.

Найдите простое кратное делителя и вычтите его из делимого.

• Для этого умножьте делитель на более удобное число, такое как 100, 10, 5, 2 и т. д., чтобы получить простое кратное делителя. В примере 3 х 100 = 300.
• Кратность делителя должна быть как можно ближе к делимому (меньше или равно делимому).
• Множитель или число, на которое умножается делитель, является неполным частным.
• Запишите произведение или кратное (300) под делимым (458) и частичным частным (100) справа.
• Нарисуйте линию и вычтите кратное из делимого (458 – 300 = 158)

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Шаг 2.

Повторите процесс

Найдите другое кратное делителю .

• Вычтите кратное из разности (158) и запишите частичное частное.
• Продолжайте умножать и вычитать, пока разница не станет меньше делителя или не станет равной 0.
• Если разница меньше делителя, то эта разница является остатком .

Шаг 3. Сложите неполные частные

Сложите неполные частные, чтобы найти окончательное частное.

• Сложите частичные частные справа.
• Если есть остаток, присоедините его к конечному частному, чтобы получить ответ на деление. В примере 458 ÷ 3 = 152 R2

Те же шаги можно использовать для деления на две цифры. Найдите и вычтите кратное двузначного делителя из делимого так же, как вы сделали с однозначным делителем.

Длинному делению не хватает гибкости деления на частичные частные.

Длинное деление должно выполняться точно, но с неполными частными можно просто несколько раз вычесть из делимого кратное делителю и все равно получить правильный ответ.

Вы можете использовать метод неполных частных, чтобы усилить разрядное значение и концепцию деления как многократного вычитания.

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• Продажа Товар в продаже

  11,25 $ 9,00 $

  В корзину

  Добавить в список желаний

Использование модели района в качестве стратегии разделения.

Модель области — отличный способ для визуалов понять и осмыслить деление, а также улучшить их чувство числа.

Метод модели площади, как и метод частных частных, использует многократное вычитание.

Кроме того, площадная модель представляет собой способ выражения деления с помощью прямоугольников.

Длина и ширина прямоугольника определяются частичными частными и делителем.

В результате в прямоугольнике будет столько же столбцов, сколько и неполных частных.

Как разделить с помощью метода модели площади?

Метод модели площади подобен методу частных частных по своим шагам, с той лишь разницей, что проблема представлена.

1. Найти и вычесть простое кратное
2. Повторите процесс
3. Сложение частичных коэффициентов

Чтобы лучше понять деление модели области, давайте попробуем это на примере 458 ÷ 3 .

Шаг 1 – Найдите и вычтите простое кратное

Поставьте задачу (458 ÷ 3).

• Нарисуйте прямоугольник и разделите его на 2, 3, … столбца (которых будет столько, сколько неполных частных).
• Запишите делитель (3) слева за пределами прямоугольника и делимое (458) внутри первого столбца, оставив достаточно места под числом.

Найдите простое кратное делителя и вычтите его из делимого.

• Для этого умножьте делитель на более удобное число, такое как 100, 10, 5, 2 и т. д., чтобы получить простое кратное делителя. В примере 3 х 100 = 300.
• Кратность делителя должна быть как можно ближе к делимому (меньше или равно делимому).
• Множитель или число, на которое умножается делитель, является неполным частным.
• Запишите частичное частное (100) сверху первого столбца и кратное (300) под делимым (458) внутри столбца.
• Нарисуйте линию и вычтите кратное из делимого (458 – 300 = 158)

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Шаг 2. Повторите процесс

Запишите разницу между делимым и кратным (158) во второй колонке.

• Найдите еще одно кратное делителю, вычтите из разницы и запишите неполное частное сверху второго столбца.
• Продолжайте умножать и вычитать, пока разница не станет меньше делителя или не станет равной 0.
• Если разница меньше делителя, то эта разница является остатком.

Шаг 3. Сложите неполные частные

Сложите неполные частные, чтобы найти окончательное частное.

• Сложите числа в верхней части столбцов (частичные частные), чтобы найти окончательное частное.
• Если есть остаток, присоедините его к конечному частному, чтобы получить ответ на деление. В примере 458 ÷ 3 = 152 R2

Те же шаги можно использовать для деления на две цифры. Найдите и вычтите кратное двузначного делителя из делимого так же, как вы сделали с однозначным делителем.

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• $ 3,75

  В корзину

  Добавить в список желаний

• Продажа Товар в продаже

  11,25 $ 9,00 $

  В корзину

  Добавить в список желаний

Как проверить наш ответ на задачу о делении?

В любом факте деления делимое всегда равно произведению делителя и частного, прибавленного к остатку.

Таким образом, Дивиденд = (Делитель × Частное) + Остаток .

Приведенная выше формула помогает нам проверить значения частного и остатка, полученные после выполнения деления.

Мы можем подставить значения частного, остатка и делителя в уравнение, чтобы проверить, совпадает ли результат с делимым.

Если результат одинаковый, мы правильно выполнили шаги деления. Если нет, то в наших расчетах возникла проблема, которую необходимо исправить.

Проверим ответ нашей задачи на деление: 458 ÷ 3 = 152 R2

Дивиденд = (Делитель × Частное) + Остаток

458 = (3 × 152) + 2

458 = 456 + 2

, таким образом, 458 = 458

Результат тот же, следовательно, проверено, что мы правильно решили задачу деления.

Заключение

Как и другие математические операции, деление — это жизненный навык, которым дети или учащиеся должны овладеть в раннем возрасте, чтобы решать некоторые жизненные задачи.

В этой статье объясняются три стратегии деления многозначных чисел: длинное деление, деление на частичные частные и деление по модели области.

Вы можете получить больше ресурсов в моих магазинах.

Магазин на моем веб-сайте

Посетите мой магазин TPT

Магазин «Сделано учителями»

Нелли

Студентка магистратуры KNUST | Частный репетитор | Ассистент преподавателя | Ассистент-исследователь | Лаборант | Исследователь | Author

Elementary Mathematics 4-5th

Наш веб-сайт предназначен для предоставления семьям из Нью-Милфорда ценной информации и ресурсов в поддержку изучения математики детьми.

Начиная с 2014-15 учебного года, Нью-Милфорд проводит исследования чисел, данных и пространства в детском саду до 5 класса.  Посетите страницу «Для семей» на их веб-сайте! В этом эссе описывается роль игр в расследованиях.

Для каждого класса K-5 предусмотрены занятия и онлайн-игры по темам, помогающие учащимся учиться.

4 класс

Операции и алгебраическое мышление

Чему научится ваш ребенок

— Интерпретируйте умножение как сравнение, например, 35 в 5 раз больше 7. (4.OA.1)

— Умножайте или делите, чтобы решать текстовые задачи (4.OA. 2)
Решите многоэтапные текстовые задачи, используя четыре операции.

— Проблемы будут включать интерпретацию остатка и/или использование уравнений с буквой, обозначающей неизвестное. (4.OA.3)

— Найдите пары множителей для чисел до 100 и определите, являются ли числа простыми или составными. (4.ОА.4)
Понимание узоров с числами или формами. (4.OA.5)

Словарь

— Фактор: число, умноженное на другое
(множитель х множитель = произведение)

— Перегруппировка: обмен суммами равной стоимости для переименования числа

— Расширенная форма: график, показывающий частоту данных вдоль числовой прямой

— Множественное число: произведение данного целого числа на другое целое число

— Сравните: расскажите, как одно число связано с другим числом
с использованием >, <, = или других

— Массив: расположение объектов в строках и столбцах

— Свойство идентичности: (Любое число, умноженное на 1, является этим числом

— Коммутативное свойство: 5 x 7 равно то же, что и 7 x 5

— Ассоциативное свойство: (2 x 3) x 4 = 2 x (3 x 4)

— Свойство нуля: любое число, умноженное на 0, равно 0

— Произведение: ответ на задача на умножение

— Остаток: Сумма, оставшаяся после того, как число нельзя разделить поровну

— Делитель: число, на которое делится делимое

— Делимое: число, которое делится

— Частное: результат деления

— Оценка: Чтобы найти число, близкое к точной сумме

Деятельность Дома

• Рисуйте фигуры и делите их на разные дроби

• Создавайте числа, чтобы использовать их в дробях

• Используйте мерные чашки при выпечке или готовке

• Выбирайте числа, чтобы составлять дроби — тренируйтесь упрощать их

• Составляйте числа, бросайте числа с помощью кубика или находите числа (на этикетках) и сравнивайте их

• Находите числа и записывайте их в развернутой форме

• Составляйте числа и скажите, какое место (и/или значение) занимает каждое из них. цифра представляет

• Размещайте большие числа на числовой прямой

• Собирайте предметы (например, Cheerios) и оцените их количество

• Рисуйте картинки и моделируйте числа

• Практикуйтесь в сложении и вычитании

Ссылки на обучение

• Взломать код
• Алгебраическое рассуждение
• Образцы чисел и правила
• Сбалансированные уравнения
• Головоломки с числами
• Обручи
• Математика Большого шлема
• Текстовые задачи
• Подразделение по сносу
• Prime и Composite Fruit Shoot
• Простой и составной Кинг-Конг

Числа и операции с основанием 10

Что выучит ваш ребенок

— Понимание многозначного разряда до 1 000 000. (4.NBT.1)

— Чтение, запись и представление многозначных целых чисел в стандартной и расширенной форме. (4.NBT.2)

— Сравните два многозначных числа, используя >, = и
Округлите многозначные целые числа. (4.NBT.3)

— Быстрое сложение и вычитание многозначных чисел. (4.НБТ.4)

— Умножайте многозначные числа и объясняйте расчеты с помощью уравнений, прямоугольных массивов
и/или моделей площадей. (4.NBT.5)

— Разделить многозначные дивиденды на однозначные делители, включая интерпретацию остатков. (4.NBT.6)

* Учащиеся 4 класса работают с целыми числами, меньшими или равными 1 000 000.

Словарь

— Разрядное значение: значение цифры в числе

— Цифра: символ, используемый для обозначения числа

— Оценка: приблизительное вычисление, близкое к точному числу, основанное на округлении ближайший десяток, сотня или тысяча (и так далее).
Например, 391 округляет до 400, а 331 округляет до 300.

— Расширенная форма: запись числа в виде суммы значений каждой цифры номер

Занятия дома

• Составляйте числа, бросайте числа кубиком или находите числа (на этикетках) и сравнивайте их

• Находите числа и записывайте их в развернутой форме

• Составляйте числа и скажите, какой разряд (и/или значение) каждая цифра представляет

• Разместите большие числа на числовой прямой • Соберите предметы (например, Cheerios) и оцените их количество

• Рисуйте картинки и моделируйте числа • Практика сложения и вычитания

Ссылки на обучение

• Десять кадров
• Быстрая математика
• Место Значение
• Головоломки с числами
• Расширенная форма
• Глубоководная дуэль
• Базовые десять блоков
• Округление чисел
• Округление до десятков космических кораблей
• Округление до сотен акул
• Частичное умножение метода
• Фактор Кафе
• Сравнить числа кроссворд

Числа и операции с дробями

Чему научится ваш ребенок

— Понимание эквивалентных дробей. (4.NF.1)

— Сравнение дробей с символами >,< или =. (4.NF.2)

— Сложение и вычитание дробей, включая смешанные числа с одинаковыми знаменателями. (4.NF.3)

— Разложить дробь на сумму дробей с одинаковым знаменателем более чем одним способом.
Пример: 3/8=1/8+1/8+1/8; 3/8= 1/8+2/8; 2 1/8= 1+1+1/8= 8/8+8/8+1/8. (4.NF.3)

— Сложение и вычитание дробей для решения текстовых задач. (4.NF.3)

— Умножение дроби на целое число. Пример: 3 х 2/5 = 2/5+2/5+2/5. (4.NF.4)

— Понять, что дробь кратна единичной дроби. Пример: 5/4 как произведение 5 x (1/4). (4.NF.4)

— Умножьте дробь на целое число, чтобы решить текстовые задачи. (4.NF.4)

— Выразите и сложите дроби со знаменателем 10 и 100. (4.NF.5)

— Читать, писать и представлять десятичные дроби со знаменателем 10 или 100. (4.NF.6)

— Сравнивать две десятичные дроби с сотыми, используя символы >, < или =, и обосновывать выводы. (4.NF.7)                   

Словарь

— Знаменатель: число под чертой в дроби, показывающее, сколько равных частей в целом

— Сравните: укажите, как одно число связано с другим число с помощью <, > или =.

— Числитель: число над чертой в дроби, показывающее, сколько частей целого

— Единица дроби: одна часть целого, представленная как 1/a.

— Эквивалент: (=) с тем же значением

— Десятичная система счисления (на основе 10) с одной или несколькими цифрами справа от запятой.

— Смешанное число: число, состоящее из целого числа и дроби.

— Десятичная точка: символ, разделяющий доллары и центы в деньгах, а также разряд единиц от десятых долей в десятичных числах.

Занятия дома

— Рисуйте разные фигуры. Разделите их на разные фракции.

— Создание чисел для дробей. Изобразите эти дроби как части целого или набора.

— Используйте мерные чашки при выпечке или приготовлении пищи.

— Используйте сантиметровую бумагу для рисования десятичных знаков.

— Соотнесите десятицентовики с десятыми и пенни с сотыми и составьте десятичные дроби, используя десятицентовики и пенни.

— Используйте меню для сравнения денег.

— Бросьте кости, чтобы составить десятичные числа и сравнить их.

— Запись десятичных чисел в развернутом виде.

— Запись десятичных чисел в словесной форме.

— Определите десятичные знаки в газете.

— Практика умножения и деления фактов.

Ссылки на обучение

• Место Value Пираты
• Сравнение дробей
• Порядок десятичных знаков
• Эквивалентные дроби
• фракционная гонка
• Видео эквивалентных дробей
• Эквивалентные дроби Видео 2
• Видео с задачами на эквивалентные дроби
• Добавление фракций видео
• Умножение дроби на целое число
• Математика поп-музыки

Измерения и данные

Чему научится ваш ребенок

— Преобразуйте эквивалентные измерения в ту же систему измерений. Бывший. 12 дюймов = 1 фут (4.MD.1)

— Решайте задачи на измерение расстояния, времени, объема жидкости, массы объектов и денег. (4.MD.2)

— Применение формул площади и периметра для прямоугольников. (4.MD.3)

— Сложение и вычитание дробей на линейном графике. (4.MD.4)

— Понимать и измерять углы. (4.MD.5)

— Измерение и построение углов с помощью транспортира. (4.MD.6)

— Разделить угол на 2 меньших угла и знать, что больший угол является суммой двух меньших углов (4.MD.7)     

Словарь

— Периметр: Расстояние вокруг и объект.

— Вместимость: максимальный объем, который может вместить контейнер.

— Площадь: мера в квадратных единицах внутренней части плоской фигуры.

— Линейный график: График, показывающий частоту данных вдоль числовой линии.

— Объем: количество кубических единиц, которое помещается внутри сплошной фигуры.

— Углы: Фигура, образованная, когда два луча или отрезка линии имеют одну и ту же конечную точку.

— Прошедшее время: количество времени, которое проходит между двумя моментами.

— Транспортир: Инструмент для измерения углов.

Занятия дома

— Используйте измерительные инструменты при выпечке или приготовлении пищи.

— Сравните предметы по длине или весу.

— Практика планирования событий для определения прошедшего времени.

— С помощью веревки измерьте запястье, шею и талию и сравните их.

— Чтение аналоговых часов в течение дня.

. Используйте секундомер, чтобы отслеживать, сколько времени вы смотрите телевизор в течение недели и сколько времени тратите на выполнение домашних заданий, и сравнивайте эти два количества времени.

— Возьмите предмет и оцените вес, затем используйте весы, чтобы определить точный вес, и сравните два значения.

— Используйте линейку для измерения предметов вокруг дома в дюймах или сантиметрах.

— Изучите площадь и объем коробки с хлопьями.

— Определение углов реального мира как острых, прямых или тупых.

— Рисование фигур. Определите их углы как тупые, острые и прямые.

— Рисование изображений с пересекающимися линиями, перпендикулярными линиями и параллельными линиями.

— Используйте линейку, чтобы найти периметр плоских фигур.

— Практика умножения и деления фактов.

Ссылки на обучение

• Площадь и периметр Шодора
• Измерить это
• Углы
• Правитель игры
• Угол атаки
• Создание линейного графика видео 1
• Создание линейного графика видео 2
• График целых чисел
• Площадь и периметр
• Время истекло; истекшее время

Геометрия

Чему научится ваш ребенок

— Находить и рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые),
, а также перпендикулярные и параллельные прямые в двухмерных фигурах (4. Ж.1)

— Классифицировать двумерные фигуры. (4.G.2)

— Понятие линии симметрии двумерной фигуры. (4.G.3)

Словарь

— Точка: точное положение или местоположение.

— Углы: Фигура, образованная, когда два луча или отрезка линии имеют одну и ту же конечную точку.

— Линия: прямой путь, проходящий в обоих направлениях
без конечных точек.

— Перпендикулярные линии: линии, которые пересекаются, образуя прямые углы.

— Сегменты линии: часть линии, которая включает
две точки, называемые конечными точками, и все точки
между ними.

— Параллельные линии: линии на плоскости, которые никогда не пересекаются.

— Луч: часть линии с одной конечной точкой,
продолжающаяся без конца в одном направлении.

— Двухмерная фигура: Замкнутая плоская фигура с длиной и шириной.

— Симметрия: Когда одна половина фигуры выглядит как зеркальное отражение другой половины.