Умножение на 6 | Таблица умножения
На этой странице представлены примеры, описывающие умножение на 6 и умножение числа 6, деление, некоторые способы произношения и записи, таблица умножения на 6 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы.
1 x 6 = 6
2 x 6 = 12
3 x 6 = 18
4 x 6 = 24
5 x 6 = 30
6 x 6 = 36
7 x 6 = 42
8 x 6 = 48
9 x 6 = 54
10 x 6 = 60
Первый вариант произношения:
1 x 6 = 6 (1 умножить на 6, равно 6)
2 x 6 = 12 (2 умножить на 6, равно 12)
3 x 6 = 18 (3 умножить на 6, равно 18)
4 x 6 = 24 (4 умножить на 6, равно 24)
5 x 6 = 30 (5 умножить на 6, равно 30)
6 x 6 = 36 (6 умножить на 6, равно 36)
7 x 6 = 42 (7 умножить на 6, равно 42)
8 x 6 = 48 (8 умножить на 6, равно 48)
9 x 6 = 54 (9 умножить на 6, равно 54)
10 x 6 = 60 (10 умножить на 6, равно 60)
Второй вариант произношения:
1 x 6 = 6 ( по 1 взять 6 раз, получится 6)
3 x 6 = 18 ( по 3 взять 6 раз, получится 18)
4 x 6 = 24 ( по 4 взять 6 раз, получится 24)
5 x 6 = 30 ( по 5 взять 6 раз, получится 30)
6 x 6 = 36 ( по 6 взять 6 раз, получится 36)
7 x 6 = 42 ( по 7 взять 6 раз, получится 42)
8 x 6 = 48 ( по 8 взять 6 раз, получится 48)
9 x 6 = 54 ( по 9 взять 6 раз, получится 54)
10 x 6 = 60 ( по 10 взять 6 раз, получится 60)
От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 6, можно легко найти результаты умножения числа 6. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример со знаком « x », в этот раз сделаем запись с помощью приподнятой точки ( ∙ ).
В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример со знаком « x », в этот раз сделаем запись с помощью приподнятой точки ( ∙ ).
Умножение числа 6:
6 ∙ 1 = 6
6 ∙ 2 = 12
6 ∙ 3 = 18
6 ∙ 4 = 24
6 ∙ 5 = 30
6 ∙ 6 = 36
6 ∙ 7 = 42
6 ∙ 8 = 48
6 ∙ 9 = 54
6 ∙ 10 = 60
Варианты произношения:
6 ∙ 1 = 6 (по 6 взять 1 раз, получится 6)
6 ∙ 2 = 12 (по 6 взять 2 раза, получится 12)
6 ∙ 3 = 18 (по 6 взять 3 раза, получится 18)
6 ∙ 4 = 24 (по 6 взять 4 раза, получится 24)
6 ∙ 5 = 30 (по 6 взять 5 раз, получится 30)
6 ∙ 6 = 36 (по 6 взять 6 раз, получится 36)
6 ∙ 7 = 42 (по 6 взять 7 раз, получится 42)
6 ∙ 8 = 48 (по 6 взять 8 раз, получится 48)
6 ∙ 9 = 54 (по 6 взять 9 раз, получится 54)
6 ∙ 10 = 60 (по 6 взять 10 раз, получится 60)
6 ∙ 1 = 6 (6 умножить на 1, равно 6)
6 ∙ 2 = 12 (6 умножить на 2, равно 12)
6 ∙ 3 = 18 (6 умножить на 3, равно 18)
6 ∙ 4 = 24 (6 умножить на 4, равно 24)
6 ∙ 5 = 30 (6 умножить на 5, равно 30)
6 ∙ 6 = 36 (6 умножить на 6, равно 36)
6 ∙ 7 = 42 (6 умножить на 7, равно 42)
6 ∙ 8 = 48 (6 умножить на 8, равно 48)
6 ∙ 9 = 54 (6 умножить на 9, равно 54)
6 ∙ 10 = 60 (6 умножить на 10, равно 60)
Деление на 6:
6 ÷ 6 = 1 (6 разделить на 6, равно 1)
12 ÷ 6 = 2 (12 разделить на 6, равно 2)
24 ÷ 6 = 4 (24 разделить на 6, равно 4)
30 ÷ 6 = 5 (30 разделить на 6, равно 5)
36 ÷ 6 = 6 (36 разделить на 6, равно 6)
42 ÷ 6 = 7 (42 разделить на 6, равно 7)
48 ÷ 6 = 8 (48 разделить на 6, равно 8)
54 ÷ 6 = 9 (54 разделить на 6, равно 9)
60 ÷ 6 = 10 (60 разделить на 6, равно 10)
Картинка:
Деление. Картинка:
Картинка:
Таблица умножения и деления на 6 без ответов (по порядку и вразброс):
| 1 ∙ 6 = | 5 ∙ 6 = | 6 ÷ 6 = | 48 ÷ 6 = |
| 2 ∙ 6 = | 6 ∙ 6 = | 12 ÷ 6 = | 60 ÷ 6 = |
| 3 ∙ 6 = | 1 ∙ 6 = | 18 ÷ 6 = | 54 ÷ 6 = |
| 4 ∙ 6 = | 4 ∙ 6 = | 24 ÷ 6 = | 18 ÷ 6 = |
| 5 ∙ 6 = | 2 ∙ 6 = | 30 ÷ 6 = | 24 ÷ 6 = |
| 6 ∙ 6 = | 7 ∙ 6 = | 36 ÷ 6 = | 12 ÷ 6 = |
| 7 ∙ 6 = | 10 ∙ 6 = | 42 ÷ 6 = | 36 ÷ 6 = |
| 8 ∙ 6 = | 3 ∙ 6 = | 48 ÷ 6 = | 30 ÷ 6 = |
| 9 ∙ 6 = | 9 ∙ 6 = | 54 ÷ 6 = | 42 ÷ 6 = |
| 10 ∙ 6 = | 8 ∙ 6 = | 60 ÷ 6 = | 6 ÷ 6 = |
Способы записи таблицы умножения на 6:
| x | Приподнятая точка | * | Знак не указан |
|---|---|---|---|
| 1 x 6 = 6 | 1 ∙ 6 = 6 | 1 * 6 = 6 | 1 __ 6 = 6 |
| 2 x 6 = 12 | 2 ∙ 6 = 12 | 2 * 6 = 12 | 2 __ 6 = 12 |
| 3 x 6 = 18 | 3 ∙ 6 = 18 | 3 * 6 = 18 | 3 __ 6 = 18 |
| 4 x 6 = 24 | 4 ∙ 6 = 24 | 4 * 6 = 24 | 4 __ 6 = 24 |
| 5 x 6 = 30 | 5 * 6 = 30 | 5 __ 6 = 30 | |
| 6 x 6 = 36 | 6 ∙ 6 = 36 | 6 * 6 = 36 | 6 __ 6 = 36 |
| 7 x 6 = 42 | 7 ∙ 6 = 42 | 7 * 6 = 42 | 7 __ 6 = 42 |
| 8 x 6 = 48 | 8 ∙ 6 = 48 | 8 * 6 = 48 | 8 __ 6 = 48 |
| 9 x 6 = 54 | 9 ∙ 6 = 54 | 9 * 6 = 54 | 9 __ 6 = 54 |
| 10 x 6 = 60 | 10 ∙ 6 = 60 | 10 * 6 = 60 | 10 __ 6 = 60 |
Способы записи таблицы деления на 6:
| / | : | ÷ | Знак не указан |
|---|---|---|---|
| 6 / 6 = 1 | 6 : 6 = 1 | 6 ÷ 6 = 1 | 6 __ 6 = 1 |
| 12 / 6 = 2 | 12 : 6 = 2 | 12 ÷ 6 = 2 | 12 __ 6 = 2 |
| 18 / 6 = 3 | 18 : 6 = 3 | 18 ÷ 6 = 3 | 18 __ 6 = 3 |
| 24 / 6 = 4 | 24 : 6 = 4 | 24 ÷ 6 = 4 | 24 __ 6 = 4 |
| 30 / 6 = 5 | 30 : 6 = 5 | 30 ÷ 6 = 5 | 30 __ 6 = 5 |
| 36 / 6 = 6 | 36 : 6 = 6 | 36 ÷ 6 = 6 | 36 __ 6 = 6 |
| 42 / 6 = 7 | 42 : 6 = 7 | 42 ÷ 6 = 7 | 42 __ 6 = 7 |
| 48 / 6 = 8 | 48 : 6 = 8 | 48 ÷ 6 = 8 | 48 __ 6 = 8 |
| 54 / 6 = 9 | 54 : 6 = 9 | 54 ÷ 6 = 9 | 54 __ 6 = 9 |
| 60 / 6 = 10 | 60 : 6 = 10 | 60 ÷ 6 = 10 | 60 __ 6 = 10 |
Умножение на:
‹ Умножение на 5 Вверх Умножение на 7 ›
Таблица умножения и деления с числом 6
Урок 11.
 Математика 3 класс ФГОС
Математика 3 класс ФГОСНа этом уроке Матюша не только помогает составить таблицу умножения и деления с числом 6, но и подсказывает, как её легче выучить на память. Для закрепления таблицы решаются задачи и в конце урока проводится игра «Снежки».
Конспект урока «Таблица умножения и деления с числом 6»
Цифра как дверной замок: сверху крюк, внизу кружок.
Здравствуйте, дети! Вы, конечно догадались, о какой цифре идет речь. Это цифра шесть. А вспомнил я этот стишок Самуила Яковлевича Маршака потому, что сегодня мы с вами будем составлять таблицы умножения и деления с числом шесть.
Но сначала давайте вспомним примеры на умножение и деление с числом шесть, которые нам уже встречались при изучении таблиц с числами один, два, три, четыре, пять.
Вы уже люди грамотные, опытные. Помните, как
изменялись результаты умножения в таблицах на два, три, четыре, пять. Когда мы
составляли таблицу умножения на два, каждое новое произведение увеличивалось на
два. В таблице умножения с числом три каждое новое произведение увеличивалось
на три. В таблице с числом четыре – увеличивалось на четыре. В таблице с числом
пять – на пять.
Когда мы
составляли таблицу умножения на два, каждое новое произведение увеличивалось на
два. В таблице умножения с числом три каждое новое произведение увеличивалось
на три. В таблице с числом четыре – увеличивалось на четыре. В таблице с числом
пять – на пять.
Ну а теперь на сколько увеличиваются произведения? Конечно, на шесть. Начинаем составлять новые примеры. И первый из них – шесть умножить на шесть. Я думаю, вы слышали песенку про таблицу умножения, и никогда не забудете: шестью шесть – тридцать шесть. Очень просто запомнить: шестью шесть – тридцать шесть.
Тридцать шесть разделить на шесть будет шесть.
Шестью семь – сорок два. И семью шесть – сорок два. Эти выражения почему-то некоторые трудновато запоминают. Но вы-то, я уверен, не забудете, что шестью семь и семью шесть – сорок два. А сорок два разделить на шесть будет семь. Ну а частное чисел сорок два и семь – шесть.
Шестью восемь сорок восемь. Восемью шесть
сорок восемь. Сорок восемь делим на шесть получается восемь, сорок восемь делим
на восемь – шесть.
Восемью шесть
сорок восемь. Сорок восемь делим на шесть получается восемь, сорок восемь делим
на восемь – шесть.
Шестью девять пятьдесят четыре. Тоже тяжковато запоминается. Но, у меня для запоминания есть одна хитрость: шестью девять – пятьдесят четыре. А девять – это пять и четыре. Шесть, пять четыре. Ну и девятью шесть – пятьдесят четыре. А пятьдесят четыре делим на шесть – девять. Пятьдесят четыре делим на девять – шесть. Ну, и самое простое – шесть умножаем на десять – шестьдесят. Десять умножить на шесть –шестьдесят. Шестьдесят разделить на шесть – десять. Шестьдесят разделить на десять – шесть.
Все, таблица составлена.
Не таблица, а песня! А точнее, стихи. Вы
спросите, почему стихи? Да потому, что в ней есть примеры, которые весело
произносятся в рифму. Шестью четыре – двадцать четыре. Шестью шесть – тридцать
шесть. Шестью восемь – сорок восемь. Только не вздумайте все остальные примеры
рифмовать, а то такого наговорите.
А теперь я предлагаю вам вот такую задачку.
В прошлом году у деда выросла репка массой семь килограммов, а в этом – в шесть раз тяжелее. Деду даже пришлось бабку, внучку и всех остальных на помощь звать. Чему равна масса репки в этом году?
Ну, кто уже знает ответ на этот вопрос?
7 · 6 = 42 (кг)
Ответ: масса репки 42 кг.
А такую задачку решите?
Робин-Бобин вчера съел пятьдесят четыре коровы, а сегодня пока только шесть. Во сколько раз больше коров он съел вчера?
Вижу-вижу! Почти все решили. А вот правильно ли? Проверьте.
54 : 6 = 9 (р.)
Ответ: в 9 раз больше.
Ну, а теперь я предлагаю вам поиграть в игру «снежки».
6 · * = 36 54 : * = 6
* · 6 = 48 36 : * = 6
6 · * = 54 42 : * = 6
* · 6 = 60 24 : * = 6
Ну, а теперь проверьте, такие числа вы вставили?
6 · 6 = 36 54 : 9 = 6
8 · 6 = 48 36 : 6 = 6
6 · 9 = 54 42 : 7 = 6
10 · 6 = 60 24 : 4 = 6
Так-так. Я понял, что мне вас не запутать. Вы –
умные. Так что, надо закругляться. Только не забудьте. Вот эти примеры вам надо
повторить.
Я понял, что мне вас не запутать. Вы –
умные. Так что, надо закругляться. Только не забудьте. Вот эти примеры вам надо
повторить.
А вот эти – выучить.
Предыдущий урок 10 Задачи на кратное и разностное сравнение чисел
Следующий урок 12 Задачи на нахождение четвёртого пропорционального
Получите полный комплект видеоуроков, тестов и презентаций Математика 3 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Примеры на умножение и деление .Первое полугодие.
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна.
 Часть 2
Часть 2 - Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
| | Математика 3 класс ->> Примеры Первое полугодиеВторое полугодие |
| 2 * 4 = 8 | 7 * 2 = 14 | 9 * 8 = 72 | 16 : 2 = 8 | 6 : 2 = 3 | 56 : 7 = 8 |
| 28 : 4 = 7 | 3 * 4 = 12 | 9 * 3 = 27 | 8 * 8 = 64 | 56 : 8 = 7 | 81 : 9 = 9 |
| 4 * 2 = 8 | 4 * 7 = 28 | 7 * 8 = 56 | 24 : 8 = 3 | 16 : 2 = 8 | 3 * 5 = 15 |
| 5 * 9 = 45 | 5 * 1 = 5 | 18 : 6 = 3 | 35 : 5 = 7 | 18 : 3 = 6 | 8 * 4 = 32 |
| 5 * 7 = 35 | 5 * 2 = 10 | 27 : 9 = 3 | 24 : 8 = 3 | 8 : 2 = 4 | 6 * 7 = 42 |
| 7 * 2 = 14 | 8 * 7 = 56 | 28 : 4 = 7 | 16 : 8 = 2 | 16 : 4 = 4 | 3 * 8 = 24 |
| 9 * 5 = 45 | 7 * 3 = 21 | 24 : 4 = 6 | 12 : 3 = 4 | 32 : 8 = 4 | 6 * 4 = 24 |
| 6 * 1 = 6 | 45 : 5 = 9 | 6 : 2 = 3 | 4 * 3 = 12 | 5 * 4 = 20 | 4 * 7 = 28 |
| 8 : 4 = 2 | 30 : 5 = 6 | 40 : 5 = 8 | 7 * 4 = 28 | 5 * 3 = 15 | 2 * 4 = 8 |
| 4 : 2 = 2 | 28 : 4 = 7 | 56 : 8 = 7 | 3 * 2 = 6 | 9 * 9 = 81 | 1 * 6 = 6 |
| 9 : 9 = 1 | 63 : 79 | 32 : 4 = 8 | 5 * 3 = 15 | 4 * 5 = 20 | 8 * 9 = 72 |
| 6 * 8 = 48 | 3 * 6 = 36 | 8 * 7 = 56 | 40 : 5 = 8 | 4 : 2 = 2 | 2 * 4 = 8 |
| 2 * 7 = 14 | 4 * 5 = 20 | 42 : 7 = 6 | 16 : 8 = 2 | 30 : 5 = 6 | 5 * 8 = 40 |
| 12 : 6 = 2 | 56 : 7 = 8 | 21 : 3 = 7 | 6 * 2 = 12 | 2 * 2 = 4 | 7 * 2 = 14 |
| 10 : 2 = 5 | 18 : 6 = 3 | 20 : 4 = 5 | 32 : 4 = 8 | 8 * 2 = 16 | 2 * 5 = 10 |
| 36 : 4 = 9 | 9 * 3 = 27 | 3 * 5 = 15 | 5 * 9 = 45 | 9 : 3 = 3 | 3 * 8 = 24 |
| 7 * 5 = 35 | 5 * 8 = 40 | 8 : 4 = 2 | 6 : 2 = 3 | 9 * 4 = 36 | 6 * 3 = 18 |
| 24 : 8 = 3 | 27 : 9 = 3 | 4 * 6 = 24 | 8 * 5 = 40 | 5 * 3 = 15 | 40 * 5 = 8 |
| 63 : 7 = 9 | 72 : 9 = 8 | 54 : 6 = 9 | 21 : 7 = 3 | 4 * 4 = 16 | 5 * 5 = 25 |
| 4 * 7 = 28 | 5 * 9 = 45 | 9 * 3 = 27 | 6 * 6 = 36 | 8 * 3 = 24 | 3 * 5 = 15 |
| 9 * 2 = 18 | 18 : 3 = 6 | 7 * 7 = 49 | 42 : 6 = 7 | 70 : 10 = 7 | 20 : 10 = 2 |
| 12 * 4 = 3 | 32 : 4 = 8 | 2 * 7 = 14 | 4 * 9 = 36 | 81 : 9 = 9 | 30 : 3 = 10 |
| 48 : 6 = 8 | 25 : 5 = 5 | 40 : 8 = 5 | 6 : 2 = 3 | 12 : 6 = 2 | 2 * 5 = 10 |
| 3 * 9 = 27 | 6 * 5 = 30 | 4 * 2 = 8 | 16 : 4 = 4 | 28 : 7 = 4 | 7 * 8 = 56 |
| 54 : 9 = 6 | 9 * 10 = 90 | 10 : 2 = 5 | 5 * 4 = 20 | 3 * 9 = 27 | 4 : 2 = 2 |
| 10 : 10 = 1 | 35 : 7 = 5 | 36 : 9 = 4 | 4 * 7 = 28 | 18 : 9 = 2 | 49 : 7 = 7 |
| 2 * 2 = 4 | 5 * 1 = 5 | 42 : 7 = 6 | 25 : 5 = 5 | 24 : 6 = 4 | 32 : 8 = 4 |
| 54 : 9 = 6 | 63 : 7 = 9 | 9 * 9 = 81 | 12 : 2 = 6 | 27 : 3 = 9 | 42 : 6 = 7 |
| 64 : 8 = 8 | 3 * 3 = 9 | 2 * 8 = 16 | 9 * 3 = 27 | 18 : 2 = 9 | 30 : 10 = 3 |
| 10 * 10 = 100 | 10 * 9 = 90 | 80 : 10 = 8 | 1 * 1 = 1 | 70 : 7 = 10 | 6 * 6 = 36 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
Умножения шести и на 6, соответствующие случаи деления.
 | План-конспект урока по математике (3 класс) по теме:
| План-конспект урока по математике (3 класс) по теме:Скопина Елена Валерьевна
УМК «Школа России»
Тема: Умножения шести и на 6, соответствующие случаи деления.
Тип урока: изучение нового материала.
Цель: знакомство с таблицей умножения шести и на 6, соответствующие случаи деления.
Задачи:
Обучающие:
- повторить табличные случаи умножения и деления на 2, 3, 4, 5;
- составить таблицы умножения на 6 и соответствующие случаи деления;
- совершенствовать умения записывать выражения с переменной, решать уравнения;
Развивающие:
- развивать логическое мышление, анализировать, рассуждать; развивать математическую речь, память;
Воспитательные:
- воспитывать доброжелательность, трудолюбие, взаимопомощь.
Пособия:
- картинка Знайка,
- карточки с ответами примеров,
- учебник по математике.
Ход урока
Этапы урока | Речь и деятельность учителя | Речь и деятельность учащихся |
I. | Ну-ка проверь, дружок, | |
II. Сообщение темы урока | На уроке мы продолжим таблицу составлять И Знайка – математик будет нам в этом помогать. Он сегодня загадку приготовил для нас, Секрет этой цифры узнает весь класс. Но сначала, ребятки, для «ума зарядка». | |
III. Устный счёт 2*3= 5*4= 6*3= 7*4= 8*4= 9*5= 9*2= 6*5= 5*5= 8*2= 7*3= | 1. Среди данных чисел назовите числа, кратные 5 (на доске числа) 9, 8, 15, 2, 28, 10, 25, 17, 5, 23, 11, 37, 20, 18, 16, 30, 12, 42, 45, 14. 2. Повторение табличного умножения и деления — Только тот, кто дружит и помогает другу всегда и везде сможет выполнить следующее задание Знайки. Счет «цепочкой» у доски: 2*3= 5*4= 6*3= 7*4= 8*4= 9*5= 9*2= 6*5= 5*5= 8*2= 7*3= | — Учащиеся называют признаки делимости на 5: Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5, т. е. если она 0 или 5. — 15, 10, 25, 5, 20, 30, 45 — Задание выполняется учениками каждого ряда, ученики по очереди выходят к доске и решают пример. — Побеждают учащиеся того ряда, которые быстро и правильно напишут ответы. 2*3= 5*4= 6*3= 7*4= 8*4= 9*5= 9*2= 6*5= 5*5= 8*2= 7*3= |
III. | — Запись на доске (в 1 столбик): 1*5+1= 4*5+4= 7*5+7= 2*5+2= 5*5+5= 8*5+8= 3*5+3= 6*5+6= 9*5+9= — Чем похожи данные выражения? — Чем отличаются выражения? — Замените суммы произведением, запишите в тетради. — Чем похожи получившиеся записи? — Кто сможет назвать тему нашего урока? — Правильно, сегодня мы с вами знакомимся с таблицей умножения шести, на 6 и соответствующими случаями деления. | — В каждом выражении второй множитель 5, первое действие умножение, а второе сложение. — Первые множители разные. — Учащиеся выполняют преобразование и записывают примеры (в 1 столбик): 1*6= 4*6= 7*6= 2*6= 5*6= 8*6= 3*6= 6*6= 9*6= — Во всех примерах одинаковый второй множитель – 6. — Таблица умножения на 6. |
IV. 1. Составление таблицы умножения на 6. 2. Волшебные слова. 3. Составление таблицы деления на 6. V. Физкультминутка VI. Проверка усвоенного материала VII. Работа над пройденным материалом 1. Работа над задачей 2.Выражение с переменной 3.Работа над уравнением | — Найдите значения произведений. Как вы получили ответы? — Давайте проверим, правильно ли выполнены вычисления. — Какого равенства не хватает? Запишите это равенство в таблицу. — Какой закон умножения применил Знайка, чтобы получились примеры такого вида? 6*1= 6 6*4=24 6*7=42 6*10=60 6*2= 12 6*5=30 6*8=48 6*3= 18 6*6=36 6*9=54 — Давайте вспомним, как он звучит. — Для лучшего запоминания таблицы Знайка предлагает нам запомнить следующие рифмы (подчеркните зелёной ручкой примеры, которые вы сейчас услышите). Шестью четыре – двадцать четыре, — Эти рифмы станут для нас «узелками на память». — Что получим, если из данных произведений будем отнимать (вычитать) 6? (24-6=18, 36-6=30, 48-6=42). — Мы получим соседей слева. — А если будем прибавлять 6? (24+6=30, 36+6=42, 48+6=54). — Получим соседей справа. — Значит, пользуясь тремя «узелками на память» мы сможем найти ответы ещё шести примеров. — Используя таблицу умножения, составьте соответствующие случаи деления на 6. — Какой закон математики будете использовать? На разминку На разминку становись! Вправо-влево покрутись Повороты посчитай, Раз-два-три, не отставай, Начинаем приседать — Раз-два-три-четыре-пять. Тот, кто делает зарядку, Может нам сплясать вприсядку. А теперь поднимем ручки И опустим их рывком. Будто прыгаем мы с кручи Летним солнечным деньком. А теперь ходьба на месте, Левой-правой, стой раз-два. Мы за парты сядем, вместе Вновь возьмёмся за дела. — Открываем учебник стр.40 — Как вы думаете, почему авторы учебника записали таблицу с равенства 6*6=36? — Давайте повторим таблицу умножения на 6 и соответствующие случаи деления. — Я называю пример, а тот, у кого карточка с ответом встаёт и называет ответ. — Прочитайте задание № 6 стр. 40 учебника — Какое задание надо выполнить? — Какой вопрос можно поставить? — Составим краткую запись. Выделите главные слова. — Какой поставили вопрос? — Как обозначить это в краткой записи? — Самостоятельно дополните краткую запись и решите задачу, с последующей взаимопроверкой в парах. — Сейчас мы с вами вспомним, как решать выражения с переменной. 1 вариант выполнит № 3, а второй вариант № 5. — Прочитайте задание № 4. Что необходимо выполнить? — Какие правила мы должны вспомнить, решая данные уравнения? — Давайте вспомним эти правила. — При решении каких уравнений, допущены ошибки? — Давайте решим уравнения, 1 вариант решает 1 уравнение, 2 вариант – 2 уравнение. — Поменяйтесь тетрадями и проверьте друг друга. | — Учащиеся записывают ответы, которые получили, пользуясь таблицей умножения на 5 и прибавляя числа. 1*6= 6 4*6=24 7*6=42 2*6= 12 5*6= 30 8*6=48 3*6= 18 6*6= 36 9*6=54 — Взаимопроверка. — 10*6=60 — Учащиеся сравнивают примеры, которые они уже вычисляли и те, которые записаны на листе (в 1 столбик). — Знайка применил переместительный закон умножения. — Учащиеся хором проговаривают переместительный закон умножения: от перестановки множителей произведение не меняется. 6*1= 6 6*4=24 6*7=42 6*10=60 6*2= 12 6*5=30 6*8=48 6*3= 18 6*6=36 6*9=54 — Учащиеся составляют примеры на деление рядом со столбиком примеров на умножение. 6: 1=6 6:6=1 12:2=6 12:6=2 18:3=6 18:6=3 24:4=6 24:6=4 30:5=6 30:6=5 36:6=6 42:7=6 42:6=7 48:8=6 48:6=8 54:9=6 54:6=9 60:10=6 60:6=10 — Если произведение разделить на один из множителей получим другой множитель. — Вращение туловищем вправо и влево. — Приседания. — Дети поднимают прямые руки над головой, потом резким движением опускают их и отводят назад, потом резким движением снова вверх и т. д. — Ходьба на месте. — Дети садятся за парты. — Предыдущие равенства мы уже изучали. — У учащихся на столе лежат карточки с числами, которые являются ответами к примерам на умножение. — Дополнить условие и поставить вопрос так, чтобы задача решалась в два действия, и решить её. — Сколько стоят тетрадь и учебник вместе? — Тетрадь, учебник. — Фигурная скобка и знак вопроса. — Учащиеся решают задачу, меняются тетрадями и выполняют взаимопроверку. — Учащиеся по вариантам выполняют задания. — Два ученика работают у доски, но класс не видит их решения. — Когда работа выполнена, осуществляется проверка работы учащихся у доски и самопроверка по образцу на доске. — Надо найти ошибки и правильно решить уравнения. — Как найти вычитаемое и как найти неизвестное слагаемое. — Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность. — Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. — Ответы учащихся. — Учащиеся решают уравнения и выполняют взаимопроверку. |
VI. Рефлексия VIII. Итог урока | — Что больше понравилось на уроке? Что запомнилось? — Над какой темой мы работали сегодня на уроке? | — Ответы учащихся. — Познакомились с таблицей умножения шести, на 6 и соответствующими случаями деления. — Тренировались считать быстро и правильно. — Вспомнили признаки делимости на 5. — Узнали, какие бывают «узелки на память» и т.д. |
VII. Домашнее задание. | Знайка прощается с вами и желает вам успехов в познании нового. № 2, № 7 стр.40, выучить таблицу умножения на 6. |
Цели, поставленная на уроке, была достигнута. Образовательные, развивающие и воспитательные задачи были реализованы.
Введение сказочного персонажа и получение заданий от его имени внесло игровой момент в ход урока и способствовало положительного эмоциональному настрою учащихся.
Повторение изученных правил (хором) помогло сделать каждого ученика участником работы над данным материалом, помогло некоторым учащимся (которые плохо знают взаимосвязь компонентов) выполнить задание.
Повторение переместительного закона умножение дало возможность дважды повторить таблицу умножения: сначала разобрали умножение шести, затем умножение на шесть.
При работе над темой урока были задействованы все способы восприятия информации, что способствовало лучшему усвоению материала:
- для аудиалов – проговаривание и прослушивание,
- для визуалов – зрительное восприятие таблицы,
- для кинестетиков – запись примеров, работа с карточками.
Запоминание «узелков на память» способствовало лучшему запоминанию таблицы, помогло понять, как владея одной информацией получить другую (зная один пример, решить другие).
Самостоятельное создание таблицы деления способствовало формированию умения применять полученную информацию для получения новой.
При повторении изученных случаев использовался соревновательный момент, что так же вызывает заинтересованность учащихся, способствует формированию ответственность за совместно выполненную работу.
Работа с карточками (ответы примеров) способствовало развитию внимания, повторению изученных на уроке случаев табличного умножения и деления.
Взаимопроверка, осуществляемая на уроке, способствовала развитию внимания, навыка сотрудничества, взаимопомощи.
Источники:
1.Интернет – ресурс.
…в 3-м классе по теме «Таблица умножения и деления на 6» : Статьи…
Урок проводится с целью повторить табличные случаи умножения и деления на 2, 3, 4, 5; составить таблицы умножения на 6 и соответствующие случаи деления; совершенствовать умения записывать выражения с переменной, решать уравнения…
festival.1september.ru›Урок математики в 3-м классе
2. Мокрушина О.А. Поурочные разработки по математике: 3 класс. – М.: ВАКО, 2012.
3…Знайка», в котором приняли участие дети старшего
http://www. yar-edudep.ru/znayk…
yar-edudep.ru/znayk…
Таблица умножения и деления на 6 | План-конспект урока по математике (2 класс):
Урок математики во 2-м классе по теме:
«Таблица умножения и деления на 6»
Тип урока: ОНЗ
Цель урока: составить и выучить таблицу умножения и деления на 6.
Задачи:
- совершенствовать умения находить значения выражений, сравнивать выражения;
- развивать логическое мышление, анализировать, рассуждать;
- развивать математическую речь, память;
- воспитывать доброжелательность, дружбу, взаимопомощь.
Дети стоят.
— Ребята, у нас сегодня необычный урок. К нам пришли гости. Повернитесь и поздоровайтесь с гостями.
Дети кивают головой, потом поворачиваются к учителю.
— Садитесь.
Ход урока:
1. Мотивация к учебной деятельности.
-Ребята, какое сейчас время года?
Случилась беда. Злая колдунья заколдовала все деревья в лесу, чтобы не было зелёных листьев и мы с вами не радовались теплу и красоте природы. Нужно срочно помочь лесу. Добрый Лесовичок передал нам волшебную карту с заданиями, при выполнении которых колдовские чары колдуньи перестанут действовать! Если мы справимся, то спасём природу! Слайд 1
Нужно срочно помочь лесу. Добрый Лесовичок передал нам волшебную карту с заданиями, при выполнении которых колдовские чары колдуньи перестанут действовать! Если мы справимся, то спасём природу! Слайд 1
-Нам нужно быть смелыми и решительными. И мы обязательно справимся со всеми трудностями! Вперёд!
2. Актуализация знаний.
-Я буду читать вам задания, а вы записывайте только ответы. Слайд 2
(Работа в тетрадях)
1.Сумма чисел 26 и 7. (33)
2.Разность чисел 43 и 8. (35)
3.Произведение чисел 3 и 6. (18)
4.Частное чисел 35 и 5. (7)
5.Сколько нужно прибавить к 38, чтобы стало 50? (12)
6.Сколько нужно вычесть из 72, чтобы стало 30? (42)
7.Увеличь число 4 в 7 раз. (28)
8.Уменьши 20 в 5 раз. (4)
Слайд 3
-Ребята, посмотрите на экран. У кого совпали все ответы, поднимите руку.
-У кого получилось по-другому? В каком задании? Почему?
3.Проблемное объяснение нового материала.
Слайд 4
-Ребята, мы справились с первым заданием и нужно идти дальше.
Посмотрите на эти примеры.
3х9=27
4х8=32
5х7=35
7х5=35
8х4=32
9х3=27
-Давайте вспомним, как называются компоненты действия умножения?
(Множитель, множитель, произведение)
-Что обозначает каждый множитель?
-Давайте проведём исследование данного столбика примеров. Что интересного вы увидели сами?
-По какому принципу составлены примеры?
-А почему мы смогли решить эти примеры?
-Посмотрите внимательно ещё раз на данный столбик примеров и скажите, а какого примера не хватает в столбике?
-Как вы думаете, почему он пропущен?
Как какова же тема нашего урока? (Тема вывешивается на доску)
Составление таблицы.
-Давайте вспомним то, что мы уже знаем.
6х2=12
6х3=18
6х4=24
6х5=30
6×6=
-Ребята давайте поищем закономерность и скажем, какое число будет в ответе следующего примера!
Закономерности:
- первый множитель неизменный, а второй множитель увеличивается на1;
- произведение увеличивается на 6 (сверху вниз, а снизу вверх уменьшается на 6),
- все произведения двузначные числа.

-Сколько раз взяли число 6 в этом примере?
Заполнение таблицы на доске и в учебниках-тетрадях.
6х6=36
6х7=42
6х8=48
6х9=54
При умножении 6 на чётное число произведение оканчивается той же цифрой на которую умножали (пример).
Слышится рифма, волшебные слова. Слайд 5
Проговорить:
6х2=12
6х4=24
6х6=36
6х8=48
-А теперь заполняем второй столбик таблицы в учебнике.
Кто знает, какому правилу нужно следовать?
(От перестановки множителей произведение не меняется)
Заполняем таблицу деления. Для это вспомним, как найти неизвестный множитель?
(Произведение разделить на известный множитель)
-А теперь наша задача состоит в том, чтобы научиться практически использовать таблицу и запомнить её, насколько это возможно!
4.Физкультминутка № 1
Мы считали и устали,
Дружно все мы тихо встали,
Ручками похлопали,
Раз, два, три. (Хлопки в ладоши под счет учителя. )
)
Ножками потопали,
Раз, два, три. (Шаги ногами на месте.)
Сели, встали, встали, сели,
И друг друга не задели.
(Приседания.)
Мы немножко отдохнем
И опять считать начнем. (Повороты туловища. Ходьба на месте.)
5.Закрепление.
Первичное закрепление во внешней речи.
-Ребята, мы выполнили два важных задания Лесовичка, и в лесу стало теплее. Но нам нужно дойти до конца! Злая колдунья спрятала цифры в таблице умножения, чтобы мы не справились с заданиями. Давайте это исправим.
Фронтальная работа. (Таблица умножения) Слайд 6
6 * …= 30
6 * 6 = …
6 * … = 42
6 * 8 = …
6 * 9 = …
Работа в парах. Жёлтая карточка.
-Берём жёлтую карточку. Задание: найти значение выражений. Слайд 7
63 — 8×6 7×6 + 38 89 – 9×6 25 – 6×0 57 – 6×6 +14
Пока дети работают, можно включить спокойную музыку, как только первая пара все сделала и дает знак — поднимает руки домиком, музыку выключить. Затем вывести на экран слайд с правильным выполнением.
Затем вывести на экран слайд с правильным выполнением.
— Итак, проверяем. Слайд 8
-Кто допустил ошибки? Поднимите руку.
-В чем они?
-Исправьте ошибки.
-Кто не допустил ошибки. Поднимите руку. Вы молодцы!
Самостоятельная работа с самопроверкой.
— Ребята, мы почти справились со всеми заданиями, идём дальше!
Зелёная карточка.
-Читаем задание. Что значит сравнить?
(Поставить знак больше, меньше или равно)
6×3…6×5
8×6…6×8
1×6…1×5
4×6…4×7
6×0…0x9
Слайд 9
-Посмотрите на экран. Итак, проверяем.
-Кто выполнил работу без ошибок? Поднимите руку.
-Молодцы!
-У кого по-другому. Проверяем.
6. Физкультминутка №2
-Если я называю число, кратное 6, если нет — ходьба на месте.
Что значит кратное?
(Число, которое можно разделить)
-Если это число не кратно 6,вы ходите.
Будьте внимательными. Приготовились.
14 (ходьба), 18 (хлопок), 12 (хлопок), 9 (ходьба), 24 (хлопок), 32 (ходьба), 45(ходьба), 30 (хлопок).
7.Включение в систему знаний и повторение.
— Когда мы используем таблицу умножения?
(При решения уравнений и задач)
-Я предлагаю решить задачу — стр.31 № 6
-Читаем задачу про себя два раза. Чтение задачи вслух.
-Сколько банок малинового варенья изготовили на зиму? (6 банок)
-Что известно про вишнёвое варенье? (в 2 раза больше)
-Что известно про клубничное варенье? (на 4 банки меньше, чем вишнёвого)
-Что нужно узнать в задаче?
Решение задачи у доски и в тетрадях.
Решение уравнений (если есть время).
-Ребята, пока мы решали задачу, у меня на столе появилось письмо от Лесовичка.
(Читает)
Дорогие ребята, вы молодцы! Злая ведьма больше не страшна нам! Спасибо, что спасли мой дом, но природа – это и ваш дом тоже! Всегда буду вам рад. Лесовичок.
8.Итог урока.
С какого тревожного сообщения начался урок? (Ответы детей.)
Вы смогли навести порядок в лесу?
Какое новое знание вам помогло навести порядок?
(Знание таблицы умножения и деления на 6)
9. Рефлексия учебной деятельности на уроке .
Учитель проводит рефлексию оценивания учащихся.
-Те ребята, кто считает, что запомнил таблицу умножения и деления на 6, поднимают солнышко.
-Ученики, которые сомневаются в ответе, поднимают облачко.
-Спасибо за урок.
Умножение. Умножение Примеры таблица на 2
На этой странице представлены примеры, описывающие умножение на 2 и умножение числа 2, деление, некоторые способы записи и произношения, таблица умножения на 2 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать таблицу умножения и деления на 2.
Умножение на 2:
1 x 2 = 2
2 x 2 = 4
3 x 2 = 6
4 x 2 = 8
5 x 2 = 10
6 x 2 = 12
7 x 2 = 14
8 x 2 = 16
9 x 2 = 18
10 x 2 = 20
Первый вариант произношения:
1 x 2 = 2 (1 умножить на 2, равно 2)
2 x 2 = 4 (2 умножить на 2, равно 4)
3 x 2 = 6 (3 умножить на 2, равно 6)
4 x 2 = 8 (4 умножить на 2, равно 8)
5 x 2 = 10 (5 умножить на 2, равно 10)
6 x 2 = 12 (6 умножить на 2, равно 12)
7 x 2 = 14 (7 умножить на 2, равно 14)
8 x 2 = 16 (8 умножить на 2, равно 16)
9 x 2 = 18 (9 умножить на 2, равно 18)
10 x 2 = 20 (10 умножить на 2, равно 20)
Второй вариант произношения:
1 x 2 = 2 (по 1 взять 2 раза, получится 2)
2 x 2 = 4 (по 2 взять 2 раза, получится 4)
3 x 2 = 6 (по 3 взять 2 раза, получится 6)
4 x 2 = 8 (по 4 взять 2 раза, получится 8)
5 x 2 = 10 (по 5 взять 2 раза, получится 10)
6 x 2 = 12 (по 6 взять 2 раза, получится 12)
7 x 2 = 14 (по 7 взять 2 раза, получится 14)
8 x 2 = 16 (по 8 взять 2 раза, получится 16)
9 x 2 = 18 (по 9 взять 2 раза, получится 18)
10 x 2 = 20 (по 10 взять 2 раза, получится 20)
Иногда еще произносят, например, так:
2 ∙ 2 = 4 (дважды два — четыре)
От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 2, можно легко найти результаты умножения числа 2. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки (∙)
В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки (∙)
Умножение числа 2:
2 ∙ 1 = 2
2 ∙ 2 = 4
2 ∙ 3 = 6
2 ∙ 4 = 8
2 ∙ 5 = 10
2 ∙ 6 = 12
2 ∙ 7 = 14
2 ∙ 8 = 16
2 ∙ 9 = 18
2 ∙ 10 = 20
Варианты произношения:
2 ∙ 1 = 2 (по 2 взять 1 раз, получится 2)
2 ∙ 2 = 4 (по 2 взять 2 раза, получится 4)
2 ∙ 3 = 6 (по 2 взять 3 раза, получится 6)
2 ∙ 4 = 8 (по 2 взять 4 раза, получится 8)
2 ∙ 5 = 10 (по 2 взять 5 раз, получится 10)
2 ∙ 6 = 12 (по 2 взять 6 раз, получится 12)
2 ∙ 7 = 14 (по 2 взять 7 раз, получится 14)
2 ∙ 8 = 16 (по 2 взять 8 раз, получится 16)
2 ∙ 9 = 18 (по 2 взять 9 раз, получится 18)
2 ∙ 10 = 20 (по 2 взять 10 раз, получится 20)
2 ∙ 1 = 2 (2 умножить на 1, равно 2)
2 ∙ 2 = 4 (2 умножить на 2, равно 4)
2 ∙ 3 = 6 (2 умножить на 3, равно 6)
2 ∙ 4 = 8 (2 умножить на 4, равно 8)
2 ∙ 5 = 10 (2 умножить на 5, равно 10)
2 ∙ 6 = 12 (2 умножить на 6, равно 12)
2 ∙ 7 = 14 (2 умножить на 7, равно 14)
2 ∙ 8 = 16 (2 умножить на 8, равно 16)
2 ∙ 9 = 18 (2 умножить на 9, равно 18)
2 ∙ 10 = 20 (2 умножить на 10, равно 20)
Деление на 2:
2 ÷ 2 = 1 (2 разделить на 2, равно 1)
4 ÷ 2 = 2 (4 разделить на 2, равно 2)
6 ÷ 2 = 3 (6 разделить на 2, равно 3)
8 ÷ 2 = 4 (8 разделить на 2, равно 4)
10 ÷ 2 = 5 (10 разделить на 2, равно 5)
12 ÷ 2 = 6 (12 разделить на 2, равно 6)
14 ÷ 2 = 7 (14 разделить на 2, равно 7)
16 ÷ 2 = 8 (16 разделить на 2, равно 8)
18 ÷ 2 = 9 (18 разделить на 2, равно 9)
20 ÷ 2 = 10 (20 разделить на 2, равно 10)
Картинка:
Деление. Картинка:
Картинка:
Таблица умножения и деления на 2 без ответов (по порядку и вразброс):
| 1 ∙ 2 = | 7 ∙ 2 = | 2 ÷ 2 = | 10 ÷ 2 = |
| 2 ∙ 2 = | 8 ∙ 2 = | 4 ÷ 2 = | 2 ÷ 2 = |
| 3 ∙ 2 = | 9 ∙ 2 = | 6 ÷ 2 = | 4 ÷ 2 = |
| 4 ∙ 2 = | 10 ∙ 2 = | 8 ÷ 2 = | 6 ÷ 2 = |
| 5 ∙ 2 = | 1 ∙ 2 = | 10 ÷ 2 = | 8 ÷ 2 = |
| 6 ∙ 2 = | 2 ∙ 2 = | 12 ÷ 2 = | 16 ÷ 2 = |
| 7 ∙ 2 = | 3 ∙ 2 = | 14 ÷ 2 = | 18 ÷ 2 = |
| 8 ∙ 2 = | 4 ∙ 2 = | 16 ÷ 2 = | 12 ÷ 2 = |
| 9 ∙ 2 = | 5 ∙ 2 = | 18 ÷ 2 = | 14 ÷ 2 = |
| 10 ∙ 2 = | 6 ∙ 2 = | 20 ÷ 2 = | 4 ÷ 2 = |
Эта часть таблицы обычно бывает если не первой, то одной из первых в изучении. Мы уже говорили о способах записи, теперь рассмотрим пример с умножением на 2, связать старые знания с новыми
Мы уже говорили о способах записи, теперь рассмотрим пример с умножением на 2, связать старые знания с новыми
Здесь 5 — это первый множитель, 2 — второй множитель, а 10 — значение произведения
Часто в качестве знака умножения также используют приподнятую точку (5 ∙ 2) и «звездочку» или «снежинку» (5 * 2) , можно встретить и другие обозначения.
Мы уже говорили в основной части о том, что, если записать таблицу умножения на числа от 1 до 10, то можно увидеть, что при перемене мест множителей значение произведения не меняется (на основании этого формулируют переместительный закон умножения), поэтому можно выучить только половину таблицы умножения и, зная её, быстро найти ответы для оставшейся половины. Кстати, есть еще и другие способы быстро выучить таблицу, а также способы быстро считать без заучивания таблицы.
Итак, мы только что сказали, что при умножении числа 2 на 5 получится такое же число как и при умножении 5 на 2:
5 x 2 = 2 x 5 = 10.
Но здесь нужно быть очень внимательными, когда дело доходит уже не просто до чисел, а до конкретных задач и примеров. Во многих учебниках рекомендуют с помощью первого множителя обозначать то, что складывают, а с помощью второго указывать, сколько раз.
Во многих учебниках рекомендуют с помощью первого множителя обозначать то, что складывают, а с помощью второго указывать, сколько раз.
Приведем в качестве примера такую ситуацию: Вася и Петя собирались рисовать. Мама дала каждому по 5 листов бумаги, значит всего листов будет 10. Это можно записать привычным способом с помощью знака плюс (5 + 5 = 10), а можно записать с помощью двух множителей и знака умножения.
Исходя из того, что каждый множитель при записи выполняет определенную роль, можно прийти к выводу о том, что, если от перемены мест множителей значение произведения не меняется, то это еще не значит, что всегда можно записывать множители в любом порядке. О порядке записи множителей периодически разгораются жаркие споры, надеемся, что скоро по этому вопросу будет достигнуто взаимопонимание. Чтобы понять логику рекомендаций о порядке множителей, необходимо еще раз провести параллель с уже известным сложением, на самом деле при вышеописанном способе записи первый множитель показывает, какое число нужно складывать (в нашем случае 5), а второй — сколько таких чисел нужно складывать, т. е. запись «5 x 2» говорит о том, что нужно по пять листов взять два раза. В любом случае важно понимать смысл того, что записано на бумаге.
е. запись «5 x 2» говорит о том, что нужно по пять листов взять два раза. В любом случае важно понимать смысл того, что записано на бумаге.
Также может возникнуть вопрос: зачем вообще нужна такая запись? Зачем вводить новый способ записи, если уже есть «плюс»?
В принципе в данном случае по удобству записи «5 x 2» мало отличается от «5 + 5». А вот если бы по 5 листов бумаги нужно было бы раздать 10 детям?
Тогда пришлось бы записывать 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 50. А если нужно было бы раздать по 5 листов целому классу? С помощью сложения записывать это было бы уже не очень удобно. Итак, если нужно раздать по пять листов десяти детям, с помощью знака умножения это можно записать коротко:
5 x 10 = 50. Но вернемся пока к основной теме.
Способы записи таблицы умножения на 2:
| x | Приподнятая точка | * | Знак не указан |
|---|---|---|---|
| 1 x 2 = 2 | 1 ∙ 2 = 2 | 1 * 2 = 2 | 1 __ 2 = 2 |
| 2 x 2 = 4 | 2 ∙ 2 = 4 | 2 * 2 = 4 | 2 __ 2 = 4 |
| 3 x 2 = 6 | 3 ∙ 2 = 6 | 3 * 2 = 6 | 3 __ 2 = 6 |
| 4 x 2 = 8 | 4 ∙ 2 = 8 | 4 * 2 = 8 | 4 __ 2 = 8 |
| 5 x 2 = 10 | 5 ∙ 2 = 10 | 5 * 2 = 10 | 5 __ 2 = 10 |
| 6 x 2 = 12 | 6 ∙ 2 = 12 | 6 * 2 = 12 | 6 __ 2 = 12 |
| 7 x 2 = 14 | 7 ∙ 2 = 14 | 7 * 2 = 14 | 7 __ 2 = 14 |
| 8 x 2 = 16 | 8 ∙ 2 = 16 | 8 * 2 = 16 | 8 __ 2 = 16 |
| 9 x 2 = 18 | 9 ∙ 2 = 18 | 9 * 2 = 18 | 9 __ 2 = 18 |
| 10 x 2 = 20 | 10 ∙ 2 = 20 | 10 * 2 = 20 | 10 __ 2 = 20 |
Способы записи таблицы деления на 2:
| / | : | ÷ | Без знака |
|---|---|---|---|
| 2 / 2 = 1 | 2: 2 = 1 | 2 ÷ 2 = 1 | 2 __ 2 = 1 |
| 4 / 2 = 2 | 4: 2 = 2 | 4 ÷ 2 = 2 | 4 __ 2 = 2 |
| 6 / 2 = 3 | 6: 2 = 3 | 6 ÷ 2 = 3 | 6 __ 2 = 3 |
| 8 / 2 = 4 | 8: 2 = 4 | 8 ÷ 2 = 4 | 8 __ 2 = 4 |
| 10 / 2 = 5 | 10: 2 = 5 | 10 ÷ 2 = 5 | 10 __ 2 = 5 |
| 12 / 2 = 6 | 12: 2 = 6 | 12 ÷ 2 = 6 | 12 __ 2 = 6 |
| 14 / 2 = 7 | 14: 2 = 7 | 14 ÷ 2 = 7 | 14 __ 2 = 7 |
| 16 / 2 = 8 | 16: 2 = 8 | 16 ÷ 2 = 8 | 16 __ 2 = 8 |
| 18 / 2 = 9 | 18: 2 = 9 | 18 ÷ 2 = 9 | 18 __ 2 = 9 |
| 20 / 2 = 10 | 20: 2 = 10 | 20 ÷ 2 = 10 | 20 __ 2 = 10 |
С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!
Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Смотрите ниже шпаргалки в полной форме.
Умножение прямо на сайте (онлайн)
*
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Ни для кого не секрет, как важно знание таблицы умножения и деления, в частности при выполнении арифметических расчётов и решении примеров по математике .
Однако, что если ребёнка пугает этот огромный набор цифр, именующийся «Таблицей умножения и деления », а уж знать его наизусть, представляется совсем непосильной задачей?
Тогда спешим успокоить – Выучить всю таблицу умножения очень просто! Для этого необходимо запомнить всего лишь 36 комбинаций чисел (связки трех чисел) . Здесь мы не учитываем умножение на 1 и 10, так как это является элементарным действием не требующим особых усилий в запоминании.
Описание работы онлайн тренажера
Данный тренажер работает на основе специально разработанного алгоритма повышения сложности примеров: начиная с самых простых цифр «2 x 2», постепенно повышая сложность до «9 x 9». Тем самым плавно завлекая в процесс изучения.
Таким образом, запоминать таблицу умножения придётся небольшими порциями, что существенно снизит нагрузку, так как дети будут направлять своё внимание всего лишь на несколько примеров, забыв про весь «большой» объём.
В Тренажере есть меню настроек для выбора режима изучения таблицы. Имеется возможность выбора дейстия — «Умножение» или «Деление», диапазона примеров «Вся таблица» или «На какое-то число». Все это является рассширенным функционалом сайта и доступно после оплаты .
Каждый новый пример сопровождается справочной подсказкой , так ребёнку будет легче начать своё изучение и запоминать новые неизвестные ему комбинации.
Если же по ходу обучения, какой либо пример вызывает трудность, можно быстро напомнить себе его результат, воспользовавшись дополнительной подсказкой , это поможет эффективнее справляться с запоминанием трудных примеров.
Процентная шкала быстро даст вам понять каким уровнем знания таблицы умножения Вы обладаете.
Пример считается полностью выученным, если правильный ответ был дан 4 раза подряд . Однако при достижении 100% , призываем не бросать изучение, а вернуться на следующий день и освежить свои знания, повторно пройдя все примеры. Ведь именно регулярные занятия развивают память и закрепляют навыки!
Ведь именно регулярные занятия развивают память и закрепляют навыки!
Описание интерфейса онлайн тренажера
Во-первых, в тренажере присутствует «панель быстрого доступа», включающая в себя 4 кнопки. Они позволяют: перейти на главную страницу сайта, включить или отключить звуковые сигналы, сбросить результаты обучения (начать изучение сначала), а также попать на страницу отзывов и комментариев.
Во-вторых, это основная структура программы.
Выше всех находится процентная шкала , отобржающая примерный уровень знания таблицы умножения.
Ниже идет поле с примером , на который необходимо дать ответ. Во время ответа оно будет изменять свой цвет: станет красным — если был дан неверный ответ, зеленым — в случае правильного, голубым — после использования подсказки, и желтоватым — во время показа нового примера.
Следом располагается строка сообщений . В ней выводятся текстовая информация об ошибках, правильных ответах, а также справочной и дополнительной подсказками.
В конце находится экранная клавиатура , содержащая только необходимые для работы кнопки: все цифры, «забой» — если нужно исправить ответ, кнопки «Проверить» и «Дополнительная подсказка».
Мы уверены, что данный тренажер «Таблица умножения за 20 минут», поможет .
И умножение. Как раз об операции умножения и пойдет речь в этой статье.
Умножение чисел
Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.
Пример 2*5 . Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.
Пример 4*3 . Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.
Пример 5*3 . Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.
Формулы умножения
Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:
Где, а – любое число, n – число слагаемых а. 2)
2)
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Умножение дробей
Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо ! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.
Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.
Умножение 2 класс
Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения. Давайте рассмотрим задачи на умножение уровня второго класса:
Давайте рассмотрим задачи на умножение уровня второго класса:
Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?
В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?
Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?
В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?
Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?
В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?
Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?
В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?
Умножение 3 класс
В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление .
Помимо умножения будет так же проходиться Деление .
Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.
Умножение столбиком:
Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.
1 шаг . Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.
2 шаг . Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.
Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.
3 шаг . Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.
Складываем полученную двойку с четверкой от предыдущего умножения.
4 шаг . Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.
Итак, умножив 427 на 6, получился ответ 2562
ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!
5 шаг . Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281
6 шаг . Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.
Умножение 4 класс
Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.
Например, найти произведение следующих пар чисел:
- 988 * 98 =
- 99 * 114 =
- 17 * 174 =
- 164 * 19 =
Презентация на умножение
Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!
Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!
Таблица умножения
Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Примеры на умножение
Умножение на однозначное
- 9 * 5 =
- 9 * 8 =
- 8 * 4 =
- 3 * 9 =
- 7 * 4 =
- 9 * 5 =
- 8 * 8 =
- 6 * 9 =
- 6 * 7 =
- 9 * 2 =
- 8 * 5 =
- 3 * 6 =
Умножение на двузначное
- 4 * 16 =
- 11 * 6 =
- 24 * 3 =
- 9 * 19 =
- 16 * 8 =
- 27 * 5 =
- 4 * 31 =
- 17 * 5 =
- 28 * 2 =
- 12 * 9 =
Умножение двузначное на двузначное
- 24 * 16 =
- 14 * 17 =
- 19 * 31 =
- 18 * 18 =
- 10 * 15 =
- 15 * 40 =
- 31 * 27 =
- 23 * 25 =
- 17 * 13 =
Умножение трехзначных чисел
- 630 * 50 =
- 123 * 8 =
- 201 * 18 =
- 282 * 72 =
- 96 * 660 =
- 910 * 7 =
- 428 * 37 =
- 920 * 14 =
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Быстрый счет»
Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Игра «Математические матрицы»
«Математические матрицы» великолепное упражнение для мозга детей , которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».
Игра «Числовой охват»
Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.
Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Математические сравнения»
Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Подходит детям и взрослым, читающим до 5000 слов в минуту.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление на 6 — Математика 3 класса
Деление означает разбиение числа на равные группы.
На прошлом уроке вы научились делить числа на 5.
Теперь давайте научимся делить числа на 6. число на 6.
1. Деление на группировку.
2. Деление на повторное вычитание.
3. Деление на умножение (самый быстрый способ)
Вы можете использовать любой из этих способов! 🤗
👉 Разберем на примере.
24 ÷ 6 = ?
Метод 1: Группировка
Чтобы разделить число на 6 с помощью группировки, просто разделите на 6 равные группы. Число в каждой группе является ответом.
24 разделены на 6 групп по 4 элемента в каждой.
24 ÷ 6 = 4
Метод 2: Повторная вычитание
, чтобы отделить число на 6 с использованием повторного вычитания, 6 от более и 6 . снова, пока не достигнете 0. Количество вычитаний — это ответ на задачу о делении.
снова, пока не достигнете 0. Количество вычитаний — это ответ на задачу о делении.
Попробуем и этот метод! 😃
24 ÷ 6 = ?
Начните с 24 и вычтите 6 снова и снова.
Сколько раз вы вычитали? 🤓
Очень хорошо! 👍 4 раза.
Итак,
24 ÷ 6 = 4
Отличная работа! 👏
Метод 3: Использование умножения
Быстро превратите любую задачу на деление в задачу на умножение , связанную с !
Решить 24 ÷ 6 = ? , подумайте о диаграмме целой части:
Можете ли вы написать уравнение умножения для этой же диаграммы?
Да!
6 х ? = 24
Знаете ли вы, какое число умножить на 6 будет 24?
Отличная работа! Это 4.
Итак, вы поняли, что 24 ÷ 6 = 4.
Умножение и деление являются противоположностями друг друга. Как только вы знаете умножение, вы также знаете свое деление!
Разделение на 6 Повторить
Это может помочь запомнить!
6 ÷ 6 = 1
12 ÷ 6 = 2
18 ÷ 6 = 3
24 ÷ 6 = 4
30 ÷ 5 9797979799999949494994999999499499999499994994999999994997947 9004
30.36019090 30. 6 = 660004999999999999999797
42 ÷ 6 = 7
48 ÷ 6 = 8
54 ÷ 6 = 9
60 ÷ 6 = 10
Отличная работа! А теперь попробуйте практику. Вы запомните их к тому времени, как закончите.
Глава 6: Таблица умножения 6, 7, 8 и 9
Математика в фокусе Глава 6: Таблица умножения 6, 7, 8 и 9
Триместр 2
*Привяжите к области 904
Большая идея: Многие модели можно использовать для умножения.
| Основные иллюстрации/упражнения:
|
Словарь глав: пропуск, точка, числовая линия, переместительное свойство умножения, ассоциативное свойство умножения, мультипликативное свойство единицы, мультипликативное свойство нуля, модель массива, модель площади
Предварительный просмотр урока:
|
из Математика в фокусе Учебная программа
Обучающие видео: | Обучающие ссылки: |
| Глава 6 Фоновое видео для родителей
| ||||||||
Практика умножения: 6-9 — Игры с таблицами умножения:
Свойства игр на умножение:
| Видео с рабочими тетрадями (от Дэниела Лу):
Сайт Даниэля Лу для рабочей тетради |
Стандарты Common Core State:
Операции и алгебраическое мышление:
Представлять и решать задачи на умножение и деление.
- CCSS.MATH.CONTENT.
 3.OA.A.1
3.OA.A.1
Интерпретировать произведения целых чисел, например, интерпретировать 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7 . - CCSS.MATH.CONTENT.3.OA.A.3
Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом неизвестного числа для представления задачи.1 - CCSS.MATH.CONTENT .3.OA.A.4
Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
Понимать свойства умножения и связь между умножением и делением.
- CCSS.MATH.CONTENT.
 3.OA.B.5
3.OA.B.5
Применение свойств операций как стратегий умножения и деления.2 Примеры. Если известно 6 × 4 = 24, то 4 × 6 = 24 также известен. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)
Умножать и делить в пределах 100.
- CCSS.MATH.CONTENT.3.OA.C.7
Свободно умножать и делить в пределах 100, используя такие стратегии, как связь между умножением и делением (например, зная что 8 × 5 = 40, известно 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Обзор главы 6
Семейное письмо
Дополнительные ресурсы
из Math in Focus Curriculum
Массивы/множества
Из Everyday Math Online: Interactive My Reference Book
Умножение и деление показателей степени — правила, примеры
Показатель степени показывает, сколько раз данная переменная или число умножается само на себя. Например, 6 4 означает, что мы умножаем 6 четыре раза. В расширенной форме это записывается как 6 × 6 × 6 × 6. При умножении двух экспоненциальных членов с одним и тем же основанием их степени складываются, а основание остается прежним. Однако при делении двух экспоненциальных членов, имеющих одно и то же основание, их степени вычитаются. Давайте узнаем больше об умножении и делении показателей в этой статье.
Например, 6 4 означает, что мы умножаем 6 четыре раза. В расширенной форме это записывается как 6 × 6 × 6 × 6. При умножении двух экспоненциальных членов с одним и тем же основанием их степени складываются, а основание остается прежним. Однако при делении двух экспоненциальных членов, имеющих одно и то же основание, их степени вычитаются. Давайте узнаем больше об умножении и делении показателей в этой статье.
| 1. | Делительные экспоненты |
| 2. | Как умножать и делить дробные степени? |
| 3. | Как умножать и делить экспоненты с переменными? |
| 4. | Часто задаваемые вопросы об умножении и делении показателей степени |
Делительные экспоненты
Законы экспонент облегчают процесс упрощения выражений. Основное правило деления показателей степени с одинаковым основанием состоит в том, что мы вычитаем данные степени. Это также известно как частное свойство показателей.
Это также известно как частное свойство показателей.
Как разделить показатели степени?
Деление показателей становится простым, если мы следуем свойствам показателей. Например, давайте решим следующий вопрос обычным способом: 6 5 ÷ 6 3 = (6 × 6 × 6 × 6 × 6)/(6 × 6 × 6 ) = 6 2 . Это требует дополнительных расчетов. Однако, когда мы используем законы экспонент, это сокращает все эти вычисления. Давайте разберемся, как разделить показатели в разных сценариях, используя разные свойства.
Деление показателей степени с одинаковым основанием
Чтобы разделить показатели степени с одинаковым основанием, мы используем основное правило вычитания степеней. Рассмотрим a m ÷ a n , где «a» — общее основание, а «m» и «n» — показатели степени. Это «частное свойство экспонентов» говорит: а m ÷ a n = a m-n . Теперь давайте разберемся в этом на примере.
Пример: Разделить 6 5 ÷ 6 3
Решение: Мы видим, что в данном выражении основания одинаковы. Используя «частное свойство экспоненты», мы получим 6 5 — 3 = 6 2 . Следовательно, ответ 6 2 .
Используя «частное свойство экспоненты», мы получим 6 5 — 3 = 6 2 . Следовательно, ответ 6 2 .
Деление показателей степени с разными основаниями
Чтобы разделить показатели степени с разными основаниями и одним и тем же показателем степени, мы используем «степень частного свойства», которая равна (a/b) m = a m /b м . Рассмотрим m ÷ b m , где выражения имеют разное основание и один и тот же показатель степени. Например, решим: 12 3 ÷ 3 3 . Используя «Свойство степени частного», это можно решить следующим образом: случаи, мы должны разделить выражения, которые имеют коэффициенты. Эти коэффициенты, привязанные к их основаниям, можно легко разделить так же, как мы делим любую другую дробь. Следует отметить, что коэффициенты можно делить даже в том случае, если выражения имеют разные основания.
Пример: Разделить 12a 7 ÷ 4a 2
Решение: Применим следующие шаги для деления выражений с коэффициентами. В данном случае 12 и 4 — коэффициенты, а остальные — переменные.
В данном случае 12 и 4 — коэффициенты, а остальные — переменные.
- Сначала перепишем выражение в виде дроби, то есть 12а 7 / 4а 2 .
- Затем делим коэффициенты, то есть 12/4 = 3.
- После этого шага мы можем применить частное свойство показателей и решить переменную, то есть 7 / 2 = 7 — 2 = 5 .
- Итак, теперь у нас есть коэффициент 3 и переменная 5 . Это дает ответ как 3a 5
Умножение экспоненциальных членов
Умножение показателей степени с одинаковым основанием и разными основаниями включает определенные правила показателей степени. Давайте разберемся с этим в следующем разделе.
Умножение показателей степени с одинаковым основанием
Когда мы умножаем два выражения с одинаковым основанием, мы применяем правило a m × a n = a (m + n) , , где «a» — общее основание, а «m» и «n» — показатели степени. Например, умножим 2 2 × 2 3 . Используя правило, 2 2 × 2 3 = 2 (2 + 3) = 2 5 .
Например, умножим 2 2 × 2 3 . Используя правило, 2 2 × 2 3 = 2 (2 + 3) = 2 5 .
Умножение показателей степени с разным основанием и одинаковой степенью
Когда мы умножаем выражения с разными основаниями и одинаковой степенью, мы применяем правило: a m × b м = (a × b) м . Например, умножим: 11 4 × 3 4 . Это можно решить как 11 4 × 3 4 = (11 × 3) 4 = 33 4 .
Как умножать и делить дробные степени?
Чтобы умножать и делить дробные степени, мы используем те же правила, что и для целых чисел. Дробные показатели степени — это те выражения, в которых степени — дроби, например, 2 ½ , 6 ¾ и так далее.
Умножение дробных степеней с одинаковым основанием
Для умножения дробных степеней с одинаковым основанием мы используем правило a m × a n = a m+n 0. Например, упростим: 2 ½ × 2 ¾ = 2 (½ + ¾) = 2 5/4 .
Например, упростим: 2 ½ × 2 ¾ = 2 (½ + ¾) = 2 5/4 .
Деление дробных степеней с одинаковым основанием
Для деления дробных степеней с одинаковым основанием мы используем правило a m ÷ a n = a m-n . Например, давайте решим 3 3/2 ÷ 3 1/2 . Используя правило, получаем 3 (3/2 — 1/2) = 3 1 = 3.
Как умножать и делить экспоненты с переменными?
Правила, которые используются в числах, также используются в показателях степени с переменными. Вспомним их и затем используем в следующих примерах:
- а м × a n = a m+n
- а м × b м = (а × b) м
- а м ÷ а н = а м-н
- а м ÷ б м = (а ÷ б) м
Переменная как основа
Давайте посмотрим, как использовать эти правила, когда база является переменной. Например, решить: у 2 × (2y) 3
Например, решить: у 2 × (2y) 3
We will apply the rule: a m × b m = (a × b) m , y 2 × (2y) 3 = y 2 × 2 3 × y 3 = 2 3 × y (2+3) = 8y 5
Variable as the Exponent
Давайте посмотрим, как использовать правила, когда показатель степени является переменной. Например, решить: 5 (2x -1) ÷ 5 (x + 1)
We will apply the rule: a m ÷ a n = a m-n , we получить 5 (2x -1 — x — 1) = 5 (x -2)
Советы по умножению и делению показателей
- a 0 90 7 7 908 m 8 ÷ 8 908 m = 1 = a m-m = a 0 ]
- Следует также отметить, что отрицательный показатель степени можно преобразовать в положительный показатель, написав обратную величину числа.
 Например, 6 -3 можно записать как 1/6 3 .
Например, 6 -3 можно записать как 1/6 3 . - Если мы умножим два показателя степени с одним и тем же основанием, их степени будут складываться.
- Если мы разделим два показателя степени с одинаковым основанием, то их степени вычитаются.
Связанные темы
- Rational Exponents
- Иррациональные Показатели
Часто задаваемые вопросы об умножении и делении показателей степени
Как умножать и делить степени?
Чтобы умножать и делить показатели степени, мы используем набор правил степени. При перемножении двух экспоненциальных членов с одним и тем же основанием их степени складываются, а основание остается прежним. Например, умножим 6 3 × 6 5 = 6 (3 + 5) = 6 8 . Однако при делении двух экспоненциальных членов, имеющих одно и то же основание, их степени вычитаются. Например, 7 8 ÷ 7 5 = 7 3 . Точно так же есть и другие правила, которые помогают легко упростить показатели степени.
Точно так же есть и другие правила, которые помогают легко упростить показатели степени.
Каковы правила деления показателей степени?
Есть несколько правил экспоненты, которые помогают в делении экспонент. Эти правила также помогают упростить числа со сложными степенями, включая дроби, десятичные дроби и корни. Например, чтобы разделить числа или переменные с одинаковым основанием, применим правило: а m ÷ a n = a m-n . Чтобы разделить числа или переменные с разными основаниями, применим правило: a m ÷ b m = (a ÷ b) m
Как вы решаете показатели степени в скобках?
Показатель степени в скобках можно решить, используя тождество (a m ) n = a mn . Например, (4 2 ) 3 = 4 (2 × 3) = 4 6 = 4096
Можем ли мы распределить показатели по делению?
Да, мы можем распределять показатели по делению. Например, (7/2) 3 = 7 3 ÷ 2 3 = 343/8
Например, (7/2) 3 = 7 3 ÷ 2 3 = 343/8
Как умножать и делить отрицательные степени?
Когда мы умножаем и делим отрицательные степени, мы следуем тем же правилам, которые используются для положительных степеней. Например, мы используем свойство: a m ÷ a n = a m-n , чтобы решить: 2 -3 ÷ 2 -4 . Это будет: 2 (-3-(-4)) = 2 (-3 + 4) = 2 1 = 2. Соблюдайте правило упрощения целых чисел, которое меняет знак после раскрытия скобок . Следует также отметить, что отрицательный показатель степени можно преобразовать в положительный показатель, написав обратную величину числа. Например, 7 -3 можно также записать как: 1/7 3 . Это означает, что если нам нужно разделить выражения с отрицательными показателями степени, мы можем просто переместить основание на другую сторону дробной черты. Например, если у нас в знаменателе дроби 4 -2 , мы можем перенести его в числитель. Это означает, что y -2 /y -3 = y 3 /y 2 = y 3 — 2 = y 1 = y.
Это означает, что y -2 /y -3 = y 3 /y 2 = y 3 — 2 = y 1 = y.
Как разделить экспоненты с разными степенями?
Чтобы разделить степени с разными степенями, но одинаковыми основаниями, мы вычитаем данные степени. Здесь используется следующее свойство: a m ÷ a n = a (m-n) . Например, давайте разделим показатели степени, 8 6 ÷ 8 4 . После применения свойства показателей степени, мы получаем, 8 6 — 4 = 8 2
Как разделить показатели степени на дроби?
Чтобы разделить степени на дроби, мы используем то же правило, что и для целых чисел, то есть m ÷ a n = a m-n . Например, разделим следующие показатели степени: 2 3/4 ÷ 2 1/2 = 2 3/4 -1/2 = 2 1/4 .
Как разделить показатели степени с разными основаниями и одинаковыми степенями?
Чтобы разделить показатели степени с разными основаниями и одинаковыми степенями, мы применяем «Степень частного свойства», которая составляет: Например, разделим, 14 3 ÷ 2 3 = (14 ÷ 2) 3 = 7 3 .
Как делить экспоненты с отрицательными основаниями?
Когда нам нужно разделить показатели степени с отрицательным основанием, правила степени остаются прежними. Например, разделим (-4) 8 ÷ (-4) 2 = (-4) 8 — 2 = (-4) 6
Умножение и деление во 2-м году (6 лет). –7)
Во втором классе ваш ребенок будет решать задачи на умножение и деление, используя таблицы умножения на 2, 5 и 10. Они будут использовать символы «×», «÷» и «=» для записи вычислений.
Ключевые слова в этом разделе – коммутативные, массивные и обратные операции.
Чему научится ваш ребенок
Ознакомьтесь с требованиями Национальной учебной программы к умножению и делению для 2-го класса (возраст 6–7 лет):
Изучите таблицы умножения на 2, 5 и 10
Вашему ребенку будут представлены к таблице умножения в этом году. Дети будут работать и начнут узнавать факты в таблицах умножения на 2, 5 и 10 и связывать их друг с другом. Они также смогут выяснить связанные факты разделения. Например:
Они также смогут выяснить связанные факты разделения. Например:
Ваш ребенок может знать, что 5 × 7 = 35 .
Из этого они могут вычислить соответствующие факты деления: 35 ÷ 7 = 5 и 35 ÷ 5 = 7 .
Ваш ребенок также должен распознавать нечетные и четные числа до 100.
Использовать знаки умножения (×), деления (÷) и равенства (=)
Во втором классе дети будут решать умножение и деление задачи с использованием таблиц умножения на 2, 5 и 10. Ожидается, что они будут правильно использовать символы «×», «÷» и «=» для записи расчетов.
Покажите, что умножать можно в любом порядке (а делить нельзя).
Ваш ребенок узнает, что при умножении чисел получается одно и то же произведение независимо от того, в каком порядке они умножают числа. Это означает, что умножение коммутативно. Например:
10 × 5 = 50
5 × 10 = 50
Ваш ребенок узнает, что порядок чисел не имеет значения при делении. Это означает, что, в отличие от умножения, деление равно 9.0003, а не коммутативный. Например:
Это означает, что, в отличие от умножения, деление равно 9.0003, а не коммутативный. Например:
10 ÷ 5 = 2
5 ÷ 10 = 0,5
Решайте задачи в контексте, используя множество различных методов
Ваш ребенок научится различным методам вычисления задач на умножение и деление. Для умножения они могут включать:
- Счет в уме с шагом 2, 5 или 10
- Использование предметов или рисование изображений
- Использование числовых строк для прямого счета в шагах
- Использование стержневой модели или метода площади/сетки.
Они могут решать задачи на деление по:
- Равное совместное использование или группировка объектов
- Использование цифровой строки для обратного счета с шагом 2, 5 или 10
- Используя свое понимание обратного, чтобы использовать умножение для решения задач на деление. Например, решая 8 ÷ 2, дети могут считать по два, чтобы узнать, сколько групп по 2 в числе 8.

Ожидается, что ваш ребенок выберет метод решения задачи и сможет проверить свой ответ, используя другой метод. Также ожидается, что они объяснят, как они решили проблему, и расскажут, почему они выбрали тот или иной метод.
Как помочь дома
Существует множество простых и быстрых способов помочь ребенку понять умножение и деление. Вот лишь несколько идей, которые помогут вашему ребенку в обучении:
1. Расскажите о нечетных и четных числах
Попросите ребенка объяснить, что он знает о нечетных и четных числах. Например, вы можете спросить своего ребенка, является ли 8 нечетным или четным числом. Если вы хотите помочь им лучше понять, повседневные предметы, такие как пуговицы или макароны, отлично подходят для изучения нечетных и четных чисел.
Четные числа можно разделить поровну на два целых числа, а нечетные нельзя. Поэтому, чтобы узнать, является ли группа объектов четной или нечетной, ваш ребенок может разделить их на две равные группы. Если объекты может быть поровну разделен между двумя группами, тогда количество объектов будет четным. Если объекты не могут быть поровну разделены между двумя группами, то число объектов нечетное.
Если объекты может быть поровну разделен между двумя группами, тогда количество объектов будет четным. Если объекты не могут быть поровну разделены между двумя группами, то число объектов нечетное.
Спрашивайте ребенка о нечетных или четных числах при каждой возможности. Например, есть ли в супермаркетах нечетное количество яблок в пакетах? Сегодня ужинает четное или нечетное количество людей?
Помогите ребенку понять, что последняя цифра («единицы») четных чисел всегда будет 0, 2, 4, 6 или 8, а последняя цифра нечетных чисел всегда будет 1, 3, 5, 7. , или 9. Остальные цифры в номере значения не имеют. Покажите ребенку число, например 36, и спросите его, четное это число или нечетное, и попросите его объяснить, почему. Например, 36 четное, потому что цифра единиц равна 6, а это четное число.
2. Практика умножения
Массивы
Ваш ребенок будет изучать умножение с помощью массивов. Массивы — это наборы объектов, расположенных в строках и столбцах так, чтобы получился прямоугольник. Помогите ребенку распознать массивы в реальном мире. Ящики для яиц, лотки для кубиков льда и окна в здании могут быть массивами.
Помогите ребенку распознать массивы в реальном мире. Ящики для яиц, лотки для кубиков льда и окна в здании могут быть массивами.
По дороге в школу или на прогулке вы можете сыграть с ребенком в игру, чтобы находить массивы. Также может быть хорошей идеей попросить вашего ребенка построить массивы из небольших предметов, таких как виноград или пуговицы. Могут ли они расположить объекты в разных массивах? Например, 6 объектов можно превратить в несколько разных массивов:
Таблица умножения
Ваш ребенок познакомится с таблицей умножения в школе. В этом году основное внимание будет уделено таблицам умножения на 2, 5 и 10.
Узнайте, какие факты об умножении уже знает ваш ребенок, а затем посмотрите, сможет ли он умножить их. Например:
Возможно, ваш ребенок уже знает, что 2 × 5 = 10.
Они могли бы использовать это, чтобы вычислить 2 × 6, добавив еще одну группу из 2, чтобы получить 12.
Запишите таблицы умножения на 2, 5 и 10 на отдельных листах бумаги или на стикерах. Попросите ребенка выбрать способ умножения, например 8 × 5, и объясните, как он решит эту задачу. Если ваш ребенок сразу знает ответ, спросите его, какие еще факты ему известны. Бросьте им вызов, чтобы побить время, когда они рассказывают свои факты умножения!
Попросите ребенка выбрать способ умножения, например 8 × 5, и объясните, как он решит эту задачу. Если ваш ребенок сразу знает ответ, спросите его, какие еще факты ему известны. Бросьте им вызов, чтобы побить время, когда они рассказывают свои факты умножения!
4. Найдите связи в умножении и делении
Вашему ребенку будет полезно, если он сможет установить связи в умножении и делении. Предложите им исследовать связи между умножением, массивами и повторяющимся сложением.
Что касается разделения, предложите ребенку:
- Использовать группировку, совместное использование и массивы
- Подумайте о связи между делением и повторным вычитанием
- См. связь между дробями и делением (например, 40 ÷ 2 = 20, 20 — половина 40).
Вы также можете помочь своему ребенку использовать коммутативность и обратные отношения для выполнения вычислений. Например:
Если они знают, что 4 × 5 = 20 , то они знают, что 5 × 4 = 20 , потому что умножение коммутативно (то есть может выполняться в любом порядке).
Если они знают, что 4 × 5 = 20 , то они знают, что 20 ÷ 5 = 4 и 20 ÷ 4 = 5 , потому что умножение и деление являются обратными операциями.
Массивы также дают детям прекрасную возможность изучить связь между умножением и сложением, а также умножением и делением. Дайте вашему ребенку вычисление умножения из таблиц умножения на 2, 5 или 10 и попросите его рассказать вам или записать любые другие связанные факты сложения, умножения или деления. Обсуждение того, как они узнают каждый факт, поможет им понять, как операции связаны друг с другом.
5. Используйте язык умножения и деления
Полезно уметь использовать язык умножения и деления при разговоре с ребенком. Язык умножения включает произведение , умножить , умножить на , умножить на , повторить сложение , равно сгруппировать и 1 массив. Язык разделения включает разделить , разделить поровну , сгруппировать поровну , массивы , и остаток .
Язык разделения включает разделить , разделить поровну , сгруппировать поровну , массивы , и остаток .
Вы можете помочь своему ребенку выучить эти термины, попросив его использовать этот язык, чтобы объяснить, как он решил проблему. Может быть полезно, чтобы математические слова были написаны на карточках, чтобы ваш ребенок мог обращаться к ним.
Вы также можете сделать или распечатать карточки со словами для умножения и деления и карточки с символами «×» и «÷». Помогите ребенку прочитать каждую карточку, а затем рассортируйте карточки по словам, описывающим умножение (×) или деление (÷). Какие слова можно отнести к обеим группам? Поговорите с ребенком о том, почему эти слова. Это поможет им понять связь между умножением и делением.
Деление дробей | Математика для гуманитарных наук Corequisite
Результаты обучения
- Разделение дробей
- Найдите обратное число
- Разделить дробь на целое число
- Разделить дробь на дробь
Введение
Прежде чем мы начнем, приведем несколько важных терминов, которые помогут вам понять принципы работы с дробями в этом разделе.
- произведение: результат умножения
- фактор: что-то умножается — для [latex]3 \cdot 2 = 6[/latex] , и 3, и 2 являются множителями 6
- числитель: верхняя часть дроби – числитель дроби [latex]\frac{2}{3}[/latex] равен 2
- знаменатель: нижняя часть дроби – знаменатель дроби [латекс]\фракция{2}{3}[/латекс] равен 3
Примечание об инструкциях
Учебники по математике и учителя используют много разных слов, чтобы дать учащимся инструкции о том, что они должны делать с данной задачей. Например, вы можете увидеть такие инструкции, как «Найти» или «Упростить» в примере в этом модуле. Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список слов, которые вы можете встретить и которые помогут вам понять, как работать с проблемами в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические действия, которые могут включать сложение, вычитание, умножение, деление. |
| Упрощение | 1) Выполнять указанные математические действия, включая сложение, вычитание, умножение, деление 2) Напишите математическую формулировку в наименьших выражениях, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценка | Выполнение указанных математических операций, включая сложение, вычитание, умножение, деление |
| Уменьшить | Запишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением |
Разделение дробей
Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для нанесения одного слоя краски на стены комнаты требуется 3 литра краски, а у вас есть ведро с 6 литрами краски, сколько слоев краски вы можете нанести на стены? Вы делите 6 на 3 для ответа 2 пальто. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их произведение равно 1 (не волнуйтесь, мы покажем вам примеры того, что это означает.)
- частное: результат деления
Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:
| Исходный номер | Взаимный | Продукт |
|---|---|---|
| [латекс] \frac{3}{4}[/латекс] | [латекс] \frac{4}{3}[/латекс] | [латекс] \frac{3}{4}\cdot \frac{4}{3}=\frac{3\cdot 4}{4\cdot 3}=\frac{12}{12}=1[/ латекс] |
| [латекс] \frac{1}{2}[/латекс] | [латекс] \frac{2}{1}[/латекс] | [латекс]\frac{1}{2}\cdot\frac{2}{1}=\frac{1\cdot}{2\cdot1}=\frac{2}{2}=1[/latex] |
| [латекс] 3=\frac{3}{1}[/латекс] | [латекс] \frac{1}{3}[/латекс] | [латекс] \frac{3}{1}\cdot \frac{1}{3}=\frac{3\cdot 1}{1\cdot 3}=\frac{3}{3}=1[/ латекс] |
| [латекс]2\фракция{1}{3}=\фракция{7}{3}[/латекс] | [латекс] \frac{3}{7}[/латекс] | [латекс]\frac{7}{3}\cdot\frac{3}{7}=\frac{7\cdot3}{3\cdot7}=\frac{21}{21}=1[/latex] |
Иногда мы называем обратное «переворотом» другого числа: переверните [латекс] \frac{2}{5}[/latex], чтобы получить обратное [латекс]\frac{5}{2}[ /латекс].
Деление на ноль
Вы знаете, что значит делить на 2 или делить на 10, но что значит делить количество на 0? Это вообще возможно? Можно ли разделить 0 на число? Рассмотрим дробь
[латекс]\фракция{0}{8}[/латекс]
. Мы можем прочитать ее как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.
[латекс]\текст{?}\cdot{8}=0[/латекс].
Мы можем сделать вывод, что неизвестное должно быть равно 0, так как это единственное число, которое даст результат 0 при умножении на 8.
Теперь давайте рассмотрим обратное число [латекс]\фракция{0}{8}[/латекс], которое будет [латекс]\фракция{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, то получим
[латекс]\текст{?}\cdot{0}=8[/латекс].
Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8. Обратная величина [латекс]\фракция{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено.
Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа а [латекс]\фракция{а}{0}[/латекс] не определена. Кроме того, обратная величина [latex]\frac{0}{a}[/latex] всегда будет неопределенной.
Деление дроби на целое число
Когда вы делите целое число, вы умножаете его на обратное. В примере покраски, где вам нужно 3 литра краски для слоя и у вас есть 6 литров краски, вы можете найти общее количество слоев, которые можно покрасить, разделив 6 на 3, [латекс]6\div3=2[/латекс ]. Вы также можете умножить 6 на обратную величину 3, то есть [латекс] \frac{1}{3}[/latex], поэтому задача умножения будет выглядеть так:
[латекс] \frac{6}{1}\cdot \ frac{1}{3}=\frac{6}{3}=2[/latex].
Деление — это умножение на обратное число
Для любого деления можно превратить операцию в умножение, используя обратное число. Деление равносильно умножению на обратное.
Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:
Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:
[латекс] \frac{1}{5}\text{ of }\frac{3}{4}=\frac{1}{5}\cdot \frac{3}{4}= \frac{3}{20}[/латекс]
Каждый человек получает [латекс]\фрак{3}{20}[/латекс] целого шоколадного батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на 2 или умножить каждый ингредиент на [латекс]\frac{1}{2}[/latex] , чтобы найти новое количество .
Например, деление на 6 равносильно умножению на обратную величину 6, то есть [латекс]\frac{1}{6}[/латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), между 6 людьми?
Каждый человек получает один кусок, поэтому каждый человек получает [латекс] \frac{1}{4}[/latex] пиццы.
Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.
Разделить дробь на дробь
Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже разрезана на 4 куска. Сколько существует фрагментов [latex]\frac{1}{2}[/latex]?
Есть 8 ломтиков. Вы видите, что деление 4 на [latex] \frac{1}{2}[/latex] дает тот же результат, что и умножение 4 на 2.
Что произойдет, если вам нужно разделить каждый срез на трети?
У вас получится 12 частей, что равносильно умножению 4 на 3.
Деление дробями
- Найдите обратную величину числа, следующего за символом деления.
- Умножьте первое число (то, что перед знаком деления) на обратную величину второго числа (после знака деления).
Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть». Это означает СОХРАНИТЬ первое число, ИЗМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Десятичные дроби: умножение и деление десятичных дробей
Урок 3: умножение и деление десятичных дробей
/en/decimals/adding-and-subtracting-decimals/content/
Умножение с десятичными дробями
В разделе «Сложение и вычитание десятичных дробей» вы научились складывать десятичных числа. Возможно, вы сможете вспомнить случаи, когда вы добавляли десятичные дроби в реальной жизни. Например, допустим, вы идете в магазин и находите рубашку, которая вам очень нравится. На ценнике написано, что он стоит $15,60. Вам так понравилась рубашка, что вы решили купить пять штук.
Чтобы узнать общую стоимость, вы можете добавить цены.
Добавление такого количества номеров может занять много времени. На уроке по умножению мы узнали, что при умножении вы получаете , многократно увеличивая число. Поскольку все цены на футболки равны и , умножение может помочь вам решить эту проблему немного быстрее.
Когда вы умножаете десятичные числа, полезно сформулировать задачу так, чтобы вам было легче решать ее шаг за шагом .
Нажмите на слайд-шоу ниже, чтобы узнать, как решить задачу на умножение с десятичными дробями.
Instead of adding $15.60 + $15.60 + $15.60 + $15.60 + $15.60…
Instead of adding $15.60 + $15.60 + $15.60 + $15.60 + $15.60…we’ll multiply $15.60 by 5.
Давайте настроим наше выражение умножения: $15,60 x 5. Мы сложим числа одно поверх другого.
Это хорошая привычка ставить число с большинство цифр на сверху . Это облегчает решение проблемы.
Давайте посмотрим на количество цифр в каждом числе. 15.60 имеет четыре цифры…
Давайте посмотрим на количество цифр в каждом числе. 15.60 имеет четыре цифры … а 5 — это одна цифра .

15.60 имеет более цифр . Это означает, что мы напишем 15,60 выше 5,9.0005
Так как мы умножаем это число, мы запишем знак раз (X) к левым числам.
Вместо знака равенства (=) мы поместим строку под числом внизу.
При написании выражения умножения с накоплением с десятичными числами числа должны быть выстроены по справа .
Давайте посмотрим на другой пример. Складываем это выражение: 4,5 x 38,12.
Сначала посмотрим, сколько цифр содержится в каждом числе. 4.5 имеет две цифры…
Во-первых, посмотрите, сколько цифр содержится в каждом числе. 4.5 имеет две цифры … а 38.12 имеет четыре цифры .
38.12 имеет еще цифр.
 Это означает, что мы поместим 38,12 выше 4,5.
Это означает, что мы поместим 38,12 выше 4,5.Затем мы убедимся, что цифры до справа от выровнены. 2 верно выше 5.
Решение задач на умножение с десятичными дробями
Умножение десятичных чисел очень похоже на умножение больших чисел. Если разделить большую проблему на несколько более мелких, ее будет легче решить. Давайте посмотрим, как это работает, решив следующую задачу: 2,3 x 4.
Щелкните слайд-шоу, чтобы узнать, как умножать десятичные дроби.
Чтобы решить нашу задачу, мы будем использовать знакомый инструмент: таблицу умножения на 9.0004 .
При умножении сложенных чисел начните с правой цифры на нижней . Нижнее число состоит только из одной цифры: 4.
Умножим 4 на верхнее число, 2,3. Поскольку в таблице умножения нет числа 2,3, нам придется умножать по одной цифре за раз.
Как обычно, решим задачу от справа налево .
 Итак, мы умножим 4 на цифру в правом верхнем углу . Вот, это 3.
Итак, мы умножим 4 на цифру в правом верхнем углу . Вот, это 3.Теперь пришло время решить 4 x 3. Мы можем использовать таблицу умножения .
4 x 3 равно 12, но нет места для записи обеих цифр под 4 и 3.
Помните, это означает, что нам придется нести . Мы узнали о переносе чисел на уроке по умножению больших чисел.
Запишем правую цифру 2 под чертой…
Запишем правую цифру 2 под чертой… затем запишем левую цифру 1 , до следующий набор цифр в задаче.
Теперь пришло время для следующего шага. Умножим 4 х 2.
4 х 2 = 8. Но 8 под чертой пока писать не будем. Помните, есть еще один шаг.
Нам нужно убедиться, что мы добавляем номер, который мы носили: 1.
Мы настроим нашу задачу на сложение.
1 + 8 = 9.
Под чертой напишем 9.

В нашей задаче мы умножили десятичное число: 2,3. Это означает, что наш ответ также должен быть десятичным числом.
Давайте разберемся, где ставить десятичную точку ( . ).
В задаче 2.3 одна цифра до справа десятичной точки.
Это означает, что наш ответ также будет иметь одну цифру до справа десятичной точки.
Поставим запятую так, чтобы только одна цифра была справа от : 2.
Наша задача решена. Итого 9,2. Мы знаем, что 2,3 х 4 = 9,2. Мы можем прочитать этот ответ как девять и две десятых .
Давайте попробуем другую задачу. На этот раз мы умножим деньги: 3,05 доллара x 2.
Сначала мы умножим нижнее число 2 на цифру справа вверху. Это 5.
2 x 5 = 10.
Напишем 0 под чертой.
 ..
..Напишем 0 под чертой… и перенесем 1. Разместим над следующей цифрой.
Следующая цифра 0.
Любое число, умноженное на ноль, равно нулю, поэтому мы знаем, что 2 x 0 = 0.
Помните, нам нужно убедиться, что мы добавили 1, которую мы несли.
0 + 1 = 1. Под чертой напишем 1.
Наконец, мы умножим 2 и 3.
2 x 3 = 6, поэтому мы напишем 6 под чертой.
Пришло время поставить нашу десятичную точку. Нам нужно подсчитать цифр до справа десятичной точки в нашей задаче.
3.05 имеет две цифры справа от десятичной точки. Это 0 и 5.
Это означает, что наш ответ должен содержать две цифры справа от запятой.
Мы поместим десятичную точку так, чтобы две цифры были справа: 1 и 0.
слева от номера.

Мы решили проблему. 3,05 доллара x 2 = 6,10 доллара. Мы можем прочитать это как шесть долларов и десять центов .
Примечание : При определении места десятичной точки в ответе подсчитайте общее количество цифр справа от 9.0003 каждые десятичных знака в вашей задаче. Например, если вы упрощаете 3,25 x 2,3, вы должны подсчитать две цифры в 3,25 плюс одну цифру в 2,3. Следовательно, мы должны поставить запятую в нашем ответе так, чтобы три цифры были справа (3,25 х 2,3 = 7,475).
Попробуйте это!
Попробуйте решить эти задачи на умножение. Затем проверьте свой ответ, введя его в поле.
7,15 х 5 =
2,67 х 3 =
6,66 х 4 =
Деление десятичных дробей
Давайте рассмотрим другую ситуацию. Представим, что у вас есть забор, и вы хотите посадить перед ним 5 кустов. Ваш забор имеет длину 20 футов. Вы хотели бы разместить кусты на одинаковом расстоянии друг от друга, поэтому вы знаете, что вам нужно будет разделить забор на 5 равных частей. Это означает, что вам нужно разделить 20 на 5.
Это означает, что вам нужно разделить 20 на 5.
В уроке о делении мы научились составлять выражения для деления. Для приведенной выше ситуации выражение будет выглядеть так:
В нашем выражении 20 — это целое число . Но что, если длина забора равна десятичному числу ? Например, предположим, что это 20,75 футов в длину. Хотите верьте, хотите нет, но деление десятичной дроби ничем не отличается.
Когда вы настраиваете выражение для деления десятичного числа, важно убедиться, что вы всегда делите на целое число . В приведенном выше примере 20,75 делится на целое число 5. Деление на целое число упрощает управление делением в длину.
Нажмите на слайд-шоу ниже, чтобы узнать, как решать задачи на деление десятичных дробей.
Составим это выражение: 20,75 / 5.
На уроке деления мы узнали, что делить числа легче, когда выражение записывается немного по-другому.

Как обычно, вместо того, чтобы писать числа рядом с символом деления …
Как обычно, вместо того, чтобы писать числа рядом с символ деления …мы будем использовать скобку деления .
Число, которое мы делим, идет под скобкой деления . Это 20,75.
К слева от дробной скобки припишем число, на которое делим. В нашей задаче это 5.
Помните, скобка деления также является знаком равенства .
Частное или ответ записывается выше ит.
Давайте составим другое выражение. На этот раз оба числа являются десятичными числами: 80,1 / 4,2.
Сначала напишем скобку деления.
Далее запишем делимое число: 80.1.
Наконец, напишем число, на которое делим: 4.
 2.
2.Поскольку мы делим десятичное число на десятичное число, нам нужно сделать еще один шаг.
Чтобы упростить деление, мы изменим число, на которое мы делим, на целое число . Это означает, что мы изменим 4.2.
Чтобы сделать 4.2 целым числом, нам нужно переместить десятичную точку на так, чтобы она стояла после последней цифры в числе.
Это означает, что мы переместим его так, чтобы он стоял после 2.
Теперь все цифры до слева десятичной точки. Мы создали целый номер . 4.2 становится 42.
Целое число обычно записывается без десятичной точки после него…
Целое число обычно записывается без десятичной точки после него… так что мы отбросить десятичную точку.
Видите, как мы это сделали? Мы переместили десятичную точку на вправо , а затем опустили десятичную точку.

Поскольку мы передвинули запятую в одном числе…
Поскольку мы переместили запятую в одном числе… нам также нужно переместить запятую в другом числе: 80.1.
Итак, мы переместим эту десятичную точку столько же раз .
80.1 становится 801.
801 — это целое число, поэтому мы опустим десятичную точку .
Теперь выражение деления 801 / 42.
Перемещение десятичных дробей может быть сложным, поэтому важно изменить число, которое вы разделить на на целое число сначала.
Попробуем еще раз с другим выражением: 0,4 / 0,02.
Сначала мы превратим 0,02 в целое число.
Мы переместим десятичную точку один раз на вправо .
0,02 становится 0,2.
У нас все еще есть цифра до справа от десятичной точки: 2.
 Это означает, что наша десятичная дробь еще не является целым числом.
Это означает, что наша десятичная дробь еще не является целым числом.Итак, мы переместим десятичную точку на вправо во второй раз.
0,2 становится 2. Все цифры теперь до слева десятичной точки.
Нули и десятичная точка больше не нужны. Мы сбросим их.
Поскольку мы передвинули первую десятичную точку на два раза вправо…
Поскольку мы переместили первую десятичную точку два раза вправо… мы проделаем то же самое до второго десятичного знака.
Мы переместим его один раз…
Мы переместим его один раз…затем мы добавим ноль …
0,4 становится 40.
Поскольку 40 — целое число, мы будем удалить ноль и десятичную точку.
Теперь выражение деления равно 40/2. Наша задача готова к решению.
1 Мы’ сдвинем его на один раз… затем мы добавим ноль … и затем мы переместим его на секунды раз.
Деление десятичных чисел
В предыдущем слайд-шоу вы практиковались в настройке выражений деления с десятичными числами. Рассмотрим подробнее, как делить десятичную дробь. Деление десятичного числа на очень похоже на деление целого числа на . В конце всего один дополнительный шаг.
Щелкните слайд-шоу, чтобы узнать, как делить десятичные дроби.
Для решения этой задачи мы будем использовать деление в длинное число: 6,5/2. завершено.
Начнем с левого разряда под скобкой деления. Это означает, что мы начнем с 6…
Мы начнем с оставил цифру под скобкой деления. Это означает, что мы начнем с 6.
 .. и выясним, сколько раз его можно разделить на 2.
.. и выясним, сколько раз его можно разделить на 2.Мы будем использовать таблицу умножения на , чтобы помочь нам. Помните, если вам нужно повторить, как использовать таблицу умножения, вы можете вернуться к уроку по умножению. Теперь пришло время решить 6 / 2.
6 / 2 = 3.
Мы напишем 3 над 6.
Затем мы умножим на 9.0004 3 и 2.
3 x 2 = 6.
Мы напишем 6 под 6.
Далее мы поставим задачу на вычитание .
6 — 6 = 0. Под чертой напишем 0.
Теперь мы запишем 5 и перепишем его рядом с 0.
05 означает то же самое, что и 5. 5 достаточно велико, чтобы его можно было разделить, поэтому мы выясним, сколько раз 5 можно разделить на 2.
В столбце 2 мы будем искать число, ближайшее к 5, но не превышающее 5. Это 4.
4 находится в ряду 2.
 Это означает, что 2 входит в число 5 два раза по .
Это означает, что 2 входит в число 5 два раза по .Мы напишем 2 выше 5.
Теперь пришло время Умножение 2 и 2.
2 x 2 = 4.
. 5.
Теперь пришло время настроить наши вычитание задача.
5 — 4 = 1. Под чертой напишем 1.
Поскольку наш ответ на задачу на вычитание равен 1, мы посмотрим под скобкой , чтобы увидеть, есть ли еще одна цифра, которую мы можем записать.
Нам больше нечего сбивать. На уроке деления мы узнали, что мы можем написать ноль рядом с числом под скобкой деления.
Итак, рядом с 6,5 мы напишем 0,
Теперь мы можем продолжить решение этой задачи. Мы запишем 0 и перепишем его рядом с 1.
Давайте посмотрим, сколько раз 10 можно разделить на 2. до 10, но не больше 10. В колонке 2 есть 10.
 Это именно то, что нам нужно!
Это именно то, что нам нужно!10 находится в 5-м ряду. Это означает, что 2 входит в число 10 пять раз .
Напишем 5 над 0.
Теперь пора умножить 5 на 2.
5 x 2 = 10.
Далее мы создадим задачу на вычитание .
Теперь пришло время решить. 10 — 10 = 0.
Поскольку ответ на задачу на вычитание равен 0, а цифр для вычитания больше нет, мы закончили деление. Остался последний шаг, который нам нужно сделать.
В этой задаче мы разделили десятичное число: 6,5. Это означает, что наше частное или ответ будет иметь десятичную точку.
Мы просто напишем десятичную точку непосредственно над другой десятичной точкой. Видите, где мы поместили его между 3 и 2?
Мы решили задачу. Коэффициент равен 3,25. Итак, 6,5/2 = 3,25. Мы можем прочитать это как три и двадцать пять сотых .

 Часть 2
Часть 2 Организационный момент
Организационный момент
 Актуализация знаний учащихся
Актуализация знаний учащихся Изучение нового материала
Изучение нового материала


 Услышав пример, карточка с ответом на который на парте, учащийся встаёт, показывает карточку и называет ответ.
Услышав пример, карточка с ответом на который на парте, учащийся встаёт, показывает карточку и называет ответ.

 60004999999999999999797
60004999999999999999797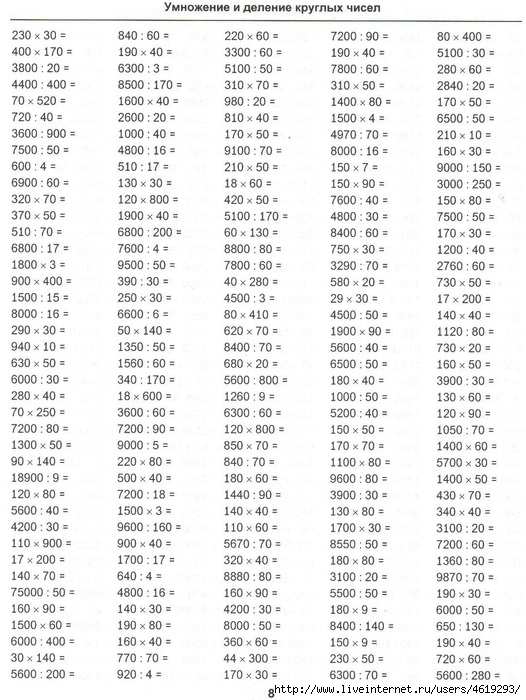

 1.
1. 0242
0242 pdf
pdf 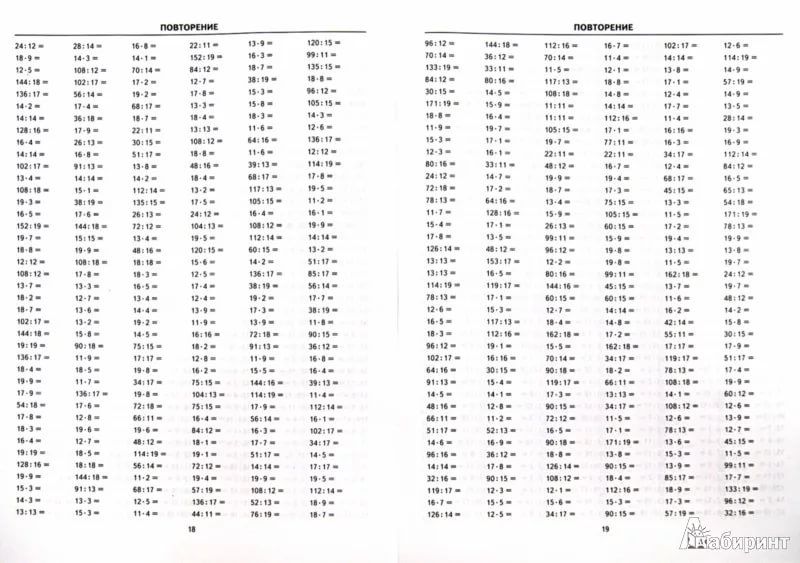 — Блоки умножения (целевой номер)
— Блоки умножения (целевой номер) 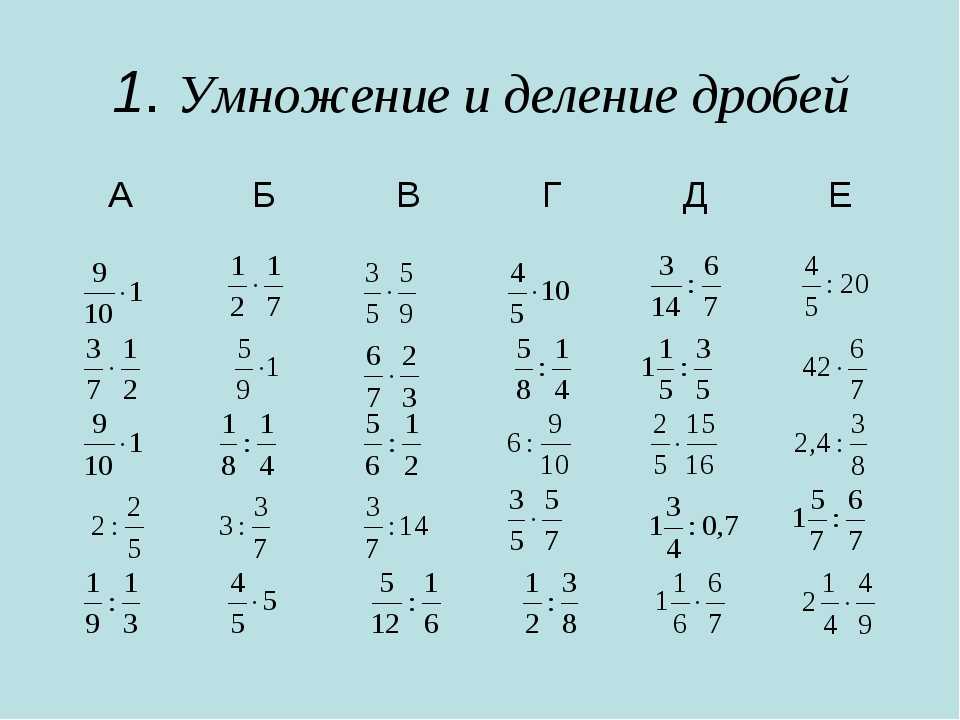 93-94
93-94 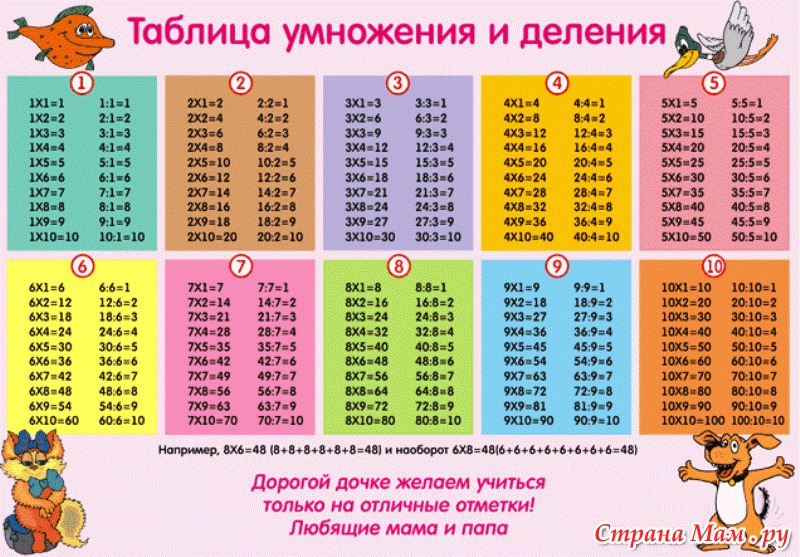 3.OA.A.1
3.OA.A.1  3.OA.B.5
3.OA.B.5  Например, 6 -3 можно записать как 1/6 3 .
Например, 6 -3 можно записать как 1/6 3 .


 Это означает, что мы поместим 38,12 выше 4,5.
Это означает, что мы поместим 38,12 выше 4,5. Итак, мы умножим 4 на цифру в правом верхнем углу . Вот, это 3.
Итак, мы умножим 4 на цифру в правом верхнем углу . Вот, это 3.
 ..
..
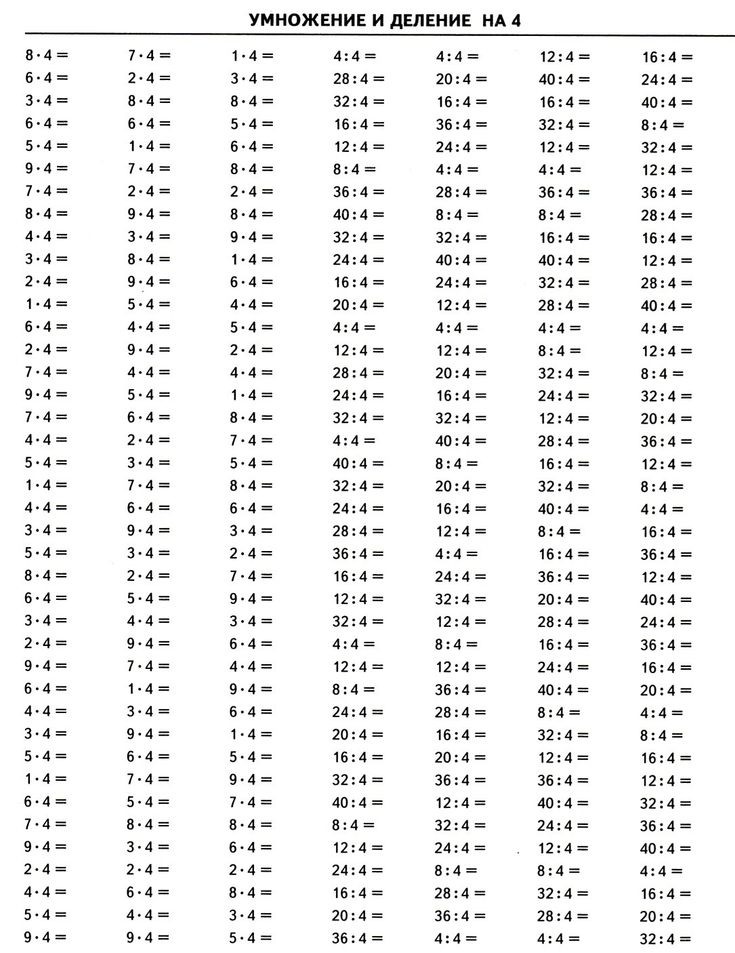 2.
2.
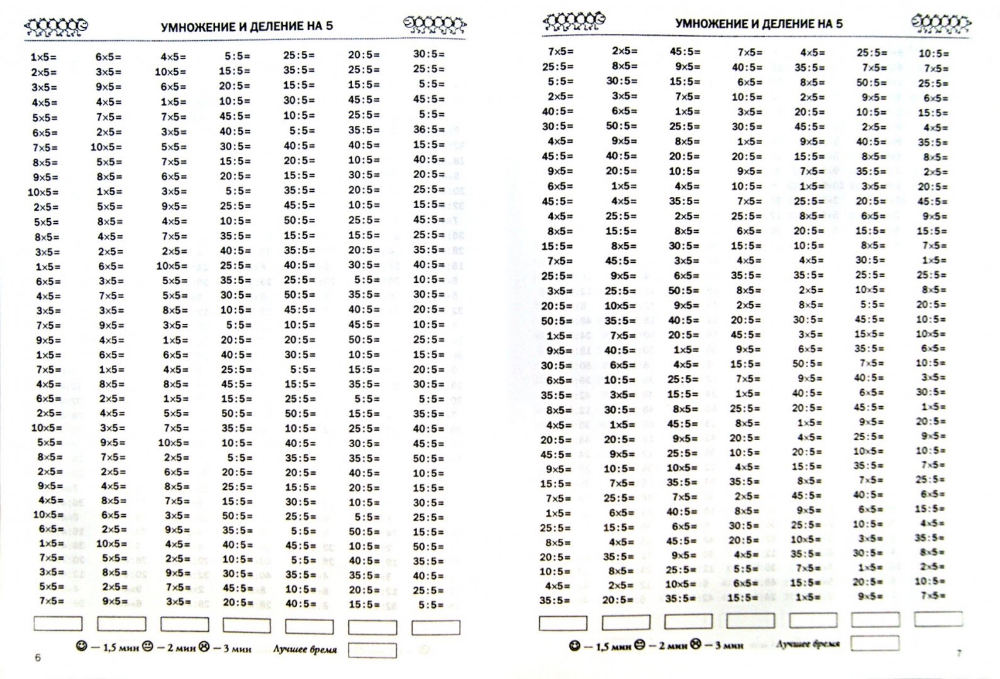 Это означает, что наша десятичная дробь еще не является целым числом.
Это означает, что наша десятичная дробь еще не является целым числом. .. и выясним, сколько раз его можно разделить на 2.
.. и выясним, сколько раз его можно разделить на 2. Это означает, что 2 входит в число 5 два раза по .
Это означает, что 2 входит в число 5 два раза по . Это именно то, что нам нужно!
Это именно то, что нам нужно!