примеры в столбик для 3, 4 класса, алгоритм, двузначное на двузначное, проверка, формула, основные правила, видеоурок
Деление с остатком – это арифметическая операция, в ходе которой проводится деление одного числа на другое, а в результате получается 2 целых числа: неполное частное и остаток от деления. Причем сам остаток всегда должен быть меньше делителя. В то же случае, если во время данной операции в результате образовался ноль, говорят, что делимое делится нацело.
Находясь в строгих рамках только натуральных чисел, во время проведения арифметических операций приходится различать деление с остатком и нацело. Здесь важно помнить, что 0 – это не натуральное число. Также еще один важный момент, на который нужно обратить внимание – неполное частное при делении меньшего на большее должно приравниваться к 0. Это также несколько выходит за рамки натуральных чисел. Все эти искусственные ограничения усложняют формулировку и дальнейшие вычисления. Деление с остатком может были проведено не только с целыми числами, но и с другими математическими объектами. Например, с многочленами.
Например, с многочленами.
Делению дети начинают обучаться еще в младших классах. Это одна из основных операций, которые можно проводить с цифрами. Можно сказать, что это основа для того, чтобы в дальнейшем проводить более сложные подсчеты. Поэтому правила нужно запоминать обязательно.
На первый взгляд может показаться, что деление с остатком никогда в будущем не пригодится. Но это не так. Данную операцию часто применяют в компьютерной технике и телекоммуникационном оборудовании с целью получения случайных и создания контрольных чисел. Сама операция исчисления ост-ка в разных языках программирования указывается по-своему.
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример для детального объяснения:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель. Основная черта обозначена оранжевым цветом.
- Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается.
 Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ). - Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
[warning]При делении таким образом, остаток всегда должен быть меньше делителя.[/warning]
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо приводить в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику подсчета ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
[warning]Существует правило для случаев, когда делитель больше делимого: НЧ равно 0, ост-к равен делимому. [/warning]
[/warning]
Как разделить число 5 на число 6? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6>5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. После всех подсчетов получаем: НЧ = 0, ост-к = 5.
Эту тему начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры: 14:3
Находим НЧ: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Ост-к: 3*4=12, 14-12=2.
Ответ: НЧ 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача:
- 3 пирожка надо разделить на двоих;
- 4 пирожка на двоих;
- 5 пирожков на двоих.

Читайте также: Натуральные числа
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами свыше 100.
Данное действие удобнее всего выполнять в столбик, так как НЧ также будет двузначным (в большинстве случаев), а алгоритм столбика облегчает подсчет и делает его более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя подсчет проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить ост-к.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у последнего первые две левые цифры – это 38. Сравниваем их с делителем. 38>25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
38>25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50>38, возвращаемся на один шаг назад.
Ответ – 1. Вписываем единицу в зону не полного частного.
Далее:
38-25=13. Вписываем 13 под чертой.
Второй уровень
13>25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136>25? Да – значит можно его вычесть. Определяем, сколько 25 поместиться в 136.
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150>136 – возвращаемся назад на один шаг. Добавляем цифру 5 в зону неполного частного, справа от единицы.
Определяем остаток:
136-125=11. Приводим под чертой. 11>25? Нет – действие провести нельзя. У делимого не остались цифры. Значит, делить больше нечего. Подсчет закончен.
Ответ: НЧ равно 15, в ост-ке 11.
Если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого, то в таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в подсчете сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38>75? Нет – деление провести нельзя. Берем все 3 цифры. 386>75? Да – действие провести можно. Проводим расчет.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450>386 – возвращаемся на шаг назад. Вписываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11>75? Нет. Также не остались цифры у делимого. Подсчет закончен.
Результат: НЧ = 5, в ост-ке — 11.
119:35
Выполняем проверку: 11>35? Нет – математическую операцию провести нельзя. Подставляем третье число – 119>35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140>119 – возвращаемся на один шаг назад. Вписываем 3 в зону неполного ост-ка.
Находим ост-к: 119-105=14. 14>35? Нет, и у делимого не остались цифры. Вычисления закончены.
Результат: НЧ = 3, осталось — 14.
1195:99
Проверяем: 11>99? Нет – подставляем еще одну цифру. 119>99? Да – начинаем вычисления.
11<99, 119>99.
99*1=99, 99*2=198 – перебор. Вписываем 1 в неполное частное.
Находим ост-к: 119-99=20. 20<99. Опускаем 5. 205>99. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим ост-к: 205-198=7.
Результат: НЧ = 12, остаток — 7.
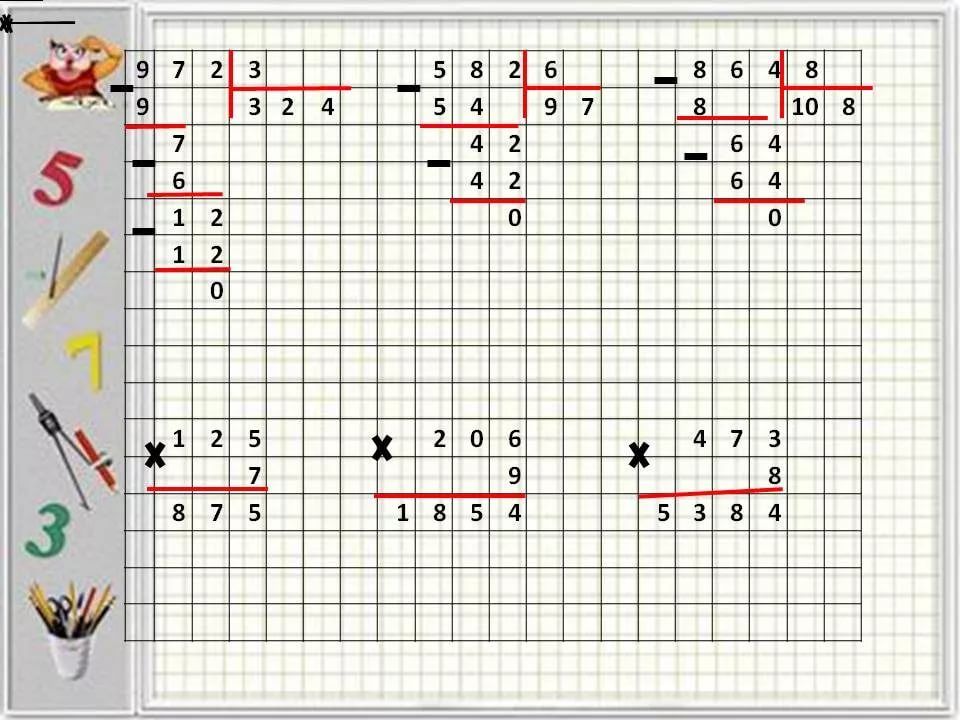
Деление с остатком — примеры:
Учимся делить в столбик с остатком:
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно. Этой теме необходимо уделить больше внимания, чтобы разобраться со всеми тонкостями подсчета. В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
Читайте также: Легкие правила округления чисел после запятой
как объяснить ребенку деление в столбик
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса.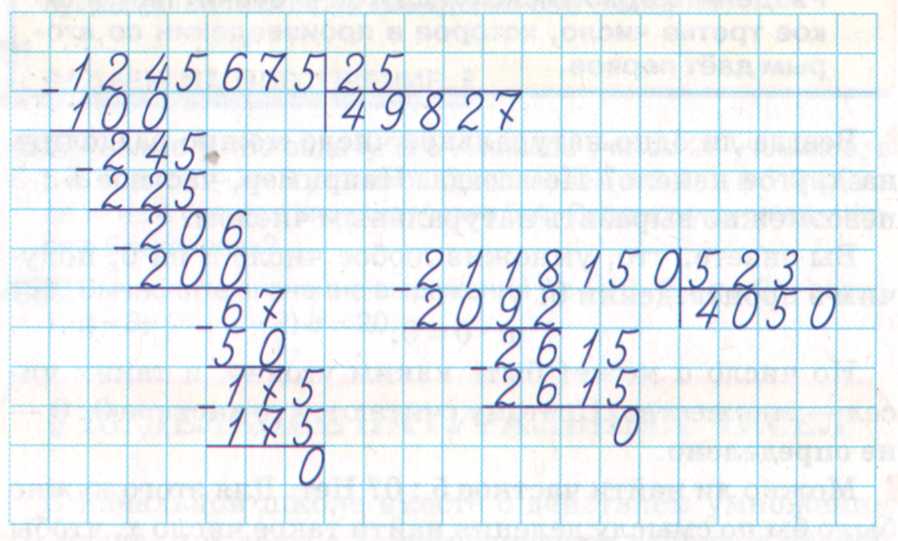 А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое
. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.Примеры 76
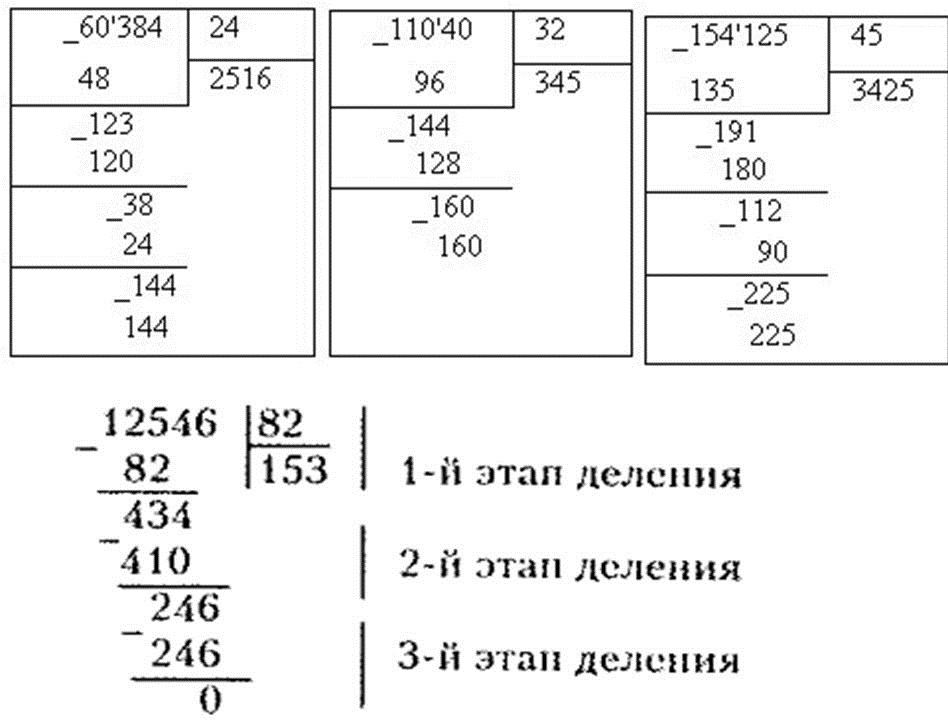
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.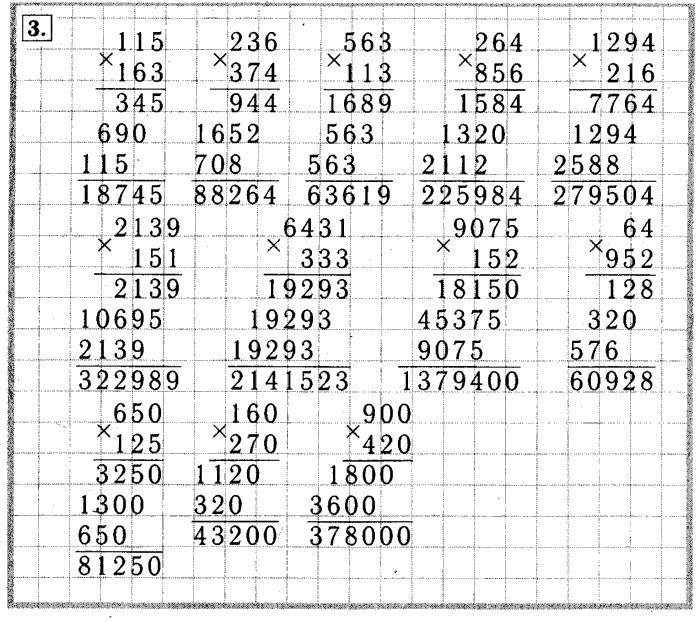
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2.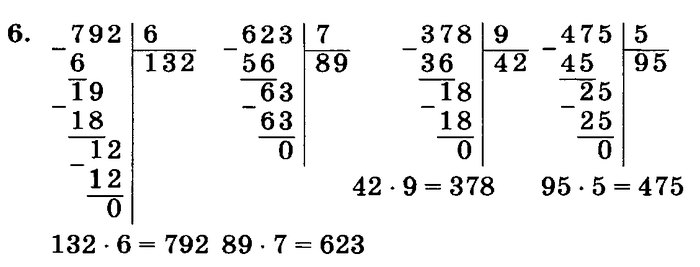 Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
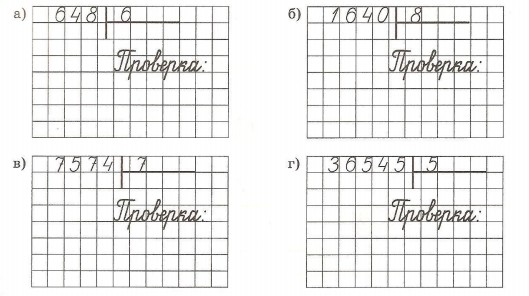
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.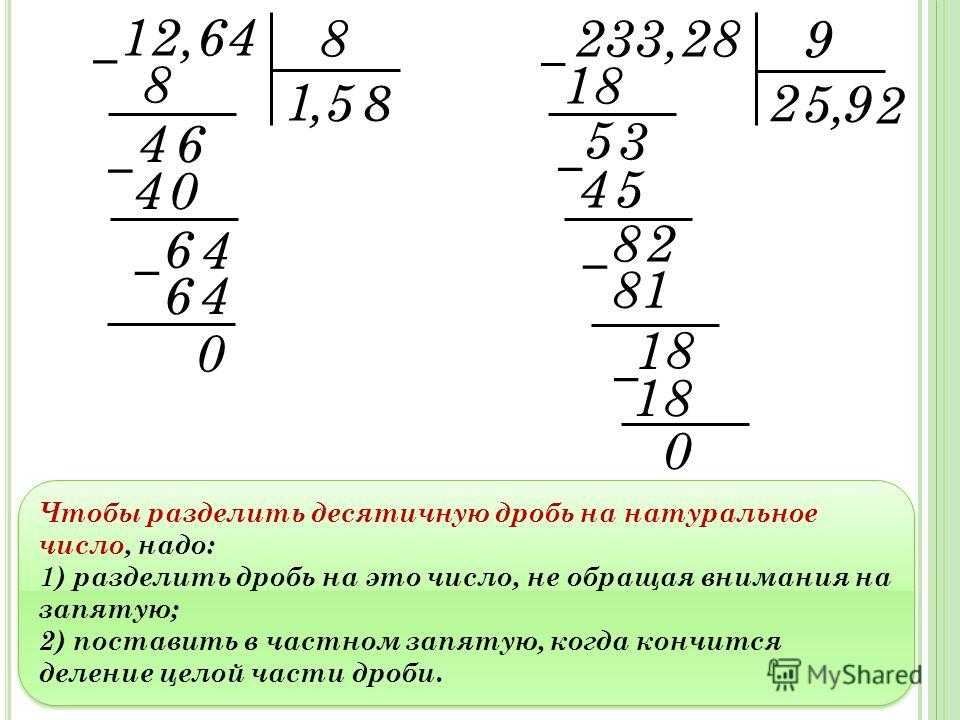
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.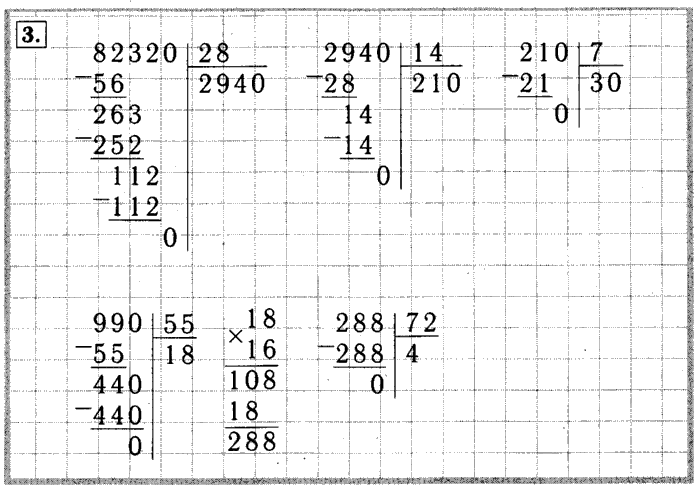
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.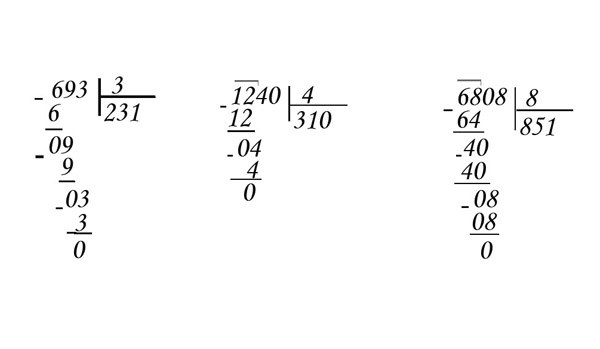
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.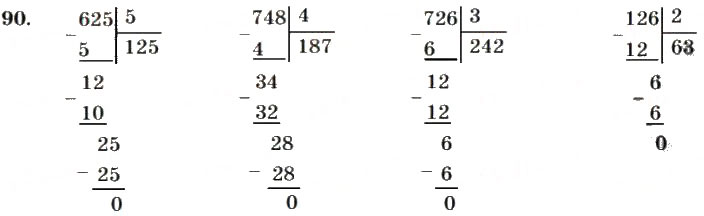
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере.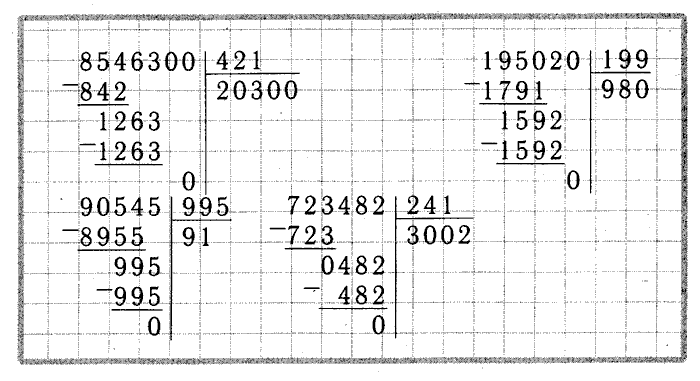 Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток. )
)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Как научиться делению столбиком, 3 класс,4 класс. Деление столбиком 3 двухзначных чисел. Деление столбиком 4 трёхзначных чисел. Пример деления столбиком без остатка, с остатком
Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Содержание статьи
- Как научиться делить столбиком 3 класс
- Как научиться делить столбиком 4 класс
- Как научиться делить столбиком на двузначное
- Видео как научиться делить в столбик
- Как научиться делить в столбик с остатком
- Как научиться делить столбиком трехзначные числа
- Как научиться делить в столбик многозначные числа
Как научиться делить столбиком 3 класс
Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100. На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Алгоритм деления в столбик:
Например, 98 необходимо разделить в столбик на 7.
В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.
Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.
Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно. Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».
Полученный ответ запишем рядом с «1».
От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».
Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.
Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.
Как научиться делить столбиком 4 класс
Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.
Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.
Делитель 8 умножим на 1 и получим — 8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.
Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4.
 Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.
Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.Как научиться делить столбиком на двузначное
В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.
Для примера выполним действие: 144 : 24
Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
После постепенного освоения простых примеров, можно перейти к более сложным.

Разделим 1035 на 23.
Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.
Видео как научиться делить в столбик
Как научиться делить в столбик с остатком
Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.
Для примера разделим 235 на 14.
235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Методом подбора разделим 90 : 10 = 9, но в нашем случае 14 х 9= 126, что больше 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.
Во время решения примеров с остатком, ответ может быть записан двумя способами:
- в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
- но чаще всего ответ записывают словами: 6 целых и 11 в остатке.
Как научиться делить столбиком трехзначные числа
Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.
Для примера рассмотрим следующие действия: 146676 : 719
146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».
Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.
Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676. Ответ верен.
Как научиться делить в столбик многозначные числа
Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное. В первом случае учитываем только первую цифру делителя, а при делении на многозначное берем во внимание количество всех цифр делителя. Рабочее число обязательно должно быть больше делителя. В других случаях – добавляем цифру следующего разряда и производим деление по алгоритму.
Как решать примеры в столбик на деление. Деление многочлена на многочлен (двучлен) столбиком (уголком)
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки).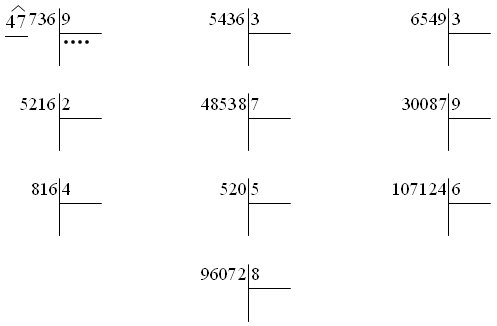 Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно .
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно .
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.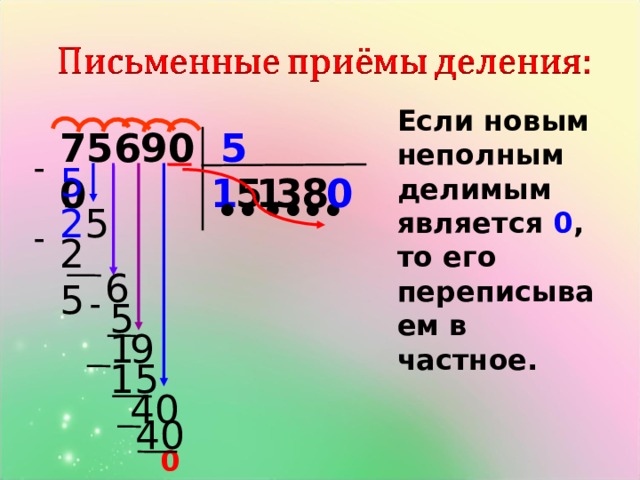
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) .
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.

- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10 .
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).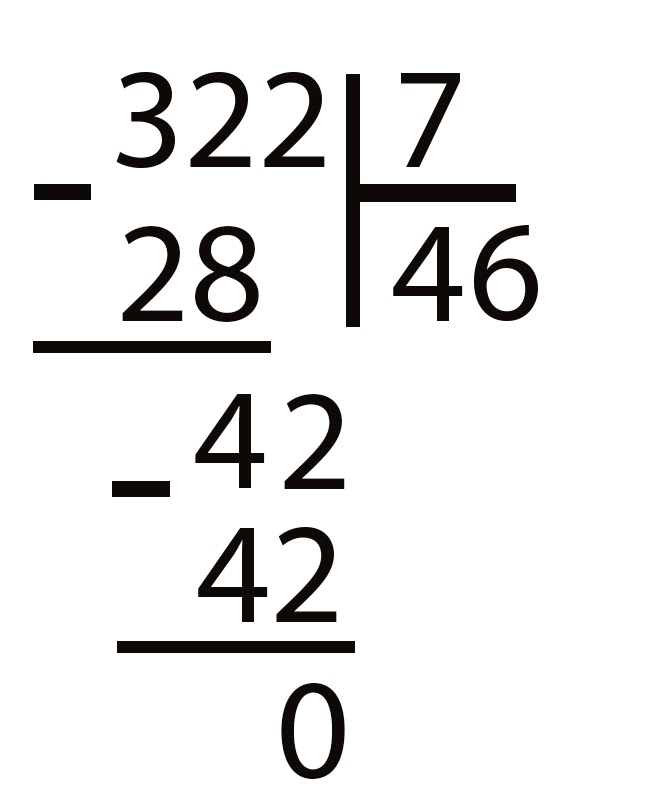
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление .
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое.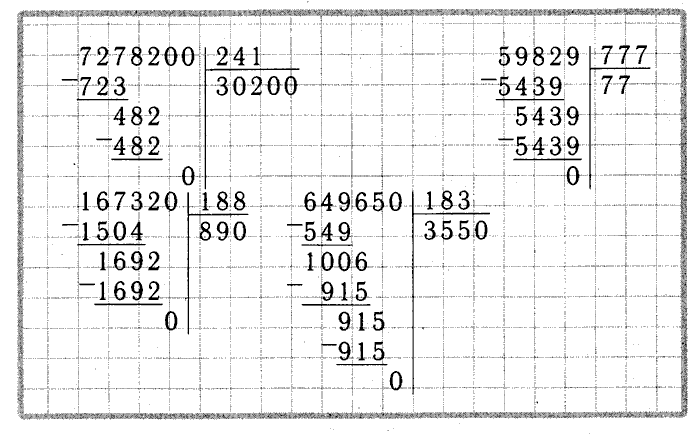 Формула:
Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.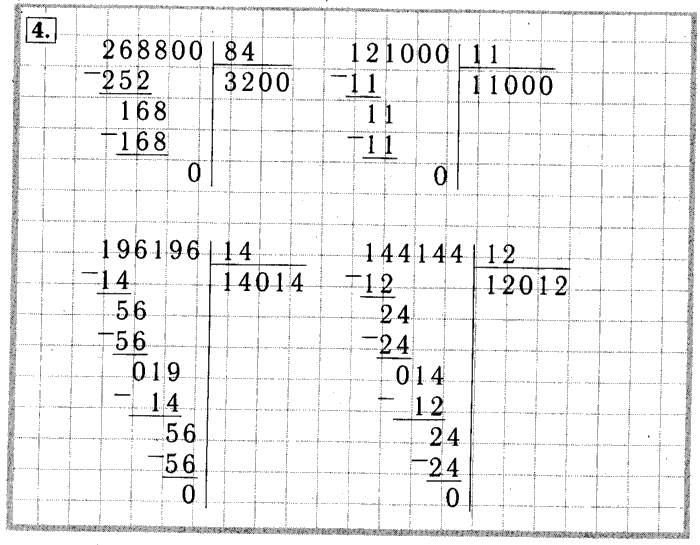
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.

- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265.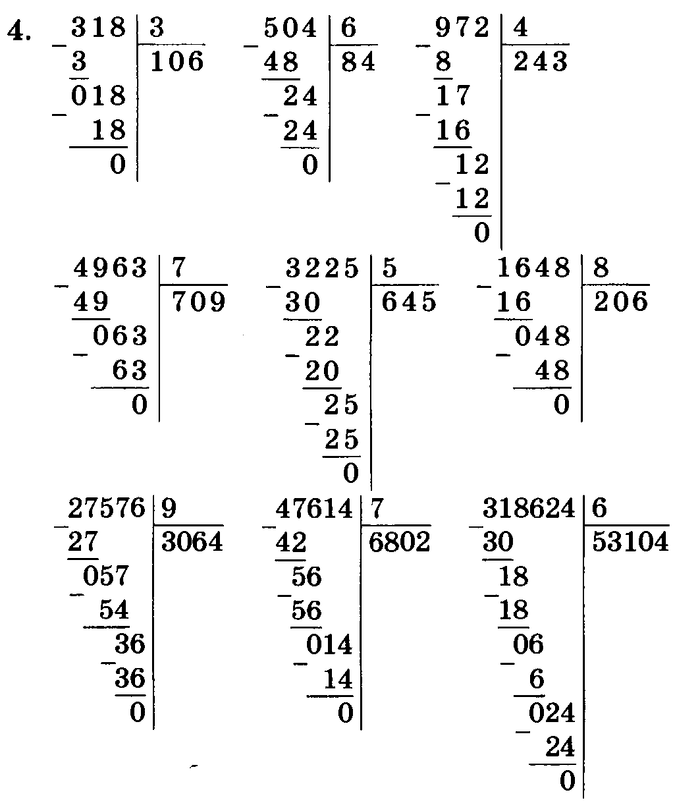 Больше в делимом цифр нет. Значит в частном будет однозначное число.
Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Примеры в столбик онлайн калькулятор. Деление натуральных чисел столбиком, примеры, решения
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).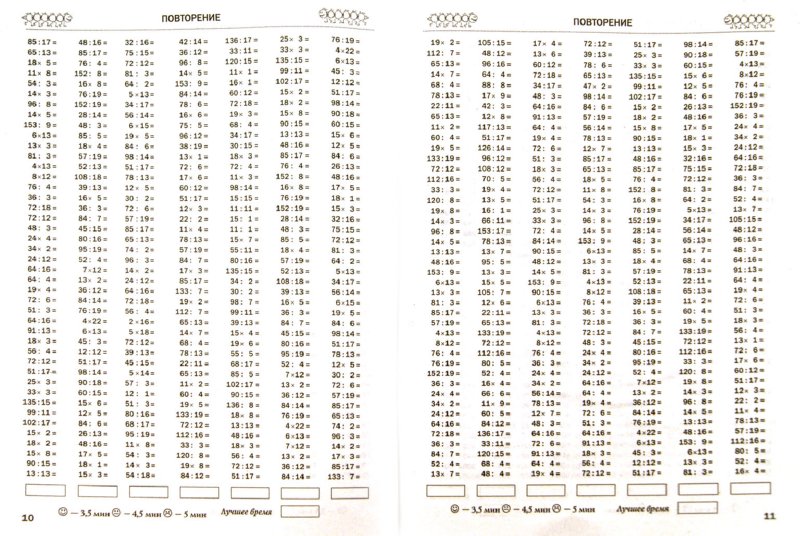
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения.
Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3.
 Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа - Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6.
 Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 - Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30.
 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 - Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.

- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.

- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть
❤️️Ответ к странице 35. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Номер 12.
Выполни деление с остатком и сделай проверку.
Ответ:
Номер 13.
Ответ:
Номер 14.
Реши уравнения.
Ответ:
Номер 15.
Реши задачу разными способами.
1) В магазин привезли 5 мешков риса, по 40 кг в каждом, и 5 мешков пшена, по 35 кг в каждом. В первый день продали 120 кг риса и 140 кг пшена. Сколько килограммов крупы осталось продать?
2) Столовая расходовала одну неделю по 70 л молока в день, а другую неделю – по 80 л молока в день. Сколько литров молока израсходовали за эти две недели, если столовая работала 5 дней в неделю? 6 дней?
Ответ:
Задача 1:
1 способ:
1) 5 ∙ 40 = 200 (кг) — риса привезли. 2) 5 ∙ 35 = 175 (кг) — пшена привезли.
3) 200 − 120 = 80 (кг) — риса осталось.
4) 175 − 140 = 35 (кг) — пшена осталось.
5) 80 + 35 = 115 (кг) — крупы осталось продать.
Ответ: 115 кг крупы.
2) 5 ∙ 35 = 175 (кг) — пшена привезли.
3) 200 − 120 = 80 (кг) — риса осталось.
4) 175 − 140 = 35 (кг) — пшена осталось.
5) 80 + 35 = 115 (кг) — крупы осталось продать.
Ответ: 115 кг крупы.
2 способ:
1) 5 ∙ 40 = 200 (кг) — риса привезли в магазин.
2) 35 ∙ 5 = 175 (кг) — пшена привезли в магазин.
3) 200 + 175 = 375 (кг) — крупы привезли всего.
4) 120 + 140 = 260 (кг) — крупы продали.
5) 375 − 260 = 115 (кг) — крупы осталось продать.
Ответ: 115 кг крупы осталось продать.
Задача 2:
1 способ:
1) 5 ∙ 70 = 350 (л) — молока за неделю израсходовали когда столовая работала 5 дней.
2) 5 ∙ 80 = 400 (л) — молока израсходовали за другую неделю когда столовая работала 5 дней.
3) 350 + 400 = 750 (л) — израсходовали за две недели в пятидневном режиме работы.
Ответ: 750 литров израсходовали за 2 недели работы по 5 дней в неделю.
2 способ:
1) 70 ∙ 6 = 420 (л) — молока использовала первая столовая за 6 дней работы. 2) 80 ∙ 6 = 480 (л) — молока использовала вторая столовая за 6 дней работы.
3) 420 + 480 = 900 (л) — молока израсходовали обе столовые за 2 недели работы по 6 дней.
Ответ: 900 литров.
2) 80 ∙ 6 = 480 (л) — молока использовала вторая столовая за 6 дней работы.
3) 420 + 480 = 900 (л) — молока израсходовали обе столовые за 2 недели работы по 6 дней.
Ответ: 900 литров.
Номер 16.
Ответ:
Номер 17.
Ответ:
Номер 1.
Сколько разрядов содержится в каждом классе?Как называются разряды и классы?
Ответ:
Три разряда. Разряды – единицы, десятки, сотни. Классы – единиц, тысяч, миллионов, миллиардов.
Номер 2.
Покажи на примере, что 10 единиц любого разряда образуют единицу следующего разряда.
Ответ:
10 ∙ 10 = 100 100 ∙ 10 = 1000
Номер 3.
Покажи на примере, что 1000 единиц одного класса образуют единицу следующего класса.
Ответ:
1 ∙ 1000 = 1000 10 ∙ 1000 = 10000
Номер 4.
Сколько цифр используется для записи чисел?Назови их. Покажи, как можно одними и теми же цифрами записать разные числа.
Ответ:
10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 127, 271, 172, 721 …
Номер 5.
Покажи на примере, как изменяется значение цифры при изменении её места в записи числа.
Ответ:
247 – 7 единиц 274 – 7 десятков 724 – 7 сотен
Номер 6.
Как получить число, которое больше данного в 10 раз? в 100 раз? в 1000 раз?
Ответ:
Умножить на 10 (в 10 раз больше), умножить на 100 (в 100 раз больше), Умножить на 1000 (в 1000 раз больше).
Номер 7.
Объясни, как можно сравнить числа.
Ответ:
Числа сравниваются по классам и по разрядам.
Например: сравним 351 и 349
Разряд сотен у чисел равны. Сравниваем разряд десятков 5 > 4, поэтому 351 > 349.
Сравниваем разряд десятков 5 > 4, поэтому 351 > 349.
Задание на полях страницы
Цепочка.
Ответ:
14 ∙ 8 = 112 112 : 2 = 56 56 : 4 = 14 14 ∙ 5 = 70
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Числа до 4-х цифр — Разложение, Советы и рекомендации
Серия 4-значных чисел начинается с числа 1000 и заканчивается числом 9999. 4-значные числа — это числа, имеющие 4 цифры, и мы можем сформировать 4-значные числа, используя любые цифры от 0 до 9, но число должно начинаться с цифры 1 или числа больше 1. Числа классифицируются в соответствии с числом цифр, которые они имеют, и значение разряда числа помогает понять значение каждой цифры.
4-значные числа — это числа, имеющие 4 цифры, и мы можем сформировать 4-значные числа, используя любые цифры от 0 до 9, но число должно начинаться с цифры 1 или числа больше 1. Числа классифицируются в соответствии с числом цифр, которые они имеют, и значение разряда числа помогает понять значение каждой цифры.
| 1. | Что такое четырехзначные числа? |
| 2. | Как записывать числа до 4 цифр? |
| 3. | Как разложить числа до 4 цифр? |
| 4. | Советы и подсказки по номерам до 4 цифр |
| 5. | Часто задаваемые вопросы о номерах до 4 цифр |
Что такое четырехзначные числа?
4-значные числа — это числа, состоящие только из 4 цифр, в которых первая цифра должна быть 1 или больше 1, а остальные цифры могут быть любым числом от 0 до 9. Например, 5693, 1023 и 9825 — четырехзначные числа.
Как записывать числа до 4 цифр?
Четырехзначные числа записываются или читаются в соответствии со значением разряда цифр. В четырехзначных числах четыре цифры соответствуют четырем разрядам — единицам, десяткам, сотням и тысячам. Когда число записывается в стандартной форме, каждая группа цифр отделяется запятой, образующей точку. Первый период, известный как «период единиц», состоит из первых трех цифр числа, если считать с правой стороны. Следует отметить, что расстановка запятых начинается с 4-значных чисел. Мы ставим запятую непосредственно перед разрядом сотен, потому что заканчивается первый период (единицы) и начинается второй период тысяч. Например, 3210 — это 4-значное число, и после запятой оно записывается как 3210.
Наименьшее четырехзначное число — 1000, а самое большое четырехзначное число — 9999, а всего существует 9000 чисел от 1000 до 9999. Мы можем составить много четырехзначных чисел, используя цифры от 0 до 9, но мы нужно помнить, что разряд тысяч в 4-значном числе не должен быть 0. Например, 0875 не является четырехзначным числом, число считается трехзначным, то есть 875.
Например, 0875 не является четырехзначным числом, число считается трехзначным, то есть 875.
4- числовые числа могут быть записаны в трех формах, т. е. в числовой форме, словами и в развернутой форме. Например, 2345 — это четырехзначное число. В числовой форме это записывается как 2345. Прописью это записывается так: Две тысячи триста сорок пять. В развернутом виде это записывается так: 2000 + 300 + 40 + 5, или 2 тысячи + 3 сотни + 4 десятка + 5 единиц.
Как разложить числа до 4 цифр?
Как уже говорилось выше, четырехзначное число имеет следующие разрядные значения — Тысячи, Сотни, Десятки и Единицы. Чтобы разложить 4-значные числа, мы умножаем каждую цифру 4-значного числа на его значение, то есть 1000, 100, 10 и 1 соответственно. Например, данное 4-значное число 5627 можно разложить следующим образом:
- 5 находится в тысячном разряде, а его разрядное значение равно 5 × 1000 = 5000 .
- 6 стоит на разряде сотен и его разрядное значение равно 6 × 100 = 600
- 2 стоит на разряде десятков и его разрядное значение равно 2 × 10 = 20
- 7 стоит на одном месте, и его разрядное значение равно 7 × 1 = 7 .

Итак, расширенная форма 5627 = 5000 + 600 + 20 + 7
Обратите внимание на следующий рисунок, на котором показано, как записать 4-значное число в соответствии с его разрядными значениями. В данном случае мы взяли пример с 4-значным числом: 4123. Здесь 4 пишется в разряде тысяч, 1 — в разряде сотен, 2 — в разряде десятков и 3 — в разряде единиц.
Советы и подсказки по номерам до 4 цифр
Ниже приведены некоторые советы и рекомендации по числам до 4 цифр, которые могут помочь при решении проблем, связанных с этими числами.
- При умножении любого однозначного числа (от 1 до 9) на 1000 получается четырехзначное число. Например, 5 × 1000 = 5000 .
- При умножении любого двузначного числа на 100 получается четырехзначное число. Например, 44 × 100 = 4400
- При умножении любого трехзначного числа на 10 получается четырехзначное число. Например, 678 × 10 = 6 780 .
- При умножении любого четырехзначного числа на 1 получается четырехзначное число.
 Например, 2345 × 1 = 2345 .
Например, 2345 × 1 = 2345 . - Наименьшее четырехзначное число, состоящее из разных цифр, равно 1023.
- Наименьшее четырехзначное число, состоящее только из одной цифры, — 1111.
- Наименьшее четырехзначное число, состоящее из двух разных цифр, равно 1000. (1000 также является наименьшим четырехзначным числом).
- Наибольшее четырехзначное число, использующее только одну цифру, равно 9 999 (9 999 также является наибольшим четырехзначным числом).
- Наибольшее четырехзначное число, состоящее из двух разных цифр, равно 9998.
- Наибольшее четырехзначное число, состоящее из всех цифр, равно 9876.
Важные примечания
Ниже приведены некоторые важные примечания, относящиеся к числам до 4 цифр, которые мы изучали в этой статье.
- Есть 4 числа (любое число от 0 до 9) в виде 4-значного числа, а начальное число должно быть 1 или больше 1.
- Разряд тысяч в четырехзначном числе не может быть равен 0.

- Наименьшее четырехзначное число — 1000, а наибольшее четырехзначное число — 9999.
- Всего существует 9000 четырехзначных чисел.
Наименьшее 4-значное число
Наименьшее 4-значное число — 1000, поскольку предшествующее ему число — 999, является 3-значным числом. Четырехзначные числа начинаются с 1000 и заканчиваются на 9.999.
Наибольшее 4-значное число
Наибольшее 4-значное число — 9999, потому что за ним следует 10000, которое является 5-значным числом. 4-значные числа начинаются с 1000 и заканчиваются на 9999.
☛ Похожие статьи
- Числа до 2 цифр
- Номера до 3 цифр
- Номера до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Числа до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Часто задаваемые вопросы о номерах до 4 цифр
Что такое четырехзначные числа?
Простыми словами, 4-значное число является 4-значным числом. Первая цифра 4-значного числа должна быть 1 или больше единицы, а остальные цифры могут быть любым числом от 0 до 9. Четырехзначные числа начинаются с 1000 и заканчиваются на 9999. Значения разрядов в 4-значном числе, начиная справа, это единицы, десятки, сотни и тысячи.
Первая цифра 4-значного числа должна быть 1 или больше единицы, а остальные цифры могут быть любым числом от 0 до 9. Четырехзначные числа начинаются с 1000 и заканчиваются на 9999. Значения разрядов в 4-значном числе, начиная справа, это единицы, десятки, сотни и тысячи.
Какое самое большое четырехзначное число?
9999 — самое большое четырехзначное число. Мы можем прочитать это число словами как девять тысяч девятьсот девяносто девять. Число после 9 999 равно 10 000 и является пятизначным числом, поэтому наибольшее четырехзначное число равно 9 999.
Какое самое маленькое четырехзначное число?
1000 — наименьшее четырехзначное число. Мы можем прочитать число словами как тысяча. Число до 1000 равно 999 и является трехзначным числом, поэтому наименьшее четырехзначное число равно 1000.
Сколько существует четырехзначных чисел?
Есть 9000 четырехзначных чисел, и они начинаются с числа 1000 и заканчиваются числом 9999.
Как поставить запятую в четырехзначном числе?
В четырехзначных числах четвертая крайняя слева цифра представляет разряд тысяч. Запятая в четырехзначном числе ставится между четвертой и третьей цифрой справа, то есть между разрядом тысяч и разрядом сотен. Например, четырехзначное число 3674 записывается как 3674.
Запятая в четырехзначном числе ставится между четвертой и третьей цифрой справа, то есть между разрядом тысяч и разрядом сотен. Например, четырехзначное число 3674 записывается как 3674.
Каковы простые делители наибольшего четырехзначного числа?
Простые делители наибольшего четырехзначного числа 9999 равны 3, 11 и 101.
Какое наибольшее четырехзначное число является полным квадратом?
Наибольшее четырехзначное число, являющееся полным квадратом, равно 9801.
4.3 Распределение частот
Содержание
Текст начинается
Тематическая навигация
- 4 Исследование данных
- 4.1 Инструменты исследования данных
- 4.2 Типы переменных
- 4.3 Распределение частот
- 4.4 Меры центральной тенденции
- 4.5 Меры рассеивания
- 4.6 Упражнения
- 4.
 7 Ответы
7 Ответы
частота ( f ) определенного значения – это количество раз, когда это значение встречается в данных. Распределение переменной представляет собой шаблон частот, означающий набор всех возможных значений и частот, связанных с этими значениями. Распределения частот изображаются в виде частотных таблиц или диаграмм.
Частотные распределения могут отображать либо фактическое количество наблюдений, попадающих в каждый диапазон, либо процент наблюдений. В последнем случае распределение называется относительное частотное распределение .
Таблицы частотного распределения можно использовать как для категориальных, так и для числовых переменных. Непрерывные переменные следует использовать только с интервалами классов, что будет объяснено в ближайшее время.
Давайте рассмотрим несколько примеров частотного распределения и относительного частотного распределения для дискретных переменных.
На Мейпл-авеню было проведено обследование. В каждом из 20 домов людей спрашивали, сколько автомобилей зарегистрировано на их домохозяйства. Результаты были записаны следующим образом:
1, 2, 1, 0, 3, 4, 0, 1, 1, 1, 2, 2, 3, 2, 3, 2, 1, 4, 0, 0
Используйте следующие шаги для представления этого данные в таблице частотного распределения.
- Разделите результаты ( x ) на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
- Составьте таблицу с отдельными столбцами для номеров интервалов (количество автомобилей на домохозяйство), подсчитанных результатов и частоты результатов в каждом интервале. Обозначьте эти столбцы Количество автомобилей , Сумма и Частота .

- Прочитайте список данных слева направо и поставьте отметку в соответствующей строке. Например, первый результат — 1, поэтому поставьте отметку в строке рядом с тем местом, где 1 появляется в столбце интервала ( Количество автомобилей ). Следующим результатом будет 2, поэтому поставьте отметку в ряду рядом с 2 и так далее. Когда вы достигнете пятой контрольной отметки, проведите контрольную линию через предыдущие четыре отметки, чтобы облегчить чтение окончательных расчетов частоты.
- Сложите количество контрольных точек в каждой строке и запишите их в последний столбец, озаглавленный Частота .
Ваша таблица распределения частот для этого упражнения должна выглядеть следующим образом:
| Количество вагонов (х) | Частота (f) |
|---|---|
| 0 | 4 |
| 1 | 6 |
| 2 | 5 |
| 3 | 3 |
| 4 | 2 |
Быстро взглянув на эту таблицу частотного распределения, мы увидим, что из 20 обследованных домохозяйств в 4 домохозяйствах не было автомобилей, в 6 домохозяйствах была 1 машина и т. д.
Пример 2. Составление таблицы кумулятивного распределения частот Таблица кумулятивного распределения частот является более подробной таблицей. Она выглядит почти так же, как таблица распределения частот, но в нее добавлены столбцы, которые также показывают совокупную частоту и совокупный процент результатов.
Она выглядит почти так же, как таблица распределения частот, но в нее добавлены столбцы, которые также показывают совокупную частоту и совокупный процент результатов.
На недавнем шахматном турнире все 10 участников должны были заполнить форму, в которой были указаны их имена, адреса и возраст. Возраст участников был записан следующим образом:
36, 48, 54, 92, 57, 63, 66, 76, 66, 80
Используйте следующие шаги, чтобы представить эти данные в таблице распределения совокупной частоты.
- Разделите результаты на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае подходят интервалы 10. Поскольку 36 лет — самый низкий возраст, а 92 — самый высокий, начните интервалы с 35 до 44 и закончите интервалы с 85 до 94.
- Создайте таблицу, аналогичную таблице частотного распределения, но с тремя дополнительными столбцами.
Совокупная таблица распределения частот должна выглядеть так:
Таблица 4.  3.2
3.2
Возраст участников шахматного турнира
Сводка таблицы
В этой таблице отображаются результаты Возрастов участников шахматного турнира. Информация сгруппирована по нижнему значению (отображается в виде заголовков строк), верхнему значению, частоте (f), совокупной частоте, проценту и совокупному проценту (отображается в виде заголовков столбцов).Нижнее значение Верхнее значение Частота (f) Суммарная частота Процент Совокупный процент 35 44 1 1 10,0 10,0 45 54 2 3 20,0 30,0 55 64 2 5 20,0 50,0 65 74 2 7 20,0 70,0 75 84 2 9 20,0 90,0 85 94 1 10 10,0 100,0
Интервалы классов
Если переменная принимает большое количество значений, то проще представлять и обрабатывать данные, группируя значения в интервалы классов. Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
Для иллюстрации предположим, что мы установили возрастные диапазоны для исследования молодых людей, допуская при этом возможность того, что некоторые пожилые люди также могут попасть в сферу нашего исследования.
Частота интервала класса — это количество наблюдений, происходящих в конкретном предопределенном интервале. Так, например, если в данных нашего исследования фигурируют 20 человек в возрасте от 5 до 9 лет, частота для интервала 5–9 будет равна 20.
. Итак, интервалы в нашем исследовании составляют от 0 до 4 лет, от 5 до 9 лет.лет, от 10 до 14 лет, от 15 до 19 лет, от 20 до 24 лет и от 25 лет и старше. Конечные точки первого интервала равны 0 и 4, если переменная дискретна, и 0 и 4,999, если переменная непрерывна. Таким же образом будут определены конечные точки других интервалов класса.
Ширина интервала класса — это разница между нижней конечной точкой интервала и нижней конечной точкой следующего интервала. Таким образом, если непрерывные интервалы нашего исследования равны от 0 до 4, от 5 до 9 и т. д., ширина первых пяти интервалов равна 5, а последний интервал открыт, поскольку ему не назначена более высокая конечная точка. Интервалы также могут быть записаны как от 0 до менее 5, от 5 до менее 10, от 10 до менее 15, от 15 до менее 20, от 20 до менее 25, от 25 и более.
Правила для наборов данных, содержащих большое количество наблюдений
Таким образом, следуйте этим основным правилам при построении таблицы распределения частот для набора данных, содержащего большое количество наблюдений:
- найдите наименьшее и наибольшее значения переменные
- принять решение о ширине интервалов классов
- включают все возможные значения переменной.
При выборе ширины интервалов классов вам придется найти компромисс между интервалами, достаточно короткими, чтобы не все наблюдения попадали в один и тот же интервал, и достаточно длинными, чтобы не остаться только с одним наблюдения за интервал.
Также важно убедиться, что интервалы классов являются взаимоисключающими и в совокупности исчерпывающими.
Пример 3. Составление таблицы частотного распределения для большого количества наблюденийТридцать батареек типа АА были протестированы, чтобы определить, как долго они будут работать. Результаты с точностью до минуты были записаны следующим образом:
423, 369, 387, 411, 393, 394, 371, 377, 389, 409, 392, 408, 431, 401, 363, 391, 405, 382 , 400, 381, 399, 415, 428, 422, 396, 372, 410, 419, 386, 390
Используйте шаги из примера 1 и приведенные выше правила, чтобы составить таблицу частотного распределения.
Ответ
Наименьшее значение – 363, а наибольшее – 431.
Используя данные и интервал классов, равный 10, интервал для первого класса составляет от 360 до 369 и включает 363 (наименьшее значение). Помните, всегда должно быть достаточно интервалов занятий, чтобы было включено самое высокое значение.
Заполненная таблица частотного распределения должна выглядеть следующим образом:
| Срок службы батареи, мин ( x ) | Частота (f) |
|---|---|
| 360–369 | 2 |
| 370–379 | 3 |
| 380–389 | 5 |
| 390–399 | 7 |
| 400–409 | 5 |
| 410–419 | 4 |
| 420–429 | 3 |
| 430–439 | 1 |
| Итого | 30 |
 Составление таблиц относительной частоты и частоты в процентах
Составление таблиц относительной частоты и частоты в процентахАналитик, изучающий данные из примера 3, может захотеть узнать не только о том, как долго работают батареи, но и о том, какая доля батарей попадает в каждый класс интервалов срока службы батарей.
Эта относительная частота конкретного наблюдения или интервала класса находится путем деления частоты ( f ) по количеству наблюдений ( n ): то есть ( f ÷ n ). Таким образом:
Относительная частота = частота ÷ количество наблюдений
Частота процентов находится путем умножения каждого значения относительной частоты на 100. Таким образом:
Частота в процентах = относительная частота X 100 = f ÷ n X 100
Используйте данные из Примера 3, чтобы составить таблицу, содержащую относительную частоту и процентную частоту каждого интервала срока службы батареи.
Вот как выглядит эта таблица:
| Срок службы батареи, мин ( х ) | Частота (f) | Относительная частота | Процентная частота |
|---|---|---|---|
| 360–369 | 2 | 0,07 | 7 |
| 370–379 | 3 | 0,1 | 10 |
| 380–389 | 5 | 0,17 | 17 |
| 390–399 | 7 | 0,23 | 23 |
| 400–409 | 5 | 0,17 | 17 |
| 410–419 | 4 | 0,13 | 13 |
| 420–429 | 3 | 0,1 | 10 |
| 430–439 | 1 | 0,03 | 3 |
| Итого | 30 | 1 | 100 |
Аналитик этих данных теперь может сказать, что:
- 7% батарей типа АА имеют срок службы от 360 минут до, но менее 370 минут, и что
- вероятность того, что любая случайно выбранная батарея типа АА будет иметь срок службы в этом диапазоне, составляет приблизительно 0,07.

Как показано ранее в примере 2, кумулятивная частота используется для определения количества наблюдений, которые лежат ниже определенного значения в наборе данных. Совокупная частота рассчитывается путем добавления каждой частоты из таблицы распределения частот к сумме ее предшественников. Последнее значение всегда будет равно сумме по всем наблюдениям, так как все частоты уже будут добавлены к предыдущей сумме. Давайте рассмотрим еще один пример расчета кумулятивной частоты.
Ежедневное количество скалолазов в Лейк-Луизе, Альберта, регистрировалось за 30-дневный период. Результаты следующие:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56 , 4, 54, 39, 52, 35, 51, 63, 42.
Количество скалолазов колеблется от 4 до 65. Для составления таблицы частот данные лучше сгруппировать по классам с интервалом 10. Каждый интервал может быть одной строкой в таблице частот. В столбце Частота указано количество наблюдений, найденных в пределах интервала класса. Например, в интервале от 10 до 20 всего два значения, тогда его частота равна 2 в таблице соответственно.
Каждый интервал может быть одной строкой в таблице частот. В столбце Частота указано количество наблюдений, найденных в пределах интервала класса. Например, в интервале от 10 до 20 всего два значения, тогда его частота равна 2 в таблице соответственно.
Используйте столбец Частота для расчета совокупной частоты.
- Сначала добавьте число из столбца Частота к его предшественнику. Например, в первой строке у нас есть только одно наблюдение и нет предшественников. Суммарная частота равна единице.
1 + 0 = 1 - Однако во второй строке есть два наблюдения. Добавьте эти два к предыдущей кумулятивной частоте (один), и в результате получится три.
1 + 2 = 3 - Запишите результаты в столбец Суммарная частота .
Другие записи в таблице можно рассчитать аналогичным образом. Результаты представлены в таблице 4. 3.5.
3.5.
| Количество скалолазов | Частота (f) | Суммарная частота |
|---|---|---|
| <10 | 1 | 1 |
| от 10 до <20 | 2 | 1 + 2 = 3 |
| от 20 до <30 | 3 | 3 + 3 = 6 |
| от 30 до <40 | 5 | 6 + 5 = 11 |
| от 40 до <50 | 6 | 11 + 6 = 17 |
| от 50 до <60 | 9 | 17 + 9 = 26 |
| >= 60 | 4 | 26 + 4 = 30 |
Кумулятивная относительная частота — это еще один способ выражения частотного распределения. Он получается путем вычисления процента кумулятивной частоты в пределах каждого интервала.
Он получается путем вычисления процента кумулятивной частоты в пределах каждого интервала.
Накопленный процент рассчитывается путем деления совокупной частоты на общее количество наблюдений ( n ), затем умножая на 100 (последнее значение всегда будет равно 100%). Таким образом,
кумулятивная относительная частота = (кумулятивная частота ÷ n) x 100
В четвертом столбце таблицы 4.3.6 показан расчет кумулятивной относительной частоты ежедневного числа скалолазов, зарегистрированных в Лейк-Луизе.
| Количество скалолазов | Частота (f) | Суммарная частота | Кумулятивная относительная частота (%) |
|---|---|---|---|
| <10 | 1 | 1 | 1 ÷ 30 х 100 = 3 |
| от 10 до <20 | 2 | 1 + 2 = 3 | 3 ÷ 30 х 100 = 10 |
| от 20 до <30 | 3 | 3 + 3 = 6 | 6 ÷ 30 х 100 = 20 |
| от 30 до <40 | 5 | 6 + 5 = 11 | 11 ÷ 30 х 100 = 37 |
| от 40 до <50 | 6 | 11 + 6 = 17 | 17 ÷ 30 х 100 = 57 |
| от 50 до <60 | 9 | 17 + 9 = 26 | 26 ÷ 30 х 100 = 87 |
| >= 60 | 4 | 26 + 4 = 30 | 30 ÷ 30 х 100 = 100 |
Кумулятивное распределение относительной частоты можно визуализировать с помощью гистограммы или линейной диаграммы, как на диаграмме 4. 3.1 ниже. Значение на горизонтальной оси является верхней границей интервала класса.
3.1 ниже. Значение на горизонтальной оси является верхней границей интервала класса.
| Верхняя граница интервала классов суточной численности скалолазов | Кумулятивная относительная частота (%) |
|---|---|
| 9 | 3 |
| 19 | 10 |
| 29 | 20 |
| 39 | 37 |
| 49 | 57 |
| 59 | 87 |
| 69 | 100 |
На графике 4. 3.1 видно, что в течение большей части дней (57%) в период количество скалолазов было меньше или равно 49.
3.1 видно, что в течение большей части дней (57%) в период количество скалолазов было меньше или равно 49.
Распределение частот можно визуализировать с помощью:
- круговой диаграммы (номинальная переменная),
- гистограмма (номинальная или порядковая переменная),
- линейная диаграмма (порядковая или дискретная переменная),
- или гистограмма (непрерывная переменная).
Эти типы диаграмм будут представлены в разделе 5 по визуализации данных. Но сначала мы рассмотрим другие методы обобщения данных с использованием показателей центральной тенденции и дисперсии.
- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Умножение и деление: Введение в деление
Урок 4: Введение в деление
/en/multiplicationdivision/video-multiplication/content/
Что такое деление?
Подразделение делит что-то поровну. Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Вы делите билетов между друзьями. Каждый друг получает равное количество билетов.
Видите, у каждого из них по 2 билета? Когда вы делите 10 билетов между пятью друзьями, вы создаете 5 равных групп по 2 билета.
Деление происходит в реальной жизни часто. Например, рассмотрим ситуацию ниже.
Представьте, что у нас есть 6 кексов…
Представьте, что у нас есть 6 кексов.
 .. и 2 пустых лотка.
.. и 2 пустых лотка.Мы положим на каждый поднос одинаковое количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы будем разделить кексы между двумя лотками.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.
На каждый поднос мы положим равное количество кексов.
 Другими словами, мы разделим кексов между двумя подносами.
Другими словами, мы разделим кексов между двумя подносами.Шесть кексов были разделены на 2 равные группы.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.
На каждом подносе по 3 кекса. Если вы начнете с шести кексов и разделите их на две равные группы, то в каждой группе будет по три кекса.
Написание выражений деления
В слайд-шоу вы видели, что мы разделили шесть кексов на две равные группы. Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления примерно так:
Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления примерно так:
6 / 2
Вы также можете написать выражение следующим образом:
6 ÷ 2
Вы можете прочитать любое выражение как шесть разделить на два . Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставили после первого числа — было 6 кексов, и мы разделили их на 2 группы.
Многие жизненные ситуации можно выразить с помощью деления. Например, представьте, что вы расставляете 15 банок на 3 полках. Вы можете разделить, чтобы убедиться, что вы поставили одинаковое количество банок на каждой полке. Другими словами, 15 банок, разделенных тремя полками, или 15/3.
Попробуйте это!
Попробуйте настроить эти ситуации как выражения деления. Пока не пытайтесь их решить.
У учительницы есть 16 карандашей, которые она распределяет поровну между 4 учениками.
У флориста есть 18 роз, и он делит их поровну между 3 вазами.
У вас есть 6 угощений, которыми вы поровну делитесь с 3 собаками.
Решение задач на деление
Вы можете использовать , считая , для решения простых задач на деление. Например, допустим, у нас есть 12 саженцев. Решаем посадить их в два ровных ряда. Сколько растений в каждом ряду? Мы могли бы написать этот вопрос так:
12 / 2
Помните, что это выражение означает 12 разделить на два , или 12 саженцев разделить на 2 ряда. Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.
В то время как подсчет работает для задач, которые начинаются с маленьких чисел, задача, которая начинается с большого числа , может занять много времени, чтобы решить ее с помощью подсчета. По этой причине большинство людей запомнить общих задачи на деление, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. С некоторой практикой вы сможете быстро запомнить ответы.
Если это звучит сложно, не волнуйтесь. С некоторой практикой вы сможете быстро запомнить ответы.
В разделе Введение в умножение вы познакомились с таблицей умножения на . На этом уроке вы использовали его для решения задач на умножение. Вы также можете использовать таблицу умножения для решения задач на деление.
Начнем с проблемы, с которой мы уже знакомы. Как бы мы решили задачу о ростке с таблицей умножения?
Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.
Помните, что каждое число в верхней части таблицы умножения находится в начале столбца .
Например, это столбец, который идет с 7.
Каждое число в левой части таблицы умножения является началом строки . Этот ряд идет с 9.
Давайте попробуем решить задачу о ростке: 12 / 2.
Сначала найдите число, на которое вы делите, справа от знака деления.
 В 12/2 мы делим на 2.
В 12/2 мы делим на 2.Найдите столбец 2.
Затем найдите число, которое вы делите, слева от знака деления. В 12/2 это 12.
Найдите 12 в колонке 2.
Найдите число в начале ряда, которое перекрывает 12. В данном случае это 6-й ряд.
Итак, ответ или частное для 12/2 равно 6.
Попробуем еще раз. На этот раз мы решим 15 / 5.
Сначала мы найдем 5-й столбец, так как мы делим на 5.
Затем мы найдем 15 в 5-м столбце, так как это число, которое мы делим.
Наконец, мы найдем число в начале ряда, которое перекрывает 15. Это 3. Итак, 15/5 = 3.
Попробуйте!
Решите эти задачи на деление. Если вам нужна помощь, вы можете использовать таблицу умножения.
42 ÷ 7 =
5 ÷ 1 =
33 ÷ 3 =
Остаток
На предыдущих страницах мы делили числа поровну. Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что происходит, когда число нельзя разделить поровну?
Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что происходит, когда число нельзя разделить поровну?
Например, рассмотрим ситуацию ниже.
Допустим, у нас есть 10 билетов…
Допустим, у нас есть 10 билетов… которые мы делим между 3 друзьями.
Попробуем решить задачу 10 / 3.
Посмотрим, сколько билетов мы сможем дать каждому из наших друзей…
Посмотрим, сколько билетов мы сможем дать каждому из наши друзья…
Посмотрим, сколько билетов мы можем подарить каждому из наших друзей… Один…
Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей… Один …
Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей… Один…
Посмотрим, сколько билетов мы можем подарить каждому из наших друзей… Один… Два…
Посмотрим, сколько билетов мы можем подарить каждому из наших друзей.
 .. Один. .. Два…
.. Один. .. Два…Посмотрим, сколько билетов мы можем подарить каждому из наших друзей… Один… Два…
Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей. друзья… Раз… Два… Три.
Что теперь? У нас 3 друга и остался только 1 билет.
Это означает, что 1 — это остаток или оставшаяся сумма.
Мы готовы написать наше частное.
У каждого друга по три билета, поэтому запишем 3.
Затем запишем остаток. Это 1. Видите, как мы написали это рядом со строчной буквой r ?
Итак, 10/3 = 3 r1. Мы можем прочитать это частное как три остатка один . 10 билетов, разделенных на 3 друзей, означает, что каждый друг получает 3 билета, а 1 билет остается.
Из слайд-шоу видно, что остаток (1) меньше, чем число, на которое мы делим (3). Так будет всегда, когда у проблемы есть остаток. Например, взгляните на каждую из этих задач ниже:
Например, взгляните на каждую из этих задач ниже:
21/5 = 4 r1
Остаток от 1 меньше 5.
76/6 = 12 r4
Остаток от 4 меньше 6.
Если остаток больше, это означает, что остаток слишком велик. Вам нужно будет попробовать разделить еще раз. Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.
Практика!
Практика разделения с этими проблемами. Если хотите, можете воспользоваться таблицей умножения на . Имеется 3 набора задач по 5 задач в каждом.
Установите 1
72 ÷ 9 =
64 ÷ 8 =
70 ÷ 10 =
55 ÷ 11 =
21 ÷ 3 =
Установка 2
35 ÷ 5 =
322 322. 322 322. 322 322. 322 322 322 322 322 322 322 322 322 322 322 322 322 322. =
72 ÷ 6 =
12 ÷ 2 =
28 ÷ 7 =
Набор 3
6 ÷ 1 =
81 ÷ 9 =
24 ÷ 3 =
49 ÷ 7 =
144 ÷ 12 =
ПродолжатьПредыдущий: Видео: Умножение
Далее:Длинная дивизия
/en/multiplicationdivision/long-division/content/
Как рассчитать проценты в Excel? (с использованием формул)
Процент рассчитывается как доля на сотню.
Другими словами, числитель делится на знаменатель, а результат умножается на 100. Процентная формула в Excel: = Числитель/Знаменатель (используется без умножения на 100). Чтобы преобразовать выходные данные в проценты, нажмите «Ctrl + Shift +%» или щелкните «%» в группе «число» на вкладке «Главная».
Рассмотрим простой пример.
В 15-дневном отпуске г-н А провел 10 дней в своем родном городе и 5 дней в США. Какой процент дней он провел в США?
Расчеты даны следующим образом:
- Формула процента = Часть дней / Общее количество дней * 100
- Процент дней, проведенных в США = 5/15 * 100 = 33,33%
- Процент дней, проведенных в родном городе = 10 /15*100=66,66%
Следовательно, г-н А провел примерно 33% своего отпуска в США.
Содержание
- Как рассчитать процент с помощью формул Excel?
- Пример №1
- Пример №2
- Пример №3
- Часто задаваемые вопросы
- Рекомендуемые статьи
с помощью следующих примеров, чтобы понять концепцию процента в Excel.
Пример №1
В следующей таблице показаны предметные оценки 6 учащихся одной школы. Поскольку результаты относятся к ежегодным экзаменам, максимальное количество баллов по каждому предмету равно 100.
Нам нужно рассчитать процентное соотношение оценок для всех студентов.
Шаги для расчета процентов в Excel перечислены ниже:
- Подсчитайте общие оценки, полученные учащимися. Для этого добавляются оценки по каждому предмету.
- Перетащите формулу ячейки h3, чтобы получить общие оценки, полученные всеми учащимися. Результат показан на следующем изображении.
- Разделите общее количество баллов на 600. Значения столбца «Всего баллов» становятся числителем. Так как предметов 6, максимальное количество баллов 600 (100*6=600). Это становится знаменателем.
- Примените следующую формулу.
Процент=Набранные баллы/Общее количество баллов*100.
Для процентных значений (показанных на следующем изображении) измените форматирование ячейки. Выберите столбец I и нажмите «Ctrl+Shift+%». Либо выберите «%» в группе «число» на вкладке «Главная».
Пример №2
В следующей таблице представлены студенты, проходящие стажировку в организации. Их задача — продавать товары на основе заранее определенных целей.
Мы хотим определить уровень эффективности (в процентах) каждого ученика.
Шаги для расчета уровня эффективности перечислены ниже:
Шаг 1: Примените формулу «продажи/цель».
Шаг 2: Отформатируйте столбец D, чтобы получить уровни эффективности в процентах. Для двух последних учеников (Gulp и Ganapathi) формула возвращает «#DIV/0!» errorExcel ErrorОшибки в Excel распространены и часто возникают во время применения формул. Список из девяти наиболее распространенных ошибок Excel: #DIV/0, #N/A, #NAME?, #NULL!, #NUM!, #REF!, #VALUE!, #####, Circular Reference. read. более.
read. более.
Примечание: Если числитель равен нулю, деление числителя на знаменатель возвращает «#ДЕЛ/0!#ДЕЛ/0!#ДЕЛ/0! это ошибка деления в Excel, которая возникает каждый раз, когда число делится на ноль. Проще говоря, мы получаем эту ошибку, когда делим любое число на пустую или нулевую ячейку.
Шаг 3: Чтобы устранить ошибку, измените существующую формулу на «=ЕСЛИОШИБКА(C2/B2,0)». Это означает, что ЕСЛИОШИБКА ЕСЛИОШИБКА Функция ЕСЛИОШИБКА в Excel проверяет формулу (или ячейку) на наличие ошибок и возвращает указанное значение вместо ошибки. Подробнееотображает ноль, если деление C2 на B2 возвращает ошибку.
Другими словами, «#DIV/0!» ошибка заменяется нулем с помощью модифицированной формулы.
Примечание: Функция ЕСЛИОШИБКАФункция ЕСЛИОШИБКАФункция ЕСЛИОШИБКА в Excel используется для определения того, что делать при возникновении ошибки перед выполнением какой-либо функции. Подробнее помогает избавиться от процентных ошибок.
Шаг 4: Результат использования функции ЕСЛИОШИБКА показан на следующем рисунке. Уровни эффективности студентов Gulp и Ganapathi равны нулю. Это связано с пробелом (нулем) в столбце B и/или столбце C.
Пример №3
Объем продаж организации за январь и февраль за 2018 год представлен в следующей таблице.
Мы хотим рассчитать рост или снижение (в процентах) месячных продаж.
Шаги для расчета увеличения (роста) или уменьшения (падения) в процентах перечислены ниже:
Шаг 1: Примените формулу «=(C2-B2)/B2».
Продажи в феврале (57500) больше, чем продажи в январе (53250). Разница (рост) между двумя продажами делится на продажи в начальный месяц (январь).
Шаг 2: Отформатируйте столбец D, чтобы получить процент роста.
Таким образом, февральские продажи выросли на 7,98% по сравнению с январскими.
Примечание: При расчете процента роста или снижения, если числитель или знаменатель меньше нуля, на выходе будет отрицательное значение.
1. Что такое процентная формула Excel?
Основная формула расчета процентов: «(часть/всего)*100» . Эта формула используется в Excel без последней части (*100). Это связано с тем, что при выборе процентного формата результирующее число автоматически изменяется на проценты.
Кроме того, удаляются десятичные точки, и результат отображается в виде округленного процента. Например, 26/45 равно 0,5777. Применяя процентный формат, это десятичное число становится равным 58%.
Чтобы преобразовать вывод в проценты, нажмите «Ctrl+Shift+%» или выберите «%» в группе «числа» на вкладке «Главная».
2. Что такое формула Excel для расчета процентного изменения?
Формула для расчета изменения в процентах выглядит следующим образом:
«(Новое значение-Начальное значение)/Начальное значение»
Эта формула помогает вычислить процентное увеличение или уменьшение между двумя значениями. Положительный процент означает увеличение, а отрицательный процент показывает уменьшение.
Положительный процент означает увеличение, а отрицательный процент показывает уменьшение.
Примечание: Чтобы получить окончательный ответ (процентное изменение), к выводу формулы применяется процентный формат.
3. Что такое формула Excel для расчета процента от суммы?
Формула для расчета процента от суммы: «(часть/всего)». Например, в столбце A перечислены ежемесячные расходы из ячейки A2 в ячейку A11. Ячейка A2 содержит 2500 долларов в качестве уплаченной арендной платы. Ячейка A12 содержит общие расходы $98700.
Формула «=A2/$A12» возвращает 3% после применения процентного формата. Это означает, что арендная плата составляет 3% от общей суммы оплаченных расходов.
Так как A2 должен измениться при перетаскивании формулы в остальные ячейки, она вводится как относительная ссылка. С другой стороны, сумма должна оставаться фиксированной для всех ячеек, поэтому A12 вводится как абсолютная ссылка.
- Процент – это доля на сотню.
- Для вычисления процентов числитель делится на знаменатель и результат умножается на 100.
- Для получения процентов выходной столбец форматируется нажатием «Ctrl+Shift+%» или выбором «%» на вкладке «Главная». .
- Деление числителя на знаменатель возвращает «#ДЕЛ/0!» ошибка, если первое равно нулю.
- Процентные ошибки можно удалить с помощью функции ЕСЛИОШИБКА.
- Процент увеличения или уменьшения рассчитывается путем деления разницы между двумя числами на начальное число.
Рекомендуемые статьи
Это руководство по формуле для вычисления процентов в Excel. Здесь мы обсуждаем вычисление процентов Excel с использованием формулы ЕСЛИОШИБКА вместе с примерами Excel и загружаемыми шаблонами Excel. Вы также можете посмотреть на эти полезные функции в Excel –
- Формула изменения в процентах
- Формула прибыли в процентах
- Вычисление увеличения в процентах в Excel
- Разница в процентах в Excel
css — Как заставить столбец Bootstrap занимать несколько строк?
Спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 181k раз
Я пытаюсь понять, как сделать следующую сетку с помощью Bootstrap.
Я не знаю, как создать поле (номер 1), которое занимает две строки. Блоки генерируются программно в том порядке, в котором они расположены. Вставка 1 — приветственное сообщение.
Любые идеи о лучшем способе пойти с этим?
- css
- твиттер-бутстрап
6
Для Bootstrap 3:
<дел>
<дел>
<дел>1
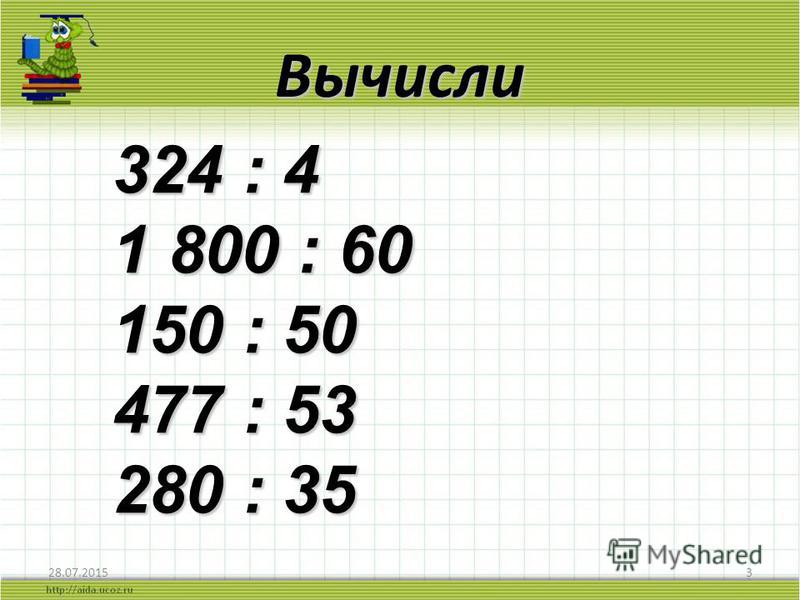 Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).