Примеры для абакуса для начинающих: Базовые упражнения в Ментальной Арифметики

Содержание

Базовые упражнения в Ментальной Арифметики

Главная » Ментальная Арифметика

15.04.202109.03.2018

Это самый большой раздел нашего обучения. Мы изучим все правила счёта и к концу этого раздела сможем совершать операции сложения и вычитания с любыми числами!
Итак, в первую очередь познакомимся с соробаном / абакусом— он станет нашим другом надолго!
Как он выглядит вы можете познакомится в статье >>>Построение урока Ментальной Арифметики

«Простым» мы называем счёт на соробане / абакусе без правил — формул. Такие примеры легко решит любой, поняв принцип. А принцип очень прост. Желая прибавить число, нужное количество косточек мы придвигаем к планке ответа. Нижние косточки — единицы -поднимаем, а верхнюю — пятёрку- опускаем. Если нам нужно вычесть число, то косточки от планки ответа нужно убрать к раме. Таким образом, ответом в примере будет количество косточек, находящихся у планки ответа. Не забываем, что верхняя косточка равна пяти.

Рассмотрим пример:

2+1+5-3

У планки осталась одна верхняя косточка, равная пяти, значит, ответ в примере-5. Рассмотрим ещё пару примеров:
83-31

11+25

Простое сложение и вычитание можно закрепить, решив примеры в рабочей тетради на страницах 7-18. А мы переходим к формулам.

Сложение с помощью пятёрки

Простым сложением и вычитанием, конечно же, мы не обойдемся. И первые формулы, которые мы начнем изучать — это помощь пятёрки — верхней косточки. Самое важное -хорошо объяснить детям самое первое правило. Так как все остальные имеют общую основу.
Но, перед тем, как мы начнём изучать эти правила, нам необходимо объяснить детям и хорошо закрепить состав числа пять. Сделать это можно разнообразными способами. Включаем пары чисел в составе пятёрки в занятия письмом. Используем пальцы на руке.

Загибаем один палец — осталось четыре.

Загибаем два пальчика — осталось три. Можно использовать палочки Кюизенера. Можно изобразить пятёрку, как домик, в котором живут друзья — 1 и 4, 2 и 3. Мы должны убедиться, что все дети хорошо запомнили эти пары чисел, перед тем, как начнём объяснять первое правило.

Итак, первая формула:
+1=+5-4

Для того, чтобы объяснить это правило, мы начинаем прибавлять единицу к каждому числу с нуля. 0+1, 1+1, 2+1, 3+1. Пока у нас всё получается. Теперь пробуем прибавить единицу к четырём. Тут возникает вопрос: как это сделать? Снизу косточек больше нет. Где мы можем взять эту единицу? Мы можем попросить помощи у пятёрки. У неё единица есть. Но, прибавить единицу мы сможем только с другом — четвёркой. Ведь в пятёрке они живут вместе. И тогда нам придётся отнять друга единицы — четыре. Так как нам нужно прибавить всего единицу. Таким образом получается, что 4+1 = +5-4

На соробане / абакусе это действие выполняется одним движением — указательный палец опускает пятёрку, а большой в это время опускает нижние четыре косточки.

4+1 =+5-4

Конечно, это объяснение для детей, оно образно демонстрирует принцип сложения с помощью пятёрки. Получив от нее нужное число, мы должны отнять лишние единицы.
Теперь пришло время ввести понятие «Базовые упражнения».

Базовые упражнения — это все примеры, содержащие данную формулу

То есть, это именно те упражнения, с помощью которых мы будем заучивать движения пальцами и доводить их до автоматизма. Очень важно выполнять действие каждый раз одинаково, тогда, с помощью моторно-мышечной памяти, наши руки через некоторое время сами будут делать нужные движения.

Базовые упражнения к каждой формуле мы будем выполнять на каждом уроке в качестве разминки. Эти упражнения — как гаммы для музыканта. Они выполняют ту же функцию и так же необходимы. И выполнять мы их будем схожим образом — прорешивая каждое упражнение на всех спицах соробана / абакуса, обязательно проговаривая каждое действие, сначала справа налево правой рукой, затем слева направо левой рукой.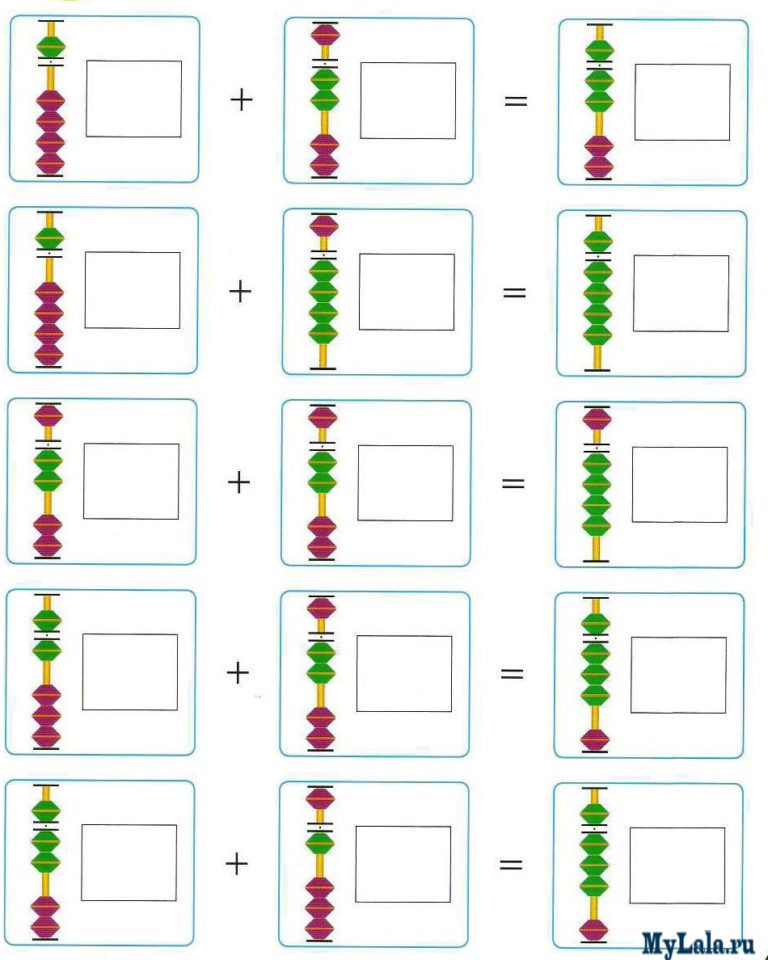

Итак, формулу+1=+5-4 содержит только одно базовое упражнение: 4+1

Формула и Базовые упражнения

+1=+5-4

4+1

До того, как мы начинаем изучение фэрмул, базовыми упражнениями тоже нужно заниматься. В этом случае мы тренируем сначала набор всех чисел на всех спицах соробана, затем решаем простые примеры без формул на всех спицах. Нам необходимо приучить пальцы к мелкомоторным движениям, которые не всем даются легко, особенно левой рукой. Для левой руки существует два вида постановки: такая же, как у правой и вторая — работают только указательный (на нижних) и средний (на верхних) пальцы. Каждый может решить, какудобнее для него и сделать выбор всамом начале занятий. Но менять постановку в дальнейшем не стоит. Очень важно заучивать движения в упражнениях одними и теми же пальцами.

Закрепляем первое правило решением упражнений из рабочей тетради.
Следующая формула:
+2=+5-3
Объяснение то же, что и в первом случае. Только прибавить два мы не сможем уже к трём и четырём. Поэтому базовых упражнений в этом правиле два.

Формула Базовые упражнения
+2=+5-3 3+2 4+2

Выполняется на соробане / абакусе, аналогично первой формуле, одним движением: указательный палец опускает пятёрку, одновременно большой палец опускает три косточки.

Закрепляем правило решением упражнений из рабочей тетради. Следующая формула:
+3=+5-2

Формула Базовые упражнения

+3=+5-2 2+3 3+3 4+3
На соробане/ абакусе выполняется одним движением: указательный палец опускает пятёрку, одновременно большой палец опускает две косточки.

Закрепляем правило решением упражнений из рабочей тетради.

И последняя формула в данной теме:
+4=+5-1

Формула Базовые упражнения
+4=+5-1 1+4
2+4 3+4 4+4
На соробане/ абакусе выполняется одним движением: указательный палец опускает пятёрку, одновременно большой палец опускает одну косточку.

1+4=+5-1

4+4=+5-1

Закрепляем правило решением упражнений из рабочей тетради.
Обратите внимание детей на то, что друг числа всегда идёт в туже сторону, что и пятёрка.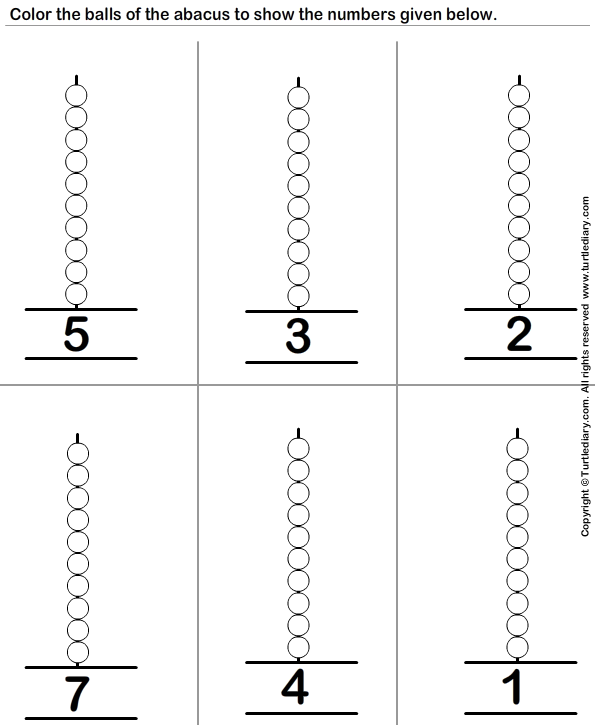
Мы закончили тему «Сложение с помощью пятёрки». Не забывайте каждый урок выполнять базовые упражнения. Это имеет большое значение в формировании моторного навыка.

Как считать на абакусе | Правила счета

24.12.2020

Система ментального счета или ментальная арифметика позволяет научить детей очень быстро выполнять в уме все арифметические действия. Для обучения используется специальная счетная доска – абакус. Сначала дети учатся выполнять арифметические действия с помощью этого приспособления, а затем начинают производить все действия в уме.

Содержание:

Как считать на абакусе
Правила счета
Сложение и вычитание на абакусе
Умножение и деление

Изобрели абакус еще в Месопотамии примерно в третьем тысячелетии до нашей эры. Подобные счетные приборы применялись практически во всех странах – Древней Греции, Риме, Египте, Китае, Индии, Японии.

В наши дни все расчеты ведутся с помощью вычислительной техники. А абакус стал главным инструментом методики развития интеллектуальных способностей – ментальной арифметики. Начинать занятия можно с раннего возраста, когда ребенок научится считать до десяти.

Как считать на абакусе

Счеты представляют собой прямоугольную рамку с вертикальными спицами. Рамка поделена поперечной перекладиной на две неравные части. На спицах нанизаны костяшки – снизу по четыре штуки, а сверху по одной. Общее количество спиц может отличаться в зависимости от модели счетной доски.

Для счета на абакусе надо запомнить несколько основных правил:

числа на счетной доске набирают слева направо;
нижние костяшки обозначают числа от 1 до 4, верхняя костяшка – соответствует числу 5;
опущенная верхняя косточка обозначает, что число больше пяти;
каждая спица соответствует одному разряду – единицы, десятки, сотни, тысячи и так далее.

Чтобы изобразить число на счетах, необходимо подвести к внутренней перекладине соответствующее количество костяшек.

К примеру, для числа 6 нужно подвинуть на крайней левой спице вниз верхнюю косточку (5) и поднять одну нижнюю (1). Аналогично отображается, например, число 66. Только для этого надо задействовать две спицы – одну для единиц, вторую для десятков.

См. также Японские счеты соробан

Правила счета

Дети очень быстро учатся считать на абакусе, достаточно объяснить им принцип и показать несколько примеров. Для счета единиц используется одна рука – правая, если нужно считать десятки и единицы, то используются обе руки.

Руку нужно сжать в кулак, выпрямив большой и указательный пальцы. Нижние косточки поднимают большим пальцем, а опускают – указательным. С верхней костяшкой работают только указательным пальцем. Если надо добавить косточки сверху и снизу, то это делают одновременно двумя пальцами. Аналогично осуществляют и удаление костяшек.

Сложение и вычитание на абакусе

Складывать и вычитать с помощью счетной доски очень просто. Сначала на абакусе набирают первое число, к нему на соответствующих спицах добавляют второе число. Складывать начинают с меньшего из двух чисел. Если на спице получается больше 9 косточек, то добавляют одну костяшку на соседней.

При вычитании из первого числа убирают нужное количество косточек на каждой спице. В этом случае первым на абакусе устанавливают большее число.

Сложение и вычитание двух- и трехзначных чисел задействует обе руки. В результате одновременно работают оба полушария мозга и стимулируется мелкая моторика. Через некоторое время сам счетный прибор становится уже ненужным, ребенок начинает работать с косточками на воображаемой доске.

Умножение и деление

Для умножения на абакусе ребенок должен выучить таблицу умножения от 1 до 10. Умножение идет по принципу от большего к меньшему. Для двузначных чисел это означает, что сначала десятки умножают на единицы, потом перемножают между собой единицы.

Рассмотрим простой пример – 11х6. Он считается в два действия:

10х6 = 60
1х6 = 6

Сначала набираем на абакусе число 60, потом к нему добавляем 6. В итоге получаем нужный ответ 66.

Деление на счетной доске производится по аналогичному принципу, только числа не складываются, а вычитаются.

См. также Что такое абак

Лучший способ использовать счеты для основных математических операций

25 ноября 2020 г.

Время чтения: 6 минут

Содержание

1.	Введение
2.	Как считать на счетах?
3.	Как использовать счеты для сложения?
4.	Как использовать счеты для вычитания?
5.	Как использовать счеты для умножения?
6.	Заключение
7.	Часто задаваемые вопросы (FAQ)
7.	Внешние ссылки

Введение

Вы когда-нибудь задумывались, как люди решали математические задачи до изобретения калькулятора или компьютера?

Если вы думаете, что они всегда носили с собой ручку и бумагу, то вы ошибаетесь.

На протяжении веков жители Азии использовали китайский калькулятор «суанпан», также известный как счеты.

Это простое счетное устройство, состоящее из прямоугольной деревянной рамы, разделенной горизонтальной перекладиной на верхнюю и нижнюю секции.

Имеется ряд вертикальных проволок, к которым прикреплены 7 бусин (две в верхнем ряду и пять в нижнем ряду), которые проходят сверху вниз по раме.

Две бусины в верхнем ряду имеют значение пять, а пять бусин в нижнем ряду – значение в единицу каждая.

Проволочки представляют степени числа 10. Традиционные счеты состоят из 13 проволочек, чтобы представлять очень большие числа. Китайские счеты предназначены для шестнадцатеричных вычислений.

Загружаемый PDF-файл

Если вы когда-нибудь захотите прочитать его столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.

📥

Лучший способ использовать счеты для основных математических операций

Скачать

Как считать на счетах?

Каждая бусинка в нижнем ряду, как указано, имеет значение 1.

После подсчета 5 нижних бусинок результат «переносится» в верхний ряд.

После подсчета обеих верхних бусин в верхнем ряду результат (например, 10) переносится в крайний левый соседний столбец.

Крайний правый столбец представляет столбец единиц измерения; следующий соседний столбец слева — это столбец десятков и так далее.

Как использовать счеты для сложения?

После того, как вы научились считать удары 1 на счетах, это первая операция, которую мы можем освоить дополнительно. Существуют различные стратегии, которые можно применять при обучении сложению.

Стратегия 10

Например, если нам нужно добавить 9+6, мы введем 6 и 9 в первые два столбца. Затем перешли от 6 к 9, так что 9 стало 10, а 6 стало 5.

Итак, теперь мы можем легко оперировать 10+5=15. Как только ваш ребенок освоит эту стратегию на счетах, вы можете заставить его попробовать делать это мысленно.

Стратегия двух пятерок

Например, если нам нужно добавить 6+7, мы введем 6 и 7 в первые два провода. Две пятерки составят 10, и мы останемся с тремя бусинками. Теперь выполнить 10+3=13 легко.

Эта стратегия работает в задачах, где два добавляемых числа больше пяти.

Допустим, нам нужно сложить 65+89. Студенты должны будут представить 89 на счетах.

Первый провод справа будет иметь 9, а второй провод будет иметь 8. Начните с первого провода и добавьте 5 к 9.

Получится 14. Сохраните цифру 4 и переходите от 1 к 8, тем самым получается 9.

Теперь выполните 9+6, что даст 15. Таким образом, фактический результат будет 154.

Для получения дополнительной информации ознакомьтесь с Abacus Addition.

Как пользоваться счетами для вычитания?

Следующая операция, которую вы изучите, это как использовать счеты в пошаговом методе для выполнения вычитания?

Вычитание — это процесс, обратный сложению. Все, что вам нужно сделать, это позаимствовать цифры из предыдущего столбца, а не переносить их. Например, если вы хотите вычесть 867 из 932.

901:30 После ввода 932 на счетах начните вычитать столбец за столбцом слева. Если вы вычтете 8 из 9, вы получите 1, поэтому вы оставите одну бисеринку на разряде сотен.
Теперь перейдем к разряду десятков. Вы не можете вычесть 6 из 3, поэтому вам придется занять 1 в разряде сотен, оставив 0. Теперь вам нужно вычесть 6 из 13, чтобы получить 7.
Теперь переходим к месту юнита. Повторите процесс. Поскольку вы не можете вычесть 7 из 2, вы должны занять 1 из разряда десятков, что превратит 7 в разряде десятков в 6. Теперь вычтите 7 из 12, чтобы получить 5.
Таким образом, наш окончательный ответ будет 932 — 867 = 65.

Регулярная практика облегчит работу. Счеты — это тренировка ума. Поэтому требует терпения и регулярных тренировок.

Как использовать счеты для умножения?

Теперь давайте перейдем к самой важной базовой математической операции — умножению. Как умножать на счетах?

Чтобы умножать небольшие числа, например, 6×4, мы можем попросить учащихся проследить за процессом сложения. Все, что им нужно сделать, это ввести 6 в четырех разных проводах.

Затем следуйте стратегии пяти, как указано выше. Итак, теперь они должны выполнить 5+5+5+5 = 20 и 1+1+1+1 = 4. Наконец, им нужно будет добавить 20+4 = 24.

Хорошо, но вышеупомянутая стратегия может использовать только в случае небольших чисел. Могут быть ситуации, когда учащийся сталкивается с большими числами. В этих случаях мы будем следовать другому подходу.

Например, если вы умножаете 34×12.

Шаг 1 — Назначьте по одной букве в каждый столбец. Таким образом, это станет «3», «4», «X», «1», «2» и «=».

Это заставляет нас чувствовать первые шесть проводов. Остальные столбцы оставьте справа, как для ответа.

Помните, что «X» и «=» будут представлены пустыми столбцами.

Шаг 2 — Умножьте 3 на 1, а затем 3 на 2. Затем вы умножите 4 на 1, а затем 4 на 2.

Понять схему. Это та часть, которую мы будем применять для всех видов чисел.

Шаг 3 — Запишите результаты продуктов в правильном порядке. Начните запись первого произведения т.е. 3х1=3 в седьмой провод.

Далее, 3×2 = 6, запишите его после столбца, в котором вы записали 3 т.е. восьмой провод.

Шаг 4 — Когда вы умножаете 4×1, прибавьте результат, т.е. 4, к предыдущему умножению, которое мы сделали, т.е. 3×2 = 6. Теперь 4+6 становится 10.

Перенесите единицу на седьмой провод, который был 3, и теперь он становится 4, а восьмой провод становится 0.

Шаг 5 — Выполните последнее умножение, которое равно 4×2 = 8. Записано в девятом проводе. Итак, наш ответ: 408.

. Для получения дополнительной информации ознакомьтесь с умножением счетов.

Заключение

Вышеупомянутые были одними из самых основных операций, которые можно выполнять с помощью счетов.

Счеты — это инструмент, который также можно использовать для выполнения высокоуровневых вычислений и операций.

Существуют определенные видео и уроки счетов, которые доступны на различных платформах, как онлайн, так и офлайн.

С такими значительными преимуществами использования счетов все больше и больше школ проводят это обучение и образование, особенно в младших классах.

Поэтому мы рекомендуем вам начать понимать основные принципы работы на счетах.

Если вам понравился этот пост, не стесняйтесь поделиться им со своими друзьями, которые также могут извлечь пользу из изучения счетов.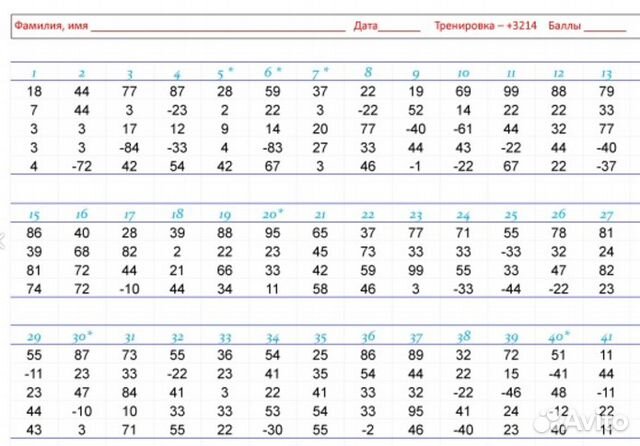

О Cuemath

Cuemath, удобная для учащихся математическая платформа, проводит регулярные интерактивные онлайн-занятия для ученых и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей. развить несколько навыков.

Ознакомьтесь со структурой оплаты для всех классов и запишитесь на пробный урок уже сегодня!

Часто задаваемые вопросы (FAQ)

Что такое счеты?

Счеты — это ручное вспомогательное средство для счета, состоящее из бусин, которые можно перемещать вверх и вниз на ряде палочек или веревок внутри обычно деревянной рамы. Сами по себе счеты не считают; это просто средство, помогающее человеку считать, запоминая то, что было подсчитано.

Где впервые использовались счеты?

Счеты (множественное число abaci или abacus), также называемые счетной рамкой, представляют собой вычислительный инструмент, использовавшийся на древнем Ближнем Востоке, в Европе, Китае и России за столетия до принятия письменной арабской системы счисления.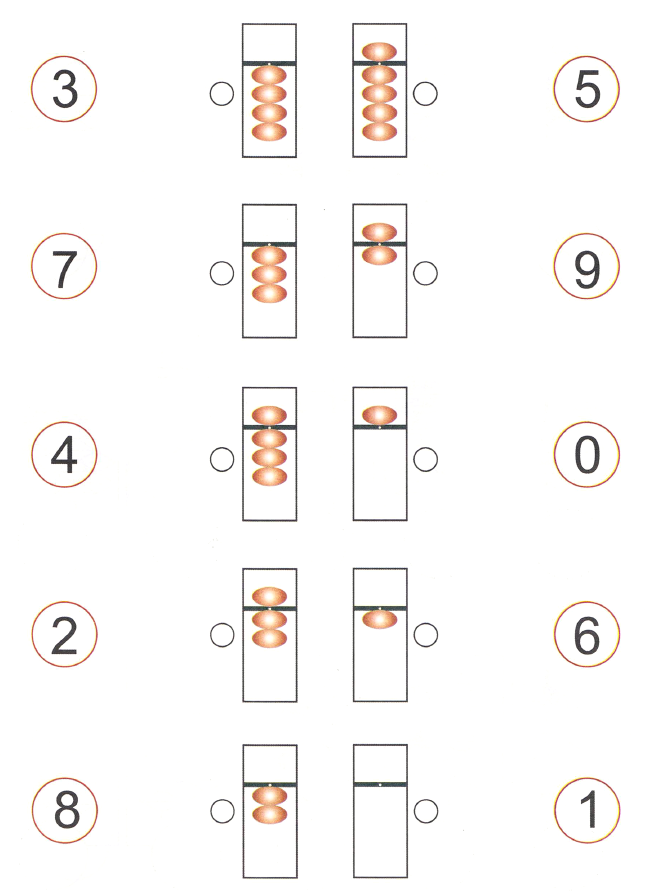 Точное происхождение абака до сих пор неизвестно.

Каковы преимущества обучения использованию счетов?

Математические навыки закладывают прочную основу для поступления в высшие классы.
Обучение счету улучшает навыки

Визуализация (фотографическая память)
Концентрация
Навыки слушания
Память, Скорость
Точность
Творчество
Уверенность в себе
Уверенность в себе, приводящая к развитию всего мозга

Как пользоваться счетами?

Это простое устройство для счета, очень полезное для слабовидящих. Если вы

знаете основы счета на счетах, вы можете легко выполнять на нем различные операции.

Ниже приведены основные шаги, которые необходимо выполнить:

Присвойте каждому столбцу разрядное значение.
Начинайте считать с бусинок нижнего ряда.
Завершить обмен 4/5.
Повторите шаблон для более высоких чисел.

Как научиться счету?

Мы можем легко научиться счету. Начните с изучения базовой структуры и расположения бусин абака. Затем вы можете перейти к изучению основных операций Abacus.

Что такое счеты и как использовать счеты в математике

Дом
>
Блог
>
Как использовать счеты?

Джессика Камински

9 минут чтения

26 апреля 2022 г.

Вы когда-нибудь использовали счеты для быстрого счета? Инструмент оказался не только полезным, но также может быть развлекательным и образовательным. В этой части вы узнаете о математике на счетах и о том, как использовать счеты, в частности, как выполнять операции сложения, вычитания, умножения, деления и расчета процентов.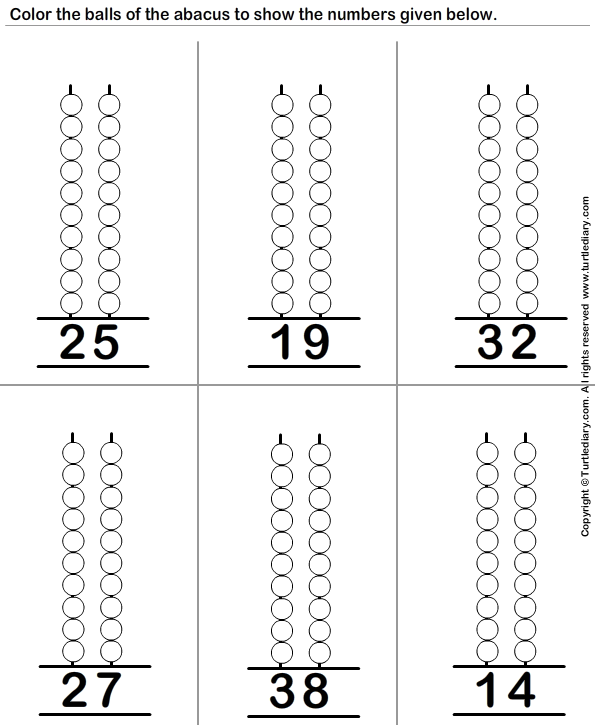 Мы шаг за шагом расскажем вам, как использовать счеты для всех расчетов.

Что такое счеты?

Счеты – счетное устройство, состоящее из бусин, нанизанных на проволоку и удерживаемых в рамке. Счеты обычно состоят из прямоугольной деревянной стойки с вертикальными стержнями. Бусины нанизаны на каждый стержень и могут свободно скользить вверх и вниз.

Счеты также иногда называют счетной рамкой.

Каждая проволока представляет разрядное значение, при этом ближайшая к пользователю бусина представляет единицы, следующая бусина представляет пятерки и т. д. Пользователи могут складывать, вычитать, умножать и делить числа, перемещая бусины вверх или вниз.

Количество бусин на стержне представляет собой разряд этой цифры. Например, крайний левый стержень может иметь три бусинки, а следующий справа от него стержень — две бусины и так далее. Крайняя правая цифра представляет единицы, двигаясь влево к сотням, тысячам и далее.

Сколько существует различных видов счетов? Это зависит от происхождения; например, существует два основных типа абаков: китайские и японские. Китайские счеты представляют собой деревянную или металлическую рамку с бусами, расположенными в вертикальных столбцах, в то время как японские счеты (соробан) имеют металлический каркас с бусами, расположенными по горизонтальной линии.

Интересно узнать, кто изобрел счеты. Точное происхождение математических счетов до сих пор неизвестно. Сегодня абаки представляют собой бамбуковые рамки с бусинами, скользящими по проволоке, но изначально это были бобы или камни, перемещаемые по канавкам в песке или на деревянных, каменных или металлических табличках.

Самая ранняя форма счетных счетов, вероятно, представляла собой доску с пятью линиями и четырьмя промежуточными промежутками, используемыми в качестве счетчиков или счетных меток. Счеты можно использовать для подсчета животных, отмечая каждый раз, когда животное проходит через ворота.

1:1 Уроки математики

Хотите воспитать гения?
Начните изучать математику с Brighterly Давайте начнем изучать математику!

Как использовать счеты для сложения?

Использование счетов может быть забавным.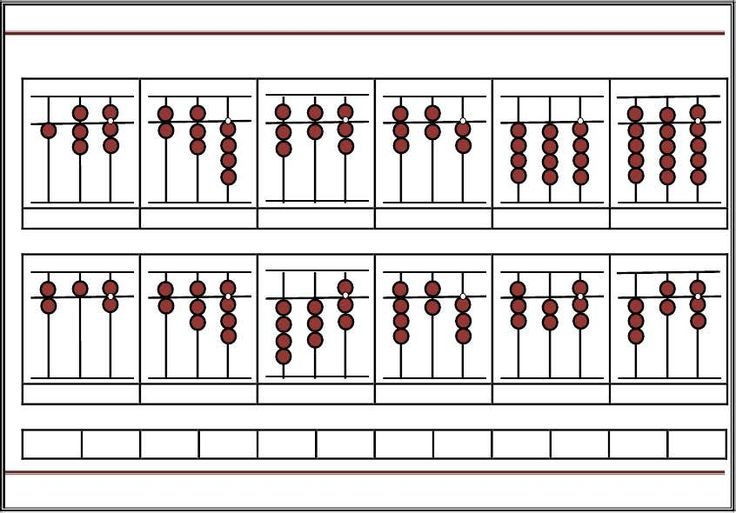 Это может помочь добавить числа, разбив задачу на столбцы, начиная с самой правой цифры и работая слева. Как работает счет? Принцип счета на счетах остается прежним: правая колонка представляет единицы, а каждая колонка слева представляет числа, кратные десяти.

Чтобы сложить два числа на счетах, вам нужно знать, сколько цифр в самом расширенном числе. Он скажет вам, сколько колонок вам понадобится на ваших счетах.

Столбцы представляют степени 10: единицы, десятки, сотни и т. д. Вот как можно читать на счетах.

Давайте рассмотрим простой пример, где мы должны добавить 7 и 6. Сначала мы можем разместить бусины для 7 в первом ряду. Итак, мы поместим бусину во вторую колонку справа, что соответствует 1, а пять бусинок поместим в третью колонку, что эквивалентно 5.

Точно так же поместим бусину во второй столбец справа, что соответствует 1, и одну бусину в третий столбец, что соответствует 5. Теперь мы можем сложить их, перемещая все бусины из третьего столбца на четвертый, так как значение пятого столбца равно 10.

После сложения получаем по одной бусине в каждом из второго, третьего, четвертого и шестого столбцов справа, что дает нам окончательный ответ – 13

Как пользоваться счетами для вычитания?

Как вы используете счеты для вычитания? Вычитать числа на счетах очень просто, как и складывать. Сначала вы должны работать с верхним рядом, а затем переходить к нижнему. Вы должны правильно настроить счеты, чтобы получить правильный ответ. Шаги следующие:

Если вы вычитаете число из пяти или менее цифр, поместите символ вычитания слева от счетов. Если вы вычитаете число из 6 или более цифр, поместите символ вычитания справа от счетов.
Введите меньшее число в нижний ряд счетов, а затем введите большее число в верхний ряд счетов, перемещая бусины от центральной полосы вниз к себе.
Чтобы вычесть два числа одинаковой длины, переместите все бусины верхнего ряда так, чтобы перед каждой цифрой верхнего ряда осталась только одна бусинка. Перед крайней левой цифрой должно быть пять бусин. В этом случае 0 должен отображаться как «00000» (пять нулей).
Далее, это приведет к тому, что некоторые из ваших бусин верхнего ряда перейдут в отрицательные числа.

1:1 Уроки математики

Хотите воспитать гения?
Начните изучать математику с Brighterly Давайте начнем изучать математику!

Как использовать счеты для умножения?

Вы сможете продемонстрировать свои навыки и произвести впечатление на своих друзей, если узнаете шаги, которые необходимо выполнить при умножении на счетах:

Создайте число, равное или превышающее число, которое вы хотите умножить, но меньше 100.
Выберите кратное число, часто меньшее или равное первому числу.
Используя кратное десяти, умножьте первое число с помощью умножения на счетах и запишите результат на листе бумаги. Это будет ваша общая сумма.
От числа, кратного десяти, отнимите единицу и прибавьте 1 к первому числу. Новый кратный должен быть на единицу меньше, чем последний кратный.
Умножьте это новое число, используя умножение на счетах, и добавьте его к промежуточной сумме из шага 3.

Возьмем для примера 664 x 10:

Ø Чтобы умножить 664 x 10, сначала положите на счеты 664

Ø Затем добавьте еще один ряд (10-й разряд) поверх цифры 664 и переместите 3-ю бисеринку. справа налево в этот ряд

Ø Затем переместите все остальные бусины 1-го ряда на одну позицию влево

Ø В итоге получится 6640.

Так работают счеты.

Использование абака для счета

Счеты, также называемые счетной рамкой, представляют собой вычислительный инструмент, который использовался в Европе, Китае и России за столетия до принятия письменной индийско-арабской системы счисления. Когда были изобретены счеты? Точная дата происхождения абака до сих пор остается загадкой.

Существует много типов счетов. Некоторые бусины разделены на десятки и единицы и называются десятичными счетами. У других есть бусины, разделенные только на тысячи и сотни, называемые абаками цифрового типа; один тип имеет бусины, расположенные только рядами из десятков, и называется двоично-десятичным счетом.

В своей простейшей форме счеты представляют собой инструмент для выполнения арифметических действий. Он состоит из прямоугольной рамы, установленной горизонтально на основании с стержнями, натянутыми поперек рамы. На каждый стержень нанизано десять бусин, по пять с двух сторон разделительной планки в центре. Шарики перемещаются из одного положения в другое для выполнения вычислений.

Для чего нужны счеты? Древние счеты были первым помощником в математических вычислениях. Его ценность в том, что он помогает памяти человека, выполняющего вычисления. Современные счеты, приобретенные в надежном месте, недороги и могут использоваться для легкого и быстрого выполнения вычислений.

Заключение

Счеты — очень мощное устройство для вычислений. Для работы с ним нужно иметь навыки, но если вы освоите метод и достаточно попрактикуетесь, у вас никогда не возникнет проблем с решением задач на деление или умножение.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7