Примеры.Умножение и деление обыкновенной дроби на натуральное чсло.Математика 5 класс. Зубарева И.И. Параграф 26.Задание 503 – Рамблер/класс

Примеры.Умножение и деление обыкновенной дроби на натуральное чсло.Математика 5 класс. Зубарева И.И. Параграф 26.Задание 503 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Вычисляли такое?

ответы

Да, конечно. Делай так:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

3 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

Решение задач суравнениями. Математика 5 класс.Зубарева И.И.Параграф 10, задание191

ЗАДАЧУ ЗАДАЛИ:
  От посёлка Левино до посёлка Новопокровское можно доехать
по шоссе, длина которого 8 км, а можно проехать (Подробнее…)

ГДЗЗубарева И.И.Математика5 класс

Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191

Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)

ГДЗЗубарева И.И.Математика5 класс

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

   Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Математика — страница 2

Сейчас читают:

• Как оформлять реферат правильно — образец
• Оформление курсовой работы по ГОСТу: образец
• Как оформить титульный лист реферата?
• Оформление рисунков в дипломе (примеры)
• Правила оформления приложений в курсовой работе
• Оформление списка литературы по ГОСТу 2020, 2021 образец
• Оформление диплома в 2022 году
• Оформление курсовой работы по госту 2020, 2021

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.

Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Математика

12.11.21

6 мин.

Обыкновенные правильные дроби, определение и их примеры

При изучении обыкновенных дробных выражений ученики сталкиваются с проблемой идентификации неправильной и правильной дробей в примерах при решении задач. Но это не особо влияет на результат вычислений, однако особенности этих двух числовых тождеств должен знать каждый. Специалисты разработали специальный алгоритм, который очень просто реализуется на практике и позволяет найти различия между ними. Общие сведения Обыкновенные дроби и операции…

Читать полностью

Математика

12.11.21

6 мин.

Правило и примеры признака делимости на 11

В школе в 5 классе изучается подробно признак делимости на 11. Правила и примеры основаны на определенной методике, разработанной специалистами и позволяющей за короткое время освоить эту тему. Обучение начинается с изучения делителей, находящихся в диапазоне от двух до десяти включительно. Математики рекомендуют на начальном этапе разобраться в теоретических основах, а затем переходить к практике. Общие сведения Любая арифметическая операция…

Читать полностью

Математика

12.11.21

6 мин.

Основные правила и свойства вычитания для 5 класса

Учащиеся средних образовательных школ изучают в 5 классе свойства вычитания и сложения. Они применяются для решения примеров, ускорения вычислений в устной форме и т. д. В высших учебных заведениях правила используются для упрощения выражений, нахождения корней дифференциальных уравнений и пределов, а также для выполнения других операций. Общая информация Вычитание — операция уменьшения числа на…

Читать полностью

Математика

12.11.21

6 мин.

Взаимно обратные числа и их объяснение в математике 6 класса

При сокращении выражений дробного типа ученики иногда сталкиваются с понятием «взаимно обратных чисел». В математике 6 класса эта тема рассматривается подробнее, поскольку количество задач на упрощение тождеств увеличивается по следующим причинам, а именно: доказательства теорем и различных соотношений, выведение формул и выполнение операций вычисления. Специалисты сначала рекомендуют изучить теорию, а затем переходить к практике. Общие сведения Одним из…

Читать полностью

Математика

12.

11.21

12 мин.

Понятие дроби в математике 5 класса и основные ее свойства

Не всегда числа выражаются целыми величинами. Понятие дроби в математике 5 класса рассматривается более подробно, поскольку каждый ученик должен понимать основные принципы работы с числами любого формата. Это позволит грамотно выполнять вычисления, используя свойства дробных выражений. Специалисты рекомендуют изучить теорию, а затем перейти к ее практическому применению. Общие сведения Числа делятся на целые и дробные.…

Читать полностью

Математика

12.11.21

12 мин.

Способ перевести десятичную дробь в обыкновенную: правила

При изучении математики важно не только знать, как перевести десятичную дробь в обыкновенную, но и уметь применять полученные знания на практике. Обучают этой науке в четвертом классе средней школы. Преобразование выражений позволяет упрощать различные задачи, делая решение простым и понятным.

Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.

Читать полностью

Математика

12.11.21

13 мин.

Примеры смешанных дробей в математике для 5 класса

Ученики изучают на уроках математики в 5 классе смешанные дроби и примеры работы с ними. Однако не всегда усваивают теоретический материал, а на практике не могут решать задачи с обыкновенными дробными величинами. Специалисты нашли выход с этой ситуации, предложив специальные алгоритмы для оптимизации вычислений без ошибок. Для их изучения необходимы определенные базовые знания. Общие сведения…

Читать полностью

Математика

12.11.21

12 мин.

Примеры умножения обыкновенных дробей (математика, 6 класс)

Расчеты выполняются не только с натуральными целыми числами, но и с дробными. На уроках математики в 6 классе примеры умножения обыкновенных дробей изучаются более подробно. Для правильного вычисления необходимо применить определенную методику, которую разработали специалисты для этой цели. Они рекомендуют сначала приобрести базовые знания, а затем перейти к их практической реализации. Общие сведения Процесс нахождения произведения двух обыкновенных…

Читать полностью

Математика

12.11.21

13 мин.

Деление с остатком для примеров в математике 5 класса

Изучение арифметических операций подробно начинается на уроках математики в 5 классе на примерах, а деление с остатком не является исключением. Некоторые ученики не представляют, какой важной для дальнейшего изучения дисциплин с физико-математическим уклоном считается эта тема. Однако сначала требуется рассмотреть теорию, а затем переходить к практическому применению знаний, полученных в процессе обучения.

Общие сведения Деление с остатком —…

Читать полностью

Математика

12.11.21

13 мин.

Правила по сложению и вычитанию дробей (математика, 5 класс)

После рассмотрения натуральных чисел и действий над ними переходят к изучению правил сложения и вычитания дробей. На математике в 5 классе этой теме уделяется несколько уроков. Преподаватель не только даёт алгоритм вычислений, но и учит школьников применять знания на практике. Научиться правильно и быстро выполнять эти алгебраические действия важно, так как в дальнейшем это умение приходиться использовать практически при изучении любой науки.

Читать полностью

Математика

12.11.21

13 мин.

Правила сравнения обыкновенных дробей и пример решения задач

В пятом классе изучаются правила сравнения обыкновенных дробей. Однако некоторые ученики не могут понять эту тему, хотя она, на первый взгляд, кажется очень простой. Не всегда получается сравнить оба дробных выражения, так как школьная методика преподносится не совсем верно. Чтобы исправить этот недочет, специалисты разработали универсальный алгоритм, который будет понятен каждому. Общие сведения Для применения правил сравнения дробей…

Читать полностью

Математика

12.11.21

14 мин.

Нахождение простых и составных чисел (математика, 6 класс)

Выявление принадлежности величины в математике (6 класс) к простому или составному числу — задача непростая, когда под рукой нет специальных таблиц или средств вычислительной техники (компьютеров, планшетов, смартфонов) с предустановленным специализированным программным обеспечением. Однако специалисты предлагают уникальную методику, позволяющую решить поставленную задачу. Общие сведения Для использования алгоритма идентификации чисел нужны определенные знания. Начинать следует с расшифровки терминов. Любое число состоит…

Читать полностью

Математика

12.11.21

12 мин.

Формулы для решения линейных уравнений (математика, 5 класс)

Очень часто необходимо находить корни равенств с неизвестными на уроках математики в 5 классе. Формулы уравнений линейного типа применяются как раз для этих целей. Для их решения нужно следовать некоторой методике, которая называется алгоритмом. Однако для этого нужен определенный «багаж» знаний, включающий приведение подобных компонентов и упрощение выражения. Общие сведения Большая часть учебников по математике для…

Читать полностью

Математика

12.11.21

13 мин.

Методика перевода числа в восьмеричную систему счисления

Перевод чисел на язык, который понятен любой электронно-вычислительной машине, осуществляется по определенному алгоритму в некоторое представление. Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8). Общие сведения Для работы с системами счисления (СС) необходимо разобрать их…

Читать полностью

Математика

12.11.21

11 мин.

Как найти наибольший общий делитель для двух чисел

При решении задач по математике в начальных классах иногда требуется найти наибольший общий делитель, или сокращенно — НОД. Однако не все учащиеся знают правильный алгоритм этой операции, а также путают ее с НОК (наименьшим общим кратным). Чтобы не совершать таких ошибок, специалисты-математики разработали универсальные алгоритмы отличия и нахождения искомых значений. Общие сведения Специалисты…

Читать полностью

Математика

12. 11.21

12 мин.

Алгоритм приведения дробей к общему знаменателю в 5 классе

Операция приведения дробей к общему знаменателю в 5 классе используется при выполнении сложения и вычитания, а также для упрощения выражений. Делать это позволяет определенная методика, которой следует придерживаться. Она также оптимизирует вычислительный процесс, экономя драгоценное время и уменьшая число ошибок на начальной стадии обучения. Перед ее изучением математики рекомендуют получить базовые знания. Базовая информация Обыкновенная дробь…

Читать полностью

Математика

12.11.21

9 мин.

Правила умножения и деления натуральных чисел для 5 класса

Одними из базовых математических операций являются умножение и деление натуральных чисел. В 5 классе они изучаются более подробно с учетом всех «тонкостей». Специалисты разработали специальные алгоритмы, позволяющие произвести расчеты без ошибок.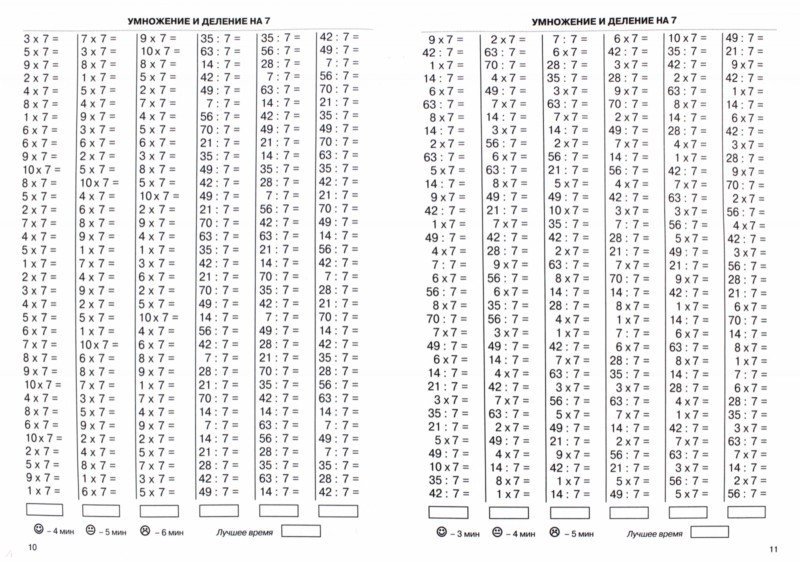 Однако перед обучением нужно разобрать основные определения и понятия, а затем приступать к практике. Общие сведения Умножением двух или нескольких чисел называется математическая операция, состоящая…

Читать полностью

Математика

12.11.21

14 мин.

Правила вычитания дробей с разными знаменателями

Пожалуй, одной из самых популярных арифметических операций в алгебре является вычитание дробей с разными знаменателями. Алгоритм выполнения этого действия несложен и ничем не отличается, по сути, от сложения. Базируется он на основном свойстве отношений, позволяющем домножить числитель и знаменатель на одно и то же число. Следует отметить, что знание операции позволяет в…

Читать полностью

Математика

12.11.21

14 мин.

Примеры и способы решений неполных квадратных уравнений

Неполные квадратные уравнения чаще всего встречаются в различных математических задачах школьной программы.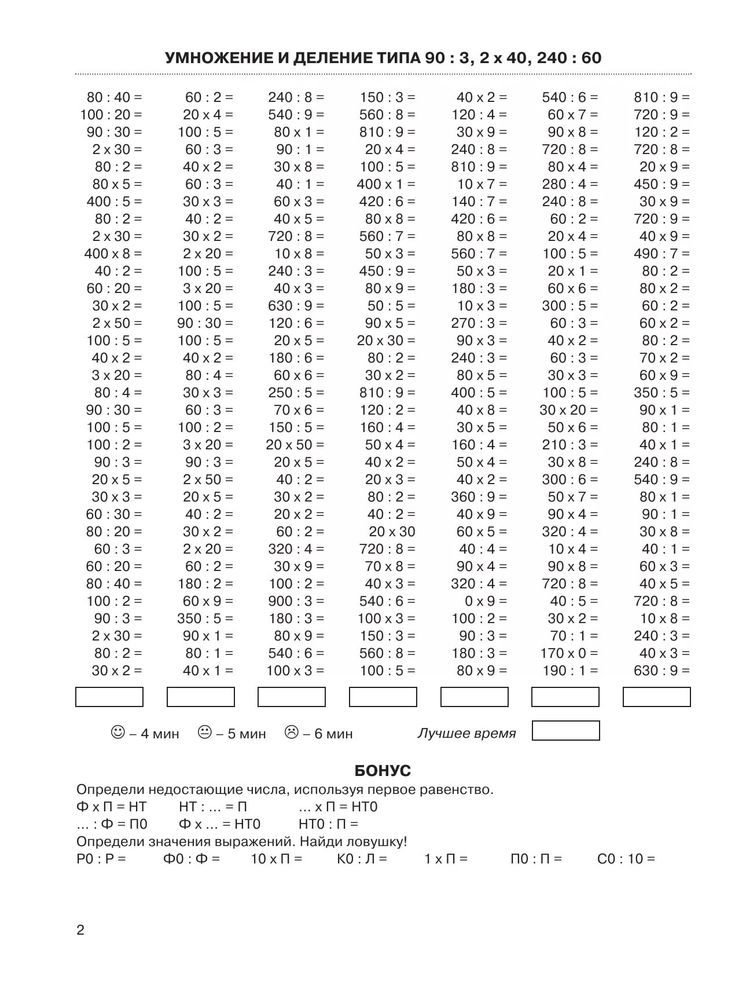 Главное их отличие от обычных в том, что они содержат меньше членов, поэтому и решать их довольно легко. Минимум существует 3 способа. Зная их, можно будет решить пример любой сложности, в некоторых случаях даже устно, причём даже за считаные секунды. Понятие и термины Под…

Читать полностью

Математика

12.11.21

9 мин.

Сочетательное свойство и законы умножения для 5 класса

Арифметические операции произведения, сложения, вычитания и деления применяются в различных дисциплинах с физико-математическим уклоном. У каждой из них существуют определенные законы, позволяющие оптимизировать процессы вычисления. Для сложения и произведения следует применять распределительное, переместительное и сочетательное свойства умножения или сложения. Общие сведения Для удобства описания арифметических операций следует ввести буквенные обозначения. Пусть первый коэффициент эквивалентен переменной «о»,…

Читать полностью

Математика

12. 11.21

13 мин.

Правила вычитания десятичных дробей и примеры решений

Арифметические действия относятся к элементарным операциям алгебры. Одним из важных умений является вычитание десятичных дробей. Этот навык используется не только в классических вычислениях, но и при изучении высшей математики. Понимая суть и зная алгоритм, можно громоздкое, сложное к восприятию выражение преобразовать к простому виду, что поможет правильно и быстро найти ответ. Общие сведения Под дробью в математике понимают…

Читать полностью

Математика

12.11.21

13 мин.

Как находить в 6 классе взаимно простые числа и что это такое

Одним из основных понятий в арифметике является деление. Каждая величина характеризуется делимостью. В зависимости от неё определяют и взаимно простые числа. Что это такое и какую пользу несёт знание правила их нахождения, изучают в шестом классе средней школы.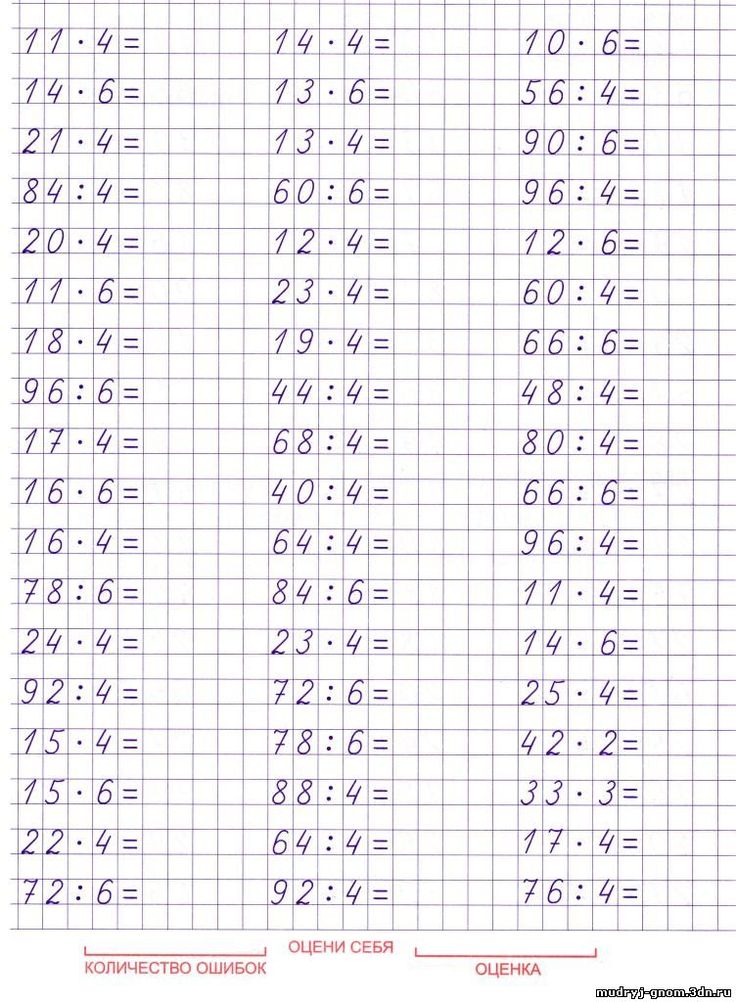 Это базисное понятие, которое позволяет в дальнейшем выполнять различные математические упрощения и преобразования как при решении элементарных задач, так и сложного уровня на уроках высшей математики.

Читать полностью

Математика

12.11.21

8 мин.

Правило деления обыкновенных дробей для 5 класса

В различных дисциплинах с физико-математическим уклоном встречается операция упрощения выражений. Иногда последние представлены в виде обыкновенных дробей. Правила деления и умножения дробных тождеств нужно знать, чтобы не совершать ошибок при вычислениях. Специалисты рекомендуют изучить теорию, а потом перейти к ее практическому применению. Общие сведения Многие начинающие математики путают правила работы с обыкновенными выражениями, поскольку при делении…

Читать полностью

Математика

12.11.21

7 мин.

Деление с остатком в столбик для 5 класса с примерами

Деление с остатком в столбик является распространенной операцией, которая применяется не только в физике и математике, но и в программировании. Это следует знать, поскольку не всегда под рукой оказываются средства для выполнения вычислений (онлайн-калькулятор и компьютер). Математики рекомендуют изучить сначала теорию, а затем перейти к практике. Общие сведения Практически любую арифметическую операцию возможно выполнить в столбик.…

Читать полностью

мостов по классам Уровень: 5

Анонс мостов по математике, третье издание!

Узнайте, что нового в учебной программе!

Первый блок посвящен объему и включает в себя обзор фактов умножения и стратегий умножения многозначных чисел. В модуле 2 учащиеся используют свои знания об эквивалентных дробях для сложения и вычитания дробей. Модуль 3 расширяет понимание учащимися разрядного значения и свойств операций, чтобы помочь учащимся разработать мощные стратегии для беглых вычислений с десятичными знаками. В Модуле 4 совершенствуются мощные стратегии умножения и деления, включая модель массива и стандартный алгоритм умножения.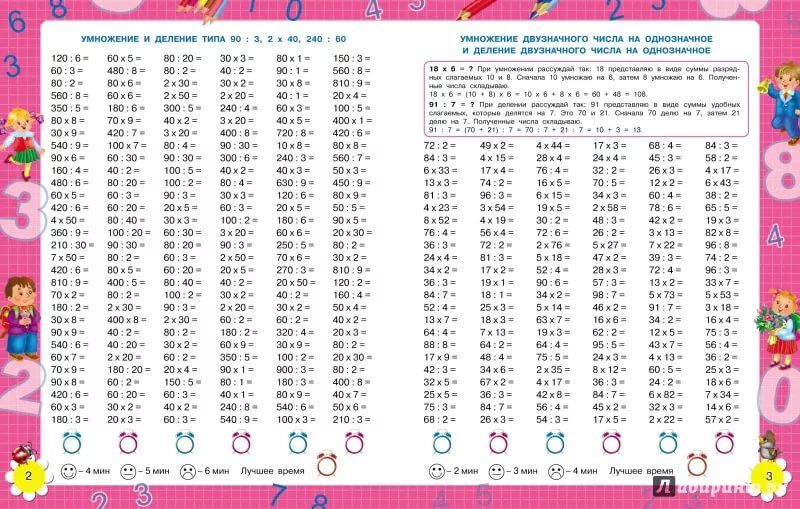

В 5 классе учащиеся учатся умножать и делить дроби. Модуль 6 вводит новые геометрические концепции, включая построение координатных графиков и использование иерархий для классификации двумерных фигур по их свойствам.

В Разделе 7 учащиеся разрабатывают точные и эффективные стратегии деления целых чисел, десятичных дробей и дробей (дробные единицы на целые числа и целые числа на дробные части). Блок 8 объединяет естественные науки, инженерию и математику. В этом последнем разделе учащиеся применяют знания и навыки, которые они приобрели в течение года, изучая солнечную энергию и проектируя солнечные дома.

Краткое содержание и образцы

Модуль 1

Выражения, уравнения и объем

• Умножение и объем
• Факторы, кратные и ассоциативное свойство
• Стратегии умножения
• От умножения к делению

Раздел 2

Сложение и вычитание дробей

• Сложение и вычитание дробей
• Дроби как операторы и частные
• Общие знаменатели
• LCM и GCF

Единица 3

Разрядное значение и десятичные разряды

• Целое число и десятичное разрядное значение
• Сложение и вычитание десятичных знаков
• Преобразования
• Отдел и район Модель

Модуль 4

Умножение и деление целых чисел и десятичных дробей

• Стратегии умножения и деления
• Другие стратегии умножения и деления
• От массива к алгоритму
• Умножение для деления

Модуль 5

Умножение и деление дробей

• Умножение целых чисел на дроби
• Умножение дробей на дроби
• Больше Умножение дроби на дробь
• Деление дробей и целых чисел

Блок 6

Графики, геометрия и объем

• Графики упорядоченных пар
• Классификация полигонов
• Том
• Баннеры и флаги

Раздел 7

Деление и десятичные дроби

• Деление дробей и целых чисел
• Интерпретации и стратегии отдела
• Силы десяти
• Десятичное умножение и деление

Блок 8

Solar Design

• Изучение солнечной энергии
• Исследование конструкции пассивной солнечной батареи
• Проектирование солнечных домов
• Отделка наших моделей

Угловой номер

• Календарная сетка
• Сборщик календарей
• Вычислительная беглость
• Проблемные строки
• Решение проблем

Сопроводительная документация

Подробнее о стандартах нумерации Корреляции Обзор EdReports Список обучения Обзор Область действия и последовательность Руководство по оценке Обзор Просмотр страницы в магазине

35 математических вопросов для 5-х классов: рабочие примеры

В 5-м классе самыми сложными вопросами по математике часто являются логические вопросы. В этой статье мы собрали подборку математических вопросов для пятиклассников, организованных по разным типам логических вопросов, с которыми учащиеся могут столкнуться в стандартных тестах и ​​за их пределами.

Зачем фокусироваться на математических рассуждениях?

Большинство пятиклассников считают логические вопросы самыми трудными. Неудивительно, что за несколько недель до стандартизированных тестов мы обучаем тысячи студентов. Обучение их навыкам математического мышления на начальном уровне — большая часть того, чем мы занимаемся здесь, в Third Space Learning.

Недавно мы даже приняли решение реструктурировать наши элементарные уроки, чтобы ввести математические рассуждения на более ранних этапах обучения, поскольку уровень сложности в конце урока был слишком высок. Мы определенно чувствуем боль учителей пятого класса!

Какого бы уровня в математике ни достигли ваши ученики в настоящее время, математические рассуждения будут появляться в начальной и средней школе, так что это важный навык в будущем.

Если вы обнаружите, что в вашем классе есть дети, которым нужно наверстать упущенное гораздо больше, чем другим, то мы можем помочь им с индивидуальными занятиями один на один, если вы свяжетесь с нами.

35 вопросов по математике для пятиклассников

Существует 7 типов вопросов по математике, с которыми могут столкнуться пятиклассники:

Для каждого из этих типов мы рассмотрим пример задачи, рассмотрев вопрос, правильный ответ и способ решения этой задачи.

Мы также рассмотрим дополнительные примеры каждого типа вопросов и ответов по математическому рассуждению, опять же с рабочими примерами и объяснением того, как ответить на каждый из них.

Наша цель — предоставить вам примеры типов математических рассуждений и способы обучения навыкам рассуждения и решения проблем, которые им потребуются для их решения.

Чтобы узнать больше о подобных задачах, ознакомьтесь с нашей коллекцией двухэтапных и многоэтапных текстовых задач. Чтобы получить советы о том, как научить детей решать подобные задачи, ознакомьтесь с этими стратегиями решения математических задач.

Тип вопроса по математике 1: одношаговые задачи со словами

Самый простой тип вопросов-рассуждений, с которым могут столкнуться учащиеся, одношаговые задачи — это именно то, что: учащимся предлагается интерпретировать письменный вопрос и выполнить один математический шаг, чтобы реши.

Взгляните на приведенный ниже вопрос:

Обоснование Вопрос 1

Ответ: $0,65

Относительно простой вопрос для толкования — первым шагом будет переписать приведенные суммы так, чтобы они могли правильно выстроиться значения места, чтобы решить. Отсюда простой математический шаг — вычитание, то есть 2,00 доллара — 1,35 доллара = 0,65.

Наиболее важным навыком для школьников в этом вопросе является твердое понимание денег как их стоимости. Если это понимание присутствует, то сам математический шаг довольно прост.

Ниже приведены еще несколько примеров:

Обоснованный вопрос 2

Ответ : 7 часов 24 минуты

Учащиеся должны понимать, что один час равен 60 минутам. Отсюда единственный математический шаг — деление: 444/60, чтобы найти целочисленный ответ с остатком.

Обоснованный вопрос 3

Ответ : 48 см ³

Учащиеся должны умножить длину на ширину на высоту, используя суммы, указанные в вопросе.

Обоснование вопроса 4

Ответ : 1,488 кубических см

Достаточно простое вычисление (умножение), если учащиеся знают, что объем прямоугольной призмы можно найти, умножив площадь основания на высоту.

Обоснование Вопрос 5

Ответ : 7,590

Единственная, относительно простая задача на округление. Учащиеся должны понимать, что «94» — это то место, на котором они должны сосредоточиться в этой задаче.

Тип вопроса по математике 2: Сложные задачи с несколькими шагами

Более сложная версия одношаговой текстовой задачи, многошаговые задачи требуют, чтобы учащиеся интерпретировали письменную задачу, но затем ее решение требует использования двух или трех математических задач. навыки и умения.

Например, рассмотрите следующий вопрос:

Обоснование Вопрос 1

Ответ: $1,85

Этот вопрос включает в себя три различных математических навыка: умножение (и деление) десятичных дробей, сложение и вычитание. Учащиеся могут сначала решить умножение или деление, но они должны выполнить и то, и другое, прежде чем двигаться дальше.

После того, как эти значения будут вычислены, следующие шаги относительно просты — сложение двух значений вместе и вычитание общей суммы из 5 долларов.

Многошаговые задачи особенно ценны для включения в практические тесты, поскольку они требуют от детей применения своих знаний математического языка и навыков рассуждения несколько раз в ходе одного вопроса, обычно в немного разных контекстах.

Еще примеры:

Обоснование вопроса 2

Ответ : $5,520

Эта задача состоит из двух шагов, но оба они представляют собой умножение. Первый — вычислить, сколько денег зарабатывается в день — 92 х 15 долларов. Затем этот продукт умножается на 4 — количество дней — чтобы получить ответ.

Обоснованный вопрос 3

Ответ : 1360 миль

Еще одна двухэтапная задача. Первый шаг — отработать 4 из 3400 миль. Затем разделите это на 10, чтобы найти 4/10 от 3400.

Обоснование Вопрос 4

Ответ : 153$

Для решения этой задачи требуется четыре шага: умножение (удвоение 51$), деление (деление 51$ пополам), повторное умножение (удвоение половины 51$– некоторые учащиеся могут признать, что последние два шага были ненужными, поскольку это возвращает нас к 51 доллару), и добавление (объединение двух затрат).

Учитывая количество шагов, учащиеся могут легко допустить арифметические ошибки.

Обоснованный вопрос 5

Ответ : 11,45 фунтов

Снова двухшаговая задача: умножить 3,45 фунта на 4, а затем вычесть из суммы 2,35 фунта.

Математические вопросы Тип 3: задачи, связанные с измерениями

Как следует из названия, эти вопросы требуют от учащихся решения задачи, включающей одну или несколько единиц измерения.

Слайд из репетиторского урока Third Space Learning 1-to-1, на котором обучают чтению единиц измерения.

Вопрос-обоснование 1

Ответ: 40 стирок

Это двухшаговая задача; учащиеся должны сначала уметь читать и переводить килограммы в граммы (и, следовательно, знать взаимосвязь и преобразование между двумя единицами — 1000 граммов в 1 килограмм), умножать 2,6 на 1000, что равно 2600, а затем делить 2600 на 65. Частное — это возможное количество стирок.

Другие примеры:

Обоснование вопроса 2

Ответ : 50 г

Относительно простая задача на деление, полагающаяся на знания учащихся о том, что 200 г — это одна пятая часть килограмма.

Обоснованный вопрос 3

Ответ : 5,12 мили

Еще одна трехшаговая задача, требующая от учеников вычитания и деления десятичных дробей – вычитания 12,63 мили из общей суммы, взятия разницы, 13,91 мили и вычитания 3,6 мили. , а затем разделив эту разницу, 10,24, пополам, чтобы получить расстояние, которое пробежали два других друга.

Обоснованный вопрос 4

Ответ : 84 дюйма/7 футов

Чтобы найти 8 футов в дюймах, учащиеся должны умножить 8 на 12. Это дает ответ 96 дюймов. Затем учащиеся должны разделить 96 на 40, чтобы найти высоту одной коробки: 2,4 дюйма. Умножьте 2,4 на 5 и вычтите это из исходной 96-дюймовой башни.

Интересно отметить, что единицы измерения для ответа могут быть указаны, а могут и не быть указаны – ответ, указанный в дюймах или футах, будет принят, однако иногда единица измерения будет указана в поле для ответа. Вот почему мы рекомендуем учащимся следить за тем, указаны ли единицы измерения в поле для ответов.

Обоснованный вопрос 5

Ответ : 0,05 фунта

Как и в случае с текущим вопросом, для решения этой задачи необходимо выполнить три шага: вычесть самый тяжелый автомобиль из общего количества (3,85 – 1), вычислить вес из оставшихся трех автомобилей (2,85/3) и вычитая 0,95 из 1, чтобы получить оставшуюся сумму в 0,05 фунта.

Тип вопроса 4: Задачи на рисование

Задачи на рисование требуют, чтобы учащиеся построили точный рисунок, следуя набору инструкций или путем отражения, перевода или масштабирования.  

Обоснование Вопрос 1

Ответ: Любая пара прямых, образующих квадрат из 4 единиц, прямоугольник из 6 единиц и квадрат из 25 единиц.

Этот вопрос значительно сложнее, чем кажется, и включает в себя аспекты умножения, а также пространственного восприятия. Одним из возможных решений является вычисление площади карты (35), а затем вычисление возможных квадратных чисел, которые поместятся (понимая, что квадратные числа образуют квадрат, когда их рисуют, как на сетке), и которые затем оставляют одно целое. прямоугольник сзади.

Много работы за одну точку!

Еще несколько примеров:

Обоснование Вопрос 2

Ответ : Любой четырехугольник, образованный соединением точек, который имеет 3 острых угла, например. форма наконечника стрелы.

Обоснованный вопрос 3

Ответ : Точно проведенный угол.

Этот вопрос требует от учащихся понимания и умения точно пользоваться транспортиром. Часто схема оценки допускает некоторую ошибку – «между 34 и 36 градусами» допустимо.

Логический вопрос 4

Ответ : Точно проведенный угол.

Как и в предыдущем вопросе, допускается небольшая погрешность, так как допустимо значение между 139 и 141 градусом.

Обоснование Вопрос 5

Ответ : Точки проведены в (2,1), (5,1) и (2,4).

Тип вопроса по математике 5: вопросы-пояснения

В этих задачах детям предлагается объяснить математическое утверждение или ошибку.

Например:

Обоснованный вопрос 1

Ответ: Если расстояние от P до R равно 800 ярдам, а расстояние от P до Q равно (Q -> R x 4), оно должно быть равно 4 /5 от 800 = 640 ярдов. Следовательно, Оливия неправа.

В большей степени, чем в большинстве других задач, этот тип требует от учащихся активной демонстрации навыков рассуждения, а также математических навыков. Здесь учащиеся должны сформулировать либо словами, либо (где это возможно) численно, что они понимают, что Q до R составляет 1/5 от общего числа, что, следовательно, P до Q составляет 4/5 от общего расстояния, а затем вычислить, что это такое, путем деления и умножение.

Другие примеры ниже:

Обоснование вопроса 2

Ответ : Нет; 20/100 равно 20, деленному на 100, что равно 0,2

Обоснованный вопрос 3

Ответ : Нет; умножение и деление имеют одинаковый приоритет в порядке операций, поэтому в задаче типа 40 x 6 ÷ 2 вы должны выполнить умножение первым, поскольку оно происходит первым.

Вопрос-рассуждение 4

Ответ : Нет

Допустимо любое объяснение, содержащее контрпример, т.е. «Нет, если число равно 1», «Не для 0», «Нет, если число меньше 1» и т. д.

Обоснованный вопрос 5

Ответ : Любой ответ, который относится к тому факту, что существует 5 в сотом разряде и 9 в тысячном разряде, так что число должно быть округлено до десятитысячного разряда.

Тип вопроса по математике 6: Вопросы последовательности

Еще один относительно простой вид логических вопросов. Задачи на последовательность предполагают выполнение учащимися математических последовательностей.

Рассмотрим этот пример:

Рассуждение Вопрос 1

Ответ: 35 , 42, 49, 56 , 63, 70

Остановка вопросов Указывает к решению: выяснить, что выяснить. увеличение между числами, затем примените это сложением или вычитанием, чтобы найти недостающие числа.

Учащиеся с более высокими показателями могут быстро понять, что это на самом деле таблица умножения на 7, и положиться на свои знания фактов умножения, чтобы получить ответ — это следует поощрять, если они затем проверяют свой ответ обычным методом, чтобы убедиться, что они не ошибся.

Еще примеры:

Обоснование 2

Ответы : 5/8 и 2 1/8 (ИЛИ 17/8)

Оба ответа должны быть правильными, чтобы получить балл. Учащиеся должны признать, что 3/4 — это то же самое, что 6/8, поэтому следующее число должно быть на три восьмых больше. Затем они должны уметь складывать и вычитать дроби, чтобы получить ответы.

Вопрос о рассуждении 3

Ответ (ы) : 4,2 и 7

Вопрос 4

Ответ (S) : 128, 135 и 156.

Вопрос 5

Вопрос 5

9000.

. Ответ(ы) : 0 и 24

Этот вопрос числовой строки может быть немного сложным; учащиеся должны выяснить, что отметки на линии представляют собой приращения по 1½, и считать в прямом и обратном порядке по 1½, чтобы получить недостающие числа.

Тип вопроса по математике 7: Вопросы на порядок

Немного более сложный вариант вопроса на последовательность, задачи на порядок требуют, чтобы учащиеся расположили набор чисел, дробей или мер в правильном порядке.

Хорошим примером является приведенный ниже вопрос по математике для пятого класса:

Вопрос-рассуждение 1

Ответ: 3/5, 3/4, 6/5

дробь, но это вряд ли необычно. Такого рода вопросы — это как раз то место, где можно найти другие «кривые шары», такие как эквивалентные дроби, смешанные числа, десятичные числа и дроби, смешанные в одной задаче.

Здесь необходимо хорошее знание основ дробей: учащиеся должны понимать, что означает больший знаменатель, и значение дроби, числитель которой больше знаменателя.

Другие примеры:

Обоснование вопроса 2

Ответ : D,C,A,B

Предложите учащимся привести все дроби к одному значению знаменателя, чтобы упростить порядок.

Вопрос-рассуждение 3

Ответ : (вниз по колонке «Место») 3, 5, 2, 4

Учащиеся могут использовать множество стратегий для решения этой задачи. Больше всего времени заняло бы приведение всех дробей к общему знаменателю. Более эффективные стратегии включают в себя рассуждения о размере дробей по сравнению с ½ или 1. Например, учащийся может заметить, что ⅜ — единственная дробь меньше ½, что ставит Бена на 5-е место. 4/8 ровно ½, тогда как остальные больше ½, что ставит Майкла на 4-е место. Затем учащийся может признать, что 10/12 ближе к 1, чем ¾, и дополнить остальную часть таблицы.

Рассуждение Вопрос 4

Ответ : C, B, D, A

Вопрос о расчиваниях 5

Ответ : D, C, B

7 Верхние Math Reasoning Questions

Теперь, когда мы рассмотрели, как отвечать на некоторые конкретные типы логических вопросов, вот еще несколько общих советов для успешного прохождения стандартизированных тестов. Не все они могут быть применимы к каждому отдельному вопросу, но применимы по крайней мере к двум, а обычно и к большему числу вопросов.

• Приучите учащихся определять, какая информация им предоставляется в вопросе и что им нужно знать для решения проблемы. Это помогает им начать формировать шаги, необходимые для поиска решения.
• Попросите учащихся «найти математику» в вопросе – какие операции или навыки им действительно необходимы для решения задачи? Это полезно даже для арифметических вопросов — неудивительно, как часто дети могут неправильно понять вопрос.
• Проверить агрегаты! Особенно в вопросах, связанных с несколькими показателями, может быть легко дать неверный ответ. В поле для ответа может быть указана определенная единица измерения, поэтому учащиеся должны работать над тем, чтобы дать свой ответ в этой единице.
• В том же духе напомните учащимся, что нужно преобразовывать разные единицы измерения в вопросе в одну и ту же единицу, чтобы упростить расчеты, например. фунты в унции.
• По возможности поощряйте числовые ответы. Даже в поясняющих вопросах демонстрация математического уравнения является лучшим объяснением, чем попытка его записать.
• Гистограмма может быть полезным способом визуализации многих различных типов вопросов и может облегчить определение «шагов», необходимых для решения.
• Проверь свою работу! Даже если работа в конечном итоге не имеет отношения к вопросу, вы можете потерять баллы, если она неверна.

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью индивидуального обучения элементарной математике с их собственным онлайн-репетитором по математике.