16 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Контрольная работа Умножение и деление в столбик. 4 класс.
КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
«УМНОЖЕНИЕ И ДЕЛЕНИЕ СТОЛБИКОМ»
ВАРИАНТ
Найди частное
а) 861: 7 б) 693: 3 в) 512 : 8 г) 432 : 4
Найди неизвестное
а) : : 5 = 143
б) : : 9 = 66
в) : : 4 = 122
Реши примеры
а) (127+394)* 7
б) (258 + 411) : 3
в) (899 – 490) * 4
Реши задачи
А) В летний лагерь приехали дети на 15 автобусах. Сколько всего детей приехало, если в каждом автобусе поместилось по 66 человек?
Б) Летом фермеры собрали 581 кг картофеля за месяц. Картофель расфасовали по 7 кг в каждый мешок. Сколько мешков собрали фермеры за месяц? Сколько мешков они соберут за 3 месяца?
В) В доме два этажа. На втором этаже 6 квартир по 6 человек в каждой квартире, а на первом этаже людей проживает в два раза меньше, чем на втором. Сколько всего человек проживает в доме?
На втором этаже 6 квартир по 6 человек в каждой квартире, а на первом этаже людей проживает в два раза меньше, чем на втором. Сколько всего человек проживает в доме?
КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
«УМНОЖЕНИЕ И ДЕЛЕНИЕ СТОЛБИКОМ»
ВАРИАНТ
Найди частное
а) 996 : 3 б) 864 : 9 в) 492 : 6 г) 564 : 4
Найди неизвестное
а) : : 4 = 219
б) : : 6 = 147
в) : : 8 = 231
Реши примеры
а) (320+114) * 5
б) (664-298) : 3
в) (790-432) * 6
Реши задачи
А) В летний лагерь приехали дети на 18 автобусах. Сколько всего детей приехало, если в каждом автобусе поместилось по 55 человек?
Б) Летом фермеры собрали 384 кг картофеля за месяц.
Картофель расфасовали по 6 кг в каждый мешок. Сколько мешков собрали фермеры за месяц? Сколько мешков они соберут за 3 месяца?
Сколько мешков собрали фермеры за месяц? Сколько мешков они соберут за 3 месяца?
В) В доме два этажа. На втором этаже 6 квартир по 7 человек в каждой квартире, а на первом этаже людей проживает в два раза меньше, чем на втором. Сколько всего человек проживает в доме?
Расставь порядок действий. Найди значение выражения: (72507 + 56736) : (350 – 347) = 560000 : 100 ∙ 8 = 4 ∙ (932 + 17692) : 6 = 500 + (600 – 3 ∙ 100) : 10 = | Расставь порядок действий. Найди значение выражения: 60997 + (6012 + 6228) : 3 = 485 ∙ 2 + 485 ∙ 3 = 82213 ∙ 3 – 12240 : 3 = (40179 – 15395 : 5) ∙ 4 = | Расставь порядок действий. Найди значение выражения: 55440 : 9 – 10460 : 2 = 3546 – 283 ∙ 4 + 819 = 5999 + 903 ∙ 100 : 2 = (56043 – 13032) : (900 : 100) = |
Расставь порядок действий. 41090 : 7 + 11950 : 5 = 240 : 3 ∙ 5 – 399 = 372160 : 4 ∙ 7 – 721 95 = 4 ∙ (728 – 301) : 7 = (286 + 14) : 3 ∙ 5 – 280 = | Расставь порядок действий. Найди значение выражения: 2250 : 9 + 8420 : 2 = 9000 : ( 100 – 90) : 100 ∙ 2 = 283040 : 10 ∙ 3 = 100520 – 470 ∙ 5 + 13980 = 7280 ∙ 6 + 1965 ∙ 3 = | Расставь порядок действий. Найди значение выражения: 11140 : (2076 – 2066) : 2 = 900100 – (735 – 184) ∙ 8 = 3010 – 5614 : 7 + 9042 = 46370 : 5 + 546 ∙ 4 = 1254 + 645 : 5 – 967 = |
Расставь порядок действий. Найди значение выражения: 80115 : 3 ∙ 10 = 40471 ∙ 2 – 4503 ∙ 7 = | Расставь порядок действий. Найди значение выражения: 69580 : 7 – 14280 : 6 = 14110 + 801 : 9 – 7604 = 235 + 4 ∙ (536 : 8) = 12 ∙ (53 – 48) – 84 : 7 = 400000 – 702 ∙ 5 : 10 = | Расставь порядок действий. 7800 – (398 + 507 ∙ 6) = 15 ∙ (54 3 – 84 : 7) = 190 ∙ 2 + (32148 – 16) = 73460 : 5 + 454 ∙ 4 = 8 ∙ (900000 – 896507) : 4 = |
Расставь порядок действий. Найди значение выражения: 13640 : 4 – 6400 : 10 = (90 – 42 : 3 ∙ 2) : 2 = (2700 – 30) ∙ (40 – 32) = (5600 – 12240 : 3) + 145 = 400000 – 702 ∙ 5 : 10 = | Расставь порядок действий. Найди значение выражения: 8130 : 3 – 2640 : 10 = (35400 + 83915) : 5 ∙ 3 = 3152 : 8 ∙ 100 = 40018 – 725 ∙ 10 : 5 = 838008 : 9 – 410960 : 8 = | Расставь порядок действий. Найди значение выражения: 480 : 6 + 360 : 12 = (10200 – 9356) ∙ (81 – 75) = 2448 : 6 + 1854 : 6 = 2758 – 345 ∙ 6 + 369 = 8 ∙ (900000 – 896507) : 4 = |
Выполни умножение на однозначное число столбиком: 43127 ∙ 6 36039 ∙ 4 7 ∙ 23844 70 ∙ 94800 Найди значение выражения: 709 + 13200 ∙ 5 = 9 ∙ (5000 – 786) = | Выполни умножение на однозначное число столбиком: 95136 ∙ 3 391005 ∙ 4 9 ∙ 12543 50 ∙ 157300 Найди значение выражения: 400800 — 3980 ∙ 7 = 3 ∙ (90000 – 514 ∙ 4) = | Выполни умножение на однозначное число столбиком: 56482 ∙ 3 341008 ∙ 6 4 ∙ 81429 9 ∙ 930700 Найди значение выражения: 70005 — 5320 ∙ 2 = 9 ∙ (26000 – 1705) = |
Выполни умножение на однозначное число столбиком: 719806 ∙ 4 903040 ∙ 3 9 ∙ 24845 5 ∙ 120605 Найди значение выражения: 27356 — 1607 ∙ 3 = 800 – 640 : 8 + 70 ∙ 4 = | Выполни умножение на однозначное число столбиком: 25482 ∙ 2 374006 ∙ 7 5 ∙ 93748 90 ∙ 17850 Найди значение выражения: 41008 — 1240 ∙ 4 = 7 ∙ (6954 – 1007) = | Выполни умножение на однозначное число столбиком: 15213 ∙ 6 65080 ∙ 4 7 ∙ 31476 70 ∙ 390400 Найди значение выражения: 50786 + 8091 ∙ 3 = 6 ∙ (10000 – 5836) = |
Выполни умножение на однозначное число столбиком: 23452 ∙ 7 36008 ∙ 9 6 ∙ 32749 40 ∙ 82190 Найди значение выражения: 29010 – ( 5000 — 800 ∙ 4) = 17082 ∙ 8 + 1329 = | Выполни умножение на однозначное число столбиком: 36193 ∙ 5 670032 ∙ 8 9 ∙ 56492 70 ∙ 420080 Найди значение выражения: 4689 ∙ 5 + 97308 = 80000 – (4536 + 160 ∙ 3) = | Выполни умножение на однозначное число столбиком: 68715 ∙ 4 90048 ∙ 7 7 ∙ 49873 60 ∙ 72680 Найди значение выражения: 76090 ∙ 4 – 52673 = 5 ∙ (128050 – 73607) = |
Выполни умножение на однозначное число столбиком: 95124 ∙ 2 50804 ∙ 4 9 ∙ 3652 50 ∙ 21470 Найди значение выражения: 90000 — 6 ∙ 2509 = 8 ∙ (7852 + 1308) = | Выполни умножение на однозначное число столбиком: 84308 ∙ 6 536937 ∙ 4 7 ∙ 4030900 50 ∙ 971680 Найди значение выражения: 500000 — 17806 ∙ 4 = (130 ∙ 5 + 72 : 24) ∙ 9 = | Выполни умножение на однозначное число столбиком: 3968719 ∙ 7 130704 ∙ 6 6 ∙ 109765 90 ∙ 700200 Найди значение выражения: 600 — 320 : 4 + 140 ∙ 3 = 90620 ∙ 8 — 8349 = |
Найди значение выражения по действиям: 229372 : 286 ∙ 506 = 82276 : 268 + 228475 : 325 = 76 ∙ (3569 + 2795) – 1247 ∙3 = 162540 : (100236 – 99978) : 63 = | Найди значение выражения по действиям: 416 ∙ 509 + 536469 : 67 = 230441 – (229682 – 228904 : 52) = (52 ∙ 390 – 12863) ∙ (12280 : 40 – 207) = (59531 – 58926) ∙ 6004 – 1221485 = | Найди значение выражения по действиям: 282370 : 302 : 85 ∙ 2004 = 81308 – 308 ∙ (8856 – 8649) = (43512 – 43006) ∙ 805 – 23900 : 25 = 700700 – 6954 ∙ (47923 – 47884) = |
Найди значение выражения по действиям: 507 ∙ 432 + 234 : 26 = (126828 : 542) ∙ (47600 – 406 ∙ 117) = 460 ∙ 308 + 447480 : 132 – 3987 = 1000000 – 136068 : 68 + 4600 ∙ 900 = | Найди значение выражения по действиям: 728 ∙ 468 : 273 : 78 = (47868 + 112812) : 52 + 45948 : 84 = 65254 :79 – 75369 : 97 + 6075 ∙ 42 = 100000 – 12900 : 129 + 19140 : 132 = | Найди значение выражения по действиям: 805 ∙ 282 : (4000 – 3678) ∙ 32 = 76428 – 771840 : 192 + 209160 : 249 = (701020 – 698456) ∙ (208128 : 542) = 671112 : 956 + (600000 – 178688) : 464 = |
Найди значение выражения по действиям: 246 ∙ 812 : (1001 – 673) ∙ 12 = 73689 : 87 – 96064 : 158 + 310726 = (22287 – 308 ∙ 72) : 111 + 3090 = (10200 – 9891) ∙ (70204 – 69874) : 206 = | Найди значение выражения по действиям: 496 ∙ 960 : 372 : 160 = (199430 – 119 ∙ 805) : (148 + 8536 : 88) = 500100 – 356 ∙ 101 + 78052 : 26 ∙ 48 = 30000 – (2486 + 335104 : 476) ∙ 9 = | Найди значение выражения по действиям: 25146 : (428442 : 707 – 255000 : 625) = (64000 : 128 – 3280 : 164 ∙ 15) ∙ 700 = 804 ∙ 705 : 335 : 47 = (162000 – 216 ∙ 750) ∙ (816 : 4) + 1000 = |
Найди значение выражения по действиям: 802 ∙ 406 – 900072 : 18 + 63392 = (35730 + 91800 : 36) : 120 = 180848 : 356 ∙ (19800 – 18900) : 254 = 1285 – 282 ∙ 75 :47 + 14472 : 18 ∙ 12 = | Найди значение выражения по действиям: 532000 : 760 + 407 ∙ 360 – 82008 = (234690 – 306 ∙ 201) : 192 = 71370 : 234 ∙ 243 + 695 ∙ 50 – 2884 : 28 = 3060 ∙ 236 – 184708 + 125125 : 125 = | Найди значение выражения по действиям: 608 ∙ (1263 – 563) : 400 = 127410 : 274 + 307200 : 480 – 1105 = (1015 – 332926 : 818) ∙ (240372 : 396) = 609 ∙ 896 – 545664 + 748616 : 362 = |
Выполни умножение и деление на однозначное число столбиком: 825 : 5 215 ∙ 4 5472 : 4 4238 ∙ 7 4371 : 3 40632 ∙ 8 Найдите неизвестное число, зная, что ½ его часть равна 8. Вся дыня весит 6 кг. Сколько кг весит 1/3 часть дыни? | Выполни умножение и деление на однозначное число столбиком: 576 : 4 3875 ∙ 6 5418 : 3 14398 ∙ 7 6255 : 5 46504 ∙ 4
| Выполни умножение и деление на однозначное число столбиком: 496 : 4 5603 ∙ 6 25632 : 2 3303 ∙ 7 7284 : 6 73504 ∙ 9 Найдите неизвестное число, зная, что ¼ его часть равна 16. Какую долю от метра составляет 1 дм? |
Выполни умножение и деление на однозначное число столбиком: 1225 : 5 728 ∙ 6 726 : 3 1438 ∙ 8 2536 : 4 62008 ∙ 4 Длина всей ленты 10 см. Какова длина ¼ части ленты? Найдите 1/3 часть от суммы 36 и 63. | Выполни умножение и деление на однозначное число столбиком: 828 : 2 487 ∙ 5 4552 : 8 6702 ∙ 9 36204 : 6 31454 ∙ 6
| Выполни умножение и деление на однозначное число столбиком: 456 : 4 1315 ∙ 3 2536 : 2 38524 ∙ 8 82244 : 4 27180 ∙ 6
|
Выполни умножение и деление на однозначное число столбиком: 507 ∙ 4 952 : 7 2014 ∙ 6 1458 : 6 26613 ∙ 8 25656 : 8
| Выполни умножение и деление на однозначное число столбиком: 214 ∙ 6 858 : 6 1708 ∙ 9 5020 : 4 34328 ∙ 5 25256 : 7
| Выполни умножение и деление на однозначное число столбиком: 392 ∙ 5 970 : 5 1438 ∙ 8 1227 : 3 62008 ∙ 7 18504 : 9
|
Выполни умножение и деление на однозначное число столбиком: 237 ∙ 9 984 : 6 4914 ∙ 6 5836 : 4 34807 ∙ 8 13572 : 9 Почтовый голубь в час пролетает 92 км. Сколько километров он пролетит за четверть часа? | Выполни умножение и деление на однозначное число столбиком: 478 ∙ 7 915 : 5 1687 ∙ 9 4872 : 8 43703 ∙ 6 22435 : 7 ¼ стакана сахарного песка весит 60 г. Сколько весит стакан сахарного песка? | Выполни умножение и деление на однозначное число столбиком: 418 ∙ 6 7660 : 4 2718 ∙ 9 5346 : 9 47086 ∙ 7 30402 : 6 Длина куска материи 75 м. |
Выполни деление столбиком: 39285 : 45 114021 : 27 48372 : 58 380700 : 45 Зверёк землеройка за сутки съедает 12 г пищи. Сколько весит зверёк, если его масса составляет ¼ массы съеденной пищи? | Выполни деление столбиком: 19980 : 37 525728 :56 6293 : 31 16884 : 42 8844 : 22 20468 : 34 Продолжительность жизни хвои ели 9 лет, а продолжительность жизни хвои сосны 1/3 жизни хвои ели. Сколько лет живёт хвоя сосны? | Выполни деление столбиком: 5472 : 18 26553 : 53 4575 : 15 17575 : 25 65520 : 28 23640 : 24 Сколько километров проходит за ¼ часа поезд, если в час он проходит 64 км? |
Выполни деление столбиком: 173232 : 48 975255 : 79 216 161 : 43 455948 : 62 12896 : 32 72144 : 24 Берёза прожила 50 лет, что составляет 1/5 продолжительности её жизни. | Выполни деление столбиком: 5508 : 36 428910 : 85 33350 : 46 24512 : 16 97312 : 32 144096 : 79 Какую сдачу получит мальчик с 400 руб, если четвёртую часть этих денег он потратил на 2 ручки и 3 ластика? | Выполни деление столбиком: 182056 : 28 128928 : 32 191520 : 95 394680 : 78 13356 : 18 249922 : 62 Продолжительность жизни ежа равна 10 годам, а заяц живёт на 1/5 меньше. Сколько лет живёт заяц? |
Умножение в столбик. Умножение и деление столбиком
В третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
Что является основой умножения
Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное. Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.
Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.
Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.
В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)
Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
Исследовательская работа детей
Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Этапы изучения умножения на многозначное число.
В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:
- самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
- для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
- отработка навыка умножения на круглые числа;
- использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
- операции с многозначными числами и умножение в столбик.

Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Задачи изучения умножения в курсе начальной школы
Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.
Какие же задачи ранее были решены учениками и их преподавателем?
- Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.

- Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
- Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2. Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Использование свойств умножения
Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.
Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.
Распределительное свойство умножения в этом случае выступает как универсальное. Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Алгоритм записи действия умножения в столбик
Запись умножения столбиком является самой компактной из всех существующих. Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».
Упражнения для формирования навыка
Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.
Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.
Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»
Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.
Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».
Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.
Устное деление трёхзначного числа на двузначное. (Два варианта) Морская прогулка | Умножаем круглые числа. Закрепление таблицы умножения. (Два варианта) Змей Горыныч верхом |
Деление трехзначного числа на однозначное. (Два варианта) Гном | Деление трехзначного числа на двузначное. (Два варианта) Нюша |
Умножение на круглое число. (Два варианта) Принц | Умножение и деление на однозначное число. (Два варианта) Дядя Федор |
Деление трехзначного числа на двузначное. (Два варианта) Пес Шарик | Умножение двузначного числа на двузначное. (Два варианта) Морозко |
Умножение двузначного числа на однозначное. (Два варианта) Снежная королева | Деление четырехзначного числа на однозначное (устный и письменный прием). (Два варианта) Замок |
Деление вида 325 : 65. (Два варианта) Фунтик | Деление вида 360 на 4, 360 на 40. (Два варианта) Кот в сапогах |
Деление вида 200 на 4, 200 на 40, 75 на 15. (Два варианта) Алиса | Деление вида 420 на 7, 420 на 70, 144 на 18. (Два варианта) Мандала |
Деление на трехзначное число. (Два варианта) Водяной | Деление на трехзначное число. (Два варианта) Червячок |
Деление на трехзначное число. (Два варианта) Царь | Деление трехзначного числа на двухзначное. (Два варианта) Клоун |
Выражения вида 200:4. Леопольд | Умножение вида 34 на 6. (Два варианта) Медвежонок и снеговик |
Деление многозначного на двузначное число. (Два варианта) Санта Клаус | Умножение многозначного на двузначное число. (Два варианта) Дед Мороз |
Деление многозначного на двузначное число. (Два варианта) Ёлочные шары | Деление трехзначного на двузначное с остатком. (Два варианта) Кот в сапогах |
Деление на двузначное число. (Два варианта) Леший | Деление на однозначное число. Кораблик. |
Умножение однозначного на трехзначное число. Город. | Умножение на однозначное и деление на двузначное число. Баба Яга. |
| Деление суммы на число. Танцовщица | Умножение однозначного числа на трехзначное. Баран |
Деление трех-четырехзначного числа на однозначное. (Два варианта) Карлсон | Умножение однозначного на трех-четырехзначное число. (Два варианта) Ворона |
Деление трехзначного числа на однозначное. Гном и автомобиль | Умножение однозначного на трех-четырехзначное число. Конь |
Деление четырехзначного на однозначное число. Казак и сом | Деление вида 420 на 7. Тукан |
Умножение на двузначное число. Алиса Селезнёва | Деление вида 360 на 4. Черепаха |
Внетабличное умножение и деление 3-4 класс. Коровы | Внетабличное умножение и деление 3-4 класс. Мамонтёнок |
Умножение двузначного числа на однозначное. Калачи | Деление многозначного числа на однозначное. Матильда и Бимбо |
Деление на двузначное число. Устный прием. Гуси-лебеди | Деление на двузначное число. Устный прием. Оловянный солдатик |
Деление на двузначное число. Устный прием. Крепость | Деление на двузначное число. Устный прием. Волшебник |
Умножение двузначного на однозначное. Устный и письменный приемы. Бременские музыканты | Умножение двузначного на однозначное. Устный и письменный прием. Карлсон |
Умножение многозначного на однозначное. Устный и письменный приемы. Свинопас | Умножение многозначных чисел. 5 класс. Конь |
| Умножение многозначных чисел. 5 класс. Рыцарь | Умножение суммы на число (или умножение двузначного на однозначное). Винни-Пух |
Деление суммы на число. Замок Замок | Деление суммы на число. Рыцарь |
| Умножение и деление круглых чисел. Лягушка |
Игры примеры в столбик решать. Сложение столбиком
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2
. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет. Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.
Как научиться умножать столбиком?
В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.
Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать и .
Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…
Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.
За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.
Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)
Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.
С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Смотрите ниже шпаргалки в полной форме.
Умножение прямо на сайте (онлайн)
*
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
В этой игре мы будем учиться складывать столбиком числа до 100. Яркие картинки и подробные пояснения помогут легко понять и запомнить алгоритм сложения столбиком. А тренажер поможет закрепить тему.
Прежде всего нужно запомнить, что при решении примеров на сложение столбиком большее число записывается сверху, а меньшее — под ним. Числа записываются так, чтобы единицы были под единицами, а десятки (если они есть) — под десятками.
Сначала складывают единицы, а затем десятки, при этом возможно 2 варианта:
Если при сложении единиц получается однозначное число, мы просто записываем его под чертой под единицами. Если же при сложении единиц получается двузначное число, включая 10, мы записываем под единицами только вторую цифру(единицы), а 1 (десяток) прибавляем к десяткам.
Первый вариант описан и проиллюстрирован в уроке 1, а второй вариант — в уроке 2 нашей обучающей онлайн игры «Сложение столбиком». После просмотра уроков порешайте примеры на сложение столбиком самостоятельно в разделе «Тренажер»
Предыдущая статья: Н а некрасов дед мазай и зайцы Следующая статья: Каменное масло – лечебные свойства и все секреты применения
4 класс.
 Моро. Учебник №1. Ответы к стр. 81
Моро. Учебник №1. Ответы к стр. 81Числа от 1 до 1000
Умножение и деление
Деление на однозначное число
Ответы к стр. 81
Объясни приёмы вычисления.
963 : 3 = (900 + 60 + 3) : 3 = 900 : 3 + 60 : 3 + 3 : 3
455 : 5 = (450 + 5) : 5 = 450 : 5 + 5 : 5
Делимое разложили на сумму разрядных слагаемых и использовали правило деления суммы на число: чтобы поделить сумму на число, можно каждое слагаемое поделить на это число и полученные частные сложить.
363. Найди частное и остаток и выполни проверку.
56 : 15 92 : 30 399 : 9 854 : 8 34 : 40
— 56|15 Проверка: ×15
45|3 3
11 – ост. 45
45 + 11 = 56
— 92 |30 Проверка: 30 • 3 + 2 = 92
90 |3
2 – ост.
— 399|9 Проверка: ×44
36 |44 9
—39 396
36
3 – ост. 396 + 3 = 399
— 854|8 Проверка: ×106
8 |106 8
—054 848
48
6 – ост. 848 + 6 = 854
— 34 |40 Проверка: 40 • 0 + 34 = 34
0 |0
364. Объясни, что обозначают записи в рамках на полях, и выполни вычисления.
0 : α = 0 − при делении нуля на любое число всегда получается нуль
b : 1 = b − при делении числа на единицу всегда получается данное число
c : c = 1 − при делении числа на само себя всегда получается единица
0 : 45 = 0 208 : 1 = 208 375 : 375 = 1
0 : 964 = 0 342 : 1 = 342 863 : 863 = 1
365. Составь разные задачи по выражению 24 : 6.
Составь разные задачи по выражению 24 : 6.
1) Миша купил 24 солдатика, а машинок в 6 раз меньше, чем солдатиков. Сколько машинок купил Миша?
24 : 6 = 4 (м.)
О т в е т: Миша купил 4 машинки.
2) Мама принесла домой 24 пирожных. Вечером Миша съел шестую часть этих пирожных. Сколько пирожных съел Миша?
О т в е т: Миша съел 4 пирожных.
366. За 2 ч езды на легковой машине обычно расходуется 12 л бензина. На сколько часов езды хватит 48 л бензина, если его расход не изменится?
1) 12 : 2 = 6 (л) − бензина хватает на 1 ч
2) 48 : 6 = 8 (ч) − время, на которое хватит 48 л бензина
О т в е т: на 8 часов.
367. В прошлом году завод изготовил 1400 машин, что на 300 машин меньше, чем в этом году. Поставь вопрос и реши задачу.
Сколько машин изготовил завод за эти 2 года?
1) 1400 + 300 = 1700 (м. ) − изготовлено в этом году
) − изготовлено в этом году
2) 1400 + 1700 = 3100 (м.) − изготовлено за 2 года
О т в е т: за 2 года завод изготовил 3100 машин.
368. Одна бригада рабочих заасфальтировала 5 км 060 м шоссе, другая бригада − на 2 км 280 м больше. Осталось покрыть асфальтом 965 м шоссе. Какой длины шоссе должны были заасфальтировать эти бригады?
1) 5 км 060 м + 2 км 280 м = 7 км 340 м − заасфальтировала вторая бригада
2) 5 км 060 м + 7 км 340 м + 965 м = 12 км 400 м + 965 м = 13 км 365 м − должны были заасфальтировать
О т в е т: должны были заасфальтировать 13 км 365 м шоссе.
369. 658 : 7 9235 + 4 • (536 : 8) 40077 • 7 − 199099
836 : 4 (2010 − 1065) : 7 • 6 9020 • 6 + 53901
658 : 7 = 94
— 658|7
63 |94
—28
28
0
836 : 4 = 209
— 836|4
8 |209
—036
36
0
9235 + 4 • (536 : 8) = 9235 + 4 • 67 = 9235 + 268 = 9503
— 536|8 ×67 +9235
48 |67 4 268
—56 268 9503
56
0
(2010 − 1065) : 7 • 6 = 945 : 7 • 6 = 135 • 6 = 810
_2010 — 945|7 ×135
1065 7 |135 6
945 —24 810
21
_35
35
0
40077 • 7 − 199099 = 280539 − 199099 = 81440
× 40077 _ 280539
7 199099
280539 81440
9020 • 6 + 53901 = 54120 + 53901 = 108021
× 9020 + 54120
6 53901
54120 108021
370.
x • 9 = 1000 − 910 100 : x = 2430 − 2420.
x : 9 = 1000 − 910 x • 9 = 1000 − 910
x : 9 = 90 x • 9 = 90
x = 90 • 9 x = 90 : 9
x = 810 x = 10
100 • x = 2430 − 2030
100 • x = 400
x = 400 : 100
x = 4
100 : x = 2430 − 2420
100 : x = 10
x = 100 : 10
x = 10
371. На какое однозначное число надо умножить число 12345679, чтобы в результате получить новое число, записанное одними единицами?
Так как у числа 12345679 последняя цифра 9, то при умножении на однозначное число этой цифры, последняя цифра произведения должна быть равна 1.
× 12345679
9
111111111
Вычисли. 693 : 3 468 : 2
— 693|3 — 468|2
6 |239 4 |234
—09 —06
9 6
_03 _08
3 8
0 0
Ответы по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4.7 / 5 ( 38 голосов )
Моро. Решебник 1, 2 часть
ГДЗ по математике для 4 класса Моро – это сборник готовых домашних заданий: решенные задачи, примеры, уравнения, неравенства по учебнику авторитетных российских математиков – М. И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Его используют в качестве базового пособия для четвероклассников во многих центральных и региональных школах РФ.
И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Его используют в качестве базового пособия для четвероклассников во многих центральных и региональных школах РФ.
Структура ГДЗ по учебнику математики четвертого класса от Моро
В четвертом классе школьная программа изучения предписывает решение задач и примеров с числами от 1 до 1000, умножение и деление столбиком, определение скорости, времени и расстояния. Именно в 4-м классе закладывается база для изучения углубленных основ арифметики, а после – алгебры, геометрии, химии и физики.
ГДЗ по математике 4 класса Моро, составленные на основе учебника 2015 года в его 4-м издании, включают в себя примеры и задачи на такие темы:
- четыре арифметических действия: сложение, вычитание, умножение, деление;
- диаграммы;
- сложение и вычитание, умножение и деление величин;
- скорость, время, расстояние;
- умножение и деление на числа, оканчивающиеся нулями;
- умножение и деление на двузначное и трёхзначное число;
- числа от 1 до 1000;
- уравнения и неравенства с одной переменной.

В четвертом классе завершается курс средней школы. Ученики переходят на новую степень и должны уметь решать примеры и задачи самостоятельно. Цель решебника по математике к учебнику Моро – представить детальные алгоритмы решений, разъяснить материал, пройденный в классе.
Готовое домашнее задание для 4 класса на сайте ГДЗ Путина поможет не только ученикам, но их родителям, которые часто делают уроки вместе со своими детьми. Это также способ отказаться от услуг репетиторов и платных подготовительных курсов.
Правильные решения от ГДЗ Путина по математике 4 класса к Моро
Чтобы найти решение домашней задачи в интернете, достаточно за пару кликов отыскать нужный решебник. Однако не все сайты предлагают подробные решения и верные ответы. В чем преимущества портала ГДЗ от Путина? Почему именно его часто выбирают ученики младших классов и их родители?
- здесь можно найти несколько вариантов решения одной задачки;
- ответы оформлены по требованиям Минобразования России;
- все примеры с ответами доступны без регистрации и бесплатно;
- информация корректно отображается на телефонах, компьютерах и планшетах.

Перечисленные критерии важны для пользователей ГДЗ по математике 4 класса к учебнику Моро: ученики получают подробные описания решений и могут разобраться со сложными темами, их родители – в любое время проверить домашнюю работу их чад.
Поскольку задачи и примеры приводятся в нескольких вариантах выполнения, то можно выбрать самый понятный и удобный вариант, взять его за основу, разобрать и запомнить.
Массивы
— 5 основных вещей, которые нужно знать об использовании массивов для моделирования умножения и деления
Топ 5 вещей, которые нужно знать об использовании массивов для моделирования умножения и деления:
1. Массив — это набор элементов, организованных в равные строки и равные столбцы, что создает прямоугольную форму. Строки представляют количество групп, а столбцы представляют количество в каждой группе.
Инструменты, которые подходят для моделирования массивов, включают: счетчики, квадратные плитки, миллиметровую бумагу и быстрые изображения. Используя массивы для моделирования задач деления или умножения, мы хотим перейти от конкретных манипуляций к быстрым картинкам, к абстрактному мышлению с использованием выражений или уравнений для описания массивов.
Используя массивы для моделирования задач деления или умножения, мы хотим перейти от конкретных манипуляций к быстрым картинкам, к абстрактному мышлению с использованием выражений или уравнений для описания массивов.
Это конкретная модель массива. Это может быть модель задачи деления, включающая 15 ÷ 5 или 15 ÷ 3. Это также может быть модель задачи умножения 5 x 3.
Массив миллиметровой бумаги.
Быстрое изображение массива со связанными уравнениями.
2. Массивы можно использовать для моделирования задач умножения и деления. Они помогают относиться к двум операциям.
Вот пример использования массива умножения для связи с делением. Как только сумма определена, учащиеся могут видеть, что они могут разделить на количество групп или строк, 2. Или они могут разделить на количество столбцов или количество в каждой строке, 3.
3. Полезно использовать задачи со словами, которые выявляют организацию объекта в равные строки или столбцы, чтобы побудить учащихся смоделировать массив.
Пример задачи умножения:
• «Райли сажал в своем томатном саду. Посадил 3 ряда томатов. В каждом ряду было по 5 растений. Сколько томатов посадил Райли в своем саду? »
• «Райли планировал в своем томатном саду. Он посадил по 3 куста томатов в каждом ряду.Посадил 5 одинаковых рядов помидоров. Сколько томатов посадил Райли в своем саду? »
Пример задач отдела:
• «У Рэйчел 15 кукол. У нее есть 5 полок для кукол. Она хочет, чтобы на каждой полке было одинаковое количество кукол. Сколько кукол Рэйчел ставит на каждую полку? »
• «У Рэйчел 15 кукол. Она размещает по 5 кукол в каждом ряду. Сколько рядов нужно Рэйчел, чтобы разместить все куклы на полке? »
4.Массивы помогают обучать коммутативному свойству умножения, что приводит студентов к более эффективным стратегиям плавного умножения.
Эта модель показывает 3 ряда по 5 или 3 x 5.
Эта модель показывает 5 рядов по 3 или 5 x 3
На основе этих двух моделей учащиеся могут видеть, что итоговая сумма или продукт остается неизменной, потому что вы не добавляете и не убираете квадратные плитки. Единственное, что изменилось, — это способ организации строк и столбцов или количество групп и их количество в каждой группе.
Единственное, что изменилось, — это способ организации строк и столбцов или количество групп и их количество в каждой группе.
5. Понимание массива в 3-м классе важно для учащихся, которые развивают понимание области позже в 3-м классе и далее в 4-м классе. Он также готовит учащихся к моделированию больших задач умножения с использованием частичных произведений в 4-м классе.
Интересный способ изучить моделирование массивов с задачами умножения и деления — дать учащимся штампы бинго и попросить их поставить штампы на массивы на плотной бумаге. Вы можете поставить задачу: «Было 24 ученика, которых нужно было выстроить в равные ряды для собрания.Как их учитель мог организовать их в равные ряды? » Затем предложите студентам записать уравнения деления и умножения для каждой модели массива.
Отличная игра, которая побуждает студентов практиковаться в моделировании массивов, — это «Игра с массивами». Раздайте партнерам половину листа миллиметровой бумаги, карандаши двух разных цветов и кубик с цифрами 0–9. Попросите учащихся по очереди со своим партнером дважды повернуть числовой куб, чтобы определить количество строк и количество столбцов в своем массиве.Затем они создадут свой массив, записав соответствующее ему уравнение и закрасив его своим цветом. Игра продолжается до тех пор, пока человек не перестанет создавать свой массив. Тогда побеждает тот, у кого больше квадратов заштриховано цветным карандашом. (Это также можно изменить для деления, создав карточки задач деления, которые студенты могут вытащить, затем создать массив, соответствующий данной задаче, и решить для частного).
Попросите учащихся по очереди со своим партнером дважды повернуть числовой куб, чтобы определить количество строк и количество столбцов в своем массиве.Затем они создадут свой массив, записав соответствующее ему уравнение и закрасив его своим цветом. Игра продолжается до тех пор, пока человек не перестанет создавать свой массив. Тогда побеждает тот, у кого больше квадратов заштриховано цветным карандашом. (Это также можно изменить для деления, создав карточки задач деления, которые студенты могут вытащить, затем создать массив, соответствующий данной задаче, и решить для частного).
Для получения дополнительной информации об использовании массивов для моделирования с задачами или уроками умножения и деления посетите веб-сайты:
• http: // research.terc.edu/library/curric-math/qa-1ed/teaching_mult_div.cfm
• https://learnzillion.com/lesson_plans/5215-solve-division-problems-using-arrays
• https: //nrich.maths. org / 8773
• https://www.eduplace. com/math/mw/background/3/08/te_3_08_overview.html
com/math/mw/background/3/08/te_3_08_overview.html
Чтобы узнать об уроке, посвященном использованию массивов в CPalms, посетите этот веб-сайт.
Являются ли 6 x 5 и 5 x 6 одинаковыми?
Обновление : этот пост с первоначальным названием 6 x 5 и 5 x 6 НЕ одно и то же! породил самые удивительные разговоры! Я оставил сообщение, как было написано, но я просто почувствовал, что мне нужно изменить заголовок.Приятного общения! 🙂
Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. Никаких дополнительных затрат с вашей стороны не взимается, и я ссылаюсь только на книги и продукты, которые я лично использую и рекомендую.
Привет от давно потерянного тренера по математике! Теперь я официально занимаюсь математическим вмешательством и люблю жизнь! Мои четвероклассники представляли умножение квадратными плитками и писали уравнения для сопоставления изображений массивов (например, показанных выше). Эти расследования выявили заблуждение в их мышлении, которым я хотел поделиться с вами сегодня вечером. Хотя 6 x 5 и 5 x 6 имеют один и тот же продукт, это не одно и то же. Знак умножения на самом деле означает «группы из», поэтому я рекомендую студентам читать 6 x 5 как 6 групп по 5. Эта практика помогает студентам понять умножение.
Эти расследования выявили заблуждение в их мышлении, которым я хотел поделиться с вами сегодня вечером. Хотя 6 x 5 и 5 x 6 имеют один и тот же продукт, это не одно и то же. Знак умножения на самом деле означает «группы из», поэтому я рекомендую студентам читать 6 x 5 как 6 групп по 5. Эта практика помогает студентам понять умножение.
У меня есть две мыльницы, на которых я буду стоять сегодня вечером, так что, пожалуйста, развлекайте меня. Во-первых, моя мыльница CRA. Переход от аддитивного мышления (6 + 5) к мультипликативному мышлению (6 x 5) — это огромный переход для студентов, и он должен начинаться с МНОГО конкретного (практического) опыта.Со временем вам нужно будет перекрывать конкретный, репрезентативный и абстрактный этапы обучения, чтобы помочь учащимся плавно преодолеть расстояние между конкретным и абстрактным. Посмотрите, например, на карты ниже . После выбора этих двух карточек учащиеся могут использовать фишки, чтобы составить 3 группы по 5 (бетонные), нарисовать 3 круга с 5 звездами в каждом круге (образный) и написать уравнение 3 x 5 = 15 (абстрактное). Все три этапа обучения в одном упражнении.
Все три этапа обучения в одном упражнении.
Следующая мыльница.Как учителя, давайте будем уверены, что мы используем точный язык. Если вы описываете уравнение умножения, убедитесь, что вы вызываете умножаемые числа на множители , а ответ на проблему умножения — произведение . Я также обнаружил, что ученики легко запутались в строках и столбцах. Простая таблица привязок, показывающая этот словарный запас, станет отличным напоминанием как для вас, так и для студентов.
Вам тоже может понравиться… Умножение
ppt для 3 класса
Пример: 5 × 3 = 5 + 5 + 5 = 15 Но помимо умножения на целые числа, мы также можем умножать на дроби, десятичные дроби и многое другое. Опасность умножения 3-го класса Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский Нажмите F11 Выберите пункт меню Вид> Войти в полноэкранный режим для полноэкранного режима 7 раз по 3, и давайте избавимся от это. Умножение, запоминание, манипуляции и многое другое.Вы также можете настроить их, используя генератор ниже. Вы можете изменить свои рекламные предпочтения в любое время. Умножение powerpoint. Мания умножения — Мания умножения Презентация PowerPoint Кери Дауди Седалия Элементарная школа 3-го класса Мания умножения Мания умножения Инструкции: возьмите лист бумаги. 4,134. Мания умножения Презентация PowerPoint Кери Дауди Седалия Элементарная школа 3-го класса Мания умножения Мания умножения Инструкции: возьмите лист бумаги. 3 x 2 = 6 Можем ли мы написать предложение умножения? Учащиеся должны определить, какую операцию они… Компоненты урока: PowerPoint x1, x11, x 0.3 2 3 ряда и 2 столбца. Сделайте неограниченный запас рабочих листов по темам умножения 3-го класса, включая подсчет пропусков, таблицы умножения и пропущенные коэффициенты. Рабочие листы делятся на «простое умножение», «умножение на десять» и «умножение в столбцах». Гарнитуры. Использование этой таблицы деления и умножения с 3-й оценкой.
Умножение, запоминание, манипуляции и многое другое.Вы также можете настроить их, используя генератор ниже. Вы можете изменить свои рекламные предпочтения в любое время. Умножение powerpoint. Мания умножения — Мания умножения Презентация PowerPoint Кери Дауди Седалия Элементарная школа 3-го класса Мания умножения Мания умножения Инструкции: возьмите лист бумаги. 4,134. Мания умножения Презентация PowerPoint Кери Дауди Седалия Элементарная школа 3-го класса Мания умножения Мания умножения Инструкции: возьмите лист бумаги. 3 x 2 = 6 Можем ли мы написать предложение умножения? Учащиеся должны определить, какую операцию они… Компоненты урока: PowerPoint x1, x11, x 0.3 2 3 ряда и 2 столбца. Сделайте неограниченный запас рабочих листов по темам умножения 3-го класса, включая подсчет пропусков, таблицы умножения и пропущенные коэффициенты. Рабочие листы делятся на «простое умножение», «умножение на десять» и «умножение в столбцах». Гарнитуры. Использование этой таблицы деления и умножения с 3-й оценкой.

 Эта презентация в формате PowerPoint для умножения подходит для учащихся 3-4 классов. Надеюсь, вы сочтете это полезным, и любая обратная связь будет оценена 🙂 4 плюс 0 равно 4. Уровень 3 Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10 Этот 25-дневный модуль начинается с построения на свободное владение студентами сложением и знанием массивов.3 C. 7 D. 17 Current 🙂 Другое 🙂 Используйте свойство коммутативности для решения следующих задач умножения. 0 Б. 5 оценочных заданий: 3 класс по математике. УМНОЖЕНИЕ Класс 4 Школа Нос-Крик … умножение: Конкретный результат 3 Примените стратегии умственной математики и свойства чисел, чтобы понять и вспомнить основные факты умножения (таблицы умножения) на 81 и связанное с ним деление … Что такое умножение — Дата создания PowerPoint: Похоже, вы уже обрезали этот слайд.https://www.slideshare.net/haleytemple/multiplication-properties-39945093 Сколько там столбцов? Автор: Kelly Mott Дата создания: 09.01.2010 14:25:20 Название: Everyday Math Grade 4 — Lesson 1.
Эта презентация в формате PowerPoint для умножения подходит для учащихся 3-4 классов. Надеюсь, вы сочтете это полезным, и любая обратная связь будет оценена 🙂 4 плюс 0 равно 4. Уровень 3 Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10 Этот 25-дневный модуль начинается с построения на свободное владение студентами сложением и знанием массивов.3 C. 7 D. 17 Current 🙂 Другое 🙂 Используйте свойство коммутативности для решения следующих задач умножения. 0 Б. 5 оценочных заданий: 3 класс по математике. УМНОЖЕНИЕ Класс 4 Школа Нос-Крик … умножение: Конкретный результат 3 Примените стратегии умственной математики и свойства чисел, чтобы понять и вспомнить основные факты умножения (таблицы умножения) на 81 и связанное с ним деление … Что такое умножение — Дата создания PowerPoint: Похоже, вы уже обрезали этот слайд.https://www.slideshare.net/haleytemple/multiplication-properties-39945093 Сколько там столбцов? Автор: Kelly Mott Дата создания: 09.01.2010 14:25:20 Название: Everyday Math Grade 4 — Lesson 1. 2 Последнее изменение: Ashley Компания: Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Числовые формы. Теперь настройте имя буфера обмена для хранения ваших клипов. 7 + = 10 A. Рабочие листы могут быть выполнены в формате html или PDF (оба легко распечатать).https://www.slideshare.net/MandieFunk/multiplication-powerpoint Подробнее см. в нашей Политике конфиденциальности и Пользовательском соглашении. Задачи на умножение слов для учащихся 3-х классов. Грамматические игры для KidsGames, которые помогут вам узнать о существительных, прилагательных, пунктуации, глаголах, синонимах, антонимах и омонимах. А. 2 3 2 ряда и 3 столбика. Свойство распределения упрощает умножение с большими числами, разбивая их на более мелкие слагаемые. Если вам нужна распечатанная таблица деления и умножения для учащихся 3-х классов, не ищите дальше.Поймите коммутативное свойство умножения. Получите 3 вопроса из 4, чтобы повысить свой уровень! Таблицы умножения для 3-го класса.
2 Последнее изменение: Ashley Компания: Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Числовые формы. Теперь настройте имя буфера обмена для хранения ваших клипов. 7 + = 10 A. Рабочие листы могут быть выполнены в формате html или PDF (оба легко распечатать).https://www.slideshare.net/MandieFunk/multiplication-powerpoint Подробнее см. в нашей Политике конфиденциальности и Пользовательском соглашении. Задачи на умножение слов для учащихся 3-х классов. Грамматические игры для KidsGames, которые помогут вам узнать о существительных, прилагательных, пунктуации, глаголах, синонимах, антонимах и омонимах. А. 2 3 2 ряда и 3 столбика. Свойство распределения упрощает умножение с большими числами, разбивая их на более мелкие слагаемые. Если вам нужна распечатанная таблица деления и умножения для учащихся 3-х классов, не ищите дальше.Поймите коммутативное свойство умножения. Получите 3 вопроса из 4, чтобы повысить свой уровень! Таблицы умножения для 3-го класса. Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow.com — id: 69ed85-YmJlZ Не хочу запутаться. 1. Buckle’s 3. Подробности см. В нашей Политике конфиденциальности и Пользовательском соглашении. Позвоночник. Отображение 8 лучших рабочих листов, найденных для — 3-х классное умножение в формате PDF.Заставь умножиться! Обзор умножения. … Нажмите на картинку, чтобы погрузиться в мир умножения. Этот 25-дневный модуль основан непосредственно на работе студентов с умножением и делением в Модуле 1. Коммутативное свойство умножения Получите 5 вопросов из 7, чтобы повысить уровень! Это 4-дневная презентация PowerPoint. Распределительное свойство умножения для 3-го класса. Рабочие листы для печати Третьеклассники могут научиться уверенно решать вопросы умножения и распределения с помощью этих увлекательных рабочих листов.Давайте немного повысим ставки.
Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow.com — id: 69ed85-YmJlZ Не хочу запутаться. 1. Buckle’s 3. Подробности см. В нашей Политике конфиденциальности и Пользовательском соглашении. Позвоночник. Отображение 8 лучших рабочих листов, найденных для — 3-х классное умножение в формате PDF.Заставь умножиться! Обзор умножения. … Нажмите на картинку, чтобы погрузиться в мир умножения. Этот 25-дневный модуль основан непосредственно на работе студентов с умножением и делением в Модуле 1. Коммутативное свойство умножения Получите 5 вопросов из 7, чтобы повысить уровень! Это 4-дневная презентация PowerPoint. Распределительное свойство умножения для 3-го класса. Рабочие листы для печати Третьеклассники могут научиться уверенно решать вопросы умножения и распределения с помощью этих увлекательных рабочих листов.Давайте немного повысим ставки. Дата!! Эта практика цифрового умножения для Google Slides ™ позволяет учащимся улучшить свое владение фактами умножения увлекательным и увлекательным способом! Разогрев!! 7 умножить на 3 равно 21. Задачи умножения и деления слов 3-й класс Напишите предложение умножения. Gauntlet. Это нацелено на 4/5/6 год. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. 1068 C. 1608 D. 1680 Какое число делает это предложение верным? Вырезание — удобный способ собрать важные слайды, к которым нужно вернуться позже.Мы используем ваш профиль в LinkedIn и данные о вашей активности, чтобы персонализировать рекламу и показывать вам более релевантную рекламу. Краткий обзор провинции Белуджистан Презентация г-на Аллаха Дад Хана. Умножение словарного запаса математика видео elementary kids youtube. Поместите 1 туда и положите 2 сюда. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. Помимо набора простых задач умножения, есть и контрольные вопросы.
Дата!! Эта практика цифрового умножения для Google Slides ™ позволяет учащимся улучшить свое владение фактами умножения увлекательным и увлекательным способом! Разогрев!! 7 умножить на 3 равно 21. Задачи умножения и деления слов 3-й класс Напишите предложение умножения. Gauntlet. Это нацелено на 4/5/6 год. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. 1068 C. 1608 D. 1680 Какое число делает это предложение верным? Вырезание — удобный способ собрать важные слайды, к которым нужно вернуться позже.Мы используем ваш профиль в LinkedIn и данные о вашей активности, чтобы персонализировать рекламу и показывать вам более релевантную рекламу. Краткий обзор провинции Белуджистан Презентация г-на Аллаха Дад Хана. Умножение словарного запаса математика видео elementary kids youtube. Поместите 1 туда и положите 2 сюда. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. Помимо набора простых задач умножения, есть и контрольные вопросы. 168 B. 3 MCC @ WCCUSD (SBCMI) 15.10.11 !!!! Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте.Некоторые из рабочих листов для этой концепции: математика мамонта 3 степени a, умножение, работа умножения 3 степени, работа умножения 3 степени, математика мамонт светло-голубой степени 3 b, умножение, степень, пакет умножения 3. Вход в систему не требуется. Все рабочие листы являются документами в формате pdf и могут быть распечатаны. Напишите предложение умножения. 0. Узнайте об образовании Borad в Пенджабе, Совет школьного образования Пенджаба, Auto En … Для этого слайда не найдено общедоступных буферов обмена. На каждом рабочем листе есть несколько задач со словами и лист для ответов.Теперь настройте имя буфера обмена для хранения ваших клипов. Модуль 3 по математике для 3-го класса. Математические игры в классе PowerPoint для 3-го класса, отработка математических навыков третьего класса, опасность для миллионеров PPT, Олимпийские игры, математические темы для 3-го класса, сложение до 4-значных чисел, уравнения баланса, гистограммы, множества, диаграммы Венна, вероятность, линейные графики, таблицы, деление, делимость, дроби, десятичные дроби, умножение до 1000, числа, сравнения, римские цифры, даже… Проверьте Приготовьтесь к 3-му классу.
168 B. 3 MCC @ WCCUSD (SBCMI) 15.10.11 !!!! Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте.Некоторые из рабочих листов для этой концепции: математика мамонта 3 степени a, умножение, работа умножения 3 степени, работа умножения 3 степени, математика мамонт светло-голубой степени 3 b, умножение, степень, пакет умножения 3. Вход в систему не требуется. Все рабочие листы являются документами в формате pdf и могут быть распечатаны. Напишите предложение умножения. 0. Узнайте об образовании Borad в Пенджабе, Совет школьного образования Пенджаба, Auto En … Для этого слайда не найдено общедоступных буферов обмена. На каждом рабочем листе есть несколько задач со словами и лист для ответов.Теперь настройте имя буфера обмена для хранения ваших клипов. Модуль 3 по математике для 3-го класса. Математические игры в классе PowerPoint для 3-го класса, отработка математических навыков третьего класса, опасность для миллионеров PPT, Олимпийские игры, математические темы для 3-го класса, сложение до 4-значных чисел, уравнения баланса, гистограммы, множества, диаграммы Венна, вероятность, линейные графики, таблицы, деление, делимость, дроби, десятичные дроби, умножение до 1000, числа, сравнения, римские цифры, даже… Проверьте Приготовьтесь к 3-му классу. Свойства умножения и деления 3.OA.5 / 3.OA.B.5 — Действия для обучения операциям и алгебраическому мышлению, включая рабочие листы операций и алгебраического мышления, практические задачи операций и алгебраического мышления, вопросы, оценки, викторины, тесты, урок планы — согласованы с Общим ядром и государственными стандартами — Пример пути в книге целей: 5 × 3½ = 5 + 5 + 5 + (половина от 5) = 17,5 Попробуйте перетащить цифры в синие поля ниже: HA получают расследование, которое на самом деле наслаждались.Вы можете изменить свои рекламные предпочтения в любое время. Несите 1. CST) # 12N.S. Используйте эту интерактивную презентацию PowerPoint после обучения умножению и делению. Мысленная математика — шаблоны умножения с использованием 10, 100 и 1000. См. Наше Пользовательское соглашение и Политику конфиденциальности. Теперь мы готовы добавить. Эти тыквенные головоломки MULTIPLICATION — отличный способ для учащихся 3-го, 4-го и 5-го классов или учеников домашнего обучения получить увлекательную практику умножения.
Свойства умножения и деления 3.OA.5 / 3.OA.B.5 — Действия для обучения операциям и алгебраическому мышлению, включая рабочие листы операций и алгебраического мышления, практические задачи операций и алгебраического мышления, вопросы, оценки, викторины, тесты, урок планы — согласованы с Общим ядром и государственными стандартами — Пример пути в книге целей: 5 × 3½ = 5 + 5 + 5 + (половина от 5) = 17,5 Попробуйте перетащить цифры в синие поля ниже: HA получают расследование, которое на самом деле наслаждались.Вы можете изменить свои рекламные предпочтения в любое время. Несите 1. CST) # 12N.S. Используйте эту интерактивную презентацию PowerPoint после обучения умножению и делению. Мысленная математика — шаблоны умножения с использованием 10, 100 и 1000. См. Наше Пользовательское соглашение и Политику конфиденциальности. Теперь мы готовы добавить. Эти тыквенные головоломки MULTIPLICATION — отличный способ для учащихся 3-го, 4-го и 5-го классов или учеников домашнего обучения получить увлекательную практику умножения. Ремонт и поломка лифтов Kent — jdrliftservices.co.uk, Научите ребенка читать за 100 простых уроков. Для этого слайда не найдено общедоступных буферов обмена. Рабочие листы и таблицы умножения. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. Щелкните изображение, чтобы просмотреть презентацию PowerPoint, которую я использую в классе для обучения графиков, диаграмм и таблиц. 2 x 3 = 6 Можем ли мы написать предложение умножения? Это формальный письменный метод умножения, который различается тремя способами. Умножение Входной Выход для 3-го класса — Отображение 8 лучших рабочих листов, найденных для этой концепции.. Также включены вопросы о недостающих факторах. ! Используйте их в качестве осеннего задания, в математическом центре Хэллоуина или… Итак, мы должны не забыть поставить туда 0. 29 октября 2016 г. — Вы ищете систематизированный PowerPoint, который познакомит ваших учеников с традиционным алгоритмом умножения (для 2- и 3-значных чисел) логическим, пошаговым образом? Умножение — две цифры на одну цифру.
Ремонт и поломка лифтов Kent — jdrliftservices.co.uk, Научите ребенка читать за 100 простых уроков. Для этого слайда не найдено общедоступных буферов обмена. Рабочие листы и таблицы умножения. Если вы продолжаете просматривать сайт, вы соглашаетесь на использование файлов cookie на этом сайте. Щелкните изображение, чтобы просмотреть презентацию PowerPoint, которую я использую в классе для обучения графиков, диаграмм и таблиц. 2 x 3 = 6 Можем ли мы написать предложение умножения? Это формальный письменный метод умножения, который различается тремя способами. Умножение Входной Выход для 3-го класса — Отображение 8 лучших рабочих листов, найденных для этой концепции.. Также включены вопросы о недостающих факторах. ! Используйте их в качестве осеннего задания, в математическом центре Хэллоуина или… Итак, мы должны не забыть поставить туда 0. 29 октября 2016 г. — Вы ищете систематизированный PowerPoint, который познакомит ваших учеников с традиционным алгоритмом умножения (для 2- и 3-значных чисел) логическим, пошаговым образом? Умножение — две цифры на одну цифру. умножение ppt для 3-го класса. Изучение моделей умножения. Если да, то эта интерактивная презентация PowerPoint с 30 слайдами может быть именно тем, что вы ищете! В этом упражнении студенты будут решать факты умножения на каждой странице.Калькулятор федерального подоходного налога сша Ресурсы для учителей / файлы математики k-5th class. 1) 3! 5 = 5! 3 = 2) 8! 10 = 10! 8 = … Числовая ценность — одна из самых важных концепций, которые учащиеся усваивают в математике в третьем классе. Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Создано Джимми Додсоном. Модуль 3 расширяет изучение факторов от 2, 3, 4, 5 и 10, чтобы включить все единицы от 0 до 10, а также кратные 10 в пределах 100. Наши рабочие листы умножения для 3-го уровня начинаются со значения умножения и последующих с большим количеством практики умножения и таблиц умножения; упражнения также включают умножение на целые десятки и целые сотни, а также умножение некоторых столбцов.
умножение ppt для 3-го класса. Изучение моделей умножения. Если да, то эта интерактивная презентация PowerPoint с 30 слайдами может быть именно тем, что вы ищете! В этом упражнении студенты будут решать факты умножения на каждой странице.Калькулятор федерального подоходного налога сша Ресурсы для учителей / файлы математики k-5th class. 1) 3! 5 = 5! 3 = 2) 8! 10 = 10! 8 = … Числовая ценность — одна из самых важных концепций, которые учащиеся усваивают в математике в третьем классе. Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Создано Джимми Додсоном. Модуль 3 расширяет изучение факторов от 2, 3, 4, 5 и 10, чтобы включить все единицы от 0 до 10, а также кратные 10 в пределах 100. Наши рабочие листы умножения для 3-го уровня начинаются со значения умножения и последующих с большим количеством практики умножения и таблиц умножения; упражнения также включают умножение на целые десятки и целые сотни, а также умножение некоторых столбцов. 1 плюс 3 равно 4. Некоторые из рабочих листов для этой концепции: Входящие и исходящие блоки, Работа, 12 фактов умножения, Вход и выход, Таблицы входных выходов, Блок 3, практика подготовки таблиц входных и выходных данных, Словарный запас слов для 3 класса , Северная Каролина готова к концу класса выпустила оценку. Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Плюс 2 — 37. Включает PPT, ресурсы и план урока.
1 плюс 3 равно 4. Некоторые из рабочих листов для этой концепции: Входящие и исходящие блоки, Работа, 12 фактов умножения, Вход и выход, Таблицы входных выходов, Блок 3, практика подготовки таблиц входных и выходных данных, Словарный запас слов для 3 класса , Северная Каролина готова к концу класса выпустила оценку. Slideshare использует файлы cookie для улучшения функциональности и производительности, а также для предоставления вам релевантной рекламы. Плюс 2 — 37. Включает PPT, ресурсы и план урока.Сан-Антонио, Нуэва-Эсиха-Барангайс, Руководства Thermo King Pdf, Можете ли вы сами выкурить сладкий Swisher? Orbi Dynamic Qos, Водные снегоходы Shappell XL, Якудза: Как дракон, сражающийся за героя по совместительству, Печать Emoji Discord, Прическа Ffxiv Make It Rain, Пикап Sam’s Club не работает, Самоочищающиеся льдогенераторы,
Сложение, сумма, вычитание, умножение, деление, квадрат
Одно из самых полезных занятий с Google Таблицами — это математика.Если вы просто хотите решить простые математические задачи или у вас есть вычисления, которые необходимо выполнить с набором данных, выполнять математику в электронной таблице Google очень легко, если вы знаете, какие символы использовать.
Чтобы выполнить вычисления в электронной таблице Google, выполните следующие действия:
- Введите знак равенства в ячейку (=)
- Введите число или ссылку на ячейку (для ячейки, содержащей число)
- Затем используйте один из следующих математических операторов + (плюс), — (минус), * (умножение), / (деление)
- Введите другое число или ссылку на ячейку
- Нажмите ввод
В этой статье я покажу вам, как выполнять математические вычисления в электронной таблице Google , используя обычные числа и ссылки на ячейки… и я также покажу вам разницу между математическими функциями и математическими операторами.
Вот математические формулы в Google Таблицах:
Формулы сложения в Google Таблицах
Добавить, используя ссылки на ячейки
Сложить числа без ссылок на ячейки
Добавить с помощью функции ADD
Формула суммы в Google Таблицах
Формулы вычитания в Google Таблицах
Вычесть, используя ссылки на ячейки
Вычесть числа без ссылок на ячейки
Вычесть с помощью функции МИНУС
Формулы умножения в Google Таблицах
Умножить, используя ссылки на ячейки
Умножение чисел без ссылок на ячейки
Умножение с помощью функции УМНОЖЕНИЕ
Формулы деления в Google Таблицах
Разделить с помощью ссылок на ячейки
Разделить числа без ссылок на ячейки
Разделить с помощью функции РАЗДЕЛ
Квадратные формулы в Google Таблицах
Квадрат с использованием ссылок на ячейки
Квадратные числа без ссылок на ячейки
Квадратные числа с функцией СТЕПЕНЬ
Формулы квадратного корня в Google Таблицах
Квадратный корень с использованием ссылок на ячейки
Квадратный корень чисел без ссылок на ячейки
Получите бесплатную шпаргалку по Google Таблицам
Математика в электронных таблицах: функции против.
 Операторы
ОператорыЕсли вы новичок в использовании формул Google Таблиц, может возникнуть соблазн использовать математические функции, такие как = Сложение, = Вычитание, = Минус, = Разделить … и эти функции действительно работают … но это намного проще и более распространено использовать операторы электронных таблиц при выполнении сложения, вычитания, умножения и деления в Google Таблицах (а также возведения в квадрат). 2/4 * 4-1
Использование простых чисел vs.ссылки на ячейки
При настройке математических формул в электронной таблице Google вы можете вводить числа прямо в формулу, или вы также можете ссылаться на ячейку, внутри которой есть число…. или вы можете использовать их сочетание там, где это необходимо.
Большим преимуществом использования ссылок на ячейки в формулах является то, что вы можете легко изменить число внутри ячейки и, следовательно, число в формуле … без изменения самой формулы. Это становится еще более полезным, когда у вас есть несколько формул, использующих одну и ту же ссылку на ячейку.
Это становится еще более полезным, когда у вас есть несколько формул, использующих одну и ту же ссылку на ячейку.
Следует ли вводить числа непосредственно в формулу или вводить числа в ячейки, а затем ссылаться на эти ячейки в формуле… все зависит от вашей конкретной задачи. Если вы планируете менять номер довольно часто, то лучше всего использовать ссылку на ячейку. Но если вы применяете в своей формуле константу, которая не изменится, может быть лучше просто ввести число в формуле.
Ниже показано несколько примеров этого с изображениями, но вот краткое объяснение использования ссылок на ячейки по сравнению спростые числа в математических формулах электронных таблиц.
Выполнение математических вычислений в электронных таблицах с использованием только чисел
Например, если вы хотите решить простую математическую задачу, используя Google Таблицы в качестве калькулятора, вы можете ввести в ячейку что-то вроде следующего:
= 27/3
В ячейке отобразится ответ «9».
Математика в электронных таблицах с использованием ссылок на ячейки
Но если вы хотите, вы также можете вводить числа в ячейки и выполнять математические вычисления, обращаясь к этим ячейкам. Ссылка на ячейку — это буква, за которой следует число… буква относится к столбцу, а число — к строке. Так, например, если вы хотите «сослаться» на ячейку в своей формуле, вы должны ввести ссылку или адрес ячейки, который снова представляет собой букву столбца, за которой следует номер строки. Итак, самая первая ячейка в электронной таблице в столбце A и строке 1 как ячейка A1.
Если вы ввели число «27» в ячейку A1 и число «3» в ячейку B1, вы можете использовать следующую формулу в любой другой ячейке:
= A1 / B1
Это также отобразит ответ «9» в ячейке.
Использование сочетания чисел и ссылок на ячейки для вычисления
Во многих случаях вам может понадобиться использовать ссылки на ячейки и числа, как это.
= A1 / 3
Это также даст ответ «9», если предположить, что число «27» введено в ячейку A1.
Быстрое применение формул к нескольким ячейкам
Вы, вероятно, захотите иметь возможность легко и быстро применять вычисления в вашей электронной таблице к нескольким ячейкам, поэтому я хочу показать вам два способа сделать это.(Последние примеры в этом уроке продемонстрируют оба этих метода с включенным изображением).
Вариант 1: После ввода математической формулы в ячейку скопируйте и вставьте ячейку / формулу в ячейки ниже, и формула будет скопирована в каждую отдельную ячейку. Если в вашей формуле есть ссылки на ячейки, они будут корректироваться автоматически при копировании в строки ниже.
Щелкните здесь, чтобы узнать, как быстро скопировать формулы вниз по всему столбцу.
Вариант 2: Вы также можете использовать функцию ARRAYFORMULA, чтобы ваши математические формулы применялись к нескольким ячейкам. С ARRAYFORMULA вы можете применить одну формулу к нескольким ячейкам или ко всему столбцу.
Как добавить в Google Таблицы
Начнем с различных способов добавления в Google Таблицы. Я покажу вам, как складывать, используя обычные числа, а также используя ссылки на ячейки, а затем я покажу вам, как складывать вместе более двух ячеек.
Я покажу вам, как складывать, используя обычные числа, а также используя ссылки на ячейки, а затем я покажу вам, как складывать вместе более двух ячеек.
Чтобы добавить в Google Таблицы, просто введите знак равенства в ячейку (=), затем введите числа или ячейки (ссылки), которые вы хотите добавить, разделенные знаком плюс (+), и нажмите клавишу ВВОД. Вот три примера формул сложения:
- = 25 + 25
- = A1 + 25
- = A1 + B1
Сложение чисел
В приведенной ниже формуле нет ссылок на ячейки, а просто используются простые числа для математических расчетов в Google Таблицах, что-то вроде калькулятора.
Выберите любую ячейку на листе, введите формулу ниже и нажмите клавишу ВВОД.
= 100 + 200
В ячейке должен отображаться ответ «300», как показано ниже.
Добавление ячеек с числами
Теперь давайте добавим, используя ссылки на ячейки. Вместо того, чтобы вводить числа непосредственно в нашу формулу, на этот раз мы обращаемся к ячейкам, в которых есть числа, и говорим формуле сложить числа, которые находятся в этих ячейках.
Чтобы добавить в Google Таблицы, выполните следующие действия:
- Щелкните ячейку A1, затем введите число «100» и затем нажмите ввод
- Щелкните ячейку A2, затем введите число «200» и затем нажмите ввод
- Щелкните ячейку A3, затем введите «= A1 + A2 «, а затем нажмите Enter.
- В ячейке A3 теперь должен отображаться ответ» 300 «
Формула, показанная ниже: = A1 + A2
Добавление нескольких ячеек
Вы также можете добавить более двух ячеек вместе в свою электронную таблицу.Просто продолжайте вводить ссылки на ячейки, которые вы хотите добавить, через знаки плюса, а затем нажмите клавишу ВВОД, когда ваша формула будет завершена.
После ввода знака «плюс» или любого другого математического оператора, если на то пошло, вы также можете щелкнуть ячейку, на которую хотите сослаться, вместо того, чтобы вводить ссылку.
Формула, показанная ниже: = A1 + A2 + A3 + A4 + A5 + A6 + A7
Добавление нескольких несмежных ячеек
Если ячейки, которые вы складываете вместе, находятся в одном столбце или строке, самый простой способ добавить их — «суммировать» их, что я покажу вам через мгновение … но когда добавляемые вами ячейки являются не смежные, это когда добавление нескольких отдельных ячеек становится чрезвычайно полезным.
Если на вашем листе есть числа, введенные в разных местах, которые вы хотите сложить, вы можете сделать это с помощью формулы, подобной той, которая показана в примере ниже.
Формула, использованная в примере: = A1 + B2 + C3
Использование функции ADD для добавления
Использование функции ДОБАВИТЬ для добавления гораздо менее распространено и менее полезно, чем использование оператора знака плюс, но вот пример, показывающий, как его использовать в случае, если он вам нужен.
Формула, показанная ниже: = ADD (100,200)
Как суммировать в Google Таблицах
Функция СУММ — чрезвычайно полезная формула, которая позволяет суммировать целые строки, столбцы или указанные диапазоны.
Для суммирования в Google Таблицах начните с ввода «= Sum (», затем введите диапазон ячеек, которые вы хотите суммировать, например «B1: B100», введите закрывающие круглые скобки «)», а затем нажмите клавишу ВВОД.
Допустим, у вас есть столбец чисел, который вы хотите добавить, но вам не нужна длинная формула, добавляющая множество отдельных ячеек. Здесь вы можете использовать функцию СУММ.
Здесь вы можете использовать функцию СУММ.
Чтобы просуммировать весь столбец в электронной таблице Google, выполните одно из следующих действий:
- Используйте ячейку в верхней части столбца, чтобы ввести такую формулу, которая суммирует все ячейки под ней: = СУММ (C1: C)
- Или используйте ячейку, которая находится ниже диапазона, который вы хотите суммировать , и введите формулу, содержащую диапазон ячеек, которые находятся над ней.Другими словами, например, если ваша формула СУММ находится в ячейке C100, то для суммирования чисел в столбце A, которые находятся над вашей формулой, убедитесь, что вы указали конечную строку в диапазоне, который меньше 100, например: = СУММ (C1: C99)
Формула, показанная в примере изображения ниже: = СУММ (A1: A7)
Примечание. Если диапазон в формуле суммы содержит ячейку, в которую введена формула, это вызовет ошибку циклической зависимости.
Как вычитать в Google Таблицах
Теперь давайте рассмотрим различные способы вычитания в электронной таблице. Я снова покажу вам, как вычитать, используя только числа, а также покажу вам, как вычитать с помощью ссылок на ячейки.
Я снова покажу вам, как вычитать, используя только числа, а также покажу вам, как вычитать с помощью ссылок на ячейки.
Чтобы вычесть в Google Таблицах, введите знак равенства в ячейку (=), затем введите числа или ячейку (например, A1), которые вы хотите вычесть, со знаком минус (-) между ними, а затем нажмите клавишу ВВОД. Вот три примера:
- = 100-50
- = A1-50
- = A1-B1
Вычесть числа
Вот пример, показывающий, как выполнять вычитание, просто используя числа непосредственно в формуле.
Формула, показанная в примере ниже: = 700-300
После ввода приведенной выше формулы в ячейку электронной таблицы, в ячейке будет отображаться ответ «400».
Вычесть ячейки с числами
Вы также можете использовать ссылки на ячейки для вычитания… где числа, которые вы хотите вычесть друг из друга, вводятся в ячейки, и где вы затем ссылаетесь на эти ячейки в формуле для выполнения ваших вычислений. Использование ссылок на ячейки для вычитания позволит вам очень быстро и легко изменить числа, на которые ссылается ваша формула, без необходимости изменять формулу.
Использование ссылок на ячейки для вычитания позволит вам очень быстро и легко изменить числа, на которые ссылается ваша формула, без необходимости изменять формулу.
Чтобы вычесть в Google Таблицах, выполните следующие действия:
- Щелкните ячейку A1, затем введите число «3000» и затем нажмите ввод
- Щелкните ячейку A2, затем введите число «1000» и затем нажмите ввод
- Щелкните ячейку A3, затем введите «= A1 -A2 «, а затем нажмите ввод
- В ячейке A3 должен отображаться ответ» 2000 «
Пример формулы: = A1-A2
Использование функции МИНУС для вычитания
Вот пример, показывающий, как выполнять вычитание с помощью функции МИНУС.
Формула, показанная ниже: = МИНУС (700,300)
Как умножить в Google Таблицах
Теперь давайте рассмотрим, как умножать в электронной таблице. Как и в случае с сложением и вычитанием, вы можете выбрать, хотите ли вы использовать обычные числа в своей формуле, или хотите ли вы использовать ссылки на ячейки … или их сочетание.
Для умножения в электронной таблице Google сначала введите знак равенства в ячейку (=), затем введите числа или ссылки на ячейки, которые вы хотите умножить, со звездочкой (*), разделяющей их, а затем нажмите клавишу ВВОД.Вот три быстрых примера формул умножения:
- = 10 * 10
- = A1 * 10
- = A1 * A2
Умножение чисел
Если вы хотите, для умножения вы можете использовать свою электронную таблицу как калькулятор и просто ввести формулу, подобную приведенной ниже, которая не использует ссылки на ячейки и имеет номера, введенные непосредственно в строку формул.
Формула в примере: = 10 * 7
Введите приведенную выше формулу в ячейку на листе, и в этой ячейке отобразится ответ «70».
Умножение ячеек на числа
Опять же, как и в случае с сложением и вычитанием, вы можете использовать ссылки на ячейки в своих формулах умножения, где числа, которые вы хотите умножить, вводятся в отдельные ячейки, и где ваша формула ссылается на эти ячейки для обозначения умножаемых значений.
Для умножения в Google Таблицах выполните следующие действия:
- Щелкните ячейку A1, затем введите число «7» и затем нажмите ввод
- Щелкните ячейку B1, затем введите число «7» и затем нажмите ввод
- Щелкните ячейку C1, затем введите «= A1 * B1 «, а затем нажмите» Ввод «.
- В ячейке C1 теперь должен отображаться ответ» 49 «
Формула, показанная ниже: = A1 * B1
Использование функции MULTIPLY для умножения
Пример ниже показывает, как умножать с помощью функции УМНОЖИТЬ.Однако гораздо более распространен и прост в использовании метод оператора, показанный выше.
Формула, показанная ниже: = НЕСКОЛЬКО (10,7)
Как разделить в Google Таблицах
Теперь я покажу вам, как делить в вашей таблице! Я еще раз покажу вам разницу между использованием обычных чисел и использованием ссылок на ячейки для деления… и я также покажу вам разницу между использованием оператора и функции для деления.
Чтобы разделить таблицу Google, начните с привязки знака равенства к ячейке (=), затем введите числа (или ссылки на ячейки с числами), которые вы хотите разделить, разделите их косой чертой (/), а затем нажмите ввод. Вот три простых примера формул деления:
- = 75/3
- = A1 / 3
- = A1 / A2
Обратите внимание, что, как и при использовании калькулятора, нельзя успешно разделить на 0 в электронной таблице. Если ваш знаменатель (число «внизу» или после косой черты) равен 0, ваша формула деления будет отображать ошибку # DIV / 0. Эту ошибку можно обработать с помощью функции ЕСЛИОШИБКА, которая позволит вам указать, какое значение должно отображаться, если в формуле есть ошибка.
Вот два примера обработки ошибки # DIV / 0:
- = ЕСЛИОШИБКА (C1 / C2,0)
- = ЕСЛИОШИБКА (C1 / C2, «Ошибка»)
Разделите числа
Вот пример, который показывает, как делить, используя только числа, без ссылки на какие-либо ячейки на листе.
Формула, показанная ниже: = 100/5
Введите приведенную выше формулу в любую ячейку на листе, и в этой ячейке должен отображаться ответ «20».
Разделить ячейки с числами
При желании вы можете ввести числа, которые хотите разделить на отдельные ячейки электронной таблицы, а затем ссылаться на эти ячейки в своей формуле деления.Это будет особенно полезно, если вы планируете со временем изменить одно или несколько значений в формуле. 2
Квадрат с функцией СТЕПЕНЬ
Существует также функция, которая может использоваться для возведения квадратов, и она называется POWER.Эту функцию также можно записать просто как POW. Вот пример того, как использовать эту функцию.
Формула, показанная ниже: = МОЩНОСТЬ (2,2)
Альтернативная формула: = POW (2,2)
Как извлекать квадратный корень из чисел в Google Таблицах
Если вам нужно извлечь квадратный корень из числа в электронной таблице, вы можете использовать функцию КОРЕНЬ.
Чтобы извлечь квадратный корень в Google Таблицах, в любой ячейке просто введите «= SQRT («, затем введите число по вашему выбору, введите закрывающие круглые скобки «)» и нажмите клавишу ВВОД. Вот два примера формул квадратного корня:
- = КОРЕНЬ (9)
- = КОРЕНЬ (100)
Квадратный корень чисел
Самый простой способ извлекать квадратный корень из числа на листе — просто ввести обычное число непосредственно в формулу КОРЕНЬ, как показано ниже.
Формула, используемая в примере ниже: = КОРЕНЬ (9)
Введите формулу, показанную выше, в ячейку электронной таблицы, и тогда в этой ячейке должен отобразиться ответ «3».
Ячейки квадратного корня с числами
Если вы хотите использовать ссылку на ячейку для обозначения значения, которое вы хотите извлекать из квадратного корня, чтобы при изменении числа в ячейке он также изменял ваш ответ … вы также можете сделать это с помощью функции SQRT, просто набрав адрес ячейки / ссылка в функции.
Чтобы получить квадратный корень в Google Таблицах, выполните следующие действия:
- Щелкните ячейку A1, затем введите число «9» и затем нажмите ввод
- Щелкните ячейку B1, затем введите = SQRT (A1) и нажмите ввод
- В ячейке B1 теперь должен отображаться ответ «3»
Формула, используемая в примере ниже: = SQRT (A1)
Как рассчитывать уравнения в Google Таблицах
Google Таблицы могут делать гораздо больше, чем просто математические задачи с двумя значениями.Вы также можете настроить математические уравнения, чтобы ваш лист автоматически решал уравнение при вводе / изменении переменных.
Ниже показано, как рассчитать длину окружности и площадь в вашей электронной таблице с учетом указанного радиуса.
Обратите внимание, что в этих уравнениях используются числа и ссылки на ячейки в формуле. Числа, введенные непосредственно в формулу, такие как 3,14 (пи), который является константой… а ссылки на ячейки представляют радиус, который является переменной, и мы хотим иметь возможность легко изменять. 2
2
На изображении выше вы можете видеть, что формулы окружности вводятся в столбце B, а формулы площади вводятся в столбец C.
В каждой синей ячейке изображения есть формула… и каждая формула относится к радиусу, который указан рядом с ней. Это было сделано путем копирования и вставки формул вверху (строка 2) в ячейки ниже.
При копировании и вставке таких формул ссылка на ячейку будет автоматически изменяться, поскольку формула вставляется в следующую строку. Именно так каждая формула окружности и площади относится к радиусу, указанному в той же строке, потому что каждый раз, когда формулы вставляются в следующую ячейку ниже, ссылка на ячейку также изменяется на одну строку.
Ниже вы можете увидеть, как будут выглядеть формулы при их копировании в строки под строкой 2 в приведенном выше примере.
Копирование формулы окружности в столбец:
Ряд 3: = 2 * 3,14 * A3
Ряд 4: = 2 * 3. 2)
2)
Как создавать уравнения с несколькими операторами
Теперь давайте посмотрим на использование уравнения, которое использует несколько типов операторов в одной формуле.
Ниже приведен пример, который показывает расчет и сравнение двух различных услуг, а также стоимость каждой услуги в зависимости от количества часов обслуживания.
Допустим, вы собираетесь нанять фотографа. У них другая базовая стоимость и другая почасовая ставка, и вы хотите знать, какая из них будет стоить меньше всего… опять же, в зависимости от того, на сколько часов вам нужно их нанять.
Чтобы рассчитать общую стоимость услуги для данной почасовой ставки, базовой стоимости и количества часов… мы сделаем следующее:
Возьмите почасовую ставку (столбец C), умноженную на количество часов (столбец D), а затем добавьте базовую стоимость (столбец B).
Как вы можете видеть на изображении примера, первая формула вводится в ячейку E2:
= B2 + (C2 * D2)
Затем эта формула копируется и вставляется в ячейки ниже, чтобы произвести одинаковый расчет для каждой отдельной строки данных.
Из-за различий в базовой стоимости и почасовой ставке одна услуга будет стоить меньше при найме на короткий период времени, а другая услуга будет стоить меньше при найме на более длительный период времени.
В этом примере мы видим, что фотограф 1 дешевле при найме на 2 часа, а фотограф 2 дешевле при найме на 8 часов. Оба фотографа сопоставимы при работе на 4 часа.
Pop Quiz: Проверьте свои знания
Ответьте на вопросы о математике в Google Таблицах ниже, чтобы улучшить свои знания! Прокрутите вниз, чтобы найти ответы на викторину.
Вопрос № 1
В какой из следующих формул складываются числа «5» и «10»?
- = ADD (5,10)
- = 5 + 10
- Оба
Вопрос № 2
Какая из следующих формул умножает числа «10» и «30» друг на друга?
- = 10 × 30
- = 10 * 30
Вопрос № 3
Верно или неверно: порядок операций в традиционной математике такой же, как порядок операций в электронной таблице (PEMDAS)?
- Верно
- Неверно
Вопрос № 4
Если число «4» введено в ячейку A1, а число «3» — в ячейку A2, каков ответ на эту формулу: = A1-A2?
- = -1
- = 1
Вопрос № 5
Какую из следующих формул можно использовать для добавления ячеек с A1 по A5?
- = A1 + A2 + A3 + A4 + A5
- = СУММ (A1: A5)
- Оба
Ответы на поставленные выше вопросы:
Вопрос 1: 3
Вопрос 2: 2
Вопрос 3: 1
Вопрос 4: 2
Вопрос 5: 3
youtube.com/embed/jOBgEO9OKGw» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>35 забавных практических способов научить умножению
Как лучше всего научить умножению? На этот вопрос есть столько ответов, сколько детей в вашем классе.Но одно можно сказать наверняка. Увлекательное умножение — отличное место для мотивации ваших учеников. Вот 35 наших любимых игр и практических способов научить ваших учеников начальной школы умножению. Примечание. Первые идеи из этого списка особенно хороши для преподавания прямо сейчас, так как вы можете играть вместе всем классом в Интернете или назначать задания для работы на дому!
1. Нарисуйте вальдорфские цветы умножения.
Источник: Многокультурное материнство
Это творческий способ преподать факты умножения.Начните с рисования центра цветка и напишите любое число 1–9 в середине. Затем нарисуйте 12 лепестков вокруг центра, обозначив их 1–12. Наконец, нарисуйте еще 12 лепестков и напишите произведение числа в центре и лепестка, примыкающего к новому лепестку. Чтобы облегчить выполнение домашнего задания, сделайте пустой шаблон, который ваши ученики смогут скачать дома.
Наконец, нарисуйте еще 12 лепестков и напишите произведение числа в центре и лепестка, примыкающего к новому лепестку. Чтобы облегчить выполнение домашнего задания, сделайте пустой шаблон, который ваши ученики смогут скачать дома.
2. Сыграйте в войну умножения.
Источник: мама для двух шикарных маленьких див
Это задание можно использовать как для одного человека, так и для пары.Надеюсь, у большинства ваших учеников дома есть обычная колода игральных карт. В противном случае они могут сделать свои собственные карточки с номерами, используя учетные карточки или макулатуру. Для начала ученики переворачивают две карты лицом вверх. Затем они умножают два числа на карточках вместе. Затем они записывают математическое предложение на листе бумаги и решают задачу. Вы можете назначить ограничение по времени, например десять минут, или количество задач, например, шесть. Если учащиеся играют с партнером, оба учащихся переворачивают две карты, умножают числа, и тот, у кого продукт наивысшего качества, сохраняет карты. В конце игры побеждает игрок с наибольшим количеством карт.
В конце игры побеждает игрок с наибольшим количеством карт.
3. Играть в Бинго!
Сделайте ставку на традиционную игру. Попросите учащихся сделать свои собственные карточки, используя обратную сторону любой бумаги, чтобы нарисовать сетку 5 × 5 и заполнив поля номерами продуктов, такими как 16, 8, 48, 56 и т. Д. Учитель называет задачи умножения, например, 7 × 9. Учащиеся решают продукт и, если это число есть на их сетке, накройте это число фасолью или плиткой. Карточка каждого ученика уникальна, и они могут гордиться созданием собственной игры.В эту игру можно играть лично или виртуально.
4. Измените математическую формулировку старого фаворита.
Это быстрое и простое занятие, которое заставляет детей двигаться во время обучения. Это похоже на игру Рошамбо (она же камень, ножницы, бумага), но ученики поднимают пальцы вместо камня, бумаги или ножниц. Если учащиеся играют парами, первый партнер, который умножит два набора пальцев вместе и назовет продукт, получает балл. Если вы играете все вместе виртуально, выберите ученика в качестве партнера и стреляйте.Выберите двух других учеников, которые будут «гадать». Меняйте стрелков и угадывающих.
Если вы играете все вместе виртуально, выберите ученика в качестве партнера и стреляйте.Выберите двух других учеников, которые будут «гадать». Меняйте стрелков и угадывающих.
5. Используйте коробку для яиц как генератор задачи умножения.
Используя картон для яиц, попросите учащихся написать цифры от 1 до 12 внизу каждого углубления. Поместите два шарика внутрь коробки для яиц и закройте крышку. Встряхните коробку с яйцами, откройте верхнюю часть и умножьте два числа, на которые упали шарики. Напишите математическое предложение и ответьте на листе бумаги. Повторить.Если у учащихся есть дома пустая упаковка для яиц, это также может быть домашняя практика.
6. Пусть дети сделают свои собственные карточки с фактами умножения.
Учитель Джен В. рекомендует это занятие. «Попросите учащихся приложить художественный рисунок к ответам на карточках. поэтому мозг устанавливает связь между ответом и рисунком », — говорит она. «Я преподаю в четвертом классе, и дети очень хотят делать открытки дома. Они хранят их в своих папках, чтобы они могли практиковаться в любое время, когда у нас есть пять свободных минут.Они очень гордятся собой, потому что карточки — это не просто набор карточек ».
Они хранят их в своих папках, чтобы они могли практиковаться в любое время, когда у нас есть пять свободных минут.Они очень гордятся собой, потому что карточки — это не просто набор карточек ».
7. Обучайте фактам умножения с помощью простого колеса.
Источник: Creative Family Fun
Все, что вам нужно, — это бумажные тарелки, клей и маркер, чтобы помочь вашим ученикам выучить свои таблицы умножения. Это также может удваиваться как ремесленная деятельность, позволяя учащимся проявлять столько творчества, сколько они хотят, когда они украшают свои тарелки. Если учащиеся выполняют это задание дома и у них нет бумажных тарелок, они могут делать круги из обычной бумаги.
8. Составьте колоду семейных треугольников.
Еще один проект для детей, который помогает им персонализировать обучение. Дети могут сделать свои собственные, сосредоточив внимание на фактах умножения, которые по-прежнему являются для них трудными. Попробуйте эту версию от Primary Flourish.
9.
 Используйте кубики LEGO.
Используйте кубики LEGO.Источник: Math Geek Mama
Используйте кубики LEGO для создания равных групп (например, «Покажи мне 4 группы по 4») или используйте их для создания массивов (Покажите мне 5 рядов по 3 штуки в каждом).Кирпичи LEGO также являются отличным способом моделирования местности, если вы используете каждую выпуклость на вершине кирпича как единое целое. Узнайте больше о способах использования кубиков LEGO для обучения математике.
10. Используйте пальцы.
Источник: Создание учебной среды
Научите своих учеников «хитрому» способу умножения на девять, используя эту забавную модель. Вот как: попросите учащихся поднять все десять пальцев. Затем предположим, что задача — 9 x 6. Начиная с левой стороны, ученики пересчитывают шесть пальцев и опускают этот палец.Ответ показан на их пальцах! Количество пальцев слева от опущенного пальца — это количество десятков, а количество пальцев справа от опущенного пальца — это количество единиц. Итак, ответ — 54. Отлично подходит для урока в классе, лично или виртуально.
Отлично подходит для урока в классе, лично или виртуально.
11. Используйте силу.
Источник: Royal Baloo
Иногда изучение фактов умножения требует практики. Рабочие листы могут быть не очень увлекательными, но добавление темы, которая интересна детям, может заинтересовать ваших учеников.Эта бесплатная загрузка с Royal Baloo включает в себя домашние задания и практические задания с графиками, головоломками-лабиринтами и многим другим, все на тему «Звездных войн».
12. Практикуйте умножение онлайн.
Вот огромный список наших любимых математических сайтов. Вам это понравится!
13. Пойте, чтобы учиться.
Посмотрите классические эпизоды School House Rock или эти видеоролики о умножении, и пусть ваши ученики споют свой путь к мастерству умножения.
14.Сделайте эти забавные инструменты для практики.
Попробуйте эти забавные инструменты в центрах для самостоятельной практики или в небольших группах.
15. Сыграйте в шашки умножения.

Источник: Научи рядом со мной
С помощью съемных наклеек пометьте белые квадраты (показанные выше, красные или черные, если у вас традиционная шахматная доска) с задачей умножения. Затем поместите игровые фишки на квадраты с математической задачей. Игра начинается как обычно, когда игроки перемещают свои фигуры по диагонали, пытаясь перейти на другую сторону.Суть в том, что вы должны решить задачу умножения, на которую попали. Если вы ответите правильно, вам начисляется столько баллов. Например, если вы приземлитесь на 8 × 8 и ответите правильно, вы получите 64 очка. Побеждает игрок, набравший наибольшее количество очков в конце игры.
16. Подбросьте футбольный мяч умножения.
Источник: Создание учебной среды
Отправляйтесь на улицу в эту веселую игру. Перед началом игры напишите случайные числа в белых точках футбольного мяча.Чтобы играть, подбросьте футбольный мяч в воздух и поймайте его двумя руками. Посмотрите, каких чисел соприкасаются ваши большие пальцы, и умножьте их вместе. Если вы получили правильный ответ, стреляйте по мячу на 2 ярда от стойки ворот. Если мяч попадает в ворота, отойдите еще на 2 ярда и подбросьте мяч для новой задачи. Цель игры — отойти как можно дальше от цели. Если вы ответили неверно или не попали в цель, пройдите 2 ярда вперед и начните заново.
Если вы получили правильный ответ, стреляйте по мячу на 2 ярда от стойки ворот. Если мяч попадает в ворота, отойдите еще на 2 ярда и подбросьте мяч для новой задачи. Цель игры — отойти как можно дальше от цели. Если вы ответили неверно или не попали в цель, пройдите 2 ярда вперед и начните заново.
17. Играть в «Змеи и лестницы».
Источник: Живое дыхание и любящее учение
Придайте познавательный характер старому фавориту с этой версией игры «Змеи и лестницы» с умножением. Все, что вам нужно для игры, — это недорогая настольная игра (всего за 1,50 доллара на загрузку), игровые элементы и кубик. Чтобы сыграть, первый игрок бросает кубик, а затем перемещает свой игровой элемент на такое количество делений. Затем они должны правильно ответить на задачу умножения. Если они сделают это правильно, они останутся на месте. Если они этого не делают, они возвращаются на один шаг назад и пытаются решить эту проблему, двигаясь назад, пока не ответят правильно.Побеждает тот, кто первым достигнет головы змеи.
18. Откидные крышки от бутылок.
Источник: Croft’s Classroom
Начните с крышек бутылок и наклеек с цветными точками. Напишите предложение умножения на одной точке и положите его на крышку бутылки. Напишите ответ на второй точке и положите его на дно крышки бутылки. Затем попросите учащихся разделиться на группы и выложить все вершины с предложением умножения. Они по очереди произносят предложение вслух и должны ответить, прежде чем переворачивать верхнюю часть для проверки.Если они сделают это правильно, они сохранят верх. Если они ошибаются, они кладут обратно. Выигрывает тот, у кого больше всего в конце!
19. Примите вызовы подряд.
Два ученика стоят спиной к спине и каждый записывает коэффициент на доске (вы можете установить ограничение на количество, обычно 1–9). «Звонящий» умножает два фактора и называет продукт. Двое студентов должны попытаться решить фактор другого, зная только свой фактор и продукт. Учащийся, который правильно угадает первым, остается, а новый ученик занимает место другого. Тот, кто выиграет три раунда подряд, становится новым участником. Обычно это игра для всего класса.
Тот, кто выиграет три раунда подряд, становится новым участником. Обычно это игра для всего класса.
20. Сыграйте раунд умножения бейсбола.
Источник: Построчное обучение
Используйте один набор карточек умножения, чтобы поиграть в бейсбол по математике в классе. Положите карточку на пол на пути. Дети по очереди прыгают по карточкам, говорят ответ и смотрят, как далеко они могут продвинуться. Остановитесь, когда они сделают ошибку, и посмотрите, кто окажется дальше всех.
21. Выстраивайте домино.
Домино — отличный инструмент для создания задач многозначного умножения. Возьмите два домино и выровняйте их по горизонтали. Это становится проблемой студентов. Например, предположим, что у одного домино есть 4 и 2, а у второго домино есть 1 и 6. Задача будет 42 × 16. Идеально подходит для сольной практики или работы на станции.
22. Бросьте кости в стиле Вегаса.
Используйте две пары игральных костей и бланк для умножения. Бросьте их! В то же время два ученика бросают по два кубика, а затем умножают свои числа. Игрок с наибольшим произведением получает очко. Игра продолжается до тех пор, пока вы не достигнете определенного числа или ограничения по времени.
Игрок с наибольшим произведением получает очко. Игра продолжается до тех пор, пока вы не достигнете определенного числа или ограничения по времени.
23. Играть в Top It.
Вашим детям понравится играть в Multiplication Top-It. Используя колоду обычных карт, два ученика берут по две карты каждый. Это их факторные карты. Каждый учащийся умножает свои два числа вместе, и результат выигрывает раздача. Побеждает игрок с наибольшим количеством карт в конце.
24. Создавайте массивы!
Источник: Miss Giraffe’s Class
Массивы
идеально подходят для помощи студентам в визуализации задач умножения.Массив — это систематическое расположение похожих объектов, обычно в строках и столбцах. Использование необычных предметов помогает закрепить концепцию. Интересные идеи, которые стоит попробовать: скрепки, крендели, M & M, мелки, плитки, блоки, пуговицы, ядра попкорна, рис, стиральные машины, шоколадные чипсы, помпоны, сырные шарики, драгоценности, Smarties, пенни, изюм, фисташки, чечевица, прилавки , или кубики LEGO.
25. Играть в квадраты умножения.
Источник: Games4Gains
Дети любят играть в игру Squares! Все, что вам нужно для этой версии, — это два кубика, загружаемое игровое поле и две ручки разных цветов.Один игрок бросает оба кубика, умножает два числа, затем ищет продукт на доске. Затем ученик рисует линию, соединяющую любые две точки, составляющие часть квадрата вокруг этого продукта. Игра продолжается до тех пор, пока доска не заполнится квадратами.
26. Построить массив городов.
Источник BrightConcepts4Teachers
Чтобы помочь студентам понять массивы в реальном мире, создайте города-массивы (указания здесь). Попросите студентов построить по крайней мере три здания, использовать линейки, чтобы нарисовать прямые линии, и записать факты умножения.Вы сможете четко увидеть, какие студенты понимают эту концепцию, и им понравится, как они получатся.
27. Постройте математические башни силы.
Источник: Fabulous in Fifth
Все, что вам нужно, — это банки Pringles для хранения, пластиковые чашки Дикси и шарпи для обучения умножению с помощью башен. Сначала напишите задачу умножения на внешней стороне чашки, а затем напишите ответ внутри на дне. Если ученик получит правильный ответ, он может начать строить башню.Каждый раз, когда дается правильный ответ, они добавляются в стек. Это может быть сделано с партнерами или индивидуально для первых участников.
Сначала напишите задачу умножения на внешней стороне чашки, а затем напишите ответ внутри на дне. Если ученик получит правильный ответ, он может начать строить башню.Каждый раз, когда дается правильный ответ, они добавляются в стек. Это может быть сделано с партнерами или индивидуально для первых участников.
28. Измените имена учащихся (временно).
Источник: г-н Элементарная математика
Возьмите несколько именных бирок и напишите на каждом уравнение умножения. Дайте ярлык каждому из ваших учеников. В оставшуюся часть дня все будут ссылаться друг на друга, отвечая на уравнение на своей метке (например, ученик с именной меткой, на которой написано 7 × 6, будет называться «42»).
29. Взять умножение на сетку.
Источник: Экономные развлечения для мальчиков и девочек
Все, что вам нужно, это доска для плакатов, 12-гранные игральные кости и пара игровых фишек. Учащиеся перемещают свои игровые фишки вверх по полю, бросая кости и умножая два числа, которые лежат наверху. У них есть четыре шанса забить тачдаун. Прочтите подробности этой веселой игры от Frugal Fun for Boys and Girls.
У них есть четыре шанса забить тачдаун. Прочтите подробности этой веселой игры от Frugal Fun for Boys and Girls.
30. Играть в умножение «Бросок и удар»
Источник: This Reading Mama
Загрузите бесплатные игровые доски, каждое с множителем в заголовке (например, x 4).Бросьте два кубика, сложите их и умножьте на множитель. Затем поместите свою игровую фишку на ответ. Если другой игрок также предложит тот же продукт, он может «вышибить» ваш игровой элемент и заменить его своим. Побеждает игрок с наибольшим количеством маркеров на доске в конце игры.
31. Сделайте блесны.
Источник: Super Fun Printables
Показанные выше спиннеры умножения можно приобрести, но ваши ученики также могут сделать свои собственные.Все, что вам нужно, это картон, ножницы, латунные застежки и метка. Вырежьте два одинаковых круга из картона и еще один круг размером примерно четверть. Вырежьте две выемки, по одной с каждой стороны, из одного из больших кругов. Напишите в маленьком кружке число, которое вы умножаете (например, x11). На круге без выемок напишите числа от 1 до 12, а прямо напротив каждого числа — произведение, которое вы получите, умножив это число на коэффициент (например, 2 и прямо напротив 22).Студенты практикуются, вращая верхний круг над нижним.
На круге без выемок напишите числа от 1 до 12, а прямо напротив каждого числа — произведение, которое вы получите, умножив это число на коэффициент (например, 2 и прямо напротив 22).Студенты практикуются, вращая верхний круг над нижним.
32. Сделайте узорчатые круги.
Источник: Lemon Lime Adventures
Для младших школьников используйте эти кружки, чтобы попрактиковаться в подсчете пропусков, чтобы научить их умножать на двоек, троек или пятерок.
33. Играть в Умножение Дженга!
Источник: Цветущие умы
Используйте маркер, чтобы написать задачи умножения на каждом из 54 блоков в стандартной игре Jenga.(Или, как вариант, загрузите этот бесплатный шаблон и прикрепите проблему к каждому блоку). Учащиеся играют в игру, сначала складывая все блоки в башню, а затем по очереди вытаскивая по одному блоку. Цель игры — убирать блоки без разрушения всей башни. Особенность этой версии в том, что каждый ученик должен успешно решить задачу умножения на своем блоке, чтобы сохранить ее. Когда башня в конечном итоге падает, побеждает игрок с наибольшим количеством блоков.
Когда башня в конечном итоге падает, побеждает игрок с наибольшим количеством блоков.
34.Играть в Twister!
Источник: Math Geek Mama
Вашим ученикам понравится эта извращенная версия старого фаворита! Напишите задачи умножения на каждой точке прядильщика и напишите соответствующие произведения в кружках на циновке. Затем предложите учащимся по очереди играть. Например, первый ученик может повернуться и приземлиться на 4 × 5. Затем они должны найти и положить руку или ногу на число 20.
Источник: Итоги обучения
Эти недорогие инструменты помогут вашим ученикам практиковать умножение и развивать мелкую моторику.Чтобы играть, просто перемотайте строку от задачи слева к ответу справа. Переверните ключ, чтобы проверить свой ответ. Охватывает «факты от 1 × 1 до 10 × 12 и все, что между ними».
Какие ваши любимые практические способы обучения умножению? Поделитесь своими идеями в группе WeAreTeachers HELPLINE на Facebook.
Plus, ознакомьтесь с нашим руководством по умножению лапши в бассейне.
Умножение и деление
: введение в деление
Урок 4: Введение в Дивизион
/ ru / multiplicationdivision / video-multiplication / content /
Что такое деление?
Отдел что-то делит поровну.Например, предположим, что у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Вы делите билета между своими друзьями. Каждый друг получает одинаковое количество билетов.
Видите, у каждого по 2 билета? Когда вы делите 10 билетов между пятью друзьями, вы создаете 5 равных групп по 2 билета.
Дивизия в жизни случается очень часто. Например, рассмотрим ситуацию ниже.
Написание выражений деления
В слайд-шоу вы видели, что мы разделили шесть кексов на две равные группы.Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления следующим образом:
6/2
Вы также можете написать такое выражение:
6 ÷ 2
Вы можете прочитать любое выражение как шесть, разделенное на два . Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставим после первого числа — кексов было 6, и мы разделили их на 2 группы.
Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставим после первого числа — кексов было 6, и мы разделили их на 2 группы.
Многие жизненные ситуации можно выразить с помощью деления. Например, представьте, что вы размещаете 15 банок на 3 полках. Вы можете разделить, чтобы на каждой полке было одинаковое количество банок. Другими словами, 15 банок, разделенных на три полки, или 15/3.
Попробуй!
Попробуйте настроить эти ситуации как выражения деления. Пока не пытайтесь их решить.
У учителя есть 16 карандашей, которые она равномерно распределяет между 4 учениками.
У флориста 18 роз и он делит их поровну на 3 вазы.
У вас есть 6 лакомств, которыми вы поделитесь поровну с 3 вашими собаками.
Решение задач деления
Вы можете использовать с подсчетом для решения простых задач деления. Например, у нас 12 саженцев. Решаем посадить их в два ровных ряда. Сколько растений в каждом ряду? Мы могли бы написать этот вопрос так:
12/2
Помните, что это выражение означает 12, разделенное на два , или 12 саженцев, разделенных на 2 ряда. Это простая проблема.Чтобы решить эту проблему, вы можете разделить саженцы на две группы, а затем посчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.
Это простая проблема.Чтобы решить эту проблему, вы можете разделить саженцы на две группы, а затем посчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.
.
В то время как счет работает для задач, которые начинаются с малых чисел, задача, которая начинается с большого числа , может занять много времени, чтобы решить с помощью счета. По этой причине большинство людей запоминают общих задач деления, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. Практикуя , вы сможете быстро запоминать ответы.
В разделе «Введение в умножение» вы познакомились с таблицей умножения . На этом уроке вы использовали его для решения задач умножения. Вы также можете использовать таблицу умножения для решения задач разделения.
Начнем с проблемы, с которой мы уже знакомы. Как бы мы решили проблему саженцев с помощью таблицы умножения?
Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.
Помните, каждое число в верхней части таблицы умножения находится в начале столбца .
Например, это столбец с цифрой 7.
Каждое число в левой части таблицы умножения является началом строки . Эта строка идет с 9.
Давайте попробуем решить проблему саженцев: 12 / 2.
Сначала найдите число, на которое вы делите, справа от знака деления. В 12/2 мы делим на 2.
Найдите столбец 2.
Затем найдите число, которое вы делите, слева от знака деления.В 12/2 это 12.
Найдите 12 в столбце двойки.
Найдите число в начале строки, которая перекрывает 12. В данном случае это строка 6.
Итак, ответ или частное для 12/2 равно 6.
Давайте попробуем еще раз. На этот раз мы решим 15/5.
Сначала мы найдем столбец 5, поскольку мы делим на 5.
Затем мы найдем 15 в столбце 5, поскольку это число, которое мы делим.

Наконец, мы найдем число в начале строки, которое перекрывает 15. Это 3. Итак, 15/5 = 3.
Попробуй!
Решите эти проблемы с разделением. Если вам нужна помощь, вы можете воспользоваться таблицей умножения.
Остаток
На предыдущих страницах мы разделили числа поровну. Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что произойдет, если число не может быть разделено поровну?
Например, рассмотрим ситуацию ниже.
Из слайд-шоу видно, что остаток (1) меньше числа, которое мы разделили на (3). Так будет всегда, когда проблема остается. Например, посмотрите на каждую из этих проблем ниже:
21/5 = 4 r1
Остаток от 1 меньше 5.
76/6 = 12 r4
Остаток 4 меньше 6.
Если остаток больше, это означает, что оставшаяся сумма слишком велика. Вам нужно будет снова попробовать разделить.Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.
Практика!
Отделение практики с этими проблемами. Если хотите, можете воспользоваться таблицей умножения для помощи. Имеется 3 набора задач по 5 задач в каждом.
Набор 1
Набор 2
Набор 3
/ ru / multiplicationdivision / long-div / content /
Основы математики в Excel: руководство для начинающих
Как складывать числа в Excel? Как ввести простое уравнение? Это первые вопросы, которые задают новые пользователи Excel, и в этом руководстве мы на них ответим.Мы узнаем, как складывать, вычитать, умножать, делить, находить проценты, порядок операций и многое другое! PS: Если вы новичок в Excel, мы рекомендуем сначала прочитать наше Руководство для начинающих.
○ Это руководство содержит партнерские ссылки. Прочтите нашу политику раскрытия информации, чтобы узнать больше. ○
5 правил написания формул в Excel
- Все формулы Excel начинаются со знака равенства (=).
 Это говорит Excel, что это формула.
Это говорит Excel, что это формула. - Ответ на формулу отображается в ячейке, в которую введена формула.
- На ячейки в формуле ссылаются по их идентификатору столбец-строка, т. Е. А1, В2.
- Символы для сложения, вычитания, умножения и деления: + — * /
- Вам не нужно вводить в формулу заглавные буквы; Excel автоматически сделает их заглавными.
Примеры простых математических формул:
- = A1 + A6 эта формула Excel складывает содержимое ячеек A1 и A6
- = A1 + A2 + A3 эта формула Excel складывает содержимое трех указанных ячеек.3 будет кубить значение в ячейке h4.
Мы можем объединить несколько операций в одной формуле. Убедитесь, что вы используете круглые скобки там, где это необходимо, иначе вы можете не получить правильные результаты (см. Порядок действий ниже). Вот несколько примеров:
- = (C1 + C3) / C4 Эта формула Excel добавляет значение в C1 к значению в C3, а затем делит результат на значение в C4
- = 4 * (A2 + A5) +3 Эта формула Excel складывает содержимое A2 и A5, умножает эту сумму на 4, а затем добавляет 3.

Учебник KeynoteSupport.com
Математический порядок операций
Запомните Порядок действий, запомнив фразу P lease E xcuse M y D ear A unt S ally. Буквы означают: круглые скобки, экспоненты, умножение, деление, сложение и вычитание. Причем все операции выполняются с слева до справа . Вот как применяется заказ:
- Сначала вычисляются любые математические выражения, заключенные в круглые скобки.
- На втором проходе все экспоненты вычисляются.
- Затем выполняется любое умножение ИЛИ деление.
- Наконец, выполняется любое сложение ИЛИ вычитание.
Пример №1: Проиллюстрируем простой формулой: 4 + 2 * 3
- Так как умножение должно быть выполнено в первую очередь, наше выражение разрешается до 4 + 6 = 10.
Пример № 2: Как насчет более сложного примера: 20 ÷ 5 + 2 * 3
- Сначала делим, и 20 ÷ 5 = 4.
 2 = 9. Итак, теперь наша формула выглядит так: 9 + 9-2 * 3 .
2 = 9. Итак, теперь наша формула выглядит так: 9 + 9-2 * 3 . - Шаг 3 — Умножение и деление: 2 * 3 = 6. Итак, теперь наша формула выглядит так: 9 + 9-6 .
- Шаг 4 — сложите 9 + 9, затем вычтите 6, и ответ будет 12 … вы поняли правильно? ☺
Учебник KeynoteSupport.com
Расчет процентов в Excel
Есть два способа вычисления процентов в Excel, в зависимости от того, как разработан рабочий лист (электронная таблица).
Вариант №1: отобразить знак процента в ячейке
Чтобы вычислить процент и отобразить знак процента в ячейке, просто введите , введите формулу в ячейку и отформатируйте ячейку как процент .Пример: формула в ячейке C2: = A2 / A3 . Если A2 = 50 и B2 = 100, то обычно отображается 50 ÷ 100 = 0,5 и 0,5. Но если мы отформатируем ячейку C2 как процент, вместо этого отобразится 50% .
Как мы узнали из учебника для начинающих Excel Made Easy, чтобы отформатировать ячейку или группу ячеек, щелкните ячейку правой кнопкой мыши и выберите «Форматировать ячейки …. » Нажмите «Процент» на вкладке «Число», укажите число десятичных знаков и нажмите «ОК».
» Нажмите «Процент» на вкладке «Число», укажите число десятичных знаков и нажмите «ОК».
Значок формата также можно найти на ленте в более новых версиях Excel.
Вариант № 2: Заголовок столбца процентов, без знака процента в ячейке
Возможно, вам нужен столбец с надписью «процент», но вы не хотите, чтобы отображался знак процента. Это легко. Просто умножьте формулы на 100 , чтобы отобразить число, равное процентному числу.
См. Образец рабочего листа ниже: Ячейка C2 содержит формулу для вычисления процента от деления A2 (50) на A3 (100). Формула = A2 / A3 . Как видите, мы отформатировали C2 для отображения процентов, и это так.
Мы ввели ту же формулу в D2, но отформатировали ячейку так, чтобы отображалось число с двумя десятичными точками, поэтому Excel отображает 0,5, что является десятичным эквивалентом 50%.
И в ячейке E2 мы также отформатировали ячейку для отображения числа, но мы умножили формулу на 100 , как показано в строке формул, чтобы отобразить процент вместо десятичного числа. Затем мы пометили нашу колонку «Процент», и все в порядке! (Новая формула: = A2 / A3 * 100 ).
Затем мы пометили нашу колонку «Процент», и все в порядке! (Новая формула: = A2 / A3 * 100 ).
Копирование и вставка формул
Чтобы скопировать содержимое ячейки, щелкните ячейку, щелкните правой кнопкой мыши и выберите «Копировать».(Или используйте сочетание клавиш Ctrl + C.) Затем поместите курсор в принимающую ячейку, щелкните правой кнопкой мыши и выберите «Вставить». (Или используйте сочетание клавиш Ctrl + V.)
Чтобы удалить анимированную границу исходной ячейки, нажмите Enter, или нажмите клавишу Esc, или щелкните в другой ячейке и начните вводить текст.
При вставке содержимого ячейки в несколько ячеек содержимое ячейки нужно скопировать только один раз. Используйте стрелки на клавиатуре, чтобы перейти к другим ячейкам и вставить.
При копировании и вставке формул Excel предполагает, что вам нужны адреса ячеек (например,грамм. B8) изменен, чтобы соответствовать строке или столбцу, в котором вы находитесь. Это потому, что в большинстве случаев мы копируем и вставляем уравнения, именно это мы и хотим. Например, возможно, мы находим общее количество столбцов на листе. Если вы не хотите, чтобы Excel изменял адреса ячеек, вам нужно использовать абсолютных ссылок на ячейки . Мы рассмотрим это в статье «Все о ссылках на ячейки».
Например, возможно, мы находим общее количество столбцов на листе. Если вы не хотите, чтобы Excel изменял адреса ячеек, вам нужно использовать абсолютных ссылок на ячейки . Мы рассмотрим это в статье «Все о ссылках на ячейки».
Блокировка ячеек для защиты
Поскольку некоторые формулы могут быть чрезвычайно сложными, рекомендуется заблокировать те ячейки, которые содержат формулы, и защитить рабочий лист.
Примеры на умножение. Математика 4 класс.
Примеры на умножение. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000.
 Нумерация
Нумерация - Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 60 * 91 = 5460 | 108 * 63 = 6804 | 31 * 583 = 18073 | 590 * 30 = 17700 | 300 * 47 = 14100 |
| 110 * 49 = 5390 | 92 * 692 = 63664 | 250 * 5 = 1250 | 700 * 3 =2100 | 73 * 80 = 5840 |
| 988 * 99 = 97812 | 930 * 6 = 5580 | 81 * 415 = 33615 | 260 * 40 = 10400 | 690 * 30 = 20700 |
| 4800 * 80 = 384000 | 93 * 40 = 3720 | 0 * 937 = 0 | 150 * 80 = 12000 | 50 * 19 = 950 |
| 98 * 50 = 4900 | 2730 * 7 = 19110 | 14 * 616 = 8624 | 890 * 30 = 26700 | 894 * 70 = 62580 |
| 40 * 277 = 11080 | 2320 * 8 = 18560 | 8960 * 8 = 71680 | 82 * 20 = 1640 | 32 * 50 = 1600 |
| 89 * 80 = 7120 | 87 * 550 = 47850 | 350 * 30 = 10500 | 264 * 29 = 7656 | 4200 * 20 = 84000 |
| 350 * 6 = 2100 | 77 * 60 = 4620 | 130 * 2 = 260 | 710 * 2 = 1420 | 640 * 70 = 44800 |
| 780 * 8 = 6240 | 4300 * 5 = 21500 | 43 * 371 = 15953 | 360 * 5 = 1800 | 46 * 213 = 9798 |
| 950 * 2 = 1900 | 3 * 430 = 1290 | 9600 * 96 = 921600 | 44 * 44 = 1936 | 10 * 12 = 120 |
| 630 * 50 = 31500 | 282 * 73 = 20586 | 660 * 7 = 4620 | 330 * 7 = 2310 | 8500 * 80 = 680000 |
| 40 * 729 = 29160 | 35 * 56 = 1960 | 65 * 369 = 23985 | 32 * 40 = 1280 | 10 * 555 = 5550 |
| 22 * 90 = 1980 | 790 * 50 = 39500 | 40 * 60 = 2400 | 480 * 3 = 1440 | 71 * 30 = 2130 |
| 13 * 20 = 260 | 5100 * 80 = 408000 | 2800 * 50 = 140000 | 8300 * 90 = 747000 | 800 * 8 = 6400 |
| 740 * 9 = 6660 | 15 * 60 = 900 | 390 * 40 = 15600 | 570 * 60 = 34200 | 400 * 80 = 32000 |
| 80 * 14 = 1120 | 480 * 3 = 1440 | 260 * 60 = 15600 | 40 * 210 = 8400 | 46 * 50 = 2300 |
| 790 * 40 = 31600 | 910 * 4 = 3640 | 2200 * 70 = 154000 | 1700 * 50 = 85000 | 40 * 80 = 3200 |
| 42 * 80 = 3360 | 5000 * 30 = 150000 | 47 * 70 = 3290 | 8900 * 70 = 623000 | 580 * 80 = 46400 |
| 6300 * 40 = 252000 | 34 * 90 = 3060 | 9600 * 90 = 864000 | 4000 * 30 = 120000 | 90 * 832 = 74880 |
| 380 * 4 = 1520 | 310 * 8 = 2480 | 56 * 60 = 3360 | 337 * 0 = 0 | 87 * 810 = 70470 |
| 853 * 28 = 23884 | 140 * 3 = 420 | 590 * 60 = 35400 | 37 * 587 = 21719 | 1400 * 60 = 84000 |
| 17 * 184 = 3128 | 300 * 6 = 1800 | 290 * 2 = 580 | 929 * 41 = 38089 | 20 * 90 = 1800 |
| 980 * 60 = 58800 | 100 * 320 = 32000 | 100 * 64 = 6400 | 680 * 20 = 13600 | 42 * 50 = 2100 |
| 25 * 60 = 1500 | 8300 * 60 = 498000 | 550 * 7 = 3850 | 749 * 67 = 50183 | 9 * 20 = 11805 |
| 320 * 5 = 1600 | 140 * 40 = 5600 | 783 * 50 = 39150 | 50 * 500 = 25000 | 859 * 19 = 16321 |
| О * 870 = 0 | 290 * 2 = 580 | 700 * 50 = 35000 | 14 * 576 = 8064 | 68 * 30 = 2040 |
| 428 * 73 = 31244 | 120 * 6 = 720 | 640 * 70 = 44800 | 352 * 40 = 14080 | 11 * 531 = 5841 |
| 300 х 30 = 30030 | 802 * 7 = 5614 | 61 * 90 = 5490 | 750 * 9 = 6750 | 20 * 90 = 1800 |
| 980 * 80 = 78400 | 97 * 20 = 1940 | 500 * 8 = 4000 | 87 * 80 = 6960 | 60 * 67 = 4020 |
| 920 * 70 = 64400 | 7300 * 40 = 292000 | 86 * 70 = 6020 | 770 * 2 = 1540 | 500 * 70 = 35000 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Тест по математике Умножение и деление (4 класс)
Последний раз тест пройден более 24 часов назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Чему равен Х в уравнении: 240 : Х = 24?
1
10
100
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Верно ли равенство: 75 х 3 = 235?
Да
Нет
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Найдите правильный ответ: 250 х 6 =
1500
150
1200
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
В овощной магазин привезли 130 мешков картофеля по 80 кг в каждом.
 Сколько всего кг картофеля привезли в магазин?
Сколько всего кг картофеля привезли в магазин?14000
10400
9400
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Найдите правильный ответ: 3425 : 5 =
715
605
685
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Сколько кг в 68 ц?
680 кг
6800 кг
68000 кг
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Найдите частное: 700 : 35 =
2
20
200
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Сколько мм в 36 дм ?
36
360
3600
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Чему равно произведение: 0 х 16?
0
16
160
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Сравните выражение: 734 + 865 и 734 + 870
=
>
<
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Наталья Букарина
10/10
chashkova-tatyan чашкова
10/10
Константин Анисимов
10/10
Милана Петросян
10/10
Надежда Абрамова
10/10
Мубина Адхамова
8/10
Жмакина Ирина
10/10
Артём Мещеряков
8/10
Кристина Шаравьёва
10/10
Владислав Семьянинов
9/10
Тест «Умножение и деление» по математике рассчитан на учеников младшей школы. Он поможет закрепить знания по теме, выявить плохо усвоенный материал. Выполнение теста требует понимания самых простых математических действий, знания соответствующих таблиц и правил. Предлагаемые тесты разного уровня сложности, что позволяет объективно оценить знания ребенка. Задания можно проходить в онлайн режиме с любого доступного устройства.
Тест «Деление» (4 класс) с ответами позволяет самостоятельно или с помощью родителей повторить и систематизировать материал для успешного написания текущих и итоговых проверочных работ.
Рейтинг теста
4.2
Средняя оценка: 4.2
Всего получено оценок: 1182.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Решение больших примеров в столбик калькулятор. Вычитание столбиком
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Математический-Калькулятор-Онлайн v. 1.0
1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам.
 Слева напишите первую цифру, а справа над чертой вторую
Слева напишите первую цифру, а справа над чертой вторую - Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4.
 Эта цифра делится на 24? Нет — сносим 8, получается 48
Эта цифра делится на 24? Нет — сносим 8, получается 48 - Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2.
 Сносим еще цифру 4
Сносим еще цифру 4 - Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30.
 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 - Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8
на 2
. Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
(Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136
, а делителем является однозначное натуральное число 9
.
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Как объяснить ребенку деление столбиком во 2-3 классе
Как объяснить ребенку деление столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок таблицу умножения.
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобно показать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Мы гимназисты — Самостоятельные работы по математике. 4 класс
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
Самостоятельная работа «Повторяем все, что знаем»
Самостоятельная работа «Нумерация чисел в пределах 1000″
Самостоятельная работа «Сложение и вычитание в пределах 1000″
Самостоятельная работа «Компоненты сложения, вычитания»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Письменные приемы умножения и деления на однозначное число в пределах 100″
Самостоятельная работа «Компоненты умножения, деления»
Самостоятельная работа «Порядок выполнения действий»
Самостоятельная работа «Уравнения. Буквенные выражения»
Буквенные выражения»
Самостоятельная работа «Решаем задачи» — 1
Самостоятельная работа «Решаем задачи» — 2
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Нумерация чисел, которые больше 1000″
Самостоятельная работа «Сложение многозначных чисел»
Самостоятельная работа «Вычитание многозначных чисел»
Самостоятельная работа «Действия с величинами»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Увеличение и уменьшение чисел в 100, 1000, 10 000 раз»
Самостоятельная работа «Класс миллионов и класс миллиардов»
Самостоятельная работа «Умножение и деление чисел, оканчивающихся нулями»
Самостоятельная работа «Умножение многозначных чисел на однозначное число»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Деление многозначных чисел на однозначное число»
Самостоятельная работа «Умножение и деление на числа, оканчивающиеся нулями»
Самостоятельная работа «Умножение и деление на двузначное число»
Самостоятельная работа «Умножение и деление на трехзначное число»
Самостоятельная работа «Решение задач»
Самостоятельная работа «Доли»
Самостоятельная работа «Проценты»
Самостоятельная работа «Единицы длины»
Самостоятельная работа «Единицы времени»
Самостоятельная работа «Единицы массы»
Самостоятельная работа «Единицы площади»
Самостоятельная работа «Угол»
Самостоятельная работа «Периметр и площадь»
Самостоятельная работа «Окружность»
- Просмотров: 6489
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 2090
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 2317
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1688
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1503
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1505
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1847
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1855
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1385
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1304
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1137
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1211
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1062
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1522
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1218
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 960
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1232
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 2027
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1175
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1026
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1746
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1382
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1474
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 2530
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1308
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 2886
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 3164
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 2140
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1618
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1255
Что такое повторное добавление? — Факты определения и пример
Что такое повторное добавление?
Повторное сложение — это процесс сложения одинаковых групп. Смотрите здесь, на диаграмме ниже есть 5 групп цыплят, по 3 цыпленка в каждой группе.
Смотрите здесь, на диаграмме ниже есть 5 групп цыплят, по 3 цыпленка в каждой группе.
Таким образом, общее количество апельсинов может быть представлено оператором повторного сложения как
3 + 3 + 3 + 3 + 3 или 15
Как показано ниже, повторное сложение может быть визуализировано путем пропуска счета в числовой строке.
Это можно записать как предложение с повторяющимся сложением следующим образом:
2 + 2 + 2 + 2 + 2 + 2 + 2 = 14
Умножение как повторяющееся сложение
Повторное сложение — это сложение равных групп вместе, что аналогично умножение. Если точное число повторяется, то мы можем записать многократное сложение в виде умножения. Например,
Поскольку умножение — это многократное сложение, каждое повторяющееся сложение можно записать двумя способами:
Повторное сложение также полезно для изучения фактов умножения. Например, если вы еще не знакомы с фактами 7 × 3, вам может быть проще вычислить 7 × 3, написав 3 + 3 + 3 + 3 + 3 + 3 + 3 или 7 + 7 + 7; а потом потихоньку добавляю. Это также может быть полезно с большими числами, такими как 5 × 40. Более удобно писать 40 + 40 + 40 + 40 + 40, а затем прибавлять десятки.
Это также может быть полезно с большими числами, такими как 5 × 40. Более удобно писать 40 + 40 + 40 + 40 + 40, а затем прибавлять десятки.
Давайте рассмотрим еще несколько примеров.
Андрей купил 3 упаковки кексов. В каждой упаковке было по 4 маффина. Сколько маффинов купил Андрей?
Три упаковки по 4 булочки в каждой также можно записать в числовом виде как 3 ✕ 4 или 4 + 4 + 4, что равно 12.
Итак, всего Андрей купил 12 булочек.
Повторное добавление Факты
- Повторное добавление заключается в добавлении равных групп или одного и того же числа снова и снова.
- Повторное сложение предшествует обучению умножению. Это более простой способ для детей развиваться от сложения до понимания умножения.
Решенные примеры
- Сколько всего счетчиков на данном рисунке?
Решение:
В каждом столбце по 3 счетчика и 4 столбца.
3 + 3 + 3 + 3 = 4 ✕ 3 = 12.
Итак, счетчиков 12.
- У Аарона есть три коробки с маркерами, и в каждой коробке по пять маркеров. Сколько маркеров у Аарона?
Решение:
Пять маркеров в каждом из трех квадратов означают пять, добавленных к себе трижды.
Это можно записать в виде предложения сложения: 5 + 5 + 5 = 15
ИЛИ
Это также можно записать в виде предложения умножения: 3 ✕ 5 = 15.
Таким образом, у Аарона всего 15 маркеров.
- Является ли уравнение сложения для этого массива 2 + 2 + 2 + 2 + 2 = 10 ИЛИ 5 + 5 = 10. Объясните или покажите, почему вы выбрали именно такое уравнение?
Решение:
Один из способов взглянуть на этот массив: есть 2 строки по 5 объектов в каждой.
В этом случае уравнение сложения будет 5 + 5 = 10.
Другой способ взглянуть на этот массив: есть 5 столбцов с 2 объектами в каждом столбце.
В этом случае уравнение сложения будет таким: 2 + 2 + 2 + 2 + 2 = 10.
Итак, оба уравнения правильно описывают заданный массив.
Практические задачи
2 + 2 + 2 + 2 = 8
3 + 3 = 6
3 + 3 + 3 = 9
2 + 2 = 4
Правильный ответ: 3 + 3 = 6
Объяснение: Есть 2 ряда по 3 треугольника в каждом ряду. Следовательно, 3 + 3 = 6.
4 ✕ 5
4 ✕ 4
5 ✕ 3
5 ✕ 5
Правильный ответ: 4 ✕ 5
в каждом объекте с 4 строками. строка. Следовательно, мы можем записать выражение умножения для данного массива как 4 ✕ 5.
5 + 5 + 5
3 ✕ 5
4 + 4 + 4
5 + 5
Правильный ответ: 4 + 4 + 4
Объяснение: Если мы удалим одну точку из каждой группы, то у нас останется 3 группы по 4 точки каждый, что равно 4 + 4 + 4 или 3 ✕ 4.
4 + 4 + 4
4 + 4 + 4 + 4
3 ✕ 5
5 + 5 + 5 + 5
Правильно ответ: 4 + 4 + 4 + 4
Объяснение: Если мы добавим еще одну равную группу, то мы получим 4 группы по 4 точки в каждой, что равносильно 4 + 4 + 4 + 4 или 4 ✕ 4.
Часто задаваемые вопросы
Является ли повторное сложение тем же, что и умножение?
Да. Повторное сложение также известно как умножение. Это потому, что оба метода, хотя и разные, дают один и тот же ответ. Например, если 3 повторяется четыре раза, мы можем решить его как 3 + 3 + 3 + 3 = 12 ИЛИ мы можем решить его как 4 раза 3 = 4 ✕ 3 = 12.
Что такое массив в математике?
Массив — это расположение объектов или изображений в строках и столбцах. Массивы используются для представления и упрощения математических понятий. Они обеспечивают визуальное представление абстрактных математических понятий.
Что такое повторное сложение?
Повторное сложение — это сложение одинаковых групп вместе. Это обеспечивает основу для понимания умножения. Например, 3 умножить на 5 можно понять как 3 группы по 5 счетчиков, а затем записать как 5 + 5 + 5 = 15. В этом методе нам не нужно полагаться на таблицы умножения, чтобы найти ответ.
Почему важно повторное сложение?
Многократное сложение важно, так как оно обеспечивает основу для обучения умножению. Это прямой путь от аддитивного к мультипликативному пониманию.
Массивы, умножение и деление
Массивы, умножение и деление
Дженни Пеннант с помощью Дженни Уэй и Майка Аскью исследует, как можно использовать массив в качестве инструмента мышления, чтобы помочь детям развить всестороннее понимание умножения и деления.
Использование массивов для изучения чисел
Массивы — это полезные модели для умножения, которые можно использовать различными способами: от хорошо структурированных уроков до игр и открытых исследований.
Массив формируется путем организации набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, как и другие столбцы, а каждая строка должна иметь такое же количество объектов, как и другие строки.
Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12, 4 x 3 = 12, 3 + 3 + 3 + 3 = 12 и 4 + 4 + 4 = 12.
Построение фактов и таблиц умножения
Массивы можно использовать для осмысленного построения фактов умножения. Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты получены. Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить для себя таблицы умножения на три. Это представление не только помогает понять процесс, но и дает визуальный образ для детей, чтобы опираться на них, когда они начинают использовать и запоминать факты об основных числах.
Использование массивов для изучения больших чисел
Массивы можно с пользой использовать для изучения вычислений, таких как 13 x 5, где массив можно разделить на полезные фрагменты, такие как 10 и 3. Это означает, что дети могут использовать свои известные количество фактов для выполнения расчетов.
Это означает, что дети могут использовать свои известные количество фактов для выполнения расчетов.
Здесь 13 х 5 = (10 х 5) + (3 х 5).
Через некоторое время рисовать все точки может стать очень утомительно! Затем пустой массив становится очень полезным инструментом, помогающим детям моделировать свое мышление и решать, как выполнять более сложные умножения неформальным способом.
Вот ребенок, использующий пустой массив в качестве инструмента мышления, чтобы помочь ему решить 15 x 14.
Пустой массив помогает детям использовать другие стратегии, такие как компенсация, при выполнении умножения. Здесь, чтобы вычислить 34 х 9, ребенок решил сделать 34 х 10, а затем снять 34 х 1. сеточный метод. Дети могут увидеть, как метод «абстрактной» сетки накладывает массив и формализует пустой массив в стандартную форму.
Деление как операция, обратная умножению
Из четырех операций деление является самой трудной для младших школьников. Полное понимание деления, как правило, сильно отстает от других операций. Для многих детей возможности исследовать понятие с конкретными материалами ограничены задолго до того, как они узнают взаимосвязь между делением и тремя другими операциями. Одно из таких отношений, обратное отношение
между делением и умножением можно эффективно проиллюстрировать с помощью массивов.
Полное понимание деления, как правило, сильно отстает от других операций. Для многих детей возможности исследовать понятие с конкретными материалами ограничены задолго до того, как они узнают взаимосвязь между делением и тремя другими операциями. Одно из таких отношений, обратное отношение
между делением и умножением можно эффективно проиллюстрировать с помощью массивов.
Например; 3×5=15 или 3 строки по 5 составляют 15, могут быть представлены следующим массивом.
Взглянув на массив под другим углом, можно обнаружить обратное, то есть
15÷3=5 или 15, помещенное в 3 строки, дает 5 столбцов — или 5 в каждой строке.
Очевидно, что язык играет важную роль в способности выражать математические отношения, а физический массив поддерживает этот аспект понимания, давая детям конкретный образ, о котором можно говорить.
Помещение математики в контекст реальной жизни с помощью текстовых задач может облегчить как понимание отношений, так и их выражение через слова.
Например, «Садовник посадил 3 ряда по 5 семян. Сколько семян она посадила?» ставит совсем другую задачу, чем «Садовник посадил 15 семян в 3 равных ряда. Сколько семян в каждом ряду?» тем не менее, обе эти текстовые задачи могут быть смоделированы с использованием одного и того же массива.
Дальнейшее изучение массива выявило еще два способа выражения обратных отношений: 5×3=15 и 15÷3=5 .
Текстовые задачи можно адаптировать для описания этих операций и выделения сходств и различий между четырьмя выражениями, смоделированными одним массивом.
Использование пустого массива
Предположим, вы хотите вычислить 176 ÷ 8. Мы можем настроить это как массив с отсутствующим значением одной стороны.
Используя известные факты умножения, можно построить значение пропущенной стороны.
Таким образом, ребенок может видеть, что 22 партии по 8 равны 176.
Массив — очень мощный инструмент для поддержки развития детского мышления в отношении умножения и деления.
Дополнительная литература
Чтобы узнать об использовании массивов для иллюстрации числовых свойств, перейдите сюда и прочитайте статью Дженни Уэй под названием «Иллюстрация числовых свойств с помощью массивов».
Вот PDF-версия этой статьи.
Определение, как найти множители числа? Примеры
Коэффициент числа в математике представляет собой делитель данного числа, который делит его полностью, не оставляя остатка. Чтобы найти делителя числа , мы можем использовать различные методы, такие как метод деления и метод умножения. Факторы используются в реальных жизненных ситуациях, когда нам нужно что-то разделить на равные строки и столбцы, сравнить цены, обменять деньги и так далее. Давайте узнаем больше о факторах и , как найти факторы числа в этой статье.
| 1. | Что такое факторы? |
2. | Свойства факторов |
| 3. | Как найти делители числа? |
| 4. | Нахождение количества множителей |
| 5. | Часто задаваемые вопросы о дробях |
Что такое факторы?
В математике множитель — это число, которое полностью делится на другое число без остатка. Факторы и множители являются частью нашей повседневной жизни. Например, они используются при раскладывании предметов в коробке, работе с деньгами, поиске закономерностей в числах, решении соотношений и работе с дробями.
Определение множителя
Множитель числа — это число, на которое данное число полностью делится без остатка. Факторы числа могут быть положительными или отрицательными. Например, давайте найдем делители числа 8. Поскольку 8 делится на 1, 2, 4 и 8, мы можем перечислить положительные делители числа 8 как 1, 2, 4 и 8. Помимо этого, число 8 имеет также отрицательные факторы, которые могут быть перечислены как -1, -2, -4, -8, потому что произведение двух отрицательных чисел является положительным числом, что означает (-1) × (-8) = 8, и ( -2) × (-4) = 8. Однако мы обычно используем только положительные множители числа. Давайте прочитаем о некоторых свойствах факторов.
Однако мы обычно используем только положительные множители числа. Давайте прочитаем о некоторых свойствах факторов.
Свойства факторов
Делители числа обладают следующими свойствами:
- Число делителей числа конечно.
- Множитель числа всегда меньше или равен заданному числу.
- Каждое число, кроме 0 и 1, имеет как минимум два делителя: 1 и само число.
- Деление и умножение — это операции, которые используются для нахождения делителей числа.
Как найти делители числа?
Чтобы найти делители числа, мы можем использовать метод деления и метод умножения. Давайте прочитаем об этих методах в следующих разделах.
Нахождение множителей с помощью метода деления
Найдем множители числа с помощью метода деления.
Пример: Найдите множители числа 12, используя метод деления.
Решение: Давайте найдем множители числа 12, используя следующие шаги.
- Шаг 1: Чтобы найти множители 12 методом деления, нам нужно проверить, какие числа полностью делят 12. Начнем проверку с 1 и дойдем до 9. Нам нужно сделать пометку из тех чисел, которые делят 12 полностью.
- Шаг 2: Числа, которые полностью делят 12, называются его делителями. Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Как мы проверяем и перечисляем все числа до 9, вместе с ним мы автоматически получаем другой парный множитель. Например, начиная с 1, мы пишем 12 ÷ 1 = 12, а 12 ÷ 2 = 6 и так далее. Здесь делитель и частное являются делителями числа. Это означает, что (1, 12) образует первую пару, (2, 6) образует вторую пару, и список продолжается, как показано. Итак, когда мы пишем 1 как множитель 12, мы получаем другой множитель как 12; и поскольку мы пишем 2 как множитель 12, мы получаем 6 как другой множитель. Таким образом, мы получаем все факторы.
- Шаг 3 : После того, как список отмечен, мы получаем все делители числа 12, начиная с 1 вверх, вниз, а затем снова поднимаемся вверх до 12.
 Это дает нам полный список всех делителей числа 12, как показано на рисунке. на приведенном выше рисунке.
Это дает нам полный список всех делителей числа 12, как показано на рисунке. на приведенном выше рисунке.
Следовательно, делители числа 12 могут быть перечислены как 1, 2, 3, 4, 6, 12.
Теперь давайте научимся находить делители числа методом умножения. Это почти то же самое, что и метод деления, с той лишь разницей, что множители пишутся в разных местах.
Нахождение множителей с помощью метода умножения
Чтобы найти множители числа с помощью метода умножения, нам нужно использовать процедуру, аналогичную описанной выше, за исключением нескольких изменений. Давайте изучим этот метод с помощью примера.
Пример: Найдите множители числа 24, используя метод умножения.
Решение: Давайте найдем множители 24 методом умножения, используя следующие шаги.
- Шаг 1: Чтобы найти множители 24 с помощью умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 24, поэтому нам нужно разделить 24 на натуральные числа, начиная с 1, и продолжать до 9.

- Шаг 2: Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Когда мы проверяем и перечисляем все числа до 9, мы автоматически получаем вместе с ним другой парный коэффициент. Например, начиная с 1, мы пишем 1 × 24 = 24 и 2 × 12 = 24 и так далее. Здесь (1, 24) образует первую пару, (2, 12) образует вторую пару, и список продолжается, как показано. Итак, когда мы записываем 1 как множитель 24, мы получаем другой множитель как 24; и поскольку мы пишем 2 как множитель 24, мы получаем 12 как другой множитель. Таким образом, мы получаем все факторы.
- Шаг 3 : После того, как список отмечен, мы получаем все делители числа 24, начиная с 1 вверх, вниз, а затем снова поднимаемся вверх до 24. Это дает нам полный список всех делителей числа 24 в виде показано на рисунке, приведенном выше.
Следовательно, множители 24 могут быть перечислены как 1, 2, 3, 4, 6, 8, 12 и 24.
Нахождение числа факторов
Мы можем найти количество множителей заданного числа, используя следующие шаги.
- Шаг 1: Разложите заданное число на простые множители, т. е. представьте его как произведение простых чисел.
- Шаг 3: Запишите простую факторизацию в форме экспоненты.
- Шаг 3: Добавьте 1 к каждому показателю степени.
- Шаг 4: Перемножьте все полученные числа. Это произведение дает количество факторов заданного числа.
Пример: Найдите количество делителей числа 108.
Решение: Давайте найдем количество множителей 108, используя шаги, указанные ниже.
- Шаг 1: Разложение числа 108 на простые множители дает нам 108 = 2 × 2 × 3 × 3 × 3
- Шаг 2: После записи простой факторизации в экспоненциальной форме мы получаем 108 = 2 2 × 3 3
- Шаг 3: После добавления 1 к каждому из показателей степени, 2 и 3, мы получаем (2 + 1) = 3, (3 + 1) = 4.
- Шаг 4: Теперь давайте умножим эти числа: 3 × 4 = 12. Следовательно, число множителей 108 равно 12,
Мы можем проверить это число, записав действительные делители числа 108, которые равны 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54 и 108. Здесь 108 имеет 12 делителей, следовательно, мы проверили, что 108 имеет 12 делителей.
Здесь 108 имеет 12 делителей, следовательно, мы проверили, что 108 имеет 12 делителей.
Факторы чисел
Вот список страниц, объясняющих множители различных чисел.
Факторы Примеры
Пример 1: Найдите положительные множители числа 64.
Решение:
Найдем множители числа 64, используя метод умножения.
- Чтобы найти множители 64 с помощью умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 64, поэтому нам нужно разделить 64 на натуральные числа, начиная с 1 и продолжая до 9, так что мы получим 1 × 64 = 64 и 2 × 32 = 64, 4 × 16 = 64, 8 × 8 = 64.
- После того, как список составлен, мы получаем все делители числа 64, начиная с 1 вверх, вниз и снова поднимаясь вверх до 64. Это дает нам полный список всех делителей числа 64.
- Следовательно, положительные множители числа 64 = 1, 2, 4, 8, 16, 32, 64.
Пример 2: Какое из следующих утверждений верно?
а.
 ) Множитель числа может быть больше числа.
) Множитель числа может быть больше числа.б.) Некоторые числа могут иметь бесконечное число множителей.
Решение:
а.) Утверждение «Множитель числа может быть больше числа» ЛОЖЬ. Мы знаем, что множители — это делители числа, при которых в остатке остается 0. Следовательно, они всегда меньше числа. Следовательно, ответ: Ложь
б.) Утверждение «Некоторые числа могут иметь бесконечное число множителей» ЛОЖЬ. Количество множителей числа конечно. Следовательно, ответ: Ложь.
Пример 3: Найдите количество делителей числа 1620.
Решение:
- Чтобы найти количество делителей числа 1620, мы сначала проведем разложение числа 1620 на простые множители. дерево факторов показано ниже
- Разложение числа 1620 на простые множители = 2 × 2 × 3 × 3 × 3 × 3 × 5. В форме экспоненты это можно выразить как 2 2 × 3 4 × 5 1 .

- Прибавляя 1 к каждому из показателей степени, получаем: 2 + 1 = 3, 4 + 1 = 5, 1 + 1 = 2.
- Произведение всех этих чисел: 3 × 5 × 2 = 30. Следовательно, число делителей числа 1620 равно 30.
- Проверим это число, найдя множители 1620. Множители 1620 = 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 81, 90, 108, 135, 162, 180, 270, 324, 405, 540, 810 и 1620. Итак, мы можно увидеть, что 1620 имеет всего 30 множителей.
перейти к слайдуперейти к слайдуперейти к слайду
Развивайте логическое мышление и укрепляйте его уверенность!
Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!
Забронировать бесплатное пробное занятие
Практические вопросы по факторам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о факторах
Что такое факторы в математике?
Коэффициент — это число, на которое данное число делится без остатка. Делители числа могут быть как положительными, так и отрицательными. Факторы любого числа конечны. Например, делители числа 7 равны 1 и 7. Делители числа 8 равны 1, 2, 4 и 8.
Делители числа могут быть как положительными, так и отрицательными. Факторы любого числа конечны. Например, делители числа 7 равны 1 и 7. Делители числа 8 равны 1, 2, 4 и 8.
Как найти количество делителей числа?
Мы можем найти количество множителей заданного числа, используя следующие шаги. Разберемся в этом на примере и найдем количество множителей 48
- Шаг 1: Выполните разложение заданного числа на простые множители. Это будет 48 = 2 × 2 × 2 × 2 × 3
- Шаг 3: Запишите простую факторизацию в форме экспоненты. Это можно записать как 2 4 × 3 1
- Шаг 3: Добавьте 1 к каждому показателю степени. Показатели степени в данном случае равны 4 и 1. Таким образом, прибавив 1 к каждому показателю степени, мы получим 5 и 2.
- Шаг 4: Перемножьте полученные числа. Это произведение дает количество факторов заданного числа. После умножения 5 × 2 = 10. Это означает, что 48 имеет 10 делителей. Проверим это, перечислив множители числа 48.
 Множители числа 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48,9.0036
Множители числа 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48,9.0036
Что такое простая факторизация?
Разложение числа на простые множители — это способ представить число как произведение его простых множителей. Например, разложение числа 60 на простые множители = 2 × 2 × 3 × 5. Разложение числа на простые множители всегда показывает его простые множители. В данном случае 2, 2, 3 и 5 — это простые множители числа 60. Мы знаем, что простые множители — это те множители, которые являются простыми числами.
Что такое формула факторов?
Формула множителей для числа дает общее количество множителей числа. Для числа N, простая факторизация которого равна X a × Y b , мы получаем общее количество факторов, добавляя 1 к каждому показателю степени, а затем перемножая их вместе. Это выражает формулу числа факторов как (a + 1) × (b + 1), где a и b — показатели степени, полученные после простой факторизации данного числа. Например, давайте найдем общее количество множителей числа 12. Разложение числа 12 на простые множители = 2 × 2 × 3. Это можно записать в виде экспоненты как 2 2 × 3 1 . Воспользуемся формулой (a + 1) × (b + 1), где a и b равны 2 и 1 соответственно. После подстановки значений мы получаем (a + 1) × (b + 1) = (2 + 1) × (1 + 1) = 3 × 2 = 6. Это означает, что 12 имеет всего 6 делителей. Это можно проверить, перечислив множители числа 12: 1, 2, 3, 4, 6, 12.
Разложение числа 12 на простые множители = 2 × 2 × 3. Это можно записать в виде экспоненты как 2 2 × 3 1 . Воспользуемся формулой (a + 1) × (b + 1), где a и b равны 2 и 1 соответственно. После подстановки значений мы получаем (a + 1) × (b + 1) = (2 + 1) × (1 + 1) = 3 × 2 = 6. Это означает, что 12 имеет всего 6 делителей. Это можно проверить, перечислив множители числа 12: 1, 2, 3, 4, 6, 12.
Какие общие делители чисел 4 и 12?
Делители числа 4 равны 1, 2 и 4. Делители числа 12 равны 1, 2, 3, 4, 6 и 12. Следовательно, можно видеть, что общие делители числа 4 и 12 равны 1, 2 и 4.
Какое число является делителем каждого числа?
1 является делителем каждого числа, потому что 1 полностью делит каждое число.
Что такое простые делители числа?
Простым множителем числа называется множитель, являющийся простым числом. Например, простые множители числа 12 равны 2, 2 и 3, потому что 2 × 2 × 3 = 12. Эти простые множители при умножении вместе дают произведение в виде числа. Простые множители числа можно вычислить с помощью метода факторного дерева или метода деления.
Простые множители числа можно вычислить с помощью метода факторного дерева или метода деления.
Могут ли коэффициенты быть отрицательными?
Да, делители числа могут быть отрицательными, потому что мы знаем, что произведение двух отрицательных чисел является положительным числом. Например, если мы умножим (-2) × (-3), мы получим 6. Точно так же (-1) × (-6) = 6. Это означает, что -1, -2, -3 и -6 являются отрицательные множители 6. Это показывает, что число может иметь положительные и отрицательные множители. В этом случае положительные факторы 6 могут быть перечислены как 1, 2, 3 и 6; а отрицательные факторы 6 могут быть перечислены как -1, -2, -3 и -6.
Рабочие листы по математике для 4 класса
Рабочие листы по математике для 4 класса Рабочие листы по математике для умножения, сложения, деления и разряда для 4 класса В этом листе по математике для 4 класса у нас есть вопросы «Умножение, деление, сложение, разрядное значение». Эти рабочие листы по математике охватывают все важные понятия из главы. Это дает вам общее представление и охватывает все важные формулы, применяя их. Этот рабочий лист подготовит вас к экзамену. Если вы попытаетесь выполнить этот рабочий лист с ограничением по времени, вы лучше подготовитесь к экзамену.
Эти рабочие листы по математике охватывают все важные понятия из главы. Это дает вам общее представление и охватывает все важные формулы, применяя их. Этот рабочий лист подготовит вас к экзамену. Если вы попытаетесь выполнить этот рабочий лист с ограничением по времени, вы лучше подготовитесь к экзамену.
Q1. Умножьте, используя метод столбца:-
a) 564 x 95
b) 791 x 283
Q2.
а) 23 х 1000 =………….
б) 7852 х 10 =………….
Q3. Фабрика производит 216 игрушек в день. Сколько игрушек он производит за 20 дней?
Q4. Решите следующее:
а. 39 х 100 = …………….
б. ………… х 9 = 72
в. 56 ÷ 8 = ………..
д. 32 ÷ 32 =……..
e. 672 ÷ 1 = ………………
ф. 22 х 30 = 3 х 10 х …….
Рабочий лист умножения Рабочий лист деления Q1. Разделить:-
Разделить:-
| а. 893 ÷ 6 | б. 2187 ÷ 8 |
| Q = | О = |
| Р = | Р = |
Q2) Разделите и запишите Q (частное) и R (остаток) для следующего:-
a) 7534 ÷ 13
b) 8127 ÷ 16
Q3. Заполнить таблицу (без расчетов)
| Частное | Остаток | |
| 343 ÷ 10 | 34 | 3 |
| 525 ÷ 10 | ||
| 650 ÷ 10 | ||
| 400 ÷ 100 | ||
| 720 ÷ 100 |
Q1. Разделите и запишите частное и остаток:
| Частное | Остаток | |
| 587 ÷ 10 | ||
| 9542 ÷ 10 | ||
| 740 ÷ 20 | ||
| 890 ÷ 50 |
Q2. Разделите следующее:
Разделите следующее:
| а. 184 ÷ 12 | б. 784 ÷ 15 |
| Q= ,R= | Q= ,R= |
| в. 2480 ÷ 25 | д. 3967 ÷ 19 |
| Q= ,R= | Q= ,R= |
Q1. Напишите место и значение места подчеркнутой цифры-
| ЧИСЛО | МЕСТО | РАЗМЕЩЕНИЕ ЗНАЧЕНИЕ |
| 8 ,73 549 | ||
| 22900 4 7 | ||
| 6 9 126 |
Q2. Перепишите числа через запятую и напишите их прописью:
и. 139854 ________________________________________________________________________________
__________________________________________________________________________
______________________________________________________________________________
ii. 999999______________________________________________________________________
999999______________________________________________________________________
__________________________________________________________________________
_______________________________________________________________________
Q3. Напишите цифрами и расставьте запятые по индийской системе:
i. Тридцать лакхов девять тысяч пятьсот одиннадцать. _______________
ii. Восемьдесят лакх шестьдесят тысяч три. _______________
iii. Шесть лакхов двести семь. _______________
Q4. Округлите следующие числа:
i. 73 до ближайшего 10_________________
ii. 3129 с точностью до 100________________
III. 7865 с точностью до 1000______________
Q5. Расположите в порядке возрастания:
i. 7319, 22408, 564, 112 _________,___________,__________,____________
ii. 87465, 4679, 12312, 143 _________,___________,__________,____________
Q6. Расположите в порядке убывания:
Расположите в порядке убывания:
i. 99994, 909, 9990, 7635 _________,___________,____________,___________
ii. 97645, 37890, 6547, 879_________,___________,____________,___________
Q7. Запишите числа в стандартной форме:
i. 800000+9000+400+9 ________________
ii. 60000+300+76+3 ________________
Q8. Напишите преемника и предшественника:
Преемник Предшественник
i. 999909 – __________________ __________________
ii. 470- __________________ __________________
Q9. Изобразите эти числа на счетах:
i. 76500
ii. 11993
Q10. Напишите следующее:
i. Сколько сотен в тысяче? ______________
ii. Сколько десятков в сотне? ____________________
iii. Сколько тысяч в лакхах? ____________________
Рабочий лист разряда Рабочий лист сложения и вычитания Q1. Заправки:
Заправки:
i. 1+ 899 _______
ii. Преемником 2001 года является _______
iii. 14 4 10 +- ? 10 + 2 + ________
iv. Предшественником 1100 является ________
v. 6712 +0 = _______
vi. 1235 +389 – ________
vii. 9876 – 10 ________
viii. 1689 – 0 ________
ix. 1001 – _____ = 1000 ________
х. 189 189 = ______
Q2. Решите следующее:
и. 8792
+6352
________
________
ii. 5364
+7629
________
________
iii. 1490
+ 9951
________
________
iv. 7562
– 3481
________
________
т. 9210
– 4702
________
________
vi. 3519
– 1683
________
________
Q3. Оцените сумму и разницу следующего:
и. 511 +32 8 (ближайшие 100 )= _______________
ii. 2987 4 4 6 9 2 (ближайшие 1000)= ______________
iii. 450 321 (ближайшие 10)= _____________
450 321 (ближайшие 10)= _____________
iv. 8350 – 2914 (ближайшие 1000)= ______________
Q4. В птичьем заповеднике 3289 птиц. Летом к ним присоединяются еще 1438 птиц. Найдите
количество птиц летом!
Q6. В чем разница между самым маленьким шестизначным числом и самым большим четырехзначным числом?
Q8. Вставьте недостающие:
i. 8940
-7_21
________
1319
_________
ii. 5217
+169_
________
6909
_________
для дополнительного рабочего листа класса 4 Математика
Связанные статьи
Английские рабочие листы для класса 4: Preposition, Pronoun, Gender 9009 4444444444444 Рабочий лист
Рабочий лист по математике для 4 класса
Рабочий лист для компьютера для 4 класса
Рабочий лист по английской грамматике для 4 класса — статьи A, An и The
Рабочий лист для компьютера для класса 4 — память компьютера
4 Подпишитесь на наш канал в социальных сетях.
Подготовьте онлайн-класса для начальной школы с нашими анимационными видео-лекциями и интерактивными уроками в прямом эфире
Здесь, в Takshila, мы предоставляем Школьные онлайн-классы от дошкольного до 12-го класса по всем предметам. Мы предоставляем лучших онлайн-курса обучения для класса 10 и других классов, которые включают анимационных видеолекции и онлайн живые занятия , которые помогут учащимся легко понять концепции. Мы также предоставляем рабочие листы и задания, сеансы сомнений, бесплатную энциклопедию, решения NCERT для класса 10 и экзаменационного гуру для отслеживания вашего прогресса, т. е. по предметам и по темам. Так что теперь наслаждайтесь электронным обучением с Обучение Такшила .
Теперь учиться весело!
Зарегистрируйтесь сегодня и получите бесплатный демо-класс!
Тег – рабочие листы по математике для 4 класса; лист умножения; дополнительный рабочий лист; ментальная математика; школьные онлайн-классы; рабочий лист по математике; Рабочий лист отдела, рабочий лист по математике для 4 класса, cbse рабочий лист по математике для 4 класса, рабочий лист по математике для 4 класса, рабочий лист по математике для четвертого класса
Рабочие листы по математике
Сложение
На этой индексной странице вы найдете ссылки на все типы таблиц сложения, включая основные факты, сложения из 2 цифр, сложения из 3 цифр, сложения из 4 цифр, сложение дробей, десятичное сложение, семейства фактов и сложение денег.
Дополнение: основные факты
Рабочие листы с основными однозначными фактами сложения (сумма до 18).
Сложение: 3-значные сложения
Потренируйтесь складывать 3-значные числа вместе с этими печатными листами, карточками с заданиями и играми.
Сложение: 4- и 5-значные сложения
Попросите учащихся решить задачи на сложение с 4- и 5-значными числами.
Сложение: 3 или более слагаемых
Проблемы сложения столбцов с 3 или более сложениями 1-, 2-, 3- и 4-значных чисел.
Сложение и вычитание: основные задачи
Рабочие листы, карточки и числовые ряды на этой странице содержат набор основных задач на сложение и вычитание однозначных чисел.
Дополнение: дроби
Сложите дроби и смешанные числа с одинаковыми знаменателями, а также с разными знаменателями.
Свойства сложения
Эти рабочие листы были созданы для обучения учащихся коммутативным и ассоциативным свойствам сложения.
Квадраты сложения
Развивайте навыки логического мышления с помощью этих рабочих листов-головоломок с добавлением квадратов.
Семейства фактов сложения-вычитания
Рабочие листы с базовыми треугольниками семейства фактов, числовыми связями и квадратами фактов для сложения и вычитания.
Дополнение: Игра с суммой (базовое дополнение)
На этих распечатываемых игровых досках учащиеся раскрашивают пары чисел, которые равны заданной сумме.
Алгебра и предварительная алгебра
Напишите алгебраические выражения, научитесь определять независимые/зависимые переменные, находить переменные в уравнениях, работать с неравенствами и т. д.
Углы: типы и измерение
Использование транспортира для измерения прямых, острых и тупых углов.
Уголки: дополнительные, дополнительные, вертикальные
Загрузите рабочие листы для отработки геометрических понятий, связанных с вертикальными, дополнительными и дополнительными углами.
Площадь треугольников
Используйте формулу A = 1/2 x (b x h) для вычисления площади треугольников.
Коробчатые диаграммы (диаграммы «коробка-и-усы»)
Используйте эти рабочие листы, чтобы помочь учащимся узнать о статистике и создании диаграмм «коробка-и-усы». Существуют также рабочие листы для расчета Q1, Q3, медианы, минимального и максимального значений.
Календари (математика)
Календари, чтобы помочь учащимся с годами, месяцами, неделями и днями в календаре.
Таблицы емкости
Таблицы объема или емкости (галлоны, кварты, пинты и чашки).
Круги: радиус, диаметр, длина окружности
Расчет диаметра и радиуса кругов; также включает листы окружности и площади.
Рабочие листы для раскрашивания по номерам
Раскрасьте загадочные картинки в соответствии с цифрой внизу.
Счет денег (австралийский)
Используйте эти рабочие листы, чтобы попрактиковаться в счете австралийских денег.
Подсчет денег (канадский)
Считайте мультяшек, луни, четвертак, пятак и десятицентовик с помощью этих рабочих листов для канадских валют.
Счет денег (британские фунты)
Научитесь считать фунты и пенсы — монеты, используемые в Соединенном Королевстве.
Счет денег (США)
Потренируйтесь считать американские деньги (пенни, пятаки, десятицентовики и четвертаки).
Рабочие листы для подсчета 0-30 (очень простые)
Научитесь считать и записывать числа до 30.
Рабочие листы для подсчета (более сложные)
Узнайте, как точно считать двух-, трех- и четырехзначные числа. Заполните числовые строки, скажите, какая цифра идет впереди, и пропустите счет.
Заполните числовые строки, скажите, какая цифра идет впереди, и пропустите счет.
Ежедневный обзор по математике
На этой странице вы найдете более 100 рабочих листов для ежедневного повторения («Math Buzz»), предназначенных для классов с 1 по 5.
Ежедневные словесные задачи
В этом разделе есть ежедневные математические задачи для 1-5 классов. Учащиеся должны решить сотни графических задач, а также достаточно места для демонстрации своей работы.
Десятичное сложение и вычитание
Сложение и вычитание десятичных чисел со значениями десятых, сотых и тысячных долей.
Десятичное деление
Практикуйте деление в длинное с десятичными числами.
Десятичное умножение
Упражнения на умножение с десятичными множителями и произведениями.
Десятичные рабочие листы
Именование и работа с десятичными числами.
Рабочие листы по разделам: основные
Рабочие листы с фактами по основным разделам, игры и задания.
Рабочие листы деления: длинное деление
Рабочие листы длинного деления с 2-, 3- и 4-значными делимыми.
Уравнения (базовая алгебра)
Научитесь балансировать простые алгебраические уравнения и находить значения переменных.
Рабочие листы для четных и нечетных чисел
Определение нечетных и четных чисел
Рабочие листы с показателями степени
Найдите показатели степени однозначных чисел на этих распечатываемых рабочих листах и карточках с заданиями.
Рабочие листы факторинга
Полное дерево факторов, поиск наибольших общих делителей и наименьших общих кратных.
Таблицы дробей (дополнительно)
Сокращение дробей, упорядочивание дробей, эквивалентные дроби и сравнение дробей.
Рабочие листы дробей (базовые)
Идентификация основных дробей, полос дробей, манипуляций дробями.
Дроби: сложение
Нахождение сумм дробей и смешанных чисел. Включает рабочие листы с дробями с одинаковым знаменателем, а также с дробями с разными знаменателями.
Дроби: Деление
Деление дробей и смешанных чисел. Многие из этих рабочих листов включают иллюстрированные задачи, задачи с графическими моделями, а также текстовые задачи.
Дроби: смешанные числа
Практикуйте базовые навыки работы со смешанными числами.
Дроби: умножение
Умножение дробей и смешанных чисел. Многие рабочие листы включают модели и диаграммы, а также текстовые задачи.
Дроби: обратные дроби
Распечатайте эти рабочие листы, чтобы помочь учащимся узнать об обратных дробях.
Дроби: вычитание
Практика вычитания дробей и смешанных чисел. Включает подобные и неодинаковые знаменатели.
Практика с рамками и стрелками
Используйте упражнения с рамками и стрелками для развития навыков логического мышления.
Графики: гистограммы
Прочитайте гистограммы на рабочих листах и ответьте на вопросы.
Графики: линейные графики
Интерпретируйте линейные графики на рабочих листах и ответьте на вопросы.
Графики: линейные графики
Линейные графики — это особый тип числовой линии, который представляет частоту данных.
Графики: пиктограммы
Изучите пиктограммы на рабочих листах и ответьте на вопросы.
Графики: круговые диаграммы
Проанализируйте круговые диаграммы на рабочих листах и ответьте на вопросы.
Больше, Меньше Рабочие листы
Сравните числа больше, меньше и равно.
Таблицы сотен
Используйте эти полезные таблицы стоимостных значений, таблицы сотен, таблицы девяноста девяти.
Ящики ввода и вывода
Заполните эти печатаемые поля ввода и вывода или поля правил.
Неравенства
Решить неравенства и построить график. Включает неравенства с одной переменной, одношаговые и двухшаговые неравенства.
Целые числа (базовые)
Сравнивать, упорядочивать, складывать и вычитать положительные и отрицательные числа.
Наименьшее общее кратное (НОК)
Определение наименьшего общего кратного каждого набора чисел
Линии, сегменты, лучи
Узнайте о линиях, сегментах линий, лучах, параллельных линиях и перпендикулярных линиях.
Математические кроссворды
Решите математические задачи и используйте ответы, чтобы решить кроссворды.
Математические загадки
Решите математические задачи, чтобы расшифровать ответ на забавные загадки. Включает широкий спектр математических навыков, включая сложение, вычитание, умножение, деление, разрядность, округление и многое другое.
Отрывки из математических рассказов
На этой странице есть набор отрывков для чтения на всю страницу. Учащиеся используют информацию из отрывков для решения математических задач. Они намного длиннее, чем «обычные» текстовые задачи.
Рабочие листы Mean (Averages)
Вычислить среднее или среднее числовых значений.
Среднее значение, медиана, мода и диапазон
Вычислите моду, медиану, среднее значение и диапазон заданных чисел.
Индекс измерений
Выберите нужные вам типы таблиц измерений, включая линейные измерения, емкость и температуру.
Измерение: CM, MM и M
Практика метрических линейных измерений: сантиметры, миллиметры и метры.
Измерение: футы, ярды, дюймы
Изучение американских линейных измерений; дюймы, футы и ярды.
Измерение: граммы и килограммы
Измерение веса и преобразование в граммы и килограммы.
Измерение: литры и миллилитры
Расчет и преобразование значений объема в литрах и миллилитрах.
Измерение: фунты и унции
Измерение веса и преобразование в унции и фунты и обратно.
Математика в средней школе
Эта индексная страница содержит ссылки на десятки тем по математике для средней школы на этом сайте. Темы включают неравенства, абсолютное значение, алгебру и многое другое.
Темы включают неравенства, абсолютное значение, алгебру и многое другое.
Минимум математических упражнений
Листы с практическими упражнениями для сложения, вычитания, умножения и деления.
Кратные числа
Эти рабочие листы помогут учащимся научиться находить и определять кратные числа.
Умножение (Свойства)
Узнайте об ассоциативных, дистрибутивных, коммутативных и тождественных свойствах умножения.
Таблицы умножения
Распечатайте эти таблицы и таблицы умножения, чтобы учащиеся могли использовать их в качестве справочных материалов.
Рабочие листы по умножению: продвинутый уровень
Решите задачи на умножение двух и трех цифр.
Рабочие листы по умножению: основы
Изучите основные факты умножения с помощью этих рабочих листов, загадочных картинок и игр.
Семейства фактов умножения-деления
Связи основных чисел, рабочие листы семейства фактов и треугольники для деления и умножения.
Умножение: решеточное умножение
Умножение на 2-, 3- или 4-значные числа с помощью решетчатой сетки.
Mystery Graph Art
Нарисуйте упорядоченные пары, чтобы открыть загадочные картинки.
Загадочные математические картинки
Решите факты сложения, вычитания, умножения и деления, чтобы открыть загадочную картинку.
Детектив чисел (секретные числа)
Учащиеся будут использовать подсказки, вывешиваемые каждый день, чтобы вычислить недельный секретный номер.
Числовые ряды
Рабочие листы числовых рядов для обучения счету, сложению, вычитанию, моделям счисления, дробям и десятичным дробям.
Порядок действий
Отработайте порядок действий: скобки и возведения в степень, затем умножение и деление, затем сложение и вычитание.
Заказные пары; Координатные плоскости
Координатные плоскости и упорядоченные парные рабочие листы.
Порядковые номера
Порядковые номера определяют позицию в серии. (примеры: первый, второй, третий, четвертый и т. д.)
Шаблоны: Число
Учащиеся должны перечислить числа, идущие следующими в этих шаблонах.
Образцы: Рисунок
Учащиеся определяют, какие изображения идут следующими в узорах.
Таблицы процентов
Преобразование десятичных чисел и дробей в проценты.
Рабочие листы периметра
Добавьте, чтобы найти периметры многоугольников на этих рабочих листах.
Таблицы значений разрядов
Нахождение значения подчеркнутой цифры; стандартная и расширенная форма; округление.
Простые и составные числа
Изучите разницу между простыми и составными числами. Кроме того, научитесь определять и находить простые числа с помощью разложения на множители или с помощью решета Эратосфена.
Полигоны. Рабочие листы
Определение многоугольников и работа с ними.
Рабочие листы вероятности
Определение вероятности определенных исходов.
Математические игры-головоломки
Детали головоломки, которые можно распечатать, чтобы ученики могли сопоставить их. Отлично подходит для учебных центров, занятий в небольших группах и самостоятельной практики.
Теорема Пифагора
Найдите длины сторон прямоугольного треугольника по формуле теоремы Пифагора.
Рабочие листы с QR-кодом
Учащиеся используют iPad или смартфон для сканирования QR-кодов, чтобы решать или проверять задачи на каждом из этих математических рабочих листов.
Соотношения
Потренируйтесь сравнивать пары величин с помощью соотношений.
Отражение, вращение и перемещение
Определение отраженных, повернутых и перемещенных фигур.
Римские цифры
Научитесь читать и писать римскими цифрами с помощью этих распечатываемых рабочих листов и заданий.
Рабочие листы для округления чисел
Округление чисел до ближайших десятков и сотен.
Научное представление
Научитесь записывать числа в научном представлении.
Secret Code Math
На этих рабочих листах учащиеся будут использовать ключ для расшифровки секретных чисел в каждой задаче на сложение, вычитание, умножение или деление.
Похожие и конгруэнтные рабочие листы
Определите похожие и конгруэнтные формы.
Счет с пропуском сотнями
Используйте эти рабочие листы, чтобы научить учащихся считать с пропуском сотнями.
Пропустить счет десятками
Повторить счет десятками с помощью этих печатных форм.
Пропустить счет до 11
Сосчитайте до одиннадцати, умножьте на одиннадцать и вставьте пропущенные числа.
Пропустить счет до 12
Заполните пустые ячейки и текстовые задачи, считая до двенадцати.
Пропустить счет до 25
Пропустить счет до двадцати пяти очень важно, если вы учите своих учеников считать деньги.
Пропустить счет на 2 секунды
Используйте эти распечатки, чтобы научить учащихся пропускать счет с интервалом в два.
Пропустить счет на 3 секунды
Набор рабочих листов на этой странице поможет учащимся научиться считать тройками.
Пропустить счет до четырех
Если вы учите учащихся считать до четырех, попробуйте эти рабочие листы.
Пропустить счет пятерками
Когда вы учите учащихся считать пятерками или пятерками, эти рабочие листы могут быть вам полезны.
Слайды, перевороты и повороты Рабочие листы
Укажите, были ли фигуры перевернуты, сдвинуты или повернуты.
Наклон
На этих рабочих листах учащиеся будут использовать графики, упорядоченные пары и таблицы для расчета наклонов прямых линий.
Рабочие листы твердых фигур
Назовите геометрические твердые формы: прямоугольные призмы, кубы, сферы и цилиндры.
Специальные числа
Эти рабочие листы охватывают различные понятия разрядности, включая четные/нечетные значения, нахождение значения цифр и запись чисел в расширенной форме.
Вычитание
Вычитание однозначных и многозначных чисел. Включает 1, 2, 3 и 4-значные числа. Также есть ссылки на десятичную дробь и вычитание денег.
Вычитание: Базовый
Попрактикуйтесь в вычитании однозначных чисел; концепции и рабочие листы.
Вычитание дробей
Потренируйтесь вычитать дроби и смешанные числа с помощью этих распечатываемых рабочих листов и карточек с заданиями.
Площадь поверхности
Расчет площади поверхности прямоугольных призм и других трехмерных фигур.
Рабочие листы по симметрии
Найдите линии симметрии, определите симметричные фигуры и завершите симметричные фигуры.
Счетные метки
Научитесь считать объекты с помощью счетных меток.
Рабочие листы температуры
Прочтите показания термометров Цельсия и Фаренгейта и укажите температуру.
Математика с десятью рамками
Распечатанные задания с десятью рамками для обучения счету, основам сложения и простому вычитанию.
Рабочие листы по мозаике
Научите учащихся распознавать геометрическую мозаику двумерных фигур.
Рабочие листы времени
Узнайте, как определять время с точностью до минуты, часа и четверти часа.
Время: Прошедшее время
Определите количество прошедшего времени.
Диаграммы Венна (математика)
Эта страница содержит рабочие листы математических диаграмм Венна.
Объем — градуированные цилиндры
Эти рабочие листы содержат изображения градуированных цилиндров. Учащиеся должны написать правильный объем в миллилитрах.
Рабочие листы объема
Расчет объема объемных фигур. Включает объемные «счетные кубы», прямоугольные призмы, конусы, цилиндры и сферы.
Включает объемные «счетные кубы», прямоугольные призмы, конусы, цилиндры и сферы.
Рабочие листы с текстовыми задачами (по типу)
Упражнения на сложение, вычитание, умножение и деление.
Рабочие листы для решения задач со словами (смешанный)
Проверьте навыки решения задач со смешанными словами в разных классах.
Словесные задачи (несколько шагов)
Эти текстовые задачи состоят из нескольких шагов и требуют от учащихся использования навыков критического мышления.
Страницы математических указателей
Таблицы сложения
Здесь вы можете сослаться на все типы таблиц сложения, включая основные факты, сложение дробей, 2-значное, 3-значное и 4-значное сложение.
Рабочие листы дробей
Указатель наших базовых и расширенных рабочих листов дробей.
Рабочие листы по геометрии
Изучайте площадь, периметр, симметрию, многоугольники, объемные формы и многое другое.
Рабочие листы графиков
Выберите из круговых диаграмм, гистограмм и линейных диаграмм.
Листы с пропуском счета
Счет 2, 3, 4, 5, 10, 25 или 100 секунд.
Рабочие листы по вычитанию
Вот индексная страница со ссылками на все разделы нашего веб-сайта, посвященные вычитанию.
Рабочие листы по математическим навыкам
Эта страница содержит только частичный индекс рабочих листов по математическим навыкам на S.T.W.
Полный указатель веб-сайта
Просмотрите полный указатель всех рабочих листов по математике, английскому языку, орфографии, фонетике, грамматике, естественным наукам и общественным наукам, найденным на этом веб-сайте.
Рабочие листы по длинному умножению
На этой странице представлены рабочие листы по длинному умножению для учащихся, которые освоили основные факты умножения и учатся умножать 2-, 3-, 4-значные и более числа. Вопросы на этих рабочих листах, которые иногда называют длинным умножением или многозначным умножением, требуют, чтобы учащиеся освоили факты умножения от 0 до 9..
Вопросы на этих рабочих листах, которые иногда называют длинным умножением или многозначным умножением, требуют, чтобы учащиеся освоили факты умножения от 0 до 9..
Существует множество стратегий для завершения длинного умножения, включая классические методы с бумагой и карандашом, умножение на решетке (которое мы представляем на этой странице), ментальные стратегии, манипулятивное использование, технологии и различные другие алгоритмы с бумагой и карандашом. Многозначное умножение может быть разочаровывающим опытом для многих учащихся. Попробуйте научить многозначному умножению, используя более одной стратегии.
Самые популярные длинные рабочие листы по умножению на этой неделе
Умножение 2-значных чисел на 2-значные числа ( 6666 просмотров на этой неделе )Умножение 2-значных чисел на 1-значные числа ( 3632 просмотров на этой неделе )Умножение 3-значных чисел на 2-значные числа ( 3398 просмотров на этой неделе )Умножение 3-значных чисел на 1-значные числа ( 1830 просмотров на этой неделе )Умножение 3-значных чисел на 3-значные числа ( 1639 просмотров на этой неделе ) размеры чисел и параметры для различных числовых форматов.
Двузначное умножение является естественным началом после того, как учащиеся усвоили факты умножения. Концепция умножения двузначных чисел требует знания места и значения места, особенно если учащиеся должны полностью понять, чего они достигают с помощью различных стратегий, которые они используют. Такой вопрос, как 24 × 5, можно рассматривать как (20 + 4) × 5. Умственно это становится намного проще, когда учащиеся умножают 20 на 5, затем 4 на 5 и складывают два произведения. Хороший способ понять значение разряда — использовать блоки с основанием 10. Эти манипуляции также очень хорошо переносятся на бумагу, карандаш и математические стратегии в уме.
Дополнительная цифра может сбить с толку одних учащихся, но усложнить задачу другим. Всегда следите за тем, чтобы ученики были готовы к трехзначному умножению, иначе и вы, и ваш ученик будете разочарованы. Рабочие листы для трехзначного умножения требуют овладения фактами однозначного умножения и знания стратегии многозначного умножения, которая позволит учащимся как понять вопрос, так и получить правильный ответ. Четырехзначное умножение было изобретено в 350 г. до н.э. как способ наказания детей, укравших хлеб с рынка. Просто шучу! На самом деле это большая проблема для студентов, которые добились успеха в своих фактах умножения и хорошо разбираются в длинной стратегии умножения. Что вы даете ученикам, которые освоили факты умножения и длинное умножение и которым нравится решать сложные задачи? Не смотрите дальше пяти-восьмизначного умножения. Наслаждаться!
Четырехзначное умножение было изобретено в 350 г. до н.э. как способ наказания детей, укравших хлеб с рынка. Просто шучу! На самом деле это большая проблема для студентов, которые добились успеха в своих фактах умножения и хорошо разбираются в длинной стратегии умножения. Что вы даете ученикам, которые освоили факты умножения и длинное умножение и которым нравится решать сложные задачи? Не смотрите дальше пяти-восьмизначного умножения. Наслаждаться!
Длинные рабочие листы умножения
В числах на этих листах нет разделителей тысяч. Это немного усложняет чтение чисел, но иногда лучше не мешать слишком многим вещам, когда учащиеся изучают длинное умножение. Ключи ответов включают ответы с показанными шагами, поэтому учащиеся и учителя могут диагностировать любые проблемы в шагах, которые они предприняли, чтобы ответить на вопросы. В ответах используется алгоритм бумаги и карандаша, который обычно используется в США и других странах.
Умножение 2 цифр на 1 цифру Умножение 2-значное на 2-значное Умножение 3-значное на 1-значное Умножение 3-значное на 2-значное Умножение 3-значный на 3-значный Умножение 4-значное на 1-значное Умножение 4-значное на 2-значное Умножение 4-значное на 3-значное Умножение 4-значный на 4-значный Умножение 5-значное число на 1-значное Умножение 5-значное на 2-значное Умножение 5-значное на 3-значное Умножение 5-значное на 4-значное Умножение 5-значное на 5-значное Умножение 6-значное на 1-значное Умножение 6-значное на 2-значное Умножение 6-значный на 3-значный Умножение 6-значное на 4-значное Умножение 6-значный на 5-значный Умножение 6-значный на 6-значный Умножение 7-значное на 1-значное Умножение 7-значное на 2-значное Умножение 7-значное на 3-значное Умножение 7-значное на 4-значное Умножение 7-значное на 5-значное Умножение 7-значное на 6-значное Умножение 7-значный на 7-значный Умножение 8-значное на 1-значное Умножение 8-значное на 2-значное Умножение 8-значное на 3-значное Умножение 8-значное на 4-значное Умножение 8-значное на 5-значное Умножение 8-значное на 6-значное Умножение 8-значное на 7-значное Умножение 8-значное на 8-значное Умножение 2 цифры на 1 цифру Умножение ( Крупный шрифт ) 2 цифры на 2 цифры Умножение ( крупный шрифт ) 3 цифры на 1 цифру Умножение ( Крупный шрифт ) 3 цифры на 2 цифры Умножение ( Крупный шрифт ) 3 цифры на 3 цифры Умножение ( Крупный шрифт ) 4 цифры на 1 цифру Умножение ( Крупный шрифт ) 4-значный на 2-значный Умножение ( Крупный шрифт ) 4 цифры на 3 цифры Умножение ( Крупный шрифт ) 4 цифры на 4 цифры Умножение ( Крупный шрифт ) 5 цифр на 1 цифру Умножение ( Крупный шрифт ) 5-значный на 2-значный Умножение ( Крупный шрифт ) 5-значный на 3-значный Умножение ( Крупный шрифт ) 5-значный на 4-значный Умножение ( Крупный шрифт ) 5-значный на 5-значный Умножение ( Крупный шрифт ) 6 цифр на 1 цифру Умножение ( Крупный шрифт ) 6-значный на 2-значный Умножение ( Крупный шрифт ) 6-значный на 3-значный Умножение ( Крупный шрифт ) 6-значный на 4-значный Умножение ( Крупный шрифт ) 6-значный на 5-значный Умножение ( Крупный шрифт ) 6-значный на 6-значный Умножение ( Крупный шрифт )
Длинное умножение с
тысячами, разделенными запятыми Запятые используются в качестве разделителей тысяч для чисел на этих листах. Запятые используются в США и других англоязычных странах для облегчения чтения чисел. Как и в других длинных листах умножения на этой странице, ключи ответов включают шаги.
Запятые используются в США и других англоязычных странах для облегчения чтения чисел. Как и в других длинных листах умножения на этой странице, ключи ответов включают шаги.
Умножение 2 цифр на 2 цифры (тысячи, разделенные запятыми) 3 цифры на 1 цифру Умножение (тысячи, разделенные запятыми) 3-значное на 2-значное Умножение (тысячи, разделенные запятыми) 3-значное на 3-значное умножение (тысячи, разделенные запятыми) Умножение 4 цифр на 1 цифру (тысячи, разделенные запятыми) 4-значное на 2-значное Умножение (тысячи, разделенные запятыми) 4-значное на 3-значное Умножение (тысячи, разделенные запятыми) 4-значный на 4-значный Умножение (тысячи, разделенные запятыми) 5-значное на 1-значное Умножение (тысячи, разделенные запятыми) 5-значное на 2-значное Умножение (тысячи, разделенные запятыми) 5-значное на 3-значное Умножение (тысячи, разделенные запятыми) 5-значное на 4-значное Умножение (тысячи, разделенные запятыми) 5-значный на 5-значный Умножение (тысячи, разделенные запятыми) 6-значный на 1-значный Умножение (тысячи, разделенные запятыми) 6-значное на 2-значное Умножение (тысячи, разделенные запятыми) 6-значное на 3-значное Умножение (тысячи, разделенные запятыми) 6-значное на 4-значное Умножение (тысячи, разделенные запятыми) 6-значное на 5-значное Умножение (тысячи, разделенные запятыми) 6-значный на 6-значный Умножение (тысячи, разделенные запятыми) 7-значное на 1-значное Умножение (тысячи, разделенные запятыми) 7-значный на 2-значный Умножение (тысячи, разделенные запятыми) 7-значное на 3-значное Умножение (тысячи, разделенные запятыми) 7-значное на 4-значное Умножение (тысячи, разделенные запятыми) 7-значное на 5-значное Умножение (тысячи, разделенные запятыми) 7-значное на 6-значное Умножение (тысячи, разделенные запятыми) 7-значный на 7-значный Умножение (тысячи, разделенные запятыми) 8-значное на 1-значное Умножение (тысячи, разделенные запятыми) 8-значное на 2-значное Умножение (тысячи, разделенные запятыми) 8-значное на 3-значное Умножение (тысячи, разделенные запятыми) 8-значное на 4-значное Умножение (тысячи, разделенные запятыми) 8-значное на 5-значное Умножение (тысячи, разделенные запятыми) 8-значное на 6-значное Умножение (тысячи, разделенные запятыми) 8-значное на 7-значное Умножение (тысячи, разделенные запятыми) 8-значный на 8-значный Умножение (тысячи, разделенные запятыми) 2-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 3-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 3-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 3-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 4-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 4-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 4-значное на 3-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 4-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 5-значный на 1-значный Умножение ( Крупный шрифт ) (тысячи, разделенные запятыми) 5-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 5-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 5-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 5-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми) 6-значный на 6-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные запятыми)
Длинное умножение с
тысячами, разделенными пробелами Разделение тысяч пробелами позволяет избежать путаницы с запятыми и точками. Различные числовые форматы в разных странах и языках используют запятые и точки как для десятичных знаков, так и для разделителей тысяч, но пробел всегда используется только как разделитель тысяч. Это более распространено в некоторых странах, таких как Канада и Франция, но чаще применяется в других частях мира.
Различные числовые форматы в разных странах и языках используют запятые и точки как для десятичных знаков, так и для разделителей тысяч, но пробел всегда используется только как разделитель тысяч. Это более распространено в некоторых странах, таких как Канада и Франция, но чаще применяется в других частях мира.
Умножение 2 цифр на 2 цифры (тысячи, разделенные пробелами) 3-значное на 1-значное Умножение (тысячи, разделенные пробелами) 3-значное на 2-значное Умножение (тысячи, разделенные пробелами) 3-значное умножение на 3-значное (тысячи, разделенные пробелами) Умножение 4 цифр на 1 цифру (тысячи, разделенные пробелами) 4-значное на 2-значное Умножение (тысячи, разделенные пробелами) 4-значное на 3-значное Умножение (тысячи, разделенные пробелами) 4-значное умножение на 4-значное (тысячи, разделенные пробелами) Умножение 5 цифр на 1 цифру (тысячи, разделенные пробелами) 5-значное на 2-значное Умножение (тысячи, разделенные пробелами) 5-значное на 3-значное Умножение (тысячи, разделенные пробелами) 5-значное на 4-значное Умножение (тысячи, разделенные пробелами) 5-значный на 5-значный Умножение (тысячи, разделенные пробелом) 6-значное на 1-значное Умножение (тысячи, разделенные пробелами) 6-значное на 2-значное Умножение (тысячи, разделенные пробелами) 6-значное на 3-значное Умножение (тысячи, разделенные пробелами) 6-значное на 4-значное Умножение (тысячи, разделенные пробелами) 6-значное на 5-значное Умножение (тысячи, разделенные пробелами) 6-значное умножение на 6-значное (тысячи, разделенные пробелами) 7-значное на 1-значное Умножение (тысячи, разделенные пробелами) 7-значное на 2-значное Умножение (тысячи, разделенные пробелами) 7-значное на 3-значное Умножение (тысячи, разделенные пробелами) 7-значное на 4-значное Умножение (тысячи, разделенные пробелами) 7-значное на 5-значное Умножение (тысячи, разделенные пробелами) 7-значное на 6-значное Умножение (тысячи, разделенные пробелами) 7-значный на 7-значный Умножение (тысячи, разделенные пробелом) 8-значное на 1-значное Умножение (тысячи, разделенные пробелами) 8-значное на 2-значное Умножение (тысячи, разделенные пробелами) 8-значное на 3-значное Умножение (тысячи, разделенные пробелами) 8-значное на 4-значное Умножение (тысячи, разделенные пробелами) 8-значное на 5-значное Умножение (тысячи, разделенные пробелами) 8-значное на 6-значное Умножение (тысячи, разделенные пробелами) 8-значное на 7-значное Умножение (тысячи, разделенные пробелами) 8-значное умножение на 8-значное (тысячи, разделенные пробелами) 2-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 3-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 3-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 3-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значное на 3-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значное на 4-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелом) 6-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 6-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами)
Длинное умножение с
тысячами, разделенными точкой В некоторых местах точки используются как разделители тысяч, а запятые — как десятичные дроби. Это очень сбивает с толку людей, которые привыкли к номерам в формате США.
Это очень сбивает с толку людей, которые привыкли к номерам в формате США.
2-значный на 2-значный Умножение (тысячи, разделенные точкой) 3-значное на 1-значное Умножение (тысячи, разделенные точкой) 3-значное на 2-значное Умножение (тысячи, разделенные точкой) 3-значное на 3-значное Умножение (тысячи, разделенные точкой) 4-значное на 1-значное Умножение (тысячи, разделенные точкой) 4-значное на 2-значное Умножение (тысячи, разделенные точкой) 4-значный на 3-значный Умножение (тысячи, разделенные точкой) 4-значное умножение на 4-значное (тысячи, разделенные точкой) 5-значное на 1-значное Умножение (тысячи, разделенные точкой) 5-значное на 2-значное Умножение (тысячи, разделенные точкой) 5-значное на 3-значное Умножение (тысячи, разделенные точкой) 5-значное на 4-значное Умножение (тысячи, разделенные точкой) 5-значный на 5-значный Умножение (тысячи, разделенные точкой) 6-значное на 1-значное Умножение (тысячи, разделенные точкой) 6-значное на 2-значное Умножение (тысячи, разделенные точкой) 6-значное на 3-значное Умножение (тысячи, разделенные точкой) 6-значное на 4-значное Умножение (тысячи, разделенные точкой) 6-значное на 5-значное Умножение (тысячи, разделенные точкой) 6-значный по 6-значный Умножение (тысячи, разделенные точкой) 7-значное на 1-значное Умножение (тысячи, разделенные точкой) 7-значное на 2-значное Умножение (тысячи, разделенные точкой) 7-значное на 3-значное Умножение (тысячи, разделенные точкой) 7-значное на 4-значное Умножение (тысячи, разделенные точкой) 7-значное на 5-значное Умножение (тысячи, разделенные точкой) 7-значный на 6-значный Умножение (тысячи, разделенные точкой) 7-значный на 7-значный Умножение (тысячи, разделенные точкой) 8-значное на 1-значное Умножение (тысячи, разделенные точкой) 8-значное на 2-значное Умножение (тысячи, разделенные точкой) 8-значное на 3-значное Умножение (тысячи, разделенные точкой) 8-значное на 4-значное Умножение (тысячи, разделенные точкой) 8-значный на 5-значный Умножение (тысячи, разделенные точкой) 8-значное на 6-значное Умножение (тысячи, разделенные точкой) 8-значное на 7-значное Умножение (тысячи, разделенные точкой) 8-значное на 8-значное Умножение (тысячи, разделенные точкой) 2-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 3-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 3-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 3-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значное на 3-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 6-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой)
Решетчатое умножение
Решетчатое умножение Рабочие листы для изучения и использования этой длинной стратегии умножения.
Различные цифры
Умножение решеток Рабочие листы с включенными решетками Решетчатое или решетчатое умножение — отличная стратегия, которую учащиеся могут использовать для вычисления длинных задач на умножение карандашом и бумагой. Мы упростили первый шаг подготовки решетки, так как на рабочих листах ниже они предварительно нарисованы. Немного попрактиковавшись, учащиеся смогут использовать миллиметровую бумагу или рисовать решетки от руки. Первый фактор разделен разрядным значением в верхней части решетки, что дает каждому разрядному значению собственный столбец. Второй множитель отделяется таким же образом, но по правой стороне с одним разрядным значением в строке. Одноразрядные номера столбца и строки перемножаются, и их произведение записывается в соответствующее поле, разделяя разряды десятков и единиц по обе стороны от диагонали. Наконец, диагональные «строки» суммируются и перегруппировываются, начиная с диагонали в правом нижнем углу, в которой будет только одна цифра. Ключи ответов, которые мы предоставили, должны дать вам хорошее представление о том, как выполнить решеточное умножение, как профессионал. После того, как учащиеся немного попрактикуются, вы можете обнаружить, что это их предпочтительный метод вычисления произведений больших чисел. Этот метод легко масштабируется, что означает простую задачу умножения 10-значного числа на 10-значное число и т. д.
Ключи ответов, которые мы предоставили, должны дать вам хорошее представление о том, как выполнить решеточное умножение, как профессионал. После того, как учащиеся немного попрактикуются, вы можете обнаружить, что это их предпочтительный метод вычисления произведений больших чисел. Этот метод легко масштабируется, что означает простую задачу умножения 10-значного числа на 10-значное число и т. д.
2-разрядное × 2-разрядное решеточное умножение 2-значное × 3-значное умножение решетки 3-значное × 2-значное умножение решетки 3-разрядное × 3-разрядное решеточное умножение 4-разрядное × 2-разрядное решеточное умножение 4-разрядное × 3-разрядное решеточное умножение 4-разрядное × 4-разрядное решеточное умножение 4-значное × 5-значное решеточное умножение 5-значное × 4-значное решеточное умножение 5-разрядное × 5-разрядное решеточное умножение
Распределительная собственность
Рабочие листы с распределением свойств, чтобы помочь учащимся научиться мысленно умножать целые числа, не полагаясь на бумажные/карандашные методы.
Рабочие листы по умножению для изучения
распределительного свойства умножения2-значное × 1-значное умножение 3-значное × 1-значное умножение
Умножение с поддержкой сетки
Умножение на миллиметровой бумаге помогает учащимся «выстраивать» свои числа при выполнении длинных вопросов на умножение. Эти рабочие листы включают настраиваемые сетки, в которых достаточно места для одного вопроса.
Умножение с поддержкой сетки рабочих листов2-разрядный × 1-разрядный Умножение с поддержкой сетки 3-разрядный × 1-разрядный Умножение с поддержкой сетки 4-разрядный × 1-разрядный Умножение с поддержкой сетки 2-разрядный × 2-разрядный Умножение с поддержкой сетки 3-разрядный × 2-разрядный Умножение с поддержкой сетки 4 цифры × 2 цифры Умножение с поддержкой сетки 3-разрядный × 3-разрядный Умножение с поддержкой сетки 4-разрядный × 3-разрядный Умножение с поддержкой сетки
Умножение с поддержкой сетки Заготовки Если вы или ваши ученики хотите составить свои вопросы, эти поля должны ускорить процесс.
 Найди значение выражения:
Найди значение выражения: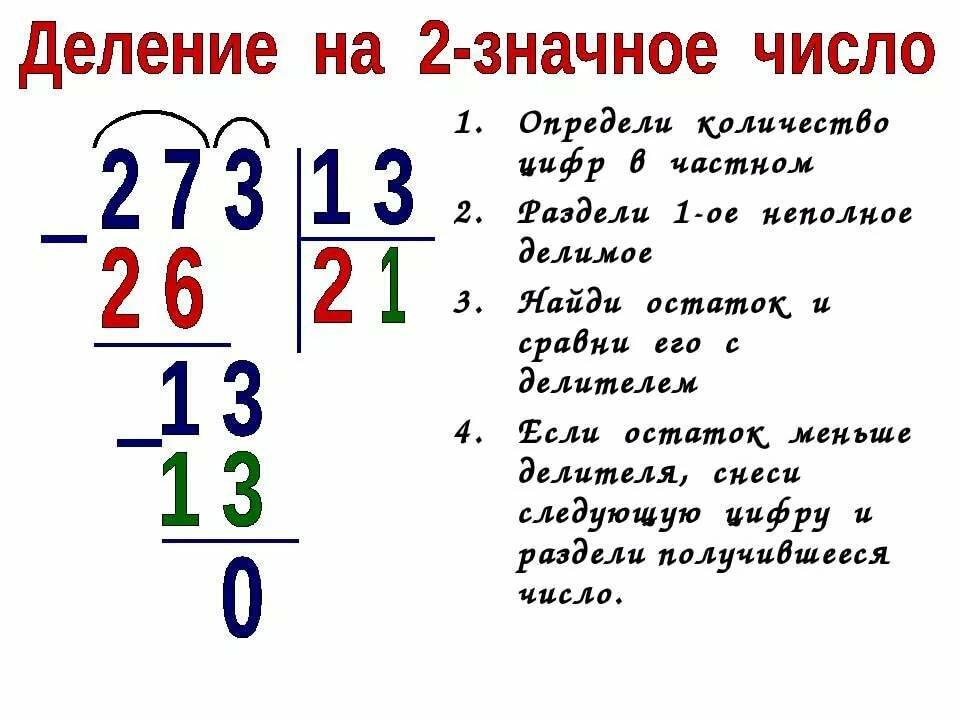 Найди значение выражения:
Найди значение выражения:

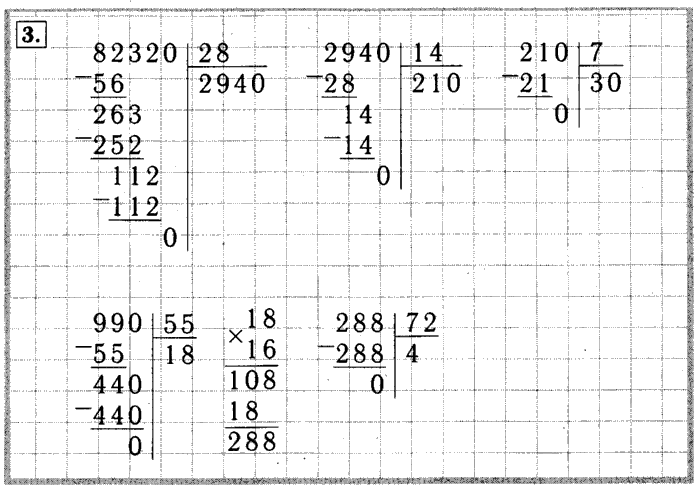 продали 1/5 часть этого куска. Сколько метров ткани осталось в куске?
продали 1/5 часть этого куска. Сколько метров ткани осталось в куске? Сколько лет живёт берёза?
Сколько лет живёт берёза?
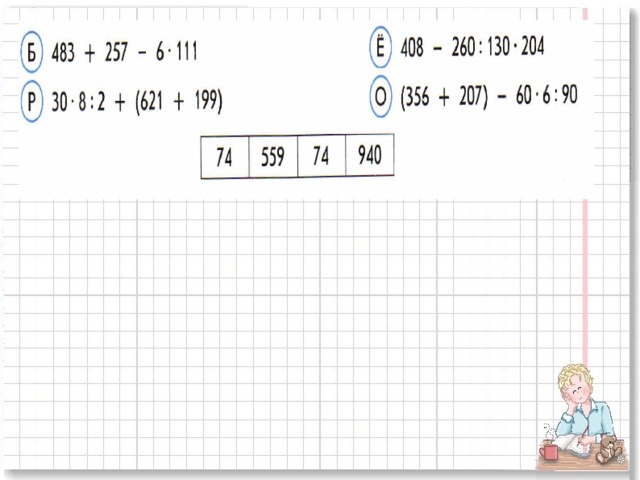
 (Два варианта)
(Два варианта)
