16 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
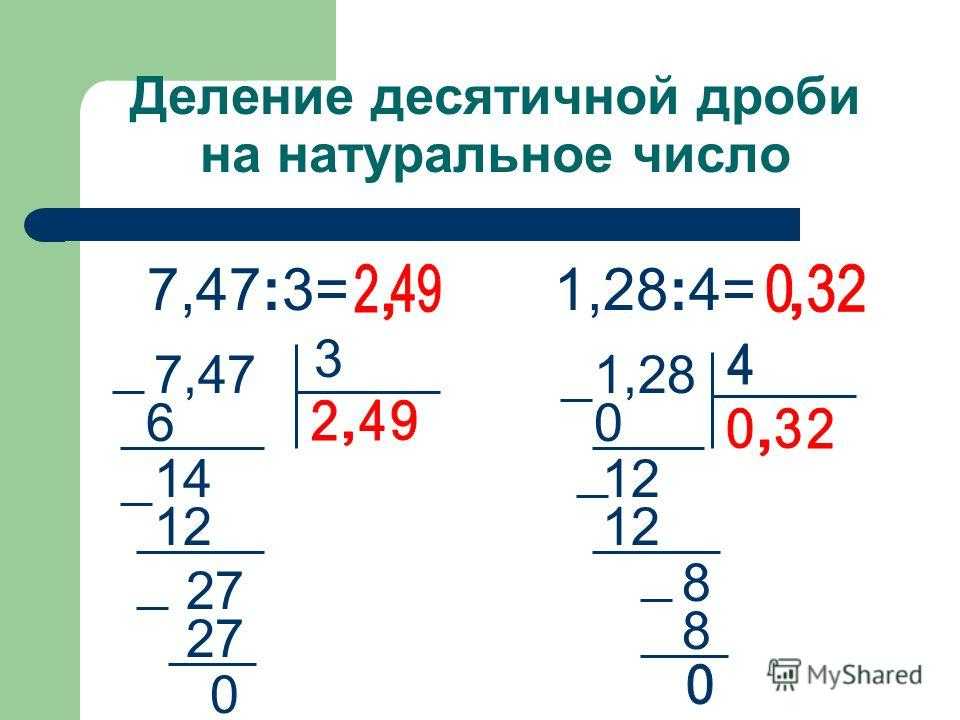
§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
Математика 5 класс
Математика 6 класс
Алгебра 7 класс
Геометрия 7 класс
Алгебра 8 класс
Алгебра 9 класс
Алгебра 10 класс
Алгебра 11 класс
Не браните погоду — если бы она не менялась, девять человек из десяти не смогли бы начать ни одного разговора.
Записываем цифру «6» в частное.
Записываем «48» под «51».
Запомните!При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус). Вычтем по правилам вычитания в столбик «48» и под чертой запишем результат.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8».
И опять по таблице умножения на «8», найдем ближайшее произведение.
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
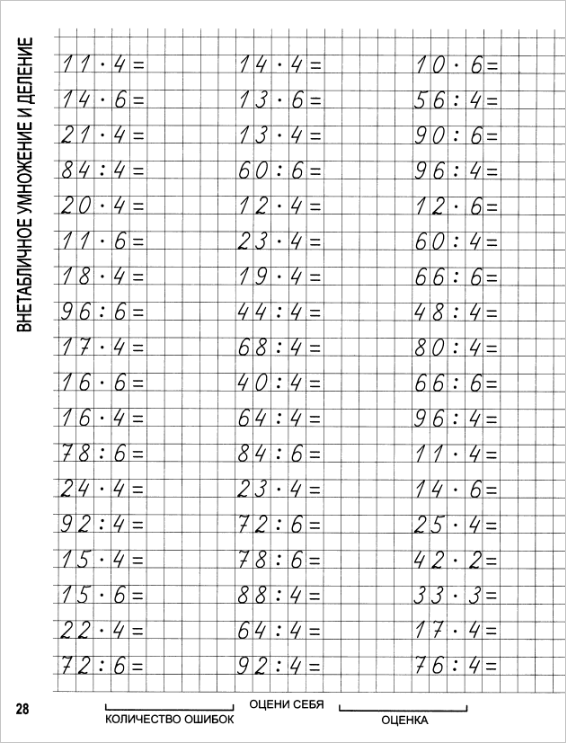
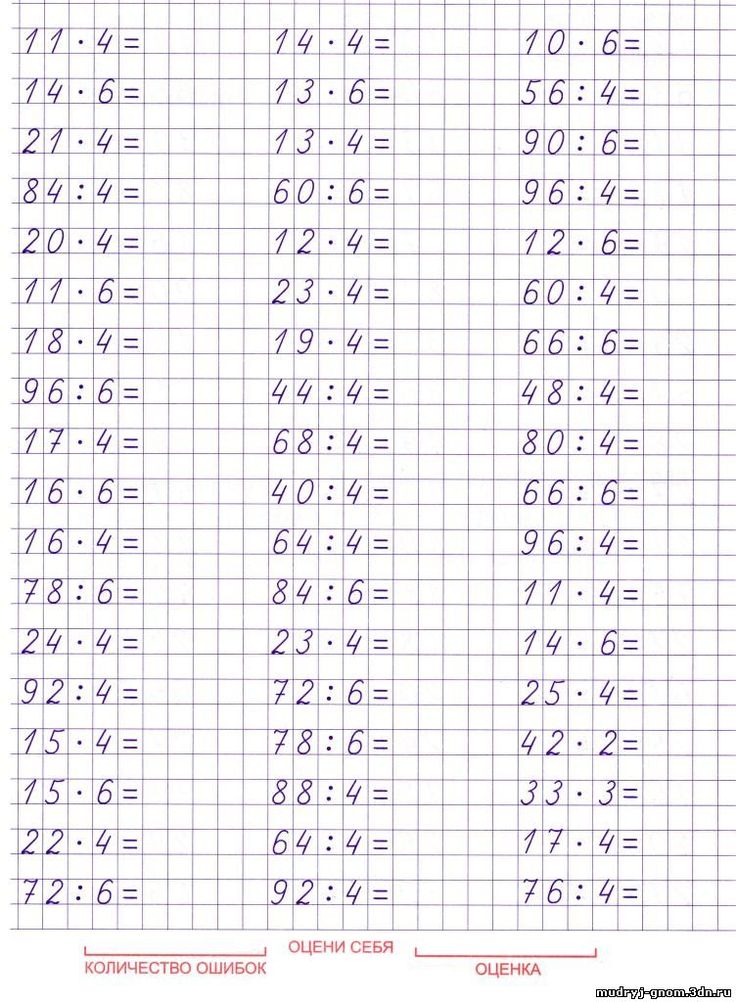
4 класс. Моро.
 Учебник №2. Ответы к стр. 31
Учебник №2. Ответы к стр. 31Числа от 1 до 1000
Деления на числа, оканчивающиеся нулями
Письменное деление на числа, оканчивающиеся нулями
Ответы к стр. 31
Объясни, как выполнено деление.
_ 49800 |600 _ 22900 |300
4800 |83 2100 |76
_ 1800 _1900
1800 1800
0 100 — ост.
О б ъ я с н е н и е:
Надо разделить 49800 на 600.
Первое неполное делимое — 4980 десятков. В записи частного будет 2 цифры.
Разделю 4980 на 600. Для этого разделю 498 на 60, получу 8 — столько десятков будет в частном.
Умножу 60 на 8, получу 480 — столько десятков разделили.
Вычту 480 из 498, получу 18 — столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 600.
Второе неполное делимое — 1800 единиц.
Умножу 600 на 3, получу 1800. Все единицы разделили.
Читаю ответ: частное равно 83.
Надо разделить 22900 на 300.
Первое неполное делимое — 2290 десятков. В записи частного будет 2 цифры.
Разделю 2290 на 300. Для этого разделю 229 на 30, получу 7 — столько десятков будет в частном.
Умножу 30 на 7, получу 210 — столько десятков разделили.
Вычту 210 из 229, получу 19 — столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 300.
Второе неполное делимое — 1900 единиц.
Разделю 1900 на 300. Для этого разделю 19 на 3, получу 6 — столько единиц будет в частном.
Умножу 300 на 6, получу 1800 — столько единиц разделили.
Вычту 1800 из 1900, получу 100 — это остаток.
Сравню остаток с делителем: единиц осталось меньше, чем 300.
Читаю ответ: частное равно 76, остаток 100.
114. 22200 : 300 34400 : 400 121500 : 500
55800 : 600 47600 : 700 276800 : 800
— 22200|300 — 55800|600
2100 |74 5400 |93
—1200 —1800
1200 1800
0 0
— 34400|400 — 47600|700
3200 |86 4200 |68
—2400 —5600
2400 5600
0 0
— 121500|500 — 276800|800
1000 |243 2400 |346
—2150
2000 3200
_1500 _4800
1500 4800
0 0
115. Выполни деление с остатком.
Выполни деление с остатком.
6739 : 80 4193 : 50 289460 : 700 350525 : 400
— 6739|80 — 4193|50
640 |84 400 |83
—339 —193
320 150
19 — ост. 43 — ост
— 289460|700 — 350525|400
2800 |413 3200 |876
—946 —3052
700 2800
_2460 _2525
2100 2400
360 — ост. 125 — ост.
116. Сравни задачи и их решения.
1) Для ремонта школы привезли 475 штук одинаковых по массе красных кирпичей и 425 штук таких же по массе белых кирпичей. Масса всех кирпичей 3600 кг. Найди массу красных и белых кирпичей в отдельности.
Масса всех кирпичей 3600 кг. Найди массу красных и белых кирпичей в отдельности.
2) Для ремонта школы привезли 900 штук белых и красных кирпичей, одинаковых по массе. Масса всех красных кирпичей 1900 кг, а масса белых 1700 кг. Найди количество красных и белых кирпичей в отдельности.
1-я задача
1) 475 + 425 = 900 (к.) − привезли всего
2) 3600 : 900 = 4 (кг) − масса одного кирпича
3) 4 • 475 = 1900 (кг) − масса красных кирпичей
4) 4 • 425 = 1700 (кг) − масса белых кирпичей
О т в е т: 1900 кг весят красные кирпичи, 1700 кг весят белые кирпичи.
2-я задача
1) 1900 + 1700 = 3600 (кг) − масса всех кирпичей
2) 3600 : 900 = 4 (кг) − масса одного кирпича
3) 1900 : 4 = 475 (к.) − красных
4) 1700 : 4 = 425 (к.) − белых
О т в е т: 475 красных и 425 белых кирпичей.
Это обратные задачи. В первой задаче мы знаем общую массу и количество кирпичей каждого вида, а во второй − общее число кирпичей и массу кирпичей каждого вида.
117. Два лыжника вышли одновременно из одного пункта в противоположных направлениях. Скорость одного лыжника 15 км/ч, а другого 10 км/ч. На сколько километров они удалятся друг от друга за 1 ч? за 2 ч? за 3 ч?
1) 15 + 10 = 25 (км/ч) − скорость удаления лыжников
2) 25 • 1 = 25 (км) − будет между лыжниками через 1 ч
3) 25 • 2 = 50 (км) − будет между лыжниками через 2 ч
4) 25 • 3 = 75 (км) − будет между лыжниками через 3 ч
О т в е т: на 25 км через 1 ч, на 50 км через 2 ч, на 75 км через 3 ч.
118. Сравни выражения.
586 • 10 • 7 и 586 • 70 1200 : 20 и 1200 : 100 : 2
36 • 800 и 36 • 8 • 100 900 : 10 : 5 и 900 : 50
586 • 10 • 7 = 586 • 70
586 • (10 • 7) = 586 • 70
586 • 70 = 586 • 70
36 • 800 = 36 • 8 • 100
36 • 800 = 36 • (8 • 100)
36 • 800 = 36 • 800
1200 : 20 > 1200 : 100 : 2
120 : 2 > 12 : 2
900 : 10 : 5 = 900 : 50
90 : 5 = 90 : 5
119. Проверь, все ли равенства верны. Исправь неверные равенства, поставив скобки.
Проверь, все ли равенства верны. Исправь неверные равенства, поставив скобки.
9 • 3 + 45 : 9 = 72 6 • 16 − 8 • 2 = 80
9 • 3 + 45 : 9 = 32 6 • 16 − 8 • 2 = 96
9 • 3 + 45 : 9 = 8 6 • 16 − 8 • 2 = 176
9 • 3 + 45 : 9 = 27 + 5 = 32
9 • 3 + 45 : 9 = 72 − неверно
9 • (3 + 45 : 9) = 9 • (3 + 5) = 9 • 8 = 72
9 • (3 + 45
9 • 3 + 45 : 9 = 27 + 5 = 32
9 • 3 + 45 : 9 = 32 – верно
9 • 3 + 45 : 9 = 27 + 5 = 32
9 • 3 + 45 : 9 = 8 − неверно
(9 • 3 + 45) : 9 = (27 + 45) : 9 = 72 : 9 = 8
(9 • 3 + 45) : 9 = 8 — верно
6 • 16 − 8 • 2 = 96 − 16 = 80
6 • 16 − 8 • 2 = 80 – верно
6 • 16 − 8 • 2 = 96 − 16 = 80
6 • 16 − 8 • 2 = 96 − неверно
6 • (16 − 8) • 2 = 6 • 8 • 2 = 48 • 2 = 96
6 • (16 − 8) • 2 = 96 — верно
6 • 16 − 8 • 2 = 96 − 16 = 80
6 • 16 − 8 • 2 = 176 − неверно
(6 • 16 − 8) • 2 = (96 − 8) • 2 = 88 • 2 = 176
(6 • 16 − 8) • 2 = 176 — верно
Вычисли и проверь.
37800 : 700
— 37800|700 Проверка:
3500 |54 × 54
—2800 700
2800 37800
0
ЗАДАНИЕ НА ПОЛЯХ
РЕБУС
— 906|2
8 |453
—10
10
_6
6
0
ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №2. Ответы к стр. 31
4.5 (90. 83%) от 24 голосующих
83%) от 24 голосующих
Деление с остатком | Математика
Если одно натуральное число не делится на другое нацело, можно выполнить деление с остатком.
Как и при делении нацело, числа, которые делим, называются делимое и делитель.
Результат деления называется неполным частным.
Число, которое остаётся от делимого в результате деления (это число меньше делителя), называется остаток.
Чтобы выполнить проверку, надо:
- Неполное частное умножить на делитель.
- К полученному произведению прибавить остаток.
- В результате должно получиться делимое.
Рассмотрим конкретные примеры деления с остатком.
Примеры.
Выполнить деление чисел с остатком и сделать проверку:
1) 29 : 8;
2) 613 : 6;
3) 279 : 10;
4) 784 : 23;
5) 4057 : 35;
6) 8591 : 62;
7) 52779 : 2524;
8) 15 : 79.
Решение: 1)
29 : 8 = 3 (остаток 5).
Проверка:
3 · 8 + 5 = 24 + 5 = 29.
2)
513 : 6 = 85 (остаток 3).
513 — делимое, 6 — делитель, 85 — неполное частное, 3 — остаток.
Проверка:
85 · 6 + 3 = 510 + 3 = 513.
3)
279 : 10 = 27 (остаток 9).
279 — делимое, 10 — делитель, 27 — неполное частное, 9 — остаток.
Проверка:
27 · 10 + 9 = 270 + 9 = 279.
4)
784 : 23 = 34 (остаток 2).
784 — делимое, 23 — делитель, 34 — неполное частное, 2 — остаток.
Проверка:
34 · 23 + 2 = 782 + 2 = 784.
5)
4057 : 35 = 115 (остаток 32).
4057 — делимое, 35 — делитель, 115 — неполное частное, 32 — остаток.
Проверка:
115 · 35 + 32 = 4025 + 32 = 4057.
6)
8591 : 62 = 138 (остаток 35).
8591 — делимое, 62 — делитель, 138 — неполное частное, 35 — остаток.
Проверка:
138 · 62 + 35 = 8556 + 35 = 8591.
7)
52779 : 2524 = 20 (остаток 2299).
52779 — делимое, 2524 — делитель, 20 — неполное частное, 35 — 2299.
Проверка:
20 · 2524 + 2299 = 50480 + 2299= 52779.
8) 15 : 79 = 0 (остаток 15).
15 — делимое, 79 — делитель, 0 — неполное частное, 15 — остаток.
( Если делимое меньше делителя, неполное частное всегда равно нулю, а остаток — делимому).
9520 : 8 = 2610 : 9 = 8720 : 4 = 5820 : 6 = 6120 : 9 = 98000 : 50 = 98000 : 70 = 53700 : 30 = 81900 : 90 = 203000 : 70= 790 * 400 = 8500 * 80 = 2800 * 50 = 4200 * 200 = 300 * 470 = 6300* 50 = 4309 * 5 = 8960 * 8 = 89448 * 7= 405028 * 3 = | 7400 : 200 = 32000 : 400 = 3200 : 8 = 4000 : 200 = 5400 : 900 = 170000 : 17 = 2100 : 70 = 90300 : 300 = 10000 : 20 = 7200 : 72 = 10 * 555 = 700 * 3 = 300 * 30 = 0* 870 = 700 * 50 = 100 * 320 = 300 * 6 = 500 * 8 = 120 * 6 = 130 * 2 = | 9520 : 8 = 2610 : 9 = 8720 : 4 = 5820 : 6 = 6120 : 9 = 98000 : 50 = 98000 : 70 = 53700 : 30 = 81900 : 90 = 203000 : 70= 790 * 400 = 8500 * 80 = 2800 * 50 = 4200 * 200 = 300 * 470 = 6300* 50 = 4309 * 5 = 8960 * 8 = 89448 * 7= 405028 * 3 = | 7400 : 200 = 32000 : 400 = 3200 : 8 = 4000 : 200 = 5400 : 900 = 170000 : 17 = 2100 : 70 = 90300 : 300 = 10000 : 20 = 7200 : 72 = 10 * 555 = 700 * 3 = 300 * 30 = 0* 870 = 700 * 50 = 100 * 320 = 300 * 6 = 500 * 8 = 120 * 6 = 130 * 2 = | 9520 : 8 = 2610 : 9 = 8720 : 4 = 5820 : 6 = 6120 : 9 = 98000 : 50 = 98000 : 70 = 53700 : 30 = 81900 : 90 = 203000 : 70= 790 * 400 = 8500 * 80 = 2800 * 50 = 4200 * 200 = 300 * 470 = 6300* 50 = 4309 * 5 = 8960 * 8 = 89448 * 7= 405028 * 3 = | 7400 : 200 = 32000 : 400 = 3200 : 8 = 4000 : 200 = 5400 : 900 = 170000 : 17 = 2100 : 70 = 90300 : 300 = 10000 : 20 = 7200 : 72 = 10 * 555 = 700 * 3 = 300 х 30 = 0 * 870 = 700 * 50 = 100 * 320 = 300 * 6 = 500 * 8 = 120 * 6 = 130 * 2 = | 9520 : 8 = 2610 : 9 = 8720 : 4 = 5820 : 6 = 6120 : 9 = 98000 : 50 = 98000 : 70 = 53700 : 30 = 81900 : 90 = 203000 : 70= 790 * 400 = 8500 * 80 = 2800 * 50 = 4200 * 200 = 300 * 470 = 6300* 50 = 4309 * 5 = 8960 * 8 = 89448 * 7= 405028 * 3 = | 7400 : 200 = 32000 : 400 = 3200 : 8 = 4000 : 200 = 5400 : 900 = 170000 : 17 = 2100 : 70 = 90300 : 300 = 10000 : 20 = 7200 : 72 = 10 * 555 = 700 * 3 = 300 х 30 = 0 * 870 = 700 * 50 = 100 * 320 = 300 * 6 = 500 * 8 = 120 * 6 = 130 * 2 = |
Урок математики в 4 классе «Алгоритм деления столбиком» УМК ПНШ
8
Урок математики в 4 классе
УМК «Перспективная начальная школа»
Тема: Алгоритм деления столбиком
Цель
Создание условий для усвоения учащимися математического понятия алгоритм деления столбиком и применения его для решения;
Задачи:
— учить анализировать запись деления четырехзначного числа на двузначное столбиком;
— формировать умение формулировать алгоритм деления столбиком, отвечая на вопросы;
— развивать математическую речь учащихся,
— Формировать соответствующие УУД
Личностные УУД:- способствовать самооценке на основе критерия успешности учебной деятельности.
Регулятивные УУД:- умение определить и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; высказывать свое предположение; выбирать для выполнения посильные задания.
Коммуникативные УУД:- умение оформлять свои мысли в устной и письменной речи, слушать, понимать речь других; договариваться о правилах поведения и общения при работе в парах и следовать им.
Познавательные УУД:-выполнять действия по заданному алгоритму; строить логическую цепь рассуждений; отличать новое от уже известного с помощью учителя.
Прогнозируемые результаты:
Предметные:
Метапредметные:
Личностные:
Усваиваемые математические термины: «алгоритм деления столбиком», «запись делимого», «первое промежуточное делимое», «остаток первого промежуточного деления», «число цифр в записи неполного частного».
Оборудование: проектор, презентация, учебник, таблицы для рефлексии, пошаговый алгоритм в конверте.
ХОД УРОКА
1этап. Этап организации направленного внимания на начало учебного занятия
Цель этапа: организовать направленное внимание на начало урока.
Деятельность учителя | Деятельность учащихся |
— Для успешной работы на уроке нам необходимы следующее: учебник, рабочая тетрадь, ручка, карандаш, линейка. Если все необходимое на парте, садитесь | Ученики проверяют необходимое на уроке оборудование, если все в наличии садятся, если нет достают все необходимое |
2 этап. Этап целеполагания
Цель этапа: Сформировать представления детей о том, что нового они узнают на уроке и чему научатся
Чтобы раскрыть название темы урока необходимо разгадать ребус. Он зашифрован в следующем задании:
— Запишите остаток от деления данных чисел в тетрадь: слайд1
70 : 8 47: 5 18 : 7 82 : 9 45 : 6 37 : 8 7 : 14 35 : 9
6 2 4 1 3 5 7 8
— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.
— Расставьте числа в порядке возрастания. Какое слово получилось? (алгоритм)
— Что значит слово алгоритм?
— С какими алгоритмами мы уже знакомы? (письменного сложения, вычитания, умножения столбиком)
— С каким алгоритмом мы еще не знакомы? Назовите тему нашего урока.
( Алгоритм письменного деления ) слайд 2
Кто сформулирует цель нашего урока? Используйте для этого слова: составление, знакомство, применение, решение слайд 3
Итак, цель урока: составление алгоритм деления столбиком и применение его для решения
3 этап. Этап актуализации знаний
Цель этапа: повторить понятие, правило, алгоритм и способ использования алгоритма
Открыли учебники записали число, тему слайд 4 и выключить
Работа по учебнику
З а д а н и е 38. Не забудьте, что обозначает условное обозначение. (не торопись с ответом, подумай) Учащиеся выполняют деление столбиком.
– Как определить первое промежуточное делимое? (выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число)
Как с его помощью определить число цифр в записи неполного частного? (Так как первое промежуточное делимое выражает число сотен25 сотен, то запись неполного частного будет состоять из трех цифр;)
Как найти первую цифру в записи неполного частного? (Нужно найти результат деления первого промежуточного делимого 25 на делитель 5 и записать соответствующую этому результату цифру 5 в старший разряд искомого неполного частного. )
)
– Нужно ли записывать остаток, если он промежуточный и равен 0? (Нет.)
Как получается следующее промежуточное делимое? (запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым )
Как найти следующую цифру в записи неполного частного? (следующую цифру в записи неполного частного определяет результат деления второго промежуточного делимого на делитель
Какую цифру нужно писать в неполном частном, если промежуточное делимое меньше делителя?(Цифру 0.)
– Когда нужно заканчивать процесс деления? (деление нужно заканчивать тогда, когда будет выполнен деление последнего промежуточного делимого)
Какое число следует считать окончательным остатком деления? (остаток, который получается при делении последнего промежуточного делимого на делитель, и будет окончательным остатком деления)
4 этап. Этап объяснения
Цель этапа: сформировать понятие (алгоритм деления столбиком), обучение УУД (выполнять действия по заданному алгоритму; строить логическую цепь рассуждений;)
З а д а н и е 39 учащиеся переписывают запись деления столбиком в тетрадь
Этап физической разрядки
Цель этапа: смена вида деятельности
Физминутка Если число, которое я назову, является значением произведения таблицы умножения,то руки вверх поднимают девочки ,если же нет –то мальчики. 64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
З а д а н и е 40. Учащиеся объясняют деление с остатком в столбик, отвечая на вопросы, система вопросов аналогична системе вопросов из №38, но только теперь речь пойдет о случае деления с остатком столбиком на двузначное число, при этом соответствующая запись деления уже перенесена детьми в готом виде в тетрадь, таким образом учащиеся самостоятельно составляют алгоритм деления столбиком, работа направлена на среднего ученика
— выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число
— Так как первое промежуточное делимое выражает число сотен 35 сотен, то запись неполного частного будет состоять из трех цифр;
— Нужно найти результат деления первого промежуточного делимого 35 на делитель 17 и записать соответствующую этому результату цифру 2 в старший разряд искомого неполного частного.
— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым, если остаток равен 0, то записывают только соответствующую цифру делимого
— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым
— Если промежуточное делимое меньше делителя, то в неполном частном на соответствующем месте нужно писать цифру 0.
— Деление нужно заканчивать тогда, когда будет выполнен деление последнего промежуточного делимого
— Остаток, который получается при делении последнего промежуточного делимого на делитель, и будет окончательным остатком деления
5 этап. Этап применения и первичного закрепления теоритических положений в условиях выполнения упражнений и задач
Цель этапа: сформировать учебные действия по использованию алгоритма деления столбиком, продолжить формирование УУД по работе со словарем учебника
З а д а н и е 41. Что обозначает это условное обозначение (проверь правильность выполнения задания), что обозначает звездочка (посмотри в словарь)
( Учащиеся формулируют алгоритм деления столбиком, используя не только дважды прозвучавшие ответы на эти же вопросы, но и пользоваться для ответов готовым алгоритмом приведенный в соответствующей статье словаря с.123)
Работаем в паре у одного открыто задание 41, у другого алгоритм. Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.
Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.
Правильно записать пример деления в столбик
Найти первое промежуточное делимое и определить количество цифр в неполном частном
Найти результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать)
Найти второе промежуточное делимое.
Найти результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать)
Действия из пунктов 4) и 5) повторит пока не будут использованы все цифры делимого.)
– Как нужно записать делимое и делитель? (Сначала записывают делимое, после этого справа от делимого ставят ├ (знак деления столбиком), в котором в верхней части записывают делитель, а нижнюю часть оставляют для записи искомого результата. )
)
– Как найти первое промежуточное делимое? (Отделяя последовательно цифры в записи делимого, находят первое промежуточное делимое и отмечают его в записи делимого с помощью дуги.)
– С помощью какого знака можно показать, какое число будет первым промежуточным делимым?
– Где записывается полученный результат первого промежуточного деления и как вычисляется остаток этого случая деления? (Находят результат деления с остатком первого промежуточного делимого на делитель и записывают полученное число в старший разряд искомого результата. После этого умножают полученный результат на делитель и записывают результат этого умножения под первым промежуточным делимым столбиком. Выполняют вычитание столбиком с целью получения остатка первого промежуточного деления.)
– Нужно ли записывать промежуточный остаток, если он равен 0? (Если остаток равен 0, то его не записывают.)
– Как получить второе промежуточное делимое и где оно записывается? (Запись второго промежуточного делимого получают с помощью приписывания к записи полученного ранее остатка цифры, которая в записи исходного делимого находится в старшем из неиспользуемых пока разрядов. )
)
– Где записывается полученный результат второго промежуточного деления и как вычисляется остаток этого случая деления?
– Если вычисленный остаток равен 0, то в каком случае его не нужно записывать? Можно ли утверждать, что все последующие случаи промежуточного деления повторяют процедуру второго случая промежуточного деления? Когда следует заканчивать процесс деления? (До тех пор пока в построении промежуточных делимых не будут использованы все цифры записи исходного делимого.)
– Где будет записано окончательное неполное делимое и окончательный остаток? Проверка на слайде алгоритма
6 этап. Этап формирование УУД
Цель этапа: закрепить, повторить, продолжить формирование УУД
Решение примеров записанных на доске 21 553 : 7; 53 132 :14по алгоритму
Для этого вы распределитесь в паре один в паре консультирует, другой записывает решение.
У кого возникают вопросы просят помощи (поднятая рука), оказывает индивидуальную помощь, через 2-3 минуты выполнившие решение проверяет учитель и просит помочь одноклассникам, которые работают медленнее других
7 этап. Этап контроля результатов деятельности учащихся или хода усвоения нового материала
Этап контроля результатов деятельности учащихся или хода усвоения нового материала
Цель этапа: проконтролировать умение учеников использовать математические термины, алгоритм деления столбиком при решении примеров, ответах на вопросы
Учитель контролирует ответы детей, при решении примеров в течении всего урока
8 этап. Этап рефлексии
Цель этапа: сформировать личную ответственность за результаты коллективной деятельности
-Какую цель мы поставили в начале нашего урока?
— Достигли мы цели урока? ( познакомились с алгоритмом деления столбиком, учились его применять при решении примеров.)
— А теперь каждый оценит себя – достиг ли он цели урока — насколько хорошо вы усвоили алгоритм деления столбиком. Оценивайте свои умения по этапам.
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
— Если же какой-либо этап вы не усвоили, не надо переживать, потому что мы с вами на следующих уроках будем продолжать работу над закреплением алгоритма, но дома в качестве домашнего задания ученик должен еще раз изучить алгоритм письменного деления и галочками отметить неустраненные затруднения.
Дома. Р.Т. № 4
Спасибо за урок
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
ГДЗ по Математике 5 класс Мерзляк
Никто не станет спорить, что математика важный предмет. На его изучение выделяется очень много часов в общеобразовательной школе. Поэтому следует пользоваться благоприятной возможностью и повышать уровень своего физико-математического мышления. Если старательно учиться и решать сложные задачи, уравнения и неравенства, то потом можно будет поступить в техническое высшее учебное заведение и получить квалификацию инженера в той или иной области техники.
На его изучение выделяется очень много часов в общеобразовательной школе. Поэтому следует пользоваться благоприятной возможностью и повышать уровень своего физико-математического мышления. Если старательно учиться и решать сложные задачи, уравнения и неравенства, то потом можно будет поступить в техническое высшее учебное заведение и получить квалификацию инженера в той или иной области техники.
А.Г. Мерзляк, В.Б. Полонский, М.С. Якир предложили собственный учебно-методический комплекс по математике для пятиклассников. Эти книги издаются известной компанией «Вентана-Граф» с 2016 года, которая готовит красочные обложки и полезные иллюстрации для школьников. Новые версии пособий появляются в продаже каждые 2-3 года. Они содержат усовершенствованные упражнения, а также способы их решения. Основная цель знаменитых авторов-методистов состоит в том, чтобы помочь ребятам лучше справляться с непростой программой по данному предмету.
Почему без ГДЗ Мерзляка, Полонского, Якира сложно преуспеть в математике (5 класс)?
На уроке присутствуют сразу 25-30 учеников, а его длительность составляет лишь 45 минут. Поэтому не всегда учителю удается оказать методическую помощь всем, кто в этом нуждается. У школьников могут оставаться вопросы, которые не были своевременно прояснены. Естественно, что накопление таких проблем выливается в непонимание последующих параграфов, а то и в вовсе отставание. Не беда, когда можно подсмотреть в решебник, найти аналогичный образец и понять тему на новом уровне.
Поэтому не всегда учителю удается оказать методическую помощь всем, кто в этом нуждается. У школьников могут оставаться вопросы, которые не были своевременно прояснены. Естественно, что накопление таких проблем выливается в непонимание последующих параграфов, а то и в вовсе отставание. Не беда, когда можно подсмотреть в решебник, найти аналогичный образец и понять тему на новом уровне.
Правильно используя сборник, можно избежать многих проблем. Не будет «двоек» на контрольных работах, нервных срывов, бессознательного отторжения от математики и тому прочего. Даже если способности ребенка к точным наукам невелики, все равно можно получать хорошие отметки и переходить из одного класса в другой без приложения экстраординарных усилий. Поэтому решебник по математике, созданный Мерзляком, может быть рекомендован ученикам, которые обладают прилежанием, но часто не понимают объяснения учителя с первого раза. В таком случае верные ответы на нашем сайте придутся весьма кстати:
- быстрый поиск решений;
- поддержка мобильных устройств;
- круглосуточная доступность;
- большое количество вариантов;
- соответствие рабочим программам на 2020 год.

Пользуйтесь пособием, и ваши успехи не заставят себя ждать. Школьник если и не полюбит математику, то перестанет иметь с ней какие-либо проблемы.
Онлайн-решебник автор: Мерзляк для 5 класса станет заменой дополнительным занятиям
Да, вполне. По сути, работа с пособием и является еще одним уроком. Единственная разница состоит в том, что учитель физически отсутствует, но зато есть подробные комментарии. Таким образом, будто создается эффект присутствия педагога. Работая с книгой, пятиклассникам стоит обратить внимание на следующие параграфы:
- дроби. Целая и десятичная части числа;
- углы и использование транспортира для их измерения;
- решение задач практического толка, требующих вычисления в столбик.
Пособие, авторы которого Полонский и Якир, пригодится пятиклассникам. Также по нему удобно повторять пройденные разделы более старшим учащимся.
Калькулятор онлайн — Решение показательных уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. n} \)
n} \)
6) an > 0
7) an > 1, если a > 1, n > 0
8) anm, если a > 1, n
9) an > am, если 0
В практике часто используются функции вида y = ax, где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.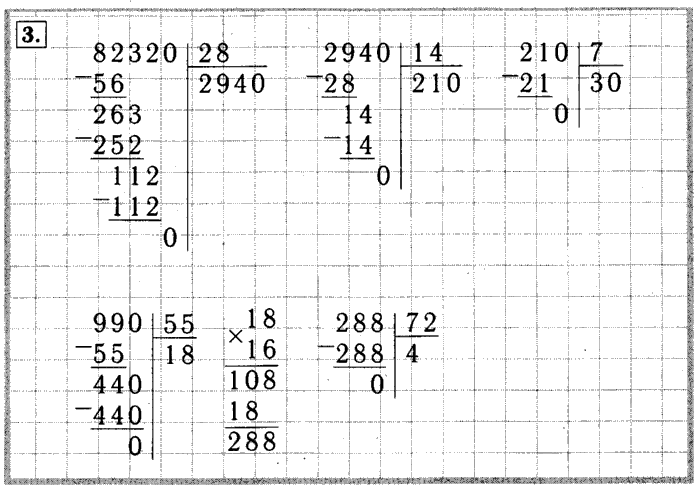
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, \( a \neq 1\), не имеет корней,
если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т. е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, \( a \neq 1\),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны
тогда и только тогда, когда равны их показатели.
е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, \( a \neq 1\),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны
тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде
8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2
Решить уравнение 3х + 1 — 2 • 3x — 2 = 25
Вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2(33 — 2) = 25,
3х — 2 • 25 = 25,
откуда 3х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3х = 7х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac{3^x}{7^x} = 1 \), откуда \( \left( \frac{3}{7} \right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9х — 4 • 3х — 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 — 4t — 45 = 0. {x-2} = 1 \)
{x-2} = 1 \)
x — 2 = 0
Ответ х = 2
Решить уравнение 3|х — 1| = 3|х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1)2 = (х + 3)2, откуда
х2 — 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Урок четвертого класса Разделение с оставшимися
Я призываю учеников к ковру, пока мы готовимся к дискуссии в классе. На смарт-плате уже есть розетка. Мне нравится, когда мои ученики находятся рядом, чтобы я мог полностью сосредоточиться на них, пока я нахожусь на доске Smart.
Я начну с перебора важной лексики для этого урока. Студентам необходимо знать эти термины, чтобы понять урок.
Словарь:
частное — ответ на задачу деления
делитель — число, на которое делится другое число
дивиденды — сумма, которую вы хотите разделить
остаток — часть, которая остается после деления
Задача 1:
У Томаса 15 шариков. Он хочет положить одинаковое количество шариков в 4 разных контейнера. Сколько шариков будет в каждой емкости? Сколько шариков останется в остатке?
Он хочет положить одинаковое количество шариков в 4 разных контейнера. Сколько шариков будет в каждой емкости? Сколько шариков останется в остатке?
Во-первых, я прошу студентов определить, какая операция будет использоваться для решения этой проблемы. «Дивизия», — слышу я большинство из них. Основываясь на прошлых знаниях, ключевые слова «одинаковое число» позволяют нам понять, что нужно разделить. Следовательно, это проблема разделения. Задача состоит из 15, разделенного на 4. Кроме того, ключевое слово «left» сообщает нам, что мы собираемся вычесть, чтобы найти остаток.
Мы можем использовать наши единичные блоки, чтобы создать модель проблемы. Мы знаем, что будет 4 группы. Мы можем взять наши 15 единичных блоков и начать разделять их на 4 группы, 1 на 1. Помните, что когда вы закончите разделять единичные блоки, в каждой группе должно быть одинаковое количество блоков. Оставшиеся блоки будут вашим остатком.
Частное к этой задаче равно 3, потому что в каждой группе по 3 шарика (4 x 3 = 12). Остается 3 шарика (15 — 12 = 3).Следовательно, остаток равен 3.
Остается 3 шарика (15 — 12 = 3).Следовательно, остаток равен 3.
Попробуем еще.
Задача 2: 37 разделить на 8.
Мы можем использовать наши единичные блоки, чтобы создать модель проблемы. Мы знаем, что будет 8 групп. Мы можем взять наши 37 единичных блоков и начать разделять их на 8 групп, 1 на 1. Помните, что когда вы закончите разделять единичные блоки, в каждой группе должно быть одинаковое количество блоков. Оставшиеся блоки будут вашим остатком.
| хххх | хххх | хххх | хххх |
хххх | хххх | хххх | хххх |
Частное к этой задаче равно 4, потому что в каждой группе по 4 элемента (4 x 8 = 32). Остается 5 шариков (37 — 32 = 5). Таким образом, остаток равен 5.
How to Teach Long Division
Итак, ваш ребенок освоил свою таблицу умножения и теперь переходит к делению в столбик. Деление в столбик может показаться легким, но на самом деле его довольно сложно научить и понять. Давайте разберемся, как понимать деление в столбик.
Деление в столбик может показаться легким, но на самом деле его довольно сложно научить и понять. Давайте разберемся, как понимать деление в столбик.
Шаги длинного деления
- Разделить
- Умножить
- Вычесть
- Выпадающий
Прежде чем мы начнем
Прежде чем мы сможем обучать делению в столбик, мы должны понять связанные с ним термины. Делимое число называется делимым , число, которое делится, называется делителем , и, наконец, число, которое является ответом на проблему деления, называется частным .Бонус: если делитель не делится равномерно на дивиденд, останется остатка .
Например,
3234 ÷ 6 = 539
3234 делится на 6 , то есть 6 делится на 3234 . Ответ на эту проблему деления: 539 или 539 — это частное от 3234 , деленного на 6 .
Но если бы у нас было 3237 ÷ 6, наш ответ был бы 539 с остатком из 3 , 3237 ÷ 6 = 539 R3
ШАГ 1: РАЗДЕЛИТЬ
Хорошо, вернемся к 3234 ÷ 6. В формате длинного деления это будет иметь вид
.
Убедитесь, что вы не сказали «шесть, разделенные на три тысячи двести тридцать четыре», что выглядело бы как
Во-первых, взгляните на крайнюю левую цифру делимого.
Спросите своего ребенка: «Может ли 6 перейти в 3?» Нет, это слишком мало.Теперь вам нужно объединить следующую позицию, 2 (сто), с 3 (тысячами) цифрами (3200).
Может ли 6 перейти в 32? Да, оно может. Это первая отправная точка для многих студентов. 32 не делится на 6, но его можно разделить на 6, оставив что-то еще. Когда вы говорите об этом со своим ребенком, и они говорят, что 32 нельзя разделить на 6, они не ошибаются.
Вы можете спросить своего ребенка: «Сколько групп по 6 человек вы можете составить из 32?» Они могут нарисовать 32 круга и сгруппировать их в группы по 6, после создания 5 групп они увидят, что осталось только 2 круга, и они могут образовать только 5 групп по 6 из 32. Однако по мере того, как они получают больше практики с делением в столбик, им нужно иметь возможность представить группы в своей голове и сделать вывод, что они могут составить 5 групп по 6 штук без необходимости рисовать круги.
Однако по мере того, как они получают больше практики с делением в столбик, им нужно иметь возможность представить группы в своей голове и сделать вывод, что они могут составить 5 групп по 6 штук без необходимости рисовать круги.
В качестве альтернативы вы можете спросить их: «Какое число, кратное 6, ближе всего к 32?» Ответят 30. Отлично! Теперь спросите: «сколько 30 делится на 6?» Ответят 5.
ШАГ 2: НЕСКОЛЬКО
Теперь ваш ребенок знает, что 6 может превратиться в 32 максимум 5 раз. Что дальше? Умножить. 5 x 6 = 30. 5 находится в верхней части панели ответов как первое число нашего ответа. 30 идет под дивиденды для подготовки к Шагу 3.
ШАГ 3: ВЫЧИСЛЕНИЕ
Затем вычитаем 32-30 = 2. В длинном делении это выглядит как
ШАГ 4: ПРИНИМАЙТЕ
Мы должны что-то сделать с этими двумя оставшимися. 6 не может перейти в 2, как ваш ребенок с радостью подтвердит. Теперь мы опускаем следующую цифру дивиденда, и наш новый дивиденд составляет 23
Теперь мы опускаем следующую цифру дивиденда, и наш новый дивиденд составляет 23
.
ПОВТОР
Начните снова с ШАГА 1.Может ли 6 войти в 23 ? Да 3 раз. ШАГ 2, что такое 3 x 6 ? 18. ШАГ 3. Что такое 23–18? 5 . ШАГ 4 выведите из строя 4 .
СЕЙЧАС ПОПРОБУЙТЕ
Может ли 6 перейти в 54? Сколько раз? Куда девается 9? Что дальше? Вычтем 54-54 = 0. Осталось что-нибудь сбить?
Что ж, похоже, мы все закончили, и вы знаете, как объяснить деление в столбик! Несмотря на то, что для некоторых учеников это сложно понять, с помощью этого метода ваш ребенок будет выполнять деление в столбик в кратчайшие сроки.Вот несколько полезных листов с длинными разделами, которые можно использовать дома.
Метод прямоугольников или площадей: альтернатива традиционному делению в столбик
Длинное деление часто считается одной из самых сложных тем для преподавания. К счастью, есть стратегии, которым мы можем научить, чтобы упростить понимание и выполнение многозначного деления.
К счастью, есть стратегии, которым мы можем научить, чтобы упростить понимание и выполнение многозначного деления.
Блочный метод , также известный как Area Model , является одной из таких стратегий.Это подход, основанный на ментальной математике, который улучшит понимание чисел. Учащиеся решают уравнение, вычитая кратные, пока они не уменьшатся до 0 или как можно ближе к 0.
Если вы планируете преподавать стратегию частичных частных в классе (что я настоятельно рекомендую), блочный метод — отличный способ начать. Он использует те же шаги, что и частные, но организован немного иначе.
Давайте узнаем, как использовать блочный метод / модель площади для деления в столбик!
Ниже я включил видеоурок и пошаговые инструкции.
ВИДЕО ОБУЧЕНИЕ
ПОШАГОВАЯ ИНСТРУКЦИЯ
Предположим, что мы хотим решить уравнение 324 ÷ 2.
Шаг 1:
Сначала рисуем прямоугольник. Записываем делимое внутри квадрата, а делитель слева.
Шаг 2:
Мы хотим выяснить, сколько групп по 2 можно сделать из 324. Мы будем делать это по частям, чтобы упростить задачу.Мы могли бы начать с создания 100 групп по 2 человека, поскольку мы знаем, что у нас есть по крайней мере такое количество групп. Итак, мы умножаем 100 × 2, чтобы получить 200, а затем убираем это 200 из 324. Теперь у нас осталось 124.
Шаг 3:
Делаем еще одну коробку и переносим в нее 124. Теперь давайте возьмем еще одно простое умножение на 2. Как насчет 50 групп по 2? Мы знаем, что можем удалить еще 50 групп по 2 из 124. 50 × 2 = 100, поэтому мы берем 100 из 124. Теперь у нас осталось 24.
Шаг 4:
Делаем еще одну коробку и переносим в нее 24.Мы знаем, что 12 групп по 2 составляют 24, поэтому давайте напишем 12 сверху и уберем 24 из 24. Теперь у нас получается 0, так что мы знаем, что мы закончили наше уравнение.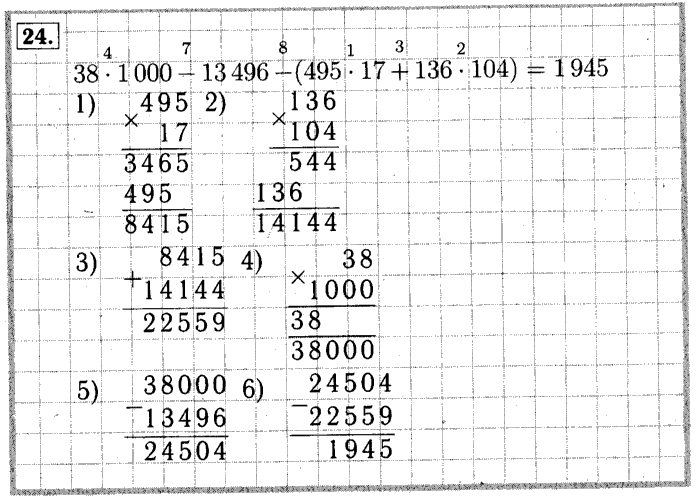
Шаг 5:
Теперь мы складываем «части» из верхней части полей, чтобы найти наше частное. 100 + 50 + 12 = 162, поэтому мы знаем, что 324 ÷ 2 = 162.
ЕЩЕ ОДИН ПРИМЕР (С ОСТАВЛЕНИЕМ)
Рассмотрим еще один пример. В этом примере мы решим 453 ÷ 4.
- Сначала мы написали дивиденды внутри коробки, а наш делитель — в левой части.
- Сначала мы взяли 100 групп по 4 человека. Получилось 400. Мы вычли 400 из 453, и в итоге осталось 53.
- Мы отнесли 53 к следующему ящику, а затем вынули еще 10 групп по 4, чтобы получилось 40. Мы убрали 40 из 53 и остались с 13.
- Мы перенесли 13 к следующему ящику, а затем вынули 3 группы по 4, чтобы получилось 12. Мы убрали 12 из 13 и остались с 1.
- Мы не можем брать больше групп по 4, поэтому наш остаток равен 1. Чтобы найти наше окончательное частное, мы прибавляем 100 + 10 + 3 + остаток 1, чтобы получить 113 R1.
ПОЛЕЗНЫЕ РЕСУРСЫ ДЛЯ СТРАТЕГИИ БЛОКА / МОДЕЛЬ ОБЛАСТИ ДЛЯ ПОДРАЗДЕЛЕНИЯ
Я с удовольствием помогу вам научить блочной стратегии деления в столбик в вашем классе. Вам могут быть полезны следующие ресурсы:
Вам могут быть полезны следующие ресурсы:
БЕСПЛАТНЫЙ МИНИ-КУРС
Зарегистрируйтесь здесь, чтобы получить бесплатный мини-курс многозначного умножения и деления.Это займет у вас всего около часа, и вы уйдете с множеством новых идей, стратегическим планом действий, бесплатными ресурсами, сертификатом PD и многим другим!
ЯЩИК СТРАТЕГИИ / ОБЛАСТЬ МОДЕЛИ КАРТОЧКИ ЗАДАЧ
Эти карточки с заданиями дают учащимся возможность попрактиковаться в использовании прямоугольного метода / модели площади для деления в столбик множеством различных способов. Учащиеся будут вычислять частные, решать задачи деления, вычислять недостающие дивиденды и делители, думать о том, как эффективно решить уравнение, используя метод ящика, и многое другое.См. Карточки задач метода коробок ЗДЕСЬ или большую пачку карточек задач длинного деления ЗДЕСЬ.
СТАНЦИЯ ДЛИННОГО РАЗДЕЛА
Станция «Длинное деление» — это математическая станция для самостоятельного обучения, ориентированная на учащихся, для деления в столбик. Студенты постепенно осваивают различные стратегии деления в столбик, одна из которых — метод ячеек. Одно из самых больших преимуществ этой математической станции заключается в том, что она позволяет вам ориентироваться на каждого ученика и его уникальные способности, чтобы каждый мог получить соответствующие вызовы.См. Станцию «Длинная дивизия» ЗДЕСЬ.
Студенты постепенно осваивают различные стратегии деления в столбик, одна из которых — метод ячеек. Одно из самых больших преимуществ этой математической станции заключается в том, что она позволяет вам ориентироваться на каждого ученика и его уникальные способности, чтобы каждый мог получить соответствующие вызовы.См. Станцию «Длинная дивизия» ЗДЕСЬ.
ИЛИ ПОСМОТРЕТЬ ВСЕ РЕСУРСЫ
рабочих листов с длинными делениями и онлайн-упражнения
Расширенный поиск
Содержание:
Язык: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan стандарт, тибетский, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld церковнославянский, церковнославянский, Старый BulgarianChuvashWelshDanishGermanDivehi, Мальдивский, MaldivianDzongkhaEweGreek (современный) EnglishEsperantoSpanishEstonianBasquePersian (фарси) Фуле, фулах, пулар, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish гэльский, GaelicGalicianGuaraníGujaratiManxHausaHebrew (современный) HindiHiri MotuCroatianHaitian, гаитянский CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut , Гренландский, кхмерский, каннада, корейский, канури, кашмирский, курдский, коми, корний, киргизский, латинский, люксембургский, латинский, лимбургский, лимбургский, лимбургский, лингала, литовский, люба-катанга, латышский, малагасийский, маршалльский, маори, македонский, mMongolianMarathi (маратхи) MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern пенджаби, Восточная PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (санскрит) SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Остров Тонга) TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu Предмет:
Оценка / уровень: Возраст: 3456789101112131415161718+
Поиск: Все рабочие листы Только мои подписанные пользователи Только мои любимые рабочие листы Только мои собственные рабочие листы
Ресурсы с длинным разделением (однозначный делитель)
Эти ресурсы предназначены для того, чтобы помочь студентам практиковать навыки деления на столбики. Они обращаются к CCSS для операций по математике четвертого класса. Мы включили карточки с номерами и страницу записи для быстрого центра или проверки партнеров, 12 карточек с рассказами о проблемах и страницу с практическими проблемами.
Они обращаются к CCSS для операций по математике четвертого класса. Мы включили карточки с номерами и страницу записи для быстрого центра или проверки партнеров, 12 карточек с рассказами о проблемах и страницу с практическими проблемами.
Задание по вытягиванию карточки с длинным разделением — Для этого задания просто распечатайте, вырежьте и ламинируйте карточки делителей и дивидендов. Мы закодировали карточки цветом, так что желтые карточки — делители, а синие карточки — дивиденды. (Студенты должны будут знать, как проверять деление с помощью умножения.) Разложите карты в две отдельные стопки. Учащиеся рисуют по одному, чтобы создать задачу. Они записывают проблему в поле на листе регистрации, а затем решают проблему. Затем они могут либо выполнить самопроверку с помощью умножения в соседнем поле, либо попросить партнера проверить их работу с помощью умножения.
Страница записи делительных и дивидендных карт
Карты задач-рассказов — Прежде чем использовать эти карты, учащиеся должны быть знакомы с интерпретацией остатков в задачах-рассказах. Они должны уметь взглянуть на историю проблемы, чтобы определить, что им делать с остальным. Это набор из 12 карточек задач по разделам (ответы с остатками и без). Распечатайте, вырежьте и ламинируйте для центра, скут-игры или билета быстрого выхода.
Они должны уметь взглянуть на историю проблемы, чтобы определить, что им делать с остальным. Это набор из 12 карточек задач по разделам (ответы с остатками и без). Распечатайте, вырежьте и ламинируйте для центра, скут-игры или билета быстрого выхода.
Практические страницы — Шесть различных практических страниц для студентов.
без остатков с остатками
С остатками и без остатков
Вот несколько интересных видео, которые, по нашему мнению, понравятся вашим ученикам:
Вашим детям нужна помощь в запоминании шагов? Послушайте The Long Division Song by Mr.Питерс. Это определенно цепляет! Песня длинной дивизии
Мистер Дуэи также иллюстрирует шаги к делению в столбик, используя рэп и Smartboard. Бит заставит ваших детей читать рэп. Мистер Дуэи — Длинное деление (также включает подсказки по десятичному разделению.)
Math Antics — хороший выбор, если вашим ученикам нужно объяснять процесс деления другим учителем. Иногда, когда дети застревают, полезно найти другое объяснение. Посмотрите здесь: Long Division by Math Antics.
Посмотрите здесь: Long Division by Math Antics.
«Песня о длинном делении» Карла Ремера — еще один отличный вариант, если вы ищете способ помочь своим ученикам запомнить этапы деления. Нам нравится, что эта песня включает в себя реальные приложения для разделения.
Длинная дивизия, длинный бой
Ужасные слова, от которых мурашки по спинам пробираются по спинам учеников и учителей… Long Division! Существует так много препятствий на пути эффективного обучения учащихся тому, как выполнять длинное деление, и каждый класс, в котором необходимо обучать этому навыку, имеет свой собственный набор трудностей.
Когда ученики начинают деление в столбик в четвертом классе, они сразу же следуют за беглостью умножения. Некоторые студенты так близко отстали, что у них не было времени закрепить беглость фактов умножения до такой степени, чтобы легко получить эту информацию. Длинное деление превращается в агонию повторного подсчета пропусков.
К шестому классу все еще есть ученики, которые все еще борются с теми же проблемами, которые преследовали их в четвертом классе, но возникают новые проблемы. В первых классах учащимся часто говорили: «Большое количество идет домой.«Что ж, трудно убедить подростка в том, что их любимая учительница четвертого класса была не совсем правильной, потому что теперь размер числа не имеет ничего общего с тем, является ли число делителем или делимым. Чтобы усложнить это, студенты с удивлением обнаруживают, что больше не будет записывать остатки, а вместо них будут дроби и десятичные дроби.
В первых классах учащимся часто говорили: «Большое количество идет домой.«Что ж, трудно убедить подростка в том, что их любимая учительница четвертого класса была не совсем правильной, потому что теперь размер числа не имеет ничего общего с тем, является ли число делителем или делимым. Чтобы усложнить это, студенты с удивлением обнаруживают, что больше не будет записывать остатки, а вместо них будут дроби и десятичные дроби.
Мне потребовалось много времени, чтобы научиться делать все типы деления в столбик. В четвертом классе меня впервые учили делению в столбик.Я скажу, что учил, а не учил, потому что я определенно не усвоил это до того, как перешел в следующий класс. Было так много шагов, и мне всегда казалось, что я их запутываю. Учительница пыталась помочь, давая мне мнемонику об известных ресторанах и их чизбургерах. (Учителя математики, я уверен, что вы знакомы с этим!) Она пыталась спросить меня, сколько раз это число «переходило» в другое. Я всегда был невероятно буквальным в своем мышлении, поэтому я представлял себе дивиденд в виде маленького домика с дверью, а делитель подходил к двери, стучал и просил чизбургер! Смешно, но это не помогло мне научиться разделять.
Я наконец научился делать большинство длинных делений достаточно хорошо, чтобы дотянуть до тех пор, пока я не перешел в математические классы, достаточно высокие, чтобы пользоваться калькулятором. Я должен сделать шокирующее признание — особенно для учителя математики — я никогда не учился делить, когда делитель был двухзначным! Я наконец научился делить на двузначные числа около года назад — после 10 лет обучения в классе, успешного обучения в колледже, в котором я получил высшее образование, и трех лет изучения математики в средней школе.
Поскольку я сам плохо разбирался в делении, я чувствую особую связь со своими учениками, которые также борются с этим навыком. Я часто замечаю мелочи, которые мешают студентам, которые в остальном хорошо разбираются в математике, не могут разделить. (… А также ученики, которые тоже не очень хороши в математике!)
Вот некоторые вещи, которые могут сбивать с толку ваших учеников, и что вы можете с этим сделать:
- «Большой номер идет в дом».
 Большой номер НЕ идет в дом! Хотя это может быть верно в отношении словесных задач, встречающихся на младших классах, это неверное с математической точки зрения утверждение.Это вызывает всевозможные проблемы, когда учащиеся достигают оценок, в которых они делятся, чтобы найти десятичные или дробные значения. Скорее правильнее было бы сказать, что делимое число идет в дом.
Большой номер НЕ идет в дом! Хотя это может быть верно в отношении словесных задач, встречающихся на младших классах, это неверное с математической точки зрения утверждение.Это вызывает всевозможные проблемы, когда учащиеся достигают оценок, в которых они делятся, чтобы найти десятичные или дробные значения. Скорее правильнее было бы сказать, что делимое число идет в дом. - «Сколько раз это число входит в то число ». Студенты, которые думают очень буквально, могут не понять значения этого утверждения. Я спросил многих учеников, которые не умеют делиться и находятся в более старших классах, могут ли они объяснить, что означает эта фраза, а они не могут.Я спрашиваю, было бы больше смысла, если бы я сказал что-то вроде «сколько групп из , этого числа я могу сделать из , этого числа », и это обычно имеет для них больше смысла. Они могут представить себе, как число делится на части, но не повторение делителя для получения делимого.
- Грязные обезьяны и чизбургеры.
 Мнемоника отлично помогает вспомнить то, что у вас уже есть хотя бы базовое понимание, но они не являются обучающими инструментами.Слишком раннее введение мнемоники может оказать негативное влияние на учащихся, которым необходимо закрепить конкретные навыки, прежде чем они попытаются перейти к абстрактному. Хотя мнемоника забавна и подходит для студентов, которые уже понимают концепцию деления и просто нуждаются в подкреплении последовательности шагов, слишком ранний переход к этим устройствам не поможет студентам, которые не понимают, что на самом деле означает каждый шаг. . Если вы не знакомы с приведенной выше мнемоникой и вам интересно: Dirty Monkeys плохо пахнут (разделить, умножить, вычесть, сбить) или McDonald’s продает сырные бургеры (разделить, умножить, вычесть, сравнить, уничтожить).Есть, конечно, много других, а также их вариации.
Мнемоника отлично помогает вспомнить то, что у вас уже есть хотя бы базовое понимание, но они не являются обучающими инструментами.Слишком раннее введение мнемоники может оказать негативное влияние на учащихся, которым необходимо закрепить конкретные навыки, прежде чем они попытаются перейти к абстрактному. Хотя мнемоника забавна и подходит для студентов, которые уже понимают концепцию деления и просто нуждаются в подкреплении последовательности шагов, слишком ранний переход к этим устройствам не поможет студентам, которые не понимают, что на самом деле означает каждый шаг. . Если вы не знакомы с приведенной выше мнемоникой и вам интересно: Dirty Monkeys плохо пахнут (разделить, умножить, вычесть, сбить) или McDonald’s продает сырные бургеры (разделить, умножить, вычесть, сравнить, уничтожить).Есть, конечно, много других, а также их вариации.
Так что же делать с этими сложными навыками? Не волнуйтесь, я не оставлю вас без дополнительных стратегий!
Стратегия разделения сверху и снизу
Это тот, который я использовал, который больше всего помог студентам, которые не совсем свободно владели языком или испытывали трудности с количеством шагов, используемых в стандартном методе обучения.
- Шаг 1. Составьте таблицу умножения делителя.Обозначьте столбец множителя буквой «Т» для вершины и столбец продукта буквой «В» для нижней части. Начните таблицу с 0, а не с 1, и пройдите через 9.
- Шаг 2: Спросите , какое наибольшее число я могу вычесть из дивиденда. Попросите учащегося определить этот номер в «нижнем» столбце.
- Шаг 3: Запишите верхнюю и нижнюю пару. Напишите «верх» над цифрой в «доме» и напишите «низ» ниже.
- Шаг 4: Попросите ученика вычесть, опустить и повторять, пока все деление не будет решено.
Преимущества этого метода заключаются в том, что после того, как ученик несколько раз практикуется, он состоит из трех шагов: вверх и вниз, вычитание, опускание вниз. Кроме того, настаивание на таблице фактов для начала работы полезно для студентов, которые еще не владеют свободно. Кроме того, в этом процессе особое внимание уделяется навыкам записи фактов умножения и вычитания. Студент не должен уметь визуализировать деление числа. Однако из-за этого мне нравится этот метод для старших учеников, которые в остальном не смогли добиться успеха с традиционным методом, а не методом перехода к целому классу.
Однако из-за этого мне нравится этот метод для старших учеников, которые в остальном не смогли добиться успеха с традиционным методом, а не методом перехода к целому классу.
Частные частные
Это замечательный метод, который наконец-то позволил мне делить на двузначные делители! Этот метод, хотя раньше нечасто использовался, в настоящее время становится все более и более распространенным из-за акцента на альтернативных методах в новых государственных стандартах, а также в общих основных стандартах.
В этом методе вам не нужно использовать максимально возможное частное, но вы можете выбрать частное. Это похоже на метод повторного вычитания деления.Основным камнем преткновения для этого метода является то, что пользователь должен иметь некоторое представление о совместимых числах и умножении, чтобы использовать его эффективно.
- Шаг 1: Выберите число для умножения, которое вам будет легко вычислить в уме. Часто это будут числа, оканчивающиеся на нули, кратные или кратные 1, 2, 5 или 10, потому что с помощью числового ощущения это можно сделать мысленно.
 Напишите это число над «домом». Выровняйте разрядные значения.
Напишите это число над «домом». Выровняйте разрядные значения. - Шаг 2: Умножьте в уме делитель на число.Напишите этот номер под номером в «домике». Выстроить разряды
- Шаг 3: Вычтите, убедившись, что ваши разрядные значения совпадают. В этом методе вы не будете «сбивать» вас с ног. Теперь разница — это ваш новый дивиденд при следующем повторении.
- Шаг 4: Повторите с другим совместимым частным. Сложите его друг над другом, выровняв числовые значения. Продолжайте выполнять шаги, пока ваше разделение не будет завершено
- Шаг 5: Сложите все частные частные, чтобы получить окончательный ответ.
Что вы делаете, чтобы помочь своим ученикам выучить длинное деление?
Как научить практическую длинную дивизию — Кейт Сноу
Разочарование в преподавании длинного деления? Деньги-монополисты спешат на помощь! Вы узнаете, как научить своего ребенка КАК выполнять деление в столбик и ПОЧЕМУ это работает.
Когда я был учителем начальной школы, я всегда знал, когда в четвертом классе была неделя с длинными разделами. Мои обычно позитивные и энергичные коллеги приходили в учительскую, обессиленные и измученные, сочувствуя и жаловавшись на утомительную работу и разочарование, связанные с обучением стольких детей этому сложному процессу.Я особенно вспоминаю день, когда одна учительница, обычно очень замкнутая и тихая, продемонстрировала «танец с длинными разделами», который она создала в отчаянии, чтобы помочь своим ученикам выучить шаги!
Мои обычно позитивные и энергичные коллеги приходили в учительскую, обессиленные и измученные, сочувствуя и жаловавшись на утомительную работу и разочарование, связанные с обучением стольких детей этому сложному процессу.Я особенно вспоминаю день, когда одна учительница, обычно очень замкнутая и тихая, продемонстрировала «танец с длинными разделами», который она создала в отчаянии, чтобы помочь своим ученикам выучить шаги!
Несмотря на то, что длинное деление может вселить страх в сердце даже опытных учителей, у меня для вас есть две хорошие новости:
- Мамам, обучающимся на дому, мы должны обучать делению в столбик только одного ребенка за раз. (Ну, может быть, двое, если у вас есть близнецы. Но не 25.)
- При практическом подходе дети могут не только научиться , как делать длинное деление, но и , почему это работает.Это экономит много времени в долгосрочной перспективе, потому что они могут легче запоминать шаги, находить свои собственные ошибки и иметь дело с более сложными ситуациями с длинным делением.

Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.
2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.
3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
24 : 6 = 4
Этот пример можно прочитать по-разному.
- 24 разделить на 6 равняется 4.
- 24 уменьшить в 6 раз – получится 4.

- Делимое – 24, делитель – 6, частное – 4.
- Частное от деления числа 24 на 6 равно 4.
Деление на 1
4 : 1 = 4
23 : 1 = 23
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
составим схему:
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Вывод: Если в задаче есть слова «в . .. раз меньше», то задача решается делением.
.. раз меньше», то задача решается делением.Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Правило встречается в следующих упражнениях:
2 класс
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 103, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 80. Урок 33,
Петерсон, Учебник, часть 2
Урок 33,
Петерсон, Учебник, часть 2
Страница 94. Урок 39, Петерсон, Учебник, часть 2
Страница 108. Урок 44, Петерсон, Учебник, часть 2
Страница 54. Урок 19, Петерсон, Учебник, часть 3
Страница 71. Урок 26, Петерсон, Учебник, часть 3
Страница 100. Повторение, Петерсон, Учебник, часть 3
Страница 102. Повторение, Петерсон, Учебник, часть 3
3 класс
Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 63, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 53, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 56, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 31. Вариант 2. № 1,
Моро, Волкова, Проверочные работы
Вариант 2. № 1,
Моро, Волкова, Проверочные работы
Страница 47. Вариант 2. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 59. Вариант 2. Тест 1, Моро, Волкова, Проверочные работыСтраница 13, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 59, Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 20, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 48, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 13.
Страница 15. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 40. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 441, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 673, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 36, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 520, Мерзляк, Полонский, Якир, Учебник
Номер 656, Мерзляк, Полонский, Якир, Учебник
Номер 657, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 1050, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 1211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1222, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1262, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1266, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
2 класс — деление, задачи и примеры на деление с ответами
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Деление чисел. Текстовые задачи на деление (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 2 класса
Математика, русский, информатика для 1–4 классов, обучающие тренажеры «МИР»
«Математика – копилка знаний», обучающее пособие для начальной школы
Деление предметов на равные группы
1. Раздели стулья на группы по 3 стула в каждой. Сколько всего групп получилось?
2. Раздели уточек на группы по 5 птиц в каждой. Сколько всего групп получилось?
3. Раздели собак на группы по 4 собаки в каждой. Сколько всего групп получилось?
4. Раздели яблоки на группы по 6 штук в каждой. Сколько всего групп получилось?
5. Раздели автомобили на 3 равные группы.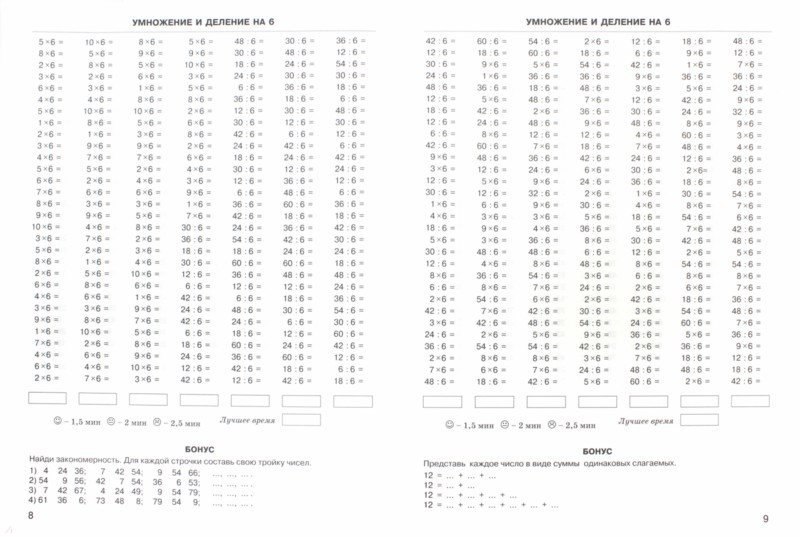 Сколько групп получилось?
Сколько групп получилось?
Деление чисел от 1 до 30
6. Реши примеры на деление и подчеркни делимое.
| 15 : 3 = | 21 : 7 = | 16 : 4 = |
7. Реши примеры на деление и подчеркни делитель:
| 18 : 6 = | 25 : 5 = | 24 : 3 = |
8. Реши примеры на деление и подчеркни частное:
| 10 : 5 = | 28 : 4 = | 20 : 4 = |
9. Раздели кружочки на 7 групп. Сколько всего кружочков оказалось в каждой группе?
10. Раздели квадратики на 10 групп. Сколько всего квадратиков оказалось в каждой группе?
11. Напиши делимое и реши примеры.
12. Используя числовую прямую, реши примеры на деление.
13. Реши примеры.
| 2 : 1 = | 2 : 2 = | 3 : 3 = | 3 : 1 = |
| 4 : 1 = | 4 : 2 = | 4 : 4 = | 5 : 1 = |
| 5 : 5 = | 6 : 1 = | 6 : 2 = | 6 : 3 = |
| 1 : 1 = | 2 : 2 = | 3 : 3 = | 4 : 4 = |
| 3 : 1 = | 4 : 2 = | 6 : 3 = | 8 : 4 = |
| 6 : 1 = | 6 : 2 = | 9 : 3 = | 12 : 4 = |
| 9 : 1 = | 8 : 2 = | 12 : 3 = | 16 : 4 = |
| 12 : 1 = | 10 : 2 = | 15 : 3 = | 5 : 5 = |
| 15 : 1 = | 12 : 2 = | 18 : 3 = | 10 : 5 = |
14. Заполни пропуски числами.
Заполни пропуски числами.
| 6 : __ = 6 | 2 : __ = 1 | 4 : 4 = __ |
| 9 : __ = 3 | __ : 2 = 3 | 8 : __ = 2 |
| __ : 5 = 2 | 6 : __ = 2 | 9 : __ = 3 |
| 8 : 2 = __ | __ : 4 = 3 | 16 : __ = 4 |
| __ : 1 = 7 | 10 : __ = 5 | __ : 3 = 5 |
| 15 : 3 = __ | __ : 2 = 6 | 18 : __ = 3 |
15. Составь числовое выражение на деление к каждому рисунку.
16. Текстовые задачи на деление.
16.1. В больницу привезли 48 рулонов бинтов. Бинты упакованы в пачки по 8 штук в каждой. Сколько пачек с бинтами привезли в больницу?
16.2. Лесники засадили участок земли молодыми саженцами. Всего получилось 9 рядов деревьев. Сколько деревьев было посажено в каждом ряду, если всего было посажено 72 дерева?
16.3. Школьный повар разложил 35 пирожков на 7 тарелок. Сколько пирожков оказалось в каждой тарелке?
16. 4. Ребята из 2 класса пошли в музей. Они шли по 2 человека в ряду. Сколько рядов получилось, если в классе учится 24 школьника? Сколько рядов получится, если идти по 3 человека в ряд, а если по 4 человека в ряд?
4. Ребята из 2 класса пошли в музей. Они шли по 2 человека в ряду. Сколько рядов получилось, если в классе учится 24 школьника? Сколько рядов получится, если идти по 3 человека в ряд, а если по 4 человека в ряд?
16.5. На склад привезли 56 кг картошки. Их надо разложить в 8 мешков. Сколько кг картошки надо положить в каждый мешок?
16.6. В школу надо завести 81 стол. За один раз машина может привезти только 9 столов. Сколько нужно сделать рейсов, чтобы привезти все столы?
16.7. Рыбак поймал 64 кг рыбы и разложил их в 8 ящиков. Сколько кг рыбы поместилось в каждый ящик?
Задачи на деление на две равные части
1. Положите на парты 8 треугольников и разложите их в 2 коробки поровну. Поскольку треугольников будет в каждой коробке? Как записать решение этой задачи?2. Разложите в 2 коробки поровну сначала 10 квадратов, затем 12 кружков, 14 прямоугольников, 16 палочек. Поскольку квадратов, кружков, прямоугольников и палочек будет в каждой коробке? Запишите решение.
3. Положите на парту 8 одинаковых треугольников, разделите их на 2 равные части. Поскольку треугольников будет в каждой части?
99. Начертите отрезки длиной 8 см, затем 12 см и 16 см и разделите каждый из них черточкой на 2 равные части, а затем запишите деление.
Указание. Надо сообщить учащимся названия членов действия деления: делимое, делитель, частное.
Деление на три равные части
1. Положите на парты 6 монет по 1 коп. и разложите их поровну в 3 коробки. Поскольку копеек будет в каждой коробке? Указание. Можно взять спичечные коробки.2. Разложите 9 двухкопеечных монет в 3 коробки поровну. Поскольку копеек будет в каждой коробке?
3. Разложите в 3 коробки поровну: 1) 12 треугольников; 2) 15 квадратов; 3) 18 кружков. Поскольку треугольников, квадратов и кружков будет в каждой коробке?
4. Начертите отрезки длиной 9 см, 12 см, 15 см, раз¬делите каждый из них на 3 равные части и затем запишите деление.
Деление на четыре равные части.
5. Р изложите в 4 коробки поровну: 1) 12 треугольников; 2) 16 квадратов; 3) 20 прямоугольников. Поскольку треугольников, квадратов и прямоугольников бу¬дет в каждой коробке?
Поскольку треугольников, квадратов и прямоугольников бу¬дет в каждой коробке?6. Катя разложила 8 котлет на 4 тарелки поровну. Поскольку котлет положила Катя на каждую тарелку? Вместо котлет разложите кружочки на 4 кучки. Указание. Деление на 5, 6, 7, 8, 9, 10 равных частей также полезно проделать на геометрических фигурах и монетах. Дети должны проявить инициативу в самостоятельном составлении задач на деление и их реше¬нии при помощи дидактического материала.
7. Начертите отрезки длиной 8 см, 12 см, 16 см и разделите каждый из них на 4 равные части, а затем запишите деление.
8. Назовите в пределах 20 все числа, делящиеся: 1) на 2; 2) на 3; 3) на 4; 4) на 5; 5) на 6; 6) на 7; 7) на 8; 8) на 9; 9) на 10.
9. Раздели на 3 следующие числа: 3, 6, 9, 12, 15, 18.
10. Раздели на 4 следующие числа: 4, 8, 12, 16, 20.
11. Раздели
на 5 — 5, 10, 15, 20; , на 8 — 8, 16;
на 6 — 6, 12, 18; на 9 — 9, 18; на 7 — 7, 14; на 10— 10, 20.
Указание. В выполнении упражнений 108—ПО участвуют трое учеников: один называет число — делимое, другой сразу должен говорить ответ — частное, третий подсчитывает ошибки того и другого. Затем учащиеся меняются ролями, так чтобы каждый из них проделал одно и то же, после чего выявляется «победитель» соревнования. Такую игру-упражнение можно использовать для самостоятельной работы. По окончании игры каждая тройка играющих сообщает учителю о результатах соревнования.
Затем учащиеся меняются ролями, так чтобы каждый из них проделал одно и то же, после чего выявляется «победитель» соревнования. Такую игру-упражнение можно использовать для самостоятельной работы. По окончании игры каждая тройка играющих сообщает учителю о результатах соревнования.
12. Решите на монетах следующие примеры:
1) 2 коп.-9:3 3) 20 коп.: 5-3
2) 5 коп.-4 : 2 4) 18 коп.: 6-5
13. Если литр воды разлить в стаканы, то сколько стаканов потребуется для этого. Проверьте и скажите, на сколько же частей вы разделили лигр, разлив воду в стаканы.
Указание. Эту задачу лучше задать на дом. Надо иметь в виду, что тонких стаканов в литре 4, а граненых — 5.
113. Заполните таблицу:
Делимое 12 18 15 20 20 18 18 14 14 16 16 20 50
Делитель 2 2 3 4 5 3 6 2 7 2 8 2 5
Частное
ЗАДАЧИ ПО ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ
1. Сколько потребуется тарелок, чтобы разложить в них 20 яблок, по 5 яблок в каждую? Решите эту задачу с помощью кружков. Указание. Ученик, решающий эту задачу, должен брать по 5 кружков столько раз, сколько можно (значит, он отнимает от 20 кружков по 5 кружков и подсчитывает, сколько раз он отнял).
Дети должны уяснить, что смысл деления по содержанию иной по сравнению с делением на равные части. В самом деле, ведь при делении по содержанию мы всегда находим (по отношению к прямому действию — умножению) множитель, а множитель есть всегда число отвлеченное, при делении же на равные части мы всегда находим множимое, вот почему частное в этом случае всегда имеет то наименование, какое имеет множимое.
Для учащихся II класса различение этих смыслов деления — дело нелегкое, но к нему учитель должен вести своих учеников путем упражнений на конкретном ма¬териале в продолжение всех лет начального обучения.
Таким образом, и деление на равные части, и деление по содержанию — это два вида деления, только в первом случае — это нахождение неизвестного множимого, а во втором — неизвестного множителя. С точки же зрения формы эти два вида деления записываются одинаково: 20:5 = 4.
Читать эти виды деления во II классе желательно различно: для деления на равные части: «20 яблок раз-делить на 5 равных частей (или просто на 5), получится по 4 яблока» (или просто 4), а для деления по содержанию: «20 яблок разделить по 5 яблок, получится 4» (под-разумевается 4 раза).

А затем, когда оба вида деления будут обобщены, то при чтении не следует делать различия, а читать в обоих случаях одинаково: «20 разделить на 5, будет 4».
2. В классе два ряда парт. За каждой партой сидят подвое: в первом ряду — 18, во втором — 16 человек. Сколько парт в первом и во втором ряду в отдельности? Сделайте рисунок к задаче. Составьте такую задачу.
Указание. В тетрадях учащихся получатся примерно такие иллюстрации:
1-й ряд
2-й ряд
3. Положите на парты маленькие линейки и при помощи их ответьте на следующие вопросы: 1) сколько раз! в 20 см содержится по 1 см, по 2 см, по 4 см, по 5 см? Сколько раз в 15 см содержится по 1 см, по 3 см, по 5 см? Запишите правильно решение этих вопросов.
Указание. Ученик считает по линейке или лучше без линейки, а затем проверяет по линейке. В тетради должна быть такая запись:
1) 20 см: 1 см=20;
2) 20 см\2 см— 10 и т. д.
117. Положите на парты монеты и подсчитайте, сколько в рубле содержится монет по 10 коп. , по 20 коп. Как записать решение этих вопросов?
, по 20 коп. Как записать решение этих вопросов?
118. Сколько раз в метре содержится отрезок длиной 10 см, 20 см? Проверьте решение, пользуясь метром.
119. Для работы в саду вышли 24 девочки и 16 мальчиков. Для удобства их распределили по бригадам, по 10 человек в каждой. Сколько получилось бригад?
Составьте подобную задачу из своей школьной жизни.
Ответы:
1. 4.2. 3.
3. 4.
4. 3.
5. 5.
6. 15 : 3 = 5; 21 : 7 = 3; 16 : 4 = 4;
7. 18 : 6 = 3; 25 : 5 = 5; 24 : 3 = 8;
8. 10 : 5 = 2; 28 : 4 = 7; 20 : 4 = 5;
9. 2
10. 2
11. 10 : 2 = 5; 9 : 3 = 3; 8 : 4 = 2; 15 : 5 = 3; 18 : 6 = 3.
12.
13.
1 1 1 1 3 2 2 2 6 3 3 3 9 4 4 4 12 5 5 1 15 6 6 214.
6 : 1 = 6 2 : 2 = 1 4 : 4 = 1 9 : 3 = 3 6 : 2 = 3 8 : 4 = 2 10 : 5 = 2 6 : 3 = 2 9 : 3 = 3 8 : 2 = 4 12 : 4 = 3 16 : 3 = 4 7 : 1 = 7 10 : 2 = 5 15 : 3 = 5 15 : 3 = 5 12 : 2 = 6 18 : 6 = 315.
 15 : 5 = 3; 20 : 4 = 5; 28 : 4 = 7;
15 : 5 = 3; 20 : 4 = 5; 28 : 4 = 7;16.
1. 6 пачек;
2. 8 деревьев;
3. 5 конфет;
4. 12 рядов; 8 рядов; 6 рядов;
5. 7 кг;
6. 9 рядов;
7. 8 кг;
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) com (впр-класс) Последние новости ГИА и ЕГЭ 2017. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.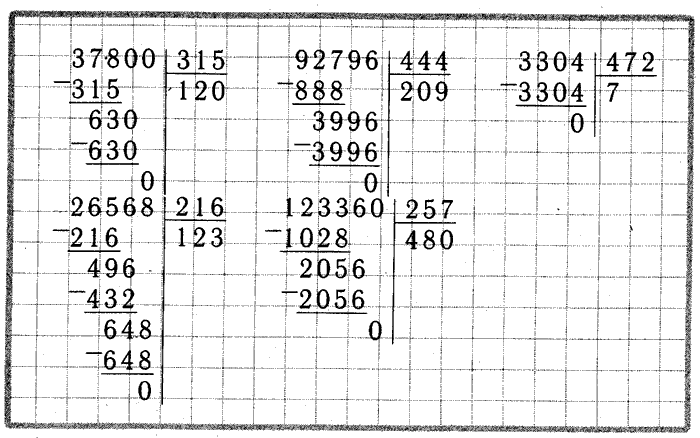 xml
xml
Индивидуальные карточки по теме «Примеры на табличное деление с остатком» | Материал по математике (3 класс) по теме:
Опубликовано 14.05.2012 — 11:22 — Тихонова Ольга Ивановна
Индивидуальные карточки содержат уже готовые примеры, достаточно записать ответ. Данный вид работы можно использовать на этапах повторения и закрепления.
Скачать:
Предварительный просмотр:
Примеры на табличное деление с остатком
65 : 8 = (ост. ) | 34 : 8 = (ост. ) | 76 : 8 = (ост. ) | 51 : 7 = (ост. ) |
44 : 7 = (ост. ) | 41 : 8 = (ост. ) | 76 : 8 = (ост. ) | 58 : 8 = (ост. ) |
22 : 8 = (ост. ) | 25 : 7 = (ост. ) | 66 : 7 = (ост. ) | 62 : 7 = (ост. ) |
1 : 7 = (ост. | 46 : 8 = (ост. ) | 55 : 8 = (ост. ) | 79 : 8 = (ост. ) |
34 : 8 = (ост. ) | 18 : 7 = (ост. ) | 65 : 7 = (ост. ) | 14 : 8 = (ост. ) |
23 : 7 = (ост. ) | 29 : 8 = (ост. ) | 77 : 8 = (ост. ) | 78 : 8 = (ост. ) |
57 : 8 = (ост. ) | 4 : 8 = (ост. ) | 42 : 8 = (ост. ) | 64 : 7 = (ост. ) |
22 : 7 = (ост. ) | 30 : 7 = (ост. ) | 68 : 7 = (ост. ) | 39 : 8 = (ост. ) |
35 : 8 = (ост. ) | 1 : 8 = (ост. ) | 44 : 8 = (ост. ) | 67 : 7 = (ост. ) |
8 : 7 = (ост. ) | 54 : 8 = (ост. | 61 : 7 = (ост. ) | 43 : 8 = (ост. ) |
15 : 8 = (ост. ) | 31 : 7 = (ост. ) | 17 : 8 = (ост. ) | 69 : 7 = (ост. ) |
19 : 7 = (ост. ) | 59 : 8 = (ост. ) | 73 : 8 = (ост. ) | 49 : 8 = (ост. ) |
37 : 8 = (ост. ) | 71 : 8 = (ост. ) | 30 : 8 = (ост. ) | 3 : 8 = (ост. ) |
43 : 7 = (ост. ) | 29 : 8 = (ост. ) | 16 : 7 = (ост. ) | 29 : 7 = (ост. ) |
36 : 8 = (ост. ) | 59 : 7 = (ост. ) | 57 : 7 = (ост. ) | 45 : 7 = (ост. ) |
20 : 7 = (ост. ) | 15 : 7 = (ост. ) | 52 : 8 = (ост. | 68 : 7 = (ост. ) |
38 : 8 = (ост. ) | 27 : 7 = (ост. ) | 18 : 8 = (ост. ) | 31 : 8 = (ост. ) |
24 : 7 = (ост. ) | 2 : 7 = (ост. ) | 8 : 8 = (ост. ) | 60 : 7 = (ост. ) |
45 : 8 = (ост. ) | 75 : 8 = (ост. ) | 19 : 8 = (ост. ) | 13 : 7 = (ост. ) |
25 : 7 = (ост. ) | 33 : 8 = (ост. ) | 27 : 8 = (ост. ) | 51 : 8 = (ост. ) |
47 : 8 = (ост. ) | 17 : 7 = (ост. ) | 12 : 8 = (ост. ) | 46 : 7 = (ост. ) |
2 : 8 = (ост. ) | 58 : 7 = (ост. ) | 7 : 8 = (ост. ) | 33 : 7 = (ост. ) |
53 : 8 = (ост. | 50 : 8 = (ост. ) | 47 : 7 = (ост. ) | 67 : 8 = (ост. ) |
60 : 8 = (ост. ) | 3 : 7 = (ост. ) | 55 : 7 = (ост. ) | 40 : 7 = (ост. ) |
9 : 8 = (ост. ) | 5 : 8 = (ост. ) | 11 : 8 = (ост. ) | 62 : 8 = (ост. ) |
61 : 8 = (ост. ) | 4 : 7 = (ост. ) | 34 : 7 = (ост. ) | 9 : 7 = (ост. ) |
69 : 8 = (ост. ) | 12 : 7 = (ост. ) | 68 : 8 = (ост. ) | 26 : 8 = (ост. ) |
13 : 8 = (ост. ) | 10 : 8 = (ост. ) | 39 : 7 = (ост. ) | 23 : 8 = (ост. ) |
36 : 7 = (ост. ) | 32 : 7 = (ост. ) | 63 : 8 = (ост. | 48 : 7 = (ост. ) |
66 : 8 = (ост. ) | 70 : 8 = (ост. ) | 53 : 7 = (ост. ) | 25 : 8 = (ост. ) |
38 : 7 = (ост. ) | 41 : 7 = (ост. ) | 10 : 7 = (ост. ) | 5 : 8 = (ост. ) |
28 : 8 = (ост. ) | 47 : 7 = (ост. ) | 52 : 7 = (ост. ) | 37 : 7 = (ост. ) |
6 : 7 = (ост. ) | 2 : 8 = (ост. ) | 21 : 8 = (ост. ) | 38 : 7 = (ост. ) |
25 : 8 = (ост. ) | 26 : 8 = (ост. ) | 66 : 8 = (ост. ) | 36 : 7 = (ост. ) |
74 : 8 = (ост. ) | 8 : 8 = (ост. ) | 50 : 8 = (ост. ) | 7 : 8 = (ост. ) |
20 : 8 = (ост. | 46 : 7 = (ост. ) | 13 : 7 = (ост. ) | 2 : 7 = (ост. ) |
37 : 7 = (ост. ) | 13 : 8 = (ост. ) | 61 : 8 = (ост. ) | 70 : 8 = (ост. ) |
11 : 7 = (ост. ) | 51 : 8 = (ост. ) | 25 : 7 = (ост. ) | 10 : 8 = (ост. ) |
54 : 7 = (ост. ) | 45 : 8 = (ост. ) | 3 : 7 = (ост. ) | 75 : 8 = (ост. ) |
5 : 7 = (ост. ) | 19 : 8 = (ост. ) | 62 : 8 = (ост. ) | 2 : 8 = (ост. ) |
50 : 7 = (ост. ) | 39 : 7 = (ост. ) | 60 : 8 = (ост. ) | 3 : 7 = (ост. ) |
5 : 8 = (ост. ) | 40 : 7 = (ост. ) | 38 : 8 = (ост. | 27 : 7 = (ост. ) |
Предварительный просмотр:
Примеры на табличное деление с остатком
26 : 5 = (ост. ) | 39 : 4 = (ост. ) | 13 : 6 = (ост. ) | 57 : 6 = (ост. ) |
29 : 4 = (ост. ) | 1 : 5 = (ост. ) | 1 : 4 = (ост. ) | 9 : 5 = (ост. ) |
13 : 3 = (ост. ) | 26 : 3 = (ост. ) | 6 : 5 = (ост. ) | 2 : 6 = (ост. ) |
9 : 2 = (ост. ) | 30 : 4 = (ост. ) | 37 : 5 = (ост. ) | 32 : 6 = (ост. ) |
19 : 6 = (ост. ) | 13 : 2 = (ост. ) | 18 : 4 = (ост. ) | 2 : 5 = (ост. ) |
22 : 3 = (ост. | 7 : 3 = (ост. ) | 48 : 5 = (ост. ) | 43 : 6 = (ост. ) |
3 : 4 = (ост. ) | 12 : 5 = (ост. ) | 8 : 6 = (ост. ) | 25 : 4 = (ост. ) |
34 : 5 = (ост. ) | 29 : 6 = (ост. ) | 31 : 5 = (ост. ) | 27 : 6 = (ост. ) |
21 : 6 = (ост. ) | 8 : 3 = (ост. ) | 52 : 6 = (ост. ) | 20 : 3 = (ост. ) |
15 : 4 = (ост. ) | 23 : 5 = (ост. ) | 1 : 2 = (ост. ) | 10 : 4 = (ост. ) |
28 : 3 = (ост. ) | 7 : 5 = (ост. ) | 29 : 3 = (ост. ) | 8 : 5 = (ост. ) |
3 : 6 = (ост. ) | 47 : 6 = (ост. ) | 4 : 6 = (ост. | 49 : 6 = (ост. ) |
7 : 4 = (ост. ) | 16 : 5 = (ост. ) | 11 : 6 = (ост. ) | 56 : 6 = (ост. ) |
16 : 3 = (ост. ) | 37 : 4 = (ост. ) | 43 : 5 = (ост. ) | 38 : 6 = (ост. ) |
15 : 2 = (ост. ) | 19 : 4 = (ост. ) | 27 : 5 = (ост. ) | 22 : 6 = (ост. ) |
36 : 5 = (ост. ) | 31 : 6 = (ост. ) | 5 : 2 = (ост. ) | 13 : 4 = (ост. ) |
3 : 2 = (ост. ) | 11 : 4 = (ост. ) | 19 : 5 = (ост. ) | 15 : 6 = (ост. ) |
18 : 5 = (ост. ) | 14 : 6 = (ост. ) | 5 : 3 = (ост. ) | 27 : 4 = (ост. ) |
7 : 2 = (ост. | 14 : 4 = (ост. ) | 47 : 5 = (ост. ) | 41 : 6 = (ост. ) |
46 : 6 = (ост. ) | 9 : 4 = (ост. ) | 17 : 5 = (ост. ) | 2 : 3 = (ост. ) |
19 : 3 = (ост. ) | 17 : 3 = (ост. ) | 37 : 4 = (ост. ) | 21 : 5 = (ост. ) |
19 : 2 = (ост. ) | 22 : 4 = (ост. ) | 29 : 5 = (ост. ) | 25 : 6 = (ост. ) |
2 : 4 = (ост. ) | 11 : 5 = (ост. ) | 7 : 6 = (ост. ) | 51 : 6 = (ост. ) |
41 : 5 = (ост. ) | 35 : 6 = (ост. ) | 23 : 3 = (ост. ) | 3 : 5 = (ост. ) |
1 : 6 = (ост. ) | 34 : 4 = (ост. ) | 6 : 4 = (ост. | 14 : 5 = (ост. ) |
5 : 4 = (ост. ) | 13 : 5 = (ост. ) | 11 : 2 = (ост. ) | 17 : 4 = (ост. ) |
44 : 5 = (ост. ) | 39 : 6 = (ост. ) | 4 : 3 = (ост. ) | 26 : 4 = (ост. ) |
10 : 3 = (ост. ) | 31 : 4 = (ост. ) | 38 : 5 = (ост. ) | 33 : 6 = (ост. ) |
17 : 2 = (ост. ) | 21 : 4 = (ост. ) | 28 : 5 = (ост. ) | 23 : 6 = (ост. ) |
14 : 3 = (ост. ) | 35 : 4 = (ост. ) | 42 : 5 = (ост. ) | 37 : 6 = (ост. ) |
5 : 6 = (ост. ) | 50 : 6 = (ост. ) | 24 : 5 = (ост. ) | 20 : 6 = (ост. |
49 : 5 = (ост. ) | 44 : 6 = (ост. ) | 10 : 6 = (ост. ) | 55 : 6 = (ост. ) |
33 : 5 = (ост. ) | 28 : 6 = (ост. ) | 25 : 3 = (ост. ) | 4 : 5 = (ост. ) |
22 : 5 = (ост. ) | 17 : 6 = (ост. ) | 46 : 5 = (ост. ) | 40 : 6 = (ост. ) |
9 : 6 = (ост. ) | 53 : 6 = (ост. ) | 45 : 6 = (ост. ) | 16 : 6 = (ост. ) |
11 : 3 = (ост. ) | 33 : 4 = (ост. ) | 39 : 5 = (ост. ) | 34 : 6 = (ост. ) |
1 : 3 = (ост. ) | 23 : 4 = (ост. ) | 31 : 5 = (ост. ) | 26 : 6 = (ост. ) |
29 : 5 = (ост. | 41 : 5 = (ост. ) | 19 : 2 = (ост. ) | 22 : 4 = (ост. ) |
25 : 6 = (ост. ) | 9 : 4 = (ост. ) | 14 : 3 = (ост. ) | 46 : 6 = (ост. ) |
25 : 6 = (ост. ) | 28 : 3 = (ост. ) | 36 : 5 = (ост. ) | 11 : 4 = (ост. ) |
2 : 3 = (ост. ) | 27 : 5 = (ост. ) | 31 : 6 = (ост. ) | 19 : 5 = (ост. ) |
По теме: методические разработки, презентации и конспекты
Индивидуальная карточка по теме «Случаи табличного деления»
Индивидуальная карточка содержит уже готовые примеры для 2-3 класса, достаточно записать ответ. Данный вид работы можно использовать на этапах повторения и закрепления….
карточки для проверки знаний табличных случаев умножения и деления
Карточки используют на уроках математики для проверки усвоения детьми табличных случаев умножения и деления в 3 классе. использование карточек позволяет экономить время на уроке….
использование карточек позволяет экономить время на уроке….
Индивидуальные карточки по математике на тему «Деление с остатком»
Индивидуальные карточки по математике на тему «Деление с остатком» разработаны для учащихся 3 класса для тренировки навыков вычисления, закрепления знаний таблицы умножения и деления….
Раздаточный материал — карточки примеров по математике на деление с остатком для 3 класса
Раздаточный материал представляет собой карточки (4 варианта) примеров на деление с остатком, которые позволяют проверить вычислительные навыки учащихся….
Индивидуальные карточки по таблице умножения и деления 2 -3 класс УМК Перспектива
Индивидуальные карточки для отработки и проверки таблицы умножения и деления 2 -3 класс УМК Перспектива…
Карточки для индивидуальной работы «Деление с остатком», 3 класс
Карточки предназначены для индивидуальной работы на этапе закрепления вычислительных навыков по теме «Деление с остатком» с каждым обучающимся. ..
..
Карточки по математике 3 класс «Деление с остатком».
Карточки по математике 3 класс «Деление с остатком»….
Поделиться:
Генератор примеров по математике
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
На данной странице вы можете создать свой уникальный pdf файл с примерами по математике.
 Просто укажите тип, уровень сложности и количество примеров. Далее нажмите кнопку скачать pdf.
Использование материалов в скаченных pdf файлах в коммерческих целях запрещено
Просто укажите тип, уровень сложности и количество примеров. Далее нажмите кнопку скачать pdf.
Использование материалов в скаченных pdf файлах в коммерческих целях запрещеноТип примеров
| Сложение |
| Вычитание |
| Умножение |
| Деление |
| Сложение столбиком |
| Вычитание столбиком |
| Умножение столбиком |
| Деление столбиком |
Уровень сложности
| Уровень 1 |
| Уровень 2 |
| Уровень 3 |
| Уровень 4 |
Количество примеров 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300
Подтвердите, что вы не робот
| Вам могут также быть полезны следующие сервисы |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
Раздел: Целые числа
Разделение это математическая операция, записанная с использованием символа ÷ , это можно рассматривать двумя способами: а ÷ б размер каждой группы, когда а объекты делятся на б группы одинакового размера, ИЛИ а ÷ б это количество групп, когда а объекты разбиты на группы б объекты каждый.
Например,
20
÷
4
можно найти, разделив
20
точки в
4
группы одинакового размера.
Мы находим, что каждая из четырех групп содержит 5 точки, так 20 ÷ 4 знак равно 5 .
В качестве альтернативы мы можем найти 20 ÷ 4 путем формирования групп 4 точки каждая, а затем подсчет количества групп:
Есть 5 группы.
Дивизия – это обратная операция умножения. То есть,
а ÷ б знак равно с если и только если с × б знак равно а .
Здесь а называется дивиденд , б называется делитель , а также с (результат) называется частное .
Разделение по
0
не определено; чтобы понять почему, замените
б
знак равно
0
в приведенных выше уравнениях. С
с
×
0
знак равно
0
независимо от того, какое значение
с
, так
а
также должен быть равен
0
; и если
а
а также
б
оба
0
,
с
может равняться чему угодно!
С
с
×
0
знак равно
0
независимо от того, какое значение
с
, так
а
также должен быть равен
0
; и если
а
а также
б
оба
0
,
с
может равняться чему угодно!
Деление на целые числа может привести к остатку. Например, если мы разделим 20 ÷ 6 путем деления 20 на группы 6 , мы получаем 3 группы с 2 осталось:
Иногда мы пишем 20 ÷ 6 знак равно 3 р 2 , куда 2 это остаток .
Или мы можем записать один числовой ответ в виде дробная часть или десятичное.
Длинный дивизион
Чтобы разделить многозначное число на однозначное, мы можем использовать длинное деление.
Пример 1:
Разделять. 496 ÷ 8
Поместите делимое внутри символа деления, а делитель снаружи символа деления.
8 496
Здесь, 8 не может содержаться в 4 , так что рассмотрим и следующую цифру. Есть 6 восьмерки в 49, так что пиши 6 в десятках частного.
Умножить 6 на делитель 8 и вычесть.
6 8 49 6 48 _ 1
Теперь снова
8
не может содержаться в
1
, поэтому опустите следующую цифру
6
.
6 8 49 6 48 _ 16
Там 2 восьмерки в 16 , так что пиши 2 на тех местах.
Умножить 2 на делитель 8 и вычесть.
6 2 8 496 48 _ 16 16 _ 0
Чтобы разделить многозначное число на многозначное число, процесс аналогичен.
Пример 2:
Разделять 1036 по 32 . Поместите делимое внутри символа деления, а делитель снаружи символа деления.
32 1036
Здесь, 32 не может содержаться в 1 , рассмотрим следующую цифру, еще 32 не может содержаться в 10 . Итак, рассмотрим также следующую цифру. Есть 3 тридцать два в 103 , так что пиши 3 в десятках частного.
Умножить 3 на делитель 32 и вычесть.
3 32 103 6 96 _ 7
Теперь снова
32
не может содержаться в
7
, поэтому опустите следующую цифру
6
.
3 32 1036 96 _ 76
Там
2
тридцать два в
76
, так что пиши
2
на тех местах.
Умножить 2 на делитель 32 и вычесть.
Вот и остаток 12 .
3 2 32 103 6 96 _ 76 64 _ 12
В отличие от сложения и умножения, для
вещественные числа
, операция деления нет коммутативный
. То есть порядок имеет значение:
40
÷
8
знак равно
5
, но
8
÷
40
знак равно
1
5
(дробное значение).
То есть порядок имеет значение:
40
÷
8
знак равно
5
, но
8
÷
40
знак равно
1
5
(дробное значение).
Точно так же деление нет ассоциативный ; то есть группировка имеет значение. Например,
( 80 ÷ 10 ) ÷ 2 знак равно 8 ÷ 2 знак равно 4 , но
80 ÷ ( 10 ÷ 2 ) знак равно 80 ÷ 5 знак равно 16 .
Формулы деления — объяснение, примеры решений и часто задаваемые вопросы
Существует четыре математических операции, а именно: сложение, вычитание, умножение и деление. Деление в математике считается самым сложным среди четырех основных математических операций. Деление – это способ деления числа на равное количество частей. Например, 20 ÷ 4; в нем говорится, что 20 вещей разделены на 4 равные группы, что также означает, что 5 вещей находятся в одной группе. На приведенной ниже диаграмме показано, что есть 20 вещей, которые разделены на 4 равные группы, и в каждой группе по 5 вещей.
Деление – это способ деления числа на равное количество частей. Например, 20 ÷ 4; в нем говорится, что 20 вещей разделены на 4 равные группы, что также означает, что 5 вещей находятся в одной группе. На приведенной ниже диаграмме показано, что есть 20 вещей, которые разделены на 4 равные группы, и в каждой группе по 5 вещей.
(Изображение скоро будет загружено)
В этой статье мы обсудим деление в математике, формулы деления, символы деления, примеры деления, правила деления и т. д.
Символ деления
Существуют различные символы деления, которые используются для представляют раздел математики. Наиболее часто используемый символ деления — ÷, но иногда для представления деления в виде дроби также используется обратная косая черта «/», где значение числителя записывается вверху, а значение знаменателя — внизу.
Пример
«p разделить на q»:
p÷q
Или
p/q
Делимое, делитель, частное и остаток в делении в математике
Когда любое число делится на другое число получить термины, а именно делимое, делитель, частное и остаток.
Делимое определяется как число, которое нужно разделить на другое число.
Делитель — это число, на которое делится другое число без остатка.
Частное — это результат, который получается после деления.
Остаток — это число, которое осталось после деления.
The above concept can be clearly understood through the image given below:
(Image Will be Uploaded Soon)
The division formula is:
Division Formula
Dividend ÷ Divisor = Частное Или, Делимое / Делитель = Частное |
Правила деления
Некоторые правила деления приведены ниже:
При делении цифры 0 на другое число всегда получается 0.
 Например, 0 ÷ 3 = 0. Это предложение означает, что 0 шоколадок распределены между 3 девочками.
Например, 0 ÷ 3 = 0. Это предложение означает, что 0 шоколадок распределены между 3 девочками.Когда любое число делится на 0, это означает, что мы вообще не делим число. Например, 3 ÷ 0 = в математике невозможно. Это предложение означает, что у нас есть 3 шоколадки, но нет девочек, чтобы раздать шоколадки, потому что мы не можем делить ни одно число на 0.
При делении любого числа на 1 всегда получается одно и то же число. Например, 3 ÷ 1 = 3. Это предложение означает, что 1 девочке дали 3 шоколадки.
При делении любого числа на одно и то же число всегда получается число 1. Например, 3 ÷ 3 = 1. Каждая девочка получила по 1 шоколадке.
Числа всегда должны быть разделены в точном порядке. Например, 15 ÷ 3 = 5 и 3 ÷ 15 = 0,2 — это два разных случая.
 15 шоколадок, разделенных на 3 девочек, отличаются от 3 шоколадок, разделенных на 15 девочек.
15 шоколадок, разделенных на 3 девочек, отличаются от 3 шоколадок, разделенных на 15 девочек.
Такие дроби, как \[\frac{1}{2}\], \[\frac{1}{3}\], \[\frac{1}{4}\] и т. д. считаются суммами деления. Например, \[\frac{1}{4}\] равно 1÷3. Это означает, что одна шоколадка делится на 3 девушек.
Использование разделения в реальной жизни:
Разделение используется, когда вам нужно разделить работу между людьми. Например, группа, исполняющая песню, разделяет разные части этой песни между участниками группы.
Вы также можете использовать разделение, когда делаете проект вместе со своими одноклассниками или друзьями. Это даст вам ясность в отношении того, кто выполняет конкретную работу, а также позволит избежать дублирования работы.
Разделение также используется в концепциях устойчивого развития.
 Многие страны объединяются, чтобы пообещать устойчивое будущее. Они делят цель, которую необходимо достичь, в зависимости от своих возможностей.
Многие страны объединяются, чтобы пообещать устойчивое будущее. Они делят цель, которую необходимо достичь, в зависимости от своих возможностей.Разделение используется, когда мы должны распределить товары, такие как фрукты, шоколад, рис, овощи среди «n» людей в нашей повседневной жизни. Эта математическая операция играет ключевую роль при разделе имущества, особенно земли.
Раздел Примеры
Некоторые примеры деления приведены ниже:
1. Найдите значение 60000 ÷ (- 10)
Решение:
60000 ÷ (-10)
= (60000 ) / (-10)
5 5 5 = (-60000) /(10)
= — 6000
2. Найдите частное 516 ÷ 12
Решение:
(Изображение скоро будет загружено)
Следовательно, частное 516 ÷12 = 43
Решенные примеры
Некоторые примеры деления с его решениями приведены ниже:
1. Найдите значение (-15625) ÷ (-125)
Найдите значение (-15625) ÷ (-125)
Решение:
(-15625) ÷ (-125)
= (-15625) / (-125)
= 1 25625/1
= 125
2. Разделите -112 на -14.
Решение:
-112 ÷ (-14)
= (-112) /(-14)
= 112 / 14
= 8
3. Разделите и найдите значение частного числа ÷ 12
Решение:
(изображение скоро будет загружено)
Следовательно, значение частного 1728 ÷ 12 = 144
Quiz Time
1. Если 6 девочек поровну поделят 145 шоколадок, сколько конфет останется?
24
0
6
1
2. (25 ÷ 5) ÷ ( 6-1)
(25 ÷ 5) ÷ ( 6-1)
5
1
625
25
3. Чему равно 323 ÷ 1
323
1
0
Не могу найти ответ
Методы деления: знание формулы, примечания и примеры
- Автор Srotaswini
- Последнее изменение 20 июля 2022 г.
- Автор Шротасвини Мохапатра
- Последнее изменение 20 июля 2022 г.
Методы деления: Значение деления состоит в том, чтобы разделить число на две или более равные части, классы, области, группы и категории. Простыми словами, смысл деления в том, чтобы разделить целое число на группу равными частями или сделать равными части. Предположим, что диагональ прямоугольника делит его на два равных треугольника. Результат деления всегда может быть или не быть целым числом. Иногда результат деления будет в виде дроби или десятичной дроби.
Простыми словами, смысл деления в том, чтобы разделить целое число на группу равными частями или сделать равными части. Предположим, что диагональ прямоугольника делит его на два равных треугольника. Результат деления всегда может быть или не быть целым числом. Иногда результат деления будет в виде дроби или десятичной дроби.
Способ деления чего-либо называется способом деления. Способы деления бывают трех видов по уровню сложности. Это метод фрагментации или деления повторным вычитанием, метод короткого деления или метод автобусной остановки и метод длинного деления. В этой статье будет подробно рассмотрена одна из самых важных арифметических операций под названием «Деление или деление» и ее методы.
В математике есть четыре основных арифметических действия. Это сложение, вычитание, умножение и деление. Исходя из задач, которые мы собираемся решить, в соответствии с этим должен быть выбран тип арифметической операции.
Пример 1: Чтобы разделить \(50\) карандашей поровну между \(25\) детьми, нам нужно разделить \(50\) на \(25\). Таким образом, каждый ребенок получит \(2\) карандаша.
Таким образом, каждый ребенок получит \(2\) карандаша.
Пример 2: \(20\) разделить на \(4\).
Если мы возьмем \(20\) объектов и разделим их на четыре равные группы, то в каждой группе будет \(5\) объектов.
Таким образом, \(20÷4=5\).
Изучите концепции 11-го экзамена CBSE
Символ деления
Разделение может быть представлено символом \( \div \), косой чертой (/) или горизонтальной линией (_). Эти символы используются для удобства при решении различных задач и расчетов. Кроме того, \(\frac{a}{b}\) можно прочитать как «\(a\) через \(b\)».
Например, деление \(60\) на \(12\) может быть выражено как:
\(60 \дел 12 = 5\)
Или \(\frac{{60}}{{12}} = 5\)
Таким образом, результат деления одинаков во всех представленных выше представлениях.
Терминология, используемая в Подразделении
Терминология означает термин. В делении используются четыре важных термина. Это делимое, делитель, частное и остаток.
Делимое: Число, которое нужно разделить на другое число, называется делимым.
Делитель: Число, на которое мы делим другое число (делимое) на равные части, называется делителем.
Частное: Результат деления называется частным.
Остаток: Число, оставшееся после деления, называется остатком.
Графическое представление приведенной выше терминологии приведено ниже.
Деление по числовой строке
Деление — это процесс многократного вычитания.
Пример: \(18 \дел 3\)
В этом методе начните с числа (делимого) в числовой строке и продолжайте вычитать число (делитель), пока не достигнете \(0\) (остаток), а количество шагов, которые мы идем в обратном счете, является частным (или результат деления).
\(3\) многократно вычитается из 18 с помощью числовой строки.
Когда \(3\) вычитается \(6\) раз из \(18\) в числовой строке, мы получаем остаток \(0\).
Таким образом, \(3\) вычитается из \(18\) шесть раз.
Следовательно, \(18÷3=6\), частное равно \(6\).
Дивизион Формула
\({\bf{Дивиденд}} = {\bf{Делитель}} \times {\bf{Частное}} + {\bf{Остаток}}.\)
После деления мы можем подставить все значения в формулу, чтобы проверить или проверить правильность нашего деления или нет.
Пример: \(200÷25=8\)
Здесь делимое \(=200\), делитель \(=25\), частное \(=8\) и остаток \(=0\)
Подставим все вышеперечисленные значения в формулу
\({\rm{Дивиденд = Делитель \умножить на Частное + Остаток}}\)
\(⇒200=25×8+0\)
\(⇒200÷25=8\)
Значит, наше деление верное.
Определить методы деления
Методы деления можно определить как то, как мы выполняем операцию деления. Существует три типа методов. Давайте обсудим каждый из них.
Метод фрагментации
Метод фрагментирования также известен как метод повторного вычитания. Этот метод используется в младших классах при обучении базовому разделу. В методе фрагментации дети будут неоднократно вычитать делитель из делимого, пока мы не получим 0 или число меньше делителя.
Этот метод используется в младших классах при обучении базовому разделу. В методе фрагментации дети будут неоднократно вычитать делитель из делимого, пока мы не получим 0 или число меньше делителя.
Метод короткого деления (метод автобусной остановки)
Метод деления на автобусной остановке также известен как метод короткого деления. Он получил свое название от идеи, что дивиденд находится внутри автобусной остановки, а делитель ждет снаружи.
Короткое деление — это быстрый и эффективный метод деления с большими числами. После того, как дети освоятся с методом фрагментации, они перейдут к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым на однозначный делитель.
Метод длинного деления
Метод длинного деления — наиболее распространенный метод, используемый для решения задач, основанных на делении. В этом методе делитель записывается за пределами правой скобки или левой боковой панели, в то время как делимое помещается внутри, а частное записывается над чертой над делимым.
Это метод, который используется при делении большого числа (обычно двузначного, трехзначного и более) на однозначное, двузначное (или большее) число.
Пример методов раздела
Пример метода фрагментации
Разделить \(12÷3\).
Давайте поймем это по некоторым картинкам,
\(12÷3\) означает, что нам нужно разделить \(12\) яблок на \(3\) в каждой группе.
Шаг 1: Вычтите или вычеркните \(3\) яблок, теперь осталось \(9\) яблок, т. е. \(12-3=9\).
Практические экзаменационные вопросы
Шаг 2: Вычтите или вычеркните еще \(3\) яблок, теперь осталось \(6\) яблок, т. е. \(12-6=3\).
Шаг 3: Вычтите или вычеркните еще \(3\) яблок, теперь осталось \(3\) яблок, т.е. \(12-9=3\).
Шаг 4: Вычтите или зачеркните еще \(3\) яблок, теперь осталось \(0\) яблок, т.е. \(12-12=0\).
Чтобы получить результат в виде \(0\), мы выполнили четыре шага или вычитали \(3\) несколько раз четыре раза.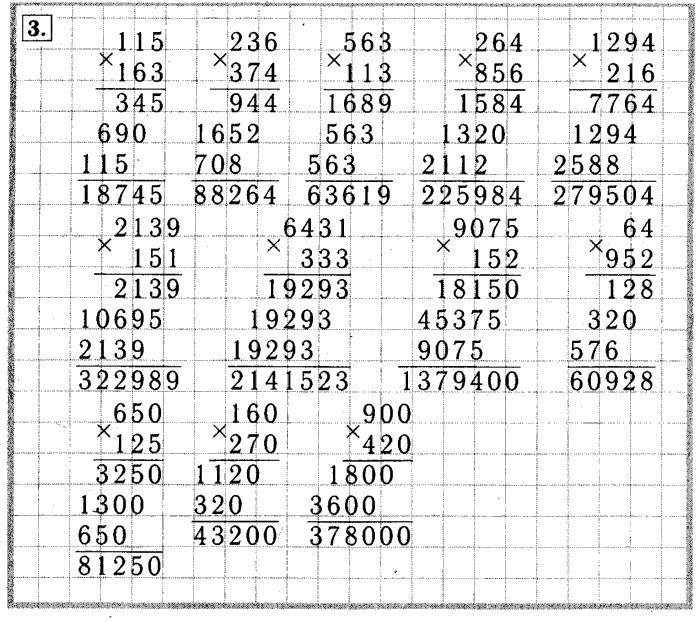 Итак, становится ясно, что ответ равен \(4\).
Итак, становится ясно, что ответ равен \(4\).
Следовательно, \(12÷3=4\).
Пример метода короткого деления
Пример: \(90÷6\)
Здесь нам нужно разделить \(90\) на \(6\) методом короткого деления.
Теперь \(6×1=6\) и остается остаток \(3\).
Остаток затем передается следующему числу, т. е. \(0\), чтобы получилось \(30\).
Теперь, \(6×5=30\), остается остаток \(0\).
Итак, если сложить вместе, ответ будет \(15\).
Следовательно, результат равен \(15\).
Примеры длинного отдела
Пример, \(436÷4\)
- Здесь \(4\) — первая цифра делимого, равная делителю. Итак, \(4 \div 4 = 1.\) Итак, \(1\) написано сверху.
- Теперь вычтите: \(4-4=0\),
- Уменьшите вторую цифру делимого и поместите ее справа от \(0\).
- Теперь \(3<4\). Таким образом, мы можем записать \(0\) как частное и уменьшить следующую цифру делимого и поместить ее справа от \(3\).
- Теперь у нас есть \(36\) в качестве нового делимого.
 \(36>4\) и \(36\) делится на \(4\). Как, \(4×9=36\).
\(36>4\) и \(36\) делится на \(4\). Как, \(4×9=36\). - Запишите \(9\) как частное.
- Теперь вычтите: \(36-36=0\).
- Таким образом, остаток равен \(0,\), а частное равно \(109.\)
Методы разделения Примечание
1. Если число разделить на \(1\), то частное будет таким же, как делимое.
Пример: \(98÷1=98\)
2. Если делимое и делитель одинаковы, то частное будет \(1\).
Пример: \(45÷45=1\)
3. Если \(0\) разделить на любое число, результатом будет \(0\).
Пример: \(0÷13=0\)
4. Если делимое разделить на \(0\), то результат не определен.
Пример, \(106÷0=∞\) (не определено)
Разделение дроби
Фракции можно разделить. При делении дробей оператор деления нужно преобразовать в умножение.
Пример: Разделите \(\frac{3}{5}\) на \(\frac{7}{5}\).
Здесь числитель равен \(\frac{3}{5}\), а знаменатель равен \(\frac{7}{5}\).
Теперь \(\frac{3}{5} \div \frac{7}{5}\) можно записать как \(\frac{3}{5} \times \frac{5}{7}\ )
Таким образом, \(\frac{3}{5} \times \frac{5}{7} = \frac{3}{7}\)
Следовательно, результат равен \(\frac{3}{7}\).
Десятичное деление
В математике разделение десятичных знаков можно наблюдать во многих понятиях, таких как алгебра, геометрия и другие числовые понятия. Деление десятичных дробей очень похоже на дроби.
Пример: Разделите \(0,2\) на \(0,3\).
Сначала преобразуем заданную десятичную дробь \(0,2\) на \(0,3\) в виде дроби.
\(0,2 = \фракция{2}{{10}}\)
\(0,3 = \фракция{3}{{10}}\)
Теперь \(\frac{{0.2}}{{0.3}} = \frac{2}{{10}} \div \frac{3}{{10}}\)
\( = \frac{2}{{10}} \times \frac{{10}}{3}\)
\( = \фракция{2}{3}\)
\(=0,666\).
Следовательно, результат равен \(0,666\)
Деление многочлена
В отличие от чисел и дробей, многочлены также можно разделить на другой многочлен. Полиномиальное деление можно выполнить двумя способами. Одним из них является полиномиальное длинное деление, которое похоже на деление чисел, но вместо чисел будут появляться полиномиальные выражения. Другой метод деления многочленов — метод синтетического деления.
Полиномиальное деление можно выполнить двумя способами. Одним из них является полиномиальное длинное деление, которое похоже на деление чисел, но вместо чисел будут появляться полиномиальные выражения. Другой метод деления многочленов — метод синтетического деления.
Решенные примеры – методы раздела
В.1. Разделите \(125\) на \(5\) методом короткого деления.
Ответ: Здесь нам нужно разделить \(125\) на \(5\) методом короткого деления.
Теперь \(5×2=10\) и остается остаток \(2\).
Остаток затем передается следующему числу, т. е. \(5\), чтобы получилось \(25\).
Теперь, \(5 × 5 = 25\), остается остаток \(0\).
Таким образом, при суммировании ответ будет \(25\).
Следовательно, результат равен \(25\).
В.2. Найдите значение: \([32 + 2 \times 17 + ( – 6)] \div 15\)
Ответ:
Дано, \([32 + 2 \times 17 + ( – 6)] \div 15 \)
Теперь \([32 + 34 + ( – 6)] \div 15\)
\( = (66 – 6) \div 15\)
\( = 60 \div 15 = \frac{{60 }}{{15}} = 4\)
Следовательно, искомый ответ равен \(4\).
В.3. Разделите \(0,214\) на \(0,02\).
Ответ: Сначала преобразуем заданную десятичную дробь \(0,214\) на \(0,02\) в виде дроби.
\(0,214 = \frac{{214}}{{1000}}\)
\(0,02 = \frac{2}{{100}}\)
Теперь \(\frac{{0,214}}{{0,02}} = \frac{{214}}{{1000}} \div \ frac{2}{{100}}\)
\( = \frac{{214}}{{1000}} \times \frac{{100}}{2}\)
\( = \frac{{214 }}{{20}} = \frac{{107}}{{10}}\)
\(= 10,7\)
Следовательно, результат равен \( 10,7.\)
В.4. Разделите \(\frac{2}{5}\) на \(\frac{5}{7}\)
Ответ: Здесь числитель равен \(\frac{2}{5}\), а знаменатель равно \(\frac{5}{7}\).
Теперь \(\frac{2}{5} \div \frac{5}{7}\) можно записать как \(\frac{2}{5} \times \frac{7}{5}\ ) 92} + 3x + 1 = (x + 2)(2x – 1) + 3\)
Следовательно, \({\rm{Дивиденд = Делитель \умножить на частное + остаток}}\)
Следовательно, ответ правильный
Попытка пробных тестов
Резюме
В этой статье было рассмотрено, что такое деление, различные методы деления, формулы для проверки правильности деления, терминология, используемая при делении, примеры различных методов, деление по числовой прямой, некоторые решенные примеры и т. д. Это очистит все ваши сомнения, связанные с делением.
д. Это очистит все ваши сомнения, связанные с делением.
Часто задаваемые вопросы о методах подразделения
В.1. Сколько существует способов деления?
Ответ: Существует три типа методов деления в зависимости от уровня сложности.
(i) Метод деления на части или метод многократного вычитания
(ii) Метод короткого деления или метод автобусной остановки
(iii) Метод длинного деления
В.2. Какой метод деления предпочтительнее?
Ответ: Метод длинного деления предпочтительнее для лучшего понимания деления любого числа, особенно когда результат частного не является целым числом.
В.3. Что такое метод короткого деления?
Ответ: В кратком делении шаги выполняются в уме и не записываются. Короткое деление обычно используется в задачах на деление, имеющих однозначные делители.
В.4. Как сделать простое деление шаг за шагом?
Ответ: Давайте воспользуемся каким-нибудь трюком, чтобы запомнить все шаги, используемые при делении в большую сторону. Вот трюк, чтобы освоить длинное деление. Используйте аббревиатуру DMSB,
Вот трюк, чтобы освоить длинное деление. Используйте аббревиатуру DMSB,
D 9.0004 стоит D IVIDE
M Стенд на M Ultiply
S СООБЩЕНИЯ S UBTRACTION
B Стоит за B DOWN
.
Q.5. Какова \(4\) терминология деления?
Ответ: Существуют \(4\) основные термины деления. Это делимое, делитель, частное и остаток.
Пройдите бесплатные пробные тесты, относящиеся к методам Раздела
Точки и прямоугольники – Математика для учителей начальных классов
Числа и операции
Предположим, вас попросили вычислить 3906 ÷ 3. Один из способов интерпретации этого вопроса (есть и другие):
«Сколько групп по 3 вписывается в число 3906?»
Определение
В квотной модели деления вам дается дивиденд (здесь это 3906), и вас просят разделить его на группы равного размера, где размер группы определяется делитель (здесь это 3).
В нашей модели точек и прямоугольников делимое 3906 выглядит следующим образом:
и три точки выглядит так:
Итак, мы действительно просим:
«Сколько групп вписывается в картинку 3906?»
Пример: 3906 ÷ 3
Существует одна группа из 3 на уровне тысяч и три на уровне сотен, ни одной на уровне десятков и две на уровне единиц.
Обратите внимание, что у нас на картинке:
• Одна группа из 3 в поле тысяч.
• Три группы по 3 в поле сотен.
• Нулевые группы по 3 в поле десятков.
• Две группы по 3 штуки в коробке для единиц.
Это показывает, что 3 входит в число 3906 одну тысячу, три сотни и две единицы раз. То есть
Попробуем посложнее! Рассмотрим 402 ÷ 3. Вот картинка:
Мы все еще ищем группы из трех точек:
Определенно есть одна группа на уровне 100.
, и теперь, кажется, мы застряли, групп по три больше нет!
Подумай / Соедини / Поделись
Что мы можем сделать сейчас? Мы действительно застряли? Сможете решить задачу на деление?
Пример: 402 ÷ 3
Вот детали, разработанные для 402 ÷ 3. Но не читайте это, пока не подумаете об этом сами!
Но не читайте это, пока не подумаете об этом сами!
Поскольку каждая точка соответствует десяти точкам в поле справа, мы можем написать:
Теперь мы можем найти больше групп из трех:
До сих пор есть лишняя точка. Давайте разобьем его тоже
Это даст нам больше групп из трех:
На картинке у нас есть:
• Одна группа из 3 в поле сотен.
• Три группы по 3 в поле десятков.
• Четыре группы по 3 штуки в коробке для единиц.
Наконец-то у нас есть ответ!
Подумай / Соедини / Поделись
Решите каждое из этих упражнений, используя метод точек и прямоугольников:
62124 ÷ 3 61230 ÷ 5
Пример: 156 ÷ 12
Давайте увеличим сложность на ступеньку выше. Рассмотрим 156 ÷ 12. Здесь мы ищем группы по 12 на этой картинке:
Как выглядит 12? В одной ячейке может быть двенадцать точек:
Но чаще всего мы записываем 12 так, как десятку и 2 единицы:
Некоторые из них мы, безусловно, видим на картинке. На уровне десятков наверняка есть один:
На уровне десятков наверняка есть один:
Примечание: При невзрыве это будет двенадцать точек в поле десятков, поэтому мы отмечаем одну группу из 12 над полем десятков.
Мы также видим три группы из двенадцати единиц:
Итак, на картинке мы имеем:
• Одна группа из 12 точек в поле десятков.
• Три группы по 12 точек в блоке единиц.
Значит
156 ÷ 12 = 13.
Задача 6
Используйте модель точек и прямоугольников для вычисления каждого из следующего:
13453 ÷ 11
4853 ÷ 23
214506 ÷ 102
Задача 7
Помните, что числа с основанием пять находятся в системе 1 ← 5 точек и квадратов. Каковы значения места в системе 1 ← 5? Заполните пробелы:
- Нарисуйте число в точках и квадратиках .
- Нарисуйте число в виде точек и прямоугольников .
- Используйте метод точек и прямоугольников, чтобы найти .

- Перепишите предложение о делении в десятичной системе счисления и проверьте правильность.
- Используйте точки и прямоугольники, чтобы найти . Не преобразовывать в 10-ю систему!
Подумай / Соедини / Поделись
- Используйте точки и прямоугольники для их вычисления.
2130 ÷ 10
41300 ÷ 100
- Какие картинки вы использовали для 10 и 100? Можете ли вы описать словами, что происходит при делении на 10 и на 100 и почему?
Мы использовали точки и прямоугольники, чтобы показать, что 402 ÷ 3 = 134.
В начальной школе вы, возможно, научились решать эту задачу на деление, используя схему, подобную следующей:
На первый взгляд это кажется очень загадочным, но на самом деле это ничем не отличается от метода точек и прямоугольников. Вот что означает таблица.
Чтобы вычислить 402 : 3, мы сначала делаем большую оценку того, сколько групп по 3 есть в 402. Давайте предположим, что есть 100 групп по три.
Давайте предположим, что есть 100 групп по три.
Сколько осталось после удаления 100 групп по 3 человека? Мы вычитаем, чтобы найти, что осталось 102.
Сколько групп по 3 в числе 102? Попробуем 30:
Сколько осталось? Осталось 12 и есть четыре группы по 3 в 12.
На это приходится все число 402. И где нам найти окончательный ответ? Просто добавьте общее количество групп из трех, которые мы подсчитали:
.402 ÷ 3 = 100 + 30 + 4 = 134.
Подумай / Соедини / Поделись
- Сравните две приведенные ниже диаграммы делений. В чем они одинаковы? Чем они отличаются?
- Также обратите внимание на метод точек и прямоугольников. В чем она совпадает или отличается от двух диаграмм?
- Почему нам нравится стандартный алгоритм? Потому что это быстро, не так много нужно записать, и это работает каждый раз.

- Почему нам нравится метод точек и прямоугольников? Потому что это легко понять. (А рисовать точки и прямоугольники — одно удовольствие!)
Мы видели, что 402 делится на 3 без остатка: 402 ÷ 3 = 134. Это означает, что 403, еще одно, не должно делиться на три. Это должно быть на одну точку больше.
Пример: 403 ÷ 3
Увидим ли мы лишнюю точку, если вычислим 402 ÷ 3 с точками и прямоугольниками?
Да, есть! У нас осталась одна точка в конце, которую нельзя разделить. Вот как это выглядит в стандартном алгоритме.
В школе мы говорим, что у нас есть остаток от единицы и иногда пишем:
Но что это на самом деле означает? Это означает, что у нас есть 134 группы по три с одной точкой. Так
Пример: 263 ÷ 12
Попробуем другой: 263 ÷ 12. Вот что у нас есть:
И мы ищем такие группы:
Вот так!
Unexploding больше не поможет, и у нас действительно останется одна оставшаяся точка в позиции десятков и точка в позиции единиц. У нас есть 21 группа из двенадцати человек и остальные из одиннадцати.
У нас есть 21 группа из двенадцати человек и остальные из одиннадцати.
Подумай / Соедини / Поделись
- Используйте метод точек и прямоугольников для вычисления каждого частного и остатка:
5210 ÷ 4
4857 ÷ 23
31533 ÷ 101
- Теперь используйте стандартный алгоритм (пример показан ниже) для вычисления каждого из приведенных выше частных и остатков.
- Какой метод вам больше нравится: точки и прямоугольники или метод стандартного алгоритма? Или это зависит от проблемы, которую вы решаете?
Что такое деление? — Математика 3 класса
Представьте, что у вас есть 12 печенюшек. 🍪
Вы хотите поделиться своими куки поровну с 3 друзьями.
Сколько печенья должен получить каждый друг? 🤔
Правильно! 🤗
✅ Каждый человек должен получить по 4 печенья.
Знаете, что мы только что сделали? 😎 Мы только что использовали деление!
Разделение числа на равные группы называется делением .
👉 Здесь мы разделили 12 печений на 3 группы и получили по 4 печенья в каждой группе.
Символ для Дивизион — ÷
. Давайте написать наше первое уравнение дивизии:
12 ÷ 3 = 4
12 Разделен на 3 равных 4
Уравнения деления имеют 3 главные части: делимое , делитель и частное .
Делимое — это число, которое делится. Это число обычно больше!
Делитель — это число, которое делит делимое поровну. Это число меньше!
Частное — это результат, который мы получаем после деления.
Совет: Вы также увидите деление, написанное следующим образом:
Это называется символом long Division .
Такой способ написания задач на деление полезен при делении больших чисел. Вы узнаете об этом позже. 😃
Теперь давайте научимся делить числа.
Деление вычитанием
Сначала давайте воспользуемся вычитанием, чтобы понять деление.
Чтобы разделить , используя вычитание, вычесть меньшее число из большего числа снова и снова, пока не достигнете нуля. Затем вы считаете, сколько раз вы вычитали. Это ответ!
Давайте попробуем! 😃
9 ÷ 3
✅ Сначала вычтите 3. Продолжайте вычитать 3, пока не получите ноль.
✅ Затем посчитайте, сколько раз вы вычли.
3 раза!
9 ÷ 3 = 3
Использование вычитания для решения деления работает, но довольно медленно. 🐌
🐌
Давайте посмотрим на другой способ мышления о делении.
Деление как противоположность умножению
Деление противоположно умножению.
Если вы знаете, что 2 x 3 = 6, вы также знаете, что 6 ÷ 3 = 2!
Почему?
Представьте, что вы умножаете число на некоторый коэффициент.
Затем вы можете разделить произведение или ответ на тот же коэффициент, чтобы снова получить исходное число.
Рассмотрим пример:
12 ÷ 3 = ?
Вы помните, какое число умножить на 3 равно 12? 🤔
Правильно!
4 x 3 = 12
Итак, вы только что выяснили, что 12 ÷ 3 = 4!
Разделение по группам
Теперь давайте попробуем разделить по группам!
На разделим с помощью группировки , разобьем большее число на группы меньшего числа.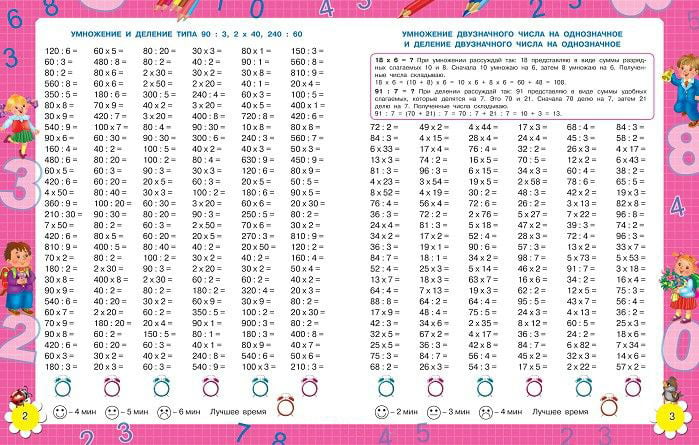
Давайте рассмотрим пример.
10 ÷ 2 = ?
На этот раз мы будем делать группы по 2, пока не достигнем 10. Давайте попробуем!
Затем подсчитайте количество групп, которые вы смогли создать.
Это твой ответ.
10 ÷ 2 = 5
Пока это работает, рисование групп происходит немного медленно. Попробуйте запомнить уравнения деления, как и с умножением.
👉 Попробуем снова разделить с группировкой
6 ÷ 2 = ?
Разделите 6 на группы по 2:
Сколько существует групп по 2? 3!
6 ÷ 2 = 3
Отличная работа! 🤗
Теперь вы понимаете основы деления! 🎉
Далее завершите практику.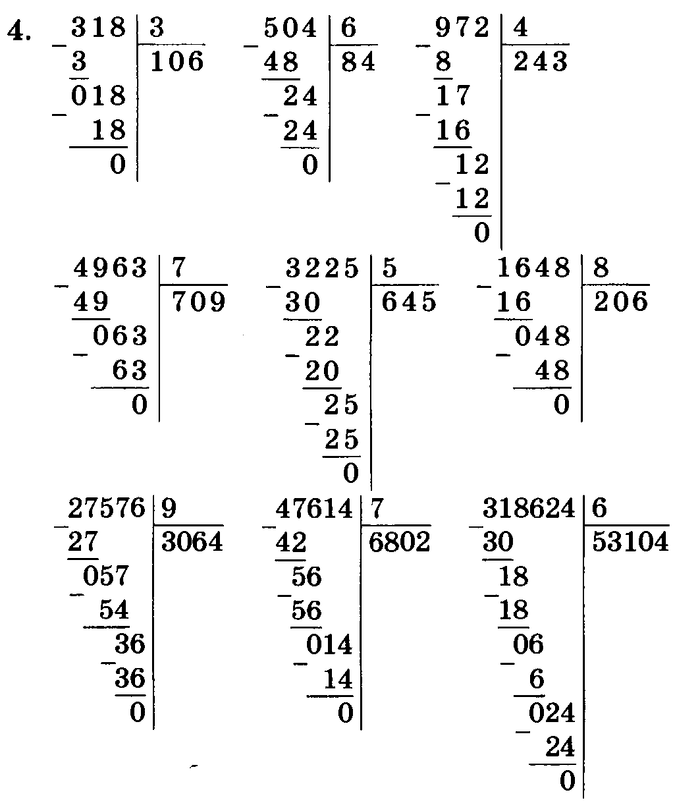 🏋 Вы узнаете больше и будете помнить дольше.
🏋 Вы узнаете больше и будете помнить дольше.
Как делить числа
Домашний
Узнать
Базовая математика
- Дополнение
- Вычитание
- Умножение
- Подразделение
- Целые числа
- Натуральные числа
- Четное нечетное
множители и множители Ссылки
Предварительная алгебра Ссылки
Вычитание определенного количества объектов снова и снова — это деление.
Примечание:
- Деление обозначается знаком «÷».
- Результат выражается знаком «=».
- С помощью таблиц мы можем выполнять деление без вычитания объектов.

Пример
Если есть 10 шоколадок. Сколько групп можно составить из этих 10 конфет с поровну в каждой группе?
5 групп по 2 шоколадки в каждойОбъяснение :
Сначала уберем 2 шоколадки из 10. Остается 8 шоколадок.
Теперь, когда мы уберем 2 шоколадки из 8, останется 6 шоколадок.
Когда мы уберем 2 шоколадки из 6, останется 4 шоколадки.
Из оставшихся 4, когда мы уберем 2 шоколадки, останется 2 шоколадки.
Когда мы удаляем группу из 2 штук в пятый раз, конфет не остается.
Получаем 5 таких групп по 2 шоколадки в каждой.
Таким образом, мы можем сказать, что 10÷2= 5
Таблицы сообщают нам результат во сколько раз число.

Если мы скажем, что 2 × 5 = 10. Это означает, что для получения 10 в качестве произведения скажем таблицу от 2 до 10, получаем 5.
Итак, 10 ÷ 2= 5.
Примечание:
Делимое число и есть делимое. Число, на которое мы делим, и есть делитель.
Если 8 ÷ 2 = 4. Здесь делимое равно 8, делитель 2, частное 4 и остаток 0.
Простой пример
Раздел: задачи со словами
Пример 1:
Пример 2:
В книге 64 страницы. Элизабет читает по 2 страницы каждый день. За сколько дней она завершит книга?
Элизабет заканчивает книгу за 32 дня.

Объяснение :
Чтобы найти дни для завершения книги, нужно разделить 64 на 2.
64 ÷ 2 = Сколько?
Чтобы разделить, сначала посмотрите на цифру слева в делимом. Скажи 2 раза
стол до 6.
Две тройки шесть. Произведение 3 и 2 равно 6. Вычтите это произведение из 6 T.
Осталось ноль десятков.
Запишите цифру 3 над чертой в разряде десятков делимого.
Запишите 4 единицы перед 0. Разделите 4 единицы на 2. Произнесите таблицу умножения на 2.
до 4.
Частное равно 2. Произведение 2 на 2 равно 4. Вычтите это произведение из 4 U. Осталось ноль десятков.
Осталось ноль десятков.
Остаток 0,
Частное равно 32.
Таким образом, 64 ÷ 2 = 32.
Простой пример
Раздел: задачи Word
3876 рубашек расставлены на 17 полках. Если на каждом лежит одинаковое количество рубашек. полка, сколько рубашек на каждой полке?
На каждой полке 228 рубашек.
Объяснение :
Чтобы найти количество рубашек на каждой полке, разделите 3876 на 17.
Чтобы разделить, сначала посмотрите на разряд тысяч в делимом. что 3.
3 меньше делителя 17. 3 нельзя разделить на 17. Возьмите 38, чтобы разделить на
17.
Разделите 38 на 17. Вычтите 34 из 38. Частное равно 2. Остаток равен 4.
Запишите 7 десятков перед 4. Разделите 47 на 17. Вычтите 34 из 47.
Частное равно 2. Остаток равен 13.
Запишите 6 единиц перед 13. Разделите 136 единиц на 17.
Произнесите таблицу умножения на 17 до 136.
Частное равно 8. Вычтите это произведение из 136 U. Остаток 0,
.
Частное равно 228.
Следовательно, 3876 ÷ 17 = 228
Набор фактов, связанных с делением, представляет собой семейство фактов .

- Скажем, 35 ÷ 7. Получим 5.
- А также 35 ÷ 5. Получим 7.
- Таким образом, 5,7 и 35 составляют фактическую семью.
Что нужно помнить
Деление на 1
Если мы разделим любое число на 1, мы получим само число.
Допустим, 78 ÷ 1. Получится 78.
Советы
- Мы всегда должны начинать делить числа с первого места заданного числа.
- Порядок деления некоторого числа: тысячи, сотни, десятки… и так далее…
- При делении любого числа делитель должен быть меньше числа делимого.
- Каждый раз вычитайте произведение из числа делимого, а затем берите следующее
число, пока все число не закончилось.




 Большой номер НЕ идет в дом! Хотя это может быть верно в отношении словесных задач, встречающихся на младших классах, это неверное с математической точки зрения утверждение.Это вызывает всевозможные проблемы, когда учащиеся достигают оценок, в которых они делятся, чтобы найти десятичные или дробные значения. Скорее правильнее было бы сказать, что делимое число идет в дом.
Большой номер НЕ идет в дом! Хотя это может быть верно в отношении словесных задач, встречающихся на младших классах, это неверное с математической точки зрения утверждение.Это вызывает всевозможные проблемы, когда учащиеся достигают оценок, в которых они делятся, чтобы найти десятичные или дробные значения. Скорее правильнее было бы сказать, что делимое число идет в дом. Мнемоника отлично помогает вспомнить то, что у вас уже есть хотя бы базовое понимание, но они не являются обучающими инструментами.Слишком раннее введение мнемоники может оказать негативное влияние на учащихся, которым необходимо закрепить конкретные навыки, прежде чем они попытаются перейти к абстрактному. Хотя мнемоника забавна и подходит для студентов, которые уже понимают концепцию деления и просто нуждаются в подкреплении последовательности шагов, слишком ранний переход к этим устройствам не поможет студентам, которые не понимают, что на самом деле означает каждый шаг. . Если вы не знакомы с приведенной выше мнемоникой и вам интересно: Dirty Monkeys плохо пахнут (разделить, умножить, вычесть, сбить) или McDonald’s продает сырные бургеры (разделить, умножить, вычесть, сравнить, уничтожить).Есть, конечно, много других, а также их вариации.
Мнемоника отлично помогает вспомнить то, что у вас уже есть хотя бы базовое понимание, но они не являются обучающими инструментами.Слишком раннее введение мнемоники может оказать негативное влияние на учащихся, которым необходимо закрепить конкретные навыки, прежде чем они попытаются перейти к абстрактному. Хотя мнемоника забавна и подходит для студентов, которые уже понимают концепцию деления и просто нуждаются в подкреплении последовательности шагов, слишком ранний переход к этим устройствам не поможет студентам, которые не понимают, что на самом деле означает каждый шаг. . Если вы не знакомы с приведенной выше мнемоникой и вам интересно: Dirty Monkeys плохо пахнут (разделить, умножить, вычесть, сбить) или McDonald’s продает сырные бургеры (разделить, умножить, вычесть, сравнить, уничтожить).Есть, конечно, много других, а также их вариации. Напишите это число над «домом». Выровняйте разрядные значения.
Напишите это число над «домом». Выровняйте разрядные значения.

 Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года.
Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года. 

 )
)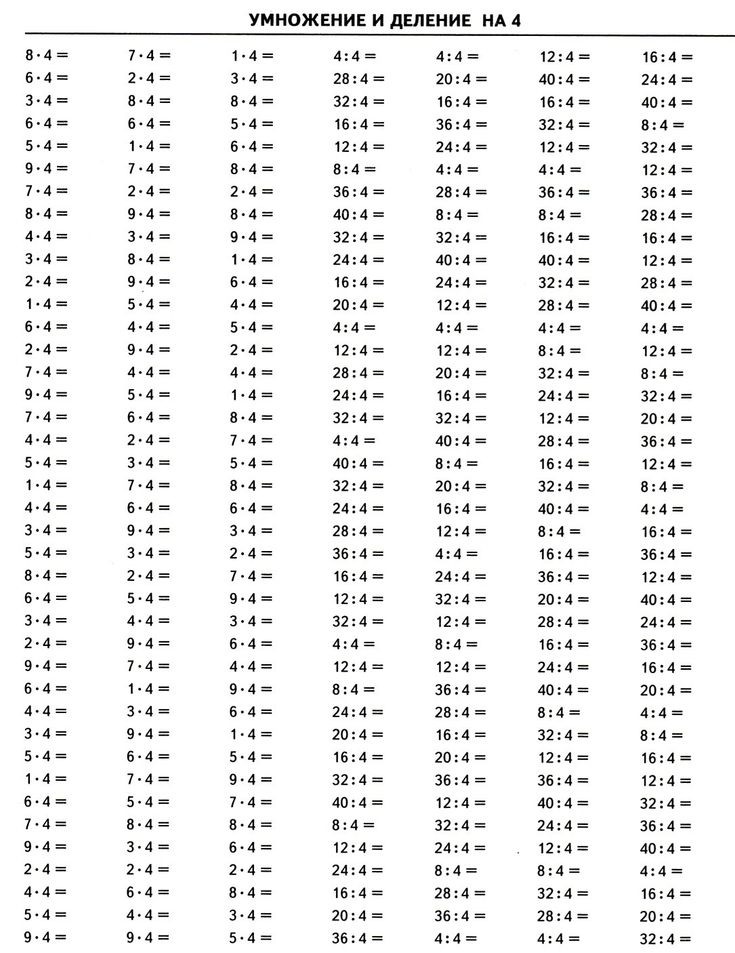 )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) Например, 0 ÷ 3 = 0. Это предложение означает, что 0 шоколадок распределены между 3 девочками.
Например, 0 ÷ 3 = 0. Это предложение означает, что 0 шоколадок распределены между 3 девочками.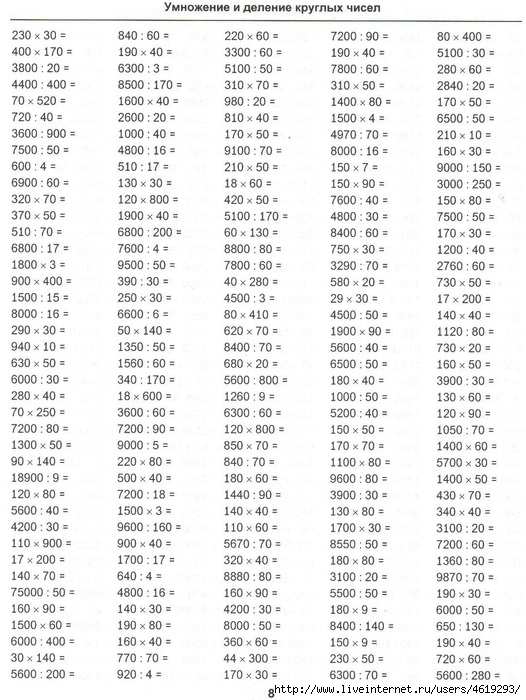 15 шоколадок, разделенных на 3 девочек, отличаются от 3 шоколадок, разделенных на 15 девочек.
15 шоколадок, разделенных на 3 девочек, отличаются от 3 шоколадок, разделенных на 15 девочек. Многие страны объединяются, чтобы пообещать устойчивое будущее. Они делят цель, которую необходимо достичь, в зависимости от своих возможностей.
Многие страны объединяются, чтобы пообещать устойчивое будущее. Они делят цель, которую необходимо достичь, в зависимости от своих возможностей. \(36>4\) и \(36\) делится на \(4\). Как, \(4×9=36\).
\(36>4\) и \(36\) делится на \(4\). Как, \(4×9=36\).