Примеры на деление. Математика 4 класс.
Примеры на деление. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 9520 : 8 = 1190 | 21000 : 210 = 100 | 5500 : 11 = 500 | 22000 : 20 = 1100 | 6860 : 7 = 980 |
| 78400 : 56 = 1400 | 228000 : 38 = 6000 | 905000 : 50 = 18100 | 844000 : 20 = 42200 | 18000 : 450 = 40 |
| 2610 : 9 = 290 | 29600 : 740 = 40 | 2400 : 48 = 50 | 80000 : 80 = 1000 | 66300 : 30 = 2210 |
| 50400 : 63 = 800 | 94500 : 35 = 2700 | 264000 : 300 = 880 | 84600 : 600 = 141 | 68000 : 680 = 100 |
| 8720 : 4 = 2180 | 32000 : 400 = 80 | 51700 : 47 = 1100 | 102000 : 600 = 170 | 10000 : 200 = 50 |
| 98800 : 260 = 380 | 9880 : 26 = 380 | 282000 : 60 = 4700 | 692000 : 40 = 17300 | 426000 : 71 = 6000 |
| 76300 : 700 = 109 | 81600 : 510 = 160 | 8400 : 70 = 120 | 60900 : 70 = 870 | 136000 : 80 = 1700 |
| 777000 : 37 = 21000 | 84800 : 800 = 106 | 450000 : 900 = 500 | 72000 : 200 = 360 | |
| 83200 : 400 = 208 | 6120 : 9 = 680 | 41800 : 380 = 110 | 68400 : 6 = 11400 | 252000 : 900 = 280 |
| 69000 : 50 = 1380 | 660000 : 550 = 1200 | 48000 : 96 = 500 | 43400 : 700 = 62 | 108000 : 300 = 360 |
| 671000 : 61 = 11000 | 8520 : 2 = 4260 | 89000 : 89 = 1000 | 79200 : 880 = 90 | 312000 : 80 = 3900 |
| 390000 : 300 = 1300 | 7700 : 77 = 100 | 188000 : 940 = 200 | 405000 : 500 = 810 | 436000 : 400 = 1090 |
| 600000 : 24 = 25000 | 7400 : 200 = 37 | 884000 : 17 = 52000 | 498000 : 30 = 16600 | 74200 : 200 = 371 |
| 7200 : 72 = 100 | 940 : 94 = 10 | 83200 : 800 = 104 | 3200 : 8 = 400 | 66300 : 17 = 3900 |
| 5820 : 6 = 970 | 630000 : 900 = 700 | 910000 : 70 = 13000 | 98000 : 50 = 1960 | 1280 : 8 = 160 |
| 83000 : 830 = 100 | 15000 : 75 = 200 | 540000 : 900 = 600 | 310000 : 500 = 620 | 120000 : 10 = 12000 |
| 80000 : 80 = 1000 | 52800 : 44 = 1200 | 636000 : 40 = 15900 | 2790 : 9 = 310 | |
| 297000 : 270 = 1100 | 969000 : 300 = 3230 | 67000 : 67 = 1000 | 86000 : 40 = 2150 | 894000 : 30 = 29800 |
| 332000 : 20 = 16600 | 583000 : 530 = 1100 | 882000 : 980 = 900 | 148000 : 20 = 7400 | 9325 : 25 = 373 |
| 7790 : 41 = 190 | 350000 : 250 = 1400 | 12600 : 60 = 210 | 48000 : 600 = 80 | 2100 : 70 = 30 |
| 432000 : 540 = 800 | 90300 : 300 = 301 | 26500 : 500 = 53 | 390 : 39 = 10 | 52600 : 200 = 263 |
| 64400 : 23 = 2800 | 19200 : 960 = 20 | 78000 : 200 = 390 | 552000 : 200 = 2760 | 65000 : 95 = 67000 |
| 61000 : 610 = 100 | 3180 : 6 = 530 | 696000 : 400 = 1740 | 7100 : 71 = 100 | 738000 : 60 = 12300 |
| 98000 : 70 = 1400 | 385000 : 11 = 35000 | 1120 : 7 = 160 | 89100 : 90 = 990 | 36400 : 91 = 400 |
| 4000 : 200 = 20 | 8900 : 89 = 100 | 98000 : 50 = 1960 | 6650 : 95 = 70 | 1500 : 2 = 750 |
| 546000 : 91 = 6000 | 55300 : 7 = 7900 | 10000 : 20 = 500 | 328000 : 40 = 8200 | 192000 : 960 = 200 |
| 33000 : 110 = 300 | 540000 : 600 = 900 | 952000 : 400 = 2380 | 39600 : 44 = 900 | 860 : 2 = 430 |
| 18000 : 150 = 120 | 18200 : 26 = 700 | 4500 : 5 = 900 | 6060 : 2 = 3030 | 408000 : 51 = 8000 |
| 53700 : 30 = 1790 | 54900 : 900 = 61 | 666000 : 370 = 1800 | 71200 : 400 = 178 | 4950 : 55 = 90 |
| 48800 : 61 = 800 | 203000 : 70 = 2900 | 450 : 9 = 50 | 170000 : 17 = 10000 | 81900 : 90 = 910 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
16 тыс изображений найдено в Яндекс.
 Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7ВСЕ ПРОГРАММЫ
Математика
Рабочие листы для 4 класса
1 цикл: Космос
Сложение, вычитание, умножение и деление в пределах 100 (устно и письменно). Название компонентов действия при сложении, вычитании, умножении и делении. Алгоритм решения текстовых задач. Значение переменной. Простейшие виды письменного сложения и вычитания в пределах 10 000. Скобки и порядок действий. Вычитание суммы и разности из числа. Умножение и деление суммы на число.
1. Сложение и вычитание в пределах 100
2. Решение текстовых заданий
3. Значение переменной
4. Письменное сложение и вычитание
5. Переместительный закон сложения
6. Сочетательный закон умножения
7. Вычитание суммы из числа
8. Умножение в пределах 100
Умножение в пределах 100
9. Деление в пределах 100
10. Деление — действие, обратное умножению
11. Переместительный закон умножения
12. Законы умножения
13. Умножение суммы на число
14. Умножение суммы на число
15. Деление суммы на число
16. Деление суммы на число
17. Вычисление удобным способом. Порядок действий
18. Вычисление удобным способом. Порядок действий
19. Повторение
2 цикл: Было время…
Величины (единицы длины, массы, времени, площади) и их соотношения. Периметр квадрата и прямоугольника. Числа до 1 000 000 и их состав.
1. Деление с остатком
2. Повторение
3. Единицы длины
4. Периметр прямоугольника
5. Единицы массы
6. Денежные единицы
7. Единицы времени
8. Скорость, время и расстояние
9. Повторение
10. Разряды числа. Сумма разрядных слагаемых.
11. Разряды. Сумма разрядных слагаемых.
Сумма разрядных слагаемых.
12. Разряды тысяч
13. Десятки тысяч
14. Сотни тысяч
3 цикл: Земля в огненном кольце
Сравнение площадей предметов, вычисление площади квадрата и прямоугольника. Письменное сложение и вычитание 5- и 6-значных чисел. Проверка суммы и разности при письменном сложении и вычитании. Порядок действий и скобки. Письменное сложение и вычитание именованных величин.
1-1. Сравнение площадей фигур. Равные по площади фигуры
1-2. Квадратный сантиметр. Площадь прямоугольника
2. Площадь квадрата
3. Единицы площади
4. Повторение
5. Повторение
6. Алгоритм устного счета
7-1. Алгоритм письменных вычислений
7-2. Алгоритм письменных вычислений
8-1. Сравнение алгоритмов устного и письменного вычислений
8-2. Сравнение алгоритмов устного и письменного вычислений
9-1. Повторение
Повторение
9-2. Повторение
10. Письменное значение пяти- и шестизначных чисел
11-1. Письменное значение пяти- и шестизначных чисел
11-2. Письменное значение пяти- и шестизначных чисел
12. Сложение нескольких чисел
13. Сложение нескольких чисел
14. Письменное значение пяти- и шестизначных чисел
15-1. Письменное значение пяти- и шестизначных чисел
15-2. Письменное значение пяти- и шестизначных чисел
16. Закрепление
18. Проверка письменного сложения и вычитания
19. Повторение
20. Повторение
4 цикл: Кукольный театр
Анализ и решение задач до трех действий. Устное умножение с числами 10, 100, 1000. Умножение однозначного числа на числа, оканчивающиеся на 0. Письменное умножение на однозначное число.
1-1. Значение выражений. Скобки и порядок действий
1-2. Значение выражений. Скобки и порядок действий
2-1. Значение выражений. Скобки и порядок действий
Скобки и порядок действий
2-2. Значение выражений. Скобки и порядок действий
3-1. Письменное сложение и вычитание величин
3-2. Письменное сложение и вычитание величин
4-1. Письменное сложение и вычитание величин
4-2. Письменное сложение и вычитание величин
5-1. Повторение
5-2. Повторение
6-1. Решение текстовых заданий
6-2. Решение текстовых заданий
7-1. Решение текстовых заданий
7-2. Решение текстовых заданий
8-1. Повторение
8-2. Повторение
9-1. Повторение
9-2. Повторение
10. Сложение в уме
11. Умножение в уме
12. Деление в уме
13. Деление в уме
14-1. Повторение
14-2. Повторение
15-1. Повторение
15-2. Повторение
5 цикл: Секреты энергии
Повторение письменного умноженияна на однозначное число. Решение выражений (порядок действий). Письменное деление на однозначное число.
1-1. Письменное умножение многозначного числа на однозначное число
1-2. Письменное умножение многозначного числа на однозначное число
2. Письменное умножение многозначного числа на однозначное число
3. Письменное умножение многозначного числа на однозначное число
4. Письменное умножение многозначного числа на однозначное число
5-1. Письменное умножение многозначного числа на однозначное число
5-2. Письменное умножение многозначного числа на однозначное число
6. Значение выражений. Порядок действий
7. Повторение
8. Письменное деление многозначного числа на однозначное число
9. Письменное умножение многозначных чисел с 0 на однозначное число
10. Письменное умножение многозначных чисел с 0 на однозначное число
11. Письменное деление многозначного числа на однозначное число
12. Письменное деление многозначного числа на однозначное число
13. Письменное деление многозначного числа на однозначное число
Письменное деление многозначного числа на однозначное число
14. Письменное деление многозначного числа на однозначное число
15-1. Повторение
15-2. Повторение
6 цикл: Кем быть?
Решение выражений (порядок действий). Письменное умножение и деление на двузначное число.
1-1. Решение выражений (порядок действий)
1-2. Значение выражений (порядок действий)
2-1. Письменное умножение на двузначное число
2-2. Письменное умножение на двузначное число
3-1. Письменное умножение множителей, оканчивающихся на ноль
3-2. Письменное умножение множителей, оканчивающихся на ноль
4-1. Письменное умножение на двузначное число
4-2. Повторение
5-1. Значение выражений
5-2. Значение выражений
6-1. Значение выражений
6-2. Значение выражений
7-1. Письменное деление на двузначное число
7-2. Письменное деление на двузначное число
8-1. Письменное деление на двузначное число с 0 в частном
Письменное деление на двузначное число с 0 в частном
8-2. Письменное деление на двузначное число с 0 в частном
9-1. Письменное деление на двузначное число с 0 в частном
9-2. Письменное деление на двузначное число с 0 в частном
10-1. Письменное деление на двузначное число
10-2. Письменное деление на двузначное число
11. Письменное деление на двузначное число
12-1. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
12-2. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
13. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
7 цикл: Государство сквозь века
Повторение умножения на двузначное число. Решение выражений (порядок действий). Письменное деление с остатком. Письменное умножение на трехзначное число.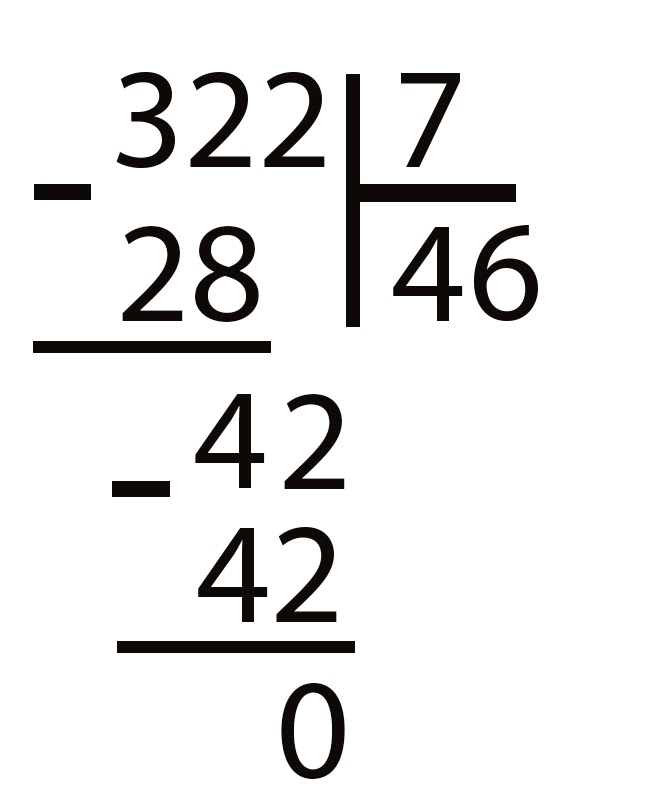 Умножение именных величин на одно- и двузначное число. Решение текстовых заданий путем составления выражений и уравнений.
Умножение именных величин на одно- и двузначное число. Решение текстовых заданий путем составления выражений и уравнений.
1-1. Письменное деление на двузначное число
1-2. Письменное деление на двузначное число
2. Значение выражения и порядок действий
3. Значение выражения и порядок действий
4. Письменное деление с остатком
5. Письменное деление с остатком
6. Повторение письменного деления и умножения
7. Умножение на трехзначное число
8. Умножение на трехзначное число
9. Письменное умножение множителей, содержащих 0
10. Письменное умножение множителей, содержащих 0
11. Повторение письменного умножения на трехзначное число
12. Умножение величин
13. Деление величин
14. Составление и решение уравнений
15. Решение текстовых заданий
16. Решение текстовых заданий
17. Повторение
18-1. Дроби
18-2. Дроби
18-3. Дроби
8 цикл: Рука об руку в политике
Решение текстовых заданий путем составления выражений и уравнений. Дроби (числительное, знаменательное, дробная черта; деление фигур на равные части; 1/2, 1/3 и 1/4 фигуры). Нахождение половины, трети и четверти числа. Нахождение части заданных величин. Нахождение дроби по закрашенной или незакрашенной части фигуры. Решение текстовых задач с дробями. Повторение и углубление: счет, составление и чтение чисел до миллиона, сравнение чисел, устное и письменное сложение и вычитание.
Дроби (числительное, знаменательное, дробная черта; деление фигур на равные части; 1/2, 1/3 и 1/4 фигуры). Нахождение половины, трети и четверти числа. Нахождение части заданных величин. Нахождение дроби по закрашенной или незакрашенной части фигуры. Решение текстовых задач с дробями. Повторение и углубление: счет, составление и чтение чисел до миллиона, сравнение чисел, устное и письменное сложение и вычитание.
1. Нахождение части величин
2. Нахождение дроби по раскрашенной части
3. Текстовые задания с дробями
4. Повторение
5. Повторение
6. Счет
7-1. Состав, чтение и запись чисел до миллиона
7-2. Сравнение чисел
8. Письменное и устное сложение в пределах миллиона
9. Устное и письменное вычитание в пределах миллиона
10. Связь сложения и вычитания
11. Устное и письменное умножение
12. Письменное умножение на двузначное число
13-1. Устное и письменное деление на однозначное число
Устное и письменное деление на однозначное число
13-2. Письменное деление на двузначное число
9 цикл: Классифицируем природу
Связь сложения и вычитания. Устное и письменное умножение на одно- и двузначное число в пределах миллиона. Письменное умножение на двузначное число в пределах миллиона. Устное и письменное деление на одно- и двузначное число в пределах миллиона. Письменное деление на двузначное число в пределах миллиона. Связь умножения и деления. Выражения и равенства. Буква в равенстве. Числа 0 и 1 и действия с ними. Порядок действий и скобки. Измерение величин (длина, вес, скорость, время, вычисление площади). Различение, называние и черчение геометрических фигур — точка, отрезок, ломаная, треугольник, четырехугольник, квадрат, прямоугольник. Вычисление периметра треугольника и четырехугольника. Решение текстовых задач до трех действий. Задачи на самоконтроль и смекалку.
1. Связь деления и умножения
2. Выражение и равенство. Переменная в равенстве.
3. Числа 0 и 1
4. Скобки и порядок
5. Измерение длины
6. Измерение массы
7. Измерение времени
8. Измерение скорости
9. Измерение стоимости
10. Измерение площади
11. Геометрические фигуры
12. Периметр прямоугольника и четырехугольника
13. Периметр и площадь треугольника и четырехугольника
14. Решение текстовых заданий
15. Задания на повторение и смекалку
Содержание
” Алгоритм умножения и деления на трехзначное число. 4 класс – Балабақша әлемі
Математика.
Краткосрочный план урока № 60.
Предмет: Математика
Урок: 60 Школа: Х. Бижанова
Дата:
05.12.19 ФИО учителя:
Отамурадова А.А
Класс: 4 А Количество
присутствующих: Количество
отсутствующих:
Раздел (сквозная тема): Раздел 2А. Умножение и деление «Культурное наследие».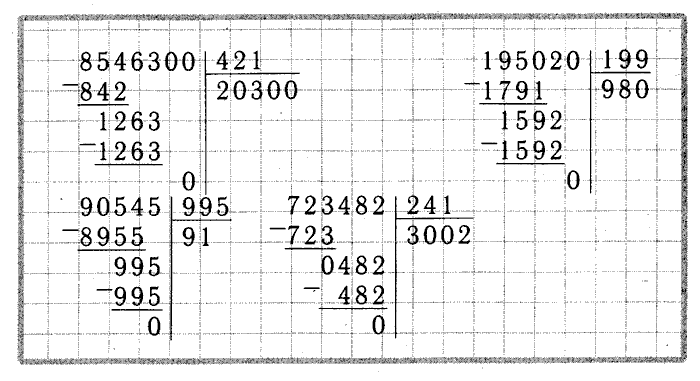
Тема урока: Обобщение изученного.
Алгоритм умножения и деления на трехзначное число.
Древние города
Цели обучения, которым посвящен урок: 4.1.2.12** – применять алгоритм умножения и деления многозначных чисел, оканчивающихся нолями, на трехзначное число;
4.1.2.13** – применять алгоритм деления многозначных чисел на двух/трехзначное число, когда в записи частного есть ноли и алгоритм обратного действия умножения
Развитие навыков: 1.2 Операции над числами
Языковые цели
Учащиеся могут:
применять алгоритм умножения и деления многозначных чисел на двузначные и трехзначные.
Предметная лексика и терминология:
названия компонентов действий, неполное произведение, неполное делимое, пробная цифра частного.
Полезные выражения для диалогов и письма:
Обсуждение
Для чего нужно определить количество цифр в частном?
Почему используется пробная цифра частного?
Письмо
Запись умножения и деления столбиком
Критерии оценивания
Применяет алгоритм деления многозначных чисел на двузначное и трехзначное. Проверяет вычисления.
Проверяет вычисления.
Материал прошедших уроков: Алгоритм умножения и деления.
Ход урока:
Этапы урока Запланированная деятельность на уроке Ресурсы
0-1 мин Создание положительного эмоционального настроя:
– Здравствуйте, те, кто родился зимой! (те, кто родился зимой, здороваются и садятся)
– Здравствуйте, те, кто родился летом! (те, кто родился летом, здороваются и садятся)
– Здравствуйте, те, кто родился весной! (те, кто родился весной, здороваются и садятся)
– Здравствуйте, те, кто родился осенью! (те, кто родился осенью, здороваются и садятся)
– Ещё раз, все, здравствуйте!
– Здороваться – это желать здоровья!
Я желаю, чтобы во все времена года у вас было отличное здоровье и мы могли дружно общаться и выполнять работу.
Эмоциональный настрой
Середина урока
2-5 мин
21-22 мин
23-28 мин
29-30 мин
31-37 мин
38-40 мин 1.Актуализация жизненного опыта.
1) Записать число, классная работа
2) Минутка чистописания
Назовите самое большое трехзначное число? (999)
– Давайте это число пропишем в мин. чистописания
чистописания
3)(К) Математический диктант:
1)Какое число надо прибавить к 12560, чтобы получить 13000? (440)
2)На сколько 10ч. меньше 1 суток? ( на 14 ч)
3) Произведение 490, первый множитель 7. Чему равен второй множитель? (70)
4)Увеличьте 67 в 100 раз (6700)
5)Найдите разность чисел 930 и 200. (730)
6)Найдите восьмую часть числа от числа 800. (100)
7)Сумма двух чисел 650, одно из них 250. Найдите другое число. (400)
8)Сколько минут составляют 180 с.? (3 мин)
9) Частное 6, делитель 50. Чему равно делимое? (300)
10)Найдите частное чисел 54000 и 6. (9000)
Проверка работы. Взаимооценивание в парах. ( на полях оценивают себя карандашами светофор)
2. Постановка цели (проблемная ситуация).
Вспомните алгоритм умножения и деления, найдите ошибки в примерах.
1235 * 201 = 248235 29200 : 73 = 4
Учащиеся находят ошибки в записи первого примера и в ответе второго.
( на доске листы с примерами дети подходят и устраняют ошибки красным маркером)
– Какова тема и цель нашего урока?
Обобщить всё, что мы изучали.
3. Выполнение задания №1 с. 72
Определи количество цифр в частном, не выполняя вычислений.
Расположи ответы (количество цифр в частном) в порядке возрастания, и ты прочтёшь, какое второе название имел древний город Испиджаб.
Р-5. А-3. М-7. С-2. А-6. Й-4 Сайрам
Выступление детей и просмотр видеоролика
4.Работа по теме урока.
Выполнение №3 с. 72 второй столбик у доски с объяснением
2210 * 402 = 888420 181944 : 361 = 504
Оценивание работы учащимися.
Физминутка
Руки в стороны и вверх
Повторяем дружно
Засиделся ученик
Разминаться нужно
Мы сначала всем в ответ
Головой покрутим НЕТ!
Энергично, как всегда
Головой покрутим ДА!
Чтоб коленки не скрипели
Чтобы ножки не болели
Приседаем глубоко
Поднимаемся легко
Раз, два, три чеканим шаг
Подает учитель знак
Это значит что пора
Нам за парты сесть УРА!
5. (И) Самостоятельная работа.
Выполнение №3 с. 72 третий столбик.
• критерии оценивания:
Знать алгоритм деления на двузначное и трехзначное числа
Применить алгоритм при вычислениях.
Я могу
Могу применить алгоритм деления многозначных чисел на двузначное и трехзначное числа.
Могу выполнить проверку
Проверка работы. Лист оценивания.
6. (П) Работа в парах.
Исследуй.
Составь выражение по схеме и обозначь в нём порядок действий.
( 2.432*203+ 40.000)+ (60.950:50+14.000)- (7.809:3*2)
Проверка работы. Самооценивание.
(Молодец, если допустили ошибку напишите старайся) Дети пишут в тетрадках сами
-Давайте повторим вместе правила работы в группе
7. Работа в группах. Решить примеры, составить слово.
4167 : 463 = 9 (о) 3918:653=6(м)
2541*205=520905 (ы) 2311*203=469133 (ц)
8400:28=300 (л) 1261*324=408564 (д)
3200*12=38400 (о)
С каждой группы выходят по два ученика находят свои ответы
Выступление групп.
– Расположите ответы в порядке возрастания и прочитайте слово «МОЛОДЦЫ»
Резерв стр 73 № 6 (устно)
Нам надо узнать сколько раз по 11л входит в 55 литров.
55:11=5(раз)
100*5=500(км)
Щучинск 239+239=478(км)
2 слайд
3 слайд
4 слайд
Учебник
тетрадь
5 слайд
Учебник
На доске
На доске
Тетрадь
6 слайд
Учебник
7 слайд
Учебник
8 слайд
9 слайд(проверка)
10 слайд
11 слайд(проверка)
Конец урока
Итог урока.
-Какую цель мы поставили на сегодняшнем уроке?
– Достигли ли мы этой цели?
– Какие затруднения были у вас на уроке?
– Что нужно сделать чтобы эти затруднения не
повторялись?
Рефлексия.
Предлагает оценить свою работу при помощи смайликов Картинки к рефлексии.
Дифференциация Оценивание Межпредметные
связи
Мотивированные дети рассказывают по схеме о живой и неживой природе о взаимосвязи в природе Формативное оценивание.
Самооценивание по «Шкале трудности» в тетради.
Взаимооценивание при работе в паре, группе классом
Результаты наблюдения учителем качества ответов учащихся
на уроке.
Определение уровня усвоения навыка по (Творческая тетрадь) – литература
– физическая культура
– самопознание
– познание мира
Рефлексия для учителя:
Важные вопросы
по уроку:
Итоговая оценка (с точки зрения преподавания и обучения)
Какие два момента были наиболее успешны?
Какие два момента улучшили урок?
Что я узнал из урока о классе и отдельных людях, что я расскажу на следующем уроке?
Приемы умножения и деления на 10. 2-й класс, «Школа России»
Тип урока: овладение новыми знаниями.
Цели: познакомить с приемами умножения и деления на 10. Совершенствовать вычислительные навыки навыки устного счёта, умение решать задачи, развивать внимание и логическое мышление.
Педагогические задачи: дать первичное представление об умножении и делении числа на 10, продолжать формировать умения находить результат действия деления с помощью примера на умножение, развивать вычислительные навыки, продолжать работу над задачами.
Планируемые образовательные результаты:
Предметные УУД: умение правильно умножать и делить на число 10, знание названия компонентов умножения и деления, понимание сути переместительного закона умножения, умение выделять геометрические фигуры, применение формулы периметра квадрата.
Метапредметные УУД:
- Регулятивные: умение формулировать учебную задачу урока на основе соотнесения того ,что уже известно и усвоено, и того, что еще неизвестно, умение контролировать и оценивать учебные действия в соответствии с поставленной задачей; способность к самопроверке, самооценке, проверке по образцу и корректировке, взаимопроверке.
- Познавательные: проявлять познавательную инициативу в учебном сотрудничестве, умение выделять необходимую информацию, создавать алгоритм деятельности, сравнивать, анализировать, устанавливать причинно-следственные связи, делать выводы.
- Коммуникативные: оказывать необходимую взаимопомощь, договариваться и приходить к общему решению в совместной деятельности, слушать, слышать и понимать партнеров, планировать учебное сотрудничество с учителем и сверстниками, достаточно полно и четко выражать свои мысли.

- Личностные УУД: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения; развитие навыков сотрудничества с взрослыми и сверстниками в разных социальных ситуациях, проявление самостоятельности, личной ответственности.
Методы и формы обучения: частично-поисковый, фронтальная и групповая работа, индивидуальная.
Оборудование: компьютер, электронная доска, доска, карточки с заданием, математический веер, карта путешествия, сундучок с призами.
1. Организационный момент
— Ребята, сегодня у нас необычный урок. Мы с вами отправимся в увлекательное морское путешествие и побудем командой моряков. С нами на борту присутствуют пассажиры. Только от нашей слаженной, дружной работы, зависит найдем ли мы сегодня клад.
2. Актуализация знаний
— Давайте вспомним правила поведения на корабле (Отвечаем по руке, задание дослушиваем до конца, сидим ровно прямо).
— Чтобы отправиться в путь нам нужно проложить курс корабля. Найдем значение данных математических выражений, показывая ответы на математическом веере.
(Выводим картинку корабля на электронную доску).
— Ребята, прочитайте данные математические выражения, назвав их компоненты и найдите значение (если дети затрудняются, необходимо напомнить арифметическое действие).
— 14 + 6 (1 слагаемое — 14, 2 слагаемое – 6, сумма равна 20).
— 43 — 4 (Уменьшаемое – 43, вычитаемое – 4, разность равна 39).
— 16 : 4 (Делимое – 16, делитель – 4, частное равно 4).
— 4 * 3 (1 множитель – 4, 2 множитель -3, произведение равно 12).
— 8 * 0 (1 множитель – 8, 2 множитель — 0, произведение равно 0).
— 40 — 33 (Уменьшаемое – 40, вычитаемое – 33, разность равна 7).
— 5 * 10 (1 множитель – 5, 2 множитель -10, произведение равно 50).
— 24 : 4 (Делимое – 24, делитель – 4, частное равно 6).
— 10 * 5 (1 множитель – 10, 2 множитель — 5, произведение равно 50).
— 17 + 15 (1 слагаемое — 17, 2 слагаемое – 17, сумма равна 32).
— Ребята, что мы сейчас с вами делали? (Считали математические выражения, вспоминали название математических компонентов).
— Молодцы! Мы отправляем наш корабль в добрый путь!
3. Самоопределение к деятельности
— Ребята, а что вы заметили, работая с данными математическими выражениями? (Мы заметили, что два выражения с одинаковыми числами и одинаковым результатом. Это 5*10 и 10*5).
Учитель записывает выражение на доске (5*10 … 10*5).
— Ребята, сравните это выражение. Какой знак мы поставим? (Равно.)
— Какое математическое свойство вы использовали для сравнения выражения? (Переместительное свойство умножения. От перестановки множителей результат умножения не изменяется).
— Вычислите значение этих выражений, заменяя умножение сложением (Один ребенок работает у доски. 5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)
5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)
— Хорошо. Ребята, чтобы дальше отправиться в путь на нашем корабле, нам нужно составить по этим выражениям два примера на деление (50 : 10 = 5 и 50 : 5 = 10)
— А как вы нашли значение выражений? (Зная значение произведения чисел 5 и 10, можно найти их частное)
— Какое правило взаимосвязи компонентов и результата действия вам помогло? (Если произведение разделить на один из множителей, то получится другой множитель)
— На сегодняшнем уроке мы продолжим учиться выполнять умножение и деление чисел и познакомимся с новым приёмом.
А кто догадался, что это за приём? (Приём умножения и деления на число 10)
— Ребята, что мы сейчас с вами делали? (Сравнивали выражения, повторяли переместительное свойство умножения и деления).
— Молодцы, отправляемся далее в наше путешествие.
— Проверьте своё предположение, откройте с. 74 и прочитайте задачи урока.
— Прочитайте объяснение вычислительного приема рядом с красной чертой.
— Послушаем объяснение и обратим наше внимание на электронную доску (Числа от 1 до 100. Приемы умножения и деления на 10).
— Что вы можете сказать о наших выводах и выводах в учебнике? (От перестановки множителей результат умножения не изменяется. Если произведение разделить на один из множителей, то получится другой ).
— Хорошо, что мы сейчас с вами сделали? (Убедились, что наши предположения правильны).
— Отправляемся дальше в наше увлекательное путешествие.
4. Физминутка
— Мы с вами моряки и нам необходимо быть внимательными, чтобы не попасть в руки к пиратам или не наткнуться на айсберг.
Игра «Запрещенное движение». Учитель говорит запретное движение, а дети должны быть внимательными и не повторять его, если учитель сказал или показал его.
5. Работа по учебнику
Работа по учебнику
Минутка чистописания.
— Откройте тетради, запишите: сегодняшнее число, Классная работа.
Цифра вроде буквы О —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним
Единицу примостим,
Он побольше станет весить,
Потому что это — десять.
— Какое число будем прописывать? (10)
— Что можно сказать о числе 10? (чётное, двузначное, круглое, 1 десяток, 0 ед., в числовом ряду стоит после числа 9, перед числом 11)
— Что в жизни бывает круглым? (Солнце, арбуз, мяч, часы, пуговица и т.п.)
— А в математике? (Круг, шар, числа)
— Какие числа называют круглыми? (Круглыми называют числа, оканчивающиеся на ноль).
— Назовите все круглые числа в числовом ряду до 100? (10, 20, 30, 40, 50, 60, 70, 80, 90).
— Назовите самое маленькое круглое двузначное число? Самое маленькое круглое трехзначное число? (10; 100).
— Прописываем число 10 через клеточку.
(Прописная цифра 1. — Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.
Прописная цифра 0. — Овал начинают писать немного левее правого верхнего угла клетки. Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем ведут руку вверх к началу овала.)
— Молодцы, наш корабль плывет дальше.
— №1 стр.74 – фронтальная работа.
Составление таблицы. Дети устно поочередно читают примеры.
— Как связаны между собой четыре столбика примеров? (При составлении 2 столбика используется переместительное свойство умножения, при составлении 3 и 4 столбика – правило о том, что если значение произведения разделить на один множитель, то получится другой множитель).
| 10 * 2 = 20 | 2 * 10 = 20 | 20 : 2 = 10 | 20 : 10 = 2 |
10 * 3 = 30 | 3 * 10 = 30 | 30 : 3 = 10 | 30 : 10 = 3 |
10 * 4 = 40 | 4 * 10 = 40 | 40 : 4 = 10 | 40 : 10 = 4 |
10 * 5 = 50 | 5 * 10 = 50 | 50 : 5 = 10 | 50 : 10 = 5 |
10 * 6 = 60 | 6 * 10 = 60 | 60 : 6 = 10 | 60 : 10 = 6 |
10 * 7 = 70 | 7 * 10 = 70 | 70 : 7 = 10 | 70 : 10 = 7 |
10 * 8 = 80 | 8 * 10 = 80 | 80 : 8 = 10 | 80 : 10 = 8 |
10 * 9 = 90 | 9 * 10 = 90 | 90 : 9 = 10 | 90 : 10 = 9 |
10 * 10 = 100 | 10 * 10 = 100 | 100 : 10 = 10 | 100 : 10 = 10 |
— Ребята, какой вывод мы можем сделать об умножении и делении на 10? (Вывод: при умножении на 10 к числу справа дописывается 0.
При делении на 10 у числа 0 убирается!)
Дети читают на электронной доске стихотворение-правило.
— Наш корабль доплыл до середины пути, продолжаем наш путь. Что мы сейчас делали? (Выявили правило умножения и деления на 10.)
6. Физминутка
— Моряки должны быть не только внимательными, но и ловкими и смелыми.
— Как мы будем плыть на спасательной шлюпке? (Упражнение гребля)
— Как будем залезать по висячей лестнице? (Упражнение как будто лезем по лестнице руками)
— Как будем смотреть вдаль? (Упражнение тянемся на мысочках)
7. Закрепление изученного материала
— Ребята, как называется кухня на корабле? (Камбуз)
— Как называют повара на корабле? (Кок)
— Кок приготовил нам пирожки, но (скажу вам по секрету) кок – это бывший пират и он не умеет считать. Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.
Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.
Задача №3.
— Прочитай задачу про себя.
— Прочитай вслух.
— Сколько пирожков раскладывал повар? (40)
— Как он их раскладывал? (Поровну).
— Что значит «поровну»? (На каждую тарелку одинаковое количество).
— Как будем раскладывать пирожки на 10 тарелок? (По 1 пирожку на каждую тарелку).
(Один ученик работает у доски. 10 магнитных тарелок закрепляем на доске, раскладываем пирожки (из бумаги) по тарелкам).
— Сколько пирожков оказалось на каждой тарелке? (1)
— Поровну разложили все 40 пирожков? (Нет).
— Уточните, как будем раскладывать пирожки? (До тех пор, пока все не закончатся).
— Сколько пирожков стало на каждой тарелке? (По 4 пирожка).
— Запишите решение задачи и ответ.
40:10=4 (п.)
Ответ: на каждой тарелке по 4 пирожка.
— Что обозначает число 40? (Количество пирожков)
— Что обозначает число 10? (Количество тарелок)
-Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Решим 2 задачи обратные данной (с помощью магнитных рисунков составляем условие задач).
1. Повар разложил 40 пирожков на тарелки. В каждой тарелке получилось по 4 пирожка. На сколько тарелок повар разложил пирожки?
40: 4 = 10 (т.)
Ответ: на 10 тарелок.
— Что обозначает число 40? (количество пирожков)
— Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Что обозначает число 10? (Количество тарелок)
2. Повар разложил на 10 тарелок пирожки. В каждой тарелке получилось по 4 пирожка. Сколько всего пирожков было?
10 * 4 = 40 (п.)
Ответ: 40 пирожков всего.
— Что обозначает число 10? (Количество тарелок)
— Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Что обозначает число 40? (Количество пирожков)
— Молодцы! Что мы сейчас с вами делали? (Решали задачу и составляли задачи обратной данной).
— Хорошо, наш корабль следует дальше. И перед нами разрушенный мост. Чтобы проплыть дальше, нам необходимо восстановить мост, решая примеры самостоятельно (Выводим картинку моста с примерами на электронную доску. Примеры из №5 с.74. Решаем в столбик. После выполнения задания проверка.)
- 74 – 58 = 16
- 46 + 37 = 83
- 83 – 29 = 54
- 64 + 36 = 100
— Молодцы! Корабль наш держит путь далее и мы с вами находим сундук с сокровищами. Чтобы открыть сундук нам надо узнать длину его стороны, зная уже периметр.
— Какую фигуру представляет сундук? (Квадрат)
— Что такое квадрат? (Прямоугольник, у которого все стороны равны)
— Что такое периметр? (Сумма длин всех сторон)
— Как найти периметр квадрата? (Сложить длины всех сторон)
— Прочитайте задание №4 на стр.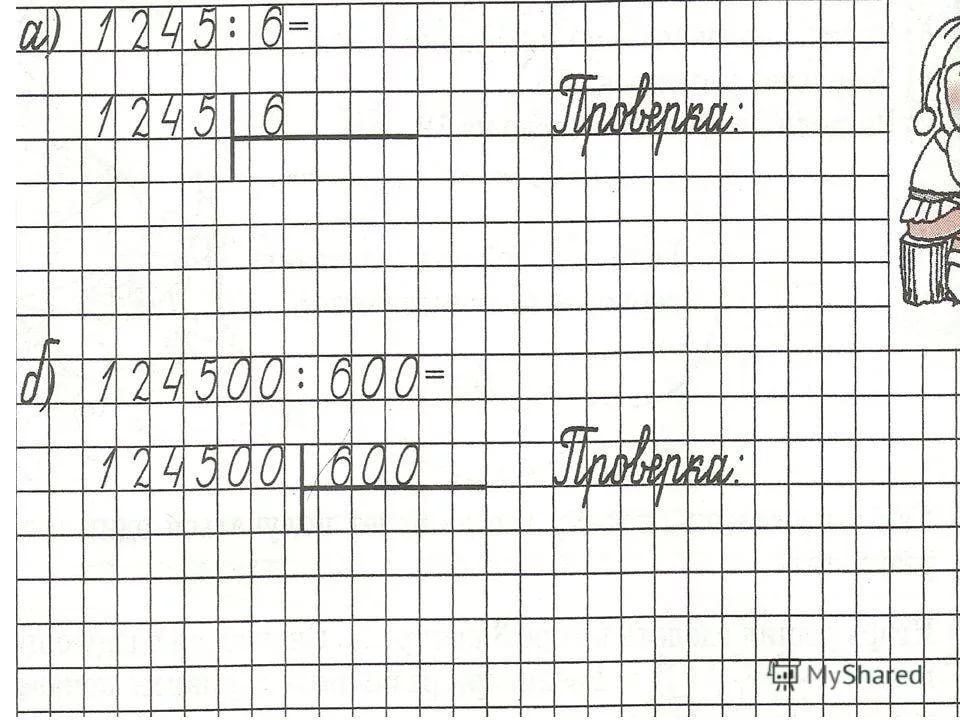 74.
74.
— Какая формула периметра квадрата?
(Р = а + а +а +а
Р = а * 4)
— Чему равен периметр квадрата по условию задачи? (20 см.)
— Подставьте это значение в равенство (а * 4 = 20.)
— Что у вас получилось? (Уравнение.)
— Решите уравнение и узнайте длину стороны этого квадрата.
а * 4 =20
а = 20:4
а =5
Ответ: а = 5 см.
— Молодцы! Что мы сейчас делали? (Закрепляли изученный материал)
8. Рефлексия
— Решение задания по компьютеру № 1.
Работа в группах.
— Мы продолжаем наше путешествие и находим на острове бутылку с посланием. На листочках детям дается задание составить числовые выражения на деление. Проверка проходит фронтально.
— Составьте числовые выражения на деление.
1) 3, 30, 10 0, 50, 4, 10, 40 60, 6, 5
30 : 3 = 10
100 : 10 = 10
50 : 5 = 10
40 : 4 = 10
60 : 6 = 10
2) 90, 70, 7, 80,9 ,10, 100, 20, 8, 2
90 : 9 = 10
70 : 7 = 10
80 : 8 = 10
100 : 10 = 10
20 : 2 = 10
Фронтальная проверка.
9. Подведение итогов урока
— Ребята, мы с вами возвращаемся домой из нашего увлекательного путешествия.
— Какую тайну математики вы сегодня открыли? Чему научились? Всем ли было легко? Какие трудности испытывали? (Мы освоили приемы умножения и деления на 10.)
— Какое правило использовали при умножении числа на 10? (При умножении на 10 к числу справа дописывается 0.)
— Как находить результат при делении круглого числа на 10? (При делении на 10 у числа 0 убирается.)
— Молодцы! Вы были сегодня активны, внимательны, сообразительны, поэтому мы справились со всеми заданиями и нашли сундук с сокровищами. Спасибо вам за хорошую работу.
Выставление отметок.
10. Домашнее задание
— Открываем наш бортовой журнал – дневник и записываем домашнее задание. Учебник – стр.74 № 6.
Сундучок с призами – шоколадные монеты.
Применение распределительного свойства умножения 6 класс онлайн-подготовка на Ростелеком Лицей
51. Применение распределительного свойства умножения.
Применение распределительного свойства умножения.
Напомню, что распределительное свойство умножения относительно сложения и вычитания записывается так.
(a + b) · c = a · c + b · c = ac + bc;
(a — b) · c = a · c — b · c = ac — bc.
Распределительное свойство умножения относительно сложения и относительно вычитания позволяет решать примеры.
Пример 1. 35-13∙15=35∙15-13∙15=3∙155-1∙153=9-5=4.
Пример 2. Найдем значение произведения
2314∙7=2+314∙7=2∙7+314∙7=14+3*714=1512.
Чтобы умножить смешанное число на натуральное число,
можно:- Умножить целую часть на это число.
- Умножить дробную часть на это число.
- Сложить полученные результаты.
Пример 3. Найдем значение выражения
538∙28+258∙28=538+258∙28=8∙28=2.
Используя распределительное свойство умножения, можно упрощать выражения вида:
58a+34a=58+34∙a=148а=134 а
34x-15x=34-15x=1520-420x=1120x.
Пример 4. Квартира состоит из двух комнат. Длина большей комнаты 5110, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3110 м. На сколько площадь одной комнаты меньше площади другой?
Площадь первой комнаты
S=a∙b=5110∙4=5+110∙4=5∙4+110∙4=20+25=2025 м2.
Площадь второй комнаты
S=a∙b=3110∙4=3+110∙4=3∙4+110∙4=12+25=1225 м2.
Разница площадей 2025-1225=8 м2.
Чтобы умножить смешанное число на смешанное число, можно:
- Перевести одно смешанное число в неправильную дробь.
- Умножить целую часть второго множителя на неправильную дробь.
-
Умножить дробную часть второго множителя на неправильную дробь.

- Сложить полученные результаты.
Пример 5. Найдем значение выражения
225∙412=225∙92=2∙92+25∙92=9+95=1045 .
Урок математики 4 класс «Деление числа на произведение»
Слайды и текст этой онлайн презентации
Слайд 1
УРОК
МАТЕМАТИКИ
4 КЛАСС
Автор: Четкина Г. В.
учитель начальных классов
МБОУ «Атратская СОШ»
Слайд 2
1
4
55
+
23
99
100
5
=
Слайд 3
560 : 7
250 * 200
15 0* 200
20180 : 10
800 * 60
200 : 2
3500 : 5
30 * 20
50150 : 10
90 * 3000
500 * 40
320 : 8
810 : 9
5400 : 6
600
5015
70
80
900
270000
40
20000
90
48000
100
30000
2018
50000
30000
2018
700
100
48000
50000
5015
900
270000
40
20000
90
Слайд 4
ВСЕХ
2
5
3
4
,
ЦАРИЦА
,
МАТЕМАТИКА
,
НАУК.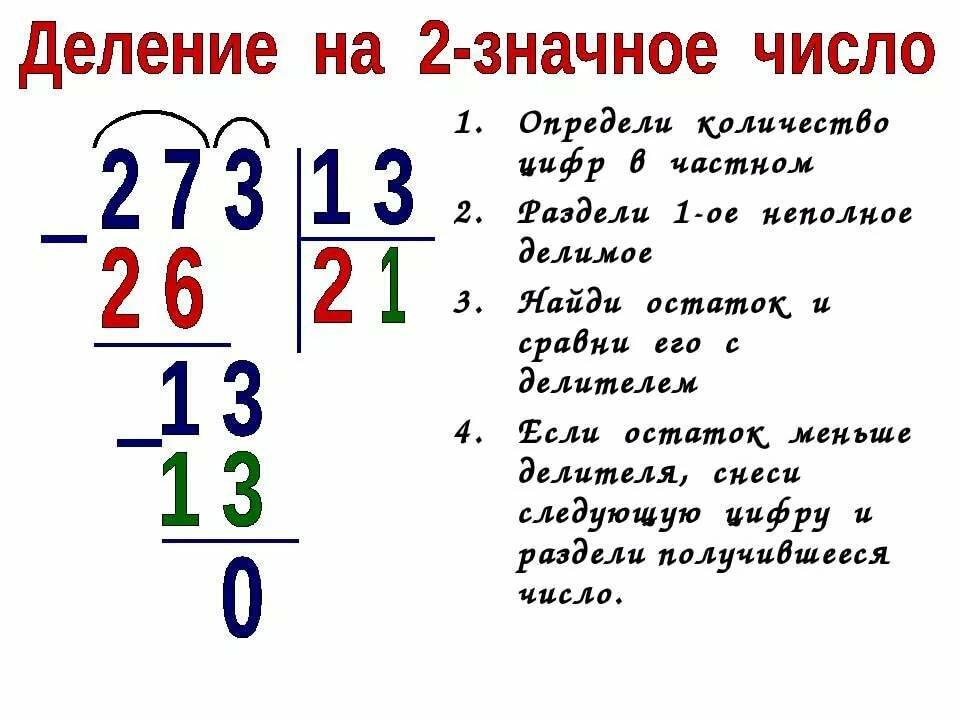
Вычислите, запишите ответ:
355 – 50*7
Реши задачу, запиши ответ:
Ученик решает 10 примеров за 40 минут. Сколько
минут в среднем идёт на решение одного примера?
Запишите номер примера, в котором допущена
ошибка: 1. 96000 : 100 = 960
2. 1250 : 10 = 125
3. 95000 : 1000 = 950
Запишите номер верного утверждения:
Чтобы найти делитель, нужно:
1. Делимое умножить на частное.
2. Делимое разделить на частное.
—
3, 5, 2, 4.
Слайд 5
Чтоб врачом, моряком
Или лётчиком стать,
Надо твёрдо на «5»
Математику знать!
Добро
пожало
вать!
МАТЕМАТИКА
Слайд 6
Частное чисел 350 и 7 увеличь на 20.
Из 800 вычти произведение чисел 30 и 9.
К 50 прибавь частное чисел 36 и 6.
Чему равно 3/5 тонны?
Найди периметр квадрата со стороной 9 см.
Чему равна ширина сада, если его S=54 кв.м, а его
длина 9 м?
70
530
56
600 кг
36 см
6 м
Сколько дм в 240 см?
24 дм
Слайд 7
500 * 6 : 100
4000 * 3 : 100
950 – 720 + 42
140 : 7 * 2
(270 – 50) * 10
Е
Н
Д
И
Л
272
30
2200
30
120
40
30
Д е л е н и е
Слайд 8
Деление числа
на произведение
познакомиться и отработать
приёмы деления числа
на произведение
Слайд 9
Составь задачу и реши её.
12км/ч t=2ч 13км/ч
?
Слайд 10
Слайд 11
Слайд 12
Молодцы!
Спасибо
за урок!
Д/З
№ 90, с. 20
20
Слайд 13
Рефлексия
ВО ВРЕМЯ ПУТЕШЕСТВИЯ БЫЛО ИНТЕРЕСНО И ЛЕГКО, ПОТОМУ ЧТО УМЕЮ БЫСТРО И ПРАВИЛЬНО ВЫЧИСЛЯТЬ, РЕШАТЬ ЗАДАЧИ
ПУТЕШЕСТВИЕ БЫЛО ИНТЕРЕСНОЕ,
НО НЕКОТОРЫЕ ЗАДАНИЯ ВЫЗЫВАЛИ
ЗАТРУДНЕНИЯ
МНЕ БЫЛО СКУЧНО! Я МЕДЛЕННО
СЧИТАЮ, МНЕ ТРУДНО БЫЛО
ВЫПОЛНИТЬ ЗАДАНИЯ.
Поколения компьютеров — история развития вычислительной техники
☰
В короткой истории компьютерной техники выделяют несколько периодов на основе того, какие основные элементы использовались для изготовления компьютера. Временное деление на периоды в определенной степени условно, т.к. когда еще выпускались компьютеры старого поколения, новое поколение начинало набирать обороты.
Можно выделить общие тенденции развития компьютеров:
- Увеличение количества элементов на единицу площади.
- Уменьшение размеров.
- Увеличение скорости работы.
- Снижение стоимости.
- Развитие программных средств, с одной стороны, и упрощение, стандартизация аппаратных – с другой.

Нулевое поколение. Механические вычислители
Предпосылки к появлению компьютера формировались, наверное, с древних времен, однако нередко обзор начинают со счетной машины Блеза Паскаля, которую он сконструировал в 1642 г. Эта машина могла выполнять лишь операции сложения и вычитания. В 70-х годах того же века Готфрид Вильгельм Лейбниц построил машину, умеющую выполнять операции не только сложения и вычитания, но и умножения и деления.
В XIX веке большой вклад в будущее развитие вычислительной техники сделал Чарльз Бэббидж. Его разностная машина, хотя и умела только складывать и вычитать, зато результаты вычислений выдавливались на медной пластине (аналог средств ввода-вывода информации). В дальнейшем описанная Бэббиджем аналитическая машина должна была выполнять все четыре основные математические операции. Аналитическая машина состояла из памяти, вычислительного механизма и устройств ввода-вывода (прямо таки компьютер … только механический), а главное могла выполнять различные алгоритмы (в зависимости от того, какая перфокарта находилась в устройстве ввода). Программы для аналитической машины писала Ада Ловлейс (первый известный программист). На самом деле машина не была реализована в то время из-за технических и финансовых сложностей. Мир отставал от хода мыслей Бэббиджа.
Программы для аналитической машины писала Ада Ловлейс (первый известный программист). На самом деле машина не была реализована в то время из-за технических и финансовых сложностей. Мир отставал от хода мыслей Бэббиджа.
В XX веке автоматические счетные машины конструировали Конрад Зус, Джорж Стибитс, Джон Атанасов. Машина последнего включала, можно сказать, прототип ОЗУ, а также использовала бинарную арифметику. Релейные компьютеры Говарда Айкена: «Марк I» и «Марк II» были схожи по архитектуре с аналитической машиной Бэббиджа.
Первое поколение. Компьютеры на электронных лампах (194х-1955)
Быстродействие: несколько десятков тысяч операций в секунду.
Особенности:
- Поскольку лампы имеют существенные размеры и их тысячи, то машины имели огромные размеры.
- Поскольку ламп много и они имеют свойство перегорать, то часто компьютер простаивал из-за поиска и замены вышедшей из строя лампы.
- Лампы выделяют большое количество тепла, следовательно, вычислительные машины требуют специальные мощные охладительные системы.

Примеры компьютеров:
Колоссус – секретная разработка британского правительства (в разработке принимал участие Алан Тьюринг). Это первый в мире электронный компьютер, хотя и не оказавший влияние на развитие компьютерной техники (из-за своей секретности), но помог победить во Второй мировой войне.
Эниак. Создатели: Джон Моушли и Дж. Преспер Экерт. Вес машины 30 тонн. Минусы: использование десятичной системы счисления; множество переключателей и кабелей.
Эдсак. Достижение: первая машина с программой в памяти.
Whirlwind I. Слова малой длины, работа в реальном времени.
Компьютер 701 (и последующие модели) фирмы IBM. Первый компьютер, лидирующий на рынке в течение 10 лет.
Второе поколение. Компьютеры на транзисторах (1955-1965)
Быстродействие: сотни тысяч операций в секунду.
По сравнению с электронными лампами использование транзисторов позволило уменьшить размеры вычислительной техники, повысить надежность, увеличить скорость работы (до 1 млн.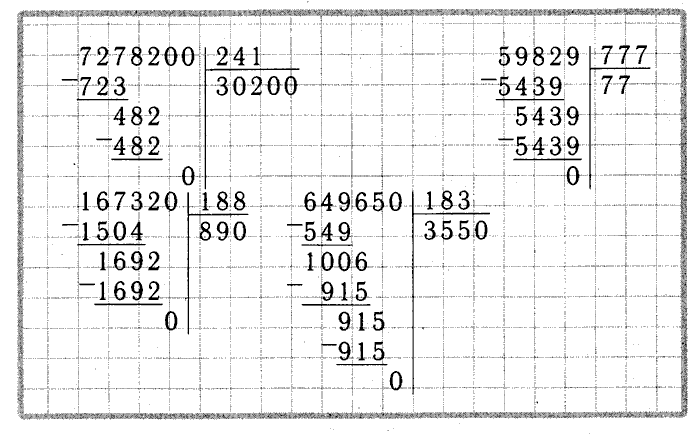 операций в секунду) и почти свести на нет теплоотдачу. Развиваются способы хранения информации: широко используется магнитная лента, позже появляются диски. В этот период была замечена первая компьютерная игра.
операций в секунду) и почти свести на нет теплоотдачу. Развиваются способы хранения информации: широко используется магнитная лента, позже появляются диски. В этот период была замечена первая компьютерная игра.
Первый компьютер на транзисторах TX стал прототипом для компьютеров ветки PDP фирмы DEC, которые можно считать родоначальниками компьютерной промышленности, т.к появилось явление массовой продажи машин. DEC выпускает первый миникомпьютер (размером со шкаф). Зафиксировано появление дисплея.
Фирма IBM также активно трудится, производя уже транзисторные версии своих компьютеров.
Компьютер 6600 фирмы CDC, который разработал Сеймур Крей, имел преимущество над другими компьютерами того времени – это его быстродействие, которое достигалось за счет параллельного выполнения команд.
Третье поколение. Компьютеры на интегральных схемах (1965-1980)
Быстродействие: миллионы операций в секунду.
Интегральная схема представляет собой электронную схему, вытравленную на кремниевом кристалле. На такой схеме умещаются тысячи транзисторов. Следовательно, компьютеры этого поколения были вынуждены стать еще мельче, быстрее и дешевле.
На такой схеме умещаются тысячи транзисторов. Следовательно, компьютеры этого поколения были вынуждены стать еще мельче, быстрее и дешевле.
Последнее свойство позволяло компьютерам проникать в различные сферы деятельности человека. Из-за этого они становились более специализированными (т.е. имелись различные вычислительные машины под различные задачи).
Появилась проблема совместимости выпускаемых моделей (программного обеспечения под них). Впервые большое внимание совместимости уделила компания IBM.
Было реализовано мультипрограммирование (это когда в памяти находится несколько выполняемых программ, что дает эффект экономии ресурсов процессора).
Дальнейшее развитие миникомпьютеров (PDP-11).
Четвертое поколение. Компьютеры на больших (и сверхбольших) интегральных схемах (1980-…)
Быстродействие: сотни миллионов операций в секунду.
Появилась возможность размещать на одном кристалле не одну интегральную схему, а тысячи. Быстродействие компьютеров увеличилось значительно. Компьютеры продолжали дешеветь и теперь их покупали даже отдельные личности, что ознаменовало так называемую эру персональных компьютеров. Но отдельная личность чаще всего не была профессиональным программистом. Следовательно, потребовалось развитие программного обеспечения, чтобы личность могла использовать компьютер в соответствие со своей фантазией.
Компьютеры продолжали дешеветь и теперь их покупали даже отдельные личности, что ознаменовало так называемую эру персональных компьютеров. Но отдельная личность чаще всего не была профессиональным программистом. Следовательно, потребовалось развитие программного обеспечения, чтобы личность могла использовать компьютер в соответствие со своей фантазией.
В конце 70-х – начале 80-х популярностью пользовался компьютера Apple, разработанный Стивом Джобсом и Стивом Возняком. Позднее в массовое производство был запущен персональный компьютер IBM PC на процессоре Intel.
Позднее появились суперскалярные процессоры, способные выполнять множество команд одновременно, а также 64-разрядные компьютеры.
Пятое поколение?
Сюда относят неудавшийся проект Японии (хорошо описан в Википедии). Другие источники относят к пятому поколению вычислительных машин так называемые невидимые компьютеры (микроконтроллеры, встраиваемые в бытовую технику, машины и др. ) или карманные компьютеры.
) или карманные компьютеры.
Также существует мнение, что к пятому поколению следует относить компьютеры с двухядерными процессорами. С этой точки зрения пятое поколение началось примерно с 2005 года.
| Домен | Кластер | Код | Единое ядро ГОСТ |
|---|---|---|---|
| Операции и алгебраическое мышление | Используйте четыре операции с целыми числами для решения проблем. | 4. OA.1 OA.1 | Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 x 7 как утверждение, что 35 в 5 раз больше 7 и 7 раз больше 5. Представьте словесные утверждения мультипликативных сравнений как уравнения умножения. |
| 4.OA.2 | Умножение или деление для решения словесных задач, включающих мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения. | ||
| 4.OA.3 | Решайте многоступенчатые задачи со словами, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление. | ||
Ознакомьтесь с факторами и мультипликаторами.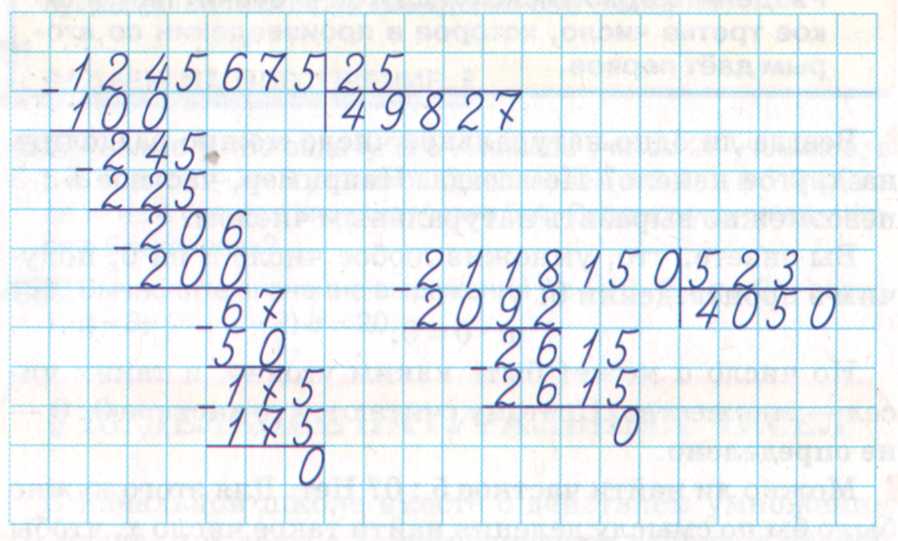 | 4.OA.4 | Найдите все пары факторов для целого числа в диапазоне 1–100. Помните, что целое число является кратным каждому из его факторов. Определите, является ли данное целое число в диапазоне 1–100 кратным заданному однозначному числу. Определите, является ли данное целое число в диапазоне 1–100 простым или составным. | |
| Создание и анализ шаблонов. | 4.OA.5 | Создает рисунок числа или фигуры в соответствии с заданным правилом.Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например: учитывая правило «сложить 3» и начальное число 1, сгенерируйте термины в результирующей последовательности и обратите внимание, что термины кажутся чередующимися между нечетными и четными числами. Неформально объясните, почему числа будут и дальше меняться таким образом. | |
| Число и операции в базе Ten | Обобщить понимание разрядов для многозначных целых чисел. | 4.NBT.1 | Помните, что в многозначном целом числе цифра в одном месте в десять раз больше, чем в месте справа. Например, узнайте, что 700 ÷ 70 = 10, применив концепции числового значения и деления. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.) |
| 4.NBT.2 | Чтение и запись многозначных целых чисел с использованием десятичных цифр, числовых имен и расширенной формы.Сравните два многозначных числа на основе значений цифр в каждом месте, используя>, = и | ||
| 4.NBT.3 | Используйте разметку знаков для округления многозначных целых чисел до любого места. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.) | ||
| Используйте понимание разряда и свойства операций для выполнения многозначной арифметики. | 4.NBT.4 | Свободно вычисляйте и вычитайте многозначные целые числа, используя стандартный алгоритм. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Можно использовать ряд алгоритмов.) (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Можно использовать ряд алгоритмов.) | |
| 4.NBT.5 | Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядах и свойствах операций. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000.Может использоваться ряд алгоритмов.) | ||
| 4.NBT.6 | Найдите целочисленные частные и остатки с дивидендами до четырех цифр и однозначными делителями, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000.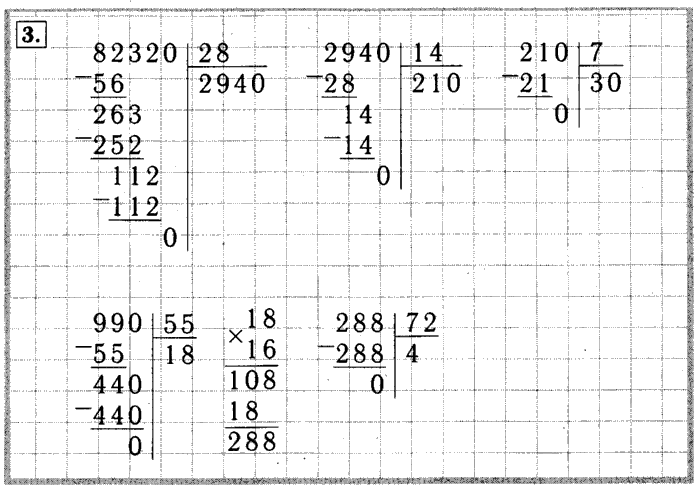 Может использоваться ряд алгоритмов.) Может использоваться ряд алгоритмов.) | ||
| Число и операции: дроби | Расширить понимание эквивалентности дробей и упорядочения. | 4.NF.1 | Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя модели визуальных дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби являются тот же размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.(Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.) |
| 4.NF.2 | Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или | ||
Постройте дроби из дробных единиц, применяя и расширяя предыдущие представления об операциях над целыми числами. | 4.NF.3 | Дробь a / b с a> 1 понимается как сумма дробей 1 / b. а. Под сложением и вычитанием дробей следует понимать соединение и разделение частей, относящихся к одному целому. г. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение по формуле . Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. г. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью, и / или используя свойства операций и взаимосвязь между сложением и вычитанием. г. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели, , например, используя визуальные модели дробей и уравнения для представления проблемы. | |
| 4.NF.4 | Применяйте и расширяйте предыдущие представления об умножении, чтобы умножать дробь на целое число. а. Дробь a / b следует понимать как кратное 1 / b. Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 × (1/4), записав вывод по уравнению 5/4 = 5 × (1/4). г. Поймите, что кратное a / b является кратным 1 / b, и используйте это понимание для умножения дроби на целое число. Например, использует модель визуальной дроби, чтобы выразить 3 × (2/5) как 6 × (1/5), распознавая этот продукт как 6/5. (Как правило, n × (a / b) = (n × a) / b.) c. Решать задачи со словами, связанные с умножением дроби на целое число, например.g., используя модели визуальных фракций и уравнения для представления проблемы. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек , сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ? | ||
| Разберитесь в десятичной системе счисления дробей и сравните десятичные дроби. | 4.NF.5 | Выразите дробь со знаменателем 10 как эквивалентную дробь со знаминателем 100 и используйте этот метод для сложения двух дробей с соответствующими знаменателями 10 и 100. Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. (Учащиеся, которые могут генерировать эквивалентные дроби, могут разработать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями в целом не является обязательным требованием в этом классе.) Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. (Учащиеся, которые могут генерировать эквивалентные дроби, могут разработать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями в целом не является обязательным требованием в этом классе.) | |
| 4.NF.6 | Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите 0,62 как 1 62/100; опишите длину как 0,62 метра; найдите 0.62 на числовой линейной диаграмме. (Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.) | ||
| 4.NF.7 | Сравните два десятичных знака с сотыми, исходя из их размера. Помните, что сравнения сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или | ||
| Измерения и данные | Решает проблемы, связанные с измерением и преобразованием измерений из более крупной единицы в меньшую. | 4.MD.1 | Знать относительные размеры единиц измерения в одной системе единиц, включая км, м, см; кг, г; фунт, унция; л, мл; час, мин, сек. В рамках единой системы измерения выразите измерения в большей единице через меньшую единицу. Запишите эквиваленты измерений в таблицу из двух столбцов. Например: знайте, что 1 фут в 12 раз больше 1 дюйма. Выразите длину 4-футовой змеи как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел (1, 12), (2, 24 ), (3, 36),…. |
| 4.MD.2 | Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкости, массами объектов и деньгами, включая задачи, связанные с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, данных в большей единице, в меньших Блок. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерений. | ||
4. MD.3 MD.3 | Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты с учетом площади пола и длины, просмотрев формулу площади как уравнение умножения с неизвестным коэффициентом. | ||
| Представление и интерпретация данных. | 4.MD.4 | Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8). Решайте задачи, связанные с сложением и вычитанием дробей, используя информацию, представленную на линейных графиках.Например, с помощью линейного графика найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземплярами в коллекции насекомых. | |
| Геометрические измерения — понимание понятий угла и измерения углов. | 4.MD.5 | Распознавать углы как геометрические формы, которые образуются там, где два луча имеют общую конечную точку, и понимать концепции измерения углов: a.  Угол измеряется относительно круга с центром в общем конце лучей, принимая во внимание долю дуги окружности Угол измеряется относительно круга с центром в общем конце лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают круг.Угол, который составляет 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов. г. Угол, который поворачивается на n углов в один градус, называется угловой мерой n градусов. | |
| 4.MD.6 | Измерьте углы в целых градусах с помощью транспортира. Нарисуйте углы указанной меры. | ||
| 4.MD.7 | Распознать угловую меру как добавочную. Когда угол разбивается на неперекрывающиеся части, угловая мера целого является суммой угловых величин частей.Решайте задачи сложения и вычитания, чтобы найти неизвестные углы на диаграмме в реальных и математических задачах, например, используя уравнение с символом для неизвестной угловой меры. | ||
| Геометрия | Нарисуйте и обозначьте линии и углы, а также классифицируйте формы по свойствам их линий и углов. | 4.G.1 | Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах. |
| 4.G.2 | Классифицируют двумерные фигуры на основании наличия или отсутствия параллельных или перпендикулярных линий либо наличия или отсутствия углов заданного размера. Считайте прямоугольные треугольники категорией и определяйте прямоугольные треугольники. | ||
| 4.G.3 | Распознает линию симметрии двумерной фигуры как линию, пересекающую фигуру, так что фигуру можно сложить вдоль этой линии на совпадающие части.Определите линейно-симметричные фигуры и проведите линии симметрии. |
Оценка: 4 — Расчет 2
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для учащихся с трудностями | |
|---|---|
Использование манипуляторов |
|
Модель / Рисование рисунка |
|
Строительные ресурсы |
|
Ежедневное подкрепление |
|
Карты памяти |
|
Взаимодействие с точками соприкосновения | |
Визуальные подсказки |
|
Несколько способов доставки |
|
% PDF-1. 5
%
1599 0 объект
>
эндобдж
xref
1599 72
0000000016 00000 н.
0000003056 00000 н.
0000003183 00000 п.
0000003883 00000 н.
0000004106 00000 п.
0000004315 00000 н.
0000004539 00000 н.
0000004747 00000 н.
0000004984 00000 н.
0000005211 00000 н.
0000005438 00000 н.
0000005650 00000 н.
0000005877 00000 н.
0000006100 00000 н.
0000006307 00000 н.
0000006514 00000 н.
0000006721 00000 н.
0000006913 00000 н.
0000007119 00000 н.
0000007345 00000 н.
0000007555 00000 н.
0000007794 00000 н.
0000008120 00000 н.
0000008446 00000 н.
0000008756 00000 н.
0000009082 00000 н.
0000009290 00000 н.
0000009529 00000 н.
0000009755 00000 н.
0000009965 00000 н.
0000010204 00000 п.
0000010426 00000 п.
0000010632 00000 п.
0000010854 00000 п.
0000011078 00000 п.
0000011304 00000 п.
0000011514 00000 п.
0000011753 00000 п.
0000011979 00000 п.
0000012152 00000 п.
0000012287 00000 п.
0000012460 00000 п.
0000012637 00000 п.
0000012877 00000 п.
0000013111 00000 п.
0000013140 00000 п.
5
%
1599 0 объект
>
эндобдж
xref
1599 72
0000000016 00000 н.
0000003056 00000 н.
0000003183 00000 п.
0000003883 00000 н.
0000004106 00000 п.
0000004315 00000 н.
0000004539 00000 н.
0000004747 00000 н.
0000004984 00000 н.
0000005211 00000 н.
0000005438 00000 н.
0000005650 00000 н.
0000005877 00000 н.
0000006100 00000 н.
0000006307 00000 н.
0000006514 00000 н.
0000006721 00000 н.
0000006913 00000 н.
0000007119 00000 н.
0000007345 00000 н.
0000007555 00000 н.
0000007794 00000 н.
0000008120 00000 н.
0000008446 00000 н.
0000008756 00000 н.
0000009082 00000 н.
0000009290 00000 н.
0000009529 00000 н.
0000009755 00000 н.
0000009965 00000 н.
0000010204 00000 п.
0000010426 00000 п.
0000010632 00000 п.
0000010854 00000 п.
0000011078 00000 п.
0000011304 00000 п.
0000011514 00000 п.
0000011753 00000 п.
0000011979 00000 п.
0000012152 00000 п.
0000012287 00000 п.
0000012460 00000 п.
0000012637 00000 п.
0000012877 00000 п.
0000013111 00000 п.
0000013140 00000 п.
Деление столбиком на двузначное число.
 Видео #
Видео #Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Для начала повторим кратко, как делить столбиком на однозначное число:
А что если деление с остатком? Смотрим в следующем видео:
youtube.com/embed/Tn-W851Arxs» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 768:24. Первое неполное делимое 76
265:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
— Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
— Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
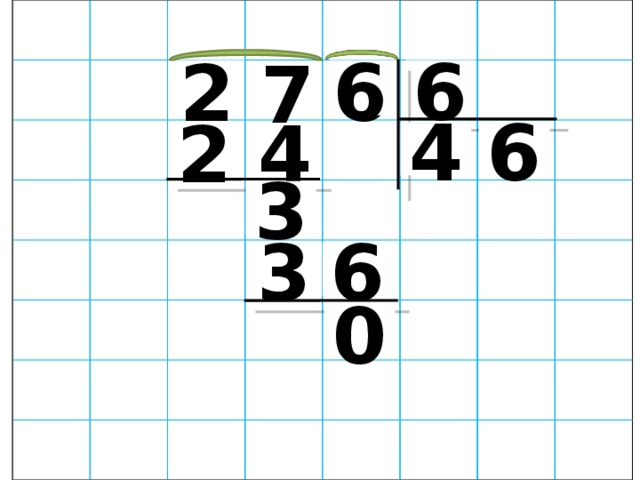
— Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
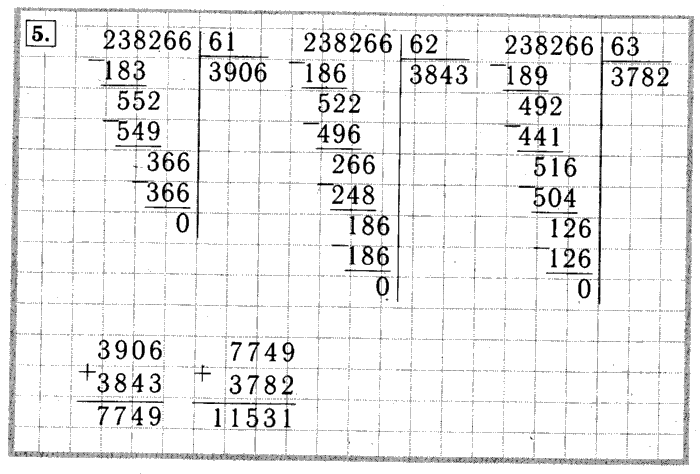
— Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
— Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
— Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428 : 42 30296 : 56 254415 : 35 16514 : 718
2924 : 68 136576 : 64 710278 : 91 15830 : 293
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге. На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0. В итоге отмечаем новое рабочее число — 20.
Важно!Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:
В последний раз повторяем пункты алгоритма 2-4 и получаем:
В самой нижней строчке записываем число 0. Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбикРазделим натуральное число 7136 на натуральное число 9.
Запишем:
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбикРазделим число 7042035 на 7.
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбикРазделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Разделим натуральное число 238079 на 34.
Ответ: 7002
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как объяснить ребенку деление в столбик, или уголком: простой принцип с примерами
Содержание статьи
- Как правильно делить в столбик?
- Что нужно знать ребенку для понимания деления столбиком?
- Методика обучения детей делению столбиком
- Работа с многозначными числами
- Как объяснить деление с остатком?
Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Как правильно делить в столбик?
Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).
Как найти частное двух чисел – 35 и 5?
- Пишем числа, участвующие в делении, так:
Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное.
Под делителем пишется частное. - Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
- Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
- Проверяем правильность действий путем умножения: 7 X 5=35. Все верно, решение выполнено точно.
Что нужно знать ребенку для понимания деления столбиком?
Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:
- отличное знание таблицы умножения;
- умение быстро считать в уме.
В конце 3 класса ученики усваивают, как разделить простые двузначные числа.
При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.
Методика обучения детей делению столбиком
Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.
Проверьте знание таблицы умножения. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).
Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.
Работа с многозначными числами
Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:
Для этого на листке бумаги производим следующие действия:
- Определяем делимое (372) и делитель (6), оформляем запись в уголок:
- Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
- Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
- Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:
- В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
Пример решен, можно проверить правильность путем умножения: 62X6=372.
Как объяснить деление с остатком?
Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:
В группе 8 учеников, на обед им выдали 18 ватрушек на подносе.
Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.
Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).
Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.
youtube.com/embed/fQA2bWiThCY» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>как объяснить ребенку деление в столбик
Деление столбиком (также можно встретить название деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при
делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком
удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида .
Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.Как делить в столбик лучше всего объяснить на примере. Вычислить :
Вычислить :
512:8=?
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения .
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не
стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в
записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.

- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число
получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего,
меньшего разряда и продолжать деление.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288
на однозначное натуральное число 4
. Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288
на однозначное натуральное число 4
, мы видим, что частным является число 35 072
, (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2
, 3
и 4
пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика.
 Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений. - Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Как в столбик делить — один из основных навыков, необходимых для работы с двух- и трёхзначными числами. Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Этот полезный математический навык необходим не только для успешного освоения школьной программы по математике и ряду других предметов. Умение делить наверняка поможет каждому в повседневной жизни.
Часть первая. ДелениеИтак, делимое, то есть число, которое нужно разделить, надо записать слева. Число, на которое делят, называют делителем и записывают справа.
Под делителем проводится черта, под которой пишут частное (решение).
Под делимым необходимо оставить место, требующееся для вычислений.
Сама задача выглядит следующим образом: пакет, где лежат шесть грибов, весит 250 грамм. Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Сейчас предстоит вычислить, сколько целых раз делится первая цифра (отсчёт ведётся с левого конца) делимого на делитель.
Для решения нашей задачи нужно узнать, сколько раз цифра 2 делится на 6. Так как это невозможно, то в ответе — 0, который записывается под делителем. В этом случае нуль является первым числом частного, однако допускается отказ от такой записи.
Теперь предстоит узнать, сколько целых раз делятся две первые цифры делимого на делитель.
Если в предшествующем действии в ответе был получен 0, надо рассмотреть две первые цифры делимого. В рассматриваемой задаче надо вычислить, сколько раз 25 делится на 6.
Если делитель является двух- и более значным числом, надо разделить на него первые три (четыре, пять и т. д.) цифры делимого. Наша цель: получить целое число.
Далее начинается работа с целыми числами. Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Результат, полученный в третьем этапе, записывается прямо под соответствующей цифрой делителя — под чертой. Данный итог будет первой цифрой искомого частного, то есть ответа.
Результат обязательно нужно писать под соответствующей цифрой делителя. Если пренебречь этим требованием, будет допущена ошибка, которая скажется и на конечном результате: он будет неверным.
В рассматриваемом случае 4 записывается под 5, так как на 6 делится число 25, а не 2.
Часть вторая. УмножениеЭтот этап представляет собой переход к новой части работы «как считать в столбик». Деление в данном случае сменятся… умножением.
Делитель умножается на число, которое было под ним записано. Это означает, что речь идёт о первой цифре искомого частного.
Результат этого произведения размещается под делимым.
В рассматриваемом примере 6 х 4 = 24. Число, стоящее в ответе, то есть 24, записывается под 25. Важно: 2 должна стоять под 2, а 4 — под 5.
Результат произведения подчёркивается. В нашем случае речь идёт о подчёркивании числа 24.
Здесь происходит переход к вычитанию и опусканию цифр.
Результат записывается под чертой, которая в свою очередь проводится под числом, поставленным под делимым.
Нам предстоит произвести вычитание 24 из 25. Получаемый при этом результат: 1.
Опускается третья цифра делимого, то есть она записывается рядом с результатом вычитания.
В нашем случае 1 не может делиться на 6. В силу этого спускают третью цифру делимого (третьей цифрой числа 250 является 0). Она размещается рядом с 1. Мы получаем число 10, которое может быть разделено на 6.
Теперь требуется повторить процесс с новым числом.
Для этого полученное число делится на наш делитель, а получаемый при этом результат размещается под делителем, в качестве которого будет выступать вторая цифра частного, то есть нашего ответа.
В решаемом примере 10 делим на 6, что даёт в итоге 1. Единичка записывается в частное — рядом с 4. После этого 6 умножается на 1 и из 10 вычитают результат. У нас должно получиться 4 (остаток).
Если делимое представляет собой двух-, трёх-, четырёх- и более значное число, изложенный процесс повторяется до тех пор, пока не будут опущены все цифры делимого. Пример для иллюстрации: если известно, что вес грибов равен 2 506 г, надо опустить цифру 6, то есть записать её рядом с 4.
Теперь переходим к записи частного с остатком или в виде десятичной дроби.
Наш остаток был равен 4, что связано с тем, что это число — 4 — не делится на 6 и у нас не осталось цифр, которые можно спустить.
Ответ при этом будет выглядеть следующим образом: 41 (ост. 4).
Вычисления на данном этапе могут быть завершены, если в задаче сформулировано требование найти что-то, выражаемое исключительно в целых числах. Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Если есть необходимость в ответе в виде десятичной дроби, можно перейти к следующим действиям алгоритма «как разделить в столбик».
Если нет желания записывать ответ с остатком, можно найти ответ в виде десятичной дроби. При получении остатка, не поддающегося делению на делитель, надо добавить десятичный знак (к частному).
В нашем случае число 250 может быть записано в виде десятичной дроби: 250.000.
Теперь, когда в наличии цифры (только нули), которые могут быть опущены, можно продолжить вычисления. Опускаем нуль и подсчитываем, сколько целых раз можно поделить полученное число на делитель.
В нашем примере после частного 41 (которое размещаем прямо под делителем) пишем десятичную запятую и приписываем 0 к остатку (4). Затем делим полученное число, то есть 40, на делитель (в роли которого выступает 6). Получаем опять 6, которую пишем в частное после десятичного знака. Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
В ряде ситуаций при поиске ответа в виде десятичной дроби приходится столкнуться с повторяющимися числами. Для этого надо прервать вычисления и округлить уже полученный ответ — вниз или вверх.
В частности, в рассматриваемом примере надо отказаться от бесконечного получения цифры 4. Нужно просто прервать вычисления и округлить частное. В силу того, что 6 больше 5, округление производится вверх, в результате чего получается ответ в виде дробного числа 41.67.
Отдел ÷ | Основы арифметики
На этой странице рассматриваются основы деления (÷) .
См. другие наши арифметические страницы для обсуждения и примеров: сложение ( + ), вычитание (-) и умножение ( × ).
Деление
Обычный письменный символ деления (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять вычисления деления. Как только мы хорошо разберемся в методе и правилах, мы сможем использовать калькулятор для более сложных вычислений, не делая ошибок.
Разделение позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте подумаем, как найти ответ на 10 ÷ 2 (десять разделить на два). Это то же самое, что «делить» 10 конфет между двумя детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ 5.
Некоторые краткие правила деления:
При делении 0 на другое число ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 конфет делится поровну между 2 детьми — каждый ребенок получает 0 сладости.
Когда вы делите число на 0, вы вообще не делите (это серьезная проблема в математике).
 2 ÷ 0 невозможно. У вас есть 2 конфеты, но нет детей, чтобы разделить их между собой. На 0 делить нельзя.
2 ÷ 0 невозможно. У вас есть 2 конфеты, но нет детей, чтобы разделить их между собой. На 0 делить нельзя.При делении на 1 ответ совпадает с числом, которое вы делили. 2 ÷ 1 = 2. Две конфеты разделить на одного ребенка.
При делении на 2 число уменьшается пополам. 2 ÷ 2 = 1.
Любое число, деленное на одно и то же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет разделить на двадцать детей — каждый ребенок получает по одной конфете.
Числа должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять конфет, разделенных на двоих детей, сильно отличаются от 2 конфет, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ равно 1 ÷ 2. Одна конфета делится на двоих детей. См. нашу страницу Фракции для получения дополнительной информации.
Множественные вычитания
Точно так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.
Например:
Если у Джона в машине 10 галлонов топлива, и он использует 2 галлона в день, сколько дней до того, как у него закончится топливо?
Мы можем решить эту задачу, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.
- В день 1 Джон начинает с 10 галлона и заканчивает 8 галлона. 10 — 2 = 8
- В день 2 Джон начинает с 8 галлона и заканчивает 6 галлона. 8 — 2 = 6
- В день 3 Джон начинает с 6 галлона и заканчивает 4 галлона. 6 — 2 = 4
- В день 4 Джон начинает с 4 галлона и заканчивает 2 галлона. 4 — 2 = 2
- В день 5 Джон начинает с 2 галлона и заканчивает 0 галлонов.
 2 — 2 = 0
2 — 2 = 0
У Джона закончилось топливо на 5-й день.
Более быстрый способ выполнить это вычисление — разделить 10 на 2. То есть, сколько раз 2 делится на 10 или сколько партий по два галлона имеется в десять галлонов? 10 ÷ 2 = 5,
Таблица умножения (см. умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (красный заштрихованный заголовок). Двигайтесь вниз по столбцу, пока не найдете нужный номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (красный заштрихованный заголовок) 5 .
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Мы можем выполнить другие простые вычисления деления, используя тот же метод. 56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки 8 .
56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки 8 .
Если возможно, вы должны попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет выполнение простых вычислений на умножение и деление.
Деление больших чисел
Вы можете использовать калькулятор для выполнения вычислений с делением, особенно когда вы делите большие числа, которые труднее вычислить в уме. Однако важно понимать, как выполнять вычисления деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также необходимо, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может показаться пугающим, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и со всей математикой, проще всего это понять, если мы рассмотрим пример:
Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине плюс запаску.
Ему нужно заменить все четыре шины на машине плюс запаску.
Дэйв получил предложение от местного гаража на 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 будет входить в 480?
Условно запишем так:
| 5 | 4 | 8 | 0 |
Работаем слева направо в логической системе.
Начнем с деления 4 на 5 и сразу наткнемся на проблему. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 входит в 4?».
Мы знаем, что 2 дважды входит в число 4 (4 ÷ 2 = 2), и мы знаем, что 1 входит в число 4 четыре раза (4 ÷ 1 = 4), но 5 не входит в число 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно входить в число, на которое мы делим (в данном случае 4), целое число раз. Как вы увидите, это не обязательно должно быть точное целое число.
Как вы увидите, это не обязательно должно быть точное целое число.
Так как 5 не входит в 4, мы ставим 0 в первую колонку (сотни). Для получения справки о столбцах сотен, десятков и единиц см. нашу страницу о числах .
| Сотни | Десятки | Единицы | |
| 0 | |||
| 5 | 4 | 8 | 0 |
Далее мы двигаемся вправо, чтобы включить столбец десятков. Теперь мы можем увидеть, сколько раз 5 входит в число 48.
5 входит в число 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно входит в число 48.
Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 число, которое мы ищем, находится между этими двумя значениями. Помните, нас интересует 90 508 – целое число, умноженное на 90 509, которое 5 входит в число 48. Десять раз – это слишком много.
Десять раз – это слишком много.
Мы видим, что 5 входит в число 48 целое число (9) раз, но не точно, с оставшимися 3.
9 × 5 = 45
48 – 45 = 3
Теперь мы можем сказать, что 5 входит в число 48 девять раз, но с остатком 3. нашли из числа, на которое мы делим: 48 — 45 = 3 .
Таким образом, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбце десятков в качестве ответа для второй части вычисления и поставить наш остаток перед нашим последним числом в единицах измерения. столбец. Наше последнее число становится 30.
| Сотни | Десятки | Единицы | |
| 0 | 9 | ||
| 5 | 4 | 8 | 30 |
Теперь разделим 30 на 5 (или узнаем, сколько раз 5 входит в 30). Используя нашу таблицу умножения, мы видим, что ответ равен ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
| Сотни | Десятки | Единицы | |
| 0 | 9 | 6 | |
| 5 | 4 | 8 | 30 |
Поскольку остатка нет, мы закончили расчет и получили ответ 96 .
Новые шины Дейва будут стоить £96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Раздел рецептов
Наш последний пример разделения основан на рецепте. Часто при приготовлении пищи рецепты сообщают вам, сколько еды они собираются приготовить, например, достаточно, чтобы накормить 6 человек.
Ингредиенты, указанные ниже, необходимы для приготовления 24 волшебных тортов, однако нам нужно сделать только 8 волшебных тортов. Мы немного изменили ингредиенты для этого примера (оригинальный рецепт: BBC Food).
Первое, что нам нужно установить, это сколько восьмерок в числе 24. Воспользуйтесь таблицей умножения выше или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Поэтому нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 сказочных пирожных.
Воспользуйтесь таблицей умножения выше или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Поэтому нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 сказочных пирожных.
Ингредиенты
- 120 г сливочного масла, размягченного при комнатной температуре
- 120 г сахарной пудры
- 3 куриных яйца, слегка взбитых
- 1 чайная ложка ванильного экстракта
- 120 г самоподнимающейся муки
- 1-2 столовые ложки молока
Количество масла, сахара и муки одинаковое, 120г. Следовательно, необходимо вычислить 120 ÷ 3 только один раз, так как ответ будет одинаковым для этих трех ингредиентов.
| 3 | 1 | 2 | 0 |
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, так как 3 больше 1. Далее мы смотрим, сколько раз 3 входит в 12. Используя таблицу умножения, если нужно, мы можем увидеть, что 3 входит в число 12 ровно 4 раза по без остатка.
Используя таблицу умножения, если нужно, мы можем увидеть, что 3 входит в число 12 ровно 4 раза по без остатка.
| 0 | 4 | 0 | |
| 3 | 1 | 2 | 0 |
120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г сливочного масла, сахара и муки.
В исходном рецепте указано 3 яйца, и мы снова делим на 3. Таким образом, 3 ÷ 3 = 1, значит, нужно одно яйцо.
Далее по рецепту требуется 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 — это то же самое, что ⅓ (одна треть). Вам понадобится ⅓ чайной ложки ванильного экстракта, хотя на самом деле может быть сложно точно отмерить ⅓ чайной ложки!
Оценка может быть полезна, и единицы измерения можно изменить!
Мы можем посмотреть на это по-другому, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам. (Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3) с 2 в остатке. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!
(Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3) с 2 в остатке. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!
Мы можем оценить ответ, чтобы убедиться, что мы правы. Три партии по 1,5 мл дают нам 4,5 мл. Таким образом, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшая оценка может быть забавой и хорошей практикой для нашей ментальной арифметики.
Далее по рецепту требуется 1–2 ст.л. молока. Это от 1 до 2 столовых ложек молока. У нас нет определенного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.
Мы уже знаем, что 1 ÷ 3 равно ⅓, а 2 ÷ 3 равно ⅔. Таким образом, нам понадобится ⅓–⅔ столовой ложки молока, чтобы приготовить восемь волшебных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому ⅓–⅔ столовой ложки соответствует 5–10 мл, то есть 1–2 чайным ложкам!
Дополнительная литература по навыкам, которые вам нужны
Основы счета
Часть руководства по навыкам, которые вам необходимы для счета
операции и начать манипулировать числами. Он также включает примеры из реальной жизни, чтобы прояснить, как эти концепции полезны в реальной жизни.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Объяснение короткого и длинного деления
Мы работали с экспертами по начальной математике, чтобы создать руководство для родителей по короткому делению (включая метод автобусной остановки) и страшному длинному делению.
Здесь мы объяснили все, что вам нужно знать, чтобы помочь вашему ребенку разобраться с этими сложными темами!
Неважно, короткое это деление или длинное, у многих детей и их родителей простое упоминание о работе на букву «Д» может вызвать мурашки по спине у многих юных математиков, но в этом нет необходимости. быть дело!
Здесь, в Third Space Learning, мы стремимся сделать математику доступной для всех, включая деление на короткое и длинное деление… задача по математике), поэтому неудивительно, что многие из нас, родителей, до сих пор испытывают трудности.
В настоящее время, когда дети проводят много времени в школе, понимая, как работает деление , а не просто запоминая метод, страх перед делением KS2 тает, но подведение итогов и помощь ребенку в выполнении деления дома поможет большая разница
Но прежде чем вы узнаете все, что вам нужно знать о дивизионах для детей, мы подготовили для вас краткий обзор дивизий!
Этот блог является частью нашей серии блогов, предназначенных для учителей, школ и родителей, поддерживающих домашнее обучение.
Рабочие листы на деление в длинное число для 3-6 классов
Этот БЕСПЛАТНЫЙ ресурс содержит 3 готовых к использованию рабочих листа для вашего класса, которые помогут им со всеми аспектами деления в длинное число, от однозначных чисел до вычисления кратных!
Кратко о методах деления
Мы знаем, как чертовски сложно деление может быть как для вас, так и для вашего ребенка, поэтому давайте начнем с некоторых определений и резюме того, что вы, возможно, забыли со школы.
Что такое деление в математике?Деление — это операция, обратная умножению и заключающаяся в разделении на равные части или группы.
В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Их:
- Разбиение на фрагменты
- Короткое деление (также известное как метод автобусной остановки)
- Длинное деление
Разбиение на части — это метод, используемый для деления больших чисел, которые невозможно разделить в уме.
При использовании метода фрагментации дети будут многократно вычитать делитель из делимого, пока не будет получен ответ. Например, 12 ÷ 3 можно решить, выполнив 12–3, чтобы получить 9, 9–3, чтобы получить 6, 6–3, чтобы получить 3, а затем 3–3, чтобы получить 0,9.0005
Когда все 3 вычитаются из 12, подсчитываются (4), становится ясно, что ответ равен 4.
Что такое короткое деление?Короткое деление — это быстрый и эффективный метод деления больших чисел.
После того, как ваш ребенок освоится с делением на фрагменты, он перейдет к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым, выполнив ряд простых шагов.
Например:
В этом примере четыре дважды превращается в девять, а в остатке остается единица.
Этот остаток затем передается следующему числу (шесть), чтобы получилось 16. Четыре входит в число 16 четыре раза, так что при суммировании получается 24.
Что такое метод автобусной остановки?
Метод деления на автобусной остановке — это еще одно название для краткого деления. Он получил свое название от идеи, что делимое (число, которое вы хотите разделить) находится внутри автобусной остановки, а делитель ждет снаружи.
Он получил свое название от идеи, что делимое (число, которое вы хотите разделить) находится внутри автобусной остановки, а делитель ждет снаружи.
Учителя расходятся во мнениях относительно того, действительно ли это изображение полезно при изучении деления, поэтому в большинстве случаев мы просто будем называть его коротким делением.
Что такое длинное деление?Длинное деление — это метод, используемый при делении большого числа (обычно трех или более цифр) на двузначное (или большее) число. Он изложен аналогично методу автобусной остановки, который используется для короткого деления.
Взгляните на наш пример ниже, чтобы увидеть, как длинное деление объясняется в наглядном примере.
Лучше всего это объяснить на примере – см. ниже.
У нас есть очень подробная статья, написанная для учителей на эту тему, которая может вам понравиться, если вы хотите более подробно изучить метод деления в KS2.
Терминология, которую необходимо знать при обучении разделу
В наших родительских блогах мы стараемся избегать слишком большого количества жаргона, но следующие три термина действительно важны для всех, кто изучает раздел.
- Дивиденд — это число, которое вы делите (число внутри «автобусной остановки»
- Делитель — это число, на которое вы делите.
- Частное — это сумма, которую получает каждый делитель, то есть ответ в большинстве случаев.
Хороший способ запомнить это делимое ÷ делитель = частное
Части задачи на деление, помеченные для детей и родителейИзучив правильный словарь всех частей задачи на деление, ваш ребенок найдете много элементов деления намного проще.0005
Что нужно знать моему ребенку о коротком и длинном делении в KS1 и KS2?
В связи с тем, что дети меняются из года в год на протяжении всей начальной школы, в кратком и длинном делениях в блоге есть что рассказать, но чтобы помочь вам, мы разбили его по годам.
Разделение 1-го года : как вы можете помочь В 1-м году деление обычно называется разделением и осуществляется с помощью конкретных предметов, таких как прилавки, блоки или даже продуктов питания, таких как макароны.
Это помогает детям понять разделение как разделение между группами.
Простой пример этого можно найти ниже.
Несколько простых задачек на деление для 1-го классаВозьмите набор кубиков и помогите ребенку решить эти задачки на деление.
Убедитесь, что вы не забыли использовать такие слова, как разделить и разделить , чтобы ваш ребенок познакомился с понятиями.
Начните с 4 блоков. Разделите их на 2 группы одинакового размера.
Начните с 10 блоков. Разделите их на 2 группы одинакового размера.
Начните с 6 блоков. Разделите их на 3 группы одинакового размера.
Дивизия 2-й класс : как вы можете помочьВо 2-м классе дети начинают более глубоко понимать, как работает деление, а это означает, что вашему ребенку предстоит еще кое-чему научиться.
Ключевая концепция, которую нужно понять и освоить в этом возрасте, — 9 лет. 0709 коммутативность .
0709 коммутативность .
Если вы изо всех сил пытаетесь вспомнить, что именно означает коммутативность, определение простое.
В математике свойство коммутативности утверждает, что порядок не имеет значения.
Умножение коммутативное ; вы можете поменять местами числа, и это не имеет значения.
2 x 3 = 6
3 x 2 = 6
Деление не коммутативное . Если вы поменяете порядок чисел, это изменит ответ.
4 ÷ 2 = 2
2 ÷ 4 = 0,5
Деление и коммутативность во 2-м классе
В этом возрасте хорошо практиковаться в изучении таблиц умножения на 2, 5 и 10 с соответствующими фактами деления. Например:
Факт умножения:
2 x 5 = 10
Соответствующие факты деления:
10 ÷ 5 = 2
10 ÷ 2 = 5
отличный пример того, почему коммутативность важна.
Если вашего ребенка устраивает разница между 10 ÷ 5 и 10 ÷ 2, даже после того, как он увидит, что 5 x 2 равно 2 x 5, он будет лучше подготовлен для комфортного перехода к короткому дивизиону KS2 и длинному KS2. разделение.
разделение.
В 3-м классе ваш ребенок сосредоточится на записи вычислений деления и решении простых задач на деление, связанных с пропущенными числами.
Здесь очень пригодятся знания об умножении и делении, поэтому, как и в случае со 2-м классом, очень важно практиковать их со своим ребенком.
Эта проблема пропущенных чисел поможет вам понять, почему знание таблицы умножения значительно упрощает деление:
5 x 4 = 20
__ ÷ 5 = 4
20 ÷ __ = 5
Также есть два письменных метода деления, которые вводятся в этом возрасте, и они разбиты ниже.
Письменные методы деления для детей
Объяснение метода деления на фрагменты
Хотя этот метод немного медленнее, чем деление на автобусной остановке, он отлично подходит для развития умственных навыков, необходимых детям для более сложного деления в дальнейшем.
Как выполнить разбиение на части метод деления Разбиение на части — это когда вы определяете, сколько раз одно число входит в другое число.
Вы вычисляете это, многократно вычитая делитель (или кратные делителю), пока не доберетесь до нуля, чтобы увидеть, сколько раз делитель может войти в число, которое вы делите (делимое).
Разделение на фрагменты — это хороший способ познакомить вашего ребенка с некоторыми из основных понятий деления, и как только они с этим смирятся, они смогут перейти к методу краткого деления.
Объяснение метода короткого деления или метода деления на автобусной остановкеЧасто упоминается как метод деления на автобусной остановке из-за того, что расчет на листе бумаги имеет некоторое визуальное сходство с автобусной остановкой, этот метод короткого деления KS2 является одним из самых популярных методов, которым обучают в школах.
Этот метод быстрее, чем фрагментация, но важно, чтобы дети понимали, что они делают (а не просто следовали методу).
Это значительно облегчит деление на части в будущем, но рекомендуется убедиться, что ваш ребенок научился разделять на фрагменты, прежде чем переходить к делению на короткие.
В этом возрасте краткое деление будет включать однозначные делители и 3- или 4-значные дивиденды.
Слайд из третьего урока Space Learning 1-to-1, на котором ученики шаг за шагом проходят короткие деления.Сядьте вместе с ребенком и посмотрите на схему ниже, чтобы узнать названия и места для каждой части задачи на деление.
Они могут выглядеть очень незнакомыми, когда вы привыкли выписывать свои суммы в строку, поэтому поработайте с ребенком, чтобы убедиться, что он знает свой делитель по делимому!
Как помочь вашему ребенку разделить трех- или четырехзначное число на однозначное числоПоскольку эти типы вопросов на деление составляют большинство вопросов, которые ваш ребенок будет решать в 3-м классе, вот рисунок, подробно описывающий, как разделить трех- или четырехзначное число на однозначное число.
Деление 4-й класс : как вы можете помочь В 4-м классе ваш ребенок будет использовать краткое деление (метод деления на автобусной остановке, описанный выше), чтобы делить числа до четырех цифр на двузначные числа.
Метод точно такой же, как и с однозначными цифрами, за исключением того, что первый шаг всегда будет включать группировку.
На этом этапе процесс деления становится гораздо более трудным, если ваш ребенок не знает наизусть таблицу умножения, поэтому лучшее, что вы можете сделать для него, — это помочь ему выучить ее.
Им также нужно будет выбрать, какой остаток использовать в зависимости от вопроса, а некоторые распространенные вопросы будут связаны с реальными ситуациями, например, с разделением групп между автомобилями или предметами между ящиками.
Вопросы на деление с остаткомОстаток может быть сложной концепцией для понимания, когда дети впервые знакомятся как с коротким, так и с длинным делением, но важно, чтобы ваш ребенок хорошо их понимал, поскольку они могут радикально измениться в зависимости от вопроса, который спрашивают.
Попрактикуйтесь в использовании пар множителей в 4 классе, чтобы облегчить письменное деление Пары множителей — это два множителя (числа), которые при умножении вместе дают определенный продукт (результат).
Упражнения с парами факторов могут помочь вашему ребенку ускорить процесс деления, так как знание того, что 4 x 5 = 20, поможет ему в вычислении 20 ÷ 4 = _ .
Попросите вашего ребенка найти как можно больше пар множителей для приведенного ниже числа, и почему бы не превратить это в игру?
Сядьте вместе со своим ребенком, возьмите ручку и лист бумаги и посмотрите, кто сможет вычислить наибольшее количество пар множителей для следующих чисел за минуту. Результаты могут быть ближе, чем вы думаете!
- 20
- 68
- 12
- 30
- 100
Подробнее: Какой самый высокий общий фактор
Дивизион Год 5 : Как вы можете помочь 9006 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9006. должен уметь быстро мысленно уменьшать сумму вдвое или вчетверо. Если им трудно, внедрение математики в реальный мир может стать отличным способом помочь им справиться с половинками и четвертинками. Например, когда вы находитесь вне дома, спросите их, сколько бы стоил предмет, если бы он был наполовину дешевле, или сколько граммов было бы в половине 1-килограммового мешка сахара.
Например, когда вы находитесь вне дома, спросите их, сколько бы стоил предмет, если бы он был наполовину дешевле, или сколько граммов было бы в половине 1-килограммового мешка сахара.
Умение быстро делить на 2 (деление пополам) и 4 (четвертование) станет важной частью деления по мере того, как ваш ребенок будет учиться в школе, поэтому будет очень полезно, если он сможет научиться этому прямо сейчас.
Сокращенное деление с десятичными знакамиСокращенное деление будет использоваться для чисел, содержащих десятичные дроби, впервые в 5-м классе.
Это означает, что самое время пересмотреть разрядность, чтобы ваш ребенок понял, как работают десятичные дроби.
Десятичные числа являются частями целого (аналогично дробям), но при делении десятичных дробей важно помнить, что столбцы разрядных значений уменьшаются в значении каждый раз, когда вы перемещаетесь вправо.
Пример деления с десятичными дробями Деление 6-й класс: как вы можете помочьВ 6-м классе ваш ребенок впервые познакомится со страшным делением на длинные числа!
Однако хорошая новость заключается в том, что как только вы освоите деление на фрагменты и короткое деление, длинное деление совсем не так уж плохо!
Ключевым моментом, когда дело доходит до деления в длину для детей, является не торопиться и поощрять их аккуратно представлять свою работу, чтобы они могли легко замечать ошибки и работать над их исправлением.
Даже зная об этом, деление в длинное число все еще может быть пугающей перспективой для детей (и родителей!), поэтому взгляните на наш пример ниже, чтобы понять, как решить задачу деления в длинное число.
Объяснение деления в длинное деление для детейВ приведенном ниже примере показан самый популярный метод деления в длинное деление для детей, а также тот, с которым вы, возможно, знакомы еще со времен начальной школы.
Все, что вам нужно для завершения вычисления 528 ÷ 24, это ручка, немного бумаги и ребенок, который хочет освоить этот метод!
После того, как вы попробуете ответить на несколько вопросов на деление на длинное деление (с вашей помощью для начала), ваш ребенок вскоре увидит, что этот метод может помочь ему понять, как решать задачи на деление на длинное, независимо от задействованных чисел, и окажется неоценимым. когда дело доходит до SAT.
Как выполнить деление в длину: простой пошаговый метод деления в длину, который можно использовать в KS2 Не беспокойтесь, если для полного внедрения процесса потребуется некоторое время. Это длинная цепочка вещей, которые нужно запомнить, поэтому потребуется регулярная практика, чтобы запомнить этот метод.
Это длинная цепочка вещей, которые нужно запомнить, поэтому потребуется регулярная практика, чтобы запомнить этот метод.
Просто запомните процесс: делить, умножать, вычитать, сводить; и повторить.
Тяжелая работа окупится в долгосрочной перспективе, поэтому стоит уделить время вашему ребенку сейчас, чтобы убедиться, что деление в столбик хорошо объяснено на раннем этапе, чтобы уменьшить количество раз, когда вы услышите неизбежное:
Откуда мы знаем, когда делить и какой метод использовать?» Мммммм…….Как ты делаешь деление в длинное…?»
Различные вопросы на деление требуют разных методов деления для их решения, но вот краткое и простое руководство, которое покажет, какой метод и когда должен использовать ваш ребенок:
- Разбиение лучше всего подходит для небольших чисел и арифметических операций.
- Сокращенное деление отлично подходит для деления больших чисел на однозначные числа.

- Длинное деление удобно для деления больших чисел на числа, состоящие из 2 и более цифр.
Конечно, могут быть случаи, когда каждый из вышеперечисленных методов можно использовать в немного разных сценариях, но, как правило, этого должно быть достаточно, чтобы помочь вашему ребенку принять правильное решение.
6-й класс SATs раздел вопросыКогда придет время сдавать экзамены SAT по математике, более чем вероятно, что вашему ребенку придется отвечать на некоторые вопросы, связанные с разделением.
Решение задач и рассуждения (бумаги 2 и 3) в 6-м классе могут быть сложными, когда речь идет о задачах на деление. Часто задачи требуют решения более чем одной операции, что может усложнить и без того напряженную обстановку, поэтому поощряйте ребенка обращать внимание на такие слова, как поделиться или , группа , чтобы помочь им определить, что необходимо сделать для решения проблемы.
Задачи на деление в задании 1 (арифметика) будут представлены в виде числовых предложений, и ваш ребенок должен будет продемонстрировать свое решение, если вопрос оценивается более чем в 1 балл.
Эти вопросы легко определить, потому что они будут использовать символы деления:
÷
или
, или они могут включать дроби.
Как правило, поощряйте ребенка к мысленному разделению, когда это возможно.
Хотя письменные методы отлично подходят для больших чисел, возможность мысленного деления даст им преимущество. Это означает, что когда они выполнят письменный метод, они смогут увидеть, является ли их ответ примерно правильным, путем оценки.
Наряду с бесплатными таблицами деления на деление вы также можете загрузить набор бесплатных вопросов SAT по делению и умножению, чтобы расширить свою практику.
Это должно было охватывать все, что вам нужно знать о делении для детей. Если вам нужны дополнительные способы помочь с домашним заданием по математике, мы рекомендуем вам также ознакомиться со следующими руководствами для родителей и детей.
- Дроби для детей: как помочь дома
- Как выучить таблицу умножения дома
- Словесные задачи с примерами
- Правила кратности
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и занятия по математике для тысяч учащихся начальных классов. С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.Обучение математике для детей от 5 до 12 лет, ориентированное на общегосударственную учебную программу и проводимое в режиме онлайн
как объяснить ребенку деление в столбик
Деление в столбик или, правильнее, письменный метод деления на угол , школьники уже в третьем классе начальной школы, но часто этой теме уделяется так мало внимания, что не все ученики могут свободно ею пользоваться к 9-11 классам. Деление столбиком на двузначное число имеет место в 4 классе, как и деление на трехзначное число, и далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, уделяя делению столбиком больше внимания, чем это заложено в школьной программе, ребенок облегчит себе выполнение задач по математике до 11 класса.
 А для этого нужно немногое — понять тему и отрабатывайте, решайте, держа алгоритм в голове, доводите навык счета до автоматизма.
А для этого нужно немногое — понять тему и отрабатывайте, решайте, держа алгоритм в голове, доводите навык счета до автоматизма.Алгоритм деления столбиком двузначного числа
Как и при делении на одну цифру, мы будем последовательно переходить от деления более крупных единиц счета к делению более мелких единиц.
1. Найдите первое неполное делимое . Это число, которое делится на делитель, чтобы получить число больше или равное 1. Это означает, что первое частично делимое всегда больше делителя. При делении на двузначное число первая неполная делимая имеет не менее 2 цифр.
Примеры 76 8:24. Первое неполное делимое 76
265:53 26 меньше 53, поэтому оно не подходит. Вам нужно добавить следующее число (5). Первый неполный дивиденд равен 265,9.00052. Определить количество цифр в частном . Для определения количества цифр в рядовом следует помнить, что одна цифра рядового соответствует неполному делимому, а еще одна цифра рядового соответствует всем остальным цифрам делимого.

Примеры 768:24. Первое неполное делимое равно 76. Оно соответствует 1 частному разряду. После первого частичного делителя следует еще одна цифра. Таким образом, в частном будет только 2 цифры.
265:53. Первое неполное делимое равно 265. Это даст 1 цифру частного. В делимом больше нет чисел. Таким образом, в частном будет только 1 цифра.
15344:56. Первое неполное делимое равно 153, а после него еще 2 цифры. Таким образом, в частном будет только 3 цифры.3. Найдите числа в каждой цифре частного . Сначала найдите первую цифру частного. Подбираем такое целое число, чтобы при умножении на наш делитель получилось число, максимально близкое к первой неполной делимой. Под уголком пишем частное число, а из неполного делителя вычитаем значение произведения в столбик. Записываем остальное. Проверяем, что он меньше делителя.
Затем находим вторую цифру привата. Перепишем в строку с остатком число, следующее за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее частное число, пока не закончатся цифры делителя.

4. Найдите остаток (если есть).
Если цифры частного закончились, а остаток равен 0, то деление производится без остатка. В противном случае значение частного записывается с остатком.
Также выполняется деление на любое многозначное число (трехзначное, четырехзначное и т.д.).
Разбор примеров деления столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда частное — однозначное число.
Найдем значение частных чисел 265 и 53.
Первое неполное делимое равно 265. В делимом больше нет чисел. Таким образом, частное будет однозначным числом.
Чтобы было проще подобрать приватный номер, делим 265 не на 53, а на близкое круглое число 50. Для этого делим 265 на 10, будет 26 (остаток 5). А 26 разделить на 5 будет 5 (остаток 1). Число 5 нельзя сразу писать в приват, так как это пробное число. Сначала нужно проверить, подходит ли он. Умножьте 53*5=265. Мы видим, что выпало число 5.
 И теперь мы можем записать это в личном уголке. 265-265=0. Деление производится без остатка.
И теперь мы можем записать это в личном уголке. 265-265=0. Деление производится без остатка.Значение частных чисел 265 и 53 равно 5.
Иногда при делении не подходит пробная цифра частного, и тогда ее нужно изменить.
Найдем значение частных чисел 184 и 23.
Частное будет однозначным.
Чтобы было проще подобрать приватный номер, делим 184 не на 23, а на 20. Для этого делим 184 на 10, будет 18 (остаток 4). И делим 18 на 2, будет 9. 9 — пробный номер, сразу в приват писать не будем, но проверим, подходит ли. Умножьте 23*9=207. 207 больше 184. Мы видим, что число 9 не подходит. В привате будет меньше 9. Попробуем, подходит ли цифра 8. Умножаем 23*8=184. Видим, что цифра 8 подходит. Мы можем записать это в частном порядке. 184-184=0. Деление производится без остатка.
Значение частных чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдите значение личных чисел 768 и 24.

Первое неполное делимое 76 десятков. Значит, в частном будет 2 цифры.
Определим первую цифру частного. Делим 76 на 24. Чтобы легче было найти приватный номер, делим 76 не на 24, а на 20. То есть 76 нужно разделить на 10, будет 7 (остаток 6). Разделите 7 на 2, чтобы получить 3 (остаток 1). 3 — пробная цифра частного. Давайте сначала проверим, подходит ли он. Умножьте 24*3=72. 76-72=4. Остаток меньше делителя. Это значит, что выпало число 3 и теперь мы можем записать его вместо десятков частных. 72 пишем под первой неполной делимой, между ними ставим знак минус, остаток пишем под чертой.
Продолжим деление. Перепишем число 8 в строке с остатком, следующим за первой неполной делимой. Получаем следующее неполное делимое – 48 единиц. Делим 48 на 24. Чтобы было проще подобрать приватный номер, делим 48 не на 24, а на 20. То есть 48 делим на 10, будет 4 (осталось 8). А 4 разделить на 2 будет 2. Это пробная цифра рядового. Мы должны сначала проверить, подойдет ли он.
 Умножьте 24*2=48. Мы видим, что выпало число 2 и, следовательно, мы можем записать его вместо единиц частного. 48-48=0, деление производится без остатка.
Умножьте 24*2=48. Мы видим, что выпало число 2 и, следовательно, мы можем записать его вместо единиц частного. 48-48=0, деление производится без остатка.Значение частных номеров 768 и 24 равно 32.
Найдите значение частных номеров 15344 и 56.
Первое неполное делимое равно 153 сотни, а значит в частном будет три цифры.
Определим первую цифру частного. Делим 153 на 56. Чтобы легче было найти приватный номер, делим 153 не на 56, а на 50. Для этого делим 153 на 10, будет 15 (остаток 3). А 15 разделить на 5 будет 3. 3 — пробная цифра частного. Помните: вы не можете сразу написать его в приват, но вы должны сначала проверить, подходит ли он. Умножьте 56*3=168. 168 больше 153. Значит, в частном будет меньше 3. Проверим, подходит ли число 2. Умножьте 56*2=112. 153-112=41. Остаток меньше делителя, значит, подходит число 2, его можно записать вместо сотен в частном.
Формируем следующий неполный дивиденд.
 153-112=41. Перепишем цифру 4 в той же строке, следующей за первой неполной делимой. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы было удобнее выбирать число частного, 414 будем делить не на 56, а на 50. 414:10=41(осталось 4). 41:5=8(ост.1). Помните: 8 — пробное число. Давайте проверим это. 56*8=448. 448 больше 414, значит, в частном будет меньше 8. Проверим, подходит ли число 7. Умножаем 56 на 7, получаем 392. 414-392=22. Остаток меньше делителя. Итак, число подошло и в частном вместо десятков можем записать 7.
153-112=41. Перепишем цифру 4 в той же строке, следующей за первой неполной делимой. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы было удобнее выбирать число частного, 414 будем делить не на 56, а на 50. 414:10=41(осталось 4). 41:5=8(ост.1). Помните: 8 — пробное число. Давайте проверим это. 56*8=448. 448 больше 414, значит, в частном будет меньше 8. Проверим, подходит ли число 7. Умножаем 56 на 7, получаем 392. 414-392=22. Остаток меньше делителя. Итак, число подошло и в частном вместо десятков можем записать 7.Пишем в строке с новым остатком 4 единицы. Значит, следующее неполное делимое равно 224 единицы. Продолжим деление. Разделите 224 на 56. Чтобы легче было подобрать частное, разделите 224 на 50. То есть сначала на 10, будет 22 (остаток 4). А 22 разделить на 5 будет 4 (остаток 2). 4 — пробный номер, давайте проверим, работает ли он. 56*4=224. И мы видим, что цифра выросла. Вместо единиц в частном пишем 4. 224-224=0, деление производится без остатка.

Значение частных номеров 15344 и 56 равно 274.
Пример деления с остатком
Для аналогии возьмем пример, аналогичный приведенному выше, но отличающийся только последней цифрой
Найдем значение приватных номеров 15345:56
Делим сначала так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. 225 делим на 56. Чтобы легче было найти личный номер, делим 225 на 50. То есть сначала к 10 будет 22 (остаток 5). А 22 разделить на 5 будет 4 (остаток 2). 4 — пробный номер, давайте проверим, работает ли он. 56*4=224. И мы видим, что цифра выросла. Вместо единиц в частном пишем 4. 225-224=1, деление производится с остатком.
Значение личных номеров 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одно из чисел оказывается равным 0, и дети его часто пропускают, отсюда и неправильное решение. Давайте разберемся, откуда может взяться 0 и как его не забыть.

Найти значение частных номеров 2870:14
Первый частичный дивиденд 28 сотен. Таким образом, частное будет состоять из 3 цифр. Ставим три точки под угол. Это важный момент. Если ребенок потеряет ноль, появится лишняя точка, которая заставит вас думать, что где-то пропущено число.
Определим первую цифру частного. Делим 28 на 14. Подбором получаем 2. Проверим, подходит ли цифра 2. Умножьте 14*2=28. Подходит цифра 2, ее можно написать вместо сотен в привате. 28-28=0.
Остаток равен нулю. Мы пометили его розовым цветом для ясности, но вам не нужно его записывать. Переписываем число 7 из делимого в строку с остатком. Но 7 не делится на 14, чтобы получить целое число, поэтому пишем вместо десятков в частном 0.
Теперь перепишем последнюю цифру делимого (количество единиц) в эту же строку.
70:14=5 Вместо последней точки в частном пишем цифру 5. 70-70=0. Нет покоя.
Значение частных номеров 2870 и 14 равно 205.

Деление нужно проверять умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Вы освоили тему, теперь потренируйтесь самостоятельно решать несколько примеров в столбик.
1428: 42 30296: 56 254415: 35 16514: 718
Колонка? Как отработать навык деления в столбик дома, если ребенок чему-то не научился в школе? Деление столбиком преподается во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно запомнить правильную запись и доступно объяснить своему ученику, что ему понадобится в жизни .
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не возникало проблем? Для начала проверим, нет ли пробелов в знаниях. Следить за тем, чтобы:
- ребенок свободно выполнял операции сложения и вычитания;
- знает цифры чисел;
- знает наизусть.

Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно все объяснить на наглядном примере.
Попросите поделиться чем-нибудь с членами семьи или друзьями. Например, конфеты, кусочки торта и т. д. Важно, чтобы ребенок понял суть – нужно делить поровну, т.е. без остатка. Практика на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно, сколько спортсменов в каждой группе и сколько мест в автобусе. Вам нужно узнать, сколько билетов нужно купить на одну и вторую группу. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите составляющие.
- Объясните, что деление противоположно умножению, умножение наизнанку.
Связь между делением и умножением удобно показать на примере таблицы.
Например, 3 умножить на 4 равно 12.

3 — первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).Если 12 (произведение) разделить на 3 (первый множитель), то получится 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимый;
Как объяснить ребенку деление двузначного числа на одно число не в столбик?
3 — делитель;
4 — частное (результат деления).Нам, взрослым, проще записать «по старинке» «уголком» — и все. НО! Дети еще не прошли деление колонной, что делать? Как научить ребенка делить двузначное число на одно число, не используя столбчатую запись?
Возьмем для примера 72:3.
Все просто! Разложим 72 на такие числа, которые легко словесно разделить на 3:
72=30+30+12.Все сразу стало понятно: 30 мы можем поделить на 3, а ребенок легко поделит 12 на 3.
Осталось только сложить результаты, т.е. 72:3=10 (получилось при делении 30 на 3) + 10 (30 разделить на 3) + 4 (12 разделить на 3).
72:3=24
Мы не использовали деление в большую сторону, но ребенок понял рассуждения и без труда выполнил вычисления.После простых примеров можно переходить к изучению деления в столбик, научить ребенка правильно писать примеры в «уголок». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа трудно делить в уме, проще пользоваться обозначениями деления столбиком. Чтобы научить ребенка правильно выполнять расчеты, следуйте алгоритму:
- Определите, где в примере находятся делимое и делитель. Попросите ребенка назвать числа (на что будем делить).
213:3
213 — делимое
3 — делитель- Запишите делимое — «угол» — делитель.
- Определите, какую часть делимого мы можем использовать для деления на заданное число.
Рассуждаем так: 2 не делится на 3, значит берем 21.
- Определить, сколько раз делитель «вписывается» в выделенную часть.

21 разделить на 3 — взять 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
Умножаем 7 на 3 — получаем 21. Записываем.
- Найдите разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понимал, что результат вычитания ВСЕГДА должен быть меньше делителя. Если получилось не так, нужно увеличить выбранное число и выполнить действие заново.
- Повторяйте шаги, пока остаток не станет равным 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить в столбик
Как объяснить ребенку деление 204:12=?
1. Пишем в столбик.
204 — делимое, 12 — делитель.2. 2 не делится на 12, поэтому берем 20.
3. Чтобы разделить 20 на 12, берем 1. Пишем 1 под «уголком».
4. Умножаем 1 на 12, получаем 12. Пишем под 20.
5. 20 минус 12 будет 8.
Проверяем сами. 8 меньше 12 (делитель)? Хорошо, верно, идем дальше.6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получилось 84?
Сразу сказать сложно, попробуем действовать методом подбора.
Возьмите, например, 8, но пока не записывайте. Считаем устно: 8 умножить на 12 будет 96. А у нас 84! Неподходящий.
Попробуем меньше… Например, возьмем 6. Проверяем себя словесно: 6 умножить на 12 равно 72. 84-72=12. Мы получили то же число, что и наш делитель, но оно должно быть либо нулем, либо меньше 12. Итак, оптимальное число — 7!7. Пишем 7 под «уголком» и выполняем вычисления. Умножьте 7 на 12, чтобы получить 84.
8. Записываем результат в столбик: 84 минус 84 равно нулю. Ура! Мы приняли правильное решение!Итак, вы научили ребенка делить в столбик, теперь осталось отработать этот навык, довести его до автоматизма.
Почему детям трудно научиться делить в столбик?
Помните, что проблемы с математикой возникают из-за невозможности быстро выполнять простые арифметические действия.
 В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить таблицу умножения «от корки до корки». Все! Остальное дело техники, и она вырабатывается практикой.
В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить таблицу умножения «от корки до корки». Все! Остальное дело техники, и она вырабатывается практикой.Наберитесь терпения, не поленитесь еще раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждое промежуточное действие перед озвучиванием готового ответа. Приводите дополнительные примеры для отработки навыков, играйте в математические игры – это принесет свои плоды, и вы очень скоро увидите результаты и порадуетесь успехам ребенка. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите своих детей делить в столбик, с какими трудностями вам пришлось столкнуться и как вы их преодолели.
Деление на столбик является неотъемлемой частью учебного материала младшего школьника. От того, насколько правильно он научится выполнять это действие, будет зависеть дальнейший прогресс в математике.

Как правильно подготовить ребенка к восприятию нового материала?
Деление столбиком — сложный процесс, требующий от ребенка определенных знаний. Для выполнения деления нужно знать и уметь быстро вычитать, складывать, умножать. Также важно знать цифры чисел.
Каждое из этих действий нужно довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать, складывать не только числа первого десятка, но и в пределах сотни за несколько секунд.
Важно сформировать правильное понятие деления как математической операции. Еще при изучении таблиц умножения и деления ребенок должен четко понимать, что делимое – это число, которое будет делиться на равные части, делитель указывает, на сколько частей нужно разделить число, частное – это сам ответ.
Как пошагово объяснить алгоритм математических действий?
Каждое математическое действие подразумевает строгое соблюдение определенного алгоритма. Примеры на длинное деление нужно делать в таком порядке:
- Написание примера в углу, при этом строго соблюдать места делимого и делителя.
 Чтобы помочь ребенку не запутаться на первых этапах, можно сказать, что слева пишем большее число, а справа меньшее.
Чтобы помочь ребенку не запутаться на первых этапах, можно сказать, что слева пишем большее число, а справа меньшее. - Выделить часть для первого деления. Его нужно разделить на делимое с остатком.
- С помощью таблицы умножения определяем, сколько раз может поместиться делитель в выбранной части. Важно указать ребенку, что ответ не должен превышать 9.
- Полученное число умножьте на делитель и запишите в левой части угла.
- Далее нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывается под чертой и записывается следующий разряд числа. Такие действия выполняются до тех пор, пока в остатке не останется 0.
Хороший пример для учащихся и родителей
На этом примере можно наглядно объяснить разделение на столбцы.
- В столбик записываются 2 числа: делимое 536 и делитель 4.
- Первая часть для деления должна делиться на 4 и частное должно быть меньше 9.
 Для этого подходит цифра 5.
Для этого подходит цифра 5. - 4 в 5 вписывается только 1 раз, поэтому в ответ пишем 1, а под 5 4.
- Далее выполняется вычитание: из 5 вычитается 4 и под чертой записывается 1.
- Следующий бит номер — 3 — сносится до единицы. В тринадцать (13) — 4 влезет 3 раза. 4х3 = 12. Двенадцать записывается под 13-м, а 3 — в ряду, как следующее разрядное число.
- Из 13 вычитается 12, в ответе получается 1. Снова сносится следующий разрядный номер — 6.
- 16 снова делится на 4. В ответ напишите 4, а в графе деления — 16, проведите черту и 0 в разнице.
Несколько раз решая вместе с ребенком задачи на укладку, вы сможете добиться успехов в быстром выполнении заданий в старшей школе.
Столбчатое деление — неотъемлемая часть школьной программы и необходимые знания для ребенка. Чтобы не было проблем на уроках и с их выполнением, необходимо с малых лет давать ребенку базовые знания.
Объяснять ребенку определенные вещи и процессы гораздо проще в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно многообразие методик обучения в разных формах).

Из этой статьи вы узнаете
Принцип деления для детей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они взялись. Ведь многие мамы в игровой форме объясняют ребенку, что папы больше тарелки, в садик идут дальше, чем в магазин и другие простые примеры. Все это дает ребенку первоначальное представление о математике еще до того, как ребенок пойдет в первый класс.
Чтобы научить ребенка делить без остатка, а потом с остатком, необходимо прямо предложить ребенку поиграть в игры с делением. Разделите, например, сладости между собой, а затем добавьте по очереди следующих участников.
Сначала ребенок поделится конфетами, раздав каждому участнику по одной. И в конце сделайте вывод вместе. Следует уточнить, что под «делением» подразумевается одинаковое количество сладостей для всех.
Если нужно объяснить этот процесс с помощью цифр, то можно привести пример в виде игры. Можно сказать, что число конфетное.
 Следует пояснить, что количество конфет, которое нужно разделить между участниками, кратно. А количество людей, на которых делятся эти сладости, делителем.
Следует пояснить, что количество конфет, которое нужно разделить между участниками, кратно. А количество людей, на которых делятся эти сладости, делителем.Тогда вам следует все наглядно показать, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он все поймет и выучит гораздо быстрее. Пока алгоритм объяснить будет сложно, да и сейчас это не нужно.
Как научить ребенка делить в столбик
Небольшое объяснение математики — хорошая подготовка к урокам, особенно к урокам математики. Если вы решили перейти к обучению ребенка делению в столбик, значит, он уже усвоил такие действия, как сложение, вычитание и что такое таблица умножения.
Если это все же вызывает у него какие-то трудности, то все эти знания нужно подтянуть. Стоит напомнить алгоритм действий предыдущих процессов, научив свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, перестанет что-либо понимать.
Чтобы упростить понимание, теперь есть разделительная таблица для малышей.
 Принцип тот же, что и для таблицы умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
Принцип тот же, что и для таблицы умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.При формировании понятия «деление» необходимо все делать в игровой форме, приводить все примеры на знакомые ребенку вещи и предметы.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было понятно, что в результате получается равные части. Это будет правильно, потому что позволит малышу осознать, что деление – это обратный процесс умножения. Если предметов будет нечетное количество, то результат выйдет с остатком и малыш запутается.
Умножение и деление с помощью электронной таблицы
Объясняя малышу взаимосвязь между умножением и делением, необходимо наглядно показать все это на каком-нибудь примере. Например: 5 х 3 = 15. Помните, что результатом умножения является произведение двух чисел.
И только после этого объясните, что это процесс, обратный умножению, и наглядно продемонстрируйте это с помощью таблицы.

Скажите, что вам нужно разделить результат «15» на один из множителей («5»/«3»), и в результате будет постоянно другой множитель, который не принимал участие в делении.
Также необходимо объяснить малышу, как правильно называются категории, осуществляющие деление: делимое, делитель, частное. Опять же, используйте пример, чтобы показать, какие из них относятся к определенной категории.
Деление столбиком — вещь не очень сложная, в ней есть свой легкий алгоритм, которому нужно учить малыша. После закрепления всех этих понятий и знаний можно переходить к дальнейшему обучению.
В принципе, таблицу умножения родители должны выучить с любимым чадом в обратном порядке, и запомнить ее наизусть, так как это будет необходимо при обучении делению столбиком.
Это необходимо сделать перед походом в первый класс, чтобы ребенку было намного легче привыкнуть к школе и не отставать от школьной программы, и чтобы класс не начал дразнить ребенка из-за мелких неудач.
 Таблица умножения есть и в школе, и в тетрадях, так что не надо таскать в школу отдельную таблицу.
Таблица умножения есть и в школе, и в тетрадях, так что не надо таскать в школу отдельную таблицу.Разделить столбиком
Перед началом урока необходимо запомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок разделить эти числа на правильные категории.
Самое главное при обучении делению столбиком — это выучить алгоритм, который, в общем-то, достаточно прост. Но сначала объясните ребенку значение слова «алгоритм», если он его забыл или не изучал раньше.
В том случае, если малыш хорошо разбирается в таблице умножения и обратном делении, трудностей у него не возникнет.
Однако долго задерживаться на полученном результате нельзя; необходимо регулярно тренировать приобретенные навыки и умения. Двигайтесь дальше, как только станет ясно, что малыш понял принцип метода.
Нужно научить малыша делить в столбик без остатка и с остатком, чтобы ребенок не боялся, что у него что-то не получилось правильно разделить.

Чтобы было легче обучать малыша процессу деления, необходимо:
- в 2-3 года понимать соотношение целое-часть.
- в 6-7 лет малыш должен свободно выполнять сложение, вычитание и знать суть умножения и деления.
Необходимо поощрять интерес ребенка к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, а не мотивировал его только на уроке, но и в жизни.
Ребенок должен носить с собой разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все нести, то не перегружайте его.
Рассмотрим простой пример:
15:5=3
В этом примере мы разделили натуральное число 15 полностью 3, без остатка.Иногда натуральное число нельзя полностью разделить. Например, рассмотрим задачу:
В шкафу было 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?Решение:
Разделите число 16 на 5 столбиком и получите:Мы знаем, что 16 умножить на 5 не делится.
 Ближайшее меньшее число, которое делится на 5, — это 15 с остатком 1. Мы можем записать число 15 как 5⋅3. В результате (16 — делимое, 5 — делитель, 3 — неполное частное, 1 — остаток). Получил формула деление с остатком что можно сделать проверка решения .
Ближайшее меньшее число, которое делится на 5, — это 15 с остатком 1. Мы можем записать число 15 как 5⋅3. В результате (16 — делимое, 5 — делитель, 3 — неполное частное, 1 — остаток). Получил формула деление с остатком что можно сделать проверка решения .и = б ⋅ с + D
A — Разделение
B — Разделение,
C — Infulte Coatient, — INCOMPLETE COAT,
.Ответ: Каждый ребенок возьмет 3 игрушки и останется одна игрушка.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то делимое делится. полностью или без остатка на делитель.
Если при делении остаток больше делителя, это означает, что найденное число не самое большое.
 Есть большее число, которое будет делить делимое, а остаток будет меньше делителя.
Есть большее число, которое будет делить делимое, а остаток будет меньше делителя.Вопросы по теме «Деление с остатком»:
Может ли остаток быть больше делителя?
Ответ: нет.Может ли остаток быть равен делителю?
Ответ: нет.Как найти делимое на неполное частное, делитель и остаток?
Ответ: подставляем значения неполного частного, делителя и остатка в формулу и находим делимое. Формула:
а=b⋅c+dПример №1:
Выполнить деление с остатком и проверить: а) 258:7 б) 1873:8Решение:
а) Разделить в столбик:258 — делимое,
7 — делитель,
36 — неполное частное,
6 — остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258б) Разделить в столбик:
1873 — делимое,
8 — делитель,
234 — неполное частное,
1 — остаток. Остаток меньше делителя 1Подставляем в формулу и проверяем, правильно ли мы решили пример:
8⋅234+1=1872+1=1873Пример #2:
Какие остатки получаются при делении натуральных чисел: а) 3 б) 8?Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть 0, 1 или 2.
В нашем случае остаток может быть 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8 В нашем случае остаток может быть 0, 1, 2, 3, 4, 5, 6 или 7.Пример №3:
Какой наибольший остаток можно получить при делении натуральных чисел: а) 9 б) 15?Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но надо указать наибольший остаток. То есть ближайшее число к делителю. Это число равно 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.Пример #4:
Найти делимое: а) а: 6 = 3 (ост. 4) б) с: 24 = 4 (ост. 11)Решение:
а) Решить по формуле:
а=b⋅с +d
(a — делимое, b — делитель, c — неполное частное, d — остаток.)
a:6=3(ост.4)
(a — делимое, 6 — делитель, 3 — неполное частное, 4 — остаток.) Подставим числа в формулу:
a=6⋅3+4=22
Ответ: a=22б) Решим по формуле:
a=b⋅c+d
(a — делимое, b — делитель, c — неполное частное, d — остаток. )
)
s:24=4(ост.11)
(c — делимое, 24 — делитель, 4 — неполное частное, 11 — остаток.) Подставляем числа в формулу:
c=24⋅4+11=107
Ответ: s=107Задача:
Провод 4м. необходимо разрезать на кусочки по 13 см. Сколько будет этих частей?
Решение:
Сначала вам нужно перевести метры в сантиметры.
4м.=400см.
Можно разделить на столбик или в уме получится:
400:13=30(остаток 10)
Проверим:
13⋅30+10=390+10=400Ответ: 30 штук получится и 10 см проволоки останется.
Как Интернет помогает людям
Правила взбивания белков
Столбцы оценок
Представления журнала оценок
Журнал оценок заполняется учащимися, когда они зачислены на ваш курс. Вы увидите всю курсовую работу, относящуюся к курсу, в котором вы находитесь. Вы можете оценивать курсовую работу, управлять элементами и публиковать оценки.
Список оцениваемых элементов — это вид журнала оценок курса по умолчанию.
 Вы можете просмотреть все назначенные вами курсовые работы и свои оценки. Вы также можете получить доступ ко всем функциям управления. Вы можете изменить порядок элементов в этом представлении. Вы можете переключиться на вкладку «Студенты», чтобы просмотреть общую картину участия каждого учащегося.
Вы можете просмотреть все назначенные вами курсовые работы и свои оценки. Вы также можете получить доступ ко всем функциям управления. Вы можете изменить порядок элементов в этом представлении. Вы можете переключиться на вкладку «Студенты», чтобы просмотреть общую картину участия каждого учащегося.Сетка учеников показывает баллы, которые набрали ученики. Имена учащихся отображаются в каждой строке, а в столбцах отображаются оцененные элементы. Вы можете оценивать элементы и управлять ими в виде сетки.
Автоматически создаваемые элементы оценок
Когда вы создаете оцениваемый элемент в своем курсе, элемент журнала оценок создается автоматически. Из списка оцениваемых элементов вы можете перетащить элемент в новое место в списке.
Если открыть посещаемость на странице «Материалы курса», можно добавить посещаемость в журнал оценок. Вы также можете добавить посещаемость на главной странице журнала оценок. Выберите знак «плюс» там, где вы хотите, чтобы строка посещаемости отображалась в списке, и выберите «Добавить посещаемость».

Подробнее о функции посещаемости
Добавление элементов оценки вручную
Вы можете добавлять элементы оценок, которые не требуют отправки, например, участие. Эти элементы оценок также называются ручными оценками, созданными вручную элементами или автономными элементами. В журнале оценок курса вы можете добавить новый элемент в список оцениваемых элементов или представление сетки учащихся.
Для элементов, добавленных вручную, нет отправок. Вы назначаете баллы и отзывы на странице списка студентов.
Элементы, добавленные вручную, не отображаются на странице Материалы курса. Элементы отображаются на общих страницах учащихся и страницах оценок курса.
Вы не можете добавлять файлы, рубрики, цели или группы к элементам, добавленным вручную. Если вы хотите добавить эти параметры к оцениваниям без отправленных материалов, см. следующий раздел: Сбор отправленных материалов в автономном режиме.
- Выберите знак «плюс» везде, где вы хотите добавить элемент, и выберите «Добавить элемент».

- На панели введите заголовок. Заголовок имеет ограничение в 255 символов. Если вы не добавите заголовок, в списке появится «Новый элемент» и дата.
- При необходимости сделайте элемент видимым для учащихся.
- Укажите подробные сведения, например описание и единицу оценки. Вы можете выбрать точки, проценты или буквы. Укажите максимально возможное количество баллов. Срок выполнения является необязательным.
- При необходимости добавьте новый элемент в категорию для использования при создании вычислений.
Вы можете выбрать только единицу оценки, с которой связана схема оценки. Например, вы не можете использовать текст в качестве единицы оценки, пока схемы оценивания текста не будут доступны в представлении курса Ultra. Вы можете изменить единицу оценки даже после начала оценивания.
Что видят ученики?
Добавленный вручную элемент можно сделать видимым для учащихся. Они видят этот элемент на своих глобальных страницах и страницах оценок курса — с оценкой или без нее.

Напоминание: Элементы, добавленные вручную, не отображаются на странице Материалы курса.
Когда вы выставляете оценку, учащиеся получают уведомление в своих лентах активности.
Собирать отправленные материалы в автономном режиме
Элементы, добавленные вручную, отображаются только в журнале оценок, а также на общих страницах и страницах оценок учащихся. Вместо этого вы можете создавать оценки, которые отображаются на странице «Материалы курса», но не требуют от учащихся загрузки отправленных материалов. Вы можете добавить инструкции, файлы, критерий оценки и цели, чтобы учащиеся могли подготовиться к автономной работе. Вы также можете включить беседы, но вы не можете добавлять вопросы или оценивать анонимно.
Примеры офлайн-работы:
- Устные презентации
- Проекты научной ярмарки
- Актёрские постановки
- Работа доставлена лично
- Упражнения по формированию команды лицом к лицу, панельные дискуссии и дебаты
Преподаватели, преподающие гибридные курсы, могут счесть этот тип оценки наиболее полезным.
 Например, вы можете использовать критерий для оценки презентации в классе, которую представляет учащийся. Нет необходимости делать заметки или добавлять счет позже.
Например, вы можете использовать критерий для оценки презентации в классе, которую представляет учащийся. Нет необходимости делать заметки или добавлять счет позже.При создании экзамена вы можете выбрать сбор материалов в автономном режиме. Учащимся сообщается, что они не могут отправить работу онлайн. Если вы создаете группы, учащиеся могут просматривать членов своей группы.
Для отправки, собранной в автономном режиме, вы не можете разрешить несколько попыток, ограничить время или использовать SafeAssign.
Подробнее об оценивании отправленных материалов, отправленных в автономном режиме
Вы можете добавить встречи к функции посещаемости для оценок, требующих присутствия учащихся вне класса. Вы можете попросить студентов посетить экскурсию или приглашенного докладчика, а затем отметить их присутствующими.
Подробнее о добавлении собрания
Что видят учащиеся?
Учащиеся могут просматривать оценку вместе с другим содержимым на странице «Материалы курса», а также на своих общих страницах и страницах оценок за курс.
 Учащимся сообщается, что они не могут отправить работу онлайн. Они могут получить доступ к другой информации, такой как инструкции и рубрика, если вы ее добавили. Учащиеся могут участвовать в обсуждениях оценки, если они включены.
Учащимся сообщается, что они не могут отправить работу онлайн. Они могут получить доступ к другой информации, такой как инструкции и рубрика, если вы ее добавили. Учащиеся могут участвовать в обсуждениях оценки, если они включены.Подробнее о рабочем процессе учащихся
Общая оценка
В списке «Оцениваемые элементы» или в представлении «Сетка учеников» в журнале оценок вы можете установить общую оценку. Общая оценка — это вычисляемый элемент, который вы создаете, чтобы показать учащимся текущий подсчет всех элементов, которые вы оцениваете и публикуете.
Выберите Настроить, чтобы создать столбец журнала оценок для общей оценки. На открывшейся странице можно настроить способ расчета общей оценки.
Не хотите отображать общую оценку? Выберите Скрыть это сообщение, чтобы убрать это приглашение с экрана. Если вы передумаете, вы всегда можете изменить этот параметр в настройках журнала оценок.
В настройках журнала оценок выберите Управление общими настройками оценок.

Для начала выберите Баллы или Взвешенный для расчета общей оценки. Список содержимого курса изменяется в зависимости от вашего выбора, и вы можете начать назначать баллы или весовые коэффициенты в процентах. Если вы используете веса категорий для расчета общей оценки, вы можете развернуть категорию, чтобы увидеть включенные оцениваемые элементы.
Создание категорий журнала оценок и управление ими
Введите балл или общий процент оценки для каждого элемента или категории в журнале оценок, чтобы придать им больший вес в оценке учащегося. Суммарное значение для всех полей процента общей оценки должно равняться 100%.
Чтобы исключить элементы или категории из общей оценки, выберите значок «Освобождение» рядом с полем балла или общей оценки в процентах. Элемент или категория становятся серыми, чтобы указать, что они не включены в расчет. Нажмите значок еще раз, чтобы снова включить элемент или категорию в расчет.
Разверните категорию, чтобы просмотреть ее элементы.
 Отсюда вы можете:
Отсюда вы можете:- Отвязать элемент от его категории. Это полезно, если вы хотите исключить элемент из правила расчета категории.
- Исключить элемент в категории из расчета общей оценки. Это удаляет очки предмета из общего количества очков, доступных в курсе .
Выберите способ отображения общей оценки в настройках общей оценки. Вы можете отобразить буквенную оценку, процент или баллы. С опцией отображения баллов преподаватели и студенты видят общую оценку в виде дроби. Например, 745/800.
Выберите Сохранить, когда закончите. Столбец «Общая оценка» отображается в журнале оценок рядом с именами учащегося, чтобы вы могли быстро увидеть, как работает каждый учащийся.
Оценки, выставленные анонимно, не включаются в расчеты, пока вы не отключите анонимность.
Расчет общей оценки по весам категорий: пример
Здесь вы найдете объяснение того, как рассчитывается общая оценка по весам категорий оценок в Learn Ultra:
Возможные баллы, веса категорий и фактические примеры баллов, общий расчет оценок Возможный балл г.
Вес категории Оценка Задания 23 25 22 Оценки 20 25 20 Журналы 20 25 10 Обсуждения 20 25 14 Расчет общей суммы баллов:
Формула общей суммы баллов:
Возможный балл по категории = (Общее количество баллов по категории / Количество элементов в категории)
Возможная оценка = (Оценка по категории / Оценка по категории * Веса) * Оценка по категории= 23/3 — > 7,6666 —> ((7,6667/7,6667) *,25) * 7,6666 = 1,
= 25/2 -> 12,5 —> ((12,5/12,5) *,25) *12,5 = 3,125
= 20/2 — > 10 —> ((10/10) *.25) *10 = 2,5
= 20/2 -> 10 —> ((10/10) *.25) *10 = 2,5Всего возможных баллов ( Всего баллов) = 10,04166
Расчет общей оценки:
Балл по категории = (Очки по категории/Количество пунктов в категории)
Общий балл = ((Оценка по категории / Общее количество баллов по категории * Вес) + (Оценка по категории / Общее количество баллов по категории * Вес) + (Категория Оценка / Общее количество баллов по категории * Вес) + (Оценка по категории / Общее количество баллов по категории * Вес) + (Оценка по категории / Общее количество баллов по категории * Вес)) * Общий вес по категории= 22/3 -> 7,33333 —> ((7,33333 /7,66666) *.
 25) —> 0,23913
25) —> 0,23913
= 20/2 -> 10 —> ((10/12,5) *,25) —> 0,2
= 10/2 -> 5 —> ((5/10) *,25) —> 0,125
= 14/2 -> 7 —> ((7/10) *.25) —> 0,175
= 0,7391 * 10,04166
= 7,42179Общая оценка = 7,4240 из 10,04166
Процент общей оценки из 100: (7,4240 /10,04166) * 100 = 73,91%Изменить общую оценку
Вы можете изменить общую оценку учащегося, если его успеваемость или участие не соответствуют схеме оценок курса.
Чтобы переопределить оценку, выберите ячейку оценки в столбце Общая оценка учащегося. Введите новое значение или выберите вариант. Вы можете переопределить оценку с помощью обозначения оценки. Переопределение полезно, если учащийся не может завершить курс или по другим причинам не соответствует требованиям для завершения. Обозначения оценок могут включать «Незавершенный», «Отзыв» и т. д. Вы можете создавать обозначения общей оценки и управлять ими в настройках журнала оценок.
Если вы хотите удалить переопределение, выберите ячейку общей оценки учащегося и выберите «Отменить переопределение».
 Общая оценка учащегося возвращается к расчету, который вы настроили для своего курса.
Общая оценка учащегося возвращается к расчету, который вы настроили для своего курса.Разница в общей оценке и рассчитанных оценках
В Blackboard Learn Ultra могут появиться незначительные различия между вычислением общей оценки и итоговой суммой, полученной с помощью функции «Добавить вычисление», из-за математического определения веса баллов в каждой формуле.
В некоторых случаях эта небольшая разница, всего 0,01, может оказать существенное влияние на вычисления, основанные на схеме оценок Ultra.
Если все элементы оценки имеют одинаковое максимальное количество баллов, оценка для обоих расчетов будет одинаковой, поскольку разница в весе будет отменена, и, таким образом, процент, назначенный схемой оценки, будет совпадать.
Подробная информация о формулах (пример расчета пяти баллов и присвоения равного веса):
Формула общей оценки:
((Оценка 1 / Сумма баллов * Вес) + (Оценка 2 / Сумма баллов * Вес) + (Оценка 3 / Сумма Очки * Вес) + (Оценка 4 / Общее количество очков * Вес) + (Оценка 5 / Общее количество очков * Вес) ) * Общий вес
Вес, присвоенный каждому пункту оценки, является частью общей суммы 100%.
 Если конкретный элемент имеет другое максимальное количество баллов (например, Score5), оно будет преобразовано в 100 % путем деления на максимальное количество баллов.
Если конкретный элемент имеет другое максимальное количество баллов (например, Score5), оно будет преобразовано в 100 % путем деления на максимальное количество баллов.Формула расчетной оценки:
(Оценка1 * Вес) + (Оценка2 * Вес) + (Оценка3 * Вес) + (Оценка4 * Вес) + (Оценка5 * Вес)
Правило взвешивания не применяется. Формула просто умножает все баллы на заданные значения и суммирует результат.
Подробнее о схемах оценивания
Подробнее о подсчете оценок
Что видят учащиеся?
Общая оценка, представленная учащимся и преподавателем, меняется по мере того, как вы создаете и оцениваете содержимое курса, которое вы включили в расчет общей оценки.
Видимость предмета не влияет на общую оценку. Однако учащиеся могут видеть только опубликованные оценки, поэтому представление учащегося об общей оценке включает только опубликованные вами оценки. Представление инструктора об общей оценке включает все оценки, независимо от того, опубликовали вы их или нет.
 В некоторых случаях вы можете увидеть общую оценку, отличную от той, которую видят ваши учащиеся.
В некоторых случаях вы можете увидеть общую оценку, отличную от той, которую видят ваши учащиеся.Подробнее о представлении учащимся общей оценки
Рабочие листы по разделам
Добро пожаловать на страницу рабочих листов по разделам на сайте Math-Drills.com! Пожалуйста, уделите нам все свое внимание, пока мы представляем эту страницу. Наши рабочие листы для деления помогут вам научить студентов очень важному понятию деления. Если учащиеся хорошо помнят факты умножения, преподавание фактов деления должно быть легким делом. Если вы хотите, чтобы ваши ученики добились успеха в изучении деления, пожалуйста, убедитесь, что они знают свои факты умножения до 81, как умножать на 0 и как умножать на 10. Если они не знают этих вещей, это займет много времени. намного дольше.
На этой странице вы найдете множество рабочих листов на деление, включая факты деления и деление в длинное с остатком и без него. Мы начнем с некоторых фактов деления, которые, как вы знаете, являются просто фактами умножения, выраженными другим способом.
 Основное отличие состоит в том, что вы не можете разделить на 0 и получить действительное число. Если вы действительно хотите, чтобы ваши ученики произвели впечатление, скажем, за обеденным столом, когда их родители спрашивают их, что они узнали сегодня, вы можете научить их тому, что деление на ноль не определено.
Основное отличие состоит в том, что вы не можете разделить на 0 и получить действительное число. Если вы действительно хотите, чтобы ваши ученики произвели впечатление, скажем, за обеденным столом, когда их родители спрашивают их, что они узнали сегодня, вы можете научить их тому, что деление на ноль не определено.Оставшаяся часть страницы посвящена длинному делению, которое почему-то не нравится некоторым представителям населения. Длинное деление является наиболее сложным, когда учащиеся не знают свои факты умножения, поэтому сначала убедитесь, что они знают их. О, мы это уже говорили. А как насчет алгоритма длинного деления… может быть, того, который вы, или ваши родители, или ваши дедушки и бабушки выучили? Мы с уверенностью говорим: да! Причина, по которой вы и ваши предки использовали его, заключается в том, что это эффективный и красивый алгоритм, который позволит вам решить некоторые из самых сложных задач на деление, с которыми не справятся даже блоки с основанием 10.
 Он работает одинаково хорошо для десятичных и целых чисел. Длинное деление на самом деле не так сложно.
Он работает одинаково хорошо для десятичных и целых чисел. Длинное деление на самом деле не так сложно.Самые популярные рабочие листы деления на этой неделе
Длинное деление — однозначный делитель и двузначное частное без остатка ( 2821 просмотров на этой неделе )4-значное на двузначное длинное деление с остатками и шагами, показанными в ключе ответа ( 1523 просмотров на этой неделе )Деление фактов до 25 без нулей ( 1432 просмотров на этой неделе )Длинное деление — однозначный делитель и трехзначное частное без остатка ( 1207 просмотров на этой неделе )Деление фактов с делителями и частное от 1 до 9с длинным символом деления ( 1069 просмотров на этой неделе )Рабочие листы с фактами о делениях
Рабочие листы с фактами о делениях, включая таблицы делений, факты о делениях и рабочие листы с отдельными фактами о делениях.
Таблицы фактов отдела
Таблицы фактов о подразделениях в Серые от 1 до 12 Таблицы фактов о подразделениях в Серые от 1 до 12 (Ответы пропущены) Таблицы фактов о подразделениях в цветах от 1 до 12 Таблица фактов о дивизионе в Монтессори-цвета от 1 до 12 Выделенные факты
Факты о горизонтальном делении рабочих листаМанипуляторы могут помочь учащимся «усвоить» концепцию деления.
 Например, учащиеся могут перегруппировать блоки с основанием десять в блоки, а затем разделить блоки на стопки. Например, 81 ÷ 9 в конечном итоге будет 9 стопками по 9 единиц.
Например, учащиеся могут перегруппировать блоки с основанием десять в блоки, а затем разделить блоки на стопки. Например, 81 ÷ 9 в конечном итоге будет 9 стопками по 9 единиц.Подразделение, по сути, задает вопрос: «Сколько _____ в _____?» На вопрос 81 ÷ 9, подсказка будет звучать так: «Сколько девяток в числе 81?» Эта подсказка пригодится учащимся при изучении математики на более поздних этапах, когда будут возникать более сложные понятия, такие как деление десятичных дробей или дробей. «Сколько третей в четырех?» или еще лучше, Сколько третьих чашек в четырех чашках?» При необходимости достаньте мерные чашки.
Факты горизонтального подразделения с дивидендами до 25 Факты горизонтального подразделения с дивидендами до 36 Факты о горизонтальном делении с дивидендами до 49 Факты горизонтального подразделения с дивидендами до 64 Факты горизонтального подразделения с дивидендами до 81 Факты горизонтального подразделения с дивидендами на 100 Факты горизонтального подразделения с дивидендами на 121 Факты горизонтального подразделения с дивидендами на 144 Факты горизонтального подразделения с дивидендами до 169 Факты горизонтального подразделения с дивидендами на 196 Факты о горизонтальном делении с дивидендами до 225
Факты о вертикальном делении рабочих листаФакты о вертикальном делении Дивиденды до 25 Со знаком деления Факты вертикального деления Дивиденды до 36 Со знаком деления Факты вертикального деления Дивиденды до 49 Со знаком деления Факты вертикального деления Дивиденды до 64 Со знаком деления Факты о вертикальном делении Дивиденды на 81 со знаком деления Факты о вертикальном делении крупным шрифтом Дивиденды до 81 Со знаком деления Факты о вертикальном делении Дивиденды до 100 Со знаком деления Факты вертикального деления Дивиденды до 121 Со знаком деления Факты вертикального деления Дивиденды до 144 Со знаком деления Факты вертикального деления Дивиденды до 169 Со знаком деления Факты о вертикальном делении Дивиденды на 196 со знаком деления Факты вертикального подразделения Дивиденды до 225 Со знаком разделения Факты о вертикальном делении Дивиденды до 25 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 36 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 49 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 64 С символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 81 с символом длинного деления (50 на странице) Факты о вертикальном разделении Дивиденды до 100 С символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 121 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 144 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 169 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 196 с символом длинного деления (50 на странице) Факты о вертикальном разделении Дивиденды до 225 С символом длинного деления (50 на странице)
Факты о горизонтальном делении рабочих листа с номерами фокусаФакты деления с делителем от 1 (частное 1-9) Факты деления с делителем от 2 (частное 1-9) Факты деления с делителем от 3 (частное 1-9) Факты деления с делителем от 4 (частное 1-9) Факты о дивизионе с Делитель 5 (Частное 1-9) Факты деления с делителем от 6 (частное 1-9) Факты деления с делителем числа 7 (частное 1-9) Факты деления с делителем числа 8 (частное 1-9) Факты деления с делителем числа 9 (частное 1-9) Факты деления с делителем 1 (частное 1-12 ) Факты деления с делителем 2 (частное 1-12 ) Факты о дивизионе с Делитель 3 (Частное 1-12 ) Факты деления с делителем 4 (частное 1-12 ) Факты деления с делителем числа 5 (частное 1-12 ) Факты деления с делителем 6 (частное 1-12 ) Факты деления с делителем числа 7 (частное 1-12 ) Факты деления с делителем числа 8 (частное 1-12 ) Факты о дивизионе с Делитель 9 (Частное 1-12 ) Факты деления с делителем числа 10 (частное 1-12 ) Факты деления с делителем числа 11 (частное 1-12 ) Факты деления с делителем числа 12 (частное 1-12 )
Факты о подразделениях рабочих листа с комбинациями фокусных чиселДеление на 1, 2, 5 и 10 (Частное 1-12) Деление на 1, 2, 5 и 10 (Частное 1-12) (Горизонтальное) Деление на 3, 4 и 6 (Частное 1-12) Деление на 7, 8 и 9(Коэффициент 1-12) Деление на 11 и 12 (Частное 1-12)
Рабочие листы на длинное деление
Рабочие листы на длинное деление для отработки различных стратегий деления на длинное, включая вопросы без остатка, остатка и десятичных частных.
Полное деление рабочих листа с без остатка
Нужен более простой способ деления больших чисел? Попробуйте этот метод, используя степени десяти. Чтобы успешно использовать этот метод, учащиеся должны уметь умножать на десять и вычитать. Студенты вычитают делимое, умноженное на убывающие степени десяти, пока не получат ноль или остаток. Пример: 1458 ÷ 54. Примечание 54 × 1 = 54, 54 × 10 = 540 (больше не нужно). 1458 — 540 — 540 = 378. Обратите внимание, что 540 было вычтено дважды, так что количество раз, когда 54 «входит» в 1458, составляет 20 раз. Продолжая, 378 — 54 — 54 — 54 — 54 — 54 — 54 — 54 = 0. Поскольку 54 было вычтено семь раз, частное увеличивается на семь и в сумме получается 27. Другими словами, 54 «входит» в 1458, 27. раз.
Мы могли бы также упомянуть, что этот метод может быть еще более сложным, если использовать степени, кратные десяти. В приведенном выше примере использование 54 × 5 = 270 помогло бы быстрее получить частное.

Делитель десяти; 2-значный коэффициент 1-значный делитель; 1-значный коэффициент 1-значный делитель; 2-значный коэффициент 1-значный делитель; 3-значный коэффициент 2-значный делитель; 2-значный коэффициент 2-значный делитель; 3-значный коэффициент 2-значный делитель; 4-значный коэффициент 3-значный делитель; 3-значный коэффициент 3-значный делитель; 4-значный коэффициент 3-значный делитель; 5-значный коэффициент
Европейское длинное деление рабочих листов без остатка1-значный делитель; 1-значный коэффициент (европейский) 1-значный делитель; 2-значный коэффициент (европейский) 1-значный делитель; 3-значный коэффициент (европейский) 2-значный делитель; 2-значный коэффициент (европейский) 2-значный делитель; 3-значный коэффициент (европейский) 2-значный делитель; 4-значный коэффициент (европейский) 3-значный делитель; 2-значный коэффициент (европейский) 3-значный делитель; 3-значный коэффициент (европейский) 3-значный делитель; 4-значный коэффициент (европейский)
Полное деление рабочих листов с остаткомВы когда-нибудь думали, что можете помочь ученику лучше понять вещи и получить более точный ответ, используя при этом остатки? Это довольно легко на самом деле.
 Остатки обычно даются вне контекста, в том числе в приведенных ниже ключах ответов. Остаток на самом деле является числителем дробного частного. Например, 19 ÷ 3 равно 6 с остатком 1, что точнее 6 1/3. Использование дробных частных означает, что ваши ученики всегда найдут точный ответ на все вопросы о делении на длинное деление, и во многих случаях ответ будет более точным (например, сравните 6 1/3 с 6,3333….).
Остатки обычно даются вне контекста, в том числе в приведенных ниже ключах ответов. Остаток на самом деле является числителем дробного частного. Например, 19 ÷ 3 равно 6 с остатком 1, что точнее 6 1/3. Использование дробных частных означает, что ваши ученики всегда найдут точный ответ на все вопросы о делении на длинное деление, и во многих случаях ответ будет более точным (например, сравните 6 1/3 с 6,3333….).Делитель десяти; 2-значный коэффициент 1-значный делитель; Двузначный дивиденд 1-значный делитель; 3-значный дивиденд 1-значный делитель; 4-значный дивиденд 2-значный делитель; 3-значный дивиденд 2-значный делитель; 4-значный дивиденд 2-значный делитель; 5-значный дивиденд 3-значный делитель; 4-значный дивиденд 3-значный делитель; 5-значный дивиденд 3-значный делитель; 6-значный дивиденд
Полное деление рабочих листа с десятичными дробями1-значный делитель; Двузначный дивиденд 1-значный делитель; 3-значный дивиденд 1-значный делитель; 4-значный дивиденд 2-значный делитель; 3-значный дивиденд 2-значный делитель; 4-значный дивиденд 2-значный делитель; 5-значный дивиденд 3-значный делитель; 4-значный дивиденд 3-значный делитель; 5-значный дивиденд 3-значный делитель; 6-значный дивиденд
Европейское длинное деление рабочих листов с остатками1-значный делитель; Двузначный дивиденд (европейский) 1-значный делитель; 3-значный дивиденд (европейский) 1-значный делитель; 4-значный дивиденд (европейский) 2-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; 4-значный дивиденд (европейский) 2-значный делитель; 5-значный дивиденд (европейский) 3-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 5-значный дивиденд (европейский) 3-значный делитель; 6-значный дивиденд (европейский)
Европейское длинное деление рабочие листы с десятичными частными1-значный делитель; Двузначный дивиденд (европейский) 1-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; Двузначный дивиденд (европейский) 2-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 3-значный дивиденд (европейский) 3-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 5-значный дивиденд (европейский)
Полное деление
с остатками рабочие листы с шагами, показанными в ключе ответаМы подумали, что было бы полезно включить несколько рабочих листов с делением на деление с показанными шагами.
 В ключах ответов для этих рабочих листов для разделения используется стандартный алгоритм, который вы могли бы изучить, если бы вы ходили в англоязычную школу. Изучение этого алгоритма само по себе иногда недостаточно, поскольку оно может не привести к хорошему концептуальному пониманию. Одним из инструментов, который помогает учащимся изучить стандартный алгоритм и развить понимание деления, является набор десятичных блоков. Обучая студентов сначала делению на блоки с основанием десять, а затем переходя к стандартному алгоритму, учащиеся получат концептуальное понимание, а также смогут использовать эффективный алгоритм для деления в длинное число. Студенты, обладающие обоими этими качествами, естественно, добьются больших успехов в своих будущих математических исследованиях.
В ключах ответов для этих рабочих листов для разделения используется стандартный алгоритм, который вы могли бы изучить, если бы вы ходили в англоязычную школу. Изучение этого алгоритма само по себе иногда недостаточно, поскольку оно может не привести к хорошему концептуальному пониманию. Одним из инструментов, который помогает учащимся изучить стандартный алгоритм и развить понимание деления, является набор десятичных блоков. Обучая студентов сначала делению на блоки с основанием десять, а затем переходя к стандартному алгоритму, учащиеся получат концептуальное понимание, а также смогут использовать эффективный алгоритм для деления в длинное число. Студенты, обладающие обоими этими качествами, естественно, добьются больших успехов в своих будущих математических исследованиях.2-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 3-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 4-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 5-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 6-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 3-значный на 2-значный Длинное деление с остатками с шагами, показанными в ключе ответа 4-значный на 2-значный Длинное деление с остатком с шагами, показанными в ключе ответа 5-значный на 2-значный Длинное деление с остатком с шагами, показанными в ключе ответа 6-значный на 2-значный Длинное деление с остатком с шагами, показанными в ключе ответа 4-значный на 3-значный Длинное деление с остатком с шагами, показанными в ключе ответа 5-значный на 3-значный Длинное деление с остатками с шагами, показанными в ключе ответа 6-значный на 3-значный Длинное деление с остатком с шагами, показанными в ключе ответа
Длинное деление на сетке
Длинное деление с помощью сетки
и НЕТ остатка рабочие листыНекоторым учащимся трудно выстроить все в ряд при выполнении алгоритма деления в длину, поэтому эти рабочие листы содержат сетку и более широкий интервал между цифрами, чтобы помочь учащимся правильно расположить элементы.
 Ключи к ответам включают типичные шаги, которые учащиеся записывают при решении каждой задачи; однако возможны небольшие вариации в реализации. Например, некоторые люди не обращают внимания на знаки вычитания, некоторые могут показывать шаги вычитания нуля и т. д.
Ключи к ответам включают типичные шаги, которые учащиеся записывают при решении каждой задачи; однако возможны небольшие вариации в реализации. Например, некоторые люди не обращают внимания на знаки вычитания, некоторые могут показывать шаги вычитания нуля и т. д.2-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 3-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 3-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 4-значный за 1-значным Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 4-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 5-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 5-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 6-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 6-значный на 2-значный Длинное деление с Поддержка сетки и подсказки и НЕТ остатка 3-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 3-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 4-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 4-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 5-значный на 1-значный Long Division с Grid Assistance и БЕЗ остатка 5-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 6-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 6-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка
Длинное деление с помощью сетки
и НЕКОТОРЫЕ остатки рабочих листа2-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 3-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 3-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 4-значный за 1-значным Длинное деление с помощью Grid Assistance и подсказками и некоторые остатки 4-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 5-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 5-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 6-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 6-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 3-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 3-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 4-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 4-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 5-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 5-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 6-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 6-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки
Правила делимости
Рабочие листы для отработки правил делимости, включая множество малых и больших чисел и сосредоточение внимания на различных делителях.
Правила делимости
Признак делимости на 2, 5 и 10
Число делится на 2, если последняя цифра (цифра в разряде единиц) четная. Следовательно, числа, оканчивающиеся на 0, 2, 4, 6 или 8, делятся на 2. Число делится на 5, если его последняя цифра — 0 или 5. Число делится на 10, если последняя цифра — 0.
Делимость на 3, 6 и 9
Число делится на 3, если сумма его цифр делится на 3. Например, 285 делится на 3, потому что 2 + 8 + 5 = 15 делится на 3. A число делится на 6, если оно делится и на 3, и на 2 (см. правила выше). Число делится на 9, если сумма его цифр делится на 9. Например, 285 не делится на 9, потому что 2 + 8 + 5 = 15 не делится на 9.
Делимость на 4, 7 и 8
Число делится на 4, если две последние цифры числа делятся на 4. Для числа 7 можно использовать несколько стратегий. Дополнительную информацию см. в разделе «Трюки с делимостью для изучения математики». Число делится на 8, если последние три цифры делятся на 8.
 Это стандартное правило, которое может быть немного поверхностным для больших чисел, например, кто знает, делится ли 680 на 8? По этой причине мы предлагаем наше решение Math-Drills.com, которое требует немного арифметических действий, но может быть довольно легко выполнено с небольшой практикой. Как вы знаете, 8 равно 2 в третьей степени, поэтому мы подумали, что если бы вы могли разделить последние три цифры числа на 2 три раза, то оно будет делиться на 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. У нас есть победитель! 680 действительно делится на 8.
Это стандартное правило, которое может быть немного поверхностным для больших чисел, например, кто знает, делится ли 680 на 8? По этой причине мы предлагаем наше решение Math-Drills.com, которое требует немного арифметических действий, но может быть довольно легко выполнено с небольшой практикой. Как вы знаете, 8 равно 2 в третьей степени, поэтому мы подумали, что если бы вы могли разделить последние три цифры числа на 2 три раза, то оно будет делиться на 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. У нас есть победитель! 680 действительно делится на 8.Делимость на 2, 5 и 10 (2 цифры) Делимость на 3, 6 и 9 (двухзначное) Делимость на 4, 7 и 8 (2 цифры) Делимость чисел от 2 до 10 (2-значные) Делимость на 2, 5 и 10 (3 цифры) Делимость 3, 6 и 9 (3-значный) Делимость на 4, 7 и 8 (3 цифры) Делимость чисел от 2 до 10 (3-значные) Делимость на 2, 5 и 10 (4 цифры) Делимость на 3, 6 и 9 (4 цифры) Делимость на 4, 7 и 8 (4 цифры) Делимость чисел от 2 до 10 (4-значные)
Деление в других основных системах счисления
Деление чисел в системах счисления, отличных от десятичных, включая двоичные, четверичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.

Деление в
других основных системах счисленияДеление двоичных чисел (основание 2) Разделение троичных чисел (основание 3) Разделение четвертичных чисел (основание 4) Разделение Квинарий Числа (база 5) Разделение порядковых номеров (основание 6) Деление восьмеричных чисел на (основание 8) Деление двенадцатеричных чисел (основание 12) Деление шестнадцатеричных чисел (основание 16) Деление десятичных чисел (основание 20) Деление шестнадцатеричных чисел (основание 36) Разделение различных чисел (различные основания)
Как сделать длинное деление: простое пошаговое руководство с иллюстрациями
Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость:
Как сделать деление в большую сторону.

Исследование 2012 года, опубликованное в журнале Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают ли они на уроках математики более высокого уровня — даже после учета различных социально-экономических факторы. Никакого давления, верно? Если при мысли об обучении делению на длинные лады у вас холодный пот и липкие ладони, не беспокойтесь — мы сделали всю работу за вас.
Как выполнить деление в длинное за шесть шагов1. Повторить
Первый шаг, который вы должны сделать, это шаг назад.
Для ученика 4-го класса деление в большую сторону представляет собой сложную смесь различных операций. Чтобы успешно научиться выполнять деление в большую сторону, им необходимо повторить эти фундаментальные понятия.
Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов, определяющих будущие математические успехи учащихся.
 Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».
Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».Убедитесь, что ваши ученики понимают, что умножение — это результат многократного сложения, а деление — это просто противоположное — многократное вычитание.
Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство числа. Запланируйте занятия, в которых учащимся будет предложено создать «семейство фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.
Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в учебе и развить уверенность в математике, прежде чем продолжить.
2. Начните с простогоДавайте начнем с урока словарного запаса. Уравнение деления на деление состоит из множества частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать.
Дивиденд — это число в правой части уравнения под чертой.
 Он представляет собой сумму, которую нужно разделить.
Он представляет собой сумму, которую нужно разделить.Делитель — это число слева — оно выполняет деление.
Частное — это число сверху. Он представляет собой ответ или количество единиц в каждом разряде после завершения уравнения.
Остаток — это число вверху справа. Он представляет оставшиеся единицы, которые не могут быть равномерно разделены на частное. Во-первых, введите уравнение, которое не имеет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что изучили:
Спросите учащихся, сколько раз 2 умещается в 4. Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?
Как только они придут к правильному ответу, поставьте 2 выше 4. Затем повторите шаг со второй цифрой в делимом.
Используйте эти простые уравнения, чтобы усилить позиционное значение.
 Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.
Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.Вместо того, чтобы сразу перейти к уравнению с остатками, начните с другого предметного урока . Разделите учащихся на группы по три, четыре или шесть человек и дайте каждой группе по 50 ватных шариков (или мармеладок, или помпонов, или зефира — любой маленький предмет, доступный в вашем классе).
Попросите учащихся разделить предметы так, чтобы у каждого члена группы было одинаковое количество предметов, а затем наблюдайте и ждите.
В конце концов, они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то предметы. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в большую сторону с помощью 9.0003 осталось .
Сначала покажите учащимся задачу с остатком в единицах:
Теперь начните со столбца десятков и проработайте задачу: 5 входит в 5 ровно один раз, так что там ничего не осталось.
 Но сколько раз 5 входит в 7, и что вы делаете с остатками?
Но сколько раз 5 входит в 7, и что вы делаете с остатками?Покажите учащимся новые шаги:
- Разделить столбец единиц делимое на делитель
- Умножить делитель на частное в нужном месте столбец
- Вычтите произведение из столбца единиц
Оставшееся число — это остаток. Обязательно смоделируйте несколько задач всем классом, чтобы учащиеся могли начать понимать этапы и то, как правильно записывать свои ответы.
Это хорошее время на уроке, чтобы научить учащихся проверять свои ответы. Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.
4. Остаток в десяткахТеперь пришло время учащимся решить задачи, в которых делитель не помещается точно в столбец десятков или единиц. Шаги почти такие же, за исключением одного нового дополнения:
- Разделить делимое в столбце десятков на делитель
- Умножить делитель на частное в столбце десятков
- Вычесть произведение из делителя
- Сократите делимое в столбце единиц и повторить .

Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому найдите время, чтобы смоделировать задачи на доске. Обсудите, почему эти шаги работают, и помогите им понять, какую важную роль в этом процессе играет значение места.
5. Постепенно вводите большие числаВот и все. Или это?
Пусть учащиеся освоятся с формулой и поработают над более мелкими задачами. Когда они обретут уверенность и начнут понимать, как выполнять деление в большую сторону, начните предлагать им задачи с трехзначным делимым, а затем задачи с двузначным делителем.
Напомните учащимся, что шаги остаются одинаковыми, независимо от того, насколько велика задача , и предложите им использовать лист бумаги, чтобы «угадать и проверить» свое умножение по ходу дела. Это хороший момент, чтобы убедиться, что у них нет проблем и что они полностью понимают взаимосвязь деления с разрядным значением и умножением.

Посмотрите это видео от Khan Academy:
0004Если вы рассмотрели весь свой контент на первых пяти шагах, поздравляем! Предложите учащимся продолжать практиковаться в делении больших и малых чисел в длинную и укреплять связь между делением и другими математическими понятиями, которые они изучают. Но процесс еще не завершен — учащиеся должны понять, как делать длинную деление с десятичной дробью. Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед.
Предложите учащимся решить задачу, как обычно. Когда они дойдут до шага, на котором они обычно останавливаются с остатком, попросите их поставить десятичную точку в конце частного и делимого и написать несколько нулей после делимого.
Предложите им продолжить обычные шаги деления на один или два знака, опуская нули.
Соедините десятичную дробь с дробью. Попросите их преобразовать частное с десятичной дробью в неправильную дробь.
Как выполнить деление в длинное число (без деления в длинное число) Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.
Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.Поздравляем! Ваш модуль подходит к концу, и вы успешно научили своих учеников выполнять деление в большую сторону.
Но знаете ли вы, что существует несколько способов деления больших чисел? Обучение учащихся другим способам проверки своей работы является важной частью математических стандартов Common Core и может улучшить понимание учащимися того, что на самом деле означает деление в столбцах в данном контексте.
Плоскостные моделиПлоскостные модели — отличный способ для визуалов понять и осмыслить деление, а также улучшить чувство числа.
Этот метод использует сетку, чтобы представить процесс деления как задачу площади: например, 148÷4 можно разделить на сетку высотой 4 единицы, площадью 148 квадратных единиц и шириной неизвестного числа единиц.

Учащиеся разбивают сетку на более удобные области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100÷4 равно 25, 40÷4 равно 10, а 8÷4 равно 2. Эти числа идут вверху модели области и могут быть сложены, чтобы получить ответ.
Частичные частныеКак и в случае с площадной моделью, частичные частные побуждают учащихся разбивать вопросы на деление на «более понятные» части. Это помогает учащимся понять, что деление — это нахождение того, сколько раз одно число может перейти в другое число.
Задайте задачу (в данном случае 450÷23) как уравнение деления на деление. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира.
Спросите, сколько раз 23 входит в число 400, но не ищите точное ближайшее число: сделайте его удобным для работы, например, 230 (десять раз). Вычтите 230 из 450 и поставьте 10 справа, чтобы отслеживать результат.
Возьмите разницу и вычтите ее из делимого.
 Ответ должен быть 220.
Ответ должен быть 220.Спросите, сколько раз 23 входит в 220. 5 x 23 равно 115, так что вычтите это из 220 и запишите 5.
Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное.
Частичные частные обладают гибкостью, которой нет в длинном делении. Длинное деление нужно делать точно, но с частичными частными можно просто многократно вычитать делитель из делимого и все равно прийти к правильному ответу.
Используйте этот метод, чтобы закрепить позиционное значение и концепцию деления как многократного вычитания.
Упражнения на деление в длинное числоЛучший способ научиться делению в длинное число – практиковаться, практиковаться и еще раз практиковаться.
Вот список из восьми заданий, которые заинтересуют ваш класс делением в длинную и помогут развить прочные математические навыки.
1. Prodigy
Prodigy — это забавный и увлекательный ресурс для занятий в классе или дома на длинные дистанции. Учащиеся исследуют мир, полный приключений, где успех зависит от правильных ответов на математические вопросы.
С помощью панели управления учителя вы можете предоставлять контент, ориентированный на урок, в зависимости от оценки, навыков или ученика. Затем ученики отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании .
Поощряйте своих учеников практиковать все математические навыки, которые они изучили в классе, включая деление в столбик. Вот как вы можете использовать Prodigy для:
- усиления уроков в классе
- разнообразия материалов по математике
- Проведение формирующего оценивания
Учащиеся играют в увлекательную игровую платформу, где они могут собирать питомцев, выполнять квесты и сражаться с друзьями.
Зарегистрируйтесь сейчас 2. Деление в натуральную величину И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!
И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!Оживите математику с помощью практической головоломки с делением в длину. Вырежьте квадраты из цветной бумаги со всеми числами, которые нужны учащимся для решения задачи на деление в длину от начала до конца. Используйте клейкую ленту, чтобы разделить линии на полу, и раздайте учащимся пронумерованные карточки.
Попросите учащихся, начиная с заданного уравнения, разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и подумать о своих шагах, и это особенно полезно для класса, который все еще хочет освоить шаги умножения.
3. Бинго с длинными дивизионамиБинго является классикой не просто так. Каждая из цифр в листе учащегося должна соответствовать вопросу, который вы задали перед классом.
 Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!
Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!Бросьте вызов своим учащимся, но убедитесь, что вы уделяете этому упражнению достаточно времени — некоторые учащиеся могут испытывать трудности с быстрым решением задач и могут расстраиваться или совершать ошибки, если не смогут справиться с заданием.
4. Книги по математикеПовысьте уровень грамотности и обучения математике с помощью забавных книг, посвященных сложным математическим понятиям. Используйте их, чтобы объяснить учащимся деление и остатки в веселой и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут учиться выполнять деление в столбик.
Некоторые книги по математике, которые охватывают подразделение:
- оставшаяся часть одного от Элинора Дж. Пинцза
- Бин.
В длинном делении много шагов, и их нужно выполнять в правильном порядке, чтобы получить правильный ответ.
 Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости.
Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости.Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в большую сторону — разделить , умножить , вычесть и свести — чтобы стимулировать творчество в вашем классе.
Предложите им создать постер, песню, мнемоническое устройство или даже небольшую сценку, которую они могут представить своим одноклассникам. Если они заинтересованы в том, чтобы найти способ запомнить шаги, они, скорее всего, быстро научатся.
6. Реле длинного деленияПревратите практику длинных дивизий в веселую классную игру с эстафетами длинных дивизий. Разделите свой класс на команды и сделайте карточки с задачами на деление в длину.
Объедините учащихся в группы. Каждая группа получает карточку для начала, и первые учащиеся выполняют первый набор шагов для своей проблемы.

Когда они закончат, второй учащийся ищет ошибки и продолжает решать задачу. Если они решат задачу, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой задачей.
Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!
7. Сундук с сокровищами
Это задание — веселый способ для вашего класса отпраздновать завершение отряда в дивизионе. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решить в группах, чтобы «открыть» коробку.
В качестве дополнительной задачи сделайте это кодом: пусть каждое частное соответствует букве алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку.
8. Генератор рабочих листовРабочие листы — это проверенный материал на уроках математики.

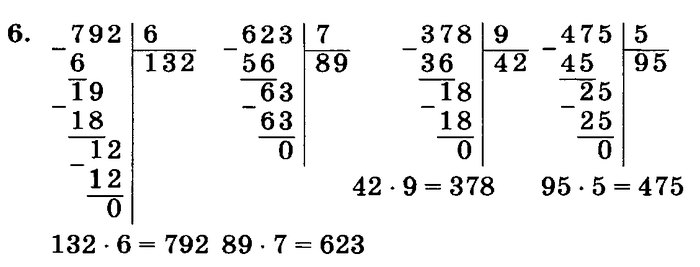


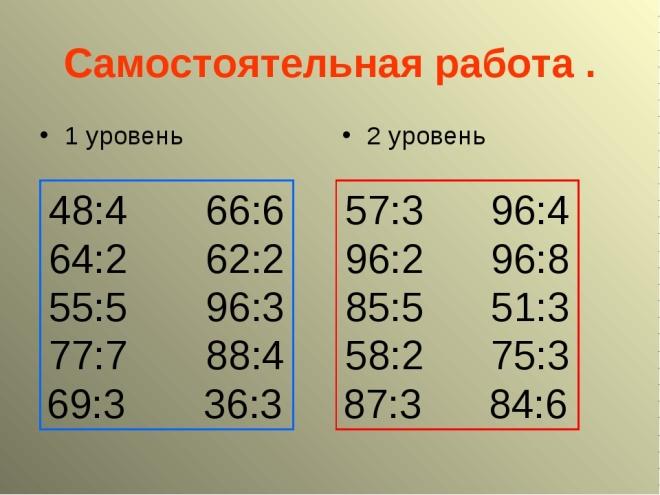
 Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и универсальных методов для вычислить произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и используйте их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые процедуры для нахождения частных, включающих многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.
Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и универсальных методов для вычислить произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и используйте их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые процедуры для нахождения частных, включающих многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.