2 класс — деление, задачи и примеры на деление с ответами
Дата публикации: .
Деление предметов на равные группы
1. Раздели стулья на группы по 3 стула в каждой. Сколько всего групп получилось?
2. Раздели уточек на группы по 5 птиц в каждой. Сколько всего групп получилось?
3. Раздели собак на группы по 4 собаки в каждой. Сколько всего групп получилось?
4. Раздели яблоки на группы по 6 штук в каждой. Сколько всего групп получилось?
5. Раздели автомобили на 3 равные группы. Сколько групп получилось?
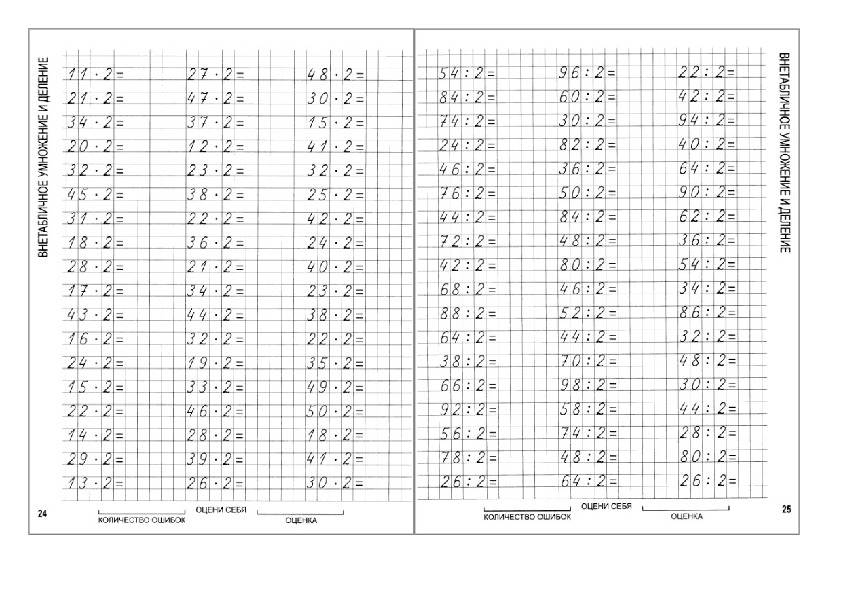
Деление чисел от 1 до 30
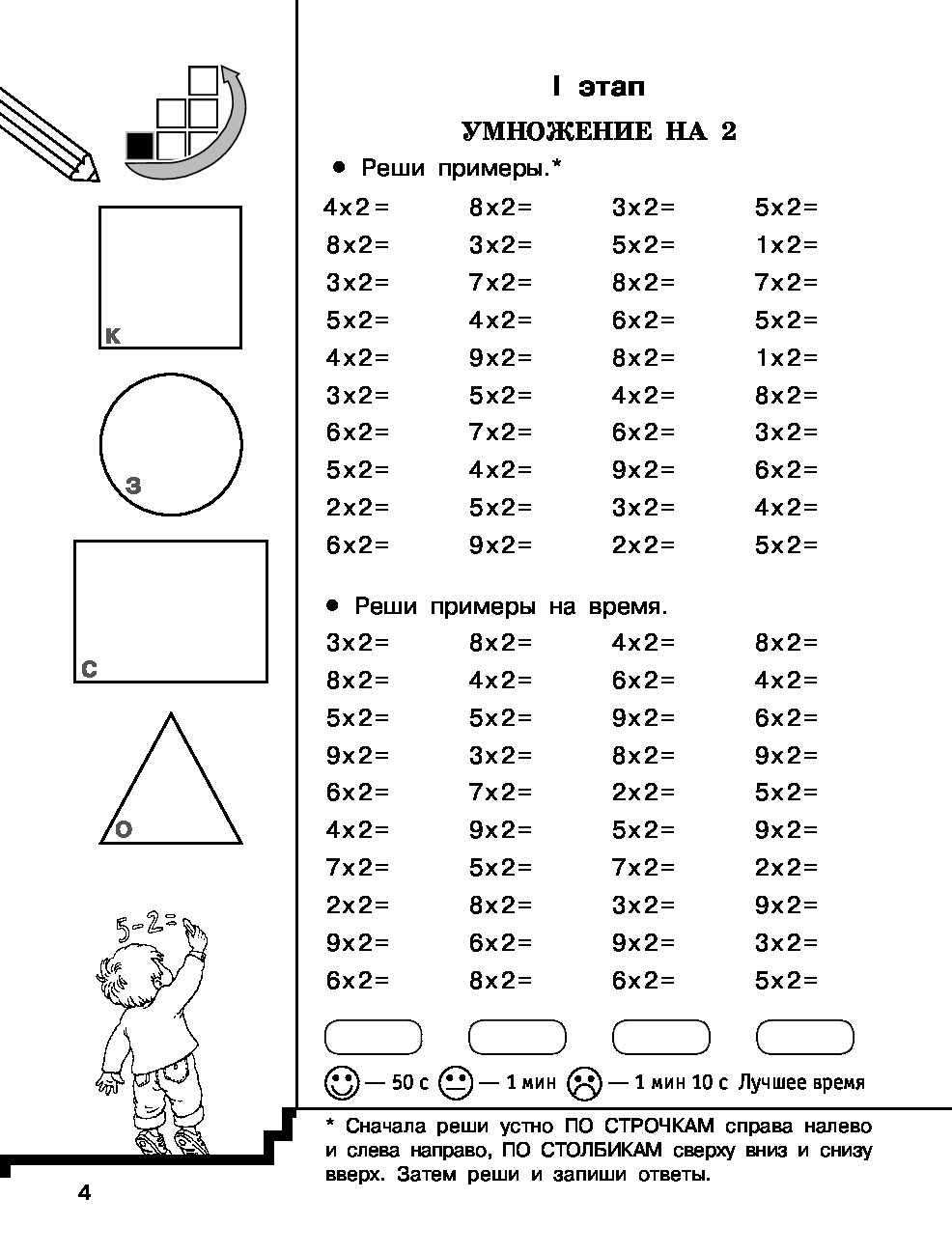
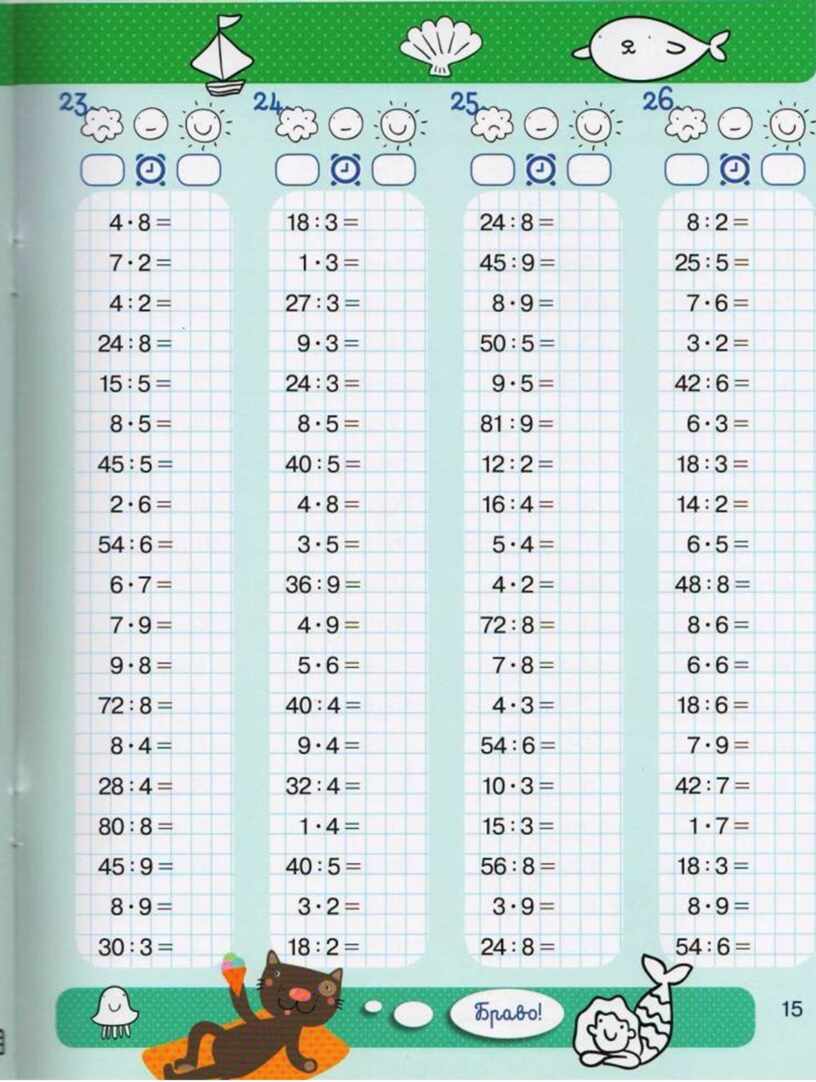
6. Реши примеры на деление и подчеркни делимое.
| 15 : 3 = | 21 : 7 = | 16 : 4 = |
7. Реши примеры на деление и подчеркни делитель:
| 18 : 6 = | 25 : 5 = | 24 : 3 = |
8. Реши примеры на деление и подчеркни частное:
| 10 : 5 = | 28 : 4 = | 20 : 4 = |
9.
10. Раздели квадратики на 10 групп. Сколько всего квадратиков оказалось в каждой группе?
11. Напиши делимое и реши примеры.
12. Используя числовую прямую, реши примеры на деление.
13. Реши примеры.
| 2 : 1 = | 2 : 2 = | 3 : 3 = | 3 : 1 = |
| 4 : 1 = | 4 : 2 = | 4 : 4 = | 5 : 1 = |
| 5 : 5 = | 6 : 1 = | 6 : 2 = | 6 : 3 = |
| 1 : 1 = | 2 : 2 = | 3 : 3 = | 4 : 4 = |
| 3 : 1 = | 4 : 2 = | 6 : 3 = | 8 : 4 = |
| 6 : 1 = | 6 : 2 = | 9 : 3 = | 12 : 4 = |
| 9 : 1 = | 8 : 2 = | 12 : 3 = | 16 : 4 = |
| 12 : 1 = | 10 : 2 = | 15 : 3 = | 5 : 5 = |
| 15 : 1 = | 12 : 2 = | 18 : 3 = | 10 : 5 = |
14.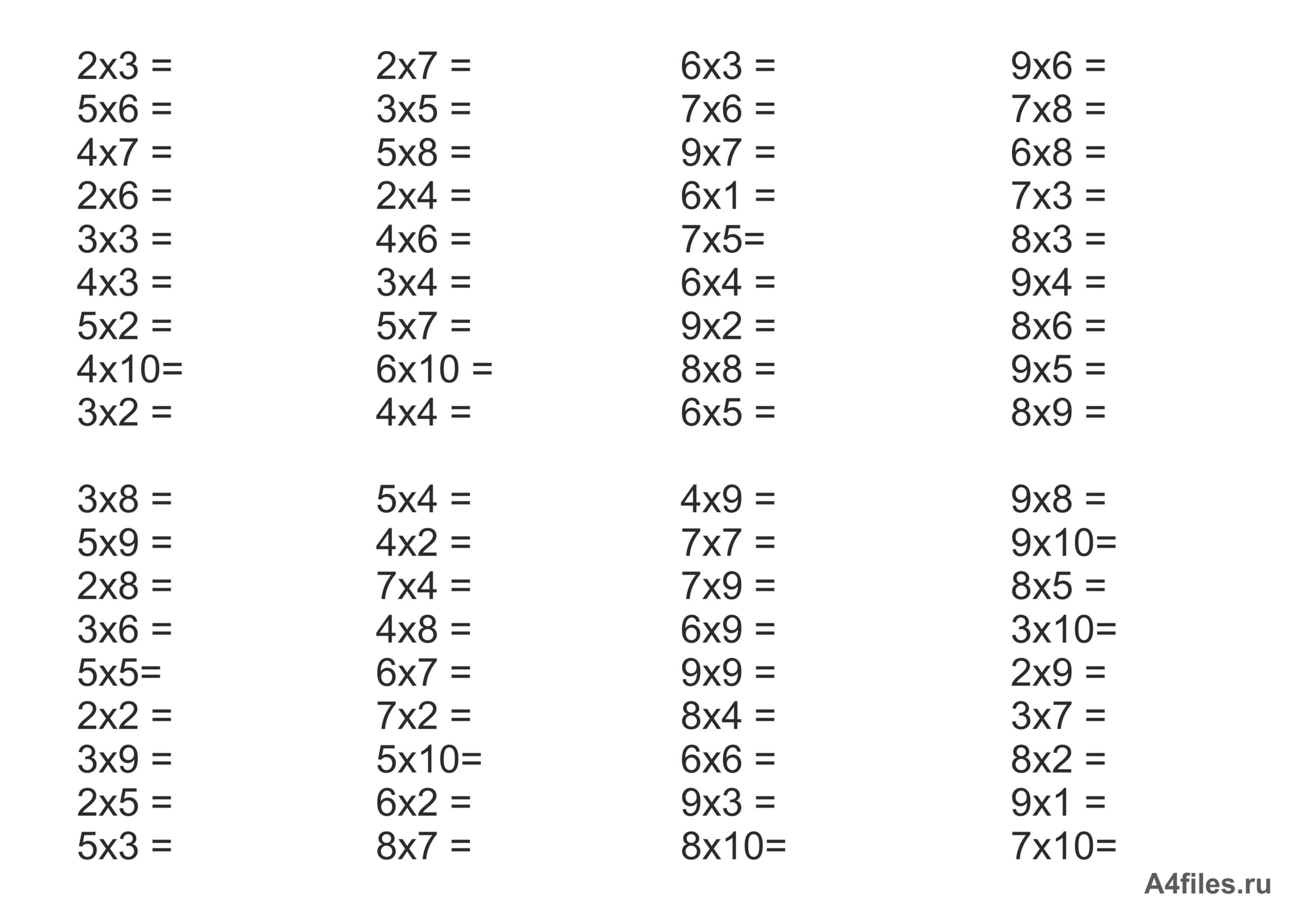 Заполни пропуски числами.
Заполни пропуски числами.
| 6 : __ = 6 | 2 : __ = 1 | 4 : 4 = __ |
| 9 : __ = 3 | __ : 2 = 3 | 8 : __ = 2 |
| __ : 5 = 2 | 6 : __ = 2 | 9 : __ = 3 |
| 8 : 2 = __ | __ : 4 = 3 | 16 : __ = 4 |
| __ : 1 = 7 | 10 : __ = 5 | __ : 3 = 5 |
| 15 : 3 = __ | __ : 2 = 6 | 18 : __ = 3 |
15. Составь числовое выражение на деление к каждому рисунку.
16. Текстовые задачи на деление.
16.1. В больницу привезли 48 рулонов бинтов. Бинты упакованы в пачки по 8 штук в каждой. Сколько пачек с бинтами привезли в больницу?
16.2. Лесники засадили участок земли молодыми саженцами. Всего получилось 9 рядов деревьев. Сколько деревьев было посажено в каждом ряду, если всего было посажено 72 дерева?
16.3. Школьный повар разложил 35 пирожков на 7 тарелок. Сколько пирожков оказалось в каждой тарелке?
16. 4. Ребята из 2 класса пошли в музей. Они шли по 2 человека в ряду. Сколько рядов получилось, если в классе учится 24 школьника? Сколько рядов получится, если идти по 3 человека в ряд, а если по 4 человека в ряд?
4. Ребята из 2 класса пошли в музей. Они шли по 2 человека в ряду. Сколько рядов получилось, если в классе учится 24 школьника? Сколько рядов получится, если идти по 3 человека в ряд, а если по 4 человека в ряд?
16.5. На склад привезли 56 кг картошки. Их надо разложить в 8 мешков. Сколько кг картошки надо положить в каждый мешок?
16.6. В школу надо завести 81 стол. За один раз машина может привезти только 9 столов. Сколько нужно сделать рейсов, чтобы привезти все столы?
16.7. Рыбак поймал 64 кг рыбы и разложил их в 8 ящиков. Сколько кг рыбы поместилось в каждый ящик?
Ответы:
1. 4.2. 3.
3. 4.
4. 3.
5. 5.
6. 15 : 3 = 5; 21 : 7 = 3; 16 : 4 = 4;
7. 18 : 6 = 3; 25 : 5 = 5; 24 : 3 = 8;
8. 10 : 5 = 2; 28 : 4 = 7; 20 : 4 = 5;
9. 2
10. 2
11. 10 : 2 = 5; 9 : 3 = 3; 8 : 4 = 2; 15 : 5 = 3; 18 : 6 = 3.
12.
13.
1 1 1 1 3 2 2 2 6 3 3 3 9 4 4 4 12 5 5 1 15 6 6 214.

6 : 1 = 6 2 : 2 = 1 4 : 4 = 1 9 : 3 = 3 6 : 2 = 3 8 : 4 = 2 10 : 5 = 2 6 : 3 = 2 9 : 3 = 3 8 : 2 = 4 12 : 4 = 3 16 : 3 = 4 7 : 1 = 7 10 : 2 = 5 15 : 3 = 5 15 : 3 = 5 12 : 2 = 6 18 : 6 = 315. 15 : 5 = 3; 20 : 4 = 5; 28 : 4 = 7;
16.
1. 6 пачек;
2. 8 деревьев;
3. 5 конфет;
4. 12 рядов; 8 рядов; 6 рядов;
5. 7 кг;
6. 9 рядов;
7. 8 кг;
3000 примеров по математике. Устный счет. Табличное умножение и деление. 2 класс — Узорова О.В. | 978-5-17-108651-0
Стоимость товара может отличаться от указанной на сайте!г. Воронеж, площадь Ленина, д.4
8 (473) 277-16-90
г. Воронеж, ул. Маршака, д.18А
Воронеж, ул. Маршака, д.18А
8 (473) 231-87-02
г. Липецк, пл.Плеханова, д. 7
8 (4742) 47-02-53г. Богучар, ул. Дзержинского, д.4
8 (47366) 2-12-90
г. Воронеж, ул. Г. Лизюкова, д. 66 а
8 (473) 247-22-55
г. Поворино, ул.Советская, 87
Поворино, ул.Советская, 87
г. Воронеж, ул. Плехановская, д. 33
8 (473) 252-57-43
г. Воронеж, ул. Ленинский проспект д.153
8 (473) 223-17-02
г. Воронеж, ул. Хользунова, д. 35
8 (473) 246-21-08
г. Россошь, Октябрьская пл., 16б
Россошь, Октябрьская пл., 16б8 (47396) 5-29-29
г. Россошь, пр. Труда, д. 26А
8 (47396) 5-28-07
г. Лиски, ул. Коммунистическая, д.7
8 (47391) 2-22-01
8 (4722) 42-48-42
г. Курск, пр. Хрущева, д. 5А
Курск, пр. Хрущева, д. 5А
8 (4712) 51-91-15
г. Губкин, ул. Дзержинского,д. 115
8 (47241) 7-35-57
г.Воронеж, ул. Жилой массив Олимпийский, д.18 (473) 207-10-96
г. Калач, пл. Колхозного рынка, д. 21
8 (47363) 21-857
г. Воронеж, ул.Челюскинцев, д 88А
Воронеж, ул.Челюскинцев, д 88А
8 (4732) 71-44-70
8 (4725) 23-38-06
г. Курск, ул.Карла Маркса, д.6
8 (4712) 54-09-50
г. Воронеж, Московский пр-т, д. 129/1
8 (473) 269-55-64
ТРЦ «Московский Проспект», 3-й этаж
Урок 64.
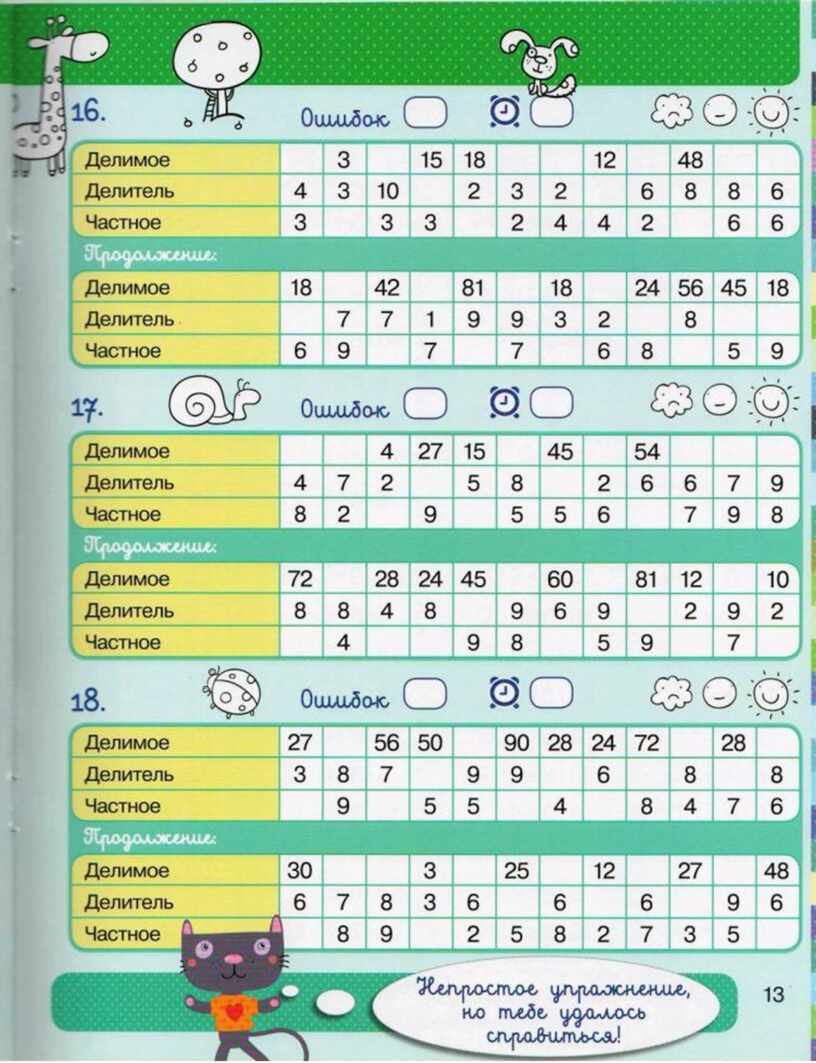 деление на 2 — Математика — 2 класс
деление на 2 — Математика — 2 классМатематика, 2 класс
Урок № 64. Деление на 2
Перечень вопросов, рассматриваемых в теме:
- Какое действие обратное умножению?
- Как найти неизвестный множитель?
- Как составить таблицу деления на 2 и таблицу, когда частное равно 2.
- Для чего необходимо знать деление на 2?
Глоссарий по теме:
Умножение – это сложение одинаковых слагаемых. Знак умножения — *, х.
Компоненты умножения: первый множитель, второй множитель.
Результат умножения – произведение.
Деление – действие обратное умножению.
Компоненты деления: делимое, делитель, частное.
Делимое – число, которое делят.
Делитель – число, на которое делят.
Частное – результат деления.
Обязательная литература и дополнительная литература:
- Моро М.И., Бантова М.А. и др. Математика 2 класс. Учебник для общеобразовательных организаций М.
 ; Просвещение, 2017. – с. 83
; Просвещение, 2017. – с. 83 - М.И.Моро, С.И.Волкова. Для тех, кто любит математику 2 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 56
Теоретический материал для самостоятельного изучения
Рассмотрим равенство. 2 • 4 = 8, где 2 – первый множитель, 4 – второй множитель, 8 – произведение.
Действие деление обратное действию умножения. Если произведение разделить на один из множителей, то получится второй множитель. Поэтому составим равенства на деление.
8 : 2 = 4
8 : 4 = 2
Перед вами таблица умножения числа 2.
Пользуясь данной таблицей, можно легко составить таблицу, где делитель равен 2.
И таблицу, где частное равно 2.
Мы составили таблицу деления на число 2 и таблицу, когда в частном получается 2. Достаточно знать хотя бы один из предложенных столбиков таблицы, можно быстро найти значения других выражений.
Для чего необходимо знать деление на 2? Знание таблицы деления на 2 помогает быстро выполнять вычисления и решать задачи.
Закончим записи, чтобы получились верные равенства.
3 • 2 = 6 2 • 5 = □ 2 • □ = 12
6 : 3 = □ 10 : □ = 5 12 : 2 = □
6 : 2 = □ 10 : □ = 2 □ : 6 = 2
Пользуясь таблицей умножения и на основе взаимосвязи между умножением и делением, выполним это задание.
3 • 2 = 6 2 • 5 = 10 2 • 6 = 12
6 : 3 = 2 10 : 2 = 5 12 : 2 = 6
6 : 2 = 3 10 : 5 = 2 12 : 6 = 2
Решим задачу.
За партами сидели 18 учеников, по 2 за каждой партой. Сколько парт заняли ученики?
Решение: 18 : 2 = 9 (п.)
Ответ: 9 парт заняли ученики.
Решим еще одну задачу.
Бабушка решила разложить 8 пирожков на 4 тарелки. Сколько пирожков на одной тарелке?
Решение: 8 : 4 = 2 (пирожка)
Ответ: 2 пирожка на одной тарелке.
Вывод:
Ответим на вопросы, поставленные в начале урока.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Действие деление обратное действию умножения.
Если произведение разделить на один из множителей, то получится второй множитель.
Зная таблицу умножения числа 2 и взаимосвязи между компонентами действия умножения, можно составить таблицу деления на 2 и таблицу, когда в частном число 2.
Знание таблицы деления на 2 помогает быстро выполнять вычисления и решать задачи.
Выполним несколько тренировочных заданий.
1. Вычислите произведение и в каждой строке, используя его, найдите частное.
9 • 2 = □ □ : 2 = □ □ : 9 = □
2 • 6 = □ □ : 2 = □ □ : 6 = □
Проверьте:
9 • 2 = 18 18 : 2 = 9 18 : 9 = 2
2 • 6 = 12 12 : 2 = 6 12 : 6 = 2
2. Решите задачу.
Все 12 вафель разложили в 2 вазочки поровну. Сколько вафель в одной вазочке?
Решение: 12 : 2 = 6 (в. )
)
Ответ: 6 вафель в одной вазочке.
3. Из чисел 4, 17, 3, 8, 10, 15, 11, 16 выпишите сначала те, которые делятся на 2. Затем выпишите те числа, которые на 2 не делятся.
Делятся на 2 – 4, 8, 10, 16.
На 2 не делятся – 17, 3, 15, 11.
Считаем быстро 2000 примеров по математике умножение и деление 2 класс — Математика Тетради 2 класс — Тетради 2 класс НУШ
Добавить отзыв
ISBN: 9789669392527
Автор книги: Солодовник С.
Издательство: Торсінг
Страниц: 16
Язык: украинский
Количество:
Добавить в корзину
Краткая информация
Это маленькое пособие содержит математические примеры на сложение и вычитание и поможет вашему ребенку тренироваться в любое время. А вы всегда сможете убедиться в том, что малыш обладает необходимыми навыками.
А вы всегда сможете убедиться в том, что малыш обладает необходимыми навыками.
Читать дальше
Скрыть
21 | 14 | 30 | |||||
Т | Р | Е | К | О | З | А | |
3000 примеров по математике. 2 класс. Устный счет. Табличное умножение и деление. Артикул: p2404373
Устному счету отведено несколько книг, включенных в общую серию «3000 примеров по математике». Каждая посвящена одной из важнейших программных тем, которые изучаются в 1-4 классах начальной школы. Количество примеров в книгах различно и увеличивается от класса к классу, от темы к теме. Всего для отработки навыков устного счета предлагается 3000 математических примеров.
В этом пособии представлен материал, направленный на формирование навыков устного счета по теме «Табличное умножение и деление» для 2 класса.
Устный счет развивает сообразительность и внимание учащихся, воспитывает математическую находчивость и укрепляет память. Правильная постановка занятий устным счетом в начальной школе предполагает ежедневные и непродолжительные (от 5 до 10 минут) упражнения. Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счета всех форм:
Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счета всех форм:
Беглый слуховой счет. (Учитель устно называет пример и устно же, спустя несколько секунд, получает ответ.)
Зрительный счет. (Примеры записаны, а ответы называются либо устно, либо записываются учениками.)
Комбинированный счет. (Учитель диктует примеры, а ученик записывает ответы.) Устное решение задач.
Устному счету отведено несколько книг, включенных в общую серию «3000 примеров по математике». Каждая посвящена одной из важнейших программных тем, которые изучаются в 1-4 классах начальной школы. Количество примеров в книгах различно и увеличивается от класса к классу, от темы к теме. Всего для отработки навыков устного счета предлагается 3000 математических примеров.
В этом пособии представлен материал, направленный на формирование навыков устного счета по теме «Табличное умножение и деление» для 2 класса.
Устный счет развивает сообразительность и внимание учащихся, воспитывает математическую находчивость и укрепляет память. Правильная постановка занятий устным счетом в начальной школе предполагает ежедневные и непродолжительные (от 5 до 10 минут) упражнения. Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счета всех форм:
Беглый слуховой счет. (Учитель устно называет пример и устно же, спустя несколько секунд, получает ответ.)
Зрительный счет. (Примеры записаны, а ответы называются либо устно, либо записываются учениками.)
Комбинированный счет. (Учитель диктует примеры, а ученик записывает ответы.) Устное решение задач.
2ЭТАП. ПОДГОТОВКА УЧАЩИХСЯ К РАБОТЕ НА ОСНОВНОМ ЭТАПЕ УРОКА 4. Проверка домашнего задания. Актуализация знаний. Реализация обще учебных умений и навыков. Цель: Организовать коррекцию выявленных пробелов в осмыслении уч-ся изученного материала. Развивать логическое мышление.
Включение детей в деятельность на личностно-значимом уровне. Цель –закрепить таблицу умножения, деления | -1 ученик работает с интерактивным заданием Дети комментируют выполнение задания записывают ответы — проверяют и оценивают сделанную работу.
Ребята ищут нужные цифры, выполняя необходимые действия, и перетаскивают их к примеру,(приём «конструктор») располагая справа от него, затем с целью проверки они проносят каждый пример сквозь трубу,(труба взята на панели инструментов, в разделе фигуры) справа «вытаскивают проверку» Если все верно, то такие же ответы дети видят на синем фоне (приём «автоматическая проверка»)
Дети определяют тему урока. (картинка взята из галереи). работают в программе panaboard, (отвечают на вопросы учителя) — формулируют тему урока и ставят цель
| — диктует задания и следит за выполнением — организует работу учащихся по проверке, -проводит инструктаж, организует фронтальную работу с сигнальными карточками (организует обратную связь) — организует работу по демонстрационному материалу — называет цель урока, чему должны научиться учащиеся . Направляет детей. | (4 страница) -Исследуйте примеры из домашнего задания, сделайте вывод? (-Есть примеры на умножение, деление и вычитание.) У: Итак, чем же мы будем заниматься на этом уроке? (Я думаю, что будем умножать и делить на 2 ) — Какую цель поставите себе на этот урок? Закрепить таблицу умножения и деления на 2) — А для чего? Чтобы потом быстро делить конфеты, решать примеры на уроках, прикидывать, сколько денег нужно отдать за 3 шоколадки в магазине, сколько чашек нужно поставить на стол, если придут 3 гостя. — Что мы должны сделать, чтобы закрепить таблицу умножения и деления на 2? (Дети формулируют задачи урока) порешать примеры, задачи, устроить отдых глазам. Ребята высказывают свои предположения, строят рассуждения, допускают существование различных точек зрения, формулируют собственное мнение (коммуникативные и познавательные УУД). Познавательные УУД. Самостоятельно выделять и формулировать познавательные задачи.
Регулятивные УУД. Целеполагание, планирование. | Докажите, что здесь лишнее? (Я думаю, что лишнее здесь 15 – 6 , т.к. этот пример на вычитание, а все остальные на умножение и деление), -Ну, раз лишний уберём. Сделайте вывод, о том, чем же мы будем заниматься на этом уроке? (пример 15-7 затеняется, «приём скрытие объекта») (5 страница) |
для класса 2
Основы подразделения
2-значное деление
3-значное деление
Дивизия с остатком
Задача со словом
Дивизионный тест
Рабочий лист отдела
Лист для ответов
Основы подразделения
Мы можем сказать, что разделение — это процесс, с помощью которого может быть выполнено равное распределение между группой, и это обозначается как.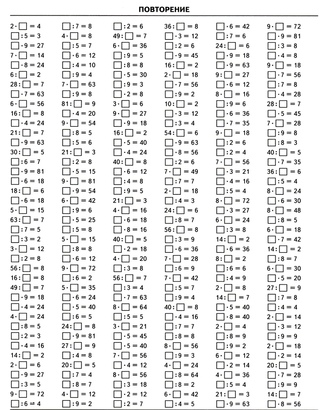 Давайте посмотрим на несколько примеров.
Давайте посмотрим на несколько примеров.
Пример 1. Есть 25 конфет, надо поровну распределить между 5 мальчиками. Сколько шоколадных конфет должен получить каждый мальчик?
Решение. Количество конфет, которые получит каждый мальчик = Общее количество конфет Количество мальчиков
= 25 5
Мы должны найти в 5 таблицах, откуда идет 25, т.е. 5 X 5 = 25
Это означает, что 25 5 = 5
Каждый мальчик должен получить по 5 шоколадных конфет.
Из приведенного выше примера мы заключаем, что деление можно производить с помощью таблиц.
2-значный раздел
Давайте узнаем еще один способ деления чисел.
Пример 1. 72 4
Решение.
Шаг 1.
Начните с десятков на первом месте.
7 десятков 4 = 1 десяток
Напишите 1 десять выше 7.
Шаг 2. Вычтите 4 из 7.
7 десятков 4 десятков = 3 десятков
Шаг 3.
Сбейте 2 с одного места.
3 десятка + 2 единицы = 32
Шаг 4.
Разделим 32 на 4. Другими словами, мы должны найти в таблице 4s, откуда приходит 32.
4 X 8 = 32
32 4 = 8
8 переходит в разряд единиц. Вычтем 32 из 32.
32 32 = 0
Итак, 72 4 = 18
Здесь 72 известно как делимое, 4 известно как делитель, а 18 известно как частное.
3-значное деление
Это похоже на двузначное деление.Давайте посмотрим на несколько примеров.
Пример 1. 456 3
Решение.
Шаг 1.
Начните с сотни.
4 сотни 3 = 1 сотня
Запишите 1 сотню выше 4.
Шаг 2.
Вычтите 3 из 4.
4 сотни 3 сотни = 1 сотню
Шаг 3.
Вычтите 5 из разряда десятков .
1 сотня + 5 десятков = 10 десятков + 5 десятков = 15 десятков
Разделите 15 на 3.Другими словами, мы должны найти в таблице 3s, откуда приходит 15.
3 X 5 = 15
15 3 = 5
5 идет до разряда десятков частного. Вычтите 15 из 15, т. Е. 15 15 = 0
Вычтите 15 из 15, т. Е. 15 15 = 0
Шаг 4.
Вычтите 6 из единицы делимого на единицу.
6 3 = 2
2 идет до единицы частного.
Итак, 456 3 = 152
Пример 2. 675 5
Решение.
Итак, ответ — 135.
с остатком
Предположим, у нас есть 6 шоколадных конфет, и мы должны поровну разделить их между 5 детьми. Если мы дадим каждому ребенку по одной шоколадке, то закончится 5 шоколадок и 1 шоколадка. останется с нами. Давайте рассмотрим несколько примеров, приведенных ниже.
Пример 1. 75 4
Решение.
Здесь 75 — делимое, 4 — делитель, 18 — частное, а 3 — остаток.
Пример 2. 93 5
Решение.
Здесь 93 — делимое, 5 — делитель, 18 — частное, а 3 — остаток.
Задача со словом
В нашей повседневной жизни разделение используется для решения разных задач. Давайте посмотрим на несколько примеров.
Пример 1. Разделите 65 конфет между 5 девушками. Сколько конфет получит каждая девушка?
Решение. Общее количество конфет = 65
Количество девушек = 5
Каждая девочка получит = Общее количество конфет Количество девочек
= 65 5
Каждая девочка получит по 13 шоколадных конфет.
Дивизионное испытание
Дивизионный тест — 1
Дивизионный тест — 2
Рабочий лист отделения 2 класса
Рабочий лист отдела — 1
Рабочий лист отдела — 2
Рабочий лист отдела — 3
Лист для ответов
Division-Answer Скачать pdf
Авторские права © LetsPlayMaths, 2021 г.com. Все права защищены.
Как ввести таблицы умножения для 2, 5 и 10
Таблицы умножения для 2, 5 и 10 — это первый набор таблиц умножения, которые студенты изучают во 2-м классе, потому что они следуют легко запоминающимся образцам и, следовательно, более «дружелюбны» чем другие таблицы умножения. В этом сообщении блога мы поговорим о некоторых из наиболее важных концепций, на которых следует сосредоточиться, расширяя то, что мы узнали во вводном уроке.
В этом сообщении блога мы поговорим о некоторых из наиболее важных концепций, на которых следует сосредоточиться, расширяя то, что мы узнали во вводном уроке.
Прежде чем мы официально представим таблицы умножения для 2, 5 и 10, сначала убедитесь, что мы знаем, что означает умножение, т.е.е. мы должны уметь интерпретировать 4 x 2 как означающие «четыре группы по два».
Затем, чтобы представить каждую из таблиц умножения для 2, 5 и 10, мы можем начать с подсчета пропусков, т. Е. 2,4,6,… и затем перейти к использованию точечной бумаги (точки в строках и столбцах, ).
Наконец, мы представим свойство распределения для умножения — выразить конечный продукт как сумму или разность двух «простых» операций умножения. Например:
Точечное представление бумаги особенно полезно при введении распределительного свойства умножения.Например, во втором примере, приведенном выше, 7 × 2 может быть организовано в «ориентирные» числа, которые мы выучили в десяти кадрах, то есть 5 и 10.
Многие ученики 2 и классов могут уже знать ответ на 7 × 2, и может не понимать, почему нам нужно разбивать числа, используя свойство распределения, но важно, чтобы мы подготовили почву для подготовки к большим числам позже.
Здесь мы возвращаемся к двум взаимосвязанным концепциям деления, например 12 ÷ 4 может означать количество объектов в каждой группе, когда 12 объектов разделены на 4 равные группы.Это также может означать количество групп, когда 12 объектов разделены на группы по 4.
Связанные факты и семейные факты — отличные инструменты для решения задач умножения и деления. Например, если 6 x 2 = 12, связанный факт будет 12 ÷ 2 = 6. Пусть учащиеся потренируются придумывать собственные связанные факты, чтобы научиться бегло говорить.
Затем попросите учащихся сгруппировать связанные факты в семейные, например,
- 2 x 4 = 8
- 4 x 2 = 8
- 8 ÷ 2 = 4
- 8 ÷ 4 = 2
Студенты могут использовать эвристики, такие как «разыграть» или «нарисовать диаграмму» для умножения и деления, и поделиться своими идеями с классом.
Пришло время представить моделирование стержней. Например,
Это позволяет учащимся освоить задачи умножения и деления в моделях столбцов, которые пригодятся при решении задач со словами.
Это может быть непросто для некоторых учащихся, если они плохо владеют своими семейными фактами умножения и деления (см. Выше). Например,
Определите неизвестное число, которое делает уравнение истинным в каждом из следующих случаев:
- 2 x? = 8
- 15 =? х 3
- 5 х 5 =?
Один из способов попрактиковаться — это написать семейство из 4 основных фактов с учетом любого из основных фактов (например,грамм. учитывая 2 x 4 = 8, найдите остальные семейные факты — 4 x 2 = 8, 8 ÷ 2 = 4 и 8 ÷ 4 = 2).
Это совокупное свойство
- (например, 2 × 5 = 5 × 2),
- ассоциативное свойство (например, 2x5x10 = (2 × 5) x10) и распределительное свойство
- (например, 7 × 5 = (5 × 5) + (2 × 5)).

На этом этапе мы не хотим подчеркивать жаргоны, но мы хотим, чтобы учащиеся понимали каждое из этих свойств и практиковались в их использовании, чтобы помочь распознавать различные способы решения проблем.
Деление можно интерпретировать как пропущенное число в задаче с неизвестным фактором. Например, мы можем начать с
2 x 6 = 12
Затем, скрывая один из факторов,
2 x? = 12
Тогда посмотрите, что пропущенное (неизвестное) число всего
? = 12 ÷ 2
Видео-объяснение и план урока (ресурс участника)
Общие основные стандарты
- A1 Расшифровка произведений целых чисел.
- A2 Интерпретация целочисленных частных целых чисел.
- A3 Используйте умножение и деление для решения задач со словами.
- A4 Определите неизвестное целое число в уравнении умножения или деления, связывающее три целых числа.
- B5 Применяйте свойства операций как стратегии умножения и деления.
- B6 Поймите разделение как проблему с неизвестным фактором.

- BC Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением или свойства операций.
Рекомендуемая серия учебников
- Учебное пособие по математике в фокусе (2A) Глава 5 — Умножение и деление (страницы 107–126)
- Учебное пособие по начальной математике (Common Core Edition) (2A) Глава 4 — Умножение и деление (страницы 112 по 134)
Дополнительные рабочие листы
Умножение и деление — целые числа | Правила | Примеры
Умножение и деление целых чисел — две основные операции, которые мы выполняем с целыми числами.Умножение включает в себя сложение определенного числа заданное количество раз. Например, 4 × 3 — это не что иное, как трехкратное сложение 4. С другой стороны, разделение означает распределение количества на равные группы. Но в случае с целыми числами мы должны позаботиться о знаке, прикрепленном к числам, который означает, является ли число положительным или отрицательным. Существуют разные правила умножения и деления целых чисел, которые мы подробно изучим в этом уроке.
Существуют разные правила умножения и деления целых чисел, которые мы подробно изучим в этом уроке.
Умножение и деление целых чисел
Четыре основные арифметические операции, связанные с целыми числами:
Умножение и деление целых чисел — наиболее часто используемые арифметические операции.Давайте подробно изучим умножение и деление целых чисел.
Умножение целых чисел
Умножение целых чисел — это процесс повторяющегося сложения положительных и отрицательных чисел или просто целых чисел. Когда мы подходим к случаю целых чисел, необходимо учитывать следующие случаи:
- Умножение 2 положительных чисел
- Умножение двух отрицательных чисел
- Умножение 1 положительного и 1 отрицательного числа
При умножении целых чисел на два положительных знака Положительное x Положительное = Положительное = 2 x 5 = 10
При умножении целых чисел на два отрицательных знака Отрицательное x Отрицательное = Положительное = –2 x –3 = 6
Когда вы умножаете целые числа на один отрицательный знак и один положительный знак, Отрицательное x Положительное = Отрицательное = –2 x 5 = –10
Следующая таблица поможет вам запомнить правила умножения целых чисел:
| Типы целых чисел | Результат | Пример |
| Оба целых положительные | Положительно | 2 х 5 = 10 |
| Оба целых числа отрицательные | Положительно | –2 x –3 = 6 |
| 1 положительный и 1 отрицательный | отрицательный | –2 x 5 = –10 |
Анна съедает 4 печенья в день. Сколько печенья она съедает за 5 дней? ⇒ 5 × 4 = 20 печенек.
Сколько печенья она съедает за 5 дней? ⇒ 5 × 4 = 20 печенек.
Деление целых чисел
Деление целых чисел включает в себя группировку элементов. Он включает как положительные, так и отрицательные числа. Как и умножение, деление целых чисел также включает те же случаи.
- Деление 2 положительных чисел
- Разделение 2 отрицательных чисел
- Деление 1 положительного и 1 отрицательного числа
При делении целых чисел на два положительных знака Положительное ÷ Положительное = Положительное 16 ÷ 8 = 2
При делении целых чисел на два отрицательных знака Отрицательное ÷ Отрицательное = Положительное = –16 ÷ –8 = 2
При делении целых чисел с одним отрицательным знаком и одним положительным знаком Отрицательное ÷ Положительное = Отрицательное = –16 ÷ 8 = –2.
Следующая таблица поможет вам запомнить правила деления целых чисел:
| Типы целых чисел | Результат | Пример |
| Оба целых положительные | Положительно | 16 ÷ 8 = 2 |
| Оба целых числа отрицательные | Положительно | –16 ÷ –8 = 2 |
| 1 положительный и 1 отрицательный | отрицательный | –16 ÷ 8 = –2 |
Чтобы подвести итог и упростить все, при умножении или делении двух целых чисел нужно помнить две самые важные вещи:
- Если знаки разные, ответ всегда отрицательный.

- Когда знаки одинаковые, ответ всегда положительный.
Примеры умножения и деления целых чисел
Несколько примеров умножения и деления целых чисел приведены в таблице ниже:
| Умножение | Дивизион |
|---|---|
| 4 × 2 = 8 | 15 ÷ 3 = 5 |
| 4 × -2 = –8 | 15 ÷ –3 = –5 |
| –4 × 2 = –8 | –15 ÷ 3 = –5 |
| –4 × -2 = 8 | –15 ÷ –3 = 5 |
Свойства умножения и деления целых чисел
Свойства умножения и деления целых чисел помогают нам идентифицировать отношения между двумя или более целыми числами, когда они связаны между собой операцией умножения или деления.Есть несколько свойств, связанных с умножением и делением целых чисел.
Свойства, связанные с умножением и делением целых чисел, перечислены ниже:
- Свойство закрытия
- Коммутативная собственность
- Ассоциативное свойство
- Распределительная собственность
- Собственность личности
Давайте подробно разберемся с каждым свойством в отношении умножения и деления целых чисел.
Закрытие собственности
Свойство закрытия указывает, что набор закрыт для любой конкретной математической операции. Целые числа закрываются при сложении, вычитании и умножении. Однако на разделение они не закрываются.
| Эксплуатация | Пример |
|---|---|
| a × b целое число | 2 × –6 = –12 |
| a ÷ b не всегда целое число | –3/4 — дробь |
Коммутационная собственность
Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат.Сложение и умножение целых чисел следуют свойству коммутативности, в то время как деление целых чисел не имеет этого свойства.
| Эксплуатация | Пример |
|---|---|
| a × b = b × a | 5 × (–6) и (–6) × 5 = –30 |
| a ÷ b ≠ b ÷ a | 15 ÷ 3 = 5, но 3 ÷ 15 = 1/5 |
Ассоциативное свойство
Согласно свойству ассоциативности изменение группировки двух целых чисел не влияет на результат операции. Свойство ассоциативности применяется к сложению и умножению двух целых чисел, но не в случае деления целых чисел.
Свойство ассоциативности применяется к сложению и умножению двух целых чисел, но не в случае деления целых чисел.
| Эксплуатация | Пример |
|---|---|
| (a × b) × c = a × (b × c) | (5 × –3) × 2 = –30 5 × (–3 × 2) = –30 |
| (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) | (20 ÷ 5) ÷ 2 = 2, но 20 ÷ (5 ÷ 2) = 8 |
Распределительная собственность
Распределительное свойство утверждает, что для любого выражения формы a (b + c), что означает a × (b + c), операнд a может быть распределен между операндами b и c как: (a × b + a × c) i .е., a × (b + c) = a × b + a × c.
| Эксплуатация | Пример |
|---|---|
| a × (b + c) = (a × b) + (a × c) | 4 × (–3 + 6) = 12 (4 × –3) + (4 × 6) = 12 |
| a × (b — c) = (a × b) — (a × c) | 2 × (5 — 3) = 4 (2 × 5) — (2 × 3) = 4 |
Идентификационная собственность
В случае сложения целых чисел 1 — это мультипликативная единица. В случае деления целых чисел элемент идентичности отсутствует.
В случае деления целых чисел элемент идентичности отсутствует.
| Идентификатор при добавлении: 0 | Удостоверение при умножении: 1 |
|---|---|
| Для любого целого числа a, a + 0 = 0 + a = a | Для любого целого числа a 1 × a = a × 1 = a |
| Например, 8 + 0 = 0 +8 = 8 | Например, (- 4) × 1 = 1 × (- 4) = — 4 |
Важные примечания
- Нет ни наименьшего целого, ни наибольшего целого числа.
- Наименьшее положительное целое число равно 1, а наибольшее отрицательное целое число равно -1.
- Правило PEMDAS применяется для операций с целыми числами. «Операциями» являются любые из следующих: скобки, квадраты, степени, квадратные корни, деление, умножение, сложение и вычитание.
Пример 1: Разделите данное выражение: (–20) ÷ (–5) ÷ (–2) =?
Решение:
Здесь мы должны разделить три целых числа, поэтому мы будем следовать правилу BODMAS, поскольку в этом выражении есть более одной операции.
 Шаг 1 равен (–20 ÷ –5) ÷ (–2). Теперь, разделив -20 на -5, мы получим 4 в качестве ответа. Итак, новое выражение (4) ÷ (–2). 4 — целое положительное число, так как отрицательное ÷ отрицательное = положительное. Теперь, если мы разделим 4 на -2, мы получим -2 как положительное ÷ отрицательное = отрицательное. Следовательно, (–20) ÷ (–5) ÷ (–2) = –2.
Шаг 1 равен (–20 ÷ –5) ÷ (–2). Теперь, разделив -20 на -5, мы получим 4 в качестве ответа. Итак, новое выражение (4) ÷ (–2). 4 — целое положительное число, так как отрицательное ÷ отрицательное = положительное. Теперь, если мы разделим 4 на -2, мы получим -2 как положительное ÷ отрицательное = отрицательное. Следовательно, (–20) ÷ (–5) ÷ (–2) = –2.Пример 2: Тест состоит из 20 вопросов. Правильные ответы получают +3, а неправильные — -1. Студент неверно ответил на 5 вопросов. Сколько баллов набрал студент?
Решение:
Если 1 ответ правильный, начисляется 3 балла.Таким образом, за 15 правильных ответов набранные баллы будут 15 × 3 = 45. Если 1 ответ неправильный, дается -1 балл. Таким образом, за 5 неправильных ответов будет получено (5 × -1) = -5. Впоследствии ученик наберет 45 — 5 = 40 баллов. Таким образом, итоговая оценка составит 40 баллов.
перейти к слайду
Часто задаваемые вопросы об умножении и делении целых чисел
Что такое целые числа?
Положительные целые числа, ноль и отрицательные числа вместе образуют целые числа.
Как складывать и вычитать целые числа?
Если нужно сложить или вычесть два целых числа, посмотрите на знаки целых чисел. Если оба числа положительны, сложите их, и сумма будет положительной. Если оба числа отрицательны, сложите их, и сумма будет отрицательной. Если одно из чисел положительное или отрицательное, вычтите, и разница будет иметь знак большего числа.
Могут ли целые числа быть отрицательными?
Да, целые числа включают в себя все отрицательные числа.Это числовые противоположности положительных чисел. Пример: -5, -63, -5, -1 и так далее.
Целые числа — целые числа?
Да. Все целые числа 0, 1, 2, 3, …….. являются целыми числами. Набор целых чисел принадлежит набору целых чисел.
Что такое правило деления целых чисел?
Правила деления целых чисел приведены ниже:
- Положительный ÷ положительный = положительный
- Отрицательный ÷ отрицательный = положительный
- Отрицательный ÷ положительный = отрицательный
Как умножать целые числа?
При умножении следуйте этой уловке, чтобы легко получить ответ:
- Умножаем без знака минус.

- Если оба целых числа отрицательные или оба положительные , окончательный ответ будет положительным .
- Если одно целое число положительно, а другое отрицательно, окончательный ответ будет отрицательным .
Как умножить несколько целых чисел?
Если целых чисел больше двух, выполните следующие простые шаги, чтобы их умножить:
- Умножаем без знака минус.
- Знак окончательного ответа можно определить по количеству отрицательных знаков.
- Если общее количество отрицательных знаков равно , окончательный ответ будет положительных .
- Если общее количество отрицательных знаков нечетное , окончательный ответ будет отрицательным .
Каковы четыре правила умножения целых чисел?
Четыре правила умножения целых чисел указаны ниже:
- Правило 1: Положительный x Положительный = Положительный
- Правило 2: Положительное x Отрицательное = Отрицательное
- Правило 3: Отрицательный x Положительный = Отрицательный
- Правило 4: Отрицательный x Отрицательный = Положительный
Как умножить положительное и отрицательное целое число?
Когда у нас есть два целых числа, одно положительное и одно отрицательное, выполните следующие простые шаги, чтобы получить их произведение:
- Умножаем без знака минус.

- Добавьте отрицательный знак к ответу, чтобы получить окончательный ответ.
Модели и стратегии умножения и деления | Scholastic
Чтобы продолжить мой последний блог о сложении и вычитании, я хотел бы рассмотреть различные стратегии и модели, используемые при умножении и делении. Очень важно, чтобы учащиеся понимали, что они делают, а не просто запоминали шаги и процедуры. Им нужно уметь анализировать и критически относиться к числам и их соотношению.Традиционные алгоритмы умножения и деления важны, и каждый студент должен знать, как их использовать, но только после того, как они укрепят свое понимание. Начиная с конкретной концепции, переходя к рисунку и, наконец, заканчивая абстрактным, учащиеся могут полностью развить мастерство.
Ниже приведены некоторые модели, которые учащиеся используют, чтобы помочь им понять взаимосвязь между умножением и делением. Надеюсь, что просмотр этих моделей и понимание того, как ими пользоваться, помогут вам, когда вы увидите, как их использует ваш ребенок.
Массивы: Это одна из самых ранних моделей, используемых для понимания концепции умножения и деления. Они помогают студентам увидеть связь между двумя операциями, а студенты могут визуально увидеть концепцию «группировки» или «совместного использования». Массивы — отличный способ помочь ученикам запомнить факты умножения и деления, а не просто использовать флеш-карточки.
Изображение: Eduplace.org
Модели области: Модель области тесно связана с вычислениями, используемыми при вычислениях по стандартному алгоритму.Разница заключается в визуальном представлении и связи с Системой Base 10, а также в понимании значения места. Студенты могут визуально видеть фактический размер каждого вычисления и узнавать, как интерпретировать частичные продукты.
Изображение: Tes.com
Модели стержней: Модели стержней основаны на концепции равных групп и частей-частей-целых. Эта модель помогает студентам отойти от конкретной фазы и начинает помогать им понять сцену изобразительного искусства.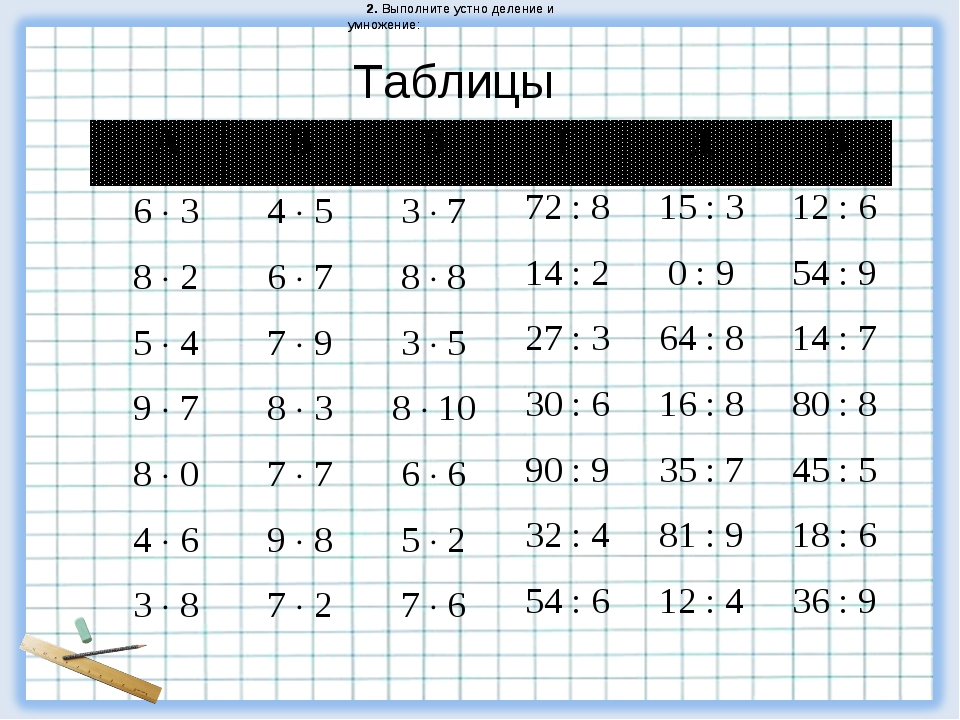 Столбчатые модели — отличный способ помочь учащимся проявить свое мышление при решении задач, особенно при решении двухэтапных задач.
Столбчатые модели — отличный способ помочь учащимся проявить свое мышление при решении задач, особенно при решении двухэтапных задач.
Изображение: Wikipedia.org
Числовые линии: Числовые линии позволяют учащимся начать понимать абстрактную стадию умножения и деления. Учащиеся начинают связывать подсчет пропусков и умножение числа с нахождением произведения фактора. Они могут «переходить» вперед или назад, чтобы представить обратную операцию. Числовые линии — отличные модели, которые помогают учащимся показать свое мышление и объяснить свои рассуждения.
Изображение: Eduplace.com
5 забавных способов научить умножению фактов
Несколько месяцев назад я написал сообщение об использовании чтения вслух для обучения умножению . Я всегда нахожусь в поиске новых идей, чтобы помочь студентам усвоить факты умножения. Интересно, что мне не всегда нравилось узнавать факты об умножении. Я помню, как сидел на кухне с папой и копировал факты на учетные карточки. Было так скучно! Я просто хотел выйти на улицу и поиграть, но я знал, что мой отец хочет для меня самого лучшего.Перенесемся на 25 лет вперед, и теперь я хочу убедиться, что изучение фактов умножения не должно быть утомительной задачей для студентов.
Было так скучно! Я просто хотел выйти на улицу и поиграть, но я знал, что мой отец хочет для меня самого лучшего.Перенесемся на 25 лет вперед, и теперь я хочу убедиться, что изучение фактов умножения не должно быть утомительной задачей для студентов. Есть много разных способов сделать изучение фактов интересным.
Итак, позвольте представить:
1- Композиции умноженияДети любят музыку и ритмы. Они могут научиться чему угодно с помощью отличной музыки. Найдите песни и видео, которые помогут вам узнать факты.
Вы можете найти большое разнообразие песен умножения на YouTube.На этом сайте есть список лучших детских песен для умножения . Если вы или ваша школа готовы потратить немного дополнительных денег, я настоятельно рекомендую Flocabulary . У них есть действительно отличные песни с отличными битами, которые понравятся детям постарше, но вам понадобится подписка. 2- Командные соревнования по математике Мотивируйте детей соревнованиями по математике! Я обнаружил, что здоровая конкуренция способствует высокой вовлеченности студентов.
- Разделите класс пополам и создайте 2 команды
- Студенты встают в 2 шеренги (1 шеренга — команда) лицом друг к другу
- Учитель может назвать факт умножения или указать уравнение
- Первая пара учеников называет ответ
- Учащийся, ответивший правильно 1-м, получает балл для своей команды
- Оба ученика садятся, и учитель переходит к следующей паре
- Этот процесс продолжается до тех пор, пока учитель не пройдёт всю строку
- Побеждает команда, набравшая наибольшее количество очков
Примечание: Если у вас нечетное количество учеников, сделайте дополнительного ученика ведением счета.Один из способов дифференцировать деятельность — объединить студентов с одинаковым академическим уровнем в пары, чтобы соревноваться друг с другом.
3- Вращение для умножения Еще один способ повысить вовлеченность студентов — это игры. В этой игре учащиеся крутятся и пытаются найти эквивалентную игровую карту. Детям нравится эта игра, потому что они стараются получить как можно больше карточек. Однако самое приятное то, что они подвергаются различным представлениям (массивам, числовым предложениям) фактов умножения для более глубокого понимания.
В этой игре учащиеся крутятся и пытаются найти эквивалентную игровую карту. Детям нравится эта игра, потому что они стараются получить как можно больше карточек. Однако самое приятное то, что они подвергаются различным представлениям (массивам, числовым предложениям) фактов умножения для более глубокого понимания.
Эта игра включена в ресурс «Таблица умножения фактов на времена». Я создал по одной для каждого факта умножения на 12. Этот ресурс великолепен, потому что он включает в себя 3 различных игры на умножение, учебные карточки для учащихся и быструю оценку.
Загрузите БЕСПЛАТНО копию таблицы умножения фактов — 11 раз, нажав на фото ниже.
4- Война умноженияЕще одна забавная игра — старая, но хорошая.Большинство детей могут быть знакомы с игрой на большую карту, но измените эту игру, чтобы она стала Войной умножения.
Как ты играешь? Это игра для двоих. Один ученик тасует карты и раздает их двумя стопками рубашкой вверх. Оба студента обратный отсчет (3, 2, 1, ВПЕРЕД!) И переворачивают верхнюю карту из своей стопки лицевой стороной вниз. Первый ученик, который точно умножит оба числа на карточках, побеждает в партии. Когда все карточки ушли, победителем становится учащийся с наибольшим количеством сетов.
Один ученик тасует карты и раздает их двумя стопками рубашкой вверх. Оба студента обратный отсчет (3, 2, 1, ВПЕРЕД!) И переворачивают верхнюю карту из своей стопки лицевой стороной вниз. Первый ученик, который точно умножит оба числа на карточках, побеждает в партии. Когда все карточки ушли, победителем становится учащийся с наибольшим количеством сетов.
Примечание: Если в колоде используются туз, дама и король, обязательно укажите их числовые значения. Например, туз может стоить 0, валет может стоить 1, дама может стоить 11, а король может стоить 12. Не забудьте вынуть джокеры.
5- Теги имен умноженияЗаставьте детей двигаться с тегами умножения имен! Это занятие понравится вашим кинестетикам.
Как ты играешь?Создавайте именные теги умножения для всех в классе, включая себя.В течение дня всех следует называть по названию продукта. Например, если у кого-то есть ярлык «8 x 3», то его или ее имя на день будет 24. У вас должно быть особое время дня, когда ученики должны встать и представиться кому-то. «Доброе утро, 25, мне 80!»
Ищете больше удовольствия от умножения?Если вы ищете забавные игры, которые подтверждают факты умножения от 2 до 12, то ознакомьтесь с моим сборником фактов об умножении.Каждый факт включает в себя 3 увлекательные игры (умножение лицом к лицу, переворот умножения, вращение для совпадения умножения), карточки для учебы учащихся и быстрое формирующее оценивание, которое можно использовать в соревнованиях всей группы.
Нажмите ЗДЕСЬ, чтобы загрузить превью из моего магазина TpT.
Есть ли у вас какие-нибудь забавные игры на умножение, которые вы используете в классе? Если да, поделитесь, пожалуйста, в разделе комментариев ниже.
225Математические решения для класса 7 по математике Глава 2
Математические решения Решения для математики класса 7 Глава 2 Умножение и деление целых чисел представлены здесь с простыми пошаговыми пояснениями.Эти решения для умножения и деления целых чисел чрезвычайно популярны среди учащихся 7-го класса по математике. Решения для умножения и деления целых чисел удобны для быстрого выполнения домашнего задания и подготовки к экзаменам. Все вопросы и ответы из книги «Математические решения» для класса 7 по математике, глава 2, предоставляются здесь для вас бесплатно. Вам также понравится возможность использования Meritnation’s Mathematics Solutions Solutions без рекламы. Все решения по математике Решения для класса 7 по математике подготовлены экспертами и имеют 100% точность.
Страница № 12:
Вопрос 1:
Умножить.
(i) -5 × -7
(ii) -9 × 6
(iii) 9 × -4
(iv) 8 × -7
(v) -124 × -1
(vi) -12 × — 7
(vii) -63 × -7
(viii) -7 × 15
Ответ:
(i) -5 × -7 = 35
(ii) -9 × 6 = -54
(iii) 9 × -4 = -36
(iv) 8 × -7 = -56
(v) -124 × -1 = 124
(vi) -12 × -7 = 84
(vii) -63 × -7 = 441
(viii) -7 × 15 = -105
Страница № 14:
Вопрос 1:
Решить:
(i) -96 ÷ 16
(ii) 98 ÷ -28
(iii) -51 ÷ 68
(iv) 38 ÷ -57
(v) -85 ÷ 20
(vi) -150 ÷ -25
(vii) 100 ÷ 60
(viii) 9 ÷ -54
(ix) 78 ÷ 65
(x) -5 ÷ -315
Ответ:
(i) -96 ÷ 16 = -6
(ii) 98 ÷ -28 = -72
(iii) -51 ÷ 68 = -34
(iv) 38 ÷ -57 = -23
(v) — 85 ÷ 20 = -174
(vi) -150 ÷ -25 = 6
(vii) 100 ÷ 60 = 53
(viii) 9 ÷ -54 = -16
(ix) 78 ÷ 65 = 65
(x) -5 ÷ -315 = 163
Страница № 14:
Вопрос 2:
Запишите три деления целых чисел так, чтобы дробная форма каждого была 245.
Ответ:
Целые числа делятся на три деления: -24-5, 4810 и -48-10.
Страница № 14:
Вопрос 3:
Запишите три деления целых чисел так, чтобы дробная форма каждого была -57.
Ответ:
-57 × 33 = -1521-57 × 44 = -2028-57 × 55 = -2535
Следовательно, целые числа делятся на три части: -1521, -2028 и -2535.
Страница № 14:
Вопрос 4:
Рыба в пруду внизу несет какие-то числа. Выберите любые 4 пары и выполните четыре умножения на эти числа. Теперь выберите четыре другие пары и выполните деление с этими числами.
Например,
1. (–13) × (–15) = 195
2. -24 ÷ 9 = -249-83
Ответ:
Четыре таких умножения:
(−13) × 9 = 117
(−15) × 12 = −180
(−8) × (−18) = 144
13 × 41 = 533
Четыре таких деления равны
. (−18) ÷ 9 = −2
(−24) ÷ 12 = −2
(−13) ÷ 13 = −1
(−27) ÷ 9 = −3
Просмотреть решения NCERT для всех глав класса 7
проверенных стратегий в специальном издании
Те дни, когда вы забываете математические факты?
Тупо уставился на задачу умножения?
Сложение или вычитание, когда они должны быть умноженными?
Готово.Прошло. Над.
Те дни остались в прошлом!
Сегодня мы собираемся научиться преподавать факты умножения нашим учащимся с ограниченными возможностями, чтобы они приобрели концептуальные знания и запомнили их.
Неправильный способ преподавать факты умножения учащихся специального образования
Когда я начинал в классе, я не мог понять, почему я тратил столько времени на изучение фактов умножения в один прекрасный день только для того, чтобы ученики пришли в класс и забыли их На следующий день!
У них не только иногда возникали проблемы с вспоминанием правильного ответа на задачу умножения, но они забывали, что такое умножение.
Например, предположим, что они решают 6 x 5. Вместо того, чтобы составлять 6 групп по 5 фишек, они добавляли бы 6 + 5. Казалось, что все стратегии обучения, которые я пробовал, не работали.
Эти карточки? Как насчет тех упражнений на умножение по времени? Если ваши ученики еще не обладают глубокими концептуальными знаниями о умножении, бросать им факты за фактами просто не сработает. Фактически, это может навредить им, увеличивая их математическую тревогу. И это дает понять, что математика помогает быстро получить правильный ответ.
Узнайте больше о том, почему беглость речи не предполагает скорости или запоминания.
Если бы я мог взмахнуть волшебной математической палочкой и заставить что-то исчезнуть из классных комнат повсюду, это были бы эти синхронизированные упражнения и механическая практика.
Отзыв — непонимание
Теперь я понимаю, что вспоминание фактов отличается от их понимания, и нам нужно использовать разные стратегии, чтобы способствовать их запоминанию и пониманию. Одна из причин, по которой я не смог помочь своим ученикам, заключалась в том, что я не согласовывал свои учебные стратегии по математике с тем, на каком уровне мои ученики развивали свои знания умножения.
Хорошо, значит, это были вещи, которые я тогда сделал не так. Но что бы я сделал сегодня по-другому? Я хочу рассказать, как правильно преподавать умножение ученикам с ограниченными возможностями в обучении математике.
Правильный способ научить учащихся специального образования фактам умножения
В этом посте мы говорили о 4 этапах усвоения фактов.
Другой способ подумать об освоении учащимися фактов умножения в континууме Конкретно-Репрезентативно-Абстрактное.
Бетон
На начальных этапах обучения умножению учащимся необходимо попрактиковаться в решении сценариев, включающих умножение, с использованием конкретных манипуляторов, таких как счетчики и кубы unifix. Студенты на конкретном этапе получают концептуальное понимание и практикуют свои стратегии счета.
Репрезентативная
После того, как вы потратите время на обучение задачам умножения с использованием конкретных материалов, вы можете посоветовать учащимся использовать рисунки или диаграммы для решения задач умножения.Эти рисунки похожи на манипулятивные в том, что они моделируют проблему, но они более абстрактны и, следовательно, требуют большего математического мышления.
Учащиеся на этапе представления укрепляют свое концептуальное понимание и стратегии счета, одновременно применяя более продвинутые навыки рассуждения для решения задач умножения.
Abstract
После того, как учащиеся получат достаточную практику, сначала решая задачи умножения с использованием конкретных манипуляций, а затем рисунков или диаграмм, они будут готовы решать уравнения умножения.Этот тип задач является абстрактным, потому что он включает символы, которые учащиеся должны интерпретировать.
Студенты на абстрактной фазе уже получили глубокие концептуальные знания в области умножения. Они практикуют свои навыки рассуждения, что приводит к усвоению фактов.
Учащимся на каждом из этих этапов нужны разные инструкции, чтобы улучшить свои навыки умножения. Прежде чем вы сможете выбрать подходящую стратегию обучения, вам нужно будет провести оценку по математике, чтобы узнать, где они находятся на пути к усвоению фактов.
Узнайте, как оценить навыки умножения и деления ваших учеников в моем БЕСПЛАТНОМ онлайн-курсе! Узнайте больше и зарегистрируйтесь здесь.
Далее, в зависимости от результатов вашей оценки, которые говорят вам, где находятся ваши учащиеся специального образования, им потребуются различные стратегии обучения математике.
Вот обучающие стратегии, которые можно использовать на каждом этапе развития умножения:
Как преподавать факты умножения, используя конкретные стратегии, которые формируют концептуальное понимание
Забудьте на мгновение об уравнениях умножения и познакомьте с концепцией умножения с помощью словесных задач и сценариев .Например:
Лили ставит свечи на торт на день рождения отца. Она делает 6 рядов свечей по 7 свечей в каждом ряду. Сколько свечей использует Лили?
Предложите учащимся решать задачу любым доступным им способом. Вовлеките класс в математические разговоры о различных способах решения каждой задачи.
Вы также можете поговорить по математике о примерах умножения, которые мы видим повсюду. Это поможет вашим ученикам рассматривать математику как нечто важное для их жизни, а не как абстрактные числа, которые существуют только на уроках математики.Например, что бы вы обсудили со своим классом по поводу этой фотографии?
Смоделируйте и подумайте вслух, как вы решите задачи умножения с помощью манипуляторов. На конкретном этапе все дело в манипуляторах! При моделировании задач и поощрении учащихся к использованию манипуляций убедитесь, что вы показываете различные представления об умножении, например:
Как преподавать факты умножения с помощью этих обучающих стратегий на этапе представления
Продолжайте использовать словесные задачи, но начинайте переводить проблема в уравнения.Например:
Лили ставит свечи на торт на день рождения отца. Она делает 6 рядов свечей по 7 свечей в каждом ряду. Сколько свечей использует Лили?
«Я заметил, что Лили сделала 6 рядов, поэтому я могу нарисовать 6 рядов по 7 в каждом ряду. 6 рядов по 7 заставляют меня думать о 6 умножить на 7.»
Продолжайте говорить по математике, но моделируйте, как преобразовать картинку в рисунок или диаграмму.
Смоделируйте, как решать задачи умножения слов, нарисовав рисунок или диаграмму.Как и в случае с конкретным этапом, покажите различные представления умножения, используя:
После того, как учащиеся сыграют в игры и упражнения на умножение и потренируются в решении задач с помощью манипуляторов и рисунков, они укрепят свое концептуальное понимание того, что значит умножение.
Пришло время поработать над улучшением процедурной беглости, чтобы у учащихся были более эффективные способы решения задач. Студенты будут готовы решать более абстрактные задачи, связанные только с символическими числами.
Как научить умножению способствовать абстрактному пониманию математических фактов
На этом этапе мы работаем над усвоением фактов. Вот некоторые учебные стратегии по математике, которые вы можете использовать:
Перевод текстовых задач непосредственно в абстрактные символы и числа.
Лили ставит свечи на торт на день рождения отца. Она делает 6 рядов свечей по 7 свечей в каждом ряду. Сколько свечей использует Лили?
«6 строк и 7 столбцов означают 6 x 7.»
Некоторые ученики смогут вспомнить эти факты умножения по памяти. Однако многие из наших учеников с нарушениями в обучении математике будут бороться с проблемами памяти. Они не смогут быстро и эффективно извлекать факты из памяти.
И это нормально!
Вместо этого вы можете научить их полагаться на известные факты. Например: умножение любого числа x3 равносильно умножению числа x2 на добавление еще одной группы.
2 x 3 = 2 x 2 + 2
3 x 3 = 3 x 2 + 3
4 x 3 = 4 x 2 + 4
5 x 3 = 5 x 2 + 5
Вы можете удвоить первое число, а затем добавить другую группу.
На этом этапе, когда учащиеся четко поймут, что такое умножение, вы также можете попросить учащихся попрактиковаться в подсчете пропусков, чтобы улучшить их память на факты умножения. Выбирайте одно число, чтобы практиковаться за раз, например, пропускайте счет на 3 секунды. Практикуйтесь в подсчете пропусков под песнопение или ритм. Хлопайте или топайте в такт. Держите его привязанным к чему-то конкретному, например к числовой прямой, чтобы учащиеся не запоминали вслепую строку слов.
УПАКОВКА…
Готовы ли вы взмахнуть своей волшебной математической палочкой и заставить эти синхронизированные упражнения и механическую практику исчезнуть из математических классов повсюду?
Как мы только что видели, есть более эффективные способы научить умножению учащихся с нарушениями в обучении математике.
 ; Просвещение, 2017. – с. 83
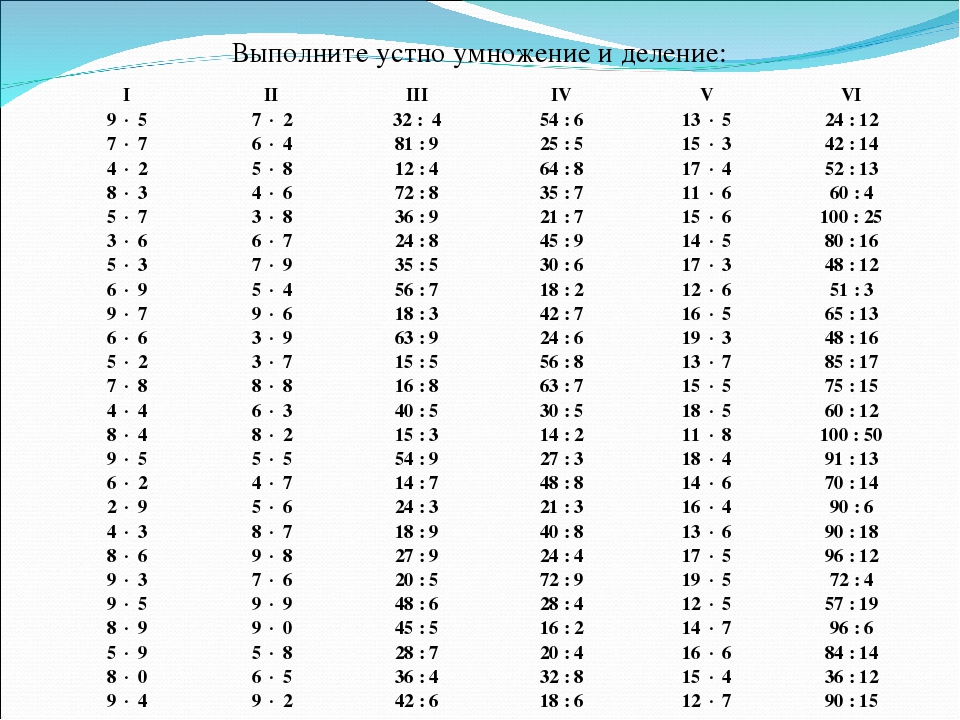
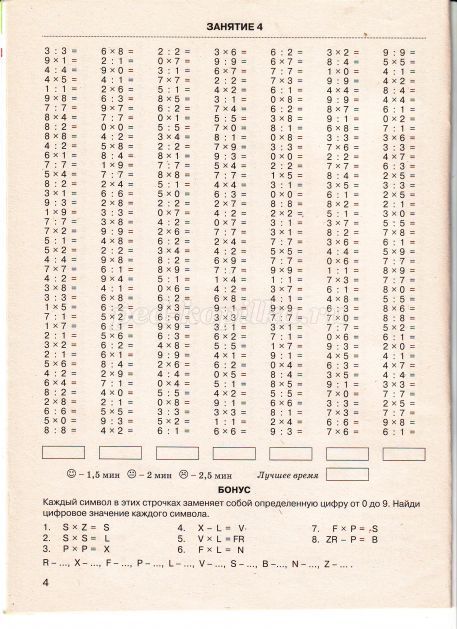
; Просвещение, 2017. – с. 83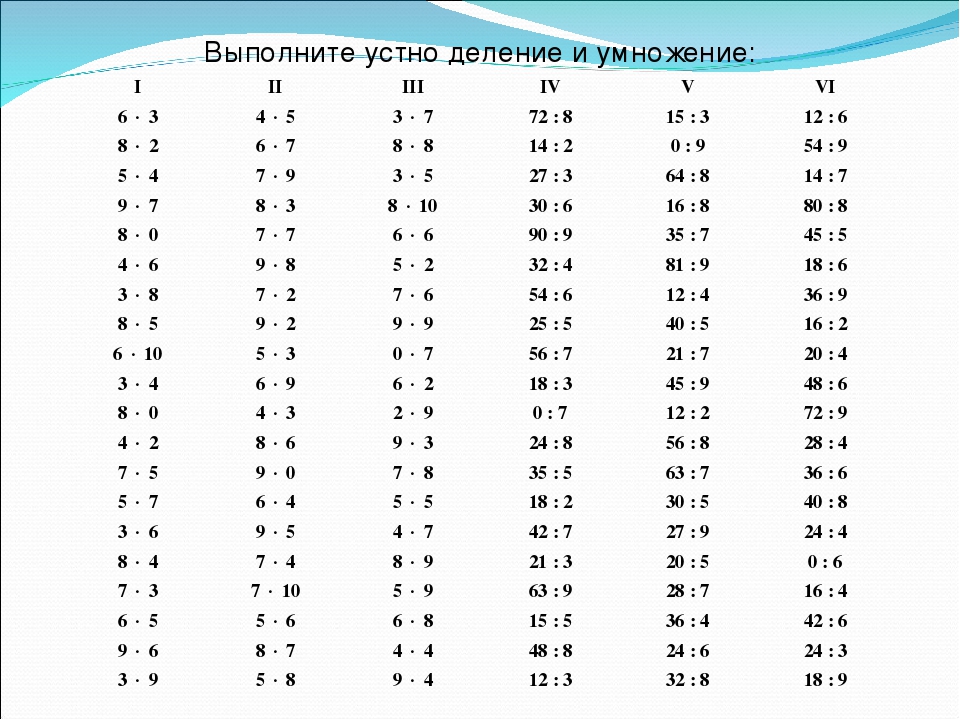 Найди значение каждого выражения.
Найди значение каждого выражения.


 . Пышкало А. М. «Сборник упражнений и проверочных работ по математике». Москва, «Просвещение», 1998 год.
. Пышкало А. М. «Сборник упражнений и проверочных работ по математике». Москва, «Просвещение», 1998 год. «Игра молчанка».
«Игра молчанка».




 Шаг 1 равен (–20 ÷ –5) ÷ (–2). Теперь, разделив -20 на -5, мы получим 4 в качестве ответа. Итак, новое выражение (4) ÷ (–2). 4 — целое положительное число, так как отрицательное ÷ отрицательное = положительное. Теперь, если мы разделим 4 на -2, мы получим -2 как положительное ÷ отрицательное = отрицательное. Следовательно, (–20) ÷ (–5) ÷ (–2) = –2.
Шаг 1 равен (–20 ÷ –5) ÷ (–2). Теперь, разделив -20 на -5, мы получим 4 в качестве ответа. Итак, новое выражение (4) ÷ (–2). 4 — целое положительное число, так как отрицательное ÷ отрицательное = положительное. Теперь, если мы разделим 4 на -2, мы получим -2 как положительное ÷ отрицательное = отрицательное. Следовательно, (–20) ÷ (–5) ÷ (–2) = –2.