3000 примеров по математике. Устный счет. Счет от 1 до 10. 1 класс — МНОГОКНИГ.ee
категории
книги
НовинкиАкции %АвтомобилиДетективы, боевикиДетская литератураДом, быт, досугИностранные языки, словариИстория, политикаКомпьютерные технологииЛюбовный романМедицина и здоровьеПодарочные изданияПсихология, философияПутеводители, атласыСовременная и классическая литератураСпорт, оружие, рыбалкаСувениры. АксессуарыФантастикаЭзотерика, астрология, магияЭкономическая литература
Подарочные карты
игры, игрушки
Игрушки Книги-игры Настольные игры Развивающие игры
товары для малышей
Прорезыватели и пустышки Шезлонги и качели Автокресла Аксессуары для защиты ребенка Вигвам Детская мебель Детская одежда Детские кроватки Кровать для путешествий Купание малыша Матрасы Подушки для беременных Развивающие игрушки для малышей Текстиль Товары для кормления Уход за малышом Ходунки
товары для праздника
Все открытки Карнавальные костюмы, маски и аксессуары Одноразовая посуда Подарочные коробки Подарочные пакеты Свечи Шарики
товары для школы
Бумажная продукция Глобусы Канцелярские товары Папки Пеналы Товары для творчества Школьные ранцы
товары для живописи, рукоделия и хобби
Декорирование Жемчуг эффект для декупажа Живопись Контур по стеклу и керамике Контур по ткани Краски для свечей Маркеры для скетчинга Моделирование Прочее Рукоделие
традиционные товары
Костровые чаши и очаги Матрёшки Платки Самовары Фарфоровые фигурки
другие товары
Аксессуары для девочек Аксессуары для мальчиков Товары для пикника Фотоальбомы
издательство
Об издательстве Многоразовые наклейки Настольные игры Рабочие тетради для дошкольников Рабочие тетради для школьников Развивающее лото Раскраски для девочек Раскраски машины и техника Раскрась водой! Учебные пособия для дошкольников
Код: 9785170598168
К сожалению, этого товара нет в наличии. Когда товар снова появится у нас, мы обновим статус, и вы сможете сделать заказ.
Когда товар снова появится у нас, мы обновим статус, и вы сможете сделать заказ.
Автор: УЗОРОВА О., НЕФЕДОВА Е.
Серия: Как научиться быстро считать
Год издания: 2009
Под заказ
Устному счету отведено несколько книг, включенных в общую серию 3000 примеров по математике» Каждая посвящена одной из важнейших программных тем, которые изучаются в 1-4 классах начальной школы. Количество примеров в книгах различно и увеличивается от класса к классу, от темы к теме. Bсего для отработки навыков устного счета предлагается 3000 математических примеров.
В этом пособии представлен материал, направленный на формирование навыков устного счета по теме «Счет от 1 до 10» для 1 класса.
Устный счет развивает сообразительность и внимание учащихся, воспитывает математическую находчивость и укрепляет память. Правильная постановка занятий устным счетом в начальной школе предполагает ежедневные и непродолжительные (от 5 до 10 минут) упражнения.
Беглый слуховой счет. (Учитель устно называет пример и устно же, спустя несколько секунд, получае ответ.).
Зрительный счет. (Примеры записаны, а ответы называются либо устно, либо записываютс учениками.).
Комбинированный счет. (Учитель диктует примеры, а ученик записывает ответы.) Устное решение задач.
Быстрота счета возникает в результате длительных тренировок. Но на первом месте должна стоят осознанность тех или иных приемов устных вычислений, а не механическое их применение. Устный счет должен предварять, дополнять или заключать ту часть урока, которой он подчинен.
Пособие можно использовать на уроках математики, а также для самостоятельной работы дома.
4 | ||
5 | 7 | |
4 | 5 | 7 |
2 | 3 | |
3 | 4 | 2 |
5 | ||
7 | 7 — 2 | 6 + 3 | 6 — 5 | 6 — 4 | 5 — 1 | 2 + 1 | 1 + 8 | 3 + 6 |
4 + 5 | 7 + 2 | 9 — 0 |
6 — 4 | 9 + 0 | 6 + 3 | 4 — 3 | 6 – 5 |
7 — 4 | 8 — 5 | 9 – 6 |
9 — 8 | 0 + 1 | 7 — 6 |
2 | ||
3 | ||
4 | ||
5 | ||
6 | ||
4 | ||
3 | ||
2 | ||
5 | 3 | 1 |
4 | 4 | 8 |
6 | 7 | ? | 10 | 8 |
4 | 5 | 1 |
6 | ? | 3 | 3 | 1 |
8 | 5 | 3 |
6 | ? | 3 |
Урок математики «Числа от 1 до 10. Закрепление». 1-й класс
Урок 35
| Педагогические цели | создание условия для закрепления состава изученных чисел; формирования умения сравнивать числа и число с числовым выражением. |
| Задачи: | учить строить отрезки и геометрические фигуры; развивать навыки устного счёта. закрепить навыки счета, сложения и вычитания; число 0. Развивать логическое мышление, привитие внимание, способствовать воспитанию доброты. |
| Планируемые результаты | Предметные: знать состав изученных
чисел; уметь выполнять порядковый счёт;
сравнивать числа и число с числовым выражением;
уметь строить отрезки и геометрические фигуры. Универсальные учебные действия (метапредметные): Регулятивные: уметь осуществлять контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона. Коммуникативные: уметь слушать и вступать в диалог, участвовать в коллективном обсуждении. Познавательные: уметь осуществлять поиск и выделение необходимой информации, применять методы информационного поиска. Личностные: проявляют познавательный интерес.. |
| Методы и формы работы | частично-поисковый, индивидуальный, фронтальный, работа в парах |
| Межпредметные связи | Математика, окружающий мир, чтение |
| Ресурсы: — основные — дополнительные | — М.И. Моро, М.А. Бантова, Г.В. Бельтюкова,
С.И. Волкова, С.В. Степанова. Математика. Учебник
для 1-го класса. Часть 1; рабочая тетрадь к
учебнику “Математика” для 1 класса; Часть 1; рабочая тетрадь к
учебнику “Математика” для 1 класса;— презентация, карточки. |
| Понятия | увеличить, уменьшить, выражение |
Ход урока
| Этапы урока | Деятельность учителя | Деятельность учащихся | Форма организации взаимодействия | Формируемые умения УУД |
| I. Орг. момент. | Отдых наш кончается, Работа начинается. Усердно будем мы трудиться, Чтобы чему-то научиться.  — Что значит учиться? — Добрый день! Улыбнитесь! Подарите улыбку своим одноклассникам | организация класса, демонстрация готовности к уроку | фронтальная | Регулятивные — учатся
контролировать свои действия. Личностные — проявляют интерес к предмету |
| II. Самоопре деление к деятельности | Ребята, посмотрите на доску. — Что вы можете сказать о числах? (числа перепутаны все перепутаны). 5, 6, 4, 1, 3, 7, 2, 8, 9, 0 — Поставить числа в порядке возрастания. — С какого числа будем ставить? (0) — Как называется этот порядок? (числовой ряд) — Все ли числа вам знакомы? (да) — Сформулируйте тему урока? (Числа от 1 до 10
. — Поставим задачи урока. (Закрепим знания чисел и будем решать примеры, будем учить работать дружно) | рассматривают числа на доске,
восстанавливают числовой ряд
ответы на вопросы,
формулируют тему урока, ставят задачи | фронтальная | Регулятивные – под руководством
учителя определяют учебные задачи Познавательные: выделяют и формулируют познавательные цели. Коммуникативные: умеют слушать и слышать и понимать партнёров в диалоге Личностные — осваивают социальную роль обучающегося |
| III. Работа по теме урока | 1) Чтобы справиться с поставленными
задачами мы пригласим в школу Лунного гостя. (слайд
2) (слайд
2)— Как его зовут? Лунтик 2) Повторение состава чисел — Но вот беда ему дед Шаршуля дал задание. (слайд 4) — Разложить 6 морковок на две кучки. Давайте поможем. — Увеличьте число 6 на 1 — Уменьшите число 6 на 2. — Назовите соседей числа 6 (5 и 7) Деда Шаршуля благодарит вас и Лунтика за работу. 2) Решение задачи Прилетела бабушка Капа. (Слайд 5) Она очень хочет, чтобы Лунтик помог набрать ягоды и фрукты на варенье. (Слайд 6-7) — Составим математический рассказ и найдём его решение. — Давайте оценим работу Лунтика и свою. | ответы детей работают в паре, раскладывают картинки- морковки на две кучки ответы детей
дети составляют условие задачи и находят решение самооценка своей работы |
работа в паре
фронтальная | Регулятивные — осуществляют
контроль своей деятельности, и деятельности
партнеров, при необходимости корректируют свои
действия, Предметные – умеют выполнять действия с выражениями, и решать задачи Коммуникативные — достаточно полно и чётко
выражают свои мысли, умеют обосновывать своё
мнение. Личностные – имеют сотрудничество со своими учениками и учителем. |
| IV. Физкультминутка. Цель: снятие утомляемости на уроке | Лунтика встретился Кузя. Он
предлагает поиграть. (Слайд 8) По дорожке, по дорожке | дети выполняют упражнения по стихотворению | фронтальная | Личностные — развитие физической
выносливости. Коммуникативные — умение вместе выполнять упражнения |
V. Закрепление материала. Цель: усвоить учащихся новый способ действия | 1) Решение примеров. (самостоятельно) (Слайд 9)На пути встретилась тётя Мотя. Она решила проверить Лунтика, как умеет считать. (Слайды-10-15) 4+1= 7+1= 9-1= 3+2= 7-2= 10-1= — Оцените работу 2) Работа по учебнику Побежали по лужайке. На берегу встретился Пескарь Иваныч. Он попросил сосчитать рыбки, которые поймали ребята.( Слайд 16-17) — Откройте учебник на стр.73 № 1 — Прочитайте математический рассказ. — Расскажите о ком рассказ. Что в нём известно? Что нужно узнать? Какое арифметическое действие следует использовать, чтобы ответить на поставленный вопрос? Почему? — Как запишем решение. — У кого получилось правильно. Оцените работу. 3) Повторение геометрического материала Продолжаем путь. На пути дядя Шнюк Дядя Шнюк сплёл паутины, но запутался в них, он просит Лунтика разобрать на группы. (Слайд 19) — На какие группы можно разделить фигуры? 4) Работа в тетради — Откройте тетради с. 27 по закладке и соедините цифры, чтобы получились фигуры. — Вставьте пропущенные числа. Самостоятельная работа. Оцените работу. | дети решают самостоятельно проверяют с сигнальными карточками, показывают ответ оценивают свою работу читают математический рассказ
решают задачу
рассматривают фигуры отвечают на вопросы выполняют задание в тетради самостоятельно выполняют выражения | индивидуальная,
фронтальная
фронтальная индивидуальная
фронтальная
индивидуальная | Регулятивные – планируют свои
действия, осуществляют контроль своей
деятельности, и деятельности партнеров. Познавательные – создают алгоритм деятельности, устанавливают причинно- следственные связи, сроят логическую цепочку действий Коммуникативные — умеют слушать и слышать и понимать партнёров в диалоге, полно и чётко выражают свои мысли, обосновывают своё мнение. Личностные – имеют сотрудничество со своими учениками и учителем. |
| VI . Итог урока. Цель: соотнесение цели урока и результата. | Бежал Лунтик по лужайке и встретил
своих друзей. — Как вы думаете, о чём расскажет своим друзьям Лунтик. — Что он узнал в школе? | дети отвечают на вопросы | фронтальная | Регулятивные – осознают
важность полученных знаний, понимают причины
успеха или неуспеха, осознают качество и уровень
усвоения. Познавательные – осваивают начальные формы рефлексии, строят цепочку умозаключений Коммуникативные — умеют выражать свои мысли, правильно строить речевые высказывания. |
| VII. Рефлексия. Цель. Оценивание свой работы на уроке. | — Оцените свою работу. Покажите свои
смалики. — Что вам понравилось на уроке? — Какая ваша роль на уроке? | дети оценивают свою работу, показывают смалики и объясняют почему выбрали такой цвет |
Список используемых источников
А) Изображение Лунтика и его друзей: http://vipsite.ws/photoshop/110738-klipart-luntik-i-druzya.html
Б) Математика, 1 класс: система уроков по
учебнику М.И. Моро,М.А. Бантовой, Г.В. Бельтюковой,
С.И. Волковой, С.В. Степановой/
авт.-сост.С.В.Савинова. — Волгоград: Учитель, 2012 г.
Моро,М.А. Бантовой, Г.В. Бельтюковой,
С.И. Волковой, С.В. Степановой/
авт.-сост.С.В.Савинова. — Волгоград: Учитель, 2012 г.
В) М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова. Математика. Учебник для 1-го класса. Часть 1. г) Рабочая тетрадь к учебнику “Математика” для 1 класса
3 супер-совета по оценке места преподавателя
Вот преуменьшение года: ценность места преподавания — это большое дело! Начиная с детского сада и заканчивая пятым классом, «Числа и действия в десятичной системе счисления» проявляются в основных математических стандартах, как часовой механизм.
Задача «понимания стоимости места» усложняется с каждым годом и действительно возрастает, начиная с 3-го класса. Ожидается, что учащиеся узнают, как «свободно складывать и вычитать в пределах 1000», используя стратегии восприятия чисел, основанные на разрядном значении. Эта трехзначная математическая стратегия может показаться неудобной, как высшая лига для детей, борющихся со значением разряда. Итак, я собираюсь поделиться:
Итак, я собираюсь поделиться:
Прежде чем я поделюсь тремя советами, давайте создадим фон. Учащиеся уже в детском саду и в первом классе приходят в школу, зная некоторые вещи о двузначных числах, например, как устно считать от 10 до 100 и считать объекты в пределах 15 или 20.
Однако их понимание чисел сильно отличается от нашего тем, что оно на основе метода счета единицами. Поэтому они обычно считают по одному и не сразу понимают связь между числом и группами десятков и единиц.
Например, если мы спросим учащегося, сколько десятков в числе 67. Он может сказать 6 в разряде десятков, потому что просто называет позицию, мало ее понимая. Но они могут не понимать, что 6 представляет собой 6 групп по десять вещей, а 7 представляет 7 отдельных вещей. Понимание того, что группа из десяти человек может представлять собой единое целое, — это огромный сдвиг!
Учащиеся, как правило, испытывают затруднения, потому что понять значение разряда совсем не просто. Это все большая головоломка, в которой нужно собрать три больших кусочка или соединения.
Первым ключом является понимание концепций счисления счисления счисления для визуального представления чисел. Хотя многие учителя могут предоставить учащимся возможность представлять числа, используя стандартные группы, для учащихся не менее важно представлять числа, используя эквивалентные группы. Я считаю это краеугольным камнем ценности места.
Учащиеся также должны уметь произносить числа в устной форме, будь то стандартные («семьдесят два») или десятичные («7 десятков и 2 единицы»).
Наконец, учащиеся должны научиться читать и писать числительные. Установление этих трех связей зависит от использования на практике различных стратегий счета: счет единицами, счет группами и одиночками, счет десятками и единицами.
Видите, как все это работает вместе? Если учащиеся пропустят одну часть, им будет сложно получить полное представление о позиционной стоимости. Вот почему так важно дать детям правильные инструменты для понимания системы ценностей места.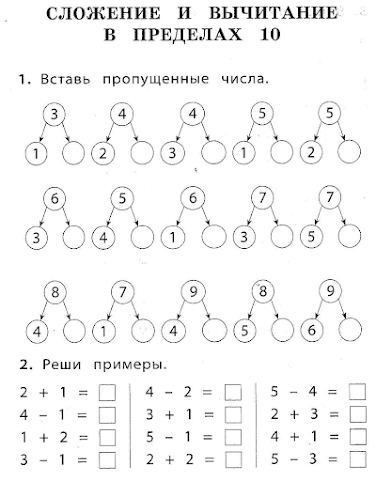
Вот несколько советов, которые развивают разрядное значение:
Совет № 1. Используйте разрядные коврики, чтобы упростить чтение и запись чиселДа, манипуляции отлично подходят для перехода учащихся от конкретного понимания к абстрактному. Коврики с расстановочными значениями хорошо работают с манипуляторами, помогая донести абстрактные концепции до сознания.
Помогите учащимся, испытывающим затруднения, сделав обучение практическим и наглядным. Это означает использование манипулятивных приемов, таких как десятичные блоки. Блоки с основанием десять — лучший инструмент в блоке. Отличительной особенностью блоков с основанием десять является универсальность построения целых чисел или десятичных дробей.
С блоком единиц, представляющим единицу, дайте учащимся время изучить взаимосвязь между единицами (маленький блок) и стержнями, а также стержнями и плоскостью на коврике с разрядным значением. Изучение этих взаимосвязей подтверждает соотношение разрядности 10:1, в том числе: 10 единиц равняются 1 десятку, 10 десятков равняются 1 сотне и так далее.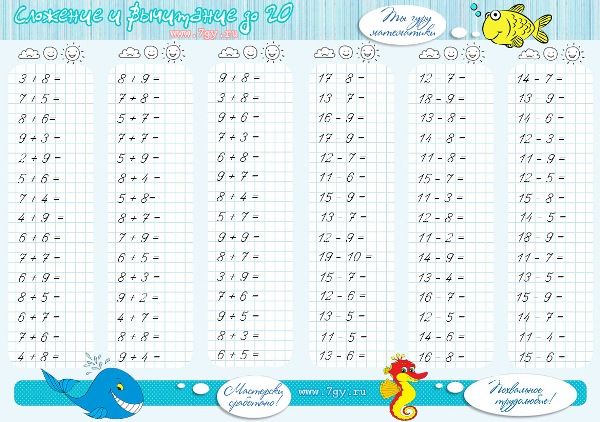
Предупреждение : Блоки с основанием 10 связаны с отношениями. Каждый блок может представлять разные суммы в зависимости от того, как они используются. Не заставляйте своих детей думать, что каждый блок может представлять ТОЛЬКО одну вещь. Например, при использовании десятичных блоков для представления десятичных дробей плоскость может представлять 1, а наименьший блок может представлять 1 сотую. В разговоре с детьми мне легко использовать фразу: В этой ситуации __________ представляет __________.
Теперь давайте поговорим о таблицах значений мест. Создавайте простые диаграммы стоимостных значений, которые можно использовать повторно, добавляя разряды для сотен, десятков и единиц. Этот макет имитирует способ написания числа слева направо. В разделе единиц убедитесь, что есть два кадра из десяти, чтобы продвигать концепцию группы из десяти и устранить необходимость подсчета один за другим. Десять кадров также помогают учащимся визуализировать, сколько еще единиц необходимо, чтобы составить полный набор из десяти.
Также дайте учащимся время представить число, используя стандартные группы и эквивалентные группы. Например, число 49.можно представить в стандартной форме как 4 десятка и 9 единиц.
Также используйте эквивалентные группы из 49, чтобы показать 3 десятка и 19 единиц. Без такого опыта детям действительно трудно понять, что обе ценности эквивалентны.
Совет № 2. Предоставьте возможность считать по группам из 10 и 100У вас могут быть дети во 2-м и 3-м классе, которые продолжают считать по единицам, а не группировать по 10. Группировка по 10 важна, потому что это мысленно легче считать, плюс наша система счисления основана на десятках! Поскольку мы хотим привить учащимся способность считать до 10 (а не навязывать им это), ознакомьтесь с этими двумя полезными упражнениями.
Упражнение на счет карандашей
Соберите учеников в круг. Найдите набор цветных мелков (или любые предметы, которые можно считать от 25 до 100) и разложите их в центре круга.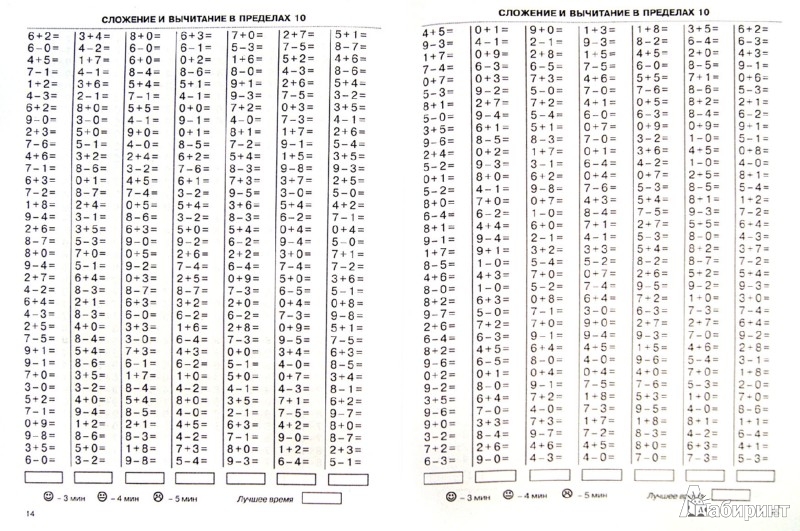 Спросите учащихся: «Как мы можем считать эти мелки так, чтобы это было проще, чем считать единицами?» Проверьте любые предложения по счету, которые дают учащиеся (например, если они говорят «сосчитай по 3», затем группируй и считай мелки по три, пока не перестанешь составлять группы по 3).
Спросите учащихся: «Как мы можем считать эти мелки так, чтобы это было проще, чем считать единицами?» Проверьте любые предложения по счету, которые дают учащиеся (например, если они говорят «сосчитай по 3», затем группируй и считай мелки по три, пока не перестанешь составлять группы по 3).
После тестирования различных стратегий обсудите, что сработало хорошо, а что не очень. Если никто не предлагает идею счета до 10, предложите ее группе и обсудите, как она работает по сравнению с другими предложениями по счету. Учащиеся обычно обнаруживают, что счет 5 или 10 — это самый простой способ группировать и считать предметы.
Занятие по оцениванию в классе
Создайте банку для оценивания в своем классе. Наполните прочную прозрачную пластиковую банку от 200 до 1000 предметов. Такие предметы, как крошечные ластики, бобы или скрепки для бумаг, хорошо работают и довольно недороги.
Сначала дайте всем учащимся возможность записать свои оценки количества предметов в банке. Например, ниже каждый ученик записывает количество ластиков, которое, по его мнению, находится в банке. После того, как учащиеся придут к своим оценкам, обсудите в классе стратегии, которые они использовали для получения записанной суммы.
Например, ниже каждый ученик записывает количество ластиков, которое, по его мнению, находится в банке. После того, как учащиеся придут к своим оценкам, обсудите в классе стратегии, которые они использовали для получения записанной суммы.
Затем высыпьте все предметы (т.е. ластики) в несколько чашек.
Объедините учащихся в пары и дайте им чашку, чтобы они могли считать и группировать предметы по 10 штук за раз.
После того, как учащиеся сгруппировали все предметы по 10, разместите все группы перед классом и задайте следующие вопросы:
- Как мы можем использовать чашки по 10, чтобы узнать, сколько всего у нас есть?
- Можем ли мы создать новые группы, используя группы по десять человек? Какие новые группы мы можем сформировать?
- Сколько человек в каждой новой группе?
После обсуждения в классе раздайте большие контейнеры для новых групп. Например, учащиеся могут сформировать новые группы по 50 или 100 человек, объединив 5 стаканчиков по 10 ластиков в один контейнер по 50 штук. Убедитесь, что у вас достаточно больших контейнеров для новых групп (т. е. 50 ластиков в каждой новой группе), и пометьте каждый. новая группа.
Убедитесь, что у вас достаточно больших контейнеров для новых групп (т. е. 50 ластиков в каждой новой группе), и пометьте каждый. новая группа.
После того, как все новые группы сформированы, считайте сотни, десятки и единицы отдельно. Запишите общее количество предметов (ластиков) на листе бумаги и обсудите, насколько их оценки были похожи или отличались от фактического подсчитанного количества.
Совет № 3. Используйте ежедневную разминку, чтобы укрепить уверенность в себеЕще одна отличная стратегия для повышения ценности места — это ежедневная разминка, особенно если она включает в себя математические рассуждения. Поскольку разрядное значение и понимание десятичной системы счисления являются основой нашей системы счисления, важно, чтобы учащиеся много практиковались.
Вы, наверное, слышали, что людям нужно что-то делать в течение 30 дней, чтобы это вошло в привычку. То же самое справедливо и для детей. Чтобы помочь вашим ученикам освоить ценность места, я разработал 30-дневную программу разминки. Эта процедура вовлекает ваш класс в содержательные математические обсуждения, помогая лучше понять разрядность в пределах 1000.
Эта процедура вовлекает ваш класс в содержательные математические обсуждения, помогая лучше понять разрядность в пределах 1000.
Каждый день проецируйте один урок математики на интерактивную доску. Учащиеся будут отвечать на 4 ежедневных вопроса. С 3 уровнями и 10 занятиями по математике, включенными в каждый уровень, у вас будет 30 дней обучения по месту.
Уровень A: начинающий
Включает 10 математических переговоров с:
- 4 Основные вопросы
- 10 больше и 10 меньше
- Понимание базовых моделей . Уровень B: средний
- 4 промежуточных вопроса
- Рассуждение о разрядных значениях
- Понимание десятичных моделей
- Сложение или вычитание кратных десяти
- Сравнение значений
- плюс 1 Дополнительный бонусный вопрос
- 4 ЗАГЛАВНЫЕ ВОПРОСЫ
- Понимание значения данной Digit
- .

- Применение понимания разрядного значения
- Нанесение чисел на числовую прямую
- Плюс 1 дополнительный ДОПОЛНИТЕЛЬНЫЙ вопрос
Домашний
- 9 класс0076
- Включает в себя различные темы, такие как сложение двузначных и трехзначных чисел.
- Подобные задачи также доступны для вычитания.
- Учащиеся учатся определять порядок возрастания и убывания.
Добавление
вычитание
Сравнение
Время
- Простые и понятные задачи на умножение, помогающие развивать навыки учащихся.
- Сложение и вычитание однозначных и двузначных чисел.
- Также включено сложение и вычитание времени.
Добавление
вычитание
Умножение
Сравнение
Время
Чувство числа
- Уроки сравнения чисел и основных задач на деление.
- Включает такие темы, как четные, нечетные, простые и составные числа.
- Также предоставляется преобразование времени и базовая алгебра.
Добавление
вычитание
Умножение
Разделение
Сравнение
Время
Дробная часть
Алгебра
Чувство числа
- Простые рабочие листы о том, как преобразовывать слова в числа.
- Планы уроков по простому и сложному сложению и вычитанию.
- Кроме того, включено введение в базовую статистику.
Добавление
вычитание
Умножение
Разделение
Время
Алгебра
Статистика
Измерение
Дробная часть
Десятичный
Чувство числа
- Умелое использование тем, включая десятичные дроби, алгебру и дроби.
- Полезные и сложные упражнения на чувство числа.
- Различные задачи статистики предназначены для того, чтобы не отставать от стандартного обучения.
Умножение
Разделение
Время
Алгебра
Статистика
Измерение
Десятичный
Дробная часть
Чувство числа
- Студентам предлагается повторять основные концепции разделения, а также изучать новые.
- Неограниченное количество уроков по умножению дробей на базовом и среднем уровне.
- Также предусмотрено сложение и вычитание целых чисел в разделе «Чувство числа».
Алгебра
Статистика
Измерение
Десятичный
Дробная часть
Чувство числа
- Подтемы включают квадрат и куб чисел, сложение и вычитание десятичных дробей и т. д.
- Учащиеся изучают и приобретают уверенность в преобразовании единиц измерения.
- Углубленное освещение таких тем статистики, как среднее значение, медиана и мода.
Алгебра
Статистика
Измерение
Десятичный
Дробная часть
Чувство числа
- Получите полное представление об алгебре.
- Развлекайтесь, решая вопросы статистики, включая диапазон, среднее значение, медиану и моду.
- Изучите взаимное преобразование единиц измерения температуры, длины и объема в разделе «Измерения».
Алгебра
Статистика
Измерение
Десятичный
Дробная часть
Чувство числа
- Вопросы по алгебре на сложение, вычитание, умножение и деление.
- Измерение представляет собой взаимное преобразование единиц длины, цены в метрах в сантиметры и наоборот.
- Улучшите понимание чисел с помощью вопросов, связанных с факторными выражениями, делением целых и отрицательных чисел.
Алгебра
Статистика
Измерение
Чувство числа
- Найдите точку, отмеченную на числе (и назовите точку)
- Поставьте точку в нужном месте
- Найдите нужное число под галочкой в числовой строке*
- Добавьте недостающий номер
- Узнайте, что числа справа больше, чем числа слева
- Определите, какое число больше, меньше или равно
- Измените диапазон числовой строки и повторите вышеуказанные навыки
- Создавайте числовые ряды, которые считают единицами, двойками, пятерками и десятками, и повторяйте описанные выше навыки .
- Устройство номерной строки
- Расходные материалы APH с крупным шрифтом, числовые строки
- Расходные материалы APH, числовые строки шрифта Брайля
- Устройство APH Number Line: виниловые весы, набор из 15 шт.

Включает 10 бесед по математике с:
Уровень C: Advanced
Включает 10 математических переговоров с:
Поднимите понимание разрядного значения учащимся на новый уровень с помощью этой процедуры. Нажмите на изображение ниже, чтобы купить.
Рекомендуемые ресурсы магазина
Метод определения разрядности
Эта математическая процедура помогает понять значение разряда за 30 дней! Студенты отвечают на 4 ежедневных вопроса, чтобы развить чувство числа в пределах 1000.
Купить сейчас
Учащиеся младших классов приходят в школу, считая единицами, но необходим переход к более эффективным стратегиям (особенно при понимании больших чисел). Проведение времени в первые годы, группируя 10 и 100, представляя числа в стандартных и эквивалентных группах, а также читая и записывая числа, безусловно, поможет закрепить понимание значения места.
Я надеюсь, что эти советы помогут вам сформировать прочную основу для оценки места у ваших учеников.
Полное цитирование таблицы значений мест и соотношений значений мест – Ван Де Валле, Дж., Карп, К.С., и Бэй Уильямс Дж.М. (2010). Математика в начальной и средней школе: обучение с развитием (7-е изд.). Бостон: Allyn & Bacon
792
Математика для разных классов | iPracticeMath
iPracticeMath имеет бесконечное количество планов уроков и рабочих листов, которые классифицируются по разным оценкам и темам. С 1 класса до 9 класса есть все, что вам нужно знать и изучать по математике. Тщательно составленные вопросы и учебные материалы призваны помочь ваши ученики учатся лучше и обеспечивают платформу для будущего изучения математики.
Перейти в 9 класс
Перейти в 10 класс
Перейти в 11 класс
Перейти в 12 класс
Перейти к 1-5 классам
Перейти в 6 класс
Перейти в 7 класс
Перейти в 8 класс
iPracticeMath предоставляет учащимся возможность проверить свои математические навыки. Эти математические задачи предназначены для первоклассников, сохраняя при этом
Имейте в виду уровень сложности и потенциал обучения.
Эти математические задачи предназначены для первоклассников, сохраняя при этом
Имейте в виду уровень сложности и потенциал обучения.
Математика 2-го класса состоит из тем, которые могут помочь развить понимание математических терминов и функций. которые ранее не были известны учащимся.
которые ранее не были известны учащимся.
Математика 3-го класса предлагает учащимся задания для совершенствования своих понятий и основных математических навыков простым, но сложным способом.
Помогите своим ученикам обучить основам математики в веселой и увлекательной форме. Превратите изучение математики в 4-м классе в отличный опыт для них!
Превратите изучение математики в 4-м классе в отличный опыт для них!
Математика для 5-го класса предназначена для того, чтобы учащиеся были в курсе тем, которые необходимо изучить и понять в школе.
Математика 6-го класса состоит из простых и сложных вопросов, чтобы увидеть, насколько хорошо учащиеся усвоили понятия.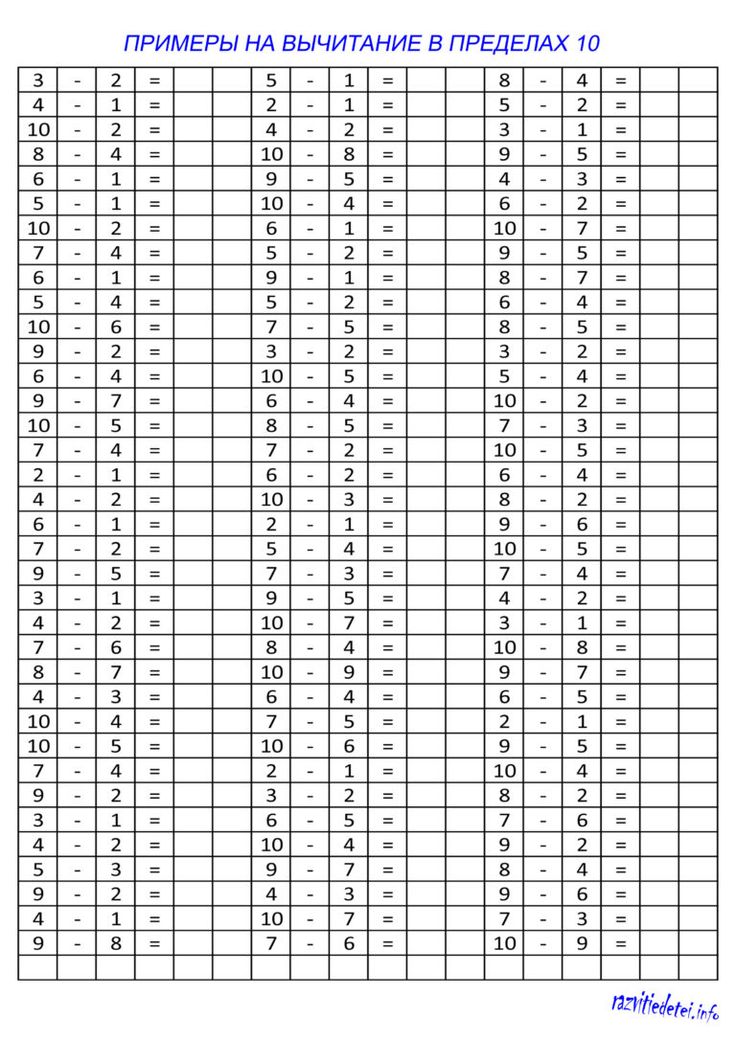
Математика 7-го класса дает учащимся возможность вовремя оттачивать базовые и продвинутые понятия. чтобы избежать проблем при выполнении математических функций.
чтобы избежать проблем при выполнении математических функций.
Математика 8-го класса в основном направлена на приобретение знаний, связанных с алгеброй, статистикой, измерениями, десятичными знаками, дробями и смыслом чисел.
iPracticeMath предлагает простые и увлекательные упражнения, помогающие освоить основы статистики, измерений, алгебры и понимания чисел.
Перейти в 9 класс
Перейти в 10 класс
Перейти в 11 класс
Перейти в 12 класс
Перейти к 1-5 классам
Перейти в 6 класс
Перейти в 7 класс
Перейти в 8 класс
Обучение математическим навыкам с числовыми линиями: часть 1
Обычные детские сады и классы для первоклассников были бы неполными, если бы на стене с гордостью не висели алфавит и числовой ряд. Часто к верхней части парты каждого учащегося приклеивается ламинированная числовая строка, к которой учащийся может легко получить доступ. Почему числовые линии занимают такое видное место в классах? Числовые линии помогают обеспечить умственную стратегию сложения и вычитания; исследования показали, что числовые линии важны, потому что они способствуют хорошему умственному восприятию чисел и арифметическим стратегиям.
Часто к верхней части парты каждого учащегося приклеивается ламинированная числовая строка, к которой учащийся может легко получить доступ. Почему числовые линии занимают такое видное место в классах? Числовые линии помогают обеспечить умственную стратегию сложения и вычитания; исследования показали, что числовые линии важны, потому что они способствуют хорошему умственному восприятию чисел и арифметическим стратегиям.
Мы все согласны с тем, что числовые линии важны. Итак, как мы учим понятиям числа и числа, особенно младших школьников с нарушениями зрения? Передовая практика для слабовидящих учащихся поддерживает использование манипулятивных средств для первоначального ознакомления с базовыми математическими навыками и концепциями восприятия чисел. В части 1 этой серии мы расскажем о различных основных действиях с числовыми линиями и проследим за тем, как молодой студент развивает базовое чувство чисел с помощью тактильных числовых линий.
Джессика Макдауэлл, опытный и творческий TVI, поделилась своими материалами и знаниями, когда она преподает концепции числовых линий этой очаровательной первокласснице. Логан умеет читать по Брайлю и получает доступ к своей математике с помощью шрифта Брайля. Первоначально Джессика познакомила Логана со стандартными линиями тактильных чисел APH (включая числовую строку APH, которая находится в диапазоне от 0 до 20), а также с меньшими числовыми линиями, созданными учителем. Его TVI предварительно научил, как получить доступ к тактильной числовой линии, и Логан последовал за своим основным классом, когда они научились использовать числовые линии для изучения основных математических понятий.
Логан умеет читать по Брайлю и получает доступ к своей математике с помощью шрифта Брайля. Первоначально Джессика познакомила Логана со стандартными линиями тактильных чисел APH (включая числовую строку APH, которая находится в диапазоне от 0 до 20), а также с меньшими числовыми линиями, созданными учителем. Его TVI предварительно научил, как получить доступ к тактильной числовой линии, и Логан последовал за своим основным классом, когда они научились использовать числовые линии для изучения основных математических понятий.
Базовые навыки работы с числовыми линиями

*Примечание. Важно, чтобы строки с тактильными номерами были созданы с делениями и с числом, напечатанным шрифтом Брайля под делением. Студентов, изучающих шрифт Брайля, нужно научить пользоваться делениями (важно для сложения и вычитания) и тому, как физически проводить пальцем прямо вниз, чтобы найти число в шрифте Брайля.
Первоначальные проблемы для Логана
Класс провел много игр и упражнений по понятиям, не используя книгу и не выполняя задания с бумагой/карандашом. Многие из этих игр требовали модификации, чтобы быть доступными, или использовались замененные игры.
Примечание. Многие классы используют мотивирующие, но недоступные приложения для отработки навыков числового ряда.
В конце концов, ученики были оценены на бумаге, и у Логана не было много времени с тактильной графикой в учебнике для числовых линий до оценивания.
Интерактивные тактильные числовые линии
Ресурсы номерной строки
Создавайте веселые интерактивные игры с числовыми рядами, чтобы практиковать основные навыки числового ряда, включая способность находить точку на числовом ряду. Начните с манипулятивных действий, таких как создание магнитной тактильной числовой строки и размещение забавной формы/объекта, магнитного на или чуть выше галочки в числовой строке Брайля. Добавьте тактильную цифру на пробковую доску и попросите ученика использовать огромную канцелярскую кнопку на отметке или чуть выше, чтобы отметить желаемое число. (См. пост «Упражнения с числовыми строками», чтобы узнать об упражнениях с пробковой доской и связанных с ними действиях с числовыми строками.) По мере продвижения ученик может наклеивать наклейки (наклейки из пеноматериала хорошо работают!) на созданную учителем числовую строку Брайля или числовую строку APH.
Начните с манипулятивных действий, таких как создание магнитной тактильной числовой строки и размещение забавной формы/объекта, магнитного на или чуть выше галочки в числовой строке Брайля. Добавьте тактильную цифру на пробковую доску и попросите ученика использовать огромную канцелярскую кнопку на отметке или чуть выше, чтобы отметить желаемое число. (См. пост «Упражнения с числовыми строками», чтобы узнать об упражнениях с пробковой доской и связанных с ними действиях с числовыми строками.) По мере продвижения ученик может наклеивать наклейки (наклейки из пеноматериала хорошо работают!) на созданную учителем числовую строку Брайля или числовую строку APH.
Основные понятия числовой линии
При вводе числовой строки объясните, что такое деления и почему они используются. Предложите учащемуся следить за отметками, чтобы найти кружок (или объект) на отметке. Как только объект найден, учащийся должен провести пальцем вниз по отметке и продолжить вниз, чтобы найти число Брайля, соответствующее этой отметке.
Предложите учащемуся определить диапазон числовой прямой и шкалы. Диапазон можно найти, указав число в крайнем левом углу и число в крайнем правом углу. Начните с единицы – каждое число и галочка увеличиваются на единицу. По мере продвижения ученика шкала может измениться на увеличение на двойки, пятерки, десятки и более.
Помните: цель состоит в том, чтобы научить ученика находить предмет по делениям (не по цифрам Брайля под числовой строкой); затем учащийся должен провести пальцем вниз, чтобы определить правильное число. (Причина: если учащийся привык следовать цифрам, а не галочкам, сложение и вычитание могут сбить с толку, так как учащийся будет считать, одновременно следуя цифрам Брайля.)
Начало игры с числовыми линиями
Выберите простую числовую строку (в зависимости от ученика диапазон может быть 1-5 или 1-10). Используя одну из манипулятивных числовых линий, упомянутых выше (магнитная доска, пробковая доска и т. д.), попросите ученика исследовать тактильную числовую линию. Определите различные части и положение/взаимосвязь каждой части: деления, прямая горизонтальная линия и числа. Начните слева и двигайтесь вправо. Учащимся, возможно, придется сначала следовать по прямой горизонтальной линии, прежде чем они смогут следовать по отметкам. Попросите учащегося начать с левой стороны и подсчитать галочки (обязательно начните с того же числа — нуля или единицы — которое указано шрифтом Брайля для этой числовой строки). Затем попросите учащегося прочитать цифры Брайля под числовой строкой. Соответствовало ли количество его делений цифрам Брайля? Вернитесь назад и пересчитайте галочки.
Определите различные части и положение/взаимосвязь каждой части: деления, прямая горизонтальная линия и числа. Начните слева и двигайтесь вправо. Учащимся, возможно, придется сначала следовать по прямой горизонтальной линии, прежде чем они смогут следовать по отметкам. Попросите учащегося начать с левой стороны и подсчитать галочки (обязательно начните с того же числа — нуля или единицы — которое указано шрифтом Брайля для этой числовой строки). Затем попросите учащегося прочитать цифры Брайля под числовой строкой. Соответствовало ли количество его делений цифрам Брайля? Вернитесь назад и пересчитайте галочки.
Теперь незаметно добавьте объект с магнитом или канцелярской кнопкой чуть выше деления; никогда не наклеивайте наклейку на число Брайля! (Сначала выбрал галочку в середине числовой строки, чтобы учащийся практиковался в том, чтобы следовать галочке, а затем считать ее.) Предложите учащемуся определить соответствующую цифру, проведя пальцем вниз к цифре Брайля.
С помощью 10-кадра ниже первоклассник Логан перемещает Пятно (трехмерную божью коровку вдоль 10-кадрового лотка, разрезанного пополам вдоль и превращенного в 1×10 (вместо 2×5). Джессика (TVI) добавлена ряд соответствующих чисел Брайля ниже десяти кадров (каждое число выровнено по центру каждого квадрата десяти кадров). На рисунке ниже соответствующие числа Брайля находятся в диапазоне от 1 до 10. Джессика сделала дополнительные соответствующие числовые строки, такие как 10 — 100 (считая на десятки), которые можно легко заменить. Внизу изображения находится числовая строка APH 0-20, которая не такая длинная, как числовая строка с 10 кадрами.0003
Джессика (TVI) добавлена ряд соответствующих чисел Брайля ниже десяти кадров (каждое число выровнено по центру каждого квадрата десяти кадров). На рисунке ниже соответствующие числа Брайля находятся в диапазоне от 1 до 10. Джессика сделала дополнительные соответствующие числовые строки, такие как 10 — 100 (считая на десятки), которые можно легко заменить. Внизу изображения находится числовая строка APH 0-20, которая не такая длинная, как числовая строка с 10 кадрами.0003
Благодаря деятельности с божьей коровкой Логан научился считать квадраты, определяя квадрат, в котором находилась божья коровка.
Следующим шагом будет попросить вашего ученика найти и поместить маркер на желаемую отметку или немного выше нее. Используя рамку 1 × 10, Логан научился считать квадраты, чтобы поместить божью коровку в нужный квадрат. Перемещение божьей коровки при подсчете квадратов более конкретно, чем подсчет делений. Он также научился находить число Брайля под десятичной рамкой.
Студенческий прогресс
Время выполнения этих заданий с числовым рядом зависит от возраста и способностей учащегося. Некоторые учащиеся могут потратить неделю на каждую часть задания, в то время как другие учащиеся могут быстро выполнить многие из этих действий за один урок. Имейте в виду, что большинству младших школьников требуется время и практика — повторение одного и того же действия или подобных действий снова и снова, прежде чем они будут готовы перейти к следующему шагу. Для учащихся со зрением учителя обычно предлагают множество игр, которые предоставляют несколько возможностей повторить один и тот же навык, прежде чем перейти к следующему навыку.
Некоторые учащиеся могут потратить неделю на каждую часть задания, в то время как другие учащиеся могут быстро выполнить многие из этих действий за один урок. Имейте в виду, что большинству младших школьников требуется время и практика — повторение одного и того же действия или подобных действий снова и снова, прежде чем они будут готовы перейти к следующему шагу. Для учащихся со зрением учителя обычно предлагают множество игр, которые предоставляют несколько возможностей повторить один и тот же навык, прежде чем перейти к следующему навыку.
Примечание. Вводите основные понятия числовых рядов в том порядке, в котором их вводят в обычном классе. Помните, цель состоит в том, чтобы учитель общего образования взял на себя ответственность за обучение ученика; Ответственность TVI состоит в том, чтобы модифицировать материалы и концепции предварительного обучения, которые являются уникальными для учащихся с нарушениями зрения, и поддерживать учителя общего образования.
Студенческие ожидания
Каждое задание поощряет максимальную самостоятельность учащихся. Ожидается, что Логан самостоятельно прочитает свою математическую задачу по Брайлю, объявит математическую задачу вслух, объявит по мере счета и будет иметь «план» того, как найти ответ. Он автоматически перемещает руки к своим манипулятивным и/или числовым линиям, чтобы выяснить проблему. Очень мало подсказок — если они вообще есть — даются. Логану разрешено делать ошибки, и, если необходимо, позже он получает дополнительные инструкции, чтобы исправить свою ошибку. Найдя ответ, Логану сначала предлагается переформулировать математическую задачу и ответить. (В части 2 этой серии Логан автоматически повторяет математическую задачу и отвечает без подсказок.) Также интересно отметить, что Логан может сидеть неподвижно во время работы, даже если у него много энергии, когда он физически не взаимодействует с манипуляторы или тактильные материалы.
Ожидается, что Логан самостоятельно прочитает свою математическую задачу по Брайлю, объявит математическую задачу вслух, объявит по мере счета и будет иметь «план» того, как найти ответ. Он автоматически перемещает руки к своим манипулятивным и/или числовым линиям, чтобы выяснить проблему. Очень мало подсказок — если они вообще есть — даются. Логану разрешено делать ошибки, и, если необходимо, позже он получает дополнительные инструкции, чтобы исправить свою ошибку. Найдя ответ, Логану сначала предлагается переформулировать математическую задачу и ответить. (В части 2 этой серии Логан автоматически повторяет математическую задачу и отвечает без подсказок.) Также интересно отметить, что Логан может сидеть неподвижно во время работы, даже если у него много энергии, когда он физически не взаимодействует с манипуляторы или тактильные материалы.
Что отсутствует Активность
Счет является обязательным навыком перед введением в действие «Чего не хватает». Заполнение пробелов для последовательности чисел и в числовой сетке — это вопрос активности и оценки, который встречается в младших начальных классах. Студенты также должны уметь читать цифры Брайля. Сначала создайте простую страницу шрифта Брайля с цифрами от 1 до 10 (оставьте два пустых места между цифрами, чтобы дать учащемуся время обработать числа, которые он только что прочитал) и попросите учащегося прочитать числа, написанные Брайлем. Затем дайте учащемуся простую страницу шрифтом Брайля с цифрами от 1 до 10, без одной цифры. (При необходимости вначале можно оставить пустое место для пропущенного числа, чтобы помочь учащемуся самостоятельно определить пропущенное число.) Повторите игру со страницами Брайля, на которых есть несколько пропущенных чисел и/или разные диапазоны чисел. Хотите вызов? Меняйте числа, считая двойками, пятерками или десятками!
Студенты также должны уметь читать цифры Брайля. Сначала создайте простую страницу шрифта Брайля с цифрами от 1 до 10 (оставьте два пустых места между цифрами, чтобы дать учащемуся время обработать числа, которые он только что прочитал) и попросите учащегося прочитать числа, написанные Брайлем. Затем дайте учащемуся простую страницу шрифтом Брайля с цифрами от 1 до 10, без одной цифры. (При необходимости вначале можно оставить пустое место для пропущенного числа, чтобы помочь учащемуся самостоятельно определить пропущенное число.) Повторите игру со страницами Брайля, на которых есть несколько пропущенных чисел и/или разные диапазоны чисел. Хотите вызов? Меняйте числа, считая двойками, пятерками или десятками!
В следующем видео Логану дается созданная учителем страница Брайля с диапазоном чисел, заканчивающихся на 101; отсутствуют различные номера. Обеими руками Логан спокойно сидит и читает цифры на странице, определяя, каких цифр не хватает.
Как только учащийся поймет концепцию определения пропущенных чисел, дайте ему созданные учителем числовых строк с пропущенными числами.
Примечание. При выполнении задания с отсутствующей числовой строкой учащийся будет следить за числами Брайля, а не за галочками в числовой строке. Однако не забудьте указать учащемуся, что для большинства операций с числовыми строками, таких как сложение и вычитание, учащийся должен считать деления, а не числа Брайля.
Больше, равно, меньше активности
Спросите учащегося, «растут» ли числа (становятся больше) по мере того, как вы перемещаетесь вправо или влево по числовой строке. Обсудите идею о том, что чем больше вы двигаетесь вправо, тем выше число. Если вы двигаетесь влево (назад по числовой строке), числа становятся меньше.
Используйте желаемую манипулятивную числовую строку; в этом примере будет использоваться кадр Логана 1 × 10, 2 божьи коровки и 2 лягушки. На трех каталожных карточках напечатайте шрифтом Брайля один из следующих математических символов: Больше, Равно или Меньше. Разместите божью коровку и манипуляторы лягушки в разных квадратах; начните с того, что божья коровка больше лягушки. Обсудите, какое число больше, божья коровка или лягушка? Введите соответствующий математический символ «Больше чем». Составьте математическое уравнение, поместив вторую божью коровку на каталожную карточку (оставив место для карточки с математическими символами), а вторую лягушку — на другую карточку. Попросите учащегося поместить символ «Больше чем» между двумя жуками. Повторите это действие несколько раз со знаком «больше чем». Если ученик готов, замените вторую божью коровку и лягушку каталожными карточками, на которых указано соответствующее число. Пример: если божья коровка на 5, а лягушка на 2, учетная карточка со шрифтом Брайля 5 будет заменена на божью коровку, а учетная карточка со шрифтом Брайля номер два будет заменена на лягушку.
Обсудите, какое число больше, божья коровка или лягушка? Введите соответствующий математический символ «Больше чем». Составьте математическое уравнение, поместив вторую божью коровку на каталожную карточку (оставив место для карточки с математическими символами), а вторую лягушку — на другую карточку. Попросите учащегося поместить символ «Больше чем» между двумя жуками. Повторите это действие несколько раз со знаком «больше чем». Если ученик готов, замените вторую божью коровку и лягушку каталожными карточками, на которых указано соответствующее число. Пример: если божья коровка на 5, а лягушка на 2, учетная карточка со шрифтом Брайля 5 будет заменена на божью коровку, а учетная карточка со шрифтом Брайля номер два будет заменена на лягушку.
Представьте процесс с помощью математических символов «меньше чем», а затем «равно». Некоторым учащимся может быть полезно просто выбрать правильный математический символ, а не составлять математическое уравнение.
Ресурсы номерной строки APH
В APH есть несколько ресурсов тактильной числовой строки, которые могут оказаться полезными:
 Д. Чурсина»
Д. Чурсина» Вставь вместо звёздочки знак «+» или «-»:
Вставь вместо звёздочки знак «+» или «-»: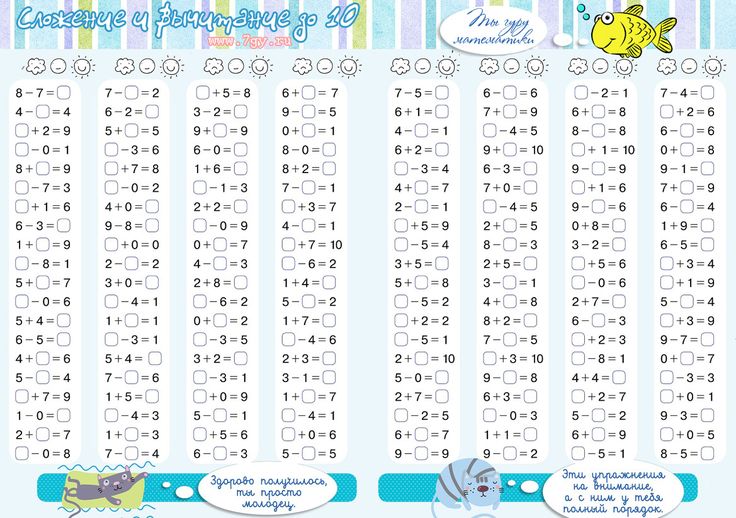 Найди ошибки:
Найди ошибки: Из каких чисел состоит?
Из каких чисел состоит? Найди закономерность. Продолжи ряды чисел влево и вправо:
Найди закономерность. Продолжи ряды чисел влево и вправо: д.;
д.; Реши кроссворд
Реши кроссворд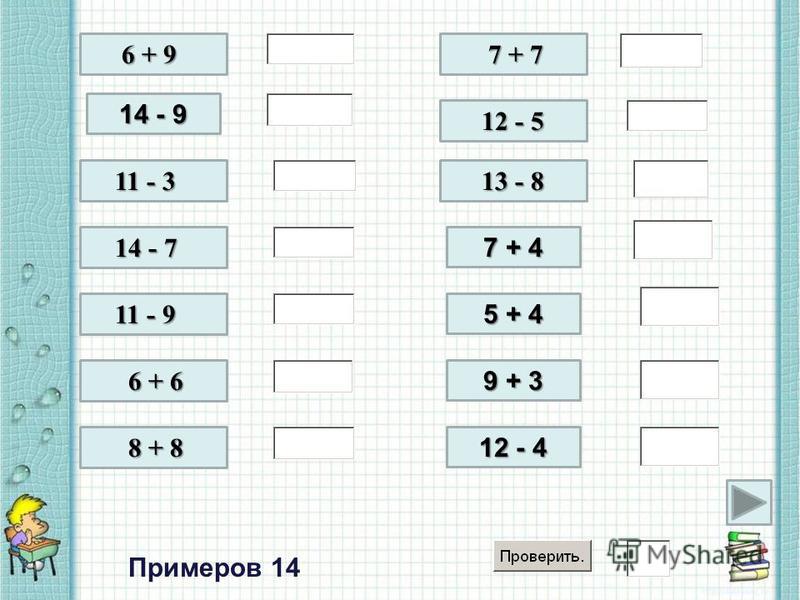
 Ф., Басов А. В. Развитие логического мышления детей – Ярославль, «Академия развития», 1997
Ф., Басов А. В. Развитие логического мышления детей – Ярославль, «Академия развития», 1997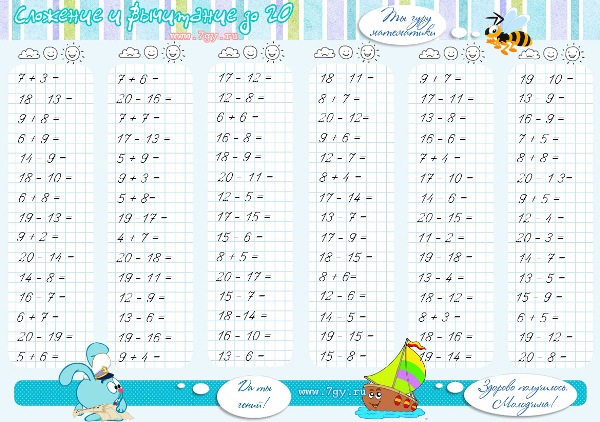 и Число 0.) Слайд 2
и Число 0.) Слайд 2
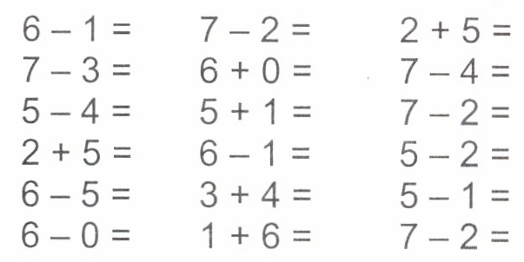 (4+2= 6)
(4+2= 6)
