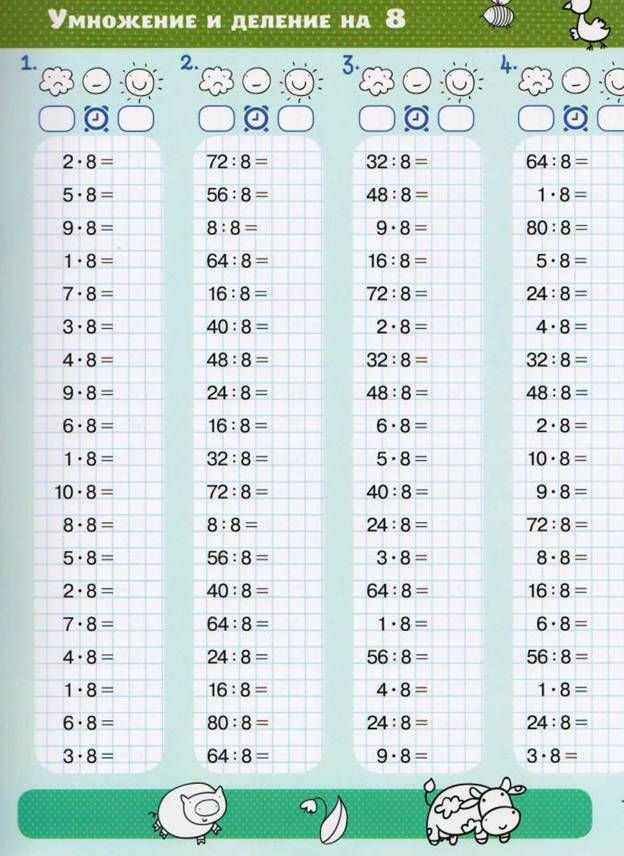
помните ли вы, как правильно

В одной из учительских групп в социальных сетях появился этот простой пример по математике. По словам автора поста, его ученики не смогли единогласно прийти к решению этой задачи. В спор в комментариях вступили коллеги преподавателя. Но всего этого не было бы, если бы участники спора помнили о базовых правилах — о том, в каком порядке выполнять математические действия. Попытайтесь и вы найти правильный ответ.

Юлиана Качанова Отвечаю за тесты

Калькулятор в сторону: решайте своим умом! Помните о порядке математических действий, чтобы найти правильный ответ.

ВОПРОС 1 ИЗ 1

98

50

51

Простые на первый взгляд математические примеры могут вызвать затруднения из-за скобок и обилия действия: сложения, вычитания, умножения и деления. Чтобы не попадаться на удочку и правильно решать подобные уравнения и примеры, необходимо помнить о порядке выполнения математических действий  — в противном случае, вы получите неверный результат.

Пример или уравнение может содержать круглые скобки, которые используются для изменения обычного порядка математических действий. Чтобы сделать все правильно, запомни такие правила:

1. При решении примера со скобками выполняй все действия слева направо — это универсальное математическое правило;
2. Сначала необходимо получить результат в скобках, соблюдая порядок действий;
3. После этого — провести оставшиеся вычисления в правильном порядке: сначала идут умножение и деление, а затем вычитание и сложение. Те же правила применяются к круглым скобкам.

Теперь стало понятнее, как решать примеры со скобками, но что делать, если в уравнении скобок нет, а найти правильный ответ все равно сложно? В этом случае помните, что в первую очередь выполняется умножение и деление (строго слева направо), а уже после — сложение и вычитание.

Чтобы закрепить свои знания, предлагаем найти решение еще одного математического примера.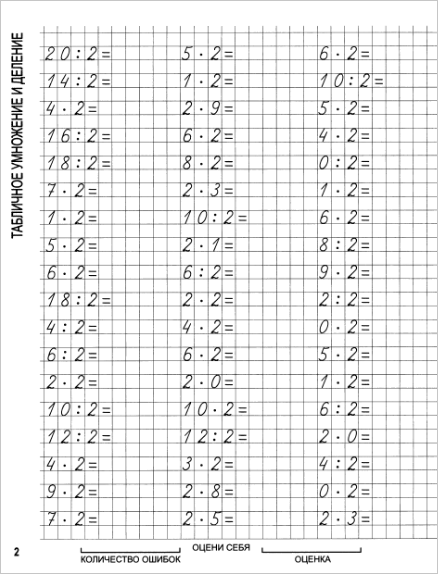 Не забывайте о порядке действий!

10 : 2 * 7 : 5 = ?

Чтобы не ошибиться во время решения, вспоминаем все правила решения примеров без скобок. В нашем случае есть только умножение и деление — значит, сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Ответ: 7.

Чтобы было проще решать сложные примеры со множеством различных действий, можно над арифметическими знаками расставлять цифры, обозначающие порядок их выполнения:

Приемы умножения и деления на 10. 2-й класс, «Школа России»

Тип урока: овладение новыми знаниями.

Цели: познакомить с приемами умножения и деления на 10.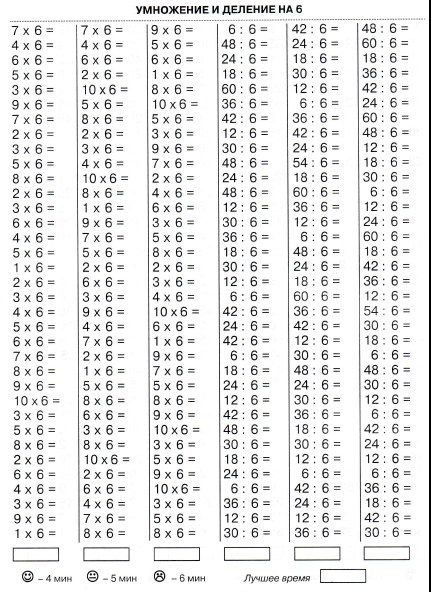 Совершенствовать вычислительные навыки навыки устного счёта, умение решать задачи, развивать  внимание и логическое мышление.

Педагогические задачи: дать первичное представление об умножении и делении числа на 10, продолжать формировать умения находить результат действия деления с помощью примера на умножение, развивать вычислительные навыки, продолжать работу над задачами.

Планируемые образовательные результаты:

Предметные УУД: умение правильно умножать и делить на число 10, знание названия компонентов умножения и деления, понимание сути переместительного закона умножения, умение выделять геометрические фигуры, применение формулы периметра квадрата.

Метапредметные УУД:

• Регулятивные: умение формулировать учебную задачу урока на основе соотнесения того ,что уже известно и усвоено, и того, что еще неизвестно, умение контролировать и оценивать учебные действия в соответствии с поставленной задачей; способность к самопроверке, самооценке, проверке по образцу и корректировке, взаимопроверке.
• Познавательные: проявлять познавательную инициативу в учебном сотрудничестве, умение выделять необходимую информацию, создавать алгоритм деятельности, сравнивать, анализировать, устанавливать причинно-следственные связи, делать выводы.
• Коммуникативные: оказывать необходимую взаимопомощь, договариваться и приходить к общему решению в совместной деятельности, слушать, слышать и понимать партнеров, планировать учебное сотрудничество с учителем и сверстниками, достаточно полно и четко выражать свои мысли.
• Личностные УУД: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения; развитие навыков сотрудничества с взрослыми и сверстниками в разных социальных ситуациях, проявление самостоятельности, личной ответственности.

Методы и формы обучения: частично-поисковый, фронтальная и групповая работа, индивидуальная.

Оборудование: компьютер, электронная доска, доска, карточки с заданием, математический веер, карта путешествия, сундучок с призами.

1. Организационный момент

— Ребята, сегодня у нас необычный урок. Мы с вами отправимся в увлекательное морское путешествие и побудем командой моряков. С нами на борту присутствуют пассажиры. Только от нашей слаженной, дружной работы, зависит найдем ли мы сегодня клад.

2. Актуализация знаний

— Давайте вспомним правила поведения на корабле (Отвечаем по руке, задание дослушиваем до конца, сидим ровно прямо).

— Чтобы отправиться в путь нам нужно проложить курс корабля. Найдем значение данных математических выражений, показывая ответы на математическом веере.

(Выводим картинку корабля на электронную доску).

— Ребята, прочитайте данные математические выражения, назвав их компоненты и найдите значение (если дети затрудняются, необходимо напомнить арифметическое действие).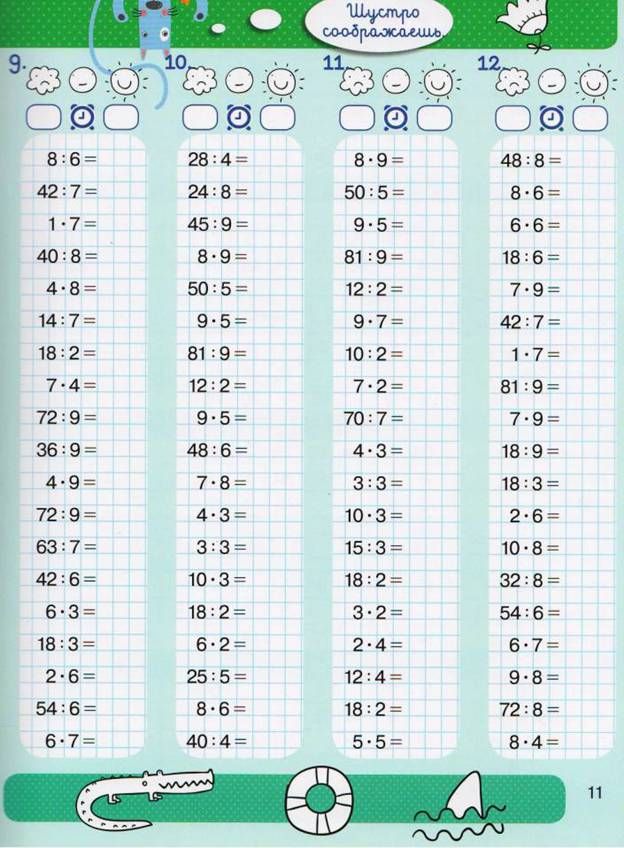

— 14 + 6 (1 слагаемое — 14, 2 слагаемое – 6, сумма равна 20).

— 43 — 4 (Уменьшаемое – 43, вычитаемое – 4, разность равна 39).

— 16 : 4 (Делимое – 16, делитель – 4, частное равно 4).

— 4 * 3 (1 множитель – 4, 2 множитель -3, произведение равно 12).

— 8 * 0 (1 множитель – 8, 2 множитель — 0, произведение равно 0).

— 40 — 33 (Уменьшаемое – 40, вычитаемое – 33, разность равна 7).

— 5 * 10 (1 множитель – 5, 2 множитель -10, произведение равно 50).

— 24 : 4 (Делимое – 24, делитель – 4, частное равно 6).

— 10 * 5 (1 множитель – 10, 2 множитель — 5, произведение равно 50).

— 17 + 15 (1 слагаемое — 17, 2 слагаемое – 17, сумма равна 32).

— Ребята, что мы сейчас с вами делали? (Считали математические выражения, вспоминали название математических компонентов).

— Молодцы! Мы отправляем наш корабль в добрый путь!

3. Самоопределение к деятельности

— Ребята, а что вы заметили, работая с данными  математическими выражениями?

(Мы заметили, что два выражения с одинаковыми числами и одинаковым результатом. Это 5*10 и 10*5).

Учитель записывает выражение на доске (5*10 … 10*5).

— Ребята, сравните это выражение. Какой знак мы поставим? (Равно.)

— Какое математическое свойство вы  использовали для сравнения выражения? (Переместительное свойство умножения. От перестановки множителей результат умножения не изменяется).

 — Вычислите  значение этих выражений, заменяя умножение сложением  (Один ребенок работает у доски. 5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)

— Хорошо. Ребята, чтобы дальше отправиться в путь на нашем корабле, нам нужно составить по этим выражениям два примера на деление (50 : 10 = 5  и 50 : 5 = 10)

— А как вы нашли значение  выражений? (Зная значение произведения чисел 5 и 10, можно найти их частное)

— Какое правило взаимосвязи компонентов и результата действия вам помогло?

(Если произведение разделить на один из множителей, то получится другой множитель)

— На сегодняшнем уроке мы продолжим учиться выполнять умножение и деление чисел и познакомимся с новым приёмом.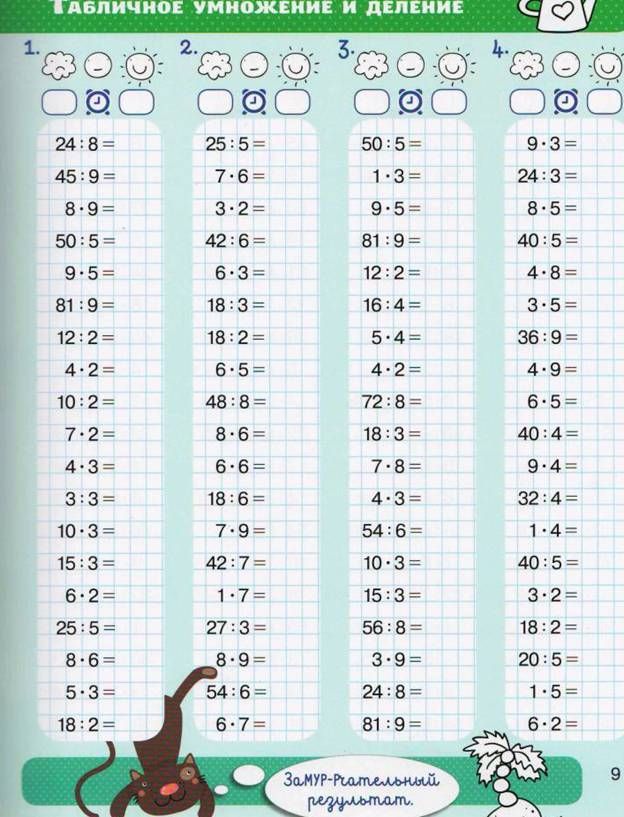
А кто догадался, что это за приём? (Приём умножения и деления на число 10)

— Ребята, что мы сейчас с вами делали? (Сравнивали выражения, повторяли переместительное свойство умножения и деления).

— Молодцы, отправляемся далее в наше путешествие.

— Проверьте своё предположение, откройте с. 74 и прочитайте задачи урока.

— Прочитайте объяснение вычислительного приема рядом с красной чертой.

— Послушаем объяснение и обратим наше внимание на электронную доску (Числа от 1 до 100. Приемы умножения и деления на 10).

— Что вы можете сказать о наших выводах и выводах в учебнике?

(От перестановки множителей результат умножения не изменяется. Если произведение разделить на один из множителей, то получится другой ).

— Хорошо, что мы сейчас с вами сделали? (Убедились, что наши предположения правильны).

— Отправляемся дальше в наше увлекательное путешествие.

4. Физминутка

— Мы с вами моряки и нам необходимо быть внимательными, чтобы не попасть в руки к пиратам или не наткнуться на айсберг.
Игра «Запрещенное движение». Учитель говорит запретное движение, а дети должны быть внимательными и не повторять его, если учитель сказал или показал его.

5. Работа по учебнику

Минутка чистописания.

— Откройте тетради, запишите: сегодняшнее  число, Классная работа.

Цифра вроде буквы О —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним
Единицу примостим,
Он побольше станет весить,
Потому что это — десять.

— Какое число будем прописывать? (10)

— Что можно сказать о числе 10? (чётное, двузначное, круглое, 1 десяток, 0 ед., в числовом ряду стоит после числа 9, перед числом 11)

— Что в жизни  бывает круглым? (Солнце, арбуз, мяч, часы, пуговица и т.

п.)

— А в математике? (Круг, шар, числа)

— Какие числа называют круглыми? (Круглыми называют числа, оканчивающиеся на ноль).

— Назовите все круглые числа в числовом ряду до 100? (10, 20, 30, 40, 50, 60, 70, 80, 90).

— Назовите самое маленькое круглое двузначное число? Самое маленькое  круглое трехзначное число? (10; 100).

— Прописываем число 10 через клеточку.

(Прописная цифра 1. — Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.

Прописная цифра 0. — Овал начинают писать немного левее правого верхнего угла клетки. Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем ведут руку вверх к началу овала.)

— Молодцы, наш корабль плывет дальше.

— №1 стр.74 – фронтальная работа.

Составление таблицы. Дети устно поочередно читают примеры.

— Как связаны между собой четыре столбика примеров? (При составлении 2 столбика используется переместительное свойство умножения, при составлении 3 и 4 столбика – правило о том, что если значение произведения разделить на один множитель, то получится другой множитель).

10 * 2 = 20	2 * 10 = 20	20 : 2 = 10	20 : 10 = 2
10 * 3 = 30	3 * 10 = 30	30 : 3 = 10	30 : 10 = 3
10 * 4 = 40	4 * 10 = 40	40 : 4 = 10	40 : 10 = 4
10 * 5 = 50	5 * 10 = 50	50 : 5 = 10	50 : 10 = 5
10 * 6 = 60	6 * 10 = 60	60 : 6 = 10	60 : 10 = 6
10 * 7 = 70	7 * 10 = 70	70 : 7 = 10	70 : 10 = 7
10 * 8 = 80	8 * 10 = 80	80 : 8 = 10	80 : 10 = 8
10 * 9 = 90	9 * 10 = 90	90 : 9 = 10	90 : 10 = 9
10 * 10 = 100	10 * 10 = 100	100 : 10 = 10	100 : 10 = 10

— Ребята, какой вывод мы можем сделать об умножении и делении на 10? (Вывод: при умножении на 10  к числу справа дописывается 0.

При делении на 10 у числа 0 убирается!)

Дети читают на электронной доске стихотворение-правило.

— Наш корабль доплыл до середины пути, продолжаем наш путь. Что мы сейчас делали? (Выявили правило умножения и деления на 10.)

6. Физминутка

— Моряки должны быть не только внимательными, но и ловкими и смелыми.

— Как мы будем плыть на спасательной шлюпке? (Упражнение гребля)

— Как будем залезать по висячей лестнице? (Упражнение как будто лезем по лестнице руками)

— Как будем смотреть вдаль? (Упражнение тянемся на мысочках)

7. Закрепление изученного материала

— Ребята, как называется кухня на корабле? (Камбуз)

— Как называют повара на корабле? (Кок)

— Кок приготовил нам пирожки, но (скажу вам по секрету) кок – это бывший пират и он не умеет считать. Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.

Задача №3.

— Прочитай задачу про себя.

— Прочитай вслух.

— Сколько пирожков раскладывал повар? (40)

— Как он их раскладывал? (Поровну).

— Что значит «поровну»? (На каждую тарелку одинаковое количество).

— Как будем раскладывать пирожки на 10 тарелок? (По 1 пирожку на каждую тарелку).

(Один ученик работает у доски. 10 магнитных тарелок закрепляем на доске, раскладываем пирожки (из бумаги) по тарелкам).

— Сколько пирожков оказалось на каждой тарелке? (1)  

— Поровну разложили все 40 пирожков? (Нет).

— Уточните, как будем раскладывать пирожки? (До тех пор, пока все не закончатся).

— Сколько пирожков стало на каждой тарелке? (По 4 пирожка).

— Запишите решение задачи и ответ.

40:10=4 (п.)

Ответ: на каждой тарелке по 4 пирожка.

— Что обозначает число 40?  (Количество пирожков)

— Что обозначает число 10? (Количество тарелок)

-Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Решим 2 задачи обратные данной (с помощью магнитных рисунков составляем условие задач).

1. Повар разложил 40 пирожков на тарелки.  В каждой тарелке получилось по 4 пирожка. На сколько тарелок повар разложил пирожки?

40: 4 = 10 (т.)

Ответ: на 10 тарелок.

— Что обозначает число 40?  (количество пирожков)

— Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Что обозначает число 10? (Количество тарелок)

2. Повар разложил на 10 тарелок пирожки. В каждой тарелке получилось по 4 пирожка. Сколько всего пирожков было?

10 * 4 = 40 (п.)

Ответ: 40 пирожков всего.

— Что обозначает число 10? (Количество тарелок)

— Что обозначает число 4? (Сколько пирожков на каждой тарелке).

— Что обозначает число 40?  (Количество пирожков)

— Молодцы! Что мы сейчас с вами делали? (Решали задачу и составляли задачи обратной данной).

— Хорошо, наш корабль следует дальше. И перед нами разрушенный мост. Чтобы проплыть дальше, нам необходимо восстановить мост, решая примеры самостоятельно (Выводим картинку моста с примерами на электронную доску. Примеры из №5 с.74. Решаем в столбик. После выполнения задания проверка.)

• 74 – 58 = 16
• 46 + 37 = 83
• 83 – 29 = 54
• 64 + 36 = 100

— Молодцы! Корабль наш держит путь далее и мы с вами находим сундук с сокровищами. Чтобы открыть сундук нам надо узнать длину его стороны, зная уже периметр.

— Какую фигуру представляет сундук? (Квадрат)

— Что такое квадрат? (Прямоугольник, у которого все стороны равны)

— Что такое периметр? (Сумма длин всех сторон)

— Как найти периметр квадрата? (Сложить длины всех сторон)

— Прочитайте задание №4 на стр.74.

— Какая формула периметра квадрата?

(Р = а + а +а +а
Р = а * 4)

— Чему равен периметр квадрата по условию задачи? (20 см. )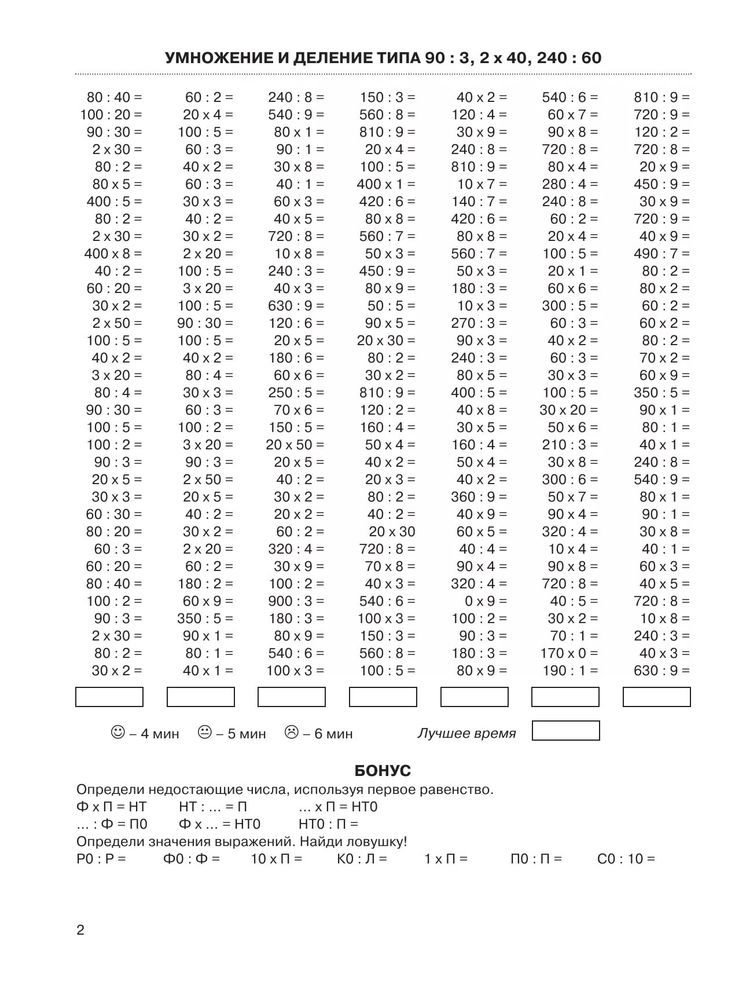

— Подставьте это значение в равенство (а * 4 = 20.)

— Что у вас получилось? (Уравнение.)

— Решите уравнение и узнайте длину стороны этого квадрата.

а * 4 =20
а = 20:4
а =5

Ответ: а = 5 см.

— Молодцы! Что мы сейчас делали? (Закрепляли изученный материал)

8. Рефлексия

— Решение задания по компьютеру № 1.

Работа в группах.

— Мы продолжаем наше путешествие и находим на острове бутылку с посланием. На листочках детям дается задание составить числовые выражения на деление. Проверка проходит фронтально.

— Составьте числовые выражения на деление.

1) 3, 30, 10 0, 50, 4, 10, 40 60, 6, 5
30 : 3 = 10
100 : 10 = 10
50 : 5 = 10
40 : 4 = 10
60 : 6 = 10

2) 90, 70, 7, 80,9 ,10, 100, 20, 8, 2
90 : 9 = 10
70 : 7 = 10
80 : 8 = 10
100 : 10 = 10
20 : 2 = 10

Фронтальная проверка.

9. Подведение итогов урока

— Ребята, мы с вами возвращаемся домой из нашего увлекательного путешествия.

— Какую тайну математики вы сегодня открыли? Чему научились? Всем ли было легко? Какие трудности испытывали? (Мы освоили приемы умножения и деления на 10.)

— Какое правило использовали при умножении числа на 10? (При умножении на 10 к числу справа дописывается 0.)

— Как находить результат при делении круглого числа на 10? (При делении на 10 у числа 0 убирается.)

— Молодцы! Вы были сегодня активны, внимательны, сообразительны, поэтому мы справились со всеми заданиями и нашли сундук с сокровищами. Спасибо вам за хорошую работу.

Выставление отметок.

10. Домашнее задание

— Открываем наш бортовой журнал – дневник и записываем домашнее задание. Учебник – стр.74 № 6.

Сундучок с призами – шоколадные монеты.

Умножение и деление дробей — Криста Кинг Математика

Превращение задач на деление дробей в задачи на умножение дробей

При умножении дробей мы умножаем их числители, чтобы найти числитель результата, и умножаем их знаменатели, чтобы найти знаменатель результата.

???\frac34\times\frac17???

???\frac{3\times1}{4\times7}???

???\frac{3}{28}???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Когда мы делим дроби, мы фактически превращаем задачу деления в задачу умножения, переворачивая делитель (вторую дробь) вверх ногами (поменяв местами числитель и знаменатель) и одновременно заменяя символ деления символом умножения. Мы называем этот процесс «умножением на обратное». обратное дроби ???a/b??? дробь ???b/a??? (где числитель и знаменатель перевернуты.

???\frac34\div\frac17???

???\frac34\times\frac71???

???\frac{3\times7}{ 4\times1}???

???\frac{21}{4}???

Ничего страшного, что в последней дроби числитель больше знаменателя. В этом случае дробь называется «неправильная» дробь

Примеры умножения и деления дробей

Пройти курс

Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого.

🙂

Учить больше

Простой пример умножения дробей

Пример

Умножение дробей.

???\frac23\times\frac{4}{11}???

Чтобы умножить дроби, мы умножаем числители и знаменатели отдельно.

???\frac{2\times4}{3\times11}???

???\frac{8}{33}???

Когда мы делим дроби, мы фактически превращаем задачу деления в задачу умножения, переворачивая делитель вверх ногами.

Давайте сделаем пример с делением.

Пример

Разделите дроби.

???\frac23\div\frac{4}{11}???

Чтобы выполнить деление дробями, мы переворачиваем вторую дробь вверх ногами и одновременно меняем символ деления на символ умножения.

???\frac23\times\frac{11}{4}???

Тогда мы рассматриваем это как задачу на умножение, умножая числители и знаменатели отдельно.

???\frac{2\times11}{3\times4}???

???\фракция{22}{12}???

Нам всегда нравится давать ответ в наименьших выражениях, поэтому мы упростим эту дробь, сократив ???2??? из числителя и знаменателя.

???\frac{22}{12}=\frac{2\cdot11}{2\cdot6}???

???\frac22\cdot\frac{11}{6}???

???1\cdot\frac{11}{6}???

???\фракция{11}{6}???

Получите доступ к полному курсу Pre-Algebra

Начать

Изучение математикиКриста Кинг 2 мая 2019 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, основы, основы математики, дроби, арифметика дробей, операции с дробями, операции с дробями, умножение дробей, умножение дробей, умножение дробей, деление дробей , деление дробей, дробное деление, обратное преобразование дробного деления в дробное умножение, преалгебра, преалгебра

0 лайков

6. Умножение и деление дробей

Вспомните следующие факты дроби:

Умножение дробей

При умножении на дробь умножьте числители и умножить знаменатели:

`2/3xx 5/7=(2xx5)/(3xx7)=10/21`

Если можете, сначала упростите .

В этом примере мы можем отменить «13» и «39», чтобы получить «1/3»:

`\cancel{13}/24xx 12/\cancel{39}=1/24 xx 12/3`

Затем отмените «12» на «24», чтобы получить «1/2»:

`1/\отмена{24} хх \отмена{12}/3=1/2 хх 1/3`

Теперь мы умножаем вершины и основания, чтобы получить:

`1/2 х х 1/3 = 1/6`

Напомним: Мы можем только умножить вершин и низов таким образом. Мы не можем сложить вершины и основания двух дробей, потому что это не даст правильного ответа.

Деление дробей

Когда разделить на дробь, инвертировать и умножить:

`3/5-:2/7=3/5xx7/2=(3xx7)/(5xx2)` `=21/10` `=2 1/10`

(я умножил на обратную величину 2/7, что равно 7/2).

Когда мы делаем то же самое с алгебраическими выражениями, не забудьте УПРОСТИТЬ СНАЧАЛА , чтобы проблему было легко решить выполнять.

Пример 1

Упростить 92`

Упражнения

Упростить:

(1) `5/16-:25/13`

Ответ

Этот включает инвертирование «25/13», чтобы получить «13/25», а затем умножение на это «13/25».

`5/16 -: 25/13=5/16xx13/25`

Затем мы отменяем 5 сверху и 25 снизу, чтобы получить «1/5».

`=1/16 xx 13/5`

`=13/80`

Последняя строка просто:

92− 16)` и получить `(3x + 4)(3x − 4)`, используя разность квадратов, которую мы изучили ранее.

`((3x+4)(3x-4))/(x+1)xx1/(4-3x)`

Далее мы используем следующий полезный прием:

`(4 − 3x) = −(3x − 4)`

(Чтобы понять, почему это работает, просто умножьте правую часть.)

`((3x+4)(3x-4))/(x+1)xx1/-(3x-4)`

После отмены у нас остается коэффициент (−1) от сокращенной дроби, и этот минус для удобства помещается впереди.