§ Смешанные числа. Целая часть дроби. Правильные и неправильные дроби
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
Обратите внимание, что в двух первых дробях (
и
) числители меньше знаменателей. Такие дроби называют правильными.
Запомните!
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
имеет числитель равный знаменателю (такие дроби равны единицы), а дробь
имеет числитель больший знаменателя. Такие
дроби называют неправильными.
Такие
дроби называют неправильными.
Запомните!
У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
.
- Разделим в столбик числитель на знаменатель.
- Теперь запишем ответ.
Запомните!
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
Любое смешанное число можно представить как сумму целой и дробной части.
Запомните!
Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
3 особенности чисел в Python, о которых вы, возможно, не знали / Хабр
Если вы писали код на Python, то весьма высока вероятность того, что вы, хотя бы в одной из своих программ, пользовались числами. Например, это могли быть целые числа для указания индекса значения в списке, или числа с плавающей точкой, представляющие суммы в некоей валюте.
Но числа в Python — это гораздо больше, чем, собственно, их числовые значения. Поговорим о трёх особенностях чисел в Python, с которыми вы, возможно, не знакомы.
№1: у чисел есть методы
В Python практически всё — это объект. Один из первых объектов, о котором узнаёт тот, кто начинает изучать Python — это str, используемый для представления строк. Возможно, вы сталкивались с использованием методов строк, вроде
Возможно, вы сталкивались с использованием методов строк, вроде .lower(), который возвращает новую строку, все символы которой приведены к нижнему регистру:
>>> "HELLO".lower() 'hello'
Числа в Python тоже, как и строки, являются объектами. У них тоже есть методы. Например, целое число можно преобразовать в байтовую строку с помощью метода .to_bytes():
>>> n = 255 >>> n.to_bytes(length=2, byteorder="big") b'\x00\xff'
Параметр length указывает на количество байт, которые нужно использовать при составлении байтовой строки, а параметр byteorder определяет порядок байт. Например, установка параметра byteorder в значение «big» приводит к возврату байтовой строки, в которой старший байт расположен первым, а установка этого параметра в значение
255 — это максимальное значение, которое может принимать 8-битное целое число. Поэтому в нашем случае при вызове метода
Поэтому в нашем случае при вызове метода .to_bytes() можно без проблем воспользоваться параметром length=1:
>>> n.to_bytes(length=1, byteorder="big") b'\xff'
А вот если записать в n число 256 и вызвать для него .to_bytes() с параметром length=1, будет выдана ошибка OverflowError:
>>> n = 256 >>> n.to_bytes(length=1, byteorder="big") Traceback (most recent call last): File "<stdin>", line 1, in <module> OverflowError: int too big to convert
Преобразовать байтовую строку в целое число можно, воспользовавшись методом .from_bytes() класса int:
>>> int.from_bytes(b'\x06\xc1', byteorder="big") 1729
Методы класса вызывают, используя имя класса, а не его экземпляр. Именно поэтому в предыдущем примере метод .from_bytes() вызывают, обращаясь к int.
Любопытный факт: 1729 — это самое маленькое положительное число, которое можно представить в виде суммы кубов двух положительных чисел двумя способами.
Исторический анекдот связывает это число с индийским математиком Сринивасой Рамануджаном, который рассказал о нём своему наставнику Готфри Харолду Харди.
Харди часто навещал Рамануджана, когда тот, умирая, находился в больнице в Патни. Именно в одно из таких посещений произошёл «инцидент» с номером такси. Харди приехал в Патни на такси, воспользовавшись своим излюбленным транспортным средством. Он вошёл в палату, где лежал Рамануджан. Начинать разговор Харди всегда было мучительно трудно, и он произнёс свою первую фразу: «Если не ошибаюсь, то номер такси, на котором я приехал, 1729. Мне кажется, это скучное число». На что Рамануджан тотчас же ответил: «Нет, Харди! О нет! Это очень интересное число. Это самое малое из чисел, представимых в виде суммы двух кубов двумя различными способами».
Один из способов представления числа 1729 в виде суммы двух кубов — это 13 + 123. Можете отыскать второй способ?
У чисел с плавающей точкой тоже есть методы. Возможно, самый полезный из них — это
Возможно, самый полезный из них — это .is_integer(). Его используют для проверки того, есть ли у числа с плавающей точкой дробная часть:
>>> n = 2.0 >>> n.is_integer() True >>> n = 3.14 >>> n.is_integer() False
Вот — интересный метод .as_integer_ratio(). Он, вызванный для числа с плавающей точкой, возвращает кортеж, содержащий числитель и знаменатель дроби, представляющей это число:
>>> n.as_integer_ratio() (1, 2)
Правда, из-за ошибки представления чисел с плавающей точкой, иногда этот метод возвращает неожиданные результаты:
>>> n = 0.1 >>> n.as_integer_ratio() (3602879701896397, 36028797018963968)
Если надо — можно вызывать методы на числовых литералах, заключённых в круглые скобки:
>>> (255).to_bytes(length=1, byteorder="big") b'\xff' >>> (3.14).is_integer() False
Если обойтись без скобок — при попытке вызова метода на целочисленном литерале будет выдана ошибка SyntaxError. SyntaxError: invalid syntax
>>> 3.14.is_integer()
False
SyntaxError: invalid syntax
>>> 3.14.is_integer()
False
Полный список методов числовых Python-типов можно найти в документации.
№2: числа обладают иерархией
В математике числа обладают естественной иерархией. Например, все натуральные числа являются целыми, а все целые числа — рациональными. Все рациональные числа — это вещественные числа, а все вещественные числа — это комплексные числа.
Похожие рассуждения применимы и к представлению чисел в Python. Здесь «числовая башня» выражается через абстрактные типы, содержащиеся в модуле numbers.
Числовая башня
Все числа в Python являются экземплярами класса Number:
>>> from numbers import Number >>> # Целые числа являются наследниками Number >>> isinstance(1729, Number) True >>> # Числа с плавающей точкой являются наследниками Number >>> isinstance(3.14, Number) True >>> # Комплексные числа являются наследниками Number >>> isinstance(1j, Number) True
Если нужно узнать о том, является ли некое Python-значение числовым, но при этом неважно то, каким именно числовым типом оно представлено, воспользуйтесь конструкцией isinstance(value, Number).
В Python имеется четыре дополнительных абстрактных типа, иерархия которых, начиная с наиболее общего числового типа, выглядит так:
Класс
Complexиспользуется для представления комплексных чисел. Тут имеется один встроенный конкретный тип —complex.Класс
Real— это представление вещественных чисел. Его единственный встроенный конкретный тип —float.Класс
Rationalпредставляет рациональные числа. Его единственным встроенным конкретным типом являетсяFraction.Класс
Integralприменяют для представления целых чисел. В нём имеется два встроенных конкретных типа —intиbool.
Так, погодите, а значения типа bool — это разве числа? Да — числа. Можете это проверить, воспользовавшись REPL:
>>> import numbers >>> # Комплексные числа являются наследниками Complex >>> isinstance(1j, numbers.Complex) True >>> # Комплексные числа не являются наследниками Real >>> isinstance(1j, numbers.Real) False >>> # Числа с плавающей точкой являются наследниками Real >>> isinstance(3.14, numbers.Real) True >>> # Числа с плавающей точкой не являются наследниками Rational >>> isinstance(3.14, numbers.Rational) False >>> # Объекты Fractions - это не наследники Rational >>> from fractions import Fraction >>> isinstance(Fraction(1, 2), numbers.Rational) True >>> # Объекты Fractions - это не наследники Integral >>> isinstance(Fraction(1, 2), numbers.Integral) False >>> # Целые числа - это наследники Integral >>> isinstance(1729, numbers.Integral) True >>> # Логические значения - это наследники Integral >>> isinstance(True, numbers.Integral) True >>> True == 1 True >>> False == 0 True
Всё это, на первый взгляд, выглядит вполне нормально. Правда, порядок несколько нарушает то, что значения типа
Правда, порядок несколько нарушает то, что значения типа bool являются числами.
Странность Python: так как тип bool относится к классу Integral (на самом деле он — прямой наследник int), со значениями True и False можно вытворять довольно необычные вещи.
Например, True можно использовать в роли индекса для того чтобы получить второй элемент итерируемого объекта. А если поделить число на False — будет выдана ошибка ZeroDivisionError.
Попробуйте выполнить «False»[True] и 1 / False в REPL!
Но если присмотреться к числовым типам поближе, окажется, что в иерархии Python-чисел имеется пара своеобразных моментов.
Числа типа Decimal не укладываются в иерархию
Как уже было сказано, в «числовой башне» Python есть 4 конкретных числовых типа, соответствующих четырём абстрактным типам: complex, float, Fraction и int. Но в Python имеется и пятый числовой тип, представленный классом
Но в Python имеется и пятый числовой тип, представленный классом Decimal. Этот тип используется для точного представления десятичных чисел и для преодоления ограничений арифметических операций с плавающей точкой.
Можно предположить, что числа типа Decimal являются наследниками Real, но это, на самом деле, не так:
>>> from decimal import Decimal
>>> import numbers
>>> isinstance(Decimal("3.14159"), numbers.Real)
FalseЕдинственный класс, наследником которого является класс Decimal — это Number:
>>> isinstance(Decimal("3.14159"), numbers.Complex)
False
>>> isinstance(Decimal("3.14159"), numbers.Rational)
False
>>> isinstance(Decimal("3.14159"), numbers.Integral)
False
>>> isinstance(Decimal("3.14159"), numbers.Number)
TrueЛогично то, что класс Decimal не является наследником Integral. В некоторой степени смысл есть и в том, что Decimal не является наследником Rational. Но почему
Но почему Decimal не является наследником Real или Complex?
Ответ кроется в исходном коде CPython:
Объекты Decimal обладают всеми методами, определёнными в классе Real, но эти объекты не должны регистрироваться в виде наследников Real, так как Decimal-числа не взаимодействуют с двоичными числами с плавающей точкой (например, результат операции Decimal(‘3.14’) + 2.71828 не определён). Но ожидается, что числа, классы которых являются наследниками абстрактного класса Real, способны взаимодействовать друг с другом (то есть — R1+R2 должно вычисляться в том случае, если числа R1 и R2 представлены типами, являющимися наследниками Real).
Получается, что объяснение странностей сводится к особенностям реализации.
Числа с плавающей точкой — странные создания
А вот числа с плавающей точкой, с другой стороны, реализуют абстрактный базовый класс Real. Они используются для представления вещественных чисел. Но, из-за того, что компьютерная память не является неограниченным ресурсом, числа с плавающей точкой — это лишь конечные аппроксимации вещественных чисел. Это приводит к возможности написания «ненормальных» образцов кода вроде такого:
Но, из-за того, что компьютерная память не является неограниченным ресурсом, числа с плавающей точкой — это лишь конечные аппроксимации вещественных чисел. Это приводит к возможности написания «ненормальных» образцов кода вроде такого:
>>> 0.1 + 0.1 + 0.1 == 0.3 False
Числа с плавающей точкой хранятся в памяти в виде двоичных дробей. Это приводит к появлению некоторых проблем. Например, у дроби 1/3 нет конечного десятичного представления (после десятичной точки идёт бесконечное множество троек). А у дроби 1/10 нет конечного представления в виде двоичной дроби.
Другими словами, в компьютере нельзя совершенно точно представить число 0,1 — если только этот компьютер не обладает бесконечной памятью.
Со строго математической точки зрения все числа с плавающей точкой — это рациональные числа, за исключением float(«inf») и float(«nan»). Но программисты используют их в роли аппроксимаций вещественных чисел и воспринимают их, по большей части, как вещественные числа.
Странность Python: float(«nan») — это особое значение с плавающей точкой, представляющее собой «не число». Такие значения часто обозначают как NaN. Но, так как float — это числовой тип, isinstance(float(«nan»), Number) возвращает True.
Получается, что «не числа» — это числа.
В общем, числа с плавающей точкой — странные создания.
№3: набор числовых типов Python можно расширять
Абстрактный числовой базовый тип Python позволяет программисту создавать собственные абстрактные и конкретные числовые типы.
В качестве примера рассмотрим класс ExtendedInteger, который реализует числа в форме a+b√p, где a и b — целые числа, а p — простое число (обратите внимание: класс не обеспечивает то, что число p является простым):
import math import numbers class ExtendedInteger(numbers.Real): def init(self, a, b, p = 2) -> None: self.a = a self.b = b self.p = p self._val = a + (b * math.sqrt(p)) def repr(self): return f"{self.class.name}({self.a}, {self.b}, {self.p})" def str(self): return f"{self.a} + {self.b}√{self.p}" def trunc(self): return int(self._val) def float(self): return float(self._val) def hash(self): return hash(float(self._val)) def floor(self): return math.floor(self._val) def ceil(self): return math.ceil(self._val) def round(self, ndigits=None): return round(self._val, ndigits=ndigits) def abs(self): return abs(self._val) def floordiv(self, other): return self._val // other def rfloordiv(self, other): return other // self._val def truediv(self, other): return self._val / other def rtruediv(self, other): return other / self._val def mod(self, other): return self.
_val % other def rmod(self, other): return other % self._val def lt(self, other): return self._val < other def le(self, other): return self._val <= other def eq(self, other): return float(self) == float(other) def neg(self): return ExtendedInteger(-self.a, -self.b, self.p) def pos(self): return ExtendedInteger(+self.a, +self.b, self.p) def add(self, other): if isinstance(other, ExtendedInteger): # Если оба экземпляра имеют одно и то же значение p, # вернуть новый экземпляр ExtendedInteger if self.p == other.p: new_a = self.a + other.a new_b = self.b + other.b return ExtendedInteger(new_a, new_b, self.p) # В противном случае вернуть значение типа float else: return self._val + other._val # Если other - значение класса Integral, прибавить значение other к значению self.
a elif isinstance(other, numbers.Integral): new_a = self.a + other return ExtendedInteger(new_a, self.b, self.p) # Если other - значение класса Real, вернуть значение типа float elif isinstance(other, numbers.Real): return self._val + other._val # Если тип other неизвестен, позволить другим принять решение # о том, что делать в такой ситуации else: return NotImplemented def radd(self, other): # Сложение коммутативно, поэтому прибегнуть к add return self.add(other) def mul(self, other): if isinstance(other, ExtendedInteger): # Если оба экземпляра имеют одно и то же значение p, # вернуть новый экземпляр ExtendedInteger if self.p == other.p: new_a = (self.a * other.a) + (self.b * other.b * self.p) new_b = (self.a * other.b) + (self.b * other.a) return ExtendedInteger(new_a, new_b, self.
p) # в противном случае вернуть значение типа float else: return self._val * other._val # Если other - значение класса Integral, умножить его компоненты a и b на other elif isinstance(other, numbers.Integral): new_a = self.a * other new_b = self.b * other return ExtendedInteger(new_a, new_b, self.p) # Если other - значение класса Real, вернуть значение типа float elif isinstance(other, numbers.Real): return self._val * other # Если тип other неизвестен, позволить другим принять решение # о том, что делать в такой ситуации else: return NotImplemented def rmul(self, other): # Умножение коммутативно, поэтому прибегнуть к mul return self.mul(other) def pow(self, exponent): return self._val ** exponent def rpow(self, base): return base ** self._val
Для того чтобы обеспечить правильность реализации интерфейса Real конкретным типом — нужно создать реализации множества методов, в именах которых есть два символа подчёркивания. Ещё нужно поразмыслить о том, как методы вроде
Ещё нужно поразмыслить о том, как методы вроде .add() и .mul() взаимодействуют с другими типами, являющимися наследниками Real.
Обратите внимание: вышеприведённый пример не создавался в расчёте на его полноту или абсолютную правильность. Его цель — продемонстрировать читателю возможности работы с числами.
При наличии реализации ExtendedInteger можно заниматься следующими вычислениями:
>>> a = ExtendedInteger(1, 2) >>> b = ExtendedInteger(2, 3) >>> a ExtendedInteger(1, 2, 2) >>> # Проверяем то, что a - это наследник Number >>> isinstance(a, numbers.Number) True >>> # Проверяем то, что a - это наследник Real >>> isinstance(a, numbers.Real) True >>> print(a) 1 + 2√2 >>> a * b ExtendedInteger(14, 7, 2) >>> print(a * b) 14 + 7√2 >>> float(a) 3.8284271247461903
Иерархия числовых типов в Python — довольно гибкая структура. Но, конечно, всегда стоит очень внимательно относиться к реализации типов, являющихся наследниками встроенных абстрактных базовых типов Python. Нужно обеспечить их корректную работу друг с другом.
Но, конечно, всегда стоит очень внимательно относиться к реализации типов, являющихся наследниками встроенных абстрактных базовых типов Python. Нужно обеспечить их корректную работу друг с другом.
В документации по Python можно найти несколько советов по реализации собственных типов, которые стоит прочесть тому, кто решит заняться созданием собственных числовых типов. Такому человеку ещё полезно будет ознакомиться с реализацией Fraction.
Итоги
Вот — те три особенности Python-чисел, которые мы здесь обсуждали:
У чисел есть методы, как и у практически всех остальных объектов в Python.
Числа обладают иерархией, даже несмотря на то, что их чёткие взаимоотношения несколько портит наличие типов
Decimalиfloat.Программисты могут создавать собственные числовые типы, которые вписываются в иерархию числовых типов Python.
Может быть, вы узнали из этого материала не только об этих особенностях чисел, но и ещё о чём-нибудь, что вам пригодится.
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Присоединяйтесь к нашей команде.
Сложение дробей с целыми числами (примеры вопросов)
Смешанное число — это число, состоящее из целой части и дробной части.
Сложение дробей с целыми числами Примеры вопросов
Вот визуальное представление смешанного числа.
В этой модели показаны два полностью заштрихованных прямоугольника, которые представляют целые числа, и один частично заштрихованный прямоугольник, представляющий дроби.
Эта дробная модель представляет собой смешанное число \(2\frac{3}{8}\).
При сложении смешанного числа с целым числом мы сначала складываем целые числа, а затем добавляем дробь.
Пример:Чему равна сумма \(11\frac{2}{3}\) и \(19\)?
Мы начнем со сложения целых чисел, то есть \(11+19=30\). Затем добавляем дробную часть в конец.
Следовательно, сумма \(11\frac{2}{3}\) и \(19\) равна \(30\frac{2}{3}\).
Вот пример того, где это можно использовать в реальной жизни:Моника выбирает два пакета персиков, чтобы купить их на фермерском рынке. Она кладет каждую сумку на весы, и первая сумка весит \(5\) фунтов. а второй мешок весит \(6\frac{2}{3}\) фунтов. Сколько фунтов персиков покупает Моника?
При сложении целого числа и дроби мы сначала складываем целые числа, затем добавляем дробь.
\(5+6=11\), теперь мы включаем \(\frac{2}{3}\), следовательно, Моника покупает всего \(11\frac{2}{3}\) фунтов. персиков.
персиков.
Вот несколько примеров вопросов о сложении дробей с целыми числами.
Вопрос №1:
Вычислите сумму \(14\frac{5}{6}\) и \(38\).
\(54\)
\(52\frac{5}{6}\)
\(56\frac{2}{5}\)
\(55\)
Показать ответ
Ответ:
При сложении дробей и целых чисел сначала вычислите целое число плюс целое число, а затем включите в ответ оставшуюся дробь. Например, \(14+38=52\), поэтому ответом будет \(52\frac{5}{6}\).
Скрыть ответ
Вопрос №2:
Вычислите сумму \(45\) и \(2\frac{1}{3}\).
\(47\frac{2}{3}\)
\(45\frac{2}{3}\)
\(46\frac{3}{5}\)
\(47 \frac{1}{3}\)
Показать ответ
Ответ:
Еще раз, при сложении дробей и целых чисел сначала вычисляйте целое число плюс целое число, а затем включайте оставшуюся дробь в отвечать. Например, \(45+2=47\), поэтому ответом будет \(47\frac{1}{3}\).
Например, \(45+2=47\), поэтому ответом будет \(47\frac{1}{3}\).
Скрыть ответ
Вопрос №3:
Добавить \(4\frac{3}{2}+5\).
\(10\frac{1}{5}\)
\(11\frac{3}{5}\)
\(9\frac{1}{5}\)
\(10 \frac{1}{2}\)
Показать ответ
Ответ:
Первым шагом является рассмотрение неправильной дроби в смешанном числе \(4\frac{3}{2}\). Дробь \(\frac{3}{2}\) — это то же самое, что и \(1\frac{1}{2}\), поэтому перепишите \(4\frac{3}{2}\) как \ (5\разрыв{1}{2}\). Теперь просто объедините \(5\frac{1}{2}\) и \(5\), чтобы получить \(10\frac{1}{2}\).
Скрыть ответ
Вопрос № 4:
Добавить \(3+3\frac{5}{4}\).
\(6\frac{1}{4}\)
\(7\frac{1}{4}\)
\(6\frac{3}{4}\)
\(7 \frac{3}{4}\)
Показать ответ
Ответ:
Первым шагом является рассмотрение неправильной дроби в смешанном числе \(3\frac{5}{4}\). Дробь \(\frac{5}{4}\) — это то же самое, что и \(1\frac{1}{4}\), поэтому перепишите \(3\frac{5}{4}\) как \ (4\разрыв{1}{4}\). Теперь просто объедините \(3\) и \(4\frac{1}{4}\), чтобы получить \(7\frac{1}{4}\).
Дробь \(\frac{5}{4}\) — это то же самое, что и \(1\frac{1}{4}\), поэтому перепишите \(3\frac{5}{4}\) как \ (4\разрыв{1}{4}\). Теперь просто объедините \(3\) и \(4\frac{1}{4}\), чтобы получить \(7\frac{1}{4}\).
Скрыть ответ
Вопрос № 5:
Вставьте пропущенное значение, чтобы уравнение было верным.
\(3\frac{4}{5}+\) ______\(=18\frac{4}{5}\)
\(13\)
\(14\frac{1}{5} \)
\(15\)
\(16\frac{1}{5}\)
Показать ответ
Ответ:
Чтобы составить сбалансированное уравнение, смешанное число \(18 \frac{4}{5}\) должны быть с каждой стороны. Если добавить \(3\frac{4}{5}+15=18\frac{4}{5}\), то \(15\) будет пропущенным значением.
Скрыть ответ
Вернуться к примерам вопросов по математике
Калькулятор смешанных чисел
Использование калькулятора
неправильные дроби.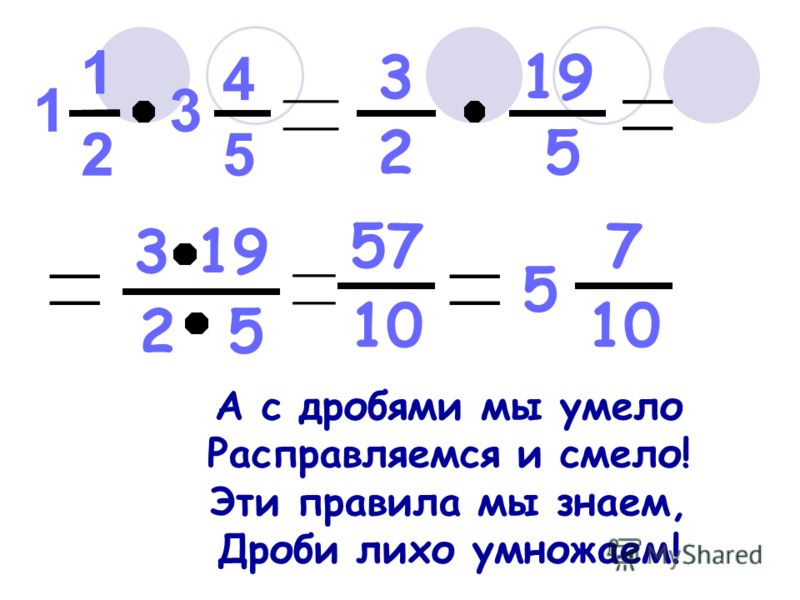 Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.Калькулятор смешанных чисел (также известный как смешанные дроби):
Этот онлайн-калькулятор выполняет простые операции с целыми числами, целыми числами, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения. Ответ дается в сокращенной дроби и смешанном числе, если оно существует.
Введите смешанные числа, целые числа или дроби в следующих форматах:
- Смешанные числа: введите 1 1/2, что составляет полторы секунды, или 25 3/32, что составляет двадцать пять и три тридцать секунд. Оставьте ровно один пробел между целым числом и дробью и используйте косую черту для ввода дробей. Вы можете ввести до 3 цифр для каждого целого числа, числителя или знаменателя (123 456/789).
- Целые числа: до 3 цифр в длину.
- Дроби: введите 3/4, что составляет три четвертых, или 3/100, что составляет три сотых.
 Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Сложение смешанных чисел с помощью формулы сложения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу сложения дробей:
a/b + c/d = (ad + bc) / bd - Сократите дроби и упростите, если возможно
Формула сложения дробей
\( \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{(a \times d) + (b \times c)}{b \times d} \)
Пример
Добавить 1 2/6 и 2 1/4
\( 1 \dfrac{2}{6} + 2 \dfrac{1}{4} = \dfrac{8}{6} + \dfrac{9}{4} \)
\( = \dfrac{(8 \times 4) + (9 \times 6)}{6 \times 4} \)
\( = \dfrac{32 + 54}{24} = \dfrac{86}{24} = \dfrac{43}{12} \)
\( = 3 \dfrac{7}{12} \)
1 2/6 + 2 1/4 = 8/6 + 9/4 = (8*4 + 9*6) / 6*4 = 86 / 24
Получаем 86/24 и упрощаем до 3 7/12
Вычитание смешанных чисел по формуле вычитания дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для вычитания дробей: a/b — c/d = (ad — bc) / bd
- Сократите дроби и упростите, если возможно
Формула вычитания дробей
\( \dfrac{a}{b} — \dfrac{c}{d} = \dfrac{(a \times d) — (b \times c)}{b \times d} \)
Пример
Вычесть 2 1/4 из 1 2/6
1 2/6 — 2 1/4 = 8/6 — 9/4 = (8*4 — 9*6) / 6*4 = -22 / 24
Уменьшите дробь, чтобы получить -11/12
Умножение смешанных чисел с помощью формулы умножения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу умножения дробей: a/b * c/d = ac / bd
- Сократите дроби и упростите, если возможно
Формула умножения дробей
\( \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{a \times c}{b \times d} \)
Пример
умножить 1 2/6 на 2 1/4
1 2/6 * 2 1/4 = 8/6 * 9/4 = 8*9 / 6*4 = 72 / 24
Сократите дробь, чтобы получить 3/1 и упростите до 3
Деление смешанных чисел с помощью формулы деления дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу деления дробей: a/b ÷ c/d = ad / bc
- Сократите дроби и упростите, если возможно
Формула деления дробей
\( \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a \times d}{b \times c} \)
Пример
разделить 1 2/6 на 2 1/4
1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8*4 / 9*6 = 32 / 54
Уменьшите дробь, чтобы получить 16/27
Связанные калькуляторы
Для выполнения математических операций над простыми правильными или неправильными дробями используйте наш
Калькулятор дробей.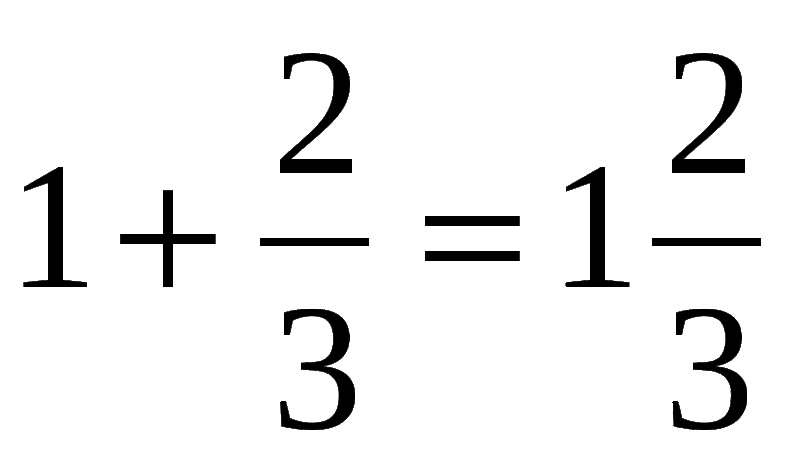
 Исторический анекдот связывает это число с индийским математиком Сринивасой Рамануджаном, который рассказал о нём своему наставнику Готфри Харолду Харди.
Исторический анекдот связывает это число с индийским математиком Сринивасой Рамануджаном, который рассказал о нём своему наставнику Готфри Харолду Харди.
 a = a
self.b = b
self.p = p
self._val = a + (b * math.sqrt(p))
def repr(self):
return f"{self.class.name}({self.a}, {self.b}, {self.p})"
def str(self):
return f"{self.a} + {self.b}√{self.p}"
def trunc(self):
return int(self._val)
def float(self):
return float(self._val)
def hash(self):
return hash(float(self._val))
def floor(self):
return math.floor(self._val)
def ceil(self):
return math.ceil(self._val)
def round(self, ndigits=None):
return round(self._val, ndigits=ndigits)
def abs(self):
return abs(self._val)
def floordiv(self, other):
return self._val // other
def rfloordiv(self, other):
return other // self._val
def truediv(self, other):
return self._val / other
def rtruediv(self, other):
return other / self._val
def mod(self, other):
return self.
a = a
self.b = b
self.p = p
self._val = a + (b * math.sqrt(p))
def repr(self):
return f"{self.class.name}({self.a}, {self.b}, {self.p})"
def str(self):
return f"{self.a} + {self.b}√{self.p}"
def trunc(self):
return int(self._val)
def float(self):
return float(self._val)
def hash(self):
return hash(float(self._val))
def floor(self):
return math.floor(self._val)
def ceil(self):
return math.ceil(self._val)
def round(self, ndigits=None):
return round(self._val, ndigits=ndigits)
def abs(self):
return abs(self._val)
def floordiv(self, other):
return self._val // other
def rfloordiv(self, other):
return other // self._val
def truediv(self, other):
return self._val / other
def rtruediv(self, other):
return other / self._val
def mod(self, other):
return self. _val % other
def rmod(self, other):
return other % self._val
def lt(self, other):
return self._val < other
def le(self, other):
return self._val <= other
def eq(self, other):
return float(self) == float(other)
def neg(self):
return ExtendedInteger(-self.a, -self.b, self.p)
def pos(self):
return ExtendedInteger(+self.a, +self.b, self.p)
def add(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = self.a + other.a
new_b = self.b + other.b
return ExtendedInteger(new_a, new_b, self.p)
# В противном случае вернуть значение типа float
else:
return self._val + other._val
# Если other - значение класса Integral, прибавить значение other к значению self.
_val % other
def rmod(self, other):
return other % self._val
def lt(self, other):
return self._val < other
def le(self, other):
return self._val <= other
def eq(self, other):
return float(self) == float(other)
def neg(self):
return ExtendedInteger(-self.a, -self.b, self.p)
def pos(self):
return ExtendedInteger(+self.a, +self.b, self.p)
def add(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = self.a + other.a
new_b = self.b + other.b
return ExtendedInteger(new_a, new_b, self.p)
# В противном случае вернуть значение типа float
else:
return self._val + other._val
# Если other - значение класса Integral, прибавить значение other к значению self. a
elif isinstance(other, numbers.Integral):
new_a = self.a + other
return ExtendedInteger(new_a, self.b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val + other._val
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def radd(self, other):
# Сложение коммутативно, поэтому прибегнуть к add
return self.add(other)
def mul(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = (self.a * other.a) + (self.b * other.b * self.p)
new_b = (self.a * other.b) + (self.b * other.a)
return ExtendedInteger(new_a, new_b, self.
a
elif isinstance(other, numbers.Integral):
new_a = self.a + other
return ExtendedInteger(new_a, self.b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val + other._val
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def radd(self, other):
# Сложение коммутативно, поэтому прибегнуть к add
return self.add(other)
def mul(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = (self.a * other.a) + (self.b * other.b * self.p)
new_b = (self.a * other.b) + (self.b * other.a)
return ExtendedInteger(new_a, new_b, self. p)
# в противном случае вернуть значение типа float
else:
return self._val * other._val
# Если other - значение класса Integral, умножить его компоненты a и b на other
elif isinstance(other, numbers.Integral):
new_a = self.a * other
new_b = self.b * other
return ExtendedInteger(new_a, new_b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val * other
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def rmul(self, other):
# Умножение коммутативно, поэтому прибегнуть к mul
return self.mul(other)
def pow(self, exponent):
return self._val ** exponent
def rpow(self, base):
return base ** self._val
p)
# в противном случае вернуть значение типа float
else:
return self._val * other._val
# Если other - значение класса Integral, умножить его компоненты a и b на other
elif isinstance(other, numbers.Integral):
new_a = self.a * other
new_b = self.b * other
return ExtendedInteger(new_a, new_b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val * other
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def rmul(self, other):
# Умножение коммутативно, поэтому прибегнуть к mul
return self.mul(other)
def pow(self, exponent):
return self._val ** exponent
def rpow(self, base):
return base ** self._val Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).