Урок 29. умножение на 1. умножение на 0 — Математика — 3 класс
Математика, 3 класс
Урок №29. Умножение на 1. Умножение на 0
Перечень вопросов, рассматриваемых в теме:
— как умножать на 1 и 0?
— какие правила используются в случаях умножения на 1 и 0?
Глоссарий по теме:
Умноже́ние – это одно из четырёх основных арифметических действий.
Правило – закономерность, устойчивая систематическая взаимосвязь между явлениями, а также высказывание, описывающее эту закономерность.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 82-83.
2. Самсонова Л. Ю. Самостоятельные работы по математике 3 классс. М.: Издательство «Экзамен», 2015 с.51-52.
3. Рудницкая В. Н. КИМ. ВПР. Математика 3 класс.
Теоретический материал для самостоятельного изучения
1 (один, единица) – наименьшее натуральное число. Цифра 1 обозначает один из нескольких, один из множества. Цифру 1 придумали арабы. Число 1 обозначает начало, что-то единственное, очень малое, но существенное.
— Единица является атомным номером водорода;
— Меркурий – первая к Солнцу планета Солнечной системы;
— Из одной клетки состоят простейшие микроорганизмы, например, амёбы;
— В спорте число 1 – это символ победы, лидерства, единства.
В математике существуют определенные правила умножения с 1 и 0.
Пользуясь переместительным свойством умножения, составим выражения и заменим умножение суммой одинаковых слагаемых.
4 ∙ 0; 8 ∙ 0; 4 ∙ 1; 8 ∙ 1.
Получились следующие выражения:
4 ∙ 0 = 0 ∙ 4 = 0 + 0 + 0 + 0 = 0
8 ∙ 0 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
4 ∙ 1 = 1 ∙ 4 = 1 + 1 + 1 + 1 = 4
8 ∙ 1 = 1 ∙ 8 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8
Заменим аналогичные выражения с буквами и сделаем вывод,
1) Если единицу умножить на число, то получится то же самое число.
2) При умножении нуля на любое число, получается ноль.
а ∙ 0 = 0 ∙ а = 0 + 0 + 0 + 0 …. = 0
а ∙ 1 = 1 ∙ а = 1 + 1 + 1 + 1 … = а
Из этого следуют правила умножения на 1 и 0:
— При умножении любого числа на 1 получается то число, которое умножали.
— При умножении любого числа на ноль получается ноль.
Задания тренировочного модуля:
Вставьте пропущенные слова
При умножении любого числа на 1 получается то число, которое___________
При умножении любого числа на 0 получается______________
Ноль
Умножали
Единица
Правильный ответ:
При умножении любого числа на 1 получается то число, которое умножали.
При умножении любого числа на 0 получается ноль.
2. Выделите цветом неверные выражения
Правильный ответ:
Приёмы умножения единицы и нуля
МБОУ Пригорская СШ
Смоленский район
Смоленская область
Тема урока:
«Приёмы умножения единицы и нуля. »
»
2 класс
Подготовила и провела:
учитель высшей категории
Чуркина Светлана Петровна
2017
Цели урока:
— познакомить с приёмами умножения на нуль и единицу; развивать внимание, логическое мышление; воспитывать чувства товарищества и взаимопомощи.
Планируемые результаты:Личностные: принимают и осваивают социальную роль обучающегося; стремятся развивать мотивы учебной деятельности, навыки сотрудничества со сверстниками, умение доказывать свою точку зрения, внимание, память, логическое мышление; проявляют самостоятельность, личную ответственность.
Предметные: формировать умения самостоятельно строить и применять новые знания; развивать умение анализировать, обобщать; развивать внимание, логическое мышление, память, воображение;
метапредметные: формировать универсальные учебные действия:
регулятивные – понимать, принимать и сохранять учебную задачу; осуществлять самоконтроль и самооценку;
познавательные – ориентироваться в материале учебника и находить по заданию учителя нужную информацию, формировать умение выделять основу для сравнения, проводить сравнение, выстраивать цепочку логических рассуждений при решении задач логического содержания; самостоятельно формулировать познавательные цели;
Тип урока: открытия новых знаний
Оборудование: ноутбук, проектор, экран, карточки для коллективной работы, карточки для самостоятельной работы, карточки для Справочника по математике, записи на маркерной доске, карточки для рефлексии, опорная таблица, картинка к задаче, презентация, диск- приложение Математика, учебник математики Школы России, М. И. Моро 2кл (2 ч),
И. Моро 2кл (2 ч),
Ход урока.
1. Психологический настрой.
— Сегодня ребята, у нас необычный урок математики, к нам пришли гости. Давайте поздороваемся.
Сегодня математика у нас.
Должны мы хорошенько поработать,
Чтоб гости, посмотрев на нас,
Все удивились: «Что за класс!»
— Пожелайте друг другу успеха и покажите, что одноклассники всегда могут рассчитывать на вашу помощь – пожмите друг другу руки и скажите: «Сам смогу и тебе помогу!»2. Орг. момент.
— Присаживайтесь на свои места. Проверьте готовность ваших рабочих мест для урока математики.
— Приготовьтесь к письму: поправьте стулья, сядьте ровно. Откройте тетради. Запишите число, название работы:
17 марта.
Классная работа.
3. Определение тему и цели урока. (Работа по индивидуальным карточкам).
— У вас на столе лежат карточки под №1.
1 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
20 + 30 = ___Н 7 + 7 = ___И 100 – 6 = ____И 15 + 15 =___Д
40 – 5 = ____Ц 12 – 2 = ___ А 34 + 6 ____ Е
2 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
2 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
45 + 16 = ___Ь 70 – 35 = ____у 43 – 7 = ____Л 37 + 13 = ___Н
3 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
74 | 50 | 14 | 99 | 40 | 12 | 20 | 44 | 8 |
2 + 10 = ___ Е 3 + 5 = ___ Е 90 – 40 = ___М
100 – 1 = ___ О 70 + 4 = ___У 28 – 8 = _____Н
20 + 20 = ___ Ж 20 – 6 = ___Н 40 + 4 = ____И
Во время решения, учитель спрашивает – Нужна ли кому-нибудь помощь? Успешно справившиеся ребята, могут оказать помощь другим.
Несколько работ берутся на проверку.
— Какие слова у вас получились: «Единица», «Нуль», «Умножение».
— Попробуйте определить тему урока — «Приёмы умножения единицы и нуля на число». Давайте проверим, правильно ли вы определи ли тему (Презентация. Слайд 1).
— Как вы думаете, чему мы будем учиться на уроке? Давайте проверим, правильно ли вы определи ли цель урока. (Презентация. Слайд 2)
4. Освоение нового материала.
а) Постановка проблемной ситуации.
— Вспомним, что такое умножение? (Сложение одинаковых слагаемых)
— Давайте заменим умножение сложением. (Презентация. Слайд 3). Дети работают, комментируют по очереди.).
3+3+3+3 52
9+9+9 13
93
2+2+2+2+2 34
04
5+5 25
— Какие выражения не имеют пары по сложению. Почему нет пары для выражения 2 5, 9 3? Какие выражения ещё не заменили сложением? Встречались ли мы раньше с такими выражениями?
б) Коллективная работа.
— Распределитесь на группы. Рассмотрите выражения на карточках, замените сложением умножением и сделайте вывод о правилах умножения на 1 и 0.
1 4 = 1+1+1+1= 4 0 4 = 0+0+0+0=0
1 8 = 1+1+1+1+1+1+1+1=8 0 8 = 0 +0+0+0+0+0+0+0=0
1 7 = 1+1+1+1+1+1+1=7 0 7 = 0+0+0+0+0+0+0=0
1 3 = 1+1+1=3 0 3 = 0 +0+0=0
1 6 = 1+1+1+1+1+1=6 0 6 = 0+0+0+0+0+0=0
!!!! Включить презентация, выключить звук.
— Вывод: при умножении 1 на любое число, получится тоже самое число.
— При умножении 0 на любое число, получится нуль.
в) – Давайте посмотрим видеоролик и посмотрим, правильный ли вывод вы сделали.(Презентация из Приложения).
г) Работа по учебнику.
– Прочитайте задание в учебнике №2 на с. 53 учебника (устно).
— При умножении 1 на любое число получается тоже самое число.
— При умножении 0 на любое число получается 0.
д) – Возьмите на столе карточку под №2. Прочитайте правило. Для чего она вам нужна?
— Вклеить в справочник по математике.
е) – Рассмотрите опорные таблицы. Как их можно прочитать, объяснить?
1 а = а 0 а = 0
Закрепление и отработка нового материала.
а) с. 53 № 1 (работа с комментированием по одному, дети пишут в тетрадях пишут в тетрадях).
1 3 = 1 + 1 + 1 = 3 1 4 = 1 + 1 +1 + 1 = 4
0 5 = 0 + 0 + 0 + 0 + 0 =0 0 6 = 0 + 0 + 0 + 0 + 0 + 0 = 0
Физкультминутка.
— Давайте отдохнём.
б) С.р. (Запись на маркерной доске)
— Выполните вычисления. Кому нужна помощь?
1 5 = 5 0 2 = 0
1 8 = 8 0 4 =0
1 10 = 10 0 7 = 0
1 6 = 6 0 10 =0
— Коллективная проверка.
— Индивидуальное задание для быстро справившихся ребят (запись на маркерной доске).
— Кто попробует решить следующие выражения
1 40 = 40 0 65 =0
0 78 = 0 1 34 = 34
1 200 =200 0 78 = 0
0 560 =0 1 1000 =1000
— А кто может придумать свой пример по новой теме?
д) подведение итога изучения нового материала:
— Что же мы узнали об умножении единицы и нуля ? Есть ли в учебнике на с. 53 правило? Где мы можем его повторить, выучить дома?
53 правило? Где мы можем его повторить, выучить дома?
— В своём справочнике.
в) Закрепление по учебнику с.53 №4. Коллективно.
— Давайте рассмотрим в каких же случаях ещё нам может понадобиться приём умножения единицы и нуля.
1 38 1 + 38 7 4 7 + 7 + 7
0 41 0 + 41 6 3 6 + 6 + 6
г) Работа по учебнику. С. 53 № 3
— Как вы думаете, как выполнить данные вычисления?
0 15 = 0
— Какое действие будем выполнять первым?
1 (30 – 23) = 7
С.р. С. 53 Внизу страницы. Кому нужна помощь?
1 26 = 26 0 (21 – 8) = 0
— Кто может сам придумать выражения на новую тему?
Самостоятельная работа в тетради.
— У вас в конвертиках лежат два листка под № 3. Те, кто считает, что хорошо усвоил данный прием вычисления, возьмет задание на жёлтом листе, а те, кто не очень уверен в своих силах, возьмет задание на голубом листе.
0 х (45-5) 1х (30-23) (78-70) х 1 (45-8) х 0 | 1 х 20 32 х 1 0 х 6 98 х 0 |
— Теперь наши новые знания применим в других заданиях.
Прочитайте задачу:
Оля купила 3 ластика, по 1 рублю каждая. Сколько стоит эта покупка?
— О чём говорится в задаче?
2. Сколько ластиков купила Оля?
3. Что значит по 1 рублю каждая?
4. Что надо найти в задаче?
5. Выполним краткую запись на доске и в тетради
6. Как записать решение?? р.
7. Как умножить один на число?
8. Какой ответ запишем?
Домашнее задание.
— У вас в конвертиках остался листик под №4. В нём записаны задания в двух вариантах. Выберите вариант, который вы сможете легко выполнить и решите его дома. От домашнего задания освобождаются ребята, которые всю неделю выполняли домашнее задание на «отлично». Откройте дневники и запишите задание – карточка. Определим, кто же освобождается от домашнего задания.
Рефлексия.
Рефлексия – осознание учеником и воспроизведение в речи того, чему научился и каким способом действовал.
— Ребята, у вас на партах лежат рожицы человечков. Если урок вам понравился, нарисуйте на них улыбку, дуга вверх. Если вы остались равнодушны к уроку и он вам не принес никаких знаний, то просто черточку. Ну, а если вам урок совсем не понравился, рисуем печальное выражение лица – дуга вниз.
Если урок вам понравился, нарисуйте на них улыбку, дуга вверх. Если вы остались равнодушны к уроку и он вам не принес никаких знаний, то просто черточку. Ну, а если вам урок совсем не понравился, рисуем печальное выражение лица – дуга вниз.
— Поднимите свои листочки и покажите их своим одноклассникам и гостям.
— Давайте посмотрим, а какое впечатление от урока, от вас останется у наших гостей? (Гости тоже рисуют улыбки на своих смайликах)
Приложение.
Замените умножение сложением. Сформулируйте правило умножения единицы на число.
1 4 = ____________________________= ______
1 8 = _____________________________=_______
1 7 = ____________________________=_______
1 3 = __________________________=________
1 6 = _______________________________=____
Замените умножение сложением. Сформулируйте правило умножения нуля на число.
0 4 = ___________________________=________
0 8 = ____________________________= _______
0 7 = ___________________________=_______
0 3 = ______________________=______
0 6 = ___________________________=_______
1 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
20 + 30 = ___Н 7 + 7 = ___И 100 – 6 = ____И 15 + 15 =___Д
40 – 5 = ____Ц 12 – 2 = ___ А 34 + 6 ____ Е
2 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
45 + 16 = ___Ь 70 – 35 = ____у 43 – 7 = ____Л 37 + 13 = ___Н
3 вариант.
Запишите свою фамилию и имя. Выполните данное задание.
__________________________________________________________________
Найдите значение выражений. Занесите результаты в таблицу и отгадайте слово.
74 | 50 | 14 | 99 | 40 | 12 | 20 | 44 | 8 |
2 + 10 = ___ Е 3 + 5 = ___ Е 90 – 40 = ___М
100 – 1 = ___ О 70 + 4 = ___У 28 – 8 = _____Н
20 + 20 = ___ Ж 20 – 6 = ___Н 40 + 4 = ____И
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
0 х (45-5)= (78-70) х 1 =
1х (30-23)= (45-8) х 0 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
1 х 20 = 0 х 6 =
98 х 0 = 32 х 1 =
Домашнее задание.
1 вариант.
Найди значение выражений.
1 6 = 1 10 = 1 20 = 1 35 =
0 6 = 0 10 = 0 20 = 0 35=
2 вариант.
Найди значение выражений. Подчеркни выражения, значение которых можно найти не выполняя вычислений.
0 (36 – 18) = 1 ( 24 + 4) =0 (7 +93) =
0 (67 + 30) = 1 (80 – 75) = 1 ( 100 – 50) =
Домашнее задание.
1 вариант.
Найди значение выражений.
1 6 = 1 10 = 1 20 = 1 35 =
0 6 = 0 10 = 0 20 = 0 35=
2 вариант.
Найди значение выражений. Подчеркни выражения, значение которых можно найти не выполняя вычислений.
0 (36 – 18) = 1 ( 24 + 4) =0 (7 +93) =
0 (67 + 30) = 1 (80 – 75) = 1 ( 100 – 50) =
Домашнее задание.
1 вариант.
Найди значение выражений.
1 6 = 1 10 = 1 20 = 1 35 =
0 6 = 0 10 = 0 20 = 0 35=
2 вариант.
Найди значение выражений. Подчеркни выражения, значение которых можно найти не выполняя вычислений.
Подчеркни выражения, значение которых можно найти не выполняя вычислений.
0 (36 – 18) = 1 ( 24 + 4) =0 (7 +93) =
0 (67 + 30) = 1 (80 – 75) = 1 ( 100 – 50) =
Домашнее задание.
1 вариант.
Найди значение выражений.
1 6 = 1 10 = 1 20 = 1 35 =
0 6 = 0 10 = 0 20 = 0 35=
2 вариант.
Найди значение выражений. Подчеркни выражения, значение которых можно найти не выполняя вычислений.
0 (36 – 18) = 1 ( 24 + 4) =0 (7 +93) =
0 (67 + 30) = 1 (80 – 75) = 1 ( 100 – 50) =
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
При умножении 1 на любое число получается тоже самое число: 1 а =а
При умножении 0 на любое число получается 0: 0 а = 0
1 а = а
0 а = 0
правила, примеры, решения, 1 умножить на 10
Имея общее представление об умножении натуральных чисел и их свойств, легче понять принцип выполнений действий над ними. Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.
Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.
Таблица умножения
Умножая два натуральных числа, получаем результат, который производится при умножении однозначных натуральных чисел. Произведение чисел 6 и 3 приравнивается к сумме, состоящей из трех слагаемых, равных числу 6. Иначе это запишем: 6·3=6+6+6=18. Таким же образом получены все результаты умноженных однозначных натуральных чисел. Все занесены в таблицу, приведенную ниже.
| 1·1=1 | 2·1=2 | 3·1=3 |
| 1·2=2 | 2·2=4 | 3·2=6 |
| 1·3=3 | 2·3=6 | 3·3=9 |
| 1·4=4 | 2·4=8 | 3·4=12 |
| 1·5=5 | 2·5=10 | 3·5=15 |
| 1·6=6 | 2·6=12 | 3·6=18 |
| 1·7=7 | 2·7=14 | 3·7=21 |
| 1·8=8 | 2·8=16 | 3·8=24 |
| 1·9=9 | 2·9=18 | 3·9=27 |
| 4·1=4 | 5·1=5 | 6·1=6 |
| 4·2=8 | 5·2=10 | 6·2=12 |
| 4·3=12 | 5·3=15 | 6·3=18 |
| 4·4=16 | 5·4=20 | 6·4=24 |
| 4·5=20 | 5·5=25 | 6·5=30 |
| 4·6=24 | 5·6=30 | 6·6=36 |
| 4·7=28 | 5·7=35 | 6·7=42 |
| 4·8=32 | 5·8=40 | 6·8=48 |
| 4·9=36 | 5·9=45 | 6·9=54 |
| 7·1=7 | 8·1=8 | 9·1=9 |
| 7·2=14 | 8·2=16 | 9·2=18 |
| 7·3=21 | 8·3=24 | 9·3=27 |
| 7·4=28 | 8·4=32 | 9·4=36 |
| 7·5=35 | 8·5=40 | 9·5=45 |
| 7·6=42 | 8·6=48 | 9·6=54 |
| 7·7=49 | 8·7=56 | 9·7=63 |
| 7·8=56 | 8·8=64 | 9·8=72 |
| 7·9=63 | 8·9=72 | 9·9=81 |
Это и есть таблица умножения. Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.
Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.
Чтобы выяснить, как пользоваться таблицей, приведем пример. Если необходимо найти произведение 6 и 8, необходимо отметить столбец верхней ячейки, где имеем 6 (8), и строку левой ячейки, где число 8 (6). Чтобы найти результат, следует найти их общую ячейку, то есть пересечение столбца и строки. На рисунке ниже изображен пример нахождения искомого умножения 6 и 8.
Умножение трех и более количества чисел
Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.
Сочетательное свойство умножения показывает равнозначность двух произведений a·(b·c) и (a·b)·c, где a, b и c могут быть любыми числами. Результат умножения данных чисел не будет зависеть от местоположения скобок. Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид a·b·c. Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.
Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид a·b·c. Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.
Сочетательное свойство умножения необходимо для того, чтобы легче было выявлять равные произведения. Это значит, что из приведенных (a·b)·(c·d), (a·(b·c))·d, ((a·b)·c)·d, a·(b·(c·d)) и a·((b·c)·d) можно сделать вывод, что они все равные. Положение скобок при умножении не играет роли. Это произведение может быть записано в виде a·b·c·d.
Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.
Если взять пять натуральных чисел и записать их в виде произведения, то получим 2·1·3·1·8. Имеется два основных способы решения.
Первый способ заключается в том, что два множителя слева будут последовательно заменяться произведением. Тогда получим, что 2·1·3·1·8=2·3·1·8. Так как 2·3=6, то 2·3·1·8=6·1·8. Далее имеем, что 6·1=6, тогда в итоге получим результат 6·8=48. Умножение пяти заданных чисел будет равняться 48. Этот способ записывается, как (((2·1)·3)·1)·8.
Тогда получим, что 2·1·3·1·8=2·3·1·8. Так как 2·3=6, то 2·3·1·8=6·1·8. Далее имеем, что 6·1=6, тогда в итоге получим результат 6·8=48. Умножение пяти заданных чисел будет равняться 48. Этот способ записывается, как (((2·1)·3)·1)·8.
Второй способ заключается в том, что скобки располагаются таким образом ((2·1)·3)·(1·8). Имеем, что 2·1=2 и 1·8=8, то ((2·1)·3)·(1·8)=(2·3)·8. При 2·3 равном 6 получим, что (2·3)·8=6·8. В итоге получим, что 6·8=48. Отсюда следует, что 2·1·3·1·8=48.
Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.
Пример 1Даны четыре числа для умножения: 3, 9, 2, 1. Их произведение записывается в виде 3·9·2·1.
При замене произведения множителей 3 и 9 или 9 и 2 получим, что следующий этап необходимо будет произвести умножение двузначных чисел 27 и 18.
Чтобы избежать это, необходимо поменять слагаемые местами, иначе расставить скобки.
Тогда получим: 3·9·2·1=3·2·9·1=(3·2)·(9·1)=6·9=54.
При перемене мест множителей можно производить наиболее удобные комбинирования для вычисления. Рассмотрим задание, где решение приводит к умножению нескольких чисел.
Пример 2Каждая коробка имеет по 3 предмета. В ящики положили 2 коробки. Какое количество предметов будет в 4 ящиках?
Решение
Нам дано, что в одном ящике 2 коробки, а в них соответственно по 3 предмета.
Тогда в одном ящике 3·2=6 предметов. Отсюда получим, что в 4 ящиках 6·4=24 предмета. Можно рассуждать иным образом. Один ящик вмещает в себя 2 коробки, отсюда в 4 ящиках 2·4=8 коробок. Каждая из коробок имеет 3 предмета, тогда имеем, что 8 коробок содержат 3·8=24 предмета.
Эти решения можно записать таким образом (3·2)·4=6·4=24 или 3·(2·4)=3·8=24.
Делаем вывод, что искомое количество предметов – это произведение 3,2,4, а значит, что 3·2·4=24.
Ответ: 24.
Подведем итоги.
При умножении трех и более чисел действия производятся последовательно. Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.
Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеУмножение суммы на натуральное число и наоборот
Благодаря распределительному свойству умножения сложение и умножение связаны. Это помогает в изучении сложения и умножения. Свойство способствует углубиться в изучение всех действий.
Если рассматривать распределительное свойство умножения относительно сложения, то получим такой вид записи с двумя слагаемыми: (a+b)·c=a·c+b·c, где a, b, c являются произвольными натуральными числами. Исходя из данного равенства при помощи метода математической индукции докажем справедливость предложенного (a+b+c)·d=a·d+b·d+c·d, (a+b+c+d)·h=a·h+b·h+c·h+d·h и т.д., где a, b, c, d, h являются натуральными числами.
Отсюда следует, что произведение суммы нескольких чисел и данного числа равна сумме произведений каждого из слагаемых с данным числом. Это правило применимо при умножении на заданное число.
Это правило применимо при умножении на заданное число.
Если взять сумму из пяти чисел 7, 2, 3, 8, 8 на 3, получим, что (7+2+3+8+8)·3=7·3+2·3+3·3+8·3+8·3. Отсюда имеем, что 7·3=21, 2·3=6, 3·3=9, 8·3=24, то 7·3+2·3+3·3+8·3+8·3=21+6+9+24+24, после чего находим сумму чисел 21+6+9+24+24=84.
Можно было сделать вычисления иначе, тогда следовало посчитать сумму, после чего умножение. Этот случай менее удобен, так как умножение двухзначного числа 7+2+3+8+8=28 на 3 мы пока не выполняли. Умножение двухзначных чисел – это тема, показанная в разделе умножения многозначного и однозначного натуральных чисел.
Используя переместительное свойство, мы можем переформулировать правило умножения суммы чисел на заданное число таким образом: произведение данного числа и суммы нескольких чисел равняется сумме произведений данного числа и каждого из слагаемых. Это правило умножения данного числа на заданную сумму.
Например, 2·(6+1+3)=2·6+2·1+2·3=12+2+6=20. Здесь применяем правила умножения числа на сумму.
Рассмотрим конкретный пример, где умножение решение сводится к умножению суммы чисел на данное число.
Пример 3В коробке находятся по 3 красных, 7 зеленых и 2 синих предмета. Какой количество предметов имеется во всех четырех коробках?
Решение
Для определения количества предметов в одной коробке, вычислим 3+7+2. Отсюда следует, что четыре коробки содержат в 4 раза больше, значит, (3+7+2)·4 предметов.
Находим произведение суммы на число, применив полученное правило, тогда (3+7+2)·4=3·4+7·4+2·4=12+28+8=48.
Ответ: 48 предметов.
Умножение натурального числа на 10, 100, 1000 и так далее
Чтобы получить правило произвольного умножения натурального числа на 10, рассмотрим подробно.
Натуральные числа вида 20, 30, 40, …, 90 соответствуют 2, 3, 4, …, 9 десяткам. Это значит, что 20=10+10, 30=10+10+10, … отсюда следует, что умножением двух натуральных чисел их смысл суммы должен быть идентичным, тогда получим 2·10=20, 3·10=30, . .., 9·10=90.
.., 9·10=90.
Таким же образом можно прийти к следующим неравенствам:
2·100=200, 3·100=300, …, 9·100=900; 2·1 000=2 000, 3·1 000=3 000, …, 9·1 000=9 000; 2·10 000=20 000, 3·10 000=30 000, …, 9·10 000=90 000; …
Выходит, что десяток десятков – это сотня, то 10·10=100;
что десяток сотен – это тысяча, тогда 100·10=1 000;
что десяток тысяч – это десять тысяч, то 1 000·10=10 000.
Исходя из рассуждений, получим 10 000·10=100 000, 100 000·10=1 000 000, …
рассмотрим пример для формулировки правила умножения произвольного натурального числа на 10.
Пример 4Необходимо произвести умножение натурального числа 7032 на 10.
Решение
Чтобы быстрее подсчитать, необходимо представить число 7032 в виде суммы разрядных слагаемых.
Применим правило умножения суммы на число из предыдущего пункта, тогда получим 7 032·10=(7 000+30+2)·10=7 000·10+30·10+2·10. Число 7000 можно представить в виде произведения 7·1 000, число 30 произведением 3·10.
Отсюда получим, что сумма 7 000·10+30·10+2·10 будет равна сумме (7·1 000)·10+(3·10)·10+2·10. Тогда сочетательное свойство умножения можно зафиксировать, как (7·1 000)·10+(3·10)·10+2·10=7·(1 000·10)+3·(10·10)+2·10.
Отсюда получим, что 7·(1 000·10)+3·(10·10)+2·10=7·10 000+3·100+2·10=70 000+300+20. Сумма, полученная в результате, представляет собой разложение по рядам числа 70320: 70 000+300+20.
Ответ: 7 032·10=70 320.
Аналогичным способом мы можем умножить любое натуральное число на 10. В таких случаях запись всегда будет оканчиваться на 0.
Приведенные примеры и рассуждения дают возможность перейти к правилу умножения произвольного натурального число на 10. Если в конце записи дописать цифру 0, тогда заданное число будет служить результатом умножения на 10. Когда в записи натурального числа дописывают 0, то полученное число применяется как результат умножения на 10.
Приведем примеры: 4·10=40, 43·10=430, 501·10=5 010, 79 020·10=790 200 и так далее.
Основываясь на правиле умножения натурального числа на 10, можно получить умножение произвольного числа на 100, 1000 и выше.
Если 100=10·10,тогда умножение натурального числа на 100 приводит к умножению числа на 10 и еще одному умножению на 10.
Тогда получим:
17·100=17·10·10=170·10=1 700; 504·100=504·10·10=5 040·10=50 400; 100 497·100=100 497·10·10=1 004 970·10=10 049 700.
Если полученная запись имеет на 2 цифры 0 больше, тогда считается, что это результат умножения всего числа на 100. Это и называется правилом умножения числа на 100.
Произведение 1 000=100·10, тогда умножение любого натурального числа на 1000 приводит к умножению заданного числа на 100 и еще одному умножению на 10. Отсюда следует, что это правило умножения произвольного натурального числа на 1000. Когда в записи имеется 3 цифры 0, тогда считают, что это результат умножения числа на 1000.
Таким же образом производится умножение на 10000, 100000 и так далее. Идет дописывание нулей в конце числа.
В качестве примера запишем:
58·1 000=58 000; 6 032·1 000 000=6 032 000 000; 777·10 000=7 770 000.
Умножение многозначного и однозначного натуральных чисел
Имея навыки для выполнения умножения, разберем все правила на примере.
Пример 5Найти произведение трехзначного числа 763 на 5.
Решение
Для начала представляем число в виде суммы разрядных слагаемых. Здесь получим, что 763=700+60+3. Отсюда получим, что 763·5=(700+60+3)·5.
Используя правило умножения суммы на число, получим, что:
(700+60+3)·5=700·5+60·5+3·5.
Произведения 700=7·100 и 60=6·10 и сумма 700·5+60·5+3·5 записывается, как (7·100)·5+(6·10)·5+3·5.
Применив переместительное и сочетательное свойство, получим (7·100)·5+(6·10)·5+3·5=(5·7)·100+(5·6)·10+3·5.
Так как 5·7=35, 5·6=30 и 3·5=15, то (5·7)·100+(5·6)·10+3·5=35·100+30·10+15.
Выполняем умножение на 100, на 10. После этого выполняем сложение 35·100+30·10+15=3 500+300+15=3 815
Ответ: произведение 763 и 5= 3815.
Чтобы закрепить материал, необходимо рассмотреть пример умножения.
Пример 6Найти произведение 3 и 104558.
Решение
3·104 558=3·(100 000+4 000+500+50+8)==3·100 000+3·4 000+3·500+3·50+3·8==3·100 000+3·(4·1 000)+3·(5·100)+3·(5·10)+3·8==3·100 000+(3·4)·1 000+(3·5)·100+(3·5)·10+3·8==3·100 000+12·1 000+15·100+15·10+3·8==300 000+12 000+1 500+150+24=313 674.
Ответ: результат умножения 3 и 104558 = 313674.
Умножение двух многозначных натуральных чисел
Умножение двух многозначных натуральных чисел производится таким образом, что один из множителей раскладывается по разрядам, после этого применяют правило умножения на сумму. Изучение предыдущих статей позволит быстрее разобраться с имеющимся разделом.
Пример 7Вычислить произведение 41 и 3806.
Решение
Необходимо произвести разложение числа 3806 по разрядам 3000+800+6, тогда 41·3 806=41·(3 000+800+6).
Правило умножения применимо для 41·(3 000+800+6)=41·3 000+41·800+41·6.
Так как 3 000=3·1 000 и 800=8·100, тогда справедливо равенство 41·3 000+41·800+41·6=41·(3·1 000)+41·(8·100)+41·6.
Сочетательное свойство способствует записи последней суммы (41·3)·1 000+(41·8)·100+41·6.
Вычисляя произведения 41·3, 41·8 и 41·6, представляем его в виде суммы
41·3=(40+1)·3=40·3+1·3=(4·10)·3+1·3=(3·4)·10+1·3=12·10+3=120+3=123; 41·8=(40+1)·8=40·8+1·8=(4·10)·8+1·8=(8·4)·10+1·8=32·10+8=320+8=328; 41·6=(40+1)·6=40·6+1·6=(4·10)·6+1·6=(6·4)·10+1·6=24·10+6=240+6=246
Получим, что
(41·3)·1 000+(41·8)·100+41·6=123·1 000+328·100+246=123 000+32 800+246
Вычислим сумму натуральных чисел:
123 000+32 800+246=156 046
Ответ: Произведение 41 и 3806 = 156046.
Теперь умеем умножать два любых натуральных числа.
Проверка результата умножения натуральных чиселУмножение всегда требует проверки. Она производится при помощи деления по правилу: полученное произведение делят на один из множителей. Если полученное число равно одному из множителей, тогда вычисление произведено правильно. Если нет, то допущена ошибка.
Если нет, то допущена ошибка.
Произвести умножение 11 на 13, равное 143. Необходимо выполнить проверку.
Решение
Проверка производится посредством деления 143 на 11. Тогда получим, что 143:11=(110+33):11=110:11+33:11=10+3=13.
Если получим число, равное одному из множителей, тогда задание решено верно.
Пример 9Произведено умножение 37 на 14. Результат равен 528. Выполнить проверку.
Решение
Для выполнения проверки необходимо разделить 528 на 37. Должны получить число 14. Производится делением столбиком:
При делении мы выявили, что 528 делится на 37, но с остатком. Отсюда следует, что умножение 37 на 14 было выполнено неверно.
Ответ: проверка показала, что умножение было выполнено неверно.
Пример 10Вычислить произведение чисел 53 и 7, после чего выполнить проверку.
Решение
Представляем число в виде суммы 50+3. Применим свойство умножения суммы двух чисел на натуральное число. Получим, что 53·7=(50+3)·7=50·7+3·7=350+21=371.
Получим, что 53·7=(50+3)·7=50·7+3·7=350+21=371.
Для выполнения проверки, разделим 371 на 7: 371:7=(350+21):7=350:7+21:7=50+3=53. Значит, умножение произведено верно.
Ответ: 53·7=371.
Умножение и деление с числами 1,0. Деление нуля на число
Технологическая карта урока
Предмет: математика
Дата проведения: 20.12.19
Тема урока: «Умножение и деление с числами 1,0. Деление нуля на число»
Тип урока: урок «открытия» нового знания
Цель: познакомить с приёмом деления нуля на число; обобщить и закрепить знания таблицы умножения
Планируемые результаты:
Личностные результаты: умение анализировать результаты учебной деятельности, объяснять причины успеха или неуспеха в своей учёбе.
Метапредметные результаты:
Регулятивные:
— умение выполнять задания по образцу;
— помнить и удерживать в памяти правило умножения (деления) нуля на число;
Познавательные:
— находить закономерности, способы решения задачи;
— определять основную и второстепенную информацию.
Коммуникативные:
— умение работать в группах, парах, участвовать в диалоге;
— задавать вопросы в ходе поиска информации
Предметные результаты:
— выполнять деление нуля на число;
— выполнять деление и умножение чисел на 1 и 0;
— решать задачи на нахождение частного.
Методы: словесный, наглядный, практический.
Формы: индивидуальная, парная, групповая, фронтальная.
Оборудование: учебник «Математика 3 класс», тетради, таблички с формулами, карточки с заданиями, снежинки с заданиями и для рефлексии, новогодняя елка, компьютер и проектор, презентация.
Ход урока:
Этапы урока | Деятельность учителя | Деятельность ученика | ||||||||||||
Организационный этап | Здравствуйте, ребята. | Приветствуют учителя. | ||||||||||||
Мотивация | — Какой сейчас месяц? (декабрь) А что можно сказать о 31 декабря? (В ночь с 31 декабря на 1 января наступает Новый год!) — Кто самый желанный гость на новогоднем празднике? Конечно, Дедушка Мороз. — Ребята, посмотрите какую елочку нам принес Дедушка Мороз. Но чего-то не хватает. Даже не знаю чего. Как вы думаете? Конечно же, нам надо ее украсить. — Поможем дедушке морозу ее украсить? Для этого нам нужно выполнять разные задания на снежинках. Вы готовы отправиться в сказочную страну Деда Мороза? Для этого нам надо стать помощниками Деда Мороза. У вас на столах лежат шапочки помощников, давайте их оденем и отправимся в путешествие. — Ваша работа на уроке должна быть обязательно оценена. Поэтому для каждого из вас есть лист помощника Деда Мороза. В течении всего урока вы будете выполнять задания и оценивать себя (подписать фамилию и имя). | Отвечают на вопрос. | ||||||||||||
3. Актуализация знаний | — Снимает снежинку под номером 1. — Ребята, вы любите фокусы? — Показать вам фокус? Содержание фокуса. Попросить учеников задумать число (однозначное). Потом это число ученик должен умножить на 2, прибавить к результату 8, разделить результат на 2 и отнять задуманное число. В результате получается число 4. — Сейчас запишите число в черновиках и покажите партнеру по плечу. — Хотите услышать ответ? Ответ будет 4. — У вас получилось? Молодцы! — Оцените себя. Нарисуйте зеленый кружок в листе помощников Деда Мороза, если ошибки не было, если было — красный. Давайте вспомним, какие правила умножения на 1 и 0 мы уже изучили. ( Формулы-подсказки я повешу на доске. а ∙ 1 = а ,а ∙ 0 = 0) — Откройте свои тетради, запишите сегодняшнее число и классная работа. Снежинка № 2 Работа в группах. Расставьте примеры в 2 группы: — Почему так распределили? . Что вы заметили? Есть ли здесь лишний пример? Все ли примеры вы смогли решить? У кого возникли затруднения? Чем этот пример отличается от остальных? Если кто-то решил, то молодец. (Проверка и отметка в Листе Помощников Деда Мороза) | Отвечают дети (При умножении любого числа на 1 получается тоже самое число. — С ответом 4 и 5 | ||||||||||||
4. Постановка цели и задач урока. | Но почему не все смогли справиться с этим примером? — Здесь есть пример с 0. А от 0 можно ожидать разные фокусы. Это необычное число. Вспомните, что вы знаете про 0? — Посмотрите, какой он коварный: когда его прибавляют, он не изменяет число, а когда умножают, превращают его в 0. — Подходят ли эти правила к нашему примеру? — Итак, какова наша цель на этом уроке? Цель: _________________ — Что для этого надо? Задача: __________ Следовательно Тема урока:_____________ | -а·0=0, 0·а=0, 0+а=а -Нет — Цель урока: «Научиться решать такие примеры». — Задача « Узнать правило деления 0 на число» — Тема урока: «Умножение и деление с числами 1,0. Деление нуля на число». | ||||||||||||
5. Первичное усвоение новых знаний. | — Сколько получится в последнем примере? Как узнали? (Если дети ответили, то объясняют как решили. Если не ответили, то я объясняю) — Деление связано с умножением. На какое число надо умножить 9, чтобы получить 0? Вывод: При делении нуля на любое другое число, получается нуль. Сравните свой вывод с тем, который есть в учебнике на стр. 85 (прочитайте и расскажите друг другу) — Итак, продолжаем выполнение заданий на снежинках. Снежинка № 3 Работа со словарем (в группе). Ребята, а вы знаете, что означает слово «Ноль»? Где мы можем узнать о значении этого слова? — Значит, какой вывод мы можем сделать? — Можно ли поделить ничего на ноль? — Какой вывод можно сделать? ПОМНИ, делить на нуль нельзя! Почему? Да потому, что какое бы число вы не умножали на 0, в ответе всегда будет 0 Физкультминутка «Снеговик» Немножко отдохнули. Продолжаем помогать Дедушке Морозу. | — На 0 (Представители групп зачитывают толкование слова ноль) — Ноль – ничего. — Нет — Ноль на число делить нельзя. | ||||||||||||
6. Первичная проверка понимания | Снежинка № 4 Работа в парах. — Кто уже чувствует в себе силу самостоятельно применить новые знания и получить звание «умников» и «умниц»? Кому нужна помощь? (Как правило, никому) — Сейчас снежинка предлагает поработать в парах. — Что нужно сделать в следующем задании? Подобрать знаки *, :, +, -. 1 вариант: 0 : 16= 16 * 0= 2 вариант 16 * 1= 16 * 0= Одна пара у доски. Проверяем по доске (взаимопроверка), оцениваем в листах Помощников Деда Мороза. (без ошибок – зеленый, 1 ошибка – желтый, 2 ошибки – красный. — Посмотрите, сколько у меня карандашей. Хотите узнать сколько? Давайте сосчитаем(48). Снежинка №5 Решение задачи. Ни один урок математики не обходится без решения задач. — Значит наша задача о чем? Решение задачи по карточкам У Маши есть 48 карандашей в коробках, 6 в каждом. Сколько у нее коробок с карандашами? А) Составление таблицы. — О чем идет речь? Какой вопрос задачи? — Прочитайте условие задачи и подумайте, как удобнее выполнить краткую запись. — Что такое 48? — 6? — Какая ещё графа должна быть в таблице? — Мы можем ответить на вопрос задачи? — Почему? — Как мы можем найти количество коробок? — Заполните таблицу, решите задачу и запишите ответ в группе.
Б) Проверка решения. 1) 48:6 = 8(кор.) Ответ: у Маши есть 8 коробок с карандашами. — Группы меняются местами и проверяют решение (по экрану). (Оценивание в листке Помощников Деда Мороза: задача решена – зеленый кружок, не решена – красный) | 1 вариант: 0:16= 0 16 *0= 0 2 вариант 16*1= 16 16*0= 0 — О карандашах — В таблице — Кол-во всех карандашей — Количество карандашей в 1 коробке — Количество коробок — Нет — Нужно найти. — Делением | ||||||||||||
7. Первичное закрепление. | Снежинка №6 Разноуровневые задания (самостоятельная работа по карточкам разного цвета) Найди ошибки, исправь и запиши правильно в свою тетрадь.
Самооценивание по образцу на экране. Доп.задача: («Проверь себя» (учебник, с. 84, 85). Проверка. Ответы записываю на доске: с. 84 — 1, 8, 12; с. 85 — 0, 0, 0.) |
| ||||||||||||
8. | 1в. Стр.85 № 6 1), № 8 (1,2 уравнения) 2в.Стр.85 № 6 2), № 8 (3,4 уравнения) | Записывают домашнее задание | ||||||||||||
9. Рефлексия (подведение итогов занятия) | — Какую цель мы сегодня поставили? — Достигли мы эту цель? -Какие правила вы узнали сегодня на уроке? -Какие правила повторили? -Какие задания ещё вызывают у вас затруднения? -За что вы можете себя похвалить? Оцените свою работу на уроке в листе Помощников Деда Мороза. Давайте нашу елочку украсим новыми снежинками. *Доволен своей работой на уроке. *Были отдельные моменты, когда я испытывал трудности. *Не доволен, много не сумел сделать. Ребята, мне очень понравилось с вами работать. Вы большие молодцы. Я вам желаю успехов. Спасибо за урок | Отвечают на вопросы — 5-6 зеленые кружочки -3-4 зеленые кружочки — 0-2 зеленые кружочки |
Урок 5. Опорное число при умножении чисел до 100
Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. В прошлом уроке, когда показывался способ умножения чисел до 20, по сути мы использовали опорное число 10.
Также стоит отметить, что подробнее вы можете ознакомиться с методикой использования опорного числа в книге «Считайте в уме как компьютер» Билла Хэндли.
Общие правила использования опорного числа
Опорное число полезно при перемножении чисел, находящихся близко и при возведении в квадрат. Как можно использовать метод опорного числа вы уже поняли из прошлого урока, теперь давайте обобщим все сказанное.
Как можно использовать метод опорного числа вы уже поняли из прошлого урока, теперь давайте обобщим все сказанное.
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным)
Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:
47*48
- Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или из 48 вычесть 3 – это всегда одно и то же)
- Дальше 45 умножаем на 50 = 2250
- Затем прибавляем 2*3 к этому результату и вуа ля – 2 256!
Схематично в уме удобно представлять приведенную ниже табличку.
|
50 (опорное число) |
48 |
* |
47 |
(48-3)*50 = 45*50 = 2 250 (или (47-2)*50 = 45*50 вспомните, что умножение на 5 – это тоже самое что деление на 2) |
|
|
2 |
* |
3 |
+6 |
|
Ответ: |
|
|
|
2 250 + 6 = 2 256 |
Опорное число пишем слева от произведения. Если числа меньше опорного, то разница между ними и опорным пишется ниже этих чисел. Справа от 48*47 пишем расчет с опорным числом, справа от остатков 2 и 3 пишем их произведение.
Если числа меньше опорного, то разница между ними и опорным пишется ниже этих чисел. Справа от 48*47 пишем расчет с опорным числом, справа от остатков 2 и 3 пишем их произведение.
Если использовать упрощенную схему, то решение выглядит так: 47*48=45*50 + 6= 2 256
Посмотрим другие примеры:
Умножить 18*19
|
20 (опорное число) |
18 |
* |
19 |
(18-1)*20 = 340
|
|
|
2 |
* |
1 |
+2 |
|
Ответ: |
|
|
|
342 |
Короткая запись: 18*19 = 20*17+2 = 342
Умножить 8*7
|
10 (опорное число) |
8 |
* |
7 |
(8-3)*10 = 50
|
|
|
2 |
* |
3 |
+6 |
|
Ответ: |
|
|
|
56 |
Короткая запись: 8*7 = 10*5+6 = 56
Умножить 98*95
|
100 (опорное число) |
98 |
* |
95 |
(95-2)*100 = 9300
|
|
|
2 |
* |
5 |
+10 |
|
Ответ: |
|
|
|
9310 |
Короткая запись: 98*95 = 100*93 + 10 = 9 310
Умножить 98*71
|
100 (опорное число) |
98 |
* |
71 |
(71-2)*100 = 6900
|
|
|
2 |
* |
29 |
+58 |
|
Ответ: |
|
|
|
6958 |
Короткая запись: 98*71 = 100*69 + 58 = 6 958
Оба числа больше опорного (над опорным)
Допустим, мы хотим умножить 54 на 53. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Но в отличие от предыдущих примеров, эти числа больше опорного. По сути, модель их умножения не меняется, но теперь нужно не вычитать остатки, а прибавлять.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Но в отличие от предыдущих примеров, эти числа больше опорного. По сути, модель их умножения не меняется, но теперь нужно не вычитать остатки, а прибавлять.
- К 54 прибавить столько, на сколько 53 превышает 50, то есть 3. Получается 57 (или к 53 прибавить 4 – это всегда одно и то же)
- Дальше 57 умножаем на 50 = 2 850 (умножение на 50 – схоже с делением на 2)
- Затем прибавляем 4*3 к этому результату. Ответ: 2862
|
|
4 |
* |
3 |
+12 |
|
50 (опорное число) |
54 |
* |
53 |
(54+3)*50 = 2 850 или (53+4)*50 = 57*50 (вспомните, что умножение на 5 – это тоже самое что деление на 2) |
|
Ответ: |
|
|
|
2 862 |
Короткое решение выглядит так: 50*57+12 = 2 862
Для наглядности еще ниже приведены примеры:
Умножить 23*27
|
|
3 |
* |
7 |
+21 |
|
20 (опорное число) |
23 |
* |
27 |
(23+7)*20 = 600
|
|
Ответ: |
|
|
|
621 |
Короткая запись: Короткая запись: 23*27 = 20*30 + 21 = 621
Умножить 51*63
|
|
1 |
* |
13 |
+13 |
|
50 (опорное число) |
51 |
* |
63 |
(63+1)*50 = 3 200
|
|
Ответ: |
|
|
|
3 213 |
Короткая запись: Короткая запись: 51*63 = 64*50 + 13 = 3 213
Одно число под опорным, а другое над
Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие.
Такие примеры решаются не сложнее, чем предыдущие.
Умножить 45*52
Произведение 45*52 считается так:
- Из 52 вычитаем 5 или к 45 прибавляем 2. В любом обоих случая получается: 47
- Дальше 47 умножаем на 50 = 2 350 (умножение на 50 – схоже с делением на 2)
- Затем вычитаем (а не прибавляем, как раньше!) 2*5. Ответ: 2 340
|
|
|
|
2 |
|
|
50 (опорное число) |
45 |
* |
52 |
(45+2)*50 = 2 350
|
|
|
5 |
|
|
-10 |
|
Ответ: |
|
|
|
2 340 |
Короткая запись: 45*52 = 47*50-10 = 2 340
Также поступаем с подобными примерами:
Умножить 91*103
|
|
|
|
3 |
|
|
100 (опорное число) |
91 |
* |
103 |
(91+3)*100 = 9400
|
|
|
9 |
|
|
-27 |
|
Ответ: |
|
|
|
9 373 |
Только одно число близко к опорному, а другое нет
Как вы уже видели из примеров, опорным числом удобно пользоваться, если даже только одно число близко к опорному. Желательно, чтобы разница этого числа с опорным составляла не более 2-x или 3-х или была равна числу, на которое удобно умножать (например, 5, 10, 25 – см. второй урок)
Желательно, чтобы разница этого числа с опорным составляла не более 2-x или 3-х или была равна числу, на которое удобно умножать (например, 5, 10, 25 – см. второй урок)
Умножить 48*73
|
|
|
|
23 |
|
|
50 (опорное число) |
48 |
* |
73 |
(73-2)*50 = 3 550
|
|
|
2 |
|
|
-46 |
|
Ответ: |
|
|
|
3 504 |
Короткое решение: 48*73 = 71*50 – 23*2 = 3 504
Умножить 23*69
|
|
3 |
|
49 |
147 |
|
20 (опорное число) |
23 |
* |
69 |
(3+69)*20 = 1440
|
|
Ответ: |
|
|
|
1 587 |
Короткая запись: Короткое решение: 23*69 = 72*20 + 147 = 1 587 — чуть сложнее
Умножить 98*41
|
100 (опорное число) |
98 |
* |
41 |
(41-2)*100 = 3900
|
|
|
2 |
* |
59 |
+118 |
|
Ответ: |
|
|
|
4018 |
Короткая запись: Короткая запись: 98*41 = 100*39 + 118 = 4 018
Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Если у вас получается хорошо умножать на 30, 40, 60, 70 или 80 – тогда, вы сможете с помощью этой методики умножать любые числа (до 100 и даже больше).
Если у вас получается хорошо умножать на 30, 40, 60, 70 или 80 – тогда, вы сможете с помощью этой методики умножать любые числа (до 100 и даже больше).
Использование нескольких опорных чисел
Методика умножения с использованием опорных чисел позволяет использовать и 2 опорных числа. Это удобно, когда опорное число одного множителя можно выразить через опорное число другого. Например, в произведении «23 * 88» удобно использовать опорное число 20 для 23 и 80 для 88. Умножение этих чисел с помощью двух опорных удобно, потому что 20=80:4.
Методика 2-х опорных чисел заключается в том, что мы сначала делим 88 на 4 и получаем 22, производим умножение 23 на 22 и произведение умножаем снова 4. То есть, мы сначала делим произведение на 4, а потом умножаем на 4. Получается: 23*22 = 250*2+6= 506, а 506*4 = 2024 – это и есть ответ!
Для визуализации можно использовать уже привычную схему. Произведение23*88 считается так:
- Записываем удобное опорное число «20» и рядом приписываем множитель 4, с помощью которого можно выразить 80 через 20.

- Дальше делаем, как и раньше, пишем, на сколько 23 превышает 20 (3), а 88 превышает 80 (8).
- Выше тройки пишем произведение 3 на 4 (то есть 3 на множитель опорного).
- К 88 прибавляем произведение 3 на 4 и умножаем на опорное (20), получается 100*20 = 2000
- Прибавляем к 2000 произведением 3-х и 8-и. Результат: 2024
|
|
3*4=12 |
|
|
|
|
|
3 |
* |
8 |
+24 |
|
20*4 (опорное число) |
23 |
* |
88 |
(88+12)*20 = 2 000
|
|
Ответ: |
|
|
|
2 024 |
Короткая запись: 23*88 = (88+3*4)*20 + 24 = 2024
Теперь давайте попробуем умножить 23*88, используя опорное число 100 для 88 и 25 для 23.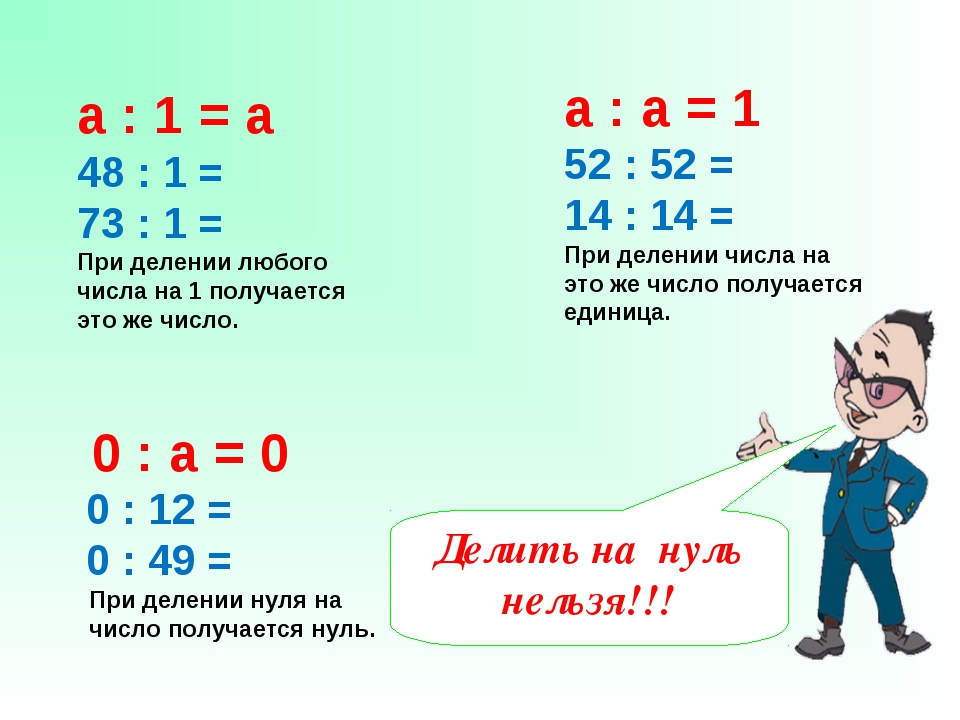 В этом случае главным опорным числом является 100. А 25 можно записать, как 100:4=25
В этом случае главным опорным числом является 100. А 25 можно записать, как 100:4=25
|
100:4 (опорное число) |
23 |
* |
88 |
(23-3)*100 = 2 000
|
|
|
2 |
|
12 |
+24 |
|
|
|
|
12:4=3 |
|
|
Ответ: |
|
|
|
2 024 |
Короткая запись: 23*88 = (23-12:4)*100 + 24 = 2024
Как видим, ответ получается один и тот же.
Способ с использованием двух опорных чисел несколько сложнее, и требует дополнительных действий. Во-первых, вы должны понять, какие 2 опорных числа вам удобно использовать. Во-вторых, нужно совершить дополнительное действие, для поиска числа, которое нужно умножать на опорное.
Эту методику применяйте лучше тогда, когда вы уже достаточно хорошо усвоили умножение с одним опорным числом.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Евгений БуяновКонспект урока по математике » Приемы умножение 1 и 0″ | План-конспект урока по математике (2 класс):
Муниципальное общеобразовательное бюджетное учреждение
средняя общеобразовательная школа д. Максимовка
Максимовка
муниципального района Стерлитамакский район
Конспект урока по математике
во 2 классе
«Приемы умножение единицы и нуля»
Подготовила:
Носова Лилия Венеровна
учитель начальных классов
2019
Тема урока: Приемы умножение единицы и нуля
Тип урока: Открытие нового знания.
Цель: Познакомить учащихся со случаями умножения 0 и 1
Задачи:
-формировать умения самостоятельно строить и применять новые знания,
-развивать умение анализировать, обобщать; развивать внимание, логическое и
критическое мышление, память, воображение;
-воспитывать интерес к математике, коммуникативные навыки общения для возможности
раскрытия потенциала каждого ребёнка
УУД, формируемые на уроке:
— личностные:
развитие способности адекватно оценивать себя и свои достижения установление
учащимися связи между целью учебной деятельности и её мотивом
— коммуникативные:
умение полно и точно выражать свои мысли в соответствии с задачами и условиями
коммуникации
— познавательные:
умение ставить и формулировать проблему, создавать алгоритм деятельности при
решении проблем поискового характера
выбор наиболее эффективных способов решения задач в зависимости от конкретных
условий,
умение использовать знаково-символические средства для создания моделей решения
учебно – познавательных задач, устанавливать причинно-следственные связи;
— регулятивные:
обучение планированию, прогнозированию, контролю, коррекции и оценке своих
действий учащимися.
Оборудование: Учебник «Школа России» Математика, презентация,ЭОР к уроку, раздаточные карточки для индивидуальной работы и работы в парах.
Ход урока:
I. Организационный момент.
Доброе утро, ребята!
Встало солнышко давно,
Заглянуло к нам в окно.
Нас оно торопит в класс
Математика у нас!
II. Актуализация знаний и формулирование проблемы урока
1. Устный счет
1) Математическая разминка.
— В комнате четыре угла. В каждом углу сидит кошка. Напротив каждой кошки по три кошки. Сколько же кошек в комнате? (4)
— Объясните, докажите свой ответ?
— Как записать число 10 четырьмя различными цифрами, соединив их знаками действия? (1+2+3+4)
— Как число 10 можно записать пятью одинаковыми цифрами, соединив их знаками действия? (2+2+2+2+2)
2 Самоопределение к деятельности. Создание проблемной ситуации. Постановка учебной задачи.
Игра «Найди ответ».
Решите примеры, заменяя умножение действием сложением, и соедините их стрелочкой с ответом.
6 х 4
5 х 2
4 х 3
9 х 2
3 х 3
7 х 4
0 х 4
5 х 1
18
9
10
28
24
12
Что обозначает первое число в примере? (слагаемое)
-Что обозначает второе число? (это число показывает количество слагаемых)
(учащиеся соединяют стрелочкой пример с ответом)
— Какие примеры мы не решили? (0 х 4 и 5 х)
— А у вас возникло затруднение?
-Почему? (Затруднение возникло, потому что не умеем умножать 0 и на число 1).
— Какая учебная задача стоит перед нами?
III. Открытие «нового способа действия».
- Построение проекта выхода из затруднения
— Сформулируйте тему урока.
(Умножение 0 и числа 1)
– Какую цель ставим? (Научиться умножать 0 и число1)
-Что для этого нужно сделать? ( Составить план действий)
Ученики составляют и проговаривают план действий с помощью учителя.
1) Сами попробуем найти способы умножения.
2) Сопоставим свои предположения с учебником.
3) Устраним затруднение.
4) Применим новое знание.
– Что нам поможет? (свой опыт, учебник страница 53, учитель)
- Реализация построенного проекта. Работа в группах.
– Сейчас мы будем работать по группам. Ученики делятся на группы, получают карточки:
Ученики действуют по плану: пробуют найти способы умножения 1 и 0 на число.
Проверка:
— Какой результат у вас получился при умножении 1 на число? (получилось тоже самое число)
— Какой вывод можно сделать? Чему равно произведение числа 1 на любое число ?
— Какой результат у вас получился при умножении 0 на число ? (0)
— Какой вывод можно сделать? Чему равно произведение нуля на любое число? (0)
Сделайте вывод, закончите предложения:
При умножении 1 на любое число получается ….
При умножении 0 на любое число получается ….
— Составьте буквенную модель решения примеров умножения 0 и числа 1, повторите вывод? (ответы учащихся)
На доске прикрепляются карточки: 1 x а = а 0 x а = 0
IV. Включение нового знания в систему знаний. Первичное закрепление с комментированием
Включение нового знания в систему знаний. Первичное закрепление с комментированием
Фронтальная форма работы.
- Пользуясь буквенными равенствами на доске: 1 x а = а 0 x а = 0 ,
выполним № 3 на странице 53 учебника (учащиеся решают у доски с комментированием)
Примеры: 0 х 15 1 х 67 1 х (33 – 30) 40 — 39 + 18 27 х 0
(рассуждения учащихся по решению каждого примера; повторение правил умножения числа 1 и 0 на любое число)
— Какие знания вам пригодились для решения примеров? (При умножении 1 на любое число получается то же число. При умножении 0 на любое число получается 0 )
Физкультурная минутка
- Поработали, ребятки!
А теперь – все на зарядку!
Влево, вправо повернитесь,
Наклонитесь, поднимитесь.
Руки вверх и руки вбок,
И на месте прыг да скок!
А теперь бежим вприпрыжку,
Молодцы вы, ребятишки!
Замедляем, дети, шаг
И на месте стой! Вот так!
А теперь мы сядем дружно,
Нам ещё работать нужно!
V. Контроль. Применение «нового знания».
Контроль. Применение «нового знания».
1) Самостоятельная работа с самопроверкой по эталону.
№ 4 на странице 53 учебника
Задание: поставьте знак > ,
1 х 38 * 1 +38 7 х 4 * 7+7+7
0 х41 *1+ 41 6 х 3 * 6+6+6
0 x 5 * 0 x 10 1 x 8 * 1 x 12
- Проверка по образцу.
— У кого всё правильно? Докажите почему надо поставить этот знак?
Исправление допущенных ошибок (у кого есть).
— Что помогло вам справиться с заданием? (применение знаний: при умножении 1 на любое число получается то же число. При умножении 0 на любое число получается 0)
VI. Рефлексия деятельности.
Чего мы не знали? (Не знали способа умножения числа 1 и 0)
— Какую учебную задачу перед собой ставили? (узнать какие числа получаются при умножении числа 1 и 0 )
Закончите предложения:
-Теперь мы знаем, при умножении 1 на любое число получается …… ( то же число). При умножении 0 на любое число получается ……( 0) .
— Где вам пригодятся эти знания? (при решении примеров, уравнений и задач)
— Сможете самостоятельно дома применить новое правило?
— Оцените свою работу на уроке по «Лестнице успеха»
Ученик помещает человечка (себя) на соответствующую ступеньку:
- уверен в своих знаниях по теме
- в основном уверен
- нужно ещё повторить
- нуждаюсь в помощи
VII. Домашнее задание.
Домашнее задание.
— Для тех, кто допустил ошибки в выполнении самостоятельной работы, предлагаю сделать ПАМЯТКИ — умножение числа 1 и 0;
— по выбору № 5 или № 6
Умножение натуральных чисел / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Умножение натуральных чисел
Умножение — одна из операций математики, предназначена для упрощения сложения одинаковых чисел.
Например: 4 + 4 + 4 = 4 · 3 = 12.
Умножение обозначают точкой «·» или крестиком «х».
Числа, которые умножаются, называют «множителями», результат умножения, называют «произведением»
Пример:
Алгоритм умножения чиселРазберем порядок умножения чисел на примере. Умножим число 25 на 16
Умножим число 25 на 16
1. Сначала записываем множители в столбик.
Второй множитель записывается под первым множителем так, что разряды второго множителя находились под соответствующими разрядами первого множителя, т.е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
2. Производим последовательное умножение.
Сначала число, обозначающее разряд единиц класса единиц второго множителя последовательно умножаем на все разряды первого множителя.
Умножим цифру 6 на 5, получаем 30 — 3 десятка 0 единиц. 0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
3. Найдем второе неполное произведение. Последовательно умножим десятки второго множителя — 1 на все разряды первого слагаемого. Сначала 1 умножим на 5, получаем 5, запишем полученное произведение под десятками. После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
4. Последовательно сложим цифры полученных неполных произведений по правилам сложения.
Свойства умножения натуральных чисел.1. Переместительное свойство умножения.
a · b = b · a
От перемены мест множителей произведение не изменится.
12 · 4 = 4 · 12
12 · 4 = 48
4 · 12 = 48
2. Сочетательное свойство умножения.
a · (b · c) = (a · b) · c
Произведение не зависит от группировки сомножителей.
2 · (3 · 6) = (2 · 3) · 6
2 · (3 · 6) = 36
1) 3 · 6 = 18; 2) 18 · 2 = 36
(2 · 3) · 6 = 36
1) 2 · 3 = 6; 2) 6 · 6 = 36
3. Распределительное свойство умножения относительно сложения.
a · (b + c) = ab + ac
При умножении числа на сумму двух других чисел, можно данное число умножить на каждое из слагаемых, а полученные результаты сложить.
3 · (5 + 4) = 3 · 5 + 3 · 4
3 · (5 + 4) = 27
1) 5 + 4 = 9; 2) 9 · 3 = 27
3 · 5 + 3 · 4 = 27
1) 3 · 5 = 15; 2) 3 · 4 = 12; 3) 12 + 15 = 27
4. Распределительное свойство умножения относительно вычитания
a · (b — c) = ab — ac
При умножении числа на разность двух других чисел, можно данное число умножить на уменьшаемое и на вычитаемое, а полученные результаты вычесть.
6 · (7 — 5) = 6 · 7 — 6 · 5
6 · (7 — 5) = 12
1) 7 — 5 = 2; 2) 2 · 6 = 12
6 · 7 — 6 · 5 = 12
1) 6 · 7 = 42; 2) 6 · 5 = 30; 3) 42 — 30 = 12
5. Свойство умножения единицы на натуральное число
a · 1 = a
При умножении единицы на любое число, получим равное ему число.
1 · 76 = 76
6. Свойство умножения нуля на натуральное число
0 · a = 0
При умножении 0 на любое число, получим 0
0 · 123 = 0
Произведение всех натуральных чисел от 1 до называют факториал, записывают: , читают: «эн факториал». Следовательно, справедливо равенство:
= 123…
Пример:
3! = 123 = 6;
5! = 12345 =120.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 566, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 603, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 628, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 837, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1162, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1515, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 421, Мерзляк, Полонский, Якир, Учебник
Номер 422, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 111, Мерзляк, Полонский, Якир, Учебник
Номер 112, Мерзляк, Полонский, Якир, Учебник
Номер 165, Мерзляк, Полонский, Якир, Учебник
Номер 175, Мерзляк, Полонский, Якир, Учебник
Номер 177, Мерзляк, Полонский, Якир, Учебник
Номер 191, Мерзляк, Полонский, Якир, Учебник
Номер 203, Мерзляк, Полонский, Якир, Учебник
Задание 252, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 779, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 797, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
Использование свойств умножения и деления нуля
Результаты обучения
- Определение свойств умножения и деления нуля
Используйте свойства нуля
Мы уже узнали, что ноль является аддитивным идентификатором, поскольку его можно добавить к любому числу, не меняя идентичности числа. Но у нуля также есть некоторые особые свойства, когда дело доходит до умножения и деления.
Умножение на ноль
Что происходит, когда вы умножаете число на [latex] 0? [/ Latex] Умножение на [latex] 0 [/ latex] делает произведение равным нулю.Произведение любого действительного числа и [латекс] 0 [/ латекс] равно [латекс] 0 [/ латекс].
Умножение на ноль
Для любого действительного числа [латекс] а [/ латекс],
[латекс] a \ cdot 0 = 0 [/ латекс]
Упражнения
Упростить:
1. [латекс] -8 \ cdot 0 [/ latex]
[латекс] -8 \ cdot 0 [/ latex]
2. [латекс] \ frac {5} {12} \ cdot 0 [/ latex]
3. [латекс] 0 \ left (2.94 \ справа) [/ латекс]
Решение:
| 1. | |
| [латекс] -8 \ cdot 0 [/ латекс] | |
| Произведение любого действительного числа на 0 равно 0. | [латекс] 0 [/ латекс] |
| 2. | |
| [латекс] \ frac {5} {12} \ cdot 0 [/ латекс] | |
| Произведение любого действительного числа на 0 равно 0. | [латекс] 0 [/ латекс] |
| 3. | |
| [латекс] 0 \ влево (2,94 \ вправо) [/ латекс] | |
| Произведение любого действительного числа и 0 равно 0. | [латекс] 0 [/ латекс] |
Деление на ноль
Как насчет разделения с помощью [latex] 0? [/ Latex] Подумайте о реальном примере: если в банке для файлов cookie нет файлов cookie и три человека хотят ими поделиться, сколько файлов cookie получит каждый человек? Есть файлы cookie [latex] 0 [/ latex], поэтому каждый человек получает файлы cookie [latex] 0 [/ latex].
[latex] 0 \ div 3 = 0 [/ latex]
Помните, что мы всегда можем проверить деление с помощью соответствующего факта умножения. Итак, мы знаем, что
[латекс] 0 \ div 3 = 0 \ text {потому что} 0 \ cdot 3 = 0 [/ latex].
Дивизия Зеро
Для любого действительного числа [latex] a [/ latex], кроме [latex] 0, \ frac {0} {a} = 0 [/ latex] и [latex] 0 \ div a = 0 [/ latex].
Ноль, деленный на любое действительное число, кроме нуля, равно нулю.
Упражнения
Упростить:
1. [латекс] 0 \ div 5 [/ латекс]
2.[латекс] \ frac {0} {- 2} [/ latex]
3. [латекс] 0 \ div \ frac {7} {8} [/ latex]
Решение:
| 1. | |
| [латекс] 0 \ div 5 [/ латекс] | |
| Ноль, деленный на любое действительное число, кроме 0, равен нулю. | [латекс] 0 [/ латекс] |
2. | |
| [латекс] \ frac {0} {- 2} [/ латекс] | |
| Ноль, деленный на любое действительное число, кроме 0, равен нулю. | [латекс] 0 [/ латекс] |
| 3. | |
| [латекс] 0 \ div \ frac {7} {8} [/ латекс] | |
| Ноль, деленный на любое действительное число, кроме 0, равен нулю. | [латекс] 0 [/ латекс] |
Теперь давайте подумаем о делении числа на ноль. Каков результат деления [латекс] 4 [/ латекс] на [латекс] 0? [/ Латекс] Подумайте о соответствующем факте умножения. Есть ли число, умноженное на [latex] 0 [/ latex], дает [latex] 4? [/ Latex]
[latex] 4 \ div 0 = [/ latex] означает [latex] \ cdot 0 = 4 [/ latex]
Поскольку любое действительное число, умноженное на [latex] 0 [/ latex], равняется [latex] 0 [/ latex] , не существует действительного числа, которое можно умножить на [латекс] 0 [/ латекс], чтобы получить [латекс] 4 [/ латекс]. Мы можем сделать вывод, что ответа на [latex] 4 \ div 0 [/ latex] нет, и поэтому мы говорим, что деление на ноль не определено.
Мы можем сделать вывод, что ответа на [latex] 4 \ div 0 [/ latex] нет, и поэтому мы говорим, что деление на ноль не определено.
Дивизион по нулю
Для любого действительного числа [latex] a, \ frac {a} {0} [/ latex] и [latex] a \ div 0 [/ latex] не определены.
Деление на ноль не определено.
Упражнения
Упростить:
1. [латекс] 7,5 \ div 0 [/ latex]
2. [латекс] \ frac {-32} {0} [/ latex]
3. [латекс] \ frac {4} {9} \ div 0 [/ латекс]
Решение:
| 1. | |
| [латекс] 7,5 \ div 0 [/ латекс] | |
| Деление на ноль не определено. | undefined |
| 2. | |
| [латекс] \ frac {-32} {0} [/ латекс] | |
| Деление на ноль не определено. | undefined |
Ниже мы суммируем свойства нуля.
Свойства нуля
Умножение на ноль: Для любого действительного числа [латекс] a [/ latex],
[латекс] \ begin {array} {c} a \ cdot 0 = 0 \ text {Произведение любого числа и 0 равно 0 .} \ hfill \ end {array} [/ latex]
Деление на ноль: Для любого действительного числа [latex] a, a \ ne 0 [/ latex]
[latex] \ frac {0} {a} = 0 [/ latex] Ноль, деленный на любое действительное число, кроме сам по себе равен нулю.
[латекс] \ frac {a} {0} [/ latex] не определено. Деление на ноль не определено.
Посмотрите следующее видео, чтобы увидеть больше примеров использования свойства нуля умножения и деления.
Что это такое и как его использовать
Число 0 давно ставит в тупик людей, изучающих математические понятия. Ноль — это число? Как мы его используем? Хотя все мы на каком-то уровне знаем, что ноль не означает ничего или ничего, это не всегда помогает нам использовать его в математических задачах.Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.
Ноль — это число? Как мы его используем? Хотя все мы на каком-то уровне знаем, что ноль не означает ничего или ничего, это не всегда помогает нам использовать его в математических задачах.Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.
Что такое число 0?
Ноль — это число? Ноль или 0 — это число , а числовая цифра, используемая для представления числа 0 , широко используется в математике и может использоваться как отдельное число или как заполнитель в уравнениях.
История
Число 0 использовалось для обозначения идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при написании чисел и уравнений.
Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.
Современное использование
Ноль обычно используется в языке, чтобы выразить концепцию отсутствия нуля, и используется в математике как целое число. Число 0 в сегодняшней математике может быть непростым; зачем что-то рассчитывать, когда на самом деле ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.
Операции с 0
Хотя этот список функций, использующих ноль , не охватывает все функции математики , эти базовые арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.
Дополнение
Закон сложения идентичности гласит, что любое число, добавленное к 0, равно самому себе .
Следовательно, вы можете сложить любое число и получить ту же сумму. Таким образом, вы можете добавить 0 к 1, 107 и 1 000 000 и все равно получить то же число, с которого вы начали.
Вычитание
Как и при сложении, если вы вычтете 0 из любого числа, вы получите ту же сумму. Например, 12-0 = 12.
.Если вы вычитаете, вам может потребоваться заимствование для решения проблемы. Заимствование — это метод, используемый для вычитания чисел с более чем одной цифрой.
Вот пример заимствования (разберемся как форматировать):
1572-125 = х
В этой задаче вы не можете вычесть 5 из 2. Итак, вам нужно взять взаймы из 7.
70 — это 7 десятков. Итак, вы можете убрать десятку, и 7 превратится в 2; тогда 2 становится 12. Теперь вы должны вычесть 5 из 12.
12-5 это 7.
6-2 это 4.
5-1 равно 4.
1-0 (пустое место) — 1.
Следовательно, ответ 1447.
Итак, если 0 — это ничто, как мы можем заимствовать из него в задаче на вычитание? Ключ в том, чтобы заимствовать следующую цифру слева. Вы можете пойти как можно дальше влево.
Итак, если бы вы сделали 306-98, вы бы сначала одолжили из 3, чтобы сделать 0 равным 10. Затем вы можете заимствовать из 10, чтобы получить 6 из 16. Итак, ваша задача будет выглядеть так: 16-8 = 8.
Затем вы можете заимствовать из 10, чтобы получить 6 из 16. Итак, ваша задача будет выглядеть так: 16-8 = 8.
9-9 = 0.
2-0 = 2.
Итак, ваш ответ — 208.
Не стесняйтесь заниматься математикой: добавит в вашу жизнь котят
Умножение
Умножение на 0 на самом деле является одной из самых простых функций 0. Когда вы умножаете на 0, ответ всегда будет 0.
12 × 0 = 0
255 × 0 = 0
1679 × 0 = 0
И знаете что? 123596395539 х 0 = 0
Дивизия
Число 0, разделенное на любое число, равно нулю.Подумайте об этом так: деление — это деление или деление вещей поровну, верно, ? Если у вас есть коробка с 8 кексами и 4 человека за вашим столом, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и коробка с 0 кексами, вам фактически нечего делить. Каждый получает 0 кексов.
К сожалению, деление числа на ноль не так очевидно логично. Любое число, деленное на ноль, считается неопределенным; если вы поместите его в калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.
Любое число, деленное на ноль, считается неопределенным; если вы поместите его в калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.
При делении вы всегда можете дважды проверить свой ответ, умножив частное (ответ на задачу деления) на делимое . В нашей задаче о кексах это 2 x 4. Число должно быть равно нашему исходному делителю, 8.
Однако это помогает нам понять, почему мы не можем разделить число на 0. Поскольку мы знаем из наших правил умножения, что все, что умножается на 0, равно 0, изложенная выше концепция не работает, если 0 является дивиденд, потому что ответ всегда будет 0, даже если это не исходный делитель.
Если по какой-то причине вы столкнулись с 0 в качестве делимого в задаче, вы можете выразить его как 1, даже если технически ответ не определен .
Возведение в степень
Как и при делении, 0 в экспоненте считается неопределенным. Однако, решая проблемы, и вы сталкиваетесь с чем-то, что равно 0 в степени другого числа или числу в степени 0, помните правило степени 0
.
Правило 0-экспоненты гласит, что любое основание с нулевым или нулевым основанием равно 1.Итак, x¹ = 1.
Между тем, 0 в любой степени равняется 0. Таким образом, 0² = 0.
Нулевой факторный
Факториал — это математическое выражение, выражаемое с помощью! что равно числу, которое получается путем умножения всех чисел от 1 до заданного целого числа.
Итак, 2! означает, что мы умножаем все числа от 1 до 2. Это означает, что 2! = 2 × 1 = 2 и, следовательно, 2! = 24
6! означает, что мы умножаем все числа от 1 до 6.Итак, 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720 и, следовательно, 6! = 720
Нулевой факториал, часто записывается как 0! Определяется как равный 1. В основном, поскольку факториал является выражением произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число от 0 до 1 — 1.
Использование числа ноль может быть непростым делом, но есть несколько правил, которые помогут вам правильно выполнять вычисления, когда используется ноль.Обязательно соблюдайте эти правила и помните, что ноль — не ваш враг. Если вы знаете, как работать с числом ноль, использовать его будет проще простого.
Что дальше?
Очарованы числом ноль? Узнайте, сколько нулей в миллиард и сколько нулей в гуголе и гуголплексе.
Нужна дополнительная помощь по математике? Узнайте, как преобразовывать десятичные дроби в дроби, складывать и вычитать дроби, а также о составных и рациональных числах.И не забудьте нашу удобную таблицу умножения.
Умножение и деление отрицательных чисел
Purplemath
Переходя от сложения и вычитания, как вы производите умножение и деление с отрицательными числами? Собственно, сложную часть мы уже рассмотрели: вы уже знаете правила «знака»:
плюс раз плюс плюс
(добавление большого количества горячих кубиков повышает температуру)
минус раз плюс минус
(удаление большого количества горячих кубиков снижает температуру)
плюс умножить на минус — минус
(добавление большого количества холодных кубиков снижает температуру)
минус умножить на минус равно плюс
(удаление большого количества холодных кубиков повышает температуру)
MathHelp.
 com
comПравила знаков действуют аналогично для деления; просто замените «раз» на «деленное на». Вот пример правил в разделе:
(Помните, что дроби — это просто еще одна форма деления! «Дроби — это деление»!)
Некоторым людям нравится думать об отрицательных числах в терминах долгов.Так, например, если вы должны 10 долларов шести людям, ваш общий долг составит 6 × 10 долларов = 60 долларов. В этом контексте имеет смысл получить отрицательный ответ. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?
Подумайте о том, чтобы перекусить в кафе. Когда вы идете платить, у ребенка возникают проблемы с использованием вашей дебетовой карты. Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.
Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.
Вы хотите подтвердить количество чрезмерных комиссий, прежде чем звонить в банк для исправления ситуации. Как в этом разобраться? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (скажем, 12,67 доллара США), которая является суммой одного платежа. Каждое списание является минусом на вашем счету, поэтому математика составляет:
.(- 76,02 $) ÷ (- 12 $.67) = 6
Итак, всего действительно было шесть зарядов. Количество зарядов, 6, при подсчете количества событий, должно быть положительным. В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.
И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.
Вы можете заметить, что люди отменяют знаки минуса.Они пользуются тем, что «минус, умноженный на минус, есть плюс». Например, предположим, что у вас есть (–2) (- 3) (- 4). Любые два отрицательных результата при умножении становятся одним положительным. Так что выберите любые два из перемноженных (или разделенных) отрицаний и «отмените» их знаки:
Упростить (–2) (- 3) (- 4).
Начну с того, что уберу одну пару знаков «минус».Потом размножу как обычно.
(–2) (- 3) (- 4)
= (–2) (- 3) (–4)
= (+6) (–4)
= –24
Если вам дано длинное умножение с отрицательными числами, просто уберите знаки «минус» попарно:
Упростить (–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1).

Первое, что я сделаю, это подсчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, оставив одну. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.
(–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1)
= (–1) (- 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (+1) (+ 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (1) (2) (–1) (- 3) (–4) (- 2) (- 1)
= (1) (2) (+1) (+ 3) (–4) (- 2) (- 1)
= (1) (2) (1) (3) (–4) (- 2) (–1)
= (1) (2) (1) (3) (+4) (+ 2) (–1)
= (1) (2) (1) (3) (4) (2) (- 1)
= (2) (3) (4) (2) (- 1)
= 48 (–1)
= –48
Я получил отрицательный ответ и знаю, что мой знак правильный.
Вот еще один пример, показывающий тот же процесс отмены в контексте разделения:
Отрицательные скобки
Основная трудность, с которой люди сталкиваются с негативом, заключается в том, чтобы иметь дело со скобками; в частности, в переносе отрицания через круглые скобки. Обычная ситуация примерно такая:
Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «над» круглыми скобками:
3 ( x + 4) = 3 ( x ) + 3 (4) = 3 x + 12
Те же правила применяются, когда вы имеете дело с негативом.Если у вас проблемы с отслеживанием, используйте маленькие стрелки:
← проведите по экрану , чтобы просмотреть изображение полностью →
Мне нужно взять 3 в круглые скобки:
3 ( x — 5) = 3 ( x ) + 3 (–5) = 3 x — 15
Здесь я возьму «минус» в скобках; Я буду распределять –2 на x и минус 3.
–2 ( x — 3) = –2 ( x ) — 2 (–3) = –2 x + 2 (+3) = –2 x + 6
Обратите внимание, как я внимательно следил за знаками в круглых скобках. «Минус» был сохранен рядом с цифрой 3 за счет использования еще одного набора круглых скобок. Не стесняйтесь использовать группирующие символы, чтобы ваш предполагаемый смысл был понятен как оценщику, так и вам самому.
Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразовывая вычитание в умножение на отрицательное значение:
Я начну с написания маленькой цифры «1» перед круглыми скобками. Затем я нарисую стрелки от этой единицы к терминам в круглых скобках, чтобы напомнить себе о том, что мне нужно сделать.
← проведите по экрану , чтобы просмотреть изображение полностью →
Не бойтесь написать эту маленькую цифру «1» и нарисовать эти маленькие стрелки.Вы должны делать все, что вам нужно, чтобы ваша работа была прямой и постоянно получала правильный ответ.
Упростить 6 — (3
x — 4 [1 — x ]).
Я буду работать изнутри, упрощая сначала символы внутренней группировки в соответствии с Порядком операций. Итак, первое, что я сделаю, это возьму –4 через скобки.Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками и, чтобы помочь мне отслеживать тот -1, который я буду распространять, я нарисую маленькие стрелки.
← проведите по экрану , чтобы просмотреть изображение полностью →
Филиал
Упростить
1 / 3 — ( x -2) / 3 .
Это непросто. Они заставляют меня вычесть дробь. Мне нужно объединить дроби, что означает объединение числителей. Чтобы не упустить из виду, что именно означает этот «минус» (а именно, что я вычитаю весь числитель второй дроби, а не только x ), я конвертирую минус с плюсом –1:
← проведите по экрану , чтобы просмотреть изображение полностью →
Обратите внимание, что я преобразовал вычитание дроби в добавление отрицательного числа, умноженного на единицу дроби.Очень легко «потерять» минус, когда вы добавляете такие беспорядочные полиномиальные дроби. Самая частая ошибка — ставить минус на x и забывать отнести его к –2. Будьте особенно осторожны с дробями!
Для дополнительной практики со скобками попробуйте здесь.
URL: https://www.purplemath.com/modules/negative3.htm
Умножение целых чисел — ChiliMath
Правила умножения и деления целых чисел очень похожи.В этом уроке мы сосредоточимся на умножении целых чисел.
Правила умножения целых чисел
Шаг 1: Умножьте их абсолютные значения.
Шаг 2: Определите знак окончательного ответа (в данном случае он называется произведением, потому что мы умножаем), используя следующие условия.
- Условие 1 : Если знаки двух чисел совпадают с , произведение всегда будет положительным числом .
- Условие 2 : Если знаки двух чисел разных , произведение всегда будет отрицательным числом .
Примеры умножения целых чисел
Пример 1 : Умножьте указанные ниже целые числа.
Решение: сначала получите абсолютное значение каждого числа.
Затем умножьте или найдите произведение абсолютных значений.
Наконец, определите знак окончательного ответа.Правило гласит, что если знаки двух целых чисел различаются, то окончательный ответ будет отрицательным.
Пример 2 : Умножьте указанные ниже целые числа.
Решение: Умножьте абсолютные значения двух чисел.
Поскольку мы умножаем целые числа с одинаковым знаком, окончательный ответ (произведение) должен быть положительным.
Пример 3 : Найдите произведение трех целых чисел ниже.
Решение: Мы также можем умножить три или более целых числа.Нам просто нужно умножить два целых числа за раз. Позвольте мне заключить в скобки, какие два числа мы умножаем в первую очередь. Произведение + 3 и — 8 равно — 24. Оно отрицательное, потому что знаки разные. Затем умножьте — 24 на — 2, чтобы получить + 48. Помните, что произведение двух целых чисел с одинаковым знаком всегда положительно.
Практика с рабочими листами
Возможно, вас заинтересует:
Целочисленное сложение
Целочисленное вычитание
Целочисленное деление
Умножение отрицательного числа дает положительный результат
Когда мы умножаем:
Да, действительно, два отрицания дают положительный результат, и мы объясним, почему , почему , на примерах!
Знаки
Поговорим о знаках .
«+» — положительный знак, «-» — отрицательный.
Когда число имеет без знака , это обычно означает, что это положительное значение .
И мы можем поставить () вокруг чисел, чтобы избежать путаницы.
Пример: 3 × −2 можно записать как 3 × (−2)
Два знака: правила
«Два одинаковых знака образуют положительный знак,
два разных знака образуют отрицательный знак»
Пример: (−2) × (+5)
Знаки — и + (отрицательный знак и положительный знак), поэтому они в отличие от знаков (они отличаются друг от друга)
Таким образом, результат должен быть отрицательным :
(-2) × (+5) = -10
Пример: (−4) × (−3)
Знаки — и — (оба являются отрицательными знаками), поэтому они похожи на знаки (похожи друг на друга)
Итак, результат должен быть положительным :
(−4) × (−3) = +12
Почему умножение двух отрицательных чисел дает положительное?
Ну, сначала объяснение «здравого смысла»:
Когда я говорю «Ешь!» Я призываю вас поесть (позитив)
Но когда я говорю «Не ешь!» Я говорю об обратном (отрицательном).
Теперь, если я скажу: «Не ешь ли , а не !», Я говорю, что не хочу, чтобы ты умирал с голоду, поэтому я снова говорю: «Ешь!» (положительный).
Итак, два отрицания дают положительный результат, и если это вас устраивает, то вам больше не нужно читать.
Направление
Все дело в направлении. Помните числовую черту?
Итак, малыш Стивен делает свои первые шаги. Он делает 2 шага за раз и делает это три раза, поэтому он делает 2 шага x 3 = 6 шагов вперед:
Теперь Малыш Стивен тоже может отступить (он умный маленький парень).Его отец ставит его в исходное положение, а затем Стивен отступает на 2 шага и делает это три раза:
И снова папа Стивена ставит его на старт, но лицом в другую сторону. Стивен делает 2 шага вперед (для него!), Но движется в отрицательном направлении. Он делает это 3 раза:
Снова на старте (спасибо, папа!), Все еще глядя в отрицательном направлении, он пробует ходить назад, снова делая два шага за раз, и он делает это три раза:
Итак, идя назад, смотря в отрицательную сторону, он движется в положительном направлении.
Попробуйте сами! Попробуйте идти вперед и назад, затем снова, но лицом в другую сторону.
Другие примеры
Пример: деньги
| Сэм дает вам три купюры по 10 долларов: | +3 × +10 = вы получаете 30 долларов | |
| Сэм дает вам три долга по 10 долларов: | +3 × −10 = вы теряете 30 долларов | |
| Сэм берет у вас три купюры по 10 долларов: | −3 × +10 = вы теряете 30 долларов | |
| Сэм берет у вас три долга по 10 долларов: | −3 × −10 = вы получаете 30 долларов |
Пример: видео бегущих людей
Люди бегут вперед, видео нормальное:
Все нормально, люди бегут вперед: +1 × +1 = +1
Люди бегут вперед, а видео назад :
Похоже, люди бегут задом наперед: +1 × −1 = −1
Люди бегут Назад , Нормальное видео:
Вы видите людей, бегущих назад: -1 × +1 = -1
Люди бегут назад , но видео назад :
Похоже, люди бегут вперед: -1 × -1 = +1
Пример: повышение / понижение уровня в резервуаре
В баке 30 000 литров, из которых ежедневно вывозится 1000 литров.Какое количество воды было в баке 3 дня назад ?
Мы знаем, что количество воды в резервуаре меняется на -1000 каждый день, и нам нужно вычесть это 3 раза (чтобы вернуться на назад на 3 дня ), поэтому изменение составит:
−3 × −1,000 = +3,000
Полный расчет:
30 000 + (-3 × -1 000) = 30 000 + 3 000 = 33 000
Итак, 3 дня назад в баке было 33 000 литров воды.
Таблица умножения
Вот с другой точки зрения .
Начните с таблицы умножения (достаточно до 4 × 4):
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Теперь посмотрим, что произойдет, если мы перейдем к негативам !
Поехали назад через ноль:
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| -4 | -4 | -8 | -12 | -16 |
| -3 | -3 | -6 | -9 | -12 |
| -2 | -2 | -4 | -6 | -8 |
| -1 | -1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Посмотрите на столбец «4»: это -16, -12, -8, -4, 0, 4, 8, 12, 16 .Каждый раз становясь на 4 больше.
Посмотрите еще раз на эту таблицу, убедитесь, что вам удобно, как она работает, потому что …
… теперь идем дальше влево , через ноль:
| × | -4 | -3 | -2 | –1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| -4 | 16 | 12 | 8 | 4 | 0 | -4 | -8 | -12 | -16 |
| -3 | 12 | 9 | 6 | 3 | 0 | -3 | -6 | -9 | -12 |
| -2 | 8 | 6 | 4 | 2 | 0 | -2 | -4 | -6 | -8 |
| -1 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| 2 | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
| 3 | -12 | -9 | -6 | -3 | 0 | 3 | 6 | 9 | 12 |
| 4 | -16 | -12 | -8 | -4 | 0 | 4 | 8 | 12 | 16 |
Тот же шаблон: мы можем следовать по строке (или столбцу), и значения меняются последовательно:
- Следуйте за строкой «4»: это идет -16, -12, -8, -4, 0, 4, 8, 12, 16 .Каждый раз становясь на 4 больше.
- Следуйте за строкой «-4»: это идет 16, 12, 8, 4, 0, -4, -8, -12, -16 . Каждый раз становится на 4 меньше.
- и т.д …
Итак, все по аккуратной схеме!
Как насчет умножения 3 или более чисел вместе?
Умножьте два за раз и следуйте правилам.
Пример: Что такое (−2) × (−3) × (−4)?
Сначала умножьте (−2) × (−3). Два подобных знака означают положительный знак, поэтому:
(−2) × (−3) = +6
Далее умножаем +6 × (−4).Два непохожих знака образуют отрицательный знак, поэтому:
+6 × (−4) = −24
Результат: (−2) × (−3) × (−4) = −24
Калькулятор умножения Добро пожаловать в калькулятор умножения Omni , где мы изучим одну из четырех основных арифметических операций: умножение . Короче говоря, мы используем его всякий раз, когда хотим добавить одно и то же число несколько раз. Например, 16 умножить на 7 (записано 16 * 7 ) — это то же самое, что добавить 16 семь раз или, что то же самое, добавить 7 шестнадцать раз.Для удобства наш инструмент работает также как калькулятор с умножением десятичных знаков . Более того, даже если у вас есть более двух чисел для умножения, вы все равно можете найти их произведение с помощью этого калькулятора.
Примечание : Если вы хотите увидеть пошаговые решения для умножения больших чисел, ознакомьтесь с калькулятором длинного умножения Omni.
Давайте не теряем ни секунды больше и посмотрим , как умножать числа !
Произведение или умножение: как умножать числа
Произведение и умножение — это одно и то же: они являются результатом умножения чисел (или других объектов, если на то пошло).К счастью, процесс очень прост: он сводится к добавлению значения подходящее количество раз. Например, 24 умножить на 5 означает, что мы добавляем 24 пять раз, то есть
24 * 5 = 24 + 24 + 24 + 24 + 24 = 120 .
Аналогично, 12 умножить на 20 преобразуется в сложение 12 двадцать раз:
12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 240 .
Однако обратите внимание, что мы всегда можем инвертировать процесс нахождения произведения с умножением. Другими словами, 24 , умноженное на 5 , также может означать двадцать четыре раза сложить 5 :
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 120 ,
, и мы можем получить 12 умноженное на 20 , добавив 20 двенадцать раз:
20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 = 240 .
Мы всегда выбираем, как умножать числа, так как результат в любом случае будет одинаковым . С математической точки зрения это означает, что произведение или умножение равно , а коммутативная операция . Обратите внимание, что то же самое верно и для сложения. С другой стороны, это не относится, скажем, к вычитанию.
Кроме того, наш калькулятор умножения работает только с числами , но математики выяснили, как умножать другие объекты. Ниже мы перечислим еще несколько калькуляторов умножения от Omni.
Однако не всегда имеет дело с целыми числами , такими как 2 , 18 или 2020 . Мы узнали, как их умножить и что, скажем, 16 умножить на 7 , но как найти произведение десятичных знаков? Например, сколько 0,2 умножить на 1,25 ? Наш калькулятор умножения также калькулятор умножения десятичных дробей ?
Да, конечно!
Умножение десятичных знаков
По сути, десятичных знака — это дроби .Таким образом, один из способов умножения десятичных дробей — это преобразовать их в обычные дроби, а затем использовать основное правило умножения числителя на числитель на знаменатель на знаменатель . Например,
0,2 * 1,25 = (2/10) * (125/100) = (2 * 125) / (10 * 100) = 250/1000 = 0,25 .
Конечно, мы могли бы также найти более простые дроби, эквивалентные двум, указанным перед умножением. В этом случае мы могли бы сказать, что 0,2 = 1/5 и 1,25 = 5/4 , поэтому
0.2 * 1,25 = (1/5) * (5/4) = (1 * 5) / (5 * 4) = 5/20 = 1/4 .
Оба ответа верны ; как умножать десятичные дроби — это всегда ваш выбор. Однако, кроме двух упомянутых, есть еще .
При умножении десятичных знаков, скажем, 0,2 и 1,25 , мы можем начать с , забывая точки . Это означает, что чтобы найти 0,2 * 1,25 , мы начнем с поиска 2 * 125 , что составляет 250 . Затем мы подсчитываем, сколько цифр справа от точек у нас было в общей сложности в числах, с которых мы начали (в данном случае их три: одна из 0.2 и два в 1,25 ). Затем мы записываем точку , которая представляет собой много цифр справа в том, что мы получили. Для нас это означает размещение точки слева от 2 , что дает 0,250 = 0,25 (мы пишем 0 , если у нас нет числа перед точкой).
В общем, мы видели , как умножать десятичные дроби тремя способами . Честно говоря, первые два были почти одинаковыми; просто промежуточные шаги были в другом порядке.Тем не менее, на этом мы завершаем часть о том, как умножать без калькулятора. Теперь подробно опишем, как это сделать с одним, а точнее с калькулятором умножения Omni.
Пример: использование калькулятора умножения
Давайте найдем 2020 умножить на 12 с помощью калькулятора умножения. Вверху нашего инструмента мы видим формулу:
результат = a₁ * a₂ .
Это означает, что для расчета 2020 * 12 нам нужно ввести:
a₁ = 2020 и a₂ = 12 .
В тот момент, когда мы даем второе число, , калькулятор умножения выдаст ответ в поле Result .
результат = 2020 * 12 = 24240
Однако предположим, что вы хотите еще умножить результат на 1,3 (помните, что наш инструмент также работает как калькулятор умножения десятичных знаков).
Мы могли бы просто очистить поля и записать ответ сверху в один из факторов, т.е., введите a₁ = 24240 и a₂ = 1,3 . В качестве альтернативы, мы можем просто выбрать много чисел под Умножить … , что позволяет нам найти произведение умножения на большее количество чисел . Если мы это сделаем, мы получим возможность ввести a₁ , a₂ , a и так далее до a (обратите внимание, что изначально есть только a и a₂ , но больше переменные появляются, когда вы начинаете заполнять поля).Затем достаточно ввести:
a₁ = 2020 , a₂ = 12 , a₃ = 1,3 ,
и прочтите ответ снизу:
результат = 2020 * 12 * 1,3 = 31512 .
Что ж, этот калькулятор умножения действительно экономит много времени. Можете ли вы представить, что напишет две тысячи двадцать умноженные на число 12 , как мы это сделали в первом разделе? Мы, например, этого не делаем.
Доказательство того, что число в нулевой степени равно единице
Вы здесь: Главная → Статьи → Доказательство нулевой степениПочему (-3) 0 = 1? Как это доказано?
Как в уроке про минус и ноль экспоненты, вы можете посмотреть следующую последовательность и спросите, что логически будет дальше:
(-3) 4 = 81
(-3) 3 = -27
(-3) 2 = 9
(-3) 1 = -3
(-3) 0 = ????
Вы можете использовать тот же шаблон для других чисел.Как только ваш ребенок обнаружит, что правило этой последовательности состоит в том, что на каждом шаге вы делите на -3, следующим логическим шагом будет то, что (-3) 0 = 1.
Видео ниже демонстрирует ту же идею: обучение нулевой экспоненты, начиная с шаблона. Это оправдывает правило и делает его логичным, а не просто кусок «анонсированной» математики без доказательств. В видео также показана идея доказательства, объясненная ниже: мы можем умножить степени одного и того же основания и сделать вывод из этого, каким должно быть число в степени нуля.
Другая идея доказательства состоит в том, чтобы сначала обратить внимание на следующее правило умножения ( n — любое целое число):
n 3 · n 4 = ( n · n · n ) · (n · n · n · n) = n 7n 6 · n 2 = ( n · n · n · n · n · n) · · · · · n · n) = n 8
Вы заметили ярлык? Для любых показателей целого числа x и y вы можете просто добавить показатели:
n x · n y = ( n · n · n ·… · n · n · n) · (n · … · n) = п х + у
Математика логична, и ее правила работают во всех случаях (теоремы применяются «для любого целого числа n » или «для всех целых чисел»). Итак, предположим, мы не знаем, что такое (-3) 0 . Что бы ни было (-3) 0 , если оно подчиняется вышеприведенному правилу, то
| (-3) 7 · (-3) 0 = (-3) 7 + 0 Другими словами, (-3) 7 · (-3) 0 = (-3) 7 | (-3) 3 · (-3) 0 = (-3) 3 + 0 Другими словами, (-3) 3 · (-3) 0 = (-3) 3 | (-3) 15 · (-3) 0 = (-3) 15 +
0 Другими словами, (-3) 15 · (-3) 0 = (-3) 15 |
…и так далее для всевозможных возможных показателей. Фактически, мы можем написать, что (-3) x · (-3) 0 = (-3) x , где x — любое целое число.
Поскольку мы предполагаем, что еще не знаем, что такое (-3) 0 , давайте заменим его P. Теперь посмотрим на уравнения, которые мы нашли выше. Зная то, что вы знаете о свойствах умножения, , что за число может быть P?
| (-3) 7 · P = (-3) 7 | (-3) 3 · P = (-3) 3 | (-3) 15 · P = (-3) 15 |
Другими словами… какое единственное число, когда вы умножаете на него, ничего не меняется? 🙂
Вопрос. Какая разница между -1 в нулевой степени и (-1) в нулевая мощность? Будет ли ответ 1 для обоих?
Пример 1: -1 0 = ____
Пример 2: (-1) 0 = ___
Ответ: Как уже объяснялось, ответ на (-1) 0 равен 1, поскольку мы возводим число -1 (отрицательное 1) в степень нуля.Однако в случае -1 0 отрицательный знак не означает отрицательное число, а вместо этого означает напротив числа следующего за ним. Итак, сначала мы вычисляем 1 0 , а затем принимаем обратное, что дает -1.
Другой пример: в выражении — (- 3) 2 первый отрицательный знак означает, что вы принимаете противоположность остальной части выражения. Итак, поскольку (-3) 2 = 9, то — (- 3) 2 = -9.
Вопрос. Почему при нулевом показателе экспоненты возникает ошибка ?? Пожалуйста, объясните, почему его не существует. Другими словами, что такое 0 0 ?
Ответ: Степень от нуля до нуля часто называют «неопределенной формой», потому что она может иметь несколько различных значений.
Поскольку x 0 равно 1 для всех чисел x, кроме 0, было бы логично определить, что 0 0 = 1.
Но мы могли бы также подумать о 0 0 , имеющем значение 0, потому что ноль для любой степени (кроме нулевой степени) равен нулю.
Кроме того, логарифм 0 0 будет равен 0 · бесконечность, что само по себе является неопределенной формой. Так что законы логарифмов с этим не сработают.
Итак, из-за этих проблем степень от нуля до нуля обычно считается неопределенной.
Однако, если для получения некоторого значения необходимо определить степень от нуля до нуля, наиболее логичным определением ее значения является 1. Это может быть «удобно», если вам нужен какой-то результат для работы во всех случаях (например, биномиальная теорема).
См. Также Что такое 0 в степени 0? от доктораМатематика.
В чем разница между степенью и экспонентой?
Вартан
Показатель степени — это небольшое повышенное число. «Степень» — это все: базовое число, возведенное в некоторый показатель степени — или значение (ответ), которое вы получите, если вычислите число, возведенное в некоторый показатель степени. Например, 8 — это степень (2), поскольку 2 3 = 8.
 Проверьте свою готовность к уроку, сядьте прямо.
Проверьте свою готовность к уроку, сядьте прямо.

 При умножении любого числа на нуль получается нуль.)
При умножении любого числа на нуль получается нуль.)


 )
)

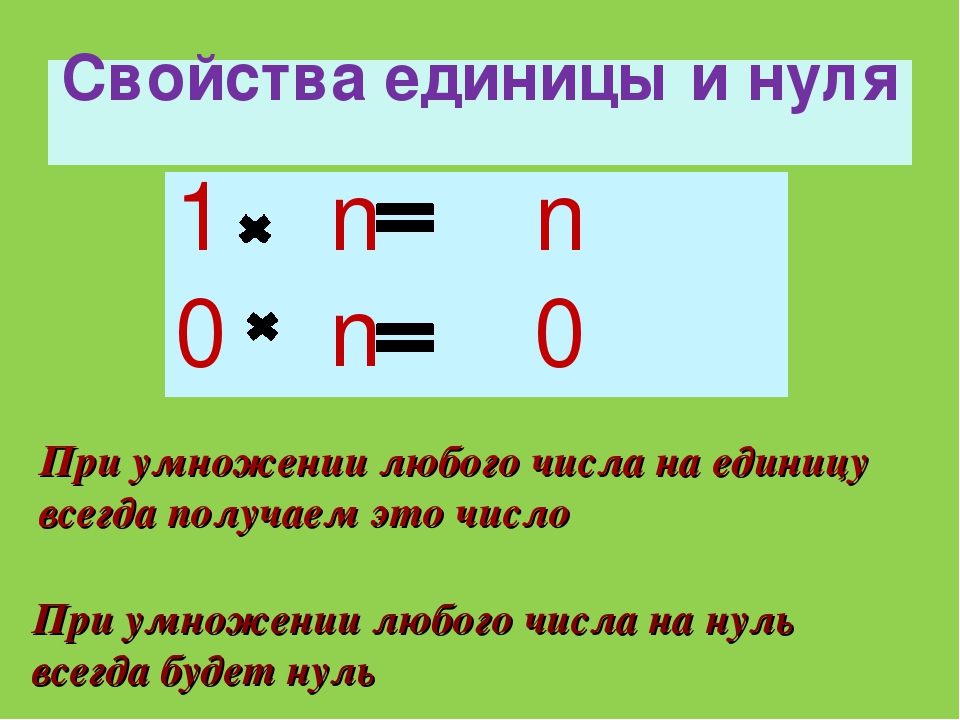
 Информация о домашнем задании, инструктаж по его выполнению
Информация о домашнем задании, инструктаж по его выполнению

