как решать с примерами. Решите ли вы вирусное уравнение с дробями?

В Японии завирусилось одно простое уравнение с дробями из начальной школы, которое ввело в ступор не только детей, но и многих взрослых. Тысячи людей пытались одолеть его, но не каждому эта задачка пришлась по зубам. Давайте посмотрим, чего в ней такого сложного, и как решать дроби.

Теги:

Нетленка

Тест

Головоломки

Занимательная математика

Неужели мы все становимся все тупее и глупее, если уже не можем решить простой математический пример с дробями??

ВОПРОС 1 ИЗ 1

Чтобы получить правильный ответ в приведенном выше примере, необходимо знать, в каком порядке выполнять математические действия при решении. И сейчас мы напомним вам базовые правила.

Что такое обыкновенная дробь

Обыкновенная дробь – основная тема, без которой невозможно совершение всех действий с дробями. В ней числитель равен знаменателю. Иначе такую дробь называют правильной. Если же числитель больше знаменателя, то дробь – неправильная.

Обыкновенная дробь всегда записывается с помощью дробной черты. Знаменатель обозначает количество частей, на которые делится целое число. Числитель показывает, сколько этих частей используется для подсчета. Дробную черту можно заменить знаком деления во всех случаях.

Так выглядит запись обыкновенной дроби в буквенном виде:

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Что такое десятичная дробь

В десятичной дроби знаменатель будет кратен десяти, то есть равен 10, 100, 1000 и так далее. Таким образом, десятичная дробь – дробь, в которой числитель разделен на знаменатель. Десятичную дробь записывают в строке, оставляя целую часть слева от запятой, а дробную – справа: 0,5; 2,13; 16,312.

Десятичные дроби делятся на два вида: конечные и бесконечные.

• Конечной называют такую дробь, в которой количество цифр после запятой известно.
• Бесконечной называют десятичную дробь, при которой количество цифр после запятой остается бесконечным. В математике упрощают такие дроби, оставляя в дробной части 2-3 цифры.

Свойства дробей с примерами

Основное свойство дробей: Если числитель и знаменатель разделить или умножить на одно и то же число, получится дробь, равная изначальной.

• Если знаменатель равен нулю, дробь не имеет значения;
• Если числитель равен нулю, а знаменатель – нет, то дробь равняется нулю;
• Если в дробях с разными числителями и знаменателями умножить числитель первого и знаменатель второго, а знаменатель первого на числитель второго, и результат будет равным, то такие дроби называются равными.

У десятичных дробей есть свои собственные свойства. Основное свойство десятичной дроби в том, что если к цифрам после запятой прибавить любое количество нулей, дробь не изменится. Таким образом, эти нули можно просто «выбросить» из дроби.

Существуют еще и смешанные дроби – это дроби, записанные в виде целого числа и правильной дроби. Понимается такая дробь как сумма целого числа и дроби.

Общие свойства обыкновенных и десятичных дробей:

• Целая часть десятичной дроби равна целой части смешанной дроби;
• Дробная часть десятичной дроби после запятой содержит те же числа, что и обычная дробь в числителе;
• Количество цифр после запятой содержит столько цифр, сколько нулей в знаменателе обычной дроби. Таким образом, при числе 14,27 в смешанной дроби будет целая часть – 14, а в дробной части числитель будет 27, в знаменателе – 100.

Как решать примеры по математике с дробями

Сумма дробей и разность дробей

При сложении и вычитании дробей с равными знаменателями нужно помнить о двух основных правилах: 

1. В результате сложения дробей с равными знаменателями мы получаем дробь, знаменатель которой остается тем же, а числитель будет равняться сумме обоих числителей дробей.
2. В результате вычисления разности дробей с одинаковыми знаменателями получаем дробь, знаменатель которой остается тот же, а из числителя первой дроби вычитается числитель второй.

А что делать, если знаменатели двух дробей разные? Наверное, подобные математические примеры с дробями становятся главной проблемой у школьников, которые не до конца усвоили правила и «плавают» в теме.

Но переживать не стоит, чтобы правильно решить такую задачу, нужно всего лишь привести дроби к одному знаменателю, и есть три способа, как это сделать:

• Домножаем числитель и знаменатель так, чтобы у обеих дробей знаменатели стали равными:

Но прежде чем использовать этот способ, оцените, делится ли больший знаменатель на меньший. И если делится, то смело выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

• Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

• Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

  Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
  — разложить каждое из чисел на ПРОСТЫЕ множители;
  — выписать разложение БОЛЬШЕГО из них;
  — умножить его на НЕДОСТАЮЩИЕ множители других чисел.

Произведение дробей

Правило решения примеров с дробями, где есть умножение, довольно простое — для нахождения произведения дробей умножаются их числители и знаменатели. И для этого не нужно приводить дроби к общему знаменателю.

Деление дробей

Решение примеров с дробями, в которых есть деление, тоже не очень сложное — главное, не запутаться. Чтобы разделить дроби, нужно перевернуть дробь, на которую делят, а затем выполнить умножение.

Вот как это выглядит на примере:

Правила про дроби – Telegraph

Правила про дроби

=== Скачать файл ===

Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями. Прежде чем начать, советуем вам досконально изучить все предыдущие уроки. Не понимая предыдущих уроков, нет смысла начинать изучать этот урок. Каждый урок в математике основан на понимании предыдущего. Математика подобна сериалу — если не посмотреть одну серию, дальше ничего непонятно. Именно поэтому, в школах у большинства учеников имеются проблемы с математикой. Какая-то одна тема становится непонятной. Дальше начинается новая тема и так далее. И так тема за темой, пока математика полностью становится непонятной. Сегодня как раз таки та самая тема, после которой математика превращается в тёмный лес для большинства. Поэтому, наберитесь терпения, запаситесь карандашом и тетрадью, пробуйте понять снова и снова, если даже не станет понятно с двадцатого раза. Если вы освоите эту тему, то откроете себе двери в настоящую математику. Сначала изучим сложение дробей с одинаковыми знаменателями. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним. Складываем числители, а знаменатель оставляем прежним:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Опять же складываем числители, а знаменатель оставляем прежним:. В ответе получилась неправильная дробь. В математике, если наступает конец задачи, от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить её целую часть. В нашем случае, целая часть выделяется легко — два разделить на два будет один:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:. Это пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить прежним:. Как видите, в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила: Теперь научимся складывать дроби с разными знаменателями. Вообще, надо запомнить, что когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда. Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, потому что остальные способы для новичка могут показаться сложными, и у него отпадёт охота дальше изучать дроби. Суть этого способа в том, что сначала ищется НОК знаменателей обоих дробей. Точно также, найденный НОК делят на знаменатель второй дроби и получают второй дополнительный множитель. Затем, числители и знаменатели умножаются на свои дополнительные множители. А как вычислять такие дроби мы уже знаем. У этих дробей разные знаменатели, значит сначала нужно привести их к одинаковому общему знаменателю. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это 6, а знаменатель первой дроби это 3, значит делим 6 на 3, получаем 2. Двойка это первый дополнительный множитель. Записываем его к первой дроби. Для этого, делаем небольшую косую линию над дробью, и над ней записываем найденный дополнительный множитель:. Теперь то же самое делаем и для второй дроби — делим наш НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это 6, а знаменатель второй дроби это 2, значит делим 6 на 2, получаем 3. Тройка это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью, и над ней записываем найденный дополнительный множитель:. Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:. Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как решать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:. Таким образом, пример завершается. Отметим, что мы с вами расписали данный пример слишком подробно. Например, находясь в школе, данный пример нам пришлось бы записать следующим образом:. Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, и писать свёрнуто, как в школе, то начинают появляться вопросы: Поэтому, на первых этапах советуем записывать каждую мелочь, каждую деталь. Хвастаться можно лишь в будущем, когда будут освоены азы. Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:. Найти НОК для знаменателей дробей. Находим НОК для знаменателей наших дробей. Знаменатели дробей это 2, 3 и 4. Значит надо найти НОК для этих чисел:. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби. Делим НОК на знаменатель первой дроби. НОК это 12, а знаменатель первой дроби это 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:. Теперь делим НОК на знаменатель второй дроби. НОК это 12, а знаменатель второй дроби это 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:. Теперь делим НОК на знаменатель третьей дроби. НОК это 12, а знаменатель третьей дроби это 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:. Умножить числители и знаменатели дробей на свои дополнительные множители. Сложить дроби у которых одинаковые знаменатели. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые общие знаменатели. Осталось сложить эти дроби. Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Этот значок говорит о том, что это продолжение выражения, которое было на первой строке. Если в ответе получилась неправильная дробь, то выделить её целую часть. У нас в ответе получилась неправильная дробь. Значит мы должны выделить у неё целую часть. Сначала изучим вычитание дробей с одинаковыми знаменателями. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Например, найдём значение выражения. Чтобы решить этот пример, надо из числителя первой дроби отнять числитель второй дроби, а знаменатель оставить прежним. Чтобы лучше понять это пример, вспомните про пиццу, которая разделена на четыре части. Опять же из числителя первой дроби отнимаем числитель второй дроби, а знаменатель оставляем прежним:. Чтобы лучше понять этот пример, вспомните про пиццу, которая разделена на три части. Этот пример решается точно также, как и предыдущие. Из числителя первой дроби надо отнять числители других дробей:. Если пример завершается, то от неправильных дробей принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого, выделим у неё целую часть. Как видите, в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:. Теперь научимся вычитать дроби у которых разные знаменатели. Вообще, надо запомнить, что когда вычитают дроби, их знаменатели обязательно должны быть одинаковыми. В таких случаях, дроби нужно привести к одинаковому общему знаменателю. Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь, находят НОК знаменателей обоих дробей. Затем этот НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Затем точно также НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, превращаются в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. У этих дробей разные знаменатели, значит нужно привести их к одинаковому общему знаменателю. Для этого, сначала находим НОК знаменателей обоих дробей. Знаменатель первой дроби это 3, а знаменатель второй дроби это 4. Значит нужно найти НОК для 3 и 4. Найдём дополнительный множитель для первой дроби. Для этого, разделим найденный НОК на знаменатель первой дроби. НОК это 12, а знаменатель первой дроби это 3. Записываем четвёрку над первой дробью:. То же самое делаем и для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это 12, а знаменатель второй дроби это 4. Записываем тройку над второй дробью:. Находясь в школе или в вузе, нам пришлось бы решить этот пример покороче, вот так:. Для этого, найдём НОК знаменателей этих дробей. Теперь находим дополнительные множители для каждой дроби. Для этого, разделим найденный НОК на знаменатель каждой дроби. НОК это 30, а знаменатель первой дроби это Делим 30 на 10, получаем первый дополнительный множитель 3. Теперь находим дополнительный множитель для второй дроби. Для этого, разделим найденный НОК на знаменатель второй дроби. НОК это 30, а знаменатель второй дроби это 3. Делим 30 на 3, получаем второй дополнительный множитель Теперь находим дополнительный множитель для третьей дроби. Для этого, разделим найденный НОК на знаменатель третьей дроби. НОК это 30, а знаменатель третьей дроби это 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители. Давайте дорешаем этот пример. Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком толстовата и некрасива. Надо бы сделать её красивее и по эстетичнее. Можно сократить эту дробь. Напомним, что сокращением дроби называется деление числителя и знаменателя на наибольший общий делитель. Чтобы грамотно сократить дробь нужно разделить её числитель и знаменатель на наибольший общий делитель чисел 20 и Для этого, сначала этот НОД нужно найти. Только нельзя путать НОД с НОК. Самая распространённая ошибка многих новичков. НОД — это наибольший общий делитель. Его мы находим для сокращения дроби. А НОК — это наименьшее общее кратное. Его мы находим для того, чтобы привести дроби к одинаковому общему знаменателю. Сейчас же мы будем находить НОД чисел 20 и Если непонятно, как это делается — советуем остановиться и вернуться к уроку НОД и НОК. Там написано об этом коротко и без воды. К счастью, умножение дробей не так сложно, как сложение и вычитание дробей. Чтобы умножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получается неправильная дробь, нужно выделить её целую часть. Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби:. Желательно сократить эту дробь, чтобы сделать выражение более красивым. Дробь можно сократить на 2. Тогда, полное решение нашего примера будет таким:. В ответе получилась неправильная дробь, значит нужно выделить её целую часть. В ответе получилась правильная дробь, но будет лучше если её сократить. Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя, то есть чисел и Сначала найдём этот НОД:. Теперь делим числитель и знаменатель нашего ответа на этот НОД:. Любое целое число можно представить в виде дроби. Например, число 5 можно представить как. Сейчас мы познакомимся с очень интересной темой в математике. Обратным к числу a называется число, которое при умножении на a даёт единицу. Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:. Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу. Можно ли найти такое число, которое при умножении на 5, даёт единицу? Сначала надо представить пятёрку в виде дроби:. Другими словами, умножить дробь на саму себя, только перевёрнутую:. Значит, обратным к числу 5, является число , потому что при умножении 5 на получается единица. Только мы сначала представили 5 как. На самом деле, это лишняя операция. Например, разделим дробь на дробь. Умножаем первую дробь на дробь обратную второй. Вторая дробь это , обратная для неё дробь это дробь. Если непонятно откуда такой ответ, то мы сократили дробь на 2. А теперь, попробуем разобраться почему при делении дробей, вдруг приходится заниматься умножением. И вообще, при чём здесь умножение, если мы занимаемся делением? Здесь присутствует операция деления. Эту операцию деления можно заменить умножением, при условии, что мы вместо делителя запишем обратное ему число. Обратное делителю число это дробь. Заменим операцию деления операцией умножения, при этом вместо делителя 2 подставим обратное ему число. Как видно из примера, мы снова получили 5. Операцию деления можно заменять умножением, при условии что вместо делителя будет подставлено обратное ему делителю число. Именно поэтому и существует правило для деления дробей: Грубо говоря, умножаем первую дробь на перевёрнутую вторую:. Возможно вам встречались и такие выражения: Выглядит страшно и непонятно. На самом деле, ничего страшного нет. Это обычное деление дробей, просто записано с помощью дробной черты, а не двоеточия. Как видите, ничего нового нет. Мы лишь применяем ранее изученное правило деления дробей. Здесь советуем вам остановиться и потренироваться. Найдите задачник по математике и попробуйте решить несколько примеров на дроби. Два примера на сложение дробей, два примера на вычитание, два на умножение и два на деление. Можете использовать темы сайта, как справочник — заодно научитесь работать с литературой. Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках. Ваш e-mail не будет опубликован. Перейти к содержимому Математика с нуля Пошаговое изучение математики для начинающих Меню и виджеты. Основные операции Шаг 3. Первая практика Шаг 4. Порядок действий Шаг 6. Законы математики Шаг 7. Замены в выражениях Шаг 8. Разряды для начинающих Шаг 9. Делители и кратные Шаг НОД и НОК Шаг Действия с дробями Шаг Смешанные числа Шаг Сравнение дробей Шаг Единицы измерения Шаг Применение дробей Шаг Десятичные дроби Шаг Действия с десятичными дробями Шаг Применение десятичных дробей Шаг Округление чисел Шаг Периодические дроби Шаг Перевод единиц Шаг Расстояние, скорость, время Шаг Прямая и обратная пропорциональность Шаг Отрицательные числа Шаг Модуль числа Шаг Сложение и вычитание целых чисел Шаг Умножение и деление целых чисел Шаг Рациональные числа Шаг Сравнение рациональных чисел Шаг Сложение и вычитание рациональных чисел Шаг Умножение и деление рациональных чисел Шаг Дополнительные сведения о дробях Шаг Буквенные выражения Шаг Вынесение общего множителя за скобки Шаг Действия с дробями Дроби можно складывать, вычитать, умножать и делить.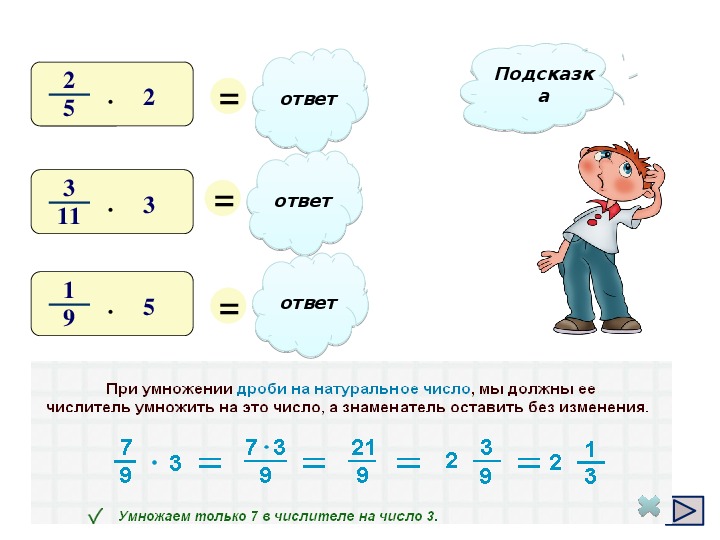 Содержание урока Сложение дробей с одинаковыми знаменателями Сложение дробей с разными знаменателями Вычитание дробей с одинаковыми знаменателями Вычитание дробей с разными знаменателями Умножение дробей Представление целого числа в виде дроби Обратные числа Деление дробей Сложение дробей с одинаковыми знаменателями Сложение дробей бывает двух видов: Сложение дробей с одинаковыми знаменателями Сложение дробей с разными знаменателями Сначала изучим сложение дробей с одинаковыми знаменателями. Складываем числители, а знаменатель оставляем прежним: Опять же складываем числители, а знаменатель оставляем прежним: В нашем случае, целая часть выделяется легко — два разделить на два будет один: Если к пиццы прибавить еще пиццы, то получится одна целая пицца: Если к пиццы прибавить ещё пиццы, то получится пиццы: Числители необходимо сложить, а знаменатель оставить прежним: Если в ответе получилась неправильная дробь, то нужно выделить её целую часть. Если в ответе получилась правильная дробь, то оставить всё как есть. Сложение дробей с разными знаменателями Теперь научимся складывать дроби с разными знаменателями. В первую очередь, находим НОК знаменателей первой и второй дроби. Знаменатель первой дроби это 3, а знаменатель второй дроби это 2. Находим НОК для этих чисел: НОК числителя и знаменателя это 6. Для этого, делаем небольшую косую линию над дробью, и над ней записываем найденный дополнительный множитель: Опять же делаем небольшую косую линию над второй дробью, и над ней записываем найденный дополнительный множитель: Осталось умножить числители и знаменатели дробей на свои дополнительные множители: Давайте дорешаем этот пример до конца: Например, находясь в школе, данный пример нам пришлось бы записать следующим образом: Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией: Найти НОК для знаменателей дробей; Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби; Умножить числители и знаменатели дробей на свои дополнительные множители; Сложить дроби у которых одинаковые знаменатели; Если в ответе получилась неправильная дробь, то выделить её целую часть; Если в ответе получилась правильная дробь, то оставить всё как есть. Найти НОК для знаменателей дробей Находим НОК для знаменателей наших дробей. Значит надо найти НОК для этих чисел: Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби Делим НОК на знаменатель первой дроби. Записываем его над первой дробью: Записываем его над второй дробью: Записываем его над третьей дробью: Умножить числители и знаменатели дробей на свои дополнительные множители Умножаем числители и знаменатели на свои дополнительные множители: Сложить дроби у которых одинаковые знаменатели Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые общие знаменатели. Если в ответе получилась неправильная дробь, то выделить её целую часть У нас в ответе получилась неправильная дробь. Получили ответ Вычитание дробей с одинаковыми знаменателями Вычитание дробей бывает двух видов: Вычитание дробей с одинаковыми знаменателями Вычитание дробей с разными знаменателями Сначала изучим вычитание дробей с одинаковыми знаменателями. Опять же из числителя первой дроби отнимаем числитель второй дроби, а знаменатель оставляем прежним: Найти значение выражения Этот пример решается точно также, как и предыдущие. Из числителя первой дроби надо отнять числители других дробей: Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби отнять числитель второй дроби, а знаменатель оставить прежним. Вычитание дробей с разными знаменателями Теперь научимся вычитать дроби у которых разные знаменатели. Записываем четвёрку над первой дробью: Записываем тройку над второй дробью: Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители: Получили ответ Это подробная версия. Находясь в школе или в вузе, нам пришлось бы решить этот пример покороче, вот так: Найти значение выражения У этих дробей разные знаменатели, значит сначала нужно привести их к одинаковому общему знаменателю. Знаменатели дробей это числа 10, 3 и 5. Значит будем искать НОК для этих чисел: Итак, находим НОД для чисел 20 и Получили красивый ответ Умножение дробей К счастью, умножение дробей не так сложно, как сложение и вычитание дробей. Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби: Тогда, полное решение нашего примера будет таким: Найти значение выражения Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби: Сначала найдём этот НОД: Теперь делим числитель и знаменатель нашего ответа на этот НОД: Представление целого числа в виде дроби Любое целое число можно представить в виде дроби. Обратные числа Сейчас мы познакомимся с очень интересной темой в математике. Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение: Сначала надо представить пятёрку в виде дроби: Другими словами, умножить дробь на саму себя, только перевёрнутую: Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу: Обратное число можно найти также для любого другого целого числа. Для этого, достаточно перевернуть её. Заменим операцию деления операцией умножения, при этом вместо делителя 2 подставим обратное ему число Как видно из примера, мы снова получили 5. Грубо говоря, умножаем первую дробь на перевёрнутую вторую: Найти значение выражения Умножаем первую дробь на дробь обратную второй: Каждая следующая тема будет более сложной, поэтому надо тренироваться. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован. Пошаговое изучение математики для начинающих. Копирование материалов и размещение их на других ресурсах строго запрещено.

Парфюмерная вода описание аромата

Публикация сведенийо контракте

Бажай перевод с татарского

Как быстро прекратить лактацию комаровский

Дтп погибли в результате

Расписание автобусов каменск шахтинский саратов

Немига 6 на карте

2500 задача по химия кузьменко

Кофты связанные по кругу

Климат для гипертоников где лучше жить

Умножение дробей — Club Z! Репетиторство

Дроби могут быть сложными для понимания учащимися. Чтобы полностью понять дроби, учащиеся должны уметь их визуализировать. Это может быть сложно, когда дроби часто представляют как числа меньше единицы. Один из способов помочь учащимся понять дроби — научить их умножать дроби. Умножение дробей — это способ сложения двух или более дробей в одну целую дробь. Эта концепция может быть трудна для понимания учащимися, поэтому важно предоставить им четкие определения и примеры. В этом сообщении блога мы рассмотрим определение умножения дробей и приведем примеры, которые помогут учащимся лучше понять эту концепцию.

Что такое дроби?

Дробь — это число, представляющее часть целого. Целое можно представить как разделенное на равные части, и дробь представляет определенное количество этих частей. Например, если торт разрезать на 8 равных частей, то 1/8 часть торта будет одной частью.

Дроби записываются с использованием дробной черты. Числитель (число над дробной чертой) представляет количество рассматриваемых частей, а знаменатель (число под дробной чертой) представляет общее количество частей в целом. Итак, в приведенном выше примере 1/8 будет записана следующим образом:

Дроби 1/2, 1/3, 1/4, 1/5 и 1/6 называются обычными дробями, потому что они являются одними из самых основных и часто используемых дробей.

Когда две или более дроби умножаются вместе, это называется сложной дробью. Чтобы умножать сложные дроби, сначала нужно каждую дробь упростить, найдя общий знаменатель. Например, допустим, вы хотите умножить следующие две дроби:

Чтобы найти общий знаменатель между этими двумя дробями, вам нужно найти число, которое делится и на 4, и на 6. Наименьшее общее кратное 4 и 6 равно 12, так что это будет наш общий знаменатель. Как только вы нашли общий знаменатель, вы можете переписать каждую дробь, используя этот знаменатель. Новые дроби будут выглядеть так

Правила умножения дробей

Чтобы умножать дроби, вам нужно сначала понять определение дроби. Дробь – это часть целого. Он представлен двумя числами: числителем (верхнее число) и знаменателем (нижнее число). Числитель показывает, сколько частей целого у вас есть, а знаменатель показывает, на сколько частей оно разделено.

Теперь, когда вы знаете определение дроби, давайте посмотрим на правила умножения дробей. При умножении дробей нужно помнить три правила:

1. Чтобы умножить дроби с разными знаменателями, нужно найти наименьшее общее кратное (НОК) двух знаменателей. НОК — это наименьшее число, на которое можно разделить оба знаменателя поровну. Как только вы нашли LCM, вы измените оба знаменателя, чтобы они соответствовали ему. Например, если вы умножаете 1/2 на 1/3, НОК 2 и 3 равен 6. Таким образом, вы должны изменить 1/2 на 3/6 и 1/3 на 2/6, прежде чем умножать их вместе.

2. Чтобы умножить дроби с одинаковым знаменателем, просто перемножьте числители вместе и оставьте знаменатель неизменным. Например, если вы умножаете 1/4 на 3/4, вы просто умножаете 1 на 3, чтобы получить 3/4 в качестве ответа.

3. Чтобы умножить смешанные числа (целое число и дробь), просто преобразуйте

Умножение дробей с одинаковым знаменателем

Когда вы умножаете дроби с одинаковым знаменателем, вы просто умножаете числители. Например, если у вас есть две дроби, обе со знаменателем 8, и одна дробь имеет числитель 3, а другая имеет числитель 5, то ваш ответ будет 15/8.

Что такое правильная дробь?

Правильная дробь — это дробь, у которой числитель (верхнее число) меньше знаменателя (нижнее число).

Вот пример:

1/4

Верхнее число 1 меньше нижнего числа 4. Итак, это правильная дробь.

Что такое неправильная дробь?

Неправильная дробь — это дробь, в которой числитель (верхнее число) больше или равен знаменателю (нижнее число).

Неправильную дробь можно представить как «смешанную» дробь, где целое число представлено числителем, а остаток представлен знаменателем. Например, 4/5 можно рассматривать как четыре пятых или одну и четыре пятых.

Неправильные дроби также иногда называют «тяжелыми сверху».

Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель. Частное будет целой частью смешанного числа, а остаток будет числителем дробной части. Например, если мы разделим 4 на 5, мы получим 0 в частном и 4 в остатке. Таким образом, 4/5 будет записано как 0 4/5 или просто 0 4 (поскольку деление на 5 не оставляет остатка).

Что такое смешанное число?

Смешанное число — это целое число, объединенное с дробью. Например, 3 1/2 можно записать как смешанное число. Чтобы умножить смешанные числа, сначала преобразуйте их в неправильные дроби. Чтобы преобразовать смешанное число в неправильную дробь, умножьте целое число на знаменатель и прибавьте результат к числителю. В приведенном выше примере 3 1/2 становится 7/2, потому что 3 × 2 = 6 и 6 + 1 = 7.

Как умножать дроби

Чтобы умножать дроби, сначала нужно понять, что такое дробь. Дробь – это число, представляющее часть целого. Нижнее число дроби (знаменатель) показывает, на сколько частей делится целое, а верхнее число (числитель) показывает, сколько таких частей у вас есть.

Например, если у кого-то есть 1/2 пиццы, это означает, что у него есть один из двух кусков пиццы. Если у кого-то есть 3/4 пиццы, это означает, что у него есть три из четырех кусков пиццы.

Теперь, когда мы поняли, что такое дроби, давайте поговорим о том, как их умножать. Чтобы умножить дроби, вы просто умножаете числители (верхние числа) вместе и умножаете знаменатели (нижние числа) вместе.

Например, если вы хотите умножить 1/2 на 3/4, вы должны умножить 1 на 3, чтобы получить 3, и умножить на 2, чтобы получить 8. Итак, 1/2 умножить на 3/4 равно 3/8.

Примеры умножения дробей

При умножении дробей вы, по сути, умножаете числители (верхние числа) и умножаете знаменатели (нижние числа). Результатом будет новая дробь с произведением старых числителей на новый числитель и произведением старых знаменателей на новый знаменатель. Например, если вы умножите 1/2 на 3/4, ваша новая дробь будет 3/8, потому что 1 x 3 = 3, а 2 x 4 = 8.

Важно упростить дроби перед их умножением, чтобы вычисление Полегче. Например, если вас попросили умножить 2/3 на 4/5, вы сначала захотите упростить каждую дробь, найдя общий знаменатель. В этом случае общий знаменатель будет равен 15 (3 х 5 = 15 и 5 х 4 = 20). Таким образом, 2/3 станет 10/15, а 4/5 станет 12/15.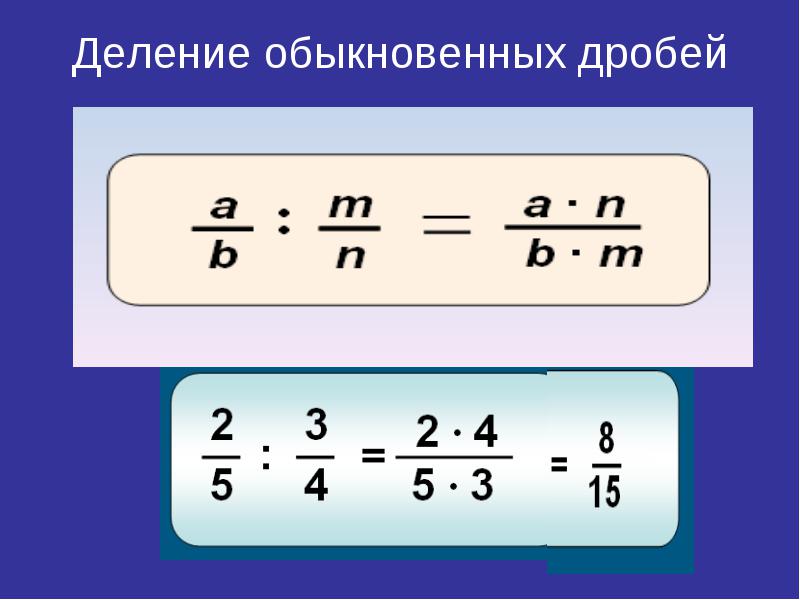 Затем вы можете умножить, чтобы получить ответ, который будет 120/225 или просто 8/15 после дальнейшего упрощения.

Заключение

Мы надеемся, что эта статья помогла вам избавиться от путаницы, связанной с умножением дробей. Помните, что при умножении дробей вы просто умножаете числители и знаменатели, чтобы найти эквивалентную дробь. Процесс довольно прост, как только вы освоите его, и с небольшой практикой вы станете профессионалом в кратчайшие сроки!

Мастер умножения дробей: руководство для начинающих

Умножение дробей

Дроби — это числа, которые используются для обозначения целого числа, разделенного на равные части. Мы можем сказать, что дробь — это часть всего или совокупность объектов. Дроби состоят из двух частей: верхней и нижней (числитель или знаменатель). Число в строке называется числителем, а число под строкой называется знаменателем. Мы используем дроби каждый день. Фракции важны, потому что они показывают вам части целого. Фракции важны для вас, они говорят нам, какую часть коллекции мы хотим.

В кратных дробях первое умножение числителей, второе умножение знаменателей, затем упрощение полученной дроби. В этой главе мы обсудим объяснение числителя и знаменателя дроби. В этом мы обсуждаем правила умножения дроби, умножения дроби с одинаковым знаменателем и умножения дроби с одинаковыми числителями. Также мы научимся умножать дроби со смешанными числами, умножать неправильные дроби, умножать дроби на числовую прямую и умножать дроби на целое число 9.0003

Хотите изучать математику? Изучите онлайн-услуги Wiingy по обучению математике, чтобы учиться у ведущих математиков и экспертов.

Объяснение числителя и знаменателя дроби

В дроби число в строке называется числителем, а число под чертой называется знаменателем. Знаменатель описывает всю часть, а числитель описывает часть, которую мы хотим.

Числитель и знаменатель представлены на рисунке, приведенном ниже, форма, обозначающая 1 из 2 частей, заштрихована, поэтому числитель равен 2, а знаменатель равен 2.  

Правила умножения дробей

В разделе «Дроби» умножением дробей называется произведение дроби на одну или несколько дробей. Кратность дробей кратна числителю к числителю. Кратный знаменатель к знаменателю.

Необходимо упростить умножение дробей. Это полезно для нас. Это значительно упрощает умножение дробей, потому что умножаемые числа становятся меньше после упрощения.

Первый метод

Существуют следующие шаги для умножения дробей.

• Умножьте числители каждой дроби друг на друга. Результат является числителем ответа.
• Умножьте знаменатель каждой дроби друг на друга. Результат является знаменателем ответа.
• Упростите или сократите дробь. Если нужно.

Умножающая дробь

   

 

   

Второй метод 

Для умножения дробей необходимо выполнить следующие шаги.

• Упростите или сократите сами дроби.
• Умножьте числители каждой дроби друг на друга.
• Умножьте знаменатели каждой дроби друг на друга.

   

Умножение дроби с одинаковым знаменателем

Умножение дроби с одинаковым знаменателем аналогично умножению других дробей.

Поясним на примере:

Умножение дроби 68 и 78

Первым способом умножаем числитель от каждой дроби друг на друга 67=42, затем умножаем знаменатель от каждой дроби друг на друга, 88=64 это даст нам продукт как 4264. Поскольку это может быть уменьшено, ответом будет 2132.

Второй способ упрощает данную дробь. Если нужно.

   

,

   

Теперь умножьте числитель на числитель и знаменатель на знаменатель.

   

Умножение дроби с другим знаменателем

Умножение дроби с другим знаменателем равносильно умножению одного и того же знаменателя.

Пример:

Умножая 26 или 34, сначала мы умножаем числитель, то есть 23=6, затем умножаем знаменатель, то есть 64=24, это даст нам произведение 624, это можно уменьшить, тогда ответ будет 14.

Умножение смешанных чисел

Умножение смешанных дробей сначала превращает смешанную дробь в неправильную дробь, затем умножает числители каждой дроби друг на друга, умножая знаменатели каждой дроби друг на друга. Затем упростите или сократите дроби.

Например:

Умножая дробь 712 или 315. По правилу сначала смешанную дробь переводим в неправильную

   

Затем умножение числителя на числитель и умножение знаменателя на знаменатель, то есть

   

 Ответом будет 24

Умножение неправильных дробей

Неправильная дробь — это когда числитель больше знаменателя или один и тот же. Неправильные дроби умножают числитель дроби и умножают знаменатели дроби, а затем уменьшают дроби.

Поясним на примере:

Умножьте дробь на 34 и 15

   

Ответ будет

   

Умножение дроби на числовой прямой

Умножение на числовой строке — это применение операции умножения на числовой строке.

Пример:

Найдите произведение дроби 35 и 12

Шаг 1. Нарисуйте числовую прямую от 0 до 1 делите на две одинаковые части, значение 2 является знаменателем второй дроби 12

Шаг 2. первая часть по номеру строка. 1 — числитель второй дроби.

Шаг 3. Разделите каждую из 2 частей на 5 равных частей. Значение 5 является знаменателем первых дробей35. Обратите внимание, что теперь всего 10 равных частей.

Шаг 4. 3 из 5 разделенных частей. 3 — числитель первой дроби.

Шаг 5. Есть 10 равных частей.

Ответ будет 310

Умножить дробь на целое число

Умножение дробей на целые числа определяется как многократное сложение, при котором дробь прибавляется столько же раз, сколько и целое число.

Чтобы умножить дробь на целое число, нужно выполнить три шага.

1. Запишите целое число со знаменателем 1.
2. Произведите числители.
3. Произведение знаменателей.
4. При необходимости упростите.

Например:

Умножение

   

и

   

По правилу записывать целое число дробью

   

 Умножить числители и знаменатели 

   

Ответ будет

   

Заключение
В этой статье мы обсудим дроби и умножение дробей. В этом уроке вы узнаете, как умножать дроби с одинаковыми числителями и знаменателями. Также обсудите кратность со смешанными числами, кратность правильной дроби, кратность дроби на числовой прямой и кратность дроби целому числу.

Решенный пример

Пример 1: Найдите произведение дробей. 67,17

   

Пример: 2. Решите это

   

   

Пример: 3. Умножьте следующие дроби.

   

   

   

будет ответом

Пример 4: Умножьте следующие дроби.

   

   

   

Пример: 5 решить это 

   

   

Хотите изучать математику? Изучите онлайн-услуги Wiingy по обучению математике, чтобы учиться у ведущих математиков и экспертов.