Вычитание ⭐ дробей с разными знаменателями: правило, способы решения
Что такое дробь? Какие бывают дроби
Определение 1Дробь является одним из вариантов записи числа в математике.
Дробь бывает:
- обыкновенная, как 12 или ab;
- десятичная, например, 0,5.
В простой записи дроби над чертой записывают делимое, то есть числитель. Под чертой расположен делитель, то есть знаменатель. Черта в дроби, разделяющая делитель и знаменатель, обозначает, что необходимо сделать, то есть выполнить деление.
Пример 1В качестве примера можно рассмотреть следующее выражение:
7÷8=78
В левой части равенства 7 является делимым, а 8 — делителем. В правой части уравнения записана дробь. Здесь 7 играет роль числителя, а 8 представляет собой знаменатель.
Основная классификация дробей:
- Числовые дроби, в состав которых входят числа, к примеру, 59, (1,5-0,2)15.
- Алгебраические дроби, состоящие из переменных, например(x+y)(x-y).

Значение алгебраических дробей определяется значением букв в выражении.
Определение 2Правильная дробь — это дробь с числителем, который по значению меньше, чем знаменатель.
Пример 2В качестве примеров правильных дробей можно привести следующие записи:
37
3145
Определение 3Неправильная дробь — это дробь с числителем, который больше, либо равен знаменателю.
Пример 3Пример неправильной дроби:
214
Данное число является смешанным. Читать его необходимо таким образом: пять целых одна четвертая. Запись числа имеет следующий вид: 514.
Использование свойств вычитания при вычитании дробей
Свойство дробей:
- В том случае, когда делитель дроби является нулем, такая дробь не имеет значения.
- Дробь равна нулю при условии, что числитель обладает нулевым значением, а знаменатель не равен нулю.
- Дроби ab и cd равны друг другу, если a×d=b×c.
- В процессе деления или умножения числителя и знаменателя дроби на одно и то же натуральное число получается равная ей дробь.

Вычитание является действием в арифметике, когда одно число отнимают от другого числа.
При вычитании справедливо использовать следующие свойства чисел:
- при вычитании суммы из числа из него допускается вычесть одно слагаемое, а затем результат уменьшить на значение второго слагаемого:
a — (b + c) = (a — b) — c,
a — (b + c) = (a — с) — b.
- скобки в выражении ((a — b) – c) не имеют смыслового значения, допустимо исключить их из выражения:
(a — b) — c = a — b — c.
- для вычитания числа из суммы необходимо воспользоваться рациональным способом решения, то есть вычесть его из одного слагаемого, а результат увеличить на значение оставшегося:
(a + b) — c = (a — c) + b, если a > c или а = с,
(a + b) — c = (b — c) + a, если b > c или b = с.
- когда из числа, в том числе, отрицательного, вычитают нуль, получается то же самое число:
a — 0 = a.
- при вычитании числа из аналогичного числа получается нуль:
a — a = 0.
Вычитание дробей с одинаковыми знаменателями
Правило 1При вычитании различных дробей с одинаковыми знаменателями требуется из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить без изменений.
Таким образом, чтобы из одной дроби вычесть дробь с аналогичным знаменателем, необходимо вычитать числители, а одинаковые знаменатели оставить прежними. Используя буквы, можно представить наглядную запись этого правила:
ac-bc=a-bc
Пример 4В качестве примеров можно решить следующие выражения:
79-59
79-59=7-59=29
1517-317
1517-317=15-317=1217
2735-1135
2735-1135=27-1135=1635
4863-2563
4863-2563=48-2563=2363
Вычитание смешанных дробей с одинаковыми знаменателями
Правило 2При вычитании смешанных дробей требуется выполнить отдельно вычитание их целых частей и отдельно вычитание их дробных частей.
В том случае, когда дробная часть уменьшаемого меньше, чем дробная часть вычитаемого, следует выполнить следующие действия:
- сначала нужно занять 1 у целой части;
- единицу необходимо представить, как дробь с числителем, равным знаменателю;
- выполнить сложение этой дроби и дробной части уменьшаемого.

Используя буквы, данное правило вычитания смешанных дробей можно записать с помощью формулы:
amc-bnc=(a-b)+m-nc
При m<n имеем:
amc-bnc=(a-1)m+cc-bnc=(a-1-b)+m+c-nc
Пример 5На нескольких примерах можно рассмотреть правило вычитания смешанных дробей:
845-235
845-235=(8-2)+4-35=615
Допустимо записать менее сложное решение:
845-235=64-35=615
527-167
527-167=42+77-167=497-167=39-67=337
1529-649
1529-649=142+99-649=14119-649=811-49=879
17323-21023
17323-21023=163+2323-21023=162623-21023=1426-1023=141623
54227-20927
54227-20927=532+2727-20927=532927-20927=3329-927=332027
Вычитание дробей с разными знаменателями
Правило 3Вычитание дробей, которые обладают разными знаменателями, выполняют путем приведения их к общему знаменателю и вычисления разности числителей.
Применение озвученного правила на практике можно рассмотреть на примере дробей, разность которых требуется определить:
29
115
В процессе решения задачи можно использовать следующий алгоритм:
- В связи с тем, что знаменатели не одинаковые, нужно определить самое маленькое общее кратное (НОК), чтобы найти единый делитель.
 Следует записать в колонку числа, составляющие в сумме значения делителей. Затем необходимо перемножить полученные значения и вычислить НОК.
Следует записать в колонку числа, составляющие в сумме значения делителей. Затем необходимо перемножить полученные значения и вычислить НОК.
НОК(9,15)=3×3×5=45
- На следующем этапе следует определить дополнительные множители. При этом НОК нужно поделить на каждый из знаменателей.
459=5
4515=3
- Числа, которые были получены в результате действий, требуется умножить на соответствующие дроби:
29=2×59×5=1045
115=1×315×3=345
- В завершении алгоритма можно выполнить вычитание заданных чисел:
1045-345=10-345=745
29-115=745
Как вычесть из обыкновенной дроби натуральное число
При вычитании натурального числа из обыкновенной дроби следует выполнить ряд действий:
- перевод натурального числа в дробь;
- перевод всех элементов выражения к единому знаменателю;
- определение разности.
Рассмотреть принцип вычитания натурального числа из обыкновенной дроби можно на примере:
8321–3
Запишем:
3=31
Таким образом:
8321-31=8321-6321=2021
В качестве альтернативного варианта решения этого примера можно записать 8321, как смешанную дробь. В процессе необходимо разделить делитель на делимое:
В процессе необходимо разделить делитель на делимое:
8321=3×2021
После вычитания получим:
3×2021–3=2021
Как вычесть обыкновенную дробь из натурального числа
Уменьшить обыкновенную дробь на натуральное число можно путем перевода данного действия к вычитанию обыкновенных дробей. Принцип решения подобной задачи можно рассмотреть на конкретном примере:
3-67
В первую очередь следует записать натуральное число, как смешанное. Для этого нужно занять единицу и перевести ее в неправильную дробь с тем же знаменателем, что у вычитаемой:
3=2×77
3=2×1
3=2×77
Таким образом:
3-67=2×77-67=2×17
Ответ прозвучит таким образом: две целых одна седьмая.
Как из единицы вычесть дробь
Если по условиям задачи из единицы нужно вычесть дробь, то в этом случае следует выполнить ряд последовательных действий:
- Перевод единицы в дробь с числителем и знаменателем, которые будут равны знаменателю вычитаемого;
- Вычитание дробей, которые обладают аналогичными знаменателями.

Используя буквы, можно записать алгоритм:
1-ab=bb-ab=b-ab
Пример 71-38=88-58=8-58=38
Если найти сумму числителя разности и числителя вычитаемого, получится в результате знаменатель вычитаемого. Таким образом, при вычитании дроби из единицы итогом является дробь с числителем, который равен разности знаменателя и числителя вычитаемой дроби, а знаменатель — остается таким же. На основании этого заключения можно упростить вычитание дроби из единицы, то есть:
1-ab=b-ab
Поэтому:
1-718=1818-718=18-718=1118
1-153200=200200-153200=200-153200=47200
1-45=5-45=15
1-316=16-316=1316
1-2531=31-2531=631
Сокращенная запись имеет вид:
1-29=79
1-911=211
1-2150=2950
Вычитание смешанного числа из целого числа
Операция вычитания из целого числа смешанного числа (смешанной дроби) выполняется по принципу, аналогичному вычитанию дроби из целого числа. При уменьшении целого числа на значение смешанного следует выполнить несколько действий:
- Перевод целого числа в смешанную дробь.
 Нужно занять единицу у целой части и перевести ее в дробь с числителем и знаменателем, которые аналогичны знаменателю дробной части вычитаемого.
Нужно занять единицу у целой части и перевести ее в дробь с числителем и знаменателем, которые аналогичны знаменателю дробной части вычитаемого. - Вычитание смешанных чисел. Вычитание вычитаемого из уменьшаемого: отдельно — целые части, отдельно — дробные.
Используя буквы, можно записать правило вычитания смешанного числа из целого:
a-bmc=(a-1)cc-bmc=(a-1-b)c-mc
Пример 88-125
8-125=755-125=65-25=635
11-378
11-378=1088-378=78-78=718
33-20211
33-20211=321111-20211=1211-211=12911
40-9750
40-9750=395050-9750=3050-750=304350
28-10514
28-10514=271414-10514=1714-514=17914
Вычитание смешанных чисел
Алгоритм действий при вычитании одного смешанного числа из другого:
- Приведение дробных частей к самому маленькому единому знаменателю.
- В том случае, когда дробная часть уменьшаемого меньше, чем дробная часть вычитаемого, следует перевести ее в вид неправильной дроби путем уменьшения на единицу целой части.
 При этом числитель уменьшаемого увеличивают на значение знаменателя.
При этом числитель уменьшаемого увеличивают на значение знаменателя. - Отдельно вычесть целые части и отдельно вычесть дробные части.
- Выполнить проверку полученной дроби на возможность сокращения.
7512-329
716-234
10-347
379-1518
В первую очередь при вычитании смешанных чисел следует найти самый маленький единый знаменатель дробных частей:
12 на 9 не делится;
12∙2=24 на 9 не делится;
12∙3=36 на 9 делится.
Таким образом, минимальный единый знаменатель этих дробей соответствует 36. Для поиска дополнительного множителя к каждой из дробей необходимо новый знаменатель разделить на старый знаменатель. Отдельно следует вычитать целые части, отдельно — дробные. В итоге получится дробная часть, которая является правильной и несокращаемой. Можно сделать вывод о том, что ответ является окончательным.
71\26-23\34=52-912=42+12-912=4512
Для вычитания смешанных чисел необходимо найти минимальный единый знаменатель для дробных частей:
6 на 4 не делится;
6∙2=12 на 4 делится.
Таким образом, 12 является минимальным единым знаменателем. Дробная часть уменьшаемого меньше по сравнению с дробной частью вычитаемого. Нужно позаимствовать единицу у целой части. В связи с тем, что знаменатель соответствует 12, единицу допустимо расписать, как 1212, то есть к числителю дробной части уменьшаемого следует прибавить знаменатель. Итоговым результатом будет дробная часть в виде правильной несократимой дроби.
10-347=977-347=637
В том случае, когда в процессе вычитания смешанных чисел в уменьшаемом нет дробной части, следует занять единицу у целой части. В связи с тем, что значение знаменателя вычитаемого соответствует 7, единицу можно представить в виде 77. В результате получена дробь, которая является правильной и не подлежит сокращению.
37\29-15\118=214-518=2918=212
Начать вычитание смешанных чисел целесообразно с определения минимального единого знаменателя. В связи с тем, что 18 делится на 9, то 18 является самым маленьким общим знаменателем. Дробь, которая получилась в результате, сокращается на 9.
Дробь, которая получилась в результате, сокращается на 9.
Как перевести смешанную дробь в обыкновенную
Смешанная дробь обладает целыми числами:
113
В обычной дроби знаменатель больше, чем числитель:
13
В действительности невозможно перевести обычную дробь в смешанную дробь и наоборот.
Неправильная дробь, в которой числитель больше по сравнению со знаменателем, имеет вид:
43
Неправильную дробь можно записать в виде смешанной дроби. Возможен и обратный перевод.
К примеру, имеется некая неправильная дробь:
173
В результате деления 17 на 3 получится 5 с каким-то остатком. Выяснять значение остатка не обязательно, так как для последующих расчетов необходимо только целое число. Затем нужно 5 умножить на 3. Из 17 следует отнять полученный результат 15. В итоге получится 2, что позволит записать 23. В результате получится 5 целых 23:
173=523
Смешанная дробь может быть преобразована в неправильную дробь. Для этого следует выполнить действия в обратном порядке:
(5×3+2)3=173
Таким образом:
523=173
Вычитание дробей.
 Вычитание дробей с разными знаменателями.
Вычитание дробей с разными знаменателями.Home » 5 класс » Вычитание дробей. Вычитание дробей с разными знаменателями.
Posted on Author admin 0
Следующее действие, которое можно выполнять с обычными дробями это вычитание. Вычитание дробей выполняется по нескольким правилам. Рассмотрим эти правила подробнее. Вычитание смешанных дробей с разными знаменателями можно посмотреть нажав на ссылку.
Вычитание дробей с одинаковым знаменателем.
Рассмотрим, пока примеры в которых уменьшаемое больше вычитаемого.
\(\frac{7}{13}-\frac{3}{13} = \frac{7-3}{13} = \frac{4}{13}\)
Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно посчитать разность числителя уменьшаемого и вычитаемого, а знаменатель оставить без изменения.
\(\frac{a}{b}-\frac{c}{b} = \frac{a-c}{b}\)
Вычитание дробей с разными знаменателями.

Чтобы выполнить вычитание дробей с разными знаменателями, нужно привести дроби к общему знаменателю, а потом применить правило вычитания дробей с одинаковыми знаменателями.
Рассмотрим пример:
Выполните вычитание дробей \(\frac{5}{6}\) и \(\frac{1}{2}\).
Общий знаменатель этих двух дробей latex]\frac{5}{6}[/latex] и \(\frac{1}{2}\) равен 6. Умножим вторую дробь \(\frac{1}{2}\) на дополнительный множитель 3.
\(\frac{5}{6}-\frac{1}{2} = \frac{5}{6}-\frac{1 \times \color{red} {3}}{2 \times \color{red} {3}} = \frac{5}{6}-\frac{3}{6} = \frac{2}{6} = \frac{1}{3}\)
Дробь \(\frac{2}{6}\) сократили и получили \(\frac{1}{3}\).
Буквенная формула вычитания дробей с разными знаменателями.
\(\bf \frac{a}{b}-\frac{c}{d} = \frac{a \times d-c \times b}{b \times d}\)
Вопросы по теме:
Как вычитать дроби с разными знаменателями?
Ответе: нужно найти общий знаменатель и далее по правилу выполнить вычитание дробей с одинаковыми знаменателями.
Как выполнить вычитание дробей с одинаковыми знаменателями?
Ответ: у числителей посчитать разность, а знаменатель оставить тот же.
Как правильно сделать проверку вычитания двух дробей?
Ответ: для проверки правильности вычитания дробей, нужно выполнить сложение вычитаемого и разности, результат их суммы будет равен вычитаемому.
\(\frac{7}{8}-\frac{3}{8} = \frac{7-3}{8} = \frac{4}{8}\)
Проверка:
\(\frac{4}{8} + \frac{3}{8} = \frac{4 + 3}{8} = \frac{7}{8}\)
Пример №1:
Выполните вычитание дробей: а) \(\frac{1}{2}-\frac{1}{2}\) б) \(\frac{10}{19}-\frac{7}{19}\)
Решение:
а) \(\frac{1}{2}-\frac{1}{2} = \frac{1-1}{2} = \frac{0}{2} = 0\)
При вычитание двух одинаковых дробей получаем нуль.
б) \(\frac{10}{19}-\frac{7}{19} = \frac{10-7}{19} = \frac{3}{19}\)
Пример №2:
Выполните вычитание и проверьте сложением: а) \(\frac{13}{21}-\frac{3}{7}\) б) \(\frac{2}{3}-\frac{1}{5}\)
Решение:
а)Найдем общий знаменатель дробей \(\frac{13}{21}\) и \(\frac{3}{7}\), он будет равен 21. Умножим вторую дробь \(\frac{3}{7}\) на 3.
Умножим вторую дробь \(\frac{3}{7}\) на 3.
\(\frac{13}{21}-\frac{3}{7} = \frac{13}{21}-\frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{13}{21}-\frac{9}{21} = \frac{13-9}{21} = \frac{4}{21}\)
Выполним проверку вычитания:
\(\frac{4}{21} + \frac{3}{7} = \frac{4}{21} + \frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{4}{21} + \frac{9}{21} = \frac{4 + 9}{21} = \frac{13}{21}\)
б) Найдем общий знаменатель дробей \(\frac{2}{3}\) и \(\frac{1}{5}\), он будет равен 15. Умножим первую дробь \(\frac{2}{3}\) на дополнительный множитель 5, вторую дробь \(\frac{1}{5}\) на 3.
\(\frac{2}{3}-\frac{1}{5} = \frac{2 \times \color{red} {5}}{3 \times \color{red} {5}}-\frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{10}{15}-\frac{3}{15} = \frac{10-3}{15} = \frac{7}{15}\)
Выполним проверку вычитания:
\(\frac{7}{15} + \frac{1}{5} = \frac{7}{15} + \frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{7}{15} + \frac{3}{15} = \frac{7 + 3}{15} = \frac{10}{15} = \frac{2}{3}\)
Category: 5 класс, Обыкновенные дроби Leave a commentКак вычитать дроби с разными знаменателями
Как вычитать дроби с разными знаменателями
Вычитание дробей с разными знаменателями — не такой простой процесс, как вычитание дробей с одинаковыми знаменателями.
Дроби представляют части целого. Дробь состоит из двух частей. Число в верхней части строки называется числителем. Он сообщает, сколько равных частей целого или набора взято. Число под чертой называется знаменателем. Он показывает общее количество равных частей, на которые делится целое, или общее количество одинаковых объектов в коллекции.
Когда целое делится на равные части, количество частей, которые мы берем, составляет дробь.
Если торт разделить на восемь равных частей, и каждый кусок торта представляет собой $\frac{1}{8}$ всего торта. Читается как «одна восьмая» или «1 на 8».
Родственные игры
Типы дробей
В зависимости от значения знаменателя существуют два типа дробей.
- Подобные дроби: Дроби с одинаковыми знаменателями известны как похожие дроби или дроби с одинаковыми знаменателями, такие как $\frac{1}{7}$ и $\frac{3}{7}; \frac{2}{5}$ и $\frac{4}{5}$.
- Непохожие дроби: Дроби с разными знаменателями известны как непохожие дроби или дроби с разными знаменателями, такие как $\frac{1}{7}$ и $\frac{3}{8}; \frac{2}{9}$ и $\frac{4}{11}$.

Операции над одинаковыми дробями достаточно просты. Предположим, нам нужно вычесть $\frac{5}{6}$ из $\frac{4}{6}$. Так как дроби одинаковые, то будут вычтены только числители, а знаменатель останется прежним, т.е. $\frac{5}{6} \;-\; \ гидроразрыва {4} {6} = \ гидроразрыва {4} {9}}$
Визуально мы представляем это так:
Когда дело доходит до дробей с разными знаменателями, это немного сложно. Как вычитать дроби с разными знаменателями? Итак, давайте научимся поэтапно вычитать дроби с разными знаменателями, используя разные методы.
Связанные листы
Методы вычитания дробей с разными знаменателями
Метод IЭто метод НОК. Основное правило вычитания дробей с разными знаменателями состоит в том, чтобы сделать знаменатели одинаковыми, найдя НОК двух знаменателей. 9{2} = 18$
Шаг 2: Преобразуйте обе дроби в одинаковые дроби, сделав знаменатели одинаковыми (т. е. найдя эквивалентные дроби). В этом примере мы получаем
В этом примере мы получаем
$\frac{5 \times 3} {6 \times 3} = \frac{15}{18}$ и $\frac{2 \times 2}{9 \times 2} = \frac{4}{18}$
Шаг 3: Вычтите числители. Знаменатель остается прежним.
$\frac{15}{18} \;-\ \frac{4}{18} = \frac{15 – 4}{18} = \frac{11}{18}$
Шаг 4: Преобразуйте полученную дробь в ее простейшую форму, если НОД числителя и знаменателя не равен 1.
В этом случае НОД $(11, 18) = 1$. Итак, это уже в самом простом виде.
Метод IIИногда бывают случаи, когда один знаменатель кратен другому знаменателю. Рассмотрим пример. Вычтем $\frac{12}{39}$ из $\frac{16}{13}$.
Умножение больших чисел может занять много времени и времени. Итак, мы будем использовать следующие шаги:
Шаг 1: Поскольку один знаменатель кратен другому, мы можем легко сделать знаменатели одинаковыми. Умножьте числитель и знаменатель $\frac{16}{13}$ на 3.
$\frac{16 \times 3}{13 \times 3} = \frac{48}{39}$
Шаг 2: Вычитание двух дробей. В этом примере мы получаем
В этом примере мы получаем
$\frac{48}{39} \;-\; \frac{12}{39} = \frac{36}{39}$
Шаг 3: Преобразуйте дробь в простейшую форму. В этом примере мы получаем
$\frac{36}{39} = \frac{12}{13}$
Метод IIIДавайте обсудим метод перекрестного умножения. Как следует из названия, мы перекрестно умножаем, как показано ниже.
Метод перекрестного умножения работает во всех случаях, но его удобно использовать, когда знаменатели являются небольшими числами.
Вычтем $\frac{5}{7}$ из $\frac{1}{2}$ перекрестным умножением.
$\frac{5}{7} \;-\; \frac{1}{2} = \frac{(5 \times 2)\;-\;(7 \times 1)}{7 \times 2} = \frac{10\;-\;7}{14 } = \frac{3}{14}$
Вычитание смешанных дробей с разными знаменателями
Смешанные числа или смешанные дроби состоят из целой части числа и дробной части. Некоторые примеры смешанных дробей с разными знаменателями: $2\frac{1}{6}$ и $5\frac{2}{5}$. Давайте разберемся, как вычитать смешанные числа с разными знаменателями, преобразовывая их в неправильные дроби. Вычитание неправильных дробей следует тем же методам, которые мы обсуждали ранее.
Вычитание неправильных дробей следует тем же методам, которые мы обсуждали ранее.
Предположим, нам нужно вычесть $2\frac{1}{6}$ из $5\frac{2}{5}$. Мы используем шаги, указанные ниже:
Шаг 1: Преобразуйте смешанные числа в неправильные дроби. В этом случае мы получаем
$2\frac{1}{6} = \frac{12 + 1}{6} = \frac{13}{6}$ и $5\frac{2}{5} = \ frac{25 + 2}{5} = \frac{27}{5}$.
Шаг 2: Найдите НОК знаменателей и сделайте знаменатели одинаковыми. В этом случае НОК $(5, 6) = 30$
$\frac{13 \times 5}{6 \times 5} = \frac{65}{30}$ и $\frac{27 \times 6 }{5 \times 6} = \frac{162}{30}$
Шаг 3: Вычтите обе дроби. В этом случае мы можем записать все шаги вместе как
$5\frac{2}{5} \;-\; 2\frac{1}{6} = \frac{27}{5}\;-\; \frac{13}{6} = \frac{162}{30} \;-\; \frac{65}{30} = \frac{162\;-\;65}{30} = \frac{97}{30}$
Шаг 4: Преобразуйте в смешанное число. В этом случае мы получаем $\frac{97}{30} = 3\frac{7}{10}$.
Вычитание дробей с разными знаменателями: визуальная модель
Рассмотрим один пример. Предположим, нам нужно вычесть $\frac{3}{8}$ из $\frac{1}{2}$.
Предположим, нам нужно вычесть $\frac{3}{8}$ из $\frac{1}{2}$.
Мы можем представить это вычитание визуально следующим образом. LCM 2 и 8 равно 8.
Итак, оба круга разделены на 8 равных частей.
$\frac{1}{2} = \frac{4}{8}$
Таким образом, для представления $\frac{1}{2}$ мы видим, что 4 части из 8 равных частей равны затененный.
Для представления $\frac{3}{8}$ круга заштрихованы 3 части из 8 частей.
Если мы уберем эти три части из первого круга, останется только 1 заштрихованная часть, которая представляет $\frac{1}{8}$.
Заключение
В этой статье мы узнали о вычитании дробей с разными знаменателями. Давайте решим несколько примеров для лучшего понимания. 9{2} \times 3 = 12$
$\frac{3 \times 3}{4 \times 3} = \frac{9}{12}$ и $\frac{5 \times 2}{6 \times 2} = \frac{10}{12}$
$\frac{5}{6}\;-\;\frac{3}{4} = \frac{10}{12}\;-\; \frac{9}{12} = \frac{10 \;-\; 9}{12} =\frac{1}{12}$
2. Найдите разницу: $\frac{1}{5}\;-\;\frac{1}{7}$ .
Решение: Здесь мы будем использовать метод перекрестного умножения.
7$ \х1 = 7$ и 5$\х1 = 5$. Кроме того, 5$ \ умножить на 7 = 35$
Итак, $\frac{1}{5}\;-\;\frac{1}{7}=\frac{7 \;-\; 5}{35} = \frac{2}{35}$
3. У Джека есть $\frac{4}{5}$ фунтов папайи. Если он даст $\frac{1}{3}$ фунтов Люси, какая часть папайи останется у Джека?
Решение: Часть папайи с Джеком $= \frac{4}{5}$
Часть папайи, которую он дал Люси $= \frac{1}{3}$
Часть папайи, оставшаяся с Джек $= \frac{4}{5} \;-\; \frac{1}{3}$
Здесь мы будем использовать перекрестное умножение
$\frac{4}{5}\;-\;\frac{1}{3} = \frac{12 \;-\; 5}{15} = \frac{7}{15}$
Доля папайи, оставшаяся у Джека $= \frac{7}{15}$
4. Найдите $\frac{3}{4} \;-\;\frac{1}{5}$.
Решение:
Нам нужно найти разность $\frac{3}{4}\;-\;\frac{1}{5}$.
Методом перекрестного умножения получаем
$\frac{15 – 4}{20} = \frac{11}{20}$
$\frac{3}{4}\;-\;\ frac{1}{5} = \frac{11}{20}$
5. Джек прыгнул на $3\frac{1}{7}$ м в соревнованиях по прыжкам в длину. Шейн прыгнул на $1\frac{2}{9}$ м. На сколько метров дольше прыгнул Джек?
Решение: Расстояние, которое преодолел Джек $= 3\frac{1}{7}$ м
Расстояние, которое преодолел Шейн $= 1\frac{2}{9}$ м
Разница $= 3\frac{1}{7}\;-\;1\frac{2}{9}$
$3\frac{1}{7}\;-\;1\frac{2}{9 } = 2\frac{2}{7}\;-\;\frac{11}{9} = \frac{198\;-\; 77}{63} = \frac{121}{63}$
Итак, Джек прыгнул дольше Шейна на $1\frac{58}{63}$ m.
Практические задачи на вычитание дробей с разными знаменателями
1
Найдите разницу: $\frac{7}{5}\;-\;\frac{5}{6}\;-\;\frac{1 {3}$.
$\frac{7}{30}$
$\frac{1}{10}$
$\frac{11}{30}$
$\frac{1}{15}$
Правильный ответ: $\frac{7}{30}$
LCM 5, 6 и $3 = 30$
$\frac{7}{5}\;-\;\frac{5}{6}\ ;-\;\frac{1}{3} = \frac{42}{30}\;-\;\frac{25}{30}\;-\;\frac{10}{30} = \frac {42\;-\;25\;-\;10}{30} = \frac{7}{30}$
2
Какой будет знаменатель результата, если $\frac{23}{49}$ вычесть из $\frac{11}{7}$?
7
49
56
343
Правильный ответ: 49
Так как 49 кратно 7, то знаменатель полученной дроби будет 49.
$\times{11} 7 \times 7} = \frac{77}{49}$
$\frac{77}{49}\;-\; \frac{23}{49} = \frac{54}{49}$
3
Расстояние от дома Алекса до его школы составляет $\frac{3}{8}$ миль. Если он уже преодолел $\frac{1}{4}$ миль пешком, сколько еще ему нужно пройти, чтобы добраться до школы?
$\frac{1}{4}$ миль
$\frac{1}{2}$ миль
$\frac{1}{16}$ миль
$\frac{1}{8} $ миль
Правильный ответ: $\frac{1}{8}$ миль
Расстояние, которое ему нужно преодолеть еще $= \frac{3}{8}\;-\;\frac{1}{4}$
НОК из 8 и $4 = 8$
$\frac{3}{8}\;-\;\frac{1}{4} = \frac{3}{8}\;-\;\frac{2 {8} =\frac{1}{8}$ миль
4
Для рецепта требуется $\frac{3}{4}$ чайной ложки сахара и $\frac{1}{5}$ чайной ложки соли. Насколько больше сахара, чем соли нужно по рецепту?
$\frac{9}{20}$
$\frac{1}{2}$
$\frac{11}{20}$
$\frac{19}{20}$
Правильный ответ: $\frac{11}{20}$
Количество сахара $= \frac{3}{4}$ чайная ложка и количество соли $= \frac{1}{5}$ чайная ложка
Разница $= \frac{3}{4}\;-\;\frac{1}{5} = \frac{15\;-\;4}{20} = \frac{11}{20}$
Часто задаваемые вопросы по Вычитание дробей с разными знаменателями
Всегда ли при вычитании двух дробей с разными знаменателями получается правильная дробь?
Нет, неправильную дробь можно получить и путем вычитания дробей с разными знаменателями. Если мы вычтем $1\frac{1}{7}$ из $3\frac{1}{2}$, мы получим $2\frac{5}{14}$.
Если мы вычтем $1\frac{1}{7}$ из $3\frac{1}{2}$, мы получим $2\frac{5}{14}$.
Как вычесть дробь из 1?
Чтобы вычесть дробь из 1, мы сначала преобразуем 1 в bb, где b — знаменатель вычитаемой дроби. Пример: $1\;-\; \frac{2}{7} = \frac{7}{7} \;-\; \frac{2}{7} = \frac{5}{7}$
В чем разница между вычитанием разнородных и одинаковых дробей?
Для вычитания разнородных дробей мы обычно используем метод перекрестного умножения или метод НОК и преобразуем разноименные дроби в одинаковые дроби, а затем вычитаем числитель. При вычитании подобных дробей мы просто вычитаем числители.
Может ли вычитание дробей с разными знаменателями дать 0?
Да, мы можем получить результат как 0, если вычесть две эквивалентные дроби. Например: $\frac{2}{6} \;-\; \frac{1}{3} = \frac{1}{3} \;-\; \frac{1}{3} = 0$
Как складывать дроби с разными знаменателями?
Мы можем складывать дроби с разными знаменателями, используя методы, которые мы использовали для вычитания. Действия по сложению дробей с разными знаменателями очень похожи. Мы просто будем использовать знак плюс вместо минуса.
Действия по сложению дробей с разными знаменателями очень похожи. Мы просто будем использовать знак плюс вместо минуса.
Как вычитать дроби с разными знаменателями
Обновлено: 06.07.2021
Учебник по тригонометрии для чайников
Исследуйте книгу Купить на Amazon
Если вы хотите вычитать дроби с разными знаменателями, у вас есть выбор методов: простой способ, быстрый прием и традиционный способ.Простой способ всегда работает, и вы должны использовать этот метод для большинства ваших потребностей в вычитании дробей. Быстрый трюк отлично экономит время, поэтому используйте его, когда можете. А что касается традиционного способа — ну, ваш учитель и другие сторонники чистоты математики, вероятно, предпочитают, чтобы вы использовали его таким образом.
Вычитание дробей простым методом
Этот способ вычитания дробей работает во всех случаях, и он прост. Вот простой способ вычитания дробей с разными знаменателями:
Вот простой способ вычитания дробей с разными знаменателями:Перемножьте две дроби и вычтите второе число из первого, чтобы получить числитель ответа.
Например, предположим, что вы хотите вычесть 6/7 – 2/5. Чтобы получить числитель, перемножьте две дроби, а затем вычтите второе число из первого числа:
.(6 5) – (2 7) = 30 – 14 = 16
После перекрестного умножения убедитесь, что вычитание выполняется в правильном порядке. (Первое число равно произведению числителя первой дроби на знаменатель второй.)
Перемножьте два знаменателя, чтобы получить знаменатель ответа.
7 5 = 35
Поставив числитель над знаменателем, вы получите ответ.
Этот пример объединяет все шаги:
При такой постановке задачи вам просто нужно упростить результат:
В этом случае вы можете уменьшить дробь:
Вычитание дробей методом быстрого трюка
Простой способ лучше всего работает, когда числители и знаменатели малы. Когда они больше, вы можете срезать путь. Прежде чем вычитать дроби с разными знаменателями, проверьте, не кратен ли один знаменатель другому. Если это так, вы можете использовать быстрый трюк:
Когда они больше, вы можете срезать путь. Прежде чем вычитать дроби с разными знаменателями, проверьте, не кратен ли один знаменатель другому. Если это так, вы можете использовать быстрый трюк:Увеличьте члены дроби с меньшим знаменателем, чтобы она имела больший знаменатель.
Например, предположим, что вы хотите найти 17/20 – 31/80. Если вы перемножите эти дроби, ваши результаты будут намного больше, чем вы хотите работать. Но, к счастью, 80 кратно 20, так что можно воспользоваться быстрым способом.
Сначала увеличьте члены 17/20 так, чтобы знаменатель был равен 80:
? = 80 ÷ 20 17 = 68
Перепишите задачу, подставив эту увеличенную версию дроби, и вычтите.
Вот задача на вычитание дробей с одинаковым знаменателем, которую решить намного проще:
В этом случае вам не придется приводить к самым низким условиям, хотя в других задачах вам, возможно, придется.
Вычитание дробей традиционным методом
Вы должны использовать традиционный способ только в крайнем случае, когда числитель и знаменатель слишком велики, чтобы использовать простой способ, и когда вы не можете использовать быстрый прием.



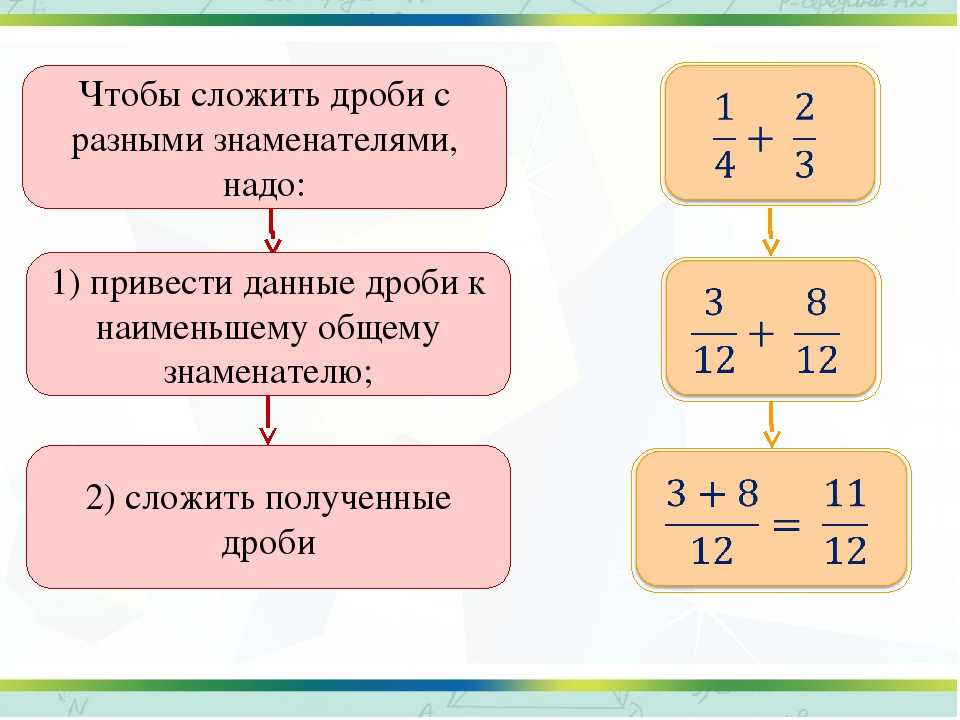 Следует записать в колонку числа, составляющие в сумме значения делителей. Затем необходимо перемножить полученные значения и вычислить НОК.
Следует записать в колонку числа, составляющие в сумме значения делителей. Затем необходимо перемножить полученные значения и вычислить НОК.
 Нужно занять единицу у целой части и перевести ее в дробь с числителем и знаменателем, которые аналогичны знаменателю дробной части вычитаемого.
Нужно занять единицу у целой части и перевести ее в дробь с числителем и знаменателем, которые аналогичны знаменателю дробной части вычитаемого. При этом числитель уменьшаемого увеличивают на значение знаменателя.
При этом числитель уменьшаемого увеличивают на значение знаменателя.