Примеры на умножения десятичных дробей на 0.1. Умножение десятичных дробей, правила, примеры, решения

Как обычные числа.

2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.

3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.

Правила умножения десятичных дробей.

1. Умножить, не обращая внимания на запятую.

2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.

Умножая десятичную дробь на натуральное число, необходимо:

1. Умножить числа, не обращая внимания на запятую;

2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.

Умножение десятичных дробей столбиком.

Рассмотрим на примере:

Записываем десятичные дроби в столбик и умножаем их как натуральные числа , не обращая внимания на запятые. Т. е. 3,11 мы рассматриваем как 311, а 0,01 как 1.

Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей. В 1-ой десятичной дроби 2 знака и во 2-рой — 2. Общее число цифр после запятых:

2 + 2 = 4

Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.

В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.

Обратите внимание:

Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.

Например :

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

Обратите внимание:

Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.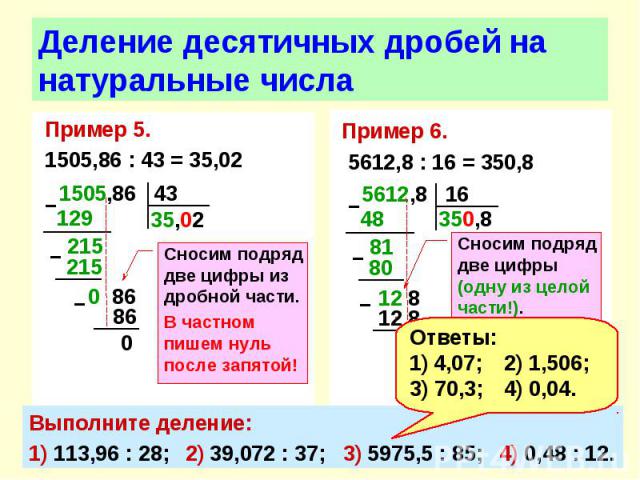

Считаем и ноль целых!

Например:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!» , – но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.

Кто в итоге прав

Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.

Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!

Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.

Что такое умножение

Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:

1. 25×3 = 75
2. 25 + 25 + 25 = 75
3. 25×3 = 25 + 25 + 25

Из этого уравнения следует вывод, что умножение — это упрощённое сложение .

Что такое ноль

Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.

Можно ли умножать на пустоту

Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

• Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
• Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
• Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0

Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.

Деление

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.

Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль – это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.

Расскажу тебе позволь,

Чтобы не делил на 0!

Режь 1 как хочешь, вдоль,

Только не дели на 0!

В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100 , 10 и др.)

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Yandex.RTB R-A-339285-1

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Пример 1

Вычислите произведение 1 , 5 и 0 , 75 .

Решение: для начала заменим десятичные дроби на обыкновенные.

Мы знаем, что 0 , 75 – это 75 / 100 , а 1 , 5 – это 15 10 . Мы можем сократить дробь и произвести выделение целой части. Полученный результат 125 1000 мы запишем как 1 , 125 .

Ответ: 1 , 125 .

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Пример 2

Умножьте одну периодическую дробь 0 , (3) на другую 2 , (36) .

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0 , (3) = 0 , 3 + 0 , 03 + 0 , 003 + 0 , 003 + . . . = 0 , 3 1 — 0 , 1 = 0 , 3 9 = 3 9 = 1 3 2 , (36) = 2 + 0 , 36 + 0 , 0036 + . . . = 2 + 0 , 36 1 — 0 , 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11

Следовательно, 0 , (3) · 2 , (36) = 1 3 · 26 11 = 26 33 .

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0 , (3) · 2 , (36) = 0 , (78) .

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см.

статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Пример 3

Вычислите произведение 5 , 382 … и 0 , 2 .

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5 , 382 … ≈ 5 , 38 . Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5 , 38 · 0 , 2 = 538 100 · 2 10 = 1 076 1000 = 1 , 076 .

Ответ: 5 , 382 … · 0 , 2 ≈ 1 , 076 .

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63 , 37 и 0 , 12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4 . Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3 , 37 · 0 , 12 = 7 , 6044 .

Пример 5

Подсчитайте, сколько будет 3 , 2601 умножить на 0 , 0254 .

Решение

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3 , 2601 · 0 , 0254 = 0 , 08280654 .

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Определение 2

Если мы умножим десятичную дробь на 0 , 1 , 0 , 01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.

Так, для умножения 45 , 34 на 0 , 1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4 , 534 .

Пример 6

Умножьте 9 , 4 на 0 , 0001 .

Решение

Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9 , 4 · 0 , 0001 = 0 , 00094 .

Ответ: 0 , 00094 .

Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0 , (18) · 0 , 01 = 0 , 00 (18) или 94 , 938 … · 0 , 1 = 9 , 4938 … . и др.

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Пример 7

Подсчитайте, сколько будет 15 · 2 , 27 .

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Ответ: 15 · 2 , 27 = 34 , 05 .

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Пример 8

Вычислите произведение 0 , (42) и 22 .

Приведем периодическую дробь к виду обыкновенной.

0 , (42) = 0 , 42 + 0 , 0042 + 0 , 000042 + . . . = 0 , 42 1 — 0 , 01 = 0 , 42 0 , 99 = 42 99 = 14 33

0 , 42 · 22 = 14 33 · 22 = 14 · 22 3 = 28 3 = 9 1 3

Итоговый результат можем записать в виде периодической десятичной дроби как 9 , (3) .

Ответ: 0 , (42) · 22 = 9 , (3) .

Бесконечные дроби перед подсчетами надо предварительно округлить.

Пример 9

Вычислите, сколько будет 4 · 2 , 145 … .

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

4 · 2 , 145 … ≈ 4 · 2 , 15 = 8 , 60 .

Ответ: 4 · 2 , 145 … ≈ 8 , 60 .

Как умножить десятичную дробь на 1000, 100, 10 и др

Умножение десятичной дроби на 10 , 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:

Определение 3

Чтобы умножить десятичную дробь на 1000 , 100 , 10 и др., нужно перенести ее запятую на 3 , 2 , 1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.

Покажем на примере, как именно это делать.

Пример 10

Выполните умножение 100 и 0 , 0783 .

Решение

Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007 , 83 ​​​​​Нули, стоящие слева, можно отбросить и записать результат как 7 , 38 .

Ответ: 0 , 0783 · 100 = 7 , 83 .

Пример 11

Умножьте 0 , 02 на 10 тысяч.

Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0 . В итоге получилось 0 , 02000 ,перенесем запятую и получим 00200 , 0 . Игнорируя нули слева, можем записать ответ как 200 .

Ответ: 0 , 02 · 10 000 = 200 .

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Пример 12

Вычислите произведение 5 , 32 (672) на 1 000 .

Решение: первым делом мы запишем периодическую дробь как 5 , 32672672672 … , так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326 , 726726 … Заключим период в скобки и запишем ответ как 5 326 , (726) .

Ответ: 5 , 32 (672) · 1 000 = 5 326 , (726) .

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Пример 13

Умножьте 0 , 4 на 3 5 6

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0 , 4 = 4 10 = 2 5 .

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1 , 5 (3) .

Ответ: 1 , 5 (3) .

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Пример 14

Вычислите произведение 3 , 5678 . . . · 2 3

Решение

Второй множитель мы можем представить как 2 3 = 0 , 6666 …. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3 , 568 и 0 , 667 . Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2 , 379856 ≈ 2 , 380 .

Ответ: 3 , 5678 . . . · 2 3 ≈ 2 , 380

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Переходим к изучению следующего действия с десятичными дробями , сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.

Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .

Навигация по странице.

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей . Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные .

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Пример.

Выполните умножение десятичных дробей 1,5 и 0,75 .

Решение.

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то . Можно провести сокращение дроби , после чего выделить целую часть из неправильной дроби , а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .

Ответ:

1,5·0,75=1,125 .

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в .

Рассмотрим пример умножения периодических десятичных дробей.

Пример.

Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .

Решение.

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда . Можно полученную обыкновенную дробь перевести в десятичную дробь :

Ответ:

0,(3)·2,(36)=0,(78) .

Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Пример.

Выполните умножение десятичных дробей 5,382… и 0,2 .

Решение.

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .

Ответ:

5,382…·0,2≈1,076 .

Умножение десятичных дробей столбиком

Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел .

Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:

• не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
• в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Рассмотрим примеры умножения десятичных дробей столбиком.

Пример.

Выполните умножение десятичных дробей 63,37 и 0,12 .

Решение.

Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:

Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12 ). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:

В итоге имеем 3,37·0,12=7,6044 .

Ответ:

3,37·0,12=7,6044 .

Пример.

Вычислите произведение десятичных дробей 3,2601 и 0,0254 .

Решение.

Выполнив умножение столбиком без учета запятых, получаем следующую картину:

Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:

На этом умножение десятичных дробей столбиком закончено.

Ответ:

3,2601·0,0254=0,08280654 .

Умножение десятичных дробей на 0,1, 0,01, и т.д.

Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.

Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.

Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .

Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Пример.

Вычислите произведение 15·2,27 .

Решение.

Проведем умножение натурального числа на десятичную дробь столбиком:

Ответ:

15·2,27=34,05 .

При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Пример.

Умножьте десятичную дробь 0,(42) на натуральное число 22 .

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .

Ответ:

0,(42)·22=9,(3) .

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Пример.

Выполните умножение 4·2,145… .

Решение.

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .

Ответ:

4·2,145…≈8,60 .

Умножение десятичной дроби на 10, 100, …

Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.

Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.

Пример.

Умножьте десятичную дробь 0,0783 на 100 .

Решение.

Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .

Ответ:

0,0783·100=7,83 .

Пример.

Выполните умножение десятичной дроби 0,02 на 10 000 .

Решение.

Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .

Умножение десятичных дробей примеры для решения. Видеоурок «Умножение десятичных дробей

1 урок

1. Организационный момент

Проверить готовность учащихся к уроку.

(Наличие учебных принадлежностей к уроку)

I .Актуализация знаний

Устная работа.

Цель: Систематизировать предыдущие знания,необходимые при изучении нового материала.

Учащиеся устно выполняют задания на умножение десятичной дроби на натуральное число и на умножение обыкновенных дробей. .

Вычислите:

Затем учитель задает вопрос:Сформулируйте как выполнить умножение десятичной дроби на натуральное число?Учащиеся вспоминают определение.Сообщаются тема урока и цели урока.

II .Одновременное разделение на группы и на пары.

Учащиеся выбирают по одной карточке со стола учителя. На одних из них записаны примеры на действия с обыкновенными дробями, а на других соответствующие ответы. Они должны будут найти соответствия, и разделится на пары.Если же будут работать в группах,то разделятся таким образом:

1 группа- это учащиеся, которым попались примеры,2 группа- это те учащиеся, у которых окажутся соответствующие ответы.(см.Приложение №1)

III .Изучение новогоматериала

Цель: Познакомить учащихся с новым материалом.

Объяснение учителя:

3.1.Групповая работа.

Цель: Самостоятельно решив задачу двумя способами сформулировать правилоумножения десятичной дроби на десятичную дробь.

Учащимся предлагается следующая задача:

Длина прямоугольника 6,3см, ширина 2,8см. Найдите его площадь.

Каждая группа выполняет данное задание по указанному ей предложенному способу.

Способ 1: Записать числовые значения измерений прямоугольника в виде натуральных чисел, выразив в миллиметрах. Вычислять площадь и полученный ответ выразить в квадратных сантиметрах.

Способ 2: Представить измерения прямоугольника в виде обыкновенных дробей, найти площадь, перемножив обыкновенные дроби и перевести в десятичную дробь.

Затем представитель каждой группы объясняет решение данного примера учащимся другой группы у доски. Учащиеся обмениваются мнениями и из результатов решения задачи делают вывод:

Сколько десятичных знаков в множителях, столько же и десятичных знаков в их произведении.

Затем учитель комментирует работу групп, подводит итоги и делает вывод.

Учащиеся записывают в тетрадях для конспектов.

Вывод: Чтобы умножить десятичные дроби надо:

1)выполнить умножение, не обращая внимания на запятые;

2)отделить в полученном произведении запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

3.2 Разбор различных примеров.

Цель: Дальнейшая отработка умений выполнять умножение десятичных дробей.

Умножим данные числа не обращая внимания на запятые, получим в произведении число 20 496. В двух множителях после запятой всего имеется три десятичных знака. Поэтому в произведении нужно отделить справа три цифры.Итак, произведение равно 20,496.

VI .Решение задач

Цель: Отработка умений применять правило умножения десятичных дробей при решении задач.

Учащиеся работают в парах.

Выполняют задания: №812 ,№814

VII . Подведение итогов урока. Рефлексия

Цель: Выяснить достигли ли учащиеся целей урока,чтобы учесть при планировании следующего урока.

Действия ученика : Обобщив свои знания, отвечают на вопросы.

Вопросы для подведения итогов .(Устно).

1. Чему мы сегодня научились на уроке?

2. Какую цель мы сегодня на уроке изучили?

3. Повторим правило умножения десятичных дробей.

В конце урока учащиеся дают рефлексию:

Урок понравился / не понравился

Цель урока понял / не понял

Что узнал, чему научился______________________________

Что не понял полностью _______________________________

Над чем надо поработать_______________________________

Оценивание: Учитель поощряет ответы и работы учеников.

Задание на дом: №813 № 815

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока:

• В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
• Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
• Воспитывать интерес к математике, активность, мобильность, умение общаться.

Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.

Ход урока

1. Организационный момент.
2. Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
3. Объяснение нового материала.
4. Задание на дом.
5. Математическая физкультминутка.
6. Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
7. Выставление оценок.

2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.

Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом на сложение и вычитание десятичных дробей, в результате решения которого ребята получают следующий код 523914687. )

5	2	3	9	1	4	6	8	7
1	2	3	4	5	6	7	8	9

Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”

Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с вами рассмотрим умножение десятичных чисел на натуральное число. Умножение десятичной дроби на натуральное число можно рассматривать как сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно этому натуральному числу. Например: 5,21·3 = 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3 = 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное число, получим

И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение. На основании сходных моментов этих способов, сделаем вывод.

Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.

На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630 . Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:

Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.

Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:

Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.

Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50% .

4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.

5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.

6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:

Задания появляются на компьютере. По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.

№ 1031 Вычисли:

Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.

№ 1035. Задача.

Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.

Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.

№ 1033. Запиши десятичные дроби в процентах.

0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.

Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово Молодцы .

Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.

Учитель подводит итоги урока и выставляет оценки.

§ 1 Применение правило умножения десятичных дробей

В этом уроке Вы познакомитесь и научитесь применять правило умножения десятичных дробей и правило умножения десятичной дроби на разрядную единицу, такую как 0,1, 0,01 и т.д. Кроме того, мы рассмотрим свойства умножения при нахождении значений выражений, содержащих десятичные дроби.

Решим задачу:

Скорость движения автомобиля составляет 59,8 км/ч.

Какой путь преодолеет автомобиль за 1,3 часа?

Как известно, чтобы найти путь, необходимо скорость умножить на время, т.е. 59,8 умножить на 1,3.

Давайте запишем числа в столбик и начнем их перемножать, не замечая запятых: 8 умножить на 3, будет 24, 4 пишем 2 в уме, 3 умножить на 9 это 27, да еще плюс 2, получаем 29, 9 пишем, 2 в уме. Теперь 3 умножаем на 5, будет 15 и еще прибавляем 2, получаем 17.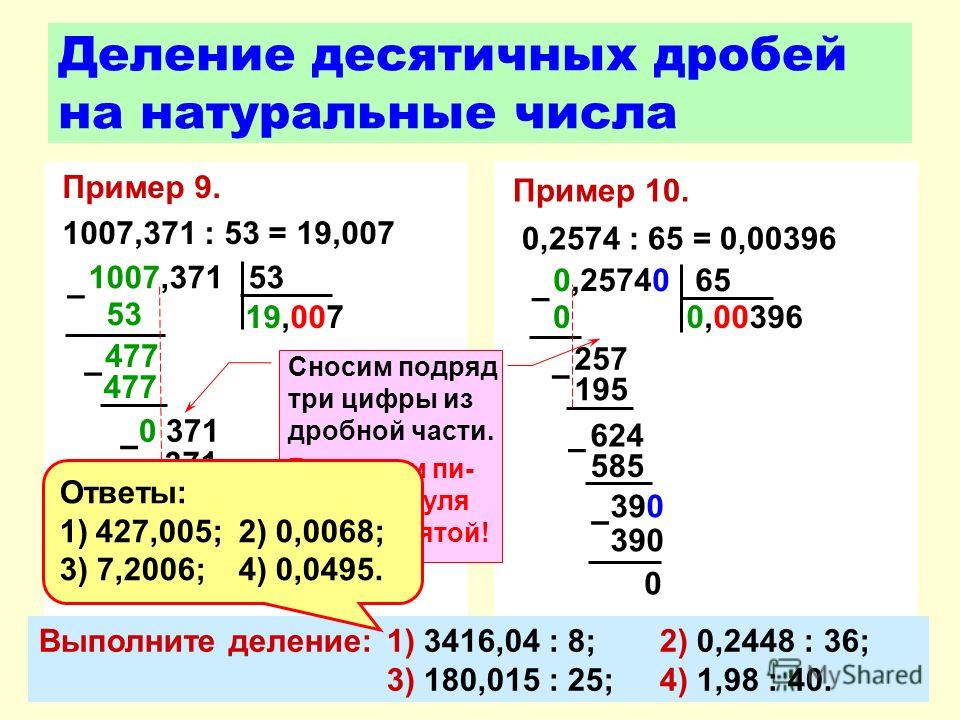

Переходим ко второй строке: 1 умножить на 8, будет 8, 1 умножить на 9, получаем 9, 1 умножить на 5, получаем 5, складываем эти две строчки, получаем 4, 9+8 равно 17, 7 пишем 1 в уме, 7+9 это 16 да еще 1, будет 17, 7 пишем 1 в уме, 1+5 да еще 1 получаем 7.

А теперь посмотрим, сколько знаков после запятых стоит в обеих десятичных дробях! В первой дроби одна цифра после запятой и во второй дроби одна цифра после запятой, всего два знака. Значит, справа в полученном результате нужно отсчитать две цифры и поставить запятую, т.е. будет 77,74. Итак, при умножении 59,8 на 1,3 получили 77,74. Значит ответ в задаче 77,74 км.

Таким образом, чтобы перемножить две десятичные дроби надо:

Первое: выполнить умножение, не обращая внимания на запятые

Второе: в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

Если же цифр в полученном произведении меньше, чем надо отделить запятой, то тогда впереди необходимо приписать один или несколько нулей.

Например: 0,145 умножить на 0,03 у нас в произведении получается 435, а запятой необходимо отделить 5 цифр справа, поэтому мы приписываем перед цифрой 4 еще 2 нуля, ставим запятую и приписываем еще один нуль. Получаем ответ 0,00435.

§ 2 Свойства умножения десятичных дробей

При умножении десятичных дробей сохраняются все те же свойства умножения, что действуют для натуральных чисел. Давайте выполним несколько заданий.

Задание №1:

Решим данный пример, применив распределительное свойство умноженияотносительно сложения.

5,7 (общий множитель) вынесем за скобку, в скобках останется 3,4 плюс 0,6. Значение этой суммы равно 4, и теперь 4 надо умножить на 5,7, получаем 22,8.

Задание № 2:

Применим переместительное свойство умножения.

2,5 сначала умножим на 4, получим 10 целых, а теперь нужно 10 умножить на 32,9 и получаем 329.

Кроме этого, при умножении десятичных дробей можно заметить следующее:

При умножении числа на неправильную десятичную дробь, т. е. большую или равную 1, оно увеличивается или не изменяется, например:

При умножении числа на правильную десятичную дробь, т.е. меньшую 1, оно уменьшается, например:

Давайте решим пример:

23,45 умножить на 0,1.

Мы должны 2 345 умножить на 1 и отделить три знака запятой справа, получим 2,345.

Теперь давайте решим другой пример: 23,45 разделить на 10, мы должны перенести запятую влево на один знак, потому что 1 ноль в разрядной единице, получим 2,345.

Из этих двух примеров можно сделать вывод, что умножить десятичную дробь на 0,1, 0,01, 0,001 и т. д. это значит разделить число на 10, 100, 1000 и т.д., т.е. надо в десятичной дроби перенести запятую влево на столько знаков, сколько нулей стоит перед 1 во множителе.

Используя полученное правило, найдем значения произведений:

13,45 умножить на 0,01

перед цифрой 1 стоит 2 нуля, поэтому перенесем запятую влево на 2 знака, получим 0,1345.

0,02 умножить на 0,001

перед цифрой 1 стоит 3 нуля, значит переносим запятую на три знака влево, получаем 0,00002.

Таким образом, в этом уроке Вы научились перемножать десятичные дроби. Для этого нужно всего лишь выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе. Кроме того, познакомились с правилом умножения десятичной дроби на 0,1, 0,01 и т.д., а также рассмотрели свойства умножения десятичных дробей.

Список использованной литературы:

1. Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
2. Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
3. Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
4. Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
5. Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
6. Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009

Умножение десятичных дробей происходит в три этапа.

Десятичные дроби записывают в столбик и умножают как обыкновенные числа.

Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.

В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.

Как умножать десятичные дроби

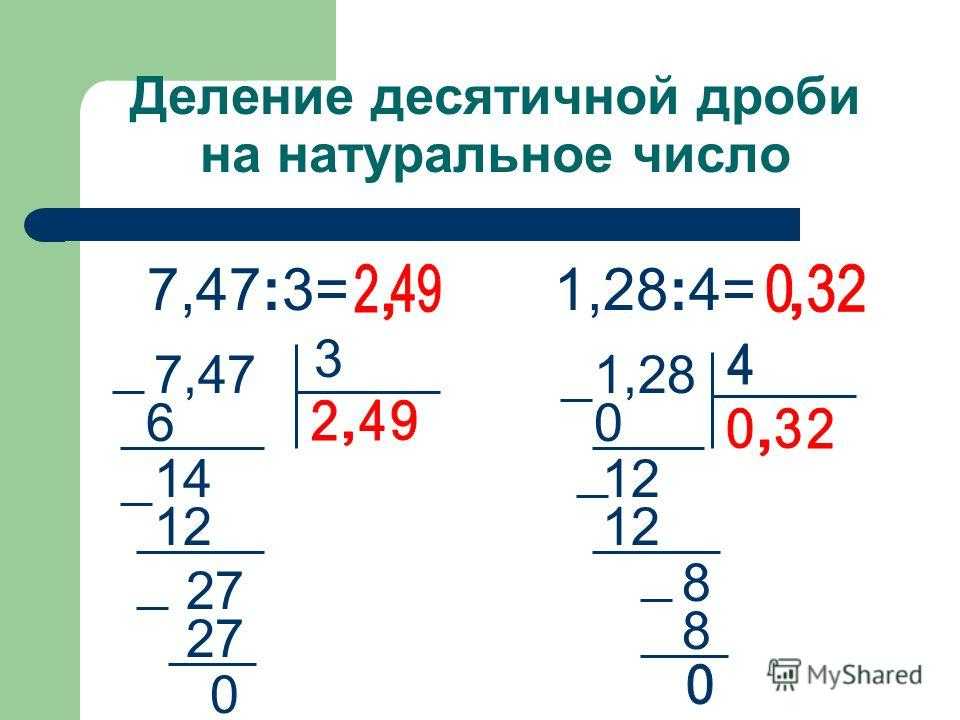
Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311 , а 0,01 как 1 .

Получили 311 . Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй — два. Общее количество цифр после запятых:

Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.

У нас не хватает одной цифры, поэтому приписываем слева один ноль.

При умножении любой десятичной дроби на 10; 100; 1000 и т.д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.

70,1 · 10 = 701

0,023 · 100 = 2,3

5,6 · 1 000 = 5 600

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.

Считаем и ноль целых!

• 12 · 0,1 = 1,2
• 0,05 · 0,1 = 0,005
• 1,256 · 0,01 = 0,012 56

Чтобы понять, как умножать десятичные дроби, рассмотрим конкретные примеры.

Правило умножения десятичных дробей

1) Умножаем, не обращая внимания на запятую.

2) В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе.

Найти произведение десятичных дробей:

Чтобы умножить десятичные дроби, умножаем, не обращая внимания на запятые. То есть мы умножаем не 6,8 и 3,4, а 68 и 34. В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе. В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.

Умножаем десятичные дроби, не принимая во внимание запятую. То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.

Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые. То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.

Умножение десятичной дроби на натуральное число выполняется аналогично. Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.

Умножение десятичных дробей начинаем с того, что умножаем натуральные числа, так как на запятые не обращаем внимания. После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.

И еще пара примеров на умножение десятичных дробей:

www.for6cl.uznateshe.ru

Умножение десятичных дробей, правила, примеры, решения.

Переходим к изучению следующего действия с десятичными дробями, сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей.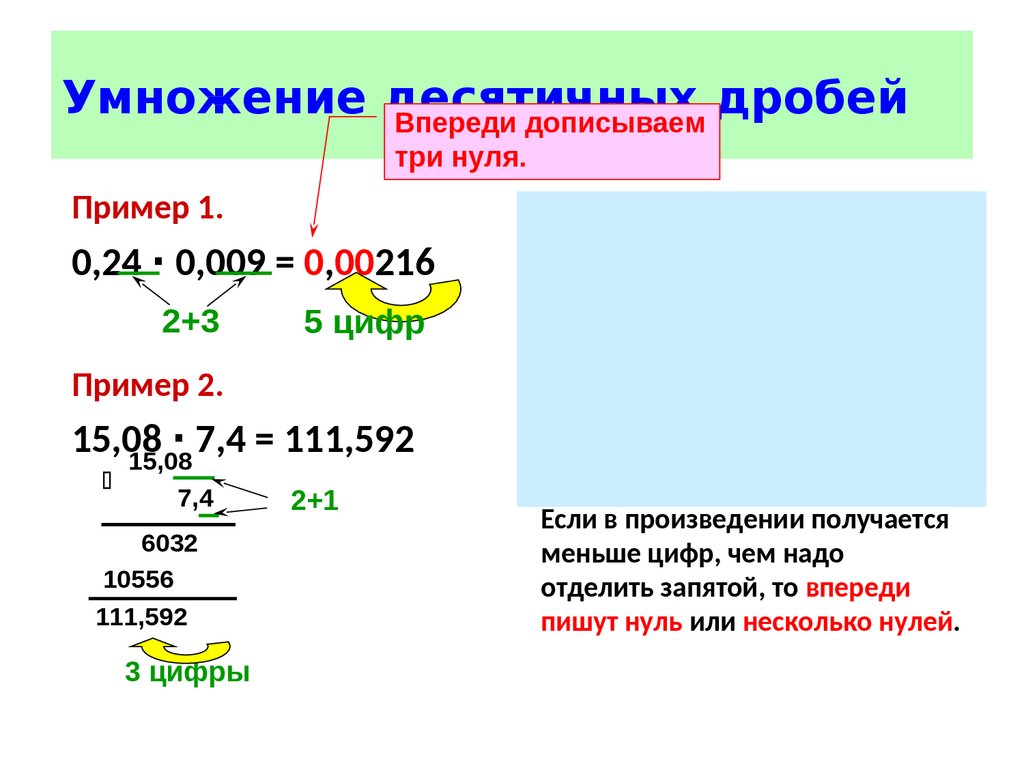 После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.

Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .

Навигация по странице.

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей. Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные.

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Выполните умножение десятичных дробей 1,5 и 0,75 .

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то. Можно провести сокращение дроби, после чего выделить целую часть из неправильной дроби, а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в следующем пункте.

Рассмотрим пример умножения периодических десятичных дробей.

Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .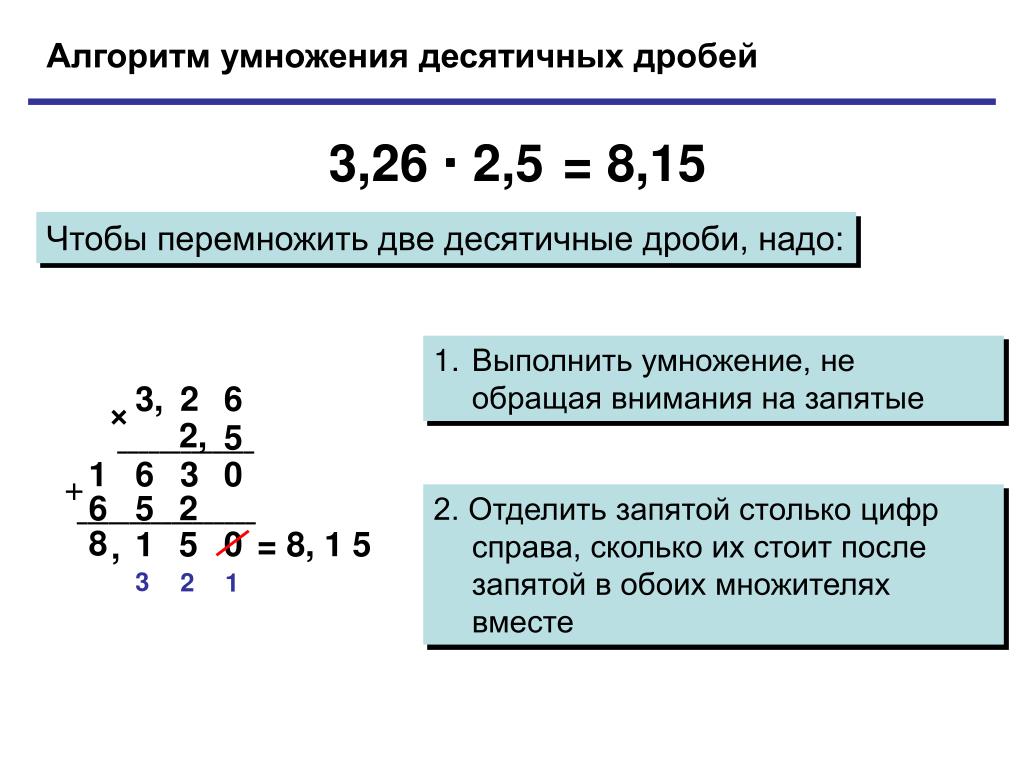

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда. Можно полученную обыкновенную дробь перевести в десятичную дробь:


Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Выполните умножение десятичных дробей 5,382… и 0,2 .

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .

Умножение десятичных дробей столбиком

Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел.

Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:

• не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
• в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Рассмотрим примеры умножения десятичных дробей столбиком.

Выполните умножение десятичных дробей 63,37 и 0,12 .

Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:


Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:


В итоге имеем 3,37·0,12=7,6044 .

Вычислите произведение десятичных дробей 3,2601 и 0,0254 .

Выполнив умножение столбиком без учета запятых, получаем следующую картину:


Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:


На этом умножение десятичных дробей столбиком закончено.

Умножение десятичных дробей на 0,1, 0,01, и т.д.

Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.

Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.

Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .

Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Вычислите произведение 15·2,27 .

Проведем умножение натурального числа на десятичную дробь столбиком:


При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Умножьте десятичную дробь 0,(42) на натуральное число 22 .

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Выполните умножение 4·2,145… .

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .

Умножение десятичной дроби на 10, 100, …

Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.

Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.

Умножьте десятичную дробь 0,0783 на 100 .

Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .

Выполните умножение десятичной дроби 0,02 на 10 000 .

Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .

Озвученное правило справедливо и для умножения бесконечных десятичных дробей на 10, 100, … При умножении периодических десятичных дробей нужно быть аккуратными с периодом дроби, которая является результатом умножения.

Умножьте периодическую десятичную дробь 5,32(672) на 1 000 .

Перед умножением распишем периодическую десятичную дробь как 5,32672672672… , это нам позволит не допустить ошибки. Теперь перенесем запятую вправо на 3 знака, имеем 5 326,726726… . Таким образом, после умножения получается периодическая десятичная дробь 5 326,(726) .

5,32(672)·1 000=5 326,(726) .

При умножении бесконечных непериодических дробей на 10, 100, … нужно предварительно провести округление бесконечной дроби до некоторого разряда, после чего проводить умножение.

Умножение десятичной дроби на обыкновенную дробь или смешанное число

Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение.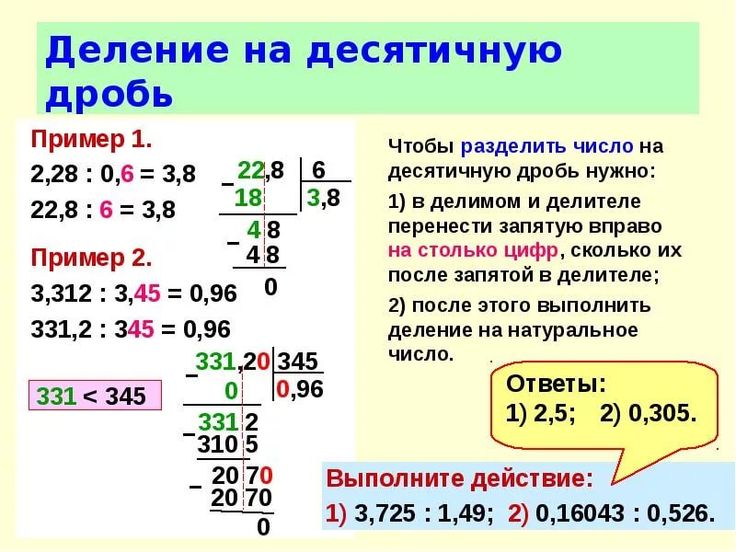

Проведите умножение десятичной дроби 0,4 на смешанное число.

Так как 0,4=4/10=2/5 и, то. Полученное число можно записать в виде периодической десятичной дроби 1,5(3) .

При умножении бесконечной непериодической десятичной дроби на обыкновенную дробь или смешанное число, обыкновенную дробь или смешанное число следует заменить десятичной дробью, после чего провести округление умножаемых дробей и закончить вычисления.

Так как 2/3=0,6666… , то. После округления умножаемых дробей до тысячных, приходим к произведению двух конечных десятичных дробей 3,568 и 0,667 . Выполним умножение в столбик:


Полученный результат следует округлить до тысячных, так как умножаемые дроби были взяты с точностью до тысячных, имеем 2,379856≈2,380 .

www.cleverstudents.ru

29. Умножение десятичных дробей. Правила


Найдем площадь прямоугольника со сторонами равными
1,4 дм и 0,3 дм. Переведем дециметры в сантиметры:

1,4 дм = 14 см; 0,3 дм = 3 см.

Теперь вычислим площадь в сантиметрах.

S = 14 3 = 42 см 2 .

Переведем квадратные сантиметры в квадратные
дециметры:

д м 2 = 0,42 д м 2 .

Значит, S = 1,4 дм 0,3 дм = 0,42 дм 2 .

Умножение двух десятичных дробей выполняется так:
1) числа перемножаются без учета запятых.
2) запятая в произведении ставится так, чтобы отделить справа
столько же знаков, сколько отделено в обоих множителях
вместе взятых. Например:

1,1 0,2 = 0,22 ; 1,1 1,1 = 1,21 ; 2,2 0,1 = 0,22 .

Примеры умножения десятичных дробей в столбик:

Вместо умножения любого числа на 0,1 ; 0,01 ; 0,001 ,
можно разделить это число на 10 ; 100 ; или 1000 соответственно.
Например:

22 0,1 = 2,2 ; 22: 10 = 2,2 .

При умножении десятичной дроби на натуральное число, мы должны:

1) перемножить числа, не обращая внимания на запятую;

2) в полученном произведении поставить запятую так, чтобы справа
от нее было столько же цифр, сколько в десятичной дроби.

Найдем произведение 3,12 10 . По указанному выше правилу
сначала умножаем 312 на 10 . Получим: 312 10 = 3120 .
А теперь отделяем запятой две цифры справа и получаем:

3,12 10 = 31,20 = 31,2 .

Значит, при умножении 3,12 на 10 мы перенесли запятую на одну
цифру вправо. Если умножить 3,12 на 100 , то получим 312 , то есть
запятую перенесли на две цифры вправо.

3,12 100 = 312,00 = 312 .

При умножении десятичной дроби на 10 , 100 , 1000 и т. д., надо
в этой дроби перенести запятую вправо на столько знаков, сколько нулей
стоит в множителе. Например:

0,065 1000 = 0065, = 65 ;

2,9 1000 = 2,900 1000 = 2900, = 2900 .

Задачи на тему «Умножение десятичных дробей»

school-assistant.ru

Сложение, вычитание, умножение и деление десятичных дробей

Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.

Правило. производится по разрядам целой и дробной части как натуральных чисел.

При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).

Сложение и вычитание десятичных дробей в строку:

243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651

843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589

Сложение и вычитание десятичных дробей в столбик:

Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток. Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.

Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.

Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).

При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:

Запись умножения десятичных дробей в столбик:

Запись деления десятичных дробей в столбик:

Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.

Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.

Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

5 класс. Математика. Десятичные дроби — Умножение и деление десятичных дробей

Комментарии преподавателя

Упраж­не­ние. Как умно­жить число 25,78 на 10?

Де­ся­тич­ная за­пись дан­но­го числа – это со­кра­щен­ная за­пись суммы. Необ­хо­ди­мо рас­пи­сать ее более по­дроб­но:

Таким об­ра­зом, нужно умно­жить сумму. Для этого можно про­сто умно­жить каж­дое сла­га­е­мое:

Вы­хо­дит, что.

Можно сде­лать вывод, что умно­жить де­ся­тич­ную дробь на 10 очень про­сто: нужно за­пя­тую сдви­нуть впра­во на одну по­зи­цию.

Упраж­не­ние. Умно­жить 25,486 на 100.

Умно­жить на 100 – это то же самое, что и умно­жить два раза на 10. Иными сло­ва­ми, необ­хо­ди­мо сдви­нуть за­пя­тую впра­во два раза:

Деление на 10, 100…

Упраж­не­ние. Раз­де­лить 25,78 на 10.

Как и в преды­ду­щем слу­чае, необ­хо­ди­мо пред­ста­вить число 25,78 в виде суммы:

Так как нужно по­де­лить сумму, то это эк­ви­ва­лент­но де­ле­нию каж­до­го сла­га­е­мо­го:

Итак, .

Вы­хо­дит, чтобы раз­де­лить на 10, нужно за­пя­тую сдви­нуть влево на одну по­зи­цию. На­при­мер:

Упраж­не­ние. Раз­де­лить 124,478 на 100.

Раз­де­лить на 100 – это то же самое, что два раза раз­де­лить на 10, по­это­му за­пя­тая сдви­га­ет­ся влево на 2 по­зи­ции:

Правило умножения и деления на 10, 100,..

Если де­ся­тич­ную дробь нужно умно­жить на 10, 100, 1000 и так далее, нужно за­пя­тую сдви­нуть впра­во на столь­ко по­зи­ций, сколь­ко нулей у мно­жи­те­ля.

И на­о­бо­рот, если де­ся­тич­ную дробь нужно по­де­лить на 10, 100, 1000 и так далее, нужно за­пя­тую сдви­нуть влево на столь­ко по­зи­ций, сколь­ко нулей у мно­жи­те­ля.

Примеры, когда необходимо перенести запятую, а цифр уже не осталось.

Умно­жить на 100 зна­чит сдви­нуть за­пя­тую впра­во на две по­зи­ции.

После сдви­га можно об­на­ру­жить, что после за­пя­той уже нет цифр, а это зна­чит, что дроб­ная часть от­сут­ству­ет. Тогда и за­пя­тая не нужна, число по­лу­чи­лось целое.

При­мер 2

Сдви­гать нужно на 4 по­зи­ции впра­во. Но цифр после за­пя­той всего две. Стоит вспом­нить, что для дроби 56,14 есть эк­ви­ва­лент­ная за­пись.

Те­перь умно­жить на 10 000 не со­став­ля­ет труда:

Если не очень по­нят­но, по­че­му можно до­пи­сать два нуля к дроби в преды­ду­щем при­ме­ре, то до­пол­ни­тель­ное видео по ссыл­ке смо­жет по­мочь в этом.

Эк­ви­ва­лент­ные де­ся­тич­ные за­пи­си

За­пись 52 озна­ча­ет сле­ду­ю­щее:

Если впе­ре­ди по­ста­вить 0, по­лу­чим за­пись 052. Эти за­пи­си эк­ви­ва­лент­ны.

Можно ли по­ста­вить два нуля впе­ре­ди? Да, эти за­пи­си эк­ви­ва­лент­ны.

Те­перь по­смот­рим на де­ся­тич­ную дробь:

Если при­пи­сать ноль, то по­лу­ча­ет­ся:

Эти за­пи­си эк­ви­ва­лент­ны. Ана­ло­гич­но можно при­пи­сать несколь­ко нулей.

Таким об­ра­зом, к лю­бо­му числу можно при­пи­сать несколь­ко нулей после дроб­ной части и несколь­ко нулей перед целой ча­стью. Это будут эк­ви­ва­лент­ные за­пи­си од­но­го и того же числа.

При­мер 3

Так как про­ис­хо­дит де­ле­ние на 100, то необ­хо­ди­мо сдви­нуть за­пя­тую на 2 по­зи­ции влево. Слева от за­пя­той не оста­лось цифр. Целая часть от­сут­ству­ет. Такую за­пись часто ис­поль­зу­ют про­грам­ми­сты. В ма­те­ма­ти­ке же, если целой части нет, то ста­вят ноль вме­сто нее.

При­мер 4

Сдви­гать нужно влево на три по­зи­ции, но по­зи­ций всего две. Если перед чис­лом на­пи­сать несколь­ко нулей, то это будет эк­ви­ва­лент­ная за­пись.

То есть при сдви­ге влево, если цифры кон­чи­лись, необ­хо­ди­мо вос­пол­нить их ну­ля­ми.

При­мер 5

В дан­ном слу­чае стоит пом­нить, что за­пя­тая все­гда стоит после целой части. Тогда:

Умножение и деление на 0,1,  0,01…

Умно­же­ние и де­ле­ние на числа 10, 100, 1000 – очень про­стая про­це­ду­ра. Точно так же дело об­сто­ит и с чис­ла­ми 0,1, 0,01, 0,001.

При­мер. Умно­жить 25,34 на 0,1.

Вы­пол­ним за­пись де­ся­тич­ной дроби 0,1 в виде обык­но­вен­ной. Но умно­жить на  – то же самое, что раз­де­лить на 10. По­это­му необ­хо­ди­мо сдви­нуть за­пя­тую на 1 по­зи­цию влево:

Ана­ло­гич­но умно­жить на 0,01 – это раз­де­лить на 100:

При­мер. 5,235 раз­де­лить на 0,1.

Ре­ше­ние дан­но­го при­ме­ра стро­ит­ся ана­ло­гич­ным об­ра­зом: 0,1 вы­ра­жа­ет­ся в виде обык­но­вен­ной дроби, а де­лить на  – это все равно, что умно­жить на 10:

То есть чтобы по­де­лить на 0,1, нужно за­пя­тую сдви­нуть впра­во на одну по­зи­цию, что рав­но­силь­но умно­же­нию на 10.

Правило умножения и деления на 0,1, 0,01…

Умно­жить на 10 и раз­де­лить на 0,1 – это одно и то же. За­пя­тую нужно сдви­нуть впра­во на 1 по­зи­цию.

Ана­ло­гич­но для 100, 1000 и так далее:

Раз­де­лить на 10 и умно­жить на 0,1 – это одно и то же. За­пя­тую нужно сдви­нуть впра­во на 1 по­зи­цию:

Ана­ло­гич­но для 100, 1000 и так далее:

123,456:0,001 = 123 456

Пра­ви­ло де­ле­ния де­ся­тич­ных дро­бей на на­ту­раль­ные числа.

Че­ты­ре оди­на­ко­вых иг­руш­ки в сумме стоят 921 рубль 20 ко­пе­ек. Сколь­ко стоит одна иг­руш­ка (см. Рис. 1)?

Рис. 1. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

Для на­хож­де­ния сто­и­мо­сти одной иг­руш­ки необ­хо­ди­мо раз­де­лить дан­ную сумму на че­ты­ре. Пе­ре­ве­дём сумму в ко­пей­ки:

 

Ответ: сто­и­мость одной иг­руш­ки 23030 ко­пе­ек, то есть 230 руб­лей 30 ко­пе­ек, или 230,3 рубля.

Можно ре­шить дан­ную за­да­чу не пе­ре­во­дя рубли в ко­пей­ки, то есть раз­де­лить де­ся­тич­ную дробь на на­ту­раль­ное число: .

Чтобы раз­де­лить де­ся­тич­ную дробь на на­ту­раль­ное число, нужно де­лить дробь на это число, как делят на­ту­раль­ные числа, и по­ста­вить в част­ном за­пя­тую тогда, когда за­кон­чит­ся де­ле­ние целой части.

Делим в стол­бик так, как делят на­ту­раль­ные числа. После того как сно­сим цифру 2 (число де­ся­тых – пер­вая цифра после за­пя­той в за­пи­си де­ли­мо­го 921,20), в част­ном ста­вим за­пя­тую и про­дол­жа­ем де­ле­ние:

Ответ: 230,3 рубля.

Пример

Делим в стол­бик так, как делят на­ту­раль­ные числа. После того как сно­сим цифру 6 (число де­ся­тых – цифра после за­пя­той в за­пи­си де­ли­мо­го 937,6), в част­ном ста­вим за­пя­тую и про­дол­жа­ем де­ле­ние:

Ответ: .

Пример

Если де­ли­мое мень­ше де­ли­те­ля, то част­ное будет на­чи­нать­ся с нуля.

1 на 19 не де­лит­ся, по­это­му в част­ном ста­вим ноль. Де­ле­ние целой части окон­че­но, в част­ном ста­вим за­пя­тую. Сно­сим 7. 17 на 19 не де­лит­ся, в част­ном пишем ноль. Сно­сим 6 и про­дол­жа­ем де­ле­ние:

Ответ: .

Деление десятичной дроби на 10,  100 и т.д.

1) 

Делим так, как делят на­ту­раль­ные числа. В част­ном по­ста­вим за­пя­тую сразу, как сне­сем 8 – первую цифру после за­пя­той в де­ли­мом 74,8. Про­дол­жа­ем де­ле­ние даль­ше. При вы­чи­та­нии  по­лу­ча­ем 8, но де­ле­ние не окон­че­но. Мы знаем, что в конце де­ся­тич­ной дроби можно при­пи­сы­вать нули – от этого зна­че­ние дроби не из­ме­нит­ся. При­пи­сы­ва­ем ноль и делим 80 на 10. По­лу­ча­ем 8 – де­ле­ние окон­че­но.

Ответ: .

2) 

Ответ: .

Чтобы раз­де­лить де­ся­тич­ную дробь на 10, 100, 1000 и т.д., надо пе­ре­не­сти за­пя­тую в этой дроби на столь­ко цифр влево, сколь­ко нулей стоит после еди­ни­цы в де­ли­те­ле.

Пример

Чтобы умно­жить дробь на целое число, нужно умно­жать, не об­ра­щая вни­ма­ния на за­пя­тую, затем в от­ве­те вер­нуть за­пя­тую на место, то есть от­де­лить ею столь­ко же цифр в дроб­ной части, сколь­ко было в ис­ход­ном числе.

При­мер: 

Вы­пол­няя умно­же­ние, не стоит об­ра­щать вни­ма­ния на за­пя­тую.

Затем необ­хо­ди­мо по­ста­вить за­пя­тую так, чтобы в дроб­ной части по­лу­чи­лось, как и рань­ше, 3 цифры.

 

Умножение десятичных дробей

Для умно­же­ния двух де­ся­тич­ных дро­бей прин­цип аб­со­лют­но такой же.

Пра­ви­ло

Чтобы пе­ре­мно­жить две де­ся­тич­ные дроби, нужно их пе­ре­мно­жить, не об­ра­щая вни­ма­ния на за­пя­тые, затем в от­ве­те от­де­лить за­пя­той столь­ко цифр, сколь­ко их было у обоих чисел вме­сте.

 

При­мер 1

Сна­ча­ла необ­хо­ди­мо пе­ре­пи­сать каж­дую дробь в виде це­ло­го числа и вспо­мо­га­тель­но­го мно­жи­те­ля. Таким об­ра­зом, каж­дая дробь будет пред­став­ле­на в виде про­из­ве­де­ния.

Затем нужно вы­пол­нить умно­же­ние целых чисел от­дель­но, вспо­мо­га­тель­ных мно­жи­те­лей от­дель­но. По­лу­чен­ный ре­зуль­тат нужно умно­жить на 0,001, то есть вы­пол­ня­ет­ся от­де­ле­ние за­пя­той дроб­ной части дли­ной в 3 цифры.

При­мер 2

Нужно вы­пол­нить умно­же­ние, не об­ра­щая вни­ма­ния на за­пя­тые. Ко­ли­че­ство цифр после за­пя­той – 3, по­это­му за­пя­тая ста­вит­ся, от­де­ляя 3 цифры. По­след­ний ноль можно убрать из за­пи­си.

При­мер 3

Вы­пол­ня­ет­ся умно­же­ние в стол­бик, при этом не об­ра­щая вни­ма­ния на за­пя­тые, но помня, что в конце надо будет также от­де­лить за­пя­той 4 цифры.

При­мер 4

В ходе урока мы уже вы­яс­ни­ли, что умно­жать де­ся­тич­ные дроби тех­ни­че­ски озна­ча­ет про­сто умно­жать целые числа. Далее в от­ве­те нужно от­де­лить за­пя­той зна­ков столь­ко, сколь­ко их было у всех чисел вме­сте.

Ко­неч­но, это пра­ви­ло рас­про­стра­ня­ет­ся и на слу­чай несколь­ких мно­жи­те­лей:

 

Деление десятичных дробей

Си­ту­а­ция с де­ле­ни­ем де­ся­тич­ных дро­бей такая же: если уметь де­лить целые числа одно на дру­гое, то тогда по­лу­чит­ся и де­ся­тич­ную дробь де­лить на дру­гую де­ся­тич­ную дробь.

При­мер

Когда за­кан­чи­ва­ет­ся целое число, ко­то­рое надо раз­де­лить, то ста­вит­ся за­пя­тая и про­дол­жа­ет­ся вы­пол­не­ние вы­чис­ле­ний:

 

При­мер

Здесь си­ту­а­ция ровно такая же: как толь­ко кон­ча­ет­ся целая часть – ста­вит­ся за­пя­тая:

То есть тех­ни­че­ски не важно, что де­лить на целое число – дробь или дру­гое целое число. Ал­го­ритм оди­на­ко­вый.

 

Источник видео: https://www.youtube.com/watch?v=97n0NvNRPP0

Источник конспекта: http://interneturok.ru/ru/school/matematika/5-klass/umnozhenie-i-delenie-desyatichnyh-drobey/umnozhenie-i-delenie-desyatichnyh-drobey?konspekt&chapter_id=1898

Источник теста: http://testedu.ru/test/matematika/5-klass/dejstviya-s-desyatichnyimi-drobyami-2.html

Умножение десятичных знаков — Примеры | Как умножать десятичные дроби?

Умножение десятичных знаков очень важно, когда мы говорим о группировке предметов.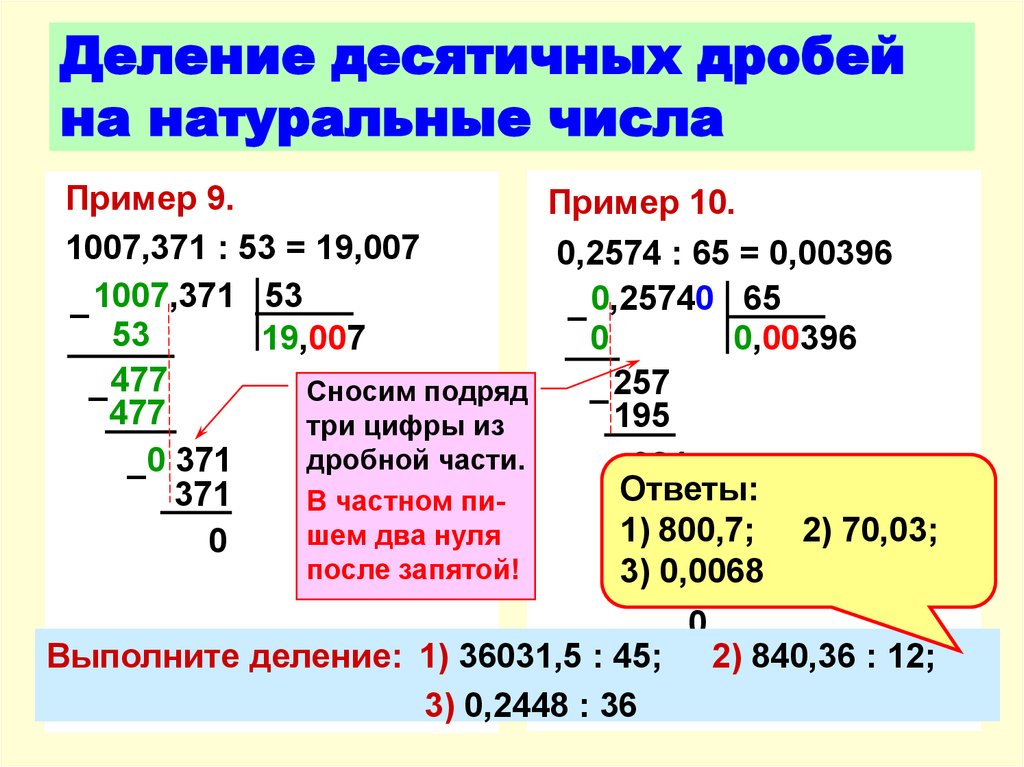 Предположим, вам нужно раздать по 0,25 части плитки шоколада каждому ребенку, а всего детей 12. Сколько плиток шоколада вам понадобится? Чтобы найти необходимое количество плиток шоколада, нужно умножить 12 на 0,25. Умножение десятичных знаков выполняется путем игнорирования десятичной точки и умножения чисел, и тогда количество знаков после запятой в произведении равно общему количеству знаков после запятой в обоих заданных числах.

1.	Как умножать десятичные дроби?
2.	Умножение десятичных дробей на целые числа
3.	Умножение двух десятичных чисел
4.	Часто задаваемые вопросы об умножении десятичных дробей

Как умножать десятичные дроби?

Умножение десятичных дробей имеет ту же процедуру, что и умножение целых чисел, за исключением размещения десятичной точки в произведении. В нашей повседневной жизни мы сталкивались с различными случаями, когда нам приходилось использовать операцию умножения на двух числах, из которых хотя бы одно или оба являются десятичными числами. Представьте, что вы идете с другом на обед. Вы оба заказываете блюдо стоимостью 6,75 долларов каждое. Общий счет составляет $ 15,75, включая налоги. Чтобы рассчитать общую стоимость тарелки в счете, вам нужно умножить 6,75 доллара на 2. Аналогичным образом предположим, что вы планируете подарить своей матери букет цветов на ее день рождения. Каждый цветок стоит 0,75 доллара, всего вы покупаете 6 цветов. Чтобы найти общую стоимость букета, вам нужно умножить 0,75 доллара на 6. В приведенных выше примерах используется умножение десятичных дробей.

Умножение десятичных дробей на целые числа

Умножение десятичных дробей на целые числа аналогично умножению целых чисел, единственное отличие заключается в расположении десятичной точки. Для умножения десятичных дробей на целые числа можно выполнить следующие шаги:

• Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа обычным образом.
• Шаг 2: После умножения подсчитайте количество знаков после запятой в десятичном числе. Произведение, полученное после умножения, будет иметь такое же количество знаков после запятой.
• Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Давайте разберемся в реальной ситуации умножения десятичных чисел на целые числа. Группа из 15 учеников решила внести свой вклад в благотворительный фонд. Каждый студент внес вклад в размере 6,5 долларов США. Какую сумму собрали со всего класса? Здесь вклад одного студента = $6,5. Общий вклад, сделанный 15 студентами = 6,5 × 15 = 9 долларов США.7.5.

Умножение десятичных дробей на 10 100 и 1000

При умножении любой десятичной дроби на 10, 100, 1000 или любую другую степень 10 мы просто сдвигаем запятую вправо на столько знаков, сколько нулей в степень числа 10.

• Если мы умножим десятичную дробь на 10, мы сдвинем запятую на одну позицию вправо, так как в числе 10 1 ноль.
• Если мы умножим любое десятичное число на 100, мы сдвинем десятичную точку на два знака вправо.
• Точно так же, если мы умножаем десятичную дробь на 1000, мы сдвигаем десятичную точку на три знака вправо и так далее.

Например, 2,32 × 10 = 23,2, 2,32 × 100 = 232, 2,32 × 1000 = 2320.

Умножение двух десятичных чисел

Этот раздел поможет вам узнать об умножении двух десятичных чисел. Это то же самое, что и у целого числа, но с той лишь разницей, что в этом случае мы должны взять сумму общего количества знаков после запятой в обоих данных числах, и это должно быть равно количеству знаков после запятой в продукт. Чтобы умножить два десятичных знака, выполните шаги, перечисленные ниже:

• Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
• Шаг 2: После умножения посчитайте общее количество знаков после запятой в обоих числах. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
• Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Давайте посмотрим на умножение двух десятичных чисел на изображении ниже:

Примеры умножения десятичных дробей:

1. Умножьте 0,567 и 13,065

Следовательно, 7,567 × 17,040 = 8,567 × 13,040 После запятой 6 цифр.

2. Найдите произведение 16,45 и 8,5

Следовательно, 16,45 × 8,5 = 139,825. Произведение имеет 3 знака после запятой.

Важные примечания:

Это несколько важных примечаний, связанных с концепцией умножения десятичных дробей. Взглянуть!

• Десятичное умножение следует той же процедуре, что и умножение целых чисел.
• Десятичная запятая должна быть поставлена ​​в произведении таким образом, чтобы произведение имело количество знаков после запятой, равное сумме знаков после запятой всех множимых и множителей.
• Убедитесь, что в произведении сохранены все нули при размещении десятичной точки.
• Если в произведении больше знаков после запятой, чем количество цифр, слева перед запятой в произведении можно вставить нули.
• Конечные нули в результирующем произведении могут быть опущены.

Попробуйте решить эти сложные вопросы:

• Чарли платят 17,45 долларов в час, и на прошлой неделе он отработал 42,5 часа. Сколько денег он заработал на прошлой неделе (округлив до цента)?
• Какое общее расстояние проедет автомобиль, если он проехал со скоростью 31,5 км/час за 7 часов 15 минут?

Умножение десятичных знаков Связанные темы

Ознакомьтесь с этими статьями, посвященными умножению десятичных дробей.

• Калькулятор деления десятичных дробей
• Калькулятор добавления десятичных знаков
• Десятичные числа и дроби
• Как добавить десятичные дроби?
• Деление десятичных дробей
• Сложение и вычитание десятичных дробей
• Десятичные числа

 

Умножение десятичных дробей Примеры

1. Пример 1: Роуз изучает десятичное умножение. Поможешь ей умножить 0,6748 на 14,9?45?

   Решение:

   Посмотрим, как умножить 0,6748 на 14,945.

   Примечание. Нули в конце можно опустить. Следовательно, 0,6748 × 14,945 = 10,084886.

2. Пример 2: Грейси пошла в продуктовый магазин со своей матерью. Ее мать купила 15 яблок по 1,25 доллара каждое. Помогите Грейси рассчитать сумму, которую должна заплатить ее мать, используя принцип умножения десятичных знаков.

   Решение:

   Стоимость одного яблока = 1,25 доллара. Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по умножению десятичных дробей

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об умножении десятичных дробей

Как умножить десятичное число на целое?

Чтобы умножить десятичное число на целое, выполните следующие действия:

• Шаг 1: Не обращайте внимания на десятичную точку и умножайте оба числа.
• Шаг 2: Подсчитайте количество знаков после запятой в десятичном числе.
• Шаг 3: Затем поставьте запятую в произведении так, чтобы количество знаков после запятой в произведении и исходное десятичное число совпадали.

Как умножить десятичные дроби на 1000?

Чтобы умножить десятичные дроби на 1000, сдвиньте запятую на три знака вправо, так как в числе 1000 три нуля.

Как научить умножать десятичные дроби?

Давайте посмотрим, как научить учащихся десятичному умножению следующими способами:

• Сначала дайте учащимся понять значение десятичного умножения с помощью демонстрации и визуализации.
• Во-вторых, познакомьте учащихся с этапами умножения двух десятичных чисел.
• Дайте практические вопросы.

Что такое правило умножения десятичных дробей?

Правила умножения десятичных дробей приведены ниже:

Правила умножения десятичных дробей:

• Выполняйте умножение так же, как и с целыми числами.
• Если в произведении больше знаков после запятой, чем количество цифр, перед размещением запятой в произведении можно вставить нули, чтобы слева от запятой был только один ноль, а знаки после запятой в произведении будут равно общему количеству знаков после запятой в обоих числах.
• Десятичная запятая должна быть поставлена ​​в произведении таким образом, чтобы произведение имело количество знаков после запятой, равное сумме знаков после запятой всех множимых и множителей.
• Конечные нули в дробной части результирующего произведения могут быть опущены.

Как умножать десятичные дроби меньше 1?

Чтобы умножить два десятичных знака меньше 1, выполните шаги, указанные ниже:

• Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
• Шаг 2: После умножения подсчитайте общее количество знаков после запятой в множимом и множитель. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
• Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Например: 0,2 × 0,4 = 0,08.

Как умножать положительные и отрицательные десятичные дроби?

Положительные и отрицательные десятичные дроби умножаются так же, как два десятичных дроби.

• Умножьте обе числовые части, как при обычном десятичном умножении.
• Так как произведение одного отрицательного числа на одно положительное число отрицательно, поэтому сохраните знак минус перед числовой частью полученного произведения.

Например, -0,5 × 0,3 = -0,15.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по умножению десятичных дробей

Умножение десятичных дробей на десятичные дроби

Это полный урок с инструкцией и упражнениями для 5-го класса по умножению десятичных дробей на десятичные дроби. Интерпретация умножения десятичного числа на десятичное состоит в том, чтобы думать об этом как о взятии дробной части десятичного числа (символ × переводится как «из»). Урок сравнивает умножение на десятичную дробь с масштабированием и сжатием палочки. Наконец, он показывает распространенный способ десятичного умножения (умножить, как если бы десятичных точек не было; в ответе столько десятичных знаков, сколько множителей в сумме).0003 В видео ниже я объясняю правило умножения десятичных дробей (поставьте в ответе столько десятичных цифр, сколько их в множителях). Я объясняю, откуда взялось это правило, используя умножение дробей. Урок продолжается под видео. Вы научились думать об умножении на целое число, например, 3 × 4 или 8 × 0,6, как повторное сложение 90 327. Однако эта концепция не работает, когда ни один из множителей не является целым числом, как в случае 9.0327 0,83 × 1,43 или 2/3 × 7/11. Вместо этого, когда вы умножаете десятичные дроби или дроби, подумайте об этом. как нахождение «определенной части» другого фактора. В этом смысле символ «×» переводится как «из». Пример. 0,1 × 80 значит найти одну десятую «из» 80. Это просто 8. Пример. 0,4 × 80 значит найти четыре десятых «из» 80. Так как одна десятая от 80 равна 8, то 0,4 от 80 в четыре раза больше много, или 32. Пример. 0,02 × 3000 означает нахождение двухсотых 3000. Поскольку одна сотая от 3000 равна 30, то 0,02 от 3000 в два раза больше. много, или 60. 1. Запишите как умножение с использованием десятичной дроби и решать. Помните, что «из» переводится как «×». Используйте верхнюю задачу     в каждой ячейке, чтобы решить нижнюю. а. одна десятая от 50 _______ × ______ =  _______ б. три десятых от 50 _______ × ______ =  _______ с. одна десятая часть 700 ______ × _______ =  _______ d. четыре десятых 700 ______ × _______ =  _______ эл. одна сотая от 4000 _______ × _______ =  _______ ф. шестисотых 4000 _______ × _______ =  _______ 2. Решить. Используйте верхнюю задачу в каждом блоке, чтобы Помогите решить нижний. а. Найти 0,1 × 30   ________     Найти 0,4 × 30   ________ б. Найти 0,1 × 400   _________     Найти 0,6 × 400   _________ с. Найти 0,01 × 600   _________     Найти 0,07 × 600   _________ д. Найти 0,1 × 520   ________     Найти 0,3 × 520   ________ эл. Найти 0,001 × 5000   _________     Найти 0,002 × 5000   _________ ф.  Найти 0,01 × 800   _________     Найти 0,11 × 800   _________ 3. Ответ. Вам не нужно рассчитывать.     а. Вы узнали, что 0,1 × 246 означает одну десятую 246.         Будет ли результат 0,1 × 246 больше или меньше 246?     б. Кроме того, 0,1 × 0,8 означает одну десятую 0,8.         Будет ли результат 0,1 × 0,8 больше или меньше 0,8?     в. Будет ли результат 1,9 × 928 больше или меньше 928? Масштабирование означает расширение или сжатие что-то по какому-то фактору. Эта красная палочка 40 пикселей длинная. Увеличим длину в четыре раза: → Мы можем написать умножение «уравнение»: 4 ×    = Использование пикселей, 4 × 40 пикселей = 160 пикселей. Теперь давайте масштабируем красную палочку до 0,4 (четыре десятых) до тех пор, пока это сначала: → Обратите внимание, он уменьшился! Мы можем написать: 0,4 ×    = В пикселях, 0,4 × 40 пикселей = 16 пикселей. Число, на которое мы умножаем (4 и 0,4 выше) называется коэффициентом масштабирования . Если коэффициент масштабирования больше 1, например 2.3, получившаяся палочка на 90 524 длиннее исходной на 90 525. Если коэффициент масштабирования меньше 1, например 0,5 или 0,66, результирующий палка короче. 4. Палка в усадке . Сколько это будет в пикселях? Сравните проблемы. а. 0,1 × =       0,1 × 40 пикселей = ________ пикселей б. 0,3 × =       0,3 × 40 пикселей = ________ пикселей в. 0,6 × =       0,6 × 40 пикселей = ________ пикселей д.  0,2 × =       0,2 × 40 пикселей = ________ пикселей эл.  0,5 × =       0,5 × 40 пикселей = ________ пикселей ф.  0,9 × =       0,9 × 40 пикселей = ________ пикселей   Давайте расширим эту палку (40 пикселей) в 1,2 раза длиннее: → Мы можем написать умножение: 1,2 ×    = Чтобы рассчитать, как долго это в пикселях, давайте сначала разберемся, что такое 0,2 от 40. Поскольку одна десятая от 40 равна 4, то 0,2 от 40 в два раза больше, или 8. 0,2 × 40 пикселей или 40 + 8 = 48 пикселей. 5. Красная палочка 50 пикселей длинная. Это расширенный или сжатый . Заполнить бланки. а. 0,5 × знак равно      0,5 × 50 пикселей = ________ пикселей б. 0,3 × знак равно      0,3 × 50 пикселей = ________ пикселей в.   1,5 × знак равно      1,5 × 50 пикселей = ________ пикселей д.   1,3 × знак равно      1,3 × 50 пикселей = ________ пикселей 6. Сообщите, получена ли палочка после «умножения» будет короче или длиннее оригинала. а. 3,1 × будет длиннее/короче б. 0,3 × будет длиннее/короче с. 0,9 × будет длиннее/короче д.   1,2 × будет длиннее/короче К короткому пути Половина 5 равна 2,5, или 0,5 × 5 = 2,5 . Это напоминает знакомое умножение 5 × 5 = 25 ! Одна десятая от 20 равна 2, поэтому три десятых 20 равно 6. Мы можем написать 0,3 × 20 = 6 . Это похоже на знакомое умножение 3 × 2 = 6 ! Ярлык для десятичного числа умножение:    1) Умножить как будто есть не было десятичных знаков. 2) Поставьте в ответе запятую. Но где мы будем ставить запятую? Давайте немного изучим это! 7. Заполните аргументацию Аниты. а. Чтобы вычислить 0,8 × 0,8, я сначала умножьте 8 × 8 = 64. Ответ на 0,8 × 0,8 должен быть немного     меньше , чем 0,8, потому что масштабирование чего-либо на 0,8 рядом с оригинально, но несколько меньше.     Итак, 0,8 × 0,8 не может быть 64, и это не может быть 6,4, но это _________! б. 0,1 × 5,6 должен составлять 1/10 размера 5,6. Значит, не может быть 56. Может ли быть 5,6? Нет, потому что     1 × 5,6 = 5,6. Итак, 0,1 × 5,6 должно равняться __________. в. 0,4 × 0,06 должно быть меньше 0,06. Это не может быть ни 24, ни 2.4. 0,24 или 0,024? ________   Ярлык десятичного умножения 1) Умножить как если бы не было десятичных знаков. 2) Поставьте в ответе запятую. количество десятичных цифр в     ответом является СУММА количества десятичных цифр в множителях. Пример 1.    0,05 × 0,7 5 × 7 равно 35. Коэффициент 0,05 имеет два, а 0,7 имеет один десятичный знак цифра. В ответе должно быть три, поэтому ответ равен 0,035. Пример 2.   12 × 2 × 0,3 × 0,2 12 × 2 × 3 × 2 = 144. Множители имеют 0, 0, 1, и 1 десятичная цифра — всего 2. Ответ имеет чтобы иметь 2 десятичных цифры, поэтому ответ 1,44. 8. Умножить сначала как будто там мы НЕТ десятичных точек. Затем добавьте к ответу десятичную точку. а. 0,5 × 0,3 = ________ б. 0,9 × 0,6 = ________ в. 0,4 × 0,08 = ________ д. 0,7 × 0,02 = ________ эл. 0,1 × 0,3 = ________ ф. 0,1 × 2,7 = ________ г. 0,2 × 0,1 = ________ ч. 0,8 × 0,1 = ________ и. 0,9 × 0,01 = ________ Дж. 0,9 × 0,1  = ________ к. 0,7 × 0,3 = ________ л. 7 × 0,03  = ________ 9. Умножение. а. 0,4 × 0,8   = ________ б. 0,7 × 1,1   = ________ в. 0,02 × 0,9 = ________ д. 0,02 × 0,5 = ________ эл. 0,002 × 9 = ________ ф. 1,1 × 0,3  = ________ г. 2,1 × 0,2 × 0,5 = _________ ч. 0,4 × 4 × 0,2   = _________ и. 6 × 0,06 × 0,2 = _________ Ответ десятичное умножение может заканчиваться одним или несколькими нулями. Это не проблема. Однако после расстановки десятичной точки вы можете упростить окончательный ответ, опуская конечные десятичные нули. 50 × 0,006 50 × 6 = 300. Множители имеют 0 и 3 десятичное число цифр, поэтому ответ должен состоять из 3. Следовательно, ответ 0,300, но это упрощает до 0,3 . 400 × 0,05 400 × 5 = 2000. Коэффициенты имеют 0 и 2 десятичное число цифр, поэтому ответ должен состоять из 2. ответ 20.00. Вы можете упростить это до 20 . 10. Решить. а. 0,4 × 0,5 = _______ б. 20 × 0,06 = _______ в. 40 × 0,05 = _______ д. 3 × 0,2 × 0,5 = _______ эл. 300 × 0,009 = ________ ф. 40 × 0,05 = __________ г. 0,6 × 0,2 × 0,5 = ________ ч. 600 × 0,004 = __________ я. 0,4 × 0,5 × 60 = ________   Картофель стоит 1,20 доллара за кг. Если вы покупаете 23 килограмма, вы умножаете 23 × $1,20, чтобы найти общую цену. Если вы покупаете 0,8 кг, вы делаете то же самое: умножаете цену на 0,8. Чтобы найти 0,8 × 1,20 доллара США, сначала умножьте без десятичной точки: 8 × 120 = 960. факторы есть 1 и 2 десятичных цифры, поэтому ответ должен состоять из трех десятичных цифр: 0,960. Мы можем опустить последние нулей, и дайте ответ как $ 0,96. Обратите внимание, что ответ также имеет смысл: 0,8 кг картофеля должен стоить чуть меньше, чем 1 кг картофеля , что было 1,20 доллара. 11. Найдите общую стоимость. Напишите умножение.       а. Лента стоит 1,10 доллара за метр, а вы покупаете 0,4 метров.       б. Гайки стоимость 8 долларов за фунт. Вы покупаете 0,3 фунта.       c. Телефон звонок стоит 7 долларов в час. Вы разговариваете 1,2 часа.       d. Кружево стоит 2,20 доллара за метр, и вы покупаете 1,5 метров. Здесь вы можете сделать рабочие листы для десятичного умножения. Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер. Он соответствует Общему базовому стандарту для 5-го класса 5.NBT.7. Mammoth Decimals 2 Учебник для самообучения для 5-6 классов, который охватывает четыре действия с десятичными знаками до трех десятичных цифр, уделяя особое внимание десятичному умножению и делению. Книга также охватывает разрядность, сравнение, округление, сложение и вычитание десятичных знаков. Есть много умственных математических задач. Скачать (6,25 долл. США) . Также доступен в виде печатной копии. => Узнайте больше и посмотрите бесплатные образцы! Меню уроков математики

Умножение десятичных знаков | Математика для гуманитарных наук Базовый курс

Результаты обучения

• Умножение двух десятичных дробей
• Умножение десятичной дроби на 10, 100 или 1000

Умножение десятичных дробей очень похоже на умножение целых чисел — нам просто нужно определить, где ставить десятичную точку. Процедура умножения десятичных дробей станет понятной, если мы сначала рассмотрим умножение дробей.

Вы помните, как умножать дроби? Чтобы умножить дроби, нужно умножить числители, а затем умножить знаменатели.

Итак, давайте посмотрим, что мы получим как произведение десятичных дробей, если сначала преобразуем их в дроби. Мы сделаем два примера рядом друг с другом ниже. Ищите образец.

А	Б
[латекс]\влево(0,3\вправо)\влево(0,7\вправо)[/латекс]	[латекс]\влево(0,2\вправо)\влево(0,46\вправо)[/латекс]
Преобразование в дроби.	[латекс]\влево({\Большой\гидроразрыва{3}{10}}\право)\влево({\Большой\гидроразрыва{7}{10}}\право)[/латекс]	[латекс]\влево({\Большой\гидроразрыва{2}{10}}\право)\влево({\Большой\гидроразрыва{46}{100}}\право)[/латекс]
Умножить.	[латекс] {\ Большой \ гидроразрыва {21} {100}} [/латекс]	[латекс] {\ Большой \ гидроразрыва {92} {1000}} [/латекс]
Преобразование обратно в десятичные числа.	[латекс]0,21[/латекс]	[латекс]0,092[/латекс]

Есть шаблон, который мы можем использовать. В A мы умножили два числа, каждое из которых имело один десятичный знак, и в произведении было два десятичных знака. В B мы умножили число с одним десятичным знаком на число с двумя десятичными знаками, и в произведении было три десятичных знака.

Сколько знаков после запятой вы ожидаете от произведения [латекс]\влево(0,01\вправо)\влево(0,004\вправо)?[/латекс] Если вы сказали «пять», вы узнали шаблон. Когда мы умножаем два числа на десятичные дроби, мы подсчитываем все десятичные разряды в множителях — в данном случае два плюс три — чтобы получить количество знаков после запятой в произведении — в данном случае пять.

Зная, как определить количество цифр после запятой, мы можем умножать десятичные числа без предварительного преобразования их в дроби. Количество знаков после запятой в произведении равно сумме количества знаков после запятой в множителях.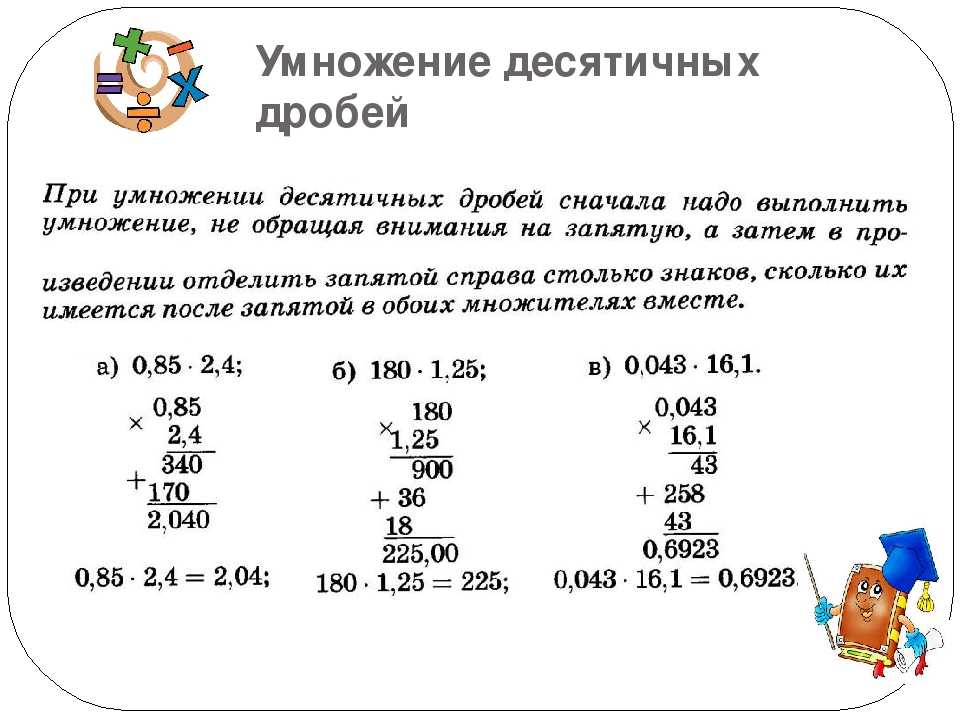

Правила умножения положительных и отрицательных чисел, конечно же, применимы и к десятичным числам.

Умножение двух чисел

При умножении двух чисел

• , если их знаки одинаковы, произведение положительное.
• , если их знаки разные, произведение отрицательное.

При умножении десятичных дробей со знаком сначала определите знак произведения, а затем умножьте, как если бы оба числа были положительными. Наконец, напишите продукт с соответствующим знаком.

Умножение десятичных чисел.

1. Определите знак произведения.
2. Напишите числа в вертикальном формате, выстраивая числа справа.
3. Умножить числа, как если бы они были целыми числами, временно игнорируя десятичные точки.
4. Поставьте десятичную точку. Количество знаков после запятой в произведении равно сумме количества знаков после запятой в множителях. При необходимости используйте нули в качестве заполнителей.
5. Запишите произведение соответствующим знаком.

 

пример

Умножить: [латекс]\влево(3.9\вправо)\влево(4.075\вправо)[/латекс]

Решение

[латекс]\вправо)\влево(3.9\вправо)\влево(3.9\вправо) (4.075\справа)[/латекс]
Определить знак произведения. Признаки те же.	Произведение будет положительным.
Напишите числа в вертикальном формате, выстраивая числа справа.
Умножьте числа, как если бы они были целыми числами, временно игнорируя десятичные точки.
Поставьте десятичную точку. Добавьте количество знаков после запятой в множители [латекс]\влево(1+3\вправо)[/латекс]. Поставьте запятую на 4 знака справа.
Продукт положительный.	[латекс]\влево(3,9\вправо)\влево(4,075\вправо)=15,8925[/латекс]

 

попробуйте

 

пример

Умножить: [латекс]\влево(-8. 2\вправо)\текст{(}5.19\текст{)}[/латекс]

6 Показать решение

 

попробуйте

В следующем видео мы покажем еще один пример умножения двух десятичных дробей.

В следующем примере нам нужно добавить несколько нулей-заполнителей, чтобы правильно разместить десятичную точку.

пример

Умножить: [латекс]\влево(0,03\вправо)\текст{(}0,045\текст{)}[/латекс]

Показать решение

 

попробуйте

Во многих областях, особенно в естественных науках, принято умножать десятичные дроби на степени [латекс]10[/латекс]. Давайте посмотрим, что произойдет, если мы умножим [латекс]1,9436[/латекс] на некоторые степени [латекс]10[/латекс].

Посмотрите на результаты без конечных нулей.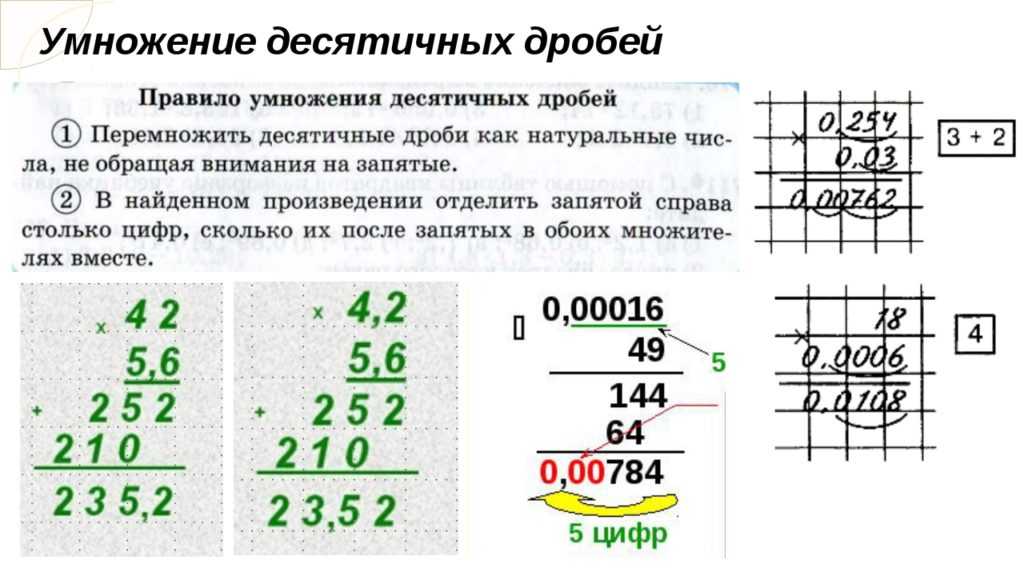 Вы замечаете закономерность?

[латекс]\begin{массив}{ccc}1.9436\влево(10\вправо)\hfill & =& 19.436\hfill \\ 1.9436\влево(100\вправо)\hfill & =& 194.36\hfill \\ 1.9436\влево(1000\вправо)\hfill & =& 1943.6 \hfill \end{array}[/latex]

Количество знаков, на которые переместилась десятичная точка, равно количеству нулей в степени десяти. В таблице ниже представлены результаты.

Умножить на	Количество нулей	Количество мест, на которые перемещается десятичная точка
[латекс]10[/латекс]	[латекс]1[/латекс]	[латекс]1[/латекс] место справа
[латекс]100[/латекс]	[латекс]2[/латекс]	[латекс]2[/латекс] места справа
[латекс]1000[/латекс]	[латекс]3[/латекс]	[латекс]3[/латекс] места справа
[латекс]10 000[/латекс]	[латекс]4[/латекс]	[латекс]4[/латекс] места справа

Мы можем использовать этот шаблон как ярлык для умножения на степени десяти вместо умножения с использованием вертикального формата. Мы можем подсчитать нули в степени [latex]10[/latex] и затем переместить десятичную точку на такое же количество знаков вправо.

Например, чтобы умножить [латекс]45,86[/латекс] на [латекс]100[/латекс], переместите десятичную точку [латекс]2[/латекс] вправо.

Иногда, когда нам нужно переместить десятичную точку, не хватает десятичных знаков. В этом случае мы используем нули в качестве заполнителей. Например, давайте умножим [латекс]2,4[/латекс] на [латекс]100[/латекс]. Нам нужно переместить десятичную точку [latex]2[/latex] вправо. Так как справа от запятой стоит только одна цифра, мы должны написать [latex]0[/latex] в сотых долях.

Умножить десятичную дробь на степень [latex]10[/latex]

1. Переместить запятую вправо на количество знаков, равное количеству нулей в степени [latex]10[/latex].
2. При необходимости напишите нули в конце числа в качестве заполнителей.

 

пример

Умножить [латекс]5,63[/латекс] на

1.