Два важнейших правила комбинаторики
Эти правила записаны в общем виде в Приложении Формулы Комбинаторики (пункт 4) и весьма напоминают алгебру событий:
1) Правило сложения комбинаций. Знак «плюс» следует понимать и читать как союз ИЛИ. Вспоминаем демонстрационную задачу с яблоком, грушей и бананом:
способами можно выбрать хотя бы один фрукт.
То есть, можно взять 1 фрукт (любой из трёх) ИЛИ какое-нибудь сочетание двух фруктов (любое) ИЛИ все три фрукта. Заметьте, что сложение комбинаций предполагает безразличие выбора (в данном случае без разницы – будет ли выбран 1, 2 или 3 фрукта).
Теперь рассмотрим более содержательный пример:
Задача 7
Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать 2 человек одного
пола?
Решение: в данном случае подсчёт количества сочетаний , не годится – по той причине, множество комбинаций из двух человек включает в себя
и разнополые пары.
Условие «выбрать 2 человек одного пола» подразумевает, что нужно выбрать двух юношей или двух девушек, и уже сама словесная формулировка указывает на верный путь решения:
способами можно выбрать 2 юношей;
способами можно выбрать 2 девушек.
Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: способами.
Ответ: 123
2) Правило умножения комбинаций. Знак «умножить» следует понимать и читать как союз И.
Рассмотрим ту же студенческую группу, которая пошла на танцы. Сколькими способами можно составить пару из юноши и девушки?
способами можно выбрать 1 юношу;
способами можно выбрать 1 девушку.
Таким образом, одного юношу и одну девушку можно выбрать:
способами.
Когда из каждого множества выбирается по одному объекту, то справедлив следующий принцип подсчёта комбинаций: «каждый
объект из одного множества может составить пару с каждым объектом другого множества».
То есть, Олег может пригласить на танец любую из 13 девушек, Евгений – тоже любую из 13 девушек, и аналогичный выбор есть у остальных молодых людей. Итого:
возможных пар.
Следует отметить, что в данном примере не имеет значения упорядоченность пары, однако если принять во внимание инициативу, то
количество комбинаций нужно удвоить, поскольку каждая из 13 девушек тоже может пригласить на танец
Этот же принцип справедлив и для более сложных комбинаций, например: сколькими способами можно выбрать 2 юношей и 2 девушек для участия в сценке КВН?
Союз И недвусмысленно намекает, что комбинации следует перемножить:
возможных групп артистов.
Иными словами, каждая пара юношей (45 уникальных пар) может выступить с каждой парой девушек (78
уникальных пар). А если рассмотреть распределение ролей между участниками, то комбинаций будет ещё больше. …Очень хочется, но всё-таки
воздержусь от продолжения, чтобы не привить вам отвращение к студенческой жизни =).
А если рассмотреть распределение ролей между участниками, то комбинаций будет ещё больше. …Очень хочется, но всё-таки
воздержусь от продолжения, чтобы не привить вам отвращение к студенческой жизни =).
Правило умножения комбинаций распространяется и на бОльшее количество множителей:
Задача 8
Сколько существует трёхзначных чисел, которые делятся на 5?
Решение: для наглядности обозначим данное число тремя звёздочками: ***
Комбинации будем считать по разрядам – слева направо:
В разряд тысяч можно записать любую из цифр (1, 2, 3, 4, 5, 6, 7, 8 или 9). Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.
А вот в разряд десятков («посерединке») можно выбрать любую из 10 цифр:
По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас
устраивают 2 цифры.
Таким образом, в младшем разряде нас
устраивают 2 цифры.
Итого, существует:
трёхзначных чисел, которые делятся на
5.
При этом произведение расшифровывается так: «9 способами можно выбрать цифру в разряд сотен и 10 способами выбрать цифру в разряд десятков и 2 способами – в разряд единиц»
Или ещё проще: «каждая из 9 цифр в разряде сотен комбинируется с каждой из 10 цифр в разряде десятков и с каждой из двух цифр в разряде единиц».
Ответ: 180
…да, чуть не забыл об обещанном комментарии к Задаче 5, в которой Боре, Диме и Володе можно сдать по одной карте способами. Умножение здесь имеет тот же смысл: способами можно извлечь 3 карты из колоды
И в каждой выборке переставить их способами.
А теперь задача для самостоятельного решения… сейчас придумаю что-нибудь поинтереснее, …пусть будет про ту же русскую версию Блэкджека:
Задача 9
Сколько существует выигрышных комбинаций из 2 карт при игре в «очко»?
Справка: выигрывает комбинация 10 + ТУЗ (11 очков) = 21 очко, и давайте будем считать выигрышной комбинацию из 2 тузов (порядок карт в любой паре не имеет значения).
Кстати, не надо считать пример примитивным. Блэкджек – это чуть ли не единственная игра, для которой существует математически обоснованный алгоритм, позволяющий систематически выигрывать у казино, и желающие могут найти массу информации об оптимальной стратегии и тактике. Правда, такие мастера довольно быстро попадают в чёрный список всех заведений 🙂
1.3.6. Перестановки с повторениями
1.3.4. Размещения
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Сложение натуральных чисел столбиком: правило, примеры
Сложение столбиком, или как еще говорят, сложение в столбик — это метод, широко используемый для сложения многозначных натуральных чисел. Суть этого метода в том, что сложение двух и более многозначных чисел сводится к нескольким простым операциям сложения однозначных чисел.
В статье подробно расписано, как выполнять сложение двух и большего количества многозначных натуральных чисел. Дано правило сложения чисел в столбик и примеры решения с разбором всех самых характерных ситуаций, возникающих при сложении чисел в столбик.
Сложение двух чисел в столбик: что нужно знать?
Прежде чем мы перейдем непосредственно к операции сложения в столбик, рассмотрим некоторые важные моменты. Для быстрого освоения материала желательно:
- Знать и хорошо ориентироваться в таблице сложения.
 Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения. - Помнить свойства сложения натуральных чисел. Особенно свойства, связанные со сложением нулей. Напомним их кратко. Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому. Сумма двух нулей есть нуль.
- Знать правила сравнения натуральных чисел.
- Знать, что такое разряд натурального числа. Напомним, что разряд — это позиция и значение цифры в записи числа. Разряд определяет значение цифры в числе — единицы, десятки, сотни, тысячи и т.д.
Сложение двух натуральных чисел в столбик
Опишем алгоритм сложения чисел столбиком с использованием конкретного примера. Пусть мы складываем числа 724980032 и 30095. Сначала следует записать эти числа по правилам записи сложения в столбик.
Числа записываются одно под другим, цифры каждого разряда располагаются, соответственно, одна под другой. Слева ставим знак «плюс», а под числами проводим горизонтальную линию.
Теперь мысленно разбиваем запись на столбики по разрядам.
Все, что остается сделать — сложить однозначные числа в каждом столбике.
Начинаем с крайнего правого столбика (разряд единиц). Складываем числа, и под чертой записываем значение единиц. Если при сложении значение десятков в результате получилось отличным от нуля, запоминаем это число.
Складываем цифры второго столбика. К результату прибавляем число десятков, которое мы запомнили на предыдущем шаге.
Повторяем весь процесс с каждым столбиком, вплоть до крайнего левого.
Данное изложение — упрощенная схема алгоритма сложения натуральных чисел столбиком. Теперь, когда мы разобрались с сутью метода, рассмотрим каждый шаг подробно.
Сначала складываем единицы, то есть числа в правом столбце. Если у нас получилось число, меньшее чем 10, записываем его в том же столбике и переходим к следующему. Если же результат сложения больше или равен 10, то под чертой в первом столбике записываем значение разряда единиц, а значение разряда десятков — запоминаем.
В нашем примере, при сложении чисел первого столбика, мы получаем число 7.
7<10, поэтому записываем это число в разряд единиц результата, а запоминать нам ничего не нужно.
Далее складываем числа в следующем столбце, то есть в разряде десятков. Проводим те же действия, только к сумме нужно прибавить число, которое мы держали в уме. Если сумма получилась меньше 10, просто записываем число под вторым столбиком. Если же результат больше или равен 10, записываем во втором столбике значение единиц этого числа, а цифру из разряда десятков запоминаем.
В нашем случае мы складываем числа 3 и 9, в результате имеем 3+9=12. На предыдущем шаге мы ничего не запоминали, поэтому к этому результату ничего прибавлять не нужно.
12>10, поэтому во втором столбике записываем цифру 2 из разряда единиц, а цифру 1 из разряда десятков держим в уме. Для удобства можно записать это число над следующим столбиком другим цветом.
Для удобства можно записать это число над следующим столбиком другим цветом.
Переходя к третьему, четвертому и так далее столбику повторяем действие, пока столбики не закончатся.
В третьем столбике сумма цифр равна нулю (0+0=0). К этой сумме прибавляем то число, которое ранее держали в уме, и получаем 0+1=1. записываем:
Переходя к следующему столбцу также складываем 0+0=0 и записываем в результате 0, так как на предыдущем шаге мы ничего не запоминали.
Следующий шаг дает 8+3=11. В столбике записываем цифру 1 из разряда единиц. Цифру 1 из разряда десятков держим в уме и переходим к следующему столбцу.
Этот столбик содержит только одно число 9. Если бы у нас не было в памяти числа 1, мы бы просто переписали число 9 под горизонтальную черту. Однако, учитывая, что не предыдущем шаге мы запомнили число 1, нужно сложить 9+1 и записать результат.
9+1=10
Поэтому, под горизонтальной чертой мы записываем 0, а единицу снова держим в уме.
Переходя к следующему столбику складываем 4 и 1, результат пишем под чертой.
Следующий столбик содержит только число 2. Так на предыдущем шаге мы ничего не запоминали, просто переписываем это число под черту.
Также поступаем и с последним столбиком, содержащим число 7.
Столбцов более нет, и в памяти также ничего нет, поэтому можно сказать, что операция сложения в столбик окончена. Число, записанное под чертой — результат сложения двух верхних чисел.
Чтобы разобраться со всеми возможными нюансами, рассмотрим еще несколько примеров.
Пример 1. Сложение натуральных чисел столбикомСложим два натуральных числа: 21 и 36.
Сначала запишем эти числа по правилу записи при сложении столбиком:
Начав с правого столбика, приступаем к сложению чисел.
1+6=7
Так как 7<10, записываем 7 под чертой.
Складываем числа во втором столбике.
2+3=5
Так как 5<10, а в памяти с предыдущего шага ничего нет, записываем результат
В памяти и в следующем столбике чисел более нет, сложение закончено. 21+36=57
21+36=57
Сколько будет 47+38?
Запишем:
7+8=15, поэтому запишем 5 в первом столбике под чертой, а 1 будем держать в уме.
Теперь складываем значения из разряда десятков: 4+3=7. Не забываем о единице и прибавляем ее к результату:
7+1=8. Полученное число записываем под чертой.
Это и есть результат сложения.
47+38=85
Пример 3. Сложение натуральных чисел столбикомТеперь возьмем два трехзначных числа и выполним их сложение.
3+9=12; 12>10
Записываем 2 под чертой, 1 держим в уме.
8+5=13; 13>10
Складываем 13 и запомненную единицу, получаем:
13+1=14; 14>10
Записываем 4 под чертой, 1 держим в уме.
7+2=9
Не забываем, что на предыдущем шаге мы запомнили 1.
9+1=10
Записываем 0 под чертой, 1 держим в уме.
В последнем столбике переносим единицу, которую мы запомнили ранее, под черту, и получаем окончательный результат сложения.
783+259=1042
Пример 4. Сложение натуральных чисел столбикомНайдем сумму чисел 56927 и 90.
Как всегда, сначала записываем условие:
7+0=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
2+9=11; 11>10
Записываем 1 под чертой, 1 держим в уме и переходим к следующему столбику.
9+1=10
Записываем 0 под чертой, 1 держим в уме и переходим к следующему столбику.
Столбик содержит одно число 6. Складываем его с запомненной единицей.
6+1=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
Столбик содержит одно число 5. Переносим его под черту и заканчиваем операцию сложения.
56927+90=57017
Следующий пример приведем без промежуточных результатов и пояснений, как образец записи сложения в столбик на практике.
Пример 5. Сложение натуральных чисел столбиком5807+4137502=?
Ответ: 5807+4137502=4143309
Сложение столбиком трех и более чисел.
 Что нужно знать?
Что нужно знать?Во первых, нужно усвоить всю информацию, уже изложенную в этой статье. Во вторых, также помним, что нули не влияют на результат сложения, и сколько бы не было в выражении слагаемых нулей, их сумма будет равна нулю.
Этапы сложения в столбик трех и более чисел аналогичны этапам из уже рассмотренных примеров с двумя числами. Обратимся к практике и поясним ход решения.
Пример 5. Сложение трех натуральных чисел столбикомСложим столбиком числа 274, 3082 и 201297.
Сначала делаем запись:
Начинаем с первого столбика, справа налево.
4+2+7=13; 13>10
3 пишем, 1 в уме. Переходим ко второму столбику.
7+8+9=24; 24+1=25; 25>10
5 пишем, 2 в уме. Переходим к третьему столбику.
2+0+2=4; 4+2=6; 6<10
6 пишем, и ничего не запоминаем. Переходим к четвертому столбику.
3+1=4; 4<10
4 пишем, и ничего не запоминаем. Переходим к пятому столбику. Пятый и шестой столбики содержат по одному числу, в уме с предыдущих шагов мы ничего не держим, поэтому просто переносим числа из последних двух столбиков под черту.
Ответ: 274+3082+201297=204653
Совет: при сложении трех и большего количества чисел в столбик, если вычисления выходят слишком громоздкими, бывает удобнее последовательно сложить два числа, затем еще два и так далее.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Значение, Определение, Предложения . Что такое правило сложения
- Онлайн-переводчик
- Грамматика
- Видео уроки
- Учебники
- Лексика
- Специалистам
- Английский для туристов
- Рефераты
- Тесты
- Диалоги
- Английские словари
- Статьи
- Биографии
- Обратная связь
- О проекте
Примеры
Значение слова «ПРАВИТЬ»
Руководить, управлять, обладая властью.
Смотреть все значения слова ПРАВИТЬ
Значение слова «СЛОЖЕНИЕ»
Арифметическое действие, посредством к-рого из двух или нескольких чисел получают новое, содержащее столько единиц, сколько было во всех данных числах вместе.
Смотреть все значения слова СЛОЖЕНИЕ
Предложения с «правило сложения»
Первое правило сложения состоит в том, что могут быть добавлены только одинаковые количества; например, различные количества четвертей. | |
| Другие результаты | |
Вопрос о едином постоянном договорном органе по правам человека крайне сложен и требует самого тщательного рассмотрения. | |
Надо отметить, что этот коктейль не грандиозен и не шедеврален, его вкус не так-то уж и сложен или необычен, просто он правильный. | |
И, наконец, раздел страны сложен с точки зрения международного права, которое, как правило, стоит на стороне суверенных государств и направлено на защиту существующей единой территории. | |
Просто подтверждение того, что мир, в котором мы живем, зачастую слишком сложен для правил, которые мы создаем, чтобы контролировать его. | |
Когда книга печатается, страницы раскладываются на пластине так, чтобы после того, как печатный лист сложен, страницы были в правильной последовательности. | |
Целью должен быть код, который “очевидно прав”, в отличие от кода, который настолько сложен, что “я не вижу никаких проблем”. | |
Этап семантического анализа, как правило, более сложен и написан от руки, но может быть частично или полностью автоматизирован с использованием атрибутивных грамматик. | |
Правовой статус WikiLeaks весьма сложен. | |
Несмотря на свои относительно простые правила, Go очень сложен. | |
Вид реставрационных работ, которые делает Адам, еще более сложен, и ничто не сравнится с знанием правильных кнопок, которые нужно нажимать в Photoshop. | |
Сложена она была правильно и чрезвычайно изящно; по красивой форме ее рук можно было заключить о стройности всего тела. | |
До того, как она потеряла свои руки, которые никогда не были восстановлены, правая рука Ники, как полагают, была поднята, сложена вокруг рта, чтобы издать победный крик. | |
Для того чтобы копия правильно читалась после того, как она сложена, должен быть какой-то брак. | |
Их одежда, как правило, сложена и разложена в ящиках или шкафах, а не лежит на полу. | |
Однако прямая настройка или сложение и вычитание в регистре sp/esp/rsp также поддерживаются, поэтому инструкции enter/leave, как правило, не нужны. | |
Это правило игнорировало сложение процентов и приводило к значительной экономии налогов, когда проценты высоки или ценная бумага имеет длительный срок погашения. | |
Возможно, что они и правда были толстые, хотя я в ту пору был невелик для своих лет и не отличался крепким сложением. | |
Таким образом, синтаксическое правило APL отличается от того, что преподается в математике, где, например, умножение выполняется перед сложением в порядке операций. | |
Мисс Марпл чуть склонилась вперед и мягко, увещевающе — так малому ребенку объясняют правила сложения и вычитания — стала излагать свою теорию. | |
Логарифмические правила обычно не используются для сложения и вычитания, но тем не менее это возможно сделать с помощью двух различных методов. | |
Сундук, казалось, был волшебным, так как в нем всегда были правильные костюмы, в правильных размерах, аккуратно сложенные в верхней части груды костюмов. | |
Затем везикулы, содержащие правильно сложенные белки, поступают в аппарат Гольджи. | |
Пирамида, используемая для обозначения троп, также представляет собой набор сложенных камней, но они, как правило, более долговечны. | |
Хотя в некоторых сообщениях говорится, что Пинто отделился от планера, авиадиспетчер, наблюдавший в бинокль, сказал, что правое крыло сложено. | |
На данной странице приводится толкование (значение) фразы / выражения «правило сложения», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных.
Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «правило сложения», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «правило сложения», просим написать нам в разделе «Обратная связь».
Сложение и вычитание положительных и отрицательных чисел
Правило сложения отрицательных чисел
Если вспомнить урок математики и тему «Сложение и вычитание чисел с разными знаками», то для сложения двух отрицательных чисел необходимо:
- выполнить сложение их модулей;
- дописать к полученной сумме знак «–».
Согласно правилу сложения можно записать:
$(−a)+(−b)=−(a+b)$.
Правило сложения отрицательных чисел применяется к отрицательным целым, рациональным и действительным числам.
Пример 1
Сложить отрицательные числа $−185$ и $−23 \ 789.$
Решение.
Воспользуемся правилом сложения отрицательных чисел.
Найдем модули данных чисел:
$|-185|=185$;
$|-23 \ 789|=23 \ 789$.
Выполним сложение полученных чисел:
$185+23 \ 789=23 \ 974$.
Поставим знак $«–»$ перед найденным числом и получим $−23 \ 974$.
Краткая запись решения: $(−185)+(−23 \ 789)=−(185+23 \ 789)=−23 \ 974$.
Ответ: $−23 \ 974$.
При сложении отрицательных рациональных чисел их необходимо преобразовать к виду натуральных чисел, обыкновенных или десятичных дробей.
Пример 2
Сложить отрицательные числа $-\frac{1}{4}$ и $−7,15$.
Решение.
Согласно правилу сложения отрицательных чисел, сначала необходимо найти сумму модулей:
$|-\frac{1}{4}|=\frac{1}{4}$;
$|-7,15|=7,15$.
Полученные значения удобно свести к десятичным дробям и выполнить их сложение:
$\frac{1}{4}=0,25$;
$0,25+7,15=7,40$.
Поставим перед полученным значением знак $«–»$ и получим $–7,4$.
Краткая запись решения:
$(-\frac{1}{4})+(−7,15)=−( \frac{1}{4}+7,15)=–(0,25+7,15)=−7,4$.
Ответ: $–7,4$.
Как вычитать числа с разными знаками
Правило сложения чисел с противоположными знаками:
Для сложения положительного и отрицательного числа необходимо:
- вычислить модули чисел;
выполнить сравнение полученных чисел:
- если они равны, то исходные числа являются противоположными и их сумма равна нулю;
- если они не равны, то нужно запомнить знак числа, у которого модуль больше;
из большего модуля вычесть меньший;
- перед полученным значением поставить знак того числа, у которого модуль больше.

Сложение чисел с противоположными знаками сводится к вычитанию из большего положительного числа меньшего отрицательного числа.
Правило сложения чисел с противоположными знаками выполняется для целых, рациональных и действительных чисел.
Пример 3
Сложить числа $4$ и $−8$.
Решение.
Требуется выполнить сложение чисел с противоположными знаками. Воспользуемся соответствующим правилом сложения.
Найдем модули данных чисел:
$|4|=4$;
$|-8|=8$.
Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.
Далее от большего модуля отнимем меньший модуль, получим:
$8−4=4$.
Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$
Краткая запись решения:
$4+(–8) = –(8–4) = –4$.
Ответ: $4+(−8)=−4$.
Для сложения рациональных чисел с противоположными знаками их удобно представить в виде обыкновенных или десятичных дробей.
Вычитание чисел с разными и отрицательными знаками
Правило вычитания отрицательных чисел:
Для вычитания из числа $a$ отрицательного числа $b$ необходимо к уменьшаемому $a$ добавить число $−b$, которое является противоположным вычитаемому $b$.
Согласно правилу вычитания можно записать:
$a−b=a+(−b)$.
Данное правило справедливо для целых, рациональных и действительных чисел. Правило можно использовать при вычитании отрицательного числа из положительного числа, из отрицательного числа и из нуля.
Пример 4
Вычесть из отрицательного числа $−28$ отрицательное число $−5$.
Решение.
Противоположное число для числа $–5$ – это число $5$.
Согласно правилу вычитания отрицательных чисел получим:
$(−28)−(−5)=(−28)+5$.
Выполним сложение чисел с противоположными знаками:
$(−28)+5=−(28−5)=−23$.
Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.
Ответ: $(−28)−(−5)=−23$.
При вычитании отрицательных дробных чисел необходимо выполнить преобразование чисел к виду обыкновенных дробей, смешанных чисел или десятичных дробей.
Сложение и вычитание чисел с разными знаками
Правило вычитания чисел с противоположными знаками совпадает с правилом вычитания отрицательных чисел.
Пример 5
Вычесть положительное число $7$ из отрицательного числа $−11$.
Решение.
Противоположное число для числа $7$ – это число $–7$.
Согласно правилу вычитания чисел с противоположными знаками получим:
$(−11)−7=(–11)+(−7)$.
Выполним сложение отрицательных чисел:
$(−11)+(–7)=−(11+7)=−18$.
Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.
Ответ: $(−11)−7=−18$.
При вычитании дробных чисел с разными знаками необходимо выполнить преобразование чисел к виду обыкновенных или десятичных дробей.
Правила сложения и вычитания. — Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info) — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Правила сложения и вычитания. — Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info)
Правила сложения и вычитания.
1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения)
Пример:
13+25=38, можно записать как: 25+13=38
2. Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).
Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).
Пример:
10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т.д.
3. Единицы складываются с единицами, десятки с десятками и т.д.
Пример:
34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица).
4. Единицы вычитаются из единиц, десятки из десятков и т.д.
Пример:
53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток)
примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого.
Пример:
41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29).
Ответ 29).
5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое.
Это значит, что сложение можно проверить с помощью вычитания.
Пример:
42+7=49
Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7
Примечание:
Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка.
6. Если к разности прибавить вычитаемое, то получится уменьшаемое.
Это значит, что вычитание можно проверить сложением.
Пример:
69-50=19
Для проверки к разности прибавим вычитаемое: 19+50=69.
Примечание:
Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка.
Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой.
Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2.
На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой.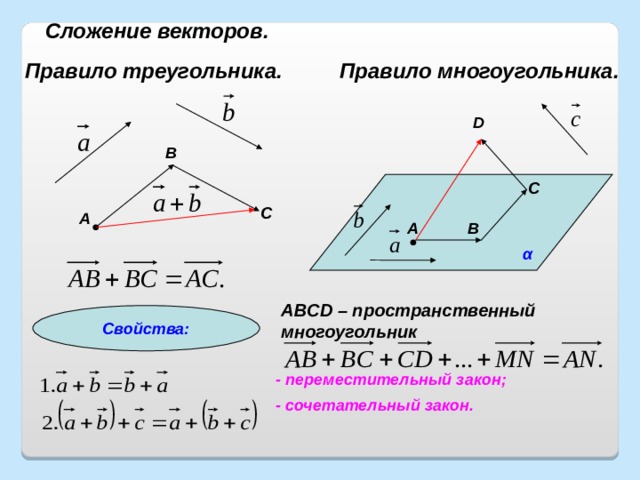 Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам.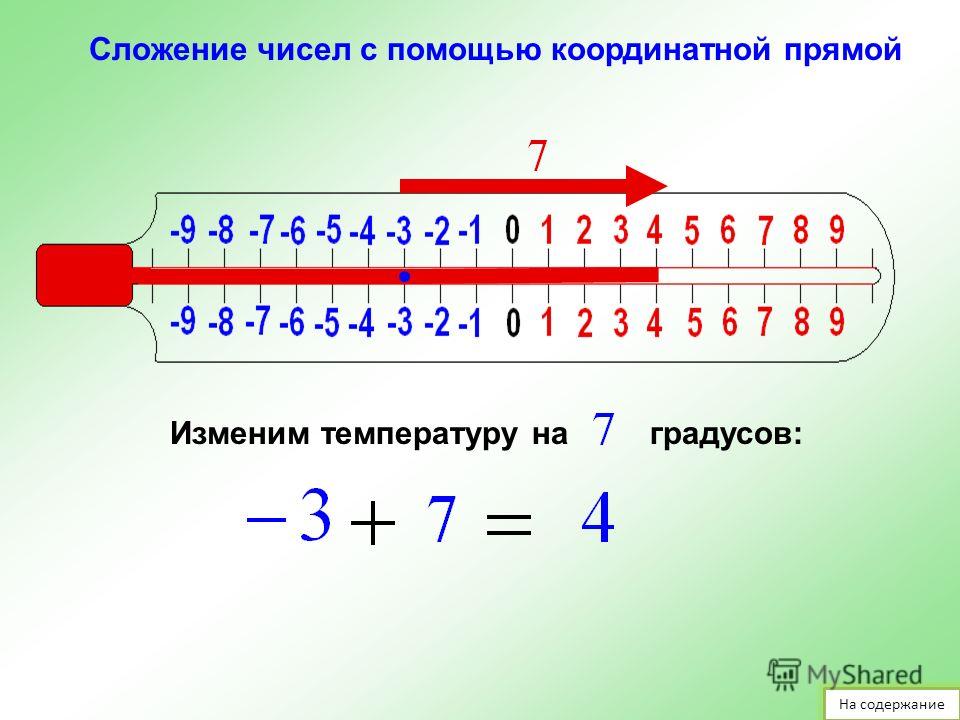
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Решение
−50 + 40 = −10
Задание 2. Найдите значение выражения:
Найдите значение выражения:
25 + (−5)
Решение
25 + (−5) = 20
Задание 3. Найдите значение выражения:
−20 + 60
Решение
−20 + 60 = 40
Задание 4. Найдите значение выражения:
20 + (−8)
Решение
20 + (−8) = 12
Задание 5. Найдите значение выражения:
30 + (−50)
Решение
30 + (−50) = −20
Задание 6. Найдите значение выражения:
27 + (−19)
Решение
27 + (−19) = 8
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Задание 11. Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Задание 12. Найдите значение выражения:
−3 + 2 − (−1)
Решение
Задание 13. Найдите значение выражения:
Найдите значение выражения:
−5 − 6 − 3
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Правила сложения и вычитания. — таблицы Tehtab.ru
Правила сложения и вычитания.
1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения)
Пример:
13+25=38, можно записать как: 25+13=38
2. Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).
Пример:
10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т. д.
3. Единицы складываются с единицами, десятки с десятками и т.д.
Пример:
34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица).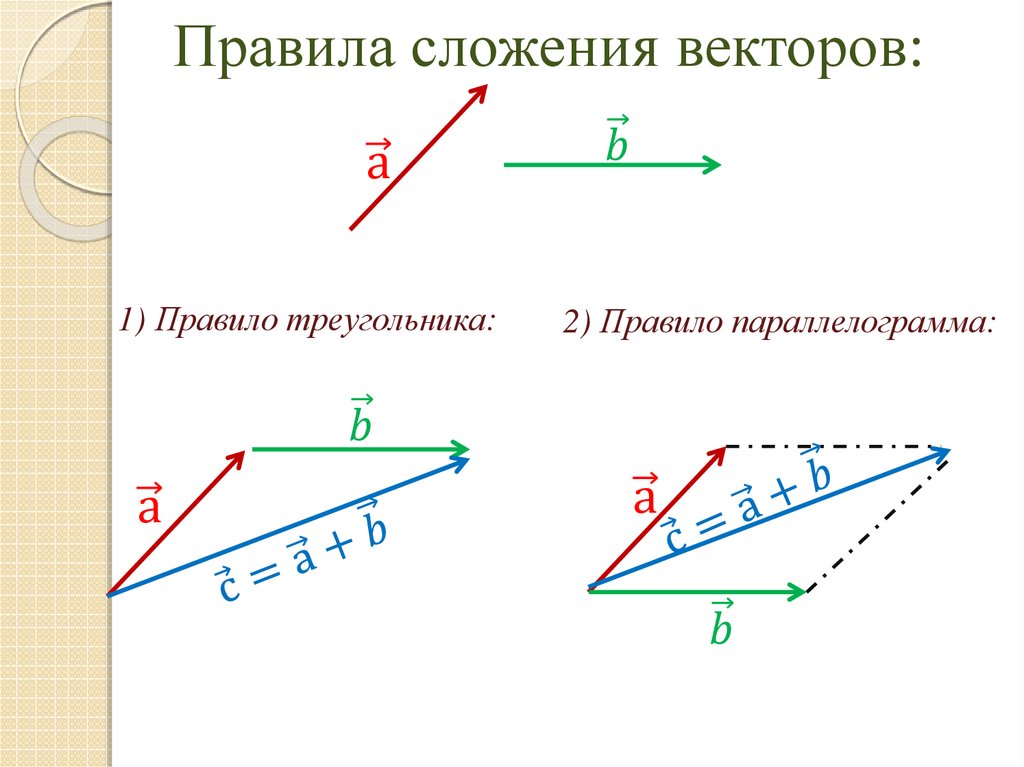
4. Единицы вычитаются из единиц, десятки из десятков и т.д.
Пример:
53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток)
примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого.
Пример:
41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29).
5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое.
Это значит, что сложение можно проверить с помощью вычитания.
Пример:
42+7=49
Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7
Примечание:
Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка.
6. Если к разности прибавить вычитаемое, то получится уменьшаемое.
Это значит, что вычитание можно проверить сложением.
Пример:
69-50=19
Для проверки к разности прибавим вычитаемое: 19+50=69.
Примечание:
Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка.
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Вычитание целых чисел, правила, примеры, сложение и вычитание целых чисел
Для полноценного разбора темы статьи введем термины и определения, обозначим смысл действия вычитания и выведем правило, согласно которому действие вычитания возможно привести к выполнению действия сложения. Разберем практические примеры. А также рассмотрим действие вычитания в геометрическом толковании – на координатной прямой.
Разберем практические примеры. А также рассмотрим действие вычитания в геометрическом толковании – на координатной прямой.
В общем, основные термины, используемые для описания действия вычитания, едины для любого типа чисел.
Определение 1
Уменьшаемое – целое число, из которого будет производиться вычитание.
Вычитаемое – целое число, которое будем вычитать.
Разность – результат выполненного действия вычитания.
Для обозначения самого действия используется знак минус, размещённый между уменьшаемым и вычитаемым. Все составные части действия, указанные выше, записываются в виде равенства. Т.е., если заданы целые числа a и b, и при вычитании из первого второго получается число c, действие вычитания запишется следующим образом: a – b = c.
Выражение вида a – b также будем обозначать как разность, как и само конечное значение этого выражения.
Смысл вычитания целых чисел
В теме вычитания натуральных чисел была установлена взаимосвязь между действиями сложения и вычитания, которая дала возможность определить вычитание как поиск одного из слагаемых по известной сумме и второму слагаемому. Примем, что вычитание целых чисел имеет такой же смысл: по заданной сумме и одному из слагаемых определяется второе слагаемое.
Примем, что вычитание целых чисел имеет такой же смысл: по заданной сумме и одному из слагаемых определяется второе слагаемое.
Указанный смысл действия вычитания целых чисел дает возможность утверждать, что c-b = a и c-a = b, если a+b = c, где a, b, c – целые числа.
Рассмотрим простые примеры для закрепления теории:
— пусть мы знаем, что -5+11 = 6, тогда разность 6-11 = -5;
— допустим, известно, что -13 + (-5) = -18, тогда -18 – (-5) = -13, а -18 – (-13) = -5.
Правило вычитания целых чисел
Указанный выше смысл действия вычитания не обозначает для нас конкретного способа вычислить разность. Т.е. мы можем утверждать, что одно из известных слагаемых – результат вычитания из суммы другого известного слагаемого. Но, если одно из слагаемых окажется неизвестным, то мы не можем знать, какова будет разность между суммой и известным слагаемым. Следовательно, для выполнения действия вычитания нам потребуется правило вычитания целых чисел:
Определение 1
Для того, чтобы определить разность двух чисел, необходимо к уменьшаемому прибавить число, противоположное вычитаемому, т. е. a – b = a+ (-b), где a и b – целые числа; b и –b – противоположные числа.
е. a – b = a+ (-b), где a и b – целые числа; b и –b – противоположные числа.
Докажем указанное правило вычитания, т.е. докажем справедливость указанного в правиле равенства. Для этого, согласно смыслу вычитания целых чисел, прибавим к a+(-b) вычитаемое b и убедимся, что получим в результате уменьшаемое a, т.е. проверим действительность равенства (a+(-b))+b = a. На основании свойств сложения целых чисел мы можем записать цепочку равенств: (a+(-b))+b = a+((-b)+b) = a+0 = a, она и будет являться доказательством правила вычитания целых чисел.
Рассмотрим применение правила вычитания целых чисел на конкретных примерах.
Вычитание целого положительного числа, примеры
Пример 1
Необходимо выполнить вычитание из целого числа 15 целого положительного числа 45.
Решение
Согласно правилу, чтобы из заданного числа 15 вычесть целое положительное число 45, нужно к уменьшаемому 15 прибавить число -45, т. е. противоположное заданному 45. Таким образом, искомая разность будет равна сумме целых чисел 15 и -45. Вычислив нужную сумму чисел с противоположными знаками, получим число -30. Т.е. итогом вычитания числа 45 из числа 15 будет число -30. Запишем все решение в одну строку: 15-45 = 15+(-45) = -30.
е. противоположное заданному 45. Таким образом, искомая разность будет равна сумме целых чисел 15 и -45. Вычислив нужную сумму чисел с противоположными знаками, получим число -30. Т.е. итогом вычитания числа 45 из числа 15 будет число -30. Запишем все решение в одну строку: 15-45 = 15+(-45) = -30.
Ответ: 15-45 = -30.
Пример 2
Необходимо вычесть из целого отрицательного числа -150 целое положительное число 25.
Решение
Согласно правилу, прибавим к уменьшаемому числу -150 число -25 (т.е. противоположное заданному вычитаемому 25). Найдем сумму целых отрицательных чисел: -150+(-25) = -175. Таким образом, искомая разность равна . Все решение запишем так: -150-25 = -150+(-25) = -175.
Ответ: -150-25 = -175.
Вычитание нуля, примеры
Правило вычитания целых чисел дает возможность вывести принцип вычитания нуля из целого числа – вычитание нуля из любого целого числа не изменяет это число, т. е. a-0 = a, где a – произвольное целое число.
е. a-0 = a, где a – произвольное целое число.
Поясним. Согласно правилу вычитания, вычитание нуля – это прибавление к уменьшаемому числа, противоположного нулю. Нуль – число, противоположное самому себе, т.е. вычесть нуль это то же самое, что прибавить нуль. На основе соответствующего свойства сложения прибавление нуля к любому целому числу не изменяет это число. Таким образом,
a-0 = a+(-0) = a+0 = a.
Рассмотрим простые примеры вычитания нуля из различных целых чисел. Например, разность 61-0 равна 61. Если же из целого отрицательного числа -874 вычесть нуль, то получится -874. Если от нуля отнять нуль, получим нуль.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Вычитание целого отрицательного числа, примеры
Пример 3
Необходимо вычесть из целого числа 0 целое отрицательное число -324.
Решение
Согласно правилу вычитания определение разности 0-(-324) необходимо произвести прибавлением к уменьшаемому числу 0 числа, противоположного вычитаемому -324. Тогда: 0-(-324) = 0+324 = 324
Тогда: 0-(-324) = 0+324 = 324
Ответ: 0-(-324) = 324
Пример 4
Определить разность -6-(-13).
Решение
Произведем вычитание из целого отрицательного числа -6 целого отрицательного числа -13. Для этого вычислим сумму двух чисел: уменьшаемого -6 и числа 13 (т. е. противоположного заданному вычитаемому -13). Получим: -6-(-13) = -6+13 = 7.
Ответ: -6-(-13) = 7.
Вычитание равных целых чисел
Если заданные уменьшаемое и вычитаемое равны, то их разность будет равна нулю, т.е. a-a = 0, где a – любое целое число.
Поясним. Согласно правилу вычитания целых чисел a-a = a+ (-a) = 0, что означает: чтобы из целого числа вычесть равное ему, нужно прибавить к этому числу число, ему противоположное, что даст в результате нуль.
Например, разность равных целых чисел -54 и -54 равна нулю; совершая действие вычитания из числа 513 числа 513, получаем нуль; отнимая от нуля нуль, получаем также нуль.
Проверка результата вычитания целых чисел
Необходимая проверка производится с помощью действия сложения. Для этого к полученной разности прибавляем вычитаемое: в итоге должно получится число, равное уменьшаемому.
Пример 5
Было произведено вычитание целого числа -112 из целого числа -300, при этом получена разность -186. Верно ли было произведено вычитание?
Решение
Выполним проверку согласно указанному выше принципу. Прибавим к заданной разности вычитаемое: -186+(-112) = -298. Мы получили число, отличное от заданного уменьшаемого, следовательно, была допущена ошибка при вычислении разности.
Ответ: нет, вычитание было произведено неверно.
Вычитание целых чисел на координатной прямой
В заключение рассмотрим геометрическое толкование действия вычитания целых чисел. Начертим горизонтальную координатную прямую, направленную вправо:
Выше мы вывели правило совершения действия вычитания, согласно ему: a-b = a+(-b), тогда геометрическое толкование вычитания чисел a и b будет совпадать с геометрическим смыслом сложения целых чисел a и –b. Из этого следует, что для вычитания из целого числа a целого числа b, необходимо:
Из этого следует, что для вычитания из целого числа a целого числа b, необходимо:
— сдвинуться из точки с координатой a на b единичных отрезков влево, если b – положительное число;
— сдвинуться из точки с координатой a на |b| (модуль числа b) единичных отрезков вправо, если b – отрицательное число;
— остаться в точке с координатой a, если b = 0.
Рассмотрим на примере с применением графического изображения:
Пусть необходимо вычесть из целого числа -2 целое положительное число 2. Для этого, согласно вышеуказанной схеме, переместимся влево на 2 единичных отрезка, попадая, таким образом, в точку с координатой -4, т.е. -2-2 = -4.
Еще один пример: вычитаем из целого числа 2 целое отрицательное число -3. Тогда, согласно схеме, переместимся вправо на |-3| = 3 единичных отрезка, попадая, таким образом, в точку с координатой 5. Получаем равенство: 2-(-3) = 5 и иллюстрацию к нему:
| 1. |
Порядок действий
Сложность: лёгкое |
3 |
| 2. |
Значение выражения. Сложение и вычитание
Сложность: среднее |
2 |
| 3. |
Значение выражения. Вычитание и сложение
Сложность: среднее |
2 |
| 4. |
Сравнение выражений
Сложность: среднее |
3 |
| 5. |
Выражение со скобками (сложение)
Сложность: среднее |
2 |
6.
|
Выражение со скобками (вычитание)
Сложность: среднее |
2 |
| 7. |
Выражение со скобками (сложение и вычитание)
Сложность: среднее |
3 |
Сложение и вычитание целых чисел с разными знаками
Сложение
При сложении двух целых чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится их общий знак.
Примеры:
(+3) + (+7) = 10,
(-3) + (-7) = -10.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух целых чисел с разными знаками нужно взять их абсолютные величины и из большей вычесть меньшую, в результате ставится знак того числа, у которого абсолютная величина больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4) + (+11) = 7, так как 11 — 4 = 7;
(-5) + (+2) = -3, так как 5 — 2 = 3.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
(-7) + 7 = 0,
(+12) + (-12) = 0.
Вычитание
Вычитание одного целого числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным.
Примеры:
(+6) — (+5) = (+6) + (-5) = 1,
(+6) — (-5) = (+6) + (+5) = 11,
(-6) — (-5) = (-6) + (+5) = -1,
(-6) — (+5) = (-6) + (-5) = -11.
Из данных примеров следует, что, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
При решении выражений, содержащих и сложение, и вычитание, можно сначала заменить вычитание сложением, затем отдельно сложить положительные и отрицательные слагаемые, а потом найти сумму получившихся чисел.
Пример.
12 — 18 + 41 — 9.
Решение: Заменим вычитание на сложение:
12 + (-18) + 41 + (-9),
сгруппируем слагаемые по их знакам и сложим отдельно положительные и отрицательные числа:
(12 + 41) + ((-18) + (-9)) = 53 + (-27).
Теперь осталось только найти сумму двух получившихся результатов:
53 + (-27) = 26, значит 12 — 18 + 41 — 9 = 26.
Правила сложения и вычитания целых чисел
Положительные целые числа, которые вы уже знаете как натуральные числа, и мы уже рассмотрели сложение и вычитание натуральных чисел, поэтому вместо этого мы сосредоточимся на отрицательных целых числах. Когда дело доходит до сложения и вычитания целых , существует несколько простых правил, и, чтобы немного изменить ситуацию, мы представим их в виде списка. Итак, вот правила сложения и вычитания отрицательных чисел.
Итак, вот правила сложения и вычитания отрицательных чисел.
1. Минус перед числом меняет знак числа.
Чтобы понять это правило, мы позвоним на помощь парочку старых друзей — числовую прямую и умножение натуральных чисел. Помните, как умножение числа на число 1 дает в результате то же самое число? Ну, поставить минус перед числом — это сокращение для умножения этого числа на -1. Расстояние от исходной точки на числовой прямой остается неизменным, но минус смещает его на противоположную сторону числовой прямой.
Итак, если мы поставим минус перед положительным целым числом, мы получим отрицательную версию того же целого числа. А если поставить минус перед целым отрицательным числом, то в результате мы получим его положительную версию.
Используя математический язык, это означает, что:
$ 2 \ cdot (-1) = — 2 $
и
$ -2 \ cdot (-1) = 2.
$
2. Если за оператором стоит отрицательное целое число, оно должно быть заключено в круглые скобки.
Это здесь, чтобы избежать путаницы, потому что знак минус также является оператором вычитания. Если поставить два оператора рядом, непонятно, если:
- один из них знак, а не оператор
- одна из них опечатка, или
- между ними отсутствует число или переменная.
Чтобы упростить задачу, было создано правило, заключающее отрицательные целые числа в квадратные скобки (скобки). Таким образом, все знают, что минус поставлен специально и что это знак.
Например: $ -3 + (-5) = -8 \ Rightarrow — 3-5 = -8 $
Хотя во время сложения и вычитания ошибок можно избежать, используя правило номер один, это правило будет незаменимым во время умножения.
3. Сложение двух отрицательных целых чисел всегда дает в результате отрицательное целое число.
Отрицательное целое число представляет собой расстояние от единственной точки, расположенной слева от исходной точки на числовой прямой, до самой исходной точки.Когда мы складываем два отрицательных целых числа вместе, мы получаем сумму расстояний до них. Но поскольку оба они расположены слева от исходной точки на числовой прямой, мы сохраняем это направление. Как это:
Но поскольку оба они расположены слева от исходной точки на числовой прямой, мы сохраняем это направление. Как это:
4. Вычитание отрицательного целого числа из другого отрицательного целого числа дает только отрицательное целое число в некоторых случаях.
Как так получилось, спросите вы? Что ж, запомните первое правило — минус перед числом меняет знак числа. Это также относится к отрицательным целым числам. Если поставить минус перед целым отрицательным числом, оно превратится в целое положительное. И когда мы добавляем положительное целое число к любому числу, мы перемещаемся вправо по числовой строке.
Итак, что произойдет, если вычитаемое (второе число) больше, чем уменьшаемое (первое число)? Когда оно превратится в положительное целое число, мы переместимся за точку отсчета и в результате получим положительное целое число.
5. Вычитание положительного целого числа из отрицательного целого числа в основном то же самое, что сложение двух отрицательных целых чисел, и в результате всегда будет получаться отрицательное целое число.
И снова правило номер один — минус перед целым положительным числом меняет знак. Когда это происходит, мы фактически складываем два отрицательных целых числа вместе, и мы рассмотрели это в правиле номер два.
6. Сложение отрицательного целого числа с положительным целым числом — это, по сути, тот же процесс, что и вычитание двух натуральных чисел.
Это простой. Такое выражение, как 5 + (-3), можно легко записать как 5-3, и результат будет тем же:
$ 5 + (-3) = 5 — 3 = 2 $
Единственное, на что мы должны обратить внимание, — это если отрицательное число больше положительного.В этом случае результатом будет отрицательное число.
7. Коммутативное свойство сложения и ассоциативное свойство сложения, которые действительны для натуральных чисел, действительны и для целых чисел.
Коммутативное свойство сложения и ассоциативное свойство сложения одинаковы как для натуральных, так и для целых чисел. Просто будьте осторожны, перемещая знаки, и все будет в порядке.
Понимание этих правил помогает нам решать практические задачи.Теперь мы знаем, как решить задачу из предыдущего урока. Повторим задачу:
Температура воздуха сегодня в полдень была 39,2 ° F, а к вечеру температура воздуха упала на 42,8 ° F. Какая была температура воздуха вечером?
Решение:
39,2–42,8 долл. США = -3,6 долл. США
долл. США
Теперь мы знаем, что температура вечером была -3,6 ° F.
Если вы хотите немного попрактиковаться, мы подготовили для вас несколько рабочих листов. Вы можете скачать их по ссылкам ниже.
Рабочие листы сложения и вычитания целых чисел
Два целых числа (96,0 КиБ, 1797 совпадений)
Три целых числа (261,5 КиБ, 1286 совпадений)
Четыре целых числа (325,1 КиБ, 1253 совпадений)
чисел — сложение и вычитание целых чисел
ср
может использовать числовую линию в качестве модели, чтобы помочь нам визуализировать сложение и вычитание
целых чисел со знаком. Просто представьте, что сложение и вычитание — это
числовая строка.Есть также несколько правил и свойств, которые определяют, как
для выполнения этих основных операций.
Просто представьте, что сложение и вычитание — это
числовая строка.Есть также несколько правил и свойств, которые определяют, как
для выполнения этих основных операций.
Чтобы добавить целые числа с тем же знаком, оставьте тот же знак и добавьте абсолютное значение каждого номер.
Чтобы добавить целые числа с разными знаками держите знак числа с наибольшим абсолютным значение и вычтите наименьшее абсолютное значение из наибольшего.
Вычесть целое число, добавив его противоположность.
Осторожно! В отрицательное отрицательное число — противоположное положительное число. То есть по-настоящему числа,
— (- а) = +
Вот как сложить два положительных целых числа:
4 + 7 =?
Если начать
при положительном числе четыре на числовой прямой и перемещении на семь единиц вправо, вы
в итоге окажется положительным одиннадцать. Кроме того, эти числа имеют одинаковый знак, поэтому вы
можно просто оставить знак и сложить их абсолютные значения, чтобы получить тот же ответ,
положительный одиннадцать.
Вот как сложите два отрицательных целых числа:
-4 + (-8) =?
Если начать при отрицательном значении четырех на числовой прямой и перемещении восьми единиц влево, вы в конечном итоге на двенадцать. Кроме того, эти числа имеют одинаковый знак, поэтому вы можно просто оставить отрицательный знак и сложить их абсолютные значения, чтобы получить тот же ответ, двенадцать отрицательных.
Вот как добавить положительное целое число к отрицательному:
-3 + 6 =?
Если начать при отрицательных трех на прямой числовой строке и переместите шесть единиц вправо, в итоге вы получите три положительных числа.Кроме того, эти числа имеют разные знаки,
так что держите знак из целого числа, имеющего наибольшее абсолютное значение, и вычесть наименьшее абсолютное значение из наибольшего.
Вычесть три от шести и сохраните положительный знак, снова дав положительный тройку.
Вот как добавить отрицательное целое число к положительному целому:
5 + (-8) =?
Если начать
при положительном пятерке на прямой числовой строке и переместите восемь единиц влево,
в итоге вы получите минус три. Кроме того, эти целые числа имеют разные знаки, поэтому
сохраните знак у целого числа, имеющего наибольшее абсолютное значение, и вычтите
наименьшее абсолютное значение из наибольшего или вычтите пять из восьми
и снова оставьте отрицательный знак
давая отрицательные три.
Кроме того, эти целые числа имеют разные знаки, поэтому
сохраните знак у целого числа, имеющего наибольшее абсолютное значение, и вычтите
наименьшее абсолютное значение из наибольшего или вычтите пять из восьми
и снова оставьте отрицательный знак
давая отрицательные три.
Вычесть число, добавьте его противоположность:
5-8 =?
Потому что они дают тот же результат, вы можете видеть, что вычитание восьми из пяти эквивалентно чтобы добавить отрицательные восемь к положительным пяти.Ответ — 3.
Вычесть число, добавьте его противоположность:
-3 — (-6) =?
Потому что они дают тот же результат, вы можете увидеть, что вычитая отрицательные шесть из отрицательных три эквивалентно добавлению положительных шести к отрицательным трем. Ответ 3.
назад наверх
Предалгебра: правила математики: вычитание
Вы помните все те правила, о которых мы рассказывали для дополнения? Мы рассказали вам о коммутативном законе , ассоциативном законе и дополнительных тождествах. Когда вы смотрите на картину в целом, ни один из этих законов не работает на вычитание. Вы не можете переупорядочить, перемешать или перегруппировать задачи вычитания так же, как сложение. С вычитанием нужно быть очень осторожным.
Когда вы смотрите на картину в целом, ни один из этих законов не работает на вычитание. Вы не можете переупорядочить, перемешать или перегруппировать задачи вычитания так же, как сложение. С вычитанием нужно быть очень осторожным.
20-8-6 = 6
8-6-20 = -18 (вы не можете переставить и получить тот же ответ)
(20-8) — 6 = 6
20 — (8-6) = 18 (вы не можете перегруппироваться и получить тот же ответ)
Некоторые правила все еще работают на вычитание. Порядок операций, который вы используете, по-прежнему работает.Найдите скобок и сначала работайте внутри этих блоков. Посмотрите, как эти проблемы выходят с очень разными ответами, если вы игнорируете круглые скобки.
(20-8) — (6-4) = 12-2 = 10
20-8-6-4 = 2
Некоторые из ваших домашних задач включают сложение и вычитание. Можете ли вы использовать какой-либо из законов сложения, чтобы решить эти проблемы или упростить задачу? Да.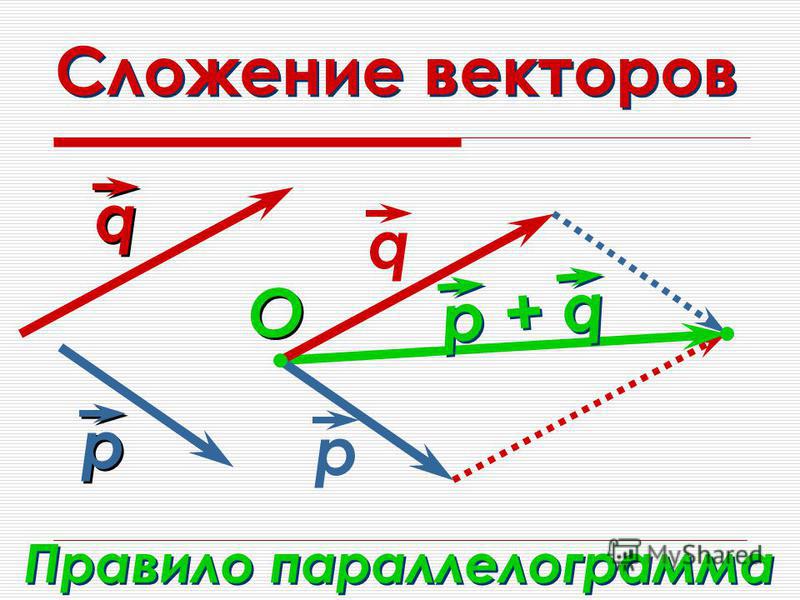 Давайте посмотрим на пример …
Давайте посмотрим на пример …
5 + 6-8-2 + 9-1 =?
Итак, как мы можем это решить? Можем ли мы перемещать вещи? Да, но только значения с символами сложения.
5 + 6-8-2 + 9-1 = 9
5 + 6 + 9-8-2-1 = 9
Тот же ответ. Мы переместили только добавляемые значения. Мы оставили значения для вычитания в том же порядке. На вычитание законы не распространяются.
Мы хотим прямо сейчас представить большую идею в математике. Мы объяснили, что вы не можете использовать какие-либо тождества сложения или законы для задач вычитания. Найдите минутку и подумайте о проблеме вычитания и о том, что это такое на самом деле. Для простых целых чисел, когда вы вычитаете, вы фактически добавляете отрицательные числа.Итак, 3-2 — это то же самое, что 3 + (-2). Этот факт означает, что каждая задача на вычитание на самом деле является замаскированной проблемой сложения.
Пример:
3 — 2 = 1
3 + (-2) = 1
18-13 = 5
18 + (-13) = 5
20-6-5-2 = 7
20 + (-6) + (-5) + (-2) = 7
Замечательная идея состоит в том, что после того, как вы создали задачу сложения, вы можете перемешать и сгруппировать вещи, как вы это делали раньше. Поскольку все наши операции являются сложением, все законы снова работают.В качестве примечания для вас: мы используем круглые скобки, чтобы упростить просмотр отрицательных чисел, когда с ними возникла проблема.
Поскольку все наши операции являются сложением, все законы снова работают.В качестве примечания для вас: мы используем круглые скобки, чтобы упростить просмотр отрицательных чисел, когда с ними возникла проблема.
20 + (-6) + (-5) + (-2) = 7
(-2) + (-6) + 20 + (-5) = 7
(-8) + 15 = 7
15 + ( -8) = 7
15-8 = 7 (мы вернули отрицательное значение в задачу вычитания)
Это не облегчит решение всех ваших проблем, но об этом важно помнить. Законы, тождества и аксиомы в математике можно использовать как маленькие уловки, когда вы начинаете решать более сложные математические задачи.Никогда не забывайте, что математические правила — ваши друзья. Они всегда помогут указать вам путь, который приведет к правильному ответу.
Четыре математических правила
Четыре правила математики
Понятия сложения, вычитания, умножения и деления — это сложные абстрактные идеи, которые взаимосвязаны.
1. Правила добавления:
положительный + положительный = (добавить) положительный
Пример: 2 + 1 = 3
отрицательный + отрицательный = (добавить) отрицательный
Пример: −3+ (−5) = −8
отрицательный + положительный = (вычесть)
Пример: 2 + (−10) = −8
Знак числа с наибольшим абсолютным значением
Пример: −14 + 16 = 2
Примечание: — (- 7) означает противоположное (−7) = 7
2.

Правила вычитания:
Замените все вычитание на сложение и возьмите знак, противоположный следующему числу, затем следуйте правилам сложения.
Пример: −7 — (9)
означает −7 + (- 9) = -16
Пример: −3 — (- 10)
−3 + (10) = 7
Пример:
−8 + (−9) — (- 1) −2 (изменить все знаки вычитания)
−8 + (−9) + (1) + (−2) (сложение и вычитание слева направо)
−17 + (1) + (−2)
−16 + (- 2) = −18
Сложение и вычитание с отрицательными числами:
При сложении и вычитании положительных и отрицательных чисел полезно помнить следующие правила.
Если операция и знак совпадают, они работают как добавление (положительного) числа, так что
— — работает как & plus; и плюс;
Если операция и знак различаются, они работают как вычитание (положительного) числа, так что
и плюс; — работает как — & plus;
3 и 4.
Правила умножения / деления:
Правила умножения и деления одинаковы.
положительный (& cross; или ÷) положительный = положительный
Пример: 10 ÷ 2 = 5
отрицательное (& cross; или ÷) отрицательное = положительное
Пример: −4 & крест; (- 3) = 12
отрицательное (& cross; или ÷) положительное = отрицательное
Пример: 18 ÷ (−2) −9
Умножение и деление на отрицательные числа:
При умножении пар положительных и отрицательных чисел полезно помнить следующие правила: Если знаки у чисел совпадают, ответ — положительное число.
(& плюс;) & крест; (& плюс;), ответ (& плюс;)
(-) и крестик; (-), ответ (& плюс;)
(& plus;) ÷ (& plus;), ответ (& plus;)
(-) ÷ (-), ответ (& плюс;)
Если знаки у чисел разные, ответ — отрицательное число.
(& плюс;) & крест; (-), ответ (-)
(-) и крестик; (& плюс;), ответ (-)
(& plus;) ÷ (-), ответ (-)
(-) ÷ (& plus;), ответ (-)
Сложение и вычитание целых чисел | Правила | Примеры
Вы уже знаете о сложении и вычитании целых чисел. Вы знаете, что целые числа являются частью целых чисел? Целые числа включают целые числа и их отрицательные числа. Каждое число в числовой строке, не имеющее дробной части, является целым числом. Но можем ли мы, как и целые числа, складывать или вычитать целые числа? Например, если температура в вашем городе была 2 º C, а она упала на 7 º C. Какая сейчас температура в вашем городе?
Вы знаете, что целые числа являются частью целых чисел? Целые числа включают целые числа и их отрицательные числа. Каждое число в числовой строке, не имеющее дробной части, является целым числом. Но можем ли мы, как и целые числа, складывать или вычитать целые числа? Например, если температура в вашем городе была 2 º C, а она упала на 7 º C. Какая сейчас температура в вашем городе?
Сложение и вычитание целых чисел — это две операции, которые мы выполняем с целыми числами для увеличения или уменьшения их значений.Давайте продолжим и узнаем больше об этих двух основных операциях с целыми числами.
Что означает сложение и вычитание целых чисел?
Целые числа — это натуральные числа, отрицательные значения этих чисел или ноль. Целое число — это целостная сущность. Целые числа — это числа, которые могут быть положительными, отрицательными или нулевыми, числами без дробной части (без десятичных знаков). Как и целые числа, мы можем складывать или вычитать целые числа.
Сложение и вычитание целых чисел означает выполнение операций сложения и вычитания двух или более целых чисел путем помещения между ними операторов сложения и вычитания.Прежде чем углубляться в концепцию, очень важно узнать, что такое абсолютное значение целого числа. В числовой строке расстояние числа от 0 называется абсолютным значением целого числа. А расстояние не указывает направление, поскольку это скалярная величина. Это всегда положительно.
Добавление обычно означает увеличение значения. Но в случае целых чисел операция сложения может привести к увеличению или уменьшению значения данного числа. Если мы добавим отрицательное целое число, значение данного числа уменьшится, а если мы добавим положительное целое число, значение увеличится.Рассмотрим следующие примеры.
У Салли 3 шарика. Еще 4 она получает от брата. Итак, у нее сейчас (3 + 4 = 7) шариков.
Температура увеличивается с -4 на 5 º по Фаренгейту. Таким образом, повышение температуры составляет (-4 + 5 = 1).
В приведенных выше примерах мы использовали концепцию сложения целых чисел. Показывая сложение целых чисел в числовой строке, мы должны двигаться вправо или в положительную сторону, когда мы добавляем положительное целое число к данному числу.С другой стороны, когда мы добавляем отрицательное число, мы перемещаемся к левой стороне числовой строки, поскольку мы вынимаем какое-то значение из данного числа, поэтому результирующее число будет меньше исходного числа.
Сложение и вычитание целых чисел лучше всего можно продемонстрировать на числовой прямой. Но работать с числовой прямой, как только возникает задача сложения, занимает очень много времени. Итак, давайте изучим все правила сложения целых чисел.
Правила сложения целых чисел
Когда мы узнаем о сложении целых чисел, три случая возникают как правило сложения целых чисел, а именно:
- Сложение двух положительных чисел
- Сложение положительного числа и отрицательного числа
- Сложение двух отрицательных чисел
Давайте изучим эти правила одно за другим.
| Правило | Пояснение | Примеры | |
| Сложение двух положительных чисел | (+ а) + (+ б) = (а + б) | При сложении двух положительных чисел мы просто складываем оба числа и получаем ответ, который является положительным значением, как при сложении целых чисел. | 3 + 4 = 7 2 + 11 = 13 |
| Сложение положительного числа и отрицательного числа | (а + (- б) = (а-б) | При сложении положительного и отрицательного числа берем разность абсолютных значений обоих чисел и к ответу добавляем знак большего числа. | 4 + (- 5) = (- 1) (-5) + 7 = 2 |
| Сложение двух отрицательных чисел | (-a) + (- b) = — (a + b) | Складывая два отрицательных числа, мы берем сумму обоих чисел и добавляем отрицательный знак к ответу. | (-2) + (- 4) = (- 6) (-5) + (- 8) = (- 13) |
На изображении ниже соблюдайте все три правила сложения для целых чисел в числовой строке.
Вычитание обычно означает уменьшение значения.Но в случае целых чисел операция вычитания может привести к увеличению или уменьшению значения данного числа. Если мы вычтем отрицательное целое число из числа, значение данного числа увеличится, а если мы вычтем положительное целое число, значение уменьшится. Рассмотрим несколько примеров, приведенных ниже, и обратите внимание на операцию, которую мы используем с целыми числами.
Рабочий спускается по лестнице на 2 ступеньки от 5 ступени, над которой он работает: (5 — 2 = 3)
Температура падает на 4 º с -1 º по Фаренгейту: (-1-4 = -5)
В приведенных выше примерах мы используем концепцию вычитания целых чисел.Показывая вычитание целых чисел в числовой строке, мы должны двигаться к левой или отрицательной стороне, когда мы вычитаем положительное число из данного числа. С другой стороны, мы перемещаемся в правую или положительную сторону, когда вычитаем отрицательное число из данного числа.
Правила вычитания целых чисел
Вы должны знать, что сложение и вычитание — обратные операции. Итак, любую задачу на вычитание можно записать как задачу сложения.Давайте узнаем, как это сделать, на нескольких примерах.
Итак, любую задачу на вычитание можно записать как задачу сложения.Давайте узнаем, как это сделать, на нескольких примерах.
2-4 = 2 + (- 4)
6-3 = 6 + (- 3)
-4-3 = -4 + (- 3)
При написании любой задачи на вычитание мы должны взять знак вычитания внутри скобок и добавить оператор сложения между обоими членами. Это один из способов решения вопросов на вычитание.
Давайте изучим правила вычитания, чтобы упростить вычисления при работе с целыми числами.
| Правило | Пояснение | Примеры | |
| Вычитание двух положительных чисел | (+ a) — (+ b) = a-b | При вычитании двух положительных чисел мы просто берем разность абсолютных значений обоих чисел и прикрепляем к ответу знак большего числа. | 3-4 = -1 11-2 = 9 |
| Вычитание положительного числа и отрицательного числа | а — (- б) = (а + б) (-a) -b = — (a + b) | При вычитании положительного и отрицательного числа мы берем сумму абсолютных значений обоих чисел и присоединяем к ответу знак уменьшаемого числа. | 4 — (- 5) = 9 (-5) -7 = -12 |
| Вычитание двух отрицательных чисел | (-a) — (- b) = ± (a-b) | При вычитании двух отрицательных чисел мы просто должны помнить одно правило: всякий раз, когда стоит отрицательный знак за пределами скобки, знак члена внутри скобки будет изменен.Затем мы должны взять разность абсолютных значений обоих чисел и приложить исправленный знак большего числа к ответу. | (-2) — (- 4) = 2 (-8) — (- 5) = (- 3) |
Что следует помнить:
- Если у числа нет знака, мы рассматриваем его как положительное число. Например, 2 можно переписать как +2.
- Каждый факт вычитания можно переписать как факт сложения. Например, 9-10 можно переписать как 9 + (- 10).
- Всегда записывайте отрицательные числа в скобках в выражении.
- Если есть выражение, в котором есть и операции сложения, и вычитания, мы можем сначала решить любой оператор. Например, 9-10 + 4.
 В этом выражении мы можем либо сначала решить (9-10), либо сначала (-10 + 4). Это не повлияет на наш ответ.
В этом выражении мы можем либо сначала решить (9-10), либо сначала (-10 + 4). Это не повлияет на наш ответ.
Какое правило сложения положительного и отрицательного целого числа?
Правило сложения положительного и отрицательного целого числа гласит, что необходимо вычислить разницу между двумя целыми числами, чтобы найти их сложение.Знак результата будет таким же, как у большего из двух целых чисел.
Что такое целое число в математике?
Целое число — это число без десятичной или дробной части из набора отрицательных и положительных чисел, включая ноль. Примеры целых чисел: -5, 0, 1, 5, 8, 97, 34 и т. Д.
Каковы правила вычитания целых чисел?
Каждый факт вычитания можно переписать как факт сложения. Итак, мы можем применять правила сложения и к задачам на вычитание.
Какое правило сложения и вычитания отрицательных чисел?
- К прибавляем два отрицательных числа, берем сумму обоих чисел и добавляем отрицательный знак к ответу.

- Пока вычитает двух отрицательных чисел, мы просто должны помнить одно правило, что всякий раз, когда есть отрицательный знак за пределами скобки, знак члена внутри скобки будет изменен. Затем мы должны взять разность абсолютных значений обоих чисел и приложить исправленный знак большего числа к ответу.
Как складывать или вычитать целые числа?
Сложение и вычитание целых чисел можно производить с помощью числовой строки и при соблюдении определенных правил сложения и вычитания.
Каковы свойства целых чисел?
С целыми числами можно выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление. Основные свойства целых чисел:
- Свойство закрытия
- Ассоциативное свойство
- Коммутативная собственность
- Распределительная собственность
- Аддитивное обратное свойство
- Мультипликативное обратное свойство
- Собственность идентичности
Каковы применения целых чисел?
Положительные и отрицательные числа применяются в реальном мире по-разному. Обычно они используются для представления двух противоречащих друг другу ситуаций.
Обычно они используются для представления двух противоречащих друг другу ситуаций.
- Целые числа часто применяются в реальной жизни для измерения температуры. Отрицательные и положительные числа и ноль на шкале обозначают разные показания температуры.
- Банковские кредитные и дебетовые отчеты также используют целые числа для представления отрицательных или положительных значений суммы.
| Вы здесь: На главную → Статьи → Целые числа В этой статье объясняются передовые методы обучения целым числам и их операциям. Узнайте, как объяснить учащимся, почему работают различные правила. В конце вы найдете две печатные информационные бюллетени для загрузки, в которых резюмируются правила сложения, вычитания, умножения и деления целых чисел. Дополнение
Вычитание У вас есть несколько вариантов, как представить вычитание целых чисел. Лично при вычитании положительного целого числа я думаю о скачках числовой строки, а при вычитании отрицательного целого числа («двойное отрицательное») я заменяю их на сложения.
На видео ниже показано, как использовать ТРИ из этих различных моделей для вычитания целых чисел: 1) модель числовой линии, 2) концепция разности и 3) счетчики. УмножениеСамый быстрый способ умножить отрицательные числа — это запомнить эти маленькие правила: отрицательный × отрицательный положительный отрицательный × положительный отрицательный Другими словами, если два целых числа имеют разный знак, то произведение отрицательное, в противном случае — положительное. Но давайте также объясним, ПОЧЕМУ это так работает.
Деление целых чиселСледуют правила деления на отрицательные числа, потому что деление — это операция, противоположная умножению. Например, что такое (−21) ÷ (−7)? Назовем ответ на это А. Итак (−21) ÷ (−7) = A. Отсюда следует, что A × (−7) = (−21) Зная правила умножения, единственное подходящее число — 3. Итак (−21) ÷ (−7) = 3. Вы можете сделать аналогичные случаи для (−21) ÷ 7 и 21 ÷ (−7). На самом деле математики использовали бы не конкретные числа, такие как 21 и 7, а переменные. Я использовал конкретные числа, чтобы аргументировать легче понять, к тому же так вы, вероятно, объяснили бы это в 6-м или 7-м классе. Конечно, студенты будут запоминать небольшие правила деления целых чисел и использовать их в вычислениях, но изучение того, откуда берутся эти правила, очень поучительно и, как мне кажется, необходимо. Информационные бюллетени по целым числам Вы можете загрузить и распечатать эти информационные бюллетени по целочисленным операциям для своих студентов. Все, что мне нужно, — это не изменять их. Эти информационные листки взяты из собрания заданий 7-го класса по математике «Мамонт». |
Правила для положительных и отрицательных чисел
Положительные и отрицательные числа — это два широких класса чисел, которые используются в математике, а также в повседневных транзакциях, таких как управление деньгами или измерение веса.
- Положительное число имеет значение больше нуля. Его знак положительный, но обычно он пишется без знака плюса перед ним (например, 4, 51, а не +4, +51).
- Отрицательное число имеет значение меньше нуля.Его знак считается отрицательным и пишется со знаком минус перед ним (например, -2, -23).
- Сумма положительного числа и равного ему отрицательного числа равна нулю.
- Ноль не является ни положительным, ни отрицательным числом.
Существуют правила сложения, вычитания, умножения и деления положительных и отрицательных чисел. Как правило, легче выполнять операции с отрицательными числами, если они заключены в квадратные скобки, чтобы разделять их. Числовые линии также упрощают понимание положительных чисел и чисел.
Числовые линии также упрощают понимание положительных чисел и чисел.
Сложение и вычитание положительных и отрицательных чисел
Когда вы складываете или вычитаете положительные и отрицательные числа, знак ответа зависит от того, похожи ли знаки или какое число имеет большее значение.
Сложить положительные и отрицательные числа просто, если оба числа имеют одинаковый знак. Просто найдите сумму чисел и держите знак. Например:
- 3 + 2 = 5
- (-4) + (-2) = -6
Найдите сумму положительного и отрицательного числа, вычтя число с меньшим значением из числа с большее значение.Знак — это знак большего числа.
- (-7) + 2 = -5
- 4 + (-8) = 4-8 = -4
- (-3) + 8 = 5
- 10 + (-2) = 10-2 = 8
- (-5) + 4 = -1
Правила вычитания аналогичны правилам сложения. Для двух положительных чисел, если первое число больше второго, результатом будет другое положительное число.
Если вы вычтите большое положительное число из меньшего положительного числа, вы получите отрицательное число.
Легкий способ сделать это — вычесть меньшее число из большего числа и изменить знак ответа на минус.
Когда вы вычитаете положительное число из отрицательного, это то же самое, что прибавлять отрицательное число. Другими словами, это делает отрицательное число более отрицательным.
- (-4) — 3 = (-4) + (-3) = -7
- (-10) — 12 = (-10) + (-12) = -24
Вычитание отрицательного числа из положительного числа отменяет отрицательные знаки и становится простым сложением.Это делает положительное число более положительным.
- 4 — (-3) = 4 + 3 = 7
- 5 — (-2) = 5 + 2 = 7
Когда вы вычитаете отрицательное число из другого отрицательного числа, отрицательные знаки снова отменяют каждое другое, чтобы стать знаком плюс. Ответ имеет знак большего числа.
- (-2) — (-7) = (-2) + 7 = 5
- (-5) — (-3) = (-5) + 3 = -2
Умножение и деление положительного числа и отрицательные числа
Если вы умножите или разделите одинаковые знаки, вы получите положительное число.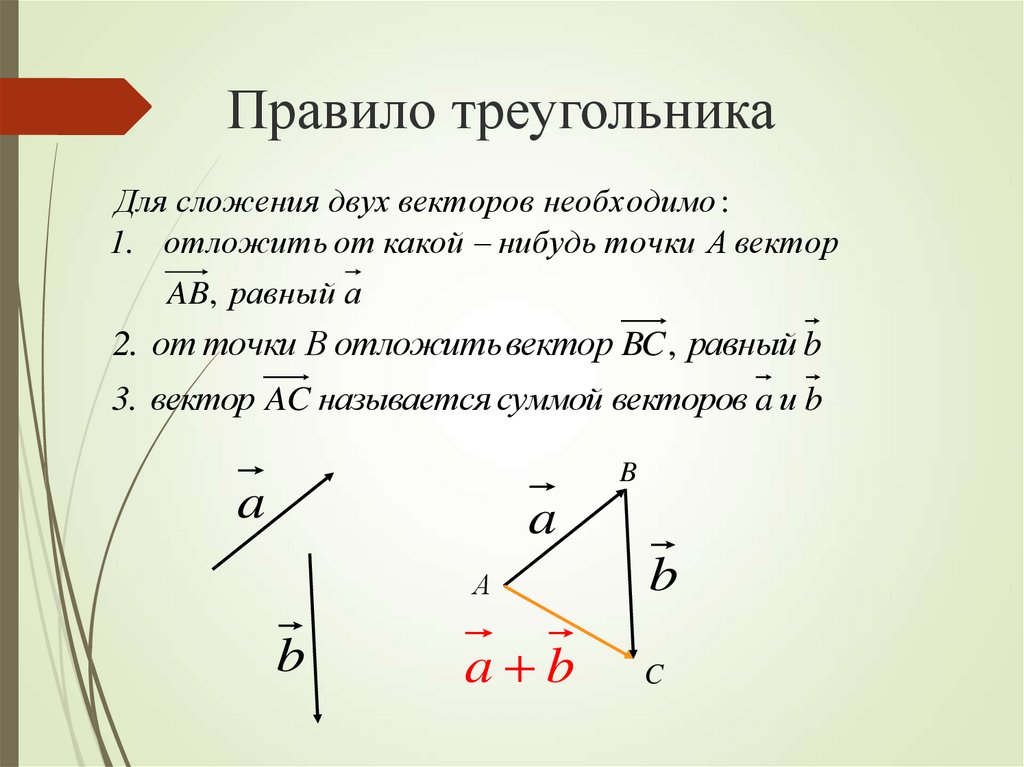 Умножение или деление положительных и отрицательных чисел дает отрицательное число.
Умножение или деление положительных и отрицательных чисел дает отрицательное число.
Правила умножения и деления просты:
- Если оба числа положительные, результат будет положительным.
- Если оба числа отрицательны, результат положительный. (По сути, два отрицательных значения компенсируют друг друга).
- Если одно число положительное, а другое отрицательное, результат будет отрицательным.
- Если вы умножаете или делите несколько чисел знаками, сложите количество положительных и отрицательных чисел.Знак избытка — знак ответа.
- Умножение любого числа (положительного или отрицательного) на ноль дает ответ 0.
- Ноль, разделенный на любые числа, равен 0.
- Любое число, деленное на ноль, равно бесконечности.
Вот несколько примеров. В этих примерах используются целые числа (целые числа), но те же правила применяются к десятичным и дробным числам.
- 4 x 5 = 20
- (-2) x (-3) = 6
- (-6) x 3 = -18
- 7 x (-2) = -14
- 2 x (-3 ) x 4 = -24
- (-2) x 2 x (-3) = 12
- 12/2 = 6
- (-10) / 5 = -2
- 14 / (-7) = -2
- (-6) / (-2) = 3
.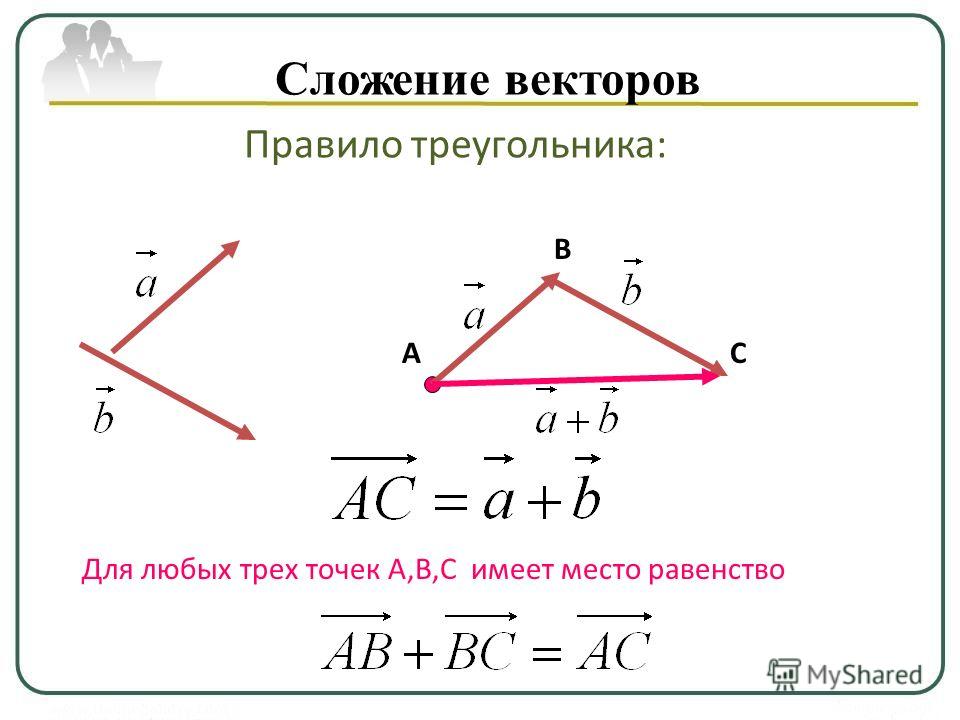
Правила сложения перемещений и скоростей при прямолинейном движении, абсолютная скорость при движении катера по реке
п.1. Правило сложения перемещений при прямолинейном движении
Рассмотрим движение катера по реке.
Можно говорить о движении катера как относительно реки, так и относительно берега.
При этом сама река также движется относительно берега.
Как было показано в §5 данного справочника, для описания движения необходимо указать тело отсчета и ввести связанную с ним систему отсчета.
Введем две системы отсчета.
Берег неподвижен. Назовем систему отсчета, связанную с берегом, неподвижной системой отсчета (НСО). Перемещение тела в НСО назовем абсолютным перемещением, \(\overrightarrow{r_a}.\)
Река подвижна. Назовем систему отсчета, связанную с рекой, подвижной системой отсчета (ПСО). Перемещение тела в ПСО назовем относительным перемещением, \(\overrightarrow{r_o}.\)
Перемещение реки относительно берега – это перемещение подвижной системы отсчета относительно неподвижной. Перемещение ПСО относительно НСО назовем переносным перемещением, \(\overrightarrow{r_п}.\)
Перемещение ПСО относительно НСО назовем переносным перемещением, \(\overrightarrow{r_п}.\)
Правило сложения перемещений
Абсолютное перемещение равно векторной сумме относительного и переносного перемещений: $$ \overrightarrow{r_a}=\overrightarrow{r_o}+ \overrightarrow{r_п} $$
Чтобы найти сумму двух векторов, нужно от конца первого вектора отложить второй вектор (см. §6 данного справочника).
При прямолинейном движении все перемещения направлены вдоль одной прямой. В этом случае сумму векторов найти проще.
Пример: правило сложения перемещений при движении катера по реке
Пусть катер плывет по течению реки.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в одну сторону, и модуль абсолютного перемещения равен сумме модулей векторов-слагаемых:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|+ |\overrightarrow{r_п}| $$
Теперь пусть катер плывет против течения.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в противоположные стороны, и модуль абсолютного перемещения равен разности модуля большего и модуля меньшего вектора:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|- |\overrightarrow{r_п}| $$
п.
 2. Правило сложения скоростей при прямолинейном движении
2. Правило сложения скоростей при прямолинейном движенииНапомним, что:
Скорость – векторная величина, равная отношению перемещения ко времени, за которое это перемещение было совершено: $$ \overrightarrow{v}=\frac{\overrightarrow{r}}{t} $$
Тогда из закона сложения перемещений получаем: $$ \overrightarrow{r_a}=\overrightarrow{r_o} +\overrightarrow{r_п} \Rightarrow \frac{\overrightarrow{r_a}}{t}=\frac{\overrightarrow{r_o}}{t} +\frac{\overrightarrow{r_п}}{t}\Rightarrow \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Правило сложения скоростей
Абсолютная скорость равна векторной сумме относительной и переносной скоростей: $$ \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Если при описании движения выбрать направление координатной оси ОХ, то можно ввести проекции скоростей \(v_x\) (см. §8 данного справочника) и получить еще одно очень полезное при решении задач правило сложения:
Правило сложения проекций скоростей при прямолинейном движении
Проекция абсолютной скорости на координатную ось ОХ равна сумме проекций относительной и переносной скоростей: $$ v_{ax}=v_{ox}+v_{пx} $$
п.
 3. Абсолютная скорость при движении катера по реке
3. Абсолютная скорость при движении катера по рекеПусть собственная скорость катера (скорость относительно реки) равна \(v\), скорость течения (переносная скорость) равна \(u\).
Направим ось ОХ в направлении скорости катера, тогда её проекция будет положительной: \(v_{ox}=v\). Если катер плывет по течению, скорость течения также направлена по ОХ и её проекция положительна: \(v_{пx}=u\). Проекция абсолютной скорости равна сумме: $$ v_{ax}=v_{ox}+v_{пx}=v+u $$
Если катер плывет против течения, при сохранении направления оси OX скорость течения направлена противоположно и её проекция отрицательна: \(v_{пx}=-u\). Проекция абсолютной скорости равна разности $$ v_{ax}=v_{ox}+v_{пx}=v-u $$ Если \(v\gt u\), проекция абсолютной скорости положительна, \(v_{ax}\gt 0\), катер поднимается вверх по реке.
При недостаточной скорости катера \(v\lt u\), проекция абсолютной скорости отрицательна, \(v_{ax}\lt 0\). Катер не сможет подниматься вверх по реке, его будет сносить вниз.
Внимание!
При описании прямолинейного движения выбор направления оси ОХ, определение знаков проекций скоростей и перемещений важны для правильного хода решения задачи и объяснения полученных результатов.
Всегда помните: скорость и перемещение – это вектора, у которых есть не только величина, но и направление.
п.4. Задачи
Задача 1. По заданным векторам относительной и переносной скоростей найдите вектор абсолютной скорости. Какой путь пройдет тело в подвижной и неподвижной системе отсчета за 5 с?
a)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=4\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=3\ \text{м/с}\) — скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=4\cdot 5=20\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=3\cdot 5=15\ \text{м}\) — путь тела в неподвижной СО
Ответ: 20 м и 15 м
б)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=30\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=50\ \text{м/с}\) — скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=30\cdot 5=150\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=50\cdot 5=250\ \text{м}\) — путь тела в неподвижной СО
Ответ: 150 м и 250 м
Задача 2. Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Дано:
\(v_1=10\ \text{км/ч}\)
\(v_2=12\ \text{км/ч}\)
\(v=15\ \text{км/ч}\)
\(d=99\ \text{км}\)
_______________
\(s-?\)
Пусть первый катер – неподвижное тело отсчета. Тогда второй катер приближается к нему со скоростью, равной сумме скоростей \((v_1+v_2)\). Время, через которое катера встретятся: $$ t=\frac{d}{v_1+v_2} $$ За это время альбатрос пролетит расстояние: $$ s=vt=v\cdot\frac{d}{v_1+v_2}=\frac{v}{v_1+v_2}d $$ Подставляем: $$ s=\frac{15}{10+12}\cdot 99=67,5\ (\text{км}) $$ Ответ: 67,5 км
Задача 3. В подрывной технике используют бикфордов шнур, пламя по которому распространяется со скоростью 0,8 см/с. Какой длины шнур понадобится подрывнику, чтобы он успел отбежать на расстояние 300 м после того, как его подожжет?
Скорость бега равна 5 м/с.
Дано:
\(u=0,8\ \text{см/с}=0,008\ \text{м/с}\)
\(v=5\ \text{м/c}\)
\(s=300\ \text{м}\)
_______________
\(L-?\)
На чертеже объект, который нужно взорвать, находится в точке B. Подрывник находится в точке O и бежит в точку A, длина шнура L=OB, расстояние AB=s.
Скорости \(u\) и \(v\) направлены противоположно. Время, за которое шнур догорит и подрывник добежит, определяется суммой скоростей \((u+v)\): $$ t=\frac{s}{u+v} $$ Длина шнура определяется временем и скоростью сгорания: $$ L=tu=\frac{su}{u+v} $$ Подставляем: $$ L=\frac{300\cdot 0,008}{5+0,008}\approx 0,48\ (\text{м})=48\ (\text{см}) $$ Ответ: 48 см
Задача 4. Из городов A и B, расстояние между которыми d=9 км, одновременно навстречу друг другу выехало два велосипедиста. В направлении от A к B дует ветер со скоростью \(v_0\). Первый велосипедист проехал расстояние между городами за 30 минут, а второй – за 45 минут. Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Пусть \(v\) — скорость велосипедистов в тихую погоду.
Переведем время в часы: \begin{gather*} t_1=30\ \text{мин}=\frac{30}{60}\text{ч}=\frac12\text{ч}\\ t_2=45\ \text{мин}=\frac{45}{60}\text{ч}=\frac34\text{ч} \end{gather*} Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й велосипедист, из А в Б | \(v+v_0\) | \(\frac12\) | \(\frac12(v+v_0)\) |
| 2й велосипедист, из Б в А | \(v-v_0\) | \(\frac34\) | \(\frac34(v-v_0)\) |
Расстояние: $$ d=\frac12(v+v_0)=\frac34(v-v_0)=9 $$ Получаем систему: $$ \begin{cases} \frac12(v+v_0)=9\\ \frac34(v-v_0)=9 \end{cases} \Rightarrow \begin{cases} v+v_0=9\cdot 2=18\\ v-v_0=9\cdot\frac43=12 \end{cases} \Rightarrow \begin{cases} 2v=18+12\\ 2v_0=18-12 \end{cases} \Rightarrow \begin{cases} v=\frac{30}{2}=15\\ v_0=\frac62=3 \end{cases} $$
Ответ:
Скорость ветра \(v_0=3\) км/ч
Скорость велосипедистов в тихую погоду \(v=15\) км/ч
Задача 5. Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Пусть \(v\) — скорость катера относительно реки (относительная скорость), \(u\) — скорость реки относительно берега (переносная скорость).
Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Катер по течению | \(v+u\) | 2 | \(2(v+u)\) |
| Катер против течения | \(v-u\) | 4 | \(4(v-u)\) |
| Плот | \(u\) | \(t\) | \(s\) |
Расстояние во всех случаях одно и то же: $$ s=2(v+u)=4(v-u)\Rightarrow (v+u)=2(v-u)\Rightarrow u+2u=2v-v\Rightarrow 3u=v $$ Скорость катера в 3 раза больше скорости течения (скорости плота).
Тогда расстояние \(s=2(v+u)=2(3u+u)=8u\)
Время для плота: $$ t=\frac su=\frac{8u}{u}=8\ (\text{ч}) $$
Ответ: 8 ч
Задача 6*. 3}=\frac16\ \text{ч}=10\ \text{мин}\)
3}=\frac16\ \text{ч}=10\ \text{мин}\)
Второй корабль подбирает контейнеры каждые 10 мин.
Значит, в течение часа второй корабль подберет еще \(N=\frac{60\ \text{мин}}{10\ \text{мин}}=6\) контейнеров.
Ответ: 6 контейнеров
Задача 7*. Автомобиль, движущийся со скоростью 72 км/ч, был пробит пулей, летевшей перпендикулярно его движению. Отверстие в дальней стенке оказалось смещено относительно отверстия в ближней стенке на 4 см. Ширина салона 1,5 м. Считая, что пуля в салоне не изменила траекторию, определите её скорость.
Дано:
\(u=72\ \text{км/ч}=20\ \text{м/с}\)
\(d=4\ \text{cм}=0,04\ \text{м}\)
\(a=1,5\ \text{м}\)
_______________
\(v-?\)
Построим чертеж движения, вид сверху. Направим ось ОХ по движению автомобиля относительно земли, ось ОУ – по движению пули относительно земли.
Если перейти в систему отсчета, связанную с автомобилем, земля «побежит» в обратном направлении со скоростью \(–u\), и траектория пули в салоне сместится (пунктирная линия на чертеже). Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$ Ответ: 750 м/с
Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$ Ответ: 750 м/с
БЕСПЛАТНЫЙ пошаговый урок по правилу вероятностного сложения с интерактивными упражнениями
Форма поиска
Поиск
Изучение правила сложения вероятностей и сложение вероятностей с помощью примеров задач и интерактивных упражнений
Эксперимент: Бросается один шестигранный кубик. Какова вероятность того, что выпадет 2 или 5?
Возможные варианты:
1. Выпавшее число может быть 2.
2. Выпавшее число может быть 5.
События: Эти события являются взаимоисключающими, поскольку они не могут происходить одновременно.
Вероятности: как найти вероятности этих взаимоисключающих событий? Нам нужно правило, чтобы вести нас.
Правило сложения 1: Когда два события, A и B, являются взаимоисключающими, вероятность того, что произойдет A или B, равна сумме вероятностей каждого события.
P(A или B) = P(A) + P(B)
Давайте воспользуемся этим правилом сложения, чтобы найти вероятность для эксперимента 1.
Эксперимент 1. Бросается один шестигранный кубик. Какова вероятность того, что выпадет 2 или 5?
Вероятности:
| P(2) | = | 1 | ||
| 6 | ||||
| Р(5) | = | 1 | ||
| 6 | ||||
| Р(2 или 5) | = | Р(2) | + | Р(5) |
| = | 1 | + | 1 | |
| 6 | 6 | |||
| = | 2 | |||
| 6 | ||||
| = | 1 | |||
| 3 | ||||
Эксперимент 2. Спиннер имеет 4 равных сектора желтого, синего, зеленого и красного цветов. Какова вероятность приземлиться на красное или синее после вращения этого блесны?
Спиннер имеет 4 равных сектора желтого, синего, зеленого и красного цветов. Какова вероятность приземлиться на красное или синее после вращения этого блесны?
Вероятности:
| P(красный) | = | 1 | ||
| 4 | ||||
| P (синий) | = | 1 | ||
| 4 | ||||
| P (красный или синий) | = | P(красный) | + | P (синий) |
| = | 1 | + | 1 | |
| 4 | 4 | |||
| = | 2 | |||
| 4 | ||||
| = | 1 | |||
| 2 | ||||
Эксперимент 3. В стеклянной банке находятся 1 красный, 3 зеленых, 2 синих и 4 желтых шарика. Если из банки наугад выбрать один шарик, какова вероятность того, что он будет желтым или зеленым?
В стеклянной банке находятся 1 красный, 3 зеленых, 2 синих и 4 желтых шарика. Если из банки наугад выбрать один шарик, какова вероятность того, что он будет желтым или зеленым?
Вероятности:
| P(желтый) | = | 4 | ||
| 10 | ||||
| P (зеленый) | = | 3 | ||
| 10 | ||||
| P (желтый или зеленый) | = | P (желтый) | + | P (зеленый) |
| = | 4 | + | 3 | |
| 10 | 10 | |||
| = | 7 | |||
| 10 | ||||
В каждом из трех вышеперечисленных экспериментов события являются взаимоисключающими. Давайте рассмотрим некоторые эксперименты, в которых события не исключают друг друга.
Давайте рассмотрим некоторые эксперименты, в которых события не исключают друг друга.
Эксперимент 4. Из стандартной колоды из 52 игральных карт случайным образом выбирается одна карта. Какова вероятность выбора короля или трефы?
Вероятности:
| P(король или трефа) | = | П(король) | + | P(клуб) | — | P(король треф) |
| = | 4 | + | 13 | — | 1 | |
| 52 | 52 | 52 | ||||
| = | 16 | |||||
| 52 | ||||||
| = | 4 | |||||
| 13 | ||||||
В эксперименте 4 события не исключают друг друга. Сложение приводит к тому, что король треф считается дважды, поэтому его вероятность необходимо вычесть. Когда два события не являются взаимоисключающими, необходимо использовать другое правило сложения.
Сложение приводит к тому, что король треф считается дважды, поэтому его вероятность необходимо вычесть. Когда два события не являются взаимоисключающими, необходимо использовать другое правило сложения.
Дополнительное правило 2: Если два события, A и B, не исключают друг друга, вероятность того, что A или B произойдут, равна:
P(A или B) = P(A) + P(B) — P(A и B)
В приведенном выше правиле P(A и B) относится к перекрытию двух событий. Применим это правило к некоторым другим экспериментам.
Эксперимент 5. В математическом классе из 30 учеников 17 мальчиков и 13 девочек. В модульном тесте 4 мальчика и 5 девочек получили оценку «А». Если ученица выбрана случайным образом из класса, какова вероятность того, что она выберет девочку или отличницу?
Вероятности: Р(девушка или А) = Р(девушка) + Р(А) — Р(девушка и А)
| = | 13 | + | 9 | — | 5 | |
| 30 | 30 | 30 | ||||
| = | 17 | |||||
| 30 | ||||||
Эксперимент 6: В канун Нового года вероятность попасть в автомобильную аварию равна 0,09. . Вероятность того, что человек будет управлять автомобилем в состоянии алкогольного опьянения, равна 0,32, а вероятность того, что человек попадет в автомобильную аварию в состоянии алкогольного опьянения, равна 0,15. Какова вероятность того, что человек за рулем в состоянии алкогольного опьянения или попадет в автомобильную аварию?
. Вероятность того, что человек будет управлять автомобилем в состоянии алкогольного опьянения, равна 0,32, а вероятность того, что человек попадет в автомобильную аварию в состоянии алкогольного опьянения, равна 0,15. Какова вероятность того, что человек за рулем в состоянии алкогольного опьянения или попадет в автомобильную аварию?
Вероятности:
| P(пьянство или несчастный случай) | = | П(в состоянии алкогольного опьянения) | + | P(авария) | — | P(пьянство и несчастный случай) |
| = | 0,32 | + | 0,09 | — | 0,15 | |
| = | 0,26 | |||||
Резюме: Чтобы найти вероятность события A или B, мы должны сначала определить, являются ли события взаимоисключающими или нет. Затем мы можем применить соответствующее правило сложения:
Затем мы можем применить соответствующее правило сложения:
Правило сложения 1: Если два события, A и B, являются взаимоисключающими, вероятность того, что произойдет A или B, равна сумме вероятностей каждого события.
P(A или B) = P(A) + P(B)
Правило сложения 2: Если два события, A и B, не являются взаимоисключающими, между этими событиями существует некоторое перекрытие. Вероятность того, что произойдет A или B, представляет собой сумму вероятности каждого события за вычетом вероятности совпадения.
P(A или B) = P(A) + P(B) — P(A и B)
Упражнения
Указания: Прочитайте каждый вопрос ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы ошиблись, выберите другую кнопку.
| 1. | День недели выбирается случайным образом. Какова вероятность того, что вы выберете понедельник или вторник? Какова вероятность того, что вы выберете понедельник или вторник? |
Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 2. | В зоомагазине есть 6 щенков, 9котят, 4 песчанки и 7 попугаев. Если домашнее животное выбрано наугад, какова вероятность того, что вы выберете щенка или попугая? |
| 1 Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 3. | Вероятность того, что у подростка из Нью-Йорка будет скейтборд, равна 0,37, велосипеда — 0,81, а того и другого — 0,36. Если наугад выбрать подростка из Нью-Йорка, какова вероятность того, что у него есть скейтборд или велосипед? Если наугад выбрать подростка из Нью-Йорка, какова вероятность того, что у него есть скейтборд или велосипед? |
| 1,18 0,7 0,82 Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 4. | Случайным образом выбирается число от 1 до 10. Какова вероятность выбрать 5 или четное число? |
Все вышеперечисленное. ОКНО РЕЗУЛЬТАТОВ: |
| 5. | Брошен один шестигранный кубик. Какова вероятность того, что выпадет число больше 3 или четное число? |
| 1 Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| Уроки вероятности |
| Введение в теорию вероятности |
| Определенные и невозможные события |
| Пространства для образцов |
| Дополнение к событию |
| Взаимоисключающие события |
| Правила сложения для вероятности |
| Независимые события |
| Зависимые события |
| Условная вероятность |
| Практические упражнения |
| Упражнения с вызовом |
| Решения |
| Цели обучения |
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
| Сопутствующая деятельность |
| Вероятностные головоломки |
| Готовые рабочие листы |
| Вероятностная игра |
математических слов: правило сложения
математических слов: правило сложения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вероятностные правила | Безграничная статистика |
Правило сложения
Правило сложения гласит, что вероятность двух событий равна сумме вероятности того, что одно из них произойдет, минус вероятность того, что произойдет оба.
Цели обучения
Рассчитайте вероятность события, используя правило сложения
Ключевые выводы
Ключевые моменты
- Правило сложения:
P(A∪B)=P(A)+P(B)−P(A∩B) .\text{P}(\text{A}\cup \text{B})=\text{P}(\text{A})+\text{P}(\text{B})-\text{ P}(\text{A}\cap \text{B}).P(A∪B)=P(A)+P(B)−P(A∩B).
- Последний член учитывался дважды: один раз в
P(A)\text{P}(\text{A})P(A)
и один раз вP(B)\text{P}(\text {B})P(B)
, поэтому его нужно вычесть один раз, чтобы он не учитывался дважды. - Если
A\text{A}A
иB\text{B}B
не пересекаются, тоP(A∩B)=0\text{P}(\text{A}\cap \text{ B})=0P(A∩B)=0
, поэтому формула принимает видP(A∪B)=P(A)+P(B).\text{P}(\text{A} \cup \ текст{B})=\text{P}(\text{A}) + \text{P}(\text{B}).P(A∪B)=P(A)+P(B).
Ключевые термины
- вероятность : Относительная вероятность события.
Дополнительный закон
Закон сложения вероятностей (иногда называемый правилом сложения или правилом сумм) утверждает, что вероятность того, что
A\text{A}A
или
B\text{B}B
представляет собой сумму вероятностей того, что
A\text{A}A
произойдет и
B \text{B}B
минус вероятность того, что произойдут оба
A\text{A}A
и
B\text{B}B
. Правило сложения резюмируется формулой:
Правило сложения резюмируется формулой:
P(A∪B)=P(A)+P(B)−P(A∩B)\displaystyle \text{P}(\text{A} \cup \text{B}) = \text{P}(\text{A})+\text{P}(\text{B})-\text{P }(\text{A} \cap \text{B})P(A∪B)=P(A)+P(B)−P(A∩B)
Рассмотрим следующий пример. Какова вероятность того, что при извлечении одной карты из колоды из
525252
карт выпадет черва или фигурная карта (король, дама или валет)? Пусть
H\text{H}H
обозначает розыгрыш сердца, а
F\text{F}F
обозначает розыгрыш лицевой карты. Так как есть
131313
червей и всего
121212
лицевых карт (
333
каждой масти: пики, червы, бубны и трефы), но только
333
лицевые карты червей, получаем:
P(H)=1352\displaystyle \text{P}(\text{H}) = \frac{13}{52}P(H)=5213
P(F)=1252\displaystyle \text{P}(\text{F}) = \frac{12}{52}P(F)=5212
P(F∩H)=352\ displaystyle \text{P}(\text{F} \cap \text{H}) = \frac{3}{52}P(F∩H)=523
Используя правило сложения, мы получаем:
P(H∪F)=P(H)+P(F)−P(H∩F)=1352+1252−352\displaystyle \начать{выравнивать} \text{P}(\text{H}\cup \text{F})&=\text{P}(\text{H})+\text{P}(\text{F})-\text{ P}(\text{H}\cap \text{F})\\ &=\frac { 13 }{ 52 } +\ frac { 12 }{ 52 } -\ frac { 3 }{ 52 } \end{align}P(H∪F)=P(H)+P(F)−P(H∩F)=5213+5212−523
Причина вычитания последнего члена заключается в том, что в противном случае мы бы считали среднюю часть дважды (поскольку
H\text{H}H
и
F\text{F}F
перекрываются).
Правило сложения для непересекающихся событий
Предположим, что
A\text{A}A
и
B\text{B}B
не пересекаются, их пересечение пусто. Тогда вероятность их пересечения равна нулю. В символах:
P(A∩B)=0\text{P}(\text{A} \cap \text{B}) = 0P(A∩B)=0
. Тогда закон сложения упрощается: \text{P}(\text{A}) + \text{P}(\text{B}) \qquad \text{когда} \qquad \text{A} \cap \text{B} = \emptysetP( A∪B)=P(A)+P(B), когда A∩B=∅
Символ
∅\emptyset∅
представляет собой пустое множество, что означает, что в данном случае
A\text{A} A
и
B\text{B}B
не имеют общих элементов (они не пересекаются).
Пример:
Предположим, из колоды из 52 игральных карт взята карта: какова вероятность получить короля или даму? Пусть
A\text{A}A
представляет событие вытягивания короля, а
B\text{B}B
представляет событие вытягивания ферзя. Эти два события не пересекаются, так как нет королей, которые были бы одновременно и королевами. Таким образом:
Эти два события не пересекаются, так как нет королей, которые были бы одновременно и королевами. Таким образом:
P(A∪B)=P(A)+P(B)=452+452=852=213\displaystyle \начать{выравнивать} \text{P}(\text{A} \cup \text{B}) &= \text{P}(\text{A}) + \text{P}(\text{B})\\&= \frac{4}{52}+\frac{4}{52}\\&=\frac{8}{52}\\&=\frac{2}{13} \end{align}P(A∪B)=P(A)+P(B)=524+524=528=132
Правило умножения
Правило умножения гласит, что вероятность появления
A\text{A}A
и
B\text{B}B
равна вероятности того, что
B\text{B}B
происходит, умноженная на условную вероятность того, что
A\text{A}A
произойдет при условии, что произойдет
B\text{B}B
.
Цели обучения
Примените правило умножения, чтобы вычислить вероятность того, что
A\text{A}A
и
B\text{B}B
встречается
Ключевые выводы
Ключевые моменты
- Правило умножения можно записать в виде:
P(A∩B) =P(B)⋅P(A∣B)\text{P}(\text{A} \cap \text{B}) = \text{P}(\text{B}) \cdot \text{P }(\text{A}|\text{B})P(A∩B)=P(B)⋅P(A∣B)
.
- Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.
Ключевые термины
- пространство выборки : Набор всех возможных исходов игры, эксперимента или другой ситуации.
Правило умножения
В теории вероятностей правило умножения гласит, что вероятность появления
A\text{A}A
и
B\text{B}B
равна вероятности того, что
A\text{A} Число
умножается на условную вероятность того, что
B\text{B}B
происходит, учитывая, что мы знаем
A\text{A}A
уже произошло. Это правило можно записать так:
P(A∩B)=P(B)⋅P(A∣B)\displaystyle \text{P}(\text{A} \cap \text{B}) = \text{P}(\text{B}) \cdot \text{P}(\text{A}|\text{B })P(A∩B)=P(B)⋅P(A∣B)
Переключение роли
A\text{A}A
и
B\text{B}B
, мы также можем записать правило как:
P(A∩B)=P(A)⋅P(B∣A)\displaystyle \text{P}(\text{A}\cap \text{B}) = \text{P}(\text{A}) \cdot \text{P}(\text{B}|\text{A })P(A∩B)=P(A)⋅P(B∣A)
Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.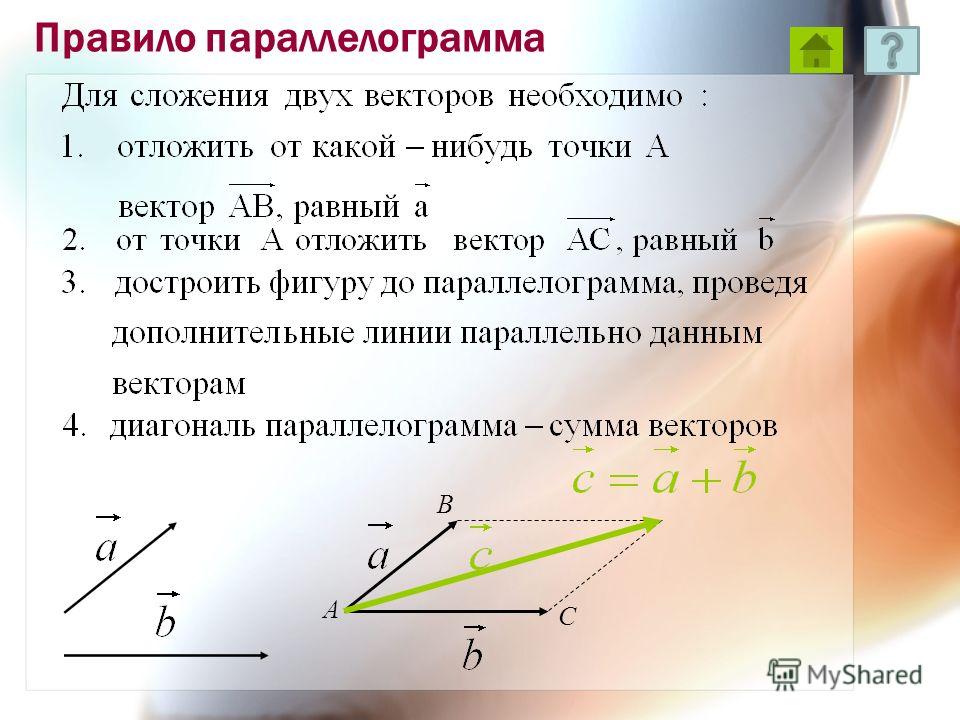 То есть в уравнении
То есть в уравнении
P(A∣B)=P(A∩B)P(B)\displaystyle \text{P}(\text{A}|\text{B})=\frac{\ текст{P}(\text{A}\cap \text{B})}{\text{P}(\text{B})}P(A∣B)=P(B)P(A∩B)
, если мы умножим обе стороны на
P(B)\text{P}(\text{B})P(B)
, мы получим правило умножения.
Правило полезно, когда мы знаем оба
P(B)\text{P}(\text{B})P(B)
и
P(A∣B)\text{P}(\text{A}|\text{B} )P(A∣B)
или оба
P(A)\text{P}(\text{A})P(A)
и
P(B∣A).\text{P }(\text{B}|\text{A}).P(B∣A).
Пример
Предположим, что мы вытащили две карты из колоды карт и пусть
A\text{A}A
будет событием, когда первая карта является тузом, а
B\text{B}B
будет если вторая карта туз, то:
P(A)=452\displaystyle \text{P}(\text{A})=\frac { 4 }{ 52 }P(A)=524
And:
P(B∣A) =351\displaystyle \text{P}\left( { \text{B} }|{ \text{A} } \right) =\frac { 3 }{ 51 }P(B∣A)=513
Знаменатель во втором уравнении равен
515151
, так как мы знаем, что карта уже вытянута. Таким образом, всего осталось
Таким образом, всего осталось
515151
. Мы также знаем, что первой картой был туз, поэтому:
P(A∩B)=P(A)⋅P(B∣A)=452⋅351=0,0045\displaystyle \начать{выравнивать} \text{P}(\text{A} \cap \text{B}) &= \text{P}(\text{A}) \cdot \text{P}(\text{B}|\text{ А})\\ &= \frac { 4 }{ 52 } \cdot \ frac { 3 }{ 51 } \\ &=0,0045 \end{align}P(A∩B)=P(A)⋅P(B∣A)=524⋅513=0,0045
Независимое событие
Обратите внимание, что когда
A\text{A}A
и
B\text{B}B
независимы, мы имеем
P(B∣A)=P(B)\text{P} (\text{B}|\text{A})= \text{P}(\text{B})P(B∣A)=P(B)
, поэтому формула принимает вид
P(A∩ B)=P(A)P(B)\text{P}(\text{A} \cap \text{B})=\text{P}(\text{A})\text{P}(\ text{B})P(A∩B)=P(A)P(B)
, с которым мы столкнулись в предыдущем разделе. В качестве примера рассмотрим эксперимент с бросанием игральной кости и подбрасыванием монеты. Вероятность того, что мы получим
В качестве примера рассмотрим эксперимент с бросанием игральной кости и подбрасыванием монеты. Вероятность того, что мы получим
222
на кубике и решка на монете
16⋅12=112\frac{1}{6}\cdot \frac{1}{2} = \frac{1}{12}61 ⋅21=121
, так как эти два события независимы.
Независимость
Сказать, что два события независимы, означает, что появление одного не влияет на вероятность другого.
Цели обучения
Объясните концепцию независимости в связи с теорией вероятностей
Ключевые выводы
Ключевые моменты
- Два события независимы, если верно следующее:
P(A∣B)=P(A)\text{P}(\text{A}|\text{B}) = \text {P}(\text{A})P(A∣B)=P(A)
,P(B∣A)=P(B)\text{P}(\text{B}|\text{ A}) = \text{P}(\text{B})P(B∣A)=P(B)
иP(AandB)=P(A)⋅P(B)\text{P} (\text{A} \\ \text{и} \\ \text{B}) = \text{P}(\text{A}) \cdot \text{P}(\text{B})P( АиВ)=П(А)⋅П(В)
.
- Если хоть одно из этих условий истинно, то все они истинны.
- Если события
A\text{A}A
иB\text{B}B
независимы, то вероятность появленияA\text{A}A
не влияет на вероятностьB\text{ Возникновение B}B
и наоборот.
Ключевые термины
- независимость : возникновение одного события не влияет на вероятность возникновения другого.
- теория вероятностей : Математическое исследование вероятности (вероятность возникновения случайных событий для прогнозирования поведения определенных систем).
Независимые события
В теории вероятности сказать, что два события независимы, означает, что появление одного не влияет на вероятность того, что произойдет другое. Другими словами, если события
A\text{A}A
и
B\text{B}B
независимы, то вероятность появления
A\text{A}A
не зависит влияет на вероятность появления
B\text{B}B
и наоборот. Концепция независимости распространяется на наборы из более чем двух событий.
Концепция независимости распространяется на наборы из более чем двух событий.
Два события независимы, если верно любое из следующих условий:
P(A∣B)=P(A)\displaystyle \text{P}(\text{A}|\text{B}) = \text{P}(\text{A})P(A∣B)=P(A)
P(B∣A)=P(B)\displaystyle \text{P}(\text{B}|\text{A}) = \text{P}(\text{B})P(B∣ А)=П(Б)
P(AandB)=P(A)⋅P(B)\displaystyle \text{P}(\text{A} \\ \text{and} \\ \text{B}) = \text{P} (\text{A})\cdot \text{P}(\text{B})P(AandB)=P(A)⋅P(B)
Чтобы показать, что два события независимы, необходимо показать только одно из перечисленных выше условий. Если хоть одно из этих условий верно, то все они истинны.
Если перевести символы в слова, первые два математических утверждения, перечисленных выше, говорят о том, что вероятность события с условием такая же, как и вероятность события без условия. Для независимых событий условие не изменяет вероятность события. Третье утверждение говорит, что вероятность появления обоих независимых событий
A\text{A}A
и
B\text{B}B
равна вероятности
A\text{A}A
появления, умноженное на вероятность появления
B\text{B}B
.
В качестве примера представьте, что вы последовательно выбираете две карты из полной колоды игральных карт. Два выбора не являются независимыми. Результат первого выбора изменяет оставшуюся колоду и влияет на вероятность второго выбора. Это называется выбором «без замены», потому что первая карта не была заменена в колоде до того, как будет выбрана вторая карта.
Однако предположим, что вы должны выбрать две карты «с заменой», вернув свою первую карту в колоду и перетасовав колоду перед выбором второй карты. Поскольку колода карт является полной для обоих вариантов выбора, первый выбор не влияет на вероятность второго выбора. При подборе карт с заменой выборы независимые.
Независимые события : Выбор двух карт из колоды путем сначала выбора одной, а затем замены ее в колоде перед выбором второй, является примером независимых событий.
Рассмотрим роль честной кости, которая представляет собой еще один пример независимых событий. Если человек разыгрывает два кубика, результат первого броска не меняет вероятность результата второго броска.
Если человек разыгрывает два кубика, результат первого броска не меняет вероятность результата второго броска.
Пример
Два друга играют в бильярд и решают подбросить монетку, чтобы определить, кто будет играть первым в каждом раунде. В первых двух раундах монета падает орлом. Они решают сыграть третий раунд и снова подбрасывают монету. Какова вероятность того, что монета снова упадет орлом?
Во-первых, обратите внимание, что каждый бросок монеты является независимым событием. Сторона, на которую падает монета, не зависит от того, что произошло ранее.
При любом подбрасывании монеты существует вероятность того, что монета упадет орлом. Таким образом, вероятность того, что монета упадет орлом в третьем раунде, равна
12{\frac{1}{2}}21
.
Пример
Какова вероятность того, что при подбрасывании монеты выпадет решка
555
раз подряд?
Напомним, что каждый бросок монеты независим, и вероятность выпадения решки равна
12{\frac{1}{2}}21
при любом броске. Также напомню, что для любых двух независимых событий A и B верно следующее утверждение:
Также напомню, что для любых двух независимых событий A и B верно следующее утверждение:
P(AandB)=P(A)⋅P(B)\displaystyle \text{P}(\text{A} \\ \text {и} \\ \text{B}) = \text{P}(\text{A})\cdot \text{P}(\text{B})P(AandB)=P(A)⋅P( B)
Наконец, понятие независимости распространяется на коллекции более
222
событий.
Следовательно, вероятность выпадения решки
444
раз подряд равна:
12⋅12⋅12⋅12=116\displaystyle {\ гидроразрыва {1} {2}} \ cdot {\ гидроразрыва {1} {2}} \ cdot {\ гидроразрыва {1} {2}} \ cdot {\ гидроразрыва {1} {2}} = {\ гидроразрыва {1}{16}}21⋅21⋅21⋅21=161
Правила и методы подсчета
Комбинаторика — это раздел математики, изучающий конечные или счетные дискретные структуры.
Цели обучения
Описать различные правила и свойства комбинаторики
Основные выводы
Ключевые моменты
- Правило суммы (правило сложения), правило произведения (правило умножения) и принцип включения-исключения часто используются для целей перечисления.

- Биективные доказательства используются для демонстрации того, что два множества имеют одинаковое количество элементов.
- Двойной подсчет — это метод, используемый для демонстрации равенства двух выражений. Принцип сортировки часто устанавливает существование чего-либо или используется для определения минимального или максимального количества чего-либо в дискретном контексте.
- Генерирующие функции и рекуррентные отношения — это мощные инструменты, которые можно использовать для управления последовательностями и которые могут описывать, если не разрешать, многие комбинаторные ситуации.
- Двойной подсчет — это метод, используемый для демонстрации равенства двух выражений.
Ключевые термины
- полином : Выражение, состоящее из суммы конечного числа членов: каждый член является произведением постоянного коэффициента и одной или нескольких переменных, возведенных в неотрицательную целую степень.
- комбинаторика : Раздел математики, изучающий (обычно конечные) наборы объектов, которые удовлетворяют определенным критериям.

Комбинаторика — это раздел математики, изучающий конечные или счетные дискретные структуры. Комбинаторные методы применимы ко многим областям математики, и знание комбинаторики необходимо, чтобы хорошо владеть статистикой. Он включает в себя перечисление, комбинирование и перестановку наборов элементов и математических отношений, характеризующих их свойства.
Аспекты комбинаторики включают в себя: подсчет структур определенного вида и размера, принятие решения о том, когда могут быть выполнены определенные критерии, а также построение и анализ объектов, удовлетворяющих критериям. Аспекты также включают поиск «самых больших», «самых маленьких» или «оптимальных» объектов, изучение комбинаторных структур, возникающих в алгебраическом контексте, или применение алгебраических методов к комбинаторным задачам.
Комбинаторные правила и методы
Несколько полезных комбинаторных правил или комбинаторных принципов общепризнаны и используются. Каждый из этих принципов используется для определенной цели. Правило суммы (правило сложения), правило произведения (правило умножения) и принцип включения-исключения часто используются для целей перечисления. Биективные доказательства используются для демонстрации того, что два множества имеют одинаковое количество элементов. Двойной подсчет — это способ показать, что два выражения равны. Принцип сортировки часто устанавливает существование чего-либо или используется для определения минимального или максимального количества чего-либо в дискретном контексте. Генерирующие функции и рекуррентные отношения — это мощные инструменты, которые можно использовать для управления последовательностями и которые могут описывать, если не разрешать, многие комбинаторные ситуации. Каждый из этих методов более подробно описан ниже.
Каждый из этих принципов используется для определенной цели. Правило суммы (правило сложения), правило произведения (правило умножения) и принцип включения-исключения часто используются для целей перечисления. Биективные доказательства используются для демонстрации того, что два множества имеют одинаковое количество элементов. Двойной подсчет — это способ показать, что два выражения равны. Принцип сортировки часто устанавливает существование чего-либо или используется для определения минимального или максимального количества чего-либо в дискретном контексте. Генерирующие функции и рекуррентные отношения — это мощные инструменты, которые можно использовать для управления последовательностями и которые могут описывать, если не разрешать, многие комбинаторные ситуации. Каждый из этих методов более подробно описан ниже.
Правило суммы
Правило суммы — это интуитивный принцип, утверждающий, что если существует
a\text{a}a
возможных способов сделать что-то и
b\text{b}b
возможных способов сделать другое, и две вещи не могут быть выполнены одновременно, тогда есть
a+b\text{a} + \text{b}a+b
всего возможных способов сделать одну из них. Формально сумма размеров двух непересекающихся множеств равна размеру объединения этих множеств.
Формально сумма размеров двух непересекающихся множеств равна размеру объединения этих множеств.
Правило продукта
Правило произведения — это еще один интуитивный принцип, утверждающий, что если существует
a\text{a}a
способов сделать что-то и
b\text{b}b
способов сделать другое, то существует
a⋅b\text{a} \cdot \text{b}a⋅b
способов сделать обе вещи.
Принцип включения-исключения
Принцип включения-исключения — это метод подсчета, который используется для получения количества элементов в объединении нескольких наборов. Этот метод подсчета гарантирует, что элементы, присутствующие более чем в одном наборе в объединении, не учитываются более одного раза. Он учитывает размер каждого набора и размер пересечений наборов. Наименьший пример, когда есть два набора: количество элементов в объединении
A\text{A}A
и
B\text{B}B
равно сумме количества элементов в
A\text{A}A
и
B\ text{B}B
минус количество элементов на их пересечении. На диаграмме ниже показан пример с тремя наборами.
На диаграмме ниже показан пример с тремя наборами.
Биективное доказательство
Биективное доказательство — это метод доказательства, который находит биективную функцию
f:A→B\text{f}: \text{A} \rightarrow \text{B}f:A→B
между двумя конечными множествами
A\text{A}A
и
B\text{B}B
, что доказывает, что они имеют одинаковое количество элементов,
∣A∣=∣B∣| \текст{А}| = |\text{B}|∣A∣=∣B∣
. Биективная функция — это функция, в которой существует однозначное соответствие между элементами двух множеств. Другими словами, каждый элемент в наборе
B\text{B}B
связан ровно с одним элементом в наборе
A\text{A}A
. Этот метод полезен, если мы хотим узнать размер
A\text{A}A
, но не может найти прямой способ подсчета его элементов. Если
Если
B\text{B}B
легче подсчитать, установление биекции от
A\text{A}A
до
B\text{B}B
решает проблему.
Двойной счет
Двойной подсчет — это метод комбинаторного доказательства равенства двух выражений. Это делается путем демонстрации того, что два выражения представляют собой два разных способа подсчета размера одного набора. В этой технике конечное множество
X\text{X}X
описывается с двух точек зрения, что приводит к двум различным выражениям для размера набора. Поскольку оба выражения равны размеру одного и того же набора, они равны друг другу.
Принцип сортировки
Принцип сортировки гласит, что если
a\text{a}a
элементов поместить в одну из
b\text{b}b
ячеек, где
a>b\text{a}>\ text{b}a>b
, то по крайней мере один из ящиков содержит более одного элемента. Этот принцип позволяет показать существование некоторого элемента множества с определенными свойствами. Например, рассмотрим набор из трех перчаток. В таком наборе должно быть либо две левые перчатки, либо две правые перчатки (или три левые или правые). Это применение принципа сортировки, позволяющее получить информацию о свойствах перчаток в наборе. 9{\text{n}}f(x)=n=0∑∞anxn
Этот принцип позволяет показать существование некоторого элемента множества с определенными свойствами. Например, рассмотрим набор из трех перчаток. В таком наборе должно быть либо две левые перчатки, либо две правые перчатки (или три левые или правые). Это применение принципа сортировки, позволяющее получить информацию о свойствах перчаток в наборе. 9{\text{n}}f(x)=n=0∑∞anxn
, коэффициенты которой дают последовательность
{a0,a1,a2,…}\left \{ \text{a} _{0}, \text{a}_{1}, \text{a}_{2},… \right \}{a0,a1,a2,…}
.
Повторяющееся отношение
Рекуррентное отношение определяет каждый член последовательности в терминах предшествующих членов. Другими словами, как только заданы один или несколько начальных членов, каждый из следующих членов последовательности является функцией предыдущих членов.
Последовательность Фибоначчи является одним из примеров рекуррентного соотношения. Каждый член последовательности Фибоначчи задается
Каждый член последовательности Фибоначчи задается
Fn=Fn−1+Fn−2\text{F}_{\text{n}} = \text{F}_{\text{n}-1} + \text{F}_{\text {n}-2}Fn=Fn−1+Fn−2
, с начальными значениями
F0=0\text{F}_{0}=0F0=0
и
F1= 1\text{F}_{1}=1F1=1
. Таким образом, начинается последовательность чисел Фибоначчи:
0,1,1,2,3,5,8,13,21,34,55,89,…\displaystyle 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…0,1,1,2,3,5,8,13,21,34,55,89 ,…
Правило Байеса
Правило Байеса выражает то, как субъективная степень убеждения должна рационально изменяться, чтобы учитывать доказательства.
Цели обучения
Объясните важность теоремы Байеса в математическом манипулировании условными вероятностями _2A2
, до (до) и после (после) обусловливания другого событияB\text{B}B
.
A1\text{A}_1A1
,A2\text{A}_2A2
, иB\text{B}B
, правило Байеса утверждает, что условные шансыA1:A2\text{A}_1:\text{A}_2A1 :A2
с учетомB\text{B}B
равны предельным шансамA1:A2\text{A}_1:\text{A}_2A1:A2
при умножении на коэффициент Байеса .A1\text{A}_1A1
илиA2\text{A}_2A2
верным, должно быть обновлено на основе наблюдения свидетельств.Ключевые термины
- Коэффициент Байеса : Отношение условных вероятностей события $B$ при условии, что имеет место событие $A_1$ или событие $A_2$ соответственно.
В теории вероятностей и статистике теорема Байеса (или правило Байеса) является важным результатом математической обработки условных вероятностей. Это результат, вытекающий из более основных аксиом вероятности. При применении вероятности, связанные с теоремой Байеса, могут иметь любую из множества вероятностных интерпретаций. В одной из этих интерпретаций теорема используется непосредственно как часть определенного подхода к статистическому выводу. В частности, с байесовской интерпретацией вероятности теорема выражает, как субъективная степень уверенности должна рационально изменяться для учета свидетельств. Это известно как байесовский вывод, который является фундаментальным для байесовской статистики.
Это результат, вытекающий из более основных аксиом вероятности. При применении вероятности, связанные с теоремой Байеса, могут иметь любую из множества вероятностных интерпретаций. В одной из этих интерпретаций теорема используется непосредственно как часть определенного подхода к статистическому выводу. В частности, с байесовской интерпретацией вероятности теорема выражает, как субъективная степень уверенности должна рационально изменяться для учета свидетельств. Это известно как байесовский вывод, который является фундаментальным для байесовской статистики.
Правило Байеса связывает вероятность события
A1\text{A}_1A1
с событием
A2\text{A}_2A2
, до (до) и после (после) обусловливания другое событие
B\text{B}B
. Шансы на
A1\text{A}_1A1
к событию
A2\text{A}_2A2
— это просто отношение вероятностей двух событий. Отношение выражается в терминах отношения правдоподобия или коэффициента Байеса. По определению это отношение условных вероятностей события
Отношение выражается в терминах отношения правдоподобия или коэффициента Байеса. По определению это отношение условных вероятностей события
B\text{B}B
при условии, что
A1\text{A}_1A1
или
A2\text{A}_2A2
соответственно. Правило просто гласит:
Апостериорные шансы равны априорным шансам, умноженным на коэффициент Байеса.
Более конкретно, учитывая события
A1\text{A}_1A1
,
A2\text{A}_2A2
и
B\text{B}B 90’805 ,910 правила Байеса что условная вероятность
A1:A2\text{A}_1:\text{A}_2A1:A2
учитывая
B\text{B}B
равны предельным шансам
A1:A2\text{ A}_1:\text{A}_2A1:A2
, умноженное на коэффициент Байеса или отношение правдоподобия. Это показано в следующих формулах:
Это показано в следующих формулах:
O(A1:A2∣B)=Λ(A1:A2∣B)⋅O(A1:A2)O(\text{A}_1:\text{A}_2| \text{B}) = \Lambda(\text{A}_1:\text{A}_2|\text{B})\cdot O(\text{A}_1:\text{A}_2)O( A1:A2∣B)=Λ(A1:A2∣B)⋅O(A1:A2)
Где отношение правдоподобия
Λ\LambdaΛ
является отношением условных вероятностей события
B\text{B}B
при условии, что
A1\text{A}_1A1
имеет место или что
A
\text{A}_2A2
соответственно:
Λ(A1:A2∣B)=P(B∣A1)P(B∣A2)\displaystyle \Lambda(\text{A}_1: \text{A}_2|\text{B}) = \frac{\text{P}(\text{B}|\text{A}_1)}{\text{P}(\text{B}| \text{A}_2)}Λ(A1:A2∣B)=P(B∣A2)P(B∣A1)
Правило Байеса широко используется в статистике, науке и технике, таких как как в: выборе модели, вероятностных экспертных системах, основанных на байесовских сетях, статистических доказательствах в судебных разбирательствах, фильтрах спама в электронной почте и т. д. Правило Байеса говорит нам, как соотносятся безусловные и условные вероятности, работаем ли мы с частотной или байесовской интерпретацией вероятность. В байесовской интерпретации часто применяется в ситуации, когда
д. Правило Байеса говорит нам, как соотносятся безусловные и условные вероятности, работаем ли мы с частотной или байесовской интерпретацией вероятность. В байесовской интерпретации часто применяется в ситуации, когда
A1\text{A}_1A1
и
A2\text{A}_2A2
являются конкурирующими гипотезами, а
B\text{B}B
являются некоторыми наблюдаемыми свидетельствами. Правило показывает, как суждение о том, является ли
A1\text{A}_1A1
или
A2\text{A}_2A2
верным, должно обновляться при наблюдении за свидетельством.
Байесовский вывод
Байесовский вывод — это метод вывода, в котором правило Байеса используется для обновления оценки вероятности гипотезы по мере получения дополнительных доказательств. Байесовское обновление является важным методом в статистике, особенно в математической статистике. Байесовское обновление особенно важно при динамическом анализе последовательности данных. Байесовский вывод нашел применение в ряде областей, включая науку, инженерию, философию, медицину и право.
Байесовское обновление особенно важно при динамическом анализе последовательности данных. Байесовский вывод нашел применение в ряде областей, включая науку, инженерию, философию, медицину и право.
Неофициальное определение
С рациональной точки зрения правило Байеса имеет большой смысл. Если доказательства не совпадают с гипотезой, следует отклонить гипотезу. Но если гипотеза крайне маловероятна 91 878 априори 91 879 , ее также следует отвергнуть, даже если доказательства действительно совпадают.
Например, представьте, что у нас есть различные гипотезы о характере новорожденного ребенка друга, в том числе:
h2\text{H}_1h2
: Младенец — темноволосый мальчик.h3\text{H}_2h3
: Девочка светловолосая.h4\text{H}_3h4
: Ребенок — собака.
Затем рассмотрим два сценария:
- Нам представлены улики в виде фотографии светловолосой девочки. Мы находим, что это свидетельство поддерживает
h3\text{H}_2h3
и противоречитh2\text{H}_1h2
иh4\text{H}_3h4
.
- Нам представили доказательство в виде изображения собачки. Хотя эти данные, рассматриваемые изолированно, подтверждают
h4\text{H}_3h4
, моя прежняя вера в эту гипотезу (о том, что человек может родить собаку) крайне мала. Поэтому апостериорная вероятность все же мала.
Важным моментом байесовского вывода, таким образом, является то, что он обеспечивает принципиальный способ объединения новых данных с предыдущими убеждениями посредством применения правила Байеса. Кроме того, правило Байеса можно применять многократно. После наблюдения некоторых свидетельств результирующую апостериорную вероятность можно рассматривать как априорную вероятность, а новую апостериорную вероятность вычислить на основе новых свидетельств. Это позволяет применять байесовские принципы к различным видам свидетельств, независимо от того, рассматриваются ли они все сразу или с течением времени. Эта процедура называется байесовской модификацией.
Теорема Байеса : Синяя неоновая вывеска Autonomy Corporation в Кембридже, демонстрирующая простое утверждение теоремы Байеса.
Дело Коллинза
Народ штата Калифорния против Коллинза был судебным процессом присяжных в 1968 году в Калифорнии, который печально известен криминалистическим использованием статистики и вероятности.
Цели обучения
Спорить о том, что вызывает ошибку прокурора
Основные выводы
Ключевые моменты
- Свидетели ограбления в Лос-Анджелесе показали, что преступниками были чернокожий мужчина с бородой и усами и белая женщина со светлыми волосами, собранными в хвост. Они скрылись на желтом автомобиле.
- Свидетель обвинения, преподаватель математики, объяснил присяжным правило умножения, но не придал значения независимости или разнице между условной и безусловной вероятностью.
- Дело Коллинза — яркий пример феномена, известного как ошибка прокурора.
Ключевые термины
- правило умножения : Вероятность того, что произойдет А и В, равна вероятности того, что произойдет А, умноженной на вероятность того, что произойдет В, при условии, что мы знаем, что А уже произошло.

- ошибка прокурора : Ошибка статистического рассуждения при использовании в качестве аргумента в судебных разбирательствах.
Народ штата Калифорния против Коллинза был судом присяжных в 1968 году в Калифорнии. Он сделал печально известное криминалистическое использование статистики и вероятности. Свидетели ограбления в Лос-Анджелесе показали, что преступниками были темнокожий мужчина с бородой и усами и белая женщина со светлыми волосами, собранными в хвост. Они скрылись на желтом автомобиле.
Прокурор вызвал для дачи показаний преподавателя математики из местного государственного колледжа. Инструктор объяснил присяжным правило умножения, но не придал значения независимости или разнице между условной и безусловной вероятностью. Затем прокурор предположил, что присяжные будут в безопасности при оценке следующих вероятностей:
- Черный мужчина с бородой: 1 из 10
- Мужчина с усами: 1 из 4
- Белая женщина с конским хвостом: 1 из 10
- Белая женщина со светлыми волосами: 1 из 3
- Желтый автомобиль: 1 из 10
- Межрасовая пара в машине: 1 из 1000
При совместном рассмотрении этих вероятностей получается 1 шанс из 12 000 000, что преступление совершила любая другая пара с аналогичными характеристиками, то есть, по мнению прокурора. Присяжные вынесли обвинительный приговор.
Присяжные вынесли обвинительный приговор.
Как видно из апелляции, Верховный суд Калифорнии отменил обвинительный приговор, раскритиковав статистическую аргументацию и не согласившись с тем, как решение было представлено присяжным. В своем решении судьи отметили, что математика:
Дело Коллинза : Дело Коллинза — классический пример ошибки прокурора. Обвинительный вердикт был отменен после подачи апелляции в Верховный суд Калифорнии в 1968 году.
Заблуждение прокурора
Дело Коллинза — яркий пример феномена, известного как ошибка прокурора — ошибка статистических рассуждений, когда она используется в качестве аргумента в судебных разбирательствах. По своей сути это заблуждение предполагает, что априорная вероятность случайного совпадения равна вероятности того, что подсудимый невиновен. Например, если известно, что преступник имеет ту же группу крови, что и подсудимый (и 10% населения имеют эту группу крови), утверждать исключительно на том основании, что вероятность виновности подсудимого равна 90% составляет заблуждение прокуроров (в очень простой форме).
Основная ошибка возникает из-за неправильного понимания условной вероятности и пренебрежения априорными шансами виновности подсудимого до того, как были представлены эти доказательства. Когда прокурор собрал какие-то доказательства (например, совпадение ДНК) и заставил эксперта засвидетельствовать, что вероятность обнаружения этих доказательств, если обвиняемые были невиновны, мала, ошибка возникает, если делается вывод, что вероятность невиновности обвиняемых должны быть сравнительно крошечными. Если совпадение ДНК используется для подтверждения вины, которая в противном случае подозревается, то это действительно веское доказательство. Однако, если доказательство ДНК является единственным доказательством против обвиняемого, и обвиняемый был выбран из большой базы данных профилей ДНК, то шансы на случайное совпадение могут быть снижены. Следовательно, это менее вредно для ответчика. Шансы в этом сценарии не связаны с шансами быть виновным; они относятся к шансам быть выбранными случайным образом.
Лицензии и авторство
Контент под лицензией CC, опубликованный ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- Вероятность. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Некоторые правила вероятности — Статистика. Предоставлено : Wikidot. Расположен по адресу : http://statistics.wikidot.com/ch5. Лицензия : CC BY-SA: Attribution-ShareAlike
- Аксиомы вероятности. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- правило добавления. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Вероятность.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - Некоторые правила вероятности — Статистика. Предоставлено : Wikidot. Расположен по адресу : http://statistics.wikidot.com/ch5. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- образец пространства. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/sample_space. Лицензия : CC BY-SA: Attribution-ShareAlike
- Независимость (теория вероятностей). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Роберта Блум, Темы вероятностей: независимые и взаимоисключающие события (модифицированный Р.
 Блум). 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Блум). 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - независимость. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- теория вероятностей. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Все размеры | Ace of Spades Card Trick Magic Macro 19.10.09 2 | Flickr — Обмен фотографиями!. Предоставлено : Flickr. Расположен по адресу : https://www.flickr.com/photos/stevendepolo/4028160820/sizes/o/in/photostream/. Лицензия : CC BY: Атрибуция
- Биекция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Принцип классификации.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Принцип включения-исключения. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Комбинаторика. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Двойной счет (метод проверки). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Биективное доказательство. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Комбинаторные принципы. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- комбинаторика. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- полином.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - Все размеры | Ace of Spades Card Trick Magic Macro 19.10.09 2 | Flickr — Обмен фотографиями!. Предоставлено : Flickr. Расположен по адресу : https://www.flickr.com/photos/stevendepolo/4028160820/sizes/o/in/photostream/. Лицензия : CC BY: Атрибуция
- Байесовский вывод. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Bayesian_inference. Лицензия : CC BY-SA: Attribution-ShareAlike
- Правило Байеса. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теорема Байеса. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Фактор Байеса.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Все размеры | Ace of Spades Card Trick Magic Macro 19.10.09 2 | Flickr — Обмен фотографиями!. Предоставлено : Flickr. Расположен по адресу : https://www.flickr.com/photos/stevendepolo/4028160820/sizes/o/in/photostream/. Лицензия : CC BY: Attribution
- Теорема Байеса MMB 01. Предоставлено : Wikimedia. Лицензия : CC BY-SA: Attribution-ShareAlike
- Люди против Коллинза. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Ошибка прокурора. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- прокурорская ошибка.
 Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Prosecutor%27s_fallacy. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Prosecutor%27s_fallacy. Лицензия : CC BY-SA: Attribution-ShareAlike - Все размеры | Ace of Spades Card Trick Magic Macro 19.10.09 2 | Flickr — Обмен фотографиями!. Предоставлено : Flickr. Расположен по адресу : https://www.flickr.com/photos/stevendepolo/4028160820/sizes/o/in/photostream/. Лицензия : CC BY: Attribution
- Теорема Байеса MMB 01. Предоставлено : Wikimedia. Расположен по адресу : https://commons.wikimedia.org/wiki/File:Bayes%27_Theorem_MMB_01.jpg. Лицензия : CC BY-SA: Attribution-ShareAlike
- Печать CA SC. Предоставлено : Wikimedia. Лицензия : Общественное достояние: Неизвестно Copyright
Дополнительное правило для вероятности — GeeksforGeeks
Как часть общества, общение с окружающими очень распространено, и не все сообщения включают факты. Факты — это универсальная истина, о которой все мы знаем, что она истинна и существует, но что, если кто-то скажет: «Сегодня может пойти дождь». Будет ли это считаться фактом? Нет, потому что это не универсальная истина и нет уверенности в том, что это событие произойдет.
Факты — это универсальная истина, о которой все мы знаем, что она истинна и существует, но что, если кто-то скажет: «Сегодня может пойти дождь». Будет ли это считаться фактом? Нет, потому что это не универсальная истина и нет уверенности в том, что это событие произойдет.
В списке ниже приведены некоторые утверждения, давайте рассмотрим их подробнее:
- Индия, вероятно, сегодня выиграет.
- Может быть, сегодня премьер-министр сделает заявление.
- Есть шанс, что известный музыкант Джон Майер приедет в Индию с туром.
- Вероятность того, что сегодня «Барселона» обыграет «Реал Мадрид», составляет 50 на 50.
Обратите внимание, что во всех этих утверждениях используются такие слова, как «вероятно», «шансы» и т. д. Эти заявления не точны, есть вероятность того, что эти вещи произойдут, но это не обязательно, что эти вещи произойдут. Таким образом, эта неопределенность, присутствующая в этих утверждениях, выражена «вероятностью» в математических терминах. Давайте определим вероятность в формальных терминах.
Давайте определим вероятность в формальных терминах.
Вероятность
Вероятность — это экспериментальный подход к азартной игре, с которой мы сталкиваемся каждый день в нашей жизни. Это способ описать эти «шансы» математическим способом, а затем проанализировать их. Это позволяет нам измерить вероятность того, что что-то произойдет.
Концепция вероятности была разработана известным философом и математиком Блезом Паскалем в 17 веке.
Давайте проведем эксперимент,
Предположим, у нас есть монета, мы подбрасываем ее несколько раз, а затем собираем данные об орлах и решках. Мы проведем этот эксперимент несколько раз и запишем данные в таблицу.
| Total Number of Times Coin Tosses | Number of Heads | Number of Tails |
| 5 | 2 | 3 |
| 10 | 7 | 3 |
| 15 | 9 | 6 |
| 20 | 11 |
Рассчитают Let’s Dealling of Two Fracts Deal Retae,
9 90000004
Теперь, если мы продолжим вычислять эти значения, мы заметим, что значения начинают сходиться к 0,5 по мере увеличения количества экспериментов.
Испытание
Испытание — это действие, которое приводит к одному или нескольким исходам.
В данном эксперименте подбрасывание монеты является испытанием.
Событие
Событие является результатом испытания
Выпадение орла или решки после подбрасывания монеты можно считать событием в нашем эксперименте. Теперь давайте определим вероятность.
Пространство выборки
Это множество всех возможных результатов
Так как пространство выборки состоит из всех возможных результатов. В нашем случае количество решек может варьироваться от 0 до количества подбрасываний монеты.
{0, 1, 2, 3, …..n}
Вероятность
Это значение, обозначающее шансы возникновения некоторого события.
Пусть «n» — общее количество испытаний, а E — событие. Вероятность возникновения этого события
Обратите внимание, что по определению числитель всегда будет меньше или равен знаменателю.
Итак,
P(E) ≤ 1
Вопрос. На основе приведенного выше эксперимента предположим, что монета была подброшена 20 раз, и мы получили 15 орлов и 5 решек. Найдите вероятность выпадения орла и решки при повторном подбрасывании этой монеты.
Решение:
Мы знаем, что монета была подброшена 20 раз, предположим, мы хотим сначала вычислить вероятность выпадения орла.
Вероятность выпадения орла:
Итак, событие, которое мы будем искать, это выпадение орла, это произошло 15 раз, когда монета была подброшена 20 раз.
Вероятность выпадения решки:
Итак, событие, которое мы будем искать, — это выпадение орла, это произошло 5 раз, когда монета была подброшена 20 раз.
Обратите внимание, что в предыдущем примере вероятность выпадения орла и вероятность выпадения решки при суммировании дают нам 1.
Вероятность с помощью диаграмм Венна
Прежде чем представить диаграммы Венна, нам нужно взглянуть на термин «Взаимоисключающие».
Взаимоисключающие: Предположим, что в испытании есть два события A и B. Если оба они не могут произойти одновременно, то оба события являются взаимоисключающими.
Например: В эксперименте с подбрасыванием монеты невозможно одновременное совпадение орла и решки. Так что это взаимоисключающие явления в природе.
Другой пример,
Предположим, что была брошена игральная кость, событие A — это выпадение нечетного числа, а событие B — число 3. Теперь, когда на кости выпадает 3, оба события A и B происходят одновременно. Таким образом, они не исключают друг друга.
На приведенных ниже диаграммах представлена диаграмма Венна для эксперимента с подбрасыванием монеты, который мы провели выше. Поскольку оба события взаимоисключающие, эти окружности не пересекаются.
В качестве примера броска кубика давайте составим диаграмму Венна для события A и события B. Обратите внимание, что исходы 1, 5 и 3 находятся в одном круге, который обозначает событие A. 3 является общим для обоих событий, а таким образом, он находится на пересечении. 4 и 6 ни в коем случае не приходят, а значит, лежат снаружи в пространстве выборки.
3 является общим для обоих событий, а таким образом, он находится на пересечении. 4 и 6 ни в коем случае не приходят, а значит, лежат снаружи в пространстве выборки.
Эти события не исключают друг друга, поэтому диаграммы пересекаются.
Сложение вероятностей
В первом примере мы видели, что вероятность выпадения орла и решки в сумме составляет 1. Отсюда возникает еще одно правило вероятности.
Для взаимоисключающих событий. Сумма всех вероятностей всех событий в эксперименте всегда равна 1. Например:
Если испытание имеет три возможных исхода, A, B и C.
P(A) + P(B) + P(C) = 1
Иногда нас интересует только один результат. Допустим, в чемпионате мира по крикету участвуют 8 команд. Нас интересует вероятность победы Индии в чемпионате мира. Нас не интересует выяснение вероятности для любой другой команды. Итак, мы сформулируем задачу следующим образом:
Допустим, событие А означает, что Индия выиграла чемпионат мира. Итак, другое событие B означает, что Индия не выиграла чемпионат мира.
Итак, другое событие B означает, что Индия не выиграла чемпионат мира.
P(A) + P(B) = 1
P(A) = 1 – P(B)
Такие события называются элементарными событиями.
Правила сложения вероятностей
Предположим, что есть два события A и B, исходя из того, являются ли оба события взаимоисключающими или нет. Описаны два разных правила,
Правило 1: когда события являются взаимоисключающими
Когда события являются взаимоисключающими, вероятность возникновения событий равна сумме обоих событий.
P(A∪B) = P(A) + P(B)
Правило 2: Когда события не исключают друг друга
Между двумя не исключающими друг друга событиями всегда есть некоторое совпадение , Следовательно, Вероятность событий примет вид
P(A∪B)= P(A) + P(B) – P(A∩B)
Давайте посмотрим на некоторые проблемы с этими понятиями.
Вопрос 1. Допустим, бросили игральную кость. Ответьте на следующие вопросы:
- Какова вероятность того, что выпадет число больше 4.
- Какова вероятность того, что выпадет четное число.
Решение:
При броске кости возможны шесть исходов.
1, 2, 3, 4, 5 и 6
Вероятность получения числа больше 4:
Количество благоприятных исходов = 2
Общее количество исходов = 6
Вероятность выпадения четного числа:
Количество благоприятных исходов = 3
Общее количество исходов = 6
Вопрос 2. Допустим, из хорошо перетасованной колоды карт была взята карта. Найдите вероятность того, что при одном розыгрыше выпадет дама.
Решение:
Мы знаем, что в колоде 52 карты.
Таким образом, всего возможны 52 исхода, если вытянута карта. Мы также знаем, что в колоде четыре дамы. Это наши благоприятные исходы.
Итак,
Общее количество исходов = 52
Общее количество благоприятных исходов = 4
Вопрос 3. В мешке лежат 3 белых, 4 черных и 2 зеленых шара. Вынимается мяч с возвратом. Найдите вероятность получения:
- A Белый шарик
- A Black Ball
- A Green Ball
Решение:
199404 . 9яйца.1. Вероятность выпадения белого шара
Общее количество шаров = 9,
Благоприятных исходов = 3
= 4
3. Вероятность выпадения черного шара
Общее количество шаров = 9,
Благоприятных исходов = 2
Вопрос 4: Спутник упал из космоса. На рисунке ниже обозначен район, в котором, по мнению ISRO, разбился спутник. Найдите вероятность того, что он упал в озеро.
Найдите вероятность того, что он упал в озеро.
Решение:
В этом случае мы не знаем количество исходов. Это сплошной случай, то есть самолет может рухнуть в любом месте района.
Итак, общая площадь региона = 10 × 5 = 50 км 2
Общая площадь озера = 5 × 3 = 15 км 2
Теперь мы можем использовать эти площади для расчета вероятности.
Общее количество возможных исходов (площадь в данном случае) = 50 км 2
Общее количество благоприятных исходов (в данном случае площадь озера) = 5 × 3 = 15 км 2
Таким образом, вероятность падения спутника в озеро равна 0,3.
Вопрос 5: Допустим, у нас есть хорошо перетасованная колода. Берем две карты, находим вероятность получить либо короля, либо даму.
Решение:
Допустим, выпадение короля представляет собой событие A, а вытаскивание ферзя представляет событие B.
Нас спрашивают о вероятности выпадения короля или ферзя. Здесь мы будем использовать закон сложения вероятностей,
Вероятность (Король или Дама) = Вероятность (Король) + Вероятность (Королева)
Мы знаем, что в колоде 4 Короля и 4 Дамы.
P(Король) =
P(Королева) =
Таким образом,
Вероятность (Король или Дама) =
белые шарики. Найти вероятность того, что выпадет один черный, один синий и один белый шар, если мы вытащим три раза с пополнением.
Решение:
Всего у нас восемь мячей.
P(выпадение черного шара) =
P(выпадение синего шара) =
P(выпадение белого шара) =
Эту вероятность мы найдем с помощью закона сложения.
Таким образом, общая вероятность получения всех трех цветов = P (черный) + P (Blue) + P (белый)
=
Обратите внимание, что вероятность суммирует до одного. Это соответствует законам вероятности.
Вопрос 7: Союзный бюджет будет объявлен правительством на этой неделе. Вероятность того, что он будет анонсирован в день, дана,
| День | Вероятность |
| в понедельник | 99 [TEX] \ FRAC \ FRAC \ FRAC \ FRAC \ FRAC. ].0040 |
| Четверг | [Tex]\frac{1}{7}[/Tex] |
| Пятница | [Tex9]\frac{1}{7} |
Найдите вероятность объявления бюджета в период с понедельника по среду.
Решение:
Нам нужно использовать закон сложения вероятностей,0005
P (вторник) =
P (среда) =
P (с понедельника по среду) = P (понедельник) + P (вторник) + P (среда)
=
=
Вопрос 8: В классе из 90 учеников 50 занимались математикой, 25 — физикой, 30 — и математикой, и физикой. Найдите количество учеников, которые изучали математику или физику.
Найдите количество учеников, которые изучали математику или физику.
Решение:
Поскольку события выбора математики и физики не являются взаимоисключающими, здесь будет применяться второе правило сложения,
P(Математика ∪ Физика) = P(Математика) + P(Физика) – P(Математика ∩ Физика)
P(Математика) = 50
P(физика) = 25
P(Математика ∩ Физика) = 30
P( Математика ∪ Физика)= 50+ 25 – 30
P(Математика ∪ Физика)= 30 учеников.
Использование правила сложения и объединение против пересечения — Криста Кинг Математика
Что такое правило сложения и когда оно применяется?
Иногда нам нужно найти вероятность того, что два события произойдут вместе в одном эксперименте. Помните, что событие – это конкретный набор результатов из выборочного пространства .
Например, какова вероятность того, что мы бросим пару кубиков с ???6???-гранями и получим хотя бы один ???1???, или четную сумму при сложении костей?
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Когда мы бросаем два кубика вместе, получается ???36??? возможные исходы. Есть ???11??? выкатывается из ???36??? где мы получим хотя бы один ???1???:
А есть ???18??? возможные исходы при четной сумме костей.
Таким образом, у нас может возникнуть соблазн сказать, что вероятность получения хотя бы одного ???1??? или четная сумма равна ???P(1\text{или даже})=(11+18)/36??? или ???29/36???. Но мы упустили из виду, что между этими двумя наборами есть некоторое совпадение. У нас есть ролики ???1-1???, ???1-3???, ???1-5???, ???3-1??? и ???5- 1??? в обоих наборах, поэтому мы дважды учитываем их при расчете вероятности.
Это означает, что мы должны вычесть перекрывающиеся значения. Так как есть ???5??? перекрывающиеся значения, вычисление вероятности на самом деле
???P(1\text{ или даже})=\frac{11+18-5}{36}???
???P(1\text{ или даже})=\frac{24}{36}???
???P(1\text{или даже})=\frac23???
Отличный способ проиллюстрировать такую вероятность перекрытия — использовать диаграмму Венна. Мы построим диаграмму Венна, чтобы показать, что существует ???11??? ролики, где мы получаем хотя бы один ???1???, что есть ???18??? катит, где сумма четная, и что там ???5??? ролики, где мы получим хотя бы один ???1??? и сумма тоже четная.
Мы построим диаграмму Венна, чтобы показать, что существует ???11??? ролики, где мы получаем хотя бы один ???1???, что есть ???18??? катит, где сумма четная, и что там ???5??? ролики, где мы получим хотя бы один ???1??? и сумма тоже четная.
Затем из диаграммы Венна мы просто добавляем ???6+5=11??? и ???5+13=18???, а затем вычтите перекрывающиеся ???5???, чтобы получить все результаты, соответствующие нашим критериям, но без двойного подсчета ни одного из результатов. И тогда наша вероятность снова равна
???P(1\text{ или даже})=\frac{11+18-5}{36}=\frac{24}{36}=\frac23???
Правило сложения
Эта идея убедиться, что мы не учитываем дважды перекрытие, называется правило сложения (или правило сумм) для вероятности и задается как:
???P(A \text{ или } B)=P(A)+P(B)-P(A\text{ и }Б)???
Что произойдет, если между ???A??? нет перекрытия? и ???Б???? В таком случае ???А??? и ???Б??? называются взаимоисключающими (или непересекающимися), а ???P(A\text{ и }B)??? будет ???0???. Это означает, что правило сложения упростится следующим образом:
Это означает, что правило сложения упростится следующим образом:
???P(A \text{ или } B)=P(A)+P(B)-P(A\text{ и }B)???
???P(A \text{ или } B)=P(A)+P(B)-0???
???P(A \text{ или } B)=P(A)+P(B)???
Что говорит нам о том, что когда события являются взаимоисключающими/непересекающимися, мы можем рассчитать вероятность любого события ???A??? происходит или событие ???B??? происходит просто путем сложения вероятности каждого события в отдельности.
Например, события на этой диаграмме Венна не пересекаются, поскольку окружности не пересекаются:
Потому что есть ???10+7=17??? общее количество событий, вероятность события ???A??? ???P(A)=10/17???. А вероятность события ???B??? ???P(B)=7/17???. Значит, вероятность того, что произойдут оба события, равна 9.0005
???P(A\text{ или }B)=P(A)+P(B)???
???P(A\text{ или }B)=\frac{10}{17}+\frac{7}{17}???
???P(A\text{ или }B)=\frac{17}{17}???
???P(A\text{ или }B)=1???
Объединение и пересечение
В первом варианте формулы правила сложения мы используем слова «или» и «и». Но мы также можем записать формулу как:
Но мы также можем записать формулу как:
???P(A\чашка B)=P(A)+P(B)-P(A\cap B)???
Эта вторая формула представляет собой тот же расчет правила сложения, но мы используем ???\cup??? и ???\шапка??? символы вместо слов «и» и «или».
???P(A\чашка B)??? называется объединением ???A??? и ???B???, а это означает вероятность того или иного ???A??? или ???Б??? или оба происходят. ???P(A\cap B)??? называется пересечением ???A??? и ???B???, а это означает вероятность ???A??? и ???Б??? оба происходят.
Использование правила сложения для расчета вероятности
Пройти курс
Хотите узнать больше о вероятности и статистике? У меня есть пошаговый курс для этого. 🙂
Учить больше
Использование правила сложения для расчета вероятностей из двусторонней таблицы данных
Пример
Мы обследовали ???100??? людей о своем любимом виде спорта и записали их пол и любимый вид спорта в таблицу.
Какова вероятность того, что участник — мужчина?
Какова вероятность того, что любимым видом спорта участника является футбол?
Какова вероятность того, что участник является женщиной или предпочитает другой вид спорта, кроме футбола или баскетбола?
Из таблицы известно, что ???60??? из ???100??? участники — мужчины, поэтому вероятность того, что участник — мужчина, составляет
???P(\text{мужской})=\frac{60}{100}=\frac35???
А из таблицы видно, что ???38??? из ???100??? участники больше всего любят футбол, поэтому вероятность того, что любимым видом спорта участника является футбол, равна
???P(\text{футбол})=\frac{38}{100}=\frac{19}{50}???
Эта идея, позволяющая избежать двойного подсчета перекрытий, называется правилом сложения (или правилом сумм) для вероятности.
Оба эти вопроса были простыми вероятностными вопросами, но третий вопрос требует от нас использования правила сложения. Есть ???40??? участницы и ???41??? участников, предпочитающих спорт, отличный от футбола или баскетбола.
Но есть ???16??? участники группы «перекрытия»: группа женщин, которые также предпочитают другой вид спорта, кроме футбола или баскетбола. Следовательно, мы применим правило сложения и скажем, что вероятность того, что участник является женщиной или любит другой вид спорта, кроме футбола и баскетбола, равна
???P(\text{женщина или кто-то другой})=\frac{40+ 41-16}{100}=\frac{65}{100}=\frac{13}{20}???
Получите доступ к полному курсу «Вероятность и статистика»
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, вероятность, статистика, статистика, вероятность и статистика, вероятность и статистика, правило сложения, объединение и пересечение, объединение и пересечение, правило сложения для вероятность
0 лайковРаздел 5.
 2: Правило сложения и дополнения
2: Правило сложения и дополненияЦели
К концу этого урока вы сможете…
- использовать правило сложения для непересекающихся событий
- используйте Общее правило добавления
- используйте правило дополнения
Дополнительное правило для непересекающихся событий
В этой главе у нас будет довольно много правил о вероятности, но мы начнем с малого. Первая ситуация, которую мы хотим рассмотреть, — это когда два события не имеют общих исходов. Мы называем подобные события непересекающимися. события .
Два события являются непересекающимися , если у них нет общих исходов. (Также обычно
известный как взаимоисключающих событий. )
)
Еще в 1881 году Джон Венн разработал отличный способ визуализации наборов. Как это часто бывает случай в математике, диаграммы взяли его имя и с тех пор его имя — Венн диаграммы. Поскольку события представляют собой наборы исходов, хорошо работает визуализация вероятности. также. Вот пример диаграммы Венна, показывающий два непересекающихся результата: Е и Ф.
Продолжим немного дальше и расставим точки на графике вот так — для обозначения результатов.
Глядя на рисунок, мы ясно видим, что P(E) = 5/15 = 1/3, так как в E 5 исходов, а всего исходов 15. Точно так же P (F) также равно 1/3.
Далее мы хотим рассмотреть все события, которые находятся либо в E, либо в F. вероятности, мы называем это событие E или F . Итак, в нашем примере P(E или F) = 10/15 = 2/3.
Но это видно только на картинке! Просто посчитайте точки, которые
Е и добавить к нему количество точек в F.
В общем, мы можем создать правило. Мы назовем это…
Правило сложения для непересекающихся событий
Если E и F являются непересекающимися (взаимно исключающими) событиями, то
P(E или F) = P(E) + P(F)
Пример 1
OK — время для примера. Давайте воспользуемся примером из предыдущего раздела о семья с тремя детьми, и определим следующие события:
E = в семье ровно два мальчика
F = в семье ровно один мальчик
Опишите событие «E или F» и найдите его вероятность.
[раскрыть ответ]
«E или F» — это событие, которое семья имеет либо один или два мальчика.
Ясно, что оба эти события не могут произойти одновременно. одновременно, поэтому они не пересекаются. Вероятность того, что в семье тогда либо один, либо два мальчика:
P(E или F) = P(E) + P(F) = 3/8 + 3/8 = 6/8 = 3/4
Конечно, часто бывают случаи, когда два события имеют исходы в
общее, поэтому нам понадобится более надежное правило для этого случая.
Общее правило сложения
Что происходит, когда два события с по имеют общие исходы? Что ж, давайте рассмотрим пример ниже. В этом случае P(E) = 4/10 = 2/5, и P(F) = 5/10 = 1/2, но P(E или F) не равно 9/10. Вы видите, почему?
Ключевым здесь являются два результата в середине, где E и F перекрываются. Официально мы называем этот регион событием E и F . Это все исходы, которые есть в и E и F. В нашем визуальном пример:
В этом случае, чтобы найти P(E или F), нам нужно сложить результаты в E с результатами в F, а затем вычесть дубликатов, которые мы сосчитаны, которые находятся в E и F. Мы называем это Общее дополнение Правило .
Общее правило сложения
P(E или F) = P(E) + P(F) — P(E и F)
Давайте рассмотрим пару быстрых примеров.
Пример 2
Рассмотрим колоду стандартных игральных карт.
Предположим, мы вытащили одну карту из колоды наугад и определили следующее события:
E = вытянутая карта туз
F = взятая карта является королем
Используйте эти определения, чтобы найти P(E или F).
[показать ответ]
Хорошо, так как E и F не имеют общих исходов, мы можем использовать правило сложения для непересекающихся событий:
P(E или F) = P(E) + P(F) = 4 /52 + 4/52 = 8/52 = 2/13
Пример 3
Рассмотрим колоду игральных карт, одна из которых вытягивается наугад. Предположим, мы определяем следующие события:
F = взятая карта является королем
G = вытянутая карта является червой
Используйте эти определения, чтобы найти P(F или G).
[показать ответ]
В отличие от предыдущего примера, события F и G, и имеют общий результат — король червей — поэтому нам нужно использовать общий Правило добавления:
P(E или F)
= P(E) + P(F) — P(E и F)
= 4/52 + 13/52 — 1/52
= 16/52 = 4/13
Итак, ключевая идея и разница между этими двумя примерами — когда вы
находка
P(E или F), обязательно ищите исходы, общие для E и F.
Правило дополнения
Я думаю, что лучший способ представить последнюю идею в этом разделе — это рассмотреть пример. Снова обратимся к колоде стандартных игральных карт:
И определим событие E = взята карта меньше короля. Если я спрошу тебя чтобы найти P(E), вы не будете их подсчитывать. (Вы не собирались, были ты?!) Нет — ты скажешь, что карт всего 52, а королей 4, поэтому должно быть на 48 карт меньше, чем у короля. Итак, P(E) = 48/52 = 12/13.
Идея, которую вы уже используете, называется дополнением . (Это дополнение, с e . Не комплимент, как в «Мой, ты выглядишь красиво сегодня!»)
Дополнение E , обозначаемое E c , представляет собой все результаты в выборочном пространстве, которые не находятся в E.
Таким образом, дополнение E равно всему, кроме результатов
на E. На самом деле, в некоторых текстах это написано как «не E».
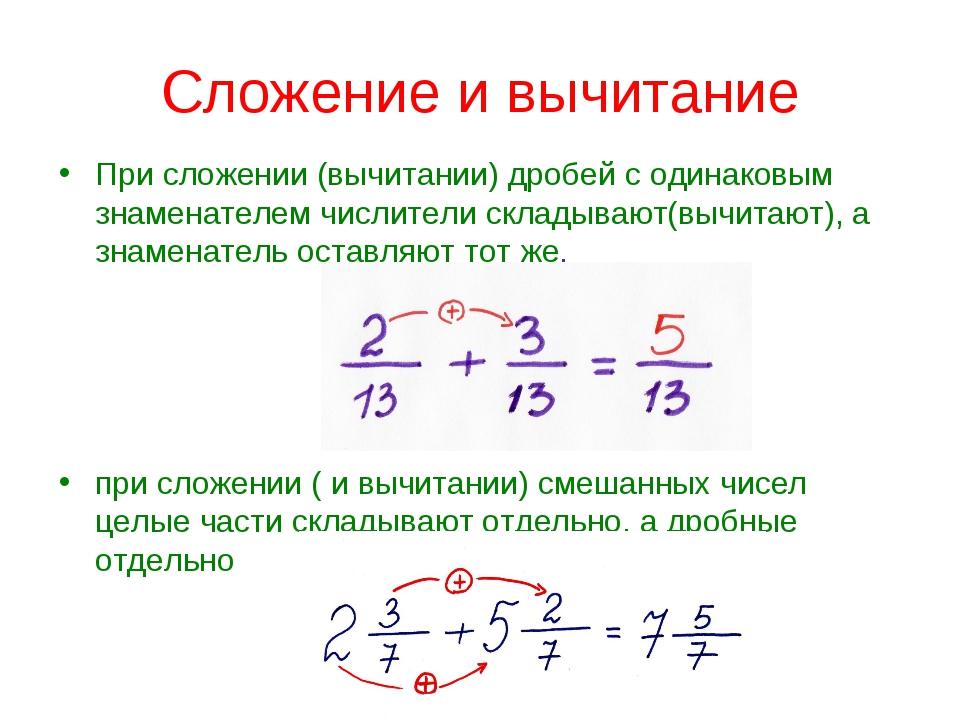 Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.





 В этом выражении мы можем либо сначала решить (9-10), либо сначала (-10 + 4). Это не повлияет на наш ответ.
В этом выражении мы можем либо сначала решить (9-10), либо сначала (-10 + 4). Это не повлияет на наш ответ.
 Если вы добавите положительное целое число, вы переместите столько единиц вправо.Если вы добавите отрицательное целое число, вы переместите столько единиц влево.
Если вы добавите положительное целое число, вы переместите столько единиц вправо.Если вы добавите отрицательное целое число, вы переместите столько единиц влево.
 Сделайте небольшой образец, который должен решить учащийся, и понаблюдайте, что происходит с ответами:
Сделайте небольшой образец, который должен решить учащийся, и понаблюдайте, что происходит с ответами: Основная идея состоит в том, чтобы интерпретировать вычитание как «удаление». Например, с (−4) — (−2) вы начинаете с 4 отрицательными счетчиками и убираете два отрицательных счетчика. У вас осталось 2 отрицательных счетчика.
Основная идея состоит в том, чтобы интерпретировать вычитание как «удаление». Например, с (−4) — (−2) вы начинаете с 4 отрицательными счетчиками и убираете два отрицательных счетчика. У вас осталось 2 отрицательных счетчика.

 Следовательно, мы получаем (например), что (−3) × (−4) = 12. Итак, отрицательное значение, умноженное на отрицательное, является положительным!
Следовательно, мы получаем (например), что (−3) × (−4) = 12. Итак, отрицательное значение, умноженное на отрицательное, является положительным! Возможно, они частично понимают это
Возможно, они частично понимают это


 или второкурсники.
или второкурсники.


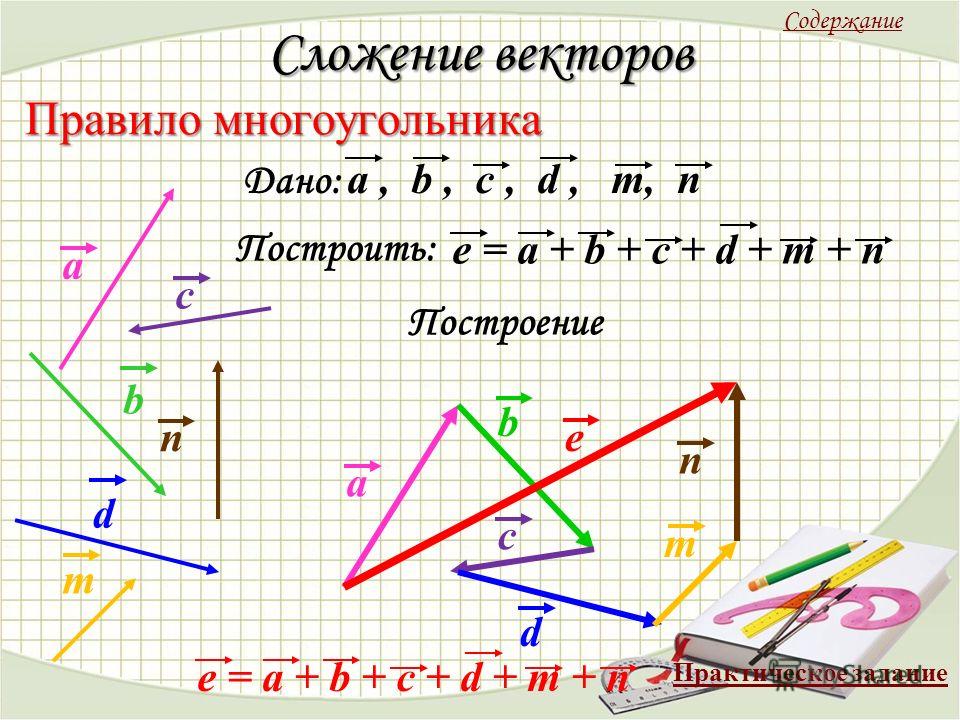



 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Блум). 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Блум). 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Prosecutor%27s_fallacy. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Prosecutor%27s_fallacy. Лицензия : CC BY-SA: Attribution-ShareAlike  Итак,
Итак,  Таким образом, всего возможны 52 исхода, если вытянута карта. Мы также знаем, что в колоде четыре дамы. Это наши благоприятные исходы.
Таким образом, всего возможны 52 исхода, если вытянута карта. Мы также знаем, что в колоде четыре дамы. Это наши благоприятные исходы. Нас спрашивают о вероятности выпадения короля или ферзя. Здесь мы будем использовать закон сложения вероятностей,
Нас спрашивают о вероятности выпадения короля или ферзя. Здесь мы будем использовать закон сложения вероятностей,