Тема сложение дробей. Сложение и вычитание дробей с разными знаменателями.

• Альфашкола
• Статьи
• Сложение дробей

Сложение – это арифметическое действие, в результате которого получают новое число, содержащее столько единиц, сколько было во всех заданных числах вместе взятых.

Дробь обозначает тип деления, который рассматривается как часть целого и  указывает на разделение целого на равные доли или части, где знаменатель показывает, на сколько частей мы разделили, а числитель — сколько взяли частей от этого целого. 

 

Сложение или вычитание дробей могут быть двух видов:

• знаменатели одинаковые;
• знаменатели разные;

Правила сложения дробей:

1. Одинаковые знаменатели. Складываем числители этих дробей. 
2. Разные знаменатели. Находим общий знаменатель с помощью наименьшего общего кратного чисел, и складываем их числители.

Чтобы вычислить НОК, необходимо разбить числа на простые множители и найти разложение большего числа, добавив к нему простые недостающие множители другого разложения. Полученные числа перемножить. Алгоритм решения для двух, трех и более чисел одинаков, если числа простые, то надо перемножить их.

 

Примеры решения задач: сложение дробей с одинаковым знаменателем.

Задача 1. Сложить две дроби с одинаковыми знаменателями \(\frac{7}{8}\) и \(\frac{1}{8}\).

Решение:

\(\frac{7}{8}+\frac{1}{8}=\)\(\frac{(7+1)}{8}\)\(=\frac{8}{8}=\frac{1}{1}\)

 

 

Ответ:\(1\).

Задача 2. Сложить две дроби с одинаковыми знаменателями \(\frac{6}{5}\)и \(\frac{3}{5}\).

Решение:

\(\frac{6}{5} +\frac{3}{5}\)\(=\frac{(6+3)}{5}\)\(=\frac{9}{5}=1\frac{4}{5}\)

 

 

Ответ:\(1\frac{4}{5}\).

3адача 3. Сложить две  дроби \(\frac{11}{3}\) и \(\frac{5}{3}\).

Решение:

\(\frac{11}{3}\) + \(\frac{5}{3}\)\(=\)\(\frac{(11+5)}{3}=\frac{16}{3}=5\frac{1}{3}\)

 

16/3 

Ответ:\(5\frac{1}{3}\).

3адача 4. Сложить две  дроби  с разными знаменателями \(\frac{11}{3}\) и \(\frac{5}{8}\).

Решение:

НОК\((3;8)\) \(=24\)

\(\frac{11*8}{3*8}+\frac{5*3}{8*3}\)\(=\)\(\frac{88}{24}+\frac{15}{24}=\)\(\frac{88+15}{24}\)\(=\frac{103}{24}=4\frac{7}{24}\)

 

 

 

Ответ: \(4\frac{7}{24}\)

Задача 5. Сложить две дроби с разными знаменателями \(\frac{27}{3}\) и \(\frac{55}{13}\).

Решение.

\(НОК(3;13) =39\)

\(\frac{(27*13)}{3*13} +\frac{(55*3)}{13*3}=\)\(\frac{351}{39}+\frac{165}{39}\)\(=\frac{351+165}{39}=\)

 

\(=\frac{516}{39}-\) сокращаем обе части дроби на 3

\(\frac{175}{13}=13\frac{6}{13}\)

Ответ: \(13\frac{6}{13}\).

Выводы:

для того чтобы сложить или вычесть два и более дробных числа нам необходимо привести их к общему знаменателю;

основное свойство дробей: значение дробного числа не изменится, если числитель и знаменатель умножить или разделить на одно и то же число.

 

 

 

`

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Наталья Николаевна Шарапова

Репетитор по математике

Стаж (лет)

Образование:

Челябинский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике с 1 по 11 класс. Подготовка к ОГЭ/ЕГЭ, профиль до 70 баллов. Репетитор по информатике для 7-9 классов. Люблю математику и информатику, потому что просто люблю. Если бывает трудно, то предлагаю идти вместе. Когда человек не один, то всегда легче и интереснее. Заодно и вспомним, что забыл и выясним, что не знал. До встречи!

Юрий Павлович Грязнов

Репетитор по математике

Стаж (лет)

Образование:

Донецкий государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов.

Математика двигает человечество вперёд. Она помогает учёным познать окружающий мир. Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума. Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата. Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.

Хикмат Мансурбек угли Бекчанов

Репетитор по математике

Стаж (лет)

Образование:

Ургенчский Государственный Университет УрГУ

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 7-10 классы. Занимаюсь подготовкой к ЕГЭ. Люблю математику за то, что у меня легко получается решать разные примеры и задачи. Всегда стараюсь сложные задачи и примеры объяснять максимально простым языком. Легко могу найти общий язык с учениками. И самое главное — наслаждаюсь процессом обучения.

Похожие статьи

• Радианная мера угла
• Объем сферы
• МГУ Факультет Фундаментальной Физико-Химической Инженерии: приемная комиссия, проходной балл
• МИФИ: факультеты и специальности, проходной балл (2018 / 2017), документы
• ЕГЭ по математике, профильный уровень. Задача с параметром
• ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 5)
• Школьная газета: для кого, про что и зачем?
• Как правильно общаться с ребенком об успеваемости?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Правила сложения обыкновенных.

Сложение дробей с целыми числами и разными знаменателями

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

• Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
• Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
• Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

• найти НОК для всех знаменателей;
• поставить для всех дробей дополнительные множители;
• умножить все числители на дополнительный множитель;
• полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
• произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Числителем, а то, на которое делят — знаменателем.

Чтобы записать дробь, напишите сначала ее числитель, затем проведите под этим числом горизонтальную черту, а под чертой напишите знаменатель. Горизонтальная , разделяющая числитель и знаменатель, называется дробной чертой. Иногда ее изображают в виде наклонной «/» или «∕». При этом, числитель записывается слева от черты, а знаменатель справа. Так, например, дробь «две третьих» запишется как 2/3. Для наглядности числитель обычно пишут в верхней части строки, а знаменатель — в нижней, то есть вместо 2/3 можно встретить: ⅔.

Чтобы рассчитать произведение дробей, умножьте сначала числитель одной дроби на числитель другой. Запишите результат в числитель новой дроби . После этого перемножьте и знаменатели. Итоговое значение укажите в новой дроби . Например, 1/3 ? 1/5 = 1/15 (1 ? 1 = 1; 3 ? 5 = 15).

Чтобы поделить одну дробь на другую, умножьте сначала числитель первой на знаменатель второй. То же произведите и со второй дробью (делителем). Или перед выполнением всех действий сначала «переверните» делитель, если вам так удобнее: на месте числителя должен оказаться знаменатель. После этого умножьте знаменатель делимого на новый знаменатель делителя и перемножьте числители. Например, 1/3: 1/5 = 5/3 = 1 2/3 (1 ? 5 = 5; 3 ? 1 = 3).

Источники:

• Основные задачи на дроби

Дробные числа позволяют выражать в разном виде точное значение величины. С дробями можно выполнять те же математические операции, что и с целыми числами: вычитание, сложение, умножение и деление. Чтобы научиться решать дроби , надо помнить о некоторых их особенностях. Они зависят от вида дроби , наличия целой части, общего знаменателя. Некоторые арифметические действия после выполнения требуют сокращения дробной части результата.

Вам понадобится

• — калькулятор

Инструкция

Внимательно посмотрите на числа. Если среди дробей есть десятичные и непрвильные, иногда удобнее вначале выполнить действия с десятичными, а затем перевести их в неправильный вид. Можете перевести дроби в такой вид изначально, записав значение после запятой в числитель и поставив 10 в знаменатель. При необходимости сократите дробь, разделив числа выше и ниже на один делитель. Дроби, в которых выделяется целая часть, приведите к неправильному виду, умножив её на знаменатель и прибавив к результату числитель. Данное значения станет новым числителем дроби . Чтобы выделить целую часть из первоначально неправильной дроби , надо поделить числитель на знаменатель. Целый результат записать от дроби . А остаток от деления станет новым числителем, знаменатель дроби при этом не меняется.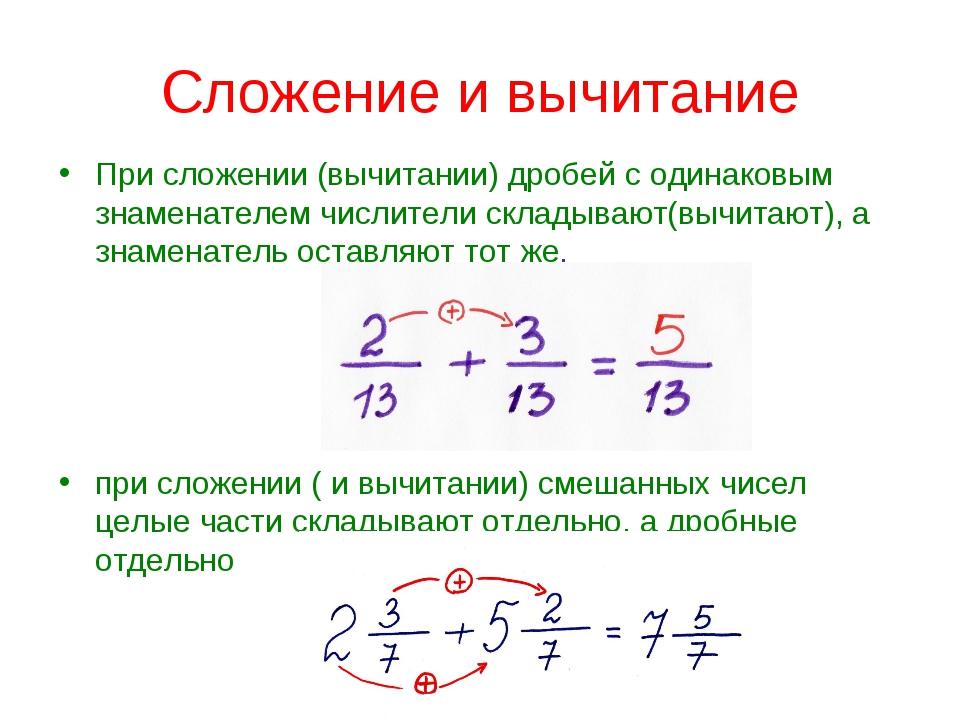 Для дробей с целой частью возможно выполнение действий отдельно сначала для целой, а затем для дробной частей. Например, сумма 1 2/3 и 2 ¾ может быть вычислена :
— Переведение дробей в неправильный вид:
— 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
— Суммирование отдельно целых и дробных частей слагаемых:
— 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾) = 3 +(8/12 + 9/12) = 3 + 17/12 = 3 + 1 5/12 = 4 5/12.

Перепишите их через разделитель «:» и продолжите обычное деление.

Для получения конечного результата полученную дробь сократите, разделив числитель и знаменатель на одно целое число, наибольшее возможное в данном случае. При этом выше и ниже черты должны быть целые числа.

Обратите внимание

Не выполняйте арифметические действия с дробями, знаменатели которых отличаются. Подберите такое число, чтобы при умножении на него числителя и знаменателя каждой дроби в результате знаменатели обеих дробей были равны.

Полезный совет

При записи дробных чисел делимое пишется над чертой. Эта величина обозначается как числитель дроби. Под чертой записывается делитель, или знаменатель, дроби. Например, полтора килограмма риса в виде дроби запишется следующим образом: 1 ½ кг риса. Если знаменатель дроби равен 10, такую дробь называют десятичной. При этом числитель (делимое) пишется справа от целой части через запятую: 1,5 кг риса. Для удобства вычислений такую дробь всегда можно записать в неправильном виде: 1 2/10 кг картофеля. Для упрощения можно сократить значения числителя и знаменателя, поделив их на одно целое число. В данном примере возможно деление на 2. В результате получится 1 1/5 кг картофеля. Удостоверьтесь, что числа, с которыми вы собираетесь выполнять арифметические действия, представлены в одном виде.

Действия с дробями.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.

Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.

Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.

Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.

А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.

Сложение и вычитание дробей.

Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:

Короче, в общем виде:

А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:

Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.

Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .

Ещё пример:

Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:

Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:

Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!

Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:

И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.

Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…

Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.

Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.

А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…

Итак, нам надо сложить два дробных выражения:

Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:

И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:

Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают.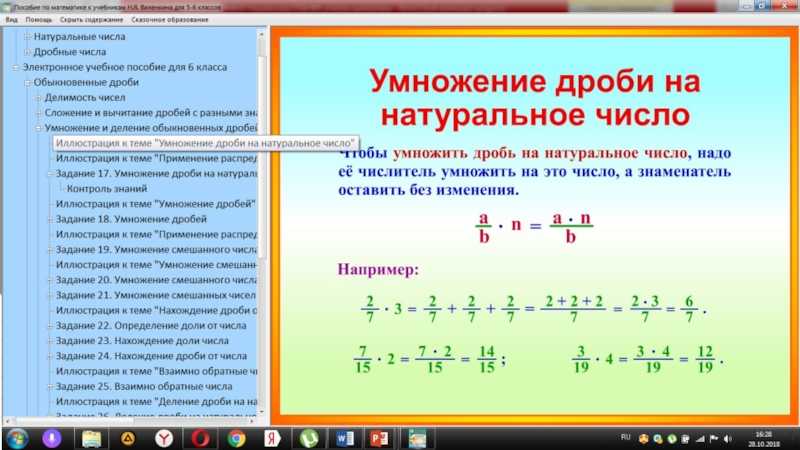 Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…

В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:

Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!

И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.

Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)

Вычислить:

Ответы (в беспорядке):

71/20; 3/5; 17/12; -5/4; 11/6

Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!

Как складывать десятичные дроби

Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:

• Разряд должен находиться под разрядом, запятая под запятой.

Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.

Сложение дробей с равными знаменателями

Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.

Сложение дробей с разными знаменателями методом нахождения общего кратного

Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:

• 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя. Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
• Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.

• Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.

Сложение дробей методом умножения крест на крест

Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.

Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.

Как вычесть дроби, знаменатели которых одинаковые

Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:

• Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы

7/19 — 3/19 = (7 — 3)/19 = 4/19.

От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».

На картинке ниже приведено еще несколько подобных примеров.

Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.

От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».

Сложение дробей, имеющих одинаковый знаменатель

Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.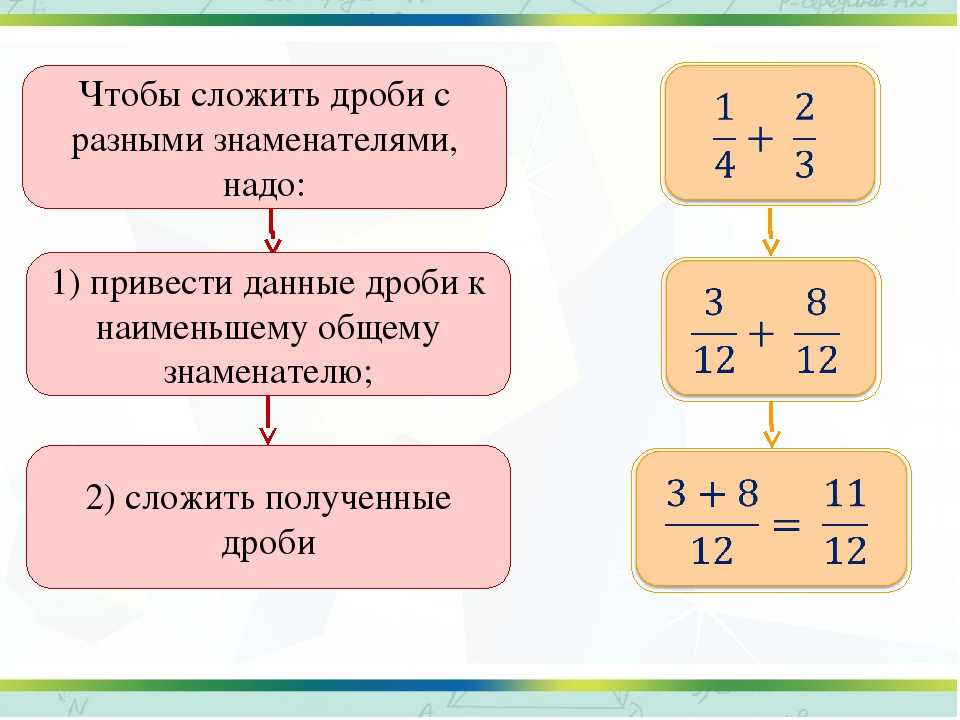

• Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:

1/4 + 2/4 = 3/4.

К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».

Дроби с различными знаменателями и их вычитание

Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.

Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.

О том, как это сделать, мы поговорим подробнее.

Свойство дроби

Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.

Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:

2/3 = 4/6 = 6/9 = 8/12…

Как привести несколько дробей к одному и тому же знаменателю

Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.

Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.

Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.

Аналогично производим действия с оставшимися дробями.

• 2/3 — в знаменателе не хватает одной тройки и одной двойки:
  2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
• 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
  7/9 = (7 х 2)/(9 х 2) = 14/18.
• 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
  5/6 = (5 х 3)/(6 х 3) = 15/18.

Все вместе это выглядит так:

Как вычесть и сложить дроби, имеющие различные знаменатели

Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.

Рассмотрим это на примере: 4/18 — 3/15.

Находим кратное чисел 18 и 15:

• Число 18 состоит из 3 х 2 х 3.
• Число 15 состоит из 5 х 3.
• Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.

• 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
• 90 поделить на 18. Полученное число «5» будет множителем для 4/18.

Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».

Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.

Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.

Аналогично производится и имеющих различные знаменатели.

Вычитание и имеющих целые части

Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:

• Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
• Если дроби имеют различные знаменатели, следует привести их к одинаковому.
• Произвести сложение или вычитание с одинаковыми знаменателями.
• При получении неправильной дроби выделить целую часть.

Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.

Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.

Вычитание дробей из целого числа

Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:

7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.

Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.

определения, правила и примеры задач

Одними из самых сложных для понимания школьника являются разные действия с простыми дробями. Это связано с тем, что детям еще сложно мыслить абстрактно, а дроби, по сути, для них именно так и выглядят. А потому, излагая материал, учителя часто прибегают к аналогиям и объясняют вычитание и сложение дробей буквально на пальцах. Хотя без правил и определений не обходится ни один урок школьной математики.

Базовые понятия

Прежде чем приступить к любым действиям с дробями, желательно усвоить несколько базовых определений и правил. Изначально важно понимать, что такое дробь. Под ней подразумевается число, представляющее собой одну или несколько долей единицы. Например, если буханку разрезать на 8 частей и 3 ломтика из них выложить в тарелку, то 3/8 и будет дробью. Причем в таком написании это будет простой дробью, где число над чертой — это числитель, а под ней — знаменатель. А вот если ее записать как 0,375, это уже будет десятичная дробь.

К тому же простые дроби подразделяют на правильные, неправильные и смешанные. К первым относят все те, числитель которых меньше знаменателя. Если наоборот, знаменатель меньше числителя, это уже будет неправильная дробь. В случае если перед правильной стоит целое число, говорят о смешанных числах. Таким образом, дробь 1/2 — правильная, а 7/2 — нет. А если ее записать в таком виде: 3¹/₂, то она станет смешанной.

Чтобы легче было разобраться в том, что такое сложение дробей, и с легкостью его выполнять, важно еще запомнить основное свойство дроби. Его суть в следующем. Если числитель и знаменатель умножить на одно и то же число, то дробь не изменится. Именно это свойство позволяет совершать простейшие действия с обыкновенными и другими дробями. По факту это означает, что 1/15 и 3/45, по сути, одно и то же число.

Сложение дробей с одинаковыми знаменателями

Выполнение этого действия обычно не вызывает больших затруднений. Сложение дробей в этом случае очень сильно напоминает подобное действие с целыми числами. Знаменатель остается без изменений, а числители просто складываются между собой. Например, если нужно сложить дроби 2/7 и 3/7, то решение школьной задачи в тетради будет вот таким:

2/7 + 3/7 = (2+3)/7 = 5/7.

К тому же такое сложение дробей можно объяснить на простом примере. Взять обычное яблоко и разрезать, например, на 8 частей. Выложить отдельно сначала 3 части, а затем добавить к ним еще 2. И в результате в чашке будет лежать 5/8 целого яблока. Саму арифметическую задачу записывают, как показано ниже:

3/8 + 2/8 = (3+2)/8 = 5/8.

Сложение дробей с разными знаменателями

Но зачастую встречаются задачи посложнее, где нужно сложить между собой, например, 5/9 и 3/5. Вот здесь и возникают первые сложности в действиях с дробями. Ведь сложение таких чисел потребует дополнительных знаний. Теперь в полной мере потребуется вспомнить об их основном свойстве. Чтобы сложить дроби из примера, для начала их нужно привести к одному общему знаменателю. Для этого необходимо просто перемножить 9 и 5 между собой, числитель «5» умножить на 5, а «3», соответственно, на 9. Таким образом, уже складываются такие дроби: 25/45 и 27/45. Теперь только осталось сложить числители и получить ответ 52/45. На листке бумаги пример будет выглядеть так:

5/9 + 3/5 = (5 х 5)/(9 х 5) + (3 х 9)/(5 х 9) = 25/45 + 27/45 = (25+27)/45 = 52/45 = 1⁷/₄₅.

Но сложение дробей с такими знаменателями не всегда требует простого перемножения чисел под чертой. Сначала ищут наименьший общий знаменатель. К примеру, как для дробей 2/3 и 5/6. Для них это будет число 6. Но не всегда ответ очевиден. В этом случае стоит вспомнить правило поиска наименьшего общего кратного (сокращенно НОК) двух чисел.

Под ним понимают наименьший общий множитель двух целых чисел. Чтобы его найти, раскладывают каждое на простые множители. Теперь выписывают те из них, которые входят хотя бы один раз в каждое число. Перемножают их между собой и получают тот самый знаменатель. На деле все выглядит немного проще.

Например, требуется сложить дроби 4/15 и 1/6. Так, 15 получается перемножением простых цифр 3 и 5, а шесть — два и три. Значит, НОК для них будет 5 х 3 х 2 = 30. Теперь, разделив 30 на знаменатель первой дроби, получим множитель для ее числителя — 2. А для второй дроби это будет число 5. Таким образом, остается сложить обыкновенные дроби 8/30 и 5/30 и получить ответ 13/30. Все предельно просто. В тетради же следует эту задачу записать так:

4/15 + 1/6 = (4 х 2)/(15 х 2) + (1 х 5)/(6 х 5) = 8/30 + 5/30 = 13/30.

НОК (15, 6) = 30.

Сложение смешанных чисел

Теперь, зная все основные приемы в сложении простых дробей, можно попробовать свои силы на более сложных примерах. И это будут смешанные числа, под которыми понимают дробь такого вида: 2²/₃. Здесь перед правильной дробью выписана целая часть. И многие путаются при совершении действий с такими числами. В действительности, здесь работают все те же правила.

Чтобы сложить между собой смешанные числа, отдельно складывают целые части и правильные дроби. А затем уже суммируют эти 2 результата. На практике все намного проще, стоит только немного поупражняться. Например, в задаче требуется сложить такие смешанные числа: 1¹/₃ и 4²/₅. Чтобы это сделать, сначала складываются 1 и 4 — получится 5. Затем суммируют 1/3 и 2/5, используя приемы приведения к наименьшему общему знаменателю. Решением будет 11/15. А окончательный ответ — это 5¹¹/₁₅. В школьной тетради это будет выглядеть гораздо короче:

1¹/₃ + 4²/₅ = (1 + 4) + (1/3 + 2/5) = 5 + 5/15 + 6/15 = 5 + 11/15 = 5¹¹/₁₅.

Сложение десятичных дробей

Помимо обыкновенных дробей, есть и десятичные. Они, кстати, намного чаще встречаются в жизни. Например, цена в магазине выглядит часто таким образом: 20,3 рубля. Это и есть та самая дробь. Конечно, такие складывать намного проще, чем обыкновенные. В принципе, нужно просто сложить 2 обыкновенных числа, главное, в нужном месте поставить запятую. Вот тут и возникают сложности.

К примеру требуется сложить такие десятичные дроби 2,5 и 0,56. Чтобы сделать это правильно, нужно к первой в конце дописать ноль, и все будет в порядке.

2,50 + 0,56 = 3,06.

Важно знать, что любая десятичная дробь может быть преобразована в простую, но не любую простую дробь можно записать как десятичную. Так, из нашего примера 2,5 = 2¹/₂ и 0,56 = 14/25. А вот такая дробь, как 1/6, будет только приблизительно равна 0,16667. Такая же ситуация будет с другими подобными числами — 2/7, 1/9 и так далее.

Заключение

Многие школьники, не понимая практической стороны действий с дробями, относятся к этой теме спустя рукава. Однако в более старших классах эти базовые знания позволят щелкать как орешки сложные примеры с логарифмами и нахождением производных. А потому стоит один раз хорошо разобраться в действиях с дробями, чтобы потом не кусать от досады локти. Ведь вряд ли педагог в старших классах будет возвращаться к этой, уже пройденной, теме. Любой старшеклассник должен уметь выполнять подобные упражнения.

Алгебраические правила работы с дробями.

Произношение: /ˈfræk.ʃən rulz/ Объяснить

Рисунок 1: Дробь

Дробные правила представляют собой набор алгебраический правила работы с дроби. Фракция имеет числитель и знаменатель. Фракция представляет собой операция деления. Числитель – делимое. Знаменатель — это делитель.

Правила дробей

Операция	Уравнения	Примеры	Описание
Добавление двух фракций [2]			к добавлению фракций, преобразование каждую фракцию, чтобы они имели общую денатор. Сложите числители и используйте общий знаменатель в качестве знаменателя. Уменьшить дробь. См. Операции с дробями: сложение и вычитание.
Вычитание двух дробей			Чтобы вычесть дроби, приведите каждую дробь к общему знаменателю. Вычтите числители и используйте общий знаменатель в качестве знаменателя. Уменьшить дробь. См. Операции с дробями: сложение и вычитание.
Умножение двух дробей [2]			Чтобы умножить дроби, умножьте числители и умножьте знаменатели. Уменьшить дробь. См. Операции с дробями: умножение.
Умножение дроби на целое число.			Чтобы умножить дробь и целое число, умножьте числитель на целое число. Знаменатель остается неизменным. Сократите дробь, если это возможно.
Деление двух дробей [2]			Чтобы разделить дроби, переверните делитель вверх дном и умножьте на делимое. Уменьшить дробь. См. Операции над дробями: деление.
Деление дроби на целое число.			Чтобы разделить дробь на целое число, преобразовать целое число в дробь, разделить дроби.
Возведение дроби в степень.			См. Операции над дробями: возведение в степень.
Преобразование смешанного числа в неправильную дробь.			Чтобы преобразовать смешанное число в неправильную дробь, умножьте целую часть на знаменатель и прибавьте произведение к числителю. Знаменатель остается неизменным. См. Как преобразовать смешанное число в дробь.
Преобразование неправильной дроби в смешанное число.			Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель с использованием остатка. Смешанное число — это частное плюс остаток, деленный на знаменатель. См. Как преобразовать дробь в смешанное число.
Нулевой числитель.			Применяя свойство умножения на ноль, нулевой числитель с нулевым знаменателем равен нулю. См. Свойство умножения на 0,9.0012
Нулевой знаменатель.			Поскольку деление на ноль не определено, нулевой знаменатель делает дробь неопределенной.
Один минус.			Поскольку , применим ассоциативное свойство умножения, чтобы получить
Два знака минус.			Так как , примените ассоциативное свойство умножения, чтобы получить
Если дробь имеет одинаковые ненулевые числитель и знаменатель, значение дроби равно 1.			Все, кроме 0, разделенного на самого себя, равно 1.
Любое целое число можно превратить в дробь.			Поскольку , применим свойство умножения на 1: . См. раздел «Свойство умножения на 1».
Сокращение дробей.			Даны два произвольных значения a и b , а также значения c , d и e такие, что а = с · d и б = с · е , . См. Сокращение дробей.
Фракции строительные.			с учетом фракции A / B и номер D , который составляет D , находка E Такой, что B · E = , а затем B · e = = = = = = = = = = = = = = = . а / б = ( а · е ) / ( б · е ).
Операции над сложными дробями.	Упростите сложные дроби, затем используйте правила для простых дробей.		Чтобы манипулировать сложной дробью, преобразуйте ее в простую дробь, затем следуйте правилам для простых дробей. См. Сложная дробь.
Преобразование десятичного числа в дробь.			Чтобы преобразовать десятичную дробь в дробь, замените десятичную дробь целым числом и разделите его на 10 n , где n — количество знаков после запятой.
Преобразование процентов в дроби.			Чтобы преобразовать проценты в дроби, используйте проценты в качестве числителя, 100 в качестве знаменателя, затем упростите.
Сравнение дробей с одинаковыми знаменателями.			Чтобы сравнить дроби с одинаковыми знаменателями, сравните числители. Соотношение между дробями такое же, как и между знаменателями.
Сравнение дробей с разными знаменателями.			Чтобы сравнить дроби с разными знаменателями, либо преобразуйте их в десятичные, либо приведите к общему знаменателю, а затем сравните их.
Таблица 1

Ссылки

1. MCADAMS, David E. DICARTION. 2-й классный выпуск 20150108-4799968. стр. 82. Life is a Story Problem LLC. 8 января 2015. Купить книгу
2. Файн, Генри Б., доктор философии. Числовая система алгебры, трактуемая теоретически и исторически . 2-е издание. стр. 12-15. www.archive.org. DC Heath & Co., Бостон, США. 1907. Последний доступ 11.07.2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n21/mode/1up/search/fraction. Купить книгу
3. Оберг, Эрик. Упрощенная арифметика . стр. 21-31. www.archive.org. Промышленный пресс. 1914. Последнее обращение 11.07.2018. http://www.archive.org/stream/arithmeticsimpli00oberrich#page/21/mode/1up/search/fraction. Купить книгу
4. Оберг, Эрик. Элементарная алгебра . стр. 23. www.archive.org. Промышленный пресс. 1914. Последний доступ 11.07.2018. http://www.archive.org/stream/elementaryalgebr00oberrich#page/n26/mode/1up/search/fraction. Купить книгу
5. Беттингер, Элвин К. и Энглунд, Джон А.. Алгебра и тригонометрия . стр. 9-11,36-40. www.archive.org. Международная Учебная Компания. Январь 1963 г. Последний доступ 11.07.2018. http://www.archive.org/stream/алгебраandtrigon033520mbp#page/n18/mode/1up. Купить книгу

Дополнительная информация

• Как умножать и делить дроби в алгебре (видео) . манекены.com. Уайли. 23.01.2010. http://www.dummies.com/how-to/content/how-to-multiply-and-divide-fractions-in-алгебра.html.

Цитируйте эту статью как:

МакАдамс, Дэвид Э. Правила дробей . 21.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/f/fractionrules.html.

Кредиты изображений

• Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

История изменений

21.04.2019:

Уравнения и выражения изменены для соответствия новому формату.

(МакАдамс, Дэвид Э.)

21.12.2018:

Пересмотрено и исправлено произношение МФА.

(МакАдамс, Дэвид Э.)

28. 08.2018:

Исправлена ​​орфография.

(МакАдамс, Дэвид Э.)

09.07.2018:

Удалены битые ссылки, обновлена ​​лицензия, реализована новая разметка, реализован новый протокол Geogebra.

(МакАдамс, Дэвид Э.)

05.02.2010:

Добавлен раздел «Справочники».

(МакАдамс, Дэвид Э.)

14.01.2009:

Первоначальная версия.

(МакАдамс, Дэвид Э.)

Правила дробей — объяснение, части и часто задаваемые вопросы

Дроби — это математический способ представления части чего-то целого. Они представлены в виде числителя и знаменателя. Мы называем верхнюю часть (или часть, которая представляет, какую часть чего-то целого мы рассматриваем) числителем, а нижнюю часть (которая представляет, сколько равных частей мы сделали из чего-то целого) называем знаменателем.

Дробь = Числитель/Знаменатель

Части дроби

Частями дроби являются:

1. Числитель: Числитель — это число, которое находится сверху. Он показывает, сколько равных частей целого или коллекции считается.

2. Знаменатель: Число под чертой является знаменателем. Он показывает общие равные части, которые мы сделали из целого.

Допустим у нас есть арбуз и мы сделали из него 8 равных частей тогда 8 будет в знаменателе дробей. Теперь, если мы хотим представить пять частей из них, тогда дробь будет ⅝. Если мы хотим представить только одну часть из них, то дробь будет ⅛. Как показано на следующем рисунке.

Правила дробей

Мы изучили множество математических операций, таких как сложение, вычитание, деление и умножение, а также получили новый способ представления дробей. Можем ли мы выполнять эти математические операции и с дробями? Ответ положительный. В этом разделе мы будем выполнять различные математические операции с правилами дробей.

1. Правило сложения дробей

Как сложить две дроби? Есть некоторые правила, которые мы должны помнить при сложении двух дробей.

• Нельзя складывать дроби с разными знаменателями.

• Чтобы сложить дроби, прежде всего, нам нужно приравнять знаменатель, взяв наименьшее общее кратное, которое является НОК чисел, присутствующих в знаменателе.

• После того, как знаменатель станет одинаковым, соответственно изменятся и числители.

• Теперь добавьте эти новые числители, чтобы получить желаемый результат.

Например: Предположим, мы хотим добавить ¼ к ¼. Затем заметьте, что знаменатель уже тот же, и даже если мы возьмем наименьшее общее кратное знаменателя, то оно тоже будет всего лишь 4. Теперь мы можем сложить числители 1 + 1 = 2. Следовательно, искомый результат будет 2/4. Кроме того, обратите внимание, что 4 является общим кратным 2 и 4. Поэтому его можно отменить. Таким образом, после упрощения мы получаем ½.

Мы также можем понять это с помощью следующей диаграммы:

2. Дробное правило вычитания

Вычитание почти то же самое, что и сложение. Вместо того, чтобы складывать числители, мы будем их вычитать. Есть некоторые правила, которые мы должны помнить при вычитании двух дробей.

• Дроби с разными знаменателями нельзя вычитать.

• Чтобы вычесть дроби, прежде всего, нам нужно приравнять знаменатель, взяв наименьшее общее кратное, то есть НОК чисел, присутствующих в знаменателе.

• После того, как знаменатель станет одинаковым, соответственно изменятся и числители.

• Теперь вычтите эти новые числители, чтобы получить желаемый результат.

Например: Предположим, мы хотим вычесть ¼ из ¾. Затем заметьте, что знаменатель уже тот же, и даже если мы возьмем наименьшее общее кратное знаменателя, то оно тоже будет всего лишь 4. Теперь мы можем вычесть числители, 3-1=2. Следовательно, искомый результат будет 2/4. Кроме того, обратите внимание, что 4 является общим кратным 2 и 4. Поэтому его можно отменить. Таким образом, после упрощения мы получаем ½.

Мы также можем понять это с помощью следующей диаграммы:

3. Правило умножения дробей

Как мы можем умножить две дроби? Будет ли это то же самое, что сложение или вычитание, когда мы должны сделать знаменатели одинаковыми? Ответ — нет. При умножении нам этого делать не нужно. Есть некоторые правила, которые мы должны помнить при умножении двух дробей.

• Дроби с разными знаменателями можно умножать.

• Числитель умножается только на числитель, а знаменатель умножается только на знаменатель.

• Мы не можем умножать числители на знаменатели, однако их можно разделить.

Например: Предположим, мы хотим умножить ⅔ на 3/15. Мы знаем, что числитель будет умножаться только на числитель. Итак, 2 × 3 = 6. Следовательно, 6 будет числителем нашего желаемого результата. Для знаменателей 3 × 15 = 45. Следовательно, 45 будет знаменателем нашей искомой дроби.

Таким образом, умножение ⅔ на 3/15 будет 6/45. Также обратите внимание, что их можно еще больше упростить. После упрощения получаем 2/15.

См. Следующее:

⅔ × 3/15

= 2 × 3/3 × 15

= 6/45

= 2/15

4. Фракция. деление дробей нам нужно помнить определенные правила и выполнять несколько шагов. Нам нужно умножить первую дробь на обратную вторую. Разделение включает в себя несколько шагов, которые необходимо выполнить-

   1. Заменить знак деления (÷) на умножение (×).

   2. Если мы меняем знак деления на умножение, то мы должны написать обратную величину второго члена или дроби.

   3. В конце концов, мы просто перемножаем их, чтобы получить требуемый ответ.

   Вот пример деления дробей:

   Предположим, нам нужно разделить 3/2 на 5/4.

   3/2 ÷ 5/4

   Шаг 1: Изменение знака на умножение от деления и запись обратной величины второго члена [÷5/4 =× 4/5].

    = 3/2 × 4/5

   Шаг 2: Умножение первой на обратную вторую дробь.

    = (3 × 4)/(2 × 5)

   = (3 × 2)/ (1 × 5)

   = 6/5

   Шаг 3: Получение упрощенного результата выражения.

   Деление дробей — это умножение дробей простым преобразованием второй дроби в обратную.

   Знаете ли вы?

   Есть еще один способ представления дробей — десятичные. Они взаимозаменяемы друг с другом. Десятичные дроби можно разделить на конечные и неконечные. Если они не заканчиваются, то далее делятся на повторяющиеся и неповторяющиеся десятичные дроби. Только отсюда идет определение рациональных чисел и иррациональных чисел. Если они либо заканчиваются, либо не прекращаются и повторяются, то мы называем их рациональными числами. Если они не прекращаются и не повторяются, то мы называем их иррациональными числами.

   Математические слова: правила дробей

   Математические слова: правила дробей

   индекс: нажмите на букву индекс: предметные области
   	Правила дробей Правила алгебры для объединения дробей. Эти правила применимы как к правильным, так и к неправильным дробям. Они применимы и ко всем рациональным выражениям.   A. Особые фракции 1. упрощается до b . 2. далее не упрощается. 3. упрощается до 0. 4. не определено. Примеры не упрощает. не определено. Так и есть. Специальное примечание: Почему нормально иметь 0 сверху (в числителе), а не внизу (в знаменателе)? Задумайтесь на мгновение, что означает деление. Причина в том, что 2·5 = 10, . Дробь    потому что 2·0 = 0. Дробь не может равняться ничему. Нет такого числа, которое можно было бы умножить на 0 и получить в ответ 10. Фракция не определена. Что насчет ? Он тоже не определен, но немного по другой причине. Если умножить 0 в знаменателе на любое число, то получится 0 в числителе. Кажется, что может равняться любому числу. В результате мы говорим, что это неопределенное выражение, которое является особым видом неопределенного выражения. B. Отрицательные дроби 1. такой же, как и 2. упрощается до   3. НЕ то же самое, что Примеры C. Аннулирование ( a ≠ 0, b ≠ 0, c ≠ 0) 1. отменяет на 1 2. Отмена на 3. отмена на 4. отмена на 5. отменяет на b 6. отменяет на b Примеры D. Дополнение 1. 2. 3. Примеры E. Вычитание 1. 2. 3. 4. Примеры F. Умножение 1. 2. 3. Примеры Осторожно!! 1. 2. Смешанные числа используются для сложения, а не для умножения. Например, значит и НЕ . Г. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт