Правило сложения и вычитание десятичных дробей
Такие арифметические вычислительные действия, как сложение и вычитание десятичных дробей, необходимы для того, чтобы, оперируя дробными числами получать искомый результат. Особая важность проведения этих операций состоит в том, что во многих сферах деятельности человека меры многих сущностей представлены именно десятичными дробями. Поэтому для осуществления определенных действий со многими предметами материального мира требуется складывать или вычитать именно десятичные дроби. Следует заметить, что на практике эти операции используются практически повсеместно.
Процедуры сложения и вычитания десятичных дробей по своей математической сути осуществляется практически точно так же, как аналогичные операции для целых чисел. При ее осуществлении значение каждого разряда одного числа нужно записывать под значением аналогичного разряда другого числа.
Вычитание десятичных дробей подчиняется следующим правилам:
• Сначала необходимо произвести уравнивание количество тех знаков, что располагаются после запятой;
• Затем нужно произвести запись десятичных дробей друг под другом таким образом, чтобы содержащиеся в них запятые располагались строго друг под другом;
• Осуществить процедуру вычитания десятичных дробей в полном соответствии с теми правилами, которые действуют для вычитания целых чисел. При этом не нужно обращать никакого внимания на запятые;
• После получения ответа запятую в нем нужно поставить строго под теми, которые имеются в исходных числах.
Операция сложения десятичных дробей осуществляется в соответствии с теми же правилами и алгоритмом, которые описаны выше для процедуры вычитания.
Пример сложения десятичных дробей
Две целых две десятых плюс одна сотая плюс четырнадцать целых девяносто пять сотых равняется семнадцать целых шестнадцать сотых.
2,2 + 0,01 + 14,95 = 17,16
| 2, | 2 |
| + 0, | 01 |
| 14, | 95 |
17, |
16 |
Пример вычитания десятичных дробей
Пятнадцать целых две десятых минус восемь целых три десятых равняется шесть целых девять десятых.
15,2 – 8,3 = 6,9
Примеры сложения и вычитания десятичных дробей
Математические операции сложения и вычитания десятичных дробей на практике используются чрезвычайно широко, причем они нередко касаются многих предметов окружающего нас материального мира. Ниже приводится несколько примеров таких вычислений.
Пример 1Согласно проектно-сметной документации, для строительства небольшого производственного объекта требуется десять целых пять десятых кубометров бетона. Используя современные технологии возведения зданий, подрядчикам без ущерба для качественных характеристик сооружения удалось использовать для проведения всех работ всего девять целых девять десятых кубометров бетона. Размер экономии составляет:
Десять целых пять десятых минус девять целых девять десятых равно ноль целых шесть десятых кубометра бетона.
10,5 – 9,9 = 0,6 м3
Двигатель, устанавливаемый на старую модель автомобиля, потребляет в городском цикле восемь целых две десятых литра топлива на сто километров пробега. Для нового силового агрегата этот показатель составляет семь целых пять десятых литров. Размер экономии составляет:
Восемь целых две десятых литра минус семь целых пять десятых литра равно ноль целых семь десятых литра на сто километров пробега в городском режиме движения.
8,2 – 7,5 = 0,7л
Операции сложения и вычитания десятичных дробей применяются чрезвычайно широко, и их осуществление не составляет никаких проблем.
В современной математике эти процедуры отработаны практически идеально, и ими практически все хорошо владеют еще со школьной скамьи.
Сложение десятичных дробей: правила и примеры
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.
Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.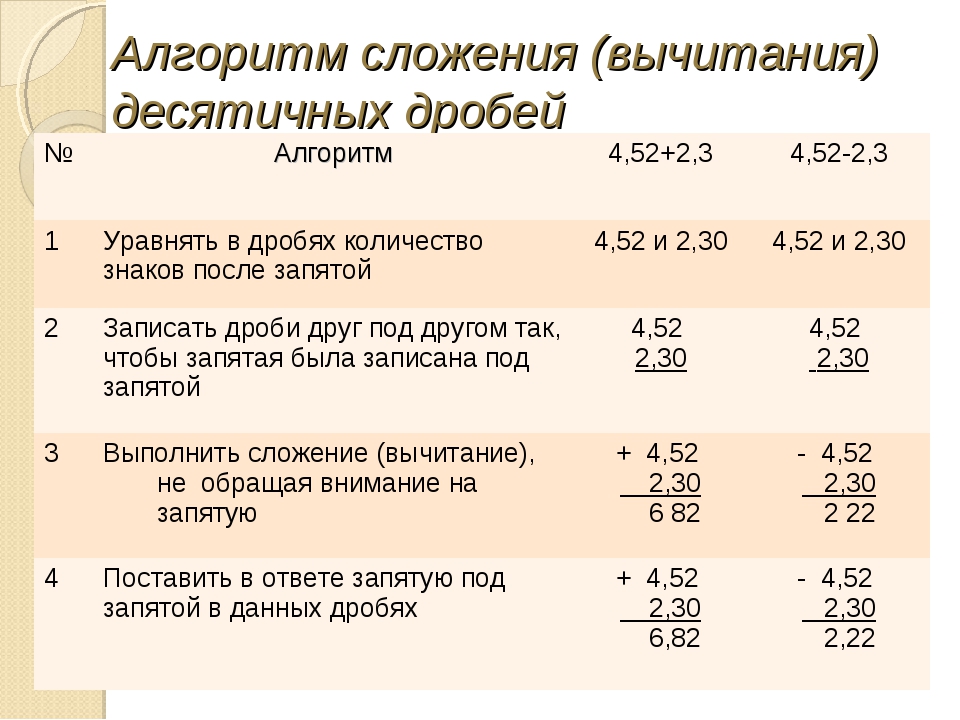
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.
- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей.
Для этого десятичная дробь переводится в обыкновенную дробь.
Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой».
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробях У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых .
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
1,5 + 3,4 = 4,9
Пример 2.
Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12.
Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0.
Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым.
Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
3 − 1,2 = 1,8
Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695.
В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880.
В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325.
В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице», то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части.
Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125.
Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке».
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9 : 5 = 1,8
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5.
А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2) : (3 × 2) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
1,7 × 10 = 17
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель.
Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
2,1 : 10 = 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1 : 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
63 : 1 = 63
Значит значение выражения 6,3 : 0,1 равно 63
6,3 : 0,1 = 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
6,3 : 0,1 = 63
Попробуем разделить 6,3 на 0,01.
В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
6,3 : 0,01 = 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3 : 0,001 = 6300
Задания для самостоятельного решения
Задание 1. Выполните сложение:
0,6 + 0,3
Решение:
Задание 2. Выполните сложение:
1,2 + 5,3
Решение:
Задание 3. Выполните сложение:
1,6 + 0,4
Решение:
Задание 4. Выполните сложение:
0,8 + 0,5
Решение:
Задание 5. Выполните вычитание:
0,9 − 0,4
Решение:
Задание 6. Выполните вычитание:
2 − 0,3
Решение:
Задание 7. Выполните вычитание:
9 − 7,8
Решение:
Задание 8. Выполните вычитание:
4 − 1,8
Решение:
Задание 9. Выполните умножение:
3,2 × 1,8
Решение:
Задание 10. Выполните умножение:
9,3 × 5,8
Решение:
Задание 11. Выполните умножение:
0,23 × 0,07
Решение:
Задание 12. Выполните умножение:
3,14 × 0,25
Решение:
Задание 13. Выполните деление:
9,36 : 6
Решение:
Задание 14. Выполните деление:
0,169 : 13
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
с другой дробью, целым натуральным числом
В данной публикации мы рассмотрим, каким образом десятичную дробь можно сложить с другой дробью (десятичной и обыкновенной) или целым натуральным числом.
Также разберем примеры для лучшего понимания представленного материала.
Правило сложения десятичных дробей
Сумма десятичных дробей находится путем их сложения столбиком. Порядок действий следующий:
1. Одноименные разряды пишем друг под другом: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т.д.
Примечание: При необходимости (если количество цифр после запятой у суммируемых дробей разное), в конце более “короткой” дроби с меньшим количеством знаков после запятой добавляем нули, чтобы выровнять ее с более “длинной”. Согласно основному свойству десятичной дроби, это никоим образом не отразится на ее величине. Когда процесс доведен до автоматизма, нули можно просто держать в уме.
2. Десятичные разделители (запятые), также, должны находится строго друг под другом.
Примеры неправильной записи слагаемых:
Примеры правильной записи слагаемых:
3. Складываем дроби, как будто имеем дело с целыми натуральными числами. Т.е. на запятые внимания не обращаем.
4. В полученном результате ставим запятую строго там же, где она стояла в суммируемых дробях.
Сумма десятичной дроби и целого натурального числа
Если к десятичной дроби требуется прибавить целое натуральное число, то в конце последнего ставим запятую, после которой добавляем столько нулей, сколько цифр содержится в дробной части десятичной дроби. Затем вычисляем сумму слагаемых.
Сложение десятичной и обыкновенной дробей
Чтобы найти сумму десятичной и обыкновенной дробей, последнюю переводим в десятичную. После этого выполняем сложение.
Можно поступить наоборот – десятичную дробь преобразовать в обыкновенную. В этом случае уже складываем обыкновенные дроби.
Примеры
Давайте найдем сумму десятичных дробей, рассмотренных выше:
Примечание: если сумма десятых в дробной части результата больше 10, то единицу держим в уме и переносим ее в целую часть.
И, напоследок, вычислим сумму десятичной дроби и целого числа:
Сложение и вычитание десятичных дробей
Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
- Записать числа в столбик таким образом, чтобы соответствующие разряды совпадали. Главный ориентир — десятичные точки. Они не являются отдельным разрядом, но должны стоять на одной вертикали;
- Сложить или вычесть полученные дроби столбиком — подобно тому, как мы складываем и вычитаем обычные числа. Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
- Полученное число и будет ответом — больше ничего делать не надо.
Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.
Задача. Найдите значение выражений: 8,125 + 17,4; 3,5 + 121,048.
Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:
Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:
Как видите, ничего общего с тем, что должно получиться на самом деле.
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке». Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.
Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:
Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.
Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.
Смотрите также:
- Умножение и деление десятичных дробей
- Как представить обычную дробь в виде десятичной
- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)
- Задача 7 — геометрический смысл производной
- Метод узлов в задаче B5
- Задача B5: площадь сектора
Сложение, вычитание, умножение и деление десятичных дробей
Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.
Правило. Сложение и вычитание десятичных дробей производится по разрядам целой и дробной части как натуральных чисел.
При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).
Примеры.
Сложение и вычитание десятичных дробей в строку:
243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651
843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589
Сложение и вычитание десятичных дробей в столбик:
Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток.
Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.
Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).
Пример:
При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:
Запись умножения десятичных дробей в столбик:
Запись деления десятичных дробей в столбик:
Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.
Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!
Сложение и вычитание десятичных дробей
Понятие десятичной дроби
Прежде, чем перейдем к тому, как выполнить сложение и вычитание десятичных дробей, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это число в математика, в которой a и b — числа или выражения.
По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Если числитель меньше знаменателя, то целая часть равна нулю.Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей нужно отдельно сложить каждую часть.
Рассмотрим пример сложения 3,2 и 5,3. Для удобства используем метод столбика.
Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть под целой частью другой. В школе это называют «запятая под запятой». Вот так:
Складываем дробные части: 2 + 3 = 5. Запишем пятерку в дробной части ответа:
Теперь целые части: 3 + 5 = 8. Запишем восьмерку в целой части ответа:
Отделим запятой целую часть от дробной, чтобы запятая была под запятой:
Получили ответ: 3,2 + 5,3 = 8,5.
Вычитание десятичных дробей
Процесс вычитания десятичных дробей очень похож на сложение. Будем использовать те же правила: «запятая под запятой» и «равное количество цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Запишем в столбик выражение так, чтобы запятая была под запятой:
Вычислим дробную часть 5 − 2 = 3. Запишем тройку в десятой части ответа:
Вычислим целую часть 2 − 2 = 0. Запишем ноль в целой части ответа:
Отделим запятой целую часть от дробной:
Вот и ответ: 2,5 − 2,2 = 0,3.
Пример 2. Вычислить: 7,353 – 3,1
В этом выражении разное количество цифр после запятой: в 7,353 три цифры после запятой, а в 3,1 только одна. Значит в дроби 3,1 в конце добавим два нуля, чтобы уравнять количество цифр в обеих дробях. То есть: 3,1 = 3,100.
Запишем в столбик и посчитаем:
Ответ: 7,353 – 3,1 = 4,253.
Пример 3. Вычислить: 3 − 1,2
В этом примере из целого числа нужно вычесть десятичную дробь. Запишем это выражение столбиком так, чтобы целая часть десятичной дроби 1,23 была под числом 3. Вот так:
Сделаем количество цифр после запятой одинаковым:
Теперь вычитаем десятые части: 0 − 2. От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
Сейчас вычтем целые части. В самом начале было число 3, но мы заняли у него единицу, поэтому оно обратилось в двойку. Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
Отделим запятой целую часть от дробной:
Ответ: 3 − 1,2 = 1,8.
Мы рассмотрели несколько примеров сложения и вычитания десятичных дробей. Чтобы каждый ученик в 5 и 6 классе мог повторить эту последовательность, есть специальный алгоритм:
Алгоритм сложения (вычитания) десятичных дробей
|
Проще говоря, правило сложения (вычитания) десятичных дробей звучит так: чтобы сложить (вычесть) две десятичные дроби, нужно записать их в столбик друг под другом, запятая под запятой. А потом сложить как обыкновенные числа и снести запятую.
Приходите практиковать сложение и вычитание десятичных дробей и решать другие увлекательные задачки по математике в интерактивном формате!
Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
знаков после запятой | SkillsYouNeed
Дроби и десятичные дроби — это два разных способа представления частей целого числа. Десятичные дроби — это способ выразить десятые, сотые, тысячные (и более) единицы.
Работа с десятичными знаками может показаться немного сложной для начала, но не волнуйтесь, это всего лишь числа, и они подчиняются правилам, как и другие числа.
Работа с десятичными знаками
Сложение и вычитание десятичных знаков
Десятичные знаки расширяют систему счисления за пределы простых «сотни, десятки, единицы» до «десятых единиц», «сотых единиц» и так далее.
Таким образом, работа с десятичными знаками аналогична работе с любыми другими числами.
Посмотрев на наши страницы, посвященные числам , сложению и вычитанию , у вас не возникнет проблем с добавлением тысяч к миксу, так зачем беспокоиться о десятых и сотых?
Если бы вы складывали числа без десятичных знаков, вы бы начали с единиц, а затем перешли к десяткам, затем тысячам и так далее. То же правило применяется, если есть десятичные дроби.Сначала добавьте их, затем единицы, затем десятки и так далее.
Самое важное правило, о котором следует помнить, — выровнять десятичные точки в вашем вычислении , следя за тем, чтобы десятичная точка в ответе также совпадала с десятичными точками над ней.
Пример 1 — Прямое добавление
123,5 + 234,2
Как и при любом сложении, выровняйте числа и складывайте столбцы, начиная с правого.
| Сот | Десятки | Единицы | Путевая точка | десятых | ||
| 1 | 2 | 3 | . | 5 | ||
| 2 | 3 | 4 | . | 2 | + | |
| Всего | 3 | 5 | 7 | . | 7 |
123,5 + 234,2 = 357,7
Пример 2 — Сложение с разными десятичными знаками
234,8 + 147,96
В этом примере мы добавляем число с одним десятичным знаком к числу с двумя десятичными знаками.Помните, не имеет значения, с каким количеством десятичных знаков мы имеем дело или имеют ли участвующие числа разное количество десятичных знаков. Самая важная часть расчета — это выровнять десятичные точки . Если это поможет вам выровнять столбцы, вы можете написать ноль в сотых столбцах первого числа или оставить это поле пустым.
| H | т | U | . | т | ч | ||
| 2 | 3 | 4 | . | 8 | 0 | ||
| 1 | 4 | 7 | . | 9 | 6 | + | |
| Всего | 3 | 8 | 2 | . | 7 | 6 |
234,8 + 147,96 = 382,76
Пример 3 — Вычитание
72,347 — 64,012
Вычтите так же, как и с целыми числами, но убедитесь, что десятичный разряд находится в правильном месте.
| т | U | . | т | ч | чт | ||
| 7 | 2 | . | 3 | 4 | 7 | ||
| 6 | 4 | . | 0 | 1 | 2 | – | |
| Всего | 0 | 8 | . | 3 | 3 | 5 |
72,347 — 64,012 = 8,335
Если вы не знаете, что такое «перенос» при сложении или вычитании, обратитесь за помощью на наши страницы Добавление и Вычитание .
Умножение десятичных знаков
При умножении и делении десятичных дробей вычисления работают так же, как и с целыми числами. Умножаем числа так, как будто десятичной точки не было.В конце расчета убеждаемся, что в нашем ответе десятичная точка стоит в правильном месте:
Начиная с ответа, который вы получили путем умножения чисел, переместите десятичную запятую на такое же количество разрядов влево, как и числа после десятичной точки в двух множителях.
Пример 1
0,5 х 0,5
5 x 5 равно 25. После десятичной точки идут два числа, по одному в каждом из умножаемых чисел, поэтому переместите десятичную точку на два разряда влево, начиная с 25 и ответ будет 0.25
Пример 2
1,2 х 0,25
Сначала удалите десятичные знаки 12 x 25 = 300
На этот раз после десятичной точки в числах умножения стоят три цифры: одна в 1,2 и две в 0,25.
Десятичная запятая в 300 стоит после второго нуля, то есть 300,0
Переместите десятичную запятую на три позиции влево, и ответ будет 0,3
Десятичные дроби
Умножение и деление на 10
Умножение на 10 перемещает десятичную запятую на одну позицию вправо ( увеличивает исходное число в 10 раз).При делении на 10 оно перемещается на одну позицию влево ( уменьшает исходное число в 10 раз).
Вы можете использовать этот факт, чтобы упростить деление десятичных дробей. Умножьте на 10 число, на которое вы делите (знаменатель), пока оно не станет целым числом. Умножьте на 10 число, которое вы делите (числитель) , такое же количество раз . Затем сделайте расчет.
Пример:
50,22 ÷ 0,2
Если вы используете стандартный формат деления (см. Нашу страницу, посвященную , раздел ), где ваш ответ ставится над чертой над числом, которое вы делите, то десятичная точка идет точно над единицей в числе, которое вы ‘ повторное разделение:
Вы можете упростить этот расчет, если умножите 0.2 на 10 один раз, чтобы получить 2. Вы умножаете 50,22 на 10 и получаете 502,2
.| H | т | U | . | т | |
| 2 | 5 | 1 | . | 1 | |
| 2 | 5 | 0 | 2 | . | 2 |
Затем произведите расчет. Делить на 2 намного проще, чем на 0.2.
Ответ: 251,1
Верхний наконечник
Если вы выполнили умножение или деление с использованием десятичных знаков, проверьте, выглядит ли ответ примерно правильным. Другими словами, если вы уберете числа после десятичной точки и округлите до целого числа в большую или меньшую сторону, все ли будет правильно?
Если ваш ответ кажется слишком большим или слишком маленьким, проверьте положение десятичной точки. Это вполне может быть позиция в любом направлении.
Преобразование дробей в десятичные
Преобразовать десятичные дроби в дроби довольно просто. Любое число можно выразить дробью, просто поставив его над единицей.
Например:
2 = 2 / 1
21 = 21 / 1
То же правило применяется к десятичным дробям.
Поставьте десятичную дробь на единицу, а затем умножьте верхнюю и нижнюю части на 10, пока у вас не перестанет быть десятичная точка.Затем, если возможно, преобразуйте дробь в смешанное число и / или уменьшите ее до наименьшего размера.
Например:
0,25 = 0,25 / 1 = 2,5 / 10 = 25 / 100 = 1 / 4
1,25 = 1,25 / 1 = 12,5 / 10 = 125 / 100 = 5 / 4 = 1 1 / 4
Подробнее см. На нашей странице Fractions .
Преобразование дробей в десятичные
Преобразование дробей в десятичные немного сложнее, но становится проще, когда вы понимаете, что дробь на самом деле вычисляется делением.
Например, половина, 1 / 2 , на самом деле равна 1, деленному на 2, что также совпадает с 5 / 10 или пятью десятыми, что выражается в десятичных дробях как 0,5. Это потому, что десятичные дроби основаны на числах, кратных десяти. (Дополнительную информацию см. На наших страницах в «Введение в к Системам измерения и ».)
Итак, чтобы преобразовать дробь в десятичную, считайте дробь вычислением деления, добавляя нули после десятичной точки, если необходимо, чтобы завершить его.
Пример 1
2 / 5 = 2,0 ÷ 5
5 переходит в 20 четыре раза, и десятичная точка идет в том же месте в верхней строке.
Таким образом, ответ будет 0,4
Пример 2
4 / 25 = 4,00 ÷ 25
25 переходит в 40 один раз, оставляя 15 в остатке.
25 точно переходит в 150 шесть раз. Наконец, проверьте правильность положения десятичной точки.
Следовательно, ответ 0,16
Всегда есть более одного пути!
По мере того, как мы все больше и больше практикуем подобные вычисления, мы начинаем находить способы облегчить поиск ответа. Рассматривая приведенный выше пример, вместо того, чтобы делать пошаговые вычисления обычным способом, мы можем остановиться и подумать: «А есть ли другой способ легко узнать, сколько раз 25 входит в 400?» Мы можем задействовать наши умственные арифметические навыки: с практикой мы будем помнить, что есть 4 лота из 25 из 100, потому что 25% — это другой способ написания ¼.Если есть четыре 25 в 100, то должно быть 4 × 4 лота 25 из 400, то есть 16. Перемещение десятичного знака на два разряда влево дает нам 0,16
Если вас беспокоит подразделение, загляните на нашу страницу Division , чтобы быстро напомнить.
Что нужно запомнить:
- Десятичные доли выражают десятые, сотые, тысячные и т.д. единиц.
- Рассматривайте их как любое целое число, но следите за позицией десятичной точки в вашем ответе.
- Если ответ кажется неправильным, проверьте положение десятичной точки.
Добавление десятичных знаков
Добавить десятичные дроби легко, если работа ведется аккуратно
Чтобы добавить десятичные дроби, выполните следующие действия:
- Запишите числа друг под другом, выровняв десятичных знаков
- Введите нули , чтобы числа имели одинаковую длину (почему это нормально, см. Ниже)
- Затем добавьте , используя сложение столбцов, не забывая поставить десятичную точку в ответе
Пример: добавить 1.452 до 1,3
| Выровняйте десятичные знаки: | 1.452 | ||
| + | 1,3 | ||
| «Pad» с нулями: | 1.452 | ||
| + | 1.300 | ||
| Добавить: | 1.452 | ||
| + | 1,300 | ||
| 2,752 |
Пример: сложить 3,25, 0,075 и 5
| Выровняйте десятичные знаки: | 3.25 | ||
| 0,075 | |||
| + | 5. | ||
| «Pad» с нулями: | 3,250 | ||
| 0,075 | |||
| + | 5.000 | ||
| Добавить: | 3,250 | ||
| 0,075 | |||
| + | 5.000 | ||
| 8,325 |
Вот и все: выровняйте десятичные точки, заполните нулями и сложите как обычно.
Вычитание
Чтобы вычесть, следуйте тому же методу: выровняйте десятичные точки, затем вычтите.
Пример: что такое 7,368–1,15?
| Выровняйте десятичные знаки: | 7,368 | ||
| – | 1,15 | ||
| «Pad» с нулями: | 7.368 | ||
| – | 1,150 | ||
| Вычесть: | 7,368 | ||
| – | 1,150 | ||
| 6,218 |
Чтобы проверить , мы можем добавить ответ к вычитаемому числу:
Пример: проверьте, что 7.368 минус 1,15 равно 6,218
Попробуем прибавить 6,218 к 1,15
| Выровняйте десятичные знаки: | 6,218 | ||
| + | 1,15 | ||
| «Pad» с нулями: | 6.218 | ||
| + | 1,150 | ||
| Добавить: | 6,218 | ||
| + | 1,150 | ||
| 7,368 |
Он совпадает с номером, с которого мы начали, поэтому проверяется.
Ввод нулей
Почему можно ставить лишние нули?
Ноль на самом деле означает, что в этом десятичном разряде нет значения.
- В таком числе, как 10, ноль означает «никто»
- В таком числе, как 2,50, ноль означает «без сотых»
Таким образом, можно безопасно взять число, например 2,5, и сделать его 2,50 или 2,500 и т. Д.
Но НЕ Берите 2,5 и не делайте 20,5, это совершенно неправильно.
Сложение и вычитание десятичных знаков
Чтобы сложить два десятичных числа, сначала проверьте, одинаковое ли количество цифр справа от десятичной точки. Если нет, добавляйте нули справа от одного из чисел, пока они не появятся.
Затем напишите одно число поверх другого, выровняв десятичные точки по вертикали. Сложите так же, как и с целыми числами, и переместите десятичную запятую прямо вниз.
Пример 1:
Добавлять 13.492 а также 7,8 .
Напишите два дополнительных нуля в конце 7,8 , и напишите числа вертикально.
13. 4 9 2 + 7. 8 0 0 _
Теперь добавлю.
1 1 3 1 . 4 9 2 + 7 . 8 0 0 _ 2 1 . 2 9 2
Ответ 21,292 .
Аналогичный метод работает и для вычитания.
Пример 2:
Вычесть 7.8 из 13,492 .
Напишите два дополнительных нуля в конце 7,8 , и напишите числа вертикально.
13. 4 9 2 — 7. 8 0 0 _
Теперь вычтите.
1 3. 4 9 2 — 7. 8 0 0 _ 5. 6 9 2
Ответ 5,692 .
Как складывать целые числа и десятичные дроби. Дополнение с перегруппировкой.
Пример 2.Напишите в столбик и прибавьте: 4785 + 9 + 2 . 307
Решение. . Показаны те:
4785 + 9 + 2 . 307
(Урок 3, вопрос 5.) Поэтому выровняйте следующим образом:
| 4785 | |
| 9 | |
| + 2 | . 307 |
| 4,796 | . 307 |
Пример 3. Запишите в столбик и прибавьте: . 58 + 5 . 8 + 58
Решение . Вот те:
_ . 58 + 5 . 8 + 58
Что касается . 58, единицы стоят с первого места до слева от десятичной запятой.
Выровняйте следующим образом:
| . 58 | |
| 5 | . 8 |
| + 58 | |
| 64 | . 38 |
Когда десятичные точки выровнены, десятичная точка в ответе будет находиться в том же месте. (Но это верно только для сложения и вычитания, а не для умножения. Урок 10.)
Что касается целого числа, такого как 58, чтобы помочь с выравниванием, мы можем вообразить десятичная точка после 8.
58 = 58 .
Целые числа, однако, обычно записываются без десятичной точки, поскольку десятичная точка означает «и».»Вот дроби
Пример 4. . 5 + . 5 + . 5
Выберите правильный ответ:
а) 15
б) . 15
в) 1 . 5
г) . 015
Ответ . в) 1 . 5
Ибо, если бы мы их выровняли и написали . 5 как 0 . 5–
| 1 |
| 0 . 5 |
| 0 . 5 |
| + 0 . 5 |
| 1 . 5 |
— мы бы увидели, что 1 (из 15 десятых) переносится в следующий столбец.
Дело:
Помимо сложения и вычитания, ответ
будет иметь такое же количество десятичных цифр, что и сами числа.
Пример 5. . 007 + . 003 + . 004
Ответ . . 014
Добавляемые числа состоят из трех десятичных цифр. Следовательно, ответ также будет состоять из трех десятичных цифр.
Пример 6. Периметры. Периметр плоской (плоской) фигуры является ее границей.
Эта фигура представляет собой прямоугольник, который представляет собой четырехстороннюю фигуру, в которой все углы являются прямыми углами. У прямоугольника противоположные стороны равны. Следовательно, периметр этого прямоугольника:
.| 12 + 12 + 6.5 + 6.5 | = | 24 + 13 |
| = | 37 дюйм. |
Пример 7. Добавляем:
| 2 | . 83 |
| 7 | . 49 |
| 6 | . 26 |
| + 8 | . 58 |
Техника. Не переписывайте задачу, записывая каждый столбец в виде отдельной суммы. Чтобы добавить столбец справа, не говорите — и не пишите — «3 плюс 9 равно 12. 12 плюс 6 равно 18.» И так далее. Скорее посмотрите вниз по столбцу и скажите , чтобы каждая частичная сумма была по .Не пиши это. (См. Урок 5, вопрос 2, пример 3.)
Чтобы добавить столбец справа, скажите
| 2 | . 83 | |
| 7 | . 49 | «12» |
| 6 | . 26 | «18» |
| + 8 | . 58 | «26» |
| 6 |
Напишите 6, перенесите 2. Чтобы добавить средний столбец, скажем,
| 2 | ||
| 2 | . 83 | «10» |
| 7 | . 49 | «14» |
| 6 | . 26 | «16» |
| + 8 | . 58 | «21» |
| . 16 |
Запись 1, перенос 2.Чтобы добавить последний столбец, скажем
| 2 | |
| «4» 2 | . 83 |
| «11» 7 | . 49 |
| «17» 6 | . 26 |
| «25» 8 | . 58 |
| 25 | . 16 |
Написать 25.
Вы можете написать десятичную точку в ответе, когда подойдете к нему; то есть после добавления среднего столбца.
Пожалуйста, «переверните» страницу и выполните несколько задач .
или
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Математические правила сложения | Sciencing
Общие правила применяются к сложению при добавлении в столбцы, нахождении суммы дробей, объединении десятичных чисел или при использовании отрицательных чисел. Вам нужно знать правила сложения, чтобы укрепить уверенность и точность.
Добавление в столбцы
При добавлении многозначных чисел в столбцы все «единицы» находятся в правом столбце, «десятки» — слева, затем «сотни» и так далее. Сложение начинается в столбце «единицы», и если сумма больше одной цифры, оставьте последнюю цифру внизу столбца и перенесите первую цифру (и) в верхнюю часть следующего столбца.
Добавление десятичных знаков
Для добавления десятичных знаков десятичные точки должны быть выровнены вертикально перед добавлением столбцов. Помните, что каждое целое число можно записать с десятичной дробью справа, за которой следует ноль, например 42.0 или 7.0.
Сложение дробей
Для сложения дробей знаменатели должны быть одинаковыми. Используйте наименьшее общее кратное для каждого знаменателя, но всякий раз, когда вы умножаете знаменатель на число, вы должны умножать числитель на то же число.
Добавление похожих терминов
При добавлении терминов переменные должны быть одинаковыми и иметь одинаковую степень. Например: 2XY + 5 X + 4XY = 5X + 6XY.
Добавление минусов
При добавлении минусов добавляйте так же, как и положительные, но ваш ответ будет отрицательным. Добавление негативов не меняет знака; у вас их просто больше.
Добавление положительных и отрицательных значений
Чтобы сложить положительное и отрицательное, вычтите два числа, а затем дайте ответу тот же знак, что и число с большим абсолютным значением.Если у вас больше отрицательных, чем положительных, ваш ответ будет отрицательным, и точно так же, если положительных ответов больше, чем отрицательных, ваш ответ будет положительным.
чисел — сложение / вычитание десятичных знаков
числа — сложение / вычитание десятичных знаков — глубинаЧтобы добавить десятичную дробь номера:
- Поставил числа в вертикальном столбце с выравниванием десятичных знаков
- Добавить столбец цифр, начиная справа и заканчивая левым. Если сумма в столбце больше десяти, «перенесите» цифры в следующий столбец на слева.
- Поместите десятичная точка в ответе непосредственно под десятичной точкой в терминах.
Вычесть десятичные числа:
- Поставил числа в вертикальном столбце, выравнивая десятичные точки.
- Вычесть каждый столбец, начиная справа и работая слева. Если цифра вычитаемое в столбце больше, чем цифра над ним, «заимствовать» цифра из следующего столбца слева.
- Поместите десятичная точка в ответе непосредственно под десятичной точкой в терминах.
- Проверьте свой ответьте, добавив результат к вычитаемому числу. Сумма должна равняться первое число.
Давайте посмотрим на пример.
Кому сложите эти числа, сначала расположите термины по вертикали, выровняв десятичную дробь очков в каждом семестре. Не забывайте, что для целого числа, такого как первый член, десятичная точка находится справа от столбца единиц. Вы можете добавить нули справа от десятичной точки, чтобы упростить выравнивание столбцов. Затем добавьте столбцы, работающие справа налево, расположив десятичный разделитель. точка в ответе прямо под десятичными точками в терминах.
Вот пример вычитания.
Кому вычтите эти числа, сначала расположите члены по вертикали, выровняв десятичную дробь очков в каждом семестре. Вы можете добавить нули справа от десятичной точки, чтобы упростить выравнивание столбцов. Затем вычтите рабочие столбцы справа налево, поставив десятичную точку в ответе напрямую под десятичными знаками в терминах.Проверьте свой ответ, добавив его ко второму члену и убедившись, что он равен первому.
назад наверх
Сложение и вычитание десятичных знаков
Когда вас просят добавить или вычесть десятичные дроби, наиболее важным шагом будет выровнять десятичных знаков.Добавление:
Пр.1) 13,6 + 17,8
Шаг 1 : Выровняйте десятичные точки так, чтобы выстроились одинаковые разряды. Другими словами, разряды десятков в обоих числах должны быть выровнены, разряды единиц в обоих числах должны быть выровнены, и т. Д.
Шаг 2 : Сложите выстроенные цифры вместе.
Пр. 2) 14,86 + 22,9
Если числа не имеют одинакового количества цифр после десятичной точки, вы можете использовать «нули-заполнители», чтобы помочь вам выровнять числа.
Пример 3.) 45 + 6.98
Распространенной ошибкой является то, что к 98 прибавляется 45. Однако здесь 45 представляет собой целое число. Это 4 десятка и 5 единиц. 98 представляет 9 десятых и 8 сотых. Эти числа не имеют одинаковых разрядов.
Вместо этого мы можем добавить десятичную точку в конце 45, а затем добавить два нуля-заполнителя, чтобы числа можно было выровнять.
45.00 + 6.98
Теперь мы готовы решить:
Вычитание:
Шаги для вычитания чисел с десятичными знаками точно такие же, как и для сложения десятичных знаков.Давайте взглянем на пару примеров.
Пр. 4) 239,83 — 125,51
Сначала мы выровняем числа, убедившись, что выстроены десятичные дроби. Затем мы просто вычитаем числа, которые находятся в обычных позициях с разрядными значениями.
Пр. 5) 98,3 — 45,67
Начнем с их выстраивания.