Деление и умножение на 0: правила для детей

23.02.2022 / 2 комментария / Математика / От admin

Тема нашей сегодняшней статьи: «Деление и умножение на 0: правила для детей». С одной стороны тема очень простая, а с другой — вызывает у деток вопросы. Так давайте разбираться вместе с весёлым клоуном Бимом, которому очень нравится задавать детям математические загадки.

Содержание статьи:

Деление и умножение на 0: правила

Сегодня день отдыха, и артисты придумывают новые вопросы для зрителей.

— Есть интересное число — 0, — говорит Бим. — Ведь это же ничего, с ним и возни мало. Давай посмотрим, какие задачи можем придумать с нулем для ребят.

Умножение на 0

— Двум или трем зрителям шариков не досталось. Значит надо складывать нули. — продолжил Бим. — Попробуем сложить два или три нуля:

0 + 0 = 0,

0 + 0 + 0 = 0.

Нет, много нулей долго писать, хотя… Сколько раз 0 в сложении ни напиши, все равно 0 выходит! Хорошо, что сложение одинаковых слагаемых заменяется умножением. Записываем:

0 + 0 = 0 ∙ 2 = 0,

0 + 0+ 0 = 0 ∙ 3 = 0,

0 + 0 + 0 + 0 = 0 ∙ 4 = 0.

Первый множитель	Второй множитель	Произведение
0	2	0
0	3	0
0	4	0

Правило. При умножении 0 на любое число произведение равно 0.

А если я наоборот запишу:

2 ∙ 0,

тогда я должен взять число 2 по 0 раз, то есть несколько раз. Так это тоже будет 0.

Первый множитель	Второй множитель	Произведение
2	0	0

Правило. При умножении любого числа на 0 произведение равно 0.

Здесь и еще одно правило работает для умножения:

Правило. От перестановки мест множителей произведение не изменяется.

Задача. Если нет ребят, сколько мы сможем подарить шариков?

Количество подаренных шариков так и останется 0. Сколько бы мы ни дарили шариков, если их некому дарить, то и число подаренных шариков равно нулю. Мы дарили по 2 шарика, но ребят 0, пишем:

2 ∙ 0 = 0 + 0 = 0.

А если по три шарика:

3 ∙ 0 = 0 + 0 + 0 = 0.

Бом и говорит:

— Давай запишем по порядку правила умножения на ноль:

• Правило 1. При умножении любого числа на 0 произведение равно 0.
• Правило 2. При умножении 0 на любое число произведение равно 0.

— Вот и еще один вопрос для зрителей: «Что получается при умножении на ноль?» — заметил Бим. — А дальше посмотрим, что получится при делении.

Деление 0 на число

— А можно ноль делить на любое число, отличное от нуля? — спросил Бом.

— Можно, только ты делишь 0 шариков, значит каждому и достанется 0 шариков, — ответил Бим.

К примеру, если пришло трое ребят, то 0 : 3 = 0.

Делимое	Делитель	Частное
0	3	0

 — Что-то уже кушать хочется. — сказал Бим. — Пойдем в буфет, мне в прошлый раз пирожное, которое было в остатке, очень понравилось. Занимательная история клоуна Бима и частное чисел в математике.

Пришли Бим и Бом в буфет, а им буфетчица говорит:

— А пирожных сегодня нет. Ведь представления нет, значит, — и пирожных мы не продаем.

— Сладкое сегодня не кушаем, — весело отвечает Бим. — Пирожных ноль.

— Да, — соглашается Бом. — Ноль, деленный на 2, — ноль. Столько пирожных и съедим.

0 : 2 = 0

Делимое	Делитель	Частное
0	2	0

Правило. При делении 0 на любое число, кроме 0, получается 0.

А почему кроме 0, узнаем дальше.

Деление на 0

Взяли они то, что было — бутерброды. Пьют чай, а Бим вздыхает:

— Там в углу шарики стоят и скучают. Нет зрителей, и некому их подарить. Выходит, что если зрителей 0, то сколько бы у нас ни было шариков, — дарить их некому, и все они у нас остаются. На ноль зрителей шарики не делятся.

Буфетчица подошла к Биму и Бому:

— Вы сегодня раздали своим зрителям по два шарика?

Бом с улыбкой говорит:

— Нет, по три.

Бим смеется:

— Сегодня не было представления! Я могу сказать, что мы раздали 0 ребятам по 4 шарика, и все мы сказали правду, так как деление проверяется умножением

2 ∙ 0 = 3 ∙ 0= 4 ∙ 0 = 0.

— Вот здорово! — обрадовался Бом. — Мы можем дать сколько угодно шариков каждому из зрителей, который не пришел!

— Значит, мы не сможем точно назвать, сколько шариков мы поделили между зрителями, которых 0 человек. — задумался Бим. — Здесь математическое деление никак не работает.

— Выходит, на ноль делить нельзя? — удивился Бом.

— Давай посмотрим правило в учебнике, — решил Бим.

Бим и Бом открыли учебник и хором прочитали:

Правило. Делить на ноль нельзя.

— Ура! И еще один вопрос для зрителей — правило деления на 0.

— Вот здорово! — обрадовался Бом. — Давай эти вопросы и правила для себя и для ребят напишем и выучим.

Заключение

Деление и умножение на ноль (правила):

Вопрос: Что получается при умножении на 0?

Правило. При умножении на 0 произведение равно 0.

Вопрос: Что получается при делении 0 на любое число, кроме 0?

Правило. При делении 0 на любое число, кроме 0, получается 0.

Вопрос: Правило деления на ноль?

Правило. На ноль делить нельзя.

Вот мы и разобрали деление и умножение на 0 (правила) с Бимом и Бобом. Вопросов по теме у Вас остаться не должно.

Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).

Не забудьте оценить наши старания. Комментарии приветствуются! По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))

• 11

  2022-03-12T22:22:37+00:00

  Алексей

  Спасибо за статью! Очень познавательно! Информация подана простым и понятным языком!

• 15

  2022-03-12T22:20:37+00:00

  Интересная история переплетена с математикой. Весёлые клоуны Бим и Бом умело объясняют тему умножения и деления на 0. Спасибо за такую неординарную подачу информации!

Деление и умножение на 0: правила для детей

23.02.2022 / 2 комментария / Математика / От admin

Тема нашей сегодняшней статьи: «Деление и умножение на 0: правила для детей». С одной стороны тема очень простая, а с другой — вызывает у деток вопросы. Так давайте разбираться вместе с весёлым клоуном Бимом, которому очень нравится задавать детям математические загадки.

Содержание статьи:

Деление и умножение на 0: правила

Сегодня день отдыха, и артисты придумывают новые вопросы для зрителей.

— Есть интересное число — 0, — говорит Бим. — Ведь это же ничего, с ним и возни мало. Давай посмотрим, какие задачи можем придумать с нулем для ребят.

Умножение на 0

— Двум или трем зрителям шариков не досталось. Значит надо складывать нули. — продолжил Бим. — Попробуем сложить два или три нуля:

0 + 0 = 0,

0 + 0 + 0 = 0.

Нет, много нулей долго писать, хотя… Сколько раз 0 в сложении ни напиши, все равно 0 выходит! Хорошо, что сложение одинаковых слагаемых заменяется умножением. Записываем:

0 + 0 = 0 ∙ 2 = 0,

0 + 0+ 0 = 0 ∙ 3 = 0,

0 + 0 + 0 + 0 = 0 ∙ 4 = 0.

Первый множитель	Второй множитель	Произведение
0	2	0
0	3	0
0	4	0

Правило. При умножении 0 на любое число произведение равно 0.

А если я наоборот запишу:

2 ∙ 0,

тогда я должен взять число 2 по 0 раз, то есть несколько раз. Так это тоже будет 0.

Первый множитель	Второй множитель	Произведение
2	0	0

Правило. При умножении любого числа на 0 произведение равно 0.

Здесь и еще одно правило работает для умножения:

Правило. От перестановки мест множителей произведение не изменяется.

Задача. Если нет ребят, сколько мы сможем подарить шариков?

Количество подаренных шариков так и останется 0. Сколько бы мы ни дарили шариков, если их некому дарить, то и число подаренных шариков равно нулю. Мы дарили по 2 шарика, но ребят 0, пишем:

2 ∙ 0 = 0 + 0 = 0.

А если по три шарика:

3 ∙ 0 = 0 + 0 + 0 = 0.

Бом и говорит:

— Давай запишем по порядку правила умножения на ноль:

• Правило 1. При умножении любого числа на 0 произведение равно 0.
• Правило 2. При умножении 0 на любое число произведение равно 0.

— Вот и еще один вопрос для зрителей: «Что получается при умножении на ноль?» — заметил Бим. — А дальше посмотрим, что получится при делении.

Деление 0 на число

— А можно ноль делить на любое число, отличное от нуля? — спросил Бом.

— Можно, только ты делишь 0 шариков, значит каждому и достанется 0 шариков, — ответил Бим.

К примеру, если пришло трое ребят, то 0 : 3 = 0.

Делимое	Делитель	Частное
0	3	0

 — Что-то уже кушать хочется. — сказал Бим. — Пойдем в буфет, мне в прошлый раз пирожное, которое было в остатке, очень понравилось. Занимательная история клоуна Бима и частное чисел в математике.

Пришли Бим и Бом в буфет, а им буфетчица говорит:

— А пирожных сегодня нет. Ведь представления нет, значит, — и пирожных мы не продаем.

— Сладкое сегодня не кушаем, — весело отвечает Бим. — Пирожных ноль.

— Да, — соглашается Бом. — Ноль, деленный на 2, — ноль. Столько пирожных и съедим.

0 : 2 = 0

Делимое	Делитель	Частное
0	2	0

Правило. При делении 0 на любое число, кроме 0, получается 0.

А почему кроме 0, узнаем дальше.

Деление на 0

Взяли они то, что было — бутерброды. Пьют чай, а Бим вздыхает:

— Там в углу шарики стоят и скучают. Нет зрителей, и некому их подарить. Выходит, что если зрителей 0, то сколько бы у нас ни было шариков, — дарить их некому, и все они у нас остаются. На ноль зрителей шарики не делятся.

Буфетчица подошла к Биму и Бому:

— Вы сегодня раздали своим зрителям по два шарика?

Бом с улыбкой говорит:

— Нет, по три.

Бим смеется:

— Сегодня не было представления! Я могу сказать, что мы раздали 0 ребятам по 4 шарика, и все мы сказали правду, так как деление проверяется умножением

2 ∙ 0 = 3 ∙ 0= 4 ∙ 0 = 0.

— Вот здорово! — обрадовался Бом. — Мы можем дать сколько угодно шариков каждому из зрителей, который не пришел!

— Значит, мы не сможем точно назвать, сколько шариков мы поделили между зрителями, которых 0 человек. — задумался Бим. — Здесь математическое деление никак не работает.

— Выходит, на ноль делить нельзя? — удивился Бом.

— Давай посмотрим правило в учебнике, — решил Бим.

Бим и Бом открыли учебник и хором прочитали:

Правило. Делить на ноль нельзя.

— Ура! И еще один вопрос для зрителей — правило деления на 0.

— Вот здорово! — обрадовался Бом. — Давай эти вопросы и правила для себя и для ребят напишем и выучим.

Заключение

Деление и умножение на ноль (правила):

Вопрос: Что получается при умножении на 0?

Правило. При умножении на 0 произведение равно 0.

Вопрос: Что получается при делении 0 на любое число, кроме 0?

Правило. При делении 0 на любое число, кроме 0, получается 0.

Вопрос: Правило деления на ноль?

Правило. На ноль делить нельзя.

Вот мы и разобрали деление и умножение на 0 (правила) с Бимом и Бобом. Вопросов по теме у Вас остаться не должно.

Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).

Не забудьте оценить наши старания. Комментарии приветствуются! По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))

• 11

  2022-03-12T22:22:37+00:00

  Алексей

  Спасибо за статью! Очень познавательно! Информация подана простым и понятным языком!

• 15

  2022-03-12T22:20:37+00:00

  Интересная история переплетена с математикой. Весёлые клоуны Бим и Бом умело объясняют тему умножения и деления на 0. Спасибо за такую неординарную подачу информации!

Что это такое и как им пользоваться

Цифра 0 уже давно ставит в тупик людей, изучающих математические понятия. Ноль это число? Как мы это используем? Хотя все мы на каком-то уровне знаем, что ноль означает ничего или ничего, это не всегда помогает нам включить его в математические задачи. Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.

 

Что такое число 0?

Является ли ноль числом? Ноль или 0 это 9Число 0009 и цифра, используемая для представления числа 0 , широко используются в математике и могут использоваться как самостоятельные числа или как заполнители в уравнениях.

 

История

Число 0 использовалось для представления идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при записи чисел и уравнений.

Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.

 

Современное использование

Ноль обычно используется в языке для выражения концепции отсутствия и используется в математике как целое число. Число 0 в сегодняшней математике может быть сложным; зачем что-то вычислять, когда на самом деле там ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.

 

Операции с 0

Хотя этот список функций с использованием нуля не охватывает все математические функции , эти основные арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.

 

Сложение

Тождество Закон сложения гласит, что любое число, добавленное к 0, равно самому себе .

Таким образом, вы можете добавить любое число и получить ту же сумму. Таким образом, вы можете добавить 0 к 1, 107 и 1 000 000 и все равно получить то же число, с которого вы начали.

 

Вычитание

Как и при сложении, если вычесть 0 из любого числа, вы получите ту же сумму. Например, 12-0 = 12.

Если вы вычитаете, вам может понадобиться заимствование для решения проблемы. Заимствование — это метод, используемый для вычитания чисел, состоящих более чем из одной цифры.

Вот пример заимствования (разберусь как форматировать):

1572-125 = х

В этой задаче из 2 нельзя вычесть 5. Значит, надо заимствовать из 7.

70 это 7 десятков. Итак, вы можете убрать десятку, и 7 станет 2; затем 2 становится 12. Теперь вам нужно вычесть 5 из 12.

12-5 равно 7.

6-2 равно 4.

5-1 равно 4.

1-0 (пустое место) равно 1.

Следовательно, ответ равен 1447.

Итак, если 0 — это ничто, как мы можем заимствовать его в задаче на вычитание? Ключ заключается в том, чтобы заимствовать из следующей цифры слева. Вы можете идти так далеко влево, как вам нужно.

Итак, если бы вы сделали 306-98 вы должны сначала позаимствовать из 3, чтобы сделать 0 равным 10. Затем вы можете позаимствовать из 10, чтобы сделать 6 равным 16. Таким образом, ваша задача будет выглядеть так: 16-8=8.

9-9=0.

2-0=2.

Таким образом, ваш ответ 208.

 

Не стесняйтесь заниматься математикой с помощью , добавляя котят в свою жизнь из самых простых функций 0. Когда вы умножаете на 0 , ответ всегда 0.

12 × 0 = 0

255 × 0 = 0

1679 × 0=0

И знаете что? 123596395539 x ​​0 = 0

 

Деление

Число 0, деленное на любое число, равно нулю. Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.

К сожалению, деление числа на ноль не столь очевидно логично. Любое число, деленное на ноль, считается неопределенным; если вы поместите его в свой калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.

При делении вы всегда можете перепроверить свой ответ, умножив частное (ответ на задачу о делении) на делимое . В нашей задаче о кексах это 2 x 4. Число должно равняться нашему исходному делителю, 8.

Однако это помогает нам понять, почему мы не можем разделить число на 0. Поскольку мы знаем из наших правил умножения, что все, что умножается на 0, равно 0, изложенная выше концепция не работает, если 0 является делимым, потому что ответ всегда будет 0, даже если это не исходный делитель.

Если по какой-то причине вы встретили 0 как делимое в задаче, вы можете выразить его как 1, даже если ответ технически не определен .

 

Возведение в степень

Как и в делении, 0 в экспоненте считается неопределенным.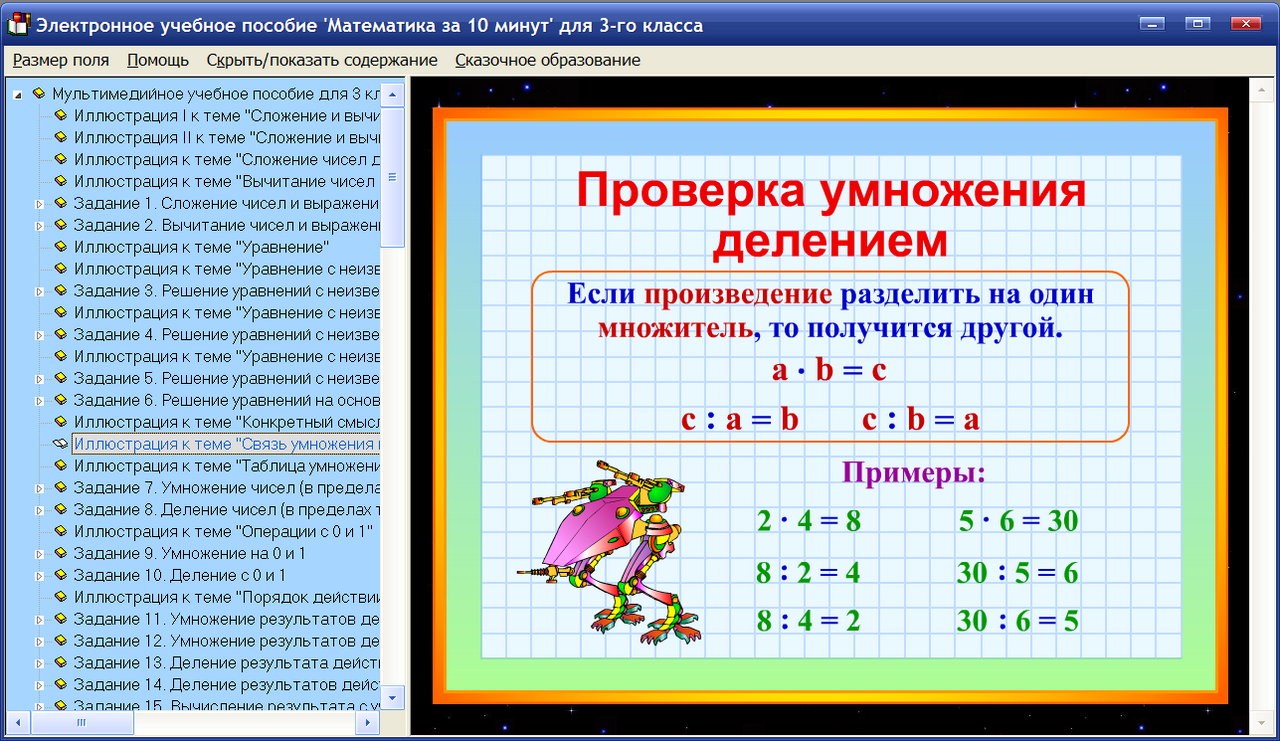 Однако, когда вы решаете задачи и сталкиваетесь с чем-то, что равно 0 в степени другого числа или числом в степени 0, помните о правиле степени 0

Правило степени 0 гласит, что любое основание с показателем степени 0 или 0 равно 1. Итак, x¹ = 1,

Между тем, 0 в любой степени равно 0. Таким образом, 0² = 0.

 

 

Факториал нуля

Факториал — это математическое выражение, выражаемое как ! равно числу, полученному путем умножения всех чисел между 1 и заданным целым числом.

Итак, 2! означает, что мы умножаем все числа от 1 до 2. Это означает, что 2! = 2×1 = 2 и, следовательно, 2! = 24

6! означает, что мы умножаем все числа от 1 до 6. Итак, 6! = 1×2×3×4×5×6 = 720 и, следовательно, 6! = 720

Нулевой факториал, часто записывается как 0! Определяется как равный 1. По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.

 

Использовать число ноль может быть сложно, но есть несколько правил, которые помогут вам правильно выполнять математические операции, когда речь идет о нуле. Обязательно придерживайтесь этих правил и помните, что ноль вам не враг. Если вы знаете, как работать с числом ноль, использовать его будет проще простого.

 

Что дальше?

Очарованы числом ноль? Узнайте, сколько нулей в миллиарде и сколько нулей в гуголе и гуголплексе.

Нужна дополнительная помощь по математике? Узнайте, как преобразовывать десятичные дроби в дроби, складывать и вычитать дроби, а также все о составных и рациональных числах. И не забудьте нашу удобную таблицу умножения.

 

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.

 

У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!

Об авторе

Кэрри имеет степень бакалавра письма, литературы и издательского дела в Колледже Эмерсон и в настоящее время получает степень магистра иностранных дел. Она несколько лет работала в издательстве и считает, что книги могут открывать новые миры. Она любит читать, гулять на свежем воздухе и узнавать что-то новое.

Деление на ноль | Brilliant Math & Science Wiki

Содержание

• Деление вида \(\frac{a}{0}\), \(a\neq 0\)
• Разделение формы \(\frac{0}{0}\)
• 2=1?

В математике при делении на ноль делитель (знаменатель) равен нулю и имеет вид \(\frac{a}{0}\). Предположим теперь, что мы применили эту операцию к некоторым числам \(x\) и \(a\). Предположим \(a\neq 0\).

\[x=\frac{a}{0}\]

Так как деление обратно умножению,

\[x\times 0=a\]

Из правил умножения мы знаем, что любое число умноженное на ноль равно нулю.

\[x\times 0=0=a\]

Что противоречит нашему предыдущему предположению, что \(a\neq 0\). Это противоречие говорит нам о том, что не существует определенной формы для \(x\) , поэтому говорят, что деление на ноль равно неопределенным .

Чтобы понять это более интуитивно, давайте рассмотрим понятие деления в элементарной арифметике. Мы определяем деление на ноль в арифметике как разбиение набора объектов на равные части.

Например, если у нас есть \(15\) яблок и мы хотим поровну раздать их \(3\) людям, то по определению деления каждый ученик получит \(\frac{15}{3}=5\ ) яблок каждый.

По той же логике \(\frac{a}{0}\) означает поровну распределить \(a\) яблок среди \(0\) людей.

Это бессмысленно; нет логического способа распределить набор объектов среди \(0\) людей, поэтому мы можем сказать, что он не определен.

Другой способ понять деление на ноль: вместо простого деления на ноль мы позволяем знаменателю все ближе и ближе приближаться к нулю и экстраполируем его. Например, давайте сделаем \(a\) равным \(1\) и посмотрим, как значения меняются по мере того, как знаменатель становится все ближе и ближе к нулю.

\[\frac{1}{0.1}=10\]

\[\frac{1}{0.01}=100\]

\[\frac{1}{0.001}=1000\]

\[\frac{1}{0,0001}=10000\]……

Мы видим, что по мере того, как знаменатель становится все ближе и ближе к нулю, значение становится все больше и больше, поэтому у нас может возникнуть соблазн сказать, что \(\frac{1}{0}=+\infty\). Но мы рассмотрели только значение, когда знаменатель стремится к нулю с положительной стороны, в равной степени допустимо проверить его с отрицательной стороны.

\[\frac{1}{-0.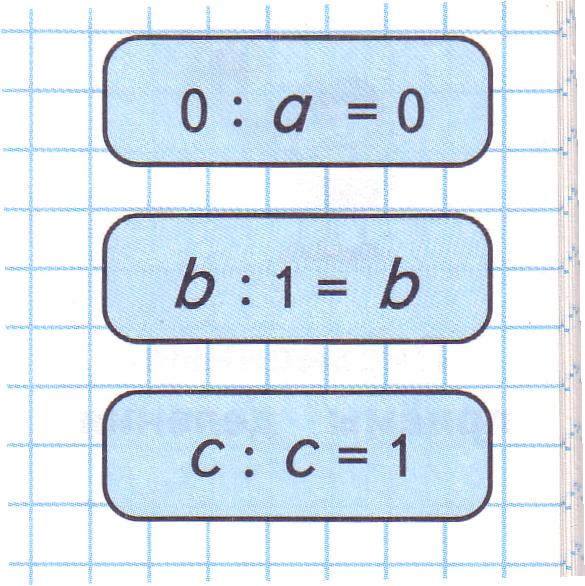 1}=-10\]

\[\frac{1}{-0.01}=-100\]

\[\frac{1}{-0.001}= -1000\]

\[\frac{1}{-0,0001}=-10000\]……

По мере того, как знаменатель становится все ближе и ближе к нулю с отрицательной стороны, \(\frac{1}{0}=-\infty\). Помимо того факта, что бесконечность — это даже не число, у нас есть два предела, к которым приближается деление по мере того, как знаменатель все ближе и ближе к нулю. Это говорит нам о том, что, хотя он определяется по мере приближения к нулю, он не определяется по мере того, как равен нулю.

Пусть значение операции равно \(x\).

\[x=\frac{0}{0}\]

\[x\times 0 = 0\]

Мы видим, что левая часть уравнения равна нулю. для любого значения \(x\), поэтому у нас есть уравнение, которое будет истинным утверждением для любого значения \(x\). Поскольку это так, у нас нет способа определить значение \(х\), говорят, что оно

неопределенное .

В элементарной арифметике \(\frac{0}{0}\) означает поровну раздать \(0\) яблок \(0\) людям.