| Табличка на двери |
Вычитание дробей. Вычитание дробей с разными знаменателями.
Следующее действие, которое можно выполнять с обычными дробями это вычитание. Вычитание дробей выполняется по нескольким правилам. Рассмотрим эти правила подробнее. Вычитание смешанных дробей с разными знаменателями можно посмотреть нажав на ссылку.
Вычитание дробей с одинаковым знаменателем.
Рассмотрим, пока примеры в которых уменьшаемое больше вычитаемого.
\(\frac{7}{13}-\frac{3}{13} = \frac{7-3}{13} = \frac{4}{13}\)Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно посчитать разность числителя уменьшаемого и вычитаемого, а знаменатель оставить без изменения.
\(\frac{a}{b}-\frac{c}{b} = \frac{a-c}{b}\)Вычитание дробей с разными знаменателями.
Чтобы выполнить вычитание дробей с разными знаменателями, нужно привести дроби к общему знаменателю, а потом применить правило вычитания дробей с одинаковыми знаменателями.
Рассмотрим пример:
Выполните вычитание дробей \(\frac{5}{6}\) и \(\frac{1}{2}\).
Общий знаменатель этих двух дробей latex]\frac{5}{6}[/latex] и \(\frac{1}{2}\) равен 6. Умножим вторую дробь \(\frac{1}{2}\) на дополнительный множитель 3.
\(\frac{5}{6}-\frac{1}{2} = \frac{5}{6}-\frac{1 \times \color{red} {3}}{2 \times \color{red} {3}} = \frac{5}{6}-\frac{3}{6} = \frac{2}{6} = \frac{1}{3}\)Дробь \(\frac{2}{6}\) сократили и получили \(\frac{1}{3}\).
Буквенная формула вычитания дробей с разными знаменателями.
\(\bf \frac{a}{b}-\frac{c}{d} = \frac{a \times d-c \times b}{b \times d}\)Вопросы по теме:
Как вычитать дроби с разными знаменателями?
Ответе: нужно найти общий знаменатель и далее по правилу выполнить вычитание дробей с одинаковыми знаменателями.
Как выполнить вычитание дробей с одинаковыми знаменателями?
Ответ: у числителей посчитать разность, а знаменатель оставить тот же.
Как правильно сделать проверку вычитания двух дробей?
Ответ: для проверки правильности вычитания дробей, нужно выполнить сложение вычитаемого и разности, результат их суммы будет равен вычитаемому.
Проверка:
\(\frac{4}{8} + \frac{3}{8} = \frac{4 + 3}{8} = \frac{7}{8}\)Пример №1:
Выполните вычитание дробей: а) \(\frac{1}{2}-\frac{1}{2}\) б) \(\frac{10}{19}-\frac{7}{19}\)
Решение:
а) \(\frac{1}{2}-\frac{1}{2} = \frac{1-1}{2} = \frac{0}{2} = 0\)
При вычитание двух одинаковых дробей получаем нуль.
б) \(\frac{10}{19}-\frac{7}{19} = \frac{10-7}{19} = \frac{3}{19}\)
Пример №2:
Выполните вычитание и проверьте сложением: а) \(\frac{13}{21}-\frac{3}{7}\) б) \(\frac{2}{3}-\frac{1}{5}\)
Решение:
а)Найдем общий знаменатель дробей \(\frac{13}{21}\) и \(\frac{3}{7}\), он будет равен 21. Умножим вторую дробь \(\frac{3}{7}\) на 3.
\(\frac{13}{21}-\frac{3}{7} = \frac{13}{21}-\frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{13}{21}-\frac{9}{21} = \frac{13-9}{21} = \frac{4}{21}\)Выполним проверку вычитания:
\(\frac{4}{21} + \frac{3}{7} = \frac{4}{21} + \frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{4}{21} + \frac{9}{21} = \frac{4 + 9}{21} = \frac{13}{21}\)б) Найдем общий знаменатель дробей \(\frac{2}{3}\) и \(\frac{1}{5}\), он будет равен 15. Умножим первую дробь \(\frac{2}{3}\) на дополнительный множитель 5, вторую дробь \(\frac{1}{5}\) на 3.
\(\frac{2}{3}-\frac{1}{5} = \frac{2 \times \color{red} {5}}{3 \times \color{red} {5}}-\frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{10}{15}-\frac{3}{15} = \frac{10-3}{15} = \frac{7}{15}\)Выполним проверку вычитания:
\(\frac{7}{15} + \frac{1}{5} = \frac{7}{15} + \frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{7}{15} + \frac{3}{15} = \frac{7 + 3}{15} = \frac{10}{15} = \frac{2}{3}\)§27. Сложение и вычитание дробей с одинаковыми знаменателями
349. Заполните пропуски.
1) Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
2) В буквенном виде правило сложения дробей с одинаковыми знаменателями записывают так: a/c+b/c=a+b/c
3) Чтобы вычесть дроби с одинаковыми элементами, нужно на числитель уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
4) В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так: a/c-b/c=a-b/c.
350. Выполните действия.
1) 6/13+5/13=11/13
2)32/45-14/45=18/45
3)13/44+18/44-15/44=16/44
4)72/95-26/95+38+95=84/95
351. В первый день туристы прошли4/15 всего пути, а во второй 6/15 пути. Какую часть пути прошли туристы за два дня?
Решение: За два дня туристы прошли
4/15 + 6/15 = 10/15 пути
Ответ: 10/15
352. Решете уравнение.
353. Решите уравнение.
354. Магазин продал 180 кг. Апельсин. В первый день было продано 13/ 36 всех апельсинов, а во второй – 19/ 36 всх апельсинов. Сколко килограммов апельсинов было продано за два дня?
Решение.
13/36 + 19/36 = 32/ 36 ( части) – продано за 2 дня.
180: 36 * 32 =160(кг.) – продано за 2 дня.Ответ: 160 кг.
355. Общая масса Пети и Коли равна 55 кг. Коли и Саши 57 кг. Пети и Саши 62 кг. Какова масса каждого мальчика?
Решение
Удвоенная масса всех мальчиков равна
55 + 57 + 62 = 174(кг), значит масса трех мальчиков 87 кг, откуда Саша – 32кг,Ответ: 32 кг; 30 кг; 25 кг. Петя – 30 кг, Коля – 25 кг.
356. Применяя знаки арифметических действий и скобки, запишите:
1) с помощью семи цифр 7выражено, значение которого равно 700:
2) с помощью восьми цифр 2 выражение, значение которого равно 200:
3) с помощью десяти цифр 6 выражение, значение которого равно 600:
4) с помощью десяти цифр 9 выражение, значение которого равно 1 000.
Ответ: 1) 777-77*7*7:
2) 222 + 22 – 2 *22:
3) 666 – 66 + 6 * ( 66 – 66):
4) 999 + 9 : 9 + 9 ( 99 – 99).
1.Организационный момент | Создать благоприятный психологический настрой на работу. Обеспечить мотивацию учения детьми, принятие ими целей урока. |
4 мин | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. (слайд№3) -Вспомните, с чем вы знакомились на прошлых уроках? К нам на урок сегодня пришёл Незнайка и попросил помочь ему разобраться с понятием обыкновенные дроби и научится задачи с помощью дробей. И как вы уже догадались, на этом уроке мы продолжим работу с обыкновенными дробями. -Тема сегодняшнего урока (слайд №1) «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». -Какие цели мы поставим на данном уроке? (слайд № 4-7) | Включаются в деловой ритм урока. С обыкновенными дробями. Научились отличать правильные и неправильные дроби и сравнивать их. Учащихся пишут дату и тему урока в тетради. Цели урока:
| Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. | 2. Актуализация знаний и умений | Актуализация опорных знаний и способов действий; повторение умения переводить текст в запись в виде дроби, восстановление определения правильной и неправильной дроби, фиксирование индивидуальных затруднений | 8 мин | И вот первые вопросы от Незнайки; -Чем натуральные числа отличаются от дробных? — Что показывает знаменатель и где его пишут? — Что показывает числитель и где его пишут? Работа с рисунками. (слайд №8-11) -Прочтите полученные ответы, а как ещё читаются эти дроби? (слайд №12) Устная работа. (слайд№13) -Помогите Незнайке собрать груши, на которых записаны неправильные дроби. -Какую дробь называют правильной? -Какую дробь называют неправильной? (слайд №14) Самостоятельная работ. (слайд №15) | Целые числа обозначают целые единицы а дробные –части единиц. Знаменатель показывает, на сколько долей делят и пишут его под чертой. Числитель показывает, сколько долей было взято и пишут его над чертой. Учащиеся пишут ответы на вопросы по слайдам в тетради. 1/2 — Половина 8/8; 17/13; 11/9. Дробь в которой числитель меньше знаменателя, называет правильной дробью. Дробь в которой числитель больше знаменателя, называет неправильной дробью. Работа в парах. Учащихся меняются тетрадями и выполняют проверку оценивая друг друга. | Личностные: оценивание усваиваемого материала. Коммуникативные: умение использовать речь для регуляции своего действия, строить понятные для окружающих высказывания. Регулятивные: контроль иоценка процесса и результатов деятельности. Познавательные: структурирование собственных знаний. | 3.Целеполагание и мотивация. | Обеспечение мотивации учения детьми, принятие ими целей урока | 8 мин | Ребята Незнайка очень удивлен, что дроби можно сравнивать так легко. Покажем ему, что ещё можно выполнит с обыкновенными дробями. Предлагаю построить ломаную из трёх отрезков по 2 см каждый и вычислить её длину в см. (слайд № 16) Проблемная ситуация; -Попробуйте вычислите длину ломаной в дм. Подсказка: -Найдите какую часть составляют 2 см от дециметра. (слайд №17-18) -Каким образом вы смогли вычислить длину в дм? А теперь попробуем вместе сформулировать правило сложения дробей с одинаковыми знаменателями. (слайд№19) Запишем правило сложения с помощью букв. Незнайка попросил помочь ему решить задачу. (слайд № 20) — К нему в гости пришли друзья, он решил угостить их яблоками положил на тарелку 10 (долей), 4 доли съели сколько долей осталось? -С помощью какого действия решили задачу? Сформулируйте правило вычитания дробей с одинаковыми знаменателями. Запишем это правило с помощью букв. (слайд № 21) | В тетради выполняют рисунок и вычисляют; 2+2+2=6см. Учащихся сталкиваются с проблемой 2см от дм., 2/10дм. Отмечают на рисунке и снова вычисляют длину ломаной. 2/10+2/10+2/10=2+2+2/10=6/10 Выполнили сложение дробей. При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляется тот же. В тетради записывают правило с помощью букв 10/10-4/10=10-4/10=6/10 При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же. В тетради записывают правило с помощью букв
| Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, строение понятные для окружающих высказывания. | 4. Применение знаний и умений в новой ситуации | Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». | 7 мин | — Итак одну из обучающих целей нашего урока вы выполнили ,выявили правила сложения и вычитания дробей с одинаковыми знаменателями осталось научиться применять эти правила на практике. Для этого поработаем с учебником; (слайд № 22) 1.Стр. 156, №1005.
— Прочитайте ответ.
— Прочитайте ответ. -Какую массу гвоздей получила первая бригада? — На сколько тонн меньше получила вторая бригада? -Сколько тонн гвоздей получила вторая бригада? | Решение задач по новой теме | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: умение оформлять свои мысли в устной форме; слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Дробью будем называть одну или несколько равных между собой долей одного целого. Дробь записывается с помощью двух натуральных чисел, которые разделены между собой чертой. Например, 1/2, 2/4, ¾, 5/9 и т.д.
Цифра, которая записана сверху над чертой, называется числителем дроби, а цифра записанная под чертой, называется знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей было поделено целое. Числитель дроби показывает, сколько таких частей взято.
Дроби, как и обычные натуральные числа, можно складывать и вычитать между собой. Разберемся, как складывать и вычитать дроби, у которых в знаменателе находится одно и тоже число.
Сложение дробей с одинаковыми знаменателями
Пусть имеется две дроби с одинаковыми знаменателями, например 3/7 и 2/7. Найти их сумму.
Основное правило сложения дробей с одинаковыми знаменателями:
- Для того, чтобы сложить две дроби с одинаковыми знаменателями, необходимо знаменатель оставить без изменения, а числители складываемых дробей сложить между собой как обычные числа.
Вернемся к нашему примеру, и сложим дроби 3/7 и 2/7. Так как, знаменатели у дробей одинаковые, то можно воспользоваться правилом, написанным выше.
Согласно этому правилу 3/7 + 2/7 будет равняться 5/7.
- 3/7 + 2/7 = (3+2)/7 = 5/7.
Вычитание дробей с одинаковыми знаменателями
Пусть имеется две дроби с одинаковыми знаменателями, например 9/13 и 5/13. Нужно найти их разность.
Основное правило вычитания дробей с одинаковыми знаменателями:
- Для вычитании дробей с одинаковыми знаменателями, необходимо знаменатель оставить без изменений, а из числителя первой дроби, вычесть числитель второй дроби.
Вернемся к нашему примеру, и вычтем из дроби 9/13 дробь 5/13. Так как знаменатели дробей равны, то можно воспользоваться правилом, написанным выше.
Согласно этому правилу 9/13 – 5/13 будет равняться 4/13.
- 9/13 – 5/13 = (9-5)/13 = 4/13.
Задача-пример на сложение и вычитание дробей
Рассмотрим одну небольшую задачку, на сложение и вычитание дробей.
Бочонок с медом был заполнен на 5/7 от своего объема. Винни-Пух съел за завтраком, 2/7 бочонка, и еще 1/7 бочонка съел Пятачок. Найти сколько меда осталось в бочонке, после завтрака героев.
Сначала определим сколько вместе съели Винни-Пух и Пятачок, для этого сложим две дроби 2\7 и 1/7.
Так как у дробей одинаковые знаменатели, то воспользуемся правилом сложения дробей с одинаковыми знаменателями.
- 2/7 + 1/7= (2+1)/7 = 3/7.
Теперь вычтем из того, что было в бочонке, то сколько съели Винни-Пух и Пятачок.
Так как дроби снова имеют одинаковые знаменатели, воспользуемся правилом вычитания дробей с одинаковыми знаменателями.
- 5/7 – 3/7 = (5-3)/7 = 2/7.
Это и будет ответом, к нашей задаче.
Нужна помощь в учебе?
Предыдущая тема: Дроби: чтение и сравнение дробей
Следующая тема:   Точка, отрезок, луч, прямая — числовая прямая | 5 класс
как делать, примеры с одинаковыми и разными знаменателями
Сложение и вычитание алгебраических дробей
Дробь — это доля числа. Она представлена в виде \frac mn, где m и n — любые натуральные числа. В данной записи m является числителем, а n — знаменателем.
Для того чтобы производить операции с дробями, необходимо знать их основное свойство. Оно состоит в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
СледствиеОдно и то же количество можно выразить разными эквивалентными дробями.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
ПримерЕсли числитель и знаменатель дроби \(\frac12\) умножить на 2, получится равная ей дробь \(\frac24.\)
Основные правила, операции без преобразования
Сложение (вычитание) дробей — это упрощение выражений вида \(\frac ab\pm\frac cb\) или \(\frac ab\pm\frac cd\), где \(c\neq d.\)
Главное правило сложения и вычитания дробей заключается в том, что операции можно проводить только между дробями с одинаковым знаменателем.
Если знаменатели двух дробей одинаковы, то можно сразу сложить или вычесть, в зависимости от задачи, числители этих дробей, а знаменатель оставить прежним. Если это возможно, дробь нужно сократить.
Общее правило сложения и вычитания дробей с одинаковым знаменателем выглядит следующим образом:
\(\frac ab\pm\frac cb=\frac{a\pm c}b,\)
где a, b и с — натуральные числа, \(b\neq0.\)
Пример\(\frac16+\frac46=\frac56;\)
\(\frac78-\frac38=\frac48=\frac12.\)
Если знаменатели разные, дроби необходимо заменить на эквивалентные с одинаковым знаменателем. Выполнить операцию необходимо уже с этими новыми дробями. Распространяется это как на положительные, так и на отрицательные дроби.
Сложение и вычитание алгебраических дробей
Приведение алгебраических дробей к общему знаменателю
Для каждой дроби существует бесконечное количество эквивалентных дробей. Это значит, что обязательно есть знаменатель, являющийся одинаковым для двух или более дробей, с которыми производится действие. Такой знаменатель называют общим.
Чтобы упростить вычисления, обычно используют метод наименьшего общего кратного.
Наименьшее общее кратное (НОК) — это такое наименьшее натуральное число, которое делится одновременно на оба числа. В данном случае это числа, стоящие в знаменателях двух дробей.
ПримерДля чисел 2 и 3 произведение и НОК = 6; для чисел 5 и 10 произведение равно 50, а НОК = 10; произведение чисел 4 и 6 равно 24, а их НОК = 12.
Как видно из последних двух примеров, НОК зачастую меньше, чем производное двух данных чисел. Благодаря НОК можно значительно сократить запись решения, поскольку отпадает нужда в ненужном сокращении дробей.
Чтобы найти НОК, необходимо разложить знаменатели обеих дробей на простые множители, а затем выбрать в разложении наименьшего знаменателя множители, не вошедшие в разложение большего знаменателя, и добавить их туда. После чего перемножить все полученные множители.
ПримерНайдем НОК чисел 12 и 18.
\(12=3\cdot2\cdot2\)
\(18=3\cdot3\cdot2\)
В разложение наименьшего знаменателя 12 вошли множители 3, 2 и 2. А в разложении наибольшего знаменателя 18 множитель 2 встречается только один раз, в нем не хватает еще одного множителя 2. Поэтому мы добавляем его к множителям числа 18. Получаем:
\(НОК\;(12;18)=3\cdot3\cdot2\cdot2=36.\)
Чтобы привести дроби к общему знаменателю, необходимо найти не только НОК, но и дополнительный множитель.2}6\)
Этап урока | Время | Деятельность преподавателя | Деятельность суворовцев |
Самоопределение к деятельнос-ти (орг. момент) | 3 мин. | Приветствие — Ребята, откройте тетради и запишите сегодняшнее число, классная работа. Слайд 1. — Ребята, какой серьёзной темой мы начали заниматься в этой четверти? Слайд 2. — В древности и в средние века учение о дробях считалось хотя и самым трудным, но и самым важным разделом арифметики. Римский оратор Цицерон писал: «Без знания дробей никто не может признаться знающим арифметику». Слайд 3. -В Древнем Египте Действия с дробями могли производить только самые просвещённые люди своего времени – жрецы, и знания свои они хранили в глубокой тайне. Сейчас действия с дробями может производить каждый уважающий себя пятиклассник. — Чему мы уже научились? — Как вы думаете, куда дальше в изучении дробей мы продолжим продвигаться? | Приветствуют преподавателя. Записывают число, «Классная работа». Отвечают на вопрос учителя: — мы начали изучать тему: «Обыкновенные дроби». Слушают объяснение преподавателя. Отвечают на вопросы преподавателя: — сокращать дроби, отмечать их на координатном луче, приводить к общему знаменателю, сравнивать дроби с равными знаменателями, с равными числителями; — мы должны научиться производить с ними арифметические действия. |
Актуализа-ция знаний и фиксация затруднений в деятель-ности | 7 мин. | Слайд 4. — Выполните задания, предложенные в презентации: — Какая из дробей лишняя; почему? ; ; — Сравните дроби:
— Какие правила сравнения дробей вы использовали? Слайд 5. Математики Древнего Египта вместо обычных знаков + и – использовали знаки «идущие ноги». Определите, какой знак они обозначали. Слайд 6. — Вычислите: — Какой пример вызвал затруднения? — Как решили первых два примера? — Как решили третий пример? — Почему получились разные ответы в 4-м примере? | Выполняют задания, предложенные в презентации, отвечают на вопросы преподавателя. (, это неправильная дробь, остальные дроби – правильные; числитель и знаменатель этой дроби – однозначные числа). — Сравнение дробей с одинаковыми знаменателями, перекрёстное правило. Выполняют задание, предложенное в презентации. Отвечают на вопросы преподавателя: — Не знаем правило сложения дробей с разными знаменателями; |
Постановка учебной задачи | 2 мин. | — Чем же мы будем сегодня заниматься? — Как будет называться тема сегодняшнего урока? -Запишите тему урока в тетрадь. Слайд 7. – Сформулируйте цели урока. Слайд 8. | — будем учиться складывать и вычитать дроби с разными знаменателями. Самостоятельно формулируют тему урока: « Сложение и вычитание дробей с разными знаменателями». Записывают тему урока в тетрадь. -Самостоятельно формулируют цели урока: 1)Построить алгоритм сложения и вычитания дробей с разными знаменателями, 2) научиться выполнять действия по построенному алгоритму. |
«Открытие» детьми нового знания | 5 мин. | Работа с презентацией. (В презентации на примере деления квадрата показано сложение и вычитание дробей с разными знаменателями) Слайд 9. — Ребята, попробуйте самостоятельно вывести правило сложения дробей с разными знаменателями. Слайд 10. Сложение и вычитание дробей с разными знаменателями:
| Работают с презентацией. Самостоятельно выводят правило сложения дробей с разными знаменателями. |
Первичное закрепление во внешней речи | 7 мин | — Выполните №440 с комментированием (5 суворовцев по очереди вызываются к доске). Слайд 11. Ответы примеров нужно записать в таблицу. — Ребята, что нужно сделать для того, чтобы достичь в чём-то успеха? Слайд 12. — Чей портрет изображён на слайде? — Алекса́ндр Васи́льевич Суво́ров — национальный герой России, великий русский полководец, не потерпевший ни одного поражения в своей военной карьере, один из основоположников русского военного искусства. — Как он достиг такого успеха? — Какие замечательные слова оставил А.В.Суворов нам в напутствие: — Дисциплина — мать победы. — Легко в учении — тяжело в походе, тяжело в учении — легко в походе. — За ученого трех неученых дают. Нам мало трех, давай нам шесть, давай нам десять на одного, — всех побьем, повалим, в полон возьмем… — Как бы плохо ни приходилось, никогда не отчаивайся, держись, пока силы есть. — Действительно, чем больше труда мы приложим на уроке, тем легче нам будет и на контрольной работе, и на экзамене. | Одновременное решение примеров на доске и в тетрадях с комментирова-нием. В результате выполнения задания получили слово «Успех». Отвечают на вопрос преподавателя: — А.В.Суворова. Отвечают на вопрос преподавателя. |
Физкультминутка | 3 мин. | Упражнения на внимание, зрение, осанку. Слайды 13, 14, 15. | Выполняют упражнения на внимание, зрение, осанку. |
Самостоя-тельная работа с самопровер-кой | 10 мин. | Самостоятельная работа с самопроверкой. Слайд 16. — Ребята, поднимите сигнальные карточки те, кто выполнил самостоятельную работу на «5», на «4». | Выполняют самостоятельную работу, затем выполняют самопроверку по образцу и выставляют себе оценки. При помощи сигнальных карточек показывают преподавателю, кто как справился с самостоятельной работой. |
Включение в систему знаний и повторение | 5 мин | — Решите задачу (слайд 17): В третьем взводе 24 суворовца. взвода занимается самбо, взвода — плаванием, — футболом. Сколько суворовцев третьего взвода занимается спортом? | Суворовцы, выполнившие самостоятельную работу на «5» и «4», решают задачу (сначала решают самостоятельно, затем сверяют свои решения). Остальные с помощью карточек-алгоритмов решают в тетрадях № 442 (а,б) |
Задание на самоподготовку | 1 мин. | — Запишите задание на самоподготовку: 1) № 447, стр.123; 2) Придумать и решить задачу на сложение и вычитание дробей с разными знаменателями. | Записывают задание на самоподготовку. |
Итог урока | 2 мин. | — Что нового узнали на уроке? – Какую цель мы ставили в начале урока? – Наша цель достигнута? – Что нам помогло справиться с затруднением? – Какие знания нам пригодились при выполнении заданий на уроке? – Оцените при помощи сигнальных карточек свою работу на уроке. Слайд 19. Пусть каждый день и каждый час | Осуществляют рефлексию собственной деятельности. |
правил вычитания дробей | Study.com
Правила вычитания дробей
Правило 1. Дроби должны иметь общий знаменатель.
Это означает, что знаменатели или нижние числа дробей должны быть одинаковыми, что мы называем общими знаменателями . Если они не совпадают, мы найдем общий знаменатель и сделаем их одинаковыми.
Правило 2: Если у вас есть общий знаменатель, он не меняется.
Другими словами, когда вы вычитаете дроби, вы вычитаете только числители или числа сверху.
Правило 3. При необходимости упростите ответ.
Если в вашем ответе числитель и знаменатель имеют общий множитель, используйте этот множитель, чтобы уменьшить дробь.
Пример с одинаковыми знаменателями
Вот пример задачи вычитания дроби, у которой уже есть общие знаменатели:
Поскольку знаменатели одинаковы, единственное, что вам нужно сделать, это вычесть верхние числа! Знаменатель останется прежним.Итак, для этой задачи 2 — 1 = 1, тогда 3 остается неизменным, поэтому
2/3 — 1/3 = 1/3
Пример с разными знаменателями
Давайте посмотрим на эту задачу вычитания дробей с разными знаменателями:
7/8 — 1/4 =?
Используя эквивалентных дробей , дробей, которые выглядят по-разному, но фактически представляют одно и то же число, мы можем найти общий знаменатель и превратить 1/4 в 2/8, которые теперь имеют тот же знаменатель, что и 7/8.
Итак, 1/4 = 2/8.Вот такая картинка!
Теперь, когда вы нашли эквивалентную дробь 1/4 (2/8), вы готовы к вычитанию!
7/8 — 2/8 = 5/8, потому что 7 — 2 = 5 и знаменатель (8) остается прежним.
Пример вычитания, требующий упрощения
В этом примере давайте объединим все, что мы узнали:
1/2 — 1/6 =?
Правило 1 гласит, что наши знаменатели должны быть одинаковыми.Поскольку это не так, давайте найдем общий знаменатель:
Используя то, что мы только что узнали об эквивалентных дробях, мы умножаем 1/2 x 3/3 и получаем 3/6, которое теперь имеет тот же знаменатель, 6, что и наша другая дробь.
Правило 2 гласит, что как только у нас есть общий знаменатель, мы просто вычитаем числители и сохраняем тот же знаменатель
3/6 — 1/6 = 2/6
Правило 3 говорит, что нужно упростить или уменьшить дробь. В 2/6 и 2, и 6 могут быть равномерно разделены на 2.
2/6 ÷ 2/2 = 1/3.
Видите, это так же просто, как Правила 1, 2 и 3 !!
Краткое содержание урока
При вычитании дробей необходимо соблюдать три правила. Первое правило — наши дроби должны иметь общих знаменателей . Если знаменатели в каждой дроби не совпадают, используйте процесс , эквивалентный дроби , чтобы сделать их одинаковыми, прежде чем переходить ко второму правилу, заключающемуся в том, что вы вычитаете только числители, сохраняя знаменатель неизменным. Наконец, третье правило гласит, что при необходимости упрощайте свой ответ!
Сложение и вычитание дробей — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Сложить или вычесть дроби с общим знаменателем
- Сложить или вычесть дроби с разными знаменателями
- Используйте порядок операций для упрощения сложных дробей
- Вычислить выражения переменных с дробями
Более подробное введение в темы, затронутые в этом разделе, можно найти в главе Prealgebra , Fractions .
Сложить или вычесть дроби с общим знаменателем
Когда мы умножали дроби, мы просто умножали числители и умножали знаменатели прямо поперек. Чтобы складывать или вычитать дроби, они должны иметь общий знаменатель.
Сложение и вычитание дробей
Если это числа, то где
Чтобы сложить или вычесть дроби, сложите или вычтите числители и поместите результат над общим знаменателем.
Выполнение упражнений по манипуляциям с математикой «Сложение дробей модели» и «Вычитание дробей модели» поможет вам лучше понять сложение и вычитание дробей.
Найдите сумму:
Решение
| Сложите числители и поставьте сумму над общим знаменателем. |
Найдите сумму:
Найдите сумму:
Найди отличия:
Решение
Найди отличия:
Найди отличия:
Найди отличия:
Найди отличия:
Теперь мы рассмотрим пример, в котором есть как сложение, так и вычитание.
Упростить:
Упростить:
Сложить или вычесть дроби с разными знаменателями
Как мы видели, для сложения или вычитания дробей их знаменатели должны быть одинаковыми. Наименьший общий знаменатель (ЖКД) двух дробей — это наименьшее число, которое может использоваться в качестве общего знаменателя дробей. ЖКД двух дробей — это наименьшее общее кратное (НОК) их знаменателей.
Наименьший общий знаменатель
Наименьший общий знаменатель (ЖКД) двух дробей — это наименьшее общее кратное (НОК) их знаменателей.
Выполнение упражнения по манипуляции математикой «Поиск наименьшего общего знаменателя» поможет вам лучше понять ЖК-дисплей.
После того, как мы найдем наименьший общий знаменатель двух дробей, мы конвертируем дроби в эквивалентные дроби с помощью ЖК-дисплея. Объединение этих шагов позволяет нам складывать и вычитать дроби, потому что их знаменатели будут одинаковыми!
Как сложить или вычесть дроби
Добавить:
Добавить:
Добавить:
Сложить или вычесть дроби.
- Есть ли у них общий знаменатель?
- Да, переходите к шагу 2.
- Нет — перепишите каждую дробь с ЖК-дисплеем (наименьший общий знаменатель). Найдите ЖК-дисплей. Измените каждую дробь на эквивалентную дробь с ЖК-дисплеем в качестве знаменателя.
- Сложите или вычтите дроби.
- Упростите, если возможно.
При нахождении эквивалентных дробей, необходимых для создания общих знаменателей, есть быстрый способ найти необходимое число для умножения числителя и знаменателя.Этот метод работает, если мы нашли ЖК-дисплей, разложив на простые числа.
Посмотрите на коэффициенты на ЖК-дисплее, а затем на каждый столбец над этими коэффициентами. «Недостающие» факторы каждого знаменателя — это числа, которые нам нужны.
В (рисунок) ЖК-дисплей, 36, имеет два множителя 2 и два множителя
.В числителе 12 два множителя равны 2, но только один множитель 3 — так что в нем «отсутствует» один 3 — мы умножаем числитель и знаменатель на 3.
В числителе 18 отсутствует один множитель 2, поэтому мы умножаем числитель и знаменатель на 2.
Мы применим этот метод, когда будем вычитать дроби в (Рисунок).
Вычесть:
Решение
Есть ли у дробей общий знаменатель? Нет, нам нужно найти ЖК-дисплей.
Не упрощайте эквивалентные дроби! Если вы это сделаете, вы вернетесь к исходным дробям и потеряете общий знаменатель!
Вычесть:
Вычесть:
В следующем примере одна из дробей имеет переменную в числителе.Обратите внимание, что мы делаем те же шаги, что и в случае, когда оба числителя являются числами.
Добавить:
Решение
У дробей разные знаменатели.
Помните, что мы можем складывать только одинаковые термины: 24 и 5 x не похожи на термины.
Добавить:
Добавить:
Теперь у нас есть все четыре операции для дробей. (Рисунок) суммирует операции с дробями.
| Умножение на дроби | Фракционное подразделение |
| Умножьте числители и умножьте знаменатели | Умножьте первую дробь на обратную величину второй. |
| Добавление фракции | Вычитание дроби |
| Сложите числители и поместите сумму над общим знаменателем. | Вычтите числители и поместите разницу над общим знаменателем. |
| Для умножения или деления дробей ЖК-дисплей НЕ нужен. Для сложения или вычитания дробей необходим ЖК-дисплей. | |
| ⓐ Что такое операция? Операция — вычитание. Есть ли у дробей общий знаменатель? № Перепишите каждую дробь как эквивалентную дробь на ЖК-дисплее. Вычтите числители и поместите разницу над общими знаменателями. Упростите, если возможно. Нет общих факторов. Дробь упрощена. | |
| ⓑ Что такое операция? Умножение. Чтобы умножить дроби, умножьте числители и знаменатели. Перепишите, указав общие множители.Удалите общие факторы. Упростить. |
Использование порядка операций для упрощения сложных дробей
Мы видели, что сложная дробь — это дробь, в числителе или знаменателе которой содержится дробь. Полоса дробей указывает на деление. Мы упростили сложную дробь, разделив на
.Теперь мы рассмотрим сложные дроби, где числитель или знаменатель содержит выражение, которое можно упростить. Поэтому сначала мы должны полностью упростить числитель и знаменатель по отдельности, используя порядок операций.Затем делим числитель на знаменатель.
Как упростить сложные дроби
Упростить:
Упростить:
Упростить:
Упростите сложные дроби.
- Упростим числитель.
- Упростим знаменатель.
- Разделите числитель на знаменатель. Если возможно, упростите.
Упростить:
Решение
Можно заключить числитель и знаменатель в круглые скобки.
Упростить:
Упростить:
Вычислить выражения переменных с помощью дробей
Раньше мы вычисляли выражения, но теперь мы можем вычислять выражения с дробями. Помните, что для оценки выражения мы подставляем значение переменной в выражение, а затем упрощаем.
ⓐⓑ
ⓐⓑ
Оценить, когда
Решение
Подставьте значения в выражение.
В следующем примере будут только переменные, без констант.
Оценить, когда
Решение
Чтобы оценить, когда мы подставляем значения в выражение.
Ключевые понятия
- Сложение и вычитание дробей: Если — числа, где тогда
и
Чтобы сложить или вычесть дроби, сложите или вычтите числители и поместите результат над общим знаменателем. - Стратегия сложения или вычитания дробей
- Есть ли у них общий знаменатель?
Да — переходите к шагу 2.
Нет — перепишите каждую дробь с помощью ЖК-дисплея (наименьший общий знаменатель). Найдите ЖК-дисплей. Измените каждую дробь на эквивалентную дробь с ЖК-дисплеем в качестве знаменателя. - Сложите или вычтите дроби.
- Упростите, если возможно. Для умножения или деления дробей ЖК-дисплей НЕ нужен. Для сложения или вычитания дробей необходим ЖК-дисплей.
- Есть ли у них общий знаменатель?
- Упростите сложные дроби
- Упростим числитель.
- Упростим знаменатель.
- Разделите числитель на знаменатель. Если возможно, упростите.
Практика ведет к совершенству
Сложение и вычитание дробей с общим знаменателем
В следующих упражнениях добавьте.
В следующих упражнениях вычтите.
Смешанная практика
Упростите следующие упражнения.
Сложить или вычесть дроби с разными знаменателями
В следующих упражнениях сложите или вычтите.
Смешанная практика
Упростите следующие упражнения.
ⓐⓑ
ⓐⓑ
Использование порядка операций для упрощения сложных дробей
Упростите следующие упражнения.
Вычислить выражения переменных с помощью дробей
Оцените в следующих упражнениях.
ⓐⓑ
ⓐⓑ
ⓐⓑ
когда
Письменные упражнения
Зачем нужен общий знаменатель для сложения и вычитания дробей? Объяснять.
Как найти жк 2 дроби?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующей главе? Почему или почему нет?
Глоссарий
- наименьший общий знаменатель
- Наименьший общий знаменатель (ЖКД) двух дробей — это наименьшее общее кратное (НОК) их знаменателей.
Сложение и вычитание дробей с непохожими знаменателями
Задача: В пиццерии было две пиццы одинакового размера, каждую нарезанную на равные части. В конце дня осталась треть одной пиццы и шестая часть другой пиццы. Сколько всего пиццы осталось?
Анализ: Эта задача требует сложить две трети и одну шестую вместе. Но мы не можем складывать эти дроби, так как их знаменатели не совпадают!
Решение: Нам нужно сделать знаменатели одинаковыми.Мы можем найти общий знаменатель , умножив знаменатели вместе: 3 x 6 = 18. Таким образом, вместо 3 или 6 кусочков пиццы мы сделаем так, чтобы у обоих было по 18 ломтиков. Теперь пицца выглядит так:
В приведенной выше задаче мы нашли общий знаменатель , умножив знаменатели исходных дробей. Однако для большинства поваров приготовить 18 ломтиков — слишком большая работа! Попробуем использовать другой метод, в котором меньше срезов.
Метод 2: Мы можем переименовать эти дроби, используя их наименьший общий знаменатель (LCD), который является наименьшим числом, которое делится на все знаменатели без остатка.Это наименьшее общее кратное знаменателя. Давайте найдем ЖК-дисплей одной трети и одной шестой.
| ||||||||||||||||||||
| Решение: | Теперь мы можем использовать 6 в качестве наименьшего общего знаменателя. |
Как видите, наименьший общий знаменатель позволяет складывать (или вычитать) дроби, используя наименьшее количество фрагментов. Не всегда целесообразно рисовать круги для решения этих задач. Итак, нам нужен арифметический метод. Мы будем использовать эквивалентные дроби, чтобы помочь нам, как показано в примерах ниже.
Пример 1:
Анализ:
Знаменатели не совпадают. Наименьший общий знаменатель (ЖКД) 4 и 6 равен 12.
Решение: Составьте эквивалентные дроби с новым знаменателем:
и
Сложите числители:
Обратите внимание, что в примере 1 числитель и знаменатель дроби должны быть умножены на одно и то же ненулевое целое число, чтобы получить эквивалентные дроби. Мы могли бы использовать общий знаменатель, например 24, для решения этой проблемы. Это показано ниже.
Как видите, использование общего знаменателя вместо ЖК-дисплея может привести к ненужному упрощению результата (например, к увеличению количества кусочков пиццы).Мы представили два метода сложения (и вычитания) дробей с разными знаменателями:
- Общий знаменатель — дает больше кусочков пиццы.
- Наименьший общий знаменатель (ЖКД) — уменьшает количество кусочков пиццы.
Вы можете использовать любой метод по своему усмотрению. Однако в оставшейся части этого урока мы будем использовать метод ЖКД. Помните, что ЖК-дисплей — это просто наименьшее общее кратное знаменателей. Давайте посмотрим на несколько примеров.
Пример 2:
Анализ: Знаменатели не совпадают. ЖК-дисплей 3 и 2 — 6.
Решение: Сделайте эквивалентные дроби с новым знаменателем:
и
Сложите числители:
Просто результат:
В примере 2 у нас была неправильная дробь, поэтому пришлось упростить результат. Рассмотрим еще несколько примеров.
Пример 3:
Анализ: Знаменатели не совпадают. ЖК-дисплей 10 и 15 — 30.
Решение: Составьте эквивалентные дроби с новым знаменателем:
и
Вычтем из числителей:
Пример 4:
Анализ: Знаменатели не совпадают. ЖК-дисплей 6, 8 и 16 — 48.
Решение: Составьте эквивалентные дроби с новым знаменателем:
Вычтем и сложим числители:
Просто результат:
Следующая процедура суммирует шаги, которые мы использовали в примерах с 1 по 4:
Процедура: Чтобы добавить или вычесть дроби с разными знаменателями:
- Найдите наименьший общий знаменатель.
- Сделайте эквивалентные дроби с помощью ЖК-дисплея.
- Сложите или вычтите числители.
- При необходимости упростите результат.
Для шага 2 помните, что числитель и знаменатель дроби должны быть умножены на одно и то же ненулевое целое число, чтобы получить эквивалентные дроби. Давайте посмотрим на некоторые проблемы со словами.
Пример 5: Член школьной команды по легкой атлетике пробежал две трети мили в понедельник и одну пятую милю во вторник.Сколько миль он всего пробежал?
Анализ: Эта задача просит нас сложить дроби с разными знаменателями:
Решение: ЖК-дисплей 3 и 5 — 15.
Пример 6: На соревновании по поеданию пирогов Спенсер съел три четверти пирога до того, как было объявлено время; Карли съела только половину пирога. Насколько больше пирога съела Спенсер, чем Карли?
Анализ: Эта задача требует от нас вычесть дроби с разными знаменателями:
Решение: На ЖК-дисплее 4 и 2 отображается 4.
Резюме: Для того, чтобы складывать или вычитать дроби, они должны иметь одинаковые знаменатели. Учитывая две или более дробей с разными знаменателями, ЖКД является наименьшим общим кратным знаменателей.
Для сложения или вычитания дробей с разными знаменателями
- Найдите наименьший общий знаменатель.
- Сделайте эквивалентные дроби с помощью ЖК-дисплея.
- Сложите или вычтите числители.
- При необходимости упростите результат.
Упражнения
Указания: складывайте дроби в каждом упражнении ниже. Обязательно упростите свой результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы записать дробь в три четверти, введите в форму 3/4. Чтобы написать смешанное число четыре и две трети, введите 4, пробел и затем 2/3 в форму.
| 1. | |
| 2. | |
| 3. | |
| 4. | Команда Марии занималась футболом две трети часа в пятницу и пять шестых часа в субботу. Сколько часов в общей сложности тренировалась ее команда в футболе? |
| 5. | Учебник истории Эми весит семь восьмых фунта, а ее учебник алгебры весит две трети фунта. Насколько больше ее учебник истории весит, чем ее учебник алгебры? |
Сложение и вычитание дробей | Математика для гуманитарных наук Corequisite
Результаты обучения
- Сложение и вычитание дробей
- Найдите общий знаменатель двух или более дробей
- Используйте общий знаменатель для сложения или вычитания дробей
- Упростите дробь до наименьшего значения
Введение
Прежде чем мы начнем, вот несколько важных терминов, которые помогут вам понять концепции работы с дробями в этом разделе.
- произведение: результат умножения
- Фактор : что-то умножается — для [latex] 3 \ cdot 2 = 6 [/ latex] и 3, и 2 являются множителями 6
- числитель: верхняя часть дроби — числитель дроби [латекс] \ frac {2} {3} [/ latex] равен 2
- знаменатель : нижняя часть дроби — знаменатель дроби [латекс] \ frac {2} {3} [/ latex] равен 3
Примечание к инструкциям
Учебники по математике и учителя используют много разных слов, чтобы дать ученикам инструкции о том, что им делать с той или иной задачей.Например, в примере этого модуля вы можете увидеть такие инструкции, как «Найти» или «Упростить». Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список слов, которые могут помочь вам понять, как решать проблемы в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические операции, которые могут включать сложение, вычитание, умножение, деление. |
| Упростить | 1) Выполните указанные математические операции, включая сложение, вычитание, умножение, деление. 2) Напишите математическое утверждение в кратчайшие сроки, чтобы не было никаких других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценить | Выполните указанные математические операции, включая сложение, вычитание, умножение, деление |
| Уменьшить | Напишите математическое утверждение в наименьшем или наименьшем значении, чтобы не было никаких других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением. |
Сложение дробей
Когда вам нужно сложить или вычесть дроби, вам нужно сначала убедиться, что дроби имеют одинаковый знаменатель.Знаменатель сообщает вам, на сколько частей было разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепцию «частей целого» можно смоделировать с помощью пиццы и кусочков пиццы. Например, представьте, что пицца разрезается на 4 части, а кто-то берет 1 кусок. Теперь [латекс] \ frac {1} {4} [/ latex] пиццы исчез, а [latex] \ frac {3} {4} [/ latex] остается. Обратите внимание, что обе эти фракции имеют знаменатель 4, который относится к количеству ломтиков, на которые была нарезана вся пицца.Что, если у вас есть еще одна пицца, которую разрезали на 8 равных частей, а 3 из них исчезли, оставив [латекс] \ frac {5} {8} [/ latex]?
Как вы можете описать общее количество пиццы, которое осталось, одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если одно число кратно другому, вы можете разделить их и не иметь остатка.
Один из способов найти наименьшее общее кратное двух или более чисел — сначала умножить каждое на 1, 2, 3, 4 и т. Д.Например, найдите наименьшее общее кратное 2 и 5.
| Сначала перечислите все числа, кратные 2: | Затем перечислите все числа, кратные 5: |
| [латекс] 2 \ cdot 1 = 2 [/ латекс] | [латекс] 5 \ cdot 1 = 5 [/ латекс] |
| [латекс] 2 \ cdot 2 = 4 [/ латекс] | [латекс] 5 \ cdot 2 = 10 [/ латекс] |
| [латекс] 2 \ cdot 3 = 6 [/ латекс] | [латекс] 5 \ cdot 3 = 15 [/ латекс] |
| [латекс] 2 \ cdot 4 = 8 [/ латекс] | [латекс] 5 \ cdot 4 = 20 [/ латекс] |
| [латекс] 2 \ cdot 5 = 10 [/ латекс] | [латекс] 5 \ cdot 5 = 25 [/ латекс] |
Наименьшее общее кратное, которое у них есть, будет общим знаменателем для двух!
Пример
Опишите оставшееся количество пиццы, используя общепринятые термины.
Показать решение Перепишите дроби [latex] \ frac {3} {4} [/ latex] и [latex] \ frac {5} {8} [/ latex] как дроби с наименьшим общим знаменателем.Найдите наименьшее общее кратное знаменателей. Это наименьший общий знаменатель.
, кратное 4: 4, 8 , 12, 16
, кратное 8: 8 , 16, 24
Наименьший общий знаменатель — 8 — наименьшее общее кратное.
Записываем [латекс] \ frac {3} {4} [/ latex] со знаменателем 8.Вы должны умножить верхнюю и нижнюю границы на 2, чтобы не изменить отношения между ними.
[латекс] \ frac {3} {4} \ cdot \ frac {2} {2} = \ frac {6} {8} [/ латекс]
Нам не нужно перезаписывать [latex] \ frac {5} {8} [/ latex], поскольку у него уже есть общий знаменатель.
Ответ
И [latex] \ frac {6} {8} [/ latex], и [latex] \ frac {5} {8} [/ latex] имеют одинаковый знаменатель, и вы можете описать, сколько пиццы осталось, с помощью общих терминов. .
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями.Тогда вы знаете, что делать! Шаги показаны ниже.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Перепишите каждую дробь, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно складывать числители.
- Упростите, отбросив все общие множители в числителе и знаменателе.
Упрощение дроби
Часто, если ответ на проблему дробный, вас просят написать его в кратчайшие сроки.Это обычное соглашение, используемое в математике, подобно тому, как предложение начинается с заглавной буквы и заканчивается точкой. В этом курсе мы не будем вдаваться в подробности о методах уменьшения фракций, потому что их много. Процесс упрощения дроби часто называют уменьшением дроби . Мы можем упростить, отбросив (разделив) общие множители в числителе и знаменателе дроби. Мы можем это сделать, потому что дробь представляет собой деление.
Например, чтобы упростить [latex] \ frac {6} {9} [/ latex], вы можете переписать 6 и 9, используя наименьшие возможные множители следующим образом:
[латекс] \ frac {6} {9} = \ frac {2 \ cdot3} {3 \ cdot3} [/ латекс]
Поскольку и в числителе, и в знаменателе стоит 3, а дроби можно считать делением, мы можем разделить 3 вверху на 3 внизу, чтобы уменьшить до 1.
[латекс] \ frac {6} {9} = \ frac {2 \ cdot \ cancel {3}} {3 \ cdot \ cancel {3}} = \ frac {2 \ cdot1} {3} = \ frac { 2} {3} [/ латекс]
Переписывание дробей с наименьшими возможными множителями часто называется разложением на простые множители.
В следующем примере вам показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Пример
Добавьте [латекс] \ frac {2} {3} + \ frac {1} {5} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не одинаковы, найдите общий знаменатель, умножив знаменатели.[латекс] 3 \ cdot5 = 15 [/ латекс]
Перепишем каждую дробь со знаминателем 15.
[латекс] \ begin {array} {c} \ frac {2} {3} \ cdot \ frac {5} {5} = \ frac {10} {15} \\\\\ frac {1} {5 } \ cdot \ frac {3} {3} = \ frac {3} {15} \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним. Убедитесь, что дробь нельзя упростить.
[латекс] \ frac {10} {15} + \ frac {3} {15} = \ frac {13} {15} [/ латекс]
Ответ
[латекс] \ frac {2} {3} + \ frac {1} {5} = \ frac {13} {15} [/ latex]
Вы можете найти общий знаменатель, найдя общие кратные знаменателей.Наименьшее общее кратное — самый простой в использовании.
Пример
Добавьте [латекс] \ frac {3} {7} + \ frac {2} {21} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не одинаковы, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) 7 и 21., кратное 7: 7, 14, 21
, кратное 21: 21
Перепишем каждую дробь со знаминателем 21.
[латекс] \ begin {array} {c} \ frac {3} {7} \ cdot \ frac {3} {3} = \ frac {9} {21} \\\\\ frac {2} {21 } \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним.Убедитесь, что дробь нельзя упростить.
[латекс] \ frac {9} {21} + \ frac {2} {21} = \ frac {11} {21} [/ latex]
Ответ
[латекс] \ frac {3} {7} + \ frac {2} {21} = \ frac {11} {21} [/ латекс]
В следующем видео вы увидите пример того, как сложить две дроби с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже.В этом примере вы будете использовать метод простой факторизации, чтобы найти НОК.
Подумай об этом
Добавьте [латекс] \ frac {3} {4} + \ frac {1} {6} + \ frac {5} {8} [/ latex]. Упростите ответ и напишите смешанное число.
Чем этот пример отличается от предыдущих? Воспользуйтесь рамкой ниже, чтобы записать несколько мыслей о том, как сложить три дроби с разными знаменателями.
Показать решение Поскольку знаменатели не одинаковы, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) 4, 6 и 8.[латекс] 4 = 2 \ cdot2 \\ 6 = 3 \ cdot2 \\ 8 = 2 \ cdot2 \ cdot2 \\\ текст {LCM}: \, \, 2 \ cdot2 \ cdot2 \ cdot3 = 24 [/ латекс]
Перепишем каждую дробь со знаминателем 24.
[латекс] \ begin {array} {c} \ frac {3} {4} \ cdot \ frac {6} {6} = \ frac {18} {24} \\\\\ frac {1} {6 } \ cdot \ frac {4} {4} = \ frac {4} {24} \\\\\ frac {5} {8} \ cdot \ frac {3} {3} = \ frac {15} {24 } \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним.
[латекс] \ frac {18} {24} + \ frac {4} {24} + \ frac {15} {24} = \ frac {37} {24} [/ latex]
Запишите неправильную дробь как смешанное число и упростите дробь.
[латекс] \ frac {37} {24} = 1 \, \, \ frac {13} {24} [/ латекс]
Ответ
[латекс] \ frac {3} {4} + \ frac {1} {6} + \ frac {5} {8} = 1 \ frac {13} {24} [/ latex]
Вычитание дробей
Когда вы вычитаете дроби, вы должны подумать, есть ли у них общий знаменатель, как при сложении дробей. Ниже приведены несколько примеров вычитания дробей, знаменатели которых не совпадают.
Пример
Вычтите [латекс] \ frac {1} {5} — \ frac {1} {6} [/ latex].Упростите ответ.
Показать решение У дробей разные знаменатели, поэтому вам нужно найти общий знаменатель. Напомним, что общий знаменатель можно найти, умножив два знаменателя вместе.[латекс] 5 \ cdot6 = 30 [/ латекс]
Записываем каждую дробь как эквивалентную дробь со знаминателем 30.
[латекс] \ begin {array} {c} \ frac {1} {5} \ cdot \ frac {6} {6} = \ frac {6} {30} \\\\\ frac {1} {6 } \ cdot \ frac {5} {5} = \ frac {5} {30} \ end {array} [/ latex]
Вычтите числители.При необходимости упростите ответ.
[латекс] \ frac {6} {30} — \ frac {5} {30} = \ frac {1} {30} [/ latex]
Ответ
[латекс] \ frac {1} {5} — \ frac {1} {6} = \ frac {1} {30} [/ latex]
Пример ниже показывает, как использовать кратные для нахождения наименьшего общего кратного, который будет наименьшим общим знаменателем.
Пример
Вычтите [латекс] \ frac {5} {6} — \ frac {1} {4} [/ latex]. Упростите ответ.
Показать решение Найдите наименьшее общее кратное знаменателей — это наименьший общий знаменатель., кратное 6: 6, 12 , 18, 24
, кратное 4: 4, 8 12 , 16, 20
12 — наименьшее общее кратное 6 и 4.
Перепишем каждую дробь со знаминателем 12.
[латекс] \ begin {array} {c} \ frac {5} {6} \ cdot \ frac {2} {2} = \ frac {10} {12} \\\\\ frac {1} {4 } \ cdot \ frac {3} {3} = \ frac {3} {12} \ end {array} [/ latex]
Вычтите дроби. При необходимости упростите ответ.
[латекс] \ frac {10} {12} — \ frac {3} {12} = \ frac {7} {12} [/ latex]
Ответ
[латекс] \ frac {5} {6} — \ frac {1} {4} = \ frac {7} {12} [/ latex]
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Сложение и вычитание дробей Факты и рабочие таблицы для детей
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатный образец. Загрузить образецЗагрузить этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже зарегистрировались? Авторизуйтесь, чтобы скачать.Этот урок представляет собой пошаговое введение через визуальный и концептуальный подход к эквивалентным дробям. Более того, мы будем использовать эквивалентные дроби как стратегию для сложения и вычитания дробей .
См. Файл фактов ниже для получения дополнительной информации о сложении и вычитании дробей или, в качестве альтернативы, вы можете загрузить нашу 33-страничную рабочую таблицу сложения и вычитания дробей для использования в классе или дома.
Основные факты и информация
ЭКВИВАЛЕНТНЫЕ ДОЛИ
- Эквивалентные дроби — это разные дроби, которые представляют одно и то же число.
- Дроби 2/3 и 4/6 эквивалентны. Две трети эквивалентны четырем шестым.
- Дроби 3/4, 6/8 и 9/12 эквивалентны. Три четверти, шесть восьмых и девять двенадцатых эквивалентны.
- Есть две простые стратегии определения эквивалентных дробей.
- Использование моделей
- Подумайте о количестве равных частей в плитках с дробями.
- Нарисуйте диаграмму
- Использование моделей
- Дроби можно выразить целыми числами в дробной форме.Возьмем для примера значение 1.
- Чтобы выразить целочисленное значение 1, всегда можно использовать дробные модели. В этом случае 4/4 представляет четыре равные части, составляющие одно целое. Следовательно, поскольку и целое число 1, и дробь 4/4 имеют одинаковое значение, они эквивалентны друг другу.
- Возьмите значение 3 или 3 целых. В этом случае каждая коробка представляет собой одно целое и состоит из 1 равной части. Следовательно, чтобы представить значение 3, мы можем выразить целое число 3 как 3/1 в дробной форме.
- Аналогично, чтобы представить целое число 2, оно может быть представлено 4 равными частями, составляющими 2 целых. Следовательно, целое число 2 равно 4/2.
ДОБАВЛЕНИЕ ИЛИ ВЫЧИСЛЕНИЕ ДРОБЕЙ — ОДИН ДЕНОМИНАТОР
- Начните складывать и вычитать дроби с одинаковым знаменателем, прежде чем пытаться работать с дробями с разными знаменателями.
- Сложите или вычтите числители, сохраняя знаменатель прежним.
- Также неплохо закончить, упростив ответ до самой низкой формы.
- Обычные дроби можно упростить до самых низких значений, применив концепцию эквивалентных дробей.
- Давайте рассмотрим. Смешанное число — это целое число и правильная дробь вместе. Давайте посмотрим на этот пример.
- Когда вы объединяете целое и дробное, вы получаете смешанное число.
- Чтобы сложить смешанные числа с одним и тем же знаменателем:
- Сложите целые числа
- Сложите числители
- Знаменатель останется прежним
ДОБАВЛЕНИЕ ИЛИ ВЫЧИСЛЕНИЕ дробей должно быть — РАЗНОЕ ЗНАЧИТЕЛЬ A
- Найдите наименьший общий знаменатель.
- Вычисляйте эквивалентные дроби с помощью ЖК-дисплея.
- Сложите или вычтите числители.
- При необходимости упростите результат.
- Сложите части целого числа.
- Измените требуемые дроби на их эквивалентные значения, чтобы у всех дробей был один и тот же знаменатель.
- Сложите или вычтите числители. Знаменатель оставьте как есть.
Это фантастический пакет, который включает в себя все, что вам нужно знать о сложении и вычитании дробей на 33 подробных страницах. Это готовых к использованию рабочих листов сложения и вычитания дробей, которые идеально подходят для предоставления студентам пошагового введения через визуальный и концептуальный подход к эквивалентным дробям.Более того, мы будем использовать эквивалентные дроби как стратегию для сложения и вычитания дробей.
Полный список включенных рабочих листов
- План урока
- Сложение и вычитание дробей
- Ты мой равный
- Эквивалентные дроби
- Разложение дробей
- Добавление смешанных дробей
- Добавление смешанных дробей
- Сложение дробных частей
- Вычитание в отличие от дробей
- Подробнее о сложении
- Подробнее о вычитании
- Проблемы с дробными словами
Ссылка / ссылка на эту страницу
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код цитировать эту страницу как первоисточник.
Сложение и вычитание дробей. Факты и рабочие таблицы: https://kidskonnect.com — KidsKonnect, 1 июля , 2020Ссылка будет отображаться как Факты и рабочие таблицы сложения и вычитания дробей: https://kidskonnect.com — KidsKonnect, 1 июля 2020 г.
Использование с любой учебной программой
Эти рабочие таблицы были специально разработаны для использования с любыми международными организациями. учебный план. Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
4.5: Сложение и вычитание дробей
Пол и Тони заказывают пиццу, разрезанную на восемь равных ломтиков. Таким образом, каждый кусок составляет 1/8 часть всей пиццы. Пол съедает два ломтика (выделены светло-серым на рис. \ (\ PageIndex {1} \)) или 2/8 всей пиццы. Тони съедает три ломтика (выделены светло-красным (или более темным оттенком серого при черно-белой печати) на рисунке \ (\ PageIndex {1} \)), или 3/8 всей пиццы.
Рисунок \ (\ PageIndex {1} \): Пол съедает два ломтика (2/8), а Тони съедает три ломтика (3/8).Должно быть ясно, что вместе Пол и Тони съедают пять ломтиков или 5/8 всей пиццы. Это отражает тот факт, что
\ [\ frac {2} {8} + \ frac {3} {8} = \ frac {5} {8}. \ Nonumber \]
Это демонстрирует, как сложить две дроби с общим (одинаковым) знаменателем. Сохраните общий знаменатель и сложите числители. То есть
\ [\ begin {align *} \ frac {2} {8} + \ frac {3} {8} & = \ frac {2 + 3} {8} ~ && \ textcolor {red} {\ text {Сохранить знаменатель; добавить числители.}} \\ & = \ frac {5} {8} ~ && \ textcolor {red} {\ text {Упростить числитель.}} \ end {align *} \]
Сложение дробей с общими знаменателями
Пусть a / c и b / c — две дроби с общим (одинаковым) знаменателем. Их сумма определена как
.\ [\ frac {a} {c} + \ frac {b} {c} = \ frac {a + b} {c} \ nonumber \]
То есть, чтобы сложить две дроби, имеющие общие знаменатели, оставить общий знаменатель и сложить их числители.
Аналогичное правило справедливо для вычитания.
Вычитание дробей с общими знаменателями
Пусть a / c и b / c — две дроби с общим (одинаковым) знаменателем. Их разница определяется как
.\ [\ frac {a} {c} — \ frac {b} {c} = \ frac {a-b} {c}. \ Nonumber \]
То есть, чтобы вычесть две дроби, имеющие общие знаменатели, оставить общий знаменатель и вычесть их числители.
Пример \ (\ PageIndex {1} \)
Найдите сумму 4/9 и 3/9.
Решение
Сохраните общий знаменатель и сложите числители.
\ [\ begin {align} \ frac {4} {9} + \ frac {3} {9} & = \ frac {4 + 3} {9} ~ & \ textcolor {red} {\ text {Сохранить знаменатель ; добавить числители.}} \\ & = \ frac {7} {9} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {1} \)
Добавить:
\ [\ frac {1} {8} + \ frac {2} {8} \ nonumber \]
- Ответ
3/8
Пример \ (\ PageIndex {2} \)
Вычтем 5/16 из 13/16.
Решение
Сохраните общий знаменатель и вычтите числители.
\ [\ begin {align} \ frac {13} {16} — \ frac {5} {16} & = \ frac {13-5} {16} ~ & \ textcolor {red} {\ text {Сохранить знаменатель ; вычесть числители.}} \\ & = \ frac {8} {16} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Конечно, как мы узнали в Разделе 4.1, мы всегда должны сводить наш окончательный ответ к минимальным условиям. Один из способов добиться этого в данном случае — разделить числитель и знаменатель на 8, наибольший общий делитель 8 и 16.
\ [\ begin {align} = \ frac {8 \ div 8} {16 \ div 8} ~ & \ textcolor {red} {\ text {Разделите числитель и знаменатель на 8.}} \\ = \ frac {1 } {2} ~ & \ textcolor {red} {\ text {Упростить числитель и знаменатель.}} \ End {align} \ nonumber \]
Упражнение \ (\ PageIndex {2} \)
Вычесть:
\ [\ frac {11} {12} — \ frac {7} {12} \ nonumber \]
- Ответ
1/3
Пример \ (\ PageIndex {3} \)
Упростить:
\ [\ frac {3} {x} — \ left (- \ frac {7} {x} \ right).\ nonumber \]
Решение
Обе дроби имеют общий знаменатель.
\ [\ begin {align} \ frac {3} {x} — \ left (- \ frac {7} {x} \ right) & = \ frac {3} {x} + \ frac {7} {x } ~ & \ textcolor {red} {\ text {Добавьте противоположное.}} \\ & = \ frac {3 + 7} {x} ~ & \ textcolor {red} {\ text {Сохраните знаменатель, добавьте числители.} } \\ & = \ frac {10} {x} ~ & \ textcolor {red} {\ text {Simplify.}} \ end {align} \ nonumber \]
Сложение дробей с разными знаменателями
Рассмотрим сумму
\ [\ frac {4} {9} + \ frac {1} {6}.\ nonumber \]
Мы не можем сложить эти дроби, потому что у них нет общего знаменателя. Так что делать?
Голы
Чтобы сложить две дроби с разными знаменателями, нам нужно:
- Найдите общий знаменатель для данных дробей.
- Составьте дроби с общим знаменателем, которые эквивалентны исходным дробям.
Если мы выполним два пункта в «Цели», мы сможем найти сумму заданных дробей.
Итак, с чего начать? Нам нужно найти общий знаменатель, а не какой-либо общий знаменатель. Согласитесь, мы хотим, чтобы числа были как можно меньше и нашли наименьший общий знаменатель .
Определение: наименьший общий знаменатель
Наименьший общий знаменатель (LCD) для набора дробей — это наименьшее число, которое делится на каждый из знаменателей данных дробей.
Рассмотрим еще раз сумму, которую мы хотим найти:
\ [\ frac {4} {9} + \ frac {1} {6}.\ nonumber \]
Знаменатели — 9 и 6. Мы хотим найти наименьший общий знаменатель, наименьшее число, которое делится как на 9, так и на 6. На ум приходит несколько кандидатов: 36, 54 и 72 делятся на 9 и 6. , назвать несколько. Но наименьшее число, которое делится как на 9, так и на 6, равно 18. Это наименьший общий знаменатель для 9 и 6.
Теперь мы переходим ко второму пункту в «Цели». Нам нужно составить дроби со знаменателем 18, которые эквивалентны 4/9 и 1/6.В случае 4/9, если мы умножим числитель и знаменатель на 2, мы получим
\ [\ begin {align} \ frac {4} {9} & = \ frac {4 \ cdot 2} {9 \ cdot 2} ~ & \ textcolor {red} {\ text {Умножьте числитель и знаменатель на 2. }} \\ & = \ frac {8} {18}. ~ & \ textcolor {red} {\ text {Упростить числитель и знаменатель.}} \ end {align} \ nonumber \]
В случае 1/6, если мы умножим числитель и знаменатель на 3, мы получим
\ [\ begin {align} \ frac {1} {6} & = \ frac {1 \ cdot 3} {6 \ cdot 3} ~ & \ textcolor {red} {\ text {Умножьте числитель и знаменатель на 3.}} \\ & = \ frac {3} {18}. ~ & \ textcolor {red} {\ text {Упростить числитель и знаменатель.}} \ end {align} \ nonumber \]
Обычно мы строим свою работу следующим образом.
\ [\ begin {align} \ frac {4} + \ frac {1} {6} & = \ frac {4 \ cdot \ textcolor {red} {2}} {9 \ cdot \ textcolor {red} {2 }} + \ frac {1 \ cdot \ textcolor {red} {3}} {6 \ cdot \ textcolor {red} {3}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с LCD = 18.} } \\ & = \ frac {8} {18} + \ frac {3} {18} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ & = \ frac {8 + 3} {18} ~ & \ textcolor {red} {\ text {Сохранять общий знаменатель; добавить числители.}} \\ & = \ frac {11} {18} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Подведем итоги процедуры.
Сложение или вычитание дробей с разными знаменателями
- Найдите на ЖК-дисплее наименьшее число, делящееся на все знаменатели данной дроби.
- Создайте дроби, используя ЖК-дисплей в качестве знаменателя, которые эквивалентны исходным дробям.
- Сложите или вычтите полученные эквивалентные дроби. Упростите, включая сокращение окончательного ответа до самых низких терминов.
Пример \ (\ PageIndex {4} \)
Упростить: \ (\ displaystyle \ frac {3} {5} — \ frac {2} {3} \).
Решение
Наименьшее число, которое делится как на 5, так и на 3, равно 15.
\ [\ begin {align} \ frac {3} {5} — \ frac {2} {3} & = \ frac {3 \ cdot \ textcolor {red} {3}} {5 \ cdot \ textcolor {красный } {3}} — \ frac {2 \ cdot \ textcolor {red} {5}} {3 \ cdot \ textcolor {red} {5}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с LCD = 15.}} \\ & = \ frac {9} {15} — \ frac {10} {15} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ & = \ frac {9- 10} {15} ~ & \ textcolor {red} {\ text {Сохранить ЖК-дисплей; вычесть числители.}} \\ & = \ frac {-1} {15} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Хотя этот ответ вполне приемлем, отрицательный, разделенный на положительный, дает нам отрицательный ответ, поэтому мы также можем написать
\ [= — \ frac {1} {15}. \ Nonumber \]
Упражнение \ (\ PageIndex {4} \)
Вычесть:
\ [\ frac {3} {4} — \ frac {7} {5} \ nonumber \]
- Ответ
-13/20
Пример \ (\ PageIndex {5} \)
Упростить: \ (- \ frac {1} {4} — \ frac {5} {6} \).
Решение
Наименьшее число, которое делится как на 4, так и на 6, равно 12.
\ [\ begin {align} — \ frac {1} {4} — \ frac {5} {6} & = — \ frac {1 \ cdot \ textcolor {red} {3}} {4 \ cdot \ textcolor {red} {3}} — \ frac {5 \ cdot \ textcolor {red} {2}} {6 \ cdot \ textcolor {red} {2}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с LCD = 12.}} \\ & = — \ frac {3} {12} — \ frac {10} {12} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ & = \ frac {-3-10} {12} ~ & \ textcolor {red} {\ text {Сохранить ЖК-дисплей; вычесть числители.}} \\ & = \ frac {-13} {12} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {5} \)
Вычесть: \ (- \ frac {3} {8} — \ frac {1} {12} \)
- Ответ
-11/24
Пример \ (\ PageIndex {6} \)
Упростить: \ (\ frac {5} {x} + \ frac {3} {4} \).
Решение
Наименьшее число, которое делится как на 4, так и на x, равно 4x.
\ [\ begin {align} \ frac {5} {x} + \ frac {3} {4} = \ frac {5 \ cdot \ textcolor {red} {4}} {x \ cdot \ textcolor {красный} {4}} + \ frac {3 \ cdot \ textcolor {red} {x}} {4 \ cdot \ textcolor {red} {x}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с ЖК-дисплеем =} 4x.} \\ = = \ frac {20} {4x} + \ frac {3x} {4x} ~ & \ textcolor {red} {\ text {Упростить числители и знаменатели.}} \\ = \ frac {20 + 3x} {4x} ~ & \ textcolor {red} {\ text {Сохранить ЖК-дисплей; добавить числители.}} \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {6} \)
Добавить:
\ [\ frac {5} {z} + \ frac {2} {3} \ nonumber \]
- Ответ
\ [\ frac {15 + 2z} {3z} \ nonumber \]
Пример \ (\ PageIndex {7} \)
Упростить: \ (\ frac {2} {3} — \ frac {x} {5} \).
Решение
Наименьшее число, которое делится как на 3, так и на 5, равно 15.
\ [\ begin {align} \ frac {2} {3} — \ frac {x} {5} = \ frac {2 \ cdot \ textcolor {red} {5}} {3 \ cdot \ textcolor {red} {5}} — \ frac {x \ cdot \ textcolor {red} {3}} {5 \ cdot \ textcolor {red} {3}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с LCD = 15 .}} \\ = \ frac {10} {15} — \ frac {3x} {15} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ = \ frac {10 — 3x } {15} ~ & \ textcolor {red} {\ text {Сохранить ЖК-дисплей; вычесть числители.}} \ конец {выровнено} \ nonumber \]
Наименьшее общее кратное
Сначала мы определяем число, кратное числу.
Определение: кратное
, кратные числа d : 1 d , 2 d , 3 d , 4 d и т. Д. То есть, кратные d — это числа nd , где n — натуральное число.
Например, число, кратное 8, равно 1 · 8, 2 · 8, 3 · 8, 4 · 8 и т. Д., или эквивалентно 8, 16, 24, 32 и т. д.
Определение: наименьшее общее кратное
Наименьшее общее кратное (НОК) набора чисел — это наименьшее число, кратное каждому числу данного набора. Процедура поиска LCM следующая:
- Список всех кратных каждого числа в данном наборе чисел.
- Перечислите общие кратные.
- Выберите наименьшее из общих кратных.
Пример \ (\ PageIndex {7} \)
Найдите наименьшее общее кратное чисел 12 и 16.
Решение
Перечислите числа, кратные 12 и 16.
, кратное 12:12, 24, 36, 48, 60, 72, 84, 96, …
, кратное 16:16, 32, 48, 64, 80, 96, 112, …
Выберите общие кратные.
Общие кратные: 48, 96, …
НОК — наименьшее из общих кратных.
НОК (12,16) = 48
Упражнение \ (\ PageIndex {7} \)
Найдите наименьший общий знаменатель 6 и 9.
- Ответ
18
Важное замечание
наименьший общий знаменатель — это наименьшее общее кратное знаменателей.
Например, предположим, что ваша проблема — 5/12 + 5/16. ЖК-дисплей — это наименьшее число, которое делится как на 12, так и на 16. Это число равно 48, что также является НОК 12 и 16. Следовательно, процедура поиска НОК также может использоваться для поиска ЖК-дисплея.
Наименьшее общее кратное с использованием простого множителя
Вы также можете найти НОК, используя разложение на простые множители.
LCM методом простой факторизации
Чтобы найти НОК для набора чисел, выполните следующую процедуру:
- Запишите факторизацию на простые множители для каждого числа в компактной форме, используя экспоненты.
- НОК находится путем записи каждого множителя, который появляется на шаге 1, в наивысшую степень этого множителя.
Пример \ (\ PageIndex {8} \)
Используйте разложение на простые множители, чтобы найти наименьшее общее кратное, найдите наименьший общий знаменатель 18 и 24.1 = 3.} \\ = 48. ~ & \ textcolor {red} {\ text {Умножить.}} \ End {align} \ nonumber \]
Обратите внимание, что этот ответ идентичен НОК, найденному в Примере 8, который был найден путем перечисления кратных и выбора наименьшего общего кратного.
Упражнение \ (\ PageIndex {8} \)
Используйте разложение на простые множители, чтобы найти наименьший общий знаменатель чисел 18 и 24.
- Ответ
72
Пример \ (\ PageIndex {10} \)
Упростить: \ (\ frac {5} {28} + \ frac {11} {42} \).
Решение
Пространство знаменателей в компактной форме с использованием экспонент.
28 = 2 · 2 · 7 = 2 92 · 104 2 92 · 105 · 7
42 = 2 · 3 · 7 = 2 1 · 3 1 · 7 1
Чтобы найти ЖК-дисплей, запишите каждый коэффициент, который появляется в наибольшей степени этого коэффициента. Появляются множители 2, 3 и 7. Наивысшая степень двойки равна 2 2 . Наивысшая степень 3, которая появляется, равна 3 1 .1 = 7.} \\ = 84 ~ & \ textcolor {red} {\ text {Умножить.}} \ End {align} \ nonumber \]
Создайте эквивалентные дроби с новым ЖК-дисплеем, затем сложите.
\ [\ begin {align} \ frac {5} {28} + \ frac {11} {42} = \ frac {5 \ cdot \ textcolor {red} {3}} {28 \ cdot \ textcolor {red} {3}} + \ frac {11 \ cdot \ textcolor {red} {2}} {42 \ cdot \ textcolor {red} {2}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с LCD = 84 .}} \\ = \ frac {15} {84} + \ frac {22} {84} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ = \ frac {37} {84} ~ & \ textcolor {red} {\ text {Сохранить ЖК-дисплей; добавить числители.}} \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {10} \)
Упростить: \ (\ frac {5} {24} + \ frac {5} {36} \)
- Ответ
25/72
Пример \ (\ PageIndex {11} \)
Упростить: \ (- \ frac {11} {24} — \ frac {1} {18} \).
Решение
Пространство знаменателей в компактной форме с использованием экспонент.2 = 9.} \\ = 72. ~ & \ textcolor {red} {\ text {Умножить.}} \ End {align} \ nonumber \]
Создайте эквивалентные дроби с новым ЖК-дисплеем, затем вычтите.
\ [\ begin {align} — \ frac {11} {24} — \ frac {1} {18} = — \ frac {11 \ cdot \ textcolor {red} {3}} {24 \ cdot \ textcolor { red} {3}} — \ frac {1 \ cdot \ textcolor {red} {4}} {18 \ cdot \ textcolor {red} {4}} ~ & \ textcolor {red} {\ text {Эквивалентные дроби с ЖК-дисплеем = 72.}} \\ = — \ frac {33} {72} — \ frac {4} {72} ~ & \ textcolor {red} {\ text {Упростите числители и знаменатели.}} \\ = \ frac {-33-4} {72} ~ & \ textcolor {красный} {\ text {Сохранить ЖК-дисплей; вычесть числители.}} \\ = \ frac {-37} {72} ~ & \ textcolor {red} {\ text {Упростить числитель.}} \ end {align} \ nonumber \]
Конечно, отрицательный, деленный на положительный, дает отрицательный ответ, поэтому мы также можем записать наш ответ в форме
.\ [- \ frac {11} {24} — \ frac {1} {18} = — \ frac {37} {72}. \ Nonumber \]
Упражнение \ (\ PageIndex {11} \)
Упростить: \ (- \ frac {5} {24} — \ frac {11} {36} \)
- Ответ
−37/72
Сравнение дробей
Самый простой способ сравнить дроби — создать эквивалентные дроби.
Пример \ (\ PageIndex {12} \)
Расположите дроби −1/2 и −4/5 в числовой строке, затем сравните их, используя соответствующий символ неравенства.
Решение
Наименьший общий знаменатель для 2 и 5 — это число 10. Сначала составьте эквивалентные дроби с ЖК-дисплеем, равным 10.
\ [\ begin {array} {c} — \ frac {1} {2} = — \ frac {1 \ cdot \ textcolor {red} {5}} {2 \ cdot \ textcolor {red} {5}} = — \ frac {5} {10} \\ — \ frac {4} {5} = — \ frac {4 \ cdot \ textcolor {red} {2}} {5 \ cdot \ textcolor {red} {2} } = — \ frac {8} {10} \ end {array} \ nonumber \]
Чтобы отобразить десятые доли, разделите интервал между -1 и 0 на десять равных приращений.
Поскольку −4/5 лежит слева от −1/2, мы имеем, что −4/5 меньше −1/2, поэтому мы пишем
\ [- \ frac {4} {5} <- \ frac {1} {2}. \ Nonumber \]
Упражнение \ (\ PageIndex {12} \)
Сравните −3/8 и −1/2.
- Ответ
\ [- \ frac {1} {2} <- \ frac {3} {8} \ nonumber \]
Упражнения
В упражнениях 1–10 перечислите кратные заданным числам, а затем перечислите общие кратные.Выберите LCM из списка общих кратных.
1. 9 и 15
2. 15 и 20
3. 20 и 8
4. 15 и 6
5. 16 и 20
6. 6 и 10
7. 20 и 12
8. 12 и 8
9. 10 и 6
10. 10 и 12
В упражнениях 11-20 для заданных чисел вычислите НОК, используя разложение на простые множители.
11. 54 и 12
12. 108 и 24
13.18 и 24
14. 36 и 54
15. 72 и 108
16. 108 и 72
17. 36 и 24
18. 18 и 12
19. 12 и 18
20. 12 и 54
В упражнениях 21-32 сложите или вычтите дроби, как показано, и упростите свой результат.
21. \ (\ frac {7} {12} — \ frac {1} {12} \)
22. \ (\ frac {3} {7} — \ frac {5} {7} \)
23. \ (\ frac {1} {9} + \ frac {1} {9} \)
24. \ (\ frac {1} {7} + \ frac {3} {7} \)
25.\ (\ frac {1} {5} — \ frac {4} {5} \)
26. \ (\ frac {3} {5} — \ frac {2} {5} \)
27. \ (\ frac {3} {7} — \ frac {4} {7} \)
28. \ (\ frac {6} {7} — \ frac {2} {7} \)
29. \ (\ frac {4} {11} + \ frac {9} {11} \)
30. \ (\ frac {10} {11} + \ frac {4} {11} \)
31. \ (\ frac {3} {11} + \ frac {4} {11} \)
32. \ (\ frac {3} {7} + \ frac {2} {7} \)
В упражнениях 33–56 сложите или вычтите дроби, как показано, и упростите свой результат.
33.\ (\ frac {1} {6} — \ frac {1} {8} \)
34. \ (\ frac {7} {9} — \ frac {2} {3} \)
35. \ (\ frac {1} {5} + \ frac {2} {3} \)
36. \ (\ frac {7} {9} + \ frac {2} {3} \)
37. \ (\ frac {2} {3} + \ frac {5} {8} \)
38. \ (\ frac {3} {7} + \ frac {5} {9} \)
39. \ (\ frac {4} {7} — \ frac {5} {9} \)
40. \ (\ frac {3} {5} — \ frac {7} {8} \)
41. \ (\ frac {2} {3} — \ frac {3} {8} \)
42. \ (\ frac {2} {5} — \ frac {1} {8 \)
43. \ (\ frac {6} {7} — \ frac {1} {6} \)
44.\ (\ frac {1} {2} — \ frac {1} {4} \)
45. \ (\ frac {1} {6} + \ frac {2} {3} \)
46. \ (\ frac {4} {9} + \ frac {7} {8} \)
47. \ (\ frac {7} {9} + \ frac {1} {8} \)
48. \ (\ frac {1} {6} + \ frac {1} {7} \)
49. \ (\ frac {1} {3} + \ frac {1} {7} \)
50. \ (\ frac {5} {6} + \ frac {1} {4} \)
51. \ (\ frac {1} {2} — \ frac {2} {7} \)
52. \ (\ frac {1} {3} — \ frac {1} {8} \)
53. \ (\ frac {5} {6} — \ frac {4} {5} \)
54. \ (\ frac {1} {2} — \ frac {1} {9} \)
55.\ (\ frac {1} {3} + \ frac {1} {8} \)
56. \ (\ frac {1} {6} + \ frac {7} {9} \)
В упражнениях 57-68 сложите или вычтите дроби, как указано, сначала применив разложение на простые множители, чтобы найти наименьший общий знаменатель.
57. \ (\ frac {7} {36} + \ frac {11} {54} \)
58. \ (\ frac {7} {54} + \ frac {7} {24} \)
59. \ (\ frac {7} {18} — \ frac {5} {12} \)
60. \ (\ frac {5} {54} — \ frac {7} {12} \)
61. \ (\ frac {7} {36} + \ frac {7} {54} \)
62.\ (\ frac {5} {72} + \ frac {5} {108} \)
63. \ (\ frac {7} {24} — \ frac {5} {36} \)
64. \ (\ frac {11} {54} + \ frac {7} {72} \)
65. \ (\ frac {11} {12} + \ frac {5} {18} \)
66. \ (\ frac {11} {24} + \ frac {11} {108} \)
67. \ (\ frac {11} {54} — \ frac {5} {24} \)
68. \ (\ frac {7} {54} — \ frac {5} {24} \)
В упражнениях 69–80 сложите или вычтите дроби, как показано, и упростите свой результат.
69. \ (\ frac {−3} {7} + \ left (\ frac {−3} {7} \ right) \)
70.\ (\ frac {−5} {9} + \ left (\ frac {−1} {9} \ right) \)
71. \ (\ frac {7} {9} — \ left (\ frac {−1} {9} \ right) \)
72. \ (\ frac {8} {9} — \ left (\ frac {−4} {9} \ right) \)
73. \ (\ frac {7} {9} + \ left (\ frac {−2} {9} \ right) \)
74. \ (\ frac {2} {3} + \ left (\ frac {−1} {3} \ right) \)
75. \ (\ frac {−3} {5} — \ frac {4} {5} \)
76. \ (\ frac {−7} {9} — \ frac {1} {9} \)
77. \ (\ frac {−7} {8} + \ frac {1} {8} \)
78. \ (\ frac {−2} {3} + \ (\ frac {1} {3} \)
79.\ (\ frac {−1} {3} — \ left (\ frac {−2} {3} \ right) \)
80. \ (\ frac {−7} {8} — \ left (\ frac {−5} {8} \ right) \)
В упражнениях 81-104 сложите или вычтите дроби, как показано, и упростите свой результат.
81. \ (\ frac {−2} {7} \) + \ frac {4} {5} \)
82. \ (\ frac {−1} {4} + \ frac {2} {7} \)
83. \ (\ frac {−1} {4} — \ left (\ frac {−4} {9} \ right) \)
84. \ (\ frac {−3} {4} −left (\ frac {−1} {8} \ right) \)
85. \ (\ frac {−2} {7} + \ frac {3} {4} \)
86.\ (\ frac {−1} {3} + \ frac {5} {8} \)
87. \ (\ frac {−4} {9} — \ frac {1} {3} \)
88. \ (\ frac {−5} {6} — \ frac {1} {3} \)
89. \ (\ frac {−5} {7} — \ left (\ frac {−1} {5} \ right) \)
90. \ (\ frac {−6} {7} — \ left (\ frac {−1} {8} \ right) \)
91. \ (\ frac {1} {9} + \ left (\ frac {−1} {3} \ right) \)
92. \ (\ frac {1} {8} + \ left (\ frac {−1} {2} \ right) \)
93. \ (\ frac {2} {3} + \ left (\ frac {−1} {9} \ right) \)
94. \ (\ frac {3} {4} + \ left (\ frac {−2} {3} \ right) \)
95.\ (\ frac {−1} {2} + \ left (\ frac {−6} {7} \ right) \)
96. \ (\ frac {−4} {5} + \ left (\ frac {−1} {2} \ right) \)
97. \ (\ frac {−1} {2} + \ left (\ frac {−3} {4} \ right) \)
98. \ (\ frac {−3} {5} + \ left (\ frac {−1} {2} \ right) \)
99. \ (\ frac {−1} {4} — \ frac {1} {2} \)
100. \ (\ frac {−8} {9} — \ frac {2} {3} \)
101. \ (\ frac {5} {8} — \ left (\ frac {−3} {4} \ right) \)
102. \ (\ frac {3} {4} — \ left (\ frac {−3} {8} \ right) \)
103. \ (\ frac {1} {8} — \ left (\ frac {−1} {3} \ right) \)
104.\ (\ frac {1} {2} — \ left (\ frac {−4} {9} \ right) \)
В упражнениях 105–120 сложите или вычтите дроби, как указано, и запишите свой ответ в виде наименьших членов.
105. \ (\ frac {1} {2} + \ frac {3q} {5} \)
106. \ (\ frac {4} {7} — \ frac {b} {3} \)
107. \ (\ frac {4} {9} — \ frac {3a} {4} \)
108. \ (\ frac {4} {9} — \ frac {b} {2} \)
109. \ (\ frac {2} {s} + \ frac {1} {3} \)
110. \ (\ frac {2} {s} + \ frac {3} {7} \)
111. \ (\ frac {1} {3} — \ frac {7} {b} \)
112.\ (\ frac {1} {2} — \ frac {9} {s} \)
113. \ (\ frac {4b} {7} + \ frac {2} {3} \)
114. \ (\ frac {2a} {5} + \ frac {5} {8} \)
115. \ (\ frac {2} {3} — \ frac {9} {t} \)
116. \ (\ frac {4} {7} — \ frac {1} {y} \)
117. \ (\ frac {9} {s} + \ frac {7} {8} \)
118. \ (\ frac {6} {t} — \ frac {1} {9} \)
119. \ (\ frac {7b} {8} — \ frac {5} {9} \)
120. \ (\ frac {3p} {4} — \ frac {1} {8} \)
В упражнениях 121–132 определите, какое из двух утверждений истинно.
121. \ (\ frac {−2} {3} <\ frac {−8} {7} \) или \ (\ frac {- 2} {3}> \ frac {−8} {7} \)
122. \ (\ frac {−1} {7} <\ frac {−8} {9} \) или \ (\ frac {- 1} {7}> \ frac {−8} {9} \)
123. \ (\ frac {6} {7} <\ frac {7} {3} \) или \ (\ frac {6} {7}> \ frac {7} {3} \)
124. \ (\ frac {1} {2} <\ frac {2} {7} \) или \ (\ frac {1} {2}> \ frac {2} {7} \)
125. \ (\ frac {−9} {4} <\ frac {−2} {3} \) или \ frac {- 9} {4}> \ frac {−2} {3} \)
126. \ (\ frac {−3} {7} <\ frac {−9} {2} \) или \ (\ frac {- 3} {7}> \ frac {−9} {2} \)
127.\ (\ frac {5} {7} <\ frac {5} {9} \) или \ frac {5} {7}> \ frac {5} {9} \)
128. \ (\ frac {1} {2} <\ frac {1} {3} \) или \ (\ frac {1} {2}> \ frac {1} {3} \)
129. \ (\ frac {−7} {2} <\ frac {−1} {5} \) или \ (\ frac {- 7} {2}> \ frac {−1} {5} \)
130. \ (\ frac {−3} {4} <\ frac {−5} {9} \) или \ (\ frac {- 3} {4}> \ frac {−5} {9} \)
131. \ (\ frac {5} {9} <\ frac {6} {5} \) или \ (\ frac {5} {9}> \ frac {6} {5} \)
132. \ (\ frac {3} {2} <\ frac {7} {9} \) или \ (\ frac {3} {2}> \ frac {7} {9} \)
Ответы
1.45
3. 40
5. 80
7. 60
9. 30
11. 108
13. 72
15 216
17. 72
19. 36
21. \ (\ frac {1} {2} \)
23. \ (\ frac {2} {9} \)
25. \ (\ frac {−3} {5} \)
27. \ (\ frac {−1} {7} \)
29. \ (\ frac {13} {11} \)
31. \ (\ frac {7} {11} \)
33. \ (\ frac {1} {24} \)
35. \ (\ frac {13} {15} \)
37.\ (\ frac {31} {24} \)
39. \ (\ frac {1} {63} \)
41. \ (\ frac {7} {24} \)
43. \ (\ frac {29} {42} \)
45. \ (\ frac {5} {6} \)
47. \ (\ frac {65} {72} \)
49. \ (\ frac {10} {21} \)
51. \ (\ frac {3} {14} \)
53. \ (\ frac {1} {30} \)
55. \ (\ frac {11} {24} \)
57. \ (\ frac {43} {108} \)
59. \ (\ frac {−1} {36} \)
61. \ (\ frac {35} {108} \)
63. \ (\ frac {11} {72} \)
65.\ (\ frac {43} {36} \)
67. \ (\ frac {−1} {216} \)
69. \ (\ frac {−6} {7} \)
71. \ (\ frac {8} {9} \)
73. \ (\ frac {5} {9} \)
75. \ (\ frac {- 7} {5} \)
77. \ (\ frac {- 3} {4} \)
79. \ (\ frac {1} {3} \)
81. \ (\ frac {18} {35} \)
83. \ (\ frac {7} {36} \)
85. \ (\ frac {13} {28} \)
87. \ (\ frac {- 7} {9} \)
89. \ (\ frac {−18} {35} \)
91. \ (\ frac {- 2} {9} \)
93.\ (\ frac {5} {9} \)
95. \ (\ frac {−19} {14} \)
97. \ (\ frac {- 5} {4} \)
99. \ (\ frac {- 3} {4} \)
101. \ (\ frac {11} {8} \)
103. \ (\ frac {11} {24} \)
105. \ (\ frac {5 + 6 q} {10} \)
107. \ (\ frac {16–27 a} {36} \)
109. \ (\ frac {6 + s} {3 s} \)
111. \ (\ frac {b — 21} {3b} \)
113. \ (\ frac {12 b + 14} {21} \)
115. \ (\ frac {2 t — 27} {3t} \)
117. \ (\ frac {72 + 7 s} {8 s} \)
119.\ (\ frac {63 b — 40} {72} \)
121. \ (\ frac {- 2} {3}> \ (\ frac {- 8} {7} \)
123. \ (\ frac {6} {7} <\ frac {7} {3} \)
125. \ (\ frac {- 9} {4} <\ frac {- 2} {3} \)
127. \ (\ frac {5} {7}> \ frac {5} {9} \)
129. \ (\ frac {- 7} {2} <\ frac {- 1} {5} \)
131. \ (\ frac {5} {9} <\ frac {6} {5} \)
Вычитание дробей с помощью Монтессори | Магазин Монтессори Ресурсы, для 6-12 начальной школы на дому и классных комнат
Вычитание дробей
Урок — ТО ЖЕ ЗНАЧИТЕЛИ
Перед этим уроком студентам потребуется
- введены для сложения дробей с тем же знаменателем
1) Имейте несколько карточек задач с различными уравнениями вычитания дробей на них
2) Иметь кусочки фракции Монтессори (лучше всего подходит коробка с разными частями)
3) Поместите 7/8 в рамку.Убедитесь, что ученики знают, что вы вложили восьмые. Затем удалите две восьмых. Представьте уравнение. Спросите: «Сколько восьмых осталось?» Напишите ответ.
4) Попросите учащихся записать и, если презентация проводится в группе, объясните своему партнеру, что делать, чтобы решить подобное уравнение.
5) Повторите, используя дробные уравнения, и попросите учащихся записать ответы в свои книги
Урок — В ОТНОШЕНИИ ДЕНОМИНАТОРОВ
До этого урока ученики должны были
- быть очень уверенным с эквивалентными дробями
1) Выходи 4/6.Выходи 1/3. Напишите уравнение 4/6 — 1/3
2) Обсудите, чем отличаются знаменатели. Спросите, знает ли кто-нибудь, как можно вычесть эти два числа. Подскажите учащимся об эквивалентных дробях. Если необходимо, покажите, как 1/3 покрывает 2/6, это должно означать, что это эквивалентно
3) Скажем, вопрос можно перефразировать как 4/6 вычесть 2/6
4) Ответ — 2/6.
5) Попросите учащихся записать и, если презентация проводится в группе, объясните своему партнеру, что делать, чтобы решить подобное уравнение.
6) Используйте вычитание дробных билетов и задайте больше вопросов.
____
Урок — ИЗМЕНЕНИЕ ОБОИХ ДЕНОМИНАТОРОВ
1) Запишите вопрос 1/2 — 2/5
2) Достаем дробные круги. Обсудите, как, как и в других вопросах, которые задал ребенок, у этих дробей разные знаменатели. Что мы делали раньше в этом случае?
3) Спросите, можем ли мы превратить 1/2 в пятые (Нет) Можем ли мы превратить 2/5 в половинки (Нет)
4) Придется поменять обе дроби.Спросите студентов, знают ли они общее кратное 2 и 5 (10). Давайте превратим все дроби в это уравнение в десятые.
5) 1/2 — это сколько десятых? (5) 2/5 — это сколько десятых (4)
6) 5/10 — 4/10 равно 1/10
7) Попросите учащихся записать и, если презентация проводится в группе, объясните своему партнеру, что делать, чтобы решить такое уравнение
8) Используйте вычитание дробных билетов, чтобы решить больше вопросов.
Легко готово к использованию вычитание дробных билетов для использования при обучении
Не забудьте также проверить
Обучение неправильным дробям с помощью Монтессори
Обучение дробям с игрой со штампом Монтессори
Сложение дробей с помощью Монтессори
Заинтересованы в дополнительных ресурсах по учебной программе Монтессори? Найдите их здесь
Вы можете присоединиться к моему списку рассылки, чтобы получать больше ресурсов Монтессори, уведомления о новых продуктах и новости здесь
. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;

 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.  Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.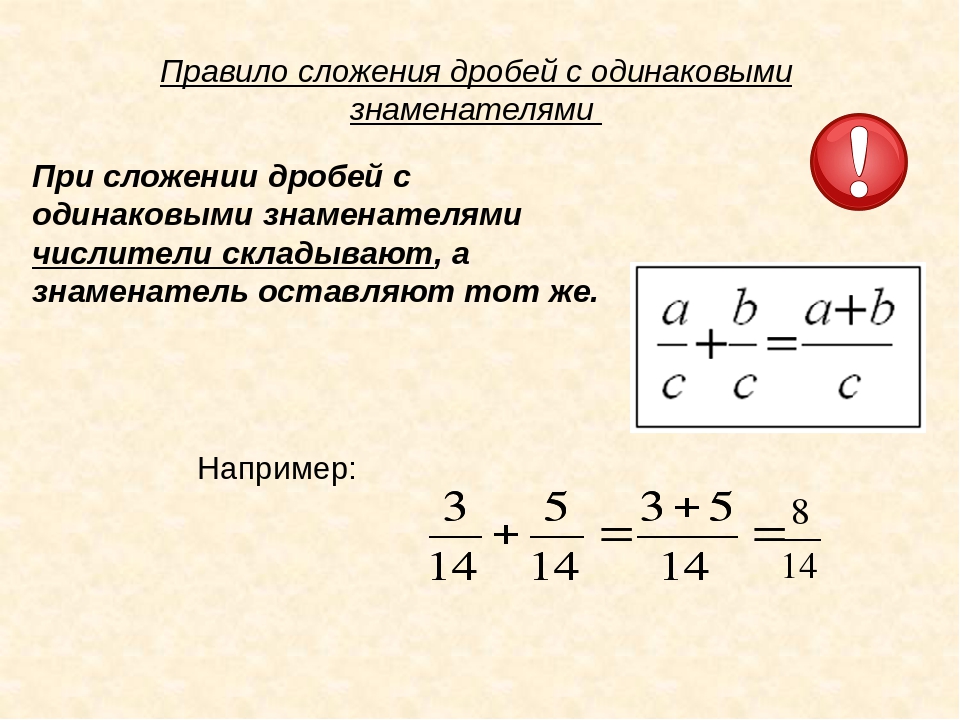 С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Теперь Ахиллес на восемьсот шагов опережает черепаху. 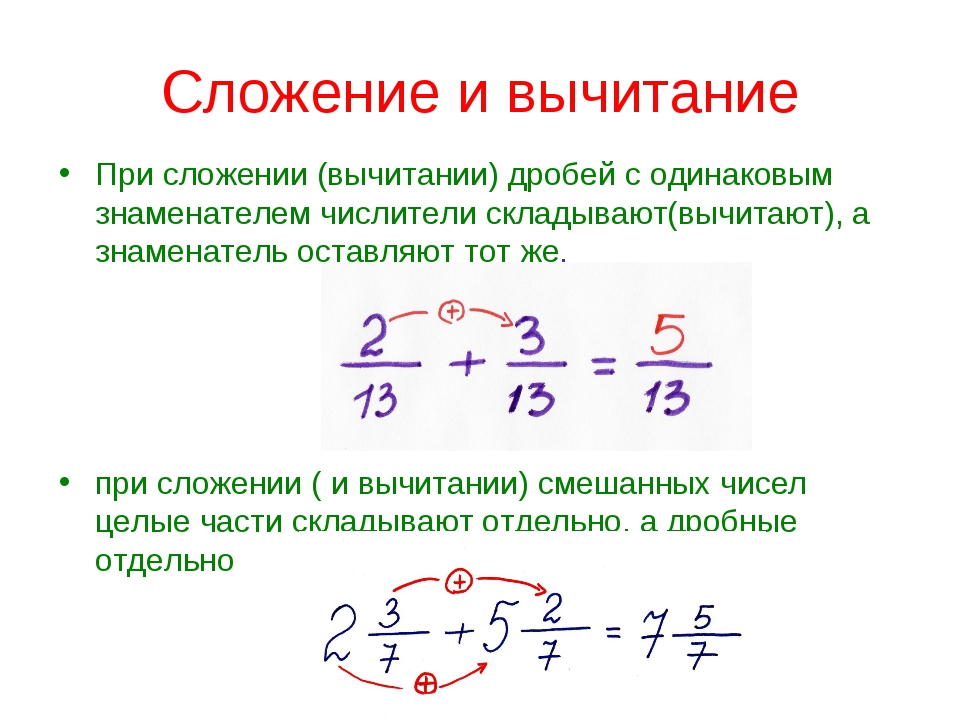 Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.

 Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет? Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения: Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы: В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6 Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца: В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы). Найти значение выражения .
Найти значение выражения . Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители  Выделяем:
Выделяем: Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы: В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью: Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю): Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью: Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке: Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
 Выделим в ней целую часть:
Выделим в ней целую часть:
 Для этого достаточно перевернуть её.
Для этого достаточно перевернуть её. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.

 В зависимости от типа выражения переходим к алгоритму решения.
В зависимости от типа выражения переходим к алгоритму решения.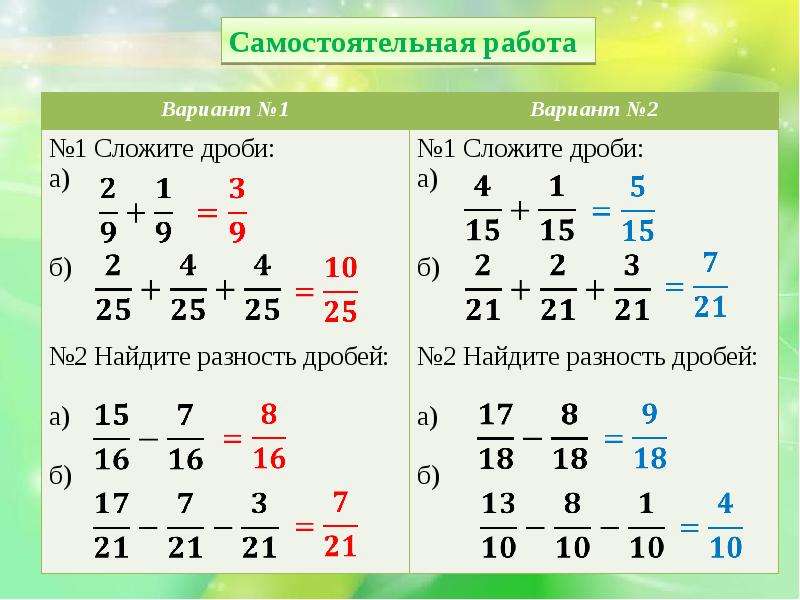
 Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
 Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например: Здесь обнаружатся новые грабли, да…
Здесь обнаружатся новые грабли, да…