Урок Сложение и вычитание дробей с одинаковыми знаменателями
Просмотр содержимого документа
«Технологич. карта матем»
Технологическая карта урока
Ф.И.О. учителя | Скосырева Лилия Васильевна |
Предмет | Математика |
Класс | 5 класс |
Тип урока | Урок «открытия новых знаний» |
Тема урока | «Сложение и вычитание дробей с одинаковыми знаменателями» |
Цель урока | Содержательная: создание условий для формирования правила сложения и вычитания дробей с одинаковыми знаменателями, обеспечение понимания учащимися правила с помощью практических заданий. Деятельностная: выполнение системы упражнений, которые позволят учащимся самостоятельно сформулировать правило сложения и вычитания дробей с одинаковыми знаменателями, формировать навыки по выполнению сложения и вычитания дробей с одинаковыми знаменателями, а также умения решать задачи на сложение и вычитание дробей с одинаковыми знаменателями. Развивающая: формировать ключевые компетенции учащихся: — информационную (умение анализировать информацию и переводить ее из одной формы в другую) — учебно-познавательную (умение осуществлять мыслительные операции: синтез, обобщение, классификация, систематизация) — коммуникативную (умение осуществлять взаимодействие с окружающими и владеть разными социальными ролями) |
Задачи урока | образовательные: актуализировать знания об обыкновенных дробях; ввести и сформулировать правила сложения и вычитания дробей с одинаковыми знаменателями. развивающие: создать условия для развития внимания, инициативы, воображения; вести работу по развитию математической речи, логического мышления; формировать умение анализировать, находить ошибки, делать выводы. воспитательные: содействовать формированию взаимоуважения, умения отстаивать своё мнение, интереса к урокам математики. |
Планируемые результаты | личностные – проявляют устойчивый и широкий интерес к новой теме и к изучению предмета; метапредметные регулятивные – обнаруживают проблему « недостатка» знаний для выполнения действия сложения и вычитания дробей с одинаковыми знаменателями познавательные — учатся осуществлять выбор наиболее эффективных способов решения образовательных задач; коммуникативные – умеют слушать других, учатся критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его. |
Формы организации образовательного пространства на уроке | Фронтальная беседа с учащимися; работа с учебником; самостоятельная работа с последующей взаимопроверкой. |
Риски | Тема урока не заинтересует учащихся. Могут возникнуть трудности при проверке работы товарища; не получится планируемая дискуссия при обсуждении ошибок самостоятельной работы. |
Средства обучения | 1. Учебник: Математика: 5 кл.: учебник для общеобразовательных учреждений / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. − М.: Вентана-Граф, 2014. 2. Технологическая карта урока. 3. Компьютер и мультимедийный проектор. Презентация по теме урока. |
СТРУКТУРА И ХОД УРОКА
Этап урока | Микроцель | Деятельность учителя | Деятельность учащихся | Планируемые результаты |
1. | Создание положительного эмоционального настроя в классе. | Приветствует учащихся. | Приветствуют учителя, настраиваются на работу. | Включение учащихся в деловой ритм урока. |
2.Проверка домашнего задания. | Актуализация опорных знаний и способов действий. Проверка усвоение учащимися предыдущей темы. | Координирует деятельность учащихся. | Взаимопроверка д/з в парах по ключам, лежащим на каждой парте. | познавательные: уметь анализировать объекты в ходе проверки домашнего задания личностные: самоопределение (умение выделять нравственный аспект поведения), смыслообразование (учебная мотивация) |
3. Устная работа (этап мотивации) | Заинтересовать учащихся. Подвести к формулированию темы урока и цели. | Ребята, мы продолжаем работать с обыкновенными дробями и предлагаю вам проверить свои знания по темам прошлых уроков при выполнении устных упражнений: Слайд 4 презентации
Слайд 5 презентации
Сравните (учебник стр. Слайд 6 презентации Расположите дроби в порядке возрастания: Слайд 7 презентации Предложен ряд чисел: ,,,2, , 5, , 7, , , . Разбейте числа на группы по определенным признакам. Вспомните, какие простейшие операции мы умеем выполнять над натуральными числами. (учебник стр.188 № 4,№ 5): 4)Из суммы чисел 19 и 23 вычесть 34. 5). К сумме чисел 18 и 16 прибавьте их разность. После проведения проверки результатов: «А если у нас будут две обыкновенные дроби можно ли с ними выполнить те же самые арифметические действия? Ведь у нас не всегда в жизни бывают только натуральные числа. Как же быть с дробями?» Учащимся предлагается выдвинуть предположение о теме урока, поставить цель урока: Слайд 8 презентации Запись на доске и тетрадях: число и тему урока «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». | 1.Участвуют в работе по повторению, в беседе с учителем отвечают на поставленные вопросы: — дают ответы на поставленные вопросы; — читают и определяют название дробей; — сравнивают дроби; — располагают числа в порядке возрастания (осуществляют сравнение дробей) — разбивают числа на группы: правильные и неправильные дроби, натуральные числа; — выделяют группу натуральных чисел; — называют операции сложение и вычитание; взаимодействуют с учителем во время устного счета, контролируют правильность ответов. 2. Постановка проблемы: выдвигают предположение о теме урока. Формулируют тему урока, цель урока. | познавательные: — развитие умения проводить наблюдения и делать самостоятельные выводы; — развитие умения применять полученные знания при решении примеров; коммуникативные : — формирование умения работать в коллективе: умение слушать и слышать, — отстаивать своё мнение; — признавать свои ошибки; регулятивные: — учить детей контролировать свою речь при выражении своей точки зрения по заданной тематике; — учить самостоятельно оценивать свои мысли и высказывания. личностные: мотивация к обучению и целенаправленной познавательной деятельности. |
4.Работа по новой теме : а)этап построения проекта выхода из затруднения; б) этап первичного закрепления; в) этап самостоятельной работы. | Сформулировать правило сложения и вычитания дробей с одинаковыми знаменателями, показать на примерах, как выполнять сложение и вычитание дробей с одинаковыми знаменателями. Сформировать умение складывать и вычитать дроби с одинаковым знаменателем. Выявление первичного осмысления изучаемого материала, коррекция выявленных пробелов, обеспечение усвоения алгоритма выполнения заданий по теме. | Дробные числа, как и натуральные числа, можно складывать и вычитать. Проблемная ситуация. Вы все знаете Тома Сойера, главного героя произведения М. Твена «Приключения Тома Сойера»,— веселого и сообразительного мальчишку, которому неведома скука, потому что ему ничего не стоит тут же придумать какую-нибудь шалость или увлекательное занятие, чтобы скоротать свободное время. Слайд 10 презентации Тому Сойеру необходимо покрасить забор из 9 досок. Он покрасил 2 доски забора, а после «уступил» это занятие другим мальчикам, которые покрасили 5 досок забора. Какую часть забора они покрасили вместе? Оказалось, что покрасили забора. Тогда можно сделать вывод, что + = = Продолжается исследование материала. Слайд 11 презентации Какую часть забора осталось покрасить? — = = Учитель организует работу по составлению алгоритма сложения и вычитания обыкновенных дробей. Слайд 12 презентации Слайд 13 презентации Слайд 14 презентации Слайд 15 презентации Учитель организует работу по отработке навыков сложения и вычитания обыкновенных дробей. (№ 743, № 745, № 747) Слайд 16 презентации Предлагает решить текстовую задачу практической направленности с зарисовкой. Для закрепления изученного на уроке материала предлагает выполнить обучающую самостоятельную работу (индивидуальную) с последующей самопроверкой (взаимопроверкой). Слайд 17 презентации Организует воспроизведение и коррекцию опорных знаний учащихся: -Как сложить дроби с одинаковыми знаменателями? — Как вычесть дроби с одинаковыми знаменателями? | Проговаривают свои предположения. Выслушивают варианты одноклассников, делают выводы. Записывают решения в тетради. Формулируют правило, работают по учебнику, сравнивают со своей формулировкой. Записывают правило сложения и вычитания обыкновенных дробей в буквенном виде в тетрадь, приводят примеры. + = — = Отрабатывают умение применять правило сложения и вычитания обыкновенных дробей при решении задач. Решают текстовую задачу с опорой на применение жизненного опыта: анализируют условие задачи, объясняют ход решения, работают с зарисовкой и сопоставляют полученный результат с реальной жизнью. Выполняют самостоятельную работу, сравнивают решение с эталоном, осуществляют взаимопроверку (самооценку), согласно критериям. Выставляют оценку, объясняют и обсуждают объективность выставленной оценки Отвечают на вопросы учителя, подводят итоги своей работы на уроке. | познавательные: — уметь анализировать объект с целью нахождения способа решения задачи; — уметь использовать графическую информацию (чертежи), формулы, строить логическую цепочку рассуждений — воспринимать текст учебника с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для ответа на поставленный вопрос. регулятивные: формировать целевые установки учебной деятельности; выстраивать алгоритм действий; коммуникативные: учить точно и грамотно выражать свои мысли. личностные: самоопределение (умение выделять нравственный аспект поведения), смыслообразование (учебная мотивация) познавательные: в ходе выполнения упражнений отрабатывать умение выполнять сложение и вычитание дробей с одинаковыми знаменателями; развивать умение применять математические знания к реальным жизненным ситуациям; регулятивные: формировать способность к мобилизации сил и энергии, к волевому усилию в преодолении препятствий; коммуникативные: уметь аргументировать свое мнение; уметь слушать и понимать речь других, оформлять мысли в устной и письменной форме управлять своим поведением (контроль, коррекция, оценка своего действия). |
5. | Обеспечение понимания детьми содержания и способов выполнения домашнего задания | Объясняет домашнее задание. (№ 744, № 746,№ 774). Задание творческого характера по желанию (составить синквейн на тему Дробь) Пример: Слайд 18 презентации | Записывают домашнее задание в дневник. | регулятивные: планировать решения учебной задачи личностные: проводить самооценку, формировать мотивацию к изучению и закреплению нового. |
6. Рефлексия. | Дать количественную оценку работы учащихся | Организует обсуждение достижений, ставя заранее подготовленные вопросы: Какую цель ставили? Удалось ли ее достичь? Какими способами? Понравился ли урок? Что вызвало затруднения? (Слайд 9) Слайд 19 презентации Благодарит за урок. Слайд 20 презентации | Отвечают на вопросы учителя. Анализируют, что при проверке знаний они проявили самостоятельность, честность, требовательность. Во время урока им потребовалась внимательность, собранность, проявление смекалки. | личностные: оценивать собственную учебную деятельность: свои достижения, самостоятельность, причины неудач. |
Организационный момент
Развивать внимание, проверить усвоение учащимися предыдущей темы
188 № 1):
Домашнее задание.
Просмотр содержимого презентации
«Сложение и вычитание обыкновенных дробей»
Урок математики в
5 классе
Работаем устно!
- Прочитайте дроби.
- Назовите правильные дроби.
- Какие дроби называют правильными?
- Назовите неправильные дроби.
- Какие дроби называют неправильными?
Работаем устно!
- Как сравнить дроби с одинаковыми знаменателями?
- Как сравнить дроби с одинаковыми числителями?
- Какая дробь больше: правильная или неправильная?
- Сравните:
=
Работаем устно!
Расположите дроби в порядке возрастания:
Работаем устно!
Предложен ряд чисел:
Разбейте числа на группы по определенным признакам
— правильные дроби
— неправильные дроби
— натуральные числа
«Сложение и вычитание дробей с одинаковыми знаменателями»
Тема урока:
Шаблон для создания презентаций к урокам математики.
Савченко Е.М.
Цели урока:
1. Сформулировать правила сложения и вычитания дробей с одинаковыми знаменателями.
2. Научиться складывать и вычитать дроби с одинаковыми знаменателями.
Тому Сойеру необходимо покрасить забор из 9 досок. Он покрасил 2 доски забора, а после «уступил» это занятие другим мальчикам, которые покрасили 5 досок забора. Какую часть забора они покрасили вместе?
Какую часть забора осталось покрасить?
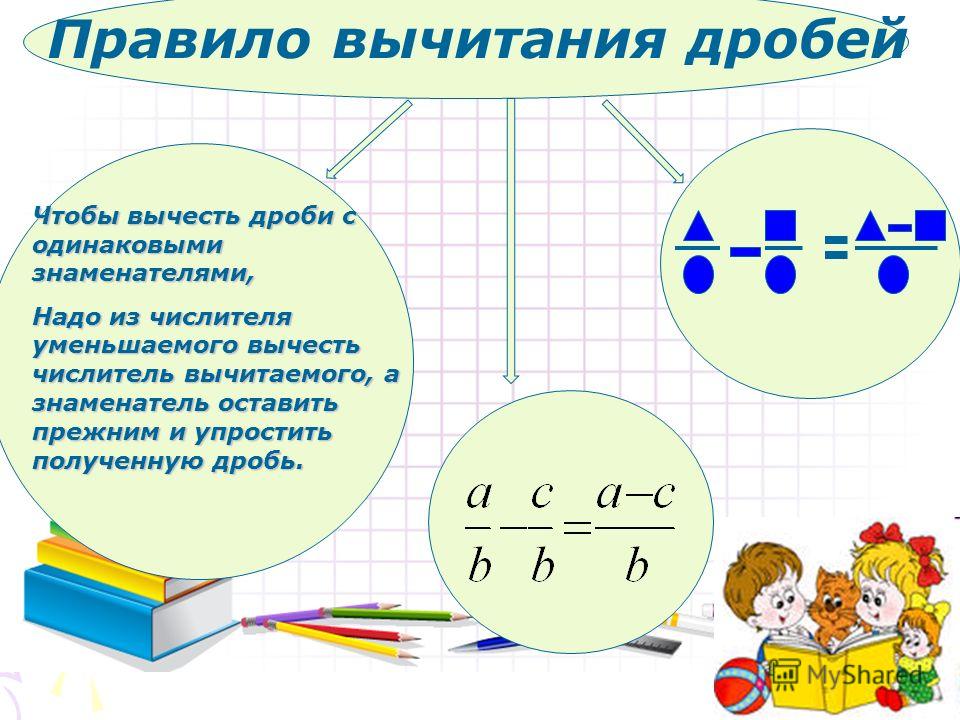
При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
С помощью букв правило сложения можно записать так:
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
С помощью букв правило вычитания можно записать так:
Физкультминутка
Проследите, в какой последовательности производятся записи при сложении дробей с одинаковыми знаменателями:
1
2
3
1 + 2
6
6
6
6
Запишите решение самостоятельно, а затем проверьте себя:
1
3
1 + 3
4
6
6
6
6
2
2
2 + 2
4
6
6
6
6
3
2
3 + 2
5
6
6
6
6
Работа в классе:
№ 743
№ 745
№ 747
Задача.
Какова масса салата?
II вариант
I вариант
10
14
4
2
6
12
=
=
1)
1)
15
12
12
15
15
12
28
12
11
2
23
30
=
=
2)
2)
25
47
25
47
47
25
19
22
15
14
5
7
=
=
3)
3)
35
43
43
35
35
43
8
6
14
=
8
2
=
10
4)
4)
17
17
17
13
13
13
8
6
5
7
6
5
=
=
5)
1
5)
1
9
9
9
8
8
8
Домашнее задание:
§27, правила
№ 744
№ 746
№ 748.
По желанию:
составить синквейн.
Рефлексия
- — На уроке я узнал…
- — Мне было легко…
- — Я пока затрудняюсь…
Спасибо за урок!
Этапы урока | Задачи этапа | Время | Деятельность учителя | Деятельность учащихся | УУД |
1.Организационный момент | Создать благоприятный психологический настрой на работу. Обеспечить мотивацию учения детьми, принятие ими целей урока. | 4 мин | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. -Вспомните, с чем вы знакомились на прошлых уроках? К нам на урок сегодня пришёл Незнайка и попросил помочь ему разобраться с понятием обыкновенные дроби и научится задачи с помощью дробей. И как вы уже догадались, на этом уроке мы продолжим работу с обыкновенными дробями. -Тема сегодняшнего урока (слайд №1) «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». -Какие цели мы поставим на данном уроке? (слайд № 4-7) -Цели поставлены, но, как вы знаете, для достижение их надо вспомнить изученное ранее. | Включаются в деловой ритм урока. С обыкновенными дробями. Научились отличать правильные и неправильные дроби и сравнивать их. Учащихся пишут дату и тему урока в тетради. Цели урока: -выявить правило и научиться выполнять сложение и вычитание дробей с одинаковыми знаменателями. -развивать внимание, логическое мышление, грамотную математическую речь. -воспитывать аккуратность при записи примеров и задач с обыкновенными дробями. | Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
2. Актуализация знаний и умений | Актуализация опорных знаний и способов действий; повторение умения переводить текст в запись в виде дроби, восстановление определения правильной и неправильной дроби, фиксирование индивидуальных затруднений | 8 мин | И вот первые вопросы от Незнайки; -Чем натуральные числа отличаются от дробных? — Что показывает знаменатель и где его пишут? — Что показывает числитель и где его пишут? Работа с рисунками.(слайд №8-11) -Прочтите полученные ответы, а как ещё читаются эти дроби? (слайд №12) Устная работа. (слайд№13) -Помогите Незнайке собрать груши, на которых записаны неправильные дроби. -Какую дробь называют правильной? -Какую дробь называют неправильной? (слайд №14) Самостоятельная работ. (слайд №15). | Целые числа обозначают целые единицы а дробные –части единиц. Знаменатель показывает, на сколько долей делят и пишут его под чертой. Числитель показывает, сколько долей было взято и пишут его над чертой. Учащиеся пишут ответы на вопросы по слайдам в тетради. 1/2 — Половина 1/3 — треть 1/4 — четверть 𝟖/𝟖; 𝟏𝟕/𝟏𝟑; 𝟏𝟏/𝟗. Дробь в которой числитель меньше знаменателя, называет правильной дробью. Дробь в которой числитель больше знаменателя, называет неправильной дробью. Работа в парах. Учащихся меняются тетрадями и выполняют проверку оценивая друг друга. | Личностные: оценивание усваиваемого материала. Коммуникативные: умение использовать речь для регуляции своего действия, строить понятные для окружающих высказывания. Регулятивные: контроль и оценка процесса и результатов деятельности. Познавательные: структурирование собственных знаний. |
3.Целеполагание и мотивация. | Обеспечение мотивации учения детьми, принятие ими целей урока | 8 мин | Ребята Незнайка очень удивлен, что дроби можно сравнивать так легко. Покажем ему, что ещё можно выполнит с обыкновенными дробями. Предлагаю построить ломаную из трёх отрезков по 2 см каждый и вычислить её длину в см. (слайд № 16) Проблемная ситуация; -Попробуйте вычислите длину ломаной в дм. Подсказка: -Найдите какую часть составляют 2 см от дециметра. (слайд №17-18) -Каким образом вы смогли вычислить длину в дм? А теперь попробуем вместе сформулировать правило сложения дробей с одинаковыми знаменателями. (слайд№19) Запишем правило сложения с помощью букв. Незнайка попросил помочь ему решить задачу. (слайд № 20) — К нему в гости пришли друзья, он решил угостить их яблоками положил на тарелку 10 (долей), 4 доли съели сколько долей осталось? -С помощью какого действия решили задачу? Сформулируйте правило вычитания дробей с одинаковыми знаменателями. Запишем это правило с помощью букв. (слайд № 21) | В тетради выполняют рисунок и вычисляют; 2+2+2=6см. Учащихся сталкиваются с проблемой 2см от дм., 2/10дм. Отмечают на рисунке и снова вычисляют длину ломаной. 2/10+2/10+2/10=2+2+2/10=6/10 Выполнили сложение дробей. При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляется тот же. В тетради записывают правило с помощью букв + = . 10/10-4/10=10-4/10=6/10 При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же. В тетради записывают правило с помощью букв | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, строение понятные для окружающих высказывания. |
4. Применение знаний и умений в новой ситуации | Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями». | 7 мин | — Итак одну из обучающих целей нашего урока вы выполнили ,выявили правила сложения и вычитания дробей с одинаковыми знаменателями осталось научиться применять эти правила на практике. Для этого поработаем с учебником; (слайд № 22) 1.
— Прочитайте ответ. 2. Стр. 156, №1006.
— Прочитайте ответ. 3. Стр. 156, №1008. -Какую массу гвоздей получила первая бригада? — На сколько тонн меньше получила вторая бригада? -Сколько тонн гвоздей получила вторая бригада? | Решение задач по новой теме №1005 (кг) салата Ответ: (кг). №1006 (т) масса станка и упаковке вмести. Ответ: (т). № 1008 (т) гвоздей получила вторая бригада. Ответ: (т). | Познавательные: формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: умение оформлять свои мысли в устной форме; слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
5. Физкультминутка | Смена деятельности. | 2 мин | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. (слайд № 23) Физкультминутка | Учащиеся сменили вид деятельности и готовы продолжить работу. | |
6. Первичное закрепление | Установление правильности и осознанности изучения темы. Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу. | 8 мин | -Далее я предлагаю вам проверить, как вы усвоили правила, выполнив самостоятельно № 1011, стр. 156. — Первые пять учеников справившихся с работой получают оценки. -А чтобы мы смогли быстро проверить правильность решения. приглашаю к доске 4 ученика. У доске каждый выполняет по одному столбику. К нам за помощью обратился Незнайка, он просит вас, проверить работу которую он выполнил. ( слайд №24) | № 1011 Решение с комментированием; а) ; в) ; б) ; г) д) ; е) ; ж); з). Самостоятельная работа: (слайд № 25) | Регулятивные: осуществление констатирующий и прогнозирующий контроль по результату и по способу действия. Познавательные: — умение ориентироваться в системе своих знаний, Коммуникативные:, контроль, коррекция, оценка. |
7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция. | Дать качественную оценку работы класса и отдельных обучаемых. | 3 мин | -Что изучили сегодня на уроке? -Кто желает сформулировать правило нахождения сложения дробей с одинаковыми знаменателями. Кто желает сформулировать правило нахождения вычитания дробей с одинаковыми знаменателями. | Учащихся формулируют правило сложения и вычитания дробей с одинаковыми знаменателями. | Личностные: формирование позитивной самооценки Коммуникативные:; умение с достаточной полнотой и точностью выражать свои мысли; Регулятивные: умение самостоятель- но анализировать правильность выполнения действий и вносить необходи- мые коррективы. |
8. Рефлексия (подведение итогов урока) | 3 мин | Было трудно … Было интересно … Я научился … Меня удивило … У меня………. | Учащихся отвечают на вопросы. Высказывают свои мнения. | Регулятивные: оценивание собственной деятельности на уроке. Коммуникативные: умение анализировать собственные успехи, неудачи, определять пути коррекции. Познавательные: рефлексия. | |
9. Информация о домашнем задании | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания | 2 мин | Сообщает домашнее задание: Прочитать теоретический материал п.26 на стр.158. Выполнить письменно №1017, №1019, №1020. (слайд № 27) | Открывают дневники, записывают домашнее задание, задают вопросы. |
(слайд№3)
Стр. 156, №1005.
настроение? (слайд № 26)Сложение и вычитание дробей
Во время сложения и вычитания дробей нам нужно проверить, имеют ли дроби одинаковые знаменатели или разные знаменатели, после чего начинается вычисление.
Давайте узнаем больше о сложении и вычитании дробей в этой статье.
| 1. | Как складывать и вычитать дроби? |
| 2. | Сложение и вычитание дробей с одинаковыми знаменателями |
| 3. | Сложение и вычитание дробей с разными знаменателями |
| 3. | Сложение и вычитание смешанных дробей |
| 4. | Сложение и вычитание дробей с целыми числами |
| 5. | Часто задаваемые вопросы о сложении и вычитании дробей |
Как складывать и вычитать дроби?
Сложение и вычитание дробей производится по аналогичным правилам, в которых перед началом сложения или вычитания проверяются знаменатели. После проверки знаменателей мы можем соответственно складывать или вычитать заданные дроби. Знаменатели проверяются следующим образом.
- Если знаменатели данных дробей совпадают, мы складываем или вычитаем только числители, а знаменатель сохраняем.
- Если знаменатели разные, мы преобразуем дроби в подобные дроби, чтобы знаменатели стали одинаковыми, а затем прибавляем или вычитаем то, что требуется.
Давайте узнаем об этом в следующих разделах.
Сложение и вычитание дробей с одинаковыми знаменателями
Процесс сложения и вычитания дробей с одинаковыми знаменателями довольно прост, потому что нам нужно только работать с числителями.
Сложение дробей с одинаковыми знаменателями
Сложим дроби 1/5 и 2/5, используя прямоугольные модели. В этом случае обе дроби имеют одинаковые знаменатели. Эти дроби называются подобные дроби . На следующем рисунке представлены обе фракции в одной и той же модели.
- 1/5 означает, что 1 из 5 частей окрашены в желтый цвет.
- 2/5 означает, что 2 из 5 частей окрашены в синий цвет.
Из 5 частей 3 части заштрихованы. В дробной форме это можно представить как 3/5.
Теперь давайте сложим дроби с одинаковыми знаменателями в числовом выражении. В этом случае нам нужно добавить 1/5 + 2/5. Давайте используем следующие шаги, чтобы понять дополнение.
- Шаг 1: Сложите числители данных дробей. Здесь числители 1 и 2, поэтому будет 1 + 2 = 3 .
- Шаг 2: Сохраните тот же знаменатель. Здесь знаменатель равен 5, .
- Шаг 3: Следовательно, сумма 1/5 + 2/5 = (1 + 2)/5 = 3/5
Следует отметить, что мы используем тот же метод для вычитания дробей.
Вычитание дробей с одинаковыми знаменателями
Вычтем дроби 2/5 и 1/5, используя прямоугольные модели. Мы представим 2/5 в этой модели, заштриховав 2 из 5 частей. Далее мы заштрихуем 1 часть из заштрихованных частей модели, что будет означать удаление 1/5.
Теперь у нас осталась 1 деталь в заштрихованных частях модели.
Теперь давайте вычтем дроби с одинаковыми знаменателями в числовом выражении. В этом случае нам нужно вычесть 2/5 — 1/5. Давайте разберемся с процедурой, выполнив следующие шаги.
- Шаг 1: Вычтем числители данных дробей. Здесь числители 2 и 1, значит будет 2 — 1 = 1
- Шаг 2: Сохраните тот же знаменатель. Здесь знаменатель равен 5,9.0056
- Шаг 3: Следовательно, разница 2/5 — 1/5 = (2 — 1)/5 = 1/5
Сложение и вычитание дробей с разными знаменателями
Для сложения и вычитания дробей с разными знаменателями нам нужно преобразовать разные дроби в одинаковые дроби, записав их эквивалентные дроби таким образом, чтобы их знаменатели стали одинаковыми. Давайте разберемся в этом с помощью примера.
Пример: Добавить 1/5 + 1/3
Решение: Для сложения разных дробей нам нужно использовать следующие шаги
- Шаг 1: Найдите наименьшее общее кратное (НОК) знаменателей. Здесь LCM 5 и 3 равно 15.
- Шаг 2: Преобразуйте заданные дроби в подобные дроби, написав эквивалентные дроби для соответствующих дробей так, чтобы их знаменатели остались прежними. Здесь это будет \(\frac {1}{5}\)×\(\frac {3}{3}\)=\(\frac {3}{15}\)
- Шаг 3: Аналогично эквивалентная дробь 1/3 со знаменателем 15 равна \(\frac {1}{3}\)×\(\frac {5}{5}\)=\(\frac { 5}{15}\)
- Шаг 4: Теперь, когда мы преобразовали данные дроби в подобные дроби, мы можем сложить числители и сохранить тот же знаменатель. Это будет 3/15 + 5/15 = 8/15
Здесь LCM 5 и 3 равно 15.Вычитание дробей с разными знаменателями
Для вычитания разнородных дробей мы выполняем те же действия, что и при сложении разнородных дробей. Давайте разберемся в этом с помощью примера.
Пример: Вычесть 5/6 — 1/3
Решение: Для вычитания разных дробей необходимо выполнить следующие шаги.
- Шаг 1: Найдите наименьшее общее кратное (НОК) знаменателей. Здесь LCM 6 и 3 равно 6.
- Шаг 2: Преобразуйте заданные дроби в подобные дроби, написав эквивалентные дроби для соответствующих дробей так, чтобы их знаменатели остались прежними. Здесь это будет \(\frac {5}{6}\)×\(\frac {1}{1}\)=\(\frac {5}{6}\)
- Шаг 3: Аналогично эквивалентная дробь 1/3 со знаменателем 6 равна \(\frac {1}{3}\)×\(\frac {2}{2}\)=\(\frac { 2}{6}\)
- Шаг 4: Теперь, когда мы преобразовали данные дроби в подобные дроби, мы можем вычесть числители и сохранить тот же знаменатель. Это будет 5/6 — 2/6 = 3/6. Это может быть дополнительно уменьшено до 1/2
Здесь LCM 6 и 3 равно 6.Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей осуществляется путем преобразования смешанных дробей в неправильные дроби, а затем сложение или вычитание выполняется в соответствии с требованием. Давайте разберемся в этом с помощью следующих примеров.
Пример: Складываем смешанные дроби: \(2\dfrac{1}{4}\) + \(1\dfrac{3}{4}\)
Решение: Сначала преобразуем смешанные дроби дроби в неправильные дроби.
- Шаг 1: Преобразуйте данные смешанные дроби в неправильные дроби. Итак, \(2\dfrac{1}{4}\) станет 9/4; и \(1\dfrac{3}{4}\) станет 7/4
- Шаг 2 : Сложите дроби, добавив числители, потому что знаменатели одинаковы. это будет 9/4 + 7/4= 16/4.
- Шаг 3: При необходимости уменьшите дробь. Это станет 16/4 = 4. Следовательно, \(2\dfrac{1}{4}\) + \(1\dfrac{3}{4}\) = 4,
Теперь давайте разберемся с вычитанием смешанных дробей, используя тот же метод.
Пример: Вычесть смешанные дроби: \(5\dfrac{1}{3}\) — \(2\dfrac{1}{3}\)
Решение: Сначала преобразуем смешанные дроби дроби в неправильные дроби.
- Шаг 1: Преобразуйте заданные смешанные дроби в неправильные дроби. Итак, \(5\dfrac{1}{3}\) станет 16/3; и \(2\dfrac{1}{3}\) станет 7/3
- Шаг 2 : Вычтите дроби, вычитая числители, потому что знаменатели одинаковы. Это будет 16/3 — 7/3 = 9/3
- Шаг 3: При необходимости уменьшите дробь. Это станет 9/3 = 3. Следовательно, \(5\dfrac{1}{3}\) — \(2\dfrac{1}{3}\) = 3
Это будет 16/3 — 7/3 = 9/3Сложение и вычитание дробей с целыми числами
Сложение и вычитание дробей с целыми числами можно выполнить следующим способом. Давайте разберемся в этом на примере.
Пример: Складываем 7/4 + 5
Решение: Складываем 7/4 + 5, используя следующие шаги.
- Шаг 1: Запишите целое число в виде дроби. В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 7/4 + 5/1
- Шаг 2: Теперь найдите НОК знаменателей и преобразуйте данные дроби в подобные дроби. Здесь НОК 4 и 1 равен 4. И после преобразования их в одинаковые дроби мы получаем (7 × 1)/(4 × 1) + (5 × 4)/(1 × 4) = 7/4 + 20/ 4
- Шаг 3: Сложите числители, не изменяя знаменатель. Здесь 7/4 + 20/4 = 27/4 = \(6\dfrac{3}{4}\)
Здесь 7/4 + 20/4 = 27/4 = \(6\dfrac{3}{4}\)Теперь давайте разберемся с вычитанием дроби из целого числа с помощью следующего примера.
Пример: Вычесть 6 — 3/5
Решение: Давайте вычтем 6 — 3/5, используя следующие шаги.
- Шаг 1: Запишите целое число в виде дроби. В этом случае целое число равно 6, что можно записать как 6/1. Итак, теперь нам нужно вычесть 6/1 — 3/5
- Шаг 2: Теперь найдите НОК знаменателей и преобразуйте данные дроби в подобные дроби. Здесь НОК 1 и 5 равен 5. И после преобразования их в одинаковые дроби мы получаем (6 × 5)/(1 × 5) — (3 × 1)/(5 × 1) = 30/5 — 3/ 5
- Шаг 3: Вычтите числители, пока знаменатель не изменится. Здесь 30/5 — 3/5 = 27/5 = \(5\dfrac{2}{5}\)
Важные замечания по сложению и вычитанию дробей
- Для сложения и вычитания одинаковых дробей мы можем напрямую работать с числителями, в то время как знаменатели остаются прежними.
- Для сложения и вычитания разных дробей никогда не складывать и не вычитать напрямую числители и знаменатели. Преобразуйте их в похожие дроби, а затем сложите или вычтите.
☛ Похожие темы
- Добавление дробей
- Вычитание дробей
- Умножение дробей
- Деление дробей
- Сложение дробей с разными знаменателями
- Вычитание дробей с разными знаменателями
- Как калькулятор дробей
- Калькулятор дробей
Часто задаваемые вопросы о сложении и вычитании дробей
Как складывать и вычитать дроби?
Для сложения и вычитания дробей сначала нужно проверить знаменатели. Если знаменатели совпадают, мы просто добавляем или вычитаем числители и сохраняем тот же знаменатель. В случае неодинаковых дробей, когда знаменатели не совпадают, мы преобразуем неодинаковые дроби в одинаковые, находя НОК знаменателей. Это помогает в написании их соответствующих эквивалентных дробей, а затем они добавляются или вычитаются по мере необходимости.
Как складывать и вычитать дроби с разными знаменателями?
Чтобы складывать и вычитать дроби с разными знаменателями, нам нужно преобразовать дроби в подобные дроби, чтобы знаменатели стали одинаковыми. Когда знаменатели совпадают, мы можем складывать или вычитать числители. Чтобы преобразовать данные дроби в подобные дроби, нам нужно найти НОК знаменателей, а затем записать их соответствующие эквивалентные дроби. Затем можно складывать или вычитать эквивалентные дроби с одинаковыми знаменателями, в зависимости от обстоятельств.
Как складывать и вычитать дроби с целыми числами?
Для сложения и вычитания дробей с целыми числами мы используем следующий метод.
- Запишите целое число в виде дроби, написав 1 в знаменателе. Например, если нам нужно сложить 8/7 + 5, мы запишем целое число в виде дроби. В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 8/7 + 5/1. Найдем НОК знаменателей и преобразуем данные дроби в подобные дроби. Здесь НОК 7 и 1 равен 7. И после преобразования их в одинаковые дроби мы получаем (8 × 1)/(7 × 1) + (5 × 7)/(1 × 7) = 8/7 + 35/ 7 = 43/7 = \(6\dfrac{1}{7}\)
- Тот же метод будет использоваться для вычитания, например, если нам нужно вычесть 7 — 2/5, мы запишем целое число 7 как 7/1, а затем вычтем. Это сделает его 7/1 — 2/5. Найдем НОК знаменателей и преобразуем данные дроби в подобные дроби. Здесь НОК 5 и 1 равен 5. И после преобразования их в одинаковые дроби мы получаем (7 × 5)/(1 × 5) — (2 × 1)/(5 × 1) = 35/5 — 2/ 5 = 33/5 = \(6\dfrac{3}{5}\)
Здесь НОК 7 и 1 равен 7. И после преобразования их в одинаковые дроби мы получаем (8 × 1)/(7 × 1) + (5 × 7)/(1 × 7) = 8/7 + 35/ 7 = 43/7 = \(6\dfrac{1}{7}\)Как складывать и вычитать дроби со смешанными числами?
Чтобы складывать и вычитать дроби со смешанными числами, мы преобразуем смешанные числа в неправильные дроби. Теперь, если они похожи на дроби, мы можем просто сложить или вычесть числители и сохранить тот же знаменатель. Чтобы сложить или вычесть разные дроби, мы преобразуем их в одинаковые дроби. Находим НОК знаменателей, преобразуем слагаемые в их эквивалентные дроби и складываем их так же, как складываем одинаковые дроби.
Каковы правила сложения и вычитания дробей?
Основные правила сложения и вычитания дробей приведены ниже:
- Нам нужно проверить, одинаковы ли знаменатели дробей или разные.
- Если знаменатели совпадают, мы можем просто сложить или вычесть числители.
- Если знаменатели не совпадают, нам нужно преобразовать их в одинаковые дроби, а затем сложить или вычесть.
Зачем им одинаковый знаменатель?
Сегодня мы узнаем почему, , когда мы складываем и вычитаем дроби, у них должен быть один и тот же знаменатель.
Если вы еще не знали, когда мы складываем и вычитаем дроби, они должны быть однородными . Подробнее об однородных и разнородных фракциях можно прочитать в этом посте.
Это действительно легко понять с помощью наглядных пособий, которые мы рассмотрим ниже. Настоящая причина связана с определением самой дроби, которая является представлением частей общего числа, которое должно быть 9.
0003 того же размера .
Когда вы складываете или вычитаете дроби, вы не можете выразить результат в виде дроби, если не разделите сумму на равные части.
Добавление фракций
Например, если вы хотите добавить 1 / 2 + 1 / 3
Мы имеем:
- 5 1 из 2 равной части а. зеленый на картинке).
- 1 из 3 равных частей юнита (фиолетовый на изображении).
Чтобы сделать сложение, мы должны принять во внимание цветные части. Поскольку каждая часть имеет разный размер, мы не можем выразить эту величину в виде дроби.
У нас есть 3 части (1 представлена зеленым прямоугольником и 2 представлена фиолетовыми прямоугольниками), но они не одного размера .
Так что мы можем сделать? Мы можем выразить дроби, которые мы хотим добавить, в виде дроби, которая позволит нам считать их частями одинакового размера .
Как вы можете увидеть на следующих изображениях, вы можете выразить фракцию 1 / 2 как 3 / 6 и фракция 1 / 3 AS /8 /8 /8 /8 /8 /8 /8 /8 /8 /8 /8 /8 / /8 / /8 / /8 / /8 / 3 .
Теперь у нас есть количества, которые мы хотим сложить, выраженные в виде дробей, состоящих из частей одинакового размера !
Теперь мы можем посчитать цветные части и выразить их в виде дроби. Есть пять равных частей: 5/6.
Итак, 1 / 2 + 1 / 3 = 5 / 6 .
Вычитание дробей
Теперь, если мы попытаемся вычесть, например, 1 / 2 и 1 / 3 , мы получим ту же проблему. Чтобы вычесть 1 / 3 из 1 / 2 , нам нужно убрать детали того же размера, что и те, что у нас есть .
Итак, нам нужно выразить обе дроби однородно, и тогда мы можем отнять части, указанные вычитанием.
, если мы выражаем 1 / 2 AS 3 / 6 и 1 / 3 AS 2 / , до 2 /
0, до 2 / 7 , до 2 / 7 , до 2 / 7, 2 / 7, 2 / 7, 2 /. / 3 , отнимаем 2 из 3 равных частей 3 / 6 , и получаем 1 часть, или 1 / 6 . Итак, находим, что 1 / 2 – 1 / 3 = 1 / 6 .Легко понять, почему знаменатели должны быть одинаковыми при сложении и вычитании дробей, не так ли?
Если вам понравился этот пост, поделитесь им, чтобы другие тоже могли узнать!
С Smartick вы можете узнать больше о дробях и других математических понятиях, а также работать над упражнениями, которые адаптируются для каждого учащегося в режиме реального времени.