Лекция 1. Правила сложения и умножения · Теория вероятностей и математическая статистика
Комбинаторика — это наука, с который каждый встречается в повседневной жизни: сколько способов выбрать 3 дежурных для уборки класса или сколько способов составить слово из данных букв. В целом, комбинаторика позволяет вычислить, сколько различных комбинаций, согласно некоторым условиям, можно составить из заданных объектов (одинаковых или разных).
Как наука комбинаторика возникла еще в 16 веке, а теперь ее изучает каждый студент (и даже школьник). Начинают изучение с понятий перестановок, размещений, сочетаний (с повторениями или без). Наиболее известные правила комбинаторики — правила суммы и произведения, которые чаще всего применяются в типовых комбинаторных задачах. Два основных правила комбинаторной теории:
Правило сложения
Возможно, это правило покажется непосвященному человеку абракадаброй, но ничего сложного нет. Рассмотрим пример – пусть в одном ящике есть
Рассмотрим пример – пусть в одном ящике есть
Закон сложения используется тогда, когда нужно выбрать только 1 элемент.
Пример 1.
Вика должна выбрать только один десерт из 8 видов коктейля, 5 видов мороженого и 5 видов йогурта. Сколькими способами она может выбрать десерт?
Решение.
Используется закон сложения, т.к. Вика должна выбрать или коктейль, или мороженое, или йогурт.
Ответ: Вика может выбрать десерт 18 способами.
При использовании закона сложения надо следить, чтобы ни один из способов выбора объекта a не совпадал с каким-либо способом выбора объекта b.
Если объект a можно получить способами, объект — способами, то объект « или » можно получить способами, где — это количество повторяющихся способов.
Пример 2.
В группе 7 человек имеют «5» по математике, 9 человек — «5» по философии. В сессии 2 экзамена. Известно, что 4 человека сдали сессию отлично. Сколько человек имеют хотя бы одну пятерку в сессии?
Решение.
Правило умножения Пусть объект А выбирается m способами, объект В выбирается n способами, то оба объекта можно выбрать m·n способами.
Все очень просто – каждый из m способов выбора объекта А комбинируется с каждым из n способов выбора объекта В, то есть количество способов просто умножается друг на друга.
Пример3.
Сколько чисел можно составить из цифр 0,1,2,3,4,5,6,7,8,9, если число должно быть двузначным?
Решение.
Можно составить 90 чисел – первую цифру числа (объект А) можем выбрать 9 способами, так как число не может начинаться с нуля. Вторую цифру числа (объект В) можем выбрать 10 способами, так как у нас есть 10 цифр.
Пример 4.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение.
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26·25=650 способами.
Пусть требуется выполнить последовательно действий. Если первое действие можно выполнить способами, второе действие способами, третье – способами и так до -го действия, которое можно выполнить способами, то все действий вместе могут быть выполнены: способами.
На стоянке такси находятся 3 автомобиля Audi, 5 автомобилей Hyundai и 7 автомобилей Toyota. Сколькими способами можно выбрать машину для поездки?
1121522В группе 7 человек имеют «5» за экзамен по математике, 9 человек — «5» за экзамен по философии. В сессии 2 экзамена: математика и философия. Известно, что 4 человека сдали сессию отлично. Сколько человек имеют хотя бы одну пятерку в сессии?
В сессии 2 экзамена: математика и философия. Известно, что 4 человека сдали сессию отлично. Сколько человек имеют хотя бы одну пятерку в сессии?
Закон сложения используется тогда, когда надо выбрать …
1 элемент2 элемента3 элементаСколько угодно элементовВ классе учится 17 мальчиков и 9 девочек. Сколькими способами можно назначить двух дежурных?
26153306650На стоянке такси находятся 3 автомобиля Audi, 5 автомобилей Hyundai и 7 автомобилей Toyota. Сколькими способами можно выбрать три машины для поездки?
Умножение одночлена на многочлен. Все правила умножения и сложения с примерами.
12+
7 месяцев назад
Математика от Баканчиковой296 подписчиков
Продолжая говорить о многочленах, сегодня мы расскажем Вам об умножении одночлена на многочлен. Но особое внимание мы уделим тому, как избежать ошибок при выполнении этого умножения. Этот урок будет полезен ученикам с 5 по 11 класс.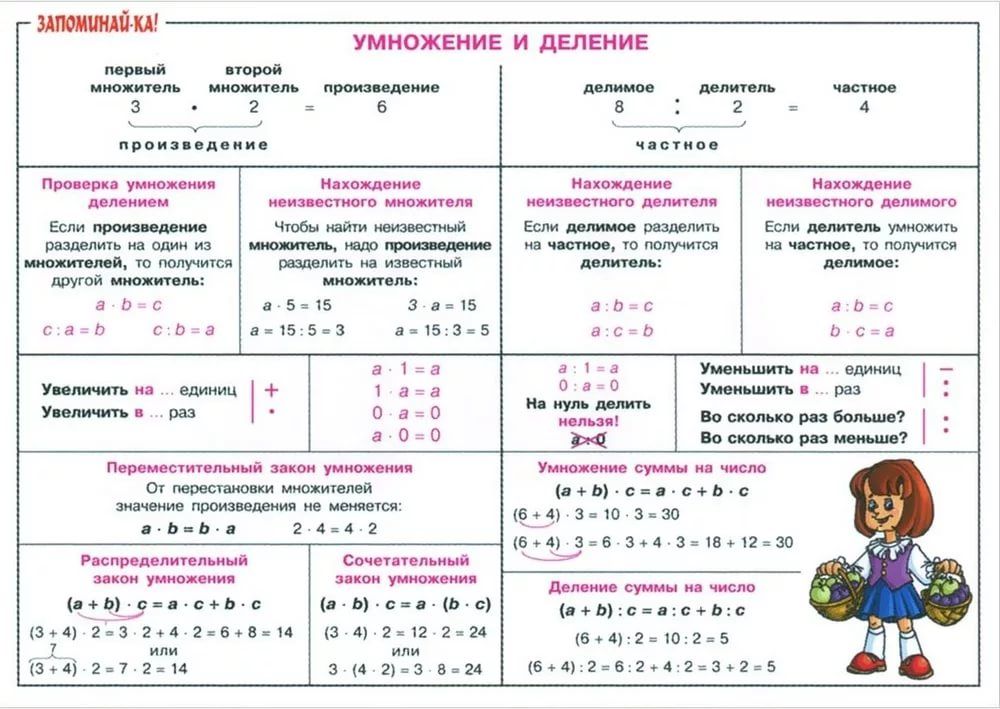 Потому что мы составили чек-лист или другими словами — склерозник, в который включили все правила умножения и сложения, которые Вы должны знать и уметь применять, чтобы без ошибок умножать одночлен на многочлен. Мы напомним Вам эти правила, дадим конкретные примеры и покажем типичные ошибки, которые допускают ученики. Следуя нашему чек-листу, Вы будете выполнять умножение одночлена на многочлен только на оценку 5.
00:00 Начало видео.
00:41 Как умножить одночлен на многочлен?
02:07 1. Правила знаков.
03:15 2. Умножение рациональных чисел. Основное правило.
04:20 2. Умножение рациональных чисел. а). Смешанные числа обращай в дробь.
05:15 2. Умножение рациональных чисел.б). Натуральные числа обращай в дробь со знаменателем 1.
06:28 3. Умножение десятичных дробей.
09:04 Примеры умножения десятичных дробей.
11:20 4. Умножение десятичной дроби на обыкновенную.
12:42 4. Умножение десятичной дроби на обыкновенную. 4.1. Как обращать обыкновенную дробь в десятичную?
16:58 Зачем повторять правила сложения?
17:31 5.
Потому что мы составили чек-лист или другими словами — склерозник, в который включили все правила умножения и сложения, которые Вы должны знать и уметь применять, чтобы без ошибок умножать одночлен на многочлен. Мы напомним Вам эти правила, дадим конкретные примеры и покажем типичные ошибки, которые допускают ученики. Следуя нашему чек-листу, Вы будете выполнять умножение одночлена на многочлен только на оценку 5.
00:00 Начало видео.
00:41 Как умножить одночлен на многочлен?
02:07 1. Правила знаков.
03:15 2. Умножение рациональных чисел. Основное правило.
04:20 2. Умножение рациональных чисел. а). Смешанные числа обращай в дробь.
05:15 2. Умножение рациональных чисел.б). Натуральные числа обращай в дробь со знаменателем 1.
06:28 3. Умножение десятичных дробей.
09:04 Примеры умножения десятичных дробей.
11:20 4. Умножение десятичной дроби на обыкновенную.
12:42 4. Умножение десятичной дроби на обыкновенную. 4.1. Как обращать обыкновенную дробь в десятичную?
16:58 Зачем повторять правила сложения?
17:31 5.

4.
 3: Правила сложения и умножения вероятностей
3: Правила сложения и умножения вероятностей- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10893
- OpenStax
- OpenStax
При вычислении вероятности необходимо учитывать два правила при определении того, являются ли два события независимыми или зависимыми, а также являются ли они взаимоисключающими или нет.
Если A и B — два события, определенные в пространстве выборок, то:
\[P(A \text{ AND } B) = P(B)P(A|B) \label{eq1}\]
Это правило также может быть записано как:
\[P(A|B) = \dfrac{P(A \text{ AND } B)}{P(B)} \nonumber\]
(Вероятность \(A\) при заданном \(B\) равно вероятности \(A\) и \(B\), деленной на вероятность \(B\). )
)
Если \(A\) и \(B\) независимы , то
\[P(A|B) = P(A). \nonumber\]
и уравнение \ref{eq1} становится
\[P(A \text{ AND } B) = P(A)P(B). \nonumber\]
Если A и B определены на выборочном пространстве, то:
\[P(A \text{ ИЛИ } B) = P(A) + P(B) — P(A \text{ AND } B) \label{eq5}\]
Если A и B являются взаимоисключающими , то
\[P(A \text{ AND } B) = 0. \nonumber\]
и уравнение \ ref{eq5} становится
\[P(A \text{ ИЛИ } B) = P(A) + P(B). \nonumber\]
Пример \(\PageIndex{1}\)
Клаус пытается выбрать, куда поехать в отпуск. У него есть два варианта: \(\text{A} = \text{Новая Зеландия}\) и \(\text{B} = \text{Аляска}\).
- Клаус может позволить себе только один отпуск. Вероятность того, что он выберет \(\text{A}\), равна \(P(\text{A}) = 0,6\), а вероятность того, что он выберет \(\text{B}\), равна \(P(\ текст{B}) = 0,35\).
- \(P(\text{A AND B}) = 0\), потому что Клаус может позволить себе только один отпуск
- Следовательно, вероятность того, что он выберет Новую Зеландию или Аляску, равна \(P(\text{A OR B}) = P(\text{A}) + P(\text{B}) = 0,6 + 0,35 = 0,95.
 \). Обратите внимание, что вероятность того, что он никуда не поедет в отпуск, должна быть равна 0,05.
\). Обратите внимание, что вероятность того, что он никуда не поедет в отпуск, должна быть равна 0,05.
Карлос играет в американский футбол. Он забивает гол в 65% случаев, когда бросает. Карлос собирается забить два гола подряд в следующем матче. \(\text{A} =\) событие Карлос успешно с первой попытки. \(P(\text{A}) = 0,65\). \(\text{B} =\) событие Карлосу удалось со второй попытки. \(P(\text{B}) = 0,65\). Карлос часто стреляет сериями. Вероятность того, что он забьет второй гол ДАННО что он забил первый гол 0,90.
- Какова вероятность того, что он забьет оба гола?
- Какова вероятность того, что Карлос забьет первый или второй гол?
- Являются ли \(\text{A}\) и \(\text{B}\) независимыми?
- Являются ли \(\text{A}\) и \(\text{B}\) взаимоисключающими?
Растворы
а. Проблема заключается в том, чтобы найти \(P(\text{A AND B}) = P(\text{B AND A})\). Поскольку \(P(\text{B|A}) = 0,90: P(\text{B AND A}) = P(\text{B|A}) P(\text{A}) = (0,90)(0,65) = 0,585\)
Карлос делает первое и второе голы с вероятностью 0,585.
б. Проблема заключается в том, чтобы найти \(P(\text{A OR B})\).
\[P(\text{A OR B}) = P(\text{A}) + P(\text{B}) — P(\text{A AND B}) = 0,65 + 0,65 — 0,585 = 0,715\]
Карлос забьет либо первый, либо второй гол с вероятностью 0,715.
в. Нет, это не так, потому что \(P(\text{B AND A}) = 0,585\).
\[P(\text{B})P(\text{A}) = (0,65)(0,65) = 0,423\]
\[0,423 \neq 0,585 = P(\text{B AND A})\ ]
Итак, \(P(\text{B AND A})\) равно , а не равно \(P(\text{B})P(\text{A})\).
д. Нет, не потому, что \(P(\text{A и B}) = 0,585\).
Чтобы быть взаимоисключающими, \(P(\text{A AND B})\) должно равняться нулю.
Упражнение \(\PageIndex{1}\)
Хелен играет в баскетбол. При штрафных бросках она бьет в 75% случаев. Теперь Хелен должна выполнить два штрафных броска. \(\text{C} =\) событие, когда Хелен делает первый выстрел. \(P(\text{C}) = 0,75\). \(\text{D} =\) событие, когда Хелен делает второй выстрел. \(P(\text{D}) = 0,75\). Вероятность того, что Елена сделает второй штрафной бросок при условии, что она сделала первый, равна 0,85. Какова вероятность того, что Хелен выполнит оба штрафных броска?
Вероятность того, что Елена сделает второй штрафной бросок при условии, что она сделала первый, равна 0,85. Какова вероятность того, что Хелен выполнит оба штрафных броска?
Ответ
\[P(\text{D|C}) = 0,85\]
\[P(\text{C AND D}) = P(\text{D AND C})\]
\[P(\text{D AND C}) = P(\text{D|C})P(\text{C}) = (0,85)(0,75) = 0,6375\]
Хелен делает первый и второй штрафной бросок с вероятностью 0,6375.
Пример \(\PageIndex{2}\)
В общественной команде по плаванию 150 членов. Семьдесят пять членов являются опытными пловцами. Сорок семь участников являются пловцами среднего уровня. Остальные — начинающие пловцы. Сорок продвинутых пловцов тренируются четыре раза в неделю. Тридцать пловцов среднего уровня тренируются четыре раза в неделю. Десять начинающих пловцов тренируются четыре раза в неделю. Предположим, случайным образом выбран один член команды по плаванию._18-500x500.jpg)
- Какова вероятность того, что участник является начинающим пловцом?
- Какова вероятность того, что участник занимается четыре раза в неделю?
- Какова вероятность того, что участник хорошо плавает и занимается четыре раза в неделю?
- Какова вероятность того, что участник является продвинутым пловцом и пловцом среднего уровня? Являются ли продвинутый пловец и пловец среднего уровня взаимоисключающими? Почему или почему нет?
- Вы начинающий пловец и тренируетесь четыре раза в неделю в независимых видах спорта? Почему или почему нет?
Ответ
- \(\dfrac{28}{150}\)
- \(\dfrac{80}{150}\)
- \(\dfrac{40}{150}\)
- \(P(\text{продвинутый И промежуточный}) = 0\), поэтому это взаимоисключающие события. Пловец не может одновременно быть продвинутым пловцом и пловцом среднего уровня.
- Нет, это не независимые события.
 \[P(\text{новичок И занимается четыре раза в неделю}) = 0,0667\]\[P(\text{новичок})P(\text{занимается четыре раза в неделю}) = 0,0996\] \[0,0667 \ нэкв 0,0996\]
\[P(\text{новичок И занимается четыре раза в неделю}) = 0,0667\]\[P(\text{новичок})P(\text{занимается четыре раза в неделю}) = 0,0996\] \[0,0667 \ нэкв 0,0996\]
Упражнение \(\PageIndex{2}\)
В школе учатся 200 старшеклассников, 140 из которых в следующем году пойдут в колледж. Сорок пойдет прямо на работу. Остальные берут год перерыва. Пятьдесят старшеклассников, поступающих в колледж, занимаются спортом. Тридцать пенсионеров, идущих прямо на работу, занимаются спортом. Пятеро старшеклассников, взявших академический отпуск, занимаются спортом. Какова вероятность того, что старшеклассник берет академический отпуск?
Ответ
\[P = \dfrac{200-140-40}{200} = \dfrac{20}{200} = 0,1\]
Пример \(\PageIndex{3}\)
Фелисити посещает Modesto JC в Модесто, Калифорния. Вероятность того, что Фелисити запишется на урок математики, равна 0,2, а вероятность того, что она запишется на урок речи, равна 0,65. Вероятность того, что она запишется на урок математики, ПРИ УСЛОВИИ, что она запишется на урок речи, равна 0,25.
Пусть: \(\text{M} =\) урок математики, \(\text{S} =\) урок речи, \(\text{M|S} =\) математика, данная речь
- Какова вероятность того, что Фелисити запишется на математику и речь?
Найдите \(P(\text{M AND S}) = P(\text{M|S})P(\text{S})\). - Какова вероятность того, что Фелисити запишется на уроки математики или речи?
Найдите \(P(\text{M ИЛИ S}) = P(\text{M}) + P(\text{S}) — P(\text{M AND S})\). - Являются ли \(\text{M}\) и \(\text{S}\) независимыми? \(P(\text{M|S}) = P(\text{M})\)?
- Являются ли \(\text{M}\) и \(\text{S}\) взаимоисключающими? \(P(\text{M AND S}) = 0\)?
Ответить
а. 0,1625, б. 0,6875, с. Кивок. №
Упражнение \(\PageIndex{3}\)
Учащийся идет в библиотеку. Пусть события \(\text{B} =\) учащийся извлекает книгу и \(\text{D} =\) учащийся извлекает DVD. Предположим, что \(P(\text{B}) = 0,40, P(\text{D}) = 0,30\) и \(P(\text{D|B}) = 0,5\).
- Найти \(P(\text{B AND D})\).
- Найти \(P(\text{B ИЛИ D})\).
Ответить
- \(P(\text{B И D}) = P(\text{D|B})P(\text{B}) = (0,5)(0,4) = 0,20\).
- \(P(\text{B OR D}) = P(\text{B}) + P(\text{D}) — P(\text{B AND D}) = 0,40 + 0,30 — 0,20 = 0,50 \)
Пример \(\PageIndex{4}\)
Исследования показывают, что примерно у одной женщины из семи (приблизительно 14,3%), доживших до 90 лет, развивается рак молочной железы. Предположим, что у тех женщин, у которых развивается рак молочной железы, тест отрицательный в 2% случаев. Также предположим, что в общей популяции женщин тест на рак молочной железы дает отрицательный результат примерно в 85% случаев. Пусть у \(\text{B} =\) женщины развился рак молочной железы, и пусть \(\text{N} =\) дал отрицательный результат. Предположим, что наугад выбрана одна женщина.
- Какова вероятность того, что у женщины разовьется рак молочной железы? Какова вероятность того, что тест женщины будет отрицательным?
- Учитывая, что у женщины рак молочной железы, какова вероятность того, что ее тест будет отрицательным?
- Какова вероятность того, что у женщины рак молочной железы И тест отрицательный?
- Какова вероятность того, что у женщины рак груди или отрицательный результат?
- Имеются ли у вас рак молочной железы и отрицательные независимые результаты тестирования?
- Являются ли наличие рака молочной железы и отрицательный результат теста взаимоисключающими?
Ответы
- \(P(\text{B}) = 0,143; P(\text{N}) = 0,85\)
- \(P(\text{N|B}) = 0,02\)
- \(P(\text{B И N}) = P(\text{B})P(\text{N|B}) = (0,143)(0,02) = 0,0029\)
- \(P(\text{B ИЛИ N}) = P(\text{B}) + P(\text{N}) — P(\text{B И N}) = 0,143 + 0,85 — 0,0029 = 0,9901 \)
- Нет.
 \(P(\text{N}) = 0,85; P(\text{N|B}) = 0,02\). Итак, \(P(\text{N|B})\) не равно \(P(\text{N})\).
\(P(\text{N}) = 0,85; P(\text{N|B}) = 0,02\). Итак, \(P(\text{N|B})\) не равно \(P(\text{N})\). - № \(P(\text{B AND N}) = 0,0029\). Чтобы \(\text{B}\) и \(\text{N}\) были взаимоисключающими, \(P(\text{B AND N})\) должно быть равно нулю
Упражнение \(\PageIndex{4}\)
В школе учатся 200 старшеклассников, 140 из которых в следующем году пойдут в колледж. Сорок пойдет прямо на работу. Остальные берут год перерыва. Пятьдесят старшеклассников, поступающих в колледж, занимаются спортом. Тридцать пенсионеров, идущих прямо на работу, занимаются спортом. Пятеро старшеклассников, взявших академический отпуск, занимаются спортом. Какова вероятность того, что старший учится в колледже и занимается спортом?
Ответ
Пусть \(\text{A} =\) студент учится в колледже.
Пусть \(\text{B} =\) студент занимается спортом.
\(P(\text{B}) = \dfrac{140}{200}\)
\(P(\text{B|A}) = \dfrac{50}{140}\)
\(P(\text{A AND B}) = P(\text{B|A})P(\text{A})\)
\(P(\text{A AND B}) = (\ dfrac{140}{200}\))(\(\dfrac{50}{140}) = \dfrac{1}{4}\)
Пример \(\PageIndex{5}\)
См. информация в примере \(\PageIndex{4}\). \(\text{P} =\) положительный результат.
информация в примере \(\PageIndex{4}\). \(\text{P} =\) положительный результат.
- Учитывая, что у женщины развился рак молочной железы, какова вероятность того, что ее тест окажется положительным. Найдите \(P(\text{P|B}) = 1 — P(\text{N|B})\).
- Какова вероятность того, что у женщины разовьется рак молочной железы и положительный результат теста? Найдите \(P(\text{B AND P}) = P(\text{P|B})P(\text{B})\).
- Какова вероятность того, что у женщины не разовьется рак молочной железы. Найдите \(P(\text{B′}) = 1 — P(\text{B})\).
- Какова вероятность того, что у женщины положительный результат теста на рак молочной железы. Найдите \(P(\text{P}) = 1 — P(\text{N})\).
Ответить
а. 0,98; б. 0,1401; в. 0,857; д. 0.15
Упражнение \(\PageIndex{5}\)
Учащийся идет в библиотеку. Пусть события \(\text{B} =\) учащийся извлекает книгу и \(\text{D} =\) учащийся извлекает DVD. Предположим, что \(P(\text{B}) = 0,40, P(\text{D}) = 0,30\) и \(P(\text{D|B}) = 0,5\).
- Найти \(P(\text{B′})\).
- Найти \(P(\text{D AND B})\).
- Найти \(P(\text{B|D})\).
- Найти \(P(\text{D AND B′})\).
- Найти \(P(\text{D|B′})\).
Ответ
- \(P(\text{B′}) = 0,60\)
- \(P(\text{D И B}) = P(\text{D|B})P(\text{B}) = 0,20\)
- \(P(\text{B|D}) = \dfrac{P(\text{B AND D})}{P(\text{D})} = \dfrac{(0,20)}{(0,30) } = 0,66\)
- \(P(\text{D И B′}) = P(\text{D}) — P(\text{D AND B}) = 0,30 — 0,20 = 0,10\)
- \(P(\text{D|B′}) = P(\text{D AND B′})P(\text{B′}) = (P(\text{D}) — P(\text {D И B}))(0,60) = (0,10)(0,60) = 0,06\)
- ДиКамилло, Марк, Мервин Филд. «Файловый опрос». Корпорация полевых исследований. Доступно на сайте www.field.com/fieldpollonline…rs/Rls2443.pdf (по состоянию на 2 мая 2013 г.).
- Райдер, Дэвид, «По данным опроса, поддержка Ford резко падает», The Star, 14 сентября 2011 г.
 Доступно на сайте www.thestar.com/news/gta/2011…_suggests.html (по состоянию на 2 мая 2013 г.).
Доступно на сайте www.thestar.com/news/gta/2011…_suggests.html (по состоянию на 2 мая 2013 г.). - «Одобрение мэра отключено». Пресс-релиз от Forum Research Inc. Доступен в Интернете по адресу www.forumresearch.com/forms/News Archives/News Releases/74209_TO_Issues_-_Mayoral_Approval_%28Forum_Research%29%2820130320%29.pdf (по состоянию на 2 мая 2013 г.).
- «Рулетка». Википедия. Доступно на сайте http://en.Wikipedia.org/wiki/Roulette (по состоянию на 2 мая 2013 г.).
- Шин, Хён Б., Роберт А. Комински. «Использование языка в Соединенных Штатах: 2007». Бюро переписи населения США. Доступно на сайте www.census.gov/hhes/socdemo/l…acs/ACS-12.pdf (по состоянию на 2 мая 2013 г.).
- Данные из Baseball-Almanac, 2013. Доступно на сайте www.baseball-almanac.com (по состоянию на 2 мая 2013 г.).
- Данные Бюро переписи населения США.
- Данные Wall Street Journal.
- Данные из The Roper Center: Архив общественного мнения Университета Коннектикута.
 Доступно на сайте www.ropercenter.uconn.edu/ (по состоянию на 2 мая 2013 г.).
Доступно на сайте www.ropercenter.uconn.edu/ (по состоянию на 2 мая 2013 г.). - Данные корпорации полевых исследований. Доступно на сайте www.field.com/fieldpollonline (по состоянию на 2 мая 2013 г.).
Правило умножения и правило сложения используются для вычисления вероятности \(\text{A}\) и \(\text{B}\), а также вероятности \(\text{A}\ ) или \(\text{B}\) для двух заданных событий \(\text{A}\), \(\text{B}\), определенных в образце пространства. При выборке с заменой каждый член совокупности заменяется после того, как он выбран, так что этот член имеет возможность быть выбранным более одного раза, а события считаются независимыми. При выборке без замены каждый член совокупности может быть выбран только один раз, и события считаются не независимыми. События \(\text{A}\) и \(\text{B}\) являются взаимоисключающими событиями, если они не имеют общих исходов.
Правило умножения: \(P(\text{A AND B}) = P(\text{A|B})P(\text{B})\)
Правило сложения: \ (P(\text{A OR B}) = P(\text{A}) + P(\text{B}) — P(\text{A AND B})\)
Используйте следующую информацию для ответьте на следующие десять упражнений. Сорок восемь процентов всех зарегистрированных избирателей в Калифорнии предпочитают пожизненное заключение без права досрочного освобождения смертной казни для человека, осужденного за убийство первой степени. Среди латиноамериканцев, зарегистрированных в Калифорнии, 55% предпочитают пожизненное заключение без права досрочного освобождения смертной казни для человека, осужденного за убийство первой степени. 37,6% всех калифорнийцев — латиноамериканцы.
Сорок восемь процентов всех зарегистрированных избирателей в Калифорнии предпочитают пожизненное заключение без права досрочного освобождения смертной казни для человека, осужденного за убийство первой степени. Среди латиноамериканцев, зарегистрированных в Калифорнии, 55% предпочитают пожизненное заключение без права досрочного освобождения смертной казни для человека, осужденного за убийство первой степени. 37,6% всех калифорнийцев — латиноамериканцы.
Пусть в этой задаче:
- \(\text{C} =\) Калифорнийцы (зарегистрированные избиратели) предпочитают жизнь в тюрьме без права досрочного освобождения смертной казни для человека, осужденного за убийство первой степени.
- \(\text{L} =\) латиноамериканцы калифорнийцы
Предположим, случайным образом выбран один калифорнийец.
Упражнение \(\PageIndex{5}\)
Найдите \(P(\text{C})\).
Упражнение \(\PageIndex{6}\)
Найдите \(P(\text{L})\).
Ответ
0,376
Упражнение \(\PageIndex{7}\)
Найдите \(P(\text{C|L})\).
Упражнение \(\PageIndex{8}\)
Что такое \(\text{C|L}\) словами?
Ответ
\(\text{C|L}\) означает, если выбранное лицо является латиноамериканцем из Калифорнии, это лицо является зарегистрированным избирателем, который предпочитает пожизненное заключение без права досрочного освобождения для лица, осужденного за убийство первой степени. .
Упражнение \(\PageIndex{9}\)
Найти \(P(\text{L AND C})\)
Упражнение \(\PageIndex{10}\)
Что такое \(\text{L AND C}\) словами?
Ответ
\(\text{L AND C}\) — это случай, когда выбранное лицо является латиноамериканцем, зарегистрированным избирателем Калифорнии, который предпочитает жизнь без права досрочного освобождения смертной казни для лица, осужденного за убийство первой степени.
Упражнение \(\PageIndex{11}\)
Являются ли \(\text{L}\) и \(\text{C}\) независимыми событиями? Покажите, почему или почему нет.
Упражнение \(\PageIndex{12}\)
Найти \(P(\text{L OR C})\).
Ответ
0,6492
Упражнение \(\PageIndex{13}\)
Что такое \(\text{L OR C}\) словами?
Упражнение \(\PageIndex{14}\)
Являются ли события \(\text{L}\) и \(\text{C}\) взаимоисключающими? Покажите, почему или почему нет.
Ответ
Нет, потому что \(P(\text{L AND C})\) не равно 0.
- Независимые события
- Возникновение одного события не влияет на вероятность возникновения другого события. События \(\text{A}\) и \(\text{B}\) независимы, если выполняется одно из следующих условий:
- \(P(\text{A|B}) = P(\text{A})\)
- \(P(\text{B|A}) = P(\text{B})\)
- \(P(\text{A И B}) = P(\text{A})P(\text{B})\)
- Взаимоисключающий
- Два события являются взаимоисключающими, если вероятность того, что они происходят одновременно, равна нулю. Если события \(\text{A}\) и \(\text{B}\) взаимоисключающие, то \(P(\text{A AND B}) = 0\).

Эта страница под названием 4.3: Правила сложения и умножения вероятности распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Включено
- да
- Теги
- Сложение вероятностей
- Независимые события
- Умножение вероятностей
- взаимоисключающие
- источник@https://openstax.
 org/details/books/introductory-statistics
org/details/books/introductory-statistics - источник[1]-stats-733
Расчет вероятностей с использованием правил сложения и умножения
Правило сложенияПравило сложения вероятностей — это правило определения, используемое для нахождения вероятности того, что произойдет событие A или событие B. Это связано с использованием союза «или». Например,
- Мы можем захотеть найти вероятность того, что на правильном кубике выпадет 3 или 6
- Страховая компания может захотеть определить вероятность того, что претензия исходит от надежного страхователя или претензия превышает 5000 долларов.
Существует две версии правила добавления в зависимости от того, являются ли задействованные события взаимоисключающими (не имеют общих элементов) или невзаимозаключающими (совместно используемые элементы). Давайте посмотрим, как выглядит каждая версия.
1.1 Правило добавления для невзаимоисключающих событий
Не взаимоисключающие события — это события, которые может произойти одновременно с . На языке вероятностей говорят, что такие события имеют некоторые общие элементы. Примеры включают проигрыш и выигрыш в игре в футбол, вождение автомобиля и прослушивание музыки или роды днем и рождение девочки. Более практические примеры в области финансов и страхования включают владение домом и наличие действующего страхового полиса, наличие кредитной карты при одновременном обслуживании автокредита или неуплату страхового взноса и попадание в аварию.
Когда два события, A и B, не являются взаимоисключающими, правило сложения говорит нам, что вероятность того, что A или B произойдут, равна сумме вероятностей того, что либо событие произойдет минус вероятность того, что произойдет и то, и другое:
$$ P(A \cup B) = P(A) + P(B) − P(A \cap B) $$
Последний член \(P(A \cap B)\) входит в уравнение дважды, т. е. один раз в P(A) и один раз в P(B). Таким образом, мы должны вычесть это один раз, чтобы оно не было двойной счет .
е. один раз в P(A) и один раз в P(B). Таким образом, мы должны вычесть это один раз, чтобы оно не было двойной счет .
Диаграмма Венна прекрасно иллюстрирует идею двойного счета. Пересечение между A и B необходимо вычесть при рассмотрении вероятности A или B.
$$ \begin{align*} \textbf{Рисунок 1.1.1 – }& \textbf{Правило сложения для невзаимоисключающих событий} \\ & \textbf{События} \end{align*} $$
Пример 1.1.1
Допустим, вы вынули одну карту из обычной колоды карт. Какова вероятность того, что карта туз или сердце?
Пусть событие A — выпадение туза, а событие B — выпадение червы.
\(P(A) = \frac {4}{52}\) и \(P(B) = \frac {13}{52}\)
\(P(A \text{ и } B) = \frac {1}{52}\)
Эти два события не исключают друг друга, потому что всегда есть шанс, что карта будет и тузом, и червой.
Итак,
$$ \begin{align*} P(A \cup B) & = P(A) + P(B) − P(A \cap B) \\ & = \frac {4}{52} + \frac {13}{52} – \frac {1}{52} \\ & = \frac {16}{52} = \frac {4}{13} \end{align*} $$
Примечание. В стандартной колоде карт четыре масти: черви, трефы, пики и бубны. В каждой масти по тринадцать карт: туз, 2, 3, 4, 5, 6, 8, 9, 10, валет, дама и король. Таким образом, во всей колоде всего 52 карты.
В стандартной колоде карт четыре масти: черви, трефы, пики и бубны. В каждой масти по тринадцать карт: туз, 2, 3, 4, 5, 6, 8, 9, 10, валет, дама и король. Таким образом, во всей колоде всего 52 карты.
Пример 1.1.2
Гендерная разбивка в математическом классе из 40 учеников: 25 мальчиков и 15 девочек. На экзамене в конце года 12 мальчиков и 5 девочек получили пятерку. Если бы мы выбрали случайного ученика из класса, какова была бы вероятность выбрать мальчика или отличника?
Пусть G — событие выбора девушки, а A — событие выбора отличника.
\(P(G) =\frac {15}{40}\) и \(P(A) = \frac {17}{40}\)
Вероятность выбора девушки, получившей оценку А, равна \(\frac {5}{40}\), т. е.
\(P(G \text{ и } A) = \frac {5}{40} \)
Эти два события не исключают друг друга, потому что всегда есть шанс, что выбранная ученица будет и девушкой, и отличницей.
Итак,
$$ \begin{align*} P(G \cup A) & = P(G) + P(A) − P(G \cap A) \\ & = \frac {15}{40} + \frac {17}{40} – \frac {5}{40} \\ & = \frac {27}{40} \end{align*} $$
Пример 1. 1.3
1.3
В консалтинговой фирме работает 100 человек. 51 из них имеют степень в области финансов, 63 — в области экономики и 28 — в обеих сферах. Какова вероятность того, что случайно выбранный работник имеет высшее финансовое или экономическое образование?
Пусть F и E — события, свидетельствующие о том, что сотрудник имеет высшее финансовое и экономическое образование соответственно.
Наш интерес равен \(P(F \cup E)\)
$$ \begin{align*} P(F \cup E) & = P(F) + P(E) − P(F \cap E) \\ & = 0,51 + 0,63 – 0,28 \\ & = 0,86 = 86\% \end{align*} $$
Примечание. Для трех невзаимоисключающих событий A, B и C правило сложения выглядит следующим образом:
$$ \begin{align*} P(A \чашка B \чашка C) & = {P(A) + P(B) + P(C) – P(A \cap B) – P(B \cap C)} \\ & {- P(A \cap C) + P(A \cap B \cap C)} \end{align*} $$
Вопрос 1.1.1
Компания по страхованию жизни подвергает потенциальных страхователей медицинскому осмотру разного уровня в зависимости от определенных факторов, таких как возраст и статус курения человека. Вероятность того, что посещение Life Office не приведет ни к анализу, ни к специалисту, составляет 50%. Из тех, кто обращается в Life Office, 25% направляют к специалистам, а 35% требуют лабораторных исследований. 9В)\)
Вероятность того, что посещение Life Office не приведет ни к анализу, ни к специалисту, составляет 50%. Из тех, кто обращается в Life Office, 25% направляют к специалистам, а 35% требуют лабораторных исследований. 9В)\)
$$ P(L \cap S) = 0,35 + 0,25 – 1 + 0,50 = 0,10 $$
1.2 Правило добавления для взаимоисключающих событий
Взаимоисключающие — это термин, описывающий два или более события, которые не могут произойти одновременно . В большинстве случаев это означает ситуацию, когда один исход заменяет другой. Бросание игральных костей является основным примером. Невозможно одновременно выбросить и четверку, и шестерку. Точно так же получение четырех на начальном броске не влияет на то, выпадет ли последующий бросок на шестерку. Все броски игральной кости независимы.
Когда два события, A и B, являются взаимоисключающими, правило сложения говорит нам, что вероятность того, что произойдет A или B , равна сумме вероятностей того, что либо событие произойдет.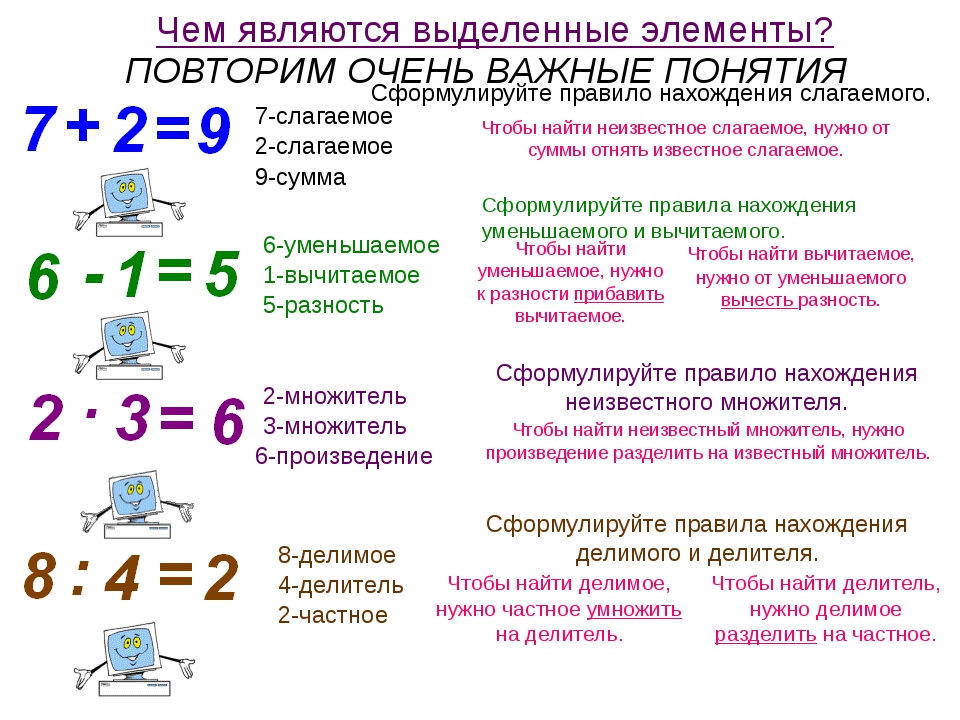
 \). Обратите внимание, что вероятность того, что он никуда не поедет в отпуск, должна быть равна 0,05.
\). Обратите внимание, что вероятность того, что он никуда не поедет в отпуск, должна быть равна 0,05. \[P(\text{новичок И занимается четыре раза в неделю}) = 0,0667\]\[P(\text{новичок})P(\text{занимается четыре раза в неделю}) = 0,0996\] \[0,0667 \ нэкв 0,0996\]
\[P(\text{новичок И занимается четыре раза в неделю}) = 0,0667\]\[P(\text{новичок})P(\text{занимается четыре раза в неделю}) = 0,0996\] \[0,0667 \ нэкв 0,0996\] \(P(\text{N}) = 0,85; P(\text{N|B}) = 0,02\). Итак, \(P(\text{N|B})\) не равно \(P(\text{N})\).
\(P(\text{N}) = 0,85; P(\text{N|B}) = 0,02\). Итак, \(P(\text{N|B})\) не равно \(P(\text{N})\). Доступно на сайте www.thestar.com/news/gta/2011…_suggests.html (по состоянию на 2 мая 2013 г.).
Доступно на сайте www.thestar.com/news/gta/2011…_suggests.html (по состоянию на 2 мая 2013 г.). Доступно на сайте www.ropercenter.uconn.edu/ (по состоянию на 2 мая 2013 г.).
Доступно на сайте www.ropercenter.uconn.edu/ (по состоянию на 2 мая 2013 г.).
 org/details/books/introductory-statistics
org/details/books/introductory-statistics