Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Задача. Найдите значение выражения:
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части.
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Смотрите также:
- Сложные выражения с дробями. Порядок действий
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Тест к уроку «Площади многоугольников на координатной сетке» (средний)
- Сложные логарифмические неравенства
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться.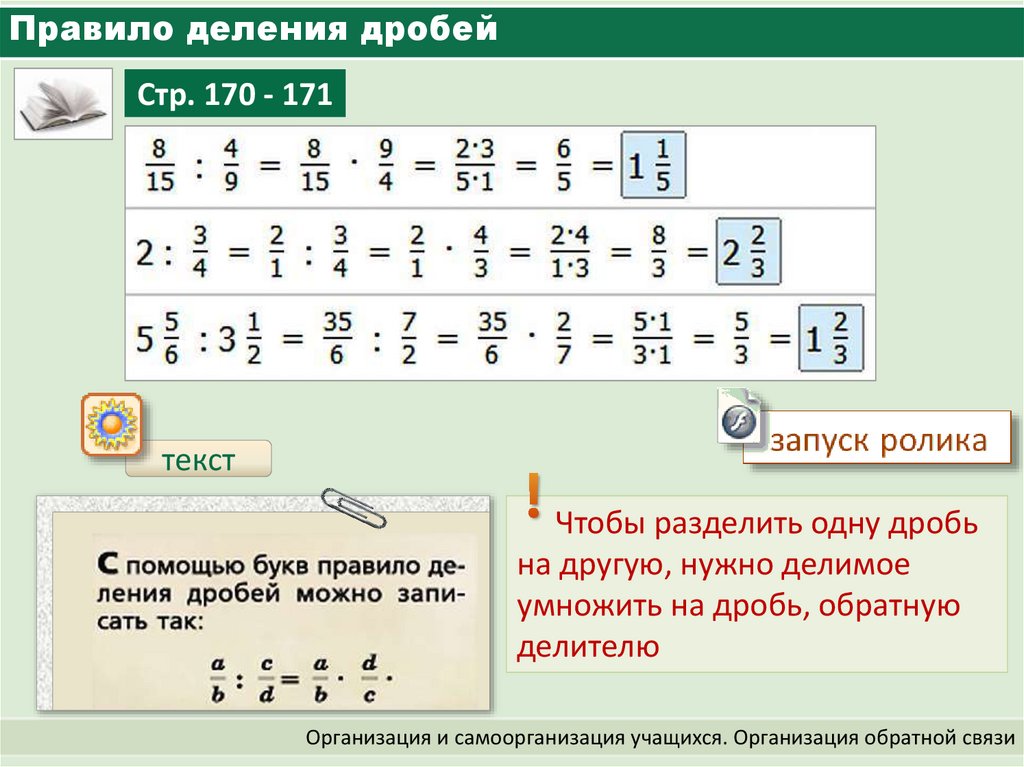 Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается.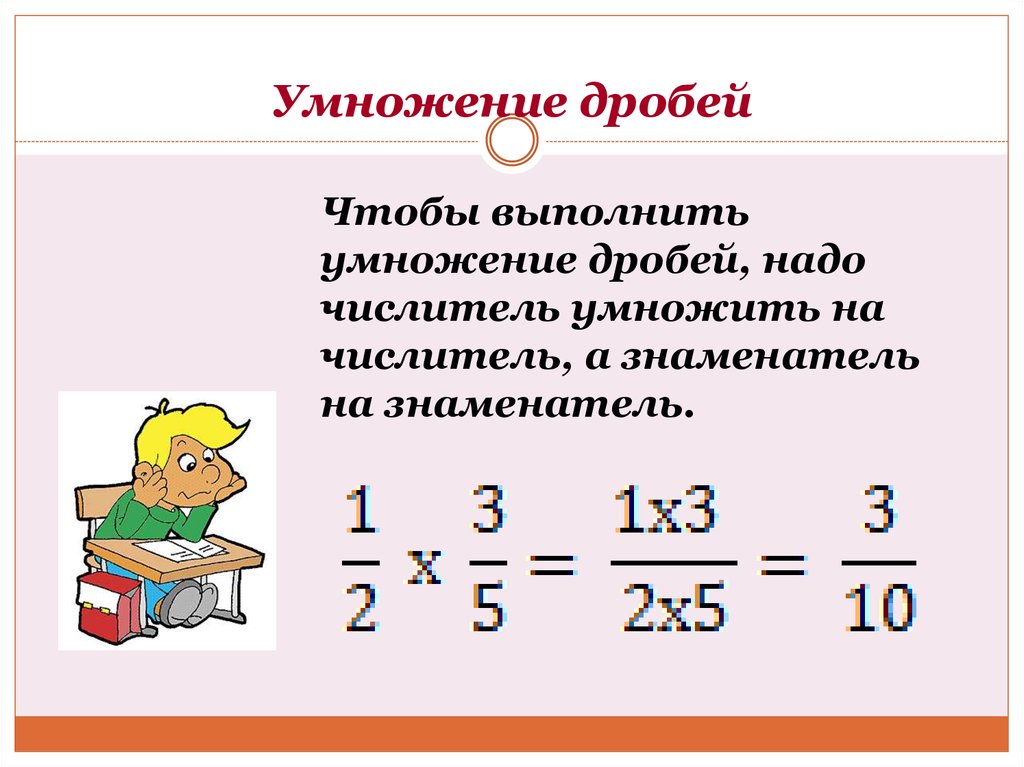 К прибавить получается .
К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз.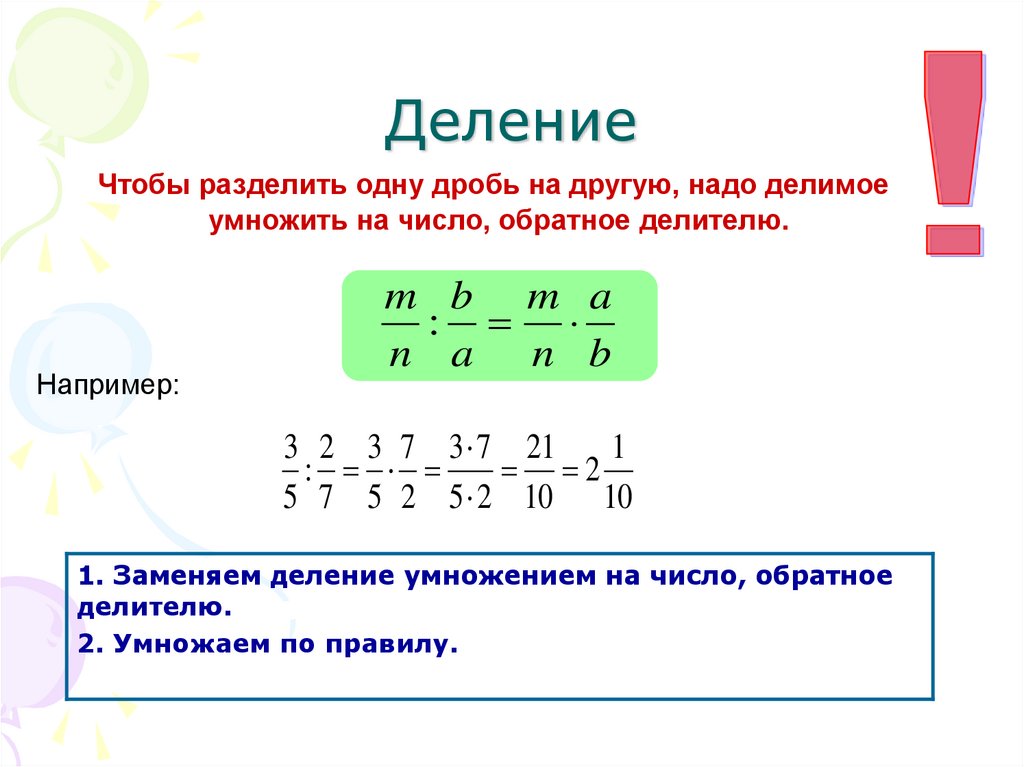 К примеру, если пиццы взять 1 раз, то получится пиццы
К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.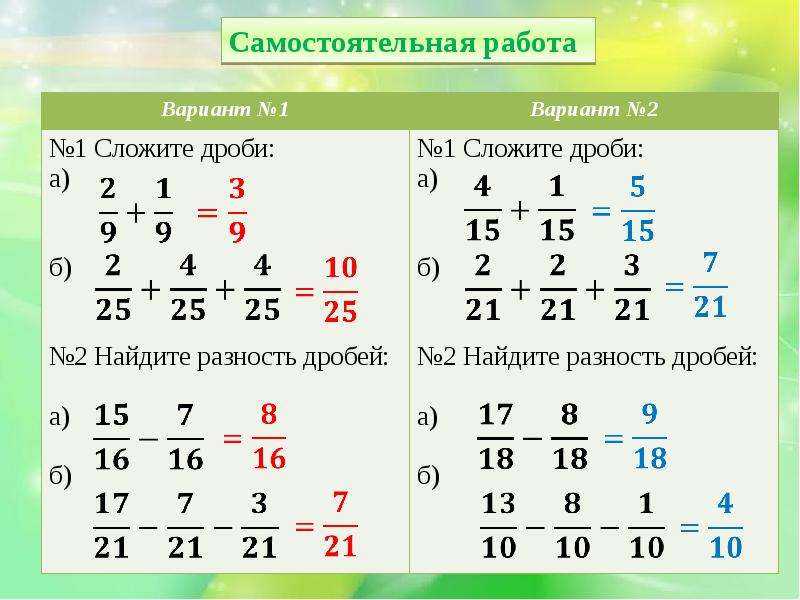
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
- для дроби обратной дробью является дробь
- для для дроби обратной дробью является дробь
- для дроби обратной дробью является дробь
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Задание 2. Найдите значение выражения:
Решение:
Показать решение
Задание 3. Найдите значение выражения:
Решение:
Показать решение
Задание 4. Найдите значение выражения:
Решение:
Показать решение
Задание 5. Найдите значение выражения:
Решение:
Показать решение
Задание 6. Найдите значение выражения:
Решение:
Показать решение
Задание 7. Найдите значение выражения:
Решение:
Показать решение
Задание 8. Найдите значение выражения:
Решение:
Показать решение
Задание 9. Найдите значение выражения:
Решение:
Показать решение
Задание 10. Найдите значение выражения:
Решение:
Показать решение
Задание 11. Найдите значение выражения:
Решение:
Показать решение
Задание 12. Найдите значение выражения:
Решение:
Показать решение
Задание 13. Найдите значение выражения:
Решение:
Показать решение
Задание 14. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
просто и понятно с примерами
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части, на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
…
Оглавление:
- Видео: Умножение дробей
- Умножение дробей с разными знаменателями
- Видео: Сложение и вычитание смешанных чисел
- Видео: Математика 6 класс. Сложение смешанных чисел с разными знаменателями
- Как происходит перемножение
- Видео: Математика 6 класс. Деление дробей
- Видео: Математика 6 класс. Умножение обыкновенных дробей
- Простейшие действия с дробями онлайн
- Видео: Обыкновенные дроби — сложение, вычитание, умножение, деление.
- Видео: Умножение смешанных дробей
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Это интересно: Как найти разность чисел в математике?
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Видео: Умножение дробей
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей:
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
Это интересно: как обозначается площадь, примеры для вычисления.
Видео: Сложение и вычитание смешанных чисел
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/b * c/d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Это интересно: что такое модуль числа?
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/9 * 6/7 = 8*6 / 9*7 = 48/63 = 16/21;
- 4/6 * 3/7 = 2/3 * 3/7<> 2*3 / 3*7 = 6/21.
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей.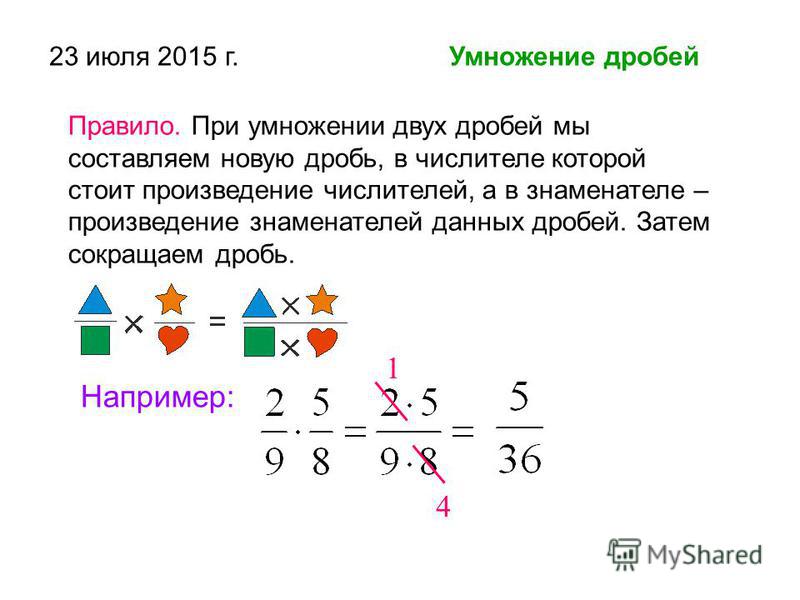 Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/11 =1 + 4/11.
Видео: Математика 6 класс. Сложение смешанных чисел с разными знаменателями
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
Пример 1.
2 1/2 * 7 3/5 = 2 + 1/2 * 7 + 3/5 = 2*7 + 2* 3/5 + 1/2 * 7 + 1/2 * 3/5 = 14 + 6/5 + 7/2 + 3/10 = 14 + 12/10 + 35/10 + 3/10 = 14 + 50/10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть, записать правило для этого действия можно формулой:
a * b/c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/15 = 12/15 + 12/15 + 12/15 + 12/15 = 48/15 = 3 1/5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/f = e/f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Видео: Математика 6 класс.
 Деление дробей
Деление дробейПример 2.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/3 * 4 1/5 = 5/3 * 21/5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
Видео: Математика 6 класс. Умножение обыкновенных дробей
Простейшие действия с дробями онлайн
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Видео: Обыкновенные дроби — сложение, вычитание, умножение, деление.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения, но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Видео: Умножение смешанных дробей
Деление дробей с разными знаменателями 6. Умножение и деление дробей
Умножение десятичных дробей
Десятичная форма записи позволяет выполнять умножение дробей практически по тем же правилам, по которым умножают натуральные числа. Отличие заключается в том, что необходимо определять место запятой в полученном произведении.
Поясним сказанное на примере; вычислим произведение 2,5 1,02.
Перенесем запятую в первом множителе на одну цифру вправо, а во втором-на две цифры вправо. Тем самым первый множитель увеличится в 10 раз, второй-в 10 2 = 100 раз, а произведение-в 10 100 = 1000 раз.
Определим произведение натуральных чисел 25 и 102:
25 102 = 2550.
Это число в 1000 раз больше, чем требуемое произведение. Поэтому необходимо число 2550 уменьшить в 1000= 10 3 раз, т. е. перенести в этом числе запятую влево на 3 цифры. Таким образом,
2,5 1,02 = 2,550 = 2,55.
Можно рассуждать по-другому:
Таким образом, чтобы перемножить две десятичные дроби9 достаточно, не обращая внимания на запятые, перемножить их как натуральные числа9 а затем в полученном произведении справа отделить запятой столько цифр, сколько их было после запятых в обоих множителях вместе.
Например,
Деление десятичных дробей
Рассмотрим пример деления десятичной дроби на натуральное число.
Пример . Вычислить 46,8: 2.
Решение . 4 десятка делим на 2-получаем цифру частного 2 (2 десятка).
6 единиц делим на 2 — получаем цифру частного 3 (3 единицы).
Деление целой части закончено-отделяем в частном целую часть запятой.
8 десятых делим на 2 — получаем цифру частного 4 (4 десятых). Остаток равен 0-деление закончено.
Деление десятичной дроби на десятичную дробь сводится к делению на натуральное число переносом запятых в делимом и делителе на столько цифр вправо, чтобы делитель стал натуральным числом.
Пример . Вычислить 4,42:0,2.
Решение . Так как в делителе одна цифра после запятой, то достаточно перенести запятые в делимом и делителе на 1 цифру вправо. Тем самым делимое и делитель увеличиваются в 10 раз, поэтому частное не изменится. При этом делитель будет натуральным числом.
Можно рассуждать и таким образом:
Но не всегда получается точный результат при делении десятичных дробей. Чаще приходится довольствоваться приближенным частным.
Пример . Найти частное 1,723:0,03.
Решение . Освободимся от запятой в делителе: 1,723:0,03= 172,3:3. Выполним деление.
Начиная с разряда сотых, цифра 3 в частном повторяется без конца, потому что остаток, начиная с третьего этапа процесса деления, все время равен одному и тому же числу 1.
Если оставить у частного первые две цифры после запятой, то получится приближенное равенство: 172,3:3 ≈ 57,43.
§ 15. Умножение и деление обыкновенных дробей — Учебник по Математикe 6 класс (Зубарева, Мордкович)
Краткое описание:
В этом параграфе учебника вас ждет более сложные операции с умножением и делением, так как следует научится не только умножению и делению целых чисел, но также и дробей. Есть множество особенностей выполнения этих действий, но если понять принцип, вы сможете решать любые выражения!
Умножение дробей кажется очень сложным при первом взгляде на эти числа. Но для того, чтобы решать такие выражения, нужно просто по порядку проделать определенные действия. Например, для умножения дробей на натуральное число, числитель умножается на множитель, а знаменатель остается таким же. После умножения эту дробь можно сократить, выявив в ней общее для числителя и знаменателя число и вынеся его как целое число. Так например, 2/3 4 = 2 4/3 = 8/3 = 2 2/3. При умножении смешанной дроби (с целым и дробью) на число, целое число и числитель умножаются между собой, а знаменатель по прежнему остается таким же. Если же нужно умножить между собой простые дроби, нужно перемножить между собой числители и записать значение в числитель и знаменатели перемножить между собой, записав значение в знаменатель. Если вам нужно умножить смешанные дроби между собой, в таком случае нужно перевести множители в неправильные дроби и определить значение выражение как в рассмотренном примере. Для деления дробей существуют другие правила, но они достаточно простые, если внимательно их изучить. При делении дроби на целое число, целое число записывают в знаменатель, но уже с действием умножения. При делении целого числа на дробь, целое число умножают на обратную дробь (тоесть перевернутый числитель и знаменатель). То же правило действует для деления дробей между собой: дробь, которая выступает за делимое, переворачивают и производят действие умножения. Еще подробней и с большими примерами вы сможете рассмотреть эту тему на страницах учебника!
При умножении смешанной дроби (с целым и дробью) на число, целое число и числитель умножаются между собой, а знаменатель по прежнему остается таким же. Если же нужно умножить между собой простые дроби, нужно перемножить между собой числители и записать значение в числитель и знаменатели перемножить между собой, записав значение в знаменатель. Если вам нужно умножить смешанные дроби между собой, в таком случае нужно перевести множители в неправильные дроби и определить значение выражение как в рассмотренном примере. Для деления дробей существуют другие правила, но они достаточно простые, если внимательно их изучить. При делении дроби на целое число, целое число записывают в знаменатель, но уже с действием умножения. При делении целого числа на дробь, целое число умножают на обратную дробь (тоесть перевернутый числитель и знаменатель). То же правило действует для деления дробей между собой: дробь, которая выступает за делимое, переворачивают и производят действие умножения. Еще подробней и с большими примерами вы сможете рассмотреть эту тему на страницах учебника!
Технологическая карта урока.
ФИО учителя: Степанова Дарья Сергеевна
Место работы: МАОУ «СОШ №76»
Должность: учитель математики
Предмет: математика
Тема урока: «Деление обыкновенных дробей».
Тип урока : урок открытия нового знания .
ЦЕЛЬ УРОКА:
Образовательные: сформировать представление о делении обыкновенных дробей, выработать первичное умение выполнять деление чисел, записанных в виде дробей.
Развивающие: развитие математического мышления учащихся и вычислительных навыков.
Воспитательные: содействовать воспитанию интереса к математике, воспитывать культуру математических записей.
Оборудование : Учебник для 6 класса общеобразовательных учреждений/ Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.- издание.- М.: Мнемозина, 2007, мультимедийный проектор, презентация к уроку по данной теме., раздаточный материал.
План:
Организационный момент (1 мин.).
Целеполагание и мотивация (7 мин. ).
).
Открытия нового знания (13 мин.).
Физкультминутка (1мин.).
Закрепление нового (15 мин.).
Подведение итогов. Рефлексия (3 мин.).
Домашнее задание (1 мин).
–Здравствуйте! Давайте проверим все ли у нас готово к уроку?
Проверяют. Достают тетради и ручки, если не достали.
–Вспомним, с каким новым понятием мы познакомились на предыдущих уроках?
–Какие числа называют взаимно обратными?
–Хорошо! Молодцы! А теперь давайте устно решим примеры на слайде.
–Из 1 вычесть мы получим?
– Что мы должны сделать, чтобы решить второй пример?
–Чему он равен?
– Тогда дополнительный множитель, для первой дроби равен?
–Молдец! Чему равен НОЗ в третьем примере?
– Как вычислим следующий пример? Как мы умножаем дробь на дробь?
–Что можно сделатьперед тем как перемножать?
–Верно, Молодец! Как умножить натуральное число на дробь?
– Что будем делать, перед тем как перемножать?
–Молодец! Как решить следующий пример?
–Верно, что получим?
Хорошо! Следующий пример.
–Молодец! Что нужно сделать, чтоб перемножить следющие два числа?
–Как будем решать следующий приер?
–С понятием взаимно обратных чисел
– Числа называют взаимно обратным, если в произведении они дают единицу.
(один ученик вслух разбирает один пример).
–Найти наименьший общий знаменатель.
–14, так как 14 делиться на 7 нацело.
–Двум. Домножим дробь на два, получим . Прибавим к дробь , получим ответ .
–Так как 7 и 5 взаимно простые числа, наименьший общий знаменатель равен 35.
Для первой дроби дополнительный множитель равен 5, для второй дроби 7. Домножим первую дробь на 5, получим , вторую дробь на 7, получим . Разность равна .
–Чтобы умножить дробь на дробь, нужно перемножить числители дробей и записать это произведение в числитель, перемножить знаменатели и записать произведение в знаменатель.
–Можно сократить 4 и 8 на 4, и 3 и 9 на 3, получим одну шестую
– Чтобы умножить натуральное число на обыкновенную дробь, нужно числитель умножить на это число, а знаменатель оставить без изменения.
–Сократим 23 и 23. Ответ 9.
– Сначала надо записать смешанное число в неправильную дробь, а потом перемножить.
–Получим дробь , перемножим ее с . Можем сократить 7 и 7. Ответ .
–Сократить ничего нельзя. Перемножаем 4 и 5,в числител запишем 20, в знаменателе 7 или .
– Нужно представить смешанные числа в виде неправильной дроби. Получим и . Можем сократить 5 и 15 на 3 и 22 и 2 на 2. В числителе получим 11 взнаменателе 3 или .
– Мы не знаем как делить.
–Как вы думаете, какая тема нашего урока на сегодня?
–Врно! Откройте тетради запишите число и тему урока.
–Какую цель мы поставим на сегоднящний урок?
–А для того, чтобы научиться делить, что нам сначала надо узнать?
–Верно! Для этого, вначале, рассмотрим задачу. Площадь прямоугольника равна
. Длина одной стороны
. Найти длину другой стороны.
– Назовите формулу площади прямугольника.
– Ширина и площадь нам известны, а длина – нет. Как мы обозначаеим неизвестную величину?
Как мы обозначаеим неизвестную величину?
– Можем мы с вами теперь составить уравнение?
–Мы с вами уже решали такие уравнения с помощью взаимно обратных чисел. Давайте решим его.
– Что получим в правой части уравнения?
–Что получим в левой части уравнения?
– Хорошо. Нашли чему равна длинна. Давайте вернемся к уравнению, и вспомним, как наити нейзвестный множитель?
–Верно! Примените это к нашему уравнению, что получим?
–Но мы уже знаем чему равен x .
– И как мы его нашли?
– А по отношению к какая дробь?
– То есть мы можем составить такое равенство:
.
– Исходя из этого равенства попробуйте сформулировать правило деления обыкновенных дробей.В этом вам поможет карточка №1, заполните пропуски в ней.
–Верно, молодцы! Запишите в тетрадь данное определение в буквенном виде, самостоятельно. Проверьте.
–Можем ли мы теперь решить тот пример, который в начале вызвал у нас затруднение(возрашаемся к примеру)?
– Деление обыкновенных дробей.
(Открывают тетради, записывают тему урока).
–Научиться выполнять деление дробей.
–Правило деления дробей.
– S = ab .
– x .
–Да.
.
– Нужно домножить обе части уравнение на обратное число, числу . То есть на .
–В правой части произведение двух взаимно обратных чисел дадут нам единицу.
–В левой части, произведение и . Сократить ничего нельзя, значит получим .
.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
–
.
–
. Мы умножили на .
–Обратная.
–Чтобы разделить одну дробь на другую, нужно делимое умножить на число обратную делителю.
– Да,
.
–А теперь разомнемся немного. Сожмите разожмите кулочки. Расправте плечики. Делайте движения головой, следуя за снежинкой.
–Верно! Учиться применять правило на практике.
(На слайде примеры. Вызываем учеников по одному к доске, остальные работают в тетрадях. )
)
–Молодцы! У вас на партах есть карточка №2. Выполните ее самостоятельно. Задание: Вставьте пропуски в примерах, чтобы получились верные равенства.
–Проверьте себя сами! Если все пропуски заполнены верно или одна ошибка – оценка «5», если 2-4 ошибки – оценка «4», если 5-7 ошибок –оценка «3».
–Решать примеры.
(выполняют карточки с заданиями №2)
(проверяют, оценивают себя)
–Давайте подведем итоги! Как вы считаете, добились ли мы поставленной в начале урока цели?
–Давайте повторим правило, которое мы сегодня узнали. (спрашиваем нескольких учеников).
–Хорошо! Молодцы! У вас на столах лежат разного цвета карточки, оцените с помощью их результат вашей работы сегодня на уроке.
– Чтобы разделить одну дробь на другую, нужно делимое умножить на число обратную делителю.
(поднимают карточки).
–Откройте дневники и запишите домашнее задание.
–Спасибо за урок!
(Записывают домашнее задание в дневники).
Раздаточный материал.
Каточка №1
Правило деления обыкновенных дробей.
Чтобы разделить одну дробь на другую, надо делимое ___________ на число, ____________ делител ю.
Карточка №2
Правила деления обыкновенных дробей с разными знаменателями. Дроби. Умножение и деление дробей
Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Как разделить простую дробь на натуральное число?
Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби. Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.
Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:
Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.
Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.
Рассмотрим на примере как разделить дробь на целое число.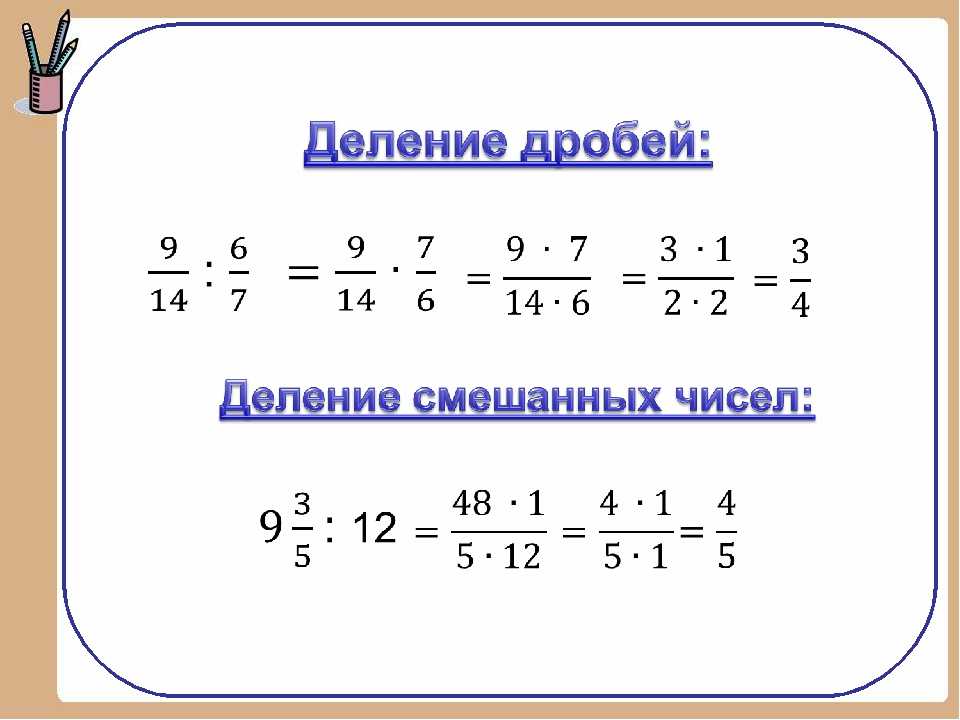 Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.
Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.
Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:
- для разделения десятичной дроби на натуральное число применяют деление в столбик;
- запятая ставится в частном тогда, когда закончено деление целой части делимого.
Применяя эти простые правила, всегда можно без особого труда разделить любую десятичную или простую дроби на целое число. Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.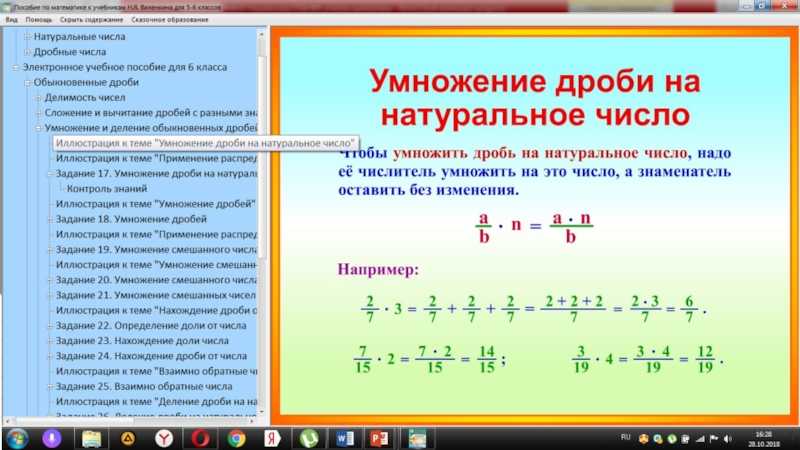
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2.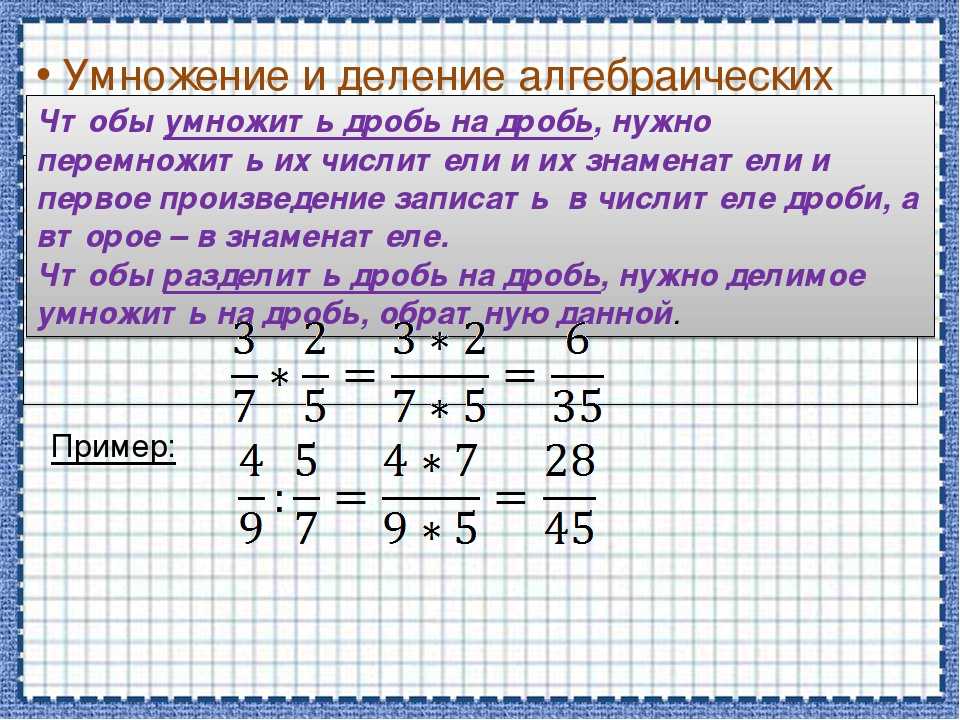 Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть.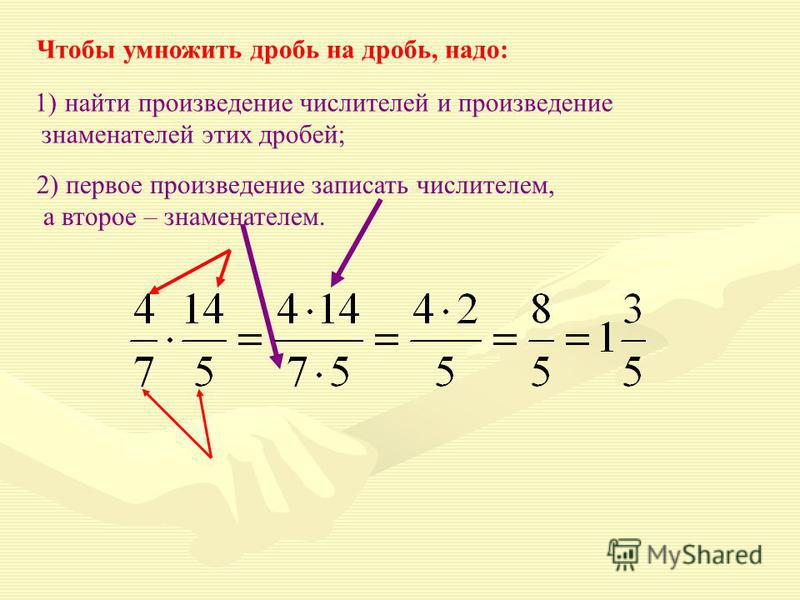 Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.
Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:
- Верхняя часть дроби называется числителем, а нижняя – знаменателем.

- При делении числа называются так: делимое: делитель = частное
Как делить дроби: простые дроби
Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:
3/77: 1/11 = 3 /77 * 11 /1 = 3/7
Как делить дроби: смешанные дроби
Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:
10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40
Как делить дробь на число
Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:
Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:
5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77
Как делить десятичные дроби
Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.
Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже. ..»)
..»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению.
 Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
В общем, будьте внимательны.
Умножение и деление алгебраических дробей
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
23·47=2·43·7=821
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
23:711=23·117=227=1121
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Сформулируем правило:
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
В буквенном виде правило можно записать как ab·cd=a·cb·d . Здесь a, b, c и d будут представлять из себя определенные многочлены, причем b и d не могут быть нулевыми.
Определение 2Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Это правило можно также записать как ab:cd=ab·dc=a·db·c . Буквы a, b, c и d здесь означают многочлены, из которых a, b, c и d не могут быть нулевыми.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a·b+1a3 дробь a3a·b+1 будет обратной.
Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a·b+1a3 дробь a3a·b+1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Пример 1Условие: умножьте дробь 1x+y на 3·x·yx2+5 , а потом разделите одну дробь на другую.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1x+y·3·x·yx2+5=1·3·x·y(x+y)·(x2+5)
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1·3·x·y(x+y)·(x2+5)=3·x·yx3+5·x+x2·y+5·y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x2+53·x·y :
1x+y:3·x·yx2+5=1x+y·x2+53·x·y
Приведем полученную дробь к стандартному виду:
1x+y·x2+53·x·y=1·x2+5(x+y)·3·x·y=x2+53·x2·y+3·x·y2
Ответ: 1x+y·3·x·yx2+5=3·x·yx3+5·x+x2·y+5·y ; 1x+y:3·x·yx2+5=x2+53·x2·y+3·x·y2 .
Довольно часто в процессе деления и умножения обыкновенных дробей получаются результаты, которые можно сократить, например, 29·38=672=112 . Когда мы выполняем эти действия с алгебраическими дробями, мы также можем получить сократимые результаты. Для этого полезно предварительно разложить числитель и знаменатель исходного многочлена на отдельные множители. Если нужно, перечитайте статью о том, как правильно это делать. Разберем пример задачи, в которой нужно будет выполнить сокращение дробей.
Пример 2Условие: перемножьте дроби x2+2·x+118·x3 и 6·xx2-1 .
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1
У нас получилась дробь, которую можно сократить:
x+12·6·x18·x3·x-1·x+1=x+13·x2·(x-1)
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
x+13·x2·(x-1)=x+13·x3-3·x2
Вот запись всего решения без пояснений:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1==x+13·x2·(x-1)=x+13·x3-3·x2
Ответ: x2+2·x+118·x3·6·xx2-1=x+13·x3-3·x2 .
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
Пример 3Условие: разделите 217·x-1 на 12·x7-x .
Решение: начнем с упрощения алгебраической дроби 217·x-1 , чтобы избавиться от дробного коэффициента. Для этого умножим обе части дроби на семь (это действие возможно благодаря основному свойству алгебраической дроби). В итоге у нас получится следующее:
217·x-1=7·27·17·x-1=14x-7
Видим, что знаменатель дроби 12·x7-x , на которую нам нужно разделить первую дробь, и знаменатель получившейся дроби являются противоположными друг другу выражениями. Изменив знаки числителя и знаменателя 12·x7-x , получим 12·x7-x=-12·xx-7 .
Изменив знаки числителя и знаменателя 12·x7-x , получим 12·x7-x=-12·xx-7 .
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
217·x-1:12·x7-x=14x-7:-12·xx-7=14x-7·x-7-12·x=14·x-7x-7·-12·x==14-12·x=2·7-2·2·3·x=7-6·x=-76·x
Ответ: 217·x-1:12·x7-x=-76·x .
Как умножить или разделить алгебраическую дробь на многочлен
Чтобы выполнить такое действие, мы можем воспользоваться теми же правилами, что мы приводили выше. Предварительно нужно представить многочлен в виде алгебраической дроби с единицей в знаменателе. Это действие аналогично преобразованию натурального числа в обыкновенную дробь. Например, можно заменить многочлен x2+x−4 на x2+x−41 . Полученные выражения будут тождественно равны.
Пример 4Условие: разделите алгебраическую дробь на многочлен x+45·x·y:x2-16 .
Решение
Начнем с замены многочлена дробью, далее действуем согласно основному правилу.
x+45·x·y:x2-16=x+45·x·y:x2-161=x+45·x·y·1×2-16==x+45·x·y·1(x-4)·x+4=(x+4)·15·x·y·(x-4)·(x+4)=15·x·y·x-4==15·x2·y-20·x·y
Ответ: x+45·x·y:x2-16=15·x2·y-20·x·y.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Как делить дроби с разными знаменателями
Когда вы складываете или вычитаете две дроби, обе дроби должны иметь одинаковые знаменатели. Но для умножения или деления дробей знаменатели вообще не имеют значения. Когда вы умножаете, вы просто работаете прямо над дробью, умножая все числители вместе, а затем все знаменатели вместе. Деление дробей работает точно так же, с добавлением еще одного шага в начале.
TL;DR (слишком длинный; не читал)
Чтобы разделить дроби независимо от знаменателей, переверните вторую дробь (делитель) вверх ногами и умножьте результат на первую дробь (делимое).
SO A / B ÷ C / D = A / B × D / C = ad / bc
Повторение: умножение дробей с разными знаменателями
Прежде чем перейти к делению дробей, найдите минутку, чтобы просмотреть процесс умножения дробей. Вам также понадобится этот навык для работы с задачами на деление.
Если перед вами стоит задача на умножение вида
\frac{a}{b} × \frac{c}{d}
, знаменатели не имеют значения. Все, что вам нужно сделать, это перемножить числители и записать их в качестве числителя вашего ответа; затем умножьте знаменатели вместе и умножьте их как знаменатель вашего ответа.
Пример 1: Вычислить
\frac{2}{5} × \frac{1}{3}
Помните, что для умножения не имеет значения, имеют ли ваши дроби одинаковые знаменатели. Все, что вам нужно сделать, это умножить прямо поперек, что дает вам:
\frac{2 × 1}{5 × 3}
, что при упрощении дает вам:
\frac{2}{15}
Если вы можете упростить свой ответ, сократив множители из числителя и знаменателя, вы должен. Но в этом случае дальнейшее упрощение невозможно, поэтому полный ответ будет следующим:
Но в этом случае дальнейшее упрощение невозможно, поэтому полный ответ будет следующим:
\frac{2}{5} × \frac{1}{3} = \frac{2}{15}
Теперь о делении. Дроби
Теперь, когда вы рассмотрели, как умножать дроби, деление дробей работает почти так же — вам просто нужно добавить один дополнительный шаг. Переверните вторую дробь (также известную как делитель) вверх ногами, а затем измените операцию на умножение вместо деления.
Итак, если ваша первоначальная задача на деление выглядит так:
\frac{a}{b} ÷ \frac{c}{d}
Первое, что вы делаете, это переворачиваете вторую дробь вверх ногами, получая д / с ; затем измените знак деления на знак умножения, что даст вам:
\frac{a}{b} × \frac{d}{c}
И поскольку вы практиковались в умножении дробей, вы знаете, как решить эту задачу. Просто умножьте числители и знаменатели, что даст вам результат:
\frac{a}{b} ÷ \frac{c}{d} = \frac{ad}{bc}
Два примера деления дробей
Теперь, когда вы знаете процесс деления дробей, пора попрактиковаться на паре примеров.
Пример 2: Вычислить
\frac{1}{3} ÷ \frac{8}{9}
Помните, что ваш первый шаг – перевернуть вторую дробь вверх ногами и изменить операцию на умножение. Это дает вам:
\frac{1}{3} × \frac{9}{8}
Теперь просто перемножьте и упростите:
\frac{1 × 9}{3 × 8} = \frac{9}{24} = \frac{3}{8}
Итак,
\frac{ 1}{3} ÷ \frac{8}{9} = \frac{3}{8}
Пример 3: Вычислить
\frac{11}{10} ÷ \frac{5}{ 7}
Обратите внимание, что одна из этих дробей неправильная (числитель больше знаменателя). Но это не меняет процесса деления дробей, поэтому переверните вторую дробь вверх ногами и измените операцию на умножение:
\frac{11}{10} × \frac{7}{5}
Как и прежде, умножьте и упростите, если сможете:
\frac{11 × 7}{10 × 5} = \frac{ 77}{50}
77 и 50 не имеют общих множителей, поэтому дальнейшее упрощение невозможно. Таким образом, ваш окончательный ответ:
\frac{11}{10} ÷ \frac{5}{7} = \frac{77}{50}
Уловка для запоминания
Если вы изо всех сил пытаетесь запомнить это , полезно вспомнить, что умножение и деление — взаимные операции; то есть одно отменяет другое. Когда вы переворачиваете дробь вверх ногами, это тоже называется обратной величиной. Итак, d / c является обратной величиной c / d , и наоборот.
Когда вы переворачиваете дробь вверх ногами, это тоже называется обратной величиной. Итак, d / c является обратной величиной c / d , и наоборот.
Это означает, что когда вы делите дробь, вы фактически выполняете обратную операцию над обратной дробью . Чтобы проблема разрешилась, должны присутствовать обе эти взаимосвязи. Если бы у вас был только один из них — скажем, если бы вы выполнили обратную операцию (умножение), не взяв сначала обратное значение этой второй дроби — ваш ответ не был бы правильным.
Итак, есть ОДНО дополнительное правило, на которое следует обращать внимание, когда речь заходит о том, какие дроби можно делить, а какие нет. Точно так же, как вы не можете делить целые числа на ноль, вы также не можете делить дробь на ноль; результат не определен. Если вы забудете об этом, вам довольно быстро напомнят, если вы попытаетесь решить такую задачу, как 5/6 ÷ 0/2.
 Это потому, что обычно вы переворачиваете вторую дробь и умножаете: 5/6 × 2/0. Но в знаменателе дроби не может быть нуля; это тоже считается неопределенным.
Это потому, что обычно вы переворачиваете вторую дробь и умножаете: 5/6 × 2/0. Но в знаменателе дроби не может быть нуля; это тоже считается неопределенным.
Как насчет деления смешанных чисел?
Если вас просят разделить смешанные числа, будьте осторожны – это ловушка! Прежде чем вы сможете продолжить, вы должны преобразовать это смешанное число в неправильную дробь. Как только это будет сделано, вы будете следовать точно такому же процессу, который вы бы использовали для правильных дробей. См. Пример 3 выше, иллюстрирующий, как это работает. Он включает неправильную дробь 11/10, которую также можно записать как смешанное число 1 1/10.
Деление дробей – Математика для торговли: Том 1
Дроби
Деление дробей следует той же логике, что и умножение дробей. Это предполагает работу с числителями и знаменателями отдельно. После того, как вы сделали свои первоначальные расчеты, вы собираете все это вместе, чтобы получить ответ. Однако есть небольшой поворот, который нам придется изучить, когда мы будем работать над некоторыми вопросами.
Однако есть небольшой поворот, который нам придется изучить, когда мы будем работать над некоторыми вопросами.
Прежде чем мы доберемся до всего этого, давайте начнем с деления целых чисел, а затем перейдем к дробям.
Начните с 20 отверток:
Теперь разделите эти 20 отверток на 10 (или на группы по 10).
[латекс]\LARGE20÷10=2[/латекс]
Вы получите 2 группы по 10 человек.
Теперь разделите эти 20 отверток на 5 (или на группы по 5).
[латекс]\БОЛЬШОЙ20÷5=4[/латекс]
Вы получите 4 группы по 5 человек.
Теперь разделите эти 20 отверток на 2 (или на группы по 2).
[латекс]\НАИБОЛЕЕ20÷2=10[/латекс]
Вы получите 10 групп по 2 человека.
Взгляните на математику здесь. Вы видите закономерность? Что ты придумал? Вы заметили, что когда вы берете исходную сумму (в данном случае 20) и делите ее на число, которое продолжает уменьшаться (10, затем 5, затем 2), мы получаем ответ, который становится больше.
[латекс]\LARGE20÷10=2[/латекс]
[латекс]\БОЛЬШОЙ20÷5=4[/латекс]
[латекс]\НАИБОЛЕЕ20÷2=10[/латекс]
Следуйте этой логике в дроби, помня, что дроби не только меньше 10, 5 и 2, но и 1. Используя этот шаблон, мы определяем, что деление 20 отверток на число меньше 1 даст нам больший ответ чем если бы мы разделили 20 на 10, 5 или 2.
Попробуйте это. Возьмите 20 отверток и разделите их на ½. Как вы думаете, каким будет ваш ответ?
[латекс]\БОЛЬШОЙ20÷\dfrac{1}{2}=?[/латекс]
Следуя нашей логике, ответ должен быть больше 10, и это действительно так.
[латекс]\БОЛЬШОЙ20÷\dfrac{1}{2}=40[/латекс]
Однако это не означает, что у нас будет 40 отверток. Это означает, что в итоге мы получим 40 частей отверток. Вы должны представить, что каждая из отверток была разделена на 2. Двадцать отверток, разделенных пополам, дадут нам в итоге 40 штук. Теперь возникает вопрос, как мы можем сделать это математически? Ответ заключается в использовании того, что известно как взаимное. Вот определение.
Вот определение.
Взаимное : Число, которое связано с другим числом таким образом, что их произведение равно 1.
Это означает, что если вы возьмете число, например 5, а затем умножите его на обратную величину, вы получите ответ 1. Мы начнем с целого числа 5. Мы также могли бы записать число 5 как дробная часть.
[латекс]\БОЛЬШОЙ5=\dfrac{5}{1}[/латекс]
Используя наше определение обратного числа, нам нужно найти число, которое при умножении на 5 / 1 дает нам ответ 1.
Чтобы найти ответ, нам нужно вернуться к умножению дробей. Помните, что когда мы умножаем дроби, мы просто умножаем числители, а затем умножаем знаменатели. Отсюда можно сделать вывод, что:
[латекс]\БОЛЬШОЙ\dfrac{5}{1}\times\dfrac{1}{5}=1[/латекс]
В конце концов, чтобы найти обратную дробь, мы просто берем числитель и делаем его знаменателем, берем знаменатель и делаем его числителем. По сути, мы просто переворачиваем дробь. Вот еще несколько примеров взаимности.
Вот еще несколько примеров взаимности.
[латекс]\БОЛЬШОЙ\dfrac{3}{8}\text{ и }\dfrac{8}{3}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{2}{9}\text{ и }\dfrac{9}{2}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{24}{17}\text{ и }\dfrac{17}{24}[/latex]
Итак, теперь, когда мы устранили взаимный вопрос, возникает вопрос, зачем нам вообще нужны взаимные вопросы? Что ж, ответ кроется в правиле деления дробей.
Правило деления дробей заключается в том, что вы берете первую дробь и умножаете ее на обратную величину второй дроби. Да, вы не ослышались: при делении вы в конечном итоге умножаете, но только после того, как сначала перевернете вторую дробь.
Переворачивание второй дроби (нахождение ее обратной величины) изменяет значение уравнения. Чтобы математически сохранить уравнение таким же, мы должны заменить вопрос на деление вопросом на умножение. Взгляните на следующий пример, чтобы увидеть, как это делается.
[латекс]\БОЛЬШОЙ\dfrac{1}{2}÷\dfrac{3}{8}=?[/latex]
Шаг 1 : Задайте вопрос в удобной для работы форме. Это включает в себя нахождение обратной величины второй дроби и последующее умножение ее на первую.
Это включает в себя нахождение обратной величины второй дроби и последующее умножение ее на первую.
[латекс]\БОЛЬШОЙ\текст{Обратное значение }\dfrac{3}{8}\text{ равно }\dfrac{8}{3}[/latex]
[латекс]\БОЛЬШОЙ\текст{Проверить : }\dfrac{3}{8}\times\dfrac{8}{3}=\dfrac{24}{24}=1[/latex]
Таким образом, мы получаем:
[латекс]\БОЛЬШОЙ \dfrac{1}{2}÷\dfrac{3}{8}\text{ становится }\dfrac{1}{2}\times\dfrac{8}{3}=?[/latex]
Шаг 2 : Следуйте той же процедуре, что и при умножении дробей. Перемножьте числители вместе, а затем умножьте знаменатели вместе.
Умножить числители вместе
[латекс]\НАИБОЛЬШИЙ1\times8=8[/латекс]
Умножить знаменатели вместе
[латекс]\НАИБОЛЬШИЙ 4 3 90/003 90[0/0 3 : Возьмите эти ответы и разделите их на дроби.
[латекс]\БОЛЬШОЙ\dfrac{1}{2}\times\dfrac{8}{3}=\dfrac{8}{6}[/latex]
Шаг 4 : Поместите ответ в самый низкий термины, а затем в смешанное число, если это необходимо.
[латекс]\БОЛЬШОЙ\dfrac{4}{3}=1\dfrac{1}{3}\text{ Смешанное число}[/latex]
Окончательный ответ:
[латекс]\БОЛЬШОЙ\dfrac{ 1}{2}÷\dfrac{3}{8}=1\dfrac{1}{3}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{5}{9}÷\dfrac{7}{4}=?[/latex]
Шаг 1 : Задайте вопрос в удобной для работы форме. Это включает в себя нахождение обратной величины второй дроби и последующее умножение ее на первую.
[латекс]\БОЛЬШОЙ\dfrac{5}{9}÷\dfrac{7}{4}\text{ становится }\dfrac{5}{9}\times\dfrac{4}{7}[/latex]
Шаг 2 : Перемножьте числители, а затем умножьте знаменатели.
Умножения числителей вместе
[latex] \ lagry5 \ times4 = 20 [/lagex]
Умножаемые знаменатели вместе
[Latex] \ lagt9 \ times7 = 63 [/lavex]
Шаг 3 . : Возьмите эти ответы и сложите их обратно в дробь.
[латекс]\БОЛЬШОЙ\dfrac{5}{9}\times\dfrac{4}{7}=\dfrac{20}{63}[/latex]
Шаг 4 : Укажите ответ в наименьшем выражении, а затем, при необходимости, в смешанном числе. В этом случае ответ и в наименьшем выражении, и уже является правильной дробью, так что мы закончили.
В этом случае ответ и в наименьшем выражении, и уже является правильной дробью, так что мы закончили.
[латекс]\БОЛЬШОЙ\dfrac{5}{9}÷\dfrac{7}{4}=\dfrac{20}{63}[/latex]
Попробуйте ответить на эти практические вопросы и посмотрите видеоответы, чтобы узнать, как вы справились.
[латекс]\БОЛЬШОЙ\dfrac{7}{8}÷\dfrac{7}{16}=[/латекс]
[латекс]\БОЛЬШОЙ4\dfrac{7}{8}÷2\dfrac{3}{4}=[/латекс]
Примечание. Это немного отличается от того, что мы делали раньше, так как включает в себя деление смешанных чисел. Как вы думаете, что вам придется делать, имея дело с этим?
ОТВЕТ : Сначала нужно преобразовать смешанное число в неправильную дробь. Затем вы можете работать над вопросом так же, как мы делали это раньше.
Ваше полное руководство — Mashup Math
Ключевой вопрос: Как делить дроби на дроби и дроби с целыми числами? Научитесь делить дроби, выполнив 3 простых шага.
Добро пожаловать в это бесплатное пошаговое руководство по делению дробей. Это руководство научит вас, как использовать простой трехэтапный метод под названием «Сохранить-изменить-перевернуть», чтобы легко делить дроби на дроби (а также дроби на целые числа).
Ниже вы найдете несколько примеров того, как делить дроби с помощью метода «Сохранить-изменить-перевернуть», а также объяснить, почему этот метод работает для любой математической задачи, связанной с делением дробей. Кроме того, это бесплатное руководство включает в себя анимированный видеоурок и бесплатный практический лист с ответами!
Вы готовы начать?
Прежде чем вы научитесь делить дроби по методу Сохранить-Изменить-Отразить, вам нужно убедиться, что вы понимаете, как умножать дроби вместе (что даже проще, чем делить!).
Поскольку умножение дробей обычно преподается перед делением дробей, возможно, вы уже знаете, как умножать две дроби. Если это так, вы можете перейти к следующему разделу.
Однако, если вы хотите быстро просмотреть, как умножать дроби, вот правило:
Правило умножения дробей: при перемножении дробей умножайте числители вместе, затем умножайте знаменатели вместе следующим образом…
Например, 3/4 x 1/2 можно решить следующим образом:
Теперь, когда вы знаете, как умножать дроби, вы готовы научиться делить дроби с помощью простого трехэтапного метода «Продолжить-Изменить-Обратить».
Начнем с простого примера
Деление дробей Пример 1Пример 1: Что такое 1/2 ÷ 1/4 ?
Чтобы решить этот пример (и любую задачу, где вам нужно разделить дроби, мы собираемся использовать метод Keep-Change-Flip)
Где:
1. ) СОХРАНИТЬ = Сохраните первую фракцию как есть и просто оставьте ее в покое.
) СОХРАНИТЬ = Сохраните первую фракцию как есть и просто оставьте ее в покое.
2.) ИЗМЕНИТЬ = Изменить знак деления на знак умножения.
3.) FLIP = Перевернуть вторую дробь (поменять местами числитель и знаменатель)
Эти шаги можно применить к примеру 1 следующим образом: исходная задача 1/2 ÷ 1/4 выглядит следующим образом:
Теперь вы можете решить задачу, перемножив дроби вместе и при необходимости упростив:
Обратите внимание, что 4/2 можно упростить.
Окончательный ответ равен 2, и мы можем заключить, что ответ на исходную задачу равен…
Окончательный ответ: 1/2 ÷ 1/4 = 2
Почему этот ответ означает? В примере 1 мы пришли к выводу, что 1/2 ÷ 1/4 = 2. Но что это на самом деле означает?
Но что это на самом деле означает?
Если мы подумаем о 1/2 ÷ 1/4 в форме вопроса: сколько 1/4 в 1/2?
И затем, если мы визуализируем 1/4 и 1/2, мы можем ясно видеть, что в 1/2 содержится 2 1/4, поэтому окончательный ответ равен 2.
Дробь, деленная на дробь: Пример 2Пример 2: Что такое 2/9 ÷ 1/3 ?
Как и в примере 01, вы можете решить эту проблему, используя метод сохранения сдачи следующим образом:
1.) Оставить первую дробь 2/9 как есть.
2.) Заменить знак деления на умножение.
3.) Переверните вторую дробь, чтобы превратить 1/3 в 3/1
Затем выполните 2/9 x 3/1 следующим образом и упростите ответ, если сможете:
В данном примере 6/9 не является окончательным ответом, так как его можно сократить до 2/3
Окончательный ответ равен 2/3, и мы можем заключить, что ответ исходной задачи равен…
Окончательный ответ: 2/9 ÷ 1/3 = 2/3
Деление дроби на целое число: пример 3Что делать, если вам нужно разделить дробь на целое число? Оказывается, процесс точно такой же, как и в предыдущих примерах!
Пример 03: Что такое 5 ÷ 2/3?
Обратите внимание, что в этом примере вы делите дробь на целое число. Но на самом деле очень просто преобразовать целое число в дробь. Все, что вам нужно сделать, это переписать число в виде дроби, где само число находится в числителе, а знаменатель равен 1.
Но на самом деле очень просто преобразовать целое число в дробь. Все, что вам нужно сделать, это переписать число в виде дроби, где само число находится в числителе, а знаменатель равен 1.
Например, 5 можно переписать как 5/1, и это правило применимо для любого целого числа!
Теперь, когда вы переписали целое число в виде дроби, вы можете использовать метод Сохранить-Изменить-Обратить для решения проблемы.
1.) Оставить первую дробь 5/1 как есть.
2.) Заменить знак деления на умножение.
3.) Переверните вторую дробь, чтобы превратить 2/3 в 3/2
Наконец, перемножьте дроби вместе и упростите, если возможно, чтобы найти окончательный ответ следующим образом:
15/2 нельзя упростить, однако его можно выразить как 7 и 1/2
В этом примере ответ может быть выражен как 15/2 или как 7 и 1/2.
И можно сделать вывод, что ответ на исходную задачу равен…
Окончательный ответ: 5 ÷ 2/3 = 15/2 или 7&1/2
Все еще запутались? Посмотрите анимационный видео-урок ниже:Посмотрите видео-урок ниже , чтобы узнать больше о том, как делить дроби на дроби и дроби на целые числа:
Бесплатный рабочий лист!
Вы ищете дополнительную практику деления дробей? Перейдите по ссылкам ниже, чтобы загрузить бесплатные рабочие листы и ключ ответа:
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ БЕСПЛАТНУЮ РАБОЧУЮ ТАБЛИЦУ
Теги: деление дробей, деление дробей на целые числа, примеры деления дробей, дробь делится на дробь
Продолжайте учиться:Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Автор: Энтони Персико Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, чтобы поделиться ими на моем 9. Интересно сравнить исходное выражение (до упрощения),
и упрощенное выражение (после отмены). в факторизованной форме: $\displaystyle
\cssId{s49}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}}$ УПРОЩЕННОЕ ВЫРАЖЕНИЕ: ГРАФИК: ГРАФИК: Разделение означает разделение предмета поровну. 2+4x+3)}}
\cssId{s25}{\cdot}
\cssId{s26}{\frac{x+1}{x+4}}$
2+4x+3)}}
\cssId{s25}{\cdot}
\cssId{s26}{\frac{x+1}{x+4}}$ фактор:
разность квадратов (числитель),
общий множитель (знаменатель) $=$ $\displaystyle
\cssId{s31}{\frac{(x-3)(x+3)}{5(x+3)(x+1)}}
\cssId{s32}{\cdot}
\cssId{s33}{\frac{x+1}{x+4}}
$ разложить трехчлен в знаменателе $=$ $\displaystyle
\ cssId {s36} {\ frac {\ hphantom {5} (x + 1) (x + 3) (x-3)} {5 (x + 1) (x + 3) (x + 4)}}
$ умножать, переупорядочивать $=$ $\displaystyle
\cssId{s39}{\frac{(x-3)}{5(x+4)}}
$ отменить два дополнительных множителя $\,1\,$ 
Хотя они равны
почти для всех значений $\,x\,$,
они немного отличаются,
из-за отмены: ЗНАЧЕНИЯ
ИЗ
$\,х\,$ 92+20х+15}
\cdot
\фракция{х+1}{х+4}}
$ СРАВНЕНИЕ $х = -4$ не определено
(деление на ноль) не определено
(деление на ноль) ведут себя одинаково:
оба не определены $х = -1$ не определено
(деление на ноль) $\displaystyle
\cssId{s60}{\frac{-1-3}{5(-1+4)} = -\frac{4}{15}}$ Наличие
$\,\фракция{х+1}{х+1}\,$
вызывает точку прокола
в
$\,х = -1\,$;
см. первый график ниже
первый график ниже $х = -3$ не определено
(деление на ноль) $\displaystyle
\frac{-3-3}{5(-3+4)} = -\frac{6}{5}$ Наличие
$\,\фракция{х+3}{х+3}\,$
вызывает
точку прокола в
$\,х = -3\,$;
см. первый график ниже все остальные
значения
$\,х\,$ оба определены;
значения равны вести себя так же:
значения равны Деление дробей – этапы, метод, примеры
 Мы узнали о делении целых чисел, теперь давайте посмотрим, как делить дроби. Дробь состоит из двух частей — числителя и знаменателя. Делить дроби почти то же самое, что и умножать их. Для деления дробей умножаем первую дробь на обратную (обратную) второй дроби. Давайте узнаем больше о делении дробей в этой статье.
Мы узнали о делении целых чисел, теперь давайте посмотрим, как делить дроби. Дробь состоит из двух частей — числителя и знаменателя. Делить дроби почти то же самое, что и умножать их. Для деления дробей умножаем первую дробь на обратную (обратную) второй дроби. Давайте узнаем больше о делении дробей в этой статье. 1. Как делить дроби? 2. Деление дробей на дроби 3. Деление дробей целыми числами 4. Деление дробей с помощью десятичных знаков 5. Деление дробей и смешанных чисел 6. Часто задаваемые вопросы о делении дробей Как делить дроби?
Мы знаем, что деление — это метод разделения поровну и объединения в равные группы. Делим целое число на делитель, чтобы получить частное. Теперь, когда мы делим дробь на другую дробь, это то же самое, что умножать дробь на обратную вторую дробь. Обратная дробь — это простой способ поменять местами числитель и знаменатель дроби. Обратите внимание на следующий рисунок, чтобы узнать простое правило деления дробей.
Обратная дробь — это простой способ поменять местами числитель и знаменатель дроби. Обратите внимание на следующий рисунок, чтобы узнать простое правило деления дробей.
В последующих разделах мы изучим деление дробей на дроби, целые числа, десятичные дроби и смешанные числа. В каждом случае мы будем использовать то же правило деления дробей, что и выше. Давайте начнем!
Деление дробей на дроби
Мы только что научились делить дроби, взяв обратную. Теперь давайте рассмотрим метод деления дроби на дробь на примере. Посмотрите на приведенную ниже формулу деления дроби на дробь. Если x/y делится на a/b, это означает, что
x/y ÷ a/b
⇒ x/y × b/a (обратная величина a/b равна b/a)
⇒ xb/ya
Теперь, если нам нужно разделить: 5/8 ÷ 15/16 подставим значения данных числителей и знаменателей.
5/8 ÷ 15/16 = 5/8 × 16/15 = 2/3
∴ Значение 5/8 ÷ 15/16 = 2/3.
Деление дробей целыми числами
Для деления дробей с целыми числами нам нужно умножить знаменатель данной дроби на данное целое число. В общем виде, если x/y — дробь, а a — целое число, то x/y ÷ a = x/y × 1/a = x/ya.
В общем виде, если x/y — дробь, а a — целое число, то x/y ÷ a = x/y × 1/a = x/ya.
Возьмем пример и разделим 2/3 на 4.
2/3 ÷ 4 = 2/3 × 1/4
= 1/6
Следовательно, 2/3 ÷ 4 дает нам 1 /6. Вот как мы делим дроби с целыми числами.
Деление дробей на десятичные дроби
Мы знаем, что десятичные числа сами по себе являются дробями по основанию 10. Мы можем представить десятичное число в дробной форме, а затем выполнить деление. Чтобы разделить дроби на десятичные дроби, выполните следующие действия:
- Преобразование заданного десятичного числа в дробь.
- Разделите обе дроби.
Рассмотрим пример 4/5 ÷ 0,5. Здесь 0,5 можно записать дробно как 5/10 или 1/2. Теперь разделите 4/5 на 1/2. Отсюда следует, что 4/5 ÷ 1/2 = 4/5 × 2/1 = 8/5. Вот как мы выполняем деление дробей с десятичными знаками. Теперь давайте научимся делить дроби со смешанными числами.
Деление дробей и смешанных чисел
Мы научились преобразовывать смешанные дроби в неправильные дроби. Для деления дробей со смешанными числами мы должны сначала преобразовать смешанную дробь в неправильную дробь, а затем разделить их, как мы делим две дроби. Рассмотрим следующий пример.
Для деления дробей со смешанными числами мы должны сначала преобразовать смешанную дробь в неправильную дробь, а затем разделить их, как мы делим две дроби. Рассмотрим следующий пример.
3/4 ÷ \(1\dfrac{1}{2}\)
Итак, первый шаг — преобразовать \(1\dfrac{1}{2}\) в неправильную дробь. \(1\dfrac{1}{2}\) равно 3/2. Теперь это можно решить следующим образом:
3/4 ÷ 3/2
⇒ 3/4 × 2/3
⇒ 6/12 = 1/2
Следовательно, 3/4 ÷ \(1\dfrac{1}{2}\) = 1/2. Если вы хотите разделить смешанное число на дробь, сначала преобразуйте смешанное число в неправильную дробь и выполните действия, описанные выше.
Разделение дробей Статьи по теме
Проверьте эти интересные статьи, связанные с концепцией деления дробей в математике.
- Калькулятор дробей
- Формула деления дробей
- Деление дробей на целые числа
- Дроби
Деление дробей Примеры
Пример 1: Найдите значение 3/16 ÷ 15/32.

Решение:
Чтобы разделить 3/16 ÷ 15/32, мы будем использовать шаги деления дробей. Первый шаг — оставить первую фракцию такой, какая она есть. Затем измените знак деления на знак умножения и, наконец, превратите вторую дробь в обратную. Отсюда следует 3/16 × 32/15. После упрощения получаем (3×32)/(16×15) = 2/5.
∴ Значение 3/16 ÷ 15/32 = 2/5
Пример 2: У Тима \(1\frac{1}{2}\) литров сока в кувшине. Он должен разлить сок по чашкам. Каждая чашка может вместить 1/4 литра сока. Сколько чашек ему понадобится, чтобы вылить весь сок?
Решение:
Для решения этого вопроса воспользуемся понятием деления дробей.
Необходимое количество чашек = Общее количество сока ÷ Вместимость 1 чашки
= 3/2 ÷ 1/4 (так как \(1\frac{1}{2}\) = 3/2)
= 3/2 × 4/1
= 12/2
= 6
Следовательно, количество чашек, необходимых для разлива сока, равно 6.

Пример 3: Используйте шаги деления дробей с целыми числами, чтобы найти значение 8/5 ÷ 5.
Решение:
Чтобы разделить дробь на целое число, мы умножаем заданное целое число на знаменатель дроби. Здесь 8/5 ÷ 5 = 8/5 × 1/5 = 8/25.
Следовательно, 8/5 ÷ 5 = 8/25.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по делению дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о делении дробей
Что означает деление дробей?
Деление дробей означает разбиение дроби на дополнительные части. Например, если вы возьмете половину (1/2) пиццы и далее разделите ее на 2 равные части, то каждая порция будет составлять 1/4 всей пиццы. Математически мы можем выразить это рассуждение как 1/2 ÷ 2 = 1/4.
Математически мы можем выразить это рассуждение как 1/2 ÷ 2 = 1/4.
Что такое умножение и деление дробей?
Умножение дробей означает прибавление дроби к самой себе определенное количество раз. Для умножения дробей используются следующие шаги:
- Шаг 1: Умножьте числители обеих дробей.
- Шаг 2: Умножьте знаменатели обеих дробей.
- Шаг 3: Упростите дробь, полученную после умножения.
С другой стороны, разделение дробей означает равное группирование или равное разделение дроби. Деление дробей связано с умножением, так как при делении двух дробей мы умножаем обратную величину второй дроби на первую.
Как визуализировать деление дробей?
Чтобы наглядно представить деление дробей, возьмите лист бумаги и сложите его на две равные части. Отрежьте 1/2 часть бумаги ножницами. Теперь у вас останется 1/2 бумаги. Теперь снова разделите эту 1/2 часть на 2 равные части. После этого у вас останется 1/4 часть бумаги. Это ответ 1/2 ÷ 2. Вот как вы можете визуализировать концепцию деления дробей.
Вот как вы можете визуализировать концепцию деления дробей.
Какое правило деления дробей?
Основное правило деления дробей состоит в том, чтобы сохранить, изменить и перевернуть. Это означает, что мы должны оставить первую дробь как есть, изменить знак деления на знак умножения и преобразовать вторую дробь в обратную. Следуя этому простому правилу, вы можете разделить любые две дроби.
Как делить дроби?
Чтобы разделить дроби, необходимо выполнить следующие шаги:
- Шаг 1: Возьмем обратную величину второй дроби.
- Шаг 2: Умножьте его на первую дробь.
- Шаг 3: Сократите полученную дробь до наименьшего значения.
Как научить делению дробей?
Делению дробей можно научиться разными способами, например, используя модели или применяя концепцию умножения дробей. Ниже перечислены некоторые способы обучения делению дробей:
- Возьмите модели круглых или прямоугольных дробей, чтобы продемонстрировать учащимся концепцию деления дробей.

- Используйте рабочие листы с картинками и текстовыми задачами.
- Используйте материалы из повседневной жизни, такие как бобы, листья, галька и т. д., чтобы показать учащимся, как делить дроби.
Как разделить число на дробь?
Чтобы разделить целое число на дробь, нужно умножить целое число на обратную величину данной дроби. Чтобы разделить дробь на дробь, нужно умножить обратную величину второй дроби на первую дробь.
Как делить дроби на целые числа?
Деление дробей на целые числа состоит из трех шагов:
- Шаг 1: Оставьте дробь как есть. Например, 3/4 ÷ 6.
- Шаг 2: Переверните целое число, что сделает его дробью формата 1/a. В этом случае 6 станет 1/6.
- Шаг 3: Измените знак на умножение. Получим 3/4 × 1/6 = 3/24 = 1/8.
Как делить дроби со смешанными числами?
Для деления дробей и смешанных чисел используются следующие шаги:
- Шаг 1: Оставьте дробь как есть.

- Шаг 2: Преобразуйте смешанное число в неправильную дробь и переверните вторую дробь.
- Шаг 3: Измените знак на умножение между дробями. Умножьте и упростите их.
Как умножать и делить дроби (видео)
СтенограммаЧасто задаваемые вопросы, Практические рабочие листы
Многие ученики очень боятся дробей. Однако, если вы помните, что представляет собой дробь , и несколько математических правил, как работать с ними алгебраически, вы сможете уверенно сталкиваться с дробями. В этом видео мы рассмотрим как умножать и делить дроби. Давайте начнем.
Начнем с точного определения дроби. Дробь представляет собой отношение «части» к «целому» или части к целому. Значение выше линии деления называется 9. 0043 числитель , а значение под чертой деления является знаменателем .
0043 числитель , а значение под чертой деления является знаменателем .
Умножение дробей
Чтобы умножить дроби, просто умножьте «прямо», что означает «числитель, умноженный на числитель», деленный на «знаменатель, умноженный на знаменатель». Давайте рассмотрим несколько простых примеров:
\(\frac{2}{3} \times \frac{2}{5}\)
Здесь мы хотим умножить \(\frac{2} {3}\) на \(\frac{2}{5}\). Как мы сказали ранее, мы собираемся умножать прямо. Итак, у нас будет 2 умножить на 2 на 3 на 5. Что равно четырем на пятнадцать. Итак, наш ответ: \(\frac{4}{15}\).
\(\frac{2}{3} \times \frac{2}{5}= \frac{2 \times 2}{3 \times 5}= \frac{4}{15}\)
Теперь попробуем еще один. Мы попробуем \(\frac{4}{7}\) раз \(\frac{3}{11}\).
\(\frac{4}{7} \times \frac{3}{11}\)
Опять та же концепция. Мы собираемся умножить 4 на 3, разделить на 7 на 11. Что дает нам \(\frac{12}{77}\).
Что дает нам \(\frac{12}{77}\).
\(\frac{4}{7} \times \frac{3}{11}= \frac{4 \times 3}{7 \times 11}= \frac{12}{77}\)
Довольно просто, правда? Теперь займемся делением дробей.
Деление дробей
Деление дробей включает несколько иной процесс. Прежде чем мы перейдем к механике процесса, давайте начнем с интуитивного примера деления дроби на два. Эффект деления на 2 заключается в простом сокращении дроби пополам или простом умножении дроби на 1 на 2.
Таким образом, \(\frac{4}{5}\) разделить на 2 на самом деле то же самое, что сказать \ (\frac{4}{5}\) раз \(\frac{1}{2}\).
\(\frac{4}{5}\)\( \div \text{ } 2 \text{ }\)\( = \frac{4}{5} \times \frac{1}{2 }\)
Затем оно будет умножено, как мы делали это раньше. Итак, у нас 4 раза 1 равно четырем, более 5 раз 2 равно 10. Что затем упрощается до \(\frac{2}{5}\).
\(\frac{4}{5}\)\( \div \text{ } 2 \text{ }\)\( = \frac{4}{5} \times \frac{1}{2 }= \frac{4}{10}= \frac{2}{5}\)
Другими словами, \(\frac{2}{5}\) вдвое меньше \( \фракция{4}{5}\).
Аналогично, деление дроби на 3 приведет к дроби, равной одной трети размера оригинала:
\(\frac{2}{5}\)\( \div \text{ } 3 \ text{ }\)\( = \frac{2}{5} \times \frac{1}{3}= \frac{2}{15}\)
\(\frac{2}{5 }\) разделить на 3 — это то же самое, что сказать \(\frac{2}{5}\) умножить на \(\frac{1}{3}\), что даст вам \(\frac{2}{15} \).
Итак, \(\frac{2}{15}\) составляет одну треть размера \(\frac{2}{5}\).
Прежде чем мы обобщим этот процесс, давайте рассмотрим некоторые важные термины. Рассмотрим связь между 2 и \(\frac{1}{2}\). Эти числа называются обратны друг другу , что означает, что числитель одного числа является знаменателем другого, и наоборот. Помните, что 2 можно записать в виде дроби, написав ее над 1, например: \(\frac{2}{1}\). Следовательно, \(\frac{2}{1}\) и \(\frac{1}{2}\) обратны. То же самое верно для 3 и \(\frac{1}{3}\), потому что 3 можно записать как \(\frac{3}{1}\). Следовательно, 3 и \(\frac{1}{3}\) обратны.
Имея это в виду, какую закономерность вы видите в процессе деления дробей?
Сохранить, изменить, перевернуть
Процесс деления дробей такой же, как умножение первой дроби на величину, обратную второй. Сокращенная версия этого многословного объяснения, которое может помочь вам запомнить процесс деления, звучит так: «Сохранить, изменить, перевернуть»:
Оставить первую дробь как есть
Изменить операцию деления на умножение;
Переверните (или возьмите обратную) вторую дробь.
После внесения этой корректировки просто следуйте правилам умножения дробей путем умножения числителей и деления на произведение знаменателей.
Вот пример использования процесса «Сохранить, изменить, перевернуть»:
Допустим, мы хотим разделить \(\frac{3}{5}\) на \(\frac{7}{5}\). Мы оставим первую дробь как есть, изменим операцию деления на умножение и перевернем второе число. Теперь мы просто умножаем наши числители, 3 умножить на 5 — это пятнадцать, более 5 умножить на 7 — это 35. А затем отсюда мы упрощаем до \(\frac{3}{7}\).
Теперь мы просто умножаем наши числители, 3 умножить на 5 — это пятнадцать, более 5 умножить на 7 — это 35. А затем отсюда мы упрощаем до \(\frac{3}{7}\).
\(\frac{3}{5} \div \frac{7}{5}= \frac{3}{5} \times \frac{5}{7}= \frac{15}{35 }= \frac{3}{7}\)
Надеюсь, это видео было полезным! Спасибо за просмотр и удачной учебы!
Перемножение дробей | Неправильные дроби и смешанные числа
Часто задаваемые вопросы
Q
Как умножать дроби на целые числа?
A
Умножьте дроби на целые числа, превратив целое число в дробь, поместив ее над 1. Любое число, разделенное само на себя, является само собой, поэтому это не меняет значения целого числа. Затем умножьте как обычные дроби.
пр. \(\frac{2}{3}×4=\frac{2}{3}×\frac{4}{1}=\frac{8}{3}=2 \frac{2}{3}\ )
Q
Как умножать смешанные дроби?
A
Умножайте смешанные дроби, сначала превращая их в неправильные дроби, а затем умножая как обычно. Если в числителе и знаменателе есть общие множители, сначала сократите их, чтобы упростить умножение. Чтобы преобразовать дробь обратно в смешанное число, разделите числитель на знаменатель. Количество полных делений становится целым числом, а остаток становится числителем дробной части исходного знаменателя.
Если в числителе и знаменателе есть общие множители, сначала сократите их, чтобы упростить умножение. Чтобы преобразовать дробь обратно в смешанное число, разделите числитель на знаменатель. Количество полных делений становится целым числом, а остаток становится числителем дробной части исходного знаменателя.
пр. \(3 \frac{1}{5}×2 \frac{7}{9}=\frac{16}{5}×\frac{25}{9}=\frac{16}{1}×\ frac{5}{9}=\frac{80}{9}=8 \frac{8}{9}\)
Пример. \(3 \frac{1}{5}×2 \frac{7}{9}=\frac{16}{5}×\frac{25}{9}=\frac{16}{5}×\ frac{5×5}{9}=\frac{16}{1}×\frac{5}{9}=\frac{80}{9}=8 \frac{8}{9}\)
Q
Как вы делите дроби?
A
Разделите дроби, используя фразу: «Сохранить, изменить, перевернуть». Оставьте первую дробь такой же. Замените знак деления на знак умножения. Переверните вторую дробь. Затем умножьте и упростите, если необходимо.
пр. \(\frac{4}{7}÷\frac{8}{13}=\frac{4}{7}×\frac{13}{8}=\frac{52}{56}=\frac{ 13}{14}\)
Q
Как вы делите дроби с целыми числами?
A
Разделите дроби на целые числа, сначала превратив целое число в дробь, а затем разделив дроби как обычно, перевернув вторую дробь и умножив ее. Любое число можно превратить в дробь, поместив его над 1.
Любое число можно превратить в дробь, поместив его над 1.
Упр. \(\frac{2}{3}÷4=\frac{2}{3}÷\frac{4}{1}=\frac{2}{3}×\frac{1}{4}=\ frac{2}{12}=\frac{1}{6}\)
Q
Как разделить смешанные дроби?
A
Разделите смешанные дроби, сначала превратив их в неправильные дроби, а затем разделив дроби как обычные.
пр. \(4 \frac{3}{5}÷2 \frac{1}{2}=\frac{23}{5}÷\frac{5}{2}=\frac{23}{5}×\ frac{2}{5}=\frac{46}{25}=1 \frac{21}{25}\)
Практические вопросы
Вопрос №1:
\(\frac{2} {3}\times\frac{7}{9}=\)
\(\frac{42}{9}\)
\(\frac{42}{47}\)
\(\frac{14}{27}\)
\(\frac{14}{9}\)
Показать ответ
Ответ:
Правильный ответ C: \(\frac{14}{27}\). Чтобы умножить дроби, просто перемножьте числители, чтобы получить новый числитель, и перемножьте знаменатели, чтобы получить новый знаменатель.
\(\frac{2}{3}\times\frac{7}{9}=\frac{2\times7}{3\times9}=\frac{14}{27}\)
Скрыть ответ
Вопрос №2:
\(\frac{7}{6}\div\frac{2}{3}=\)
\(\frac{7}{4}\)
\(\frac{9}{) 9}\)
\(\frac{14}{18}\)
\(\frac{7}{2}\)
Показать ответ
Ответ:
Правильный ответ A: \(\ гидроразрыва{7}{4}\). Чтобы разделить дроби, используйте фразу: Keep, Change, Flip. Оставьте первую дробь такой же. Заменить знак деления на знак умножения. Переверните вторую дробь, чтобы она была обратной. Этот процесс выглядит так:
\(\frac{7}{6}\div\frac{2}{3}=\frac{7}{6}\times\frac{3}{2}\)
Затем умножьте и упростите дроби.
\(\frac{7}{6}\times\frac{3}{2}=\frac{7\times3}{6\times2}=\frac{21}{12}=\frac{7}{ 4}\)
Скрыть ответ
Вопрос №3:
\(\frac{1}{4}\times\frac{6}{7}\div\frac{2}{9}= \)
\(\frac{7}{108}\)
\(\frac{47}{52}\)
\(\frac{12}{252}\)
\(\frac {27}{28}\)
Показать ответ
Ответ:
Правильный ответ D: \(\frac{27}{28}\). Согласно Порядку операций (PEMDAS), умножение и деление могут происходить одновременно. Для этого примера давайте проработаем умножение и деление по порядку слева направо. Итак, мы начнем с умножения \(\frac{1}{4}\) и \(\frac{6}{7}\), при необходимости упрощая.
Согласно Порядку операций (PEMDAS), умножение и деление могут происходить одновременно. Для этого примера давайте проработаем умножение и деление по порядку слева направо. Итак, мы начнем с умножения \(\frac{1}{4}\) и \(\frac{6}{7}\), при необходимости упрощая.
\(\frac{1}{4}\times\frac{6}{7}=\frac{1×6}{4×7}=\frac{6}{28}=\frac{3}{ 14}\)
Затем разделите \(\frac{3}{14}\) на \(\frac{2}{9}\).
\(\frac{3}{14}\div\frac{2}{9}=\frac{3}{14}\times\frac{9}{2}=\frac{27}{28}\ )
Следовательно, \(\frac{1}{4}\times\frac{6}{7}\div\frac{2}{9}=\frac{27}{28}\).
Скрыть Ответ
Вопрос № 4:
Сара Энн печет печенье, и рецепт требует \(\frac{2}{3}\) чашек масла. Ей нужно много печенья, поэтому она решает увеличить рецепт в четыре раза. Быстро сообразив, что печенья много, она решает немного отступить и сделать рецепт только в \(3\frac{1}{2}\) раза больше оригинала. Для этого сколько чашек масла понадобится Саре-Энн?
\(2\frac{1}{3}\) чашки
\(\frac{4}{21}\) чашки
\(1\frac{2}{3}\) чашки
\ (\frac{1}{7}\) чашек
Показать ответ
Ответ:
Правильный ответ: A: \(2\frac{1}{3}\) чашек. Первое, что нужно сделать, чтобы решить эту проблему, это \(3\frac{1}{2}\) нужно преобразовать в неправильную дробь.
Первое, что нужно сделать, чтобы решить эту проблему, это \(3\frac{1}{2}\) нужно преобразовать в неправильную дробь.
\(3\frac{1}{2}=\frac{3×2+1}{2}=\frac{7}{2}\)
Затем умножьте две дроби и упростите.
\(\frac{2}{3}\times\frac{7}{2}=\frac{14}{6}=\frac{7}{3}\)
Наконец, преобразуйте \(\frac {7}{3}\) в смешанное число.
\(\frac{7}{3}=2\frac{1}{3}\)
Саре Энн нужно \(2\frac{1}{3}\) чашек масла.
Скрыть ответ
Вопрос №5:
У Антонио осталось \(\frac{6}{8}\) пиццы и два голодных друга. Если Антонио и его друзья поровну поделят пиццу, какая часть пиццы достанется каждому?
\(\frac{1}{3}\)
\(\frac{3}{4}\)
\(\frac{1}{4}\)
\(\frac{2}{3}\)
Показать ответ
Ответ :
Правильный ответ C: \(\frac{1}{4}\). Этот вопрос предлагает нам разделить \(\frac{6}{8}\) на 3.