Правила умножения и деления чисел с разными знаками: Умножение и деление отрицательных чисел

Содержание

Умножение и деление отрицательных чисел

Мы уже умеем складывать и вычитать отрицательные числа.

Теперь давайте разберемся с умножением и делением.

Предположим, нам нужно умножить +3 на -4. Как это сделать?

Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.

Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.

Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом

. Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.

А как перемножить два отрицательных числа?

К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.

Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.

Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.

Положение знака при умножении изменяется таким образом:

положительное число х положительное число = положительное число;
отрицательное число х положительное число = отрицательное число;
положительное число х отрицательное число = отрицательное число;
отрицательное число х отрицательное число = положительное число.

Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число. Перемножая два числа с разными знаками, мы получаем отрицательное число.

Такое же правило справедливо и для действия противоположного умножению – для деления.

(+12):(+3)=+4;

(+12):(-3)=-4;

(-12):(+3)=-4;

(-12):(-3)=+4.

Вы легко можете в этом убедиться, проведя обратные операции умножения. Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).

Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Умножение и деление положительных и отрицательных чисел

Положительные и отрицательные числа изучаются в самом начале курса математики, в шестом классе. Хотя дальнейшее обучение требует постоянно работать с этими числами, неудивительно, что по прошествии времени некоторые мелочи забываются — и люди начинают совершать грубые ошибки.

Умножение и деление — одни из самых частых действий с числами, имеющими разные знаки.

Разберемся и вспомним, как нужно перемножать и делить такие числа между собой, ставя в ответе правильный знак.

Умножение чисел с разными знаками

Это правило — одно из самых простых в арифметике.

Если перед нами есть некое положительное число «а», и его требуется умножить на отрицательное число «z», то мы просто перемножаем числа — а потом ставим перед результатом знак «минус».
Можно сказать и так — чтобы умножить друг на друга числа с разными знаками, нужно перемножить между собой модули множителей, а потом вернуть знак «минус» в ответ.

Для утверждения справедлива следующая цифровая запись: -а*z = — (|а|*|z|). Также напомним, что для нуля действуют особые правила — если на него умножается какое-либо число, положительное или отрицательное, ответ в любом случае будет равен нулю.

Возьмем пару простых примеров.

Если выражение выглядит, как – 5*6, то решать его нужно следующим образом: -5*6 = — (|5|*|6|) = — 30.
Если выражение следующего типа — — 7*0, то в ответе сразу пишется 0.

Деление чисел с разными знаками

Для таких случаев тоже действует очень простое правило. Оно похоже на предыдущее — если задача требует разделить «–а» на «b», или «a» на «–b», то для начала мы берем модули чисел, их абсолютные значения, и совершаем процесс деления безо всякой перестановки делимого и делителя.

Таким образом находится частное — а затем к нему добавляется знак «минус». Неважно, выступает ли в роли делимого отрицательное число, или наоборот, мы делим число со знаком «плюс» на отрицательное — ответ всегда будет со знаком «минус». Иначе говоря, числовым методом мы записываем это так: -a : b = — (|a| : |b|).

Например, — 10: 2 = — (10:2) = — 5, или 21: (-3) = — (21:3) = — 7. В конечном итоге деление совсем не сложное и сводится к привычным нам действиям над модулями чисел.

И точно так же, как в предыдущем случае, на особенном положении находится нуль. Его присутствие в выражении автоматически дает нуль в ответе. И неважно, это 0:а или а:0 — и попытка деления нуля, и деление на нуль дают одинаковый результат.

7. Умножение и деление положительных и отрицательных чисел.

п. 35. УМНОЖЕНИЕ

ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.

ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.

Данный модуль представляет собой задание с пошаговым контролем и состоит из пяти шагов. Задание предназначено для отработки умения и навыков учащихся умножать положительные и отрицательные числа. Загрузить модуль.

КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.

ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.

Данный модуль представляет собой задание повышенной сложности, состоящее из трех уровней. Задание направлено на проверку знаний свойств нуля при умножении. Загрузить модуль.

п. 36. ДЕЛЕНИЕ

ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.

Правила и примеры.

ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.

КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.

ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.

п. 37. РАЦИОНАЛЬНЫЕ ЧИСЛА

ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.

ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.

Данный модуль состоит из 5 заданий. Задания предназначены для отработки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.

КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.

Данный модуль состоит из 5 заданий. Задания предназначены для проверки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.

п. 38. СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.

ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.

КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.

ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.

Данный модуль представляет собой задания повышенной сложности, состоящее из трех уровней. Задание направлено на формирование рациональных вычислительных приемов: умение применять переместительное и сочетательное свойства сложения и умножения для нахождения значения числового выражения. Загрузить модуль.

ОБОБЩЕНИЕ ПО ТЕМЕ

Игра «Плюс и минус». Можно выбрать действия с положительными и отрицательными числами, а также скорость игры. И проверить себя как вы умеете определять знак результата.

Деление отрицательных чисел и чисел с разными знаками

Министерство образования и науки РД

МКОУ «Джибахнинская СОШ»

Открытый урок по математике для

6 класса

«Деление отрицательных чисел и чисел с разными знаками»

Подготовила:

Магомедова П.М,

учитель математики

МКОУ «Джибахнинская СОШ»

2018

Конспект урока математики в 6 классе по теме

«Деление отрицательных чисел и чисел с разными знаками»

Цели урока:

Сформулировать правило деления отрицательных чисел и чисел с разными знаками.

Проверить справедливость свойств единицы и нуля при делении положительных и отрицательных чисел.

Закрепление правил по данной теме;

Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.

Развитие познавательного интереса;

Развитие логического мышления, памяти, внимания.

Задачи урока:

Образовательные:

Закрепление правил по данной теме;

Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.

Развивающие:

Развитие познавательного интереса;

Развитие логического мышления, памяти, внимания.

Воспитательные:

Воспитание активности;

Привитие учащимся навыков самостоятельной работы;

Воспитание любви к природе, привитие интереса к народным приметам.

Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.

Оборудование: Интерактивная доска, компьютер, карточки с заданиями.

План урока

Организационный момент

Актуализация знаний

Открытия новых знаний, обретения новых умений и навыков

Выполнение теста

Решение упражнений

Рефлексия. Самостоятельная работа и проверка по эталону

Итог урока

Домашнее задание.

Ход урока

1. Организационный момент.

– Здравствуйте, ребята! Проверяю визуально готовность ребят к уроку и настраиваю на получении хорошей оценки (слайд 1). Я хочу вас спросить, с чем у вас ассоциируется слово «Действие»? (слайд 2). Слушаем рассуждения детей.

2.Актуализация знаний

В математике мы знаем четыре действия с числами. Действия: сложение и вычитание. Давайте решим данные примеры вспомним правила их выполнения. (слайд 3)

Реши сам:

21 + ( — 8 ) =13;

-10 + ( — 16 ) =-26;

7 – ( -15 ) = 22;

— 32 – ( — 22 ) = -10;

-16 + 5 = -11;

Идет фронтальная работа с классом с проговариванием правил сложения и вычитания чисел с разными знаками.

Следующие действия: умножение и деление (слайд 4)

Реши сам: (слайд 5)

11 ∙ ( — 8 ) = -88;

-10 ∙ ( — 1,6 ) = 16;

-7 ∙ 0,5 = -3,5 ;

— 33 ∙ (- ) = 11;

-15 ∙ = -5;

Также идет фронтальная работа с классом с проговариванием правил умножения чисел с разными знаками. Обращаю внимание класса на последние два примера. Вопрос классу: — Каким действием можно было заменить умножение, чтобы ответ остался прежним? (Делением). Строим предположения и делаем выводы о правилах деления чисел с разными знаками.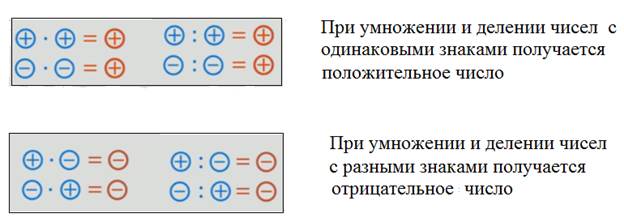 Наводящими вопросами подвожу к теме сегодняшнего урока.

3.Открытия новых знаний, обретения новых умений и навыков

Итак, тема урока: Деление (слад 6)

Вместе с классом формулируем цели данного урока(слайд 7)

Формулируем правило деления чисел с разными знаками и записываем в тетрадь (слайд 8)

Вспоминаем, записываем свойства единицы и нуля (слайд 9).

Закрепляем полученные знания при выполнении следующей работы (слайд 10)

Выполните деление:

4,8:(-8 ) = -0,6

-24:(-0,2) = 120

0:(-49) = 0

-4,9: 7 = -0,7

-15:(-1) = 15

Учащиеся меняются тетрадями, выполняют проверку и ставят оценку.

— Мы с вами плодотворно поработали, давайте отвлечемся на физминутку (слайд 11)

– Далее продолжим работать над умножением и делением положительных и отрицательных чисел. Задача каждого из вас – разобраться в том, как он освоил эту тему, и если потребуется – доработать то, что еще не совсем получается. Кроме того вы узнаете много интересного о первом месяце весны – марте.

-Когда-то в старину на Руси отсчет лет вели с 1 марта, с начала сельскохозяйственной весны, с первой весенней капели. Март был “зачинателем” года. Название месяца “март” идет от римлян. Они назвали этот месяц в честь одного из своих богов, узнать, что это за бог, вам поможет тест.

4. Выполнение теста «Составьте слово» (слайд 12).

-25:(-25)= 5. -50:(-25)=

-45: 9= 6. 32:(-2)=

-1,5×2= 7. -0,25×(-1)=

-204:2=

И	У	А	Р	С	М	Т
2	-16	— 5	-3	0,25	1	-102

Ответ: Мартиус

-У римлян один месяц года в честь бога войны Марса был назван мартиусом. На Руси это название упростили, взяв лишь первые четыре буквы (слайд 13).

В народе говорят: “ Март неверен, то плачет, то смеется”. С мартом связано много народных примет. Некоторые дни его имеют свои названия. Давайте сейчас все вместе мы составим народный месяцеслов на март.

5. Решение упражнений.

Учащиеся у доски решают примеры, ответы которых являются числами месяца. На доске появляется пример, а затем день месяца с названием и народной приметой.

-2,5:5×(-26) (слайд 14)

13 марта – Василий-капельник: с крыш каплет. Птицы гнезда завивают, а перелетные летят из теплых мест.

-29,12:(-2,08) (слайд 15)

14 марта – Евдокия (Авдотья-плющиха) – снег плющит настом. Вторая встреча весны (первая на Стретение). Какова Евдокия – таково и лето. Евдокия красна – и весна красна; на Евдокию снег – к урожаю.

(-6-36:4)×(-1)(слайд 16)

15 марта – Федот. На Федота ветер и метель – долго травы не будет.

7,15×(-4):(-1,3) (слайд 17)

22 марта – Сороки – день равен ночи. Зима кончается, весна начинается, прилетают жаворонки. По старинному обычаю из теста пекут жаворонков и куликов.

6. Рефлексия. Самостоятельная работа и проверка по эталону

Проверь себя: (слайд 18-19)

4,9: (-0,7) = -7
2. -2·(-3,4) = 6,8
3. -5,2:26 = -0,2
4. -2· = —
5. —: (-4) =

Критерии оценки:

нет ошибок —- оценка 5

1 ошибка —— оценка 4

2 ошибки —— оценка 3

По окончанию самостоятельной работы, с помощью готовых ответов на экране, учащиеся осуществили самопроверку и выставили оценку.

7.Итог урока.

– Ребята, понравился ли вам сегодняшний урок?

– Что нового вы сегодня узнали?

– Мы достигли поставленных целей урока? (слайд 20)

– Я предлагаю вам подготовить самим месяцеслов на апрель. Вы должны найти приметы апреля и составить примеры с ответами, соответствующими дню месяца.

8. Домашнее задание:

стр. 218 №1174, 1179(1) (слайд 21)

Умножение и деление целых чисел. Возведение в степень

Умножение

При умножении двух целых чисел умножаются их абсолютные величины. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные

Примеры:

3 · 5 = 15,

3 · (-5) = -15,

-3 · 5 = -15,

-3 · (-5) = 15.

Ниже представлена схема (правило знаков при умножении):

+	·	+	=	+

+	·	—	=	—

—	·	+	=	—

—	·	—	=	+

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на -1 получится число противоположное данному.

Примеры:

-15 · (-1) = 15,

25 · (-1) = -25.

Деление

При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

Примеры:

15 : 5 = 3,

15 : (-5) = -3,

-15 : 5 = -3,

-15 : (-5) = 3.

При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):

+	:	+	=	+

+	:	—	=	—

—	:	+	=	—

—	:	—	=	+

Из данных примеров следует, что

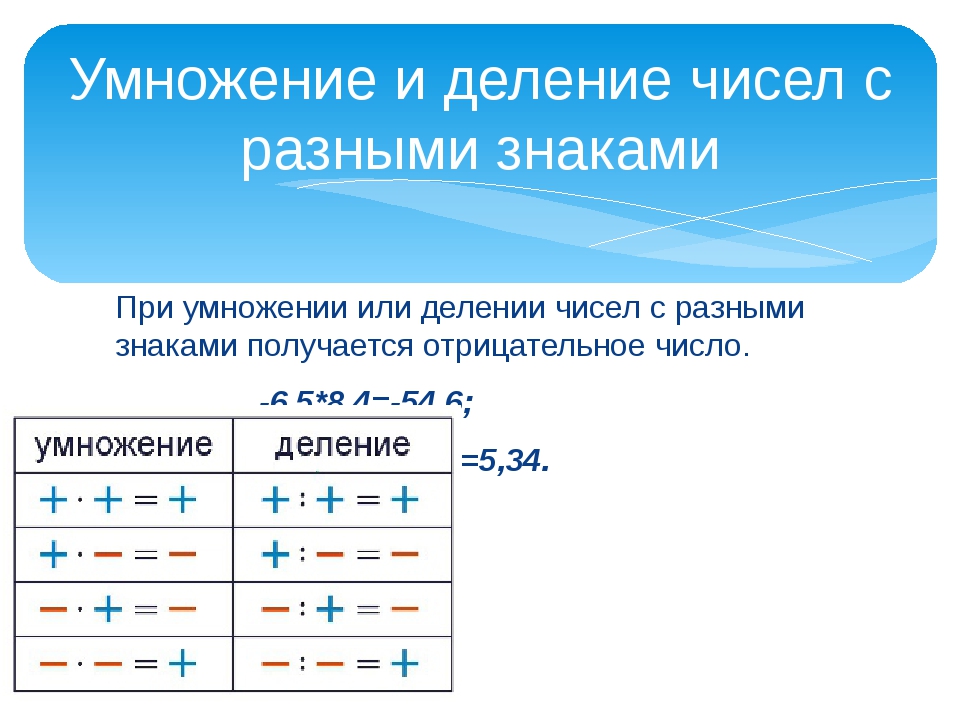
частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на -1 получится число противоположное данному.

Примеры:

-15 : (-1) = 15,

25 : (-1) = -25.

Возведение в степень

При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.

Степень положительного числа всегда будет положительным числом.

Примеры:

5² = 5 · 5 = 25,

4³ = 4 · 4 · 4 = 64.

Степень отрицательного числа может быть как положительным, так и отрицательным числом.

Примеры:

Нечётный показатель степени:

(-3)³ =	(-3) · (-3)	· (-3) =
	+

= 9 · (-3) = -27,

то есть (-3)³ < 0.

Чётный показатель степени:

(-4)⁴ =	(-4) · (-4)	·	(-4) · (-4)	=
	+		+

= 16 · 16 = 256,

то есть (-4)⁴ > 0.

следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.

Умножение и деление рациональных чисел

В данном уроке рассматривается умножение и деление рациональных чисел.

Умножение рациональных чисел

Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.

Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.

Пример 1. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.

Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками

Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.

Таким образом, значение выражения равно

Короткое решение выглядит следующим образом:

Пример 2. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:

Решение для данного примера можно записать покороче:

Пример 3. Найти значение выражения

Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

Решение для данного примера можно записать покороче:

Пример 4. Найти значение выражения

Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс

Решение для данного примера можно записать покороче:

Пример 5. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Короткое решение будет выглядеть значительно проще:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть

Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение

Решение для данного примера можно записать покороче

Пример 7. Найти значение выражения

Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.

Решение для данного примера можно записать покороче:

Пример 8. Найти значение выражения

Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.

Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.

Первое действие:

Второе действие:

Ответ: значение выражения равно −2.

Пример 9. Найти значение выражения:

Переведём смешанные числа в неправильные дроби:

Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение

Пример 10. Найти значение выражения

Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

Второе действие:

Третье действие:

Четвёртое действие:

Ответ: значение выражения равно

Пример 11. Найти значение выражения

Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.

В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:

Пример 12. Найти значение выражения

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Пример 13. Найти значение выражения

Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .

Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.

Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:

Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения равно

Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:

Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.

Пример 14. Найти значение выражения −4,2 × 3,2

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.

Пример 15. Найти значение выражения −0,15 × 4

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.

Пример 16. Найти значение выражения −4,2 × (−7,5)

Деление рациональных чисел

Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.

Пример 1. Выполнить деление:

Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.

Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение

Таким образом, значение выражения равно

Подробное решение выглядит следующим образом:

Короткое решение можно записать так:

Пример 2. Выполнить деление

Короткое решение можно записать так:

Пример 3. Выполнить деление

Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь

Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:

Пример 4. Выполнить деление

В данном случае нужно первое число −3 умножить на дробь, обратную дроби .

Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:

Пример 6. Выполнить деление

Умнóжим первую дробь на число, обратное числу 4.

Обратное числу 4 это дробь . На неё и умножим первую дробь

Пример 5. Выполнить деление

Умнóжим первую дробь на число, обратное числу −3

Обратное числу −3 это дробь

Пример 6. Найти значение выражение −14,4 : 1,8

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус

Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.

Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.

Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:

Теперь переведём полученные смешанные числа в неправильные дроби:

Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:

Пример 7. Найти значение выражения

Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0

Пример 8. Найти значение выражения −7,2 : (−0,6)

Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.

Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)

Многоэтажные дроби

Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:

В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:

В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.

При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.

Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.

Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.

После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:

И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.

Пример 2. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь

А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .

Пример 3. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2

А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.

Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.

Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.

Реализуется этот метод следующим образом:

Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!

Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:

С первого на четвёртый. Со второго на третий.

В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.

Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.

Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь пользуясь новой схемой.

Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть

В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.

Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:

В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:

Использование переменных

Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.

Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.

Использование переменных оправдано, при работе с многоэтажными дробями. Например:

Найти значение выражения

Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.

Выражение, находящееся в числителе можно занести в переменную с любым названием, например:

Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A

А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B

Теперь наше изначальное выражение принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.

Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .

Найдём значение переменной A

Найдём значение переменной B

Теперь подставим в главное выражения вместо переменных A и B их значения:

Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:

Таким образом, значение выражения равно −1.

Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.

Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как

Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.

Задания для самостоятельного решения

Задание 1. Выполните умножение:

Решение:

Задание 2. Выполните умножение:

Решение:

Задание 3. Выполните умножение:

Решение:

Задание 4. Выполните умножение:

Решение:

Задание 5. Выполните умножение:

Решение:

Задание 6. Выполните умножение:

Решение:

Задание 7. Выполните умножение:

Решение:

Задание 8. Выполните умножение:

Решение:

Задание 9. Выполните деление:

Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

Задание 16. Выполните деление:

Решение:

Задание 17. Выполните деление:

Решение:

Задание 18. Вычислите выражение:

Решение:

Задание 19. Вычислите выражение:

Решение:

Задание 20. Вычислите выражение:

Решение:

Задание 21. Вычислите выражение:

Решение:

Задание 22. Вычислите выражение:

Решение:

Задание 23. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:

Решение:

Задание 24. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:

Решение:

Задание 25. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:

Решение:

Задание 26. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:

Решение:

Задание 27. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:

Решение:

Задание 28. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:

Решение:

Задание 29. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:

Решение:

Задание 30. Найдите значение выражения:

Решение:

Задание 31. Найдите значение выражения:

Решение:

Задание 32. Найдите значение выражения:

Решение:

Задание 33. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Умножение дробей с разными знаками. Умножение и деление отрицательных чисел

В данном уроке рассматривается умножение и деление рациональных чисел.

Содержание урока

Умножение рациональных чисел

Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь

Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.

Пример 1. Найти значение выражения

Короткое решение выглядит следующим образом:

Пример 2. Найти значение выражения

Пример 3. Найти значение выражения

Решение для данного примера можно записать покороче:

Пример 4. Найти значение выражения

Решение для данного примера можно записать покороче:

Пример 5. Найти значение выражения

Короткое решение будет выглядеть значительно проще:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть

Решение для данного примера можно записать покороче

Пример 7. Найти значение выражения

Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.

Решение для данного примера можно записать покороче:

Пример 8. Найти значение выражения

Ответ: значение выражения равно −2.

Пример 9. Найти значение выражения:

Переведём смешанные числа в неправильные дроби:

Пример 10. Найти значение выражения

Третье действие:

Четвёртое действие:

Ответ: значение выражения равно

Пример 11. Найти значение выражения

Пример 12. Найти значение выражения

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Пример 13. Найти значение выражения

Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:

Третье действие:

Ответ: значение выражения равно

Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:

Пример 14. Найти значение выражения −4,2 × 3,2

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .

Пример 15. Найти значение выражения −0,15 × 4

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .

Пример 16. Найти значение выражения −4,2 × (−7,5)

Деление рациональных чисел

Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь

В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.

А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.

Пример 1. Найти значение выражения:

Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.

Итак, умножим первую дробь на дробь обратную второй.

Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.

Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение

Таким образом, значение выражения равно

Подробное решение выглядит следующим образом:

Короткое решение будет выглядеть так:

Пример 2. Найти значение выражения

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Короткое решение будет выглядеть следующим образом:

Пример 3. Найти значение выражения

Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.

Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:

Пример 4. Найти значение выражения

Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .

Обратная для дроби это дробь . На неё и умножим первое число −3

Пример 6. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.

Обратное для числа 4 это дробь . На неё и умножим первую дробь

Пример 5. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3

Обратное для числа −3 это дробь . На неё и умножим первую дробь:

Пример 6. Найти значение выражение −14,4: 1,8

Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .

Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.

Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:

Теперь переведём полученные смешанные числа в неправильные дроби:

Пример 7. Найти значение выражения

Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:

Многоэтажные дроби

После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:

Пример 2.

Пример 3. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2

Реализуется этот метод следующим образом:

Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:

С первого на четвёртый. Со второго на третий.

Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.

Попробуем вычислить многоэтажную дробь пользуясь новой схемой.

Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.

Использование переменных

Использование переменных оправдано, при работе с многоэтажными дробями. Например:

Найти значение выражения

Выражение, находящееся в числителе можно занести в переменную с любым названием, например:

А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B

Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.

Найдём значение переменной A

Найдём значение переменной B

Теперь подставим в главное выражения вместо переменных A и B их значения:

Таким образом, значение выражения равно −1.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

В этой статье мы разберемся с умножением чисел с разными знаками . Здесь мы сначала сформулируем правило умножения положительного и отрицательного числа, обоснуем его, а после этого рассмотрим применение данного правила при решении примеров.

Навигация по странице.

Правило умножения чисел с разными знаками

Умножение положительного числа на отрицательное, а также отрицательного на положительное, проводится по следующему правилу умножения чисел с разными знаками : чтобы умножить числа с разными знаками, надо умножить , и перед полученным произведением поставить знак минус.

Запишем данное правило в буквенном виде. Для любого положительного действительного числа a и действительного отрицательного числа −b справедливо равенство a·(−b)=−(|a|·|b|) , а также для отрицательного числа −a и положительного числа b справедливо равенство (−a)·b=−(|a|·|b|) .

Правило умножения чисел с разными знаками полностью согласуется со свойствами действий с действительными числами . Действительно, на их основе несложно показать, что для действительных и положительных чисел a и b справедлива цепочка равенств вида a·(−b)+a·b=a·((−b)+b)=a·0=0 , которая доказывает, что a·(−b) и a·b – противоположные числа, откуда следует равенство a·(−b)=−(a·b) . А из него следует справедливость рассматриваемого правила умножения.

Следует отметить, что озвученное правило умножения чисел с разными знаками справедливо как для действительных чисел, так и для рациональных чисел и для целых чисел . Это следует из того, что действия с рациональными и целыми числами обладают теми же свойствами, которые использовались при доказательстве выше.

Понятно, что умножение чисел с разными знаками по полученному правилу сводится к умножению положительных чисел.

Осталось лишь рассмотреть примеры применения разобранного правила умножения при умножении чисел с разными знаками.

Примеры умножения чисел с разными знаками

Разберем решения нескольких примеров умножения чисел с разными знаками . Начнем с простого случая, чтобы сосредоточиться на шагах правила, а не на вычислительных сложностях.

Пример.

Выполните умножение отрицательного числа −4 на положительное число 5 .

Решение.

По правилу умножения чисел с разными знаками нам сначала нужно перемножить модули исходных множителей. Модуль −4 равен 4 , а модуль 5 равен 5 , а умножение натуральных чисел 4 и 5 дает 20 . Наконец, осталось поставить знак минус перед полученным числом, имеем −20 . На этом умножение завершено.

Кратко решение можно записать так: (−4)·5=−(4·5)=−20 .

Ответ:

(−4)·5=−20 .

При умножении дробных чисел с разными знаками нужно уметь выполнять умножение обыкновенных дробей , умножение десятичных дробей и их комбинаций с натуральными и смешанными числами.

Пример.

Проведите умножение чисел с разными знаками 0,(2) и .

Решение.

Выполнив перевод периодической десятичной дроби в обыкновенную дробь , а также выполнив переход от смешанного числа к неправильной дроби , от исходного произведения мы придем к произведению обыкновенных дробей с разными знаками вида . Это произведение по правилу умножения чисел с разными знаками равно . Осталось лишь перемножить обыкновенные дроби в скобках, имеем .

Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet

Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:

Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.

Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.

Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом.Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:

$$ 3 \ cdot (-4) = — 12 $$

3 умножить на 4 равно 12. Поскольку существует одно положительное и одно отрицательное число, произведение отрицательное 12.

$$ (- 3) \ cdot (-4) = 12 $$

Теперь у нас есть два отрицательных числа, поэтому результат положительный.

Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель.Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,

$$ \ frac {12} {3} = 4 $$

Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):

$$ 3 \ cdot 4 = 12 $$

Что произойдет, если разделить два отрицательных числа? Например,

$$ \ frac {(- 12)} {(- 3)} = \:? $$

Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.

Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:

Когда вы делите отрицательное число на положительное, то частное отрицательное.

Когда вы делите положительное число на отрицательное, частное также становится отрицательным.

Когда вы делите два отрицательных числа, получается положительное частное.

Те же правила верны и для умножения.

Видеоурок

Вычислить следующие выражения

$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$

Умножение и деление положительных и отрицательных чисел

Правила умножения и деления чисел очень похожи. Ключ состоит в том, чтобы определить, совпадают ли знаки у данных двух чисел или разные, потому что это определит окончательный знак ответа.

Правила умножения и деления чисел со знаком

Примеры того, как найти произведение или частное числа со знаком

Пример 1 : Найдите произведение (3) (6) и частное 12 ÷ 6 .

Найдите произведение (3) (6):

Поскольку числа 3 и 6 имеют одинаковые знаки (оба положительные), их произведение положительно.

(3) (6) = 18

Найдите частное от 12 ÷ 6:

Поскольку числа 12 и 6 имеют одинаковые знаки (оба положительные), их частное положительное.

12 ÷ 6 = 2

Пример 2 : Найдите произведение (–5) (- 3) и частное — 21 ÷ (–7) .

Найдите произведение (–5) (- 3):

Числа −5 и −3 имеют отрицательные знаки. Наличие такого же знака означает, что их продукт также должен быть положительным.

(–5) (- 3) = 15

Найдите частное от — 21 ÷ (–7) :

У чисел −5 и −3 есть отрицательные знаки. Частное двух чисел с одинаковым знаком положительно.

— 21 ÷ (–7) = 3

Пример 3 : Умножьте числа (9) (- 3) и разделите числа 18 ÷ (–9) .

Число 9 имеет положительный знак, а число −3 имеет отрицательный знак. Умножение этих двух чисел на разные знаки должно дать отрицательный ответ.

(9) (- 3) = –27

Число 9 положительно, а −3 отрицательно. Разделение двух чисел с разными знаками должно дать отрицательный ответ.

18 ÷ (–9) = –2

Пример 4 : Упростите числовое выражение.

Мы можем упростить числитель, умножив два числа.Сделайте то же самое со знаменателем.

Числа в числителе имеют разные знаки, поэтому мы ожидаем, что их произведение будет отрицательным. Между тем в знаменателе есть два числа с одинаковым знаком (оба отрицательные), поэтому их произведение должно быть положительным.

Завершим это делением числителя на знаменатель. Не забывайте также о правилах деления. Числитель отрицательный, а знаменатель положительный, наличие разных знаков должно давать отрицательный ответ.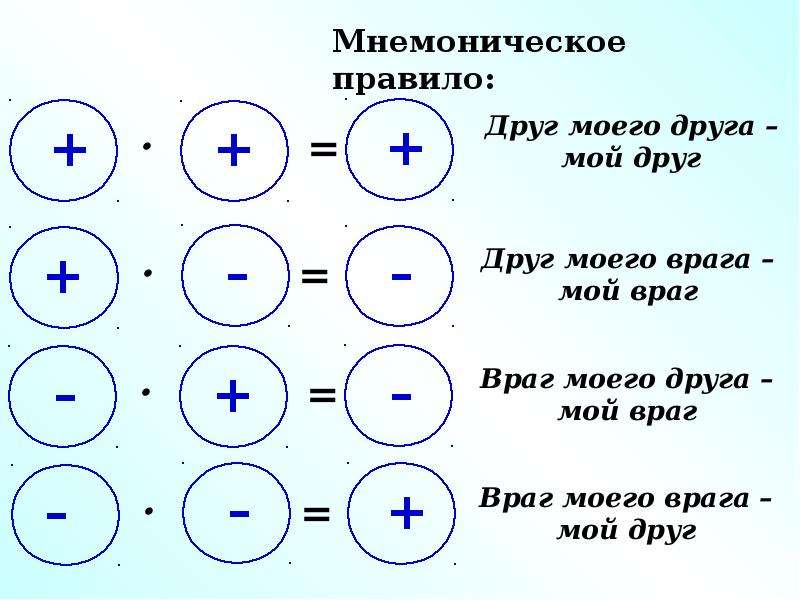

Пример 5 : Умножьте числа (–1) (- 2) (- 3) (- 4) .

До сих пор мы умножали числа по два за раз. На этот раз мы можем найти произведение трех или более чисел.

Мы можем решить это, умножая два числа за раз, потому что мы знаем, как это сделать.

Но есть быстрый способ определить знак, не умножая их по два за раз.

Обратите внимание, что у нас есть четное количество отрицательных знаков , то есть четыре отрицательных числа.Если вы столкнулись с чем-то вроде этого, воспользуйтесь правилом:

Четное число отрицательных знаков означает, что мы ожидаем положительного ответа.

(–1) (- 2) (- 3) (- 4) = +24

Пример 6 : умножить числа (–1) (–1) (–1 ) (–1) (–1) (–1) (–1) (–1) (–1) .

Эта проблема не предназначена для того, чтобы вас обмануть. Вместо этого думайте об этом как о еще одной возможности научиться решать такой вопрос.Ваш учитель может использовать что-то подобное в вашей викторине, чтобы проверить, хорошо ли вы знаете тему.

Не обращая внимания на знаки, все числа — единицы. Следовательно, мы предполагаем, что ответ может быть +1 или -1 .

Подсчитав количество отрицательных знаков, мы получим девять (9), что является нечетным!

Запомните правило:

Нечетное количество отрицательных знаков означает, что наш окончательный ответ должен быть отрицательным.

(–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) = –1

Пример 7 : Разделите числа (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) .

Правило нечетного и четного числа отрицательных чисел также работает при делении чисел.

Поскольку у нас есть семь (7) отрицательных знаков, нечетное число, ответ должен быть отрицательным.

(–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) = –1

Умножение и деление чисел со знаком — Предварительно -Алгебра

После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.

В этом видео мы научимся умножать и делить положительные и отрицательные числа.

Когда два знака совпадают +

Когда два знака разные —

Умножение и деление

Пример 1

Правило умножения целых чисел:

Если два знака совпадают, ответ положительный.

Если два знака различны, ответ отрицательный.

Поскольку оба числа положительны, ответ будет положительным.

Следовательно,

Пример 2

Правило деления целых чисел:

Если два знака совпадают, ответ положительный.

Если два знака различны, ответ отрицательный.

Поскольку у двух чисел разные знаки, ответ отрицательный.

Следовательно,

Стенограмма видеоурока

Давайте посмотрим на умножение и деление чисел со знаком.

Это означает умножение и деление положительных и отрицательных чисел.

Правило очень простое. То же самое правило для умножения и деления.

Если два знака совпадают, ответ положительный.

Если два знака различны, ответ отрицательный.

Приведем несколько быстрых примеров.

Для этого оба числа положительные, поэтому ответ положительный.

Даже если оба числа отрицательные, поскольку оба знака совпадают, ответ все равно будет положительным.

Эти два числа имеют разные знаки, поэтому ответ отрицательный.

Опять разные знаки поэтому ответ отрицательный.

Порядок здесь не имеет значения.

То же самое и с делением.

Знаки другие, значит отрицательный.

Давай

Знаки те же, значит, положительный.

Что делать, если у нас более двух чисел?

Например:

Давайте решим по два за раз.

Знаки другие, значит отрицательный. Затем переходите к умножению другого числа.

В этом случае оба числа имеют одинаковый знак, поэтому ответ положительный.

Напомню, что у нас одни и те же правила умножения и деления.

Если два знака совпадают, ответ положительный.

Если два знака различны, ответ отрицательный.

Умножение и деление целых чисел — методы и примеры

В математике арифметические операции с целыми числами включают вычитание, сложение, деление и умножение всех типов действительных чисел. В частности, целые числа — это числа, которые включают положительные, отрицательные и нулевые числа. Умножение и деление целых чисел регулируются аналогичными правилами.

Как умножать целые числа?

Умножение определяется как повторное сложение целых чисел. Умножение целых чисел включает три случая:

Умножение двух положительных целых чисел
Умножение двух отрицательных целых чисел
Умножение положительного и отрицательного целого числа.

Умножение двух целых чисел со знаком равенства всегда дает положительный результат. Это означает, что произведение двух положительных или двух отрицательных целых чисел положительно.С другой стороны, целые числа продукта со знаком отличия всегда будут отрицательными.

Многие студенты сталкиваются с проблемой запоминания приведенных выше правил умножения целых чисел. В этой статье есть сценарий, который поможет вам избежать путаницы. В этом сценарии положительный знак (+) используется для обозначения « ХОРОШО », а отрицательный знак символизирует фразу « BAD ». «Давайте взглянем на эту мнемонику.

Если хорошие (+) вещи случаются с хорошими (+) людьми, то это хорошо (+)
Если хорошие (+) вещи случаются с плохими (-) людьми, то это плохо (-)
Если плохие (-) вещи случаются с хорошими (+) людьми, тогда это плохо (-)
Если плохие (-) вещи случаются с плохими (-) людьми, то это хорошо (+)

Чтобы умножить целые числа, просто умножьте числовые числа без знака и поставьте знак на продукте, вспомнив приведенные выше правила.

Пример 1

7 x 5 = 35
7 × (-6) = -42
(-9) × 5 = -45
(-4) × (-5) = 20

Если количество отрицательных множимых в предложении умножения нечетное, произведение будет отрицательным числом.

Пример 2

(-2) × (−4) × (−3) = −24; здесь количество множимых = 3 (нечетное число)

Когда количество отрицательных множимых в предложении умножения четное, произведение будет положительным.

Пример 3

(-4) × (-3) = 12; Здесь число множимых равно 2 (четным)

Как разделить целые числа?

Если умножение — это суммирование целых чисел, то деление — это распределение целых чисел. Мы можем просто сказать, что деление — это обратное умножение. Правила деления целых чисел аналогичны правилам умножения. Единственная разница в делении состоит в том, что частное может не быть целым числом.

Давайте также посмотрим на правила деления:

Частное положительного целого числа всегда положительно. Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Частное двух отрицательных чисел всегда положительно. Это означает, что если дивиденд и делитель отрицательны, то частное всегда положительно. Например;
(- 9) ÷ (- 3) = + 3
Следовательно, при делении двух целых чисел с одинаковыми знаками мы делим числа без знака и ставим положительный знак результату.
Деление положительного и отрицательного целого числа дает отрицательный ответ. Например; (+ 16) ÷ (- 4) = — 4

Таким образом, чтобы разделить целые числа с разными знаками, числовые значения делятся без знаков, а результат ставится знаком минус.

Практические вопросы

Вы насчитали всего 120 рук в своем классе. Сколько было учтено студентов?
В тесте по математике 20 вопросов. За каждый правильный ответ дается три балла, за неправильный — 1 балл.Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент?
Дайвер спускается со скоростью 40 футов в минуту от уровня моря. Найдите положение дайвера по отношению к уровню моря через 5 минут спуска?
Мужчина должен банку 8000 долларов. Если каждый из его 4 друзей готов погасить ссуду, внося равную сумму. Определите, сколько денег вложил каждый из его друзей.
26 человек разделили между собой 5 876 долларов поровну. Сколько получил каждый?

Предыдущий урок | Главная страница | Следующий урок

Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.[Решено]

Вопрос: Перечислите правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Четыре основные арифметические операции, связанные с целыми числами:

Сложение целых чисел
Вычитание целого числа
Умножение целых чисел
Деление целых чисел

Ответ: Есть некоторые правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Прежде чем мы начнем изучать эти методы операций с целыми числами, нам нужно запомнить несколько вещей. Если перед числом нет знака, это означает, что число положительное.

Пояснение:

Ниже приведены правила сложения, вычитания, умножения и деления положительных и отрицательных чисел

Правило сложения целых чисел:

Случай 1: Знаки одинаковые

Если знаки такие же, добавить и сохранить тот же знак.

(+) + (+) = сложите числа и получите положительный ответ

Пример: 2 + 5 = 7

(-) + (-) = сложите числа, и ответ будет отрицательным

Пример: (-5) + (-4) = -9

Случай 2: Знаки разные

Если знаки разные, вычтите числа и используйте знак большего числа

(+) + (-) = вычесть числа и принять знак большего числа

Пример: 7 + (-3) = 4

(-) + (+) = вычесть числа и принять знак большего числа

Пример: (-9) + 6 = -3

Правило вычитания целых чисел:

Чтобы вычесть число из другого числа, следует изменить знак числа (которое должно быть вычтено), а затем это число с измененным знаком следует прибавить к первому числу.

(+) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа

Пример: (+6) — (+2)

= (+6) + (-2) = 6-2 = 4

(-) — (-) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа

Пример: (-9) — (-6)

= (-9) + (+6) = -9 + 6 = -3

(+) — (-) = Измените знак числа, которое нужно вычесть, и сложите их.Результат всегда положительный

Пример: (+5) — (-3)

= (+5) + (+ 3) = 5 + 3 = 8

(-) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат всегда отрицательный

Пример: (-7) — (+2)

= (-7) + (-2) = -7-2 = -9

Правило умножения и деления целых чисел:

Случай 1: Знаки одинаковые

Если знаки одинаковые, умножьте или разделите, и ответ всегда будет положительным.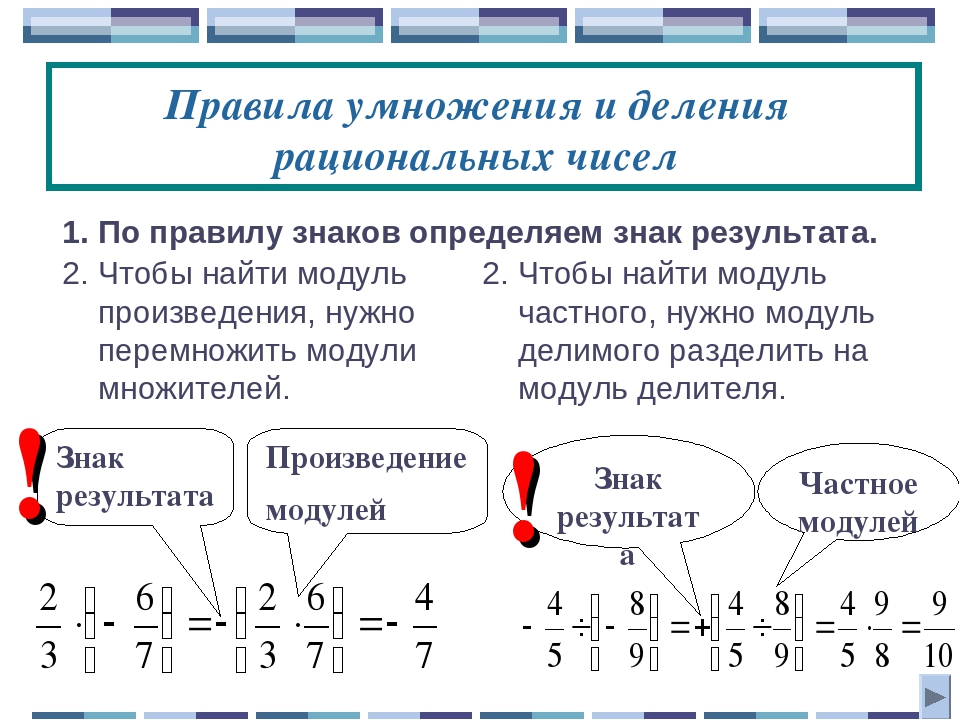

Пример: 5 × 4 = 20

Пример: 16 ÷ 4 = 4

Пример: (-7) × (-9) = 63

Пример: (-20) ÷ (-2) = 10

Случай 2: Знаки разные

Если знаки разные, умножить или разделить, ответ всегда отрицательный.

Пример: 6 × (-10) = -60

Пример: 30 ÷ (-15) = -2

Пример: -3 × 11 = 33

Пример: -25 ÷ 5 = -5

Таким образом, мы научились складывать, вычитать, умножать и делить положительные и отрицательные числа.

вещественных чисел | Начальная алгебра

Результаты обучения

Сложить и вычесть действительные числа
- Сложить вещественные числа с одинаковыми и разными знаками
- Вычесть действительные числа с одинаковыми и разными знаками
- Упростите комбинации, которые требуют как сложения, так и вычитания действительных чисел.
Умножение и деление действительных чисел
- Умножение двух или более действительных чисел.
- Разделить действительные числа
- Упростите выражения умножением и делением
- Упростите выражения с помощью действительных чисел
Распознавать и комбинировать похожие термины в выражении
- Используйте порядок операций для упрощения выражений
Упростите составные выражения с помощью действительных чисел
- Упростите выражения с помощью дробных черт, скобок и круглых скобок
- Используйте свойство распределения для упрощения выражений с помощью символов группировки
- Упростить выражения, содержащие абсолютные значения

Перед тем, как мы начнем, следует запомнить некоторые важные термины:

целые числа: подсчет чисел, таких как 1, 2, 3 и т. Д., включая негативы и ноль
вещественное число: дроби, отрицательные числа, десятичные дроби, целые числа и ноль — все это действительные числа
абсолютное значение: расстояние от нуля до числа; это всегда положительно. [латекс] | -7 | = 7 [/ латекс]
знак: это относится к положительному или отрицательному числу, мы используем [latex] + [/ latex] для положительного (справа от нуля в числовой строке) и [latex] — [/ latex] для отрицательного. (слева от нуля в числовой строке)
разница: результат вычитания
сумма: результат сложения

Умение комфортно работать с отрицательными числами необходимо для успеха в алгебре.По этой причине мы сделаем краткий обзор сложения, вычитания, умножения и деления целых чисел. Целые числа — это все положительные целые числа, ноль и их противоположности (отрицательные). Поскольку это обзор целых чисел, описания и примеры не будут такими подробными, как на обычном уроке.

Сложение и вычитание действительных чисел

При сложении целых чисел необходимо рассмотреть два случая. Первый случай — совпадают ли знаки (положительные или отрицательные). Если знаки совпадают, мы сложим числа и сохраним знак.

Если знаки не совпадают (одно положительное и одно отрицательное число), мы вычтем числа (как если бы все они были положительными), а затем используем знак из большего числа. Это означает, что если большее число положительно, ответ будет положительным. Если большее число отрицательно, ответ отрицательный.

Чтобы сложить два числа с одинаковым знаком (положительное или отрицательное)

Добавьте их абсолютных значений (без знака [latex] + [/ latex] или [latex] — [/ latex])
Поставьте сумму тем же знаком.

Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное)

Найдите разность из их абсолютных значений. (Обратите внимание, что когда вы обнаруживаете разницу абсолютных значений, вы всегда вычитаете меньшее абсолютное значение из большего.)
Укажите для суммы тот же знак, что и у числа с большим абсолютным значением.

Пример

Найдите [латекс] 23–73 [/ латекс].

Показать решение Вы не можете использовать свой обычный метод вычитания, потому что 73 больше 23.Перепишите вычитание как добавление противоположного.

[латекс] 23+ \ влево (-73 \ вправо) [/ латекс]

Слагаемые имеют разные знаки, поэтому найдите разницу их абсолютных значений.

[латекс] \ begin {array} {c} \ left | 23 \ right | = 23 \, \, \, \ text {and} \, \, \, \ left | −73 \ right | = 73 \\ 73-23 = 50 \ end {array} [/ latex]

Поскольку [латекс] \ left | −73 \ right |> \ left | 23 \ right | [/ latex], окончательный ответ отрицательный.

Ответ

[латекс] 23–73 = −50 [/ латекс]

Другой способ подумать о вычитании — это подумать о расстоянии между двумя числами на числовой прямой.В приведенном ниже примере [latex] 382 [/ latex] соответствует правому из 0 на [latex] 382 [/ latex] единиц, а [latex] -93 [/ latex] находится к левому из 0 на 93 ед. Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].

Пример

Найдите [латекс] 382– \ left (−93 \ right) [/ latex].

Показать решение Вы убираете отрицательный знак, поэтому думайте об этом как об удалении отрицательного знака. Это становится дополнительной проблемой. [латекс] -93 [/ латекс] становится [латекс] +93 [/ латекс]

[латекс] 382 + 93 = 475 [/ латекс]

Ответ

[латекс] 382 — (- 93) = 475 [/ латекс]

В следующем видео объясняется, как вычесть два целых числа со знаком.

Пример

Найдите [латекс] — \ frac {3} {7} — \ frac {6} {7} + \ frac {2} {7} [/ latex]

Показать решение Сложите первые два и дайте результату знак минус:

Так как знаки у первых двух одинаковые, найти сумму абсолютных значений дробей

Поскольку оба числа отрицательны, сумма отрицательна. Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.

[латекс] \ левый | — \ frac {3} {7} \ right | = \ frac {3} {7} [/ latex] и [latex] \ left | — \ frac {6} {7} \ right | = \ frac {6} {7} [/ латекс]

[латекс] \ begin {array} {c} \ frac {3} {7} + \ frac {6} {7} = \ frac {9} {7} \\\\ — \ frac {3} {7 } — \ frac {6} {7} = — \ frac {9} {7} \ end {array} [/ latex]

Теперь добавьте третье число.Знаки разные, поэтому найдите разницы их абсолютных значений.

[латекс] \ левый | — \ frac {9} {7} \ right | = \ frac {9} {7} [/ latex] и [latex] \ left | \ frac {2} {7} \ right | = \ frac {2} {7} [/ латекс]

[латекс] \ frac {9} {7} — \ frac {2} {7} = \ frac {7} {7} [/ latex]

Поскольку [latex] \ left | \ frac {-9} {7} \ right |> \ left | \ frac {2} {7} \ right | [/ latex], знак окончательной суммы такой же, как знак [латекс] — \ frac {9} {7} [/ латекс].

[латекс] — \ frac {9} {7} + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]

Ответ

[латекс] — \ frac {3} {7} + \ left (- \ frac {6} {7} \ right) + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]

В следующем видео вы увидите пример того, как сложить три дроби с общим знаменателем и разными знаками.

Пример

Оценить [латекс] 27,832 + (- 3,06) [/ латекс]. Когда вы добавляете десятичные дроби, не забудьте выровнять десятичные дроби так, чтобы вы добавляли десятые доли к десятым, сотые к сотым и т. Д.

Показать решение Поскольку слагаемые имеют разные знаки, вычтите их абсолютные значения.

[латекс] \ begin {array} {r} \ underline {\ begin {array} {r} 27.832 \\ — \ text {} 3.06 \, \, \, \ end {array}} \\ 24.772 \ end { array} [/ latex]

[латекс] \ влево | -3,06 \ вправо | = 3.06 [/ латекс]

Сумма имеет тот же знак, что и 27,832, абсолютное значение которого больше.

Ответ

[латекс] 27,832+ \ влево (-3,06 \ вправо) = 24,772 [/ латекс]

В следующем видео представлены примеры сложения и вычитания десятичных знаков с разными знаками.

Умножение и деление действительных чисел

Умножение и деление — это обратные операции , так же как сложение и вычитание. Вы можете вспомнить, что когда вы делите дроби, вы умножаете их на обратную.Обратные операции «отменяют» друг друга.

Умножение действительных чисел

Умножение действительных чисел ничем не отличается от умножения целых чисел и положительных дробей. Однако вы не знаете, как отрицательный знак влияет на товар.

С целыми числами вы можете думать об умножении как о повторяющемся сложении. Используя числовую линию, вы можете совершить несколько прыжков заданного размера. Например, на следующем рисунке продукт [latex] 3 \ cdot4 [/ latex] показан в виде 3 прыжков по 4 единицы каждый.

Итак, чтобы умножить [latex] 3 (−4) [/ latex], вы можете повернуться лицом влево (в отрицательную сторону) и сделать три «прыжка» вперед (в отрицательном направлении).

Произведение положительного числа и отрицательного числа (или отрицательного и положительного) дает отрицательное значение.

Произведение положительного и отрицательного числа

Чтобы умножить положительное число и отрицательное число , умножьте их абсолютные значения. Произведение минус .

Пример

Найдите [латекс] −3,8 (0,6) [/ латекс].

Показать решение Умножьте абсолютные значения, как обычно. Установите десятичную точку, считая разряды. 3.8 имеет 1 место после десятичной точки, а 0.6 имеет 1 место после десятичной точки, поэтому продукт имеет [латекс] 1 + 1 [/ latex] или 2 разряда после десятичной точки.

[латекс] \ begin {array} {r} 3.8 \\\ underline {\ times \, \, \, 0.6} \\ 2.28 \ end {array} [/ latex]

Произведение отрицательного и положительного отрицательного.

Ответ

[латекс] -3,8 (0,6) = — 2,28 [/ латекс]

Следующее видео содержит примеры умножения десятичных чисел с разными знаками.

Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)

Чтобы умножить два положительных числа , умножьте их абсолютные значения. Продукт положительный .

Чтобы умножить два отрицательных числа на , умножьте их абсолютные значения.Продукт положительный .

Пример

Найдите [латекс] ~ \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) [/ latex]

Показать решение Умножьте абсолютные значения чисел. Сначала умножьте числители, чтобы получить числитель произведения. Затем умножьте знаменатели, чтобы получить знаменатель произведения. При необходимости перепишите в минимальных терминах.

[латекс] \ left (\ frac {3} {4} \ right) \ left (\ frac {2} {5} \ right) = \ frac {6} {20} = \ frac {3} {10} [/ латекс]

Произведение двух отрицательных чисел положительно.

Ответ

[латекс] \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) = \ frac {3} {10} [/ latex]

В следующем видео показаны примеры умножения двух дробей со знаком, включая упрощение ответа.

Суммируем:

положительный [латекс] \ cdot [/ latex] положительный : Продукт положительный .
отрицательный [латекс] \ cdot [/ latex] отрицательный : Продукт положительный .
отрицательный [латекс] \ cdot [/ latex] положительный : Продукт отрицательный .
положительный [латекс] \ cdot [/ latex] отрицательный : Продукт отрицательный .

Как видите, произведение двух отрицательных чисел является положительным числом. Итак, если вы умножаете более двух чисел, вы можете подсчитать количество отрицательных множителей.

Умножение более двух отрицательных чисел

Если есть четное число (0, 2, 4,…) отрицательных множителей для умножения, произведение будет положительным .
Если имеется нечетное число (1, 3, 5,…) отрицательных факторов, произведение отрицательное .

Пример

Найдите [латекс] 3 (−6) (2) (- 3) (- 1) [/ latex].

Показать решение Умножьте абсолютные значения чисел.

[латекс] \ begin {array} {l} 3 (6) (2) (3) (1) \\ 18 (2) (3) (1) \\ 36 (3) (1) \\ 108 ( 1) \\ 108 \ end {array} [/ latex]

Подсчитайте количество отрицательных факторов. Есть три [латекса] \ left (−6, −3, −1 \ right) [/ latex].

[латекс] 3 (−6) (2) (- 3) (- 1) [/ латекс]

Поскольку существует нечетное количество отрицательных факторов, произведение отрицательное.

Ответ

[латекс] 3 (−6) (2) (- 3) (- 1) = — 108 [/ латекс]

Следующее видео содержит примеры умножения более двух целых чисел со знаком.

Разделить действительные числа

Вы можете помнить, что когда вы делили дроби, вы умножали на обратную величину . Reciprocal — это другое название мультипликативного обратного (точно так же, как напротив — другое название для аддитивного обратного).

Самый простой способ найти обратное умножение — просто «перевернуть» числитель и знаменатель, как вы это делали, чтобы найти обратное.Вот несколько примеров:

Обратное значение [latex] \ frac {4} {9} [/ latex] равно [latex] \ frac {9} {4} [/ latex], потому что [latex] \ frac {4} {9} \ left (\ frac {9} {4} \ right) = \ frac {36} {36} = 1 [/ латекс].
Обратное значение 3 равно [latex] \ frac {1} {3} [/ latex], потому что [latex] \ frac {3} {1} \ left (\ frac {1} {3} \ right) = \ frac {3} {3} = 1 [/ латекс].
Обратное значение [latex] — \ frac {5} {6} [/ latex] равно [latex] \ frac {-6} {5} [/ latex], потому что [latex] — \ frac {5} {6} \ left (- \ frac {6} {5} \ right) = \ frac {30} {30} = 1 [/ latex].
Обратное значение 1 равно 1, так как [латекс] 1 (1) = 1 [/ латекс].

Когда вы делите на положительные дроби, вы научились умножать на обратную. Вы также делаете это, чтобы разделить вещественных числа на .

Подумайте о том, чтобы разделить мешок из 26 шариков на два мешка меньшего размера с одинаковым количеством шариков в каждом. Вы также можете сказать, что каждая сумка меньшего размера содержит и половину шариков.

[латекс] 26 \ div 2 = 26 \ left (\ frac {1} {2} \ right) = 13 [/ latex]

Обратите внимание, что 2 и [latex] \ frac {1} {2} [/ latex] являются обратными величинами.

Попробуйте еще раз, разделив мешок из 36 шариков на мешочки поменьше.

Количество мешков	Деление на количество мешков	Умножение на обратное
3	[латекс] \ frac {36} {3} = 12 [/ латекс]	[латекс] 36 \ left (\ frac {1} {3} \ right) = \ frac {36} {3} = \ frac {12 (3)} {3} = 12 [/ latex]
4	[латекс] \ frac {36} {4} = 9 [/ латекс]	[латекс] 36 \ left (\ frac {1} {4} \ right) = \ frac {36} {4} = \ frac {9 \ left (4 \ right)} {4} = 9 [/ латекс]
6	[латекс] \ frac {36} {6} = 6 [/ латекс]	[латекс] 36 \ left (\ frac {1} {6} \ right) = \ frac {36} {6} = \ frac {6 \ left (6 \ right)} {6} = 6 [/ латекс]

Деление на число аналогично умножению на обратную величину. (То есть вы используете обратную величину от делителя , второго числа в задаче деления.)

Пример

Найдите [латекс] 28 \ div \ frac {4} {3} [/ latex]

Показать решение Перепишите деление как умножение на обратную. Аналог [latex] \ frac {4} {3} [/ latex] — это [latex] \ frac {3} {4} [/ latex].

[латекс] 28 \ div \ frac {4} {3} = 28 \ left (\ frac {3} {4} \ right) [/ latex]

Умножить.

[латекс] \ frac {28} {1} \ left (\ frac {3} {4} \ right) = \ frac {28 \ left (3 \ right)} {4} = \ frac {4 \ left ( 7 \ right) \ left (3 \ right)} {4} = 7 \ left (3 \ right) = 21 [/ латекс]

Ответ

[латекс] 28 \ div \ frac {4} {3} = 21 [/ латекс]

Теперь давайте посмотрим, что это значит, когда одно или несколько чисел отрицательны.Число и его обратная величина имеют один и тот же знак. Поскольку деление переписывается как умножение с использованием обратной величины делителя, а взятие обратной величины не меняет никаких знаков, деление следует тем же правилам, что и умножение.

Правила подкласса

При делении перепишите задачу как умножение, используя обратную величину делителя в качестве второго множителя.

Когда одно число — положительное , а другое — отрицательное , частное будет отрицательным .

Когда оба числа являются отрицательными , частное равно положительным .

Когда оба числа являются положительными , частное составляет положительных .

Пример

Найдите [латекс] 24 \ div \ left (- \ frac {5} {6} \ right) [/ latex].

Показать решение Перепишите деление как умножение на обратную.

[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = 24 \ left (- \ frac {6} {5} \ right) [/ latex]

Умножить.Поскольку одно число положительное, а другое отрицательное, произведение отрицательное.

[латекс] \ frac {24} {1} \ left (- \ frac {6} {5} \ right) = — \ frac {144} {5} [/ latex]

Ответ

[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = — \ frac {144} {5} [/ latex]

Пример

Найдите [латекс] 4 \, \ left (- \ frac {2} {3} \ right) \, \ div \ left (-6 \ right) [/ latex]

Показать решение Перепишите деление как умножение на обратную.

[латекс] \ frac {4} {1} \ left (- \ frac {2} {3} \ right) \ left (- \ frac {1} {6} \ right) [/ latex]

Умножить.Число отрицательных чисел четное, значит, произведение положительное.

[латекс] \ frac {4 \ left (2 \ right) \ left (1 \ right)} {3 \ left (6 \ right)} = \ frac {8} {18} [/ latex]

Запишите дробь наименьшим числом.

Ответ

[латекс] 4 \ left (- \ frac {2} {3} \ right) \ div \ left (-6 \ right) = \ frac {4} {9} [/ latex]

В следующем видео рассказывается, как делить дроби со знаком.

Помните, что черта дроби также указывает на деление, поэтому отрицательный знак перед дробью идет вместе с числителем, знаменателем или целой дробью: [latex] — \ frac {3} {4} = \ frac {-3 } {4} = \ frac {3} {- 4} [/ latex].

В каждом случае общая дробь отрицательная, потому что при делении есть только одно отрицательное число.

В следующем видео рассказывается, как делить дроби со знаком.

Упростите выражения с помощью действительных чисел

Прежде чем мы начнем, немного важной терминологии:

операции / операторы: В математике мы называем такие вещи, как операции умножения, деления, сложения и вычитания. Это глаголы математического мира, выполняющие работу с числами и переменными. 2b [/ латекс] или [латекс] -3 [/ латекс] и [латекс] 8 [/ латекс]. Если у нас есть одинаковые термины, нам разрешено складывать (или вычитать) числа перед переменными, а затем оставлять переменные такими же. Когда мы комбинируем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный. Знак всегда соответствует сроку.
Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс] 5x-2y-8x + 7y [/ latex]
Показать решение
Подобные термины в этом выражении:
[латекс] 5x [/ латекс] и [латекс] -8x [/ латекс]
[латекс] -2y [/ латекс] и [латекс] -7y [/ латекс]
Обратите внимание, как мы держали табличку перед каждым термином.
Объедините похожие термины:
[латекс] 5x-8x = -3x [/ латекс]
[латекс] -2y-7y = -9y [/ латекс]
Обратите внимание, как знаки становятся операциями, когда вы объединяете одинаковые термины.
Упрощенное выражение:
[латекс] 5x-2y-8x + 7y = -3x-9y [/ латекс]
В следующем видео вам будет показано, как комбинировать одинаковые термины, используя идею распределительного свойства. Обратите внимание, что это другой метод, чем показан в письменных примерах на этой странице, но он дает тот же результат.2 \\ — 3x + 3x = 0 \, \, \, \, \, \, \, \, \, \, \, \\ 9-1 = 8 \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
В следующем видео вам будет показан еще один пример объединения похожих терминов. Обратите внимание, почему вы не можете объединить все три термина в примере.

Порядок действий
Вы можете вспомнить или не вспомнить порядок операций для применения нескольких математических операций к одному выражению. Так же, как для нас принято ездить по правой стороне дороги, порядок операций — это набор соглашений, используемых для обеспечения порядка, когда вам необходимо использовать несколько математических операций для одного выражения.На приведенном ниже рисунке показан порядок выполнения математических операций.
Порядок работы
Пример
Упростить [латекс] 7–5 + 3 \ cdot8 [/ latex].
Показать решение Согласно порядку операций умножение предшествует сложению и вычитанию.
Умножить [латекс] 3 \ cdot8 [/ latex].
[латекс] \ begin {array} {c} 7–5 + 3 \ cdot8 \\ 7–5 + 24 \ end {array} [/ latex]
Теперь сложите и вычтите слева направо. [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 2 + 24 [/ латекс].
Наконец, доп.
[латекс] 2 + 24 = 26 [/ латекс]
Ответ
[латекс] 7–5 + 3 \ cdot8 = 26 [/ латекс]
В следующем примере вам будет показано, как упростить выражение, которое содержит как умножение, так и вычитание, используя порядок операций.

Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также необходимо вспомнить, как выполнять эти вычисления.
Пример
Упростите [латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ latex].
Показать решение Согласно порядку операций умножение и деление предшествуют сложению и вычитанию. Иногда полезно добавить круглые скобки, чтобы вы знали, что идет первым, поэтому давайте заключим в скобки умножение и деление, поскольку оно будет стоять перед вычитанием.
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ латекс]
Сначала умножьте [латекс] 3 \ cdot \ frac {1} {3} [/ latex].
[латекс] \ begin {array} {c} \ left (3 \ cdot \ frac {1} {3} \ right) — \ left (8 \ div \ frac {1} {4} \ right) \\\ текст {} \\ = \ left (1 \ right) — \ left (8 \ div \ frac {1} {4} \ right) \ end {array} [/ latex]
Теперь разделите [латекс] на 8 \ div \ frac {1} {4} [/ latex].
[латекс] \ begin {array} {c} 8 \ div \ frac {1} {4} = \ frac {8} {1} \ cdot \ frac {4} {1} = 32 \\\ text {} \\ 1-32 \ end {array} [/ latex]
Вычесть.
[латекс] 1–32 = −31 [/ латекс]
Ответ
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} = — 31 [/ латекс]
В следующем видео показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание, с помощью членов, содержащих дроби.{3}} = 72 [/ латекс]
В следующем видео выражение с показателями степени упрощено с использованием порядка операций.

Группировка символов
Группирующие символы, такие как круглые скобки (), квадратные скобки [], фигурные скобки [латекс] \ displaystyle \ left \ {{} \ right \} [/ latex] и дробные черты, могут использоваться для дальнейшего управления порядком четырех арифметических операций. . Правила порядка операций требуют, чтобы сначала были выполнены вычисления внутри символов группировки, даже если вы добавляете или вычитаете внутри символов группировки и у вас есть умножение вне символов группировки.После вычисления внутри символов группировки разделите или умножьте слева направо, а затем вычтите или сложите слева направо. Если в составе символов группировки есть символы группировки, выполняйте вычисления изнутри наружу. То есть сначала начните упрощать внутри самых внутренних символов группировки.
Помните, что скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]
Упростите составные выражения действительными числами
В этом разделе мы будем использовать навыки из последнего раздела, чтобы упростить математические выражения, которые содержат много символов группировки и множество операций. Мы используем термин составной для описания выражений, которые имеют много операций и много группирующих символов. При применении порядка операций с этими выражениями требуется больше внимания. Кроме того, вы увидите, как обрабатывать абсолютные значения при упрощении выражений.{2}} + 2} [/ латекс]
Показать решение В этой задаче есть скобки, круглые скобки, дроби, показатели, умножение, вычитание и сложение.
Сначала обрабатываются символы группировки. Скобки вокруг [latex] -6 [/ latex] не являются символом группировки; они просто дают понять, что отрицательный знак принадлежит цифре 6. Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]
Следующее видео содержит пример, аналогичный написанному выше. Обратите внимание, как числитель и знаменатель дроби упрощаются по отдельности.

Распределительная собственность
Круглые скобки используются для группировки или объединения выражений и терминов в математике. Вы можете увидеть, как они используются, когда вы работаете с формулами, и когда вы переводите реальную ситуацию в математическую задачу, чтобы найти количественное решение.
Распределительная собственность Combo Meal
Например, вы собираетесь пообщаться с друзьями и звоните им, чтобы спросить, не хотят ли они чего-нибудь из вашего любимого проезда. Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
[латекс] \ begin {array} {c} \, \, \, 3 \ left (2 \ text {tacos} + 1 \ text {drink} \ right) \\ = 3 \ cdot {2} \ text { тако} +3 \ текст {напитки} \\\, \, = 6 \ текст {тако} +3 \ текст {напитки} \ конец {массив} [/ латекс]
Свойство распределенности позволяет нам явно описать сумму, которая является результатом группы групп.В случае комбинированных блюд у нас есть три группы (два тако плюс один напиток). Следующее определение описывает, как использовать свойство распределения в общих чертах.
Распределительное свойство умножения
Для всех действительных чисел a, b, и c , [латекс] a (b + c) = ab + ac [/ latex].
Это означает, что когда число в скобках умножает выражение, вы можете распределить умножение на каждый член выражения индивидуально.
Чтобы упростить [латекс] 3 \ left (3 + y \ right) -y + 9 [/ latex], может быть полезно увидеть выражение, переведенное в слова:
умножьте три на (сумму трех и y), затем вычтите y, затем прибавьте 9
Чтобы умножить три на сумму трех и y, вы используете свойство распределения —
[латекс] \ begin {array} {c} \, \, \, \, \, \, \, \, \, 3 \ left (3 + y \ right) -y + 9 \\\, \, \, \, \, \, \, \, \, = \ underbrace {3 \ cdot {3}} + \ underbrace {3 \ cdot {y}} — y + 9 \\ = 9 + 3y-y + 9 \ end {array} [/ latex]
Теперь вы можете вычесть y из 3y и прибавить 9 к 9.
[латекс] \ begin {array} {c} 9 + 3y-y + 9 \\ = 18 + 2y \ end {array} [/ latex]
В следующем примере показано, как использовать свойство распределения, когда один из задействованных терминов отрицательный.
Пример
Упростить [латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) [/ latex]
Показать решение
Это выражение содержит два набора круглых скобок с заблокированными в них переменными. Мы будем использовать свойство distributive, чтобы убрать круглые скобки.
[латекс] \ begin {array} {c} a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) \\ = a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \ end {array} [/ latex]
Обратите внимание, как мы поместили отрицательный знак, который был на b, перед 2, когда мы применили свойство распределения.Когда вы умножаете отрицательный результат на положительный, результат будет отрицательным, поэтому [latex] 2 \ cdot {-a} = — 2a [/ latex]. При использовании распределительного свойства важно быть осторожным с отрицательными знаками.
[латекс] \ begin {array} {c} a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \\ = a + 10-2a + 3a + 12 \\ = 2a + 22 \ end {array} [/ latex]
Мы объединили все возможные условия, чтобы получить окончательный результат.
Ответ
[латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) = 2a + 22 [/ латекс]
Абсолютное значение
Выражения абсолютного значения — это последний метод группировки, который вы можете увидеть.Напомним, что абсолютное значение количества всегда положительно или равно 0.
Когда вы видите выражение абсолютного значения, включенное в большее выражение, относитесь к абсолютному значению как к символу группировки и сначала оцените выражение внутри знака абсолютного значения. Затем возьмите абсолютное значение этого выражения. Пример ниже показывает, как это делается.
Пример
Упростите [латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} [/ latex].
Показать решение В этой задаче есть абсолютные значения, десятичные дроби, умножение, вычитание и сложение.
Сначала обрабатываются символы группировки, включая абсолютное значение. Упростите числитель, а затем знаменатель.
Оценить [латекс] \ left | 2–6 \ right | [/ latex].
[латекс] \ begin {array} {c} \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
Возьмите абсолютное значение [латекс] \ left | −4 \ right | [/ latex].
[латекс] \ begin {массив} {c} \ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
Сложите числа в числителе.
[латекс] \ begin {array} {c} \ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7 } {2 \ left | 3 \ cdot 1.5 \ right | — (- 3)} \ end {array} [/ latex]
Теперь, когда числитель упростился, обратимся к знаменателю.
Сначала вычислите выражение абсолютного значения. [латекс] 3 \ cdot 1,5 = 4,5 [/ латекс], что дает
[латекс] \ begin {array} {c} \ frac {7} {2 \ left | {3 \ cdot {1.5}} \ right | — (- 3)} \\\\\ frac {7} {2 \ left | {4.5} \ right | — (- 3)} \ end {array} [/ latex]
Выражение «[латекс] 2 \ left | 4.5 \ right | [/ latex]» читается как «двойное абсолютное значение 4,5». Умножить 2 раза на 4,5.
[латекс] \ begin {array} {c} \ frac {7} {2 \ left | 4.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7} {9- \ left (-3 \ справа)} \ end {array} [/ latex]
Вычесть.
[латекс] \ begin {array} {c} \ frac {7} {9- \ left (-3 \ right)} \\\\\ frac {7} {12} \ end {array} [/ latex]
Ответ
[латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | -3 \ left (-3 \ right)} = \ frac {7} {12} [/ латекс]
В следующем видео порядок операций используется для упрощения выражения в форме дроби, которое содержит элементы абсолютного значения. Обратите внимание, как абсолютные значения обрабатываются как круглые и квадратные скобки при использовании порядка операций.

Правила деления отрицательных чисел
Учащиеся изучают правила сложения и вычитания чисел в очень раннем возрасте. Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.
Два положительных результата
При делении одно число, делимое, делится на другое число.

Умножение и деление отрицательных чисел

Умножение и деление положительных и отрицательных чисел

Умножение чисел с разными знаками

Деление чисел с разными знаками

Похожие статьи

7. Умножение и деление положительных и отрицательных чисел.

Деление отрицательных чисел и чисел с разными знаками

1. Организационный момент.

4. Выполнение теста «Составьте слово» (слайд 12).

5. Решение упражнений.

7.Итог урока.

8. Домашнее задание:

стр. 218 №1174, 1179(1) (слайд 21)

Умножение и деление целых чисел. Возведение в степень

Умножение

Деление

Возведение в степень

Умножение и деление рациональных чисел

Умножение рациональных чисел

Деление рациональных чисел

Многоэтажные дроби

Использование переменных

Задания для самостоятельного решения

Навигация по записям

Умножение дробей с разными знаками. Умножение и деление отрицательных чисел

Умножение рациональных чисел

Деление рациональных чисел

Многоэтажные дроби

Использование переменных

Правило умножения чисел с разными знаками

Примеры умножения чисел с разными знаками

Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet

Умножение и деление положительных и отрицательных чисел

Правила умножения и деления чисел со знаком

Примеры того, как найти произведение или частное числа со знаком

Умножение и деление чисел со знаком — Предварительно -Алгебра

Умножение и деление

Пример 1

Пример 2

Стенограмма видеоурока

Умножение и деление целых чисел — методы и примеры

Как умножать целые числа?

Как разделить целые числа?

Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.[Решено]

Вопрос: Перечислите правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Ответ: Есть некоторые правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Пояснение:

Правило сложения целых чисел:

Правило вычитания целых чисел:

Правило умножения и деления целых чисел:

Таким образом, мы научились складывать, вычитать, умножать и делить положительные и отрицательные числа.

вещественных чисел | Начальная алгебра

Результаты обучения

Сложение и вычитание действительных чисел

Чтобы сложить два числа с одинаковым знаком (положительное или отрицательное)

Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное)

Пример

Ответ

Пример

Ответ

Пример

Ответ

Пример

Ответ

Умножение и деление действительных чисел

Умножение действительных чисел

Произведение положительного и отрицательного числа

Пример

Ответ

Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)

Пример

Ответ

Умножение более двух отрицательных чисел

Пример

Ответ

Разделить действительные числа

Пример

Ответ

Правила подкласса

Пример