234*908. 209*905 233*630 911*992 40803: 201 826 281:909 72900:972 102555:265 242963:427 332621:683 897744:472 365216:904 решите…

 Необходимо решить примеры в столбик с проверкой:

1. 234 х 908 = 
2. 209 х 905 =
3. 233 х 630 =
4. 911 х 992 =
5. 40803 : 201 =
6. 826 281 : 909 =
7. 72900 : 972 =
8. 102555 : 265 =
9. 242963 : 427 =
10. 332621 : 683 =
11. 897744 : 472 =
12. 365216 : 904 =

Умножение в столбик

Как умножать в столбик рассмотрим на первом примере: 234*908

Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее. Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа. Сбоку слева между числами ставим знак действия. У нас это «×» (знак умножения).

Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается под чертой под самой правой цифрой. 

Умножаем число сверху по цифре (знаку) справа налево.

8 х 4 = 32
У нас получилось число большее или равное 10.

Поэтому под черту идет только последняя цифра результата. Это 2. Количество десятков произведения (у нас 3 десятка) ставим над соседом слева от 8.Умножаем 0 на 4.

0 х 4 = 0
Не забудем, что над 0 стоит 3. Это значит, что к результату умножения (произведению) надо прибавить 3.

0 + 3 = 3
Умножаем 9 на 4.

9 х 4 = 32

Переходим к умножению числа 908 на 3. Умножаем по тем же правилам, что и на 4.

Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.

Аналогично делаем и для умножения числа 908 на 2, только результат умножения на третью цифру необходимо записывать уже под третьей цифрой результата второго действия умножения.

Полученные числа под чертой складываем в столбик.

 Для выполнения проверки полученное число делим на один из множителей. В результаты должен получиться второй множитель.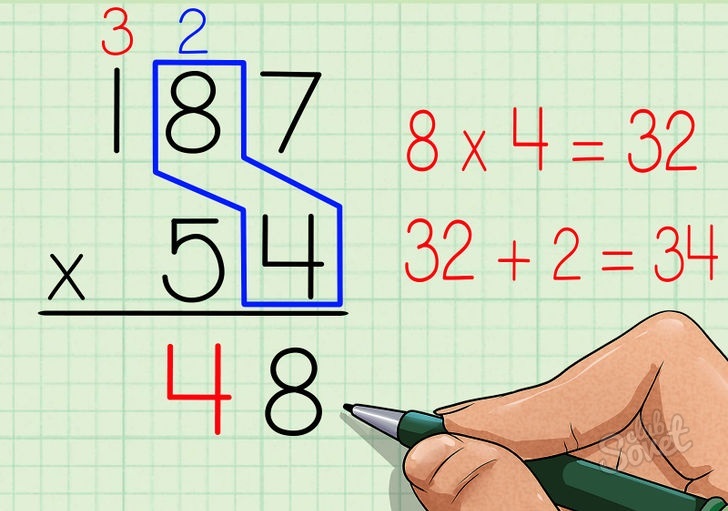

Решение примеров на умножение с проверкой http://bit.ly/2BQCsoI

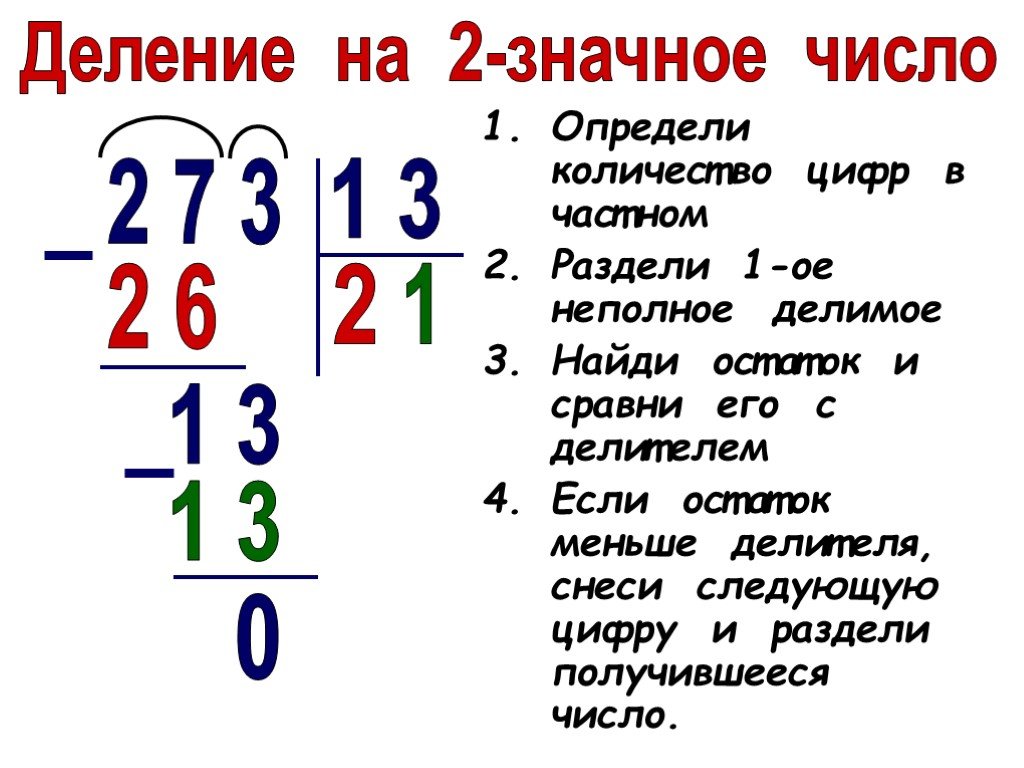
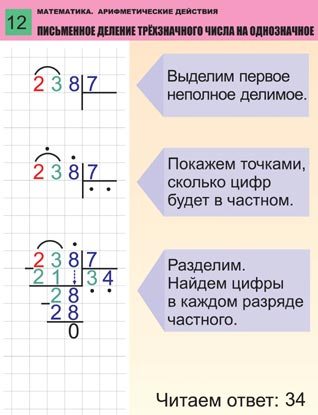
Деление в столбик

Разберёмся на примере 40803 : 201

Для начала запишем делимое и делитель в столбик. Их частное (результат) будем записывать под делителем. У нас это число 201.

Начинаем делить:

Определяем неполное частное. Для этого слева направо сравниваем цифры делимого и делитель.

• Берем 4. 4 меньше 201, значит нужно взять ещё одну цифру из делимого.
• Берем 40. 40 меньше 201
• Берем 408. 408 больше 201. Значит это неполное частное.

Приступаем к делению. Находим ближайшее к 408 произведение. 

201 х 2 = 402.

Записываем цифру 2 в частное. Далее записываем 402 под 408.

Между 408 и 402 слева поставим «−» (минус). Вычтем в столбик 402 и под чертой запишем результат.

В остатке получилось 6.

Спишем из делимого 40803 цифру 0 к 6. Число 60 меньше 201, значит списываем ещё одну цифру. Число 603 больше 201. Приступаем к делению. Находим ближайшее произведение.

201 х 3 = 603.

Вычитаем и в остатке получаем 0. Значит ответ 40803 : 201=23

Чтобы выполнить проверку нужно частное умножить на делитель, то есть 23 х 201, если в ответе получается делимое (40803), то мы посчитали верно.

Решение примеров на деление с проверкой: http://bit.ly/2B7CfR6

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 78. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник — страница 78Готовое домашнее задание

Вспомни правила умножения с числами 0 и 1. Вычисли:

Ответ:

1 ∙ 8 = 8    312 ∙ 1 = 312    0 ∙ 35 = 0 1 ∙ 1 = 1    703 ∙ 1 = 703    0 ∙ 100 = 0
918 ∙ 0 = 0    10 ∙ 1 = 10 617 ∙ 0 = 0    10 ∙ 0 = 0

Номер 340.

Ответ:

0 дес. ∙ 5 + 3 дес. = 3 дес. 0 тыс. ∙ 7 + 4 дес. = 4 дес.
0 сот. ∙ 3 + 2 сот. = 2 сот. 0 сот. ∙ 1 + 1 сот. = 1 сот.

Номер 341.

Ответ:

803 ∙ 5 = 4015 4019 ∙ 7 = 28133
50801 ∙ 4 = 203204 90048 ∙ 7 = 630336

41008 ∙ 6 = 246048 70032 ∙ 8 = 560256

Решение столбиком:

Номер 342.

Начерти три отрезка. Длина первого 8 см 5 мм, что на 7 мм больше длины второго и на 1 см 5 мм меньше длины третьего отрезка.

Ответ:

8 см 5 мм − 7 мм = 7 см 8 мм – длина второго отрезка. 8 см 5 мм + 1 см 5 мм = 10 см – длина третьего отрезка. 8 см 5 мм – длина первого отрезка.

Номер 343.

Комбайнер убирал 9 дней пшеницу на двух полях. На первом поле он собрал 400 т пшеницы, а на втором – 320 т. Сколько тонн зерна убирал комбайнер за 1 день, если ежедневная выработка была одинаковой?

Ответ:

1) 400 + 320 = 720 (т) – пшеницы убрали за 9 дней. 2) 720 : 9 = 80 (т) Ответ: 80 тонн пшеницы убирают за 1 день.

Номер 344.

На мельницу отправили пшеницу на 10 машинах, по 42 ц на каждой, а ячменя в 3 раза меньше, чем пшеницы. На сколько центнеров больше отправили пшеницы, чем ячменя?

Ответ:

1) 42 ∙ 10 = 420 (ц) – отправили пшеницы. 2) 420 : 3 = 140 (ц) – отправили ячменя. 3) 420 − 140 = 280 (ц) Ответ: на 280 ц больше отправили пшеницы.

Номер 345.

Запиши выражения и вычисли их значения.
1) Произведение чисел 8 и 3125 уменьшить на 5186.
2) Наименьшее шестизначное число увеличить в 10 раз, а результат уменьшить в 1000 раз.
3) Частное чисел 872 и 8 увеличить в 7 раз.

Ответ:

Номер 346.

Рассмотри рисунки и объясни, чем похожи и чем различаются рисунки: 1 и 2, 2 и 3, 3 и 4, 1 и 4.

Ответ:

Рисунки похожи тем, что у них есть два круга (красный и синий) и есть центр окружность. Рисунки отличаются тем, что: 1 – окружности находятся рядом; 2 – окруж. касаются друг друга; 3 – окруж. пересекаются; 4 – окна окружность находится в центре другой окружности.

Номер 347.

Сколько в числе 15400 десятков? сотен? тысяч? Сколько единиц в числе, содержащем 208 дес.? 32 сот.?

Ответ:

15400 – 1540 д., 154 сот., 15 тыс. 208 дес. – 2080 ед. 32 сот. – 3200 ед.

Номер 348.

Ответ:

Номер 349.

Переставляя карточки с цифрами сделай равенство верным.

Ответ:

62 : 31 = 3 63 : 21 = 3

Задание внизу страницы

Вычисли.

Ответ:

Задание на полях страницы

Ребус.

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Ваше сообщение отправлено!

+

Что такое длинное умножение? | TheSchoolRun

Мы объясним, что такое метод длинного умножения, и рассмотрим, как навыки умножения формируются в течение каждого года обучения в начальной школе.

или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам

Что такое длинное умножение?

Длинное умножение (или умножение в столбик ) — письменный способ умножения чисел (обычно дву- или трехзначного числа на другое большое число).

Обычно используется в 5-м и 6-м классах после того, как дети освоят метод сетки . Преимущество метода сетки заключается в том, что он побуждает детей думать о разряде и умножать числа, кратные десяти и сотням. Как только они освоятся с этим, длинное умножение станет более быстрой и эффективной техникой для использования.

Как умножать методом длинного умножения

Как и при сложении и вычитании столбцов, числа располагаются в столбце следующим образом:

Умножение в начальной школе

Навыки умножения у детей формируются во время обучения в начальной школе следующим образом.

Год 1

• Счет вперед или назад единицами, двойками, пятерками и десятками.
• Решите одношаговые задачи на умножение с использованием объектов и массивов при поддержке учителя.

Вот пример массива для демонстрации 5 x 3 или 3 x 5:

Год 2

• Вызов фактов умножения для таблиц умножения на 2, 5 и 10 и соответствующих фактов деления.
• Используйте многократное сложение (представляющее 4 партии по 3 как 3 + 3 + 3 + 3) и массивы для решения вопросов на умножение.
• Распознавать числа, кратные 2, 5 и 10.
• Используйте знаки x и = при написании предложений с числами умножения.
• Решите задачи на умножение с использованием объектов и массивов (см. схему выше).

Год 3

• Вызов фактов умножения для таблиц умножения на 2, 3, 4, 5, 8 и 10 и соответствующих фактов деления.
• Используйте письменные методы для умножения двузначных чисел на однозначные числа (например: 13 x 4).

Год 4

• Вспомнить факты умножения до 12 x 12 и соответствующие факты деления.
• Распознавание и использование пар факторов.
• Умножение двузначных и трехзначных чисел на однозначное с использованием формальной письменной схемы.

Год 5

• Определение кратных и коэффициентов.
• Распознавать простые числа, имеющие только два делителя, и определять простые числа меньше 100.
• Понимать квадратные и кубические числа.
• Умножение чисел до четырех цифр на однозначное или двузначное число с использованием формальных методов, включая длинное умножение.

Как видно из приведенных выше задач, детям не нужно умножать двузначные числа на трехзначные числа до 6-го класса, поэтому методу длинного умножения, вероятно, не будут обучать до тех пор (хотя способные дети 5-го класса могут используйте и его).

Год 6

• Умножение чисел до четырех цифр на двузначное с использованием длинного умножения.
• Определите общие делители, общие кратные и простые числа.
• Умножение однозначных чисел, содержащих до двух знаков после запятой, на целые числа.

Матричная арифметика M.2 | СТАТ ОНЛАЙН

Транспонировать матрицу Раздел

  9T \]

Чтобы выполнить сложение матрицы с , две матрицы должны иметь одинаковые размеры. Это означает, что они должны иметь одинаковое количество строк и столбцов. В этом случае просто добавьте каждый отдельный компонент, как показано ниже.

Например

\[A + B = \begin{pmatrix} 1 & -5 & 4 \\ 2 & 5 & 3 \end{pmatrix} + \begin{pmatrix} 8 & -3 & -4 \\ 4 & -2 & 9 \end{pmatrix} = \begin{pmatrix} 1 + 8 & -5 — 3 & 4 — 4 \\ 2 + 4 & 5 -2 & 3 + 9Т \]

Матричное скалярное умножение Раздел

 

Чтобы умножить матрицу на скаляр, также известное как скалярное умножение , умножьте каждый элемент матрицы на скаляр.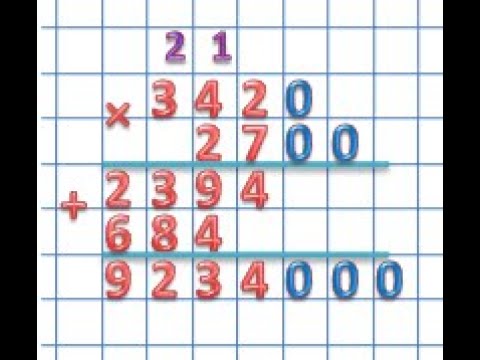

Например…

\[ 6*A = 6 * \begin{pmatrix} 1 & -5 & 4\\ 2 & 5 & 3 \end{pmatrix} = \begin{pmatrix} 6 * 1 & 6 * -5 & 6 * 4\\ 6 * 2 и 6 *5 и 6 * 3 \end{pmatrix} = \begin{pmatrix} 6 & -30 & 24 \\ 12 & 30 & 18 \end{pmatrix}\]

Чтобы умножить два вектора одинаковой длины, нужно взять скалярное произведение , также называемое внутренним произведением . Это делается путем умножения каждой записи в двух векторах вместе, а затем сложения всех произведений.

Например, для векторов x и y скалярное произведение рассчитывается ниже

\[ x \cdot y = \begin{pmatrix} 1 & -5 & 4 \end{pmatrix} * \begin{pmatrix} 4 & -2 & 5 \end{pmatrix} = 1*4 + (-5 )*(-2) + 4*5 = 4+10+20 = 34\]

Умножение матриц Раздел

 

Чтобы выполнить умножение матриц , первая матрица должна иметь такое же количество столбцов, сколько строк во второй матрице. Количество строк полученной матрицы равно количеству строк первой матрицы, а количество столбцов полученной матрицы равно количеству столбцов второй матрицы. Таким образом, матрицу 3 × 5 можно умножить на матрицу 5 × 7, получив матрицу 3 × 7, но нельзя умножить матрицу 2 × 8 на матрицу 4 × 2. Чтобы найти элементы в результирующей матрице, просто возьмите скалярное произведение соответствующей строки первой матрицы и соответствующего столбца второй матрицы.

Например,

\[ C*D = \begin{pmatrix} 3 & -9 & -8\\ 2 & 4 & 3 \end{pmatrix} * \begin{pmatrix} 7 & -3\\ -2 & 3\\ 6 & 2 \end{pmatrix} \]

\[ C*D = \begin{pmatrix} 3*7 + (-9)*(-2) + (-8)*6 & 3* (-3) + (-9)*3 + (-8)*2 \\ 2*7 + 4*(-2) + 3*6 и 2*(-3) + 4*3 + 3*2 \ end{pmatrix}\]

\[ C*D = \begin{pmatrix} 21 + 18 — 48 & — 9 — 27 — 16 \\14 — 8 + 18 & — 6 + 12 + 6 \end{pmatrix} = \begin{pmatrix} -9 & — 52\\ 24 & 12 \end{pmatrix} \]

Умножение матриц имеет некоторые из тех же свойств, что и «нормальное» умножение, например

\[ A(BC) = (AB)C\]

\[A(B + C) = AB + AC\]

\[(A + B)C = AC + BC\]

Однако умножение матриц не является коммуникативным.