Порядок выполнения действий / Натуральные числа и действия над ними / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Натуральные числа и действия над ними
5. Порядок выполнения действий

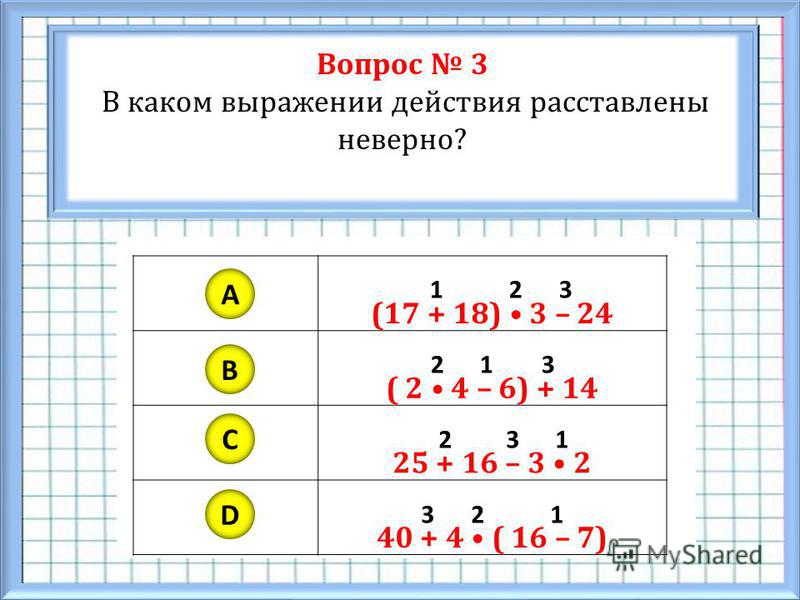
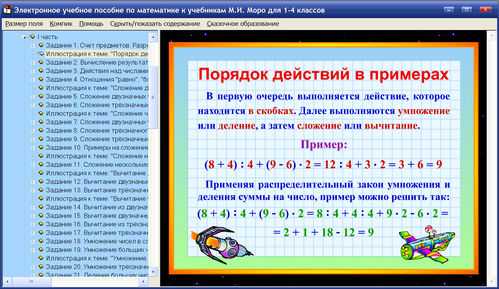
Вам уже известно из начальной школы, что при решении примеров, которые содержат несколько арифметических действий, а также могут содержать скобки, порядок выполнения действий выбираем согласно определенным правилам.

При этом, сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел — действиями второй ступени. Тогда правила, по которым мы определяем порядок выполнения действий, будут звучать так:

1) Если в выражении нет скобок и оно содержит действия только одной ступени, то действия выполняют по порядку слева направо.

Пример:

1)

1) 5 + 5 = 10;

2) 10 — 7 = 3;

3) 3 — 2 = 1;

4) 1 + 4 = 5.

2)

1) 34 = 12;

2) 12 : 2 = 6;

3) 64 = 24;

4) 24 : 8 = 3.

2) если в выражении нет скобок и оно содержит действия первой и второй ступени, то сначала выполняют действия второй ступени по порядку слева направо, а потом действия первой ступени, также по прядку слева направо.

Пример:

1) 18 : 9 = 2;

2) 2 : 2 = 1;

3) 34 = 12;

4) 9 — 1 = 8;

5) 8 + 12 = 20.

3) если в выражении есть скобки, то сначала выполняют действия в скобках, учитывая при этом правила 1 и 2.

Пример:

1) 12 : 3 = 4;

2) 6 — 4 = 2;

3) 25 = 10;

4) 7 + 10 = 17.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Понятие о натуральном числе

Сложение натуральных чисел

Вычитание натуральных чисел

Умножение натуральных чисел

Деление натуральных чисел

Степень числа. Квадрат и куб числа

Меньше или больше

Меньше или больше на сколько? во сколько раз?

Формулы

Уравнения

Натуральные числа и действия над ними

Правило встречается в следующих упражнениях:

5 класс

Задание 627, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 789, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 934, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1130, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1374, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1437, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1560, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1716, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 207, Мерзляк, Полонский, Якир, Учебник

Номер 454, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 352, Мерзляк, Полонский, Якир, Учебник

Номер 1032, Мерзляк, Полонский, Якир, Учебник

Номер 1215, Мерзляк, Полонский, Якир, Учебник

Номер 1276, Мерзляк, Полонский, Якир, Учебник

Задание 550, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 948, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1166, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1233, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1561, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

7 класс

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 5, Мерзляк, Полонский, Якир, Учебник

Номер 125, Мерзляк, Полонский, Якир, Учебник

Номер 162, Мерзляк, Полонский, Якир, Учебник

Номер 165, Мерзляк, Полонский, Якир, Учебник

Номер 170, Мерзляк, Полонский, Якир, Учебник

Номер 171, Мерзляк, Полонский, Якир, Учебник

Номер 177, Мерзляк, Полонский, Якир, Учебник

Номер 906, Мерзляк, Полонский, Якир, Учебник

Номер 1163, Мерзляк, Полонский, Якир, Учебник

---

Как раскрывать скобки в выражениях и уравнениях.

Правила математики.

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент.

В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3)  , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример.  (9 + 6) : 3=9 : 3 + 6 : 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть. 

Пример.    12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b

• Назад
• Вперед

 
умножить наподелить на

 

org/BreadcrumbList»>
• Уроки
• Математика

Вам может пригодиться:

Что такое скобки? Определение, правила, примеры

Что такое круглые скобки?

Скобки или «круглые скобки» — это знакомые ( ) символы, которые используются парами для группировки элементов или указания порядка операций в уравнении.

В математике вам часто придется использовать скобки при создании или решении уравнений. Они помогают группировать числа и определять порядок операций. В таких случаях используются три типа скобок:

• Круглые скобки или ( )
• Квадратные или квадратные скобки или [ ]
• Фигурные скобки или угловые скобки или { }

Скобки всегда идут парами, и если есть открывающая скобка, должна быть и закрывающая скобка. Открывающие скобки: (, [  и {. Соответствующие им закрывающие скобки: ), ] и }.

 В этой статье мы изучим правила использования скобок в математике.

Как использовать скобки в математике?

В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения.

Вот пример, чтобы лучше понять это:

3 + (-5) = -2

Второй способ использования скобок в математике — умножение чисел. Если в уравнении нет арифметической операции, наличие скобок означает, что вы должны применить умножение.

Разберем это на примере:

6 (4 + 2)

можно записать как 6 х (4 + 2)

Следовательно, ответ 6 х 6 = 36.

Третий и последний скобки в математике используются для группировки чисел и определения порядка операций.

Порядок операций

Скобки изменяют порядок операций.

Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:

Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на термины, присутствующие в них.

Давайте лучше разберемся на примере.

Возьмем задачу: 9 – 10 ÷ 5 – 3 x 2 + 7

Давайте решим ее, используя изученный вами порядок действий.

= 9 – 10 ÷ 5 – 3 x 2 + 7

= 9 – 2 – 3 x 2 + 7 (сначала вы делите)

= 9 – 2 – 6 + 7 (затем умножаете)

= 7 – 6 + 7 (Затем вычесть)

= 1 + 7 (Затем вычесть)

= 8 (И, наконец, сложить)

Теперь давайте рассмотрим ту же задачу со скобками: 

9 – 10 ÷ (5 – 3) x 2 + 7

Сначала нужно вычислить числа в скобках.

= 9 – 10 ÷ 2 x 2 + 7 (Решите выражение в скобках)

= 9 – 5 x 2 + 7 (Разделить)

= 9 – 10 + 7 (Умножить)

= –1 + 7 (Сложить)

= 6

Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!

Помните: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.

Давайте разберем это на примере:

Упростим выражение (2 + (3 x 4))

Здесь мы сначала решим внутреннюю скобку.

Таким образом, выражение примет вид (2 + 12) = 14

Решенные примеры

Пример 1: Упростим выражение: (2 + 4 x 6) – 4 + (2 x 3)

Решение . Начните с решения выражений в скобках.

= (2 + 24) – 4 + 6 (умножить в скобках)

= 26 – 4 + 6 (решить члены в скобках)

= 22 + 6 (сложить)

= 28

Пример 2: Упростите выражение: ( 2 x (7 – 5)) – ((6 ÷ 3) + 4)

Начните с решения самых внутренних скобок

= (2 x 2) – (2 + 4)

= 4 – 6

= –2

Пример 3: Упростите выражение: 2 (3 + 5) + 8 (4 – 1)

Сначала решите выражения в скобках.

Здесь скобки также обозначают знак умножения.

= 2 x 8 + 8 x 3

= 16 + 24

= 40

Практические задачи

1

Упростим выражение: (3 + 2 x 8) – 4 + (5 x 7)

45

50

24

5 Мы знаем, что правильный ответ 9

9000 уравнение в скобках решается первым.
Итак, 19 — 4 + 35 = 50

2

Упростим выражение: ( 4 x (6 – 2)) – ((8 ÷ 2) + 5 )

7

2

17

5

Правильный ответ: 7
Мы знаем, что сначала решается уравнение в скобках.
Итак, (4 x 4) – (4 + 5)
16 – 9 = 7

3

Упростим выражение: 4 (3 + 2) + 4 (7 – 2)

10

50

20

40

Правильный ответ: 40
Мы знаем, что скобки также обозначают умножение.
Итак, 4 x 5 + 4 x 5
20 + 20 = 40

Часто задаваемые вопросы

Что такое скобки в математике?

Скобки используются для группировки чисел или переменных в математике. Они могут изменить решение выражения и, следовательно, ответ.

Круглые скобки — это то же самое, что фигурные скобки?

Нет. Скобки, обозначенные ( ), отличаются от фигурных скобок { }. Они имеют различные применения в математике. Они используются во вложенных выражениях. Вы узнаете о них больше позже.

Есть ли другое название для скобок?

Да. Иногда скобки также называют круглыми скобками.

Порядок операций и БЕДМАС

• Дом
• О
• Страницы математики и статистики
• R Программирование
• Предметы Python

 

Привет. Эта страница будет посвящена порядку операций и БЭДМАС в алгебре. Читатель должен быть знаком с показателями степени, скобками (круглыми скобками), умножением, вычитанием, сложением и вычитанием.

---

Содержание

 

 

---

Каков порядок операций и БЭДМАС?

 

Порядок операций — это математическое и алгебраическое правило, которому мы следуем, когда имеем комбинацию сложения, вычитания, умножения, деления, возведения в степень и скобок. Термин и вспомогательное средство для запоминания BEDMAS означает скобки, показатели степени, деление, умножение, сложение и вычитание.

Альтернативой BEDMAS является PEDMAS, где скобки заменяются скобками (то же самое и в математике).

• Кронштейны
• Экспоненты
• Отдел
• Умножение
• Дополнение
• Вычитание

Скобки имеют наивысший приоритет и должны обрабатываться в первую очередь. Мы идем слева направо в BEDMAS/PEDMAS (или сверху вниз, как показано выше).

 

---

Примеры 92 = 25\), чтобы получить 24.

 

Пример четвертый

   

\[(\frac{1}{2} \times 5) — 1 + 4 = \frac{5}{2} — 1 + 4 = \frac{5}{2} + 3 = \frac{5}{2} + \frac{6}{2} = \frac{5 + 6}{2} = \frac{11}{ 2}\]

 

Скобка оценивается первой, где 5 умножается на половину. После сложения и вычитания (с дробями) мы получаем ответ \(\dfrac{11}{2} = 5,5\).

 

Пример пятый

    92 — 4) + 1 = 20 — (9 — 4) + 1 = 20 — 5 + 1 = 16\]

 

В этом примере используется комбинация компонентов BEDMAS.