Правила начальных классов (с 1 по 4 класс)
Числа. Чтение, сравнение
3 класс — миллионов 2 класс — тысяч 1 класс единиц сотни мил-лионов десят-ки мил-лионов едини-цы мил-лионов сотни тысяч десят-ки тысяч едини-цы тысяч сотни десят-ки едини-цы 9 разряд 8 разряд 7 разряд 6 разряд 5 разряд 4 разряд 3 разряд 2 разряд 1 разряд
I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 Примеры записи римских цифр. 1- I 2 – II 3 – III 4 – IV 5 – V 6 – VI 7 – VII 8 – VIII 9 – IX 10 – X 11 – XI 12 – XII 13 – XIII 14 – XIV 15 – XV 16 – XVII 17 – XVII 18 – XVIII 19 – XIX 20 – XX 21 – XXI 30 – XXX 40 – XL 50 – L 60 – LX 70 – LXX 80 – LXXX 90 – XC 99 — XCIX 100 – C 102 – CII 400 – CD 500 – D 800 — DCCC 900 – CM Арифметические действия и их свойства. Сложение 3+5=8 Знак +(плюс), действие- сложение, 3 – первое слагаемое, 5- второе слагаемое, 3+5 — сумма, 8 — значение суммы. Если из суммы вычесть одно слагаемое, то получится другое слагаемое. Вычитание 9-4=5 Знак-(минус), действие — вычитание, 9 — уменьшаемое, 4 — вычитаемое, 9 – 4 — разность, 5- значение разности. Если из уменьшаемого вычесть разность, то получится вычитаемое. Если к разности прибавить вычитаемое, то получится уменьшаемое. Умножение. 3•5=15 Знак •или х (умножить), действие- умножение, 3 – первый множитель,5- второй множитель, 3•5 — произведение, 15 — значение произведения. Если произведение разделить на один множитель, то получится другоймножитель. Деление. 20:4 = 5 Знак (:) — разделить, действие деление. 20 – делимое, 4 – делитель, 20:4 это частное, 20 – значение частного Если делимое разделить на частное, то получится делитель. Если частное умножить на делитель, то получится делимое.
Свойства и законы арифметических действий.
Свойства арифметических действий. Свойства 0 (нуля)
Свойства 1 (единицы)
Действия над числами.
Выражения. Выражения бывают числовые и буквенные.
Равенства и неравенства.
Порядок действий. Если в примере встречаются два и более арифметических действия, то их выполнение проводят в следующем порядке:
Минутная стрелка. Число на циферблате Количество минут Как прочитать 1 5 Пять минут (какого?) 2 10 Десять минут (какого?) 3 15 Пятнадцать минут (какого?) 4 20 Двадцать минут (какого?) 5 25 Двадцать пять минут (какого?) 6 30 Половина (какого?) 7 35 Без 25 минут (сколько?) 8 40 Без 20 минут (сколько?) 9 45 Без 15 минут (сколько?) 10 50 Без 10 минут (сколько?) 11 55 Без 5 минут (сколько?) 12 60 Ровно (сколько?) ЭТО НАДО ЗНАТЬ НАИЗУСТЬ !!! Таблица №1 1+1=2 2+1=3 3+1=4 2+2=4 4+1=5 3+2=5 5+1=6 4+2=6 3+3=6 6+1=7 5+2=7 4+3=7 7+1=8 6+2=8 5+3=8 4+4=8 8+1=9 7+2=9 6+3=9 5+4=9 9+1=10 8+2=10 7+3=10 6+4=10 5+5=10 Таблица №2 2+9=11 3+8=11 4+7=11 5+6=11 3+9=12 4+8=12 5+7=12 6+6=12 4+9=13 5+8=13 6+7=13 5+9=14 6+8=14 7+7=14 6+9=15 7+8=15 7+9=16 8+8=16 8+9=17 9+9=18 Таблица №3 2∙2=4 3∙2=6 3∙3=9 9∙9 = 81 4∙2=8 4∙3=12 4∙4=16 5∙2=10 5∙3=15 5∙4=20 5∙5=25 6∙2=12 6∙3=18 6∙4=24 6∙5=30 6∙6=36 7∙2=14 7∙3=21 7∙4=28 7∙5=35 7∙6=42 7∙7=49 8∙2=16 8∙3=24 8∙4=32 8∙5=40 8∙6=48 8∙7 =56 8∙8=64 9∙2=18 9∙3=27 9∙4=36 9∙5=45 9∙6=54 9∙7 =63 8∙9 = 72 Уравнения и способы их решения.
Уравнения на «+» Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. Все уравнения на «плюс» решаются обратным действием «минусом» Уравнения на «▪» Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Все уравнения на «умножение» решаются обратным действием «делением» Уравнения на «-»
Уравнение на «:»
Величины и их измерения. Единицы времени. Секунда – с Минута – мин Час – ч Сутки – сут Неделя — нед Месяц – мес. Год (лет) – год (л) Век – век 1мин – 60 с 1ч – 60 мин 1 сут = 24 ч 1 нед = 7 сут 1 год = 365(366)сут 1 век = 100 л 1 мес = 31сут, 30 сут 28 или 29 сут (февраль) Январь — 31 Февраль – 28(29) Март — 31 Апрель — 30 Май — 31 Июнь — 30 Июль — 31 Август — 31 Сентябрь — 30 Октябрь — 31 Ноябрь — 30 Декабрь — 31 Дни недели: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье. 1.Для того, чтобы перевести из большей величины в меньшую, надо значение большей умножить на соотношение между ними. Например 1 час = 60минут. 7чсасов = 7 ∙60 = 420 минут. 2.Для того, чтобы перевести из меньшей величины в большую, надо меньшую величину разделить на соотношение между ними. Например. 1 сут – 24 часа. Тогда 48ч = 48 :24 = 2 сут. Единицы длины. Миллиметр — мм, сантиметр — см, дециметр — дм, метр — м, километр — км. 1см = 10мм 1дм = 10см = 100мм 1м = 10дм = 100см = 1 000мм 1км = 1 000м = 10 000дм = 100 000см = 1000 000мм Единицы массы Грамм – г Килограмм – кг Центнер – ц Тонна – т 1 кг = 1 000г 1 ц = 100 кг = 100 000 г 1 т = 10 ц = 1000 кг = 1000 000г Единицы площади 1см2 = 100мм2 1дм2 = 100см2 = 10000мм2 1м2 = 100дм2 = 10000см2 = 1000000мм2 1км2 = 1 000000м2 1а(ар) = 100м2 1га(гектар) = 10000м2 1 га = 100а Единицы объёма 1см3 = 1000мм3 1дм3= 1000см3 = 1000000мм3 1м3 = 1000дм3 = 1000000см3 1 км3 = 1000000000м3 Если перевод их одних величин в другие идет по стрелочке вперёд, то мы добавляем нужное количество нулей, если в обратном направлении, то убираем нужное количество нулей. Чтобы найти долю меньшей величины в большей, надо посмотреть на соотношение между ними. Если 1см = 10мм, то 1мм = десятая часть см. Если 1т = 1000000г, то 1г – миллионная часть тонны. Решение задач. Для того, чтобы текст был задачей, в нем должны быть: условие, вопрос, решение, ответ. Решение простых задач по вопросу Вид решения решение Вопрос «Сколько всего?» записывается в условии «уголком». Плюс(+) Вопрос «Сколько осталось?» записывается в условии !Ост-?». Минус(-) Вопрос « На сколько меньше?» или «На сколько больше?» записывается в условии стрелочкой. Это задачи на сравнения. От большего числа отнимаем меньшее Вопрос « Во сколько меньше?» или «Во сколько больше?» записывается в условии стрелочкой. Большее число делим на меньшее По условию с прямым сравнением Условие решение Если в условие сказано «на больше» Плюс(+) Если в условие сказано «на меньше» Минус(-) Если в условие сказано «в … раз больше» Умножить (•) Если в условие сказано «в … раз меньше» Разделить (:) По условию с косвенным сравнением Если в условии сказано … решение «это или что на больше» Минус(-) «это ил что на меньше» Плюс(+) «это или что в … раз больше» Разделить (:) «это или что в … раз меньше» Умножить (•) Решение задач, с записью условия в таблице. Цена (за 1 предмет) Количество Стоимость (Всего) Решение ? Цена=стоимость:количество ? Количество=стоимость:цену ? Стоимость = цена количесво Решение задач, с записью условия в таблице. Скорость (V) Время (t) Расстояние (S) Решение ? v =S t ? t = S :v ? S = v t Правило треугольника. Составные задачи.
Памятка по решению задач на движение. Одновременное встречное движение. Нахождение общего расстояния 1 способ 1.находим S1 = V1·• t 2 способ 1. находим Vсближения = V1 + V2 2. находим Sобщее = Vсближения ·• t Нахождение одной из скоростей. 1 способ. 1. находим S1 = V1·• t 2 способ. 1. находим Vсближения = Sобщее : t 2. находим V2 = Vсближения – V1 Нахождение времени. 1 способ 1.находим Vсближения = V1 + V2 Решение задач на движение вдогонку. Нахождение времени, через которое один объект догонит другой. 1.находим Vприближения = V1 — V2 1. находим Vприближения = V1 — V2 Обратные задачи. Задачи называются обратными, если то, что было неизвестно по условию в первой задаче, становится известным во второй. А то, что было известным в первой задаче, становится неизвестным во второй. Решениями этих задач являются обратные друг другу примеры. Геометрический материал. Прямая линия (нет ни начала, ни конца) Луч (есть начало, нет конца) Отрезок (есть начало и есть конец) Прямые линии могут быть параллельными (не пересекаются), пересекающимися, перпендикулярными (при пересечении все углы прямые) Углы. Прямой Острый Тупой Развёрнутый Острый угол меньше прямого, тупой угол больше прямого. Прямоугольник Прямоугольник – это четырёхугольник, у которого все углы прямые и противоположные стороны равны. Нахождение периметра. 4 угла, 4 вершины, 4 стороны
Нахождение стороны по периметру и другой стороне. а = (Р – b – b) : 2 или b = (Р – a – a) : 2 или Р:2 – а Например. Р = 24см, а = 7 см. Найти в. в = 24:2 – 7 = 5 см Нахождение площади S = a ∙ b Нахождение стороны прямоугольника по площади и известной стороне. a = S:b или b = S:a Нахождение площади по известному периметру и стороне. Сначала надо найти вторую сторону, затем по формуле площадь. Нахождение периметра по известной площади. Сначала надо найти сторону, затем площадь. Квадрат Квадрат – это прямоугольник, у которого все стороны равны. 4 угла, S = a ∙ a = a2 4 вершины, P = a+a+a+a 4 стороны. P = 4 ∙ a Нахождение стороны квадрата по известному периметру. Если P = 4 ∙ a, то а = Р : 4 (Чтобы найти сторону, надо периметр разделить на 4) Нахождение стороны квадрата по известной площади. Чтобы найти сторону квадрата по известной площади, надо подобрать произведение равных множителей, значение которого равно значению площади. 1 = 1 ∙ 1 4 = 2 ∙ 2 9 = 3 ∙ 3 16 = 4 ∙ 4 25 = 5 ∙ 5 36 = 6 ∙ 6 49 = 7 ∙ 7 64 = 8 ∙ 8 81 = 9 ∙ 9 100 = 10 ∙ 10 121 = 11 ∙ 11 400 = 20 ∙ 20 8100 = 90 ∙ 90 и так далее Нахождение площади, если известен периметр квадрата.
Треугольник 3 угла 3 вершины 3 стороны Периметр равен сумме трёх сторон. Круг и окружность. Окружность имеет длину. Круг имеет площадь Центр окружности или круга Радиус окружности или круга – Диаметр окружности или круга — Чтобы определить полное количество десятков в числе, надо зачеркнуть последний знак (единицы). В числе 6758 – 675 десятков. Чтобы определить количество сотен, надо зачеркнуть два знака 6758 – 67 сотен |
Конспект урока по учебному предмету «Математика» в 4-ом классе по теме «Умножение и деление на 10, 100, 1000» • Наука и образование ONLINE
Главная Работы на конкурс Педагогика, психология, управление образованием Педагогика начальной школы Конспект урока по учебному предмету «Математика» в 4-ом классе по теме «Умножение и деление на 10, 100, 1000»
Автор: Ермакова Дина Климентьевна
Место работы/учебы (аффилиация): ГУО «Стайская средняя школа Лепельского района» Витебской области, Республика Беларусь, учитель начальных классов
Данная методическая разработка составлена в соответствии с требованиями Образовательного стандарта ОБЩЕЕ СРЕДНЕЕ ОБРАЗОВАНИЕ, на основании учебной программы по учебным предметам для учреждений общего среднего образования для 4 класса.
Содержание, методы, средства и формы организации познавательной деятельности на уроке подчинены выполнению поставленных целей и задач образования, развития и воспитания обучающихся. Для организации деятельности обучающихся на уроке применяются различные формы работы: индивидуальная, фронтальная, парная. На уроке имеют место элементы проблемного обучения и самостоятельная поисковая деятельность, которая способствует усвоению учащимися нового материала.
Цель: планируется, что к концу урока ученики будут уметь:
- умножать и делить числа на 10, 100, 1000;
- решать задачи с применением правила;
- знать правила умножения и деления чисел на 10, 100, 1000.
Задачи личностного развития:
- создать условия для развития у учеников умений устанавливать причинно-следственные связи, использовать алгоритм действий;
- способствовать формированию умения к самоконтролю, самооценке и самокоррекции учебной деятельности;
- способствовать воспитанию целеустремленности, позитивного отношения к учебной работе.

Оборудование: учебник «Математика 4 класс» часть 2, Г.Л. Муравьёва, М.А. Урбан; компьютер, презентация, карточки с правилами и заданиями.
Загрузка…
Педагогика начальной школы
Конспект учебного занятия «Урок обучения грамоте: Звуки [н] [н’], буквы Нн»
Доступна к просмотру полнотекстовая версия работы
Урок построен с учётом игровой, информативно-коммуникативной, здоровье сберегающей технологий, технологии проблемного обучения. Задачи: закрепить знания обучающихся о букве Н и звуках [н] [н’]; развивать навыки чтения вслух, хором: слогов, слов, пред…
Посмотреть работу
Педагогика начальной школы
Конспект урока математики «Чётные и нечётные числа»
Доступна к просмотру полнотекстовая версия работы
Урок закрепления по теме представит формы деятельности по развитию умений выполнять вычисления на основе знаний таблицы умножения и деления с числом 2, развитию внимания, образного и логического мышления, воспитанию активности в работе, целеустремлён. ..
..
Посмотреть работу
Педагогика начальной школы
Конспект урока литературного чтения «А. С. Пушкин «Сказка о царе Салтане…»»
Доступна к просмотру полнотекстовая версия работы
Посредством интеграции учебных предметов урок даст возможность детям увидеть многогранность литературного произведения, лучше осмыслить сказку, увидеть в ней добро и зло, красоту слова, музыки, изобразительного искусства, научит понимать музыку, виде…
Посмотреть работу
Педагогика начальной школы
Урок по окружающему миру «Секреты воды»
Доступна к просмотру полнотекстовая версия работы
Экспериментальная работа учащихся 3 класса по изучению свойств воды. Цели: Образовательная: познакомить с некоторыми свойствами воды, уточнить и систематизировать знания учащихся о значении воды в жизни человека. Развивающая: развивать наблюдательнос…
Развивающая: развивать наблюдательнос…
Посмотреть работу
Педагогика начальной школы
Конспект урока по окружающему миру «Средние века: время рыцарей и замков»
Доступна к просмотру полнотекстовая версия работы
Цель урока: формирование представления о Средневековье и знакомство с эпохой средних веков, достижениями, особенностями. Задачи: Образовательные: сформировать представление о средневековье; формирование представлений о религиях, получивших распростра…
Посмотреть работу
Мероприятие завершено
Блок 1.1 — 1.2: Образцы в делении
Математика 7Блоки 1.1 — 1.2: правила делимости — 0, 2, 3, 4, 5, 6, 8, 10
что нам нужно знать ?
Что значит «делить»?
отношения и части: деление и умножение
классные заметки
|
| ||||
| 7_unit_1.1_1.2_divisibility_family_tree.pdf 70025 |
| 7_unit_1.1_1.2_dr_all_solutions.pdf |
Что мы подразумеваем под «Паттернами деления»?
Давайте посмотрим на этот график:
Здесь показана взаимосвязь между умножением и делением, где числа 3, 6 и 18 связаны. 8 x 6 = 48. 48 / 6 = 8 Обратите внимание, что это семейство фактов состоит из 2 моделей деления и 2 моделей умножения. деление и 2 шаблона умножения. При делении вы можете использовать шаблоны для решения примеров вопросов, а также научиться умножать и делить на 10, 100, 1000 и т. д.!. Они образуют «СЕМЕЙСТВО ФАКТОВ». Давайте посмотрим на СЕМЕЙСТВО ФАКТОВ 6, 8 и 48:
Они образуют «СЕМЕЙСТВО ФАКТОВ». Давайте посмотрим на СЕМЕЙСТВО ФАКТОВ 6, 8 и 48:
6 x 8 = 48. 48 / 8 = 6
Давайте попробуем:
Из-за отношения, которое я упомянул между ними, мы можем обратить то, что мы сделали выше, чтобы умножить. Попробуем:
Есть несколько быстрых тестов, которые можно использовать, чтобы проверить, делится ли большее число на другое число. Те, которые мы будем использовать, называются ПРАВИЛА ДЕЛИМОСТИ.
Те, которые мы будем использовать, называются ПРАВИЛА ДЕЛИМОСТИ.
— Все числа кратные 100 (200, 300, 400 и т. д.) делятся на 4 — Все числа кратные 1000 (1000, 2000, 3000 и т. д.) делятся на 8 — Число делится на — Все числа делятся на 1 — Числа НЕ МОГУТ делиться на 0: Это потому, что мы не можем взять данное число и разделить его на ноль равных групп. Кроме того, мы не можем составлять нулевые наборы из заданного количества элементов. — ФАКТОРЫ встречаются парами. Когда мы находим один делитель числа, мы также находим второй делитель.
| факторинг | шаблоны в делении (основание 10) |
правила делимости
АКАДЕМИЯ ХАНА | МАТЕМАТИЧЕСКИЕ ИГРЫ |
АКАДЕМИЯ ХАНА |
По ссылке АКАДЕМИИ KHAN выше ищите ПРАКТИКУ — ФАКТОРЫ И ДЕЛИМОСТЬ
IXL — УМНОЖЕНИЕ |
|
| ||||||||
|
| ||||||||
|
| ||||
|
| ||||||||||||
| ||

 5 дес. – 50. Если к названию числа добавляют слово «сотня», то для записи числа надо добавить два ноля. 5 сот. – 500. Тысяча – три ноля, десятки тысяч – четыре ноля и т.д.
5 дес. – 50. Если к названию числа добавляют слово «сотня», то для записи числа надо добавить два ноля. 5 сот. – 500. Тысяча – три ноля, десятки тысяч – четыре ноля и т.д..jpg)

 Им соответствуют знаки «+», «-», «▪», «:».
Им соответствуют знаки «+», «-», «▪», «:». Для того, чтобы к сумме двух чисел прибавить третье, можно к первому числу прибавить значение суммы второго и третьего числа. или Два соседних слагаемых можно заменить их суммой.
Для того, чтобы к сумме двух чисел прибавить третье, можно к первому числу прибавить значение суммы второго и третьего числа. или Два соседних слагаемых можно заменить их суммой.  (a — b) ▪ c = a ▪ c — b ▪ c
(a — b) ▪ c = a ▪ c — b ▪ c

 В выражении 45 + 56 : 8, последним выполняют сложение. Поэтому читают так: «Сумма числа 45 и частного 56 и 8»
В выражении 45 + 56 : 8, последним выполняют сложение. Поэтому читают так: «Сумма числа 45 и частного 56 и 8»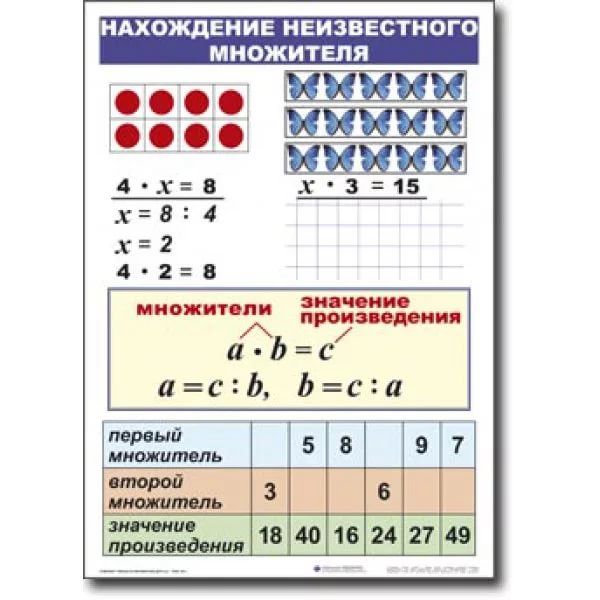

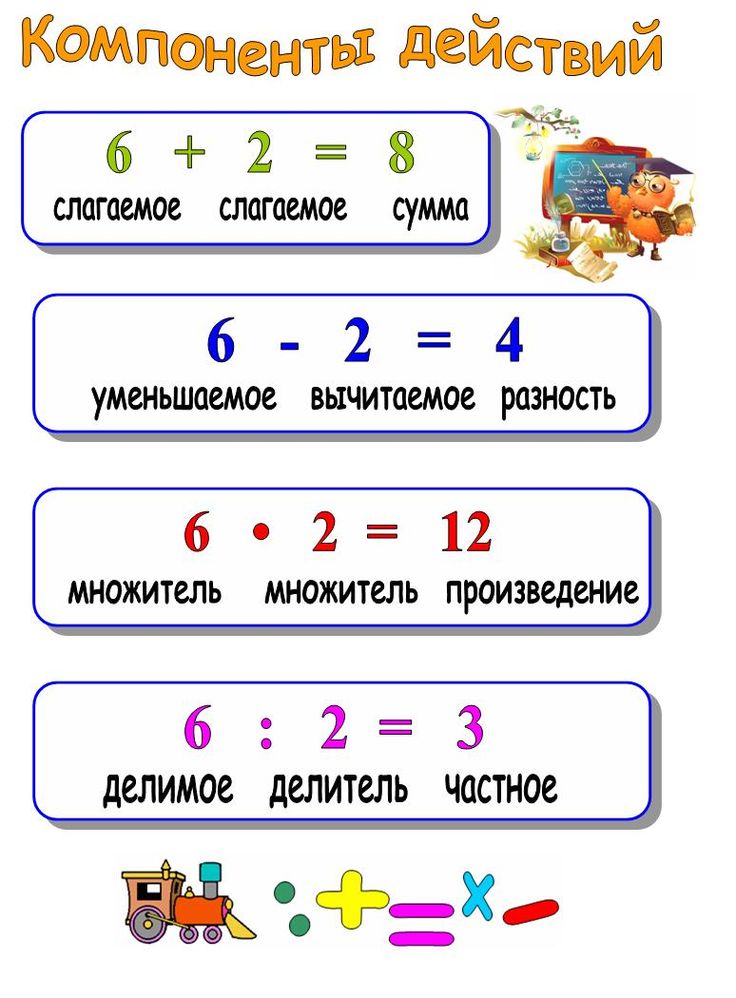 Если в уравнении навычитание неизвестное число стоит на втором месте, то уравнение решается прямым действием — вычитанием.
Если в уравнении навычитание неизвестное число стоит на втором месте, то уравнение решается прямым действием — вычитанием. Для этого надо определить порядок действий в уравнении.
Для этого надо определить порядок действий в уравнении.
 Например, 1 км = 1000м, тогда 4 км = 4000м. и 56000м= 56 км.
Например, 1 км = 1000м, тогда 4 км = 4000м. и 56000м= 56 км. Это задачи на сравнения.
Это задачи на сравнения.
 находим S2 = V2 ·• t
находим S2 = V2 ·• t


 1-1.2_unit_notes.pdf
1-1.2_unit_notes.pdf 
 pdf
pdf