Умножение и деление десятичных дробей – правила (5 класс, математика)

4.4

Средняя оценка: 4.4

Всего получено оценок: 265.

4.4

Средняя оценка: 4.4

Всего получено оценок: 265.

Умножение и деление десятичных дробей – тема достаточно простая для 5 класса. Однако ученики в примерах часто ошибаются, путаясь в правильной постановке запятой. Чтобы не допускать досадных ошибок разберемся в теме подробнее.

Что такое десятичная дробь?

Десятичной дробью называют дробь, записанную с помощью разделительной запятой. Знаменателем такой дроби всегда является степень числа 10.

В обычной форме записи нельзя увидеть знаменатель. Он спрятан за количеством знаков после запятой. Количество знаков после запятой это степень, в которую нужно возвести число 10, чтобы получить знаменатель.

Десятичная дробь может быть положительной и отрицательной. Также существуют смешанные десятичные дроби, но неправильных десятичных дробей не бывает. Это невозможно из-за самой формы записи числа.

Умножение десятичных дробей

Для того, чтобы умножить десятичные дроби нужно следовать следующему алгоритму:

• Посчитать количество знаков после запятой у обоих множителей. Причем нас интересует именно общее количество знаков после запятой. То есть нужно посчитать это значение для одного множителя, для другого, а потом сложить. Так мы получим число n – общее количество знаков после запятой у двух множителей.
• После этого запятые убираются и числа перемножаются как целые.
• С конца числа отсчитывается n количество знаков и ставится запятая.

Рассмотрим небольшой пример:

0,12*0,2 – общее количество знаков после запятой равняется 3. Уберем запятые и выполним умножение.

12*2=24 – теперь вернем запятую обратно.

0,12*0,2=0,024.

Обратите внимание, что нам не хватало знака перед числом для правильной постановки запятой, и мы просто поставили 0. Количество нулей, которые можно поставить перед или после числа неограниченно – они всегда там есть, просто их не пишут.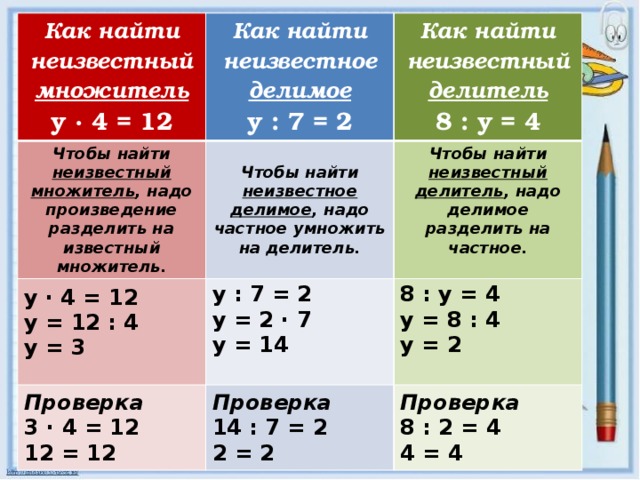

Деление дробей

Для того, чтобы разделить десятичные дроби, нужно следовать следующему алгоритму:

• Из двух чисел выбрать то, у которого знаков после запятой большей. Это и будет число m – наибольшее количество знаков после запятой.
• Нужно передвинуть в обоих числах: делимом и делителе – запятую вправо так, чтобы у чисел не оставалось дробных частей, то есть нужно у обоих чисел передвинуть запятую на m знаков.
• Выполнить деление. Полученный результат уже является ответом, никаких дополнительных запятых добавлять не нужно.

Если не хватает дробей части у одного из чисел, чтобы передвинуть запятую, следует добавить нули. Так, если передвинуть запятую в числе 0,12 на 3 знака, то получится число 120

Рассмотрим пример деления:

0,12:0,2 – наибольшее число знаков: 2, значит, передвинем запятую и выполним деление.

12:2=6 – это и есть ответ, то есть:

0,12:0,2=0,6.

Что мы узнали?

Мы вспомнили, что такое десятичная дробь. Привели правила умножения и деления десятичных дробей, а также рассмотрели несколько примеров.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Веня Светлосанов

  5/5

• Лариса Казакова

  5/5

• Валентина Бурова

  5/5

• Эрнест Хабибуллин

  5/5

• Алексей Бражников

  5/5

• Илья Сафронов

  5/5

• Егор Якушин

  4/5

• Екатерина Графкина

  5/5

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 265.

---

А какая ваша оценка?

Правила умножения и деления натуральных чисел для 5 класса

Одними из базовых математических операций являются умножение и деление натуральных чисел. В 5 классе они изучаются более подробно с учетом всех «тонкостей». Специалисты разработали специальные алгоритмы, позволяющие произвести расчеты без ошибок. Однако перед обучением нужно разобрать основные определения и понятия, а затем приступать к практике.

Общие сведения

Умножением двух или нескольких чисел называется математическая операция, состоящая из множителей и результата (произведения). Следует отметить, что ее можно заменить сложением, т. е. 2*3=2+2+2=6. Иными словами, первый множитель указывает на число, а второй обозначает, какое количество раз его необходимо сложить с эквивалентным значением. Операция умножения (при не табличных значениях) выполняется в столбик.

Деление — вид арифметической операции, при которой одно число (делимое) делится на другое (делитель), а их результатом является частное. Ее можно заменить вычитанием, т. е. 36/6=36−6−6−6−6−6−6=0. Следует отметить, что деление является сложным типом операции, поскольку классифицируется на два вида: без остатка и с его наличием.

Алгоритм деления

Деление, как и умножение, выполняется по определенному алгоритму. Однако следует учитывать факт, что результат может быть целым и с остатком. В первом и во втором случае применяется аналогичный алгоритм, но существуют некоторые особенности. Методика деления натурального числа на другое значение, принадлежащего к этому типу, имеет такой вид:

1. Записать делимое, а с правой стороны — делитель, отделяя их прямой чертой.
2. Взять количество разрядов, соответствующих делителю.
3. Подобрать множитель, а затем записать его произведение на делитель под I разрядной группой и вычислить их разность.
4. Взять II разрядную группу и выполнить аналогичную операцию.
5. Продолжать до того момента, пока не получится 0 или величина (остаток), которая меньше делителя.

Следует отметить, что операция деления имеет несколько особенностей. К ним относятся следующие:

1. Деление на 0 невозможно. Возможно только нуль разделить на любое число. Результат при этом будет равен 0. Пример деления для 5 класса имеет такой вид: 0/8=0.
2. Деление на 1 имеет эквивалентное исходное значение: 5/1=5.

После рассмотрения алгоритмов нужно перейти решению примеров на умножение и деление для 5 класса.

Примеры решений

Для примера следует разобрать задачу на перемножение чисел 25 и 25. В этом случае рекомендуется воспользоваться таким алгоритмом:

1. Записать первый множитель, а под ним второй.
2. Провести результирующую горизонтальную линию после величин в первом пункте.
3. Поставить слева знак произведения.
4. Умножить 25 на 5 (разряд единиц), а затем записать под чертой: 125.
5. Перемножить 25 и 2 (десятки): 50.
6. Записать величину, полученную в пятом пункте под десятками первого результата.
7. Сложить величины 125+50 (смещенное влево): 625.

Следующий пример — задание на операцию деления 625 на 5. Для этого следует воспользоваться вышеописанной методикой:

1. Написать делимое и делитель, разделив их вертикальной чертой.
2. Рассмотреть I разряд. Он делится на 5, но с остатком: 6/5=1 (1 — остаток).
3. Записать в поле результата число 1.
4. Перемножить 1 и 5, записав под шестеркой: 5.
5. Отделить остаток: 1.
6. Перенести к 1 второй разряд: 12.
7. Подобрать множитель: 5*2=10&lt,12.
8. Перемножить 5 и 2, записав результат под 12.
9. Выделить остаток: 2.
10. Перенести к 2 III разряд: 25.
11. Осуществить деление 25 на пятерку: 25/5=5.
12. Искомое частное: 125.

Следует отметить, что множитель при выполнении операции деления подбирается по такому принципу: его произведение на делитель не должно превышать значения делимого. Операция с остатком реализуется аналогично. Например, в выражении 4/3 остаток равен единице, а результат записывается следующим образом: 4/3=1 (+1). Последнее значение «(+1)» указывает на положительный остаток, т. е. 3*1+1=4.

Иногда в математической литературе можно встретить запись «(-1)», которая указывает на отрицательную величину остатка. Например, запись «11 (-1)» при делении неизвестного числа на тройку определяет исходную величину следующим образом: 3*11−1=33−1=32. Пример возможно править и в таком виде: 32/3=10 (+2)=11 (-1).

Таким образом, арифметические операции умножения и деления рекомендуется при отсутствии калькулятора выполнять в столбик, но для этого следует знать основные методики.

правил умножения целых чисел | умножение и деление целых чисел

Содержание

В арифметике сложение, вычитание, умножение и деление являются четырьмя основными операциями, используемыми при решении задач. Если вы знаете и соблюдаете основные правила целых чисел при умножении и делении, процесс решения задач становится гладким и легким.

Умножение и деление целых чисел

Умножение и деление есть не что иное, как многократное сложение и вычитание чисел соответственно. Вы можете выполнять умножение и деление, используя многократное сложение или вычитание целых чисел и применяя их правила к целым числам.

Но процесс многократного сложения или вычитания долгий и трудоемкий. Как и в случае сложения или вычитания целых чисел, для умножения и деления целых чисел также существуют определенные правила.

Умножение целых чисел

Умножение можно рассматривать как многократное сложение (накопление). Существуют определенные правила умножения целых чисел.

Правила умножения целых чисел:

• Умножение двух положительных чисел
• Умножение двух отрицательных чисел
• Умножение положительного числа на отрицательное число

Теперь, что касается результата умножения двух целых чисел, может произойти любое из следующего:

• Произведение двух целых чисел с одинаковые знаковые числа всегда будут положительными. Это означает, что
  • произведение двух целых положительных чисел положительно
  • произведение двух отрицательных чисел положительно
• Произведение двух целых чисел с разными знаками всегда будет отрицательным. Произведение положительного числа на отрицательное число (целые числа с разными знаками) всегда будет отрицательным.

Примечание: Произведение двух целых чисел всегда является целым числом.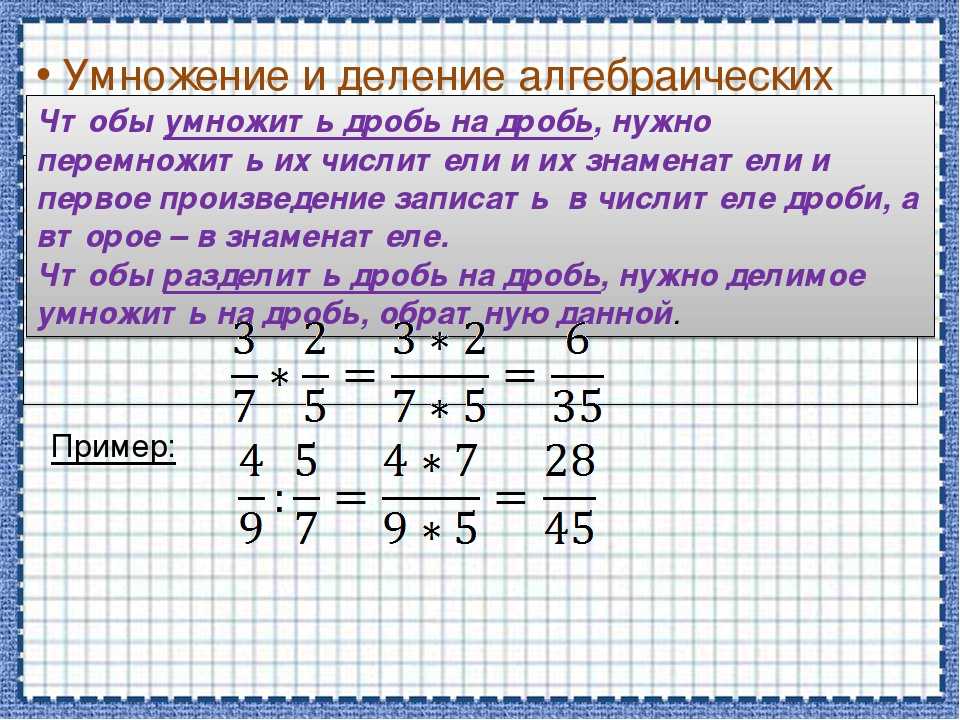

Приведенные выше правила умножения целых чисел можно обобщить следующим образом:

Тип чисел	Результат	Пример
Положительный $\times$ Положительный	Положительный $\left(+\right)$	$3 \times 7 = 21$
Отрицательный $\times$ Отрицательный	Положительный $\left( right)$	$\left(-3 \right) \times \left(-7 \right) = 21$
Положительное $\times$ Отрицательное	Отрицательное $\left(- \right)$	$3 \times \left(-7 \right) = -21$
Отрицательное $\times$ Положительное	Отрицательное $\left(- \right)$	$\left(-3 \right) \times 7 = -21$

Примечание: В случае умножения целых чисел просто умножайте числа без знака. Получив произведение, поставьте знак в соответствии с правилом умножения, приведенным в таблице выше.

Шаги при умножении целых чисел

Следующие шаги выполняются при умножении двух целых чисел:

Шаг 1: Определите абсолютное значение чисел.

Шаг 2: Найдите произведение абсолютных значений.

Шаг 3: После получения продукта определите знак числа в соответствии с правилами или условиями.

Примечание: Абсолютное значение целого числа, представляет собой целое число без знака.

Например,

• абсолютное значение $-12$ равно 12$
• абсолютное значение $+12$ равно 12$

Деление целых чисел деление — это многократное вычитание (распределение) чисел. Следовательно, деление целых чисел можно рассматривать как операцию, противоположную операции умножения. Тем не менее, правила деления целых чисел такие же, как и правила умножения.

Примечание: Результат двух целых чисел не всегда является целым числом.

• Когда остаток равен 0, результатом является целое число.
• Если остаток не равен 0, результат не является целым числом.

Правила деления:

• Результат двух положительных целых чисел всегда будет положительным.
• Результат двух отрицательных целых чисел всегда будет положительным.
• Результат положительного целого числа и отрицательного целого числа всегда будет отрицательным.

Тип номеров	Результат	Пример
Положительный $	$ $ $ \ \ №+ $ \ $ \ \ rong $ $ $ $ $ \ \ rong \ $ $ $ $ $ \ $ \ $ \ $ \ $ \ $ \ $ $ $ \ $ \ $ \ $ \ $ $ $ \ $ $ \ $ \ $ \ $. 5$
Отрицательное $\div$ Отрицательное	Положительное $\left(+\right)$	$\left(-15 \right) \div \left(-3 \right) = 5$
Положительный $\div$ Отрицательный	Отрицательный $\left(- \right)$	$15 \div \left(-3 \right) = -5$
Отрицательное $\div$ Положительное	Отрицательное $\left(- \right)$	$\left(-15 \right) \div 3 = -5$

Как и в случае умножения, разделите целые числа без знака, затем присвойте знак по правилу, указанному в таблице выше.

Шаги деления целых чисел

Следующие шаги выполняются при умножении двух целых чисел:

Шаг 1: Определите абсолютное значение чисел.

Шаг 2: Найдите произведение абсолютных значений.

Шаг 3: После получения продукта определите знак числа в соответствии с правилами или условиями.

Примечание: Абсолютное значение целого числа, представляет собой целое число без знака.

Например,

• абсолютное значение $-12$ равно 12$
• абсолютное значение $+12$ равно 12$

Известные математические соревнования для детей

Умножение и деление целых чисел с использованием числовой прямой

Как уже говорилось ранее, умножение и деление представляют собой многократное сложение и вычитание чисел. Вы можете выполнять умножение и деление, используя правила сложения и вычитания, используя числовую прямую.

Умножение целых чисел с помощью числовой строки

Чтобы выполнить умножение на числовой строке, мы начинаем с нуля $\left(0 \right)$ и двигаемся к правой стороне числовой строки заданное количество раз.

Рассмотрим пример. Умножьте $2 \times 4$ с помощью числовой прямой.

Начиная с нуля, на числовой прямой формируются четыре группы равных интервалов по $2$. Таким образом, мы достигнем 8.

Следующая числовая строка показывает $2 \times 4 = 8$.

Начать с 0Переместить 2 шагаПовторить 4 раза

Умножение положительных чисел в числовой строке

При умножении двух или более положительных чисел существует простое правило, которое следует за простым умножением. Поскольку это умножение, мы будем двигаться к правой стороне числовой прямой. Давайте решим $3 \times 5$.

Начиная с нуля, на числовой прямой образуются пять групп равных интервалов по $3$. Таким образом, мы достигнем $15$.

Следующая числовая строка показывает $3 \times 5 = 15$.

Начать с 0Переместить 3 шагаПовторить 5 раз

Умножение отрицательных чисел в числовой строке

При умножении более двух отрицательных чисел используйте правило четного-нечетного: 

• Подсчитайте количество отрицательных знаков.
• если количество отрицаний четное, результат положительный
• если количество отрицательных чисел нечетное, результат отрицательный 

Примечание: 

• Числа, входящие в таблицу умножения $2$, называются четными, например $2, 4, 6, 8, 10, 12, …$
• Числа, которые не входят в таблицу умножения 2, называются нечетными, например $1, 3, 5, 7, 9, 11, …$
• Каждое натуральное число является либо четным, либо нечетным количество.

Рассмотрим пример $-4 \times 4$.

Количество отрицательных знаков равно $1$, что нечетно. Таким образом, результат будет отрицательным (и будет лежать слева от $0$(ноль)).

Начиная с нуля, в левой части числовой прямой формируются четыре группы равных интервалов по $4$. Таким образом, мы достигнем $-16$.

Начать с 0Переместить 4 шагаПовторить 4 раза Типы систем координат

Деление на числовой прямой

Как упоминалось выше, деление есть не что иное, как многократное вычитание. Воспользуемся этим фактом и поймем представление операции деления на числовой прямой.

Предположим, что число $x$ делится на $y$.

Поскольку операцию деления можно выполнять как повторное вычитание, поэтому мы будем выполнять операцию вычитания, двигаясь влево по числовой строке.

Давайте разберемся с шагами деления на числовой прямой.

Шаг 1: Нарисуйте числовую прямую, начертите числа, кратные $y$, начиная с $0$, и отметьте делимое $x$ на числовой прямой. Мы возьмем $x$ в качестве эталона.

Шаг 2: Начиная с $x$, мы продолжаем вычитать группы по $y$ единиц, пока не достигнем числа $0$. Каждый раз, когда мы делаем вычитание, мы перемещаемся на y единиц влево от $x$, пока не достигнем $0$. Альтернативный метод сделать это, начиная с $0$ в качестве контрольной точки, мы можем двигаться вправо группами по $y$ единиц, пока не достигнем числа $x$.

Шаг 3: Количество шагов на $y$ единиц, на которые мы продвинулись влево от $x$, чтобы достичь $0$, или количество шагов на $y$ единиц, на которые мы продвинулись вправо от $0 $ для достижения $x$ даст нам частное.

Давайте рассмотрим пример деления 12$ на 6$, чтобы понять представление деления на числовой прямой.

Давайте выполним шаги, описанные выше, чтобы выполнить деление $12 \div 6$.

Начать с 0

Чтобы выполнить $12\div 6$, мы построим числовую прямую и нанесем первые несколько кратных $6$, начиная с $0$, включая делимое $12$.

Первые несколько кратных 6

Обведите дивиденд $12$.

Encircle 12

Начиная с $12$, двигайтесь влево на $6$ единиц и продолжайте повторять эти движения по $6$ единиц, пока не достигнете $0$.

Перемещение от 12 до 0

Количество ходов, сделанных для достижения $0$ с $14$, будет частным. Как мы видим, нам пришлось переместиться на $2$ прыжков, чтобы достичь $0$.

Следовательно, частное равно $2$.

Деление отрицательных чисел на числовой прямой

Теперь мы рассмотрим представление деления отрицательных чисел на числовой прямой. Шаги, чтобы показать деление, будут очень похожи на те, что обсуждались в предыдущем разделе. Возьмем два случая с примерами.

Случай I: Отрицательное число делится на положительное число

Пример: $\left(-12 \right) \div 3$

Согласно правилам работы с целыми числами, когда отрицательное число делится на положительное число или и наоборот, результат всегда является отрицательным числом.

Начать с 0

Мы наносим отрицательные числа, кратные $3$, на числовую прямую, начиная с $0$ и по крайней мере до $-12$, поскольку делимое равно $-12$.

Отрицательное число, кратное 3

Обведите делимое $-12$.

Окружность -12

Начиная с $-12$, сместитесь вправо на $3$ единиц и продолжайте повторять эти движения по $3$ единиц, пока не достигнете $0$.

Переход от -12 к 0

Мы видим, что всего было сделано $4$ прыжков, каждый из которых состоит из $3$ единиц, чтобы достичь $-12$.

Так как скачки сделаны влево от $0$ на числовой прямой, следовательно, результат равен $-4$.

Следовательно, $\left(-12 \right) \div 3 = -4$.

Случай II: Отрицательное число разделить на отрицательное число

Пример: $\left(-15 \right) \div \left(-3 \right)$

В соответствии с правилами целочисленной операции, когда отрицательное число делится на отрицательное число, результат всегда положительный количество.

Начать с 0

Наносим положительные числа, кратные как минимум $3$, до $15$, как показано на диаграмме.

Первые несколько кратных 3

Обведите дивиденд $15$.

Encircle 15

Начиная с $15$, двигайтесь влево на $3$ единиц и продолжайте повторять эти движения по $3$ единиц, пока не достигнете $0$.

Переход от 15 к 0

Мы видим, что всего сделано $5$ прыжков, каждый из которых состоит из $3$ единиц, чтобы достичь 0. 

Следовательно, $\left(-15 \right) \div \left(-3 \ справа) = 5$.

Деление на числовой прямой с остатками

При делении чисел мы сталкиваемся со многими ситуациями, когда делимое не делится на делитель полностью. Это происходит, когда делимое не кратно делителю или делитель не является множителем делимого.

При возникновении такой ситуации мы получаем ненулевой остаток.

Теперь мы поймем, как представить деление на числовой прямой с остатками на примере.

Разделим число $12$ на $5$ и представим его на числовой прямой.

Начать с 0

Поскольку делитель равен $5$, мы начинаем формировать группы по $5$ единиц и начинаем двигаться вправо от $0$, начиная с $0$, чтобы достичь числа $12$.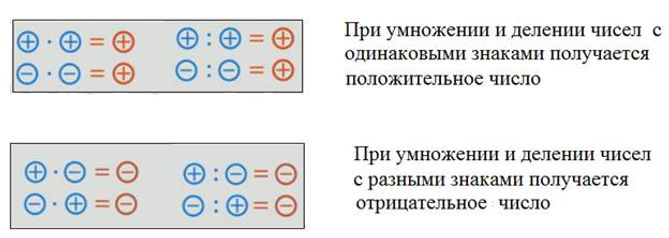

Первые несколько кратных 5

Обведите дивиденд $17$.

Encircle 17

Начните создавать группы по $5$ от $0$.

Переход от 0 к 17

Мы видим, что первая группа от 0$ до 5$, вторая группа от 5$ до 10$ и третья группа от 10$ до 15$. Таким образом, у нас есть три группы по $5$ от $0$ до $15$.

Обратите внимание, что для третьей группы нам нужно как минимум на 5$ больше единиц, но у нас есть только на 2$ больше единиц от 15$ до 17$.

Следовательно, мы можем сказать, что остаток равен $2$, так как эти $2$ единицы не образуют группу из $5$.

Следовательно, частное равно $3$, так как есть три группы по $5$, а остаток равен $2$.

Следовательно, мы можем представить это деление как $17 \div 5 =$ Частное равно $2$, а остаток равен $5$.

Ключевые выводы

• Если знаки разные, ответ отрицательный.
• Если знаки одинаковые, ответ положительный.

Практические задачи

1. $\left( +8 \right) \times \left(-1 \right)$
2. $\left(+4 \right) \times \left(+6 \right)$
3. $\left(-3 \right) \times \left(-7 \right)$
4. $\left(-9 \right) \times \left(-2 \right)$
5. $\left( -11 \вправо) \раз \влево(+5 \вправо)$
6. $\влево(+12 \вправо) \раз \влево(0 \вправо)$
7. $\влево(-20 \вправо) \раз \left(-4 \right)$
8. $\left(-15 \right) \times \left(+13 \right)$
9. $\left(-20 \right) \times \left(-5 \ вправо)$
10. $\влево(-9\вправо) \раз \влево(+4\вправо)$
11. $\влево(+3\вправо) \раз \влево(-6 \вправо)$
12. $\влево(+11\вправо)\раз\влево(0\вправо)$
13. $\влево(-7\вправо) \раз\влево(-4\вправо)$
14. $\влево(- 9 \right) \times \left(+8 \right)$
15. $0 \div \left(-8 \right)$
16. $\left(+9 \right) \div \left(-3 \right) $
17. $\left(-11 \right) \div \left(-6 \right)$
18. $\left(-12 \right) \div \left(-3 \right)$
19. $\left (-25 \right) \div \left(+5 \right)$
20. $\left(+45 \right) \div \left(-3 \right)$
21. $\left(-24 \right) \дел\влево(-4\вправо)$
22. $\left(-78 \right) \div \left(13 \right)$
23. $\left(30 \right) \div \left(-10 \right)$
24. $\left(+14 \right) \div \left(-2 \right)$
25. $\left(-16 \right) \div \left(-8 \right)$
26. $\left(-48 \right) \div \ влево(+6\вправо)$
27. $\влево(4\вправо) \дел\влево(2\вправо)$
28. $0 \дел\влево(6\вправо)$

Рекомендуемое чтение

• Дополнение и вычитание целых чисел
• Как решать радикальные уравнения?
• Что использовать — HCF или LCM?

Вам также может понравиться

Что такое вписанный четырехугольник – (определение, свойства, теоремы и доказательства)

Содержание Что такое вписанный четырехугольник? Читать больше

Что такое воздушный змей в геометрии – (определение, форма, свойства и примеры)

Содержание Что такое воздушный змей в геометрии?Свойства воздушного змеяДиагонали

Читать больше

Что такое квадрат в геометрии – (определение, форма, свойства и примеры)

Содержание Что такое квадрат в геометрии? Примеры SquareDiagonal для

Читать больше

Как применять правила умножения и деления целых чисел?

Используя правила умножения и деления, можно легко умножить или разделить два целых числа. В этом пошаговом руководстве вы узнаете эти правила.

Умножение и деление целых чисел — это две основные операции, выполняемые над целыми числами. Умножение целых чисел аналогично повторяющимся сложениям, что означает добавление целого числа определенное количество раз.

Похожие темы

• Как умножать и делить целые числа?
• Как применять правила сложения и вычитания целых чисел?

Пошаговое руководство по применению правил умножения и деления

Правила умножения целых чисел

Умножение целых чисел — это процесс многократного сложения, в котором участвуют положительные и отрицательные числа или, можно сказать, целые числа. Когда дело доходит до умножения целых чисел, следует учитывать следующее:

• Умножение \(2\) положительных чисел: Когда вы умножаете целые числа на два положительных знака, \(\color{синий}{положительный\:\times \:положительный\:=\:положительный}\)
• Умножение \ (1\) положительное и \(1\) отрицательное число: когда вы умножаете целые числа с одним отрицательным знаком и одним положительным знаком, \(\color{blue}{negative\:\times \:positive\:=\:negative\ :}\)
• Умножение \(2\) отрицательных чисел: при умножении целых чисел с двумя отрицательными знаками \(\color{синий}{отрицательный\:\times \:отрицательный\:=\:положительный}\)

Следующая таблица поможет вам запомнить правила умножения целых чисел:

Правила деления целых чисел

Целочисленное деление включает группировку элементов. В него входят как положительные, так и отрицательные числа. Как и умножение, деление целых чисел включает в себя одно и то же:

• Деление \(2\) положительных чисел: Когда вы делите целые числа с двумя положительными знаками, \(\color{blue}{positive\:\div \:positive\: =\:положительный\:}\)
• Деление \(2\) отрицательных чисел: при делении целых чисел с двумя отрицательными знаками, \(\color{синий}{отрицательный\:\div \:отрицательный\:=\:положительный}\)
• Деление \( 1\) положительное и \(1\) отрицательное число: когда вы делите целые числа с одним отрицательным знаком и одним положительным знаком, \(\color{blue}{negative\:\div \:positive\:=\:negative}\ )

Следующая таблица поможет вам запомнить правила деления целых чисел:

При умножении или делении целых чисел следует помнить о двух важных моментах:

1. Когда знаки разные, ответ всегда отрицательный.
2. При одинаковых знаках ответ всегда положительный.

Применение Правила умножения и деления – Пример 1:

Решите данное выражение, используя правила деления целых чисел: \((–30) ÷ (–5) ÷ (–2)\) .