Рассмотрите, каким образом учащиеся знакомятся с умножением и делением с числами 0 и 1 в различных учебниках математики.

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 4 из 4 М2М ч.2 с. 53. УМК «Школа России». Далее учащиеся знакомятся с особыми (частными) случаями умножения любого числа на 1 и 0.  На с.82 вводится правило умножения любого числа на 1: при умножении любого числа на 1 получается то число, которое умножали. На с.83 вводится правило умножения любого числа на 0: при умножении любого числа на нуль получается нуль. Замечается, что на 0 делить нельзя! С.84. С.85. На данной странице учащиеся знакомятся с делением нуля на число. Дается формулировка: если произведение 0 разделить на число, не равное 0, получим 0. Заданий для закрепления частных случаев умножения и деления недостаточно → дает сам учитель.   М2А ч.2 с. 76-77. УМК «Система развивающего обучения Занкова». В учебнике Аргинской 2 класс, умножение и деление на 1 и 0 изучают в одной теме «Таблица умножения». На с.76 дано задание подводящее к правилу умножение на 1, выполняя задание учащиеся формулируют вывод и сравнивают его с правилом: если 1 умножить на число, то получится это же число. Дана и другая формулировка правила: если число умножить на 1, то получится это же число. В общем виде это правило записывается так: а * 1 = 1 * а = … Ниже представлены задания для закрепления пройдённого материала. С.78. На данной странице предлагается задание, раскрывающее связь между умножением и делением. Сначала учащиеся находят значения произведений, затем с помощью получившихся равенств находят значения частных, с опорой на записи делают вывод. Формулировки правила «деление на 1» в учебнике нет󠇄 → дает сам учитель. При деление любого числа на 1, получается тоже самое число. Например, 5 : 1 = 5. Если число разделить на самого себя, получим 1. Например, 5 : 5 = 1. С.82. Учащимся предлагается сравнить выражения, вычислить их значения, заменив умножение сложением, затем сделать вывод и закончить правило: При умножение числа 0 на натуральное число получится … В качестве подсказки дается общий вид правила: 0 * а = 0 Далее рассматривается другое равенство: а * 0 = 0, учащиеся пользуясь правилом находят значения выражений: 6 * 0, 27 * 0 и т.д. С.83. Учащимся предлагается порассуждать: можно ли по материалу задания №451 сделать вывод: Если хотя бы один множитель равен 0, то и значение произведения равно 0.     С.84. Дается задание на закрепление пройденного материала, учащиеся заполняют таблицу. Затем предлагается найти значения частных, используя равенства, полученные в пункте 2, формулируется вывод. Учащиеся читают правило записанное в пункте 5: если 0 разделить на любое натуральное число, получится 0. Записывают правило в общем виде: 0 : а = 0. С.87. Учащиеся рассуждают по теме вопроса: Можно ли найти значения этих частных? После чего учитель сообщает, что на 0 делить нельзя! Потому что если делитель 0, то число не делится на части, а значит нет действия. Это правило необходимо запомнить. Упражнений на закрепление частных случаев умножения и деления в учебнике не много → дает сам учитель. М2Д ч.2 с.56. УМК «Школа 2100». В учебнике Демидовой 2 класс на уроке 2.40 вводится новая тема: «Умножение с нулем и единицей». Учащиеся находят значения произведений, заменив умножение их суммами, затем предлагается найти значение выражения 1 * 20, не заменяя его суммой. Делают вывод и сравнивают его с правилом: при умножении единицы на любое число получается то число, на которое умножали, дается общий вид правила: 1 * а = а, например, 5 * 1 = 5. Аналогичное задание выполняют и с умножением на 0. Делают вывод и сравнивают его с правилом: при умножении 0 на любое число, получается 0. Дается общий вид правила: 0 * а = 0. Аналогично формулируются правила умножения любого числа на 1 и 0. Упражнений на закрепление частных случаев умножения практически нет → дает сам учитель. М2Д ч.3 с.10. УМК «Школа 2100». На уроке 2.56 вводится новая тема: «Деление с нулем и единицей». Учащиеся находят значения произведений, отвечают на вопрос как деление связано с умножением? Затем находят значения второго выражения в каждом столбце, опираются на связь умножения с делением. Делают вывод и сравнивают его с правилом: при делении любого числа на единицу получаем это же число, дается общий вид правила: а : 1 = а, например, 5 : 1 = 5. Учащиеся рассуждают по теме вопроса: Существует ли значение выражения: 5 : 0, 7 : 0? Можно ли подобрать такое число, умножив которое на 0, получили бы 5 или 7? С опорой на уже имеющиеся знания, учащиеся приходят к выводу: на 0 делить нельзя. Учитель сообщает, что на 0 делить нельзя! Потому что если делитель 0, то число не делится на части, а значит нет действия. Это правило необходимо запомнить. Учащиеся находят значения второго выражения в каждом столбце, опираются на связь умножения с делением. Делают вывод и сравнивают его с правилом: при делении 0 на любое число, не равное 0, получим 0. Дается общий вид правила: 0 : а = 0. Аналогично формулируется правило деления любого числа на 1: при делении любого числа, не равного 0, самого на себя получаем единицу. Дается общий вид правила: а : а = 1. Упражнений на закрепление частных случаев умножения практически нет → дает сам учитель. М2Д ч.1 с.59. В данном учебнике на с.59 вводится новая тема: «Умножение чисел 0 и 1». Перед каждым правилом дано задание, которое подводит к правилу. Учащиеся выполняют задание, формулируют вывод и сравнивают его с правилом из учебника: при умножении числа 1 на любое число получается то же самое число. С.60. Учащиеся выполняют задание, формулируют вывод и сравнивают его с правилом из учебника: при умножении числа 0 на любое число получается 0. М2Д ч.2 с.85. На данной странице вводится новая тема: «умножение на 0 и на 1». Учащиеся выполняют задание, используя переместительное свойство умножения, формулируют выводы и сравнивают их с правилами из учебника: при умножении числа на 1 всегда получают то число, которое умножали. При умножении числа на 0 всегда получается 0. Упражнений на закрепление частных случаев умножения в учебнике недостаточно → дает сам учитель. М3Д ч.1 с.76. Изучая таблицы умножения, составляются таблицы деления, в которые включается частный случай деления любого числа на 1. С.83. С.98. Формулировки правил: на 0 делить нельзя; при делении 0 на любое число, не равное 0, получим 0, в данном учебнике нет → дает сам учитель. Упражнений на закрепление частных случаев деления недостаточно → дает сам учитель.   М2И ч.2 с. 57. УМК «Гармония». В данном учебнике на с. 57 учащимся предлагается найти значения выражений, заменив умножение сложением. Выполнив действия, учащиеся формулируют вывод, отвечают на вопрос: почему некоторые выражения находятся в рамках? Сверяют свои ответы с рассуждением Миши и Маши, выясняют кто из ребят прав. Затем читают правила представленные ниже. М3И ч.1 с.78. УМК «Гармония». В 3 классе так же дано задание и рассуждение Миши и Маши, но уже правило деление 1 и 0. В данном учебнике на с.78 учащимся предлагается найти значения выражения, используя равенство. Таким образом проводится связь между умножением и делением. Выполнив действия, учащиеся формулируют вывод. Сверяют свои ответы с рассуждением Миши и Маши. Затем читают правила представленные ниже.   С.79. Упражнений на закрепление частных случаев умножения и деления недостаточно → дает сам учитель.   ⇐ Предыдущая1234 Читайте также:  Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности 

Последнее изменение этой страницы: 2021-05-12; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.013 с.)

Нуль делится на число. Почему делить на ноль нельзя? Делится ли ноль на ноль

Класс: 3

Учебник: «Математика» М.И.Моро

Цели урока: создать условия для формирования умения делить 0 на число.

Задачи урока:

• раскрыть смысл деления 0 на число через связь умножения и деления;
• развивать самостоятельность, внимание, мышление;
• формировать навыки решения примеров на табличное умножение и деление.

Для достижения цели урок был разработан с учётом деятельностного подхода.

Структура урока включала в себя:

1. Орг. момент , целью которого было позитивно настроить детей на учебную деятельность.
2. Мотивация позволила актуализировать знания, сформировать цели и задачи урока. Для этого были предложены задания на нахождение лишнего числа, классификацию примеров на группы, добавление недостающих чисел . В ходе решения этих заданий, дети столкнулись с проблемой : нашёлся пример, для решения которого не хватает имеющихся знаний. В связи с этим дети самостоятельно сформулировали цель и поставили перед собой учебные задачи урока.
3. Поиск и открытие нового знания дал возможность детям предложить различные варианты решения задания. Основываясь на ранее изученный материал, они смогли найти верное решение и прийти к выводу , в котором сформулировали новое правило.
4. Во время первичного закрепления ученики комментировали свои действия,работая по правилу , дополнительно были подобраны свои примеры на это правило.
5. Для автоматизации действий и умения пользоваться правилам в нестандартных заданиях дети решали уравнения, выражения в несколько действий.
6. Самостоятельная работа и проведенная взаимопроверка показали, что большинство детей тему усвоили.
7. Во время рефлексии дети сделали вывод, что поставленная цель урока достигнута и оценили себя с помощью карточек.

В основе урока лежали самостоятельные действия учащихся на каждом этапе, полное погружение в учебную задачу. Этому способствовали такие приёмы, как работа в группах, само- и взаимопроверка, создание ситуации успеха, дифференцированные задания, саморефлексия.

Ход урока

Цель этапа	Содержание этапа	Деятельность ученика
1. Орг. момент
Подготовка уч-ся к работе, позитивный настрой на учебную деятельность.	Стимулирование на учебную деятельность . Проверьте свою готовность к уроку, сядьте ровно, облокотитесь на спинку стула. Потрите свои ушки, чтобы кровь активнее поступала в мозг. Сегодня у вас будет много интересной работы, с которой, я уверена, вы справитесь на отлично.	Организация рабочего места, проверка посадки.
2. Мотивация.
Стимулирование познавательной активности, активизация мыслительного процесса	Актуализация знаний, достаточных для приобретения нового знания. Устный счёт. Проверка знания табличного умножения:	Решение заданий, основанных на знании табличного умножения.
	А) найди лишнее число: 2 4 6 7 10 12 14 6 18 24 29 36 42 Объясните, почему оно лишнее и каким числом его надо заменить.	Нахождение лишнего числа.
	Б) вставьте пропущенные числа: … 16 24 32 … 48 …	Добавление недостающего числа.
	Создание проблемной ситуации Задания в парах: В) расставьте примеры в 2 группы: Почему так распределили? (с ответом 4 и 5).	Классификация примеров по группам.
	Карточки: 8·7-6+30:6= 28:(16:4)·6= 30-(20-10:2):5= 30-(20-10·2):5=	Сильные ученики работают по индивидуальным карточкам.
	Что вы заметили? Есть ли здесь лишний пример? Все ли примеры вы смогли решить? У кого возникли затруднения? Чем этот пример отличается от остальных? Если кто-то решил, то молодец. Но почему не все смогли справиться с этим примером?	Нахождение затруднения. Выявление недостающего знания, причины затруднения.
	Постановка учебной задачи. Здесь есть пример с 0. А от 0 можно ожидать разные фокусы. Это необычное число. Вспомните, что вы знаете про 0? (а·0=0, 0·а=0, 0+а=а)· Приведите примеры. Посмотрите, какой он коварный: когда его прибавляют, он не изменяет число, а когда умножают, превращают его в 0. Подходят ли эти правила к нашему примеру? Как же он поведёт себя при елении?	Наблюдение над известными приёмами действий с 0 и соотношение с исходным примером.
	Итак, какова наша цель? Решить этот пример верно. Таблица на доске. Что для этого надо? Узнать правило деления 0 на число.	Выдвижение гипотезы,
Как же найти верное решение? С каким действием связано умножение? (с делением) Приведите пример 2 · 3 = 6 6: 2 = 3 Можем ли мы теперь 0:5? Это значит, надо найти число, при умножении которого на 5 получится 0. х·5=0 Это число 0. Значит, 0:5=0. Приведите свои примеры.	поиск решения на основе ранее изученного,
Формулирование правила. Какое же правило теперь можно сформулировать? При делении 0 на число получается 0. 0: а = 0.	Решение типовых заданий с комментированием. Работа по схеме (0:а=0)
5. Физминутка.
Профилактика нарушения осанки, снятие усталости с глаз, общего утомления.
6. Автоматизация знаний.
Выявление границ применимости нового знания.	В каких ещё заданиях может понадобиться знание этого правила? (в решении примеров, уравнений)	Использование полученных знаний в разных заданиях. Работа в группах.
	Что неизвестно в этих уравнениях? Вспомните, как узнать неизвестный множитель. Решите уравнения. Какое решение в 1 уравнении? (0) Во 2? (нет решения, на 0 делить нельзя)	Обращение к ранее изученным умениям.
	** Составьте уравнение с решением х=0 (х·5=0)	Для сильных уч-ся творческое задание
7. Самостоятельная работа.
Развитие самостоятельности, познавательных способностей	Самостоятельная работа с последующей взаимопроверкой. №6	Активные умственные действия учащихся, связанные с поисками решения, опираясь на свои знания. Самоконтроль и взаимоконтроль. Сильные ученики проверяют и помогают более слабым.
8. Работа над ранее пройденным материалом. Отработка умения решения задач.
Формирование навыка решения задач.	Как вы думаете, часто ли в задачах используется число 0? (Нет, не часто, т.к. 0 – это ничего, а в задачах должно какое-то количество чего-либо. ) Тогда будем решать задачи, где есть другие числа. Прочитайте задачу. Что поможет решить задачу? (таблица) Какие столбики в таблице надо записать? Заполните таблицу. Составьте план решения: что надо узнать в 1, во 2 действии?	Работа над задачей с использованием таблицы. Планирование решения задачи. Самостоятельная запись решения. Самоконтроль по образцу.
9. Рефлексия. Итоги урока.
Организация самооценки деятельности. Повышение мотивации ребёнка.	Над какой темой сегодня работали? О чём вы не знали в начале урока? Какую цель ставили перед собой? Достигли вы её? С каким правилом познакомились? Оцените свою работу, выставив соответствующий значок: солнышко – я доволен собой, у меня всё получилось белое облако – всё хорошо, но я мог работать лучше; серое облако – урок обычный, ничего интересного; капелька – ничего не получилось	Осознавание своей деятельности, самоанализ своей работы. Фиксация соответствия результатов деятельности и поставленной цели.
10. Домашнее задание.

Каждый ещё со школы помнит, что на ноль делить нельзя. Младшеклассникам никогда не объясняют, почему так поступать не следует. Просто предлагают принять это как данность наравне с другими запретами вроде «нельзя совать пальцы в розетки» или «не стоит задавать взрослым глупые вопросы». АиФ.ru решил разобраться, так ли были правы школьные учителя.

Алгебраическое объяснение невозможности деления на ноль

С точки зрения алгебры, делить на ноль нельзя, так как это не имеет никакого смысла. Возьмём два произвольных числа, a и b, и умножим их на ноль. a × 0 равно нолю и b × 0 равно нолю. Получается, что a × 0 и b × 0 равны, ведь произведение в обоих случаях равно нолю. Таким образом, можно составить уравнение: 0 × a = 0 × b. А теперь предположим, что мы можем делить на ноль: разделим обе части уравнения на него и получим, что a = b. Получается, что если допустить операцию деления на ноль, то все числа совпадают. Но 5 не равно 6, а 10 не равно ½. Возникает неопределённость, о которой пытливым младшеклассникам учителя предпочитают не рассказывать.

Объяснение невозможности деления на ноль с точки зрения матанализа

В старших классах изучают теорию пределов, которая также говорит о невозможности деления на ноль. Это число там трактуется как «неопределённая бесконечно малая величина». Так что если мы в рамках этой теории рассмотрим уравнение 0 × X = 0, то обнаружим, что X нельзя найти потому, что для этого пришлось бы разделить ноль на ноль. А это также не имеет никакого смысла, так как и делимое, и делитель в таком случае представляют из себя неопределённые величины, следовательно, нельзя сделать вывод об их равенстве или неравенстве.

Когда на ноль делить можно?

В отличие от школьников, студентам технических вузов на ноль делить можно. Операцию, которая в алгебре является невозможной, можно произвести в других сферах математического знания. В них появляются новые дополнительные условия задачи, которые допускают это действие. Делить на ноль можно будет тем, кто прослушает курс лекций по нестандартному анализу, изучит дельта-функцию Дирака и ознакомится с расширенной комплексной плоскостью.

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметк и начинается отсчет координат положения точки в любой системе координат.

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль .

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль .

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль .

Пример 3

Ноль умножить на ноль равняется ноль .

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль .

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль .

0:

= 0

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.

0: 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как деление нуля на ноль , не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в ноль . Если это определено, то такому выражению, как ноль разделить на ноль , в подавляющем большинстве случаев можно придать некий смысл.

Евгений ШИРЯЕВ, преподаватель и руководитель Лаборатории математики Политехнического музея , рассказал «АиФ» о делении на ноль:

1. Юрисдикция вопроса

Согласитесь, особенную провокационность правилу придает запрет. Как это нельзя? Кто запретил? А как же наши гражданские права?

Ни конституция, ни Уголовный кодекс, ни даже устав вашей школы не возражают против интересующего нас интеллектуального действия. А значит, запрет не имеет юридической силы, и ничто не мешает прямо тут, на страницах «АиФ», попробовать что-нибудь разделить на ноль. Например, тысячу.

2. Разделим, как учили

Вспомните, когда вы только узнали, как делить, первые примеры решали с проверкой умножением: результат, умноженный на делитель, должен был совпасть с делимым. Не совпал — не решили.

Пример 1. 1000: 0 =…

Забудем на минуту про запретное правило и сделаем несколько попыток угадать ответ.

Неправильные отсечёт проверка. Перебирайте варианты: 100, 1, −23, 17, 0, 10 000. Для каждого из них проверка даст один и тот же результат:

100 · 0 = 1 · 0 = − 23 · 0 = 17 · 0 = 0 · 0 = 10 000 · 0 = 0

Ноль умножением все превращает в себя и никогда — в тысячу. Вывод сформулировать несложно: никакое число не пройдет проверку. Т. е. ни одно число не может быть результатом деления ненулевого числа на ноль. Такое деление не запрещено, а просто не имеет результата.

3. Нюанс

Чуть не упустили одну возможность опровергнуть запрет. Да, мы признаем, что ненулевое число не разделится на 0. Но может быть, сам 0 сможет?

Пример 2. 0: 0 = …

Ваши предложения для частного? 100? Пожалуйста: частное 100, умноженное на делитель 0, равно делимому 0.

Еще варианты! 1? Тоже подходит. И −23, и 17, и все-все-все. В этом примере проверка на результат будет положительной для любого числа. И, по-честному, решением в этом примере надо называть не число, а множество чисел. Всех. А так недолго договориться и до того, что Алиса — это не Алиса, а Мэри-Энн, а обе они — сон кролика.

4. Что там про высшую математику?

Проблема разрешена, нюансы учтены, точки расставлены, все прояснилось — ответом для примера с делением на ноль не может быть ни одно число. Такие задачки решать — дело безнадежное и невозможное. А значит… интересное! Дубль два.

Пример 3. Придумать, как разделить 1000 на 0.

А никак. Зато 1000 можно без трудностей делить на другие числа. Ну, давайте хотя бы делать то, что получается, пусть даже изменив поставленную задачу. А там, глядишь, увлечемся, и ответ сам собой объявится. Забываем на минуту про ноль и делим на сто:

Сотня далека от нуля. Сделаем шаг к нему, уменьшив делитель:

1000: 25 = 40,
1000: 20 = 50,
1000: 10 = 100,
1000: 8 = 125,
1000: 5 = 200,
1000: 4 = 250,
1000: 2 = 500,
1000: 1 = 1000.

Очевидная динамика: чем ближе делитель к нулю, тем больше частное. Тенденцию можно наблюдать и дальше, переходя к дробям и продолжая уменьшать числитель:

Осталось заметить, что к нулю мы можем подойти как угодно близко, делая частное сколь угодно большим.

В этом процессе нет нуля и нет последнего частного. Мы обозначили движение к ним, заменив число на последовательность, сходящуюся к интересующему нас числу:

При этом подразумевается аналогичная замена и для делимого:

1000 ↔ { 1000, 1000, 1000,. .. }

Стрелки не зря поставлены двусторонними: некоторые последовательности могут сходиться к числам. Тогда мы можем поставить в соответствие последовательности ее числовой предел.

Посмотрим на последовательность частных:

Она растет неограниченно, не стремясь ни к какому числу и превосходя любое. Математики добавляют к числам символ ∞, чтобы иметь возможность рядом с такой последовательностью поставить двустороннюю стрелку:

Сопоставление числам последовательностей, имеющих предел, позволяет предложить решение к третьему примеру:

При поэлементном делении последовательности, сходящейся к 1000, на последовательность из положительных чисел, сходящуюся к 0, получим последовательность, сходящуюся к ∞.

5. И здесь нюанс с двумя нулями

Что будет результатом деления двух последовательностей положительных чисел, сходящихся к нулю? Если они одинаковые, то тождественная единица. Если к нулю быстрее сходится последовательность-делимое, то в частном — последовательность с нулевым пределом. А когда элементы делителя убывают гораздо быстрее, чем у делимого, последовательность частного будет сильно расти:

Неопределенная ситуация. И так и называется: неопределенность вида 0/0 . Когда математики видят последовательности, подходящие под такую неопределенность, они не бросаются делить два одинаковых числа друг на друга, а разбираются, какая из последовательностей быстрее бежит к нулю и как именно. И в каждом примере будет свой конкретный ответ!

6. В жизни

Закон Ома связывает силу тока, напряжение и сопротивление в цепи. Часто его записывают в такой форме:

Позволим себе пренебречь аккуратным физическим пониманием и формально посмотрим на правую часть как на частное двух чисел. Вообразим, что решаем школьную задачу по электричеству. В условии дано напряжение в вольтах и сопротивление в омах. Вопрос очевиден, решение в одно действие.

А теперь заглянем в определение сверхпроводимости: это свойство некоторых металлов обладать нулевым электрическим сопротивлением.

Ну что, решим задачку для сверхпроводящей цепи? Просто так подставить R = 0 не выйдет, физика подкидывает интересную задачу, за которой, очевидно, стоит научное открытие. И люди, сумевшие поделить на ноль в этой ситуации, получили Нобелевскую премию. Любые запреты полезно уметь обходить!

Математическое правило относительно деления на ноль всем людям рассказывали еще в первом классе общеобразовательной школы. «Делить на ноль нельзя», — учили всех нас и запрещали под страхом подзатыльника делить на ноль и вообще обсуждать эту тему. Хотя некоторые учителя младших классов все-таки пробовали объяснить на простейших примерах, почему нельзя делить на ноль, но эти примеры были настолько нелогичны, что проще было просто запомнить это правило и не задавать лишних вопросов. Но все эти примеры были нелогичными по той причине, что логически объяснить это в первом классе нам учителя не могли, так как в первом классе мы и близко не знали, что такое уравнение, а логически это математическое правило объяснить можно только с помощью уравнений.

Все знают, что при делении любого числа на ноль выйдет пустота. Почему именно пустота, мы рассмотрим потом.

Вообще в математике только две процедуры с числами признаются независимыми. Это сложение и умножение. Остальные же процедуры считаются производные от этих двух процедур. Рассмотрим это на примере.

Скажите, сколько будет, например, 11-10? Мы все моментально ответим, что это будет 1. А как мы нашли такой ответ? Кто-то скажет, что это и так понятно, что будет 1, кто-то скажет, что от 11 яблок отнял 10 и посчитал, что получилось одно яблоко. С точки зрения логики все правильно, но вот по законам математики эта задача решается по-другому. Нужно вспомнить, что основными процедурами считаются сложение и умножение, поэтому нужно составить такое уравнение: х+10=11, а только потом х=11-10, х=1. Заметим, что сложение идет на первом месте, а только потом на основе уравнения мы можем отнимать. Казалось бы, зачем столько процедур? Ведь ответ и так очевиден. Но только такими процедурами можно объяснить невозможность деления на ноль.

Например, мы делаем такую математическую задачу: хотим 20 поделить на ноль. Итак, 20:0=х. Чтобы узнать, сколько же будет, нужно вспомнить, что процедура деления вытекает из умножения. Другими словами, деление-это производная процедура от умножения. Поэтому нужно составить уравнение из умножением. Итак, 0*х=20. Вот тут и тупик. Какое бы число мы не множили на ноль, все равно будет 0, но не 20. Вот отсюда и вытекает правило: делить на ноль нельзя. Ноль делить на любое число можно, а вот число на ноль — увы, нельзя.

Отсюда появляется еще один вопрос: а можно ли ноль делить на ноль? Итак, 0:0=х, значит 0*х=0. Это уравнение можно решить. Возьмем, например, х=4, значит 0*4=0. Получается, что если разделить ноль на ноль, получится 4. Но и здесь все не так просто. Если мы возьмем, например, х=12 или х=13, то выйдет тот же ответ (0*12=0). Вообще, какое бы мы число не подставляли, все равно выйдет 0. Поэтому, если 0:0, то получится бесконечность. Вот такая нехитрая математика. К сожалению, процедура деления ноль на ноль тоже бессмысленна.

Вообще, цифра ноль в математике самая интересная. К примеру, все знают, что любое число в нулевой степени дает единицу. Конечно, с таким примером в реальной жизни мы не встречаемся, но вот с делением на ноль жизненные ситуации попадаются очень часто. Поэтому запомним, что делить на ноль нельзя.

Умножение и деление на числа вида 10, 100, 0,1, 0,01 5 класс онлайн-подготовка на Ростелеком Лицей

Умножение чисел на 10, 100

 

 Упражнение. Как умножить число 25,78 на 10?

 

Десятичная запись данного числа – это сокращенная запись суммы. Необходимо расписать ее более подробно:

Таким образом, нужно умножить сумму. Для этого можно просто умножить каждое слагаемое:

Выходит, что.

Можно сделать вывод, что умножить десятичную дробь на 10 очень просто: нужно запятую сдвинуть вправо на одну позицию.

 

Упражнение. Умножить 25,486 на 100.

Умножить на 100 – это то же самое, что и умножить два раза на 10. Иными словами, необходимо сдвинуть запятую вправо два раза:

 

Деление чисел на 10, 100

 

 

Упражнение. Разделить 25,78 на 10.

 

Как и в предыдущем случае, необходимо представить число 25,78 в виде суммы:

Так как нужно поделить сумму, то это эквивалентно делению каждого слагаемого:

Итак, .

Выходит, чтобы разделить на 10, нужно запятую сдвинуть влево на одну позицию. Например:

 

Упражнение. Разделить 124,478 на 100.

Разделить на 100 – это то же самое, что два раза разделить на 10, поэтому запятая сдвигается влево на 2 позиции:

 

Правило умножения и деления на 10, 100, 1000

 

 

Если десятичную дробь нужно умножить на 10, 100, 1000 и так далее, нужно запятую сдвинуть вправо на столько позиций, сколько нулей у множителя.

 

И наоборот, если десятичную дробь нужно поделить на 10, 100, 1000 и так далее, нужно запятую сдвинуть влево на столько позиций, сколько нулей у множителя.

 

Примеры, когда необходимо сдвинуть запятую, а цифр уже не осталось

 

 

Пример 1

 

Умножить на 100 значит сдвинуть запятую вправо на две позиции.

После сдвига можно обнаружить, что после запятой уже нет цифр, а это значит, что дробная часть отсутствует. Тогда и запятая не нужна, число получилось целое.

 

Пример 2

Сдвигать нужно на 4 позиции вправо. Но цифр после запятой всего две. Стоит вспомнить, что для дроби 56,14 есть эквивалентная запись.

Теперь умножить на 10 000 не составляет труда:

Если не очень понятно, почему можно дописать два нуля к дроби в предыдущем примере, то дополнительное видео по ссылке сможет помочь в этом.

 

Эквивалентные десятичные записи

Запись 52 означает следующее:

Если впереди поставить 0, получим запись 052. Эти записи эквивалентны.

Можно ли поставить два нуля впереди? Да, эти записи эквивалентны.

 

Теперь посмотрим на десятичную дробь:

Если приписать ноль, то получается:

Эти записи эквивалентны. Аналогично можно приписать несколько нулей.

Таким образом, к любому числу можно приписать несколько нулей после дробной части и несколько нулей перед целой частью. Это будут эквивалентные записи одного и того же числа.

 

Пример 3

Так как происходит деление на 100, то необходимо сдвинуть запятую на 2 позиции влево. Слева от запятой не осталось цифр. Целая часть отсутствует. Такую запись часто используют программисты. В математике же, если целой части нет, то ставят ноль вместо нее.

 

Пример 4

Сдвигать нужно влево на три позиции, но позиций всего две. Если перед числом написать несколько нулей, то это будет эквивалентная запись.

То есть при сдвиге влево, если цифры кончились, необходимо восполнить их нулями.

 

Пример 5

В данном случае стоит помнить, что запятая всегда стоит после целой части. Тогда:

 

Умножение и деление на 0,1, 0,01, 0,001

 

 

Умножение и деление на числа 10, 100, 1000 – очень простая процедура. Точно так же дело обстоит и с числами 0,1, 0,01, 0,001.

 

 

Пример. Умножить 25,34 на 0,1.

Выполним запись десятичной дроби 0,1 в виде обыкновенной. Но умножить на  – то же самое, что разделить на 10. Поэтому необходимо сдвинуть запятую на 1 позицию влево:

 

Аналогично умножить на 0,01 – это разделить на 100:

 

Пример. 5,235 разделить на 0,1.

Решение данного примера строится аналогичным образом: 0,1 выражается в виде обыкновенной дроби, а делить на  – это все равно, что умножить на 10:

То есть чтобы поделить на 0,1, нужно запятую сдвинуть вправо на одну позицию, что равносильно умножению на 10.

 

Правило умножения и деления на 0,1, 0,01, 0,001

 

 

Умножить на 10 и разделить на 0,1 – это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию.

 

 

Аналогично для 100, 1000 и так далее:

 

Разделить на 10 и умножить на 0,1 – это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию:

 

Аналогично для 100, 1000 и так далее:

 

Решение примеров

 

 

1. 

 

 

2. 

 

3. 

 

4. 

 

5. 

 

6. 

 

7. 

 

8. 

 

Вывод

 

На этом уроке было изучено правила деления и умножения на 10, 100 и 1000. Кроме того, были рассмотрены правила умножения и деления на 0,1, 0,01, 0,001.

Примеры на применения данных правил были рассмотрены и решены.

 

Список литературы

1. Виленкин Н.Я. Математика: учеб. для 5 кл. общеобр. учр. 17-е изд. – М.: Мнемозина, 2005.

2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011.

3. Ершова А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006.

4. Хлевнюк Н.Н., Иванова М.В.. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Фестиваль педагогических идей» (Источник)

2. Интернет портал «Matematika-na.ru» (Источник)

3. Интернет портал «School.xvatit.com» (Источник)
 

Домашнее задание

1. Вычислите:

а)  

б)

2. Вычислите:

а)  

б)

3. Сравните значения выражений:

а)  

б)

 

 

Пределы

— Почему можно умножать на ноль

Резюме

Разрешение умножения на $0$ требует, чтобы $0=-0$. Это, по сути, никогда не проблема. Напротив, даже если мы разрешим арифметические операции с $\infty$, разрешение деления на $0$ потребует, чтобы $\infty=-\infty$. Обычно это считается неприемлемым, поскольку не интуитивно понятно и противоречит тому, как мы используем символ $\infty$ в исчислении (и по другим причинам). В ситуациях, когда мы принимаем $\infty=-\infty$, может быть разрешено деление на $0$.

Полное объяснение

Деление на ноль не запрещено, потому что оно всегда дает один и тот же ответ. Нет ничего плохого в операции, которая всегда дает один и тот же ответ. Это запрещено, потому что всегда есть более одного ответа или ноль ответов, и чтобы деление было полезным, обычно ожидается, что оно даст ровно один ответ.

Понимание того, почему деление на ноль на самом деле запрещено, позволяет быстро понять, почему умножение на ноль разрешено , поскольку проблемные ситуации, возникающие при попытке деления на ноль, не относятся к попытке умножения на ноль.

• Когда $x\neq0$, «$x/0$» не может оцениваться ничем, что является числом в обычном арифметическом смысле слова «число». В конце концов, произведение любого числа на $0$ равно $0$ и, таким образом, не будет равно $x$ при $x\neq0$.

• Когда $x=0$, «$x/0$» может быть любым числом в обычном арифметическом смысле слова «число». В конце концов, произведение любого числа на $0$ равно $0$.

Допущение бесконечности наряду с конечными числами на самом деле не сильно улучшает ситуацию; само по себе использование бесконечностей, как если бы они были числами, не устраняет проблемы, препятствующие делению на ноль. Предположим, что $x/0=\infty$. Поскольку $0=-0$,

$$\frac{x}{0} = \frac{x}{-0} = -\frac{x}{0} = -\infty.$$

Тогда мы есть $\infty=-\infty$.

Интуитивно говоря, независимо от того, сколько раз вы прибавляете $0$ к $0$, даже бесконечно много раз, нет причин думать, что склонность к достижению большего значения больше, чем склонность к достижению меньшего значения. $\infty$ иногда означает «очень большое положительное число» (при этом $-\infty$ принимает значение «очень большое отрицательное число»). А $0$ иногда означает «очень маленькое число». Но $0$ не означает конкретно «очень маленькие положительное число .»

Есть три способа решить проблему, состоящую в том, что простое деление на $0$ с получением $\infty$ превращает $\infty=-\infty$ в теорему.

1. Не допускать деления на $0$, даже если рассматривать $\infty$ и $-\infty$ как числа — например, даже при использовании (аффинно) расширенной вещественной прямой. Это типичный подход. Это не требует, чтобы мы прекращали умножив на $0$, начиная с , хотя часто трудно сказать $\infty=-\infty$, по сути всегда нормально, что $0=-0$ .

2. Принять, что $\infty=-\infty$. Это подход проективной вещественной прямой и сферы Римана.

3. Отклонение отрицательных чисел. Если нет отрицательных чисел, то разумно и естественно разрешать арифметические операции с $\infty$, считая $-\infty$ бессмысленными или неопределенными. Тогда к $0$ можно приблизиться только справа (т. е. с положительной стороны числовой прямой), и частные, подобные $1/0$, как и все другие частные в такой системе, гарантированно положительны, если они определены.

На самом деле мы редко хотим, чтобы делилось на 0$. В конце концов, $0/0$ по-прежнему будет неопределенным (или ему будет разрешено быть любым числом), так что цель деления чего угодно на что угодно еще не достигнута. Но мы очень часто хотим, чтобы числа могли быть отрицательными. И обычно нам нравится различать $\infty$ и $-\infty$ (чтобы, например, мы могли думать о пределе, который «расходится до бесконечности», и пределе, который «расходится до отрицательной бесконечности», как «равный» различным бесконечные значения). 92$. Что означает $1001$?
(Это должно проиллюстрировать вездесущность умножения на ноль.)

В шкафу Сэма только 5 сумок и вещи в сумках. Ни в одном из мешков нет яблок. (Или: в каждом мешке нет яблок.) Сколько яблок в шкафу Сэма?

Мэри и Билли едут вперед по прямой дороге, начиная с отметки «10 миль». Они прибывают бок о бок к отметке на шоссе «70 миль». Перед ними маркеры миль с более высокими значениями. Мэри продолжает ехать со скоростью 60 миль в час, в то время как Билли продолжает двигаться с такой медленной скоростью, что можно подумать, что он вообще не двигается. Как далеко от того места, где они начали, Мэри и Билли спустя три часа? (Вы можете предположить, что все отметки миль точны.)

Фрэнни обнаружила, что независимо от того, сколько раз она прибавляет к себе $0$, в сумме она получает $0$. В частности, для всех положительных целых чисел $n$, которые она пробовала, сумма $0 + 0 + … + 0$ с членами $n$ дает $0$. Есть ли общее утверждение об умножении на $0$, которое вы могли бы дать Фрэнни, чтобы объяснить (или охарактеризовать) ее результаты?

Краткое изложение алгебры — Темы предварительного исчисления

Темы в

ПРЕДВАРИТЕЛЬНАЯ РАБОТА

Содержание | Дом

1

Студент, прошедший курс алгебры, найдет здесь полный обзор. Студент, который сейчас проходит такой курс, увидит, что в магазине.

АЛГЕБРА — это метод письменных вычислений. А что такое расчет, как не замена одного набора символов другим? В арифметике мы заменяем «2 + 2» на «4». В алгебре мы можем заменить ‘ на  + (− b )’ с ‘ a  —  b .’

a + (− b ) = a − b .

Мы называем это формальным правилом. Он показывает, как выражение, написанное в одной форме, может быть заменено другой формой. Знак = означает, что «может быть переписано как» или «может быть заменено на».

Если p и q являются высказываниями (уравнениями), то правило

Если p , затем q ,

или эквивалент

p подразумевает q ,

означает:  Мы можем заменить — в смысле следования — заявление p заявлением q . Например,

x + a = b подразумевает x = b — a .

Это означает, что мы можем следовать утверждению  ‘ x + a = b ‘ с утверждением » x  =  b  −  a .’

Ибо мы решаем уравнения логической последовательностью утверждений.

Алгебра зависит от того, как все выглядит. Таким образом, мы можем сказать, что алгебра — это система формальных — грамматических — правил. Далее следует то, что нам разрешено писать.

(См. полный курс «Навыки алгебры»)

11. Аксиомы равенства

а = а		Личность
Если a = b , то b = a .		Симметрия
Если a = b и b = c , то a = c .		Транзитивность

Невозможно дать явное определение слова «равно» или его символа = . Однако эти правила являются неявным определением. Значение «равно» подразумевает эти три правила.

О том, как правило симметрии проявляется на практике, см. в Уроке 6 Алгебры. Правило симметрии применяется ко всем приведенным ниже правилам.

12.  Коммутативные правила сложения и умножения

а + б	=	б + а
а ·   б	=	б ·   а

13. Тождественные элементы сложения и умножения:

3. 0 и 1

а + 0 = 0 + а = а

a ·  1 = 1 ·   a = a

Таким образом, если мы «действуем» над числом с элементом идентичности,
возвращает это число без изменений.

14. Аддитивная обратная a :  − a

a + (− a ) = — a + a = 0

«Обратное» число отменяет то, что делает число.
Например, если вы начинаете с 5 и прибавляете 2, то чтобы вернуться к 5, вы должны добавить -2. Добавление 2 + (-2) тогда равносильно добавлению 0, что является тождеством.

15. Мультипликативное обратное или обратное число a ,
5.    обозначается как	1 а	( а 0)

и ·

1 а

=

1 а

·   и

= 1,

Два числа называются обратными друг другу, если их произведение равно 1.
Таким образом, 1/ a символизирует то число, которое при умножении на a , производит 1.

Обратное значение

р к

это

к р

.

16.  Алгебраическое определение вычитания

а − б = а + (− б )

Вычитание в алгебре определяется как сложение обратного.

17. Алгебраическое определение деления

а б

=

а ·

1 б

Деление в алгебре определяется как умножение по взаимному согласию.
Следовательно, в алгебре есть две основные операции: сложение и умножение.

18. Обратное к обратному

− (− a ) = a

19. Отношение b − a к a − b

б — а = -( а — б )

Сейчас,   b + a  равно к a + b . Но b − a — это отрицательное число числа a − b .

10. Правило знаков для умножения, деления и
10. дроби

a (− b ) = − a b . (− a ) b = − a b . (− a )(− b ) = аб.

а − б

= −

а б

.

− а    б

= −

а б

.

− а − б

=

а б

.

«Подобные знаки дают положительное число, в отличие от знаков — отрицательное».

11. Правила для 0

a ·  0 = 0 ·   a = 0,

Если а 0, то

0 и

= 0,

а 0

= Нет значения.

0 0

= Неопределенный.

Деление на 0 является исключенной операцией. (Навык алгебры, урок 5.)

12. Умножение/факторинг

м ( а + б ) = м а + м б	Распределительное правило/
	Общий коэффициент
( x − a )( x − b ) = x 2 − ( a + b ) x + ab
	Квадратичный трехчлен
( a ± b ) 2 = a 2 ± 2 ab + b 2	Совершенный квадратный трехчлен
( a + b )( a − b ) = a 2 2 2 20734 − б 2	Разница
	два квадрата
( A ± B ) (A 2 AB + B 2 ) = A B 2 ) = A B 2 ) = A B 2 ).	Сумма или разница
	два кубика

13. Одинаковая операция с обеими частями уравнения

Если					Если
	и	=	б ,			и	=	б ,
затем				, затем
a + c		=	б + в .			ак	=	б в .

Мы можем прибавить одно и то же число к обеим частям уравнения;
мы можем умножить с обеих сторон на одно и то же число.

14. Смена знака в обеих частях уравнения

Если
	− и	=	б ,
затем
	и	=	− б .

Мы можем изменить любой знак в обеих частях уравнения.

15. Смена знака в обеих частях неравенства:
15. Смена смысла

Если
	и		б ,
затем
	− и	>	− б .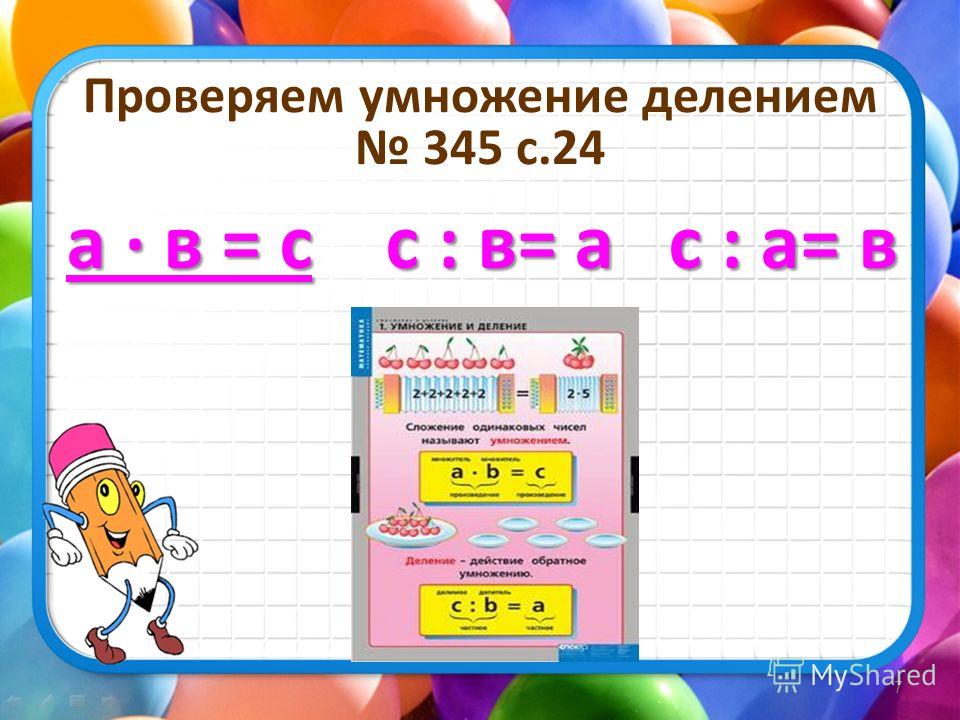

Когда мы меняем знаки в обеих частях неравенства, мы должны изменить смысл неравенства.

16. Четыре формы уравнений, соответствующие
16. Четыре операции и их обратные

Если					Если
	x + a	=	б ,			x − a	=	б ,
затем					, затем
	х	=	б − а .			х	=	а + б .

Если					Если
	топор	=	б ,			x     a	=	б ,
затем					, затем
	х	=	б а	.		х	=	аб .

См. «Навыки алгебры», урок 9..

17. Изменение смысла при решении неравенства

Если
	− топор	б,
затем
	х	> −	б а	.

18. Абсолютное значение

Если  | х | = b , тогда x = b или x = − b .

Если  | х | < b  тогда − b < x < б .

Если  | х | > b   (и b > 0), затем  x > b  или x < − b .

19. Принцип эквивалентных дробей

х у		=	топор ай
и симметрично,
топор ай		=	х у

Мы можем умножить и числитель, и знаменатель на один и тот же коэффициент; мы можем разделить оба на общий множитель.

20. Умножение дробей

а б	·	в г	=	ак бод
а ·		в г	=	ак д

21. Деление дробей (сложные дроби)

Деление — это умножение на обратное.

22. Сложение дробей

	+	б с	=	а + б     в	Тот же знаменатель
а б	+	в г	=	ад + бк     бд	Различные знаменатели с без общих делителей
а   до н. э.	+	е   cd	=	объявление + будет     bcd	Различные знаменатели с общими делителями

Общий знаменатель — НОК знаменателей.

23.  Правила показателей

а м а n	=	а м+н		Умножение или деление
а м а 0 n	=	а м-н		степени того же основания
( аб ) п	=	а н б н		Мощность произведения факторов
( a м ) n	=	а мин		Сила силы

24.  Определение отрицательного показателя степени

а − п

=

1  а п

25. Определение показателя степени 0

а ⁰ = 1

26.  Определение корня квадратного

Из квадратного корня в квадрате получается подкоренное число.

27.  Уравнения вида   a ² = b

Если
а 2		=	б ,
затем
и		=	±.

28. Умножение/факторизация радикалов

		=
и симметрично,
		=

29.  Определение n -го корня

30.  Определение рационального показателя

Умелее сначала рутировать.

31. Законы логарифмов

log xy  =  log x  +  log y .

журнал

х у

= log x  —  log y .

логарифм x ⁿ  =  n логарифм x .

журнал 1 = 0,

бревно б б = 1.

32. Определение сложной единицы i

i ² = −1

Следующая тема: Рациональные и иррациональные числа

Содержание | Дом

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: [email protected]

Объясните, почему правила деления целых чисел совпадают с правилами умножения целых чисел.

Умножение целых чисел делением

Эмма О.

спросил 20.06.16

Я вообще не понимаю этого. Если бы вы могли объяснить это подробно, я был бы очень признателен. Это для летнего урока по алгебре, который я посещаю, чтобы продвинуться вперед.

Подписаться І 6

Подробнее

Отчет

4 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Дэвид В. ответил 20.06.16

Репетитор

4. 7 (89)

Опытный профессор

Об этом репетиторе ›

Об этом репетиторе ›

Ключевое понятие здесь ВЗАИМНОЕ .

 

Число 1/x является обратным числом x.

 

Когда значение y умножается на (1/x), , мы можем записать выражение как y/x, что равно y, деленному на x . Операция умножения следует тем же правилам, что и операция деления [потому что это одна и та же операция, выраженная по-разному].

 

Примечание PLZ (поскольку вы упомянули целые числа): правила целочисленного деления обычно игнорируют остаток и сохраняют частное (например, 10\3 равно 3; «\» используется некоторыми компьютерными языками для целочисленного деления) .

Голосовать за 1 Голосовать против

Подробнее

Отчет

Ира С. ответил 20.06.16

Репетитор

5,0 (298)

Двуязычный репетитор по математике и многое другое

Смотрите таких репетиторов

Смотрите таких репетиторов

Вот как вообще работают подразделения. На самом деле деление и умножение являются операциями одного уровня в порядке операций по одной и той же причине.

 

Любую задачу на деление можно превратить в задачу на умножение!!!

 

Подумайте о делении дробей.

 

8 ÷ 1/2 = 8*2/1.

12 ÷ 2/3 = 12 * 3/2

 

Итак, поскольку деление можно преобразовать в умножение, оно должно подчиняться тем же правилам, что и умножение.

 

Надеюсь, это помогло.

Голосовать за 1 Голосовать против

Подробнее

Отчет

Майкл Дж. ответил 20.06.16

Репетитор

5 (5)

Применение простой математики в повседневной жизни

См. таких репетиторов

Смотрите таких репетиторов

отрицательное, умноженное на отрицательное, будет положительным

отрицательное, умноженное на положительное, будет отрицательным

положительное, умноженное на положительное, будет положительным

 

Умножение обратно делению. Если умножение следует этим правилам, то оно работает в обратном порядке. Обратным путем, конечно же, будет деление.

Голосовать за 1 Голосовать против

Подробнее

Отчет

Кеннет С. ответил 20.06.16

Репетитор

4,8 (62)

Экспертная помощь по алгебре/триггерам/(пред)исчислению для гарантии успеха в 2018 году

См.