Двоичная арифметика : сложение, вычитание, умножение, деление

 

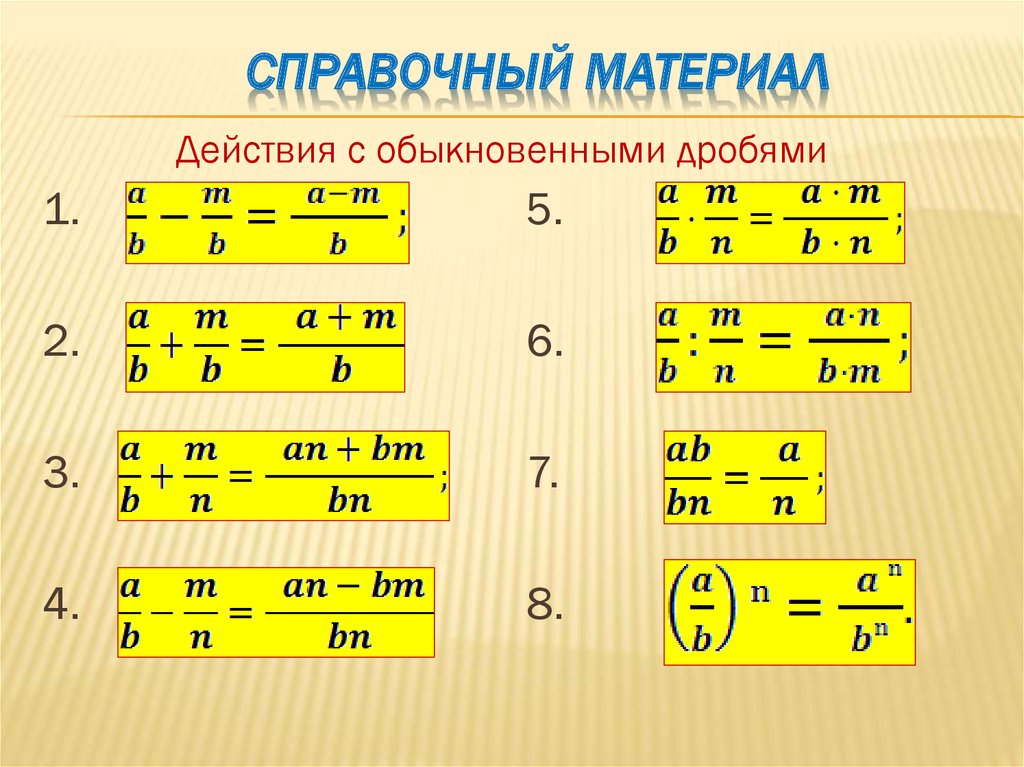
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.

Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.

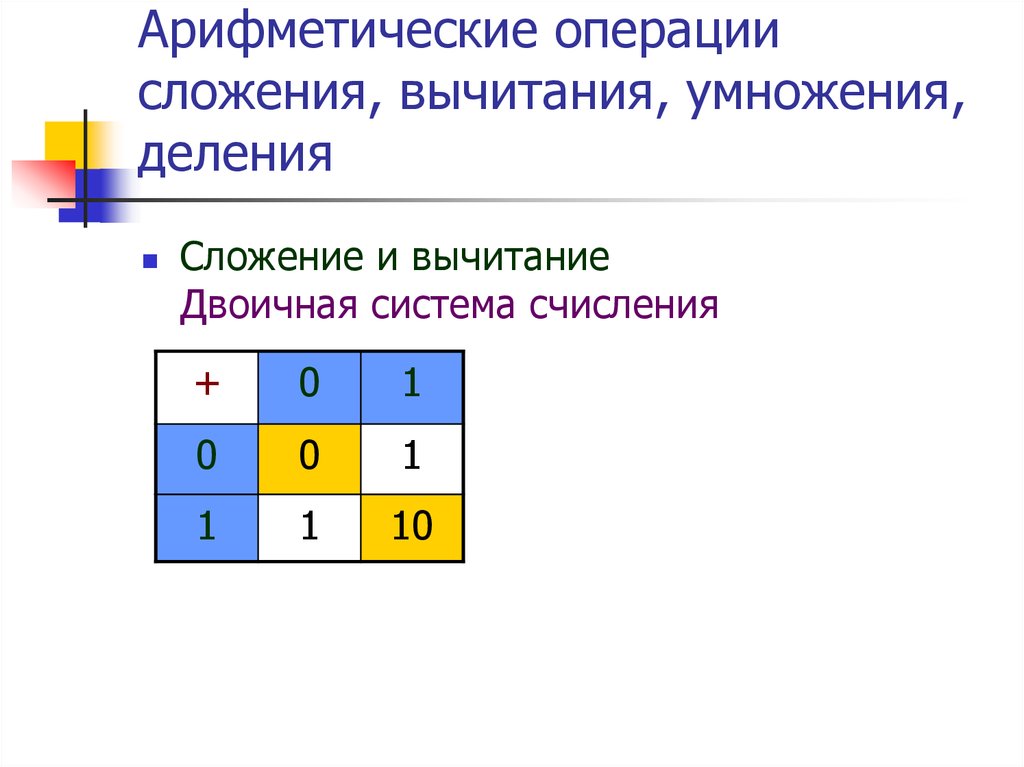
Таблица сложения, вычитания и умножения для двоичной системы счисления

Сложение	Вычитание	Умножение
0 + 0 = 0	0 — 0 = 0	0 ∙ 0 = 0
0 + 1= 1	1 — 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 — 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 — 1 = 1	1 ∙ 1 = 1

Сложение двоичных чисел

Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

Пример: 1011,1₂ + 1010,11₂

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,1₂ + 111₂ + 101,1₂

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 100₂. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 101₂. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.

Вычитание двоичных чисел

В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,01₂ — 1001,1₂

Умножение и деление двоичных чисел

Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 101111011₂ в десятичную систему счисления.
Поскольку 10₁₀ = 1010₂, запишем

Полученные остатки,  1001₂ = 9₁₀,  =111₂ = 7₁₀,  11₂ = 3₁₀. Искомое число 101111011₂ = 379₁₀.

Назад: Представление данных и архитектура ЭВМ

почему на 0 делить нельзя

«Делить на ноль нельзя! » — большинство школьников заучивает это правило наизусть, не задаваясь вопросами.

Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему? » А ведь на самом деле очень интересно и важно знать, почему же нельзя.

Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.

Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.

Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.

Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.

Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение. ) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.

Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.

Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности» , но в арифметике таких случаев не встречается. )

Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль.

правил арифметических операций — MATLAB & Simulink

Арифметика с фиксированной запятой относится к тому, как выполняются операции с двоичными словами со знаком или без знака. Простота арифметических функций с фиксированной точкой, таких как сложение и вычитание позволяет реализовать экономичное аппаратное обеспечение.

В следующих разделах описываются правила, которым следует программное обеспечение Simulink

® при выполнении арифметических операций над входными данными и параметры. Эти правила организованы в четыре группы в зависимости от задействованных операций: сложение и вычитание, умножение, деление и сдвиги. Для каждого из этих четырех группы, правила выполнения указанной операции представлены на примере используя правила.

Вычислительные блоки

Базовая архитектура многих процессоров содержит несколько вычислительных блоков включая арифметико-логические устройства (ALU), устройства умножения и накопления (MAC) и оборотни. Эти вычислительные блоки обрабатывают двоичные данные напрямую и обеспечивают поддержка арифметических вычислений различной точности. АЛУ выполняет стандартный набор арифметических и логических операций, а также деление. MAC выполняет операции умножения, умножения/сложения и умножения/вычитания. Перевертыш выполняет логические и арифметические сдвиги, нормализацию, денормализацию и другие операции.

Сложение и вычитание

Сложение — наиболее распространенная арифметическая операция, выполняемая процессором. Когда двое n-битные числа складываются вместе, всегда можно получить результат с n + 1 ненулевые цифры из-за переноса самой левой цифры. Для двух дополнений сложения двух чисел, следует рассмотреть три случая:

• Если оба числа положительные и результат их сложения имеет знак бит 1, то произошло переполнение; в противном случае результат правильный.

• Если оба числа отрицательные и знак результата равен 0, то произошло переполнение; в противном случае результат правильный.

• Если числа имеют разные знаки, переполнение не может произойти и результатом будет всегда правильно.

Процесс суммирования блоков Simulink с фиксированной точкой

Рассмотрим суммирование двух чисел. В идеале, реальные значения подчиняются уравнение

Va=±Vb±Vc,

, где В _b и В _c — входные значения, а В _a — выходное значение. Чтобы увидеть, как суммирование на самом деле реализованы, три идеальных значения должны быть заменены общим [Наклон Схема кодирования Bias] описана в Scaling:

Vi=Fi2EiQi+Bi.

Уравнение Дополнительно дает решение полученного уравнение для сохраненного целого числа, Q _и . Используя обозначения сокращения, это уравнение становится

QA = ± FSB2EB -EAQB ± FSC2EC -EAQC+BNET,

, где F _SB и F _SC являются скорректированными фракциями и _SC — это скорректированные фракционные и _SC — это скорректированные фракционные и _SC . это чистое смещение. Офлайн-конверсии и онлайн преобразования и операции обсуждаются ниже.

Офлайн-конверсии. Ф _сб , Ф _сб и B _net вычисляются в автономном режиме с использованием округления до ближайшего и насыщенность. Кроме того, B _net хранится с использованием типа выходных данных.

Онлайн-преобразования и операции. Остальные операции выполняются в режиме онлайн с фиксированной точкой процессор, и зависят от наклонов и смещений для входных и выходных данных типы. Наихудший (наиболее неэффективный) случай имеет место, когда наклоны и смещения не совпадают. Наихудшие преобразования и операции задаются этими шагов:

1. Начальное значение для Q _a задается чистым смещением, B _net :

   Qa=Bnet.

2. Первое введенное целочисленное значение, Q _b , умножается на скорректированный наклон, F _sb :

   QRawProduct=FsbQb.

3. Предыдущий продукт преобразуется в модифицированный тип выходных данных, где наклон равен единице, а смещение равно ноль:

   QTemp=конвертировать(QRawProduct).

   Это преобразование включает любой необходимый сдвиг битов, округление или обработка переполнения.

4. Выполняется операция суммирования:

   Qa=Qa±QTemp.

   Это суммирование включает любую необходимую обработку переполнения.

5. Шаги со 2 по 4 повторяются для каждого номера суммироваться.

Важно отметить, что битовый сдвиг, округление и обработка переполнения применяются к промежуточным шагам (3 и 4), а не ко всему сумма.

Дополнительные сведения см. в разделе Процесс суммирования.

Оптимизация моделирования и сгенерированного кода

Если масштабирование входных и выходных сигналов совпадает, количество операции суммирования сведены к худшему (наиболее неэффективному) случаю. Для Например, когда вход имеет тот же дробный наклон, что и выход, шаг 2 сводится к умножению на единицу и может быть устранено. Тривиальные шаги в процесс суммирования исключается как для моделирования, так и для генерации кода. Эксклюзивное использование масштабирования только двоичной точки как для входных сигналов, так и для выходных сигналы — это распространенный способ устранения несовпадающих наклонов и смещений, а результаты в наиболее эффективных симуляциях и сгенерированном коде.

Умножение

Результат умножения n-битного двоичного числа на m-битное двоичное число в продукте длиной до m + n битов как для слов со знаком, так и для слов без знака. Большинство процессоров выполняют n-битное умножение на n-битное и дают 2n-битный результат. (двойные биты) при условии отсутствия переполнения.

Процесс умножения блоков Simulink с фиксированной точкой

Рассмотрим умножение двух чисел. В идеале реальные значения подчиняться уравнению

Va=VbVc.

, где В _b и В _c — входные значения, а В _a — выходное значение. Чтобы увидеть, как умножение на самом деле реализованы, три идеальных значения должны быть заменены общим [Наклон Схема кодирования Bias] описана в Scaling:

Vi=Fi2EiQi+Bi.

Решение полученного уравнения для выходного сохраненного целого числа, Q _a , приведен ниже:

Qa=FbFcFa2Eb+Ec-EaQbQc+FbBcFa2Eb-EaQb+FcBbFa2Ec-EaQc+BbBc-BaFa2-Ea.

Умножение с ненулевыми смещениями и несовпадающими дробями Склоны. Реализация приведенного выше уравнения в наихудшем случае имеет место, когда наклоны смещения входного и выходного сигналов не совпадают. В таких случаях, требуется несколько низкоуровневых целочисленных операций для выполнения высокоуровневое умножение (или деление). Выбор реализации, сделанный в отношении эти низкоуровневые вычисления могут повлиять на вычислительную эффективность, ошибки округления и переполнение.

В блоках Simulink фактическая операция умножения или деления всегда выполняется с переменными с фиксированной точкой, которые имеют нулевые смещения. Если вход имеет ненулевое смещение, оно преобразуется в представление, имеющее масштабирование только с двоичной точкой перед операцией. Если результат должен быть ненулевое смещение, операция сначала выполняется с временными переменными, которые иметь масштабирование только с двоичной точкой. Затем результат преобразуется в данные тип и масштаб конечного вывода.

Если и входы, и выход имеют ненулевые смещения, то операция разбивается следующим образом:

V1Temp=V1,V2Temp=V2,V3Temp=V1TempV2Temp,V3=V3Temp,

, где

V1Temp=2E1TempQ1Temp,V2Temp=2E2TempQ2Temp,2E3Temp.

Эти уравнения показывают, что временные переменные имеют только двоичную точку масштабирование. Однако в уравнениях не указывается знаковость, слово длины или значения фиксированного показателя степени этих переменных. Программное обеспечение Simulink присваивает эти свойства временным переменным. исходя из следующих целей:

• Представляет исходное значение без переполнения.

  Тип данных и масштаб исходного значения определяют максимальное и минимальное реальное значение:

  VMax=F2EQMaxInteger+B,

  VMin=F2EQMinInteger+B.

  Тип данных и масштабирование временного значения должны быть в состоянии представляют этот диапазон без переполнения. Возможна потеря точности, но переполнение никогда не допускается.

• Используйте тип данных, обеспечивающий эффективность операций.

  Эта цель связана с целью, которую вы будете использовать для развертывание вашего дизайна в производстве. Например, предположим, что вы будет реализовывать проект на 16-битном процессоре с фиксированной точкой, который предоставляет 32-битный long , 16-битный целое и 8-битное короткое или символ . Для такой цели сохранение эффективность означает, что используется не более 32 бит, а меньший используются размеры 8 или 16 бит, если они достаточны для поддержания точность.

• Поддерживайте точность.

  В идеале все возможные значения, определенные исходным типом данных и масштабирование прекрасно представлено временной переменной. Однако для этого может потребоваться больше битов, чем эффективно. Биты отбрасывается, что приводит к потере точности в той мере, в какой это требуется для сохранения эффективности.

Например, рассмотрим следующее, предполагая, что 16-разрядный микропроцессор target:

VOriginal=QOriginal+-43.25,

, где Q _Original — это 8-битный беззнаковый тип данных. Для этих данных тип,

QMaxInteger=225, QMinInteger=0,

, поэтому

VMax=211,75, VMin=-43,25.

Минимально возможное значение отрицательное, поэтому временная переменная должна быть целочисленный тип данных со знаком. Исходная переменная имеет наклон 1, но смещение выражается с большей точностью двумя цифрами после двоичного точка. Чтобы получить полную точность, фиксированный показатель степени временной переменной должно быть -2 или меньше. Программное обеспечение Simulink выбирает наименьшую возможную точность, т. как правило, наиболее эффективен, если не возникают проблемы с переполнением. Для масштабирования 2 ^-2 , выбор знакового 16-битного или знакового 32-битного позволяет избежать переполнения. Для эффективности программное обеспечение Simulink выбирает меньший выбор из 16 бит. Если исходная переменная является входной, затем уравнения для преобразования в временная переменная:

uint8_T  QOriginal, uint16_TQTemp,   QTemp=((int16_T)QOriginal≪2)−173.

Умножение с нулевыми смещениями и несовпадающими дробными наклонами. Когда смещения равны нулю, а дробные наклоны не совпадают, реализация сокращается до

Qa=FbFcFa2Eb+Ec-EaQbQc.

Преобразования в автономном режиме

Количество

FNet=FbFcFa

рассчитывается в автономном режиме с использованием округления до ближайшего и насыщения. F _Net сохраняется с использованием типа данных с фиксированной точкой формы

2EnetQnet,

, где E _Net и Q _NET выбираются автоматически для Best F_{88004004.9004.} . Выбираются автоматически для Best F _NET выбираются для Best. .

Онлайн-преобразования и операции

1. Целочисленные значения Q _b и Q _c умножаются:

   QRawProduct=QbQc.

   Для обеспечения полной точности продукта двоичная точка Q _RawProduct определяется как сумма двоичных точек Q _b и Q _c .

2. Предыдущий продукт преобразуется в выходной тип данных:

   QTemp=конвертировать(QRawProduct).

   Это преобразование включает любой необходимый сдвиг битов, округление или обработка переполнения. Преобразование сигналов обсуждает преобразования.

3. Выполняется умножение

   Q2RawProduct=QTempQNet

   .

4. Предыдущий продукт преобразуется в выходной тип данных:

   Qa=convert(Q2RawProduct).

   Это преобразование включает любой необходимый битовый сдвиг, округление или обработка переполнения. Преобразование сигналов обсуждает преобразования.

5. Шаги с 1 по 4 повторяются для каждого дополнительное число, которое нужно умножить.

Умножение с нулевыми смещениями и сопоставлением дробных наклонов. Когда смещения равны нулю и дробные наклоны совпадают, реализация сокращается до

Qa=2Eb+Ec-EaQbQc.

Офлайн-преобразования

Офлайн-преобразования не выполняются.

Онлайн-преобразования и операции

1. Целочисленные значения Q _b и Q _c умножаются:

   QbProduct=

   QRawProduct.

   Для обеспечения полной точности продукта двоичная точка Q _RawProduct определяется как сумма двоичных точек Q _b и Q _c .

2. Предыдущий продукт преобразуется в тип выходных данных:

   Qa=convert(QRawProduct).

   Это преобразование включает любой необходимый сдвиг битов, округление или обработка переполнения. Преобразование сигналов обсуждает преобразования.

3. Шаги 1 и 2 повторяются для каждого дополнительного число, которое нужно умножить.

Дополнительные сведения см. в разделе Процесс умножения.

Деление

В этом разделе обсуждается деление величин с нулевым смещением.

Процесс деления блоков Simulink с фиксированной точкой

Рассмотрим деление двух чисел. В идеале, реальные значения подчиняются уравнение

Va=Vb/Vc,

, где В _b и В _c — входные значения, а В _a — это выходное значение. Чтобы увидеть, как деление на самом деле реализованы, три идеальных значения должны быть заменены общим [Наклон Схема кодирования Bias] описана в Scaling:

Vi=Fi2EiQi+Bi.

Для случая, когда поправочные коэффициенты наклона равны единице, а смещения равны ноль для всех сигналов, решение полученного уравнения для выхода сохраненное целое число, Q _a , дается следующее уравнение:

Qa=2Eb-Ec-Ea(Qb/Qc).

Это уравнение включает целочисленное деление и некоторые битовые сдвиги. Если E _a  >  E _b – E _c , то любые битовые сдвиги вправо и реализация просто. Однако, если E _a  <  E _b – E _c , то битовые сдвиги происходят влево и реализация может быть сложнее. Существенная проблема заключается в том, что на выходе больше точность, чем обеспечивает целочисленное деление. Чтобы получить полную точность, нужно дробное деление. Программирование на C язык предоставляет доступ к целочисленному делению только для типов данных с фиксированной точкой. В зависимости от размера числителя можно получить некоторые дробные битов, выполняя сдвиг перед целочисленным делением. В худшем случае это может быть необходимо прибегнуть к повторным вычитаниям в программном обеспечении.

Как правило, деление значений — это операция, которой следует избегать в встроенные системы с фиксированной точкой. Деление, где результат имеет большую точность, чем целочисленное деление (т. е. E _a  <  E _b – E _c ) следует использовать с еще большей неохотой.

Для получения дополнительной информации см. Процесс разделения.

Смены

Почти все микропроцессоры и цифровые сигнальные процессоры поддерживают четко определенные бит-сдвиг (или просто сдвиг ) операций для целых чисел. Например, рассмотрим 8-битное целое число без знака 00110101. Результаты 2-битный сдвиг влево и 2-битный сдвиг вправо показаны на следующую таблицу.

Shift Operation	Binary Value	Decimal Value
No shift (original number)	00110101	53
Shift влево на 2 бита	11010100	212
Сдвиг вправо на 2 бита 7 03	13

Вы можете выполнить сдвиг, используя Simulink Сдвиг арифметического блока. Использовать это

Сдвиг битов вправо

Частный случай сдвига битов вправо требует рассмотрения обработка самого левого бита, который может содержать информацию о знаке. Переход к право может быть классифицировано либо как логический сдвиг вправо или арифметический сдвиг вправо. Для логического сдвига вправо 0 включается в самый старший бит для каждого битового сдвига. Для арифметический сдвиг вправо, старший бит перерабатывается для каждого бита сдвиг.

Блок Shift Arithmetic выполняет арифметический сдвиг вправо и, следовательно, перерабатывает старший бит для каждого битового сдвига вправо. Например, учитывая число с фиксированной точкой 11001,011 (-6,625), сдвинутое на два разряда вправо с неподвижной двоичной точкой дает число 11110,010 (-1,75), как показано на модель ниже:

Для выполнения логического сдвига вправо числа со знаком с помощью арифметического сдвига блок, используйте блок преобразования типа данных, чтобы привести число как беззнаковое число эквивалентной длины и масштабирования. Этот модель показывает, что число фиксированной точки со знаком 11001,001 (-6,625) становится 00110.010 (6.25).

Вы щелкнули ссылку, соответствующую этой команде MATLAB:

Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Обратитесь в местное представительство

Правило знаков — Math28

Содержание

Определение положительного или отрицательного знака

Знаки, сопровождающие числа, очень важны, так как они указывают, положительное это число или отрицательное. Чтобы определить, является ли число положительным, слева от числа ставится крест, хотя во многих случаях знак не ставится, и считается, что оно положительное, с другой стороны, чтобы определить, является ли число отрицательным, средний тире или черта ставится слева от числа.

3 ← Положительный
+ 3 ← Положительный
— 3 ← Отрицательный

Примечание : Для положительного числа слева от числа у нас нет другого числа, которое можно оставить без знака.

В числовой строке вы можете увидеть разницу между числом с положительным знаком и числом с отрицательным знаком.

• -1
• 0
• 1

Ноль считается нейтральным числом, слева от нуля предыдущей строки соответствуют отрицательные числа до самой бесконечности (-inf), а справа от нуля положительные числа до самой бесконечности (+inf). обдуманный

---

Законы или правила знаков

Закон или правило знаков указывает на знак, преобладающий при выполнении операций двух одинаковых или разных знаков, и применяется по-разному для различных математических операций:

Правило знаков для сложения и вычитания

• При сложении двух положительных чисел результат будет иметь положительный знак. 3 + 5 = 8
• При сложении или вычитании двух чисел, одно с положительным знаком, а другое с отрицательным знаком, результат будет иметь знак наибольшего числа. 5 — 6 = — 1
• При сложении или вычитании двух чисел, одно с отрицательным знаком, а другое с положительным знаком, результат будет иметь знак наибольшего числа. — 7 + 4 = — 3
• При вычитании двух отрицательных чисел результат будет иметь отрицательный знак. — 5 — 4 = — 9

Упрощение вышеизложенного:

положительный y положительный = положительный
положительный + отрицательное = наибольшее число
отрицательное + положительное = наибольшее число
отрицательное y отрицательное = отрицательное

Узнать больше о: « Сумма » →

Узнать больше о: « Вычитание » →

Правило знаков для умножения и деления

• При умножении или делении двух положительных чисел результат будет иметь положительный знак.