Порядок действий в математике

Метки

Головоломки Досуг Задачи Логика Математика Смекалка

Порядок выполнения действий в математике нередко становится настоящим камнем преткновения. Мы изучали его в начальных классах школы и, по идее, должны помнить всю жизнь. Но теория, как говорил Мефистофель, суха. Да и кому, по правде говоря, интересны примеры, где порядок действий расписан заранее?

© Depositphotos

Другое дело — задания из нашей подборки. В них тебе дается лишь набор цифр и число, которое нужно получить. А какие действия и в каком порядке выполнять, решать только тебе. И тут уж ответ не вычислишь, а тем более не угадаешь. Ведь для решения необходимо мыслить и творчески, и аналитически. А это помогает нам успешно находить выход из самых сложных жизненных ситуаций.

Порядок действий в математике

1. Начнем с примеров попроще. Поставь в записи 1 * 3 * 2 * 1 * 2 = 10 вместо звездочек знаки арифметических действий, чтобы получилось верное равенство. Попробуй найти как можно больше вариантов решения со скобками и без.
   
2. У тебя есть четыре цифры: 5, 5, 5 и 1. С помощью сложения, вычитания, умножения, деления и скобок получи из них число 24, используя каждую из этих цифр только 1 раз.
   
3. Используя цифры (1, 3, 4, 6), скобки и арифметические операции (сложение, вычитание, умножение, деление), получи число 24. Разрешается использовать только эти цифры и только эти операции. Каждую цифру можно использовать только один раз. Операции и скобки можно использовать любое число раз.© Depositphotos

Ответы

1. Как я уже говорил, тут открывается широкий простор для творчества. Мне сходу удалось найти только одно решение без скобок: 1 + 3 х 2 + 1 + 2 = 10. И одно со скобками: 1 х (3 + 2) х 1 х 2 = 10. Но решений, скорее всего, намного больше. Попробуй найти недостающие!
2. Я предложил эту задачку своим друзьям. И перед тем как назвать верный ответ, расскажу вам об ошибочных, а также весьма остроумных вариантах решения.
   Самый распространенный ответ:5 х 5 – 1 = 24. Был еще такой вариант: 5 + 5 + 5 + 5 + 5 – 1 = 24. Да, ответ в обоих случаях, конечно, 24. Но как быть с условием? В нём четко сказано, что нужно использовать каждую из цифр и только 1 раз!
   © Depositphotos

   Интересное решение за пределами математики предложила девушка бариста. По ее словам, достаточно выпить 5 чашек кофе, затем еще 5 чашек и еще 5 чашек за один день, чтобы получить 24 часа бодрствования. Мы не советуем даже пробовать это повторить. Ведь больше 300 миллилитров бодрящего напитка в день способны навредить твоему здоровью. Но попытка свести воедино математику, кулинарию и физиологию заслуживает всяческого уважения.

   © Pexels

   Возвращаясь к математике, признаюсь, что найти решение для этого примера было очень непросто. У меня оно получилось таким:

   (5 — (1 : 5)) х 5= 24. Но, может, кто-нибудь из наших читателей найдет еще один вариант?

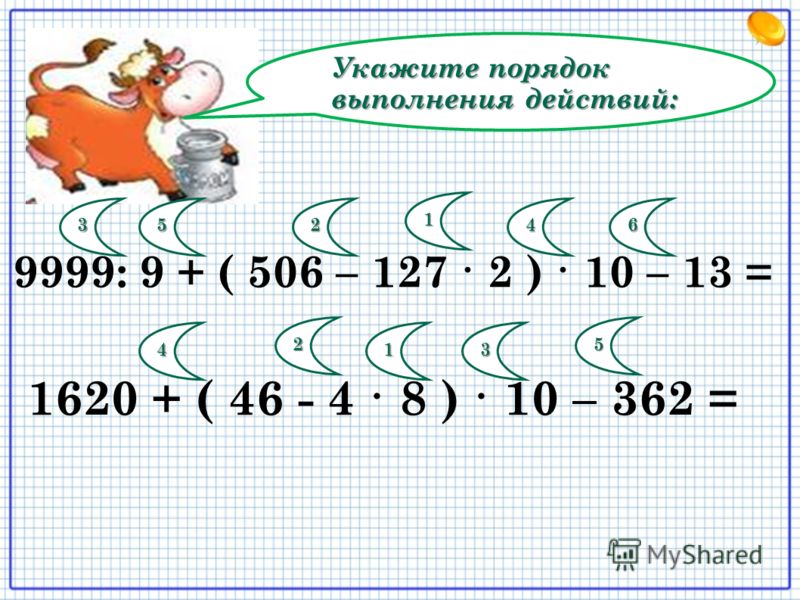
3. Мы уже решили два примера. Поэтому с последним проблем быть не должно. И опять нас выручает деление на дробь:
   6 / ( 1 — ( 3 / 4 ) ) = 24.
   © Pexels

Как видишь, наши забавные задачки помогают провести время с пользой. Ведь сообразительность помогает искать необычные, интересные и простые пути решения, достигая результата не только в игре, но и в реальной жизни кратчайшим путем.

Поделиться

Выполнение арифметических операций. Решение разобранных примеров.

• Альфашкола
• Статьи
• Порядок выполнения арифметических операций

Как правильно вычислить \(\frac{48}{2}(9+3)\) ? Один получает в ответе \(288\), второй \(2\). В таких случаях стоит помнить, что первое действие выполняется в скобках, и здесь важно знать порядок арифметических операций.

 

Порядок арифметических операций — это порядок, в котором все алгебраические выражения должны быть выполнены. Зачастую значение выражения меняется в зависимости от порядка его вычисления. Порядок выполнения арифметических  операций:

1. действия в скобках
2. радикалы, то есть корни
3. умножение и деление
4. сложение и вычитание

Круглые скобки — это изогнутые символы \(()\), которые помещаются вокруг части выражения, чтобы показать, что выражения внутри них должны быть вычислены в первую очередь. В круглых скобках следует соблюдать тот же порядок операций. Сначала вычисляются выражения в скобках, затем корни, то есть радикалы, умножение и деление и в конце сложение и вычитание. Если есть несколько одинаковых арифметических операций, то действия выполняются в порядке слева направо.

---

Пример 1. Вычислить:

 

Сначала выполняем умножение в скобках \(2*8=16\), потом деление \(16:4=4\) и затем сложение \(4+1,2=5,2\).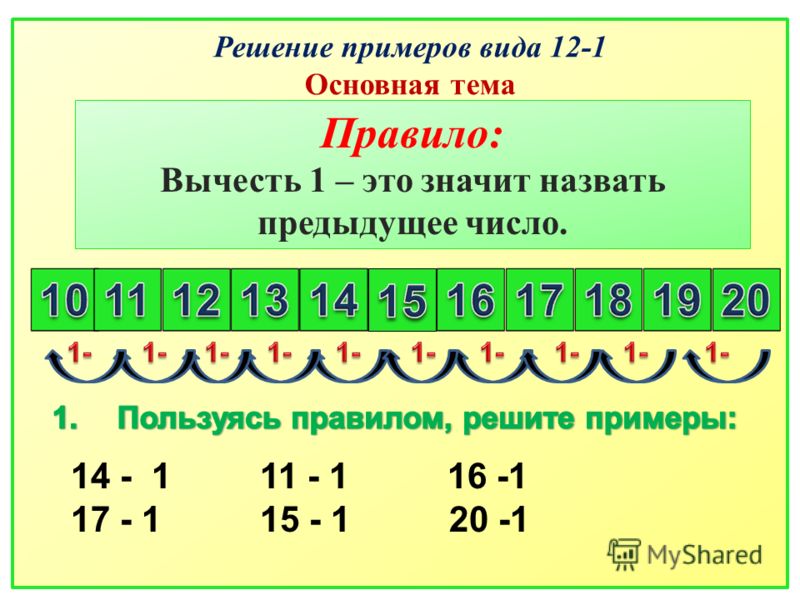 В результате выражения получаем \(5,2.\)

---

Пример 2. Вычислить:

Сначала обратим внимание, что нет скобок и корней, поэтому мы сразу переходим к умножению и делению \(3*3=9\), затем переходим к сложению и вычитанию, работая слева направо \(9-5=4\) и \(4+2=6\) . В результате выражения получаем \(6.\)

Логическое обоснование порядка арифметических операций, помимо скобок, которые, очевидно, являются первыми, заключается в том, что умножение — это повторное сложение, а возведение в степень — это повторное умножение. Кроме того, деление обратно умножению.

Например, выражение:

должно быть решено в следующем порядке: вычисляем выражение в скобках \(6+7=13\), потом выполняем умножение \(2*13=26\) и затем отнимаем от получившегося значения \(82\) и получаем \(-56\). Это и есть наш окончательный результат -56.

Если бы  желаемый порядок решения выражения был бы другим, на основе исходной задачи, то скобки были бы расположены по-другому. Порядок операций очень важен, поэтому вы должны понимать порядок арифметических операций на хорошем уровне.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Сергей Владимирович Туркенич

Репетитор по математике

Стаж (лет)

Образование:

Гомельский государственный университет им. Ф. Скорины

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Тамара Ростиславовна Промская

Репетитор по математике

Стаж (лет)

Образование:

ГГУ им. Я.Купалы

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Владимир Валерьевич Ковалев

Репетитор по математике

Стаж (лет)

Образование:

Пятигорский государственный педагогический институт иностранных языков

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ЕГЭ по математике (базовый уровень)
• Репетитор по геометрии
• Репетитор по химии для подготовки к ЕГЭ
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Репетитор по истории для подготовки к ОГЭ
• ВПР по физике
• ВПР по обществознанию
• Репетитор для подготовки к ЕГЭ по обществознанию
• Подготовка к ЕГЭ по информатике
• Программирование Pascal

Похожие статьи

• Умножения и деление отрицательных чисел
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 2)
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 10)
• Решаем ОГЭ. Задание №16
• ЕГЭ по математике, базовый уровень. Задачи на движение по прямой (вариант 1)
• 5 советов по подготовке к ЕГЭ по математике
• 7 способов избавиться от насморка у детей
• Переход в другую школу: как помочь ребенку справиться со стрессом и влиться в коллектив

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Эта математическая задача стала вирусной, потому что PEMDAS сбивает людей с толку

50,2 тыс.

Просмотров

by Персонал TeachThought

Кажется, каждые несколько недель распространяется математическая задача, которая вызывает спор и становится вирусной, потому что никто не может прийти к единому мнению относительно ответа. И это почти всегда связано с PEMDAS.

Почему PEMDAS так сбивает с толку? Это связано с математикой как своего рода языком. Википедия объясняет PEMDAS:

«В математике и компьютерном программировании порядок операций (или приоритет операций ) представляет собой набор правил, отражающих соглашение о том, какие процедуры следует выполнять в первую очередь, чтобы вычислить данное математическое выражение.

Например, в математике и большинстве компьютерных языков умножение имеет более высокий приоритет, чем сложение, и так было с момента введения современной алгебраической записи. Таким образом, выражение 2 + 3 × 4 интерпретируется как имеющее значение 2 + (3 × 4) = 14, а не (2 + 3) × 4 = 20. С введением показателей степени в 16 и 17 веках они получили приоритет над сложением и умножением и могли быть помещены только как верхний индекс справа от их основания. Таким образом 3 + 5 ²  = 28 и 3 × 5 ²  = 75.

Эти соглашения существуют для устранения двусмысленности обозначений, позволяя при этом быть как можно более краткими. Если желательно переопределить соглашения о приоритете или даже просто подчеркнуть их, можно использовать круглые скобки ( ), чтобы указать альтернативный порядок операций (или просто усилить порядок операций по умолчанию). Например, (2 + 3) × 4 = 20 заставляет сложение предшествовать умножению, а (3 + 5) ²  = 64 заставляет сложение предшествовать возведению в степень. Если в математическом выражении требуется несколько пар круглых скобок (например, в случае вложенных круглых скобок), круглые скобки могут быть заменены скобками или фигурными скобками, чтобы избежать путаницы, как в [2 × (3 + 4)] – 5 = 9».

См. также 12 вопросов, которые помогут учащимся представить себя мыслителями

Эта математическая задачка стала вирусной, потому что PEMDAS сбивает людей с толку

Так в чем же проблема? Во-первых, твиттер и характер дезинформации и разногласий, а также тип контента, которым с большей вероятностью будут делиться. Вот последний пример.

6/2(1+2)
6/2*(1+2)
6/2*3
3*3
9

PEMDAS слева направо pic.twitter.com/vQQXZ6GbQ8

— медвежонок tae-dy ⁷ (@thebangtanbabie) 13 ноября 2020 г.

Социальные сети были созданы для обмена мнениями и разногласий, так что мы здесь. Как мы уже упоминали, они часто становятся вирусными, и в 2019 году доктор философии по математике Университета Кентукки. Джаред Антробус объяснил, почему все понимают все неправильно, в «Отказе PEMDAS».

«Проблема с этой проблемой заключается в том, что деление не является ассоциативным . Если бы нас попросили оценить 12 ÷ 6 ÷ 3, у нас была бы очень похожая проблема. Какой знак деления делаем первым? Независимо от того, что сказал нам наш учитель начальной школы, мы не можем предположить, что автор задачи предполагал, что мы будем работать слева направо. На самом деле, разные калькуляторы будут давать разные ответы, в зависимости от того, как они запрограммированы!

Что делать с неассоциативными операциями?

Единственная причина, по которой мы можем отказаться от написания круглых скобок с длинными строками сложения и умножения, заключается в их ассоциативности. Для деления мы должен указать, какую операцию нужно выполнить первой. Мы должны написать либо (12 ÷ 6) ÷ 3, либо 12 ÷ (6÷3), чтобы читатель точно знал, что мы имеем в виду.

Выражение 12 ÷ 6 ÷ 3 неоднозначно. Это может означать две разные вещи. Единственный способ узнать, что имел в виду автор, — это попросить разъяснений. То же самое касается 6 ÷ 2 × 3».

Неоднозначность делает невозможным ответы на вопросы!

Неоднозначные утверждения характерны не только для математики. Столь же расстраивает следующий вопрос:

Если женщина играет в шахматы со своей сестрой и является гроссмейстером, есть ли вероятность, что она выиграет?

Опять непонятен замысел автора. К какой женщине относится каждое упоминание «она»? Единственный способ узнать это — попросить разъяснений».

Заключение

Мы просто подумали, что учителя математики могут найти хороший перерыв в почти непрерывном цикле плохих новостей, который был в 2020 году. Скорее всего, к тому времени, когда вы будете это читать, он уже не будет в тренде. , но тем не менее он есть. Посмотреть на себя.

Математика как комплексное решение задач

Джейкоб Клерляйн и Шина Херви, Generation Ready

К тому времени, когда маленькие дети поступают в школу, они уже на пути к тому, чтобы научиться решать задачи. С самого рождения дети учатся учиться: они реагируют на свое окружение и реакцию окружающих. Это осмысление опыта является непрерывным, рекурсивным процессом. Мы давно знаем, что чтение — это сложная деятельность по решению проблем. Совсем недавно учителя пришли к пониманию того, что повышение математической грамотности — это также сложная деятельность по решению проблем, которая становится более мощной и гибкой, если практиковаться чаще. Проблема в математике — это любая ситуация, которая должна быть решена с помощью математических инструментов, но для которой нет очевидной стратегии. Если путь вперед очевиден, это не проблема — это простое приложение.

Математики всегда понимали, что решение задач занимает центральное место в их дисциплине, потому что без задачи нет математики. Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века. 90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.

«Решение задач — это не только цель изучения математики, но и основное средство для этого».

(NCTM, 2000, стр. 52)

В 2011 году Стандарты Common Core State включили Стандарты процессов NCTM по решению задач, рассуждению и доказательству, общению, представлению и связям в Стандарты математической практики. Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.

«Однако учебная программа по решению задач требует от учителя другой роли. Вместо того, чтобы руководить уроком, учитель должен предоставить ученикам время для решения проблем, самостоятельного поиска стратегий и решений и научиться оценивать свои собственные результаты. Несмотря на то, что учитель должен присутствовать очень активно, главное внимание в классе должно быть сосредоточено на мыслительных процессах учащихся».

(Burns, 2000, стр. 29)

Обучение решению проблем

Чтобы понять, как учащиеся становятся способными решать задачи, нам нужно взглянуть на теории, лежащие в основе обучения математике. К ним относятся признание аспектов обучения, связанных с развитием, и тот важный факт, что учащиеся активно участвуют в изучении математики посредством «действий, разговоров, размышлений, обсуждений, наблюдений, исследований, слушания и рассуждений» (Copley, 2000, стр. 29). . Концепция совместного конструирования обучения является основой теории. Более того, мы знаем, что каждый студент находится на своем уникальном пути развития.

Убеждения, лежащие в основе эффективного преподавания математики

• Самобытность, язык и культура каждого учащегося должны уважаться и цениться.
• Каждый учащийся имеет право на доступ к эффективному математическому образованию.
• Каждый ученик может стать успешным учеником по математике.

Дети приходят в школу с интуитивным пониманием математики. Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.

Обучение происходит в социальных условиях (Выготский, 1978). Учащиеся строят понимание посредством участия в решении проблем и взаимодействия с другими в этих действиях. Благодаря этим социальным взаимодействиям учащиеся чувствуют, что они могут рисковать, пробовать новые стратегии, а также давать и получать обратную связь. Они учатся совместно, когда делятся разными точками зрения или обсуждают способы решения проблемы. Именно через разговоры о проблемах и обсуждение своих идей дети строят знания и осваивают язык, чтобы осмысливать опыт.

Учащиеся приобретают понимание математики и развивают навыки решения задач в результате решения задач, а не непосредственного обучения (Hiebert1997). Роль учителя состоит в том, чтобы создавать проблемы и представлять ситуации, которые обеспечивают форум, на котором может происходить решение проблем.

Почему важно решать проблемы?

Наши учащиеся живут в обществе, основанном на информации и технологиях, где им необходимо уметь критически мыслить о сложных вопросах, а также «анализировать и логически мыслить о новых ситуациях, разрабатывать неопределенные процедуры решения и ясно и убедительно сообщать о своем решении другим». (Баруди, 1998). Математическое образование важно не только из-за «роли контролера, которую математика играет в доступе учащихся к образовательным и экономическим возможностям», но и потому, что процессы решения задач и приобретение стратегий решения задач готовят учащихся к жизни после школы (Кобб). и Ходж, 2002).

Важность решения задач при изучении математики исходит из убеждения, что математика в первую очередь связана с рассуждениями, а не с запоминанием. Решение проблем позволяет учащимся развивать понимание и объяснять процессы, используемые для достижения решений, а не запоминать и применять набор процедур. Именно благодаря решению задач учащиеся развивают более глубокое понимание математических концепций, становятся более вовлеченными и ценят актуальность и полезность математики (Wu and Zhang, 2006). Решение задач по математике способствует развитию:

• Способность мыслить творчески, критически и логически
• Способность структурировать и организовывать
• Способность обрабатывать информацию
• Удовольствие от интеллектуальной задачи
• Навыки решения проблем, которые помогают им исследовать и понимать мир

Решение задач должно лежать в основе всех аспектов преподавания математики, чтобы учащиеся могли ощутить силу математики в окружающем их мире. Этот метод позволяет учащимся рассматривать решение задач как средство построения, оценки и уточнения своих математических теорий и теорий других.

Проблемы, которые являются «проблемными»

Требования учителя к ученикам очень важны. Учащиеся учатся справляться со сложными проблемами, только столкнувшись с ними. Учащиеся должны иметь возможность работать над сложными задачами, а не над серией простых задач, вытекающих из сложной задачи. Это важно для стимулирования математических рассуждений учащихся и создания прочных математических знаний (Энтони и Уолшоу, 2007). Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.

Учащиеся будут иметь возможность объяснить свои идеи, ответить на идеи других и бросить вызов своему мышлению. Те ученики, которые думают, что математика — это все о «правильном» ответе, нуждаются в поддержке и поощрении, чтобы пойти на риск. Терпимость к трудностям необходима для решения проблем, потому что «застревание» — это неизбежный этап решения практически любой проблемы. Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:

 

• Доступны и расширяемы
• Разрешить отдельным лицам принимать решения
• Способствовать обсуждению и общению
• Поощряйте оригинальность и изобретательность
• Поощряйте «что, если?» и «а что, если нет?» вопросы
• Содержит элемент неожиданности (адаптировано из Ahmed, 1987)

«Учащиеся учатся решать задачи по математике в первую очередь путем «действия, разговора, размышления, обсуждения, наблюдения, исследования, слушания и рассуждений».

(Copley, 2000, стр. 29)

«…когда учащиеся исследуют вместе. Оно становится мини-обществом – сообществом учащихся, занятых математической деятельностью, дискурсом и размышлениями. Учащимся должна быть предоставлена ​​возможность действовать как математики, позволяя, поддерживая и бросая вызов их «математизации» конкретных ситуаций. Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».

(Fosnot, 2005, стр. 10)

Исследования показывают, что «классы, в которых ориентация последовательно определяет результаты задач с точки зрения ответов, а не мыслительных процессов, связанных с получением ответов, негативно влияет на мыслительные процессы и математические тождества. учащихся (Энтони и Уолшоу, 2007, стр. 122).

Эффективные учителя формируют у своих учеников хорошие привычки решать проблемы. Их вопросы разработаны, чтобы помочь детям использовать различные стратегии и материалы для решения проблем. Студенты часто хотят начать без плана в виду. Посредством соответствующих вопросов учитель дает учащимся некоторую структуру для начала решения проблемы, не говоря им, что именно делать. В 1945 Полиа опубликовал следующие четыре принципа решения проблем, чтобы помочь учителям помочь своим ученикам.

1. Понять и изучить проблему
2. Найти стратегию
3. Используйте стратегию для решения проблемы
4. Оглянитесь назад и подумайте над решением

Решение проблем — это не линейный, а сложный интерактивный процесс. Учащиеся перемещаются вперед и назад между фазами Pólya и между ними. Стандарты Common Core State описывают этот процесс следующим образом:

«Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут точки входа в ее решение. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение.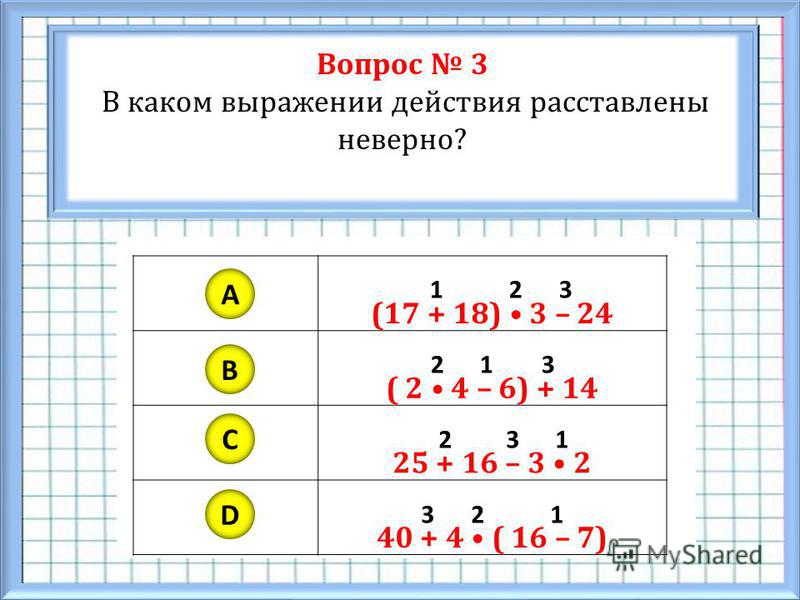 Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс». (Стандарты обучения математике нового поколения штата Нью-Йорк, 2017 г.).

Принципы решения проблем Полиа

1. Понять и изучить проблему
2. Найти стратегию
3. Используйте стратегию для решения проблемы
4. Оглянитесь назад и подумайте над решением

Учащиеся перемещаются вперед и назад по ходу решения задач.

 

Цель состоит в том, чтобы учащиеся имели ряд стратегий, которые они используют для решения проблем, и понимали, что может быть более одного решения. Важно понимать, что процесс столь же важен, если не более важен, чем получение решения, поскольку именно в процессе решения учащиеся раскрывают математику. Получение ответа — это не конец процесса. Размышление о стратегиях, используемых для решения проблемы, дает дополнительный опыт обучения. Изучение подхода, используемого для решения одной проблемы, помогает учащимся более комфортно использовать эту стратегию в различных других ситуациях.

При осмыслении идей учащиеся должны иметь возможность работать как самостоятельно, так и совместно. Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.

Реальность

Эффективные учителя математики создают для учащихся целенаправленный учебный опыт, решая задачи в релевантных и осмысленных контекстах. Хотя текстовые задачи — это способ поместить математику в контекст, он не делает ее автоматически реальной. Задача учителей состоит в том, чтобы давать учащимся задачи, основанные на их опыте реальности, а не просить их приостановить его. Реалистичность не означает, что задачи обязательно связаны с реальным контекстом, скорее они заставляют учащихся думать «настоящим» образом.

Планирование беседы

Планируя и продвигая беседу, учителя могут активно вовлекать учащихся в математическое мышление. На уроках математики, насыщенных дискурсом, учащиеся объясняют и обсуждают стратегии и процессы, которые они используют при решении математических задач, тем самым связывая свой повседневный язык со специальной лексикой математики.

Учащиеся должны понимать, как общаться математически, давать разумные математические объяснения и обосновывать свои решения. Эффективные учителя поощряют своих учеников сообщать свои идеи устно, письменно и с использованием различных представлений. Слушая учеников, учителя могут лучше понять, что знают их ученики, и неправильные представления, которые у них могут быть. Именно заблуждения открывают окно в процесс обучения студентов. Эффективные учителя рассматривают мышление как «процесс понимания», они могут использовать мышление своих учеников как ресурс для дальнейшего обучения. Такие учителя отзывчивы как к своим ученикам, так и к дисциплине математики.

«Сегодня математика требует не только вычислительных навыков, но и способности мыслить и рассуждать математически, чтобы решать новые задачи и изучать новые идеи, с которыми учащиеся столкнутся в будущем. Обучение улучшается в классах, где учащиеся должны оценивать свои собственные идеи и идеи других, им предлагается делать математические предположения и проверять их, а также им помогают развивать свои навыки рассуждения».

(Джон Ван де Валле)

«Капитал. Превосходство в математическом образовании требует справедливости — высоких ожиданий и сильной поддержки для всех учащихся».

(NTCM)

Заключение

То, как учителя организуют обучение в классе, во многом зависит от того, что они знают и думают о математике, а также от того, что они понимают в преподавании и изучении математики. Учителя должны признать, что процессы решения проблем развиваются с течением времени и значительно улучшаются за счет эффективных методов обучения.