Порядок действий в математике

Метки

Головоломки Досуг Задачи Логика Математика Смекалка

Порядок выполнения действий в математике нередко становится настоящим камнем преткновения. Мы изучали его в начальных классах школы и, по идее, должны помнить всю жизнь. Но теория, как говорил Мефистофель, суха. Да и кому, по правде говоря, интересны примеры, где порядок действий расписан заранее?

© Depositphotos

Другое дело — задания из нашей подборки. В них тебе дается лишь набор цифр и число, которое нужно получить. А какие действия и в каком порядке выполнять, решать только тебе. И тут уж ответ не вычислишь, а тем более не угадаешь. Ведь для решения необходимо мыслить и творчески, и аналитически. А это помогает нам успешно находить выход из самых сложных жизненных ситуаций.

Порядок действий в математике

1. Начнем с примеров попроще. Поставь в записи 1 * 3 * 2 * 1 * 2 = 10 вместо звездочек знаки арифметических действий, чтобы получилось верное равенство. Попробуй найти как можно больше вариантов решения со скобками и без.
   
2. У тебя есть четыре цифры: 5, 5, 5 и 1. С помощью сложения, вычитания, умножения, деления и скобок получи из них число 24, используя каждую из этих цифр только 1 раз.
   
3. Используя цифры (1, 3, 4, 6), скобки и арифметические операции (сложение, вычитание, умножение, деление), получи число 24. Разрешается использовать только эти цифры и только эти операции. Каждую цифру можно использовать только один раз. Операции и скобки можно использовать любое число раз.© Depositphotos

Ответы

1. Как я уже говорил, тут открывается широкий простор для творчества. Мне сходу удалось найти только одно решение без скобок: 1 + 3 х 2 + 1 + 2 = 10. И одно со скобками: 1 х (3 + 2) х 1 х 2 = 10. Но решений, скорее всего, намного больше. Попробуй найти недостающие!
2. Я предложил эту задачку своим друзьям. И перед тем как назвать верный ответ, расскажу вам об ошибочных, а также весьма остроумных вариантах решения.
   Самый распространенный ответ:5 х 5 – 1 = 24. Был еще такой вариант: 5 + 5 + 5 + 5 + 5 – 1 = 24. Да, ответ в обоих случаях, конечно, 24. Но как быть с условием? В нём четко сказано, что нужно использовать каждую из цифр и только 1 раз!
   © Depositphotos

   Интересное решение за пределами математики предложила девушка бариста. По ее словам, достаточно выпить 5 чашек кофе, затем еще 5 чашек и еще 5 чашек за один день, чтобы получить 24 часа бодрствования. Мы не советуем даже пробовать это повторить. Ведь больше 300 миллилитров бодрящего напитка в день способны навредить твоему здоровью. Но попытка свести воедино математику, кулинарию и физиологию заслуживает всяческого уважения.

   © Pexels

   Возвращаясь к математике, признаюсь, что найти решение для этого примера было очень непросто. У меня оно получилось таким:

   (5 — (1 : 5)) х 5= 24. Но, может, кто-нибудь из наших читателей найдет еще один вариант?

3. Мы уже решили два примера. Поэтому с последним проблем быть не должно. И опять нас выручает деление на дробь:
   6 / ( 1 — ( 3 / 4 ) ) = 24.
   © Pexels

Как видишь, наши забавные задачки помогают провести время с пользой. Ведь сообразительность помогает искать необычные, интересные и простые пути решения, достигая результата не только в игре, но и в реальной жизни кратчайшим путем.

Поделиться

Мудрый гном — Карточки по математике «Выполнение действий со скобками и без»

Порядок выполнения действий:

Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.

Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.

Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.

Рассмотрим пример:

38 – (10 + 6) = 22;

Итак, вспомним о том, что сначала вычисляются выражения в скобках

1) в скобках: 10 + 6 = 16;

2) вычитание: 38 – 16 = 22.

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

 

 

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5;

2) умножение: 5 × 4 = 20;

10 + 4 – 3 = 11, т.е.:

1) 10 + 4 = 14;

2) 14 – 3 = 11.

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9;

2) 2 × 3 = 6;

3) 12 ÷ 3 = 4;

4) 9 – 6 = 3; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54, т.е.:

1) выражение в скобках: 13 – 9 = 4;

2) умножение: 6 × 4 = 24;

3) сложение: 30 + 24 = 54;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

 

 

 

Составление выражения со скобками

1. Представь предложения в виде выражений со скобками и реши их.

а) Из числа 16 вычти сумму чисел 8 и 6.
б) К числу 34 прибавь сумму чисел 5 и 8.

в) Сумму чисел 13 и 5 вычти из числа 39.
г) Разность чисел 16 и 3 прибавь к числу 36
д) Из числа 50 отними разность чисел 48 и 28.

2. Реши задачи.

а) Папа принёс из сада корзину, в которой было 78 слив. Коля взял из корзины 25 слив. Маша взяла из корзины 18 слив. Мама тоже взяла из корзины 15 слив, но положила обратно 7 штук. Сколько слив оказалось в корзине?

б) В течении рабочего дня мастер ремонтировал детали. В начале смены ему надо было отремонтировать 38 штук. Он смог отремонтировать 23 штуки. После обеда для ремонта принесли еще столько же деталей, сколько было в начале рабочего дня. Мастер отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?

 

3. Реши примеры.

а) 45 : 5 + 12 * 2 — 21 : 3 =
б) 56 — 72 : 9 + 48 : 6 * 3 =
в) 7 + 5 * 4 — 12 : 4 =
г) 18 : 3 — 5 + 6 * 8 =

Решение выражений со скобками

1.

Реши примеры.

а) 1 + (4 + 8) =	б) 8 — (2 + 4) =	в) 3 + (6 — 5) =	г) (18 + 47) — (47 -18) =
д) 18 — (2 + 14) =	е) (2 + 9) — (5 + 2) =	ж) 59 — (2 + 5) =	з) 30 — (9 + 5) — 3 =

2. Реши примеры

а) 36 : 3 + 12 * ( 2 — 1 ) : 3 =
б) 39 — ( 81 : 9 + 48 : 6) * 2 =
в) ( 7 + 5 ) * 2 — 48 : 4 =
г) 18 : 3 + ( 5 * 6 ) : 2 — 4 =

Реши задачи

1. На складе находилось 25 упаковок стирального порошка. В течении дня в магазин А и в магазин Б отвезли по 12 упаковок порошка. Затем на склад привезли в 3 раза больше упаковок порошка, чем было утром. Сколько упаковок порошка оказалось на складе к концу дня?

2. В гостинице проживало 75 туристов. В первый день из гостиницы уехало 3 группы по 12 человек, а заехало 2 группы по 15 человек. На второй день уехало еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?

3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. Затем забрали 8 вещей. После обеда привезли ещё 18 вещей, а забрали только 5 почищенных вещей. Сколько вещей оказалось в химчистке к концу дня, если в начале рабочего дня там находилось 14 вещей?

 

 

 

 

Обратные операции: умножение и деление

Что такое обратные операции?

Обратные операции — это два разных типа вычислений, оказывающих противоположное влияние друг на друга. Например, вычитание — операция, обратная сложению, а деление — операция, обратная умножению.

В математике слово «инверсия» означает «противоположное».

Обратные операции можно использовать для отмены исходной операции. Это приводит к возврату значения, с которого мы начали до первого вычисления.

Например, мы можем начать с числа 5, а затем умножить его на 4.

5 × 4 = 20. Мы начали с 5, но теперь их 20.

Чтобы вернуться от 20 к 5, мы используем обратную операцию.

20 ÷ 4 = 5. Мы можем вернуться от 20 к 5, разделив на 4.

Мы говорим, что умножение на 4 — это операция, обратная делению на 4.

Умножение 5 на 4 дало 20.

Разделив 20 на 4, мы вернулись к 5.

Умножение и деление являются примерами обратных операций.

Что такое обратное умножению?

Обратным умножением является деление. Если вы умножите на заданное число, а затем разделите на то же число, вы получите то же число, с которого начали. Деление имеет эффект, противоположный умножению.

Например, здесь 3 × 2 = 6.

Мы начали с числа 3.

Мы умножили его на 2, чтобы увеличить от 3 до 6.

Для возврата от 6 к 3 необходимо использовать обратную операцию.

Противоположностью умножения на 2 является деление на 2.

Делим 6 на 2, чтобы вернуться к исходному числу 3.

Деление имело обратный эффект по отношению к умножению, выполненному в исходном расчете.

Деление и умножение обратны только в том случае, если деление и умножение на одно и то же число. В этом примере мы умножили и разделили на 2.

Что такое обратное делению?

Обратное деление — умножение. Если вы разделите на заданное число, а затем умножите на то же число, вы получите то же число, с которого начали. Умножение имеет эффект, противоположный делению.

Например, вот 10 ÷ 2 = 5.

Мы начали с числа 10.

Мы разделили его на 2, чтобы уменьшить 10 до 5.

Чтобы вернуться от 5 к нашему исходному числу 10, мы должны использовать обратную операцию.

Мы можем умножить 5 на 2, чтобы вернуться к исходному числу 10. 5 × 2 = 10.

Деление на 2 и умножение на 2 являются обратными операциями. Умножение на 2 привело к отмене деления на 2.

Как записать умножение в виде деления

Чтобы записать умножение как деление, выполните следующие действия:

1. Запишите ответ умножения в начале деления перед знаком деления.
2. Запишите два умножаемых числа после знака деления и после знака равенства соответственно.
3. Два числа на втором шаге можно записать в любом порядке, чтобы образовать два разных предложения с делением.

Например, вот 7 × 8 = 56. Запишем это умножение как деление.

Каждое умножение можно переписать как деление, используя те же числа, но в другом порядке.

Если вы знаете ответ на данное умножение, вы можете сразу использовать его для создания деления без выполнения каких-либо вычислений. Просто переставьте числа.

Первый шаг — написать ответ на умножение в начале предложения деления. Результат умножения теперь равен числу, на которое оно делится.

56 — это ответ на умножение 7 × 8 = 56. Мы начнем наше деление с 56.

Следующим шагом будет запись умножаемых чисел в предложении умножения после знака деления и после знака равенства в любом порядке.

Умножаются два числа: 7 и 8. Мы напишем 7 после знака деления и 8 после знака равенства.

Преобразуем умножение 7 × 8 = 56 в деление 56 ÷ 7 = 8. Используемые числа те же, но они записаны в другом порядке.

В то время как 56 должно идти в начале деления, два других числа 7 и 8 могут быть записаны в любом порядке. Для каждого умножения можно записать два разных деления.

На этот раз мы напишем эти два числа в другом порядке.

Преобразуем умножение 7×8=56 в деление 56÷8=7.

7 × 8 = 56 можно записать как 56 ÷ 7 = 8 или 56 ÷ 8 = 7.

Как записать деление как умножение

Чтобы записать деление как умножение, выполните следующие действия:

1. Запишите делимое число как ответ в конце умножения.
2. Запишите оставшиеся два числа в предложении деления, умноженные вместе в предложении умножения.
3. Два числа из второго шага можно записать в любом порядке, чтобы получились два разных предложения умножения.

Например, вот 18 ÷ 6 = 3

Первый шаг — записать делимое число в начале деления как ответ в конце умножения.

18 — это число, которое нужно разделить. Это сформирует ответ в конце умножения.

Следующим шагом будет запись оставшихся двух чисел из деления, умноженных вместе, в предложении умножения.

Два других числа в делении — это 6 и 3.

Мы можем записать 18 ÷ 6 = 3 как 6 × 3 = 18.

Мы также можем записать 18 ÷ 6 = 3 как 3 × 6 = 18. Неважно, в каком порядке умножаются два числа.

Каждое предложение деления может быть записано как два разных предложения умножения.

18 ÷ 6 = 3 можно записать как 6 × 3 = 18 или 3 × 6 = 18.

Multiplication and Division Operations Video Tutorial & Practice

Recent Channels

• General Chemistry

Chemistry

• General Chemistry
• Organic Chemistry
• Analytical Chemistry
• GOB Chemistry
• Biochemistry

Biology

• Общая биология
• Microbiology
• Anatomy & Physiology
• Genetics
• Cell Biology

Math

• College Algebra
• Trigonometry
• Precalculus

Physics

• Physics

Business

• Microeconomics
• Macroeconomics
• Финансовый учет

Социальные науки

• Психология

Начните вводить текст, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.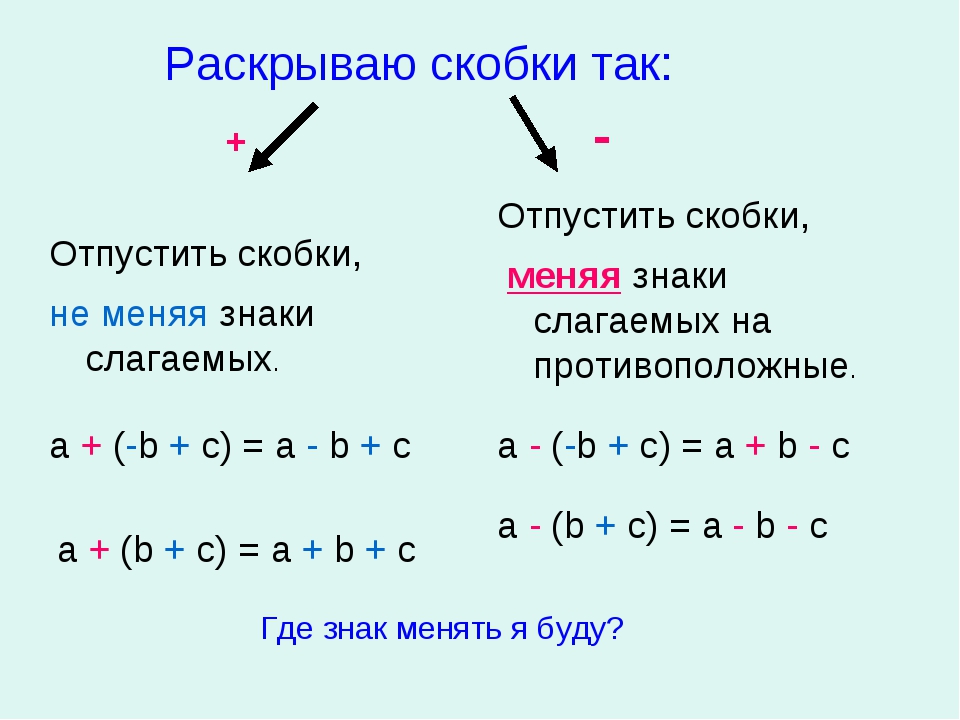

Изучите самые сложные понятия химии с помощью пошаговых видеоуроков и практических задач от преподавателей мирового уровня

5. БОНУС: математические операции и функции

Next Topic

Умножение и деление значений в научной записи.

При умножении или делении наш окончательный ответ будет иметь наименьшее количество значащих цифр.

2 м

Воспроизвести видео:

Было ли это полезно?

В этом видео мы посмотрим. Что именно мы делаем, когда у нас есть представление о числах и научных обозначениях, и мы их умножаем или делим? Теперь мы скажем, когда вы умножаете значения и экспоненциальное представление, вы умножаете коэффициенты. Помните, что в данном случае ваши коэффициенты — это значения, это переменные A и B, а затем мы собираемся добавить показатели степени, которые здесь являются нашими степенями. Наши силы X и Y. Итак, когда мы делаем а, умноженное на 10, умноженное на х, умноженное на В, умноженное на 10, на Y. Здесь мы умножаем а и В вместе, а затем складываем показатели степени. Итак, x плюс y, это будет ответом на наше выражение. Теперь, когда вы делите значения в научном представлении, вы делите коэффициенты и вычитаете степени. Итак, здесь мы собираемся разделить на B, умноженное на 10. И теперь у нас есть 10 на X, деленное на 10 на Y. Получается X минус Y. Теперь мы собираемся сказать, что мы должны помнить это после умножения и деления. Помните, что для коэффициентов у нас будет наименьшее количество значащих цифр, поэтому наименьшее количество знаков цифры, когда вы умножаете или делите его наименьшее количество больных вещей, когда вы добавляете или вычитаете наименьшее количество знаков после запятой. Теперь, когда мы ознакомились с основами умножения чисел в экспоненциальном представлении, давайте взглянем на другие примеры, которые у нас есть. Здесь. У нас есть примеры один и два. Мы собираемся применить то, что мы узнали наверху. Ответьте, что мы подойдем к ним тем же способом, о котором говорили в предыдущих двух примерах. Теперь вернитесь, взгляните на первый пример и на то, как мы к нему подходим. Если вы хотите сделать это раньше времени самостоятельно, вы также можете сделать это.

2

concept

Вычисление умножения и деления 1

2m

Воспроизвести видео:

Было ли это полезно?

, используя описанный выше метод. Определите ответ, перемножив следующие значения. Итак, здесь у нас есть эти три значения в научных обозначениях, находящихся в процессе применения. Здесь мы собираемся умножить коэффициенты, а затем запомнить, что показатели степени складываются. Итак, мы умножаем эти три коэффициента вместе на 2,134 умножить на 1,66 умножить на 3,7. Получим 10,4822. И помните, показатели степени складываются так, что получается пять плюс минус три плюс шесть. Так что это дало бы мне восемь в конце. Но помните, когда дело доходит до умножения ваших коэффициентов, когда вы выполняете умножение или деление, это должно быть наименьшее количество значащих цифр. Теперь, когда у вас есть десятичный знак, помните, мы идем слева направо, мы начинаем считать. Как только вы доберетесь до своего первого ненулевого числа, ваше первое ненулевое число здесь будет равным Итак, вы начинаете считать там и считаете до конца. Итак, 1234 Вот ваш первый нон 012 Вот ваш первый нон Так что, по крайней мере, число больных вещей должно быть. Теперь, как мы смотрим на этот ответ, он написан неправильно с точки зрения научной нотации. Помните, что ваш коэффициент должен быть числом от единицы, но меньше 10. Так что нам придется переместить эту десятичную дробь на единицу. Мы просто уменьшили количество. Он изменился с 10 до 1. Если ваш коэффициент становится меньше, это означает, что ваши показатели степени будут увеличиваться. Так становится 10 к девятке, а нам нужно шесть. Исправление для этого будет один нулевой пункт умножить на 10 до девяти. Если вы введете это в свой калькулятор, вы должны получить этот ответ сейчас. Помните, когда вы выполняете 10 повторений любой силы, вы должны указать это в скобках в своем калькуляторе. Таким образом, вы должны заключить в скобки каждое из этих чисел, а затем умножить их. Если вы этого не сделаете, ваш калькулятор, скорее всего, даст вам неверный ответ. Но исходя из того, что мы видели выше, это будет правильное значение при умножении. Эти три числа в экспоненциальном представлении пытаются сделать в следующем примере. Так же, как мы сделали это. Вернитесь и посмотрите, совпадает ли ваш ответ с моим.

3

concept

Умножение и деление 2

1m

Воспроизвести видео:

Было ли это полезно?

, так что здесь говорится, что с помощью методов, описанных выше, мы определили ответ на следующий вопрос о смешанных операциях. Таким образом, в этом вопросе мы имеем комбинацию умножения и деления. Итак, когда дело доходит до коэффициентов, это коэффициенты. Мы умножаем эти коэффициенты вместе здесь. Когда мы это сделаем, это даст нам 11,8454. А затем здесь X костей, когда они умножаются, складываются вместе, так что восемь плюс минус один, что дает мне семь.