Что обозначают буквы Е, Ё, Ю, Я
Дело в том, что в русском языке буквы Е, Ё, Ю, Я есть, а звуков таких нет. Эти буквы в разных позициях в слове могут обозначать разные звуки. В одних случаях они обозначают два звука, а в других — один звук и указывают на мягкость предыдущего согласного звука. Разберём эту тему подробнее.
Содержание:
Что обозначают буквы Е, Ё, Ю, Я
Когда Е, Ё, Ю, Я обозначают два звука
Когда Е, Ё, Ю, Я обозначают один звук
Упражнения на закрепление
В начальной школе дети знакомятся с основными правилами русского языка, узнают, чем отличаются русский язык устный и русский язык письменный. Первое, с чего начинается это знакомство, — алфавит. Урок за уроком школьники изучают буквы и звуки, узнают, что они бывают гласными и согласными, что каждая из них имеет собственные свойства, что далеко не всегда в слове пишется та буква, которая слышится, что в русском языке некоторые звуки могут быть обозначены разными буквами, а буквы порой обозначают разные звуки. Так, например, гласных букв 10, а гласных звуков, которые эти буквы обозначают, всего 6. Дело в том, что в русском языке буквы Е, Ё, Ю, Я есть, а звуков таких нет. Эти буквы в разных позициях в слове могут обозначать разные звуки. В одних случаях они обозначают два звука, а в других — один звук и указывают на мягкость предыдущего согласного звука. Разберём эту тему подробнее.
Так, например, гласных букв 10, а гласных звуков, которые эти буквы обозначают, всего 6. Дело в том, что в русском языке буквы Е, Ё, Ю, Я есть, а звуков таких нет. Эти буквы в разных позициях в слове могут обозначать разные звуки. В одних случаях они обозначают два звука, а в других — один звук и указывают на мягкость предыдущего согласного звука. Разберём эту тему подробнее.
Когда Е, Ё, Ю, Я обозначают два звука
Рассмотрим их на примере следующих слов:
- ель, ёршик, юбилей, яма;
- счастье, съёмка, вьюга, семья;
- боец, мумиё, пиявка, каюта.
В первой строчке буквы Е, Ё, Ю, Я расположены в начале слова, во второй — в середине после мягкого либо твёрдого знаков, а в третьей — после другой гласной буквы. Произнесём эти слова вслух, медленно и чётко, прислушиваясь к звучанию. Для наглядности запишем транскрипцию этих слов.
Для наглядности запишем транскрипцию этих слов.
Начнём с первой строчки: ель [й’эл’], ёршик [й’оршик], юбилей [й’уб’илей’], яма [й’ама]. Мы видим, что буквы Е, Ё, Ю, Я, расположенные в начале слова, обозначают два звука: [й’э], [й’о], [й’у], [й’а].
Вторая строчка: счастье [щ’аст’й’э], съёмка [сй’омка], вьюга [в’й’уга], семья [с’им’й’а]. И здесь, находясь после мягкого и твёрдого знаков, эти буквы также обозначают два звука: [й’э], [й’о], [й’у], [й’а].
Третья строчка: боец [бай’эц], мумиё [мум’ий’о], пиявка [п’ий’афка], каюта [кай’ута]. И в этом случае буквы Е, Ё, Ю, Я, стоящие после другой гласной буквы, обозначают по два звука: [й’э], [й’о], [й’у], [й’а].
И в этом случае буквы Е, Ё, Ю, Я, стоящие после другой гласной буквы, обозначают по два звука: [й’э], [й’о], [й’у], [й’а].
Делаем вывод:
Буквы Е, Ё, Ю, Я ещё называют йотированными гласными, так как в позициях, которые мы рассмотрели выше, они обозначают два звука, первый из которых звук [й’], называется “йот”.
Когда Е, Ё, Ю, Я обозначают один звук
Эту ситуацию рассмотрим также на примерах. Но сначала вспомним, что мы знаем о согласных звуках. Согласные звуки могут быть твёрдыми и мягкими. Сравним пары слов по их произношению.
Мэтр — метр.
Нос — нёс.
Лук — люк.
Мальчик — мячик.
Очевидно, что в первом столбике первый согласный звук — твёрдый, во втором — мягкий. Но и в первом, и во втором столбике буквы Е, Ё, Ю, Я обозначают одни и те же звуки [э], [о], [у], [а]. Произнесём слова и определим, какие звуки обозначают буквы Е, Ё, Ю, Я после согласных: метр — звук [э], нёс —звук [о], люк — звук [у], мячик — звук [а].
Делаем вывод:
Упражнения на закрепление
Не стоит забывать, что самые прочные знания — это знания осознанные, полученные учеником в результате соединения теории с практикой. Поэтому именно закрепление материала является необходимым условием формирования прочных знаний по изучаемой теме. После обсуждения правил обязательно предложите своему ребёнку выполнить задания на закрепление. Они могут быть, например, такими:
- Выпиши слова в два столбика: первый — где буквы Е, Ё, Ю, Я обозначают 1 звук, второй — 2 звука.
Ветка, пьёт, Петя, Алёша, мята, поют, друзья, берёза, люстра, съели, синие.
Проверка:
- Выпиши слова в два столбика: первый — где буква Я указывает на мягкость согласного звука, второй — где буква Я обозначает два звука.
Яркий, тянуть, Петя, деревья, ясно, мяч, растения, Аня, ястреб, швея, рябина.
Проверка:
- Прочти стихотворение, спиши его и подчеркни буквы Е, Ё, Ю, Я, обозначающие два звука.

Мы едем, едем, едем
В далёкие края,
Хорошие соседи,
Счастливые друзья
Проверка:
Мы едем, едем, едем
В далёкие края,
Хорошие соседи,
Счастливые друзья.
- Отгадай загадки. В словах-ответах найди буквы Е, Ё, Ю, Я. Объясни, в каких случаях эти буквы обозначают 1 звук, а в каких — 2 звука.
Была зелёной, маленькой,
Потом я стала аленькой.
На солнце почернела я,
И вот теперь я спелая. (Ежевика)
***
Покраснел зелёный сад —
Капли красные висят.
Всем знакомы капли эти:
Их и взрослые, и дети
С удовольствием едят,
Только косточки летят. (Вишня)
***
Само с кулачок,
Красный бочок,
Потрогаешь — гладко,
А откусишь — сладко. (Яблоко)
***
По названию она
Очень чёрной быть должна.
В слове из-за этого вышла заковыка.
Светло-фиолетова спелая (черника).
***
Осень в сад к нам пришла,
Красный факел зажгла.
Здесь дрозды, скворцы снуют
И, галдя, её клюют. (Рябина)
***
С виду он как рыжий мяч,
Только вот не мчится вскачь.
В нём полезный витамин
Это спелый (апельсин).
Проверка:
Ежевика (первая е — 2 звука, вторая — 1 звук), вишня (1 звук), яблоко (2 звука), черника (1 звук), рябина (1 звук), апельсин (1 звук).
Ещё больше заданий на закрепление изучаемого материала предлагает образовательная онлайн-платформа iSmart. С ней ваш ребёнок освоит сложные правила русского языка легко, интересно, увлекательно.
Образовательная платформа iSmart даёт прекрасную возможность совершенствовать знания по основным предметам школьной программы, подготовиться к контрольным, проверочным работам, ВПР, олимпиадам, а также изучить дополнительные предметы, не вошедшие в школьную программу.
Платформа содержит также сервис «Продлёнка», который предлагает занятия с репетитором по всем предметам в онлайн-формате в Zoom и станет прекрасным помощником родителям.
Регистрируйте своего ребёнка на платформе iSmart и начинайте заниматься!
Фонетический разбор слова
Гласные звуки
В русском алфавите всего 33 буквы.
Две из них – Ь, Ъ — не относятся ни к гласным, ни к согласным буквам, звуков не обозначают .
Гласные буквы : бывают ударными или безударными, образуют слоги. Сколько в слове гласных звуков, столько и слогов.
Гласных букв 10 : а, о, у, э, ы, я, ё, ю, е, и.
Гласных звуков 6 : [а], [о], [у], [э], [и], [ы].
А, О, У, Э, Ы – обозначают твёрдость согласных звуков.
Я, Ё, Ю, Е, И – обозначают мягкость согласных звуков.
Йотированные гласные буквы Я — [йа] Ю- [йу] Е – [йэ] Ё – [йо] (буквы, обозначающие два звука). Обозначают два звука , если стоят:
Обозначают два звука , если стоят:
* в начале слова (ёж, яблоко, юла)
* после Ъ и Ь (съешь, семья, подъём)
Буквы е, я, ю, ё обозначают один звук [э], [а], [у], [о] после согласного только под ударением.
век — [в’эк], мяч- [м’ач’], блюз — [бл’ус], мед — [м’от]
В безударном положении эти буквы после согласного
обозначают звук [и]
ряды [р’ и д ы] лесок [л’ и с о к]
Согласные звуки
Согласные звуки не образуют слог.
Согласные звуки не бывают ударными или безударными.
Согласных букв 21 : н, м, л, р, й, б, в, г, д, ж з, п, ф, к, т, ш, с, х, ц, ч, щ.
Согласных звуков в русском языке – 36.
Парные согласные звуки
|
твердые звонкие |
твердые глухие |
мягкие звонкие |
мягкие глухие |
| [б] |
[п] |
[б’] |
[п’] |
|
[в] |
[ф] |
[в’] |
[ф’] |
|
[г] |
[к] |
[г’] |
[к’] |
|
[д] |
[т] |
[д’] |
[т’] |
|
[ж] |
[ш] |
— | — |
|
[з] |
[с] |
[з’] |
[с’] |
Непарных глухих звуков – 5: [х], [х’] [ц], [ч’], [щ’].
Непарных звонких звуков – 9: [л], [л’], [м], [м’], [н], [н’], [р], [р’], [й’].
Всегда твёрдые согласные звуки: [ж], [ш], [ц].
Всегда мягкие согласные звуки: [ч’], [щ’], [й’].
Непарные звонкие звуки [л], [л’], [м], [м’], [н], [н’], [р], [р’] называются сонорными, что в переводе с латинского значит «звучные».
ПРИМЕРЫ
вода — [вада’] во — да’
[в] — согл., парн. тв., парн. звон.
[а] — гласн., безударн.
[а] — гласн., ударн.
4 б , 4 зв.
вьюга — [в’ й’у’га]
в [в’] — согл, парн. мяг., парн. звон.
ь —
[й’] — согл., непарн. мяг., непарн. звон.
ю [у] — глас., удар.
г [г] — согл., парн. твер., парн. звон.
а [а] — глас, безуд.
5 б.,
ТАБЛИЦЫ ДЛЯ ЗАПОМИНАНИЯ:
комбинаторика — Количество слов, которые можно составить с помощью ИНСТИТУЦИИ так, чтобы гласные и согласные чередовались
Задавать вопрос
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 5к раз
$\begingroup$
Вопрос:
Сколько слов можно составить из УЧРЕЖДЕНИЕ так, чтобы гласные и согласные чередовались?
Моя попытка:
Всего 11 букв в слове УЧРЕЖДЕНИЕ . 6 согласных — {NSTTTN} , а 5 гласных — {IIUIO} . Итак, если мы начнем с согласных, то получим $6!$ другое расположение согласных и $5!$ другое расположение гласных. Но I повторяется 3 раза, T повторяется 3 раза и N повторяется 2 раза. Таким образом, мы получаем $$\frac{6! \cdot 5!}{3! \cdot 3! \cdot 2!} = 1200$$ разных слов.
6 согласных — {NSTTTN} , а 5 гласных — {IIUIO} . Итак, если мы начнем с согласных, то получим $6!$ другое расположение согласных и $5!$ другое расположение гласных. Но I повторяется 3 раза, T повторяется 3 раза и N повторяется 2 раза. Таким образом, мы получаем $$\frac{6! \cdot 5!}{3! \cdot 3! \cdot 2!} = 1200$$ разных слов.
Так же возможно, что это слово начинается с гласной, таким образом у нас будет еще $1200$ слов.
Таким образом, общее количество образованных слов равно $1200 + 1200 = 2400$
Но дан ответ: 1200 .
Я что-то упустил?
- комбинаторика
0
$\begingroup$
У вас нет возможности начать с гласной или с согласной, так как вы должны чередоваться, а у вас 6 согласных и 5 гласных. Оно должно начинаться с согласного.
Оно должно начинаться с согласного.
$\endgroup$
1
$\begingroup$
НЕ возможно, что слово начинается с гласной, потому что согласных больше.
Количество способов разместить NNSTTT на нечетных местах:
$$\binom62\cdot\binom41\cdot\binom33=60$$
Количество способов разместить IIIOU на четных местах:
$$\binom53\cdot\binom21\cdot\binom11=20$$
Отсюда количество способов устроить УЧРЕЖДЕНИЕ равно:
$$60\cdot20=1200$$
$\endgroup$
$\begingroup$
Если слово начинается с гласной, то гласная закончится раньше, чем согласная.
Пусть C обозначает согласную, а V гласную, у нас в первом случае CVCVCVCVCVC, а во втором случае будет VCVCVCVCVC и у нас останется еще одна C. Который мы не можем добавить в конце.
Который мы не можем добавить в конце.
$\endgroup$
0
Сколько слов из 3 гласных и 6 согласных можно составить из 5 гласных и 10 согласных?
Перестановка известна как процесс организации группы, тела или чисел по порядку, выбор тела или чисел из набора известен как комбинации таким образом, что порядок чисел не имеет значения.
В математике перестановкой называют также процесс организации группы, в котором все члены группы располагаются в определенной последовательности или порядке. Процесс перестановки известен как перестановка компонентов, если группа уже организована. Перестановки происходят почти во всех областях математики. В основном они появляются, когда рассматриваются разные команды на определенных ограниченных наборах.
Формула перестановки
При перестановке r вещей выбираются из группы n вещей без замены. В этом порядок выбора материи.
В этом порядок выбора материи.
n P r = (n!)/(n – r)!
Здесь
n = размер группы, общее количество вещей в группе
r = размер подмножества, количество вещей, которые нужно выбрать из группы выбора числа из набора, так что (в отличие от перестановки) порядок выбора не имеет значения. В меньших случаях можно подсчитать количество комбинаций. Комбинация известна как слияние n вещей, взятых по k за раз, без повторения. В сочетании порядок не имеет значения, вы можете выбирать элементы в любом порядке. К тем комбинациям, в которых допускается повторение, часто применяют термины k-отбор или k-комбинация с репликацией.
Формула комбинации
В комбинации r предметов выбираются из набора из n предметов, причем порядок выбора не имеет значения.
n C r = n!/((n-r)! r!)
Здесь
n = количество предметов в наборе
r = количество вещей, выбранных из группы.
Сколько слов из 3 гласных и 6 согласных можно составить из 5 гласных и 10 согласных?
Ответ:
Всего № гласных = 5
Всего кол. согласных = 10
Количество слов с 3 гласными и 6 согласными
3 гласных можно выбрать из 5 гласных = 5 C 3 способов = n!/(n-r)!r!= 5!/( 5-3)!3! =10 способов
Из 10 согласных можно выбрать 6 согласных = 10 C 6 способов = n!/(n-r)!r! = 10!/(10-6)!6! = 210 способов
Общий выбор = 5 C 3 × 10 C 6
Теперь 9 букв в каждом наборе можно расположить в 9! пути
Всего кол. слов = 5 C 3 × 10 C 6 × 9!
= 10 × 210 × 9!
= 2100 × 9!
= 762 048 000 слов
Аналогичные вопросы
Вопрос 1: Если приведено 5 гласных и 6 согласных, то сколько 6 -буквенных слов можно сформировать с 3 гласными и 3 согласными?
Ответ:
Всего тел.
гласных = 5
Всего кол. согласных = 6
№. из 6 буквенных слов с 3 гласными и 3 согласными
3 гласных можно выбрать из 5 гласных = 5 C 3 способов = n!/(n-r)!r!= 5!/(5-3)!3 ! =10 способов
Из 6 согласных можно выбрать 3 согласных = 6 C 3 способов = n!/(n-r)!r! = 6!/(6-3)!3! = 20 способов
Всего выбрано = 5 C 3 × 6 C 3
Теперь 6 букв в каждом выборе можно расположить в 6! пути
Всего кол. из 6-буквенных слов = 5 C 3 × 6 C 3 × 6!
= 10 × 20 × 6!
= 200 × 6!
= 1,44 000 слов
Вопрос 2. Сколько различных слов, каждое из которых содержит 3 гласных и 5 согласных, можно составить из 5 гласных и 19 согласныхсогласные буквы?
Ответ:
Всего тел.
гласных = 5
Всего кол. согласных = 19
Количество слов с 3 гласными и 5 согласными
3 гласных можно выбрать из 5 гласных = 5 C 3 способов = n!/(n-r)!r!= 5!/( 5-3)!3! =10 способов
Из 19 согласных можно выбрать 5 согласных = 19 C 5 способов = n!/(n-r)!r! = 19!/(19-5)!5! = 11 628 способов
Всего выбрано = 5 C 3 × 19 C 5
Теперь 8 букв в каждом выборе можно расположить в 8! пути
Всего кол. слов = 5 C 3 × 19 C 5 × 8!
= 10 × 11 628 × 8!
= 116280 × 8!
= 4 688 409 600 слов
Вопрос 3. Сколько различных слов, каждое из которых содержит 2 гласных и 3 согласных, можно составить из 5 гласных и 17 согласных?
Ответ:
Всего тел.
гласных = 5
Всего кол. согласных = 17
Количество разных слов с 2 гласными и 3 согласными
2 гласных можно выбрать из 5 гласных = 5 C 2 способов = n!/(n-r)!r!= 5!/ (5-2)!2! =10 способов
Из 17 согласных можно выбрать 3 согласных = 17 C 3 способов = n!/(n-r)!r! = 17!/(17-3)!3! = 680 способов
Всего выбрано = 5 C 2 × 17 C 3
Теперь 5 букв в каждом наборе можно расположить в 5! пути
Всего кол. слов = 5 C 2 × 17 C 3 × 5!
= 10 × 680 × 5!
= 6800 × 5!
= 8,16,000 слов
Вопрос 4. Сколько различных слов, каждое из которых содержит 2 гласных и 3 согласных, можно составить из 4 гласных и 7 согласных?
Ответ:
Всего тел.


 гласных = 5
гласных = 5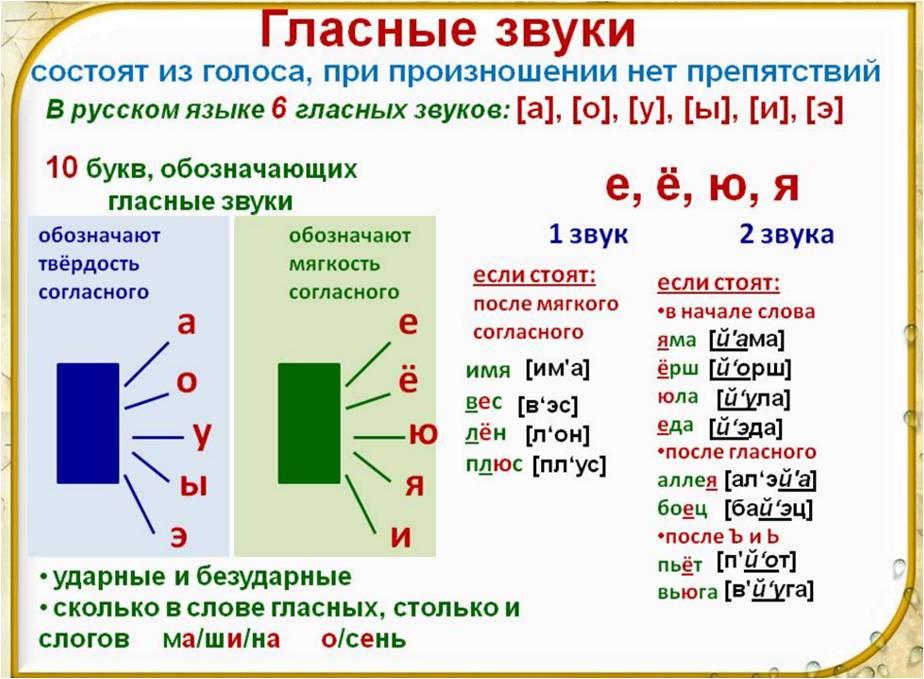 гласных = 5
гласных = 5 гласных = 5
гласных = 5