Конструируя – обучаемся. Сложение и вычитание натуральных чисел
Библиографическое описание:Прончев, Г. Б. Конструируя – обучаемся. Сложение и вычитание натуральных чисел / Г. Б. Прончев, М. А. Лазарев. — Текст : непосредственный // Молодой ученый. — 2010. — № 4 (15). — С. 368-371. — URL: https://moluch.ru/archive/15/1411/ (дата обращения: 15.04.2023).
Эта статья написана, прежде всего, для студентов, готовящихся стать учителями начальных классов. В ней описана система заданий для младших школьников, которая позволяет повысить мотивацию, активировать творческие способности учащихся, в игровой форме освоить новый материал.
Точность и чёткость формулировок при определении понятия любого объекта является главным условием в понимании самого объекта и его свойств [1]. Грамотно построенные вопросы учителя, побуждение к логическим действиям естественно подводят учащихся к восприятию учебной темы.
В предыдущей нашей работе [2] на примере учебной темы «формирование разрядов в позиционных системах счисления» был описан способ подачи нового материала, основанный на создании образа, легко запоминаемого учащимися; движении фигуры, её трансформации в другую фигуру, в которой видны все составляющие элементы, естественно воспринимаемые учащимися.
В данной работе на примере учебных тем «сложение чисел» и «вычитание чисел» будет описан подход авторов к проведению занятий по этим темам, предложена новая система заданий.
Сложение однозначных чисел.
Число – это количественная характеристика объекта.
Однозначное число – это число, в написании которого используется только один знак (символ) без повторения.
При написании чисел используются знаки (символы), которые обычно называют Цифрами. Обычно мы используем десять цифр (т.н. «арабские цифры»):
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Рассмотрим однозначные числа. Очевидно, что их всего десять, и они совпадают с арабскими цифрами. Для любого однозначного числа совокупность (множество) однозначных чисел разбивается на две части (подмножества). Первое подмножество – однозначные числа, сложение с которыми выбранного однозначного числа в сумме дает однозначное число.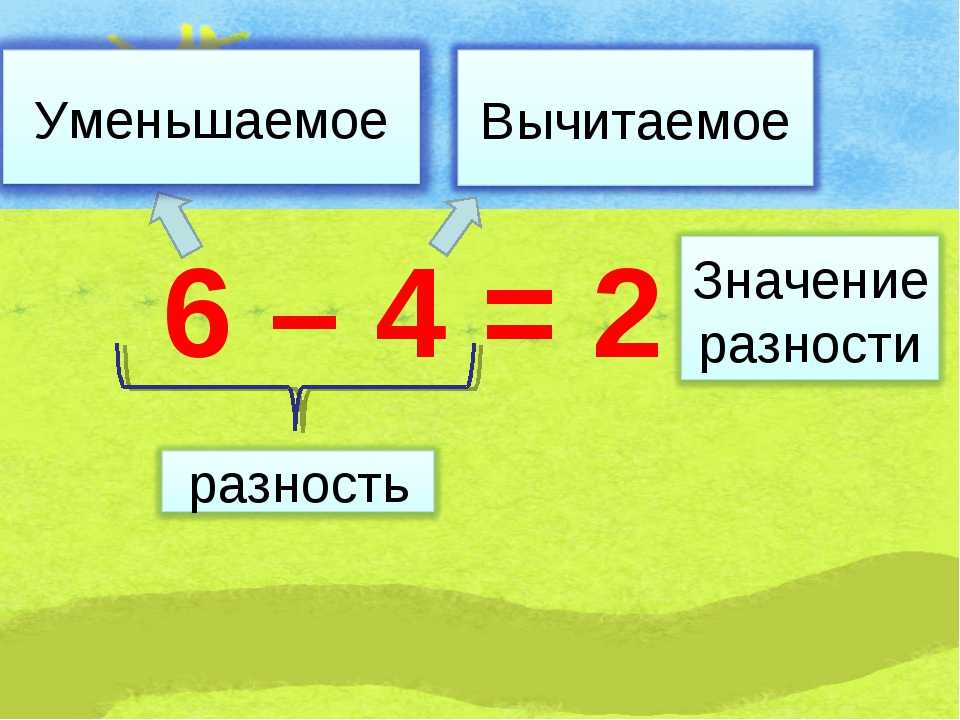
Пример.
Выберем число 6. Для этого числа множество однозначных чисел разбивается на два подмножества: первое – числа от 0 до 3; второе – числа от 4 до 9.
И так происходит с любым числом в этом множестве. Попробуйте сами и убедитесь!
Число 10.
Этому числу уделим большее внимание. Во-первых, в написании этого числа используется два различных знака: первый – 1; второй – 0. Что они обозначают? 1 – количество десятков. 0 – количество единиц следующего десятка [2].
Посмотрим, как оно записывается. Представьте себе вертикальный столбик, в котором находится десять разноцветных предметов. На какую цифру этот разноцветный столбик похож? Количество предметов в нём – десять, сколько десятков мы имеем? Ответ —
Здесь проявилась гениальная догадка человека: поставить эту цифру рядом с только что написанным числом слева, потому что оно старше написанного.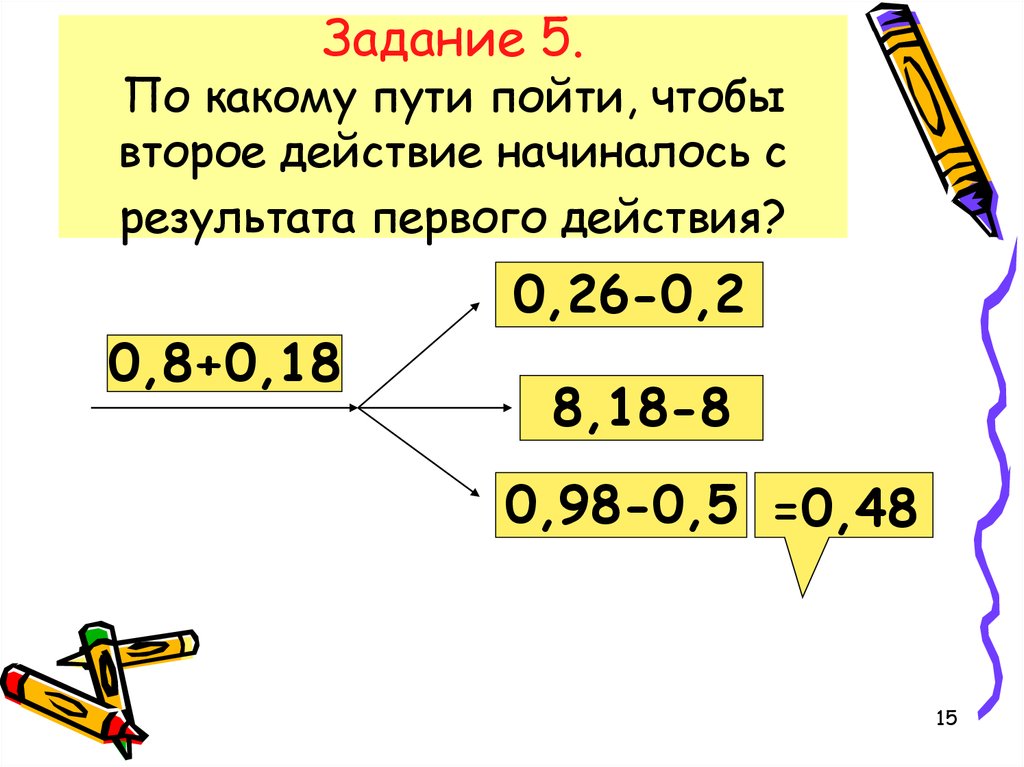 А что нам мешает сжать этот столбик до палочки, похожей на цифру 1. Поставим её рядом с написанным числом СЛЕВА и запомним, что это – один десяток, а на место, где раньше были написанные цифры, поставим цифру 0. Она будет обозначать количество единиц следующего десятка, но их нет, пусто, а пустое множество мы обозначаем цифрой 0.
А что нам мешает сжать этот столбик до палочки, похожей на цифру 1. Поставим её рядом с написанным числом СЛЕВА и запомним, что это – один десяток, а на место, где раньше были написанные цифры, поставим цифру 0. Она будет обозначать количество единиц следующего десятка, но их нет, пусто, а пустое множество мы обозначаем цифрой 0.
Так обозначилось число ДЕСЯТЬ – двумя различными цифрами. И процесс набора повторился. Так образовалась запись числа десять. Эта мысль дала возможность поместного написания цифр, обозначающих общее количество взятых предметов, а место для написания нового значения данного числа назвали разрядом числа.
Сколько цифр можно уместить на этом месте, разряде? Только десять. Потому что других цифр мы не используем. Это оказалось и не нужным. Описанный процесс можно сделать наглядным. Цифры 1, 2 и т.д. появляются с количеством единиц в следующем десятке. Это происходит до набора полного десятка. Сколько полных десятков мы набрали? Ответ – 2 десятка. В разряде десятков мы должны написать цифру 2. Цифру 0 надо поставить в разряде единиц этого числа. Этот набор производится до момента появления 10-го десятка, который по аналогии переходит в следующий разряд – одной сотни. Разряды десятков и единиц – обнуляются. Обнуление единиц младшего разряда является окончанием выполнения задания.
В разряде десятков мы должны написать цифру 2. Цифру 0 надо поставить в разряде единиц этого числа. Этот набор производится до момента появления 10-го десятка, который по аналогии переходит в следующий разряд – одной сотни. Разряды десятков и единиц – обнуляются. Обнуление единиц младшего разряда является окончанием выполнения задания.
Записывать эти примеры хорошо было бы «в столбик», т.к. вся последующая работа учащегося происходит сложением и вычитанием в столбик.
Для учащихся 1-х классов нужно давать задания такого типа: составить примеры на сложение и вычитание так, чтобы результатом было однозначное число. Примеры на вычитание дать после практической работы.
Такую практическую работу, к сожалению, ученики не выполняют ни в школе, ни в подготовительных группах. А зря! Такие задания приучают ребёнка к самостоятельности, уверенности в правильности своих действий, они перестают бояться аналогичных заданий, данных им учителем.
Приведем пример такой практической работы.
Практическая работа для учеников 1 класса.
На листе бумаги нарисовали карандашом любую замкнутую фигуру любого размера. Обозначили внутреннюю часть фигуры числом 5. Вырезали её. Внутри фигуры нарисовали ещё одну любую замкнутую фигуру. Обозначили её цифрой 3. Теперь по контуру вырезали фигуру, обозначенную цифрой 3. Удалим её. Каким числом обозначить то, что осталось? Подсознание подсказывает ответ – числом 2.
Вопрос: Что произошло с размером первоначальной фигуры?
Ответ: Он уменьшился.
Вопрос: Назовите математически действие удаления.
Ответ: Вычитание.
Вопрос: Назовите результат действия удаления.
Ответ: Остаток.
Вернёмся к примеру.
Первое число назвали уменьшаемым. Оно уменьшилось. Второе число назвали вычитаемым. Третье число назвали остатком или разностью между уменьшаемым и вычитаемым.
Продолжение. Попробуем восстановить фигуру.
Вопрос
Ответ: Объединить вырезанную фигуру с оставшейся.
Вопрос: Какое математическое действие напоминает Вам эта операция?
Ответ: Сложение.
Вывод: Действие вычитания проверяется действием сложения.
Первый тип примеров (без перехода через десяток).
Пример на сложение:
Пример на вычитание:
Первый тип примеров на сложение и вычитание без перехода через десяток в каждом разряде учащиеся усвоили и выполнили.
В первом типе примеров учащиеся понимают, что можно вычислить сумму не только записав выражение строчкой. Можно в столбик. Оказывается, можно выбрать самостоятельно такие слагаемые, которые в сумме с данным числом дадут в результате число, меньшее десятка. Таких вариантов может быть несколько.
После усвоения заданий 1-го типа, можно перейти ко 2-му типу заданий. Для этого нужно обязательно ещё раз повторить тему «образование десятка» и разобраться в теме сложение чисел с переходом через десяток.
Второй тип примеров (с переходом через десяток).
Напишем любое число, например 4. Прибавим к нему любое число из “второго подмножества”. Например, 7. Число 7 мы представим в виде суммы «удобных» слагаемых (6+1). Далее применим правило прибавления к числу суммы двух слагаемых. К числу 4 прибавляем число 6. Получаем число 10, один десяток. Этот один десяток мы переводим в число 1 и записываем эту 1 в разряде десятков, рядом со вторым слагаемым:
4 + 7 = 4 + (6 + 1) = 10 + 1 = 11.
Второй способ
Разделим вертикальными рядами разряды чисел.
В каждом одноимённом разряде напишем сумму двух слагаемых с переходом через десяток. Первое слагаемое – произвольное число. Второе слагаемое выберем из второго множества, чтобы сумма с первым слагаемым в данном разряде была двузначным числом. Найдем их сумму. Рядом с числом 4 напишем ещё произвольную цифру, например, 3 и прибавим к ней любое число из второго подмножества так, чтобы сумма этих чисел была двузначным числом. И так в каждом разряде.
Первое слагаемое – произвольное число. Второе слагаемое выберем из второго множества, чтобы сумма с первым слагаемым в данном разряде была двузначным числом. Найдем их сумму. Рядом с числом 4 напишем ещё произвольную цифру, например, 3 и прибавим к ней любое число из второго подмножества так, чтобы сумма этих чисел была двузначным числом. И так в каждом разряде.
Это уже творческий процесс. Он зависит только от действий самого ученика.
Пример на сложение:
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Первое слагаемое составляю произвольно. По одной цифре в одном разряде. Сколько цифр написать? Сколько хочу. Хоть до конца строчки. Не забыть поставить плюс слева. Перехожу ко второму слагаемому. Второе слагаемое нужно записать под первым: единицы под единицами, десятки под десятками, сотни под сотнями и т. д. Подбирая числа так, чтобы они в сумме с верхним числом давали двузначное число в данном разряде.
Ученик сам создал пример и сам подсчитал его результат. Он научился самостоятельно составлять пример на сложение и вычитание без помощи других.
Третий тип примеров (смешанный).
Назовем его смешанный тип.
А как это?
Первое слагаемое записываю произвольно. Второе слагаемое записываю под первым. При сложении, надо учитывать, в каком разряде надо переносить единицу в старший разряд, а в каком нет. Этим примером отрабатывается
Пример на сложение.
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Мы видим, что в первом и третьем разрядах сумма цифр одноименных разрядов не превышает десяти, а во втором разряде – больше десяти.
Четвёртый тип примеров (круглое число).
В четвёртом типе примеров при сложении и вычитании создаём круглое число.
Пример на сложение:
Первое слагаемое произвольное число. Второе слагаемое записываем под первым, столбиком, подбираем цифры так, чтобы сумма цифр одноименных разрядов оканчивалась на ноль, т.е. десятком.
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Пример на вычитание:
Первое число – уменьшаемое, создается учащимся произвольно. Старший разряд – число отличное от нуля, остальные разряды – нули. Под ним записывается вычитаемое – произвольно. Далее выполняется вычитание. Выбираем случай, когда цифра старшего разряда уменьшаемого меньше самого вычитаемого.
Самостоятельная работа.
Первый тип примеров (без перехода через десяток).
Пример на сложение .
Пример на вычитание.
Второй тип примеров (с переходом через десяток в каждом разряде).
Пример на сложение .
Пример на вычитание.
Третий тип примеров (смешанный).
Пример на сложение .
Пример на вычитание.
Четвертый тип примеров (с круглым числом).
Пример на сложение .
Пример на вычитание.
Выводы
Системы предложенных в работе заданий в настоящее время нет ни в одном учебнике по математике для начальной школы. Тем не менее, ее использование позволяет повысить мотивацию, активировать творческие способности учащихся, в игровой форме освоить новый материал. Считаем целесообразным дополнить такой системой новые учебники по математике для начальной школы. Необходимо использовать данный материал в контрольных работах студентов-педагогов, планирующих работать в начальной школе. Это поможет повысить профессионализм будущих преподавателей.
Считаем целесообразным дополнить такой системой новые учебники по математике для начальной школы. Необходимо использовать данный материал в контрольных работах студентов-педагогов, планирующих работать в начальной школе. Это поможет повысить профессионализм будущих преподавателей.
Литература
1. Лазарев М.А., Воробьева Н.А., Прончев Г.Б. Теоретико-дидактический подход к формированию понятия // Журнал Профессиональное образование / Приложение “Новые педагогические исследования. 2007. № 1. С. 75 – 77.
2. Лазарев М.А., Воробьева Н.А., Прончев Г.Б. Формирование понятия разряда в позиционной системе счисления / в кн.: Исследования в профессиональном образовании. Сборник статей аспирантов и докторантов. Выпуск 1, М.: НОУ “ИСОМ”, 2007, С. 37 – 40.
Основные термины (генерируются автоматически): число, десяток, цифра, Первое, слагаемое, сложение, второе, вычитание, разряд, однозначное число.
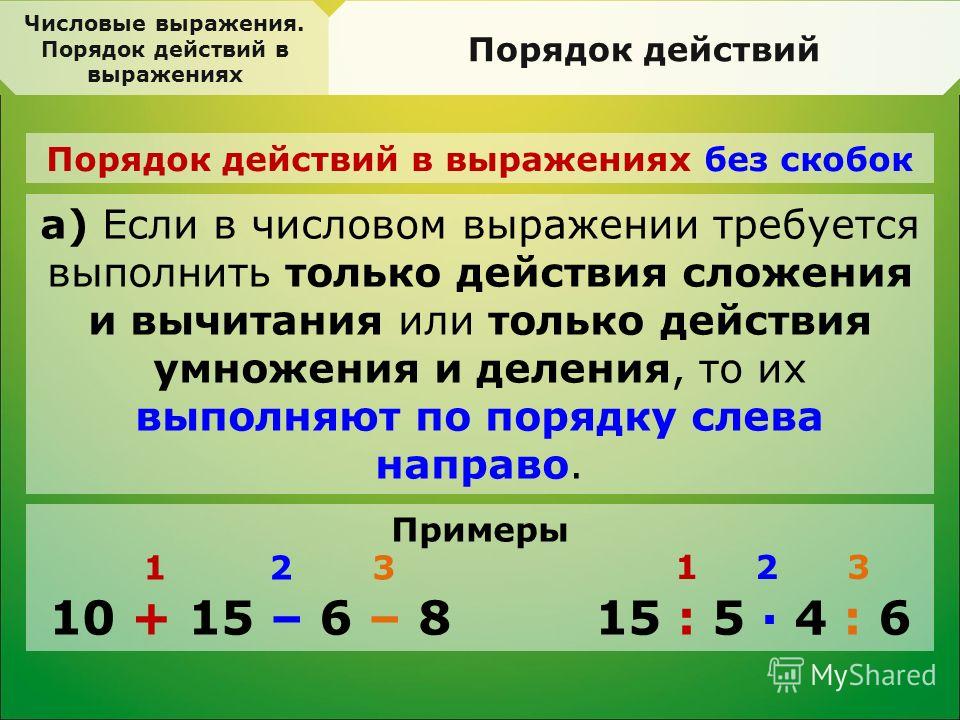
Порядок выполнения действий в примерах
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Презентация
учителя
Здравствуй, четвероклассник.
Приглашаю тебя на урок по теме «Порядок
выполнения действий ».
Сегодня тебе предстоит повторить порядок
выполнения действий в выражениях со
скобками и без скобок; совершенствовать
навык решения задач и примеров.
Надеюсь, что тебе понравится мое задание.
Буду рада прочитать твой ответ в строке
«комментарий».
Твой учитель.
Познакомься с содержанием
урока. Узнай, что ты сможешь
сделать на этом уроке.
3. Порядок выполнения действий.
Если тебе нужно выполнить несколько арифметическихдействий (сложение, вычитание, умножение и деление), то
сначала выполняют умножение и деление по порядку слева
направо, а затем сложение и вычитание по порядку слева
направо.

Например,
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим деление,
потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 — 5 = 5
4) 5 + 48 = 53
Вспомни
правило.
4. Порядок выполнения действий.
Если в выражении есть скобки, то сначала выполняютдействия в скобках, но обязательно учитывать первое и
второе правила.
Например,
Вспомни правило.
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим вычитание в
скобках, затем деление, потом умножение и сложение.
1) 25 — 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53
5. Порядок выполнения действий.
Например,В числовом выражении 4 арифметических действия: сложение,
деление, сложение и деление.

Определим порядок действий и запишем их над
арифметическими знаками: сначала производим действия в
скобках (деление, затем сложение), затем деление, потом
сложение.
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Посмотри фильм.
По ходу просмотра фильма постарайся
вспомнить материал 3 класса.
Если ты что-то не помнишь,
останавливай просмотр фильма в
непонятных местах и просматривай их
еще раз.
После просмотра фильма выполни
задания на Рабочем листе (его надо
скачать и распечатать, чтобы тебе было
удобно).
Будет здорово, если в комментариях ты
напишешь, все ли у тебя получилось.
English Русский Правила
Montessori 1st Operations — сложение и вычитание в App Store
Описание
Удивительное приложение для детей от 5 до 8 лет, посвященное изучению сложения и вычитания!
— Выбрано в iTunes!
Хотите создать прочную математическую базу для своих детей? Монтессори 1st Operations — это революционное приложение, объединяющее 100-летнюю проверенную педагогику с лучшими технологиями 21-го века и забавными монстрами, чтобы представить 4 очень важных понятия (сложение, вычитание, удвоение/половина, нечет/чет).
Он предлагает четкий и простой подход к первым операциям, который навсегда изменит отношение детей к математике, независимо от того, используют ли они ее в классе или дома. Мы внедрили алгоритм динамического прогресса, который следит за прогрессом каждого пользователя и адаптирует игры в соответствии с их уровнем.
Рекомендуемый возраст: от 5 до 8 лет
Основные характеристики:
— Играйте с материалами Монтессори: числовые стержни и счетчики
— Изучайте математику в интерактивном приложении с очаровательной графикой!
— Мастер сложения и вычитания в естественной прогрессии с числами от 1 до 99!
— Приступайте к умножению и делению, используя понятия двойного и половинного!
— Запустите игровую приставку, в которой много игр!
— Получайте удовольствие от «лаборатории монстров», создавая своего собственного монстра!
• Разработано учителями.
• Безопасен для детей! Абсолютно никакой сторонней рекламы!
Скачайте 1st Operations прямо сейчас и будьте готовы стать непобедимым в математике!
Если вам нравятся Монтессори-первые операции, вам также понравятся и другие наши образовательные приложения: http://edokiacademy. com.
com.
Если у вас есть вопросы или комментарии к нашему приложению, напишите нам по адресу: [email protected], так как мы не можем отвечать на отзывы, оставленные в iTunes.
ЗНАЙ, ЧТО ВНУТРИ
Как участник MOMs with Apps, мы следуем рекомендациям «Знай, что внутри» для детских приложений
Мы очень серьезно относимся к защите персональных данных. При использовании нашего приложения ваш ребенок никогда не встретит:
— реклама
— внутри приложений
— ссылки на социальные сети
— запрос персональных данных
Версия 1.4.3
Это приложение было обновлено компанией Apple для отображения значка приложения Apple Watch.
Веселые новые игры, невероятная лаборатория монстров и связь с нашей родительской панелью управления!
Рейтинги и обзоры
4 оценки
Отличный!
Монтессори 1-е Операции — прекрасное учебное пособие для изучения математических понятий с упором на сложение, вычитание, шансы, четы и деление чисел пополам.
С помощью визуальных подсказок и увлекательной анимации дети научатся более осмысленно обрабатывать фундаментальные математические вычисления. Я с радостью рекомендую этот продукт и предлагаю его начинающим учащимся, а также студентам, которые могут испытывать трудности с этими основными понятиями. ~отзыв L.S.Appleby
Отличное приложение для изучения ранних математических понятий
Моему 4 1/2 года нравится это приложение! Она мотивирована и чувствует себя выполненной, когда решает вопрос и получает очки, чтобы получить больше частей монстра. По общему признанию, ее любимое занятие — взрывать их, но за это время она освоила простое сложение и теперь изучает простое вычитание, простое деление (половины, четверти и т. д.) и интересуется четными и нечетными числами. Это приложение помогло ей учиться вместе со мной — в основном потому, что приложение такое же неутомимое, как и она, и я могу настроить объекты для ее расчета только так много раз, прежде чем я достигну своего предела.
Мне нравится, что я могу настроить ее обучение так, чтобы оно соответствовало ее уровню — она еще не готова к двузначным цифрам. Она расстраивалась, используя профиль старшей сестры, поэтому я создал для нее новый, где она укрепила свою уверенность и с нетерпением ждет своего времени на iPad, чтобы она могла играть в свою чудовищную математическую игру.
В целом претензий нет — редкость для дорогого приложения. Он стабилен и отзывчив на нашем iPad 2 и моем iPhone 6P. Музыка/звук приятные и не раздражающие.
Любовь любовь любовь!
должно быть приложение…
Отличное математическое приложение для детей. Весело и легко играть. Мне нравится лаборатория, где можно экспериментировать с монстрами!
Разработчик, EDOKI ACADEMY, не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Для получения дополнительной информации см. политику конфиденциальности разработчика.
Сведения не предоставлены
Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.
Информация
- Продавец
- ЭДОКИ АКАДЕМИЯ
- Размер
- 151,3 МБ
- Категория
- Образование
- Возрастной рейтинг
- 4+, для детей от 6 до 8 лет
- Авторское право
- © Академия Эдоки
- Цена
- 3,99 $
- Сайт разработчика
- Тех. поддержка
- политика конфиденциальности
Опоры
Еще от этого разработчика
Вам также может понравиться
4.
 2 — Арифметические вычисления с использованием арифметических операторов
2 — Арифметические вычисления с использованием арифметических операторовВсе, что мы сделали до сих пор, это сложили вместе переменные. Конечно, мы могли бы также вычитать, умножать, делить или возводить в степень переменные. Нам просто нужно убедиться, что мы используем символы, которые распознает SAS. Это:
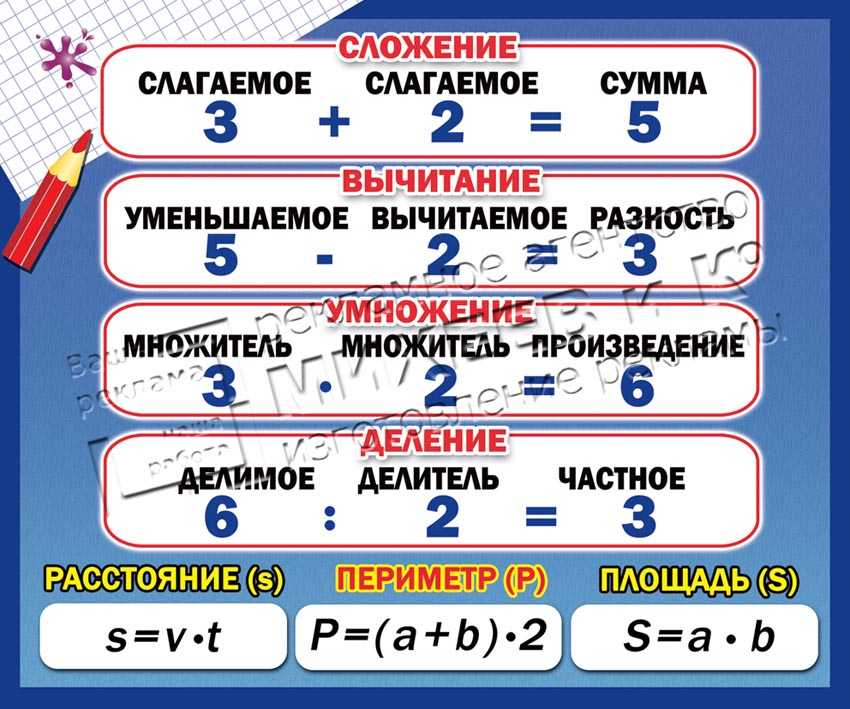
| Эксплуатация | Символ | Заявление о присвоении | Действия предприняты |
| дополнение | + | a = b + c ; | добавить b и c |
| вычитание | — | а = б — в ; | вычесть c из b |
| умножение | * | a = b * c ; | умножить b и c |
| отдел | / | a = b / c ; | разделить b на c |
| возведение в степень | ** | а = б ** в ; | поднять b в степени c |
| отрицательный префикс | — | а = — б ; | взять минус b |
Как и в других языках программирования, в операторе присваивания можно выполнять более одной операции. Операции выполняются так же, как и для любого математического выражения, а именно:
Операции выполняются так же, как и для любого математического выражения, а именно:
- сначала выполняется возведение в степень, затем умножение и деление, и, наконец, сложение и вычитание
- если в одном и том же выражении встречаются несколько экземпляров сложения, несколько экземпляров вычитания или сложения и вычитания, операции выполняются слева направо
- , если несколько экземпляров умножения, несколько экземпляров деления или умножение и деление встречаются вместе в одном выражении, операции выполняются слева направо
- если в одном выражении встречается несколько экземпляров возведения в степень, операции выполняются справа налево Сначала выполняется
- операций в скобках
Это последняя пуля, которую, я думаю, будет полезно знать. Если вы используете круглые скобки, чтобы специально указать SAS, что вы хотите вычислить в первую очередь, вам не нужно так сильно беспокоиться о других правилах. Давайте рассмотрим два примера.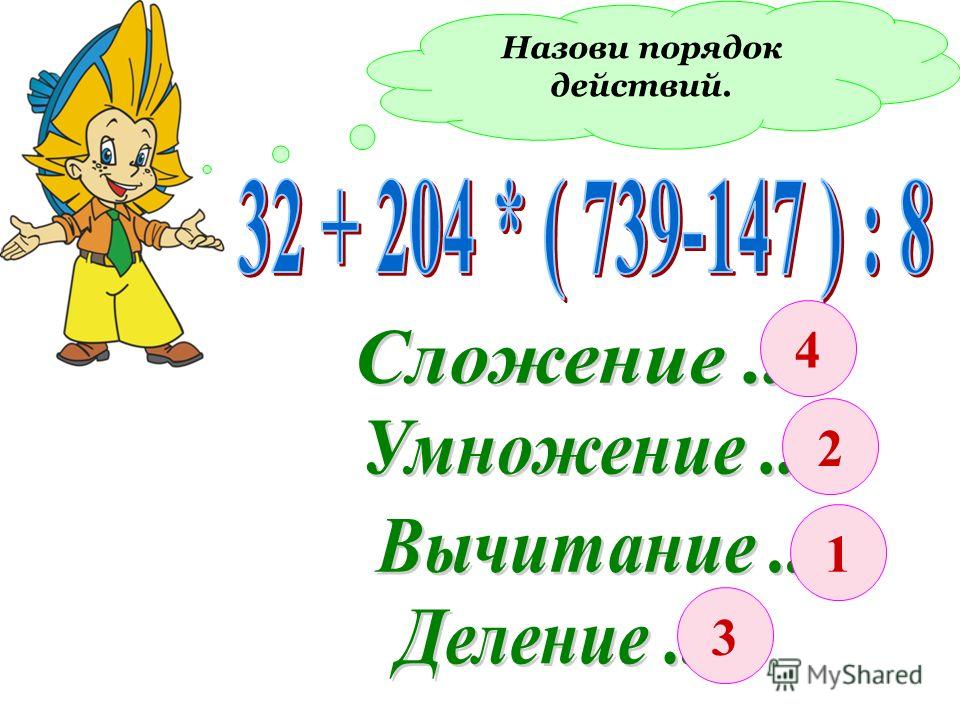
Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (неправильно) вычисляет 9 баллов учащихся.0175 окончательный классов:
DATA классов; входное имя $ 1-15 e1 e2 e3 e4 p1 f1; финал = 0,6*e1+e2+e3+e4/4 + 0,2*p1 + 0,2*f1; ДАННЫЕ; Александр Смит 78 82 86 69 97 80 Джон Саймон 88 72 86 . 100 85 Патрисия Джонс 98 92 92 99 99 93 Джек Бенедикт 54 63 71 49 82 69 Рене Портер 100 62 88 74 98 92 ; БЕГАТЬ; PROC PRINT данные = оценки; имя переменной e1 e2 e3 e4 p1 f1 final; БЕГАТЬ;
Ну да ладно, значит, инструктор должен придерживаться статистики, а не математики. Как видно из заявления о задании, преподаватель пытается указать SAS усреднить четыре экзаменационных балла, сложив их и разделив на 4, а затем умножив результат на 0,6. Давайте посмотрим, что вместо этого делает SAS. Запустить и запустить программу SAS и просмотрите результат, чтобы узнать, сможете ли вы выяснить, что сделала SAS, скажем, для первого студента Александра Смита. Если вы все еще не уверены, еще раз просмотрите правила порядка операций. Правила говорят нам, что SAS first:
Давайте посмотрим, что вместо этого делает SAS. Запустить и запустить программу SAS и просмотрите результат, чтобы узнать, сможете ли вы выяснить, что сделала SAS, скажем, для первого студента Александра Смита. Если вы все еще не уверены, еще раз просмотрите правила порядка операций. Правила говорят нам, что SAS first:
- берет первую экзаменационную оценку Александра 78 и умножает ее на 0,6, чтобы получить 46,8 .
- берет четвертый экзаменационный балл Александра 69 и делит его на 4, чтобы получить 17,25
- берет оценку проекта Александра 97 и умножает ее на 0,2, чтобы получить 19.4
- берет итоговый экзаменационный балл Александра 80 и умножает его на 0,2, чтобы получить 16,0
Затем SAS выполняет все сложения:
46,8 + 82 + 86 + 17,25 + 19,4 + 16,0
, чтобы получить окончательный результат 267,45. Теперь, может быть, это окончательная оценка, которую хочет Александр, но она все равно в корне неверна. Давайте посмотрим, сможем ли мы помочь инструктору по статистике, воспользовавшись последним правилом, согласно которому операции в скобках выполняются в первую очередь.
Давайте посмотрим, сможем ли мы помочь инструктору по статистике, воспользовавшись последним правилом, согласно которому операции в скобках выполняются в первую очередь.
Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (правильно) вычисляет итоговых оценок учащихся:
оценки DATA; входное имя $ 1-15 e1 e2 e3 e4 p1 f1; финал = 0,6*((e1+e2+e3+e4)/4) + 0,2*p1 + 0,2*f1; ДАННЫЕ; Александр Смит 78 82 86 6997 80 Джон Саймон 88 72 86 . 100 85 Патрисия Джонс 98 92 92 99 99 93 Джек Бенедикт 54 63 71 49 82 69 Рене Портер 100 62 88 74 98 92 ; БЕГАТЬ; PROC PRINT данные = оценки; имя переменной e1 e2 e3 e4 p1 f1 final; БЕГАТЬ;
Давайте еще раз разберем расчет окончательного результата Александра. Оператор присваивания для final указывает SAS:
Оператор присваивания для final указывает SAS:
- сначала сложить четыре экзаменационных балла Александра (78, 82, 86, 69), чтобы получить 315
- , а затем разделите эти 315 на 4, чтобы получить средний балл за экзамен 78,75 9.0127
- , а затем умножьте средний экзаменационный балл 78,75 на 0,6, чтобы получить 47,25 .
- , а затем возьмите оценку проекта Александра 97 и умножьте ее на 0,2, чтобы получить 19,4 .
- , а затем возьмите итоговый экзаменационный балл Александра 80 и умножьте его на 0,2, чтобы получить 16,0
Затем SAS выполняет сложение последних трех элементов:
47,25 + 19,4 + 16,0
, чтобы получить окончательный результат 82,65. Там это звучит гораздо лучше. Извините, Александр.
Запустить и запустить программу SAS, чтобы увидеть, как мы это сделали. Просмотрите результаты процедуры печати, чтобы убедиться, что окончательные оценки были рассчитаны в соответствии с пожеланиями преподавателя.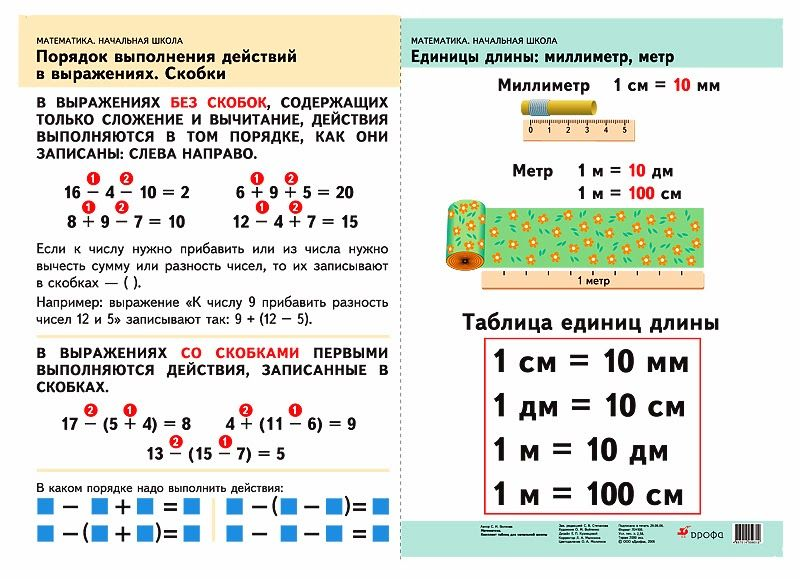
 С помощью визуальных подсказок и увлекательной анимации дети научатся более осмысленно обрабатывать фундаментальные математические вычисления. Я с радостью рекомендую этот продукт и предлагаю его начинающим учащимся, а также студентам, которые могут испытывать трудности с этими основными понятиями. ~отзыв L.S.Appleby
С помощью визуальных подсказок и увлекательной анимации дети научатся более осмысленно обрабатывать фундаментальные математические вычисления. Я с радостью рекомендую этот продукт и предлагаю его начинающим учащимся, а также студентам, которые могут испытывать трудности с этими основными понятиями. ~отзыв L.S.Appleby