«Порядок выполнения действий в выражениях. Скобки»
- Шевцова Елена Викторовна
Разделы: Начальная школа, Конкурс «Учение с увлечением, или Как полюбить математику?»
Класс: 2
Ключевые слова: математика, Порядок выполнения действий в выражениях
Тип урока: Урок «открытия» новых знаний.
Цель: создать условия для формирования умения определять порядок действий в выражениях, использовать скобки.
Планируемые результаты.
Предметные:
- дети научатся определять порядок действий в выражениях со скобками и применять алгоритм выполнения действий на практике;
- читать выражения со скобками и без скобок.

Метапредметные.
Познавательные УУД:
- дети будутсравнивать выражения с целью выделения признаков сходства и различия;
- аргументировать свои ответы;
- находить необходимую информацию в учебнике;
- проводить анализ и синтез в результате решения выражений со скобками и без скобок.
Регулятивные УУД:
- принимать и удерживать цель на протяжении всего урока;
- выполнять самопроверку по образцу;
- оценивать свою работу;
- действовать по намеченному плану.
Коммуникативные УУД:
- включаться и поддерживать учебный диалог;
- уметь слушать и понимать других.
Личностные УУД:
- самоопределение;
- смыслообразование («какое значение, смысл имеет для меня умение учиться, зачем мне знать порядок выполнения действий в выражениях со скобками»).

Оборудование: учебник – Истомина Н.Б. «Математика 2 класс» Смоленск: «Ассоциация XXI век», 2012; карточки для индивидуальной работы; презентация.
Описание урока
Урок открытия новых знаний.
Используется проблемно-диалогическая технология Е.Л.Мельниковой. Для постановки проблемы использую прием № 1, для этого предъявляю противоречивые факты. Для решения поиска проблемы использую подводящий диалог, работу в парах.
Результатом этапа поиска решения является формулирование темы и целей урока, составление алгоритма определения порядка действий в выражениях.
Используя полученные знания и алгоритм, учащиеся выполняли продуктивные задания учебника.
Это первый урок в группе уроков по данной теме. На данном уроке учащиеся изучили правило порядка действий в выражениях.
При планировании урока были учтены все особенности класса. Осуществляя индивидуальный подход, учащиеся были распределены в пары так, чтобы в каждой были и «слабые», и «сильные» ученики, так, чтобы «слабый» оказался в ситуации успеха и «сильный» участвовал в поиске правильных ответов.
Высокая работоспособность достигнута сменой деятельности, наличием наглядности в виде презентации и проведением двух динамических пауз.
Использовались различные приемы устной и письменной работы, фронтального опроса, самостоятельной работы с самопроверкой в классе.
Этапы урока | Ход урока |
1.Мотивация к учебной | — Всем, всем — (на доске карточки с равенствами и неравенствами, арифметическими действиями) Ученики называют известные им математические термины. |
2. Актуализация знаний | — У вас на столах — карточки. (Приложение 1) Что на них записано? (выражения) Как вы думаете, какое задание я вам предложу сделать с данными выражениями? (найти, вычислить значения данных выражений) |
3. Выявление места и причины затруднения и | |
4. Построение проекта выхода из затруднении («открытие детьми нового знания» (подводящий диалог) -Чем отличаются выражения? (Порядком действий.) — Мы поняли, как нужно решать эти выражения. А как показать это другим? — Чего мы не знаем? Что надо узнать? Чему научиться? (Как показать, какое действие надо выполнить первым?) Узнать … Как показать, какое действие надо выполнить первым? Научиться … определять порядок действий в выражениях (со скобками и применять алгоритм выполнения действий на практике.) и находить значения этих выражений -Для определения порядка действий иногда не хватает специального знака. (Если ученики затрудняются сделать этот вывод, то можно задать наводящий вопрос) — «Как водитель на дороге узнает, куда надо ехать и с какой скоростью?» — Какой бы вы использовали знак с этой целью? Учащиеся предлагают свои варианты. — Математики всего мира много лет назад тоже столкнулись с этой проблемой, поэтому они договорились обозначать действие, которое надо выполнить первым, скобками.  Что показывают скобки в выражении? (Какое действие выполняется первым.) — Давайте откроем учебник на с. 66 и подтвердим правильность наших выводов. Еще сегодня мы будем учиться правильно читать выражения со скобками и без них. — Прочтем текст под условным знаком «новая информация» (учебник с.66) Вывод: 1. Если в выражении стоят скобки, то действие, записанное в них, нужно выполнить вначале. 8 — (3+4) Прочтем наше выражение — В этом выражении есть скобки, значит, сначала мы должны выполнить действие, которое в скобках. (найдем сумму 3 и 4 =7, из 8 вычтем 7= 1 | 2. Если в выражении нет скобок, то действия выполняются по порядку, слева направо. (пример на доске 8-3+4 ) — Прочтем наше выражение (к разности 8 и 3 прибавить 4) — В этом выражении нет скобок, поэтому действия выполняются в порядке, в котором они записаны (слева направо).  сначала найдем разность 8 и 3=5, теперь к 5 прибавим 4=9) |
5. Первичное закрепление во внешней речи | Первичное закрепление 1) 1 хлопок учителя – поднимаются или опускаются руки, 2 хлопка – действие для ног (встать или присесть) |
6. Самостоятельная работа с самопроверкой по эталону Самостоятельная работа с самопроверкой по эталону | Самостоятельная работа с самопроверкой по образцу. Давайте вспомним, чему мы сегодня должны научиться… — Определять порядок действий в выражениях со скобками и находить значения выражений (применять алгоритм выполнения действий на практике.) |
| Работа в группах |
ПАМЯТКА №3 – Как будем действовать, чтобы определить порядок? Алгоритм: |
Работа в парах Обсудить в парах: в каких парах выражений значения одинаковые, а в каких разные. | Физминутка. |
7. Включение в систему знаний и повторение | Карточки для индивидуальной работы 2. Расставь порядок действий. Проверить (если будет время) |
8. Рефлексия учебной деятельности | Что должны были узнать?… |
9. Самооценка | «Дорожка успеха» (см. Приложение 2) |
10. | 1. №225 (5-8), тпо №103, 105 |
| ТЕМА: МЕТОДИКА ОБУЧЕНИЯ АРИФМЕТИЧЕСКИМ ДЕЙСТВИЯМ
И ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ
С арифметическими действиями учащиеся знакомятся сразу же после изучения числа 2. Изучение каждого из чисел первого десятка (кроме 1), завершается изучением действий сложения и вычитания в пределах этого числа. Действие сложение и вычитание изучаются параллельно. Учащиеся знакомятся со знаками сложения — плюсом (+), вычитания- минусом (-) и знаком равенства — равно (=). При изучении данной темы учащиеся должны овладеть приемами вычисления, получить прочные вычислительные навыки, заучить результаты сложения и вычитания в пределах 10, а также состав чисел первого 10, узнавать и показывать компоненты и результаты двух арифметических действий и понимать их названия в речи учителя. По мере овладения учащимися натуральной последовательностью чисел и свойством этого ряда нужно знакомить и с приемами сложения и вычитания, опирающимся на это свойство натурального ряда чисел. Дети учатся этим приемам прибавлять и вычитать единицу из числа, т.е. присчитывать и отсчитывать по 1. Когда учащиеся научились прибавлять и вычитать по одному, надо учить их прибавлять по два. Когда учащиеся овладели приемами присчитывания, учитель знакомит их с приемами отсчитывания. Если приемами присчитывания ученики первого класса овладевают довольно быстро, то приемами отсчитывания — намного медленнее. Трудность состоит в том, что прием отсчитывания основан на хорошем знании обратного счета, а обратный счет для многих учащихся первого класса труден. Кроме того, ученики плохо запоминают — сколько нужно отнять, сколько уже отняли, сколько ещё надо отнять. При изучении каждого числа первого десятка учащиеся получают представление и о составе этих чисел. В начале необходимо давать такие упражнения, в которых одно из слагаемых воспринимаются детьми наглядно, а второе они отыскивают по представлению. При выполнении действий сложения и вычитания в пределах данного числа вводятся решение примеров с отсутствующим компонентом. Его обозначают точками, рамками, знаками вопросов и т.д., Запишем 1-1=0 (отсутствие предметов обозначают цифры О) Решаются еще примеры, когда разность равна нулю. Нуль сравнивается с единицей. Устанавливается, что ноль меньше единицы, единица больше нуля, поэтому ноль должен стоять перед единицей. Однако учитель должен помнить, что ноль не относится к натуральным числам. Поэтому ряд натуральных чисел должен начинаться с единицы. Вводить число ноль в качестве вычитаемого, а потом и слагаемого следует на большом числе упражнений. Смысл действий с нулем будет лучше понять учащимся, если ноль в качестве вычитаемого и ноль в качестве слагаемого будет вводиться не одновременно. Полезно показать учащимся и зависимость изменения суммы от применения слагаемых, а также изменения остатка от изменения уменьшаемого. Учитель первого класса должен обращать внимание учащихся на то, что сумма всегда больше каждого из слагаемых, а остаток всегда меньше уменьшаемых. Уменьшаемое больше или равно вычитаемому, в противном случае вычитание произвести нельзя. Уже с первого класса ученики должны быть приучены к проверке правильности решения примеров.
Овладение вычислительными приемами сложения и вычитания в пределах 20 основано на хорошем знании сложения и вычитания в пределах 10, знание нумерации и состава чисел в пределах 20. При изучении действий сложения и вычитания в пределах 20, как и при изучении соответствующих действий в пределах 10, большое значение имеет наглядность и практическая деятельность с пособиями самих учащихся. Действия сложения и вычитания целесообразнее изучать параллельно после знакомства с определенным случаем сложения изучать соответствующий случай вычитания сопоставления со сложением. Во втором классе учащиеся должны знать название компонентов действий сложения и вычитания. 1. Приемы сложения и вычитания, основанные на знаниях десятичного состава чисел. 2. Сложение и вычитание без перехода через десяток: а) к двухзначному числу прибавляется однозначное число. Из двухзначного числа вычитается однозначное число; б) получение суммы 20 и вычитание однозначного числа из 20; в) вычитание из двухзначного числа двухзначного: 15-12, 20-15. Решение примеров такого вида можно объяснить разными приемами: 1. Разложить уменьшаемое и вычитаемое на десятки и единицы и вычитать десятки из десятков, единицы из единиц. 2. Разложить вычитаемое на десяток и единицы. Вычитать из уменьшаемого десятки, а из полученного числа — единицы. 3. Сложение и вычитание с переходом через ряд представляет наибольшие трудности для учащихся, с психофизическими нарушениями. вычитание с переходом через десяток тоже требует ряд операций; — уменьшаемое разложить на десяток и единицы — вычитаемое разложить на два числа, одно из которых равно числу уменьшаемого единицы — вычесть единицы — вычесть из десятка оставшееся число единиц Подготовительная работа должна заключаться в повторении: а) таблица сложения и вычитания в пределах 10, б) состава чисел первого десятка (всех возможных вариантов из двух чисел) в) дополнение чисел до 10 г) разложение двухзначного числа на десятки и единицы д) вычитание из десяти однозначных чисел е) рассмотрение случаев вида 17-7, 15-5. Сложение и вычитание в пределах 100. При обучении сложению и вычитанию в пределах 100 соблюдаются все требования, которые предъявляются к обучению выполнению действий в пределах 20. Многие трудности, которые испытывают дети при выполнении действий сложения и вычитания в пределах 20, не снимаются и при выполнении этих же действий в пределах 100. Как показывают опыт и специальные исследования, по-прежнему большие затруднения учащиеся испытывают при выполнении действия вычитания. Наибольшее количество ошибок возникает при решении примеров на сложение и вычитание: из единиц вычитаемого единицы уменьшаемого. Последовательность изучения действий сложения и вычитания обусловлено нарастанием ступени трудности при рассмотрении различных случаев. Различают: 1. Сложение и вычитание круглых десятков (30 + 20, 50-20, решение основано на знании нумерации круглых десятков) 2. Сложение и вычитание без перехода через разряд. 3. Сложение двухзначного числа с однозначным числом, когда в сумме получается круглые десятки. Вычитание из круглых десятков однозначного и двухзначного числа. 4. Сложение и вычитание с переходом через разряд. Все действия с примерами 1,2, групп выполняются приемами устных вычислений, то есть вычисления надо начинать с единиц высших разрядов. Запись примеров производится в нумерации, десятичного состава чисел, таблиц сложения и вычитания в пределах 10. Действия сложения и вычитания изучаются параллельно. Методика изучения табличного умножения и деления. В практике работы школы в начальных классах получила рассмотрение следующая система изучения действий умножения и деления: 1. Введение понятия об умножении как сумм одинаковых слагаемых. 2. Составление таблицы умножения числа 2. 3. Понятие деления на равные части. 4. Составление таблицы деления на 2. 5. Составление таблицы умножения в пределах 20. 6. Составление таблицы деления в пределах 20. 7. Деление по содержанию. 8.Сопоставление умножения и деления как взаимообратных действий. 9. Изучение умножения в пределах 100. Составление таблиц умножения и деления. Практическое знакомство с переместительным законом умножения. 10. Деление с остатками 11. Умножение на 1 и единицы. Деление на 1. Ноль как компонент умножения. Ноль как делимое. При обучении умножению и делению перед учителем стоит сложная задача — раскрыть смысл каждого арифметического действия на конкретном материале. Обучение табличному умножению и делению в пределах 20. В 2 классе учащиеся получают понятие об умножении и знакомятся с действиями умножения и деления в пределах 20. Лучшему осознанию учащимся смысла действия умножения способствует подготовительная работа: счет равными группами предметов, а также счет по 2, 3, 4, 5, до 20. После того как учащиеся получают первое представление об умножении, познакомятся со знаком умножения и записью этого действия, можно переходить к изучению таблицы умножения числа 2. Таблица умножения составляется по постоянному множимому. Этапы знакомства с табличным умножением числа 2: 1. Счет предметов от 2 до 20. 2. Счет изображений предметов по 2 на рисунках или числовых фигурках и составление примеров на сложение. 3. Замена сложения умножением и чтения таблицы умножения. Обучение табличному умножению в пределах 1000. В 2 классе повторяется табличное умножение в пределах 20 и заканчивается изучение всего табличного умножения и деления. По-прежнему много внимания уделяется наглядной основе и счета равными группами их числам. После составления таблицы умножения числа 6 учитель должен обратить внимание на то что ответ каждого последующего примера может быть получен из предыдущего путем прибавления 6 (единиц множимого). Обучение табличному делению в пределах 20. В начальных классах действие деления рассматривается в зависимости от действия умножения. Только тогда дети хорошо усваивают сущность деления, когда сопоставляется с умножением, устанавливается взаимосвязь между этими двумя действиями. Опыт показывает, что вывод деления из умножения без объявления сущности самого процесса деления оказывается малопонятным. Деление с остатком вводится после изучения табличного деления. На деление с остатком дети допускают много ошибок. Они либо не записывают, либо прибавляют его к частному, либо получают остаток больше делителя. Методика изучения арифметических действий в пределах 1000 Все действия в пределах 1000 без перехода через разряд учащиеся выполняют приемами устных вычислений с записью в строчку, а с переходом через разряд — приемами письменных вычислений с записью в столбик. Важно постепенно нарастание трудности при решении арифметических примеров, каждый последующий уровень в решении примеров должен опираться на знание предыдущих случаев. Сложение и вычитание в пределах 1000. В изучении действий сложения и вычитания в пределах 1000 можно выделить следующие этапы: 1. Сложение и вычитание без перехода через разряд. — сложение и вычитание круглых сотен. Действие производится на основе знаний нумерации, и сводятся по существу к действиям в пределах 10; — сложение и вычитание круглых сотен и единиц, круглых сотен и десятков; — сложение и вычитание круглых десятков, а также круглых сотен десяток; — сложение трехзначных чисел с однозначным числом, двухзначным и трехзначным без перехода через разряд и соответствующие случаи вычитания; — особые случаи сложения и вычитания. 2. Сложение и вычитание с переходом через разряд. Сложение и вычитание с переходом через разряд — это наиболее трудный материал. Поэтому учащиеся выполняют действия в столбик. Сложение и вычитание в столбик производятся над каждым разрядом в отдельности и сводятся к сложению и вычитанию в пределах 20. При решении примеров на сложение и вычитании с переходом на разряд соблюдается следующая последовательность: 1. Сложение и вычитание с переходом через разряд в одном разряде (единиц или десятков) 2. Сложение и вычитание с переходом через разряд в двух разрядах (единиц или десятков) 3. Особые случаи сложения и вычитания, когда в сумме или разности получается один или два нуля, когда в уменьшаемом содержится один или два нуля, когда в уменьшаемом содержится единица. 4. Вычитание трехзначных, двухзначных и однозначных чисел из 1000. Умножение и деление в пределах 1000. Умножение и деление также как сложение и вычитание, могут производиться как устными, так и письменными приемами вычислений, записываться в строчку или в столбик. 1. Устное умножение и деление в пределах 1000: — умножение и деление круглых сотен — умножение и деление круглых десятков на однозначное число: а) рассматриваются случаи умножения и деления круглых десятков, которые сводятся к табличному умножению и делению; б) рассматриваются случаи, которые сводятся к нетабличному умножению и делению без перехода через разряд. 2. Умножение и деление трехзначных чисел на однозначное число без перехода через разряд. 3. Умножение десяти и ста, умножение на десять и сто. 4. Деление на десять и сто: — письменное умножение и деление в пределах 1000; — умножение и деление на однозначное число с переходом через разряд; — умножение двухзначного числа на однозначное с переходом через разряд в разряде десятков или единиц; — умножение двухзначного числа на однозначное с переходом через разряд в разряде единиц и десятков; — умножение трехзначного числа на однозначное число с переходом через разряд в одном разряде — единиц или десятков; — умножение трехзначного числа на однозначное число с переходом через разряд в двух разрядах — единиц и десятков — особый случай умножения — первый множитель — трехзначное число с нулем на конце или в середине; — умножение двухзначного числа на круглые десятки. Деление изучается в такой последовательности. 1. Число сотен, десятков и единиц делитель без остатка на делитель. 2. Число сотен делится на делитель без остатка, а число десятков без остатка на делитель не делится. 3. Число сотен не делится без остатка на делитель. 4. Число сотен делимого меньше числа единиц делителя, в частном получается двухзначное число. 5. Особый случай деления, когда в частном на конце или в середине получается ноль. 6. Деление на круглые десятки. Сложение и вычитание многозначных чисел. Сложение и вычитание многозначных чисел, кроме случаев, указанных выше, выполняются приемами письменных вычислений. Основой алгоритмов сложения и вычитания чисел любого класса является поразрядное сложение и вычитание. Умножение и деление многозначных чисел. Умножение и деление многозначных чисел представляет гораздо больше трудностей, чем сложение и вычитание. Трудности возникают и тогда, когда надо единицы высшего разряда перевести в низший разряд, удержать их в памяти. Неумение долгое время сосредоточить внимание на выполнение действия приводит к тому, что учащиеся низшие разряды числа умножают правильно, а при умножении высших разрядов допускают ошибки. Скачать 59 Kb. Поделитесь с Вашими друзьями: |
Урок математики «Правило порядка выполнения действий в выражениях со скобками» | План-конспект урока по математике (3 класс) по теме:
Технологическая карта урока
Ф. И. О. педагога: Морозова Елена Федоровна
И. О. педагога: Морозова Елена Федоровна
Предмет: Математика, УМК «Школа 21 века»
Класс: 3а
Тип урока: Урок «открытия новых знаний»
Тема: Правило порядка выполнения действий в выражениях со скобками.
Цель: Изучить порядок выполнения действий в выражениях со скобками и научить выполнять алгоритм на практике.
Задачи:
1.Уметь решать математические выражения со скобками
2.Уметь применять алгоритм на практике
Название этапа | Деятельность учителя | Деятельность учащихся | УУД |
1.Мотивирование (самоопределение) к учебной деятельности | Здравствуйте, ребята. Посмотрите, друг другу в глаза, улыбнитесь друг другу, шёпотом пожелайте товарищу хорошего рабочего настроения на весь урок. Займите свои рабочие места. Ребята, обратите внимание, у вас на столах лежат карточки с заданиями и смайлики красного, зеленого и голубого цвета. Зеленые смайлики вы будете поднимать, если ответ верный, и вы соглашаетесь со своими товарищами, желтые – сомневаетесь или вам надо еще подумать, а голубые, если не соглашаетесь или ответ не верный. С карточками мы будем работать в течение урока. Откройте тетради, запишите число. Классная работа | Желают удачи друг другу, хорошего рабочего настроения. Садятся за парты Проверяют наличие иллюстративного материала Записывают | Личностные: |
2.Актуализация знаний и фиксирование индивидуального затруднения | — Скажите, пожалуйста, что нового вы узнали на прошлом уроке? (слайд 1) Сейчас я предлагаю проверить, как хорошо вы усвоили правило. (слайд 2) (43+57)+20= 18:(27:3)= (72-6)-2= 4*(2*3)= 94-8*8= 4*(8+1)+(25-16):3 — 81:(36:4)= Какие выражения вы записали без скобок? Почему? В каких выражениях нельзя отбросить скобки? Почему? Каков порядок действий в других выражениях? Каков порядок действий в выражении, которое не содержит скобок, а только знаки + или-, * или : | Правило с.116 Вычитание и деление не обладают сочетательным и переместительным свойством. Поэтому в таких выражениях, как 9:(3:3), 12-(7-4) скобки переставлять или отбрасывать нельзя. Сначала нужно выполнить действия в скобках Объяснение учеников Два выражения можно записать без скобок. (43+57)+20=120 4*(2*3)=24 Решая эти примеры, я использовал переместительное и сочетательное свойство сложения и умножения, т. В остальных примерах скобки отбросить нельзя, поэтому вычисления делаем сначала в скобках, потом умножение деление, сложение вычитание. 18:(27:3)=2 (72-6)-2=66 Первым- умножение и деление, потом сложение вычитание и дальше по порядку, слева направо. 94-8*8=30 | Коммуникативные: |
3.Выявление места и причины затруднения | Ребята, у нас осталось последнее выражение. Сможете его решить? Почему? Чтобы решить это выражение, что должны знать?(правило) | Думают и выявляют место и причину затруднения: Не знаем, как выполнять действия в таких выражениях; не знаем последовательность действий в выражении.- не знаем правило | Познавательные: Регулятивные: |
4Построение проекта выхода из затруднения | Значит, что сегодня мы должны изучить на уроке? Сформулируем тему урока «Порядок выполнения действий в выражениях со скобками (слайд 3) Цель нашего урока? Изучить правило выполнения действий в выражении и научиться вычислять значение выражения со скобками. | Формулируют тему и цель урока Правило выполнения действий в выражении Порядок выполнения действий в выражениях со скобками Научиться вычислять значение выражений. | Регулятивные: |
5.Реализация построенного проекта | Как будем решать это выражение? Предлагаю обсудить все возможные варианты решения в группах. Для этого используем сингапурскую структуру СИНГЛ-РАУНД-РОБИН. Сначала думаем, затем начинаем проговаривать ответ по кругу, начиная с участника №1. Итак, ваши предположения. (спросить по желанию). Какую версию выдвинул ученик по плечу? (спросить оного из учащихся) Ребята, у вас получилось две версии: решить выражение по порядку выполнения математических действий и вторая -разделить выражение на части. Рассмотрим первую версию. Для этого вспомним, по какому правилу мы выполняем математические действия в выражениях содержащих скобки, деление и умножение, сложение и вычитание. Запишите выражение в тетрадь, определим порядок действий в выражении. (слайд 4) 4*(8+1) + (25-16):3 — 81:(36:4)= Подпишем над выражением цифры в порядке выполнения действий. Сколько действий у нас получилось? Значит, сколько примеров мы должны решить? Мы можем в них запутаться? Ребята, давайте разберем 2 версию, которую вы высказали, может она окажется более простой и удобный? Попробуем разбить выражение на части. Как будем разбивать? Как определить каждую часть? Где будут границы частей? (слайд 5) Посмотрите на экран, вам подсказка. Что изменилось в нашем выражении? Знаки + и- стали красного цвета. Почему я их выделила красным цветом? Знаки заключены в скобки? Значит, по ним мы будем определять границы частей выражения. Итак, как мы будем проводить разбивку выражения на части? (слайд 6) Какое выражение сейчас получилось? Из скольких частей состоит теперь выражение? Можем мы решить такое выражение? Как? Прежде чем вы вычислите значения выражения, я попрошу вас снова поработать в группах. Ребята, прежде, как решить это выражение, давайте составить план или алгоритм выполнения действий в таких выражениях. У вас на столах лежат карточки с описанием математических действий. Выберите правильное действие и разложите карточки по порядку выполнения математических действий. Почему убрали одну карточку. Какие алгоритмы у вас получились? Как вы думаете, у вас получились правильные алгоритмы? Как и где, мы это можем проверить? Откроем учебник на с.117 прочитаем памятку. Поднимите карточки, у кого алгоритм составлен верно. (слайд 7) Теперь мы знаем алгоритм решения этого выражения, поэтому сейчас вычислим значение выражения. (слайд 8)Правильное решение на доске. У вас такой же ответ? | Обсуждают возможные варианты ответа на вопрос, используя структуру СИНГЛ-РАУНД-РОБИН. Объяснение учеников: Сосчитать слева направо по порядку; сосчитать сначала в скобках; разделить выражение на части и т. 1.В скобках 2. умножение и деление, 3. сложение вычитание 4. дальше по порядку, слева направо Один ученик у доски записывает выражение и определяет порядок действий 4 1 7 2 5 8 6 3 4*(8+1)+(25-16):3 — 81:(36:4)= 8 действий да ученик решает у доски Знаки + и — стали красного цвета знаки +, или – будут определять границы части; Сначала в выражении нужно найти знаки + или – не заключенные в скобки. Затем начинаем разбивать выражение на части слева направо, от начала до первого из знаков — это первая часть выражения, от первого знака до второго — это вторая часть, от второго знака до конца выражения. Сверху выделяем части карандашом (выделить на доске) Из трех. Да. Сначала сосчитать каждую часть, а затем выполнить действия слева направо. Составляют алгоритм в группах с раздаточным материалом. 1.Находим в выражении все знаки + или — , не заключенные в скобки – это будут границы частей выражения. 2.Определяем количество частей в выражении, от начала до первого знака + или — , не заключенных в скобки 3.Выполняем вычисления каждой части выражения. а) в скобках б) умножение/деление; в) сложение/вычитание). 4. Остальные действия в выражении выполняют слева направо 5.Выполняем вычисления каждой части выражения. а) сложение/вычитание б) умножение/деление; в) в скобках ( карточку с неверным описанием убирают) Поднимают сигнальные карточки По эталону, прочитать правило. Читают правило Поднимают сигнальные карточки. Один ученик решает у доски Поднимают сигнальные карточки | Регулятивные: |
6.Первичное закрепление с проговариванием во внешней речи | (слайд 9) Ребята, выражение вы решили успешно, поэтому сейчас я предлагаю отработать навыки решения выражений со скобками. У вас на столах карточки с математическими заданиями. Запишите их в тетрадь и разбейте выражения на части. 6*6 + 45: (13-4) + 48:8= (154-128) -(20:5+3)+152= Физкультминутка | Проговаривая алгоритм, разбивают выражения на части у доски (фронтальная работа) | Познавательные |
7.Самостоятельная работа с проверкой по эталону | С.117 №11 2*3*4 — (20:5+3)+152= 607- 6*6: (13-4) +(48:8)= Поменяйтесь тетрадями с соседом по лицу. Проверьте. (слайд 10) Вывод на экран эталона Оцените работу товарища, подняв карточки. (проверить учащихся, выполнивших 2 примера) | Выполняют задание, сильные ученики-2 примера Меняются тетрадями Дети поднимают сигнальные карточки | Регулятивные: |
8. | (слайд 11) Задача с.119 № 16 На базе было 260 кг.вишни. В школьные буфеты отправили 8 ящиков по 6 кг.вишни,в детские сады -7 ящиков по 5 кг. и в кафе-9 ящиков по 8 кг. Сколько вишни отправили на базы Сколько вишни осталось на базе? Как записать одним выражением? | Решают (1 ученик у доски). Было-260 кг Б.-8 ящ. по 6 кг, Д.с.—7 ящ. по 5 кг. К. — 9 ящ. по 8 кг. Сколько вишни отправили с базы? Сколько вишни осталось на базе? 8*6+7*5+9*8=155 260-166=105 кг Запись одним выражением 260-(8*6+7*5+9*8)=105 | Познавательные: |
9.Рефлексия учебной деятельности на уроке | Ребята, наш урок подходит к завершению. Запишите Домашнее задание Уч. с.118 №14, 1-2 выражение вычислить двумя способами. Какую задачу ставили? Удалось решить поставленную задачу? Каким способом? Где можно применить новые знания? Что на уроке у вас хорошо получалось? Над чем ещё надо поработать? Я прошу вас взять в руки красные и синие смайлики и оценить свою работу на уроке. Кому всё понятно и хорошее настроение – поднимите зеленый, а если у вас остались вопросы, желтый, кто не понял тему — красный. Ребята, я благодарю вас за работу, и тоже хочу оценить вашу работу на уроке. Скажите, какое событие ждет нашу страну в феврале 2014 года? За победу спортсменам вручают золотые, серебряные и бронзовые медали. Я вручаю вам золотые и серебряные звезды (вручение звезд) Давайте улыбнёмся друг другу и скажем спасибо. Урок закончен | Научиться решать выражения, содержащие скобки. Научились выделять части выражения и решать по порядку, слева направо. Зимняя олимпиада | Регулятивные |
Сложение и вычитание, часть 2: начальные сюжетные ситуации
Математика | К-2
Обзор
В этом материале мы обсуждаем первые типы ситуаций, с которыми учащиеся обычно сталкиваются, когда знакомятся с задачами на сложение и вычитание в детском саду. Изучение этих ситуаций позволяет учителям увидеть, как учащиеся начинают понимать основы сложения и вычитания.
Этот ресурс основан на некоторых концепциях и схемах, впервые представленных в нашем обзорном материале «Сложение и вычитание, часть 1: задачи истории».
Ключевые понятия
В дополнение к подробному рассмотрению ситуаций добавления, изъятия и объединения/разбора этот ресурс фокусируется на двух ключевых понятиях, связанных с этими исходными типами ситуаций:
- Ситуации добавления и изъятия представляют собой последовательность событий, в которых одна величина превращается в новую величину, тогда как ситуации складывания/разборки представляют собой изменение точки зрения: вы должны быть в состоянии видеть две величины как одну объединенную величину.
 , или наоборот.
, или наоборот. - Акцентирование действия при представлении сюжетных задач помогает учащимся обобщить отношения между величинами в каждом типе ситуации.
Добавление к
В нашем первом ресурсе этой серии мы подробно рассмотрели ситуацию с добавлением. Вкратце: в этой ситуации количество start всегда увеличивается на количество change , что дает нам результат количество. Мы представляем ситуацию с примером проблемы и диаграммой ниже. Мы не рекомендуем использовать диаграмму в качестве модели для учащихся, но надеемся, что она может быть полезна для понимания типа ситуации учителями.
В этом примере, как это обычно бывает с вводными задачами надстроек, результат количество неизвестно. Результатом является количество, которое проще всего решить в этой ситуации, что делает этот тип задач типичной отправной точкой для задач на сложение.
Взять из
Ситуация с взятием из очень похожа на ситуацию с добавлением (включая название количества), но имеет одно важное отличие. Вместо увеличения Start к изменение , мы снижение СТАРЬ на ИЗМЕНЕНИЕ (I.E. . Это представлено ниже.
Как и в случае с добавлением, ситуация взятия обычно начинается с того, что учащимся предлагается найти неизвестное результат количество. Этот тип задач также служит типичным введением в вычитание в детском саду.
REFLECT — Уделите несколько минут индивидуальному или коллективному размышлению над следующими вопросами.
- С каких задач вы начинаете, когда знакомите учащихся с дополнением? А вычитание?
Сложение
Другая ситуация, которая часто формирует первоначальное понимание учащимися сложения, – это сложение. Ниже приводится пример составной задачи и диаграмма, представляющая тип ситуации.
Ниже приводится пример составной задачи и диаграмма, представляющая тип ситуации.
В сложившейся ситуации есть два отдельных количества, которые оба обозначаются как , добавляет в CCSS (в нашем примере 3 золотых рыбки и 2 золотых рыбки). Затем, когда эти две величины рассматриваются вместе, они становятся новой, единой величиной, называемой 9.0021 итого (в данном случае 5 золотых рыбок). Таким образом, в сложившейся ситуации мы меняем то, как мы видим эти две величины.
Сборные ситуации всегда включают решение неизвестного всего .
Разборка
Параллельно с ситуацией сборки есть еще одна ситуация, с которой учащиеся обычно сталкиваются на первых этапах изучения вычитания: ситуация разборки. В ситуации сложения мы нашли неизвестное итого , но в ситуации разборки мы находим неизвестное дополнение . Мы показываем это ниже.
Как мы видим в приведенном выше примере задачи, в ситуации с разборкой мы находим отсутствующее сложение (количество белых кроликов), учитывая общее количество (8 кроликов) и другие дополнение (5 серых кроликов).
Теперь, когда у нас есть представление о ситуациях, с которыми учащиеся сталкиваются в детском саду, стоит изучить некоторые тонкие, но важные характеристики ситуаций «собери/разбери».
Две стороны одной медали
Возможно, вы заметили, что ситуации добавления и изъятия очень похожи. Мы сравниваем их на диаграмме ниже.
В исследовании «Когнитивно управляемые инструкции» (CGI) как ситуации «собери вместе», так и «разбери на части» рассматриваются как ситуации «часть-часть-целое». Ситуации соединения — это ситуации «часть-часть-целое», когда неизвестно целое, а ситуации «разборки» — ситуации, в которых часть неизвестна. Может быть полезно рассматривать эти ситуации вместе как ситуации часть-часть-целое, потому что это помогает нам увидеть, что сложение требуется, когда неизвестно целое, и вычитание требуется, когда неизвестна часть.
Ситуации объединения и разделения являются статическими
Ситуации добавления и извлечения представляют собой последовательность событий. Например: «Есть 8 кроликов, а уходят 3 кролика. Сколько кроликов осталось?» Поскольку учащиеся легко понимают эту последовательность, ситуации добавления и исключения (при решении неизвестного результата) часто могут быть очень интуитивными.
Например: «Есть 8 кроликов, а уходят 3 кролика. Сколько кроликов осталось?» Поскольку учащиеся легко понимают эту последовательность, ситуации добавления и исключения (при решении неизвестного результата) часто могут быть очень интуитивными.
Напротив, ситуации сборки и разборки статичны : все количества присутствуют одновременно. В нашем примере выше ученика просят увидеть белых кроликов, серых кроликов, а также комбинированный набор серых и белых кроликов. Это требует от ученика более гибкого мышления.
В общем, статическая природа ситуаций складывания и разборки делает их более абстрактными, чем последовательность событий в ситуациях добавления и извлечения, и они могут быть более сложными для учащихся. чтобы понять в своих начальных исследованиях сложения и вычитания.
РАЗМЫШЛЕНИЕ. Потратьте несколько минут на то, чтобы поразмышлять над следующими вопросами индивидуально или в команде.
- Если бы вы были детсадовцем, как бы вы смоделировали следующие задачи по извлечению и разборке с манипуляторами?
- 8 кроликов и 3 кролика уходят.
 Сколько кроликов осталось?
Сколько кроликов осталось? - Есть 8 кроликов. 3 из них белые. Сколько серых?
- 8 кроликов и 3 кролика уходят.
- Какую задачу проще было смоделировать? Почему?
Вы могли заметить руку, отталкивающую кубики в каждом примере из учебника, показанном выше. В японских учебных программах обычно делается акцент на этом типе действия в задачах на рассказ, потому что это помогает учащимся обобщать то, что происходит в каждой ситуации. Например, в ситуациях с дополнениями учащиеся приходят к пониманию того, что, хотя детали сюжетных задач могут различаться, одна величина ( change ) всегда присоединяется к существующему количеству ( начало ), и это всегда можно представить, подтолкнув одно количество к другому, как показано в блоках ниже.
Это действие (именно так учащиеся часто моделируют тип задачи) можно сделать видимым на доске с помощью стрелок, как показано ниже.
Ниже мы показываем учебник и изображения действий на доске для каждой из начальных ситуаций, которые изучают учащиеся.
Вы можете заметить, что действие связано даже со статическими ситуациями. Кролики не двигаются в задаче на разборку, так почему же мы отталкиваем блоки? Хотя в этой ситуации на самом деле никакое количество не удаляется, это может помочь учащимся визуализировать удаление известного сложения (белых кроликов) из общего числа (всего 8 кроликов), чтобы найти недостающее сложение (количество серых кроликов). Это помогает учащимся понять, что операция по поиску недостающей части — это вычитание.
Вопросы для обсуждения- Какие идеи о начальном обучении сложению и вычитанию, обсуждаемые в этом ресурсе, кажутся вам важными в вашей среде?
- Как ваша учебная программа справляется с начальными задачами на сложение и вычитание? Что в нем вам нравится и/или вы заметили, что есть возможность для улучшения?
- Какой опыт у ваших учеников в настоящее время влияет на их понимание ситуаций добавления, изъятия и складывания/разборки?
- Как вы и ваши ученики изображаете на доске задачи на сложение и вычитание?
- О чем вы хотите узнать больше и какие шаги вы можете предпринять для этого?
Следующие шаги
В нашем следующем материале мы продолжим обсуждение преподавания и изучения сложения и вычитания, показывая, как учащиеся развивают свое понимание ситуации «сравнить».
Используйте приведенные ниже ссылки, чтобы продолжить или ознакомиться с другими шагами последовательности.
Связанные темы
См. плитки ресурсов ниже для расширенного обсуждения различных тем, связанных с сложением и вычитанием.
Задачи на сложение и вычитание 1
Задачи на сложение и вычитание 1Дети решают задачи на сложение и вычитание разными способами. Во взрослом возрасте мы, вероятно, сначала подумаем об операции (+ или -), используемой для решения задачи. Но дети думают в основном о двух вещах. Сначала они думают о действии или отношениях в проблеме, а затем думают о том, что неизвестно. В ближайшие несколько недель мы будем говорить о разного рода проблемах. Мы поговорим о задачах объединения, разделения и сравнения.
Действие в задачах Word
Одним из видов действий является объединение вещей. В зависимости от того, что неизвестно, существует три различных типа соединения. проблемы. На этой неделе мы будем
покрывающий первый вид, результат соединения неизвестен. В таких задачах к ряду элементов присоединяется ряд других элементов. Ребенок должен отгадать неизвестное, т.е. сколько предметов
являются результатом этого соединения. Например, у Байрона было 7 снарядов. Его подруга Мелисса дала ему 9более
снаряды. Сколько снарядов сейчас у Байрона?
проблемы. На этой неделе мы будем
покрывающий первый вид, результат соединения неизвестен. В таких задачах к ряду элементов присоединяется ряд других элементов. Ребенок должен отгадать неизвестное, т.е. сколько предметов
являются результатом этого соединения. Например, у Байрона было 7 снарядов. Его подруга Мелисса дала ему 9более
снаряды. Сколько снарядов сейчас у Байрона?Стратегии для Решение неизвестных проблем с результатом соединения
Взрослые, скорее всего, будут решать задачи на сложение или вычитание, вспоминая факты. Дети решают проблему разными способами, называемыми стратегиями, прежде чем они дойдут до того момента, когда смогут вспомнить факты. Важно, чтобы у детей была возможность решать задачи разными способами. Решение задач более чем одним способом помогает детям больше узнать о числах. Начало обучения математике с обучения детей их «фактам» может прервать это развитие. Математика — это больше, чем просто получение ответов.| Результат неизвестен | Изменение неизвестно | Начало неизвестно | ||
У Байрона 7 снарядов. Затем Мелисса дала ему Сколько сейчас снарядов |
Лучший способ узнать, как дети выясняют проблемы, чтобы спросить их. Знать о детских типичный рост использования стратегии помогает взрослым понять, чего ожидать от детей. Дети решают задачи на соединение тремя основными способами: физическим (прямым) моделированием, счетом или использованием фактов.
- Физическое моделирование: Первая стратегия, которую вырабатывают дети, состоит в том, чтобы использовать предметы или пальцы, чтобы соединить две группы. Затем они считают их всех, начиная с единицы. Например, чтобы узнать, сколько ракушек у Байрона, дети складывают вместе 7 ракушек (или используют монеты или другие жетоны) и 9 ракушек и считают их все «1, 2, 3, 4, 5… 16».
- Стратегии счета: В другое время дети будут
использовать счетную стратегию.
 Стратегии подсчета используют числа для представления количества. Обычно дети начинают использовать стратегии подсчета для решения задач «соединение-результат-неизвестно», начиная с числа, которое было первым в задаче, и затем они будут считать. Например, поскольку они знают, что у Байрона было 7 снарядов, они будут считать: «7 (пауза) 8, 9, 10,
11, 12, 13, 14, 15, 16».
называется в расчете. Это требует больше умственных усилий, чем физическое моделирование, потому что дети должны помнить, что 7 представляет собой 7 оболочек, а 8 представляет собой первую оболочку, которую дала ему Мелисса, 9.
представляет вторую оболочку, которую ему дала Мелисса, и так до 16.
Более продвинутый счет
стратегия рассчитывает от большего числа в задаче. В этом случае ребенок начнет с 9 (самого большого числа в задаче) и будет считать «10, 11…16». Это важный шаг в понимании детьми числа, потому что сначала дети не осознают, что 7 и 9больше такое же количество, как 9 и еще 7. Хотя это может не иметь большого значения для такой проблемы, как эта, это имеет значение для таких проблем, как:
У Байрона было 2 конфеты, а Мелисса дала ему еще 8.
Стратегии подсчета используют числа для представления количества. Обычно дети начинают использовать стратегии подсчета для решения задач «соединение-результат-неизвестно», начиная с числа, которое было первым в задаче, и затем они будут считать. Например, поскольку они знают, что у Байрона было 7 снарядов, они будут считать: «7 (пауза) 8, 9, 10,
11, 12, 13, 14, 15, 16».
называется в расчете. Это требует больше умственных усилий, чем физическое моделирование, потому что дети должны помнить, что 7 представляет собой 7 оболочек, а 8 представляет собой первую оболочку, которую дала ему Мелисса, 9.
представляет вторую оболочку, которую ему дала Мелисса, и так до 16.
Более продвинутый счет
стратегия рассчитывает от большего числа в задаче. В этом случае ребенок начнет с 9 (самого большого числа в задаче) и будет считать «10, 11…16». Это важный шаг в понимании детьми числа, потому что сначала дети не осознают, что 7 и 9больше такое же количество, как 9 и еще 7. Хотя это может не иметь большого значения для такой проблемы, как эта, это имеет значение для таких проблем, как:
У Байрона было 2 конфеты, а Мелисса дала ему еще 8. С 8 рассчитывать намного проще, чем с 2.
С 8 рассчитывать намного проще, чем с 2. - Использование фактов: Дети также учатся использовать факты для решения проблем с неизвестным результатом соединения. Дети запоминают одни факты быстрее, чем другие. Часто сначала учат «двойников». Они будут использовать эти знания для выяснить ответы. Это называется получением фактов. Используя в качестве примера проблему с раковиной, ребенок, который знает, что 7+7 равно 14, может решить, что 9на 2 больше, чем 7, поэтому ответ должен быть на 2 больше, чем 14, то есть 16. Эта стратегия основана на понимании отношений между числами; и поэтому это значительный рост в понимании чисел. Наконец, дети помнят свои числовые факты и могут давать ответы, вспоминая факт 7+9=16. Когда это воспоминание основано на детских опыта с числом и с их появляющимся развитием в решении задач, то дети понимают, откуда берутся их ответы. Более важно, чтобы учащиеся понимали, как они получили ответ, чем то, как быстро они его находят.
Стратегии вычитания Прогресс | Департамент образования
Добро пожаловать в асинхронный модуль, Стратегии вычитания Прогресс . В своем собственном темпе читайте материалы, смотрите короткие видеоклипы и разбирайтесь в картинках. Этот модуль длится примерно 1 час и может быть завершен за один присест или небольшими частями. Когда вы пройдете модуль, щелкните ссылку на анкету в поле справа. После успешной отправки анкеты ваш сертификат часа контакта будет автоматически отправлен по электронной почте на адрес, указанный в анкете. Если у вас есть какие-либо вопросы об этом процессе или содержании этого модуля, свяжитесь с Джен Робитайл по адресу [email protected].
В своем собственном темпе читайте материалы, смотрите короткие видеоклипы и разбирайтесь в картинках. Этот модуль длится примерно 1 час и может быть завершен за один присест или небольшими частями. Когда вы пройдете модуль, щелкните ссылку на анкету в поле справа. После успешной отправки анкеты ваш сертификат часа контакта будет автоматически отправлен по электронной почте на адрес, указанный в анкете. Если у вас есть какие-либо вопросы об этом процессе или содержании этого модуля, свяжитесь с Джен Робитайл по адресу [email protected].
Стратегии перечислены от самых ранних до стандартного алгоритма. Многие из них используются параллельно, но важно понимать, что различные стратегии используются для более глубокого концептуального понимания и перехода к более процедурной модели, основанной на концептуальном понимании вычитания. Имейте в виду, что освоение стандартного алгоритма вычитания не ожидается до 4-го класса в соответствии с результатами обучения штата Мэн и общими базовыми стандартами штата, однако учащиеся начнут практиковать стандартный алгоритм наряду с другими стратегиями намного раньше 4-го класса.
Модели
Учащиеся впервые осваивают вычитание с помощью моделей. Они могут использовать различные манипулятивные средства, такие как кубики, счетные медведи, пуговицы, пять и десять рамок, пальцы или счетчики. Учащиеся могут также рисовать представления или картинки для моделирования математики или даже физически разыгрывать вычитание. Эти модели помогают учащимся понять действие, происходящее в самых ранних задачах на вычитание. Модели по-прежнему могут быть полезны, когда учащиеся работают над задачами «часть-часть-сумма», «изменение» и «сравнительное вычитание». Студентам также необходимо попрактиковаться в поиске пропущенных значений во всех местах задачи на вычитание — уменьшаемое, вычитаемое и разность. Дополнительные примеры ситуаций с задачами на вычитание см. в Глоссарии, таблица 1 из Общего стандарта штата по математике.
Обратный (или прямой) счет
При использовании стратегии обратного или даже прямого счета важно помнить, что вычитание означает разницу или расстояние между уменьшаемым и вычитаемым значениями. Когда ваши ученики понимают взаимосвязь значений и то, что они могут либо считать в обратном порядке от уменьшаемого, либо считать от вычитаемого, они углубляют свое понимание смысла чисел и того, как числа работают вместе. Стратегия обратного отсчета или подсчета вверх часто может сочетаться с числовой линией или открытой числовой линией, поскольку значения работают с увеличением.
Когда ваши ученики понимают взаимосвязь значений и то, что они могут либо считать в обратном порядке от уменьшаемого, либо считать от вычитаемого, они углубляют свое понимание смысла чисел и того, как числа работают вместе. Стратегия обратного отсчета или подсчета вверх часто может сочетаться с числовой линией или открытой числовой линией, поскольку значения работают с увеличением.
Числовые сетки
Числовые сетки – отличный способ поиска шаблонов для вычитания учащихся. Это начинает формировать понимание разрядности, когда учащиеся начинают смотреть на то, что они замечают в разрядах десятков и единиц. Числовые сетки уникально настроены в рядах по десять, чтобы смоделировать нашу систему счисления с основанием десять. Когда учащиеся перемещаются по строке, они должны заметить, что цифра в разряде десятков остается неизменной до конца ряда, а разряд единиц увеличивается на единицу. Двигаясь вверх или вниз по строке, они должны заметить, что разряд единиц остается прежним, а разряд десятков либо увеличивается, либо уменьшается на единицу.
Обратите внимание на разницу в этих двух сетках чисел. Одна сетка идет от 0 до 110 сверху вниз, а другая идет от 1 до 100 снизу вверх. Тот, что слева, чаще используется в классе, однако тот, что справа, более точно соответствует действиям ученика по сложению или вычитанию. По мере того, как учащиеся продолжают считать, числа увеличиваются в таблице. По мере того, как учащийся ведет обратный отсчет при вычитании, числа идут вниз по таблице.
Базовые десять блоков
Блоки с основанием 10 — это инструмент, используемый многими способами в математике. В этом случае мы будем использовать десятичные блоки, представляющие сотни, десятки и единицы, чтобы показать действие вычитания или удаления из одной группы. Учащиеся должны начать с построения представления уменьшаемого (число, от которого отнимается), затем взять от уменьшаемого значение вычитаемого (вычитаемое число), оставив разницу. По мере того как учащиеся изучают эту стратегию, начните с чисел, где не нужно разбивать группы. По мере того, как учащиеся знакомятся с действием вычитания, начните обсуждение отдельных цифр в разрядном значении, узнайте, что, по мнению учащихся, вы могли бы сделать, если не хватает одного конкретного разрядного значения. Затем учащиеся могут смоделировать справедливую торговлю. Когда учащиеся освоятся с физическими манипуляциями, переходите к визуальному представлению или эскизу десяти базовых блоков. Объясните учащимся, что им не нужно рисовать отдельные единицы, а использовать «стенографические» наброски основных десяти блоков (квадрат для сотен, линия для десятков и точка для единиц). Затем учащиеся могут связать свои модели с более абстрактным стандартным алгоритмом вычитания. Эта последовательность обучения смоделирована в видео.
По мере того, как учащиеся знакомятся с действием вычитания, начните обсуждение отдельных цифр в разрядном значении, узнайте, что, по мнению учащихся, вы могли бы сделать, если не хватает одного конкретного разрядного значения. Затем учащиеся могут смоделировать справедливую торговлю. Когда учащиеся освоятся с физическими манипуляциями, переходите к визуальному представлению или эскизу десяти базовых блоков. Объясните учащимся, что им не нужно рисовать отдельные единицы, а использовать «стенографические» наброски основных десяти блоков (квадрат для сотен, линия для десятков и точка для единиц). Затем учащиеся могут связать свои модели с более абстрактным стандартным алгоритмом вычитания. Эта последовательность обучения смоделирована в видео.
Открытая числовая строка
Мы все знакомы с числовой строкой, которую используют маленькие дети. Обычно он начинается с нуля и увеличивается до единицы. Открытая числовая строка — это пустая числовая строка, которую можно использовать для любых значений вдоль числовой строки, которые могут быть полезны при решении задач. Обычно галочки не включаются в открытую числовую строку, и по мере добавления числа в числовую строку они могут не соответствовать масштабу. Открытая числовая линия полезна для создания представления для записи шагов умственных вычислений. Посмотрите видео, чтобы увидеть пример использования незамкнутых числовых рядов с вычитанием.
Обычно он начинается с нуля и увеличивается до единицы. Открытая числовая строка — это пустая числовая строка, которую можно использовать для любых значений вдоль числовой строки, которые могут быть полезны при решении задач. Обычно галочки не включаются в открытую числовую строку, и по мере добавления числа в числовую строку они могут не соответствовать масштабу. Открытая числовая линия полезна для создания представления для записи шагов умственных вычислений. Посмотрите видео, чтобы увидеть пример использования незамкнутых числовых рядов с вычитанием.
Компенсация/отдача и получение (постоянные различия)
Компенсация — это стратегия, часто применяемая в ментальной арифметике, когда одно или несколько чисел корректируются, чтобы сделать числа более удобными для ментальной арифметики.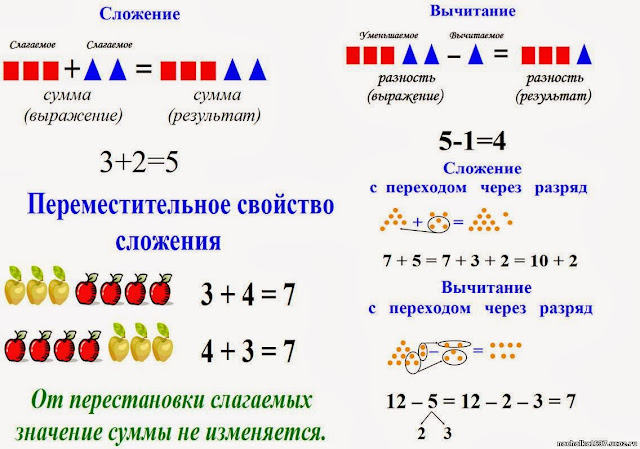 Например, некоторое значение может быть взято из уменьшаемого или вычитаемого или добавлено к нему, а затем разница корректируется, чтобы упростить решение проблемы. В задаче 59 — 32 59 всего на единицу меньше 60, и 60 будет легче вычесть, чем 59., а разбиение 32 на 30 и 2 также облегчит мысленное вычитание, что даст нам задачу 60 — 30 — 2. 60 — 30 = 30, 30 — 2 = 28. Теперь нам нужно скорректировать задачу для дополнительной, которую мы начали с, поэтому 28 — 1 = 27. Другой способ решить ту же проблему, используя постоянные разности, состоит в том, чтобы сделать то же самое для каждого уменьшаемого и вычитаемого, виртуально перемещая их положение на числовой прямой. Подумайте о расстоянии между 32 и 59 на числовой прямой, добавляя единицу к каждому значению, делая такое же расстояние, теперь это расстояние между 33 и 60; проблемы эквивалентны только в другом месте на числовой прямой. Построение смысла чисел и использование отношений разрядных значений и цифр позволяет нам углубить наше понимание операций.
Например, некоторое значение может быть взято из уменьшаемого или вычитаемого или добавлено к нему, а затем разница корректируется, чтобы упростить решение проблемы. В задаче 59 — 32 59 всего на единицу меньше 60, и 60 будет легче вычесть, чем 59., а разбиение 32 на 30 и 2 также облегчит мысленное вычитание, что даст нам задачу 60 — 30 — 2. 60 — 30 = 30, 30 — 2 = 28. Теперь нам нужно скорректировать задачу для дополнительной, которую мы начали с, поэтому 28 — 1 = 27. Другой способ решить ту же проблему, используя постоянные разности, состоит в том, чтобы сделать то же самое для каждого уменьшаемого и вычитаемого, виртуально перемещая их положение на числовой прямой. Подумайте о расстоянии между 32 и 59 на числовой прямой, добавляя единицу к каждому значению, делая такое же расстояние, теперь это расстояние между 33 и 60; проблемы эквивалентны только в другом месте на числовой прямой. Построение смысла чисел и использование отношений разрядных значений и цифр позволяет нам углубить наше понимание операций.
Компенсация разлагает (разбирает) или перекомпоновывает (собирает обратно) числа, чтобы облегчить вычитание в уме. Учащиеся должны понять, как числа можно разбить на части и собрать вместе, чтобы укрепить свои навыки восприятия чисел.
Расширенная нотация (перегруппировка)
Расширенная нотация использует разрядное значение для вычитания внутри каждого разрядного значения, а затем объединяет расширенное обозначение, чтобы получить окончательное различие. В расширенной нотации одно разрядное значение может быть перегруппировано, когда это необходимо для вычитания разрядного значения.
Стандартный алгоритм США
Стандартный алгоритм США для вычитания — это стратегия, о которой большинство взрослых думают, когда их просят вычесть числа: сложите и вычтите.


 (сумма, разность, равенство, неравенство, схема, рисунок, арифметические действия +, — и т.д.)
(сумма, разность, равенство, неравенство, схема, рисунок, арифметические действия +, — и т.д.) )
)
 Прочитай выражение.
Прочитай выражение. 
 Домашнее задание
Домашнее задание

 Затем проводятся упражнения на дифференциацию примеров, в которых ноль будет слагаемым и вычитаемым.
Затем проводятся упражнения на дифференциацию примеров, в которых ноль будет слагаемым и вычитаемым.
 Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут применение и при изучении арифметических действий.
Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут применение и при изучении арифметических действий.


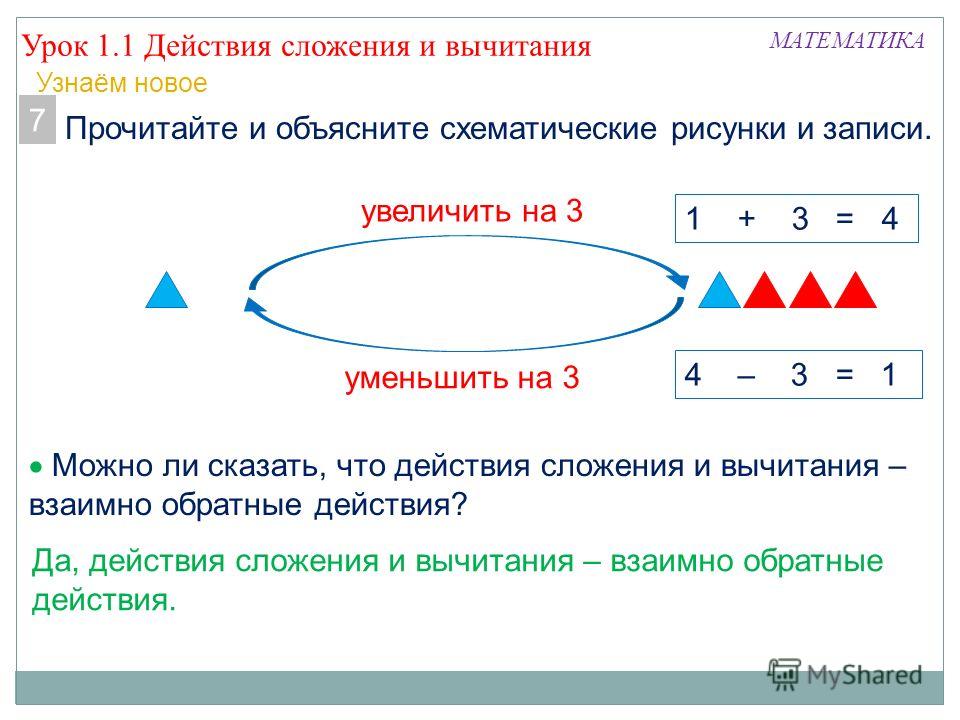
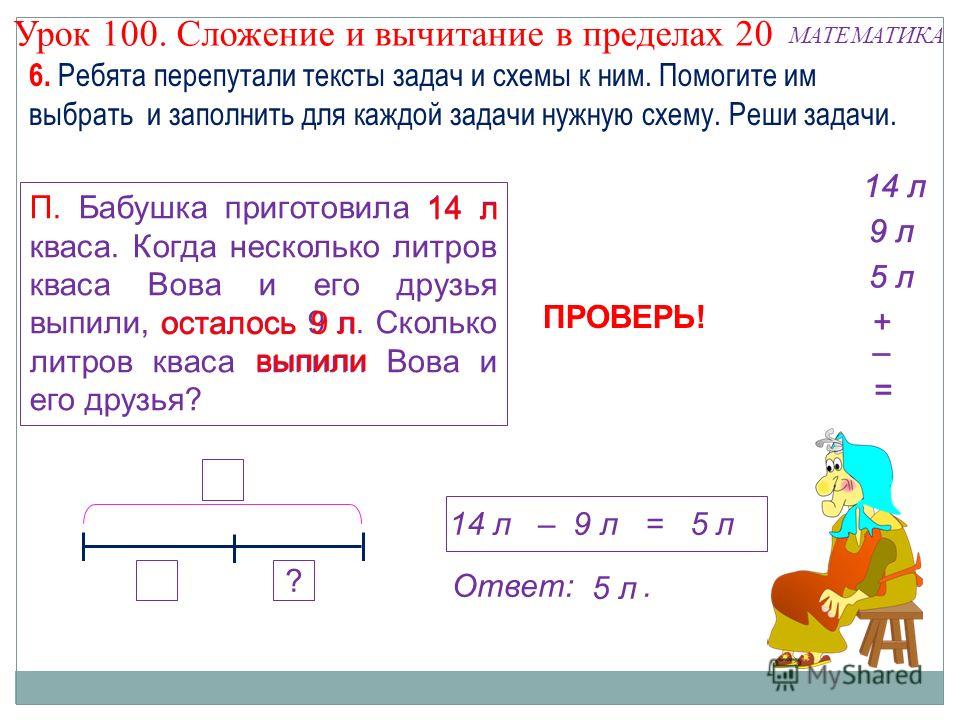


 Непреодолимые трудности для ребенка могут возникнуть при несоблюдении степени трудности решения примеров. Поэтому очень важно соблюдать последовательность в выборе примеров, учитывая их нарастающую степень трудности, и тщательно отрабатывать каждый случай.
Непреодолимые трудности для ребенка могут возникнуть при несоблюдении степени трудности решения примеров. Поэтому очень важно соблюдать последовательность в выборе примеров, учитывая их нарастающую степень трудности, и тщательно отрабатывать каждый случай. К ним относятся случаи, которые вызывают наибольшие трудности и в которых чаще всего допускают ошибки. Учащихся больше всего затрудняют действия с нулем, (ноль находится в середине или в конце)
К ним относятся случаи, которые вызывают наибольшие трудности и в которых чаще всего допускают ошибки. Учащихся больше всего затрудняют действия с нулем, (ноль находится в середине или в конце)
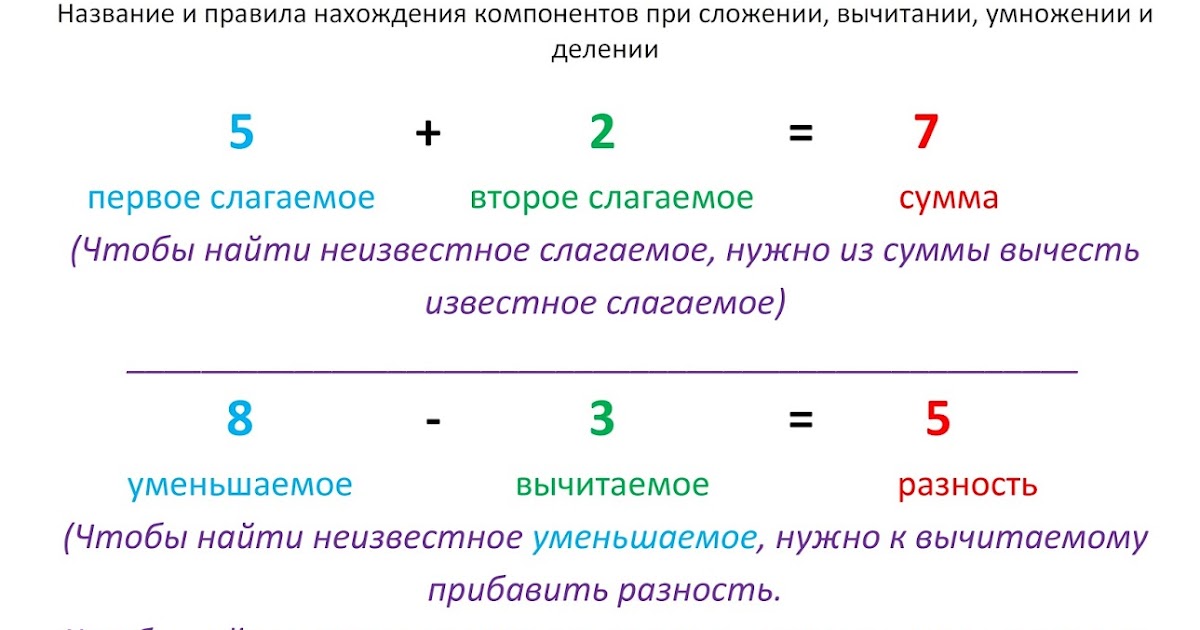
 Это связано с тем, что ученики не твердо знают таблицу умножения. Даже те учащиеся, которые запоминают таблицу умножения, затруднялись применить её при решении примера с многозначными числами, то есть актуализировать свои знания и использовать их.
Это связано с тем, что ученики не твердо знают таблицу умножения. Даже те учащиеся, которые запоминают таблицу умножения, затруднялись применить её при решении примера с многозначными числами, то есть актуализировать свои знания и использовать их.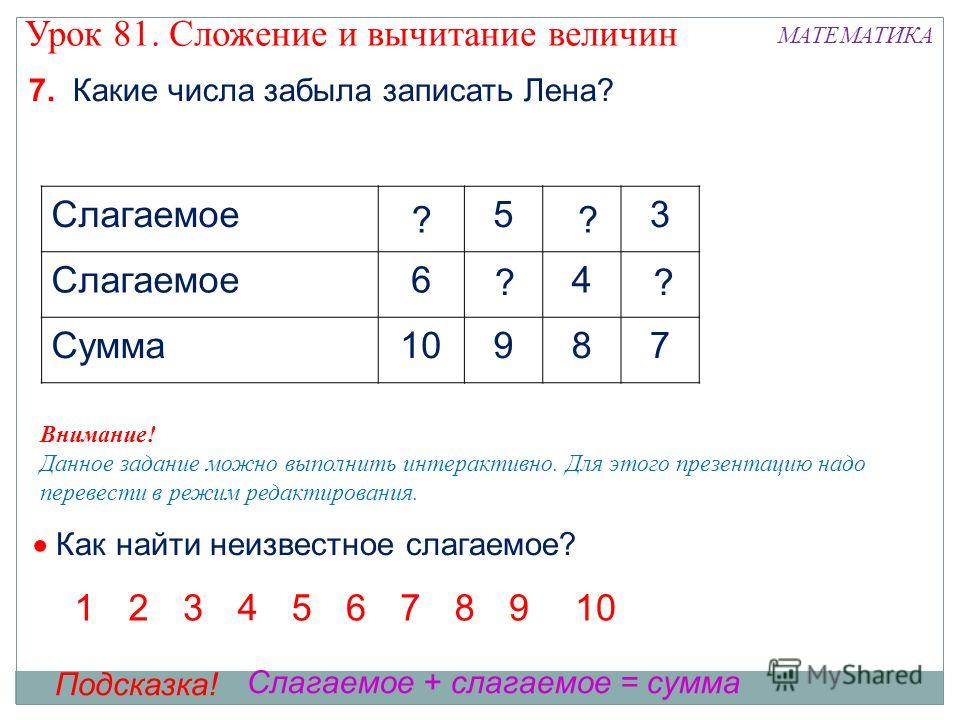 Теперь посмотрите на меня, я тоже желаю вам удачи на этом уроке, потому что «с малой удачи начинается большой успех».
Теперь посмотрите на меня, я тоже желаю вам удачи на этом уроке, потому что «с малой удачи начинается большой успех». Посмотрите на экран. Здесь даны выражения со скобками и без скобок. В каких выражениях можно отбросить скобки? Запишите эти выражения без скобок. В остальных выражениях определите порядок действий.
Посмотрите на экран. Здесь даны выражения со скобками и без скобок. В каких выражениях можно отбросить скобки? Запишите эти выражения без скобок. В остальных выражениях определите порядок действий. к. эти свойства дают возможность записывать выражения, содержащие только умножение и сложение без скобок и выполнять вычисления в любом порядке.
к. эти свойства дают возможность записывать выражения, содержащие только умножение и сложение без скобок и выполнять вычисления в любом порядке.


 д.
д.

 Включение в систему знаний и повторение
Включение в систему знаний и повторение Первый -определить порядок действий и вычислить по порядку( не вычисляли), второй путем разбиения выражения на части. И скажите, какой способ вычисления значения выражения удобнее.
Первый -определить порядок действий и вычислить по порядку( не вычисляли), второй путем разбиения выражения на части. И скажите, какой способ вычисления значения выражения удобнее.
 , или наоборот.
, или наоборот. Сколько кроликов осталось?
Сколько кроликов осталось? Стратегии подсчета используют числа для представления количества. Обычно дети начинают использовать стратегии подсчета для решения задач «соединение-результат-неизвестно», начиная с числа, которое было первым в задаче, и затем они будут считать. Например, поскольку они знают, что у Байрона было 7 снарядов, они будут считать: «7 (пауза) 8, 9, 10,
11, 12, 13, 14, 15, 16».
называется в расчете. Это требует больше умственных усилий, чем физическое моделирование, потому что дети должны помнить, что 7 представляет собой 7 оболочек, а 8 представляет собой первую оболочку, которую дала ему Мелисса, 9.
представляет вторую оболочку, которую ему дала Мелисса, и так до 16.
Более продвинутый счет
стратегия рассчитывает от большего числа в задаче. В этом случае ребенок начнет с 9 (самого большого числа в задаче) и будет считать «10, 11…16». Это важный шаг в понимании детьми числа, потому что сначала дети не осознают, что 7 и 9больше такое же количество, как 9 и еще 7. Хотя это может не иметь большого значения для такой проблемы, как эта, это имеет значение для таких проблем, как:
У Байрона было 2 конфеты, а Мелисса дала ему еще 8.
Стратегии подсчета используют числа для представления количества. Обычно дети начинают использовать стратегии подсчета для решения задач «соединение-результат-неизвестно», начиная с числа, которое было первым в задаче, и затем они будут считать. Например, поскольку они знают, что у Байрона было 7 снарядов, они будут считать: «7 (пауза) 8, 9, 10,
11, 12, 13, 14, 15, 16».
называется в расчете. Это требует больше умственных усилий, чем физическое моделирование, потому что дети должны помнить, что 7 представляет собой 7 оболочек, а 8 представляет собой первую оболочку, которую дала ему Мелисса, 9.
представляет вторую оболочку, которую ему дала Мелисса, и так до 16.
Более продвинутый счет
стратегия рассчитывает от большего числа в задаче. В этом случае ребенок начнет с 9 (самого большого числа в задаче) и будет считать «10, 11…16». Это важный шаг в понимании детьми числа, потому что сначала дети не осознают, что 7 и 9больше такое же количество, как 9 и еще 7. Хотя это может не иметь большого значения для такой проблемы, как эта, это имеет значение для таких проблем, как:
У Байрона было 2 конфеты, а Мелисса дала ему еще 8. С 8 рассчитывать намного проще, чем с 2.
С 8 рассчитывать намного проще, чем с 2.