Технологическая карта «Переместительное свойство сложения»

Просмотр содержимого документа
«Технологическая карта «Переместительное свойство сложения»»

Тема: «Переместительной свойство сложения»

Цель: Создать условия для ознакомления учащихся с переместительным свойством сложения и его особенностью, практически применять перестановку слагаемых.

Задачи:

1. формировать представление о таких терминах как (переместительное свойство сложения).

2. Развивать умение оперировать этими знаниями. Способствовать развитию математической речи, наглядно-образного мышления.

3. Воспитывать любовь и интерес к математике.

 Личностные: 

1. способность к самооценке на основе критерия успешности учебной деятельности;

Регулятивные: 

1. умение определять и формулировать цель на уроке с помощью учителя;

2. оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки;

3. планировать своё действие в соответствии с поставленной задачей;

4. вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок;

5. высказывать своё предположение.

Коммуникативные: 

1. умение оформлять свои мысли в устной форме;

2. слушать и понимать речь других;

3. совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательные: 

1. умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;

2. добывать новые знания: находить ответы на вопросы, используя учебник, ИКТ, свой жизненный опыт и информацию, полученную на уроке.

Ход урока:

Этап урока	Деятельность учителя	Деятельность учащихся	УУД
Мотивация к учебной деятельности	Здравствуйте, ребята. Громко прозвенел звонок – Начинается урок. Ваши ушки на макушке, Глазки широко раскрыты. Слушайте, запоминайте, Ни минуты не теряйте! Начнем урок математики, проверьте свою готовность к уроку.	Приветствие учителя, эмоциональный настрой на урок	К-1 К-2
Актуализация и фиксирование индивидуальных затруднений в пробном действии с выявлениями места и причины затруднения	Давайте вспомним то, что нам уже известно. а) Слайд. Три зелёные лягушки Загорают кверху брюшком. Три решили муху съесть, А всего лягушек…(3+3=6 ). б) Слайд. Семь малюсеньких котят, Что дают им – все едят. А один — сметаны просит. Сколько же котяток? (7+1=8) в) Слайд. У меня четыре лапки, А на них надеты тапки. У ребят давай-ка спросим – Вместе лап и тапок…(4+4=8)	6 8 8	К-1 К-2 Р-1 Р-4 П-1 Л-1
Построение проекта выхода из затруднений	К нам за помощью обратились животные, которые никак не могу разрешить спор. -Как вы думаете, сможем ли мы им помочь? «Лиса поймала 4 большие рыбы и 3 маленькие. А Волк поймал 3 большие рыбы и 4 маленькие. Каждый из зверей утверждает, что его улов больше» Чтобы разобраться в этом вопросе, я предлагаю вам провести небольшое исследование. Кто знает, что это? Предлагаю превратить наш класс в научно-исследовательскую лабораторию. Каждый из нас – сотрудник этой лаборатории, учёный-исследователь. Мы все равны. Мы – коллеги. Коллеги – это товарищи по работе.	Исследовать – это значит понять, установить	Р-3 К-1 К-2 Л-1 П-3
Реализация построенного проекта выходя из затруднений	-Возьмите из своего конверта треугольники. -Сколько у Лисы больших рыб? -Положите перед собой столько же больших кружочков. -Сколько у Лисы маленьких рыб? — Положите рядом с большими столько маленьких кружочков, сколько маленьких рыб у Лисы. — Запишите выражение, сколько всего рыб у Лисы. -Назовите компоненты при сложении. — Прочитайте выражение, называя числа при сложении. (Аналогичная работа выполняется с рыбами, пойманными Волком.) Сравните оба выражения. -Чем похожи? -Чем отличаются? -Что произошло со слагаемыми? (поменялись местами) -Изменился ли результат? Сравните улов зверей. -Сформулируйте правило.  Физминутка. Раз — подняться, потянуться, Два – согнуться, разогнуться. Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять – руками помахать, Шесть – за парту тихо сесть.	4 3 4+3=7 От перемены мест слагаемых сумма не меняется
Первичное закрепление с проговариванием во внешней речи	Откройте учебник на странице 14 посмотрите на упражнение 1. Рассмотрите рисунок. Сколько красных точек на первой фишке домино? Сколько синих? Назовите пример.  — Как получили второй пример?  -Сколько всего точек на первой фишке? Как изменится сумма, если фишку перевернуть?  -Объясните, как получили остальные примеры. Докажите, что ответы этих примеров будут одинаковые. -Какие выражения легче было решить?	3+2=5 Перевернули фишку Сумма не изменится К большему прибавить меньшее	К-1 К-2 Р-1 Р-2 Р-3 П-1 П-2
Самостоятельная работа с проверкой по эталону	Посмотрите на доску перед вами выражение 6+3, 8+3, 5+4. Решите его в тетрадях самостоятельно.	6+3=9	К-1 К-2 Р-1 Р-2 П-1 П-2 Л-2
Включение в систему знаний	Ребята, о чем мы сегодня говорили на уроке? Какое практическое задание мы с вами выполняли? Давайте повторим, что мы с вами изучили и на уроке. Я подготовила фразы, которые вам необходимо завершить: 1.На уроке я познакомился(ась) … 2. Больше всего на уроке мне понравилось… 3. Тема урока показалась мне…	Решали пример С переместительным свойством Решать примеры Интересной	К-1 К-2 Р-1 Р-2 Р-3 П-1 П-2
Рефлексия	Если вы справились со всеми заданиями, поднимите веселый смайлик. Если у вас возникли затруднения, поднимите грустный.		К-1 Р-5

Переместительное свойство сложения

Из курса математики вам известно, что для сложения целых неотрицательных чисел выполняются коммутативное и ассоциа­тивное свойства. В начальном курсе математики учащиеся знако­мятся с коммутативным свойством сложения, называя его «переместительное свойство сложения» или «перестановка сла­гаемых». Для его разъяснения могут быть использованы действия с предметными множествами, сравнение числовых равенств, в ко­торых переставлены слагаемые, сравнение суммы длин одинако­вых отрезков (полосок).

При формировании у детей представлений о смысле сложения полезно предлагать им такие ситуации для предметных действий, при выполнении которых они сами подмечают закономерность, связанную с переместительным свойством сложения. Например:

а} На левой тарелке 4 апельсина, на правой — 3. Покажи, сколь­ко апельсинов на двух тарелках.

Ученики выполняют схематический рисунок и записывают ра­венство, подсчитав количество апельсинов на двух тарелках.

б) Теперь на левой тарелке 3 апельсина, на правой — 4 Покажи, сколько апельсинов на двух тарелках.

Ученики выполняют схематический рисунок и записывают ра­венство, подсчитав количество апельсинов на двух тарелках.

4+3=7

Сравнивая рисунки и математические записи (в чем их сходство и различие?), дети подмечают, что количество апельсинов на двух тарелках не изменилось.

Величины, изучаемые в курсе математики начальных классов: длина, площадь, объём, ёмкость, масса, цена, стоимость, время, скорость.

Понятие величина не является чисто математическим понятием, его применяют в разных науках. В математике вся теория величин строится на их основных свойствах:

1. любые 2 величины одного рода сравнимы;

2. величины одного рода можно складывать;

3. величину умножают на действительное число и получают величину того же рода;

4. величины одного рода вычитают, делят и т.п.

Изучение величин в начальной школе имеет прикладной характер. Задача учителя: сформировать представление о величине как свойстве предметов и явлений, которое связано с измерением. В начальной школе рассматриваются такие величины: длина, масса, ёмкость, время, площадь. Также рассматриваются связи между величинами: цена, количество, стоимость.

Величина – это характеристическое свойство предмета или явления. Истомина Н. Б. в изучении величин выделяет 8 этапов:

1. Выявление представлений ребёнка о данной величине. Выделение понятия и соответствующего термина.

2. Сравнение однородных величин: визуально (на глаз), ощущением, наложением, приложением, с помощью различных мерок.

3. Знакомство с единицей измерения величины и с измеряемым прибором.

4. Сложение и вычитание однородных величин, выраженных в единицах одного наименования.

5. Знакомства с новой единицей измерения.

6. Перевод единиц одного наименования в другое.

7. + и – однородных величин, выраженных в единицах 2 наименований.

8. Умножение и деление величин.

Длина – это величина, которая характеризует протяженность предмета относительно одной из осей координат. В речи подчеркиваем, вдоль какой оси рассматривается протяженность: вдоль оси x – длина, вдоль оси z – ширина, вдоль оси y – высота (толщина). С длиной дети знакомятся по программе ДОУ.

Масса — величина, которая характеризует свойство тяжести предмета. Вес – сила, с которой предмет давит на опору. Масса определяется с помощью весов по преобразованной шкале. Операция с весами: отвешивание, взвешивание.

Ёмкость — величина, которая характеризует вместимость, то есть свойство предмета вмещать в себя определенное количество жидкого или сыпучего вещества. Вместимость определяется след. показателями:

1. показываем операцию вливания жидкости в сосуд, измеряем количество жидкости в сосуде.

2. Вместимость будет зависеть от формы сосуда.

Объём — величина, которая характеризует свойство предмета: занимать определенное место в пространстве.

Вместимость + ёмкость = объём.

Скорость – это расстояние, преодоленное телом за единицу времени. Это величина, которая характеризует свойство предмета изменять своё положение в пространстве с течением времени.

Площадь — величина, которая характеризует место, занимаемое телом или плоской геометрической фигурой на модели плоскости. Площадь вводится путем демонстрации того факто, что разные по форме и размеру фигуры занимают разное место на плоскости.

Время — величина, которая характеризует продолжительность некоторого события или явления. Представления о времени формируются в системе с опорой на временные ориентировки: до – после, раньше – позже, днем – вечером, утром – ночью и т.д. время является философской категорией и обладает след. свойствами:

— невидимо;

— неощущаемо;

— необратимо;

— периодично;

— циклично;

— условно может быть изображено.

Что такое коммутативное свойство сложения ⭐ Определение, примеры

• Дом
• >
• База знаний
• >
• Коммутативное свойство сложения – определение с примерами

Раскрытие тайн математики часто может быть похоже на грандиозное приключение, полное новых концепций и захватывающих открытий. Мы в Brighterly стремимся сделать это путешествие максимально приятным и полезным. Одним из ключевых шагов на этом пути математических исследований является коммутативное свойство сложения. Этот фундаментальный принцип — больше, чем просто математическое правило; это маяк, освещающий взаимосвязь и гармонию, присущие числам и операциям.

Коммутативное свойство сложения сродни волшебному переключателю, который позволяет числам танцевать и меняться местами без изменения окончательного результата суммы. Это свидетельство присущей математике гибкости и элегантности. Поняв этот принцип, дети смогут по-новому взглянуть на манипулирование числами, привив им чувство уверенности и любопытства, которые побудят их глубже погрузиться в увлекательный мир чисел. Итак, давайте вместе отправимся в это познавательное путешествие, исследуя и раскрывая коммутативное свойство сложения вместе с Brighterly.

Что такое коммутативное свойство сложения?

Переместительное свойство сложения — это фундаментальное понятие в арифметике и алгебре, которое помогает нам понять более сложные математические идеи. Но что именно? Термин «коммутативный» происходит от латинского слова «commutare», что означает передвигаться или менять местами. В математике это свойство утверждает, что изменение порядка сложения чисел не влияет на сумму.

Проще говоря, если вы складываете два или более чисел вместе, вы можете переставить эти числа в любом порядке, и вы все равно получите ту же сумму. Это может показаться очевидным, но это важнейший принцип, лежащий в основе большей части математических вычислений, которые мы делаем каждый день. Это позволяет нам выполнять расчеты более гибко и эффективно. Например, при добавлении нескольких чисел мы можем сгруппировать числа таким образом, чтобы упростить математику, и эта стратегия стала возможной благодаря свойству коммутативности.

Переместительное свойство формулы сложения

Итак, как выглядит переместительное свойство формулы сложения? Это довольно просто. Если у вас есть два числа, скажем, a и b, формула просто утверждает, что a + b = b + a. Это может показаться слишком простым, но это невероятно мощно.

Например, если у вас есть 3 яблока и вы добавляете еще 2, у вас будет такое же количество яблок, как если бы вы сначала взяли 2 яблока, а затем добавили 3. Результат тот же: у вас есть 5 яблок. Эта формула является отличной иллюстрацией того, как порядок добавления чисел не влияет на конечный результат.

Применение коммутативного свойства сложения

Коммутативное свойство сложения — это больше, чем просто абстрактное математическое понятие — оно имеет практическое применение в повседневной жизни. Например, при совершении покупок не имеет значения, добавляете ли вы цену яблок к цене бананов или наоборот; общая стоимость будет такой же.

Кроме того, это свойство можно применять и при решении сложных математических задач, особенно в алгебре. Это позволяет нам переставлять термины в алгебраическом выражении или уравнении, чтобы упростить вычисления или более легко идентифицировать похожие термины. Например, в уравнении 2x + y = z мы могли бы записать его как y + 2x = z без изменения его смысла или решения.

Примеры коммутативного свойства сложения

Чтобы дополнительно проиллюстрировать коммутативное свойство сложения, рассмотрим несколько примеров.

1. Если у нас есть числа 4 и 7, мы можем записать это как 4 + 7 = 11. Но мы также можем записать это как 7 + 4 = 11. Оба уравнения дают нам один и тот же результат, доказывая свойство коммутативности.

2. В реальной жизни представьте, что у вас есть 5 конфет, и ваш друг дает вам еще 2. Теперь у вас есть 5 + 2 = 7 конфет. Если бы ваш друг сначала дал вам 2 конфеты, а затем вы нашли еще 5, у вас было бы 2 + 5 = 7 конфет. Порядок добавления не меняет общее количество конфет, которые у вас есть.

Практические вопросы по переместительному свойству сложения

Теперь, когда мы поняли переместительное свойство сложения, давайте проверим наши знания, задав несколько практических вопросов.

1. Покажите, что 13 + 22 = 22 + 13.
2. Докажите свойство коммутативности, используя числа 8 и 15.
3. Приведите пример из жизни, где используется свойство коммутативности.

Помните, что ключом к освоению любой математической концепции является практика!

Заключение

Коммутативное свойство сложения — это не просто математический принцип, это бесценный инструмент, компас, который ведет нас через обширный ландшафт чисел и операций. В Brighterly мы понимаем силу, которую такие основополагающие концепции имеют в формировании математического пути ребенка. Мы считаем, что, овладев свойством перестановочности, учащиеся могут выработать более гибкий подход к решению проблем, формируя образ мышления, рассматривающий проблемы как возможности для творчества и инноваций.

Понимая и применяя коммутативное свойство сложения, дети могут легче усваивать более сложные математические концепции, закладывая прочную основу для своего будущего обучения.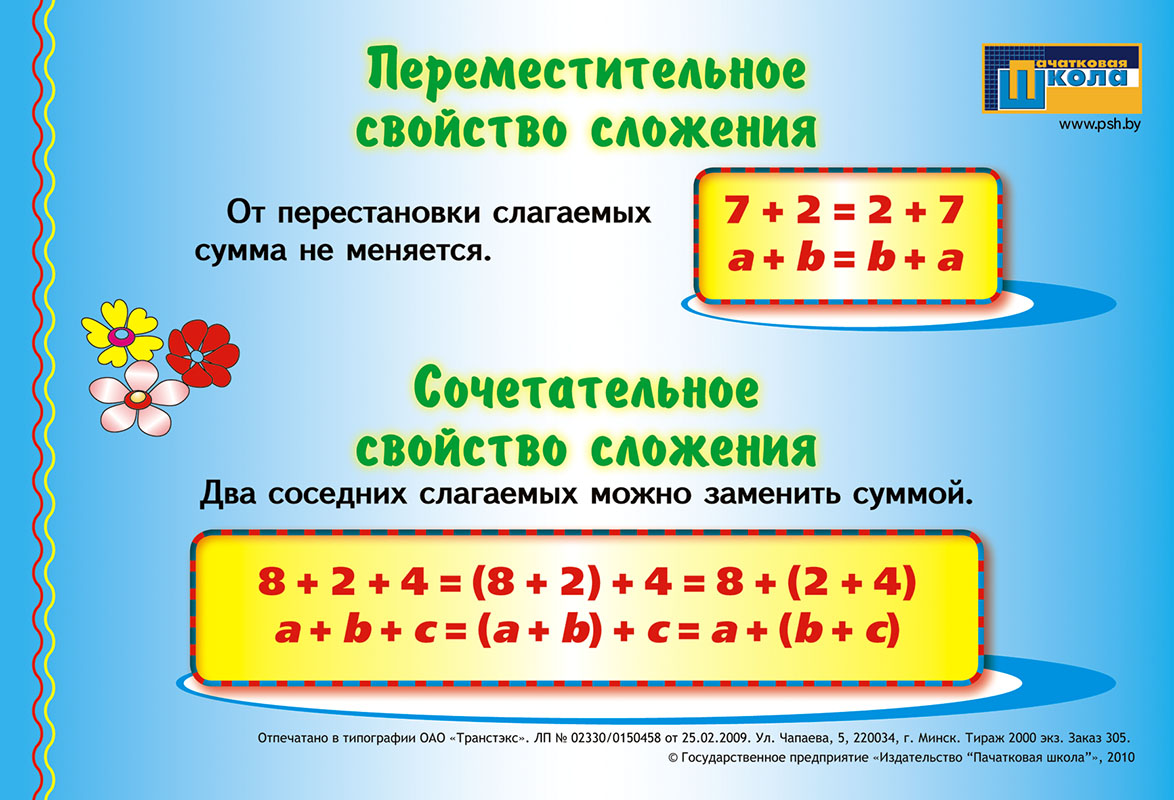 Это похоже на изучение правил игры, позволяющее им играть более эффективно и творчески. А в великой математической игре Brighterly гарантирует, что каждый ребенок будет оснащен нужными инструментами и знаниями, превратив их учебный процесс в радостное приключение, наполненное новыми открытиями и достижениями.

Часто задаваемые вопросы о коммуникативном свойстве сложения

Применяется ли коммуникативное свойство сложения к вычитанию?

Нет, свойство коммутативности не применяется к вычитанию. Это связано с тем, что порядок вычитания чисел существенно влияет на результат. Например, если мы рассмотрим числа 5 и 3, 5-3 равно 2, тогда как 3-5 равно -2. Как видите, результаты не совпадают, что указывает на то, что вычитание не является коммутативным.

Применяется ли коммутативное свойство сложения к умножению?

Да, свойство коммутативности применимо и к умножению. Это означает, что порядок умножения чисел не меняет произведения. Например, если мы возьмем числа 4 и 2, 4 * 2 равно 8, а 2 * 4 также равно 8. Это показывает, что, как и сложение, умножение является коммутативной операцией.

Переместительное свойство сложения применимо только к двум числам?

Нет, коммутативность распространяется на любое количество чисел. Этот принцип означает, что вы можете переставлять несколько чисел в любом порядке при сложении, и сумма останется прежней. Например, для чисел 2, 5 и 3 2 + 5 + 3 равно 10, как и 3 + 2 + 5 и 5 + 3 + 2.

Источники информации

1. Коммутативное свойство сложения из Википедии. всесторонний обзор коммутативного свойства в математике.
2. Факты о сложении от Национального совета учителей математики. План урока посвящен пониманию и применению свойств сложения.
3. Коммутативный закон сложения от Wolfram MathWorld — более подробное техническое исследование свойства коммутативности.

Десятичные и целые числа. Свойства целых чисел

Те же знакомые свойства целых чисел применимы и к целым числам. Если вы как и многие студенты, всякий раз, когда вы видите одно из этих «свойств», вы стонете внутри и думаете: «Зачем мне учиться всему этому?» Хотите верьте, хотите нет, но свойства чисел придумали не злые математики пытать студентов-математиков! Это основные правила нашей системы математики, и вы будете использовать их всю оставшуюся жизнь. Очень важно, чтобы ты понять, как применять каждый из них, когда вы решаете математические задачи. Когда ты доберитесь до алгебры, вы будете использовать эти свойства снова и снова! Давайте рассмотрим каждый из них подробно и простым языком.

Коммутативное имущество дополнения
Переместительное свойство умножения
Ассоциативное свойство дополнения
Ассоциативное свойство умножения
Распределительное имущество

Коммутативное свойство сложения
Коммутативное свойство свойство сложения говорит о том, что мы можем складывать числа в любом порядке. Вы можете помнить свойство коммутативности, думая о числах, «коммутирующих», или поменяться местами. Пример показывает нам, что «отрицательные два плюс положительные «четыре» — это то же самое, что «положительные четыре плюс отрицательные два».

-2 + 4 = 4 + (-2)

Коммутативный свойство умножения
Переместительное свойство умножения очень похоже. Он говорит, что мы может умножать числа в любом порядке без изменения результата. пример показывает нам, что «отрицательное два раза положительное четыре» является то же, что «положительное четыре раза отрицательное два».

-2(4) = 4(-2)

Ассоциативный имущество дополнения
Ассоциативное свойство сложения говорит нам, что мы можем группировать числа в сумму любым способом, который мы хотим, и все равно получим тот же ответ. Вы можете вспомнить ассоциативное свойство, думая о двух числах, связанных друг с другом, а затем один уходит, чтобы ассоциироваться с другим номером.

Пример показывает нам, что мы можем добавить «отрицательные два и положительные четыре» вместе, а затем добавьте эту сумму к положительным трем, чтобы получить окончательный ответ, или мы можем сначала сложить вместе «положительные четыре и положительные три» а затем добавьте эту сумму к отрицательным двум, чтобы получить окончательный ответ. Ответ будет одинаковым независимо от того, как мы это делаем.

(-2 + 4) + 3 = -2 + (4 + 3)

Ассоциативный свойство умножения
Ассоциативное свойство умножения говорит нам, что мы можем группировать номера в продукте любым способом, который мы хотим, и все равно получим тот же ответ.

Пример показывает нам, что мы можем либо умножать «отрицательные два и положительные четыре» вместе, а затем умножьте это произведение на положительное три, чтобы получить окончательный результат. ответ, или мы можем перемножить «положительные четыре и положительные три» вместе сначала, а затем умножьте это произведение на минус два, чтобы получить окончательный ответ. Ответ будет одинаковым независимо от того, как мы это делаем.

-2(4) x 3 = -2(4 x 3)

Распределительный собственность
Распределительное свойство вступает в игру, когда выражение, включающее сложение затем умножается на что-то. Это говорит нам, что мы можем сначала добавить, а затем умножить или сначала умножить, а потом добавить. В любом случае умножение «распределено» по всем терминам в круглых скобках.

В примере мы можем сначала добавить числа в скобках — 4+3 — а затем умножить результат на -2 ; или мы можем умножить -2 и каждый термин отдельно, а затем добавить два продукта вместе. Ответ одинаково в обоих случаях.

-2(4 + 3) = (-2 х 4) + (-2 х 3)

Смотреть вне!

Вычитание не является ни коммутативным, ни ассоциативным.

Подразделение ни коммутативный, ни ассоциативный.

Примеры

1. Мы можем добавить числа в любом порядке. (Переместительное свойство сложения.)

-2 + 4 = 4 + -2

2. Мы можем умножать числа в любом порядке.