Свойства умножения и деления — Тур-инфо
Математика и ее свойства
На уроках математики в 5 классе мы тренируемся умножать, делить, складывать и вычитать. Самое интересное — это хитрить и упрощать выражения. В этом помогают свойства умножения и деления, про которые мы сейчас расскажем.
О чем эта статья:
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел A и B верно равенство: A * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
- 6 * 5 = 5 * 6 = 30; 4 * 2 * 3 = 3 * 2 * 4 = 24.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел A, b и C верно равенство: A * b * c = (a * b) * c = a * (b * c).
- 3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел A, b и C верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
С учетом переместительного свойства умножения можно переформулировать правило так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел A, b и C верно равенство: (a − b) * c = a * c − b * c.
С учетом переместительного свойства умножения можно переформулировать правило так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел A, b и C верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: A * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
Деление на нуль невозможно. Деление нуля на число: 0 : a = 0. Деление равных чисел: A : a = 1. Деление на единицу: A : 1 = a. Для деления переместительное свойства не выполняется: A : b ≠ b : a. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c). Деление произведения на число:
(a * b) : c = (a : c) * b, если a делится на c;
(a * b) : c = a * (b : с), если b делится на c;
(a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c. Деление числа на произведение:
A : (b * c) = (a : b) : c = (a : c) : b.
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: A : b = (a * k) : (b * k), где K — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 2
Упростить выражение: 27a – 16a.
Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
- 3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30
Как решаем 27a 16a a 27 a 16 a 27 — 16 a 11 11a.
Skysmart. ru
23.
11.2020 18:56:58
2020-11-23 18:56:58
Источники:
Https://skysmart. ru/articles/mathematic/svojstva-umnozheniya-i-deleniya
Свойства сложения и вычитания. Переместительное и сочетательное » /> » /> .keyword { color: red; }
Математика и ее свойства
Как в сказке черепаха перехитрила и обогнала зайца, так и мы можем схитрить и решить любое выражение быстрее с помощью упрощения. Для этого разберемся в свойствах сложения и вычитания.
О чем эта статья:
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое, 5 — второе слагаемое, 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения в 1 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c)
Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
9 — это уменьшаемое,
При этом саму запись (9 — 4) тоже можно назвать разностью.
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть такое же число, то получится нуль.
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
A — (b + c) = a — b — c
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.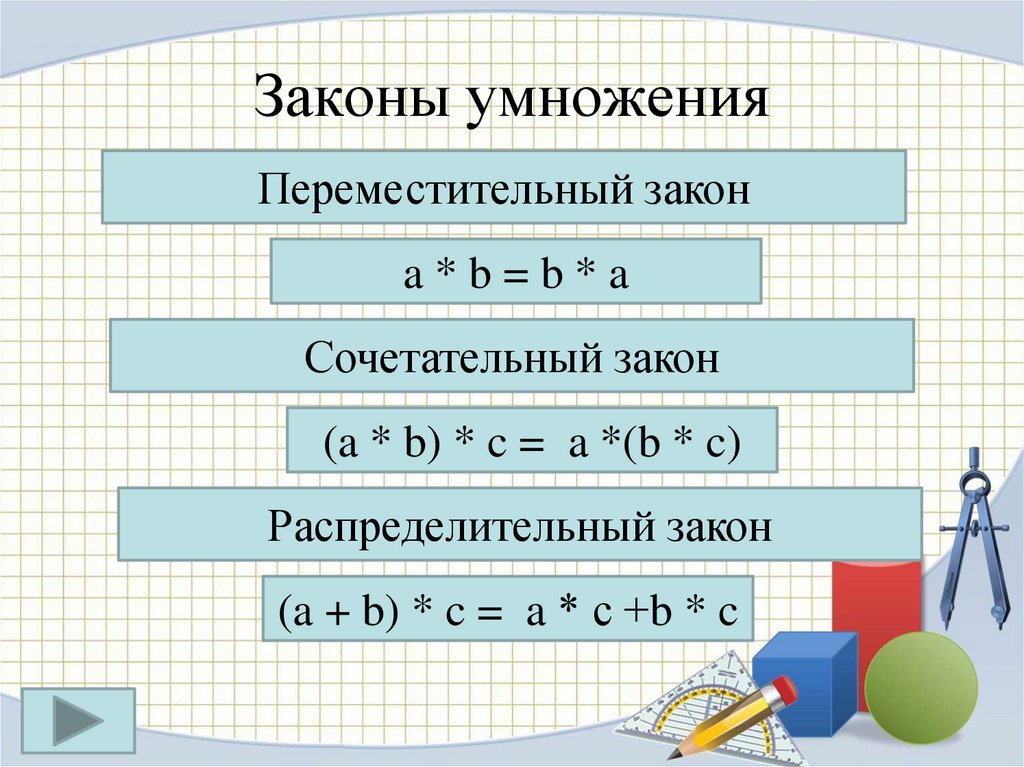
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)
Есть случаи, когда скобки не имеют значения при вычитании, и их можно опустить. Например: (a — b) — c = a — b — c.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
A b — c b — c a если b c или b с.
Skysmart. ru
21.07.2020 0:57:06
2020-07-21 00:57:06
Источники:
Https://skysmart. ru/articles/mathematic/svojstva-slozheniya-i-vychitaniya
Свойства по математике, алгебре и геометрии, основные свойства для студентов и школьников » /> » /> .keyword { color: red; }
Математика и ее свойства
В данном разделе собраны Основные свойства по математике, алгебре и геометрии, которые необходимы студентам и школьникам для подготовки к занятиям, выполнения контрольных работ и решения задач.
Свойства и формулы — это краткий теоретический материал, выучив которые вы легко сможет выполнить задания в школе или университете.
Если после изучения данного теоретического материала у Вас возникнут проблемы в решении задач или появятся вопросы образовательного характера, то вы всегда можете задать их на нашем форуме.
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
Любую работу
Поможем написать реферат или решить контрольную
Наши эксперты помогают подготовиться к сдаче курсовой, защите дипломной, решить задачу или написать реферат
Поможем в короткие сроки
Наши эксперты заботятся о том, чтобы помочь вам как можно скорее (от 3 часов) и делают все, чтобы вы сдали работу вовремя
Мы проверяем каждую работу на плагиат и помогаем писать «с нуля»
Наш отдел контроля качества проверит каждую запятую в вашей работе и при необходимости бесплатно внесет корректировки в течение гарантийного срока
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
Любую работу
Наши эксперты помогают подготовиться к сдаче курсовой, защите дипломной, решить задачу или написать реферат
Поможем в короткие сроки
Наши эксперты заботятся о том, чтобы помочь вам как можно скорее (от 3 часов) и делают все, чтобы вы сдали работу вовремя
Мы проверяем каждую работу на плагиат и помогаем писать «с нуля»
Наш отдел контроля качества проверит каждую запятую в вашей работе и при необходимости бесплатно внесет корректировки в течение гарантийного срока
Остались вопросы.
Www. webmath. ru
16.10.2018 21:25:46
2018-10-16 21:25:46
Источники:
Https://www. webmath. ru/poleznoe/svoistva. php
Переместительное свойство умножения 2 класс презентация, доклад, проект
Урок математики
2 класс
тема: «Переместительное свойство умножения»
Учитель: Пономарева Ольга Ивановна
филиал МБОУ «Покрово-Пригородная СОШ» в с.
Красносвободное
«Без
сомнения,
без волнения
Открыть важное свойство умножения!»
Слагаемое, множитель, произведение, слагаемое, множитель, сумма.
? ? ?
2 + 3 = 5
? ? ?
2 · 3 = 6
слагаемое слагаемое сумма
Сумма
множитель множитель произведение
2 · 3 = 6
произведение
2+3=3+2
Переместительное свойство сложения.
От перестановки мест слагаемых сумма не меняется.
Как назвать выражения?
7 + 7 + 7 + 7
2 + 2 + 2 + 2 + 2
3 + 3 + 3 + 3 + 3+ 3
7 + 7 + 7 + 7 = 7· 4
2 + 2 + 2 + 2 + 2 = 2 · 5
3 + 3 + 3 + 3 + 3+ 3= 3 ·6
Как назвать выражения?
6 · 4, 8 · 3, 9 · 2
Замените суммой.
6 ·4=6+6+6+6
8 ·3=8+8+8
9 ·2=9+9
Найди значения произведений –замени их суммой.
15 · 2
10 · 3
2 · 25
4 · 15
=15+15=30
=10+10+10=30
=?
=?
2· 25= ?
4· 15= ?
2· 25 =2+2+2+2+2+2+2+2+2+2+2+2+2 +2+2+2+2+2+2+2+2+2+2+2+2
4· 15=4+4+4+4+4+4+4+4+4+4+4+4+4+4+4
Как посчитать по-другому ?
Тема урока:
переместительное свойство умножения.
Цель: находить произведение, используя переместительное свойство умножения.
От перемены мест множителей, результат не меняется-
переместительное свойство умножения.
2· 25= ?
4· 15= ?
2· 25= 25· 2= 25+25=50
4· 15= 15· 4=15+15+15+15=60
84
4 · 3 = 3 · 4
9 · 2 = 2 · 9
Дядя Фёдор разделил прямоугольный огород на квадраты. Сколько в нём квадратов?
Матроскин посчитал так: 3·4=12 (кв.)
Шарик вычислил по-другому:
4·3= 12 (кв.)
Как рассуждал каждый герой?
Запиши решение и ответ.
I вариант. II вариант.
5 · 4=…· 5, 6 · 4=…· 6,
2 ·…=8 · 2, 2 ·…=7 · 2,
1 · 9=9 ·…, 1 · 8=8 ·…,
4 · 3=…· 4. 4 · 6=…· 4.
I вариант. II вариант.
4, 4,
8, 7,
1, 1,
Реши задачи.
Цель: находить произведение, используя переместительное свойство умножения.
2 · 35 = 35 · 2
Таблица умножения
До свидания, друзья !
Домашнее задание.
Рабочая тетрадь стр.82 № 1,2.
Спасибо !
Ресурсы Интернета:
Картинка Матроскина и Шарика ( 1 слайд)-http://www.igrushkispb.ru/pazly-30-detaley-ru03063-midi-lic-prostokvashino-sharik-i-matroskin-castor-land
Кот Матроскин (4 слайд)-https://my-shop.ru/shop/products/3349721.html
Шарик (7 слайд)- http://knigi.tomsk.ru/products/1434948
Дядя Фёдор (8 слайд)-https://ru.
wikipedia.org/wiki/%D0%94%D1%8F%D0%B4%D1%8F_%D0%A4%D1%91%D0%B4%D0%BE%D1%80Почтальон Печкин (14 слайд) https://www.litres.ru/eduard-uspenskiy/bolshaya-kniga-o-prostokvashino/chitat-onlayn/page-2/
Кувшин (11 слайд)-http://www.lenagold.ru/fon/clipart/k/kuvsh3.html
Прощание — https://nukadeti.ru/raskraski/pes-sharik-i-kot-matroskin
«Математика 2 класс» Г.В.Дорофеев, Т.Н. Миракова, Т.Б. Бука. Москва «Просвещение» 2015. Ч.2-109с.
Аллан Р., Bилльямс М. Математика на 5: Пособие для 1-3 классов начальной школы.-М.: АСТ-ПРЕСС, 1996.-384 с.
Скачать презентацию
Конспект урока «Переместительное свойство сложения» по математике для 1 класса
Урок математики в 1 классе
по теме: «Переместительное свойство сложения»
Цель – познакомить с переместительным свойством сложения.
Задачи:
Обучить учащихся новому приёму сложения, основанному на переместительном свойстве сложении;
Закрепить вычислительные навыки;
Развивать умения решать простые задачи;
Воспитывать интерес к изучению математики, чувства дружбы, взаимопонимания.
Сюжетная линия сказки «Теремок»
Оборудование: учебник, рабочая тетрадь по УМК «Перспектива», интерактивная доска.
Ход урока:
Организация класса
Прозвенел уже звонок
Мы в поход отправляемся смело,
В мир примеров и сложных задач.
— Сегодня мы отправимся в путешествия и встретимся со своими старыми знакомыми-героями известной сказки. А какой вы узнаете, если расположите ответы примеров в порядке увеличения.
5 – 4 = Т
2 + 8 = К
8 – 6 = Е
3 + 3 = Р
7 – 0 = Е
0 + 8 = М
10 – 1 = О
Слайд 1. Дети решают примеры, записывают ответы, составляют слово.
Устный счет
В чистом поле теремок
Он ни низок не высок,
Шла лягушка из болота,
Видит заперты ворота.
На воротах тех плакат:
«В домик тот зайдет,
Кто числа по порядку разберет» — появляется лягушка
7 3 1 5 8 4 6 2 10 9
1. По порядку возрастания
2. По порядку убывания
3. Чётные числа
4. Не четные числа
— Молодцы!
Вошла лягушка в дом.
— А вот и мышка спешит.
В чистом поле теремок
Он ни низок не высок,
Кто, кто в теремочке живёт?
Кто, кто в невысоком живёт?
А лягушка ей в ответ:
Чтобы дверь мою открыть,
Надо вам задачки решить.
На качелях две Елены,
А с мячом Иван, Игнат.
Две Ирины прибежали
Валя, Зина и Егор –
Вот и в сборе весь наш двор.
А теперь скажите мне,
Сколько деток во дворе (9)
— Решили задачки и мышка, и попала в теремок
— Ребята, а из каких геометрических фигур состоит теремок?
Слайд 2. Дети собирают теремок из геометрических фигур.
— Молодцы!
— Продолжаем наш урок,
Тема новая вас ждёт
— У теремка появляется петушок.
3. Работа над новым.
Это что за теремок?
Он не низок, не высок.
Эй, откройте петушку!
Ко-ко-ко, кукареку
Слышит он такой ответ:
«Рады мы тебя впустить, но не можем дверь открыть.
Постарайся, посмелей
Отвечать на вопросы по-быстрей.»
— Петушку нужно помочь решить задачу
На озере плавали 5 лебедей, к ним приплыли еще 2. Сколько лебедей стало на озере?
— Условие задачи?
— Вопрос задачи?
— Какое решение? (5 + 2 =7)
— Ответ задачи?
— Как по другому можно записать? (2 + 5 = 7)
— Почему?
— Как называются числа при сложении? (1 сл.
, 2сл., сумма)
— Сравните эти 2 решения?
— Что сделали со слагаемыми? (поменяли местами)
— Изменился ли результат? (нет)
— Какой вывод можно сделать?
(от перемены мест слагаемых сумма не изменяется)
— Откройте рабочие тетради на стр. 34 выполним задания 1
— Молодцы!
— Задание №2
— Задание № 3
— Задание №4
— Дверь открылась.
Стали жить друзья втроём:
Лягушка, мышка, петушок.
Физминутка под музыку.
Все дружно трудились,
Немножко устали.
Быстро все сразу
За партами встали.
Друзей водой не разольёшь.
Вдруг стучится старый ёж.
Кто, кто в теремке живёт?
Кто, кто в невысоком живёт?
Я серый ёжик,
Ни головы, ни ножек.
Разрешите здесь пожить?
Буду терем сторожить.
Лучше нас лесных ежей
Нет на свете сторожей.
Если он задачи решит,
То будет в домике жить.
4.
Закрепление — Открыли учебники на странице 27
Пустили звери в дом
И дружно живут вчетвером.
Физминутка (использование интерактивной доски)
5. Самостоятельная работа
А тут и зайчишка появился
Просит впустить его в дом,
Веселее будет жить впятером.
Звери рады зайца впустить,
Надо примеры самостоятельно решить.
Составьте примеры и решите их
__________________________________
__________________________________
2. Вставь пропущенные числа:
3+5=…+3 2+1=1+… 6+2=2+…
5+1=1+… 4+2=…+4 3+6=6+…
3. Вспомни состав числа
4. Реши примеры
5. Число «сбежало»
6. Итог урока.
Вот закончился урок,
Подведём сейчас итог.
А пока теремок на замок.
Будет спать до утра теремок
— Что нового и интересного узнали?
— Спасибо за урок!
Здесь представлен конспект к уроку на тему «Переместительное свойство сложения», который Вы можете бесплатно скачать на нашем сайте.
Предмет конспекта: Математика (1 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые,
Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Эффективные стратегии введения свойств сложения в 3-м классе
Вы учитель 3-го класса и ищете веселые и эффективные способы познакомить учащихся со свойствами сложения? Если вы новичок в обучении в третьем классе, возможно, вы никогда раньше не преподавали такие стратегии. Вам может быть интересно узнать, что именно представляют собой эти свойства сложения. В этой записи блога я расскажу о некоторых забавных способах обучения ассоциативному свойству сложения и коммутативному свойству сложения. Читайте об эффективных стратегиях и занятиях по ознакомлению со свойствами сложения, которые понравятся вашим ученикам!
Каковы свойства сложения?
Свойства сложения — это набор правил или стратегий, которые ваши учащиеся могут использовать при сложении 2 или более чисел.
Эти свойства стратегий сложения значительно облегчают учащимся решение задач и расчеты. Это особенно верно, когда они начинают решать более глубокие и сложные проблемы.
Существует 4 основных свойства сложения: переместительное свойство, ассоциативное свойство, распределительное свойство и свойство идентичности. В 3-м классе учащиеся сосредотачиваются на стратегиях изучения ассоциативного свойства сложения и коммутативного свойства сложения.
Что такое коммутативное свойство сложения?
Коммутативное свойство сложения — это когда вы берете задачу на сложение и можете изменить порядок слагаемых, но сумма останется прежней. Независимо от того, в каком порядке находятся слагаемые, вы всегда получаете один и тот же результат.
Ваши ученики, скорее всего, имеют представление об этом понятии, даже если они не узнают термин математического словаря, коммутативное свойство сложения . Во 2-м классе они могут называть это «перевернутыми фактами».
Переместительное свойство сложения Пример
При обучении математическим свойствам в 3-м классе очень важно давать учащимся конкретные примеры для моделирования рассматриваемого свойства.
Вводя свойство коммутативности сложения, вы можете использовать следующий пример:
Вы идете в продуктовый магазин и покупаете содовую и пакетик чипсов. У стойки вы передаете кассиру газировку и пакетик чипсов. Имеет ли значение, какой предмет они сканируют первым? Нет! Независимо от того, в каком порядке кассир сканирует товары, сумма всегда остается неизменной.
Используя этот пример, вы можете попросить учеников повернуться и поговорить с соседом, чтобы обсудить свои ответы. Это отличный способ поощрить математические дискуссии и расширить словарный запас в классе.
Что такое ассоциативное свойство сложения?
Ассоциативность сложения используется при сложении 3 и более многозначных чисел. Скобки используются с этим свойством, и, вероятно, это будет первый раз, когда ваши ученики столкнутся с их использованием в математике.
С помощью этого свойства 2 добавления группируются внутри круглых скобок и добавляются первыми. Неважно, какие 2 числа учащиеся группируют в скобках.
Как только эта сумма достигнута, учащиеся добавляют это число к третьему сложению. Независимо от того, как вы группируете слагаемые, сумма всегда останется неизменной.
Ассоциативное свойство сложения Пример
Чтобы представить ассоциативное свойство сложения в 3-м классе, вы можете использовать такой пример, как 31 + 11 + 5 = 47. Смоделируйте для учащихся, как независимо от того, каков порядок слагаемых и нет независимо от того, какие 2 слагаемых помещены в скобки, сумма останется прежней.
Вы можете смоделировать это с помощью следующих уравнений:
(31+11) + 5 = 47 и 31 + (11+5) = 47
Поскольку учащиеся впервые столкнулись с использованием скобок в математике. , вводя это математическое свойство в 3-м классе, важно помнить, что когда они видят скобки в задаче, это числа, которые им нужно решить в первую очередь.
Таким образом, если первые два слагаемых заключены в круглые скобки, это числа, которые нужно решить в первую очередь.
Если они находятся рядом с двумя последними слагаемыми, это числа, которые они решат первыми. Чрезвычайно важно объяснить учащимся, что порядок не имеет значения, но какие бы ни были скобки, это числа, которые решаются в первую очередь.
Учащиеся могут практиковать различные примеры, используя интерактивное задание по математике.
Свойства якорной диаграммы сложения
Когда дело доходит до введения новых стратегий и концепций, таких как свойства сложения, я всегда рекомендую начинать с введения одного свойства за раз, создавая якорную диаграмму для всего класса. На якорной диаграмме заполните только место для свойства, которое вы представляете в этот день. Заполнение всей якорной диаграммы и одновременное введение всех свойств может быть очень сложным для учащихся.
Свойство коммутативности — это первое свойство сложения, которое я ввожу. В первый день вы можете поговорить о свойстве и обсудить, что такое коммутативное свойство, заполнив эту часть свойств дополнительной якорной диаграммы.
Вы можете практиковать этот навык в течение нескольких дней, прежде чем вводить ассоциативное свойство сложения и добавлять его в якорную таблицу для всей группы.
Якорная диаграмма для всей группы является мощным визуальным подспорьем для учащихся, особенно если они впервые знакомятся с этой концепцией.
Чтобы учащиеся активно изучали эти свойства сложения и работали с ними, я предлагаю им создать соответствующую мини-версию якорной диаграммы свойств сложения в своем интерактивном математическом журнале. Это позволяет им активно работать и исследовать эту концепцию, пока мы вместе создаем якорную диаграмму для всей группы.
Это помогает им взять на себя ответственность за свое обучение, а также служит отличным ориентиром для них, чтобы оглянуться назад в течение года. Если им когда-нибудь понадобится пример того, как что-то сделать, они могут просто вернуться назад, используя вкладки организации математического журнала, и посмотреть в своем математическом журнале.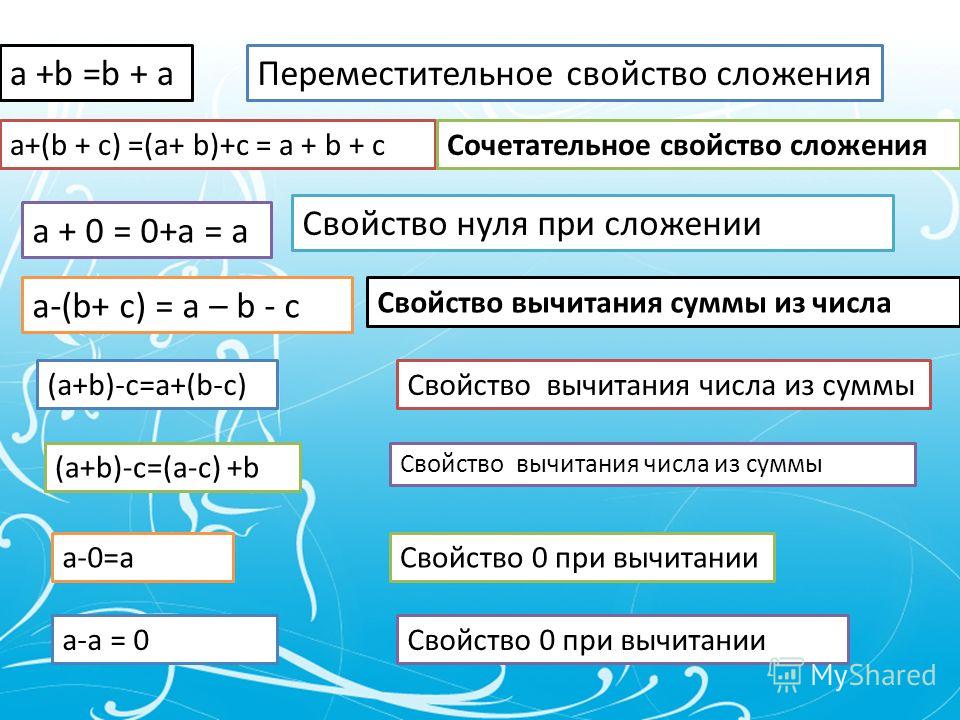
Свойства сложения Упражнения
При знакомстве и отработке коммутативных и ассоциативных свойств сложения есть несколько эффективных упражнений и игр, которые я люблю использовать для отработки этих стратегий со студентами.
Переключи и добавь
Для первого задания позовите 4 учеников к передней части комнаты. 2 ученика держат табличку с номером или просто лист бумаги с написанным на нем числом. Два других ученика держат листы бумаги со знаками + и =.
Учащиеся должны поставить каждый знак, чтобы решить задачу. Наведя порядок, учащиеся меняют слагаемые и снова складывают. Например, если задача 33 + 17 = 50, учащиеся моделируют, что независимо от того, в каком порядке находятся слагаемые, будь то 33 + 17 или 17 + 33, сумма остается неизменной.
Увидев, как учащиеся со знаками чисел физически меняются местами, не меняя суммы, учащиеся получают лучшее наглядное представление о коммутативном свойстве сложения.
Вы можете предложить учащимся, сидящим на своих местах, решить задачу на доске и показать факт перестановки, представляющий свойство коммутативности.
Они даже могут попросить студентов с плакатами поменяться местами, чтобы смоделировать факт поворота.
Вы можете выполнить аналогичное задание для моделирования ассоциативного свойства, используя 3 плаката с числами, 2 плаката со знаком +, плакат со знаком = и добавив 2 плаката со скобками. Для этого варианта требуется, чтобы 8 учащихся смоделировали, что независимо от того, как вы группируете числа или какие слагаемые заключаются в круглые скобки, сумма останется неизменной. Вы можете использовать карточки с числами и коврики со значениями мест, чтобы определить числа и позволить учащимся на своих местах решить и смоделировать задачу вместе со учащимися-добровольцами.
Брось, добавь, переверни
Другим свойством сложения, которое мне нравится использовать для отработки этой стратегии, является игра в кости. Это называется «свернуть, добавить, перевернуть». Дайте своим ученикам набор из 3 игральных костей. Если у вас недостаточно для того, чтобы у каждого ученика было 3, дайте им 1 кубик, и они могут бросить его 3 раза, чтобы получить трехзначное число.
Они бросают кости, чтобы создать задачу на сложение и найти сумму. Затем они должны показать свойство коммутативности, перевернув слагаемые и решить, совпадают ли их суммы.
Вы можете использовать то же упражнение для моделирования ассоциативного свойства сложения, предложив учащимся бросить кости столько раз, чтобы получилось 3 сложения. Затем они могут писать в скобках и моделировать различные способы группировки слагаемых внутри скобок, чтобы всегда получать одну и ту же сумму.
Drop and Add
Drop and Add — еще одна очень увлекательная игра, в которой вы можете попрактиковаться в свойствах сложения. Вы можете найти это задание, а также другие в моем разделе 3-го класса «Стратегии сложения и вычитания трехзначных чисел с подсказками по математике».
Для игры у учащихся есть лист бумаги с числовой сеткой. Они бросают шарик с помпоном на сетку с числами 3 раза. Какое бы число оно ни выпадало каждый раз, они записывают, чтобы создать трехзначное число.
Затем они повторяются, чтобы создать еще одно трехзначное число. Эти 2 числа становятся их слагаемыми, и они решают сумму.
Затем учащиеся демонстрируют переместительное свойство сложения, переворачивая слагаемые и снова находя сумму. Если они получают одинаковую сумму в обоих уравнениях, то их ответ правильный. Это также отличный способ научить студентов перепроверять свою работу.
Учащиеся могут использовать эти свойства игры на сложение, чтобы попрактиковаться в ассоциативности, бросая помпоны столько раз, чтобы получилось 3 сложения. Они могут написать уравнение и написать в скобках, моделируя различные способы группировки слагаемых, чтобы найти одну и ту же сумму.
Я надеюсь, что эти советы, стратегии и упражнения по ознакомлению со свойствами сложения и их практике в 3-м классе помогут вам чувствовать себя более уверенно при обучении этим понятиям.
Посмотрите мое видео на YouTube, чтобы узнать больше об этих концепциях и получить представление об этих свойствах операций сложения!
Хотите, чтобы планы уроков по стратегии сложения и вычитания для 3-го класса были составлены за вас? Ознакомьтесь с моим 3-м классом «Стратегии сложения и вычитания трехзначных чисел с подсказками по математике», в котором есть планы уроков на 20 дней, занятия, игры и многое другое!
Закрепите изображение ниже, чтобы вернуться к этому посту позже!
Применение свойств операций как стратегий умножения и деления.
Примеры: Если известно 6 4 = 24, то известно и 4 6 = 24. (Переместительное свойство умножения.) 3 5 2 можно найти по 3 5 = 15, тогда 15 2 = 30, или по 5 2 = 10, тогда 3 10 = 30. (Ассоциативное свойство умножения.) Зная, что 8 5 = 40 и 8 2 = 16, можно найти 8 7 как 8 (5 + 2) = (8 5) + (8 2) = 40 + 16 = 56. (Распределительное свойство.)Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого контрольного показателя для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Формирующие оценки MFAS
Разбить и собрать:
Учащимся даются два массива, один из которых представляет уравнение 7 x 9 = 63, а другой представляет уравнение (5 + 2) x 9 = 63, чтобы проверить, узнают ли они взаимосвязь между два.
Работает ли это при делении?:
Учащихся спрашивают, выполняется ли переместительное свойство при делении.
Достижение цели по чтению:
Учащимся предлагается решить две задачи, одну представленную уравнением 4 x 6 = 24, а другую уравнением 6 x 4 = 24, чтобы проверить, узнают ли они ответ на вторую задачу. на основе коммутативного свойства.
Использование ассоциативного свойства умножения:
Учащихся просят найти произведение трех чисел и наблюдают, используют ли они ассоциативное свойство для более легкого нахождения произведения.
Оригинальные учебники для учащихся по математике — классы K-5
Обезьяны с умножением: переместительное свойство:
Изучите стратегии, такие как свойство перестановочности, которые помогут вам лучше умножать в этом интерактивном учебном пособии.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом тесте.
Оригинальный учебник для студентов
Обезьяны с умножением: переместительное свойство:
Изучите стратегии, такие как свойство перестановочности, которые помогут вам лучше умножать в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Учебники
Объяснение распределительного свойства умножения:
В этом видеоруководстве от Khan Academy исследуется распределительное свойство умножения: почему оно работает? Как это работает? Зачем мне его использовать?
Тип: Учебник
Коммутативные и ассоциативные свойства умножения:
В этом видеоруководстве от Khan Academy используйте массивы для изучения коммутативных и ассоциативных свойств умножения.
Тип: Учебник
Коммутативные и ассоциативные свойства сложения и умножения:
В этом уроке рассматриваются коммутативные и ассоциативные свойства применительно к сложению и умножению. Эти свойства полезны при вычислениях в уме и при решении уравнений. Этот ресурс включает в себя видеоурок, видеопримеры и короткую викторину.
Тип: Учебное пособие
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Учебники
Объяснение распределительного свойства умножения:
В этом видеоруководстве от Khan Academy исследуется распределительное свойство умножения: почему оно работает? Как это работает? Зачем мне его использовать?
Тип: Учебник
Коммутативные и ассоциативные свойства умножения:
В этом видеоруководстве от Khan Academy используйте массивы для изучения коммутативных и ассоциативных свойств умножения.
Тип: Учебник
Коммутативные и ассоциативные свойства сложения и умножения:
В этом уроке рассматриваются коммутативные и ассоциативные свойства применительно к сложению и умножению. Эти свойства полезны при вычислениях в уме и при решении уравнений. Этот ресурс включает в себя видеоурок, видеопримеры и короткую викторину.
Тип: Учебник
Рабочие листы свойств | Бесплатно — дистанционное обучение, рабочие листы и многое другое: CommonCoreSheets
| Хотите помочь поддержать сайт и убрать рекламу? Станьте покровителем через patreon или сделайте пожертвование через paypal. |
Коммутативное свойство сложения
ссылка
Перетаскивание ⇄ для прокруткиНажмите, чтобы открыть 1oa3Использование коммутативного свойства ★M
Каждый рабочий лист содержит 14 задач на заполнение пропусков для задач на сложение с использованием свойства коммутативности.
Идентификационное свойство добавления
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть Использование свойства идентичности сложения ★
Каждый рабочий лист содержит 20 задач, для решения которых используется свойство идентичности сложения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New SheetАссоциативное свойство умножения
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть Ассоциативное свойство 3oa5 — пропущенное значение ★
Каждый рабочий лист содержит 20 задач на поиск пропущенного значения.
Каждый рабочий лист содержит 14 задач на определение пропущенной цифры в задаче на ассоциативные свойства.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3oa5Нахождение ассоциативного свойства умножения ★Каждый рабочий лист содержит 12 задач на определение второй половины задач на ассоциативные свойства.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3oa5Поиск эквивалентного ассоциативного свойства ★ Каждый рабочий лист содержит 14 задач, использующих свойство ассоциативности для поиска эквивалентных задач.
Каждый рабочий лист содержит 12 задач с множественным выбором, определяющих ассоциативное свойство умножения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New SheetКоммутативное свойство умножения
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3oa5Commutative Property — Множественный выбор ★
Каждый рабочий лист содержит 12 задач с множественным выбором, определяющих коммутативное свойство умножения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New Sheet 7ns2cУмножение рациональных чисел с коммутативным свойством ★ Каждый рабочий лист содержит 10 задач, использующих переместительное свойство умножения для решения задачи на умножение рациональных чисел.
Распределительное свойство умножения
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3oa5Использование свойства распределения ★
Каждый рабочий лист содержит 10 задач, использующих свойство распределения для решения задачи.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New Sheet 3oa5Распределительная собственность ★Каждый рабочий лист содержит 12 задач с множественным выбором, определяющих распределительное свойство умножения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Определение распределительной собственности ★ На каждом листе есть 10 задач на переписывание выражения с использованием свойства распределения и последующее решение.
Каждый рабочий лист содержит 10 задач на решение задачи на деление с использованием свойства распределения с массивом.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Использование распределительного свойства деления ★MКаждый рабочий лист содержит 10 задач на решение задачи на деление с использованием свойства распределения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Изучение распределительной собственности ★M Каждый рабочий лист содержит 20 задач на проверку распределительного свойства умножения.
Идентификационное свойство умножения
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть Свойство 3oa5Identity — множественный выбор ★
Каждый рабочий лист содержит 12 задач с множественным выбором, определяющих свойство идентичности умножения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New SheetВсе свойства умножения
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3oa5Mixed — Заполните пробел ★
Каждый рабочий лист содержит 20 рабочих листов, определяющих либо Ассоциативное, Распределительное, Коммутативное или Идентификационное свойство умножения.