Арифметические действия с целыми числами
Понятия арифметических действий
По двум или нескольким целым числам можно составить новое целое число. Способов составлять новое целое число очень много. Так, по двум целым числам 6 и 2 можно составить новое число различным образом.
Можно по двум целым числам составить такое число, которое будет заключать в себе столько единиц, сколько их содержится в обоих числах. Для 6 и 2 это будет число 8. В этом случае число 8 равно обоим числам, вместе взятым.
Можно по двум целым числам составить такое число, которое будет показывать, насколько единиц одно число больше другого. Для 6 и 2 это будет число 4.
Можно по двум целым числам составить число, которое будет показывать, сколько единиц получим, если одно число повторим количество раз, равное второму числу. Для 6 и 2 это будет число 12.
Можно попробовать по двум целым числам составить такое число, которое покажет, сколько раз второе число содержится в первом.
Таким образом, по двум числам 6 и 2 разными способами мы составили 4 новых числа: 8, 4, 12 и 3.
Арифметическое действие. Способ составлять новое число по двум или нескольким числам называется арифметическим действием.
Данные и искомые. Те числа, по которым составляют новое число, всегда даются и называются данными числами, а новое число, которое составляют по данным, называют искомым, ибо цель арифметического действия состоит в том, чтобы отыскать его. Искомое число называют также результатом действия.
Основные арифметические действия
Вообще арифметических действий много, но основных только четыре: сложение, вычитание, умножение и деление.
Они названы основными, ибо все остальные действия приводятся к ним.
По двум числам 6 и 2 найти число 8, равное двум числам, взятым вместе, значит сложить два числа. Само действие называется сложением, и связь между тремя числами выражают словесно: 6 да 2 составляют 8.
По двум числам 6 и 2 найти число 4, показывающее, чем число 6 больше 2, значит 2 отнять от 6. Отнять 2 от 6 значит вычесть 2 из 6. Само действие называется вычитанием. Связь между тремя числами выражается словесно: 6 без 2 составляет 4.
По двум числам 6 и 2 составить 12 или иначе повторить 6 два раза, значит умножить 6 на 2. Действие называется умножением. Связь между числами 6, 2 и 12 выражается словесно: 6, повторенное 2 раза, составляет 12, или 6, умноженное на 2, составляет 12.
По двум числам 6 и 2 составить число 3, указывающее, сколько раз 6 содержит число 2, значит 6 разделить на 2. Действие называется делением.
Связь между числами 6, 2 и 3 выражают словесно: 6 содержит число два 3 раза, или 6, деленное на 2, составляет 3.
Связь между числами 6, 2 и 3 выражают словесно: 6 содержит число два 3 раза, или 6, деленное на 2, составляет 3.Знак равенства. Слово «составляет» заменяют знаком =, который называется знаком равенства, ибо это слово может быть заменено словом равно.
Равенство. Совокупность равных чисел по обе стороны знака = называется равенством.
Четыре арифметических действия над двумя числами могут быть выражены словами:
Во всех этих действиях 6 и 2 являются данными числами, а 8, 4, 12 и 3 — искомыми числами.
Знаки основных действий. Слова «да», «без», «умноженное», «деленное» заменяют особыми знаками:
слово «да» — знаком + (плюс)
слово «без» — знаком — (минус)
слово «умноженное» («повторенное») — знаком × или · (точкой)
слово «деленное» — знаком : (÷)
Заменяя слова знаками, мы можем зависимость между числами выразить письменно:
6 + 2 = 8 (сложение)
6 — 2 = 4 (вычитание)
6 × 2 = 12 (умножение)
6 ÷ 2 = 3 (деление)
Знаки + и — были введены Родольфи (Rodolphi) в 1522 году, знак × ввел англичанин Отред (Oughtred) в 1631 г.
, знак = ввел английский геометр Рекор (Recort) в 1552 г.
Основные математические действия | Wikids
Чтобы продолжить просмотр зарегистрируйтесь или войдите в аккаунт
Возможности режима обучения:
- просмотр истории в виде слайдов
- возможность прослушивания озвучки по каждому слайду
- возможность добавить свою, детскую озвучку
- тесты для детей, чтобы закрепить материал
- специально подобранные коллекции картинок и видео для улучшения восприятия
- ссылки на дополнительные обучающие курсы
Озвучка доступна в режиме обучения
Сложение, вычитание, умножение и деление – это основные действия с числами.Рассмотрим по порядку.Чтобы сложить два числа друг с другом, нужно просто прибавить одно число к другому.Порядок не важен, ведь получится тот же результат.
Например, у Вани 3 яблока, а у Вовы 4, сколько всего у них яблок? Мы можем прибавить к трём четыре и наоборот. Получится всегда 7.
Числа, которые складывают друг с другом, называются слагаемые.Результат называется сумма.
Тест по основным математическим действиям.
Основные математические действия. Сложение.
При вычитании порядок чисел важен. Числа менять местами нельзя. Например, Петя купил 8 бананов, а затем съел 2. Сколько осталось?Для решения составим выражение: 8 — 2. Отнимаем от восьми два, получаем шесть.Если вычесть из двух восемь, получится другой результат.Как вычитать из меньшего числа большее, мы научимся далее.
Число, из которого вычитают, называется уменьшаемое.Число, которое вычитают – вычитаемое.Результат называется разность.
Вычитание. Тест.
Тест по вычитанию.
Умножение обозначается символами × * ∙ .Чтобы умножить два числа, нужно сложить первое число столько раз, сколько обозначает второе число.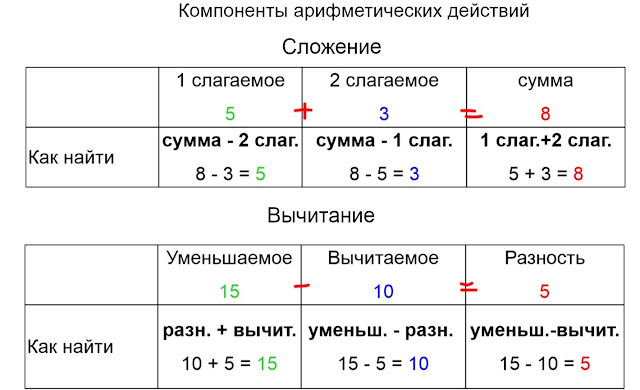
В умножении, как и в сложении, порядок чисел не важен.Если умножить 2 на 3 получится столько же, как и 3 умножить на 2.Три раза по 2 равно 6:2 + 2 + 2 = 6Два раза по 3 тоже равно 6:3 + 3 = 6Если число умножить на 1, получится это же число:5×1=57×1=7
Множители – это числа, которые умножаются.Произведение – результат умножения.
Основные математические действия. Умножение.
Основные математические действия. Умножение.
Деление позволяет найти, сколько раз одно число содержится в другом. Обозначается символами : ÷ ∕ .Например, сколько двоек содержится в восьми? Надо разделить 8 на 2. Получится 4.8 : 2 = 4 Из деления всегда можно получить сумму.Еще пример.8=4+4 – два раза по 4.10 : 5 = 2Какое число нужно сложить 5 раз, чтобы получилось 10.
Делимое – это число, которое делят.Делитель – это число, на которое делят.Результат деления называется частное.
Основные математические действия. Деление.
Основные математические действия. Деление.
Тест по основным математическим действиям
Вопросы по основным математическим действиям
Основные арифметические операции: четыре основных оператора
Изучите арифметические операции
Как сказала нам Джули Эндрюс в Звуки музыки , мы должны «начать с самого начала», потому что это «очень хорошее место для начала». В математике мы не начинаем с До-Ре-Ми, а строим на основах, известных как арифметические операции!
Овладение арифметическими операциями означает создание прочной основы для успешного изучения математики на всю жизнь, поэтому мы настоятельно рекомендуем не торопиться, чтобы действительно посвятить себя этим навыкам!
Если вам нужен более широкий обзор арифметического раздела математики, давайте сделаем шаг назад, чтобы сначала пройтись по арифметике в целом.
Готовы приступить к арифметическим операциям?
Прежде всего, что такое «арифметические операции»?
Арифметические операции являются строительными блоками для всех математических процессов и методов. (Да, они очень важны!) Эти типы операций являются частью «арифметической» ветви математики.
Арифметические операции сводят математику к основам, которыми мы пользуемся каждый день, осознаем мы это или нет. Этими основами являются сложение, вычитание, умножение и деление.
Не так уж и страшно, правда?
Базовая арифметика
Иногда можно услышать, что арифметические операции называют «основной арифметикой», что означает наиболее фундаментальные математические операции.
Основные арифметические операции
Основными арифметическими операциями обычно считаются сложение, вычитание, умножение и деление.
Через мгновение мы углубимся в каждое из них!
Некоторые школы также включают сравнение чисел и оценку степеней (или показателей степени) как часть арифметических операций.
Если вы еще не там, не волнуйтесь! Каждый движется в своем собственном темпе, и мы всегда можем помочь вам, когда вы туда доберетесь.
Четыре основных математических действия
Независимо от того, балансируете ли вы свою чековую книжку или заказываете пиццу на вечеринку, скорее всего, вы ежедневно используете некоторые из четырех основных арифметических действий.
Но иногда, когда что-то настолько второстепенно, трудно объяснить это хорошо. Вот таблица терминов и примеров, которые вы можете использовать при описании четырех основных операций:
| Операция | Глагол | Пример | Словарь результатов |
|---|---|---|---|
| Дополнение | Добавить | $1 + 1 = 2$$ | Результатом сложения является «сумма» |
| Вычитание | Вычесть | $3 — 2 = 1$$ | Результат вычитания – «разность» |
| Умножение | Умножить | $$\displaylines{4 × 2 = 8 \\ 2 * 3 = 6 \\ 5 ⋅ 2 = 10}$$ | Результат умножения — «произведение» |
| Отдел | Разделить | $$\displaylines{12 ÷ 3 = 4 \\ 10/2=5}$$ | Результат деления — «частное» |
Теперь, когда мы знаем больше о каждой операции, мы можем углубиться еще глубже и взглянуть на оператора каждой операции.
Что такое арифметические операторы?
Арифметические операторы — это символы, которые мы видим в математических задачах и которые обозначают действие, которое мы должны предпринять. Они как маленькие математические инструкции GPS, говорящие нам, что должно произойти, чтобы мы достигли конечного пункта назначения.
Другими словами, оператор говорит нам, какую операцию выполнять! Например, оператор $$-$$ говорит нам, что мы должны вычесть.
Давайте рассмотрим каждый оператор более подробно:
Арифметические операторы: руководство
Изучение арифметических операторов (и связанных с ними операций) похоже на обучение вождению автомобиля — вам нужно знать, какая педаль за что отвечает, прежде чем вы сможете нажать на педаль. газ и начать рулить.
Вот удобная таблица, объясняющая, что означает каждый оператор и как он может выглядеть на странице:
| Оператор | Операция |
|---|---|
| $$+$$ | Дополнение |
| $$-$$ | Вычитание |
| $$×, *, ⋅$$ | Умножение |
| $$÷ , /$$ | Подразделение |
Иногда вы можете увидеть более одного оператора в одной и той же задаче.
Если эти операторы разные — например, «+» и «÷» в одной и той же задаче — вам нужно следовать структуре PEMDAS.
Напоминаем, что PEMDAS означает:
- Скобки
- Экспоненты
- Умножение (слева направо)
- Подразделение (слева направо)
- Дополнение (слева направо)
- Вычитание (слева направо)
Примеры арифметических операций
Понимание контекста, лежащего в основе арифметических операций, поможет укрепить обучение, но то, что действительно укрепит эти навыки, — это попробовать их! Работа над проблемами — и, честно говоря, несколько неправильных — гарантирует, что учащийся будет полностью вовлечен.
Итак, когда будете готовы, попробуйте решить следующие примеры задач:
- $$3 + 4$$
- $$6 ÷ 2$$
- $$2 \times1$$
- 8$ – 5 + 2$
- $$3 \times4 – 1$$
- $$\frac{4}{2} + \frac{6}{3}$$
- $$5 – 1 + 3$$
- $$7 \times 3 \times 2$$
- 12$ ÷ 3 + 5$$
- $$2 \раз 0$$
Проблемы? Это нормально! Нравится нам это или нет, чувство неуверенности или застревания на самом деле является частью процесса обучения.
Хорошая новость заключается в том, что вам не нужно оставаться на месте! Отсканируйте сложную задачу с помощью приложения Photomath, и мы проведем вас через каждый шаг.
P.S.: Вы также можете проверить свои ответы на примеры задач, отсканировав их с помощью приложения!
Вот как это выглядит:
/
И еще: какие два основных арифметических действия коммутативны?
Сложение и умножение известны как «коммутативные» (другими словами, они следуют свойству коммутативности). Это означает, что вы можете изменить порядок чисел и получить тот же результат.
Вы можете заметить это при работе с примерами задач, но свойство перестановочности означает, что $$2 + 3$$ равняется той же сумме, что и $$3 + 2$$. Точно так же $$4 \times 5$$ дает нам тот же продукт, что и $$5 \times4$$.
Однако , а не означает, что мы можем переключаться между сложением и умножением.
Например, $$2 + 3 4$$ равно , а не , как и $$2\times34$$. Вот почему PEMDAS так важен!
Мы надеемся, что к настоящему времени вы уже немного освоились с арифметическими операциями. Сама математика не слишком пугающая, поэтому, если вы хорошо понимаете термины и символы, вы готовы к арифметическим операциям!
Когда вы будете готовы перейти к четырем основным операциям, мы также научим вас большему сравнению чисел и вычислению степеней!
Независимо от того, где вы находитесь в своем математическом путешествии, если вы застряли перед сложной задачей, все, что вам нужно сделать, это отсканировать ее с помощью приложения Photomath — оттуда мы можем описать каждый шаг решения процесс в деталях. Таким образом, ничего не будет упущено или забыто, и у вас будет экспертная дорожная карта на следующий раз.
Помните: математика не должна вызывать стресс, потому что мы всегда в вашей команде!
Есть домашнее задание по арифметике?
Зайдите в приложение Photomath, чтобы мгновенно найти пошаговые решения всех ваших арифметических задач.
Арифметические операторы — Основы программирования
Кеннет Лерой Басби и Дэйв Брауншвейг
Обзор
Основными арифметическими операциями являются сложение, вычитание, умножение и деление. Арифметика выполняется в соответствии с порядком операций. [1]
Обсуждение
Оператор выполняет действие над одним или несколькими операндами. Общие арифметические операторы:
| Действие | Общий символ |
| Дополнение | + |
| Вычитание | - |
| Умножение | * |
| Отдел | / |
| Модуль (связанный с целыми числами) | % |
Эти арифметические операторы являются бинарными, то есть имеют два операнда.
Операнды могут быть как константами, так и переменными.
возраст + 1
Это выражение состоит из одного оператора (сложения), который имеет два операнда. Первый представлен переменной с именем age, а второй — буквальной константой. Если бы возраст имел значение 14, то выражение оценивало бы (или было равно) 15.
Эти операторы работают так, как вы их выучили на протяжении всей жизни, за исключением деления и модуля. Обычно мы думаем о делении как о результате результата, который может иметь дробную часть (тип данных с плавающей запятой). Однако деление, когда оба операнда имеют целочисленный тип данных, может действовать по-разному. Пожалуйста, обратитесь к следующему разделу «Целочисленное деление и модуль».
Арифметические операторы присваивания
Многие языки программирования поддерживают комбинацию присваивания ( = ) и арифметические операторы (+, — , *, /, % ).
В различных учебниках они называются «составными операторами присваивания» или «комбинированными операторами присваивания». Их использование можно объяснить с точки зрения оператора присваивания и арифметических операторов. В таблице мы будем использовать переменную age и можно предположить, что она имеет целочисленный тип данных.
| Примеры арифметических назначений: | Эквивалентный код: |
|---|---|
возраст += 14; | возраст = возраст + 14; |
возраст -= 14; | возраст = возраст - 14; |
возраст *= 14; | возраст = возраст * 14; |
возраст /= 14 лет; | возраст = возраст / 14 лет; |
возраст %= 14; | возраст = возраст % 14; |
Псевдокод
Основная функция .
